Dynamic Probabilistic Modeling of Concrete Strength: Markov Chains and Regression for Sustainable Mix Design
Abstract
1. Introduction
- RQ-1: How do varying proportions of PC, FA, and BFS drive the dynamic evolution of compressive strength across diverse concrete mixes, achieving superior accuracy (R2 = 0.977) over static neural network models by modeling nonlinear material interactions?
- RQ-2: How does curing time govern compressive strength progression in PC-, FA-, and BFS-based mixes, enabling tailored curing schedules with higher precision (CoV = 15.57%) than traditional curing models?
- RQ-3: How can high-accuracy compressive strength forecasting (R2 = 0.977) optimize mix designs for specific structural applications, such as precast or high-performance structures, offering real-time adaptability beyond less practical ML models?
- RQ-4: How can predictive modeling minimize PC use while maximizing FA and BFS contributions to enhance durability and sustainability, achieving eco-friendly designs that surpass prior deterioration-focused studies?
2. Literature Review
2.1. Traditional Models for Strength Prediction
2.2. Machine Learning Approaches
2.3. The Influence of Material Composition, Curing Time, and Sustainability
2.4. Research Gaps and the Current Study’s Contributions
- Critically synthesizes limitations of conventional and machine learning-based models for dynamic strength prediction, highlighting the need for interpretable, practical, and sustainability-oriented approaches.
- Develops a hybrid modeling framework combining Markov Chain theory and regression analysis, enabling robust, time-dependent prediction of compressive strength for diverse binder compositions and curing intervals.
- Implements validation using Coefficient of Variation (CoV), providing a normalized, literature-benchmarked measure of predictive consistency and reliability for concrete strength modeling.
- Delivers actionable, real-time recommendations for sustainable mix design, facilitating reduction of the Portland Cement proportion and enhanced use of FA and BFS, supporting environmental goals without compromising performance.
3. Methodology
3.1. Data Collection
- Mix Code (Mi): identifier for each mixture, such as Control, M1, M2 etc.
- PC, FA, BFS composition (kg/m3) (xPC, xFA, xBFS): quantities of each material used per cubic meter.
- Curing time (t): the curing period in days for each measurement.
- Compressive strength (S): measured compressive strength in MPa.
3.2. Data Preprocessing
3.2.1. Categorization of Strength States
3.2.2. Curing-Time-Driven Transition State and Probability Modeling
- Pij is the probability of transitioning from state Si to state Sj;
- Cij is the count of transitions observed from state Si to state Sj (this represents the number of times the system moved directly from state Si to state Sj in the observed dataset);
- Ti is the total number of transitions originating from state Si (it is calculated by summing all the transitions from Si to any other state, i.e., the total number of transitions starting from state Si to any state Sj).
3.3. Markov Chain Model Development
3.3.1. Transition Matrix Construction
3.3.2. Steady-State Calculations
3.3.3. Expected Transitions Matrix
3.4. Regression Analysis
3.4.1. Model Structure
3.4.2. Significance Testing
3.4.3. Model Refinement
3.4.4. Model Validation
3.5. Strength Prediction Using the Markov Chain Model
4. Results
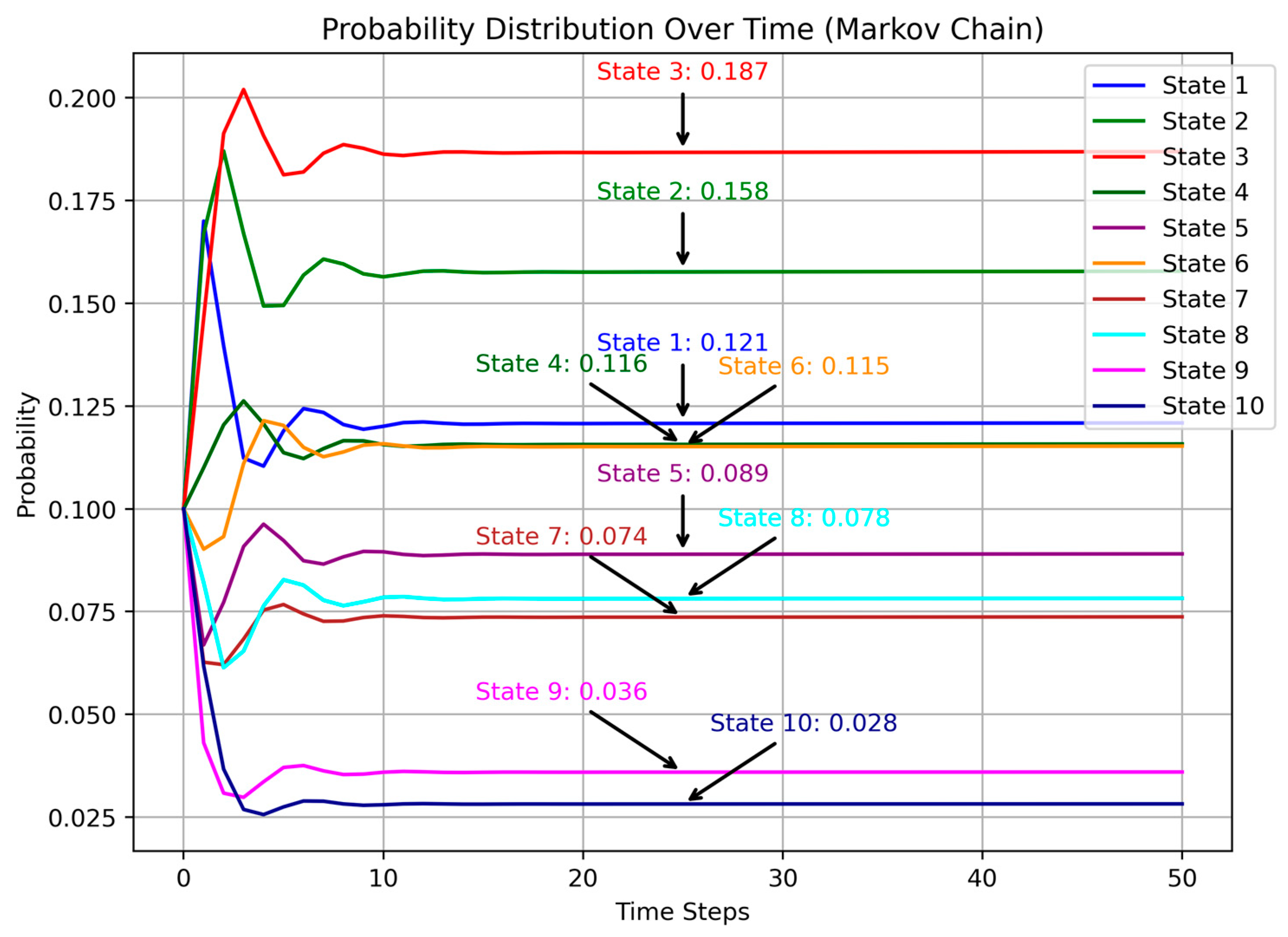
4.1. Steady-State Transitions and Markov Chain Analysis
4.2. Transition Matrix Analysis
4.2.1. Dynamic Strength Evolution Through Markov Chain Analysis
4.2.2. State-by-State Strength Insights
- Early Strength States (State 1–State 3): Early-stage curing is marked by slower strength gains, particularly in State 1, where mixes with lower PC or Blast Furnace Slag (BFS) content exhibit limited development. Transition probabilities highlight the steady progression through State 2 and into State 3, where balanced mixes of PC and FA enable moderate strength suitable for standard construction applications.
- Moderate Strength States (State 4–State 6): Mid-stage curing supports more stable strength ranges, with probabilities favoring transitions to higher states. For example, State 5 (21.0–23.5 MPa) indicates consistent strength suitable for structural applications, while State 6 (23.5–26.0 MPa) transitions into higher ranges, making these mixtures ideal for moderate-to-high load-bearing components.
- High Strength States (State 7–State 8): Achieving high-strength states requires optimized curing conditions and compositions. State 7 (26.0–28.5 MPa) and State 8 (28.5–31.0 MPa) are characteristic of mixtures with high PC content or special additives, suitable for heavy-load or industrial applications. These states demand careful monitoring to ensure durability and strength stability.
- Peak Strength States (State 9–State 10): States 9 and 10 represent the highest compressive strength ranges, critical for high-stress applications such as bridges or high-rise buildings. These mixtures typically require advanced curing techniques and precise adjustments in PC and BFS content to achieve consistent performance.
4.2.3. Practical Implications of Strength Transitions
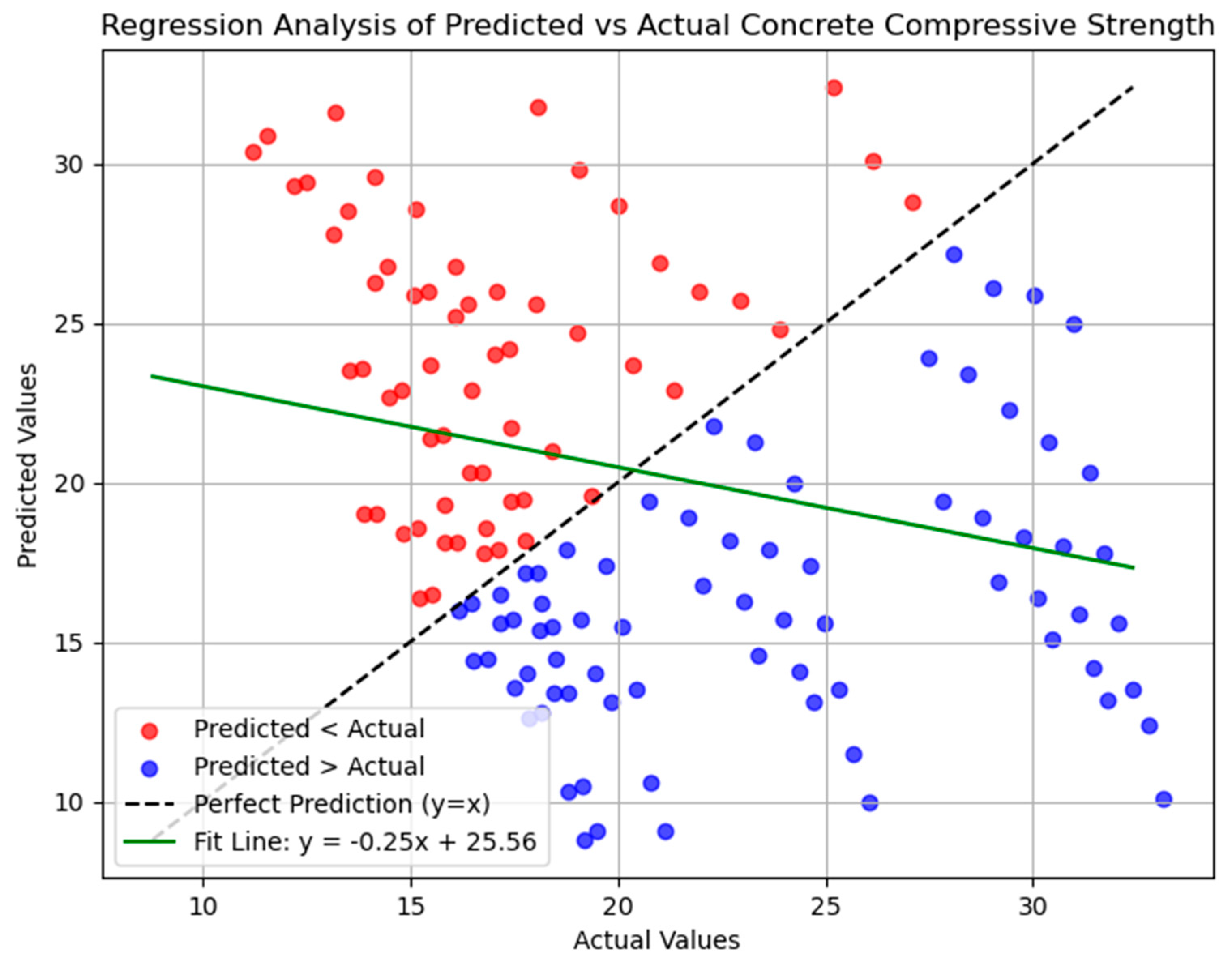
4.3. Regression Model Assessment
- PC: Essential for early strength, especially in precast applications.
- FA: Supports sustainability but requires extended curing.
- BFS: Improves durability for high-performance applications.
- Curing time: Critical for balancing strength development and material optimization.
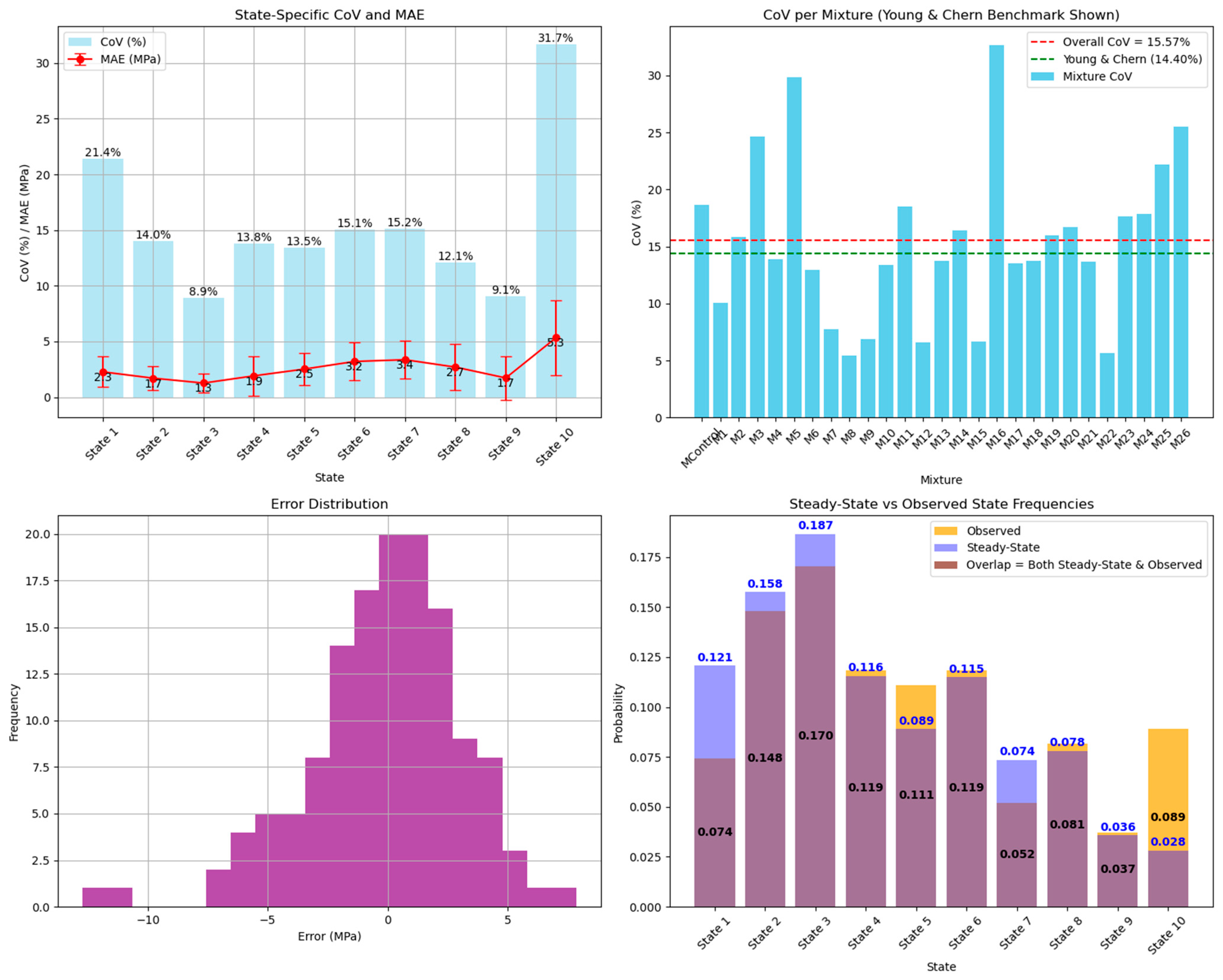
4.4. Model Validation Using Coefficient of Variation (CoV)
5. Discussions and Implications
- For early strength, increase PC content and use accelerated curing methods.
- For long-term durability, prioritize higher BFS content, especially in aggressive environments.
- For sustainable projects, incorporate FA but allow extended curing times to offset its early-stage limitations.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Mix Code | PC Composition of the Mixture (kg/m3) | FA Composition of the Mixture (kg/m3) | BFS Composition of the Mixture (kg/m3) | Curing Times—Age (Days) | Compressive Strength (MPa) |
|---|---|---|---|---|---|
| MControl | 300 | 0 | 0 | 3 | 22 |
| MControl | 300 | 0 | 0 | 7 | 25 |
| MControl | 300 | 0 | 0 | 28 | 27 |
| MControl | 300 | 0 | 0 | 90 | 32 |
| MControl | 300 | 0 | 0 | 180 | 36 |
| M1 | 270 | 0 | 30 | 3 | 19 |
| M1 | 270 | 0 | 30 | 7 | 20 |
| M1 | 270 | 0 | 30 | 28 | 23 |
| M1 | 270 | 0 | 30 | 90 | 30 |
| M1 | 270 | 0 | 30 | 180 | 33 |
| M2 | 270 | 30 | 0 | 3 | 17 |
| M2 | 270 | 30 | 0 | 7 | 20 |
| M2 | 270 | 30 | 0 | 28 | 24 |
| M2 | 270 | 30 | 0 | 90 | 30 |
| M2 | 270 | 30 | 0 | 180 | 35 |
| M3 | 240 | 0 | 60 | 3 | 11 |
| M3 | 240 | 0 | 60 | 7 | 14 |
| M3 | 240 | 0 | 60 | 28 | 18 |
| M3 | 240 | 0 | 60 | 90 | 24 |
| M3 | 240 | 0 | 60 | 180 | 32 |
| M4 | 240 | 30 | 30 | 3 | 15 |
| M4 | 240 | 30 | 30 | 7 | 16 |
| M4 | 240 | 30 | 30 | 28 | 18 |
| M4 | 240 | 30 | 30 | 90 | 24 |
| M4 | 240 | 30 | 30 | 180 | 27 |
| M5 | 240 | 60 | 0 | 3 | 10 |
| M5 | 240 | 60 | 0 | 7 | 13 |
| M5 | 240 | 60 | 0 | 28 | 14 |
| M5 | 240 | 60 | 0 | 90 | 19 |
| M5 | 240 | 60 | 0 | 180 | 27 |
| M6 | 210 | 0 | 90 | 3 | 16 |
| M6 | 210 | 0 | 90 | 7 | 17 |
| M6 | 210 | 0 | 90 | 28 | 19 |
| M6 | 210 | 0 | 90 | 90 | 22 |
| M6 | 210 | 0 | 90 | 180 | 29 |
| M7 | 210 | 30 | 60 | 3 | 16 |
| M7 | 210 | 30 | 60 | 7 | 17 |
| M7 | 210 | 30 | 60 | 28 | 20 |
| M7 | 210 | 30 | 60 | 90 | 25 |
| M7 | 210 | 30 | 60 | 180 | 29 |
| M8 | 210 | 60 | 30 | 3 | 16 |
| M8 | 210 | 60 | 30 | 7 | 17 |
| M8 | 210 | 60 | 30 | 28 | 19 |
| M8 | 210 | 60 | 30 | 90 | 23 |
| M8 | 210 | 60 | 30 | 180 | 29 |
| M9 | 210 | 90 | 0 | 3 | 13 |
| M9 | 210 | 90 | 0 | 7 | 15 |
| M9 | 210 | 90 | 0 | 28 | 17 |
| M9 | 210 | 90 | 0 | 90 | 21 |
| M9 | 210 | 90 | 0 | 180 | 29 |
| M10 | 180 | 0 | 120 | 3 | 13 |
| M10 | 180 | 0 | 120 | 7 | 17 |
| M10 | 180 | 0 | 120 | 28 | 18 |
| M10 | 180 | 0 | 120 | 90 | 23 |
| M10 | 180 | 0 | 120 | 180 | 32 |
| M11 | 180 | 30 | 90 | 3 | 14 |
| M11 | 180 | 30 | 90 | 7 | 14 |
| M11 | 180 | 30 | 90 | 28 | 19 |
| M11 | 180 | 30 | 90 | 90 | 21 |
| M11 | 180 | 30 | 90 | 180 | 26 |
| M12 | 180 | 60 | 60 | 3 | 13 |
| M12 | 180 | 60 | 60 | 7 | 16 |
| M12 | 180 | 60 | 60 | 28 | 18 |
| M12 | 180 | 60 | 60 | 90 | 24 |
| M12 | 180 | 60 | 60 | 180 | 30 |
| M13 | 180 | 90 | 30 | 3 | 13 |
| M13 | 180 | 90 | 30 | 7 | 14 |
| M13 | 180 | 90 | 30 | 28 | 18 |
| M13 | 180 | 90 | 30 | 90 | 25 |
| M13 | 180 | 90 | 30 | 180 | 26 |
| M14 | 180 | 120 | 0 | 3 | 10 |
| M14 | 180 | 120 | 0 | 7 | 15 |
| M14 | 180 | 120 | 0 | 28 | 18 |
| M14 | 180 | 120 | 0 | 90 | 24 |
| M14 | 180 | 120 | 0 | 180 | 25 |
| M15 | 150 | 0 | 150 | 3 | 16 |
| M15 | 150 | 0 | 150 | 7 | 19 |
| M15 | 150 | 0 | 150 | 28 | 20 |
| M15 | 150 | 0 | 150 | 90 | 26 |
| M15 | 150 | 0 | 150 | 180 | 33 |
| M16 | 150 | 30 | 120 | 3 | 19 |
| M16 | 150 | 30 | 120 | 7 | 21 |
| M16 | 150 | 30 | 120 | 28 | 23 |
| M16 | 150 | 30 | 120 | 90 | 36 |
| M16 | 150 | 30 | 120 | 180 | 42 |
| M17 | 150 | 60 | 90 | 3 | 13 |
| M17 | 150 | 60 | 90 | 7 | 14 |
| M17 | 150 | 60 | 90 | 28 | 19 |
| M17 | 150 | 60 | 90 | 90 | 26 |
| M17 | 150 | 60 | 90 | 180 | 27 |
| M18 | 150 | 90 | 60 | 3 | 13 |
| M18 | 150 | 90 | 60 | 7 | 15 |
| M18 | 150 | 90 | 60 | 28 | 18 |
| M18 | 150 | 90 | 60 | 90 | 26 |
| M18 | 150 | 90 | 60 | 180 | 28 |
| M19 | 150 | 120 | 30 | 3 | 16 |
| M19 | 150 | 120 | 30 | 7 | 16 |
| M19 | 150 | 120 | 30 | 28 | 18 |
| M19 | 150 | 120 | 30 | 90 | 26 |
| M19 | 150 | 120 | 30 | 180 | 29 |
| M20 | 150 | 150 | 0 | 3 | 12 |
| M20 | 150 | 150 | 0 | 7 | 14 |
| M20 | 150 | 150 | 0 | 28 | 18 |
| M20 | 150 | 150 | 0 | 90 | 26 |
| M20 | 150 | 150 | 0 | 180 | 29 |
| M21 | 120 | 0 | 180 | 3 | 16 |
| M21 | 120 | 0 | 180 | 7 | 17 |
| M21 | 120 | 0 | 180 | 28 | 21 |
| M21 | 120 | 0 | 180 | 90 | 24 |
| M21 | 120 | 0 | 180 | 180 | 26 |
| M22 | 120 | 30 | 150 | 3 | 15 |
| M22 | 120 | 30 | 150 | 7 | 16 |
| M22 | 120 | 30 | 150 | 28 | 18 |
| M22 | 120 | 30 | 150 | 90 | 24 |
| M22 | 120 | 30 | 150 | 180 | 30 |
| M23 | 120 | 60 | 120 | 3 | 11 |
| M23 | 120 | 60 | 120 | 7 | 16 |
| M23 | 120 | 60 | 120 | 28 | 19 |
| M23 | 120 | 60 | 120 | 90 | 22 |
| M23 | 120 | 60 | 120 | 180 | 26 |
| M24 | 120 | 90 | 90 | 3 | 14 |
| M24 | 120 | 90 | 90 | 7 | 16 |
| M24 | 120 | 90 | 90 | 28 | 20 |
| M24 | 120 | 90 | 90 | 90 | 26 |
| M24 | 120 | 90 | 90 | 180 | 31 |
| M25 | 120 | 120 | 60 | 3 | 9 |
| M25 | 120 | 120 | 60 | 7 | 14 |
| M25 | 120 | 120 | 60 | 28 | 16 |
| M25 | 120 | 120 | 60 | 90 | 17 |
| M25 | 120 | 120 | 60 | 180 | 23 |
| M26 | 120 | 150 | 30 | 3 | 10 |
| M26 | 120 | 150 | 30 | 7 | 19 |
| M26 | 120 | 150 | 30 | 28 | 18 |
| M26 | 120 | 150 | 30 | 90 | 18 |
| M26 | 120 | 150 | 30 | 180 | 22 |
| M27 | 120 | 180 | 0 | 3 | 9 |
| M27 | 120 | 180 | 0 | 7 | 9 |
| M27 | 120 | 180 | 0 | 28 | 12 |
| M27 | 120 | 180 | 0 | 90 | 16 |
| M27 | 120 | 180 | 0 | 180 | 20 |
| From State (Si) | To State (Sj) | Number of Transitions from State Si to State Sj (Denoted Cij) | Total Number of Transitions Starting from State Si (Denoted Ti) | Transition Probability |
|---|---|---|---|---|
| State 1 | State 1 | 3 | 17 | 0.176 |
| State 1 | State 2 | 10 | 17 | 0.588 |
| State 1 | State 3 | 3 | 17 | 0.176 |
| State 1 | State 4 | 1 | 17 | 0.059 |
| State 1 | State 5 | 0 | 17 | 0.000 |
| State 1 | State 6 | 0 | 17 | 0.000 |
| State 1 | State 7 | 0 | 17 | 0.000 |
| State 1 | State 8 | 0 | 17 | 0.000 |
| State 1 | State 9 | 0 | 17 | 0.000 |
| State 1 | State 10 | 0 | 17 | 0.000 |
| State 2 | State 1 | 0 | 22 | 0.000 |
| State 2 | State 2 | 5 | 22 | 0.227 |
| State 2 | State 3 | 12 | 22 | 0.545 |
| State 2 | State 4 | 5 | 22 | 0.227 |
| State 2 | State 5 | 0 | 22 | 0.000 |
| State 2 | State 6 | 0 | 22 | 0.000 |
| State 2 | State 7 | 0 | 22 | 0.000 |
| State 2 | State 8 | 0 | 22 | 0.000 |
| State 2 | State 9 | 0 | 22 | 0.000 |
| State 2 | State 10 | 0 | 22 | 0.000 |
| State 3 | State 1 | 0 | 26 | 0.000 |
| State 3 | State 2 | 0 | 26 | 0.000 |
| State 3 | State 3 | 6 | 26 | 0.231 |
| State 3 | State 4 | 6 | 26 | 0.231 |
| State 3 | State 5 | 5 | 26 | 0.192 |
| State 3 | State 6 | 7 | 26 | 0.269 |
| State 3 | State 7 | 2 | 26 | 0.077 |
| State 3 | State 8 | 0 | 26 | 0.000 |
| State 3 | State 9 | 0 | 26 | 0.000 |
| State 3 | State 10 | 0 | 26 | 0.000 |
| State 4 | State 1 | 0 | 16 | 0.000 |
| State 4 | State 2 | 0 | 16 | 0.000 |
| State 4 | State 3 | 1 | 16 | 0.063 |
| State 4 | State 4 | 2 | 16 | 0.125 |
| State 4 | State 5 | 6 | 16 | 0.375 |
| State 4 | State 6 | 3 | 16 | 0.188 |
| State 4 | State 7 | 3 | 16 | 0.188 |
| State 4 | State 8 | 0 | 16 | 0.000 |
| State 4 | State 9 | 0 | 16 | 0.000 |
| State 4 | State 10 | 0 | 16 | 0.000 |
| State 5 | State 1 | 2 | 13 | 0.154 |
| State 5 | State 2 | 0 | 13 | 0.000 |
| State 5 | State 3 | 0 | 13 | 0.000 |
| State 5 | State 4 | 0 | 13 | 0.000 |
| State 5 | State 5 | 1 | 13 | 0.077 |
| State 5 | State 6 | 4 | 13 | 0.308 |
| State 5 | State 7 | 0 | 13 | 0.000 |
| State 5 | State 8 | 4 | 13 | 0.308 |
| State 5 | State 9 | 1 | 13 | 0.077 |
| State 5 | State 10 | 1 | 13 | 0.077 |
| State 6 | State 1 | 2 | 16 | 0.125 |
| State 6 | State 2 | 1 | 16 | 0.063 |
| State 6 | State 3 | 1 | 16 | 0.063 |
| State 6 | State 4 | 0 | 16 | 0.000 |
| State 6 | State 5 | 0 | 16 | 0.000 |
| State 6 | State 6 | 2 | 16 | 0.125 |
| State 6 | State 7 | 4 | 16 | 0.250 |
| State 6 | State 8 | 5 | 16 | 0.313 |
| State 6 | State 9 | 1 | 16 | 0.063 |
| State 6 | State 10 | 0 | 16 | 0.000 |
| State 7 | State 1 | 2 | 10 | 0.200 |
| State 7 | State 2 | 3 | 10 | 0.300 |
| State 7 | State 3 | 0 | 10 | 0.000 |
| State 7 | State 4 | 0 | 10 | 0.000 |
| State 7 | State 5 | 0 | 10 | 0.000 |
| State 7 | State 6 | 0 | 10 | 0.000 |
| State 7 | State 7 | 1 | 10 | 0.100 |
| State 7 | State 8 | 2 | 10 | 0.200 |
| State 7 | State 9 | 2 | 10 | 0.200 |
| State 7 | State 10 | 0 | 10 | 0.000 |
| State 8 | State 1 | 6 | 11 | 0.545 |
| State 8 | State 2 | 1 | 11 | 0.091 |
| State 8 | State 3 | 2 | 11 | 0.182 |
| State 8 | State 4 | 0 | 11 | 0.000 |
| State 8 | State 5 | 0 | 11 | 0.000 |
| State 8 | State 6 | 0 | 11 | 0.000 |
| State 8 | State 7 | 0 | 11 | 0.000 |
| State 8 | State 8 | 0 | 11 | 0.000 |
| State 8 | State 9 | 1 | 11 | 0.091 |
| State 8 | State 10 | 1 | 11 | 0.091 |
| State 9 | State 1 | 0 | 5 | 0.000 |
| State 9 | State 2 | 2 | 5 | 0.400 |
| State 9 | State 3 | 1 | 5 | 0.200 |
| State 9 | State 4 | 1 | 5 | 0.200 |
| State 9 | State 5 | 0 | 5 | 0.000 |
| State 9 | State 6 | 0 | 5 | 0.000 |
| State 9 | State 7 | 0 | 5 | 0.000 |
| State 9 | State 8 | 0 | 5 | 0.000 |
| State 9 | State 9 | 0 | 5 | 0.000 |
| State 9 | State 10 | 1 | 5 | 0.200 |
| State 10 | State 1 | 2 | 4 | 0.500 |
| State 10 | State 2 | 0 | 4 | 0.000 |
| State 10 | State 3 | 0 | 4 | 0.000 |
| State 10 | State 4 | 1 | 4 | 0.250 |
| State 10 | State 5 | 0 | 4 | 0.000 |
| State 10 | State 6 | 0 | 4 | 0.000 |
| State 10 | State 7 | 0 | 4 | 0.000 |
| State 10 | State 8 | 0 | 4 | 0.000 |
| State 10 | State 9 | 0 | 4 | 0.000 |
| State 10 | State 10 | 1 | 4 | 0.250 |
References
- Altuncı, Y.T. A Comprehensive Study on the Estimation of Concrete Compressive Strength Using Machine Learning Models. Buildings 2024, 14, 3851. [Google Scholar] [CrossRef]
- Atici, U. Prediction of the strength of mineral admixture concrete using multivariable regression analysis and an artificial neural network. Expert Syst. Appl. 2011, 38, 9609–9618. [Google Scholar] [CrossRef]
- Chahar, A.S.; Pal, P. A review on various aspects of high-performance concrete. Innov. Infrastruct. Solut. 2023, 8, 175. [Google Scholar] [CrossRef]
- Ismail, L.; Abdel Razik, M.; Ateya, E.S.; Said, A. Optimizing sustainable concrete mixes with recycled aggregate and Portland slag cement for reducing environmental impact. Discov. Mater. 2024, 4, 68. [Google Scholar] [CrossRef]
- Sun, B.; Huang, Y.; Liu, G.; Wang, W. Prediction of compressive strength of concrete under various curing conditions: A comparison of machine learning models and empirical mathematical models. Innov. Infrastruct. Solut. 2024, 9, 262. [Google Scholar] [CrossRef]
- Talaei Khoei, T.; Ould Slimane, H.; Kaabouch, N. Deep learning: Systematic review, models, challenges, and research directions. Neural Comput. Appl. 2023, 35, 23103–23124. [Google Scholar] [CrossRef]
- Sang, F.; Luo, R.; Chen, Y.; Ge, X.; Xiao, M. Factor analysis evaluation of asphalt pavement performance considering structural strength and hidden cracks. Constr. Build. Mater. 2023, 408, 133651. [Google Scholar] [CrossRef]
- Vollpracht, A.; Soutsos, M.; Kanavaris, F. Strength development of GGBS and fly ash concretes and applicability of fib model code’s maturity function—A critical review. Constr. Build. Mater. 2018, 162, 830–846. [Google Scholar] [CrossRef]
- Guo, R.; Li, D.; Chen, G.; Jin, Y.; Li, H.; Zhang, Y. Nonhomogeneous Markov chains for degeneration behaviour of RC members’ durability and its Bayesian updating. Case Stud. Constr. Mater. 2025, 22, e04189. [Google Scholar] [CrossRef]
- Fib-Federation Internationale du Beton. Fib Model Code for Concrete Structures; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Young, C.; Chern, J. Practical prediction model for shrinkage of steel fiber reinforced concrete. Mater. Struct. 1991, 24, 191–201. [Google Scholar] [CrossRef]
- Wang, J.; Long, G.; Xiang, Y.; Dong, R.; Tang, Z.; Xiao, Q.; Ma, K. Influence of rapid curing methods on concrete microstructure and properties: A review. Case Stud. Constr. Mater. 2022, 17, e01600. [Google Scholar] [CrossRef]
- Smarzewski, P.; Stolarski, A. Properties and Performance of Concrete Materials and Structures. Crystals 2022, 12, 1193. [Google Scholar] [CrossRef]
- Elkafrawy, M.; Gowrishankar, P.; Aswad, N.G.; Alashkar, A.; Khalil, A.; AlHamaydeh, M.; Hawileh, R. GFRP-Reinforced Concrete Columns: State-of-the-Art, Behavior, and Research Needs. Buildings 2024, 14, 3131. [Google Scholar] [CrossRef]
- Pombo, R.; Altamirano, M.G.; Giaccio, G.M.; Zerbino, R.L. Design and execution of floors on ground and industrial pavements with fibre reinforced concrete. In Rilem-Fib International Symposium on Fibre Reinforced Concrete; Springer International Publishing: Cham, Switzerland, 2021; pp. 640–651. [Google Scholar]
- Tan, X.; Mahjoubi, S.; Zhang, Q.; Dong, D.; Bao, Y. A framework for improving bridge resilience and sustainability through optimizing high-performance fiber-reinforced cementitious composites. J. Infrastruct. Preserv. Resil. 2022, 3, 18. [Google Scholar] [CrossRef]
- Khasawneh, M.A. Geopolymer concrete in construction projects: A review. Discov. Civ. Eng. 2025, 2, 124. [Google Scholar] [CrossRef]
- Toklu, K. Investigation of mechanical and durability behaviour of high strength cementitious composites containing natural zeolite and blast-furnace slag. Silicon 2021, 13, 2821–2833. [Google Scholar] [CrossRef]
- Han, X. Design and Construction Techniques of Prestressed Concrete Structures in Bridge Engineering. Acad. J. Archit. Geotech. Eng. 2024, 6, 74–79. [Google Scholar]
- Sawab, J.; Lim, I.; Mo, Y.L.; Li, M.; Wang, H.; Guimaraes, M. Ultra-High-Performance Concrete and Advanced Manufacturing Methods for Modular Construction; No. FY-ID-13-5282 CA-13-TX-UH-0606-0122; University of Houston: Houston, TX, USA, 2016. [Google Scholar]



| State | Compressive Strength Range (MPa) | Mix Code and Curing Age Mi (t) |
|---|---|---|
| State 1 | <13.5 | M3 (3, 7), M5 (60), M9 (90), M10 (0), M12 (60), M13 (90), M14 (120), M20 (150), M23 (60), M25 (120), M26 (150), M27 (180) |
| State 2 | 13.5–16 | M3 (7), M4 (3, 7), M6 (0), M7 (30), M8 (60), M9 (90), M10 (0), M11 (30), M12 (60), M13 (90), M14 (120), M19 (120), M21 (0), M22 (30), M24 (90) |
| State 3 | 16–18.5 | M2 (3, 7), M3 (28), M4 (28), M6 (0), M7 (30), M8 (60), M9 (90), M10 (0), M11 (30), M12 (60), M13 (90), M14 (120), M17 (60), M18 (90), M19 (120), M20 (150), M21 (0), M22 (30), M24 (90) |
| State 4 | 18.5–21 | M1 (28), M2 (28), M4 (7), M5 (60), M6 (0), M8 (60), M9 (90), M10 (0), M11 (30), M12 (60), M13 (90), M14 (120), M15 (0), M16 (30), M17 (60), M19 (120), M20 (150), M22 (30), M23 (60), M24 (90) |
| State 5 | 21–23.5 | M1 (90), M2 (180), M3 (90), M4 (90), M5 (60), M6 (0), M8 (60), M9 (90), M10 (0), M11 (30), M12 (60), M13 (90), M15 (0), M16 (30), M17 (60), M19 (120), M20 (150), M23 (60), M24 (90), M25 (120), M26 (150) |
| State 6 | 23.5–26 | M1 (180), M2 (180), M3 (180), M4 (180), M5 (60), M7 (30), M8 (60), M9 (90), M10 (0), M11 (30), M12 (60), M13 (90), M14 (120), M15 (0), M16 (30), M17 (60), M18 (90), M19 (120), M20 (150), M23 (60), M24 (90), M25 (120), M26 (150) |
| State 7 | 26–28.5 | M1 (90), M2 (180), M3 (180), M5 (60), M6 (0), M7 (30), M8 (60), M9 (90), M10 (0), M11 (30), M12 (60), M13 (90), M14 (120), M15 (0), M16 (30), M17 (60), M18 (90), M19 (120), M20 (150), M22 (30), M23 (60), M24 (90), M25 (120), M26 (150) |
| State 8 | 28.5–31 | M3 (180), M5 (60), M6 (0), M7 (30), M8 (60), M9 (90), M10 (0), M11 (30), M12 (60), M13 (90), M14 (120), M15 (0), M16 (30), M17 (60), M18 (90), M19 (120), M20 (150), M22 (30), M23 (60), M24 (90), M25 (120), M26 (150) |
| State 9 | 31–33.5 | M1 (90), M2 (180), M3 (180), M5 (60), M6 (0), M7 (30), M8 (60), M9 (90), M10 (0), M11 (30), M12 (60), M13 (90), M14 (120), M15 (0), M16 (30), M17 (60), M18 (90), M19 (120), M20 (150), M23 (60), M24 (90), M25 (120), M26 (150) |
| State 10 | >33.5 | M1 (90), M3 (180), M4 (180), M5 (60), M6 (0), M7 (30), M8 (60), M9 (90), M10 (0), M11 (30), M12 (60), M13 (90), M14 (120), M15 (0), M16 (30), M17 (60), M18 (90), M19 (120), M20 (150), M22 (30), M23 (60), M24 (90), M25 (120), M26 (150) |
| From/To | State 1 | State 2 | State 3 | State 4 | State 5 | State 6 | State 7 | State 8 | State 9 | State 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| State 1 | 0.176 | 0.588 | 0.176 | 0.059 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| State 2 | 0.000 | 0.227 | 0.545 | 0.227 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| State 3 | 0.000 | 0.000 | 0.231 | 0.231 | 0.192 | 0.269 | 0.077 | 0.000 | 0.000 | 0.000 |
| State 4 | 0.000 | 0.000 | 0.067 | 0.133 | 0.400 | 0.200 | 0.200 | 0.000 | 0.000 | 0.000 |
| State 5 | 0.154 | 0.000 | 0.000 | 0.000 | 0.077 | 0.308 | 0.000 | 0.308 | 0.077 | 0.077 |
| State 6 | 0.125 | 0.063 | 0.063 | 0.000 | 0.000 | 0.125 | 0.250 | 0.313 | 0.063 | 0.000 |
| State 7 | 0.200 | 0.300 | 0.000 | 0.000 | 0.000 | 0.000 | 0.100 | 0.200 | 0.200 | 0.000 |
| State 8 | 0.545 | 0.091 | 0.182 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.091 | 0.091 |
| State 9 | 0.000 | 0.400 | 0.200 | 0.200 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.200 |
| State 10 | 0.500 | 0.000 | 0.000 | 0.250 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.250 |
| State | State 1 | State 2 | State 3 | State 4 | State 5 | State 6 | State 7 | State 8 | State 9 | State 10 |
| Probability | 0.1207 | 0.1575 | 0.1865 | 0.1156 | 0.0889 | 0.1151 | 0.0736 | 0.078 | 0.0358 | 0.0281 |
| Metric | Value | Insight |
|---|---|---|
| R2 | 0.977 | Indicates the model explains 97.7% of the variance in compressive strength. |
| Adjusted R2 | 0.97 | Confirms the robustness of the model after accounting for predictors. |
| Standard Error | 3.27 | Represents the average deviation of predicted compressive strength from observed values. |
| F-Statistic | 1474.26 | Demonstrates the overall significance of the regression model. |
| Significance F | 0.00 | Highlights the strong statistical relevance of the predictors in the model. |
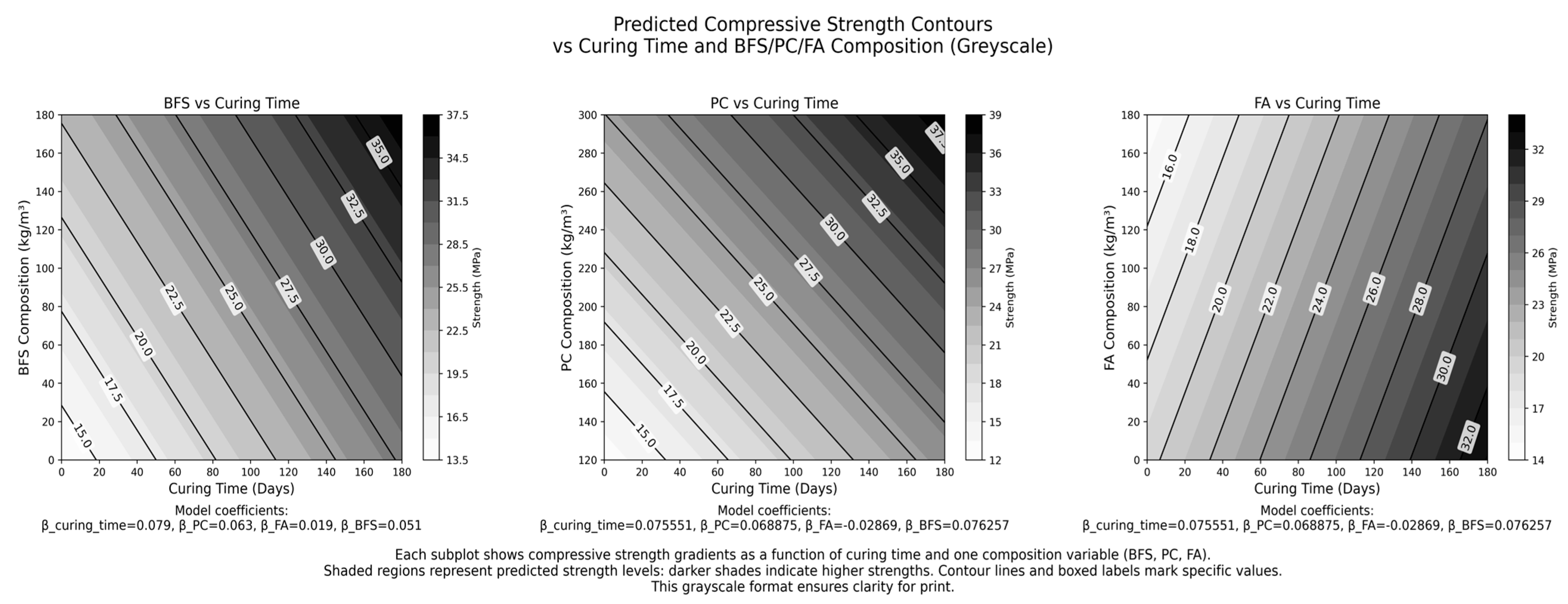
| Predictor | Coefficient | p-Value | Significance | Key Insight |
|---|---|---|---|---|
| PC Composition (kg/m3) | 0.063 | 0.000 | Highly Significant | Major contributor to early strength. |
| FA Composition (kg/m3) | 0.019 | 0.0006 | Significant | Improves strength but lags in early stages. |
| BFS Composition (kg/m3) | 0.051 | 0.000 | Highly Significant | Key for long-term durability. |
| Curing Time (Days) | 0.079 | 0.000 | Highly Significant | Strongly influences strength progression. |
| Aspect | Observation | Example Points | Implication | ||
|---|---|---|---|---|---|
| Predicted vs. Actual Strength Trends | Underestimation at Early Strength States (State 1 to 3) | Red markers dominate early curing stages. | Actual: 13.5 MPa (State 3) Predicted: 11.5 MPa (15% underestimation) | Model underestimates rapid strength gains during hydration, leading to conservative early-stage usability assessments. | |
| Actual: 14.5 MPa (State 2 to 3) Predicted: 12.9 MPa (underestimated by 11%) | |||||
| Overestimation in Higher Strength States (State 7 to 10) | Green markers dominate longer curing stages. | Actual: 30.9 MPa (State 9) Predicted: 33.1 MPa (7% overestimation) | Overestimations in long-term strength can lead to unsafe structural assumptions for high-stress applications. | ||
| Actual: 36 MPa (State 10) Predicted: 41.6 MPa (15% overestimation) | |||||
| Regression Line and Prediction Accuracy | Regression Equation | y = 0.93x + 1.25: slope slightly below 1, indicating underprediction at low MPa and overprediction at high MPa. | Actual: 15 MPa Predicted (regression): 15.2 MPa (slight bias). | Good performance in moderate MPa ranges (18–28 MPa) but poor accuracy at extremes highlights needs for calibration. | |
| Actual: 36 MPa Predicted (regression): 35.7 MPa (close to accurate but slightly underestimates) | |||||
| Material Influence on Predictions | Portland Cement (PC) Dominant Mixes | PC-rich mixes (e.g., M16, M10) show strong long-term predictions but overestimate at high MPa levels. | M16 at 180 days | Actual: 42 MPa Predicted: 45 MPa (7% overestimation) | PC-heavy mixes cause accelerated strength gain, exacerbating overpredictions for long curing periods. |
| Fly Ash (FA) and BFS Mixes | FA- or BFS-rich mixes (e.g., M13, M12) underperform during early curing. | M12 at 7 days | Actual: 16 MPa Predicted: 14.5 MPa (underestimated by 9%) | FA-rich mixes require better model representation to account for slower strength evolution. | |
| Curing Time Influence | Key Trends | Consistent underestimation for early curing and overestimation for long curing periods. | 7 days | Actual: 13.5 MPa Predicted: 11.7 MPa (underestimated) | Model struggles to balance early-stage underpredictions and long-term overpredictions. Environmental and hydration data incorporation could address this challenge. |
| 180 days | Actual: 36 MPa Predicted: 41.6 MPa (overestimated) | ||||
| State | Interpreting Markov Chain Transition Probabilities | Observed Trends | Mix Codes | Decision | Industry-Specific Recommendation |
|---|---|---|---|---|---|
| State 1 | The system has a 0.0213 chance of staying in State 1, 0.0710 chance of moving to State 2, and smaller probabilities of transitioning to other states (State 3, State 4, etc.). This tells us the likelihood of moving from a lower compressive strength range to a higher one or remaining within the same range. | In this state, transitions suggest a frequent move to lower MPa states, implying a need for better early-stage curing. The mix codes associated with this state show a diverse range of materials, which could contribute to the moderate compressive strength. There is a strong association with mixes that balance materials like M3, M5, M9, M10, etc., which suggests that this state tends to hover around the lower strength ranges (11.0–13.5 MPa). | M3, M5, M9, M10, M12, M13, M14, M17, M18, M20, M23, M25, M26, M27 | To improve early strength, increase the Portland Cement (PC) or Fly Ash (FA) content slightly. Alternatively, consider adding a moderate amount of Blast Furnace Slag (BFS) to improve density and reduce porosity, which can also contribute to durability. Higher PC content could accelerate curing, leading to higher early compressive strength. Mixtures should be closely monitored to maintain balance, but increasing PC content can ensure that this state is suitable for structural uses in moderate-stress environments. | In precast concrete construction, rapid curing methods such as steam curing, direct electric curing, and microwave curing accelerate strength development, making them ideal for non-critical structural elements or short-duration projects where moderate strength is acceptable. Increased Portland Cement (PC) content, combined with optimized curing techniques, ensures quicker hydration and early strength gain, facilitating faster production turnover while maintaining essential mechanical properties [12]. |
| State 2 | From State 2, there is a 0.0358 chance of staying in State 2, 0.0859 chance of transitioning to State 3, and smaller chances of moving to States 4 and beyond. The transition probabilities indicate a tendency to stay within a certain range but also to move upward or downward in compressive strength. | Transitions from this state show a tendency to move towards higher MPa states, with a notable shift to 13.5–16.0 MPa. This indicates that this state is part of the moderate-strength spectrum and could be optimized with slight adjustments. The mix codes M3, M4, M5, M6, and others suggest an emphasis on medium-strength mixes with some variability in the transition towards higher strengths. | M3, M4, M5, M6, M7, M9, M11, M13, M14, M17, M18, M19, M20, M22, M24, M25 | Moderately increase PC or FA content to optimize transitions towards higher-strength states. Adding a small percentage of BFS can enhance the durability and overall density, making the concrete more resilient over time. By adjusting the mix towards a higher PC content, curing time can be improved, leading to better early strength. This state is already suitable for moderate structural use and can be optimized with minor changes. | This state is well-suited for use in the manufacturing of concrete products such as pavements and utility structures where moderate strength is essential for durability, but speed in curing is also a key factor for mass production [13]. |
| State 3 | From State 3, there is a 0.0430 chance of staying in State 3, with further transitions to State 4 and higher probabilities for States 5 and 6. This suggests that the system tends to move up the compressive strength scale with higher probabilities at each step. | Strong transitions towards higher MPa states, with mix codes like M2, M3, M4, and M6, pointing to an optimal range for compressive strength around 16.0–18.5 MPa. The presence of stronger mix codes suggests the potential for more rapid curing and higher initial strength in this state. The mix transitions also show that the material can achieve good performance in structural applications, especially in moderate stress environments. | M2, M3, M4, M6, M7, M8, M9, M10, M12, M13, M14, M15, M18, M19, M21, M22, M25, M26 | Increase PC content slightly to further accelerate early-stage curing and strength gain. Additionally, BFS can be included to improve long-term strength, durability, and resistance to aggressive environments. This will also ensure better consistency in performance, especially in structural applications where moderate-to-high compressive strength is needed. | In the construction sector, this state is ideal for structural concrete elements such as beams, columns, and foundations that need to meet strength requirements early in the construction phase [14]. |
| State 4 | The transition from State 4 has 0.0077 chance of remaining in State 4 and increasing chances for transition to States 5 and 6. The transition suggests a gradual movement to higher compressive strength values. | In this state, there is a balanced transition to the higher-strength range (18.5–21.0 MPa). The mix codes suggest a more specialized mix to ensure that it stays within this range, which could be useful for certain structural applications requiring consistent strength. The trend towards slightly higher strength states makes this an ideal range for concrete used in moderate-stress environments. | M1, M6, M7, M8, M9, M10, M11, M15, M16, M17, M23, M24, M26 | For improved early strength and quicker curing, increase the PC content slightly. Adding BFS can improve the mix’s resistance to shrinkage and cracking, especially in environments with temperature variations. Monitoring the mix and ensuring balanced components will allow this state to meet the structural requirements for moderate-strength concrete. | In industrial flooring applications, where both strength and durability are key but cost-efficiency is still important, this state offers a balance between curing time and final strength. Slight increases in PC will help accelerate curing for rapid construction timelines [15]. |
| State 5 | In State 5, there is a 0.0137 chance of staying in State 5, 0.0274 to transition upward, and smaller chances to transition to lower states, indicating more movement toward higher strength states. | This state transitions moderately toward higher MPa ranges (21.0–23.5 MPa) but shows some variability in strength. The mixture, associated with codes like M1, M2, and M6, suggests a flexible approach to the mix that can be adjusted for performance. The transitions indicate potential for a mix to perform in structural environments under moderate stress, but with more focus needed on controlling the mix ratios for consistent performance. | M1, M2, M6, M8, M9, M10, M11, M16, M17, M21, M23, M25 | Slightly increase the PC, FA, or consider adding BFS to the mix. BFS will enhance durability and long-term strength while also improving the resistance to thermal cracking. Close monitoring will ensure the mix achieves the desired compressive strength for this state. | For infrastructure projects, where higher strength is required but with flexible mix options, this state is ideal for road construction and bridging elements that need moderate–high strength but still depend on flexibility in the mix for practical uses [16]. |
| State 6 | From State 6, the system has a 0.0144 chance of staying, with a 0.0288 probability of moving upward to States 7 and 8, showing a tendency to increase compressive strength. | This state shows a balanced distribution with some tendency towards higher MPa ranges (23.5–26.0 MPa). The transition patterns show a good spread across various mix codes, indicating a strong potential for the state to perform well in both early strength gain and long-term durability. The state is typically part of the higher strength spectrum. | M1, M2, M3, M4, M5, M6, M7, M9, M10, M11, M12, M14, M18, M20, M23 | This state already has a high strength level, but adding BFS can increase the mix’s durability, particularly in environments with chemical exposure. The mix ratios can be adjusted to improve consistency while maintaining compressive strength. The use of BFS can help meet the requirements for both compressive strength and durability. | This state is ideal for high-performance applications, such as high-rise construction and structural elements with heavy loads, where compressive strength and durability are paramount. BFS addition improves resistance to environmental factors, making it suitable for critical infrastructure applications [17]. |
| State 7 | The system in State 7 has a 0.0147 chance of remaining in State 7, but higher probabilities to transition to States 8 and 9. This indicates potential for further increase in compressive strength. | State 7 transitions from lower-strength states to higher MPa states in the 26.0–28.5 MPa range. Mix codes such as M4, M5, M6, and M7 are strongly represented, suggesting a well-balanced mix that allows for early strength gain and long-term durability. However, the transition matrix indicates that maintaining balance is important to prevent any decline in strength. | M4, M5, M6, M7, M9, M15, M17, M18, M20, M21, M24 | For better early-stage strength and improved curing, increasing the Portland Cement (PC) content will help accelerate the transition to higher MPa ranges. Adding Fly Ash (FA) or Blast Furnace Slag (BFS) can enhance durability, particularly in high-stress environments, without compromising early strength. BFS will also improve long-term resistance to chemical attacks and mitigate shrinkage. Close monitoring will help ensure the mix remains within the optimal strength range for structural applications. | Ideal for high-strength industrial foundations and heavy machinery platforms where the concrete needs to withstand heavy loads and high-stress conditions. This state will allow faster curing while maintaining the strength required for such heavy-duty applications. BFS can further enhance the performance in environments exposed to aggressive conditions, making it suitable for long-term durability in industrial sectors [18]. |
| State 8 | From State 8, there is a 0.0426 chance of transitioning back to lower states, with significant likelihood of transitioning to States 9 and 10, suggesting further strength development. | State 8 shows a steady increase in strength, suggesting it is in the 28.5–31.0 MPa range. The mix codes associated with this state (M1, M2, M6, M7) indicate a strong base mix capable of transitioning toward higher-strength concrete. The mix has a stable tendency to perform well, which is essential for certain structural applications in more demanding environments. | M1, M2, M6, M7, M8, M9, M12, M19, M20, M22, M24 | Slightly increase the PC content to further enhance early strength. BFS can be introduced to improve the mix’s durability, particularly in environments with high exposure to chemicals or freezing-and-thawing cycles. This state is ideal for moderate-to-high structural strength, and small adjustments in the mix will help ensure it reaches its full potential. | Prestressed concrete is widely used in bridges, tunnels, and high-rise construction due to its superior load-bearing capacity and durability. Optimized prestressing techniques, combined with slight increases in Portland Cement (PC) content, can accelerate curing time, ensuring rapid strength gain before tensioning. Additionally, the incorporation of Blast Furnace Slag (BFS) enhances long-term durability, particularly in structures exposed to aggressive environmental conditions such as bridges and tunnels [19]. |
| State 9 | In State 9, there is a 0.0143 chance of staying in State 9, and a strong 0.0072 chance of transitioning to State 10, indicating movement to the highest strength range. | The transition matrix indicates steady movement towards higher MPa states, with a clear trend towards 31.0–33.5 MPa. The mix codes (M1, M3, M9) associated with this state suggest that it is appropriate for higher-strength structural applications, but still requires close monitoring to prevent premature setting or poor workability in some mixes. | M1, M3, M9, M10, M15, M21 | Increase PC content slightly to help with early-stage strength development. Adding BFS will improve the mix’s resistance to chemical attacks and improve long-term durability without sacrificing early strength. This will also help maintain workability and prevent cracking. | This state is excellent for power plants, nuclear facilities, and dam construction, where high-strength concrete is required for durability under extreme conditions. Increasing the PC content will enhance strength gain without compromising workability. BFS addition will improve the mix’s durability, making it suitable for high-performance applications in harsh industrial environments [20]. |
| State 10 | From State 10, the system has a 0.0070 chance of staying in State 10, indicating a relatively stable compressive strength in the highest range. | State 10 tends to show a slower progression toward higher strength states, likely due to the mix’s transition behavior and specific material types. The mix codes point to a more specialized blend (M1, M2, M6) capable of achieving the 33.5–36.0 MPa range, which is suitable for high-strength structural applications. | M1, M2, M6, M9, M10, M16 | Slight increases in PC or FA content will help speed up the curing process. BFS can be introduced to further enhance the mix’s durability, particularly for high-performance applications where concrete will be subjected to severe environmental conditions. Monitoring mix ratios closely will ensure consistent performance, particularly for the highest strength applications. | For specialized industrial structures such as high-rise buildings, oil platforms, and wind turbine foundations, this state is suitable for demanding environments. Further increases in PC content will ensure that the concrete performs well under heavy loads and extreme conditions. BFS will enhance the concrete’s durability, especially in aggressive environments exposed to chemicals, moisture, or freeze-thaw cycles [3]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.S.; Tasnim, A.; Hasan, M.F.; Kabir, G. Dynamic Probabilistic Modeling of Concrete Strength: Markov Chains and Regression for Sustainable Mix Design. Infrastructures 2025, 10, 219. https://doi.org/10.3390/infrastructures10080219
Ahmed MS, Tasnim A, Hasan MF, Kabir G. Dynamic Probabilistic Modeling of Concrete Strength: Markov Chains and Regression for Sustainable Mix Design. Infrastructures. 2025; 10(8):219. https://doi.org/10.3390/infrastructures10080219
Chicago/Turabian StyleAhmed, Md. Shahariar, Anica Tasnim, Md Ferdous Hasan, and Golam Kabir. 2025. "Dynamic Probabilistic Modeling of Concrete Strength: Markov Chains and Regression for Sustainable Mix Design" Infrastructures 10, no. 8: 219. https://doi.org/10.3390/infrastructures10080219
APA StyleAhmed, M. S., Tasnim, A., Hasan, M. F., & Kabir, G. (2025). Dynamic Probabilistic Modeling of Concrete Strength: Markov Chains and Regression for Sustainable Mix Design. Infrastructures, 10(8), 219. https://doi.org/10.3390/infrastructures10080219








