Deterioration Modeling of Pavement Performance in Cold Regions Using Probabilistic Machine Learning Method
Abstract
1. Introduction
- (1)
- Construct a specific dataset for cold-region pavement performance, integrating various features related to traffic, structural design, and environmental conditions.
- (2)
- Apply Bayesian optimization to automatically select the hyperparameters of the NGBoost model and improve its predictive capability.
- (3)
- Compare the proposed approach with commonly used deterministic machine learning models, including ANN, RF, and XGBoost, in terms of both accuracy and uncertainty estimation.
2. Methodology
2.1. Data Collection and Preparation
2.2. Model Development
3. Results and Analysis
3.1. Model Performance Evaluation
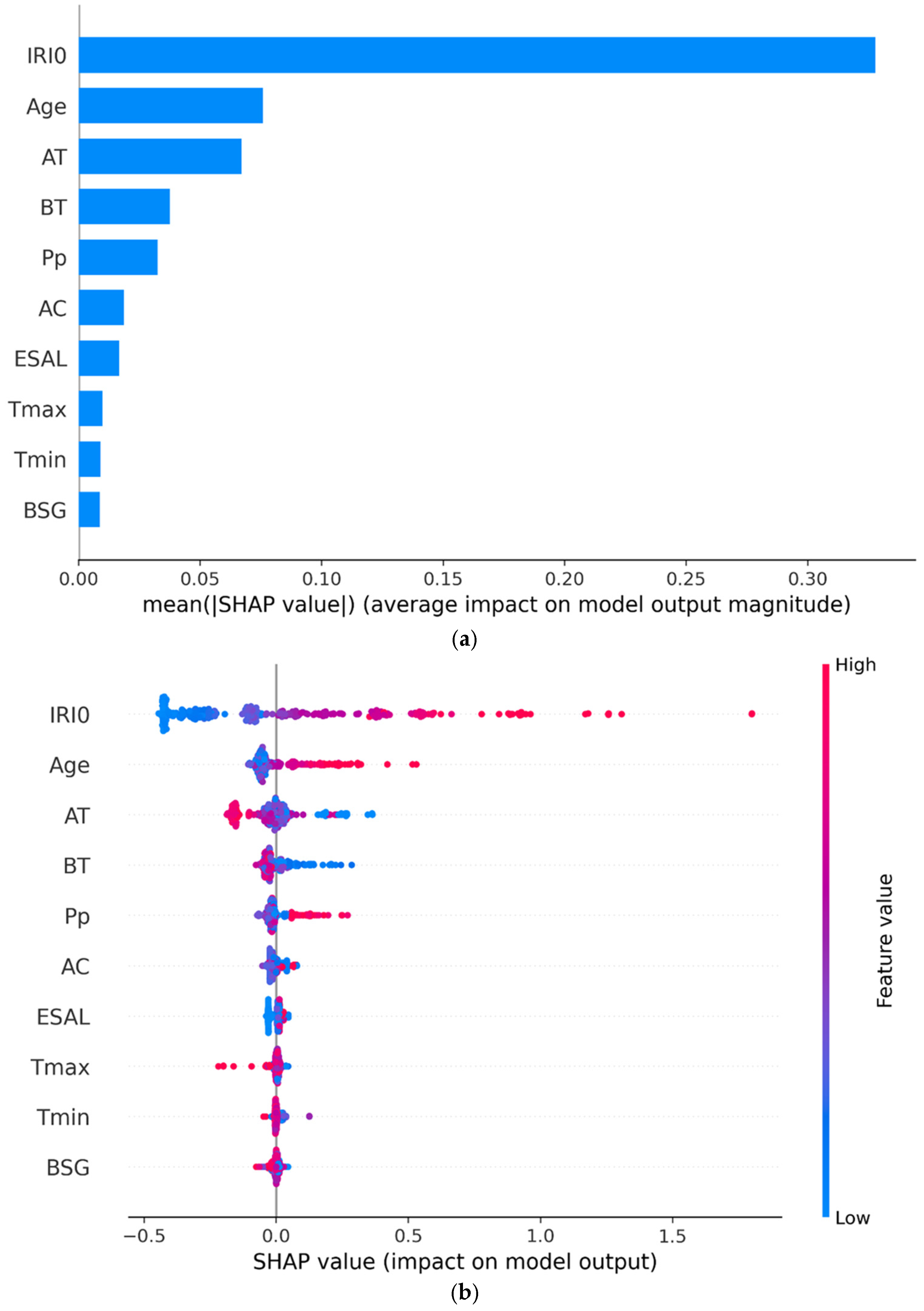
3.2. Interpretation of ML Model
3.3. Limitations and Recommendations
4. Conclusions
- (1)
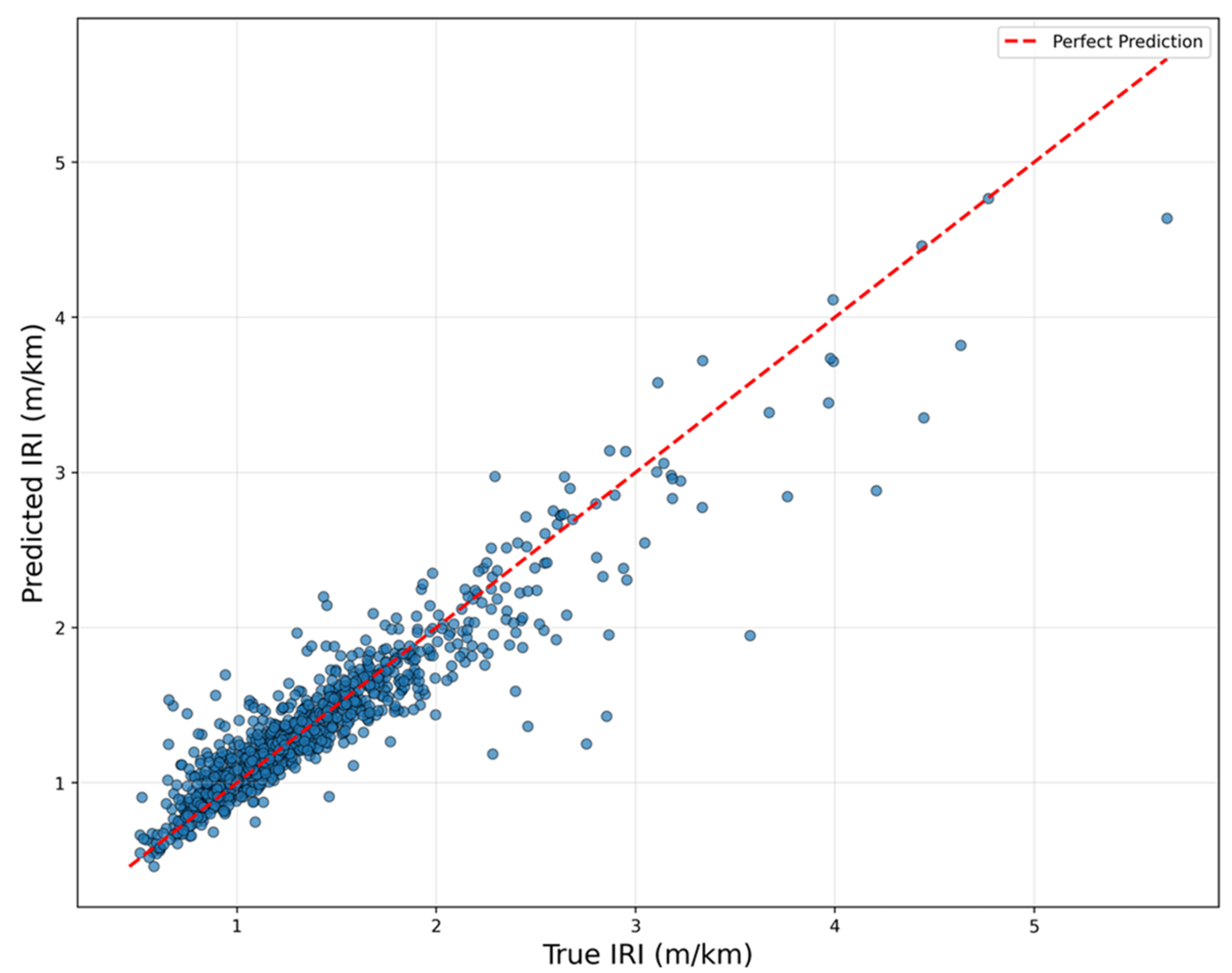
- The BO-NGBoost model outperformed traditional machine learning algorithms (ANN, RF, and XGBoost), achieving an R2 of 0.897, RMSE of 0.184, and MAE of 0.107, effectively capturing IRI growth pattern under cold-region climatic conditions.
- (2)
- Unlike conventional models that provide only point predictions, BO-NGBoost provides probabilistic predictions with uncertainty bounds. These bounds widen with pavement age, capturing the increasing variability in long-term deterioration due to cumulative damage, data variability, and environmental heterogeneity.
- (3)
- To enhance interpretability, SHAP analysis was employed. It identified initial IRI, pavement age, layer thicknesses, and precipitation as key contributors. Higher initial IRI and older pavement will lead to faster deterioration, while a thicker asphalt layer and base layer can help mitigate it.
- (4)
- Pavements in cold regions deteriorate rapidly due to freeze–thaw cycles and moisture infiltration. Low temperatures combined with high precipitation accelerate cracking and structural weakening, leading to higher surface roughness over time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- de Abreu, V.H.S.; Santos, A.S.; Monteiro, T.G.M. Climate Change Impacts on the Road Transport Infrastructure: A Systematic Review on Adaptation Measures. Sustainability 2022, 14, 8864. [Google Scholar] [CrossRef]
- Doll, C.; Trinks, C.; Sedlacek, N.; Pelikan, V.; Comes, T.; Schultmann, F. Adapting rail and road networks to weather extremes: Case studies for southern Germany and Austria. Nat. Hazards 2014, 72, 63–85. [Google Scholar] [CrossRef]
- Cui, B.; Wang, H. Predicting Asphalt Pavement Deterioration Under Climate Change Uncertainty Using Bayesian Neural Network. IEEE Trans. Intell. Transp. Syst. 2025, 26, 785–797. [Google Scholar] [CrossRef]
- Vignisdottir, H.R.; Ebrahimi, B.; Booto, G.K.; O’Born, R.; Brattebø, H.; Wallbaum, H.; Bohne, R.A. A review of environmental impacts of winter road maintenance. Cold Reg. Sci. Technol. 2019, 158, 143–153. [Google Scholar] [CrossRef]
- Hinkka, V.; Pilli-Sihvola, E.; Mantsinen, H.; Leviäkangas, P.; Aapaoja, A.; Hautala, R. Integrated winter road maintenance management—New directions for cold regions research. Cold Reg. Sci. Technol. 2016, 121, 108–117. [Google Scholar] [CrossRef]
- Cui, B.; Gu, X.; Hu, D.; Dong, Q. A multiphysics evaluation of the rejuvenator effects on aged asphalt using molecular dynamics simulations. J. Clean. Prod. 2020, 259, 120629. [Google Scholar] [CrossRef]
- Mills, L.N.O.; Attoh-Okine, N.O.; McNeil, S. Developing Pavement Performance Models for Delaware. Transp. Res. Rec. 2012, 2304, 97–103. [Google Scholar] [CrossRef]
- Morehouse, T.A. The 1962 Highway Act: A study in artful interpretation. J. Am. Inst. Plan. 1969, 35, 160–168. [Google Scholar] [CrossRef]
- Hajek, J.J.; Bradbury, A. Pavement Performance Modeling Using Canadian Strategic Highway Research Program Bayesian Statistical Methodology. Transp. Res. Rec. 1996, 1524, 160–170. [Google Scholar] [CrossRef]
- Li, N.; Haas, R.; Xie, W.C. Development of a new asphalt pavement performance prediction model. Can. J. Civ. Eng. 1997, 24, 547–559. [Google Scholar] [CrossRef]
- Heidari, M.J.; Najafi, A.; Alavi, S. Pavement deterioration modeling for forest roads based on logistic regression and artificial neural networks. Croat. J. For. Eng. J. Theory Appl. For. Eng. 2018, 39, 271–287. [Google Scholar]
- Liu, Z.; Shen, S.; Yu, S.; Jahangiri, B.; Mensching, D.J.; Haghshenas, H.F. Development of field compaction curves for asphalt mixtures based on laboratory workability tests and machine learning modeling. Constr. Build. Mater. 2025, 479, 141520. [Google Scholar] [CrossRef]
- Piryonesi, S.M.; El-Diraby, T.E. Using Machine Learning to Examine Impact of Type of Performance Indicator on Flexible Pavement Deterioration Modeling. J. Infrastruct. Syst. 2021, 27, 04021005. [Google Scholar] [CrossRef]
- Choi, S.; Do, M. Development of the Road Pavement Deterioration Model Based on the Deep Learning Method. Electronics 2020, 9, 3. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Gu, X.; Dong, Q. Non-destructive testing and intelligent evaluation of road structural conditions using GPR and FWD. J. Traffic Transp. Eng. 2025, 12, 462–476. [Google Scholar] [CrossRef]
- Kaloop, M.R.; El-Badawy, S.M.; Hu, J.W.; Abd El-Hakim, R.T. International Roughness Index prediction for flexible pavements using novel machine learning techniques. Eng. Appl. Artif. Intell. 2023, 122, 106007. [Google Scholar] [CrossRef]
- Pérez-Acebo, H.; Isasa, M.; Gurrutxaga, I.; García, H.; Insausti, A. International Roughness Index (IRI) prediction models for freeways. Transp. Res. Procedia 2023, 71, 292–299. [Google Scholar] [CrossRef]
- Elhadidy, A.A.; El-Badawy, S.M.; Elbeltagi, E.E. A simplified pavement condition index regression model for pavement evaluation. Int. J. Pavement Eng. 2021, 22, 643–652. [Google Scholar] [CrossRef]
- Luo, X.; Wang, F.; Bhandari, S.; Wang, N.; Qiu, X. Effectiveness evaluation and influencing factor analysis of pavement seal coat treatments using random forests. Constr. Build. Mater. 2021, 282, 122688. [Google Scholar] [CrossRef]
- Guo, R.; Fu, D.; Sollazzo, G. An ensemble learning model for asphalt pavement performance prediction based on gradient boosting decision tree. Int. J. Pavement Eng. 2022, 23, 3633–3646. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, W.; Liu, J. Developing an improved extreme gradient boosting model for predicting the international roughness index of rigid pavement. Constr. Build. Mater. 2023, 408, 133523. [Google Scholar] [CrossRef]
- Liu, Z.; Gu, X.; Chen, J.; Wang, D.; Chen, Y.; Wang, L. Automatic recognition of pavement cracks from combined GPR B-scan and C-scan images using multiscale feature fusion deep neural networks. Autom. Constr. 2023, 146, 104698. [Google Scholar] [CrossRef]
- Deng, Y.; Shi, X. Short-Term Predictions of Asphalt Pavement Rutting Using Deep-Learning Models. J. Transp. Eng. Part B Pavements 2024, 150, 04024004. [Google Scholar] [CrossRef]
- Yamany, M.S.; Abraham, D.M. Hybrid Approach to Incorporate Preventive Maintenance Effectiveness into Probabilistic Pavement Performance Models. J. Transp. Eng. Part B Pavements 2021, 147, 04020077. [Google Scholar] [CrossRef]
- Xiao, F.; Chen, X.; Cheng, J.; Yang, S.; Ma, Y. Establishment of probabilistic prediction models for pavement deterioration based on Bayesian neural network. Int. J. Pavement Eng. 2023, 24, 2076854. [Google Scholar] [CrossRef]
- Nicolosi, V.; Augeri, M.; D’Apuzzo, M.; Evangelisti, A.; Santilli, D. A Probabilistic Approach to the Evaluation of Seismic Resilience in Road Asset Management. Int. J. Disaster Risk Sci. 2022, 13, 114–124. [Google Scholar] [CrossRef]
- Alnaqbi, A.J.; Zeiada, W.; Al-Khateeb, G.; Abttan, A.; Abuzwidah, M. Predictive models for flexible pavement fatigue cracking based on machine learning. Transp. Eng. 2024, 16, 100243. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Gu, X.; Wang, D.; Dong, Q.; Cui, B. Intelligent Assessment of Pavement Structural Conditions: A Novel FeMViT Classification Network for GPR Images. IEEE Trans. Intell. Transp. Syst. 2024, 25, 13511–13523. [Google Scholar] [CrossRef]
- Duan, T.; Anand, A.; Ding, D.Y.; Thai, K.K.; Basu, S.; Ng, A.; Schuler, A. Ngboost: Natural gradient boosting for probabilistic prediction. In Proceedings of the International Conference on Machine Learning, Online, 13–18 July 2020; Curran Associates, Inc.: Red Hook, NY, USA, 2021; pp. 2690–2700. [Google Scholar]
- Chen, S.-Z.; Feng, D.-C.; Wang, W.-J.; Taciroglu, E. Probabilistic Machine-Learning Methods for Performance Prediction of Structure and Infrastructures through Natural Gradient Boosting. J. Struct. Eng. 2022, 148, 04022096. [Google Scholar] [CrossRef]
- Zhou, Z.; Cao, J.; Shi, X.; Zhang, W.; Huang, W. Probabilistic rutting model using NGBoost and SHAP: Incorporating other performance indicators. Constr. Build. Mater. 2024, 438, 137052. [Google Scholar] [CrossRef]
- Mei, Y.; Sun, Y.; Li, F.; Xu, X.; Zhang, A.; Shen, J. Probabilistic prediction model of steel to concrete bond failure under high temperature by machine learning. Eng. Fail. Anal. 2022, 142, 106786. [Google Scholar] [CrossRef]
- Chen, Y.; Khandelwal, M.; Onifade, M.; Zhou, J.; Ismail Lawal, A.; Oluwaseyi Bada, S.; Genc, B. Predicting the hardgrove grindability index using interpretable decision tree-based machine learning models. Fuel 2025, 384, 133953. [Google Scholar] [CrossRef]
- Shekhar, S.; Bansode, A.; Salim, A. A comparative study of hyper-parameter optimization tools. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Brisbane, Australia, 8–10 December 2021; pp. 1–6. [Google Scholar]
- Watanabe, S. Tree-structured parzen estimator: Understanding its algorithm components and their roles for better empirical performance. arXiv 2023, arXiv:2304.11127. [Google Scholar] [CrossRef]
- Li, M.; Dai, Q.; Su, P.; You, Z.; Ma, Y. Surface layer modulus prediction of asphalt pavement based on LTPP database and machine learning for Mechanical-Empirical rehabilitation design applications. Constr. Build. Mater. 2022, 344, 128303. [Google Scholar] [CrossRef]
- Cui, B.; Wang, H. Oxidative aging mechanism of asphalt binder using experiment-derived average molecular model and ReaxFF molecular dynamics simulation. Fuel 2023, 345, 128192. [Google Scholar] [CrossRef]
- Cui, B.; Wang, H. Compatibility analysis of waste polymer recycling in asphalt binder using molecular descriptor and graph neural network. Resour. Conserv. Recycl. 2025, 212, 107950. [Google Scholar] [CrossRef]
- Cui, B.; Wang, H. Molecular modeling of asphalt-aggregate debonding potential under moisture environment and interface defect. Appl. Surf. Sci. 2022, 606, 154858. [Google Scholar] [CrossRef]
- Labi, S. Introduction to Civil Engineering Systems: A Systems Perspective to the Development of Civil Engineering Facilities; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Gong, H.; Sun, Y.; Shu, X.; Huang, B. Use of random forests regression for predicting IRI of asphalt pavements. Constr. Build. Mater. 2018, 189, 890–897. [Google Scholar] [CrossRef]
- Sharma, A.; Sachdeva, S.N.; Aggarwal, P. Predicting IRI Using Machine Learning Techniques. Int. J. Pavement Res. Technol. 2023, 16, 128–137. [Google Scholar] [CrossRef]
- Zhang, T.; Smith, A.; Zhai, H.; Lu, Y. LSTM+MA: A Time-Series Model for Predicting Pavement IRI. Infrastructures 2025, 10, 10. [Google Scholar] [CrossRef]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of machine learning models using improved shapley additive explanation. Comput. Methods Programs Biomed. 2022, 214, 106584. [Google Scholar] [CrossRef]


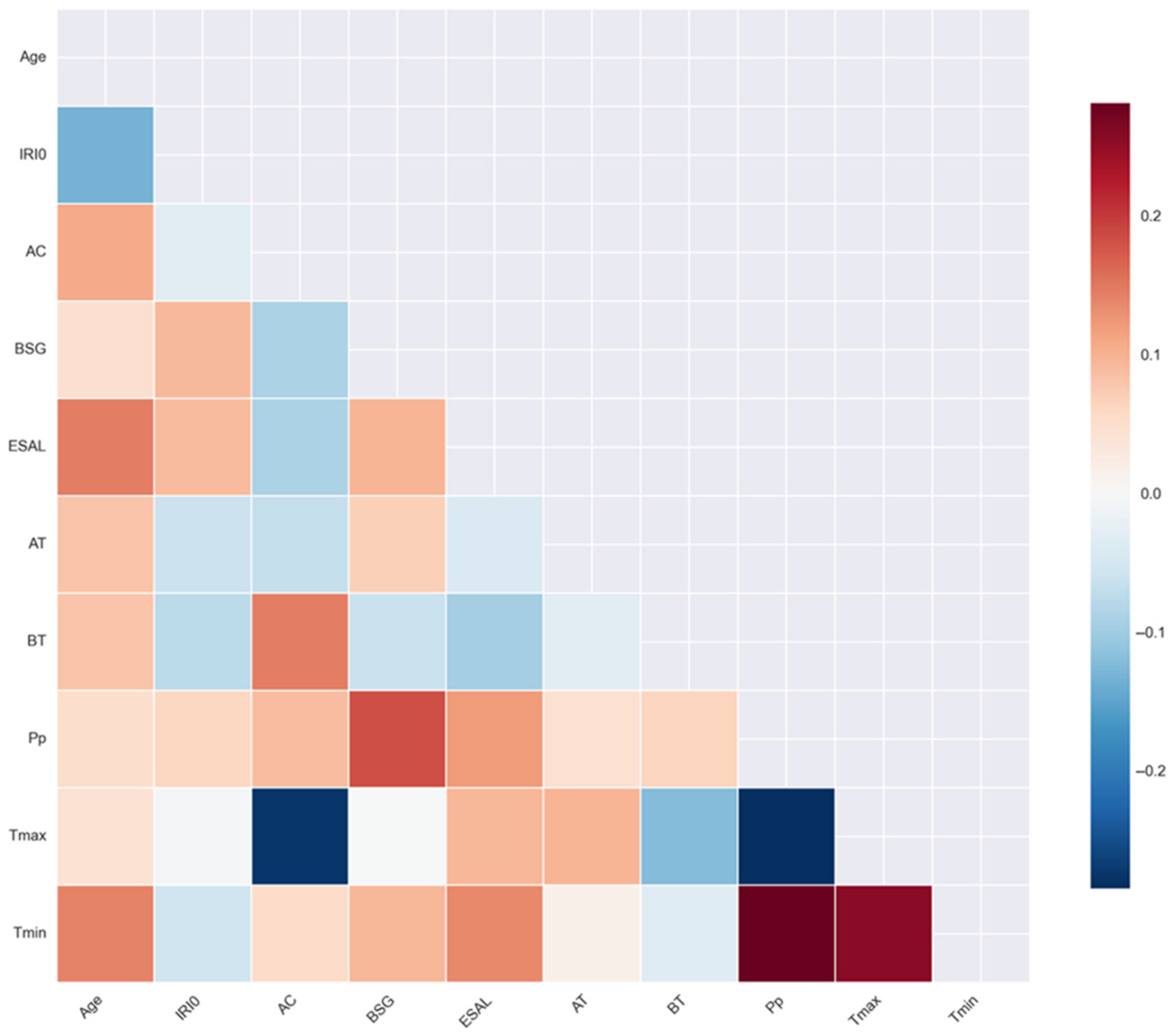
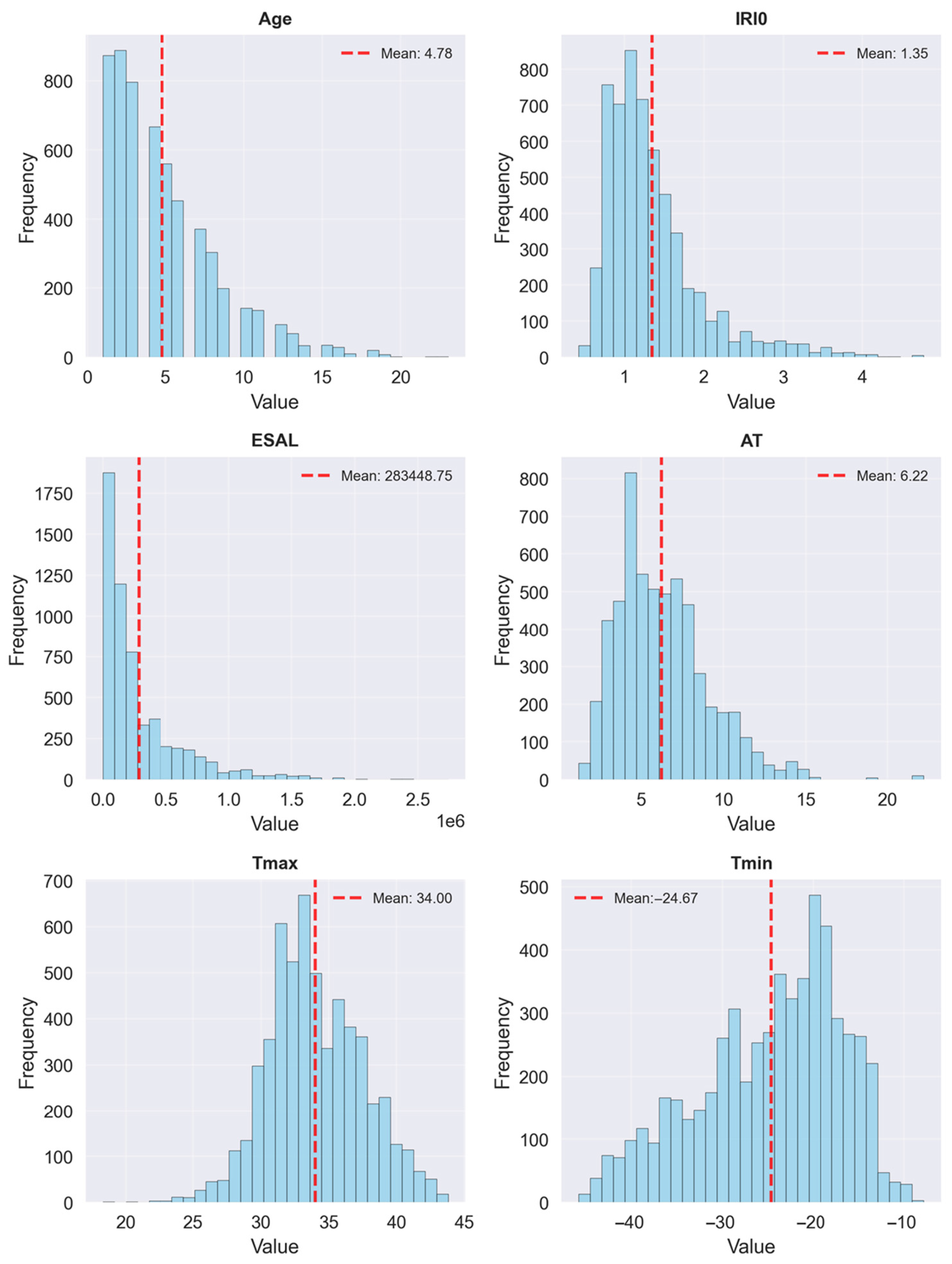
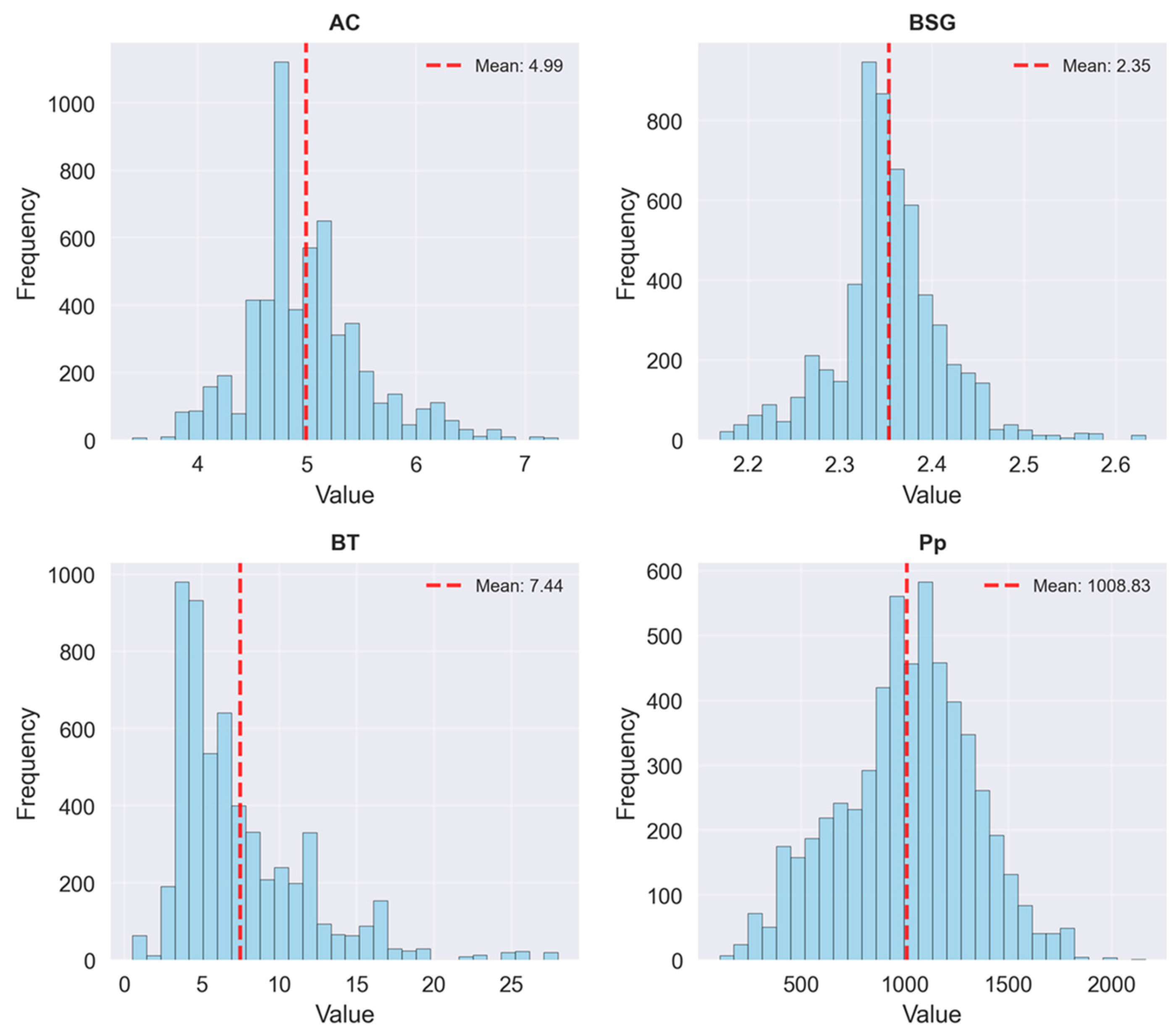

| Category | Label | Variables | Descriptions |
|---|---|---|---|
| Climate | Tmax | Maximum temperature (°C) | The maximum air temperature |
| Tmin | Minimum temperature (°C) | The minimum air temperature | |
| Pp | Precipitation (mm) | Annual water equivalent of total surface precipitation for each inspection year | |
| Structure | AT | Thickness of AC layer (inch) | Representative thickness for AC layer in a section |
| BT | Thickness of base layer (inch) | Representative thickness for unbound base layer in a section | |
| Material | AC | Average Asphalt Content (%) | Mean asphalt content (% by weight of total mixture) |
| BSG | Bulk specific gravity | Bulk specific gravity of the asphalt bound layer | |
| Traffic | ESAL | Annual generic equivalent single axle load | Estimated annual truck generic equivalent single axle load |
| Construction | IRI0 | Initial IRI (m/km) | Initial IRI after first installation |
| Age | Age (year) | Pavement age (year) | |
| Output | IRI | Measured IRI (m/km) | Measured IRI value at inspection year |
| Category | ML Model | R2test | RMSE | MAE |
|---|---|---|---|---|
| Deterministic model | ANN | 0.847 | 0.315 | 0.132 |
| Random Forest | 0.864 | 0.211 | 0.118 | |
| XGBoost | 0.870 | 0.207 | 0.116 | |
| Probabilistic model | BO-NGBoost | 0.897 | 0.184 | 0.107 |
| Study | Dataset | Model | Strengths and Limitations |
|---|---|---|---|
| This study |
| BO-NGBoost (R2test = 0.897) |
|
| Gong et al. [42] |
| Random forest (R2test = 0.974) |
|
| Choi and Do [14] |
| Recurrent neural network (R2test = 0.873) |
|
| Sharma, A. et al. [43] |
| Gradient boosting machine (R2test = 0.866) |
|
| Zhang et al. [44] |
| Long short-term memory (R2test = 0.965) |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Gu, X.; Wu, W. Deterioration Modeling of Pavement Performance in Cold Regions Using Probabilistic Machine Learning Method. Infrastructures 2025, 10, 212. https://doi.org/10.3390/infrastructures10080212
Liu Z, Gu X, Wu W. Deterioration Modeling of Pavement Performance in Cold Regions Using Probabilistic Machine Learning Method. Infrastructures. 2025; 10(8):212. https://doi.org/10.3390/infrastructures10080212
Chicago/Turabian StyleLiu, Zhen, Xingyu Gu, and Wenxiu Wu. 2025. "Deterioration Modeling of Pavement Performance in Cold Regions Using Probabilistic Machine Learning Method" Infrastructures 10, no. 8: 212. https://doi.org/10.3390/infrastructures10080212
APA StyleLiu, Z., Gu, X., & Wu, W. (2025). Deterioration Modeling of Pavement Performance in Cold Regions Using Probabilistic Machine Learning Method. Infrastructures, 10(8), 212. https://doi.org/10.3390/infrastructures10080212








