The Analysis of Axial Compression Performance of Reinforced Concrete Columns Strengthened with Prestressed Carbon Fiber Sheets

Abstract

Current research primarily focuses on using CFRP materials to strengthen small or medium-sized test specimens. To address this, our study employed ABAQUS software to analyze the axial compression behavior of large-scale reinforced concrete (RC) columns strengthened with prestressed carbon fiber reinforced polymer (CFRP) sheets. We conducted comparative analyses on key parameters: the prestress level applied to the CFRP, the width of CFRP strips, the spacing between strips, the confinement ratio, and the overall load–displacement curves of the columns. The results demonstrate that applying prestress significantly improves the efficiency of stress transfer in the CFRP sheet, effectively mitigating the stress lag phenomenon common in traditional CFRP strengthening, leading to a substantially enhanced strengthening effect. The CFRP wrapping method critically impacts performance: increasing the confinement ratio enhanced ultimate load capacity by 21.8–59.9%; reducing the strip spacing increased capacity by 21.8–50.4%; and widening the strips boosted capacity by 38.7–58%. Although full wrapping achieved the highest capacity increase (up to 73.2%), it also incurred significantly higher costs. To ensure the required strengthening effect while optimizing economic efficiency and CFRP material utilization, the strip wrapping technique is recommended. For designing optimal reinforcement, priority should be given to optimizing the confinement ratio first, followed by adjusting strip width and spacing. Proper optimization of these parameters significantly enhances the strengthened member’s ultimate load capacity, ductility, and energy dissipation capacity. This study enriches the theoretical foundation for prestressed CFRP strengthening and provides an essential basis for rationally selecting prestress levels and layout parameters in engineering practice, thereby aiding the efficient design of strengthening projects for structures like bridges, with significant engineering and scientific value.

1. Introduction

Over time, the structural load-bearing capacity and expected service life of bridges may gradually decrease due to multiple factors. These factors include long-term lack of maintenance, design deficiencies, poor construction quality, and natural environmental degradation [1]. Since demolishing old bridges involves a substantial workload and potential safety hazards, structural strengthening becomes a preferred solution. Common bridge strengthening methods include section enlargement, externally bonded Fiber Reinforced Polymer (FRP) composites, bonded steel plates, and external prestressing [2,3]. Based on material properties, FRP is primarily categorized into three types: Carbon FRP (CFRP), Glass FRP (GFRP), and Aramid FRP (AFRP). Among these, CFRP offers a high strength-to-weight ratio, excellent corrosion resistance, superior durability, and exceptional tensile strength. These properties allow CFRP to significantly enhance structural flexural/shear capacity and energy dissipation without increasing self-weight. Furthermore, CFRP features simple construction procedures, shorter project timelines, and high efficiency, leading to its growing adoption in concrete structure reinforcement. Consequently, CFRP is increasingly becoming a material of choice in strengthening design for concrete structures [4,5,6].

However, during the initial loading stage, conventional CFRP sheet strengthening exhibits stress lag, requiring the constrained concrete to reach a certain strain level before becoming fully effective [7,8]. Prestressed CFRP sheet strengthening technology overcomes this by applying prestress to the CFRP sheet in advance. This imposes active confinement on the core concrete, thereby enhancing the column’s ultimate load capacity, deformation capability, and ductility. This technique offers significant advantages: substantial material savings and reduced strengthening costs; significantly reduced structural deformation; increased structural stiffness alongside enhanced load-bearing capacity; and the suppression of crack initiation and propagation, improving member ultimate strength [9,10,11,12].

Research by Cheng Donghui et al. [13] demonstrated that preloaded concrete columns strengthened with prestressed CFRP sheets exhibited a significantly increased yield load upon reloading, with the increase proportional to the prestress level. Zhou et al. [14] experimentally analyzed the axial compression behavior of large circular concrete columns confined by transversely applied prestressed CFRP strips. They studied the effects of varying prestress levels, strip spacing, and strengthening configurations. Their results confirmed that prestressed CFRP strips effectively confine the core concrete, significantly delay stirrup strain development, and enhance both the strength and ductility of circular columns. Deng et al. [15] found that strengthening reinforced concrete (RC) box beams (both existing and new) using prestressed CFRP plates effectively increased flexural capacity, cracking resistance, and structural stiffness, though this improvement came at the expense of the beam’s ductility. Kim et al. [16] showed that prestressed CFRP sheets effectively increased the cracking strength, ultimate strength, and yield strength of beams, redistributed stresses within the beam, and reduced localized damage.

Additionally, due to limitations in testing equipment load capacity, most current research focuses on strengthening small and medium-sized specimens using CFRP materials [17,18,19]. While significant progress has been made in strengthening smaller-scale components, studies on large-scale specimens remain relatively scarce. In practical engineering, large-scale structural members are far more common, and their mechanical behavior and failure modes are notably more complex. Therefore, research on strengthening large-scale reinforced concrete structures holds significant practical importance. To address this gap, this study applies prestressed CFRP sheet strengthening technology to large-scale reinforced concrete (RC) columns with a side length of 600 mm. It systematically investigates the effects of varying CFRP sheet width, spacing, and confinement ratio on the axial compressive mechanical performance of the strengthened large-scale RC columns.

2. Material Properties and Model Verification

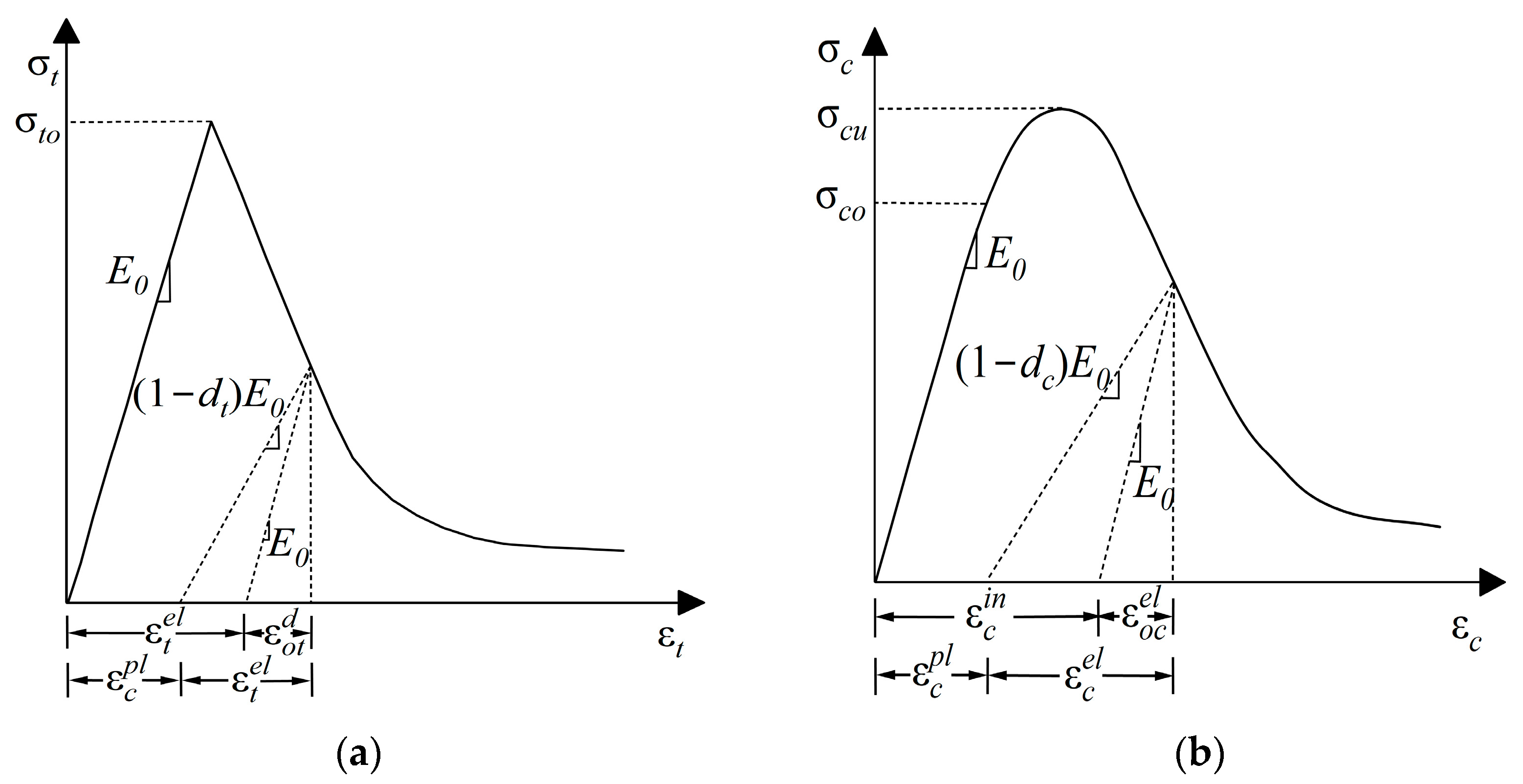
2.1. Constitutive Model of RC Columns

Concrete structures are susceptible to damage and experience stiffness degradation under repeated loading. In ABAQUS, the concrete damage plasticity model (shown in Figure 1) was adopted. This model incorporates compressive and tensile damage factors to accurately simulate the nonlinear behavior of concrete [20]. Based on the energy equivalence principle [21], these damage factors are calculated according to the following equation(s):

$$d=1-\sqrt{\sigma /E_0\epsilon }$$

(1)

In the formula, $d$ is the damage factor, $\sigma$ denotes stress, $\epsilon$ denotes strain, and E represents the elastic modulus of concrete. The constitutive relationships for concrete under both compression and tension were defined according to the Code for Design of Concrete Structures (GB 50010-2010) [22] to more realistically simulate the concrete damage and failure process under stress. Compared to concrete, reinforcing steel exhibits more stable mechanical properties. Within the ABAQUS model, it was treated as an idealized elastic–plastic material. This study employed a bilinear constitutive model for the steel reinforcement to accurately represent its mechanical behavior in both the elastic and plastic stages. The corresponding stress–strain relationship curve is illustrated in Figure 2.

2.2. Constitutive Model of CFRP

In the finite element analysis, the CFRP sheet was treated as an anisotropic, ideal linear elastic material. Its characteristic stress–strain relationship is depicted in Figure 3. To model the anisotropic damage initiation and progressive failure behavior of the CFRP sheet, this study implemented the Hashin damage criterion. This was achieved by degrading relevant components within the material’s stiffness matrix. The specific parameters for the Hashin damage model calibration are provided in

Table 1. Hashin damage parameters.

${\mathit{X}}_{\mathbf{T}}$/MPa	${\mathit{X}}_{\mathbf{C}}$/MPa	${\mathit{Y}}_{\mathbf{T}}$/MPa	${\mathit{Y}}_{\mathbf{C}}$/MPa	${\mathit{S}}_{\mathbf{L}}$/MPa	${\mathit{S}}_{\mathbf{T}}$/MPa
3461	89	185	42	120	135

Note: $X_{\mathrm{T}}$, $X_{\mathrm{C}}$, $Y_{\mathrm{T}}$, $Y_{\mathrm{C}}$, $S_{\mathrm{L}}$, and $S_{\mathrm{T}}$ represent the longitudinal tensile strength, longitudinal compressive strength, transverse tensile strength, transverse compressive strength, longitudinal shear strength, and transverse shear strength, respectively.

. The CFRP’s orthotropic material properties were defined using a layered shell/solid element formulation. The corresponding material properties defining CFRP’s elastic behavior, strength limits, and damage evolution are comprehensively listed in

Table 2. Material properties of CFRP.

${\mathit{E}}_1$/MPa	${\mathit{E}}_2$/MPa	${\mathit{N}}_{\mathbf{u}12}$/MPa	${\mathit{G}}_{12}$/MPa	${\mathit{G}}_{13}$/MPa	${\mathit{G}}_{23}$/MPa
241,000	1000	0.28	4500	4500	3600

Note: $E_1$, $E_2$ represent the elastic moduli along the longitudinal (fiber) direction and transverse direction, respectively. $N_{\mathrm{u}12}$ is the Poisson’s ratio for strain in the transverse direction (2) caused by stress in the longitudinal direction (1). $G_{12}$, $G_{13}$, and $G_{23}$ denote the shear moduli for the 1–2 plane (longitudinal–transverse), 1–3 plane (longitudinal through thickness), and 2–3 plane (transverse through thickness), respectively.

. This methodology enables the explicit simulation of CFRP’s damage initiation and ultimate failure within the numerical framework.

2.3. Model Element Selection and Meshing

Within the ABAQUS finite element analysis software, the concrete, steel reinforcement, and CFRP sheet components were modeled using distinct element types: concrete was simulated with eight-node reduced-integration linear hexahedral elements (C3D8R), steel reinforcement with two-node linear 3D truss elements (T3D2), and the CFRP sheet with four-node reduced-integration general-purpose shell elements (S4R). A structured meshing strategy was applied to the numerical model. Following iterative mesh sensitivity studies, a global element size of 60 mm was identified as optimal, balancing computational accuracy and efficiency. At this mesh size, deviations in the calculated ultimate load capacity were limited to 2.16–3.33% compared to finer (50 mm) and coarser (70 mm) meshes, while computational efficiency remained significantly higher. This configuration ensured robust solution convergence and result reliability. The meshing details for all components are illustrated in Figure 4.

2.4. Contact Relationships and Boundary Conditions

The contact conditions between distinct components critically influence computational efficiency, solution convergence, and result accuracy, necessitating precise interfacial definitions. To ensure synergistic behavior between the CFRP sheet and concrete, a tie constraint was implemented, effectively integrating both materials into a monolithic system; this approach reflects the minimal interfacial slip observed in practical engineering due to robust CFRP–concrete bonding. Reinforcement cages were embedded within the concrete matrix using the Embedded Region constraint, accurately simulating reinforced concrete’s composite mechanics while enhancing model reliability and computational precision. Within ABAQUS, reference points RP₁ (top) and RP₂ (bottom) were established for the RC column. Kinematic coupling constraints were then applied: the top surface coupled to RP₁ with all degrees of freedom fixed except Z-translation (loading direction) and the bottom surface fully constrained at RP₂. Axial load was subsequently applied to RP₁. This methodology streamlines the model, optimizes convergence efficiency, and faithfully replicates experimental loading protocols.

2.5. Finite Element Model Validation

Prior to analyzing the mechanical behavior of composite structures using finite element theory, validation against experimental data is essential to verify the accuracy of the simulation methodology. This study adopted specimens S1L1H2C and S2L2H2C from Ref. [23] as benchmark cases, comparing their experimental results with ABAQUS predictions. The material properties used in the model are specified in

Table 3. Material parameters of the finite element model.

Specimen Number	Sectional Dimension/mm	Height/mm	Thickness of the Protective Layer/mm	Longitudinal Reinforcement	Stirrup Spacing	Number of Plies CFRP	Chamfer Radius/mm
S1L1H2C	200 × 200	600	15	8C8	A6@133	1	32
S2L2H2C	400 × 400	1200	30	8C16	A8@118	2	64
S3L3H1C	600 × 600	1800	45	8C25	A10@123	3	96

,

Table 4. Material parameters of CFRP.

Species	Standard Value of Tensile Strength/MPa	Thickness of CFRP/mm	Elasticity Modulus/MPa
CFRP	3461	0.167	2.41 × 105

and

Table 5. Material parameters of reinforcing steel.

Bar Diameter/mm	Steel Bar Grade	Yield Strength/MPa	Ultimate Strength/MPa
6	HPB300	381	536
8	HPB300	386	452

, while other parameters were adopted directly from the test data in Ref. [24]. As shown in Figure 5, the load–displacement curves for both specimens demonstrate close agreement between numerical simulations and physical experiments. The maximum load discrepancy was limited to 1.13%, confirming the validity of the finite element modeling approach.

3. Parameter Analysis

3.1. Parameter Determination

Building upon the material parameters of the large-scale specimen S3L3H1C defined in Section 2.5, eighteen finite element specimen variants were designed for parametric analysis. To systematically investigate the influence of CFRP strip width and spacing on strengthening effectiveness, the confinement ratio was adopted as the primary evaluation metric, defined as:

$${\rho }_{\mathfrak{c}}={\displaystyle \frac{W}{W+T}}$$

(2)

In the equation, $W$ represents the width of the CFRP strips and s denotes the spacing between CFRP strips. To quantitatively evaluate the enhancement of CFRP confinement on the axial compression performance of concrete columns, three prestress levels were investigated: 0.1, 0.2, and 0.25, where a prestress level of 0.1 indicates the CFRP prestress equals 10% of its ultimate tensile strength. The specimen matrix detailed in

Table 6. Specimen design parameters.

Specimen Number	Width of CFRP/mm	Gap of CFRP/mm	Constraint Ratio	Prestressed Degree	Number of Plies CFRP
DBZ1	0	0	0	0	0
DBZ2	whole package	0	1	0	3
W1800-T0-0.1	whole package	0	1	0.1	3
W1800-T0-0.2	whole package	0	1	0.2	3
W1800-T0-0.25	whole package	0	1	0.25	3
W100-T250-0.2	100	250	0.29	0.2	3
W100-T200-0.2	100	200	0.33	0.2	3
W100-T150-0.2	100	150	0.4	0.2	3
W100-T100-0.2	100	100	0.5	0.2	3
W150-T100-0.2	150	100	0.6	0.2	3
W100-T60-0.2	100	60	0.63	0.2	3
W260-T100-0.2	260	100	0.72	0.2	3
W350-T100-0.2	350	100	0.78	0.2	3
W45-T45-0.2	45	45	0.5	0.2	3
W90-T90-0.2	90	90	0.5	0.2	3
W120-T120-0.2	120	120	0.5	0.2	3
W150-T150-0.2	150	150	0.5	0.2	3
W180-T180-0.2	180	180	0.5	0.2	3

follows a systematic naming convention: $W$ indicates CFRP strip width (mm), T represents spacing between strips (mm), and the numerical suffix denotes the prestress level. For instance, specimen W100-T150-0.2 corresponds to a CFRP width of 100 mm, spacing of 150 mm, and prestress level of 0.2, while DBZ1 designates the unstrengthened Control Specimen 1 serving as the baseline for comparative analysis.

3.2. Prestress Application and Temperature Drop Value Correction

This study implemented the thermal prestressing method [9,24] to apply prestress to the CFRP sheets. Within ABAQUS, a predefined temperature field was assigned to the CFRP as an initial condition. Subsequently, a controlled temperature reduction was applied, inducing thermal contraction in the CFRP elements to simulate prestress. The governing equation for this method is:

$$\Delta T={\displaystyle \frac{\sigma }{E\alpha }}$$

(3)

In the equation, ΔT represents the applied temperature reduction (°C), σ denotes the target prestress level (MPa), E is the elastic modulus of the CFRP sheet (GPa), and α signifies its coefficient of thermal expansion (CTE), taken as 7 × 10⁻⁶/°C. Direct application of the theoretical ΔT value derived from this formula often fails to achieve the intended prestress level. This discrepancy arises because the equation assumes ideally fixed-end constraints, whereas real-world specimen boundaries introduce unintended compliance, leading to prestress losses that compromise the targeted reinforcement effect.

To effectively solve the problem of prestress loss, this paper corrects the cooling method theory as follows: (1) Calculate the required theoretical temperature drop value P₁ based on the target prestress value and the theoretical formula of the cooling method; (2) input this value into the predefined field of ABAQUS and calculate the actual applied prestress value P₂; (3) since there is a difference between the target and actual prestress values, the target prestress value $c$ is divided by the actual prestress value to obtain the corresponding correction coefficient; (4) the correction coefficient is multiplied by the temperature drop value T₁ in the first step to obtain the corrected temperature drop value, and the calculation in the second step is repeated. Finally, the error between the two is reduced, and the target prestress is applied. The complete iterative correction procedure is illustrated in the flowchart shown in Figure 6.

The prestress application processes and correction outcomes for CFRP sheets under varying prestress levels are comprehensively summarized in

Table 7. Applying prestress using the temperature method.

Prestressed Degree	Target Prestress/MPa	Theoretical Temperature Drop Value/°C	Actual Prestressed Value P2/MPa	Prestress Difference ∆P1/MPa	Error Before Correction/%	Correction Factor c	The Corrected Temperature Drop Value/°C	Modified Prestress/MPa	The Corrected Prestress Difference/MPa	Corrected Error/%
0.1	346.1	−2051.6	322.4	23.7	6.8	1.07	−2109.5	345.9	0.2	0.05
0.2	692.2	−4103.1	644.8	47.4	6.8	1.07	−4326.9	692.0	0.2	0.02
0.25	865.3	−5129.2	804.1	61.2	7.1	1.08	−5484.4	863.2	2.1	0.24
0.3	1038.3	−6154.7	968.2	70.1	6.8	1.07	−6585.5	1036.9	1.45	0.14
0.4	1384.4	−8206.3	1290.2	94.2	6.8	1.07	−8780.7	1384.2	0.2	0.01

. Prior to correction, the discrepancy between target and achieved prestress ranged from 6.8% to 7.1%. After implementing the correction coefficient c, errors were drastically reduced to 0.01–0.24%. This optimization significantly mitigates prestress losses inherent in conventional thermal methods, achieving unprecedented precision in prestress activation. Representative post-correction prestress distributions across select specimens are illustrated in Figure 7, demonstrating uniform stress transfer efficacy.

4. Factors Affecting CFRP Sheet Reinforcement Effect

4.1. Effect of Initial Prestress on CFRP Sheets

Table 8. Simulated values of specimen ultimate bearing capacity.

Specimen No.	Yield Load/103 KN	Yield Load Increase Range/%	Ultimate Load/103 KN	Limit Load Increase Range/%
DBZ1	8.9	/	11.9	/
DBZ2	9.8	10.1	14.4	21.0
W1800-T0-0.1	12.8	43.8	17.3	45.4
W1800-T0-0.2	16.1	80.9	20.6	73.1
W1800-T0-0.25	16.8	88.8	22.6	89.9
W100-T250-0.2	11.2	25.8	14.5	21.8
W100-T200-0.2	11.3	27.0	14.9	25.2
W100-T150-0.2	12.3	38.2	15.6	31.1
W100-T100-0.2	13.3	49.4	16.5	38.7
W150-T100-0.2	13.4	50.6	17.4	46.2
W100-T60-0.2	14.5	62.9	17.9	50.4
W260-T100-0.2	14.3	60.7	18.2	52.9
W350-T100-0.2	14.5	62.9	18.8	58.0
W45-T45-0.2	13.2	48.3	17.1	43.7
W90-T90-0.2	11.6	30.3	16.7	40.3
W120-T120-0.2	13.1	47.2	16.5	38.7
W150-T150-0.2	12.2	37.1	16.4	37.8
W180-T180-0.2	12.5	40.4	16.1	35.3

summarizes the ultimate bearing capacities of each specimen and the corresponding improvement compared to the unreinforced specimen DBZ1. As shown in Table 8, the simulated values of specimen ultimate bearing capacity, the application of initial prestress to the CFRP sheets resulted in an increase in ultimate bearing capacity ranging from 21% to 89.9%. This indicates that prestressed CFRP sheets can significantly enhance the load-bearing capacity of large-scale reinforced concrete columns. The strengthening effect is also influenced by factors such as the level of prestress applied, the wrapping spacing, and the width of the CFRP sheets. It should be noted that although the results show that prestressing can improve the ultimate capacity by up to 89.9%, further increases in prestress level may lead to a reduction in the enhancement effect. When the prestress ratio exceeds 0.25, there is also a risk of debonding between the CFRP and the concrete interface [9]. Therefore, in practical engineering applications, it is necessary to balance safety and cost-effectiveness when selecting an appropriate level of prestress.

Figure 8a,b present the load–displacement curves for different prestressing levels and load–strain curves of CFRP sheets. Figure 8a,b present the load–displacement curves and CFRP load–strain curves under different prestress levels, respectively. From Figure 8a, it can be seen that at the beginning of loading, the load-displacement curve shows a linear variation. As the load increases, the unreinforced specimen DBZ1 is the first to show a turning point, with a reduced slope in the ascending segment and increased displacement. In contrast, the strengthened columns exhibit less damage under the same load. For the non-prestressed specimen DBZ2, the initial resistance primarily comes from the concrete and steel reinforcement. As the load continues to increase, cracks develop progressively, lateral strain increases, and the strain in the CFRP sheets rises rapidly, allowing the CFRP to effectively confine the cracked and damaged concrete, thereby enhancing the load-carrying capacity of the structure. However, due to the delayed activation of the CFRP, a certain degree of stress lag occurs, resulting in only a 21% improvement in ultimate load, indicating a relatively limited strengthening effect.

Figure 8b shows the load–displacement curves for different prestressing levels and the load–strain curves of CFRP sheets. Taking specimen W1800-T0-0.25 as an example, its initial strain was 2.08 × 10⁻³, and at the ultimate load, the CFRP strain reached 13.5 × 10⁻³, while the strain in DBZ2 was only 8.23 × 10⁻³. This demonstrates that in prestressed specimens, the CFRP participates in load resistance earlier due to the applied prestress, converting passive confinement into active confinement, and placing the concrete under a triaxial compressive stress state. Under such conditions, both the concrete and CFRP contribute to the load resistance, effectively suppressing the development of lateral cracks, increasing the ultimate compressive strain, and enhancing both the stability and the ultimate load-bearing capacity of the specimen.

4.2. Influence of Width and Space of Prestressed CFRP Sheets

The load–displacement curves and load–concrete strain curves of the specimens are shown in Figure 8. As illustrated in Figure 9a, during the initial loading stage, the ascending slopes of the load–displacement curves are nearly identical. For specimens with a CFRP width of 100 mm, the ultimate bearing capacity decreases as the spacing between CFRP strips increases. Additionally, the descending slope becomes steeper, indicating that the specimens fail more abruptly after reaching their peak load. This phenomenon can be attributed to the weakened lateral confinement of the core concrete as the CFRP spacing increases, which reduces the overall load-bearing capacity. When the spacing is large, the CFRP sheets are less effective in restraining the deformation of concrete. As a result, stress concentrates in the unconfined zones, accelerating crack propagation and ultimately leading to structural failure and reduced capacity.

Figure 9b shows that, with the same CFRP spacing, the ascending slopes remain consistent; however, as the CFRP width increases, the confined area of the concrete expands. Wider CFRP sheets provide more effective lateral restraint over a larger region, limiting the formation and propagation of cracks, reducing unconfined zones, and slowing crack development. This leads to an increase in structural bearing capacity.

Figure 9c compares the load–strain curves of confined and unconfined concrete for selected specimens. Taking specimen W100-T60 as an example, at peak load, the ultimate compressive strain of the unconfined concrete is 1.58 × 10⁻³, while that of the confined concrete reaches 2.67 × 10⁻³. These results indicate that prestressed CFRP sheet reinforcement effectively enhances the deformation capacity of the structure, improving both the energy dissipation and ductility of the specimens.

4.3. Influence of Constraint Ratio of Prestressed CFRP Sheets

In summary, both the width and spacing of CFRP sheets significantly influence their strengthening effectiveness. To more accurately reflect these effects, this study introduces the concept of the confinement ratio of CFRP sheets. The load–displacement and load–concrete strain curves under different confinement ratios are shown in Figure 10, load–displacement curves for varying prestressed CFRP confinement ratios. As illustrated in Figure 10a, the ultimate bearing capacity of the specimens increases with the confinement ratio. Among the tested specimens, W1800-T0-0.2 exhibited the best strengthening performance, followed by W350-T100-0.2, while W100-T250-0.2 showed the least improvement. This is because continuous CFRP wrapping provides the most effective lateral confinement for the core concrete, enhancing both energy dissipation capacity and ultimate strength. In contrast, when CFRP strips are used, the unconfined regions experience increased lateral strain as the load rises, leading to localized cracking and rapid damage progression, ultimately reducing load capacity. Regardless of the wrapping type, the descending slopes of the curves tend to flatten, indicating improved ductility.

Figure 10c further shows that with an increasing confinement ratio, the load–strain curves of confined concrete become smoother and more gradual in the failure stage, suggesting enhanced energy dissipation and improved structural stability under extreme loading conditions.

Figure 10b reveals that at the same confinement ratio, the ultimate bearing capacity of specimen W45-T45-0.2 is only 6.2% higher than that of W180-T180-0.2. Their load–displacement curves display similar ascending slopes and relatively gentle descending segments, indicating comparable strengthening performance. As the CFRP width and spacing increase, the confinement of the core concrete improves, while unconfined areas are more prone to cracking and deformation, resulting in performance differences. According to Table 7, the ultimate load of specimen W1800-T0-0.2 is 20.6 × 10³ kN, while that of W350-T100-0.2 is 18.8 × 10³ kN—only an 8.7% difference. These results suggest that when strip wrapping can satisfy structural performance and strengthening requirements, it is preferable due to cost-efficiency and ease of construction.

Although specimens W180-T180-0.2 and W45-T45-0.2 share the same confinement ratio, their strengthening effects differ significantly. This is mainly attributed to the non-uniform confinement caused by larger CFRP width and spacing, which compromises the effectiveness of CFRP. In addition, the larger unconfined concrete regions are more susceptible to stress concentrations, which can lead to localized failure and premature structural collapse.

5. Conclusions

• In finite element analysis, the temperature reduction method can effectively simulate the application of prestress in structures. However, partial prestress loss may occur during the application process. By employing iterative calculations of a correction factor, the prestress loss can be minimized to achieve the target prestress level.
• Prestressed CFRP sheets can effectively strengthen large-scale reinforced concrete (RC) columns by improving the bonding performance with the structure, enhancing overall stiffness, reducing deformation, and increasing load-bearing capacity. As the initial prestress level increases, the ultimate bearing capacity of the structure also improves, with a maximum increase of up to 89.9%. In addition, prestressing helps mitigate the stress lag issue of CFRP sheets, enabling them to engage earlier during loading and enhancing both the stability and capacity of structural members.
• The wrapping method of CFRP sheets significantly affects the strengthening performance. At the same width and a prestress level of 0.2, reducing the wrapping spacing increases the ultimate bearing capacity by 21.8% to 50.4%. With constant spacing, increasing the width results in an enhancement of 38.7% to 58%. Full wrapping using continuous CFRP sheets can achieve up to a 73.2% increase in ultimate load capacity, although it involves significantly higher material consumption and cost.
• When the CFRP confinement ratio varies, the ultimate bearing capacity of specimens increases with higher confinement ratios, with an improvement range of 21.8% to 59.9%. Under the same confinement ratio, increasing both width and spacing leads to a reduction in capacity improvement from 44.5% to 35.3%. This indicates that the CFRP confinement ratio should be considered as a primary factor in selecting a strengthening scheme, with spacing and width optimized accordingly to determine the most effective and efficient design.
• This study recommends that future work should focus on experimental validation of the numerical results and investigate the long-term durability of prestressed CFRP-strengthened large-scale reinforced concrete structures to further advance the practical application of this technology in engineering.