Multi-Model Intelligent Prediction of Rock Integrity in Tunnels Based on Geological Differences of Ground-Penetrating Radar Exploration Workfaces
Abstract
1. Introduction
2. Characteristics Analysis
2.1. Rock Integrity Characteristics and Fractured Rock Structure
2.2. The Interpretation Mechanism of GPR
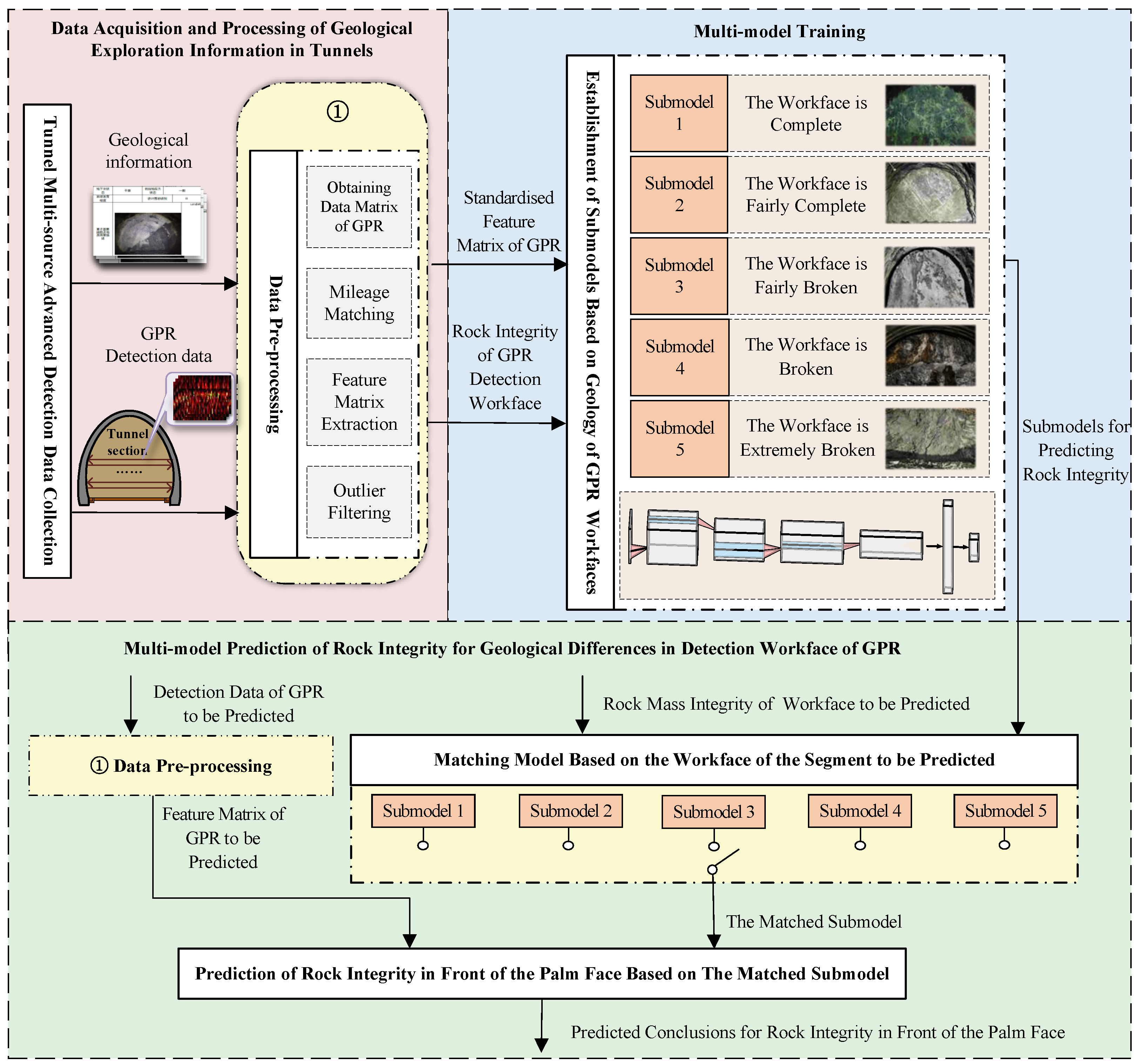
3. Methodology
3.1. Data Pre-Processing
3.1.1. Obtaining Relative Amplitude Matrix of GPR
3.1.2. Mileage Matching and Feature Matrix Extraction
3.1.3. Outlier Filtering
3.2. Multi-Model Training and Prediction
3.2.1. Data Analysis and Segmentation
3.2.2. Multi-Model Training
4. Experimental Results and Discussions
4.1. Dataset Preparation
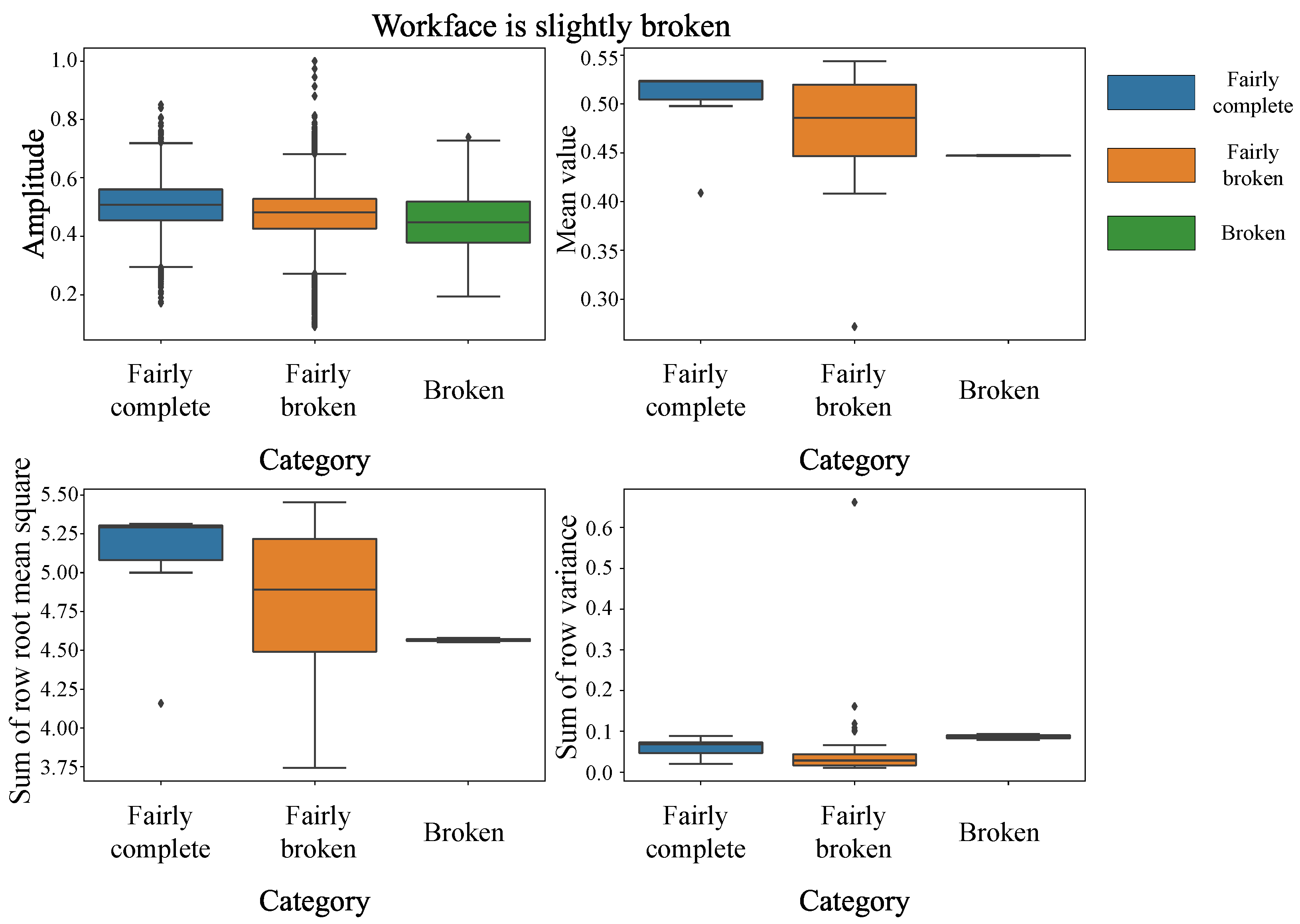
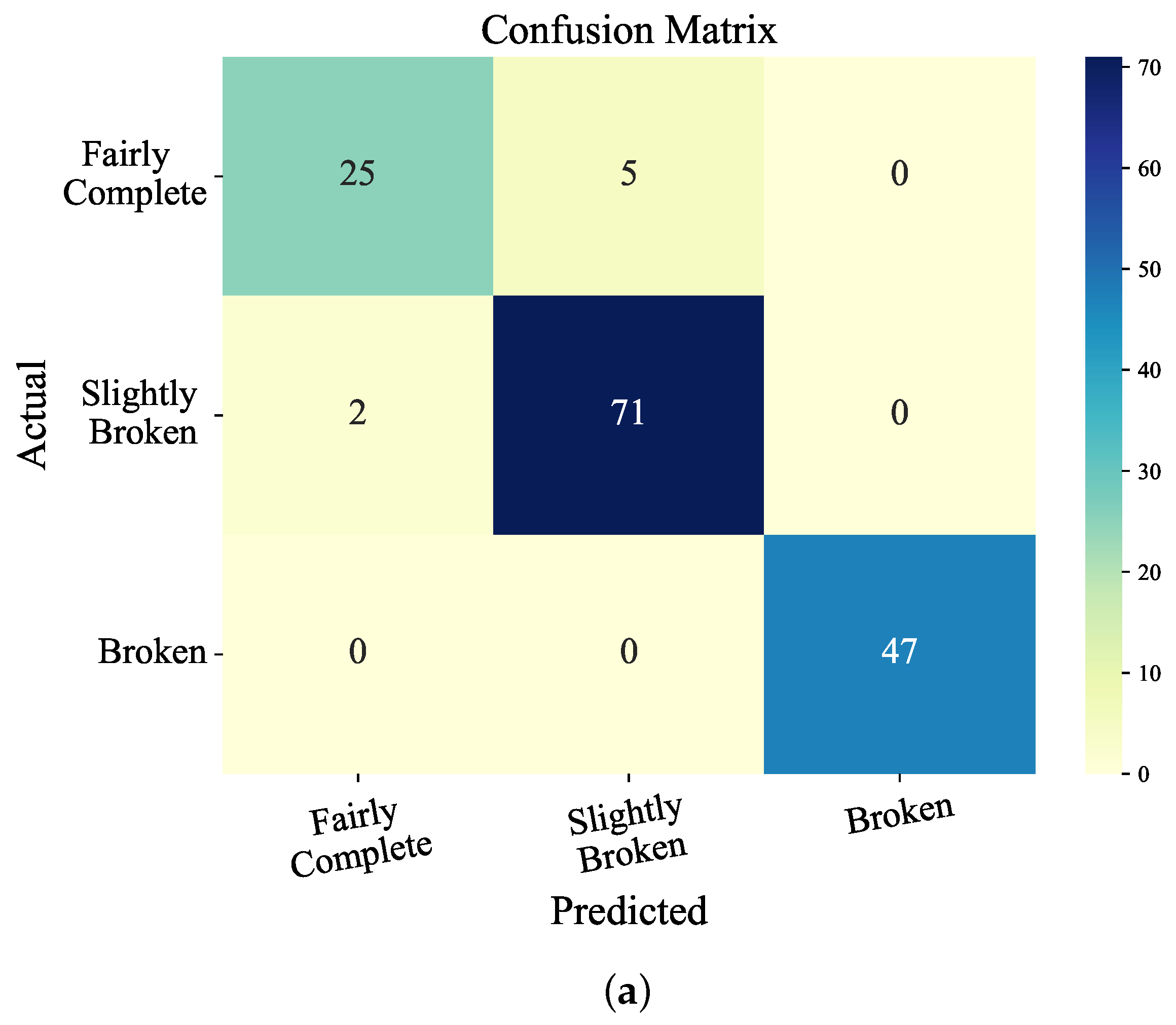
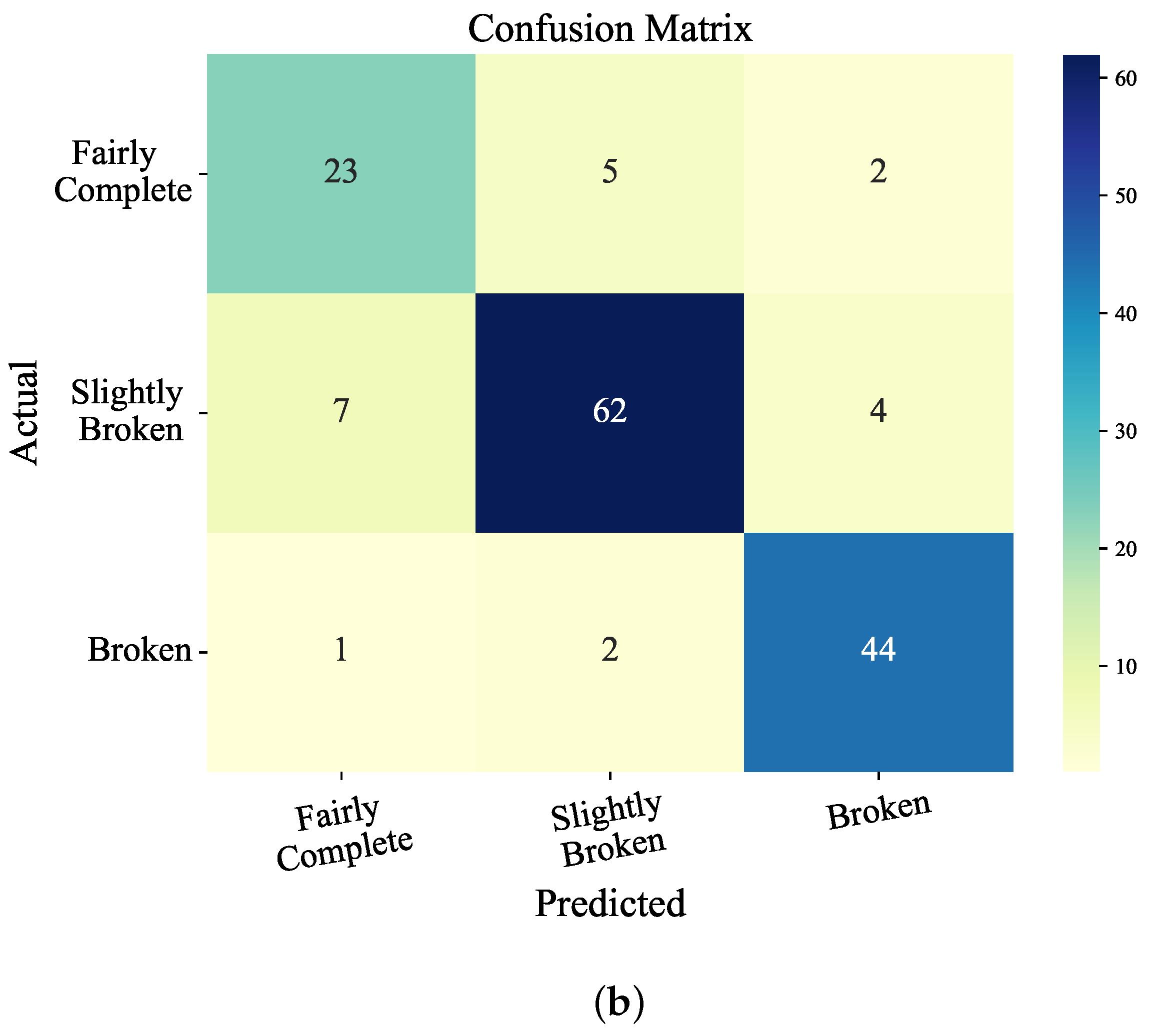
4.2. Results and Analysis
4.3. Discussions
5. Conclusions
- It proposes a method for extracting structured feature matrices from unstructured GPR detection data, addressing the challenge of converting raw radar data into analyzable formats for intelligent prediction.
- It introduces an index to measure amplitude anomaly fluctuations, namely, the sum of row variances, which provides a quantitative basis for identifying abnormal data in GPR signals.
- It considers the geological differences of GPR exploration workfaces to establish multi-models for predicting rock integrity, improving the adaptability of the prediction method to complex and variable tunnel geological conditions.
- It validates the effectiveness of the proposed method through testing in ten real tunnels and comparison with two alternative methods. The method achieved an accuracy of 95.33% in the constructed dataset, with precision rates above 90% for the prediction of fairly complete, slightly broken, and broken rock categories, demonstrating its practical application value.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, D.; Sun, Z.; Fang, Q. Scientific problems and research proposals for Sichuan–Tibet railway tunnel construction. Undergr. Space 2022, 7, 419–439. [Google Scholar] [CrossRef]
- Abbas, N.; Li, K.G.; Fissha, Y.; Lei, W.; Emad, M.Z.; Chandrahas, N.S.; Khatti, J.; Taiwo, B.O.; Sazid, M.; Gebrehiwot, Z.; et al. Stress-deformation and stability challenges in Himalayan tunnels: Impact of geological discontinuities. Discov. Mater. 2024, 4, 72. [Google Scholar] [CrossRef]
- Sazid, M.; Ahmed, H.A. Stability analysis of shallow depth tunnel in weak rock mass: 3D numerical modeling approach. J. City Dev. 2019, 1, 18–22. Available online: https://pubs.sciepub.com/jcd/1/1/3 (accessed on 10 August 2025).
- Duan, S.; Xu, X. Discussion of problems in calculation and application of rock mass integrity coefficient. J. Eng. Geol. 2013, 21, 548–553. [Google Scholar]
- Dong, F.; Wang, S.; Yang, Y.; Ren, M.; Demisa, M.; Zhang, R. Research on dynamic fuzzy prediction method for surrounding rock stability of mountain tunnels throughout the construction period. Tunn. Undergr. Space Technol. 2025, 158, 106390. [Google Scholar] [CrossRef]
- Zaki, N.F.M.; Ismail, M.A.M.; Abidin, M.H.Z. Geological prediction ahead of tunnel face in the limestone formation tunnel using multi-modal geophysical surveys. J. Phys. Conf. Ser. 2018, 995, 12114. [Google Scholar] [CrossRef]
- Yue, Y.P.; Liu, H.; Lin, C.D.; Meng, X.; Liu, C.; Zhang, X.; Cui, J.; Du, Y. Automatic recognition of defects behind railway tunnel linings in GPR images using transfer learning. Measurement 2024, 224, 113903. [Google Scholar] [CrossRef]
- Li, C.; Wang, H.C.; Wang, Y.S.; Wang, L.L.; Yang, X.; Wan, X.R. Recognition of tunnel fracture zones in seismic waves and ground-penetrating radar data. Appl. Sci. 2024, 14, 1282. [Google Scholar] [CrossRef]
- Qin, Z.; Wu, H.B.; Zhang, E.Z. Application of ground penetrating radar in urban transportation construction. West China Explor. Eng. 2018, 30, 95–98+103. [Google Scholar] [CrossRef]
- Ling, J.Y.; Qian, R.Y.; Shang, K.; Guo, L.Y.; Zhao, Y.; Liui, D. Research on the dynamic monitoring technology of road subgrades with time-lapse full-coverage 3D ground penetrating radar (GPR). Remote Sens. 2022, 14, 1593. [Google Scholar] [CrossRef]
- Sun, C.X. Application of ground penetrating radar technology in geological survey of water conservancy and hydropower engineering. Groundwater 2024, 46, 183–184. [Google Scholar] [CrossRef]
- Cui, Y.T.; Wang, S.H.; Li, J.W. GPR noise suppression algorithm based on compressed parallel non-local mean filtering method. Chin. J. Eng. Geophys. 2023, 20, 825–834. [Google Scholar] [CrossRef]
- Jin, Y.; Duan, Y.L. A new method for abnormal underground rocks identification using ground penetrating radar. Measurement 2020, 149, 106988. [Google Scholar] [CrossRef]
- He, X.K.; Wang, C.; Zheng, R.Y.; Li, X.W. GPR image noise removal using grey wolf optimisation in the NSST domain. Remote Sens. 2021, 13, 4416. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, S.; Deng, Z.W.; Ling, T.H. Geological detection of hard rocks by GPR and signal time-frequency characteristics analysis in urban underground trenchless construction. Meas. Sci. Technol. 2024, 35, 045406. [Google Scholar] [CrossRef]
- Zhang, S.; He, W.C.; Cao, F.; Hong, L. Time-frequency analysis of GPR simulation signals for tunnel cavern fillings based on short-time fourier transform. In Earth and Space 2021: Materials, Structures, Dynamics, and Control in Extreme Environments; American Society of Civil Engineers: Reston, VA USA, 2021; pp. 572–581. [Google Scholar] [CrossRef]
- Liu, M.M.; Liu, Z.H.; Zhou, D.; Lan, R.Y.; Wu, H. Recognition method of typical anomalies during karst tunnel construction using GPR attributes and Gaussian processes. Arab. J. Geosci. 2020, 13, 791. [Google Scholar] [CrossRef]
- Zhang, R.; Gan, C.; Cao, W. A novel intelligent method for extracting the multi-domain features of ground penetrating radar data. In Proceedings of the 2023 China Automation Congress (CAC), Chongqing, China, 17–19 November 2023; pp. 6069–6074. [Google Scholar] [CrossRef]
- Gao, S.Q.; Wang, Y.Q.; Mou, Y.C. Advance geological forecasting and image analysis of karst tunnel with ground penetrating radar. Chin. J. Eng. Geophys. 2021, 18, 642–646. [Google Scholar] [CrossRef]
- Chen, P.S.; Yuan, Q.; Zhang, Z.P.; Yang, L.; Chen, Z.L.; Wu, L. Image interpretation method for geological advance prediction of water-rich fracture zone in tunnel based on convolutional neural network. J. Appl. Basic Eng. Sci. 2022, 30, 196–207. [Google Scholar] [CrossRef]
- Chen, H.H.; Liu, S.M. Advanced geological prediction technology of tunnel based on image recognition. Arab. J. Geosci. 2019, 12, 601. [Google Scholar] [CrossRef]
- Li, T.B.; Meng, L.B.; Zhu, J. Comprehensive analysis method for advanced geological prediction of tunnels. J. Rock Mech. Eng. 2009, 28, 2429–2436. [Google Scholar] [CrossRef]
- Zheng, L.; Li, X.; Liu, Z.; Huang, D.; Tang, Z. Accuracy evaluation of advanced geological prediction based on improved analytic hierarchy process and ground penetrating radar. Math. Probl. Eng. 2020, 2020, 8617165. [Google Scholar] [CrossRef]
- Gan, C.; Cao, W.H.; Wu, M.; Liu, K.Z.; Chen, X.; Hu, Y.L.; Ning, F.L. Two-level intelligent modeling method for the rate of penetration in complex geological drilling process. Appl. Soft Comput. J. 2019, 80, 592–602. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, X.; Tang, S.; Liu, X.; Li, X.; Zhang, Q.; Yan, F.; Xu, C.; Liu, Q. Fast perception of rock mass strength and integrity in TBM tunnelling using in-situ penetration test. Tunn. Undergr. Space Technol. 2023, 141, 105358. [Google Scholar] [CrossRef]
- Park, J.S.; Go, Y.W.; Oh, T.M. Evaluating the relationship between RMR and Q-system for improved classification of faulted rocks and weak rocks. Sci. Rep. 2025, 15, 17121. [Google Scholar] [CrossRef]
- Bieniawski, Z. Engineering classification of jointed rock masses. Civ. Eng. Siviele Ingenieurswese 1973, 1973, 335–343. Available online: https://hdl.handle.net/10520/AJA10212019_17397 (accessed on 10 August 2025).
- Barton, N. Rock mass classification and tunnel reinforcement selection using the q-system. In Rock Classification Systems for Engineering Purposes; ASTM International: West Conshohocken, PA, USA, 1988. [Google Scholar] [CrossRef]
- GB50218-94; Standard for Engineering Classification of Rock Masses. China Planning Press: Beijing, China, 1995.
- Guo, K.; Zhang, L. Multi-source information fusion for safety risk assessment in underground tunnels. Knowl.-Based Syst. 2021, 227, 107210. [Google Scholar] [CrossRef]


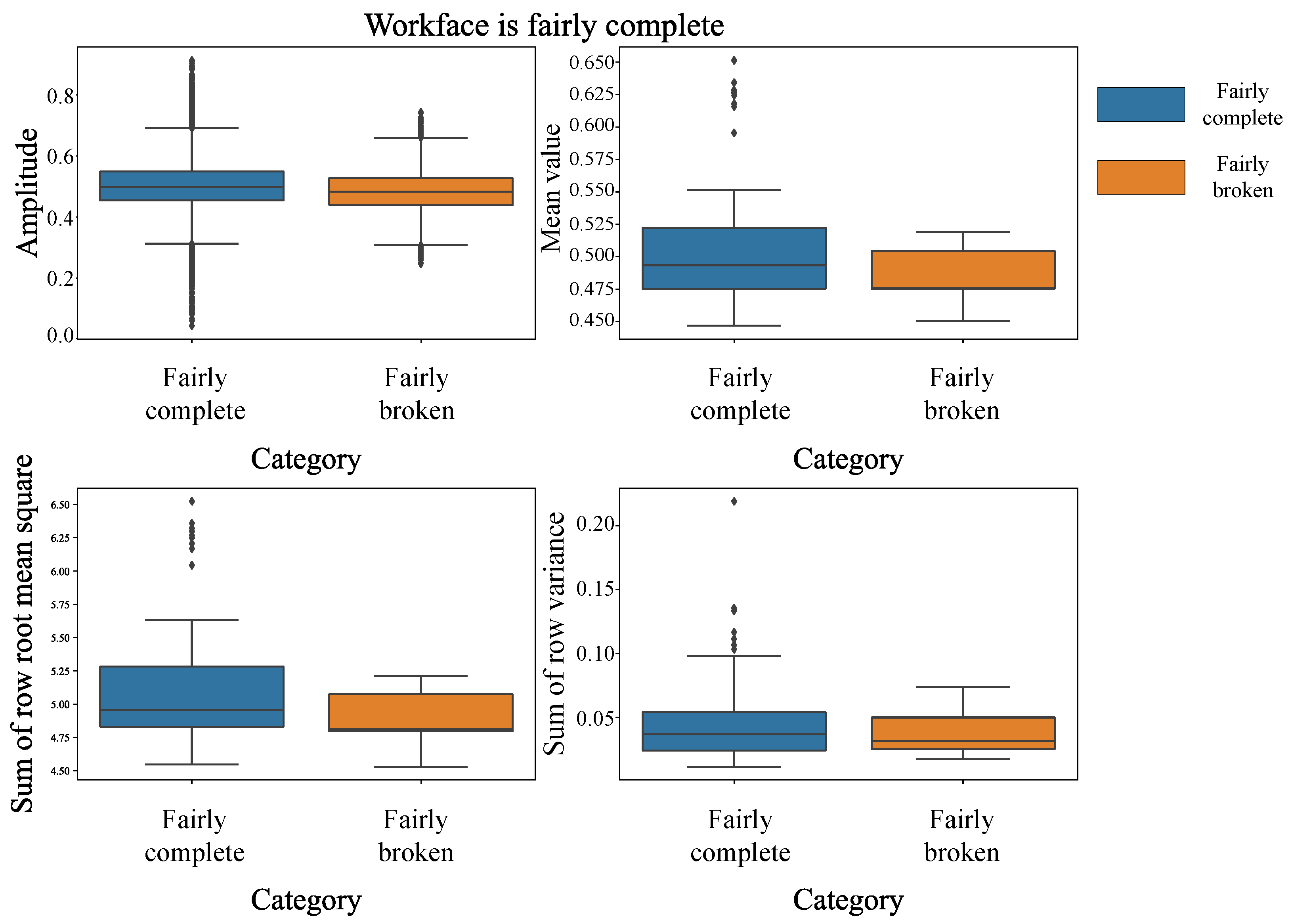


| Layer | Filters | Kernel Size | Stride | Padding | Activation | Output Size |
|---|---|---|---|---|---|---|
| Input | - | - | - | - | - | |
| Conv1 | 16 | (5,5) | 1 | 2 | ReLU | |
| MaxPool1 | - | (2,2) | 2 | 0 | - | |
| Conv2 | 32 | (5,5) | 1 | 2 | ReLU | |
| MaxPool2 | - | (2,2) | 2 | 0 | - | |
| Linear | - | - | - | - | - | 5 |
| Method | Accuracy | Macro-Precision | Macro-Recall |
|---|---|---|---|
| Proposed method | 95.33% | 95.34% | 93.53% |
| Manual prediction | 86.67% | 85.57% | 84.37% |
| Prediction without division of the exploration face | 86.00% | 84.02% | 85.07% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Fu, W.; Hu, X. Multi-Model Intelligent Prediction of Rock Integrity in Tunnels Based on Geological Differences of Ground-Penetrating Radar Exploration Workfaces. Infrastructures 2025, 10, 211. https://doi.org/10.3390/infrastructures10080211
Huang Y, Fu W, Hu X. Multi-Model Intelligent Prediction of Rock Integrity in Tunnels Based on Geological Differences of Ground-Penetrating Radar Exploration Workfaces. Infrastructures. 2025; 10(8):211. https://doi.org/10.3390/infrastructures10080211
Chicago/Turabian StyleHuang, Yong, Wei Fu, and Xiewen Hu. 2025. "Multi-Model Intelligent Prediction of Rock Integrity in Tunnels Based on Geological Differences of Ground-Penetrating Radar Exploration Workfaces" Infrastructures 10, no. 8: 211. https://doi.org/10.3390/infrastructures10080211
APA StyleHuang, Y., Fu, W., & Hu, X. (2025). Multi-Model Intelligent Prediction of Rock Integrity in Tunnels Based on Geological Differences of Ground-Penetrating Radar Exploration Workfaces. Infrastructures, 10(8), 211. https://doi.org/10.3390/infrastructures10080211




