Research on the Dynamic Response of the Catenary of the Co-Located Railway for Conventional/High Speed Trains in High-Wind Area
Abstract
1. Introduction
2. Materials and Methods
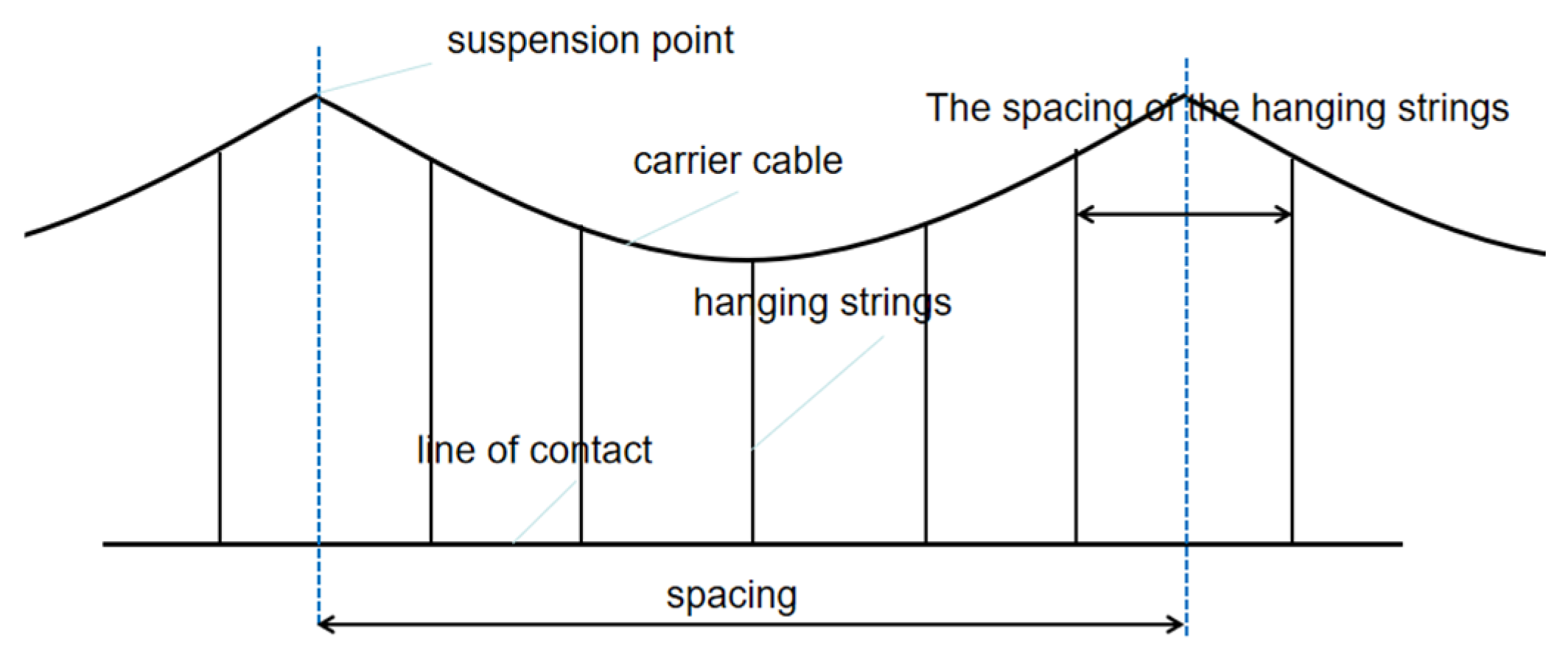
2.1. Catenary Modeling
- (1)
- The catenary, messenger cables, and support structures (pillars and cantilevers) are idealized as tensioned Euler beams with bending stiffness and uniformly distributed mass.
- (2)
- Suspension cables, positioners, and droppers are modeled as spring-damper elements.
- (3)
- Suspension cable endpoints are treated as concentrated mass points.
- (1)
- BEAM188 elements for contact wires and messenger cables.
- (2)
- COMBIN14 elements for elastic components (e.g., droppers).
- (3)
- MASS21 elements for concentrated masses (e.g., suspension clamps and positioning devices).
- (1)
- Support Constraints: The messenger cable supports are fully constrained in all displacement degrees of freedom (DOFs), effectively creating fixed boundary conditions at these locations.
- (2)
- Contact Wire Positioning Constraints: At contact wire positioning points, three critical DOFs are constrained:
- (i)
- Translational displacements along the following directions:The longitudinal direction (x-axis, parallel to train motion).The lateral direction (z-axis, perpendicular to track).
- (ii)
- Rotational displacement about the vertical axis (y-axis).These constraints prevent spurious displacements and rotations at contact wire terminations, thereby enhancing system stability and operational reliability.
- (3)
- Positioning Clamp Constraints: Similar DOF restrictions are applied at positioning clamp bases to ensure structural stability throughout the catenary system.
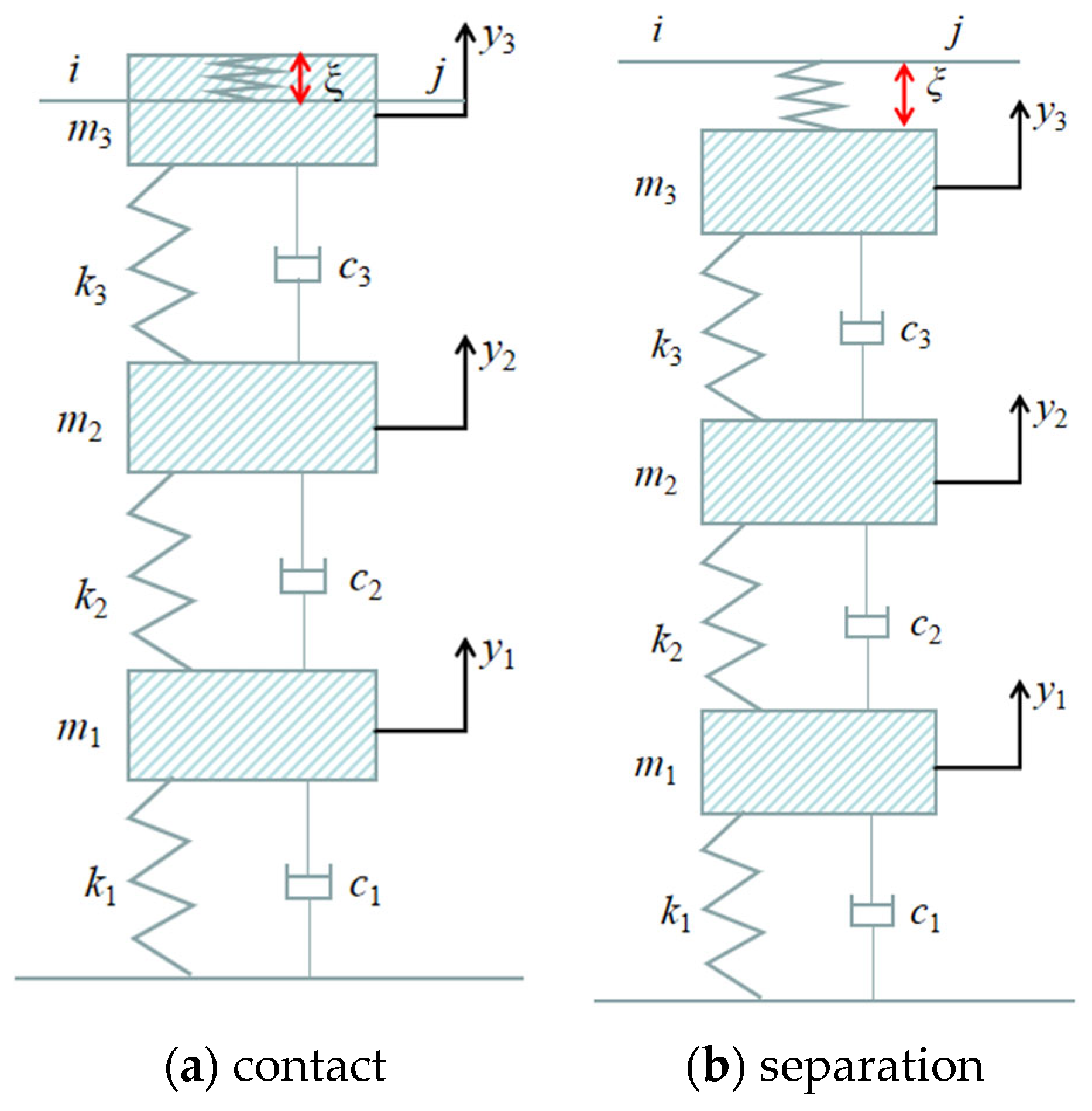
2.2. Pantograph Modeling
2.3. Pantograph–Catenary Coupling Contact Model
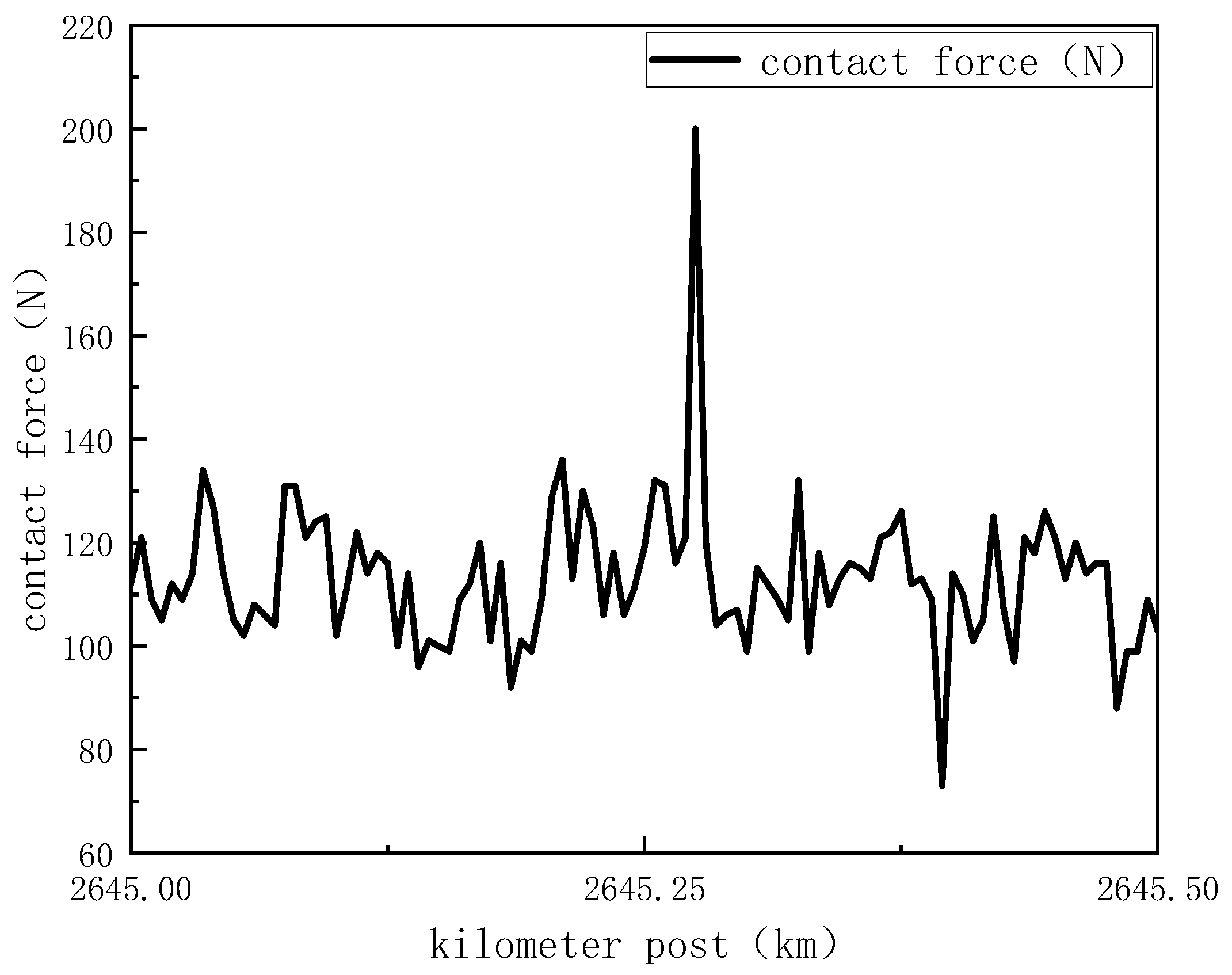
2.4. Model Verification
3. Result Analysis
3.1. Evaluation Criteria
3.2. Dynamic Response Analysis of Pantograph–Catenary in the Mainline Section
3.3. Dynamic Response Analysis of Pantograph–Catenary in the Transition Section
- (1)
- Active control
- (2)
- Passive control
- (1)
- Active control of pantograph
- (2)
- Passive control of pantograph
- (3)
- Crosswind conditions in the wind zone under pantograph passive control
4. Discussion
5. Conclusions
- (1)
- Both the conventional Tsg15B and high-speed DSA380 pantograph systems demonstrate a compliant performance in wind-affected zones, with all measured contact forces and vertical displacements remaining within the established operational limits. These results confirm that the dynamic responses of both pantograph types satisfy the essential requirements for colinear operation.
- (2)
- Due to the increase in the rated tension of the catenary and the load-bearing cable, the vertical displacement in the wind zone without crosswind conditions is lower than that in the non-wind zone. The average vertical displacement is reduced by 8.52%, and the standard deviation is significantly reduced, which improves the stability of the pantograph system.
- (3)
- Under the action of a crosswind of 20 m/s, the vibration of the overhead contact system is significant, and the maximum contact force of the high-speed train pantograph is 279.23 N. However, the pantograph still meets the requirements for safe operation. In the closed configuration operation of the pantograph, the contact force and dynamic vertical displacement of the pantograph are greater than those in the open configuration operation, and the points with large fluctuations in the catenary mainly occur in the mid-span.
- (4)
- Under active control, the dynamic response of the high-speed mainline is lower than that of the conventional mainline, while the opposite trend is observed under passive control.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Zhu, X. Research on Health Status Assessment of Highspeed Railway Catenaries Based on Gray Clustering and Combination Assigning Method. J. China Railw. Soc. 2016, 38, 57–63. [Google Scholar] [CrossRef]
- Wu, T.X.; Brennan, M.J. Basic analytical study of pantograph-catenary system dynamics. Veh. Syst. Dyn. 1998, 30, 443–456. [Google Scholar] [CrossRef]
- Zhang, W.H.; Mei, G.M.; Wu, X.J.; Shen, Z. Hybrid simulation of dynamics for the pantograph-catenary system. Veh. Syst. Dyn. 2002, 38, 393–414. [Google Scholar] [CrossRef]
- Kerstin, S.; Wolfgang, E.; Michael, K.; Willett, S.; Jenzer, M.; Willett, T. An approach to continuous on-site monitoring of contact forces in pantographs by a fiber optic sensing system. Opt. Lasers Eng. 2013, 51, 172–179. [Google Scholar]
- Collina, A.; Bruni, S. Numerical simulation of pantograph-overhead equipment interaction. Veh. Syst. Dyn. 2002, 38, 261–291. [Google Scholar] [CrossRef]
- Bocciolone, M.; Resta, F.; Rocchi, D.; Tosi, A.; Collina, A. Pantograph aerodynamic effects on the pantograph-catenary interaction. Veh. Syst. Dyn. 2006, 44, 560–570. [Google Scholar] [CrossRef]
- LI, R.; Zhou, N. Influence of high-speed trains passing through tunnel on pantograph-catenary dynamic behaviors. J. Vib. Shock 2013, 32, 33–37. [Google Scholar]
- Poetsch, G.; Evans, J.; Meisinger, R.; Kortüm, W.; Baldauf, W.; Veilt, A.; Wallaschek, J. Pantograph/catenary dynamics and control. Veh. Syst. Dyn. 1997, 28, 393–414. [Google Scholar] [CrossRef]
- Pombo, J.; Ambrósio, J.; Pereira, M.; Rauter, F.; Collina, A.; Facchinetti, A. Influence of the aerodynamic forces on the pantograph-catenary system for high speed trains. Veh. Syst. Dyn. 2009, 47, 1327–1347. [Google Scholar] [CrossRef]
- Li, R.; Zhou, N. Fluctuating wind field and wind induced vibration response of contact network based on AR model. J. Traffic Transp. Eng. 2013, 13, 56–62. [Google Scholar]
- Zhao, F.; Liu, Z. Simulation Study on Influence of Stochastic Wind Field to Dynamic Behavior of Pantograph-catenary System. J. China Railw. Soc. 2012, 34, 36–42. [Google Scholar]
- Hu, X.; Wang, H. Dynamic Inspection Evaluation and Warning Methods of the OcS on Beijing-Shanghai HSR. Chinarailway 2024, 5, 25–32. [Google Scholar] [CrossRef]
- Sun, L.; Song, W. Adaptability of Existing Freight Facilities Serving High Speed Freight EMUs. Chinarailway 2023, 4, 56–62. [Google Scholar] [CrossRef]
- Guan, J.; Wu, J. Building and confirmation for dynamic simulation model of pantograph and catenary. J. Rail Way Sci. Eng. 2017, 14, 2444–2451. [Google Scholar]
- Chen, X.; Zhang, X. Research on Dynamie Current Collection Characteristies of High-Speed Railway Double-Pantograph-Catenary System Under Environmental Wind. J. Vib. Meas. Diagn. 2024, 44, 320–329 + 411–412. [Google Scholar]
- TB 10009-2016 [S]; Code for Design of Railway Traction Power Supply. China Railway Publishing House: Beijing, China, 2016.
- EN 50367:2020/A1:2022; European Standard Railway Applications. Fixed Installations and Rolling Stock. Criteria to Achieve Technical Compatibility Between Pantographs and Overhead Contact Line. CENELEC: Brussels, Belgium, 2022.




| Form | Arguments |
|---|---|
| Span length | 50 m |
| Stagger | ±200 mm |
| Dropper clearance | 5/8/8/8/8/8/5 m |
| Catenary parameters | 150 mm2 copper alloy wire |
| Cable parameters | 120 mm2 copper alloy stranded wire |
| Rated working tension of the catenary | 28.5 Kn (wind area); 25 kN (Non-wind area) |
| Rated working tension of the load-bearing cable | 21 kN (wind area); 20 kN (Non-wind area) |
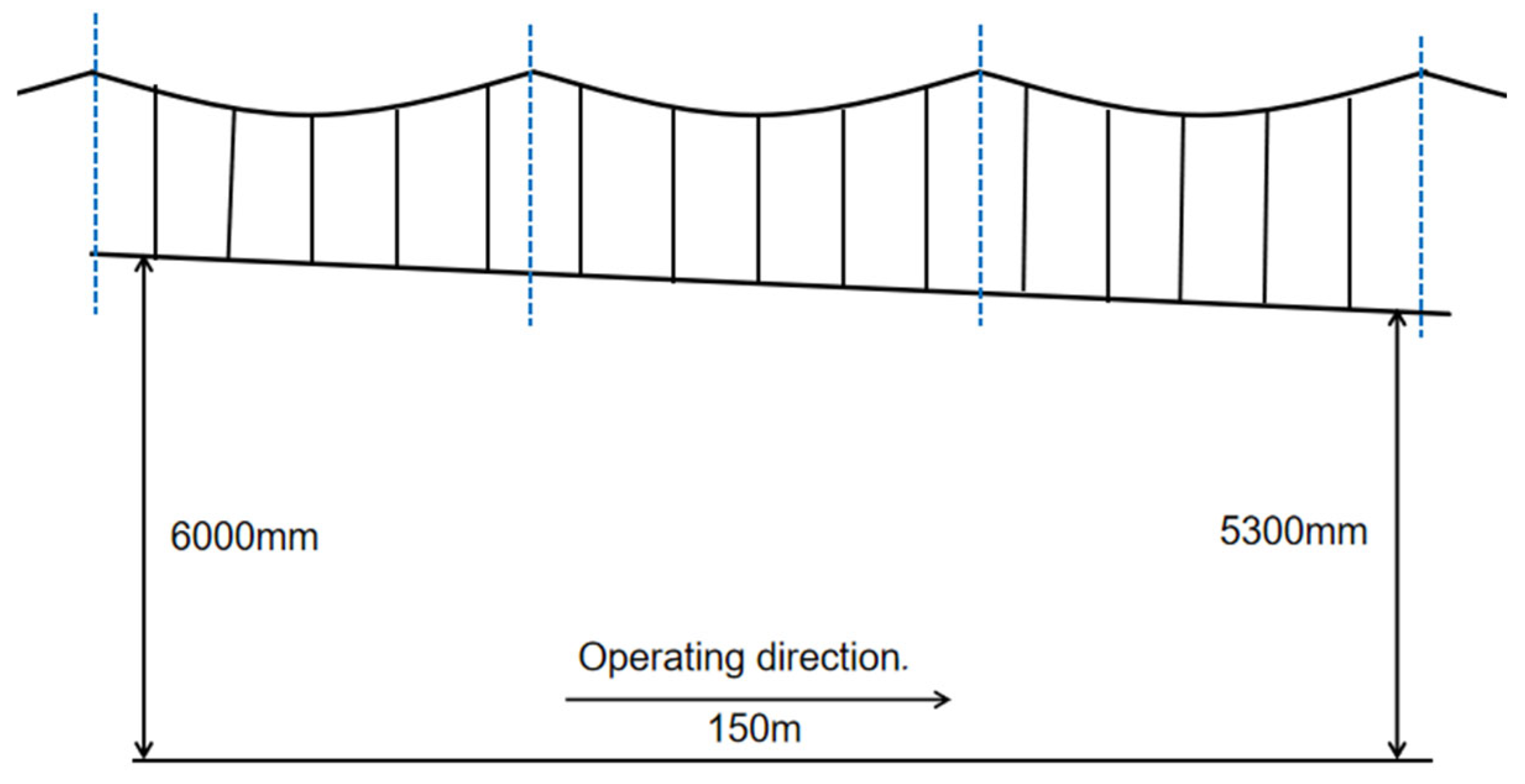
| The overhead catenary is elevated | 6000 mm (conventional speed); 5300 mm (high speed) |
| Pantograph | m1/kg | m2/kg | m3/kg | k1/(N·m−1) | k2/(N·m−1) | k3/(N·m−1) | c1/(N·s·m−1) | c2/(N·s·m−1) | c3/(N·s·m−1) |
|---|---|---|---|---|---|---|---|---|---|
| Tsg15B | 23 | 18 | 5.3 | 39 | 39 | 6000 | 0.1 | 0.1 | 0.1 |
| DSA380 | 5.8 | 7.12 | 6.0 | 0.01 | 14,100 | 9430 | 70 | 0 | 0 |
| Arguments | Contact Force | ||
|---|---|---|---|
| Simulation Result | Measured Data | Relative Error | |
| Maximum contact force Fmax/N | 192.64 | 200.00 | −3.68% |
| Minimum contact force Fmin/N | 65.30 | 68.00 | −3.97% |
| Average contact force Fm/N | 120.02 | 114.92 | 4.43% |
| Speed v (km/h) | 120 | 160 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|
| Average contact force Fm (N) | 60 < Fm ≤ 0.00047 × v2 + 90 | ≤0.00097 × v2 + 70 | ||||
| Maximum contact force Fmax (N) | 300 | 350 | ||||
| Minimum contact force Fmin (N) | 0 | 0 | ||||
| maximum standard deviation σmax (N) | 0.3Fm | |||||
| Maximum lifting capacity (mm) | 120 | 150 | ||||
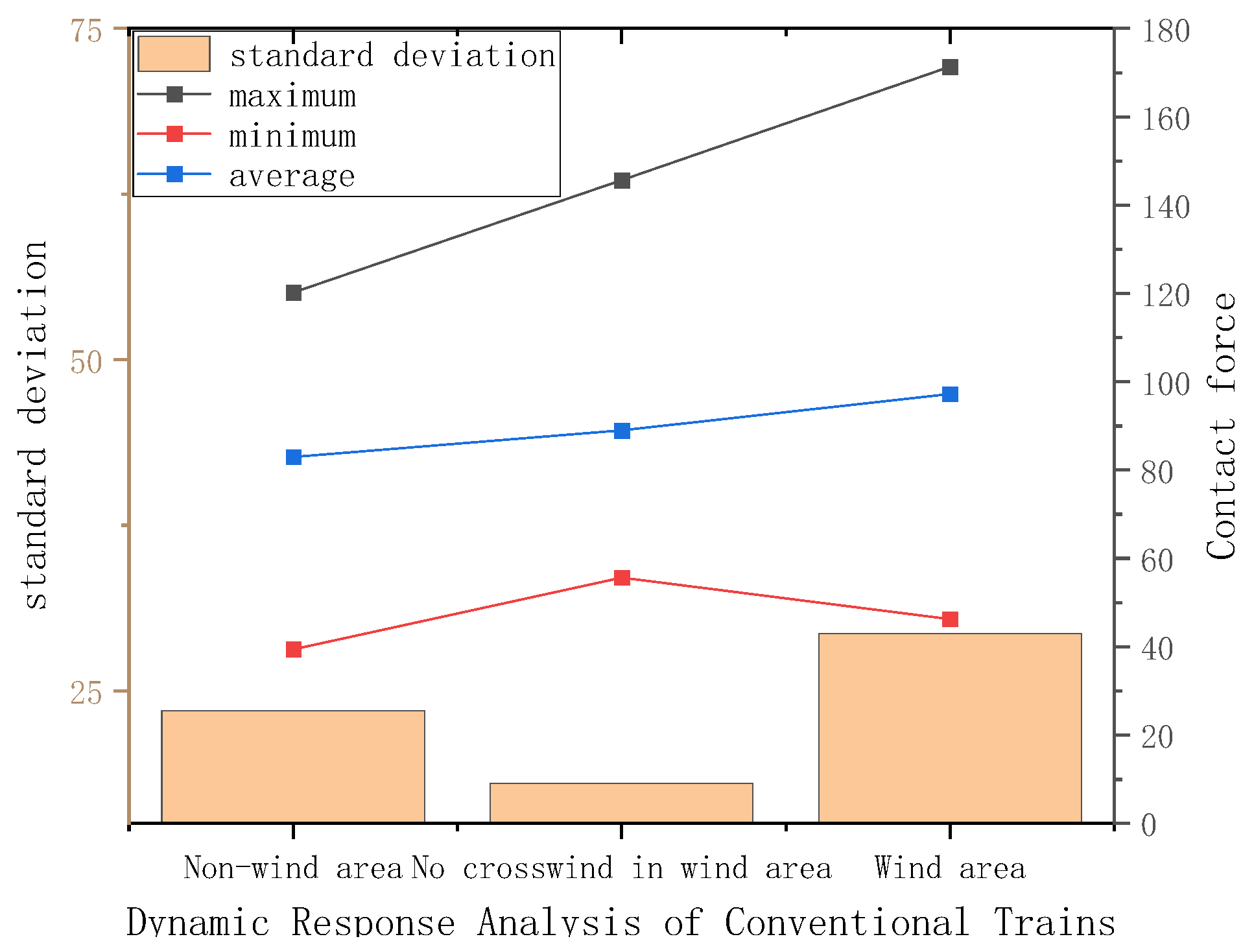
| Name of Parameter | Non-Wind Area | Wind Area with No Crosswind | Wind Area with Crosswind |
|---|---|---|---|
| Maximum contact force Fmax/N | 127.23 | 148.32 | 177.56 |
| Minimum contact force Fmin/N | 44.97 | 60.27 | 50.22 |
| Average contact force Fm/N | 90.54 | 92.62 | 94.63 |
| maximum standard deviation σ/N | 28.33 | 26.23 | 30.27 |
| Name of Parameter | Non-Wind Area | Wind Area with No Crosswind | Wind Area with Crosswind |
|---|---|---|---|
| Maximum contact force Fmax/N | 192.64 | 259.65 | 279.23 |
| Minimum contact force Fmin/N | 65.30 | 75.43 | 67.57 |
| Average contact force Fm/N | 120.02 | 142.01 | 158.01 |
| maximum standard deviation σ/N | 31.47 | 27.27 | 39.01 |
| Name of Parameter | Non-Wind Area | Wind Area with No Crosswind | Wind Area with Crosswind |
|---|---|---|---|
| Maximum lifting capacity/mm | 44.71 | 42.22 | 53.59 |
| Minimum lifting amount/mm | 10.74 | 13.57 | 15.01 |
| Average lifting amount/mm | 22.63 | 21.65 | 29.37 |
| Name of Parameter | Non-Wind Area | Wind Area with No Crosswind | Wind Area with Crosswind |
|---|---|---|---|
| Maximum lifting capacity/mm | 70.67 | 57.40 | 79.78 |
| Minimum lifting amount/mm | 24.20 | 18.00 | 23.76 |
| Average lifting amount/mm | 44.09 | 34.12 | 49.64 |
| Name of Parameter | Non-Wind Area | Wind Area with No Crosswind | Wind Area with Crosswind |
|---|---|---|---|
| Maximum contact force Fmax/N | 120.22 | 145.63 | 171.36 |
| Minimum contact force Fmin/N | 39.38 | 55.67 | 46.24 |
| Average contact force Fm/N | 83.01 | 89.03 | 92.26 |
| maximum standard deviation σ/N | 23.51 | 18.02 | 29.31 |
| Maximum Lifting Capacity/mm | Maximum Lifting Capacity/mm | Maximum Lifting Capacity/mm | Maximum Lifting Capacity/mm |
|---|---|---|---|
| Maximum lifting capacity/mm | 40.98 | 39.32 | 49.28 |
| Minimum lifting amount/mm | 11.93 | 10.27 | 14.26 |
| Average lifting amount/mm | 21.26 | 19.59 | 27.10 |
| Name of Parameter | 160 km/h Tsg15B Pantograph (Open Configuration Operation) | 160 km/h Tsg15B Pantograph (Closed Configuration Operation) |
|---|---|---|
| Maximum contact force Fmax/N | 130.32 | 135.67 |
| Minimum contact force Fmin/N | 48.32 | 52.68 |
| Average contact force Fm/N | 91.27 | 92.53 |
| Maximum Lifting Capacity/mm | 160 km/h Tsg15B Pantograph (Open Configuration Operation) | 160 km/h Tsg15B Pantograph (Closed Configuration Operation) |
|---|---|---|
| Maximum lifting capacity/mm | 43.04 | 46.13 |
| Minimum lifting amount/mm | 14.73 | 18.89 |
| Average lifting amount/mm | 23.98 | 27.70 |
| Name of Parameter | 160 km/h Tsg15B Pantograph (Open Configuration Operation) | 160 km/h Tsg15B Pantograph (Closed Configuration Operation) |
|---|---|---|
| Maximum contact force Fmax/N | 185.54 | 207.94 |
| Minimum contact force Fmin/N | 52.72 | 70.32 |
| Average contact force Fm/N | 98.42 | 102.67 |
| maximum standard deviation σ/N | 33.10 | 33.32 |
| Maximum Lifting Capacity/mm | 160 km/h Tsg15B Pantograph (Open Configuration Operation) | 160 km/h Tsg15B Pantograph (Closed Configuration Operation) |
|---|---|---|
| Maximum lifting capacity/mm | 51.27 | 55.12 |
| Minimum lifting amount/mm | 15.23 | 17.34 |
| Average lifting amount/mm | 28.33 | 30.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Gou, Y.; Guo, B.; Li, H.; Cao, E.; Ma, J. Research on the Dynamic Response of the Catenary of the Co-Located Railway for Conventional/High Speed Trains in High-Wind Area. Infrastructures 2025, 10, 182. https://doi.org/10.3390/infrastructures10070182
Li G, Gou Y, Guo B, Li H, Cao E, Ma J. Research on the Dynamic Response of the Catenary of the Co-Located Railway for Conventional/High Speed Trains in High-Wind Area. Infrastructures. 2025; 10(7):182. https://doi.org/10.3390/infrastructures10070182
Chicago/Turabian StyleLi, Guanghui, Yongzhi Gou, Binqian Guo, Hongmei Li, Enfan Cao, and Junjie Ma. 2025. "Research on the Dynamic Response of the Catenary of the Co-Located Railway for Conventional/High Speed Trains in High-Wind Area" Infrastructures 10, no. 7: 182. https://doi.org/10.3390/infrastructures10070182
APA StyleLi, G., Gou, Y., Guo, B., Li, H., Cao, E., & Ma, J. (2025). Research on the Dynamic Response of the Catenary of the Co-Located Railway for Conventional/High Speed Trains in High-Wind Area. Infrastructures, 10(7), 182. https://doi.org/10.3390/infrastructures10070182






