Dynamic Wheel Load Measurements by Optical Fiber Interferometry

Abstract

This study proposes a Fabry–Perot interferometric system and an associated evaluation method for measuring the weight of moving trains. An optical fiber sensor, comprising a sensing fiber and a supporting structure, is securely bonded to the rail foot. As a train traverses the track, the resulting localized bending induces a change in the sensing fiber’s length, which manifests as a quantifiable phase shift in the interference signal. We developed a physical–mathematical model, based on three Gaussian functions, to describe the temporal change in sensing fiber length caused by the passage of a single bogie. This model enables the determination of a proportionality constant to accurately convert the measured phase change into train weight. Model validation was performed using a train set, including a locomotive and four variably loaded wagons, traveling at 15.47 km/h. This system offers a novel and effective approach for real-time train weight monitoring.

1. Introduction

Global challenges like climate change and the reliance of many nations on imported fossil fuels highlight the critical need for sustainable transportation. Among various modes, rail and shipping stand out for their significantly lower carbon dioxide emissions per ton-kilometer of transported cargo. Consequently, rail transport is recognized as an environmentally sound system capable of moving large volumes of goods efficiently, cost-effectively, and safely over medium to long distances. Its importance is therefore expected to grow in the future [1].

The effectiveness of rail transport services is intrinsically linked to the quality of both the transport infrastructure and the rolling stock, including its maintenance and operational practices. Notably, substandard or improperly utilized rolling stock can directly compromise the integrity of railway lines. This underscores the vested interest of railway line operators in continuously monitoring the condition of rolling stock as it traverses the tracks.

Various sensing systems, often integrated with the railway track and operating on mechanical, electrical, or optical principles [2,3,4], are being developed to monitor train movement and condition [5,6,7,8,9]. These systems provide crucial data for real-time operation and help identify problematic rolling stock that could damage the tracks. While traditional methods like acoustic and visual inspection are still in use, they are increasingly being automated. Analyzing acoustic measurements and track vibrations, for example, can diagnose vehicle and track health, as well as indicate changes in wheel-to-track load [10,11].

One critical parameter affecting both vehicle and track integrity is the weight of moving trains, particularly freight. Static weighing is rarely performed before trains enter the main infrastructure due to it being time-consuming and expensive. This has spurred interest in dynamic weighing systems, or “weight-in-motion” (WIM) technologies. Early WIM systems utilized strain gauges attached to the rail [12]. Other intrusive methods involved installing sensors like quartz force sensors directly into the track [13]. Monitoring of railway traffic parameters frequently employs piezoelectric sensors. The dynamic loading and vibrations induced by a passing train are effectively detected by piezoelectric sensors integrated into the rails or sleepers, generating a proportional electrical signal [2]. These sensors exhibit high sensitivity to subtle pressure and vibration changes, facilitating comprehensive analysis. A key benefit is their passive operation; they do not require external power, thereby simplifying installation and deployment. However, accurate data acquisition is contingent upon meticulous installation and routine calibration. Moreover, environmental vibrations and noise inherent to railway operations can introduce signal interference, demanding advanced data processing. Interestingly, weight can also be estimated from wheel angular speed and train velocity [14,15]. Optical fiber-based systems are a particularly promising alternative due to their immunity to electromagnetic interference. These sensors can be attached to the side or bottom of the rail [5,16], or even secured with detachable clamps or magnets.

Fiber Bragg gratings (FBGs) are currently the most common optical systems for railway vehicle weighing due to their established technology, relatively simple application, the capacity for quasi-distributed sensing via integration of multiple FBGs into a single optical fiber, and the absence of a power requirement at the sensing point [17,18,19]. Their principle relies on measuring a Bragg wavelength shift caused by changes in the sensing fiber’s length as the rail bends under a passing vehicle. FBGs are additionally applied in structural health monitoring [20] and vibration analysis for bridges [21] and tunnels. However, FBG systems can be complex and costly due to the sophisticated equipment needed for wavelength monitoring and the production of individual gratings.

Sensors in real-world settings pick up noisy signals, especially at higher speeds. This often leads researchers to focus on static or low-speed measurements for weight determination, though they may later validate their methods for faster conditions [22].

This paper proposes a novel approach to determine the weight exerted by individual wheels of a passing train set. Our method analyzes the phase change in an interference signal, which directly correlates with the length change of a sensing optical fiber within an optical sensor. This sensor functions as a low-finesse Fabry–Perot interferometer and is strategically glued to the rail foot between two sleepers. As a train passes, the rail deforms, altering the sensing fiber’s length and consequently the phase of the interference signal. This system offers significant advantages, including sensor simplicity, straightforward signal evaluation, ultra-high sensitivity and resolution, inherent immunity to temperature–strain cross-sensitivity, proven robustness in challenging environments, and the ability to simultaneously acquire data on axle loads, axle count, train speed, and potential defects in the motion system. Therefore, our proposed optical fiber sensor system presents a compelling and effective alternative to existing FBG-based solutions.

2. Signal from the Sensor and Rail Bending

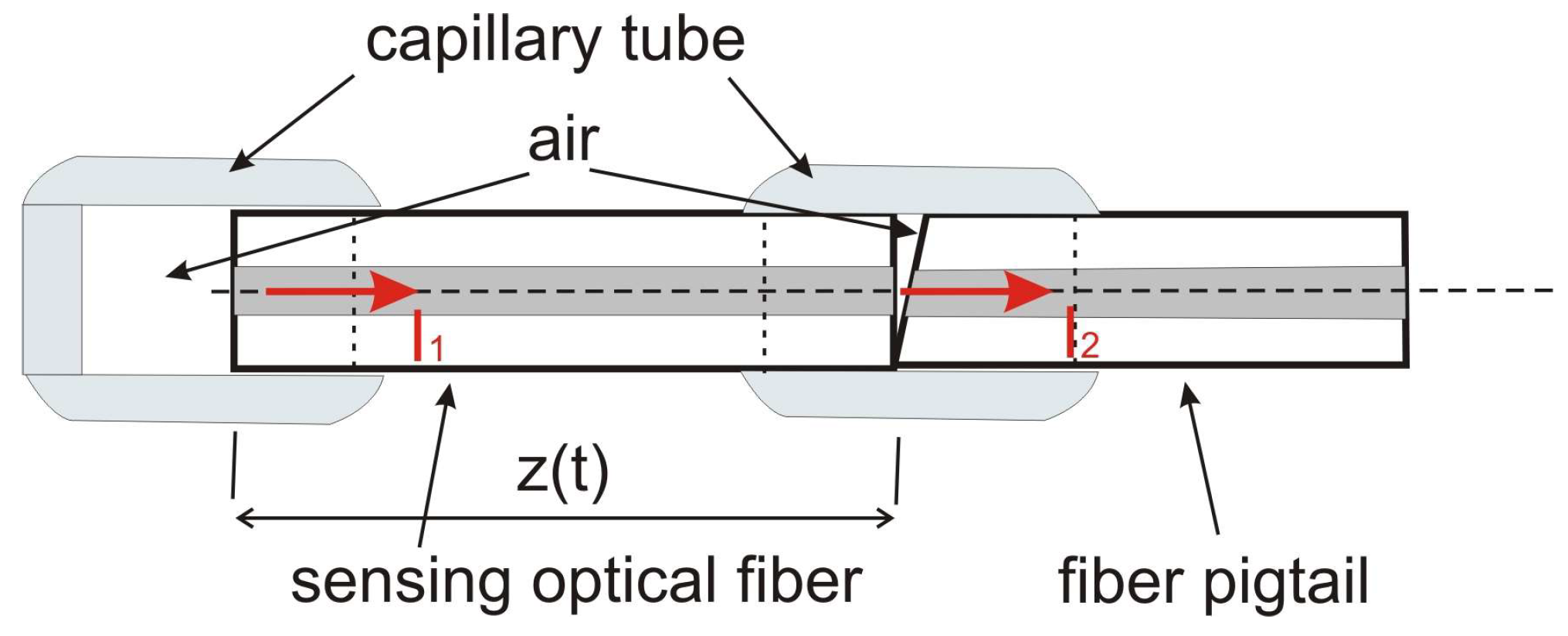
The developed optical fiber system for monitoring the dynamic operation of rolling stock comprises an optical fiber sensor, a Safibra OFLS-6-DFB-1550 laser diode operating at a wavelength of 1550 nm (Safibra s.r.o., Ricany, Czech Republic), a CIR-3-P-1550-900-1-1-FA circulator (Thorlabs Inc., Newton, NJ, USA), a Thorlabs PDA10CS-EC photodetector (Thorlabs Inc., Newton, NJ, USA), a PicoScope 5444B oscilloscope(Pico Technology, St Neots, UK), and a remote server for data storage, processing, and distribution. The sensing component of this system is based on the Fabry–Perot interferometer, where a conventional single-mode optical fiber functions as the Fabry–Perot cavity (Figure 1). The sensor’s sensitive optical fiber is integrated into an aluminum support element (Figure 2), which is then securely bonded to the rail’s foot between two sleepers (Figure 3) using an MS polymer-based adhesive.

With its end faces perpendicular to the fiber axis and surrounded by air, the sensing optical fiber reflects approximately 4 percent of the incident optical radiation. This configuration allows the fiber to operate as a low-finesse Fabry–Perot interferometer. For an interferometer functioning in the optical fiber’s single-mode regime, the monochromatic optical signal in the time domain, arising from the interference of the two beams reflected from the fiber ends, can be expressed as

$$I\left(t\right)=I_1\left(t\right)+I_2\left(t\right)+2\sqrt{I_1\left(t\right)I_2\left(t\right)}\mathrm{c}\mathrm{o}\mathrm{s}\left(2 \beta z\left(t\right)+\pi \right),$$

(1)

where I₁ and I₂ are intensities of interfering beams, β is the propagation constant of the fundamental mode of the optical fiber, t is time, and z is the length of the fiber.

The bending of the rail causes an extension of the sensing optical fiber affixed to its foot. Assuming this extension is small, the quantities I₁, I₂, and β in (1) may be treated as constant. Consequently, the interference term I_int(t) of the signal I(t) can be expressed as

$$I_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(t\right)=K \mathrm{c}\mathrm{o}\mathrm{s}\left(\Phi \left(t\right)\right),$$

(2)

where K is a constant and $\Phi \left(t\right)$ is the time change of the phase of the interference signal. Given the considered assumptions, $\Phi \left(t\right)$ is determined solely by the instantaneous length of the sensing optical fiber.

Significant vibrations lead to substantial noise in the signal, which complicates the accurate determination of the signal resulting from rail bending. Based on our observations, pronounced vibrations (which appear as elevated noise levels in our signal) correlate directly with higher wear in rolling stock. For this reason, our current investigation concentrates on low-speed scenarios, where vibration-induced noise attributable to suboptimal rolling stock technical conditions is negligible.

The interference signal from the optical fiber sensor, depicting its time dependence during a train’s passage, is shown in Figure 4. The sensor effectively captured rail deformation caused by the train, which was moving at 15.47 km/h. Notably, the train set consisted of a locomotive pushing four wagons.

The time-dependent signal data was specifically obtained during a measurement campaign dedicated to determining the number of train axles. Comprehensive details regarding this campaign can be found in our previous publication [23]. The ambient temperature during this particular measurement was 24 °C. Even though temperature variations led to changes in the optical sensing fiber’s length, because we analyzed interference in the time domain, their effect was limited to a shift in the initial phase of the signal.

Analysis of the interference signal’s phase change, predicated on the assumption that the rail undergoes convex deformation beneath the wheel, reveals that as the train traverses the sensor, the rail between its wheels exhibits both convex and concave bending. The temporal evolution of this phase change, $\Phi$(t), was obtained through phase demodulation. This $\Phi$(t) signal, which correlates with the I_int(t) signal depicted in Figure 4, is displayed in Figure 5.

Based on the phase change $\Phi$(t) analysis of the moving train set, Figure 6 schematically depicts the convex and concave rail deformation sites observed under two wagons.

As depicted in Figure 6, the rail exhibits characteristic deformations: a convex bend directly beneath the wagon wheels, a concave bend within each railway bogie (between two wheels), another concave bend occurring between adjacent bogies, and further concave bends at the train set’s leading and trailing ends. This deformation pattern propagates along the rail as a traveling wave, a direct consequence of the train set’s motion. The magnitudes of these localized convex and concave bends are contingent upon the forces transmitted by individual wheels to the track and the deformational characteristics of the railway superstructure. Assuming consistent deformational properties of the railway superstructure within a chosen section of the track, the extent of individual rail bends will solely correlate with the forces (or weights) exerted by the respective wheels. Thus, the rail bending observed during the passage of a train set offers a viable means for determining individual wheel weights.

3. Rail Deformation Model

Our subsequent analysis will be confined to the deformation of the rail and the sensing optical fiber during the traverse of a railway bogie. The passage of a bogie induces bending in the optical fiber, which, in turn, alters its length. Simultaneously, the rail undergoes vertical deformation, manifesting as both convex and concave deflections.

A maximal convex bend is observed when one of the bogie’s wheels is situated directly above the sensor fiber’s centroid (Figure 7a). Conversely, a maximal concave bend occurs when the bogie’s wheels are symmetrical to the sensor fiber’s centroid (Figure 7b). The peak extension of the optical fiber during a convex bend is individually dependent on the gravitational forces F₁ and F₂, which are exerted perpendicularly to the rail directly above the sensor’s center and are a consequence of the wheel loads m₁ and m₂ on the railway bogie. Similarly, the optical fiber’s maximum length during a concave bend is governed by the gravitational forces F₁ and F₂, corresponding to the masses m₁ and m_2, spatially distributed around the sensor fiber.

The extension of the optical fiber, caused by the train wheels during both convex and concave rail deformations, leads to a corresponding phase shift in the interference signal. Furthermore, we hypothesize that the time-varying phase change attributed to a single wheel’s passage can be modeled using a Gaussian function. Consequently, the temporal evolution of the interference signal phase, φ_convex, at a convex bend, induced by the railway bogie wheels traversing the sensor fiber, can be mathematically formulated as

$${\phi }_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{x},\mathrm{n}}\left(t\right)=A_{\mathrm{n}}\left(m_{\mathrm{n}}\right) \mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{{\left(t-B_{\mathrm{n}}\right)}^2}{{{2 C}_{\mathrm{n}}\left(v\right)}^2}}\right),$$

(3)

In this context, n ∈ {1,2}, where n signifies the index of the railway bogie wheel. t denotes time, and m_n represents the mass (weight) of the n-th railway bogie wheel. v is the speed of the railway bogie. A_n quantifies the maximum phase for the n-th wheel, correlating with the peak extension of the sensing optical fiber at the rail’s convex bend, which is induced by the weight m_n of the traversing wheel. B_n is the parameter that specifies the temporal point at which the maximal convex bends of the sensing optical fiber manifest upon the wheel’s passage over the sensor. C_n defines the temporal extent of the convex bend occurrence, with this parameter being dependent on the wheel speed. Importantly, parameters A_n and C_n remain constant for a given train wheel load and a consistent train speed.

Proceeding under these established assumptions, the temporal variation in the sensor optical fiber’s phase at the concave bend, attributed to the railway bogie’s traversal of the sensor fiber, can be formulated by the relation

$${\phi }_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{v}\mathrm{e}}\left(t\right)=-A_{\mathrm{b}}\left(m_1, m_2\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{{\left(t-B_{\mathrm{b}}\right)}^2}{{{2 C}_{\mathrm{b}}\left(v\right)}^2}}\right),$$

(4)

In this context, the parameter A_b signifies the maximum phase associated with the peak extension of the optical fiber during the rail’s concave deformation, induced by the railway bogie’s traversal. B_b specifies the temporal instant of the maximum concave rail bend, while C_b quantifies the temporal extent of the concave bend’s occurrence.

Under these assumptions, the time dependence of phase Φ(t) in (2) for the passage of a railway bogie can be expressed as

$$\Phi \left(t\right)={\phi }_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{v}\mathrm{e}}\left(t\right)+\sum _{n=1}^2{\phi }_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{x},\mathrm{n}}\left(t\right)+{\varphi }_0,$$

(5)

where φ₀ is the phase constant.

4. Results and Discussion

We utilized the described physical–mathematical model of rail deformation, which accounts for the intensity of the interference signal in the time domain, to simulate our real measured data. The sensing element employed was an optical fiber Fabry–Perot sensor, as detailed in reference [6]. This sensor detected the passage of the train set’s left side, comprising a locomotive and four wagons. Prior to the test, the individual wheel weights of the train set were statically measured using a Transporta Praha scale, designed for rolling stock wheel and axle load assessment (a location other than the one used for the experiment). The weights obtained from this static measurement are presented in

Table 1. Comparison of static weight and weight determined from phase change and proportionality constant.

Car (-)	Bogie (-)	Wheel (-)	Static Weight (kg)	An Gaussian Peak (rad)	Dynamic Weight (kg)	Percentage Difference
1	1	1	3085	3.9	2652	−14.0
		2	2310	2.9	1972	−14.6
	2	1	2390	4.0	2720	13.8
		2	2785	3.5	2380	−14.5
2	3	1	3500	4.4	2992	−14.5
		2	3985	5.8	3944	−1.0
	4	1	3735	5.9	4012	7.4
		2	4150	5.5	3760	−9.4
3	5	1	5750	5.8	3944	−31.4
		2	5700	8.8	5984	5.0
	6	1	5655	8.4	5712	1.0
		2	5020	8.6	5848	16.5
4	7	1	8095	10.6	7208	−11.0
		2	9005	14.1	9588	6.5
	8	1	8155	12.3	8364	2.6
		2	8725	12.3	8364	−4.1
5 engine	9	1	8600	13.7	9316	8.3
		2	8360	12.5	8500	1.7
	10	1	8775	14.3	9724	10.8
		2	8865	13.8	9384	5.9

. During the interference signal acquisition with the optical fiber Fabry–Perot sensor, the train was moving at a speed of 15.47 km/h.

Figure 8a, Figure 9a, Figure 10a and Figure 11a display the measured and calculated I_int(t) time dependencies. These calculations were performed using Equations (2) and (5) for the first, third, fifth, and seventh railway bogies, respectively, counting from the end of the train set (which was configured with the locomotive pushing the wagons). As is evident from these figures, there is good agreement between the measured and calculated dependencies.

Correspondingly, Figure 8b, Figure 9b, Figure 10b and Figure 11b present the theoretical phase change derived from the interference signals shown in Figure 8a, Figure 9a, Figure 10a and Figure 11a. These theoretical phase changes are calculated using Equations (3) and (4), and their sum (5).

An examination of the dependencies presented in Figure 8b, Figure 9b, Figure 10b and Figure 11b reveals that the phase change of the interference signal, quantified by φ_concave, exerts a negligible influence on the peak amplitudes of the φ_convex,n function. Across all simulations, the contribution of the φ_concave functions to the maxima of the φ_convex,n functions consistently remained below 1.3% of the maximum φ_convex,n value. Consequently, their contribution to the determination of maximum A_n values was disregarded.

Considering that the A_n values of the φ_convex,n functions are contingent upon the force (weight) exerted by each wheel of the train set, and assuming that the rail’s deformation during the train’s passage occurs strictly within elastic limits, the A_n values will exhibit direct proportionality to the weight m_n. From this premise, it follows that for the accurate determination of an individual train wheel’s weight, it is sufficient to evaluate only the maximum phase change at the rail’s convex bend. The weight per wheel can subsequently be expressed by the relation

$$m_{\mathrm{n}}=K_{\mathrm{p}} A_{\mathrm{n}},$$

(6)

where K_p is the proportionality constant.

Table 1 displays the A_n (Gaussian peak) values obtained by comparing the experimental and theoretical I_int(t) interference signal dependencies for the individual wheels of the train set’s railway bogies. Additionally, this table provides the weights subsequently determined using relation (6). The proportionality constant, K_p, used in these weight calculations was established with the aid of static weighting values.

The individual weights obtained from static scales were divided by their respective A_n values, which we determined. Recognizing that the individual proportionality constants exhibited variations across different wheels, we established the overall proportionality constant, K_p, via arithmetic averaging. The calculated K_p value, employed for determining weights from the measured A_n values, is 680 kg/rad. The weights thus calculated are presented in Table 1.

To facilitate a direct comparison between static weights and those calculated using relation (6), the weights are presented in a bar graph (Figure 12).

The most substantial percentage deviation between our calculated weight values and those obtained via static scales is observed for the first wheel of the fifth bogie (corresponding to the ninth wheel in Figure 12). Static measurements indicate that the weights for the 9th and 10th wheels are virtually identical. Nevertheless, equivalent wheel loads should theoretically result in commensurate rail bending, which would be reflected by comparable A_n values detected by the fiber optic sensor. The measured phase change (A_n Gaussian peak) for the 10th wheel, however, deviates by 3 rad, being greater than that for the 9th wheel (Figure 10). As we are unaware of any underlying physical mechanism that could account for such a considerable phase difference with the employed measurement methodology, given the almost identical loads on the 9th and 10th wheels, we postulate that the static scale data, specifically for the 9th wheel of the train set, is anomalous.

5. Conclusions

We utilized a Fabry–Perot interferometric system to measure the weight of a moving train. As train wheels traverse the track, they induce both convex and concave bending, leading to a change in the length of the sensing optical fiber. This length alteration, in turn, manifests as a phase change in the interference signal. The change in fiber length caused by track bending during a bogie’s passage was accurately described using a physical–mathematical model based on three Gaussian functions.

This model enabled us to determine the proportionality constant, K_p, which establishes the relationship between the maximum phase value of the interference signal for individual wheel passages and the corresponding wheel load. As K_p is influenced by various track and rolling stock parameters, it is imperative to determine this constant for a given sensor installation before its practical application.

We have successfully demonstrated this using data from low-speed train operations, where the influence of dynamic vibrations and noise is significantly reduced. Our results confirm reliable performance for speeds up to 20 km/h. It is important to note that the precision of phase determination can be influenced by increased vibration and noise at higher speeds. However, for instances involving low wear of rolling stock, the system’s applicability could extend to higher speeds. Therefore, the presented data evaluation technique offers a viable solution for weighing on railway tracks serving industrial facilities.