Assessment of Anisotropy in Cold In-Place Recycled Materials Using Shear Wave Velocity and Computed Tomography Analysis
Abstract
1. Introduction
2. Objectives
3. Background
3.1. Wave-Based Methods
3.2. The P-RAT
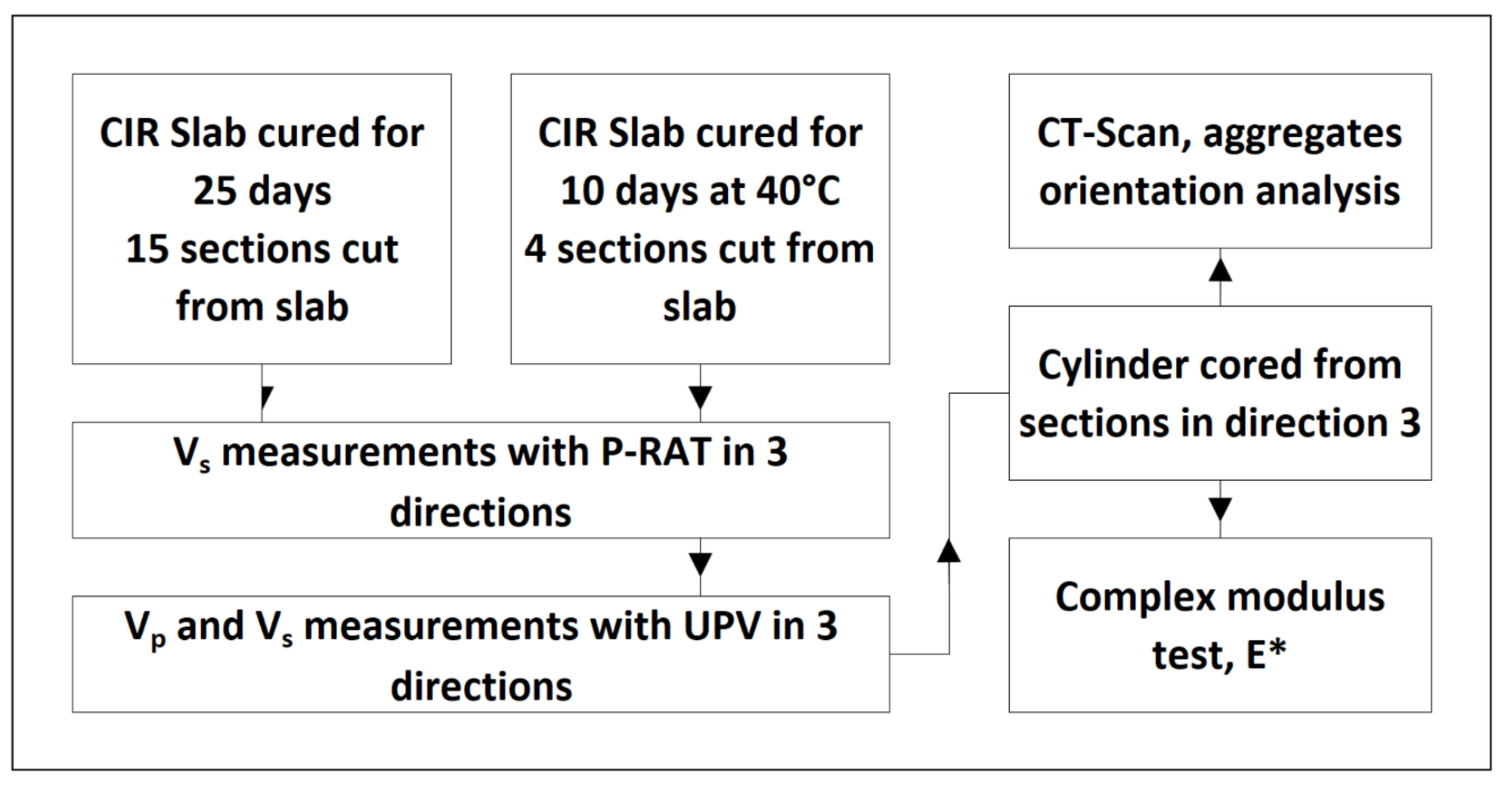
4. Materials and Methods
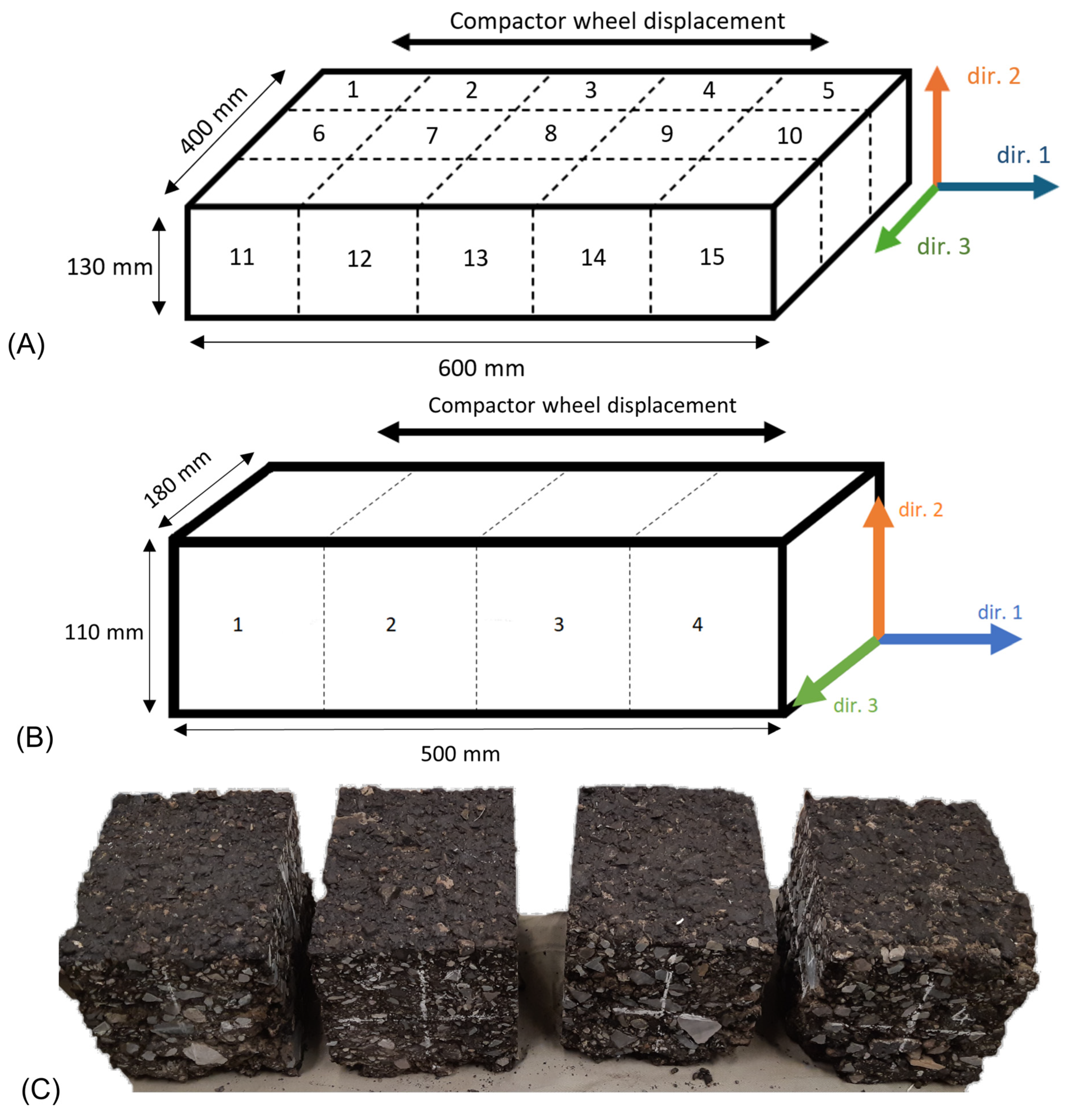
4.1. Materials Used and Specimens
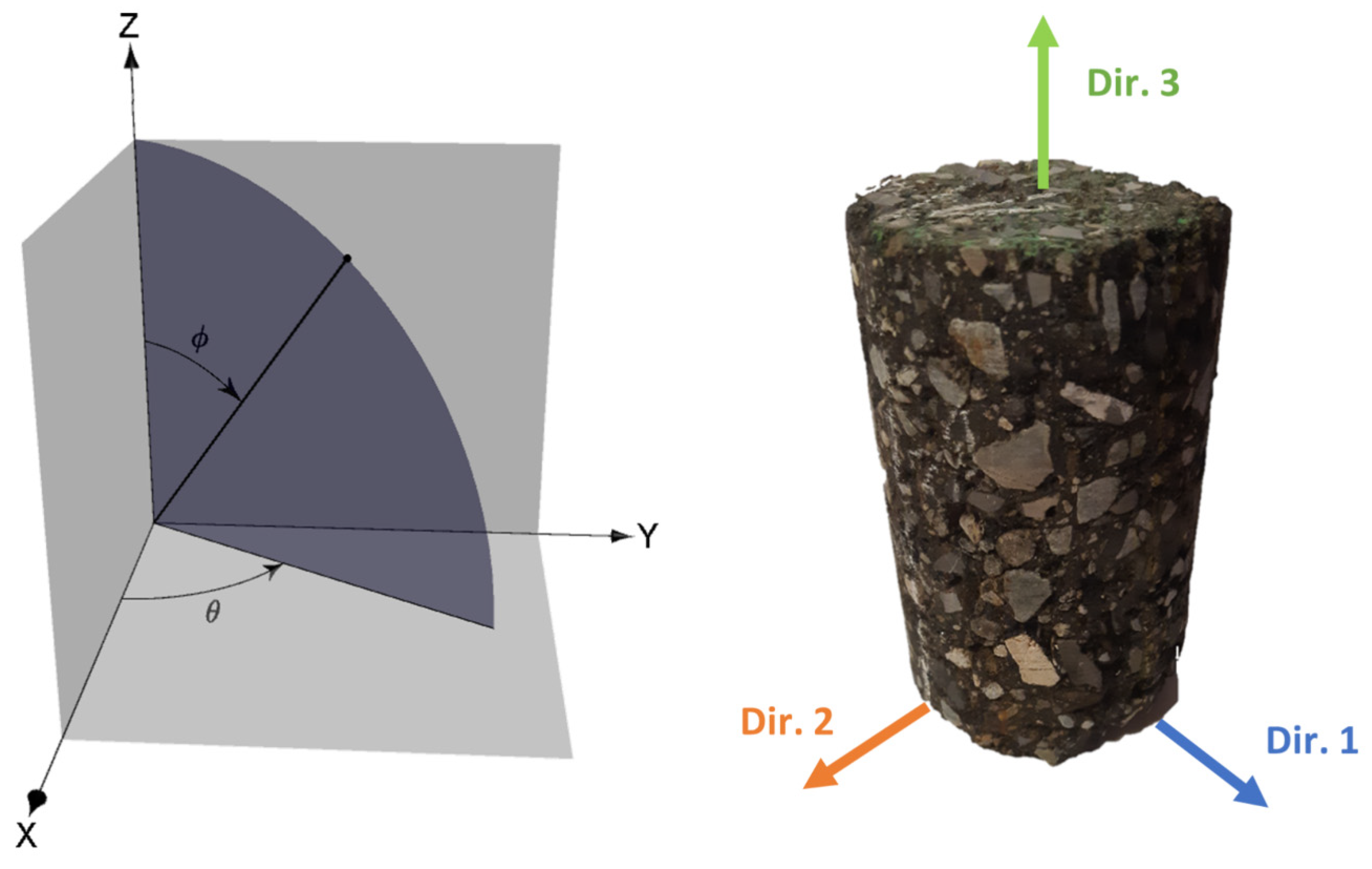
4.2. P-RAT Anisotropy Measurements
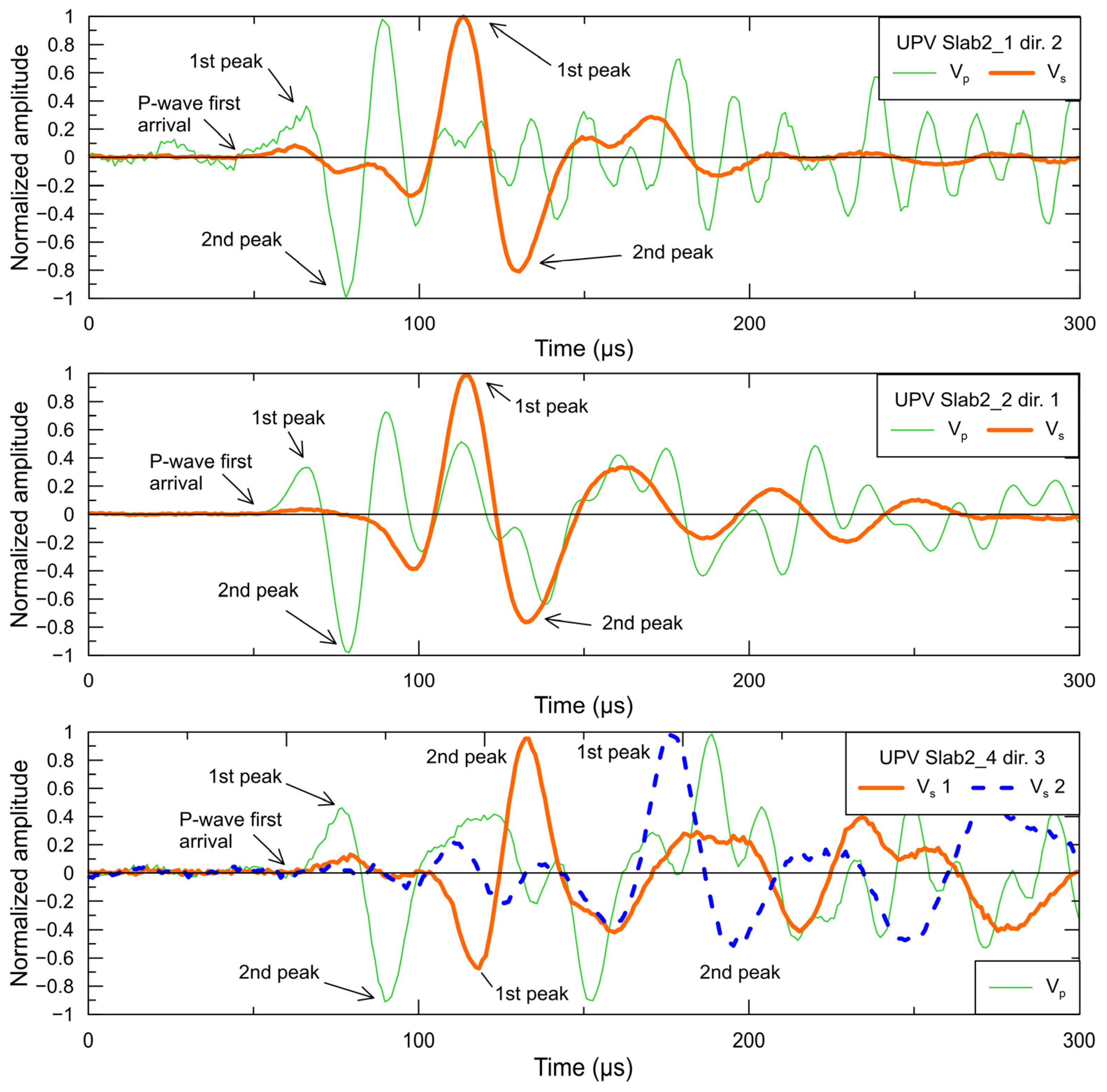
4.3. UPV
4.4. Complex Modulus E*
4.5. Computed Tomography Scan (CT-SCAN) and 3D Image Analysis
5. Results and Analysis
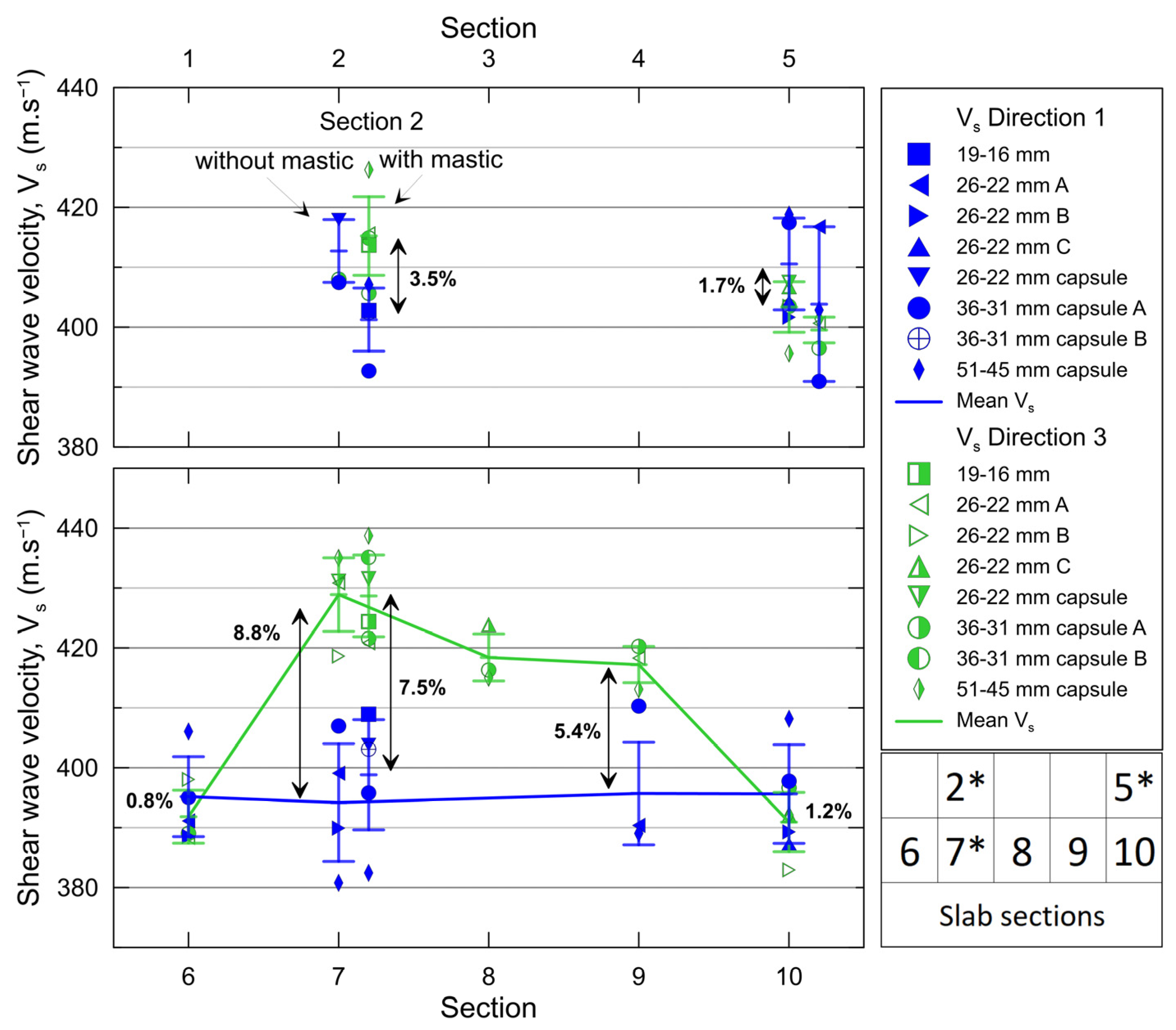
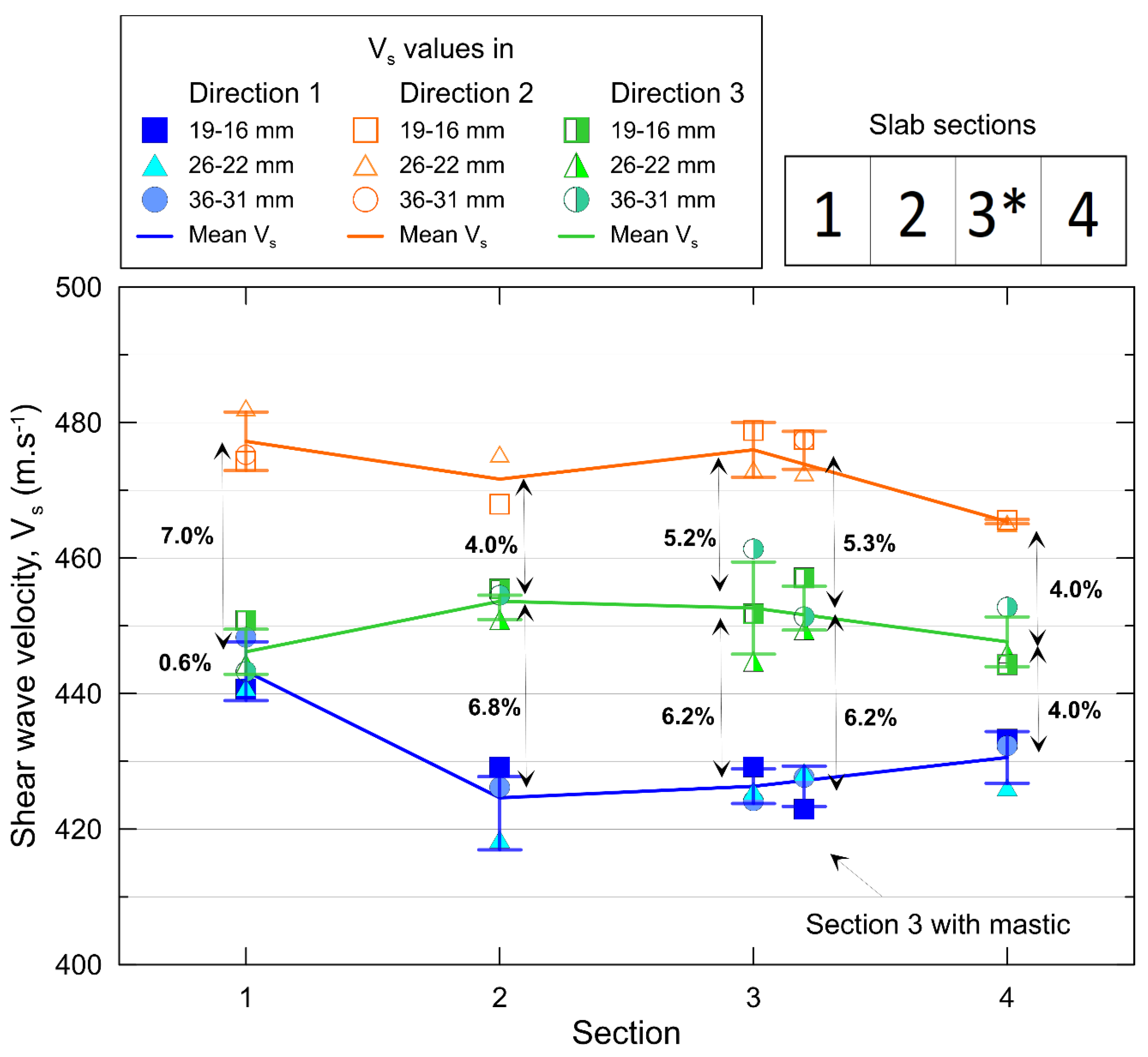
5.1. P-RAT Shear Wave Velocity (Vs) Results
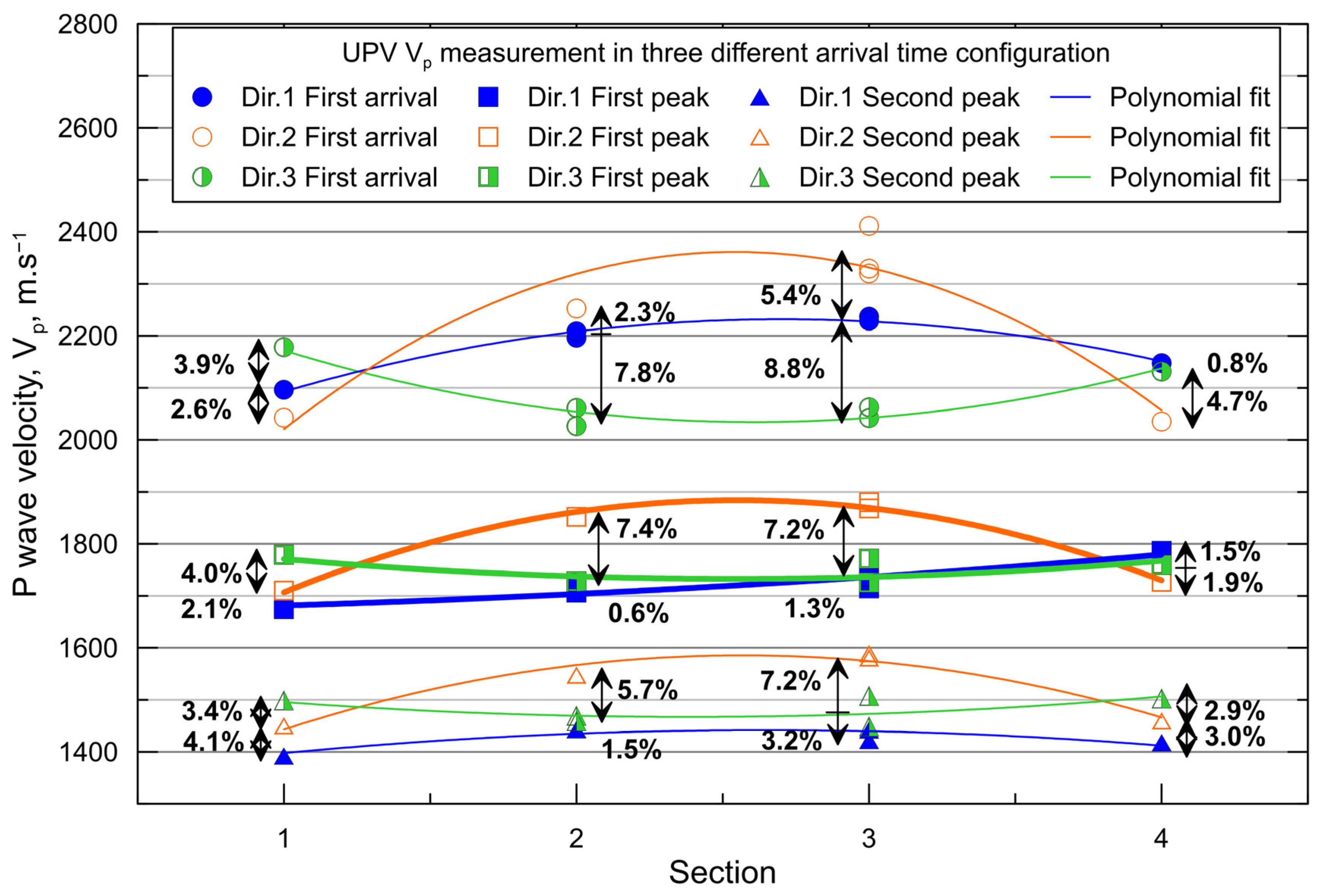
5.2. UPV Test Results
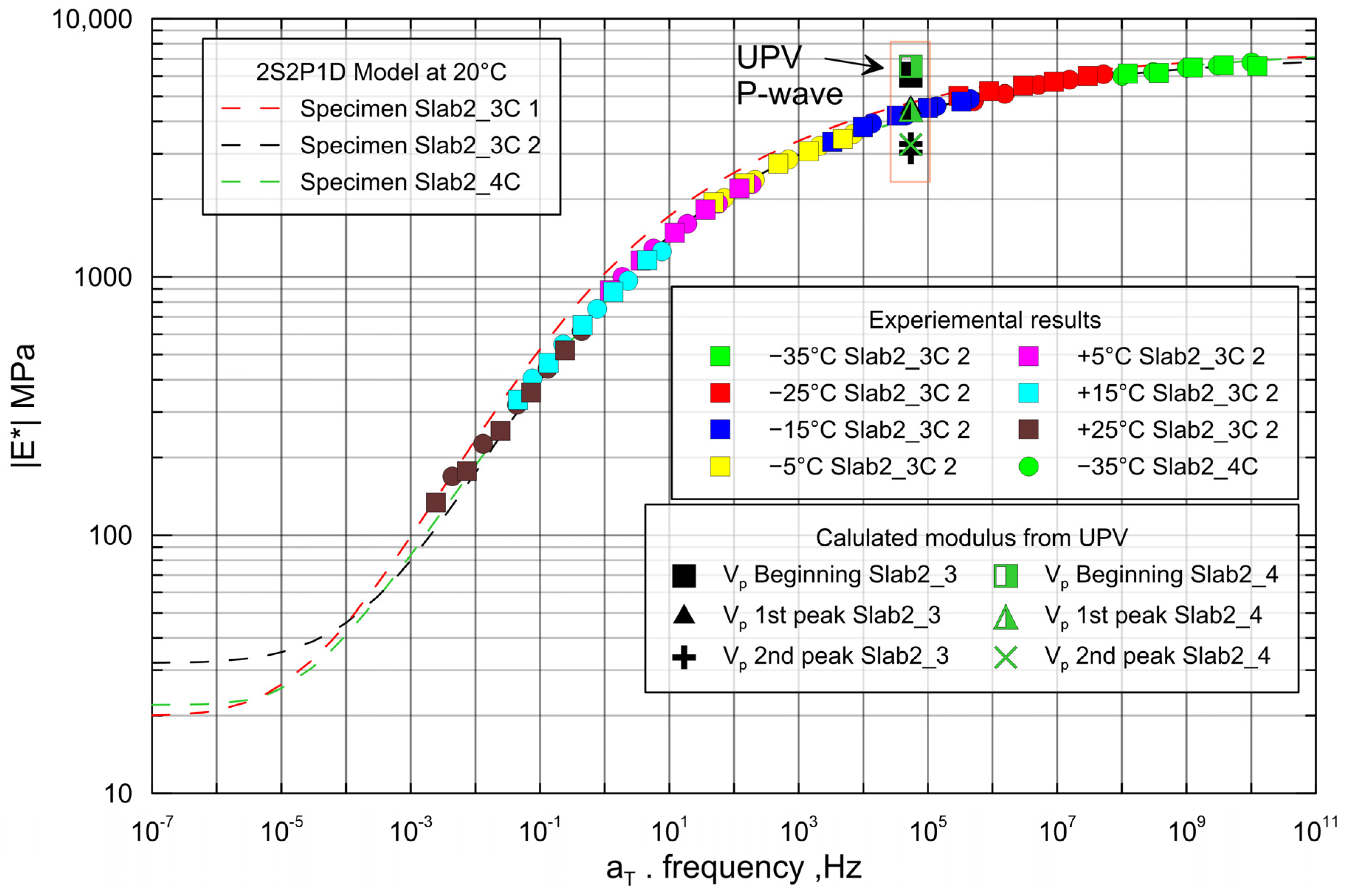
5.3. Complex Modulus
5.4. Three-Dimensional Image Analysis Results
6. Conclusions
- Vs measurements with P-RAT show a systematic anisotropy in the two tested slabs. Different sizes of P-RAT transducers were used and the variability was low. Vs in the direction of compaction is higher than Vs in the orthogonal direction of displacement of the compacting wheel, which is higher than Vs in the direction of the compacting wheel; Vs2 > Vs3 > Vs1. Differences between Vs values range from 0.6 to 11.6%. Vs values on the outer sections of the slabs tend to be closer to one another compared to the middle section. The difference in wave velocities is explained by the compaction method and the dimensions of the mold, which generate uneven confinement in the mix.
- UPV results with PUNDIT also show anisotropy. UPV Vp values are different in every direction, and the same axial symmetry relative to the middle of the slab was observed as in P-RAT results. Vs values from UPV were trickier to obtain, as the arrival time of the wave is hard to determine. Various setups of arrival time were then tested. Vs from P-RAT and Vp from UPV results are consistent one with each other.
- E* results are consistent in the tested specimens, and they were modelized with the 2S2P1D model. Moduli from UPV were plotted in the master curve and the proper arrival time setup were determined to be the first peak for P-wave.
- CT scans highlighted a preferential orientation of the aggregate in the direction of the movement of the compacting wheel, dir. 1. However, a non-negligible part of the aggregates is oriented in the two other directions.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Raschia, S.; Perraton, D.; Graziani, A.; Carter, A. Influence of low production temperatures on compactability and mechanical properties of cold recycled mixtures. Constr. Build. Mater. 2020, 232, 117169. [Google Scholar] [CrossRef]
- Sangiorgi, C.; Tataranni, P.; Simone, A.; Vignali, V.; Lantieri, C.; Dondi, G. A laboratory and filed evaluation of Cold Recycled Mixture for base layer entirely made with Reclaimed Asphalt Pavement. Constr. Build. Mater. 2017, 138, 232–239. [Google Scholar] [CrossRef]
- Orosa, P.; Orozco, G.; Carret, J.C.; Carter, A.; Pasadín, A.R. Compactablility and mechanical properties of cold recycled mixes prepared with different nominal maximum sizes of RAP. Constr. Build. Mater. 2022, 339, 127689. [Google Scholar] [CrossRef]
- Li, Y.; Lyv, Y.; Fang, L.; Zhang, Y. Effects of Cement and Emulsified Asphalt on Properties of Mastics and 100% Cold Recycled Asphalt Mixtures. Materials 2019, 12, 754. [Google Scholar] [CrossRef]
- Kuchiishi, A.K.; Vasconcelos, K.; Bernucci, L.L.B. Effect of mixture composition on the mechanical behavior of cold recycled asphalt mixtures. Int. J. Pavement Eng. 2021, 22, 984–994. [Google Scholar] [CrossRef]
- Raschia, S.; Graziani, A.; Carter, A.; Perraton, D. Laboratory mechanical characterization of cold recycled mixtures produced with different RAP sources. Road Mater. Pavement Des. 2019, 20, 233–246. [Google Scholar] [CrossRef]
- Diefenderfer, B.K.; Bowers, B.F.; Shwartz, C.W.; Farzaneh, A.; Zhang, Z. Dynamic Modulus of Recycled Pavement Mixtures. J. Transp. Res. Board 2016, 2575, 19–26. [Google Scholar] [CrossRef]
- Nguyen, L.N.; Nguyen, M.H.; Dao, D.V.; Nguyen, P.Q.; Nguyen, T.M.T.; Tran, T.D. Effect of curing regimes on the dynamic modulus of entirely RAP cold recycled asphalt mixture. J. Mater. Des. Appl. 2023, 237, 1975–1989. [Google Scholar] [CrossRef]
- Pham, N.H.; Sauzéat, C.; Di Benedetto, H.; González-Leön, J.A.; Barreto, G.; Nicolaï, A.; Jakibowski, M. Analysis and modeling of 3D complex modulus tests on hot and warm bituminous mixtures. Mech. Time-Depend Mater. 2015, 19, 167–186. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Sauzéat, C.; Clec’h, P. Anisotropy of bituminous in the linear viscoelastic domain. Mech. Time-Depend Mater. 2016, 20, 281–297. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Pham, N.H.; Di Benedetto, H.; Sauzéat, C. Anisotropic Behavior of Bituminous Mixtures in Road Pavement Structures. J. Test. Eval. 2020, 48, 178–188. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Klein, K.A.; Fam, M.A. Soils and Waves: Particulate Materials Behavior, Characterization and Process Monitoring, 1st ed.; John Wiley & Sons Ltd.: Chichester, UK, 2001; ISBN 0-471-49058-X. [Google Scholar]
- Nguyen, T.L.; Szymkiewicz, F.; Reiffsteck, P.; Bourgeois, E.; Mestat, P. Caractérisation et effet de l’anisotropie sur le comportement de sols reconstitués. Rev. Can. De Géotechnique 2011, 48, 1520–1536. [Google Scholar] [CrossRef]
- Massad, E.; Tashman, L.; Somedavan, N.; Little, D. Micromechanics-Based Analysis of Stiffness Anisotropy in Asphalt Mixtures. J. Mater. Civ. Eng. 2002, 14, 374–383. [Google Scholar] [CrossRef]
- Underwood, S.; Heidari, A.H.; Guddati, M.; Kim, R. Experimental Investigation of Anisotropy in Asphalt Concrete. J. Transp. 2005, 1929, 238–247. [Google Scholar] [CrossRef]
- Bhasin, A.; Izadi, A.; Bedgaker, S. Three dimensional distribution of the mastic in asphalt composites. Constr. Build. Mater. 2011, 25, 4079–4087. [Google Scholar] [CrossRef]
- Alanazi, N.; Kassem, E.; Jung, S.J. Evaluation of the Anisotropy of Asphalt Mixtures. J. Transp. Eng. Part B Pavements 2018, 144, 04018022. [Google Scholar] [CrossRef]
- Hassan, N.A.; Airey, G.D.; Khan, R.; Collop, A.C. Nondestructive characterization of the effect of asphalt mixture compaction on aggregate orientation and segregation using X-ray computed tomography. Int. J. Pavement Res. Technol. 2012, 5, 84–92. [Google Scholar]
- Huang, J.; Pei, J.; Li, Y.; Yang, H.; Li, R.; Zhang, J.; Wen, Y. Investigation on aggregate particles migration characteristics of porous asphalt concrete (PAC) during vibration compaction process. Constr. Build. Mater. 2020, 243, 118153. [Google Scholar] [CrossRef]
- Quinteros, V.S.; Carraro, J.A.H. The initial fabric of undisturbed and reconstituted fluvial sand. Geotechnique 2021, 73, 1–15. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Sauzéat, C.; Sohm, J. Stiffness of Bituminous Mixtures Using Ultrasonic Wave Propagation. Road Mater. Pavement Des. 2009, 10, 789–814. [Google Scholar] [CrossRef]
- Mounier, D.; Di Benedetto, H.; Sauzéat, C. Determination of bituminous mixtures linear properties using ultrasonic wave propagation. Constr. Build. Mater. 2012, 36, 638–647. [Google Scholar] [CrossRef]
- Arulnathan, R.; Boulanger, R.W.; Riemer, M.F. Analysis of benderelement tests. ASTM Geotech. Test. J. 1998, 21, 120–131. [Google Scholar] [CrossRef]
- Brandenberg, S.J.; Kutter, B.L.; Wilson, D.W. Fast Stacking and Phase Corrections of Shear Wave Signals in a Noisy Environment. ASCE J. Geotech. Geoenviron. Eng. 2008, 134, 1154–1165. [Google Scholar] [CrossRef]
- Abd Elhafeez, T.; Amer, R.; Saad, A.; El Kady, H.; Madi, M. Evaluation of Flexible Pavement Mixtures Using Conventional Test and Ultrasonic Wave Propagation. Adv. Civ. Eng. Mater. 2014, 3, 1–20. [Google Scholar] [CrossRef]
- Larcher, N.; Takarli, M.; Angellier, N.; Petit, C.; Sebbah, H. High frequency shear modulus of bitumen by ultrasonic measurements. In Proceedings of the 5th European Asphalt Technology Association Conference, Braunschweig, Germany, 3–5 June 2013; p. 13. [Google Scholar]
- Mounier, D.; Di Benedetto, H.; Sauzéat, C.; Bilodeau, K. Observation of Fatigue of Bituminous Mixtures Using Wave Propagation. J. Mater. Civ. Eng. 2016, 28, 04015083. [Google Scholar] [CrossRef]
- Zargar, M.; Banerjee, S.; Bullen, F.; Ayers, R. An investigation into the Use of Ultrasonic Wave Transmission Techniques to Evaluate Air Voids in Asphalt, GCEC 2017. In Proceedings of the 1st Global Civil Engineering Conference, Kuala Lumpur, Malaysia, 25–28 July 2017; pp. 1427–1439. [Google Scholar] [CrossRef]
- Hou, S.; Deng, Y.; Jin, R.; Shi, X.; Luo, X. Relationships between Physical, Mechanical and Acoustic Properties of Asphalt Mixtures Using Ultrasonic Testing. Buildings 2022, 12, 306. [Google Scholar] [CrossRef]
- Karray, M.; Ben Romdhan, M.; Hussien, M.H.; Ethier, Y. Measuring shear wave velocity of granular material using the piezoelectric ring-actuator technique(P-RAT). Can. Geotech. J. 2015, 52, 1302–1317. [Google Scholar] [CrossRef]
- Tavassoti-Kheiry, P.; Solaimanian, M.; Qiu, T. Characterization of High RAP/RAS Asphalt Mixtures Using Resonant Column Tests. J. Mater. Civ. Eng. 2016, 28, 04016143. [Google Scholar] [CrossRef]
- Elbeggo, D.; Hussien, M.N.; Ethier, Y.; Karray, M. Robustness of the P-RAT in the Shear-wave Velocity Measurement of Soft Clays. J. Geotech. Geoenviron. Eng. 2019, 145, 04019014. [Google Scholar] [CrossRef]
- Lecuru, Q.; Ethier, Y.; Carter, A.; Karray, M. Characterization of Cold In-Place Recycled Materials at Young Age Using Shear Wave Velocity. Adv. Civ. Eng. Mater. 2019, 8, 336–354. [Google Scholar] [CrossRef]
- Lecuru, Q.; Ethier, Y.; Carter, A.; Karray, M. Early-age stiffening of Cold Recycled Bituminous Materials using shear wave velocity. J. Test. Eval. 2025; accepted. [Google Scholar]
- Soliman, N.A.; Khayat, K.H.; Karray, M.; Omran, A.F. Piezoelectric ring actuator technique to monitor early-age properties of cement-based materials. Cem. Concr. Compos. 2015, 63, 84–95. [Google Scholar] [CrossRef]
- Naji, S.; Khayat, K.H.; Karray, M. Assessment of Static Stability of Concrete Using Shear Wave Velocity Approach. ACI Mater. J. 2017, 114, 105–115. [Google Scholar] [CrossRef]
- Naji, S.; Khayat, K.H.; Karray, M. Effect of piezoeletric ring sensor size on early-age property monitoring of self-consolidating concrete. ACI Mater. J. 2018, 115, 813–824. [Google Scholar] [CrossRef]
- Mhenni, A.; Hussien, M.N.; Karray, M. Improvement of the Piezo-Electric Ring Actuator Technique (P-RAT) Using 3D Numerical Simulations. In Proceedings of the 68th Canadian Geotechnical Conference, Québec, QC, Canada, 20–23 September 2015; p. 7. [Google Scholar]
- Ministère des Transports du Québec (MTQ). Détermination de la Densité Brute et de la Masse Volumique des Enrobés à Chaud Compactés, LC 26-040; Ministère des Transports du Québec: Québec, QC, Canada, 2023.
- Olard, F.; Di Benedetto, H. General “2S2P1D” Model and Relation Between the Linear Viscoelastic Behaviours of Bituminous Binders and Mixes. Road Mater. Pavement Des. 2003, 4, 184–224. [Google Scholar] [CrossRef]
- Perraton, D.; Di Benedetto, H.; Sauzéat, C.; Nguyen, Q.T.; Pouget, S. Three-Dimensional Linear Viscoelastic Properties of Two Bituminous Mixtures Made with the Same Binder. J. Mater. Civ. Eng. 2018, 30, 04018305. [Google Scholar] [CrossRef]
- Lin, M.; Hu, C.; Guan, H.; Easa, S.M.; Jiang, Z. Impacts of Material Orthotropy on Mechanical Behaviors of Asphalt Pavements. Appl. Sci. 2021, 11, 5481. [Google Scholar] [CrossRef]
- Pennington, D.S.; Nash, D.F.T.; Lings, M.L. Anisotropy of G0 shear stiffness in Gault Clay. Géotechnique 1997, 47, 391–398. [Google Scholar] [CrossRef]



| Method | Specimen | Slab2_1C | Slab2_2C | Slab2_3C | Slab2_4C |
|---|---|---|---|---|---|
| LC 26-040 | Volumetric bulk density (g·cm−3) | 1.910 | 1.940 | 1.985 | 1.900 |
| Air void ratio (%) | 24.1 | 22.9 | 21.1 | 24.5 | |
| Three-dimensional analysis | Air void ratio (%) | N.A. | 17.2 | 16.5 | 17.1 |
| Calculated bulk density (g·cm−3) | N.A. | 2.084 | 2.102 | 2.086 |
| Section | Vs1 (m·s−1) | Vs3 (m·s−1) | ||||
|---|---|---|---|---|---|---|
| Min. | Max. | σ% | Min | Max | σ% | |
| Slab1_2 | 407.5 | 417.9 | 1.8% | 408.0 | 408.0 | N.A. |
| Slab1_2 mastic | 388.4 | 401.9 | 1.4% | 401.4 | 420.9 | 1.7% |
| Slab1_5 | 401.6 | 418.8 | 2.1% | 395.6 | 407.4 | 1.2% |
| Slab1_5 mastic | 387.2 | 411.7 | 3.1% | 393.8 | 398.5 | 0.6% |
| Slab1_6 | 388.5 | 406.0 | 1.9% | 388.4 | 398.1 | 1.4% |
| Slab1_7 | 380.8 | 406.9 | 2.9% | 418.6 | 435.0 | 1.6% |
| Slab1_7 mastic | 378.9 | 403.9 | 2.5% | 415.8 | 432.7 | 1.7% |
| Slab1_8 | N.A. | N.A. | N.A. | 415.0 | 423.9 | 1.1% |
| Slab1_9 | 389.0 | 410.3 | 2.5% | 413.1 | 420.3 | 0.9% |
| Slab1_10 | 387.3 | 408.2 | 2.4% | 383.0 | 396.6 | 1.5% |
| Section | Vs1 (m·s−1) | Vs2 (m·s−1) | Vs3 (m·s−1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 19–16 | 26–22 | 36–31 | 19–16 | 26–22 | 36–31 | 19–16 | 26–22 | 36–31 | |
| Slab2_1 | 440.7 | 440.9 | 448.3 | 474.3 | 482.2 | 475.2 | 450.8 | 444.5 | 443.2 |
| σ% | 1.0% | σ% | 0.9% | σ% | 0.9% | ||||
| Slab2_2 | 429.1 | 418.5 | 426.2 | 467.9 | 475.4 | N.A. | 455.4 | 450.9 | 454.5 |
| σ% | 1.3% | σ% | 1.1% | σ% | 0.5% | ||||
| Slab2_3 | 429.2 | 425.6 | 424.2 | 478.8 | 473.1 | N.A. | 451.8 | 444.8 | 461.3 |
| σ% | 0.6% | σ% | 0.8% | σ% | 1.8% | ||||
| Slab2_3 mastic | 417.0 | 422.2 | 421.4 | 465.6 | 461.2 | 465.6 | 450.3 | 443.2 | 445.0 |
| σ% | 0.7% | σ% | 0.5% | σ% | 0.8% | ||||
| Slab2_4 | 433.2 | 426.2 | 432.3 | 465.6 | 465.1 | N.A. | 444.3 | 446.0 | 452.8 |
| σ% | 0.9% | σ% | 0.1% | σ% | 1.0% | ||||
| E00 | E0 | ν00 | ν0 | k | H | δ | τ | β | C1 | C2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MPa | MPa | (Tref) | |||||||||
| Slab2_3C 1 | 20 | 7500 | / | / | 0.170 | 0.475 | 2.56 | 0.2 (10.93) | 5000 | 20.00 | 159.12 |
| Slab2_3C 2 | 32 | 7200 | / | / | 0.170 | 0.490 | 2.69 | 1.1 (4.96) | 5000 | 24.02 | 158.55 |
| Slab2_4C | 22 | 7675 | / | / | 0.161 | 0.450 | 2.85 | 1.1 (4.96) | 5000 | 23.47 | 159.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lecuru, Q.; Ethier, Y.; Carter, A.; Karray, M. Assessment of Anisotropy in Cold In-Place Recycled Materials Using Shear Wave Velocity and Computed Tomography Analysis. Infrastructures 2025, 10, 115. https://doi.org/10.3390/infrastructures10050115
Lecuru Q, Ethier Y, Carter A, Karray M. Assessment of Anisotropy in Cold In-Place Recycled Materials Using Shear Wave Velocity and Computed Tomography Analysis. Infrastructures. 2025; 10(5):115. https://doi.org/10.3390/infrastructures10050115
Chicago/Turabian StyleLecuru, Quentin, Yannic Ethier, Alan Carter, and Mourad Karray. 2025. "Assessment of Anisotropy in Cold In-Place Recycled Materials Using Shear Wave Velocity and Computed Tomography Analysis" Infrastructures 10, no. 5: 115. https://doi.org/10.3390/infrastructures10050115
APA StyleLecuru, Q., Ethier, Y., Carter, A., & Karray, M. (2025). Assessment of Anisotropy in Cold In-Place Recycled Materials Using Shear Wave Velocity and Computed Tomography Analysis. Infrastructures, 10(5), 115. https://doi.org/10.3390/infrastructures10050115









