The Effect of Girder Profiles on the Probability of Fatigue Damage in Continuous I-Multigirder Steel Bridges
Abstract
1. Introduction
2. Materials and Methods
2.1. Characterization of Bridges
2.2. Representative Bridge Sample
2.3. Characterization of Truck Configurations
2.4. Structural Analysis
2.5. Reliability Analysis for Fatigue
| Variable | Unit | Parameters | Values | Distribution | Reference | |
|---|---|---|---|---|---|---|
| Truck gross weight, GVW | kN | / | Table 2 | Table 2 | Varies | This study |
| Axle weight ratio | - | Mean/COV | Table 3 | Table 3 | Normal | [67] |
| Axle spacings | m | Mean/COV | Table 4 | Table 4 | Normal | [67] |
| Fatigue damage model, | - | Mean/COV | 1.00 | 0.15 | Weibull | [40,75] |
| Average Daily Truck Traffic, | - | Mean/COV | 1236 | 1.00 | Log-normal | This study |
| Stress ratio, | - | Mean/COV | 0.97 | 0.09 | Normal | [40], This study |
| Distribution factor ratio, G | - | Mean/COV | 0.38 | 0.13 | Normal | [40] |
| Dynamic impact, I | - | Mean/COV | 1.10 | 0.11 | Normal | [40] |
| Headway factor, H | - | Mean/COV | 0.88 | 0.21 | Normal | [74] |
| Gross weight factor, | - | Mean/COV | 0.35 | 0.06 | Log-normal | [40] |
| Fatigue stress range ratio, | - | Mean/COV | Table 6 | Table 6 | Log-normal | [40] |
3. Results
3.1. Model Validation
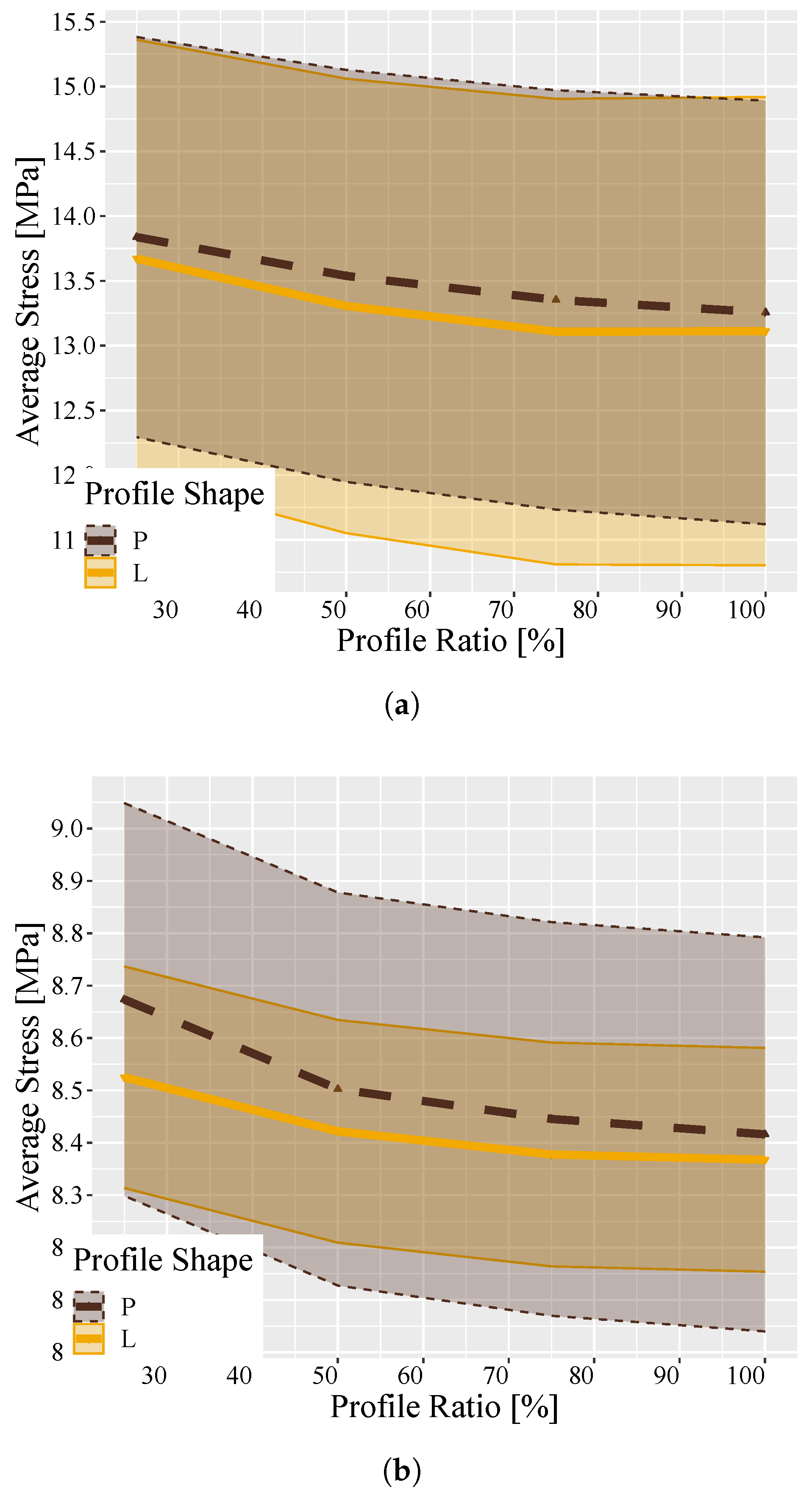
3.2. Stress Analysis
3.3. Reliability Analysis
3.4. Economic Impact of Different Shape Profiles
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AASHTO | American Association of State Highway and Transportation Officials |
| LRFD | Load and Resistance Factor Design |
| WIM | Weigh-In-Motion |
| LTPP | Long-Term Pavement Program |
| LTBP | Long-Term Bridge Program |
| FHWA | Federal Highway Administration |
References
- Han, Y.; Li, K.; Cai, C.; Wang, L.; Xu, G. Fatigue reliability assessment of long-span steel-truss suspension bridges under the combined action of random traffic and wind loads. J. Bridge Eng. 2020, 25, 04020003. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, X. Thoughts on the development of bridge technology in China. Engineering 2019, 5, 1120–1130. [Google Scholar] [CrossRef]
- Lu, D.; Wei, W.; He, X. Optimization and application of fatigue design based on AASHTO code. China J. Highw. Transp. 2017, 30, 40. [Google Scholar]
- Qin, S.; Gao, Z. Developments and prospects of long-span high-speed railway bridge technologies in China. Engineering 2017, 3, 787–794. [Google Scholar] [CrossRef]
- Timoshenko, S. History of Strength of Materials: With a Brief Account of the History of Theory of Elasticity and Theory of Structures; Dover Publications: Mineola, NY, USA, 1983. [Google Scholar]
- Fiorillo, G.; Ghosn, M. Failure Analysis of Continuous Highway Steel I-Multigirder Bridges under the Combined Effect of Fatigue and Overloading Events. J. Bridge Eng. 2025, 30, 04024105. [Google Scholar] [CrossRef]
- Sharifi, Y. Uniform corrosion wastage effects on the load-carrying capacity of damaged steel beams. Adv. Steel Constr. 2012, 8, 153–167. [Google Scholar]
- Schilling, C.G.; Klippstein, K.H. New method for fatigue design of bridges. J. Struct. Div. 1978, 104, 425–438. [Google Scholar] [CrossRef]
- Schilling, C. A new method for the fatigue design of steel highway bridges. Civ. Eng. Pract. Des. Eng. 1984, 3, 541–550. [Google Scholar]
- Agerskov, H. Fatigue in steel structures under random loading. J. Constr. Steel Res. 2000, 53, 283–305. [Google Scholar] [CrossRef]
- Schilling, C.G. Stress cycles for fatigue design of steel bridges. J. Struct. Eng. 1984, 110, 1222–1234. [Google Scholar] [CrossRef]
- Deng, L.; Nie, L.; Zhong, W.; Wang, W. Developing fatigue vehicle models for bridge fatigue assessment under different traffic conditions. J. Bridge Eng. 2021, 26, 04020122. [Google Scholar] [CrossRef]
- Moses, F. Weigh-In-Motion Systems Using Instrumented Bridges. Transp. Eng. J. 1979, 105, 233–249. [Google Scholar] [CrossRef]
- Moses, F.; Ghosn, M. Instrumentation for Weighing Trucks-In-Motion for Highway Bridge Loads, Final Report; Federal Highway Administration: Washington, DC, USA, 1983; Volume FHWA/OH-83/001. [Google Scholar]
- Ojio, T.; Carey, C.; OBrien, E.J.; Doherty, C.; Taylor, S.E. Contactless bridge weigh-in-motion. J. Bridge Eng. 2016, 21, 04016032. [Google Scholar] [CrossRef]
- Yan, D.; Luo, Y.; Lu, N.; Yuan, M.; Beer, M. Fatigue stress spectra and reliability evaluation of short-to medium-span bridges under stochastic and dynamic traffic loads. J. Bridge Eng. 2017, 22, 04017102. [Google Scholar] [CrossRef]
- Alampalli, S.; Lund, R. Estimating fatigue life of bridge components using measured strains. J. Bridge Eng. 2006, 11, 725–736. [Google Scholar] [CrossRef]
- Saberi, M.R.; Rahai, A.R.; Sanayei, M.; Vogel, R.M. Bridge fatigue service-life estimation using operational strain measurements. J. Bridge Eng. 2016, 21, 04016005. [Google Scholar] [CrossRef]
- Kwon, K.; Frangopol, D.M.; Soliman, M. Probabilistic fatigue life estimation of steel bridges by using a bilinear S-N approach. J. Bridge Eng. 2012, 17, 58–70. [Google Scholar] [CrossRef]
- Yen, B.T.; Hodgson, I.C.; Zhou, Y.E.; Crudele, B.B. Bilinear S-N Curves and Equivalent Stress Ranges for Fatigue Life Estimation. J. Bridge Eng. 2013, 18, 26–30. [Google Scholar] [CrossRef]
- Leander, J.; Norlin, B.; Karoumi, R. Reliability-based calibration of fatigue safety factors for existing steel bridges. J. Bridge Eng. 2015, 20, 04014107. [Google Scholar] [CrossRef]
- FHWA. LTBP InfoBridge; Federal Highway Administration, U.S. Department of Transportation: Washington, DC, USA, 2023. [Google Scholar]
- CNSA. Canada’s Core Public Infrastructure Survey: Roads, Bridges and Tunnels, 2016; Canada’s National Statistics Agency: Ottawa, ON, Canada, 2016. [Google Scholar]
- Ghosn, M.; Moses, F. Reliability calibration of bridge design code. J. Struct. Eng. 1986, 112, 745–763. [Google Scholar] [CrossRef]
- Tabsh, S.W.; Nowak, A.S. Reliability of highway girder bridges. J. Struct. Eng. 1991, 117, 2372–2388. [Google Scholar] [CrossRef]
- Ghosn, M.; Moses, F. Redundancy in Highway Bridge Superstructures; Number NCHRP 406; Transportation Research Board, National Cooperative Highway Research Program: Washington, DC, USA, 1998. [Google Scholar]
- Ghosn, M. Development of Truck Weight Regulations Using Bridge Reliability Model. J. Bridge Eng. 2000, 5, 293–303. [Google Scholar] [CrossRef]
- O’Connor, A.; O’Brien, E.J. Traffic load modelling and factors influencing the accuracy of predicted extremes. Can. J. Civ. Eng. 2005, 32, 270–278. [Google Scholar] [CrossRef]
- Ghosn, M.; Sivakumar, B.; Miao, F. Development of State-Specific Load and Resistance Factor Rating Method. J. Bridge Eng. 2013, 18, 351–361. [Google Scholar] [CrossRef]
- Fiorillo, G.; Ghosn, M. Procedure for statistical categorization of overweight vehicles in a WIM database. J. Transp. Eng. 2014, 140, 04014011. [Google Scholar] [CrossRef]
- Fiorillo, G.; Ghosn, M. Fragility analysis of bridges due to overweight traffic load. Struct. Infrastruct. Eng. 2018, 14, 619–633. [Google Scholar] [CrossRef]
- FHWA. LTPP InfoPave; Federal Highway Administration, U.S. Department of Transportation: Washington, DC, USA, 2023. [Google Scholar]
- Nowak, A.; Hong, Y. Bridge Live Load Models. J. Struct. Eng. 1991, 121, 1245–1251. [Google Scholar] [CrossRef]
- Fiorillo, G.; Ghosn, M. MPI Parallel Monte Carlo Framework for the Reliability Analysis of Highway Bridges. J. Comput. Civ. Eng. 2018, 32, 04017087. [Google Scholar] [CrossRef]
- Fiorillo, G.; Ghosn, M. Risk-based importance factors for bridge networks under highway traffic loads. Struct. Infrastruct. Eng. 2018, 15, 113–126. [Google Scholar] [CrossRef]
- Fiorillo, G.; Ghosn, M. Structural Redundancy, Robustness, and Disproportionate Collapse Analysis of Highway Bridge Superstructures. J. Struct. Eng. 2022, 148, 04022075. [Google Scholar] [CrossRef]
- Moses, F.; Goble, G.; Pavia, A. Truck Loading Model for Bridge Fatigue. In Proceedings of the Specialty Conference on Metal Bridges American Society of Civil Engineers; American Association of State Highway and Transportation Officials, and Transportation Research Board: St. Louis, MO, USA, 1974. [Google Scholar]
- Goble, G.; Moses, F.; Pavia, A. Applications of a bridge measurement system. Transp. Res. Rec. 1976, 579, 36–47. [Google Scholar]
- Moses, F. Structural system reliability and optimization. Comput. Struct. 1977, 7, 283–290. [Google Scholar] [CrossRef]
- Nyman, W.E.; Moses, F. Calibration of bridge fatigue design model. J. Struct. Eng. 1985, 111, 1251–1266. [Google Scholar] [CrossRef]
- Yazdani, N.; Albrecht, P. Risk analysis of fatigue failure of highway steel bridges. J. Struct. Eng. 1987, 113, 483–500. [Google Scholar] [CrossRef]
- Raju, S.K.; Moses, F.; Schilling, C.G. Reliability calibration of fatigue evaluation and design procedures. J. Struct. Eng. 1990, 116, 1356–1369. [Google Scholar] [CrossRef]
- Laman, J.A.; Nowak, A.S. Fatigue-load models for girder bridges. J. Struct. Eng. 1996, 122, 726–733. [Google Scholar] [CrossRef]
- Agerskov, H.; Nielsen, J.A. Fatigue in steel highway bridges under random loading. J. Struct. Eng. 1999, 125, 152–162. [Google Scholar] [CrossRef]
- Metzger, A.T.; Huckelbridge, A.A., Jr. Temporal nature of fatigue damage in highway bridges. J. Bridge Eng. 2009, 14, 444–451. [Google Scholar] [CrossRef]
- Wang, C.S.; Hao, L.; Fu, B.N. Fatigue reliability updating evaluation of existing steel bridges. J. Bridge Eng. 2012, 17, 955–965. [Google Scholar] [CrossRef]
- Zhang, W.; Cai, C. Fatigue reliability assessment for existing bridges considering vehicle speed and road surface conditions. J. Bridge Eng. 2012, 17, 443–453. [Google Scholar] [CrossRef]
- Bowman, M.D.; Fu, G.; Zhou, Y.E.; Connor, R.J.; Godbole, A.A. Fatigue Evaluation of Steel Bridges; Volume NCHRP Report 721; Transportation Research Board, National Academy Press: Washington, DC, USA, 2012. [Google Scholar]
- Putri, C.A.; Tateishi, K.; Shimizu, M.; Hanji, T. Failure probability for fatigue crack in web plate of bridge girder. Int. J. Steel Struct. 2022, 22, 42–55. [Google Scholar] [CrossRef]
- Croce, P. Background to fatigue load models for Eurocode 1: Part 2 Traffic Loads. Prog. Struct. Eng. Mater. 2001, 3, 335–345. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhai, H.; Bao, W.; Liu, Y. Research on standard fatigue vehicular load for highway bridges. Highway 2009, 12, 21–25. [Google Scholar]
- Chen, W.z.; Xu, J.; Yan, B.c.; Wang, Z.p. Fatigue load model for highway bridges in heavily loaded areas of China. Adv. Steel Constr. 2015, 11, 322–333. [Google Scholar]
- Liu, Y.; Li, D.; Zhang, Z.; Zhang, H.; Jiang, N. Fatigue load model using the weigh-in-motion system for highway bridges in China. J. Bridge Eng. 2017, 22, 04017011. [Google Scholar] [CrossRef]
- Han, X.; Frangopol, D.M. Fatigue reliability analysis considering corrosion effects and integrating SHM information. Eng. Struct. 2022, 272, 114967. [Google Scholar] [CrossRef]
- Fisher, J.W.; Frank, K.H.; Hirt, M.A.; McNamee, B.M. Effect of Weldments on the Fatigue Strength of Steel Beams; Number NCHRP Report 102; Transportation Research Board, National Cooperative Highway Research Program: Washington, DC, USA, 1970. [Google Scholar]
- Fisher, J.W.; Mertz, D.R.; Zhong, A. Steel Bridge Members Under Variable Amplitude Long Life Fatigue Loading; Number NCHRP Report 267; Transportation Research Board, National Cooperative Highway Research Program: Washington, DC, USA, 1983. [Google Scholar]
- Dexter, R.J.; Wright, W.J.; Fisher, J.W. Fatigue and fracture of steel girders. J. Bridge Eng. 2004, 9, 278–286. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 149–164. [Google Scholar] [CrossRef]
- McConnell, J.R.; Almoosi, Y.S. Field Evaluation of Fatigue Stresses in a Modern Highly Skewed Steel I-Girder Bridge. J. Bridge Eng. 2022, 27, 04022005. [Google Scholar] [CrossRef]
- Sivakumar, B.; Ghosn, M.; Moses, F. Protocols for Collecting and Using Traffic Data in Bridge Design; Number NCHRP Report 683; Transportation Research Board, National Academy Press: Washington, DC, USA, 2011. [Google Scholar]
- Chotickai, P.; Bowman, M.D. Truck models for improved fatigue life predictions of steel bridges. J. Bridge Eng. 2006, 11, 71–80. [Google Scholar] [CrossRef]
- Grubb, M.A.; Wilson, K.E.; White, C.D.; Nickas, W.N. Load and Resistance Factor Design (LRFD) for Highway Bridge Superstructures-Reference Manual; Technical Report; Federal Highway Administration, U.S. Department of Transportation: Washington, DC, USA, 2015. [Google Scholar]
- Ghosn, M.; Yang, J.; Beal, D.; Sivakumar, B. Bridge System Safety and Redundancy; Number NCHRP Report 776; Transportation Research Board, National Academy Press: Washington, DC, USA, 2014. [Google Scholar]
- Ghosn, M.; Fiorillo, G.; Gayovyy, V.; Getso, T.; Ahmed, S.; Parker, N. Effect of Overweight Vehicles on NYSDOT Infrastructure; Number NYSDOT C-08-13; New York State Department of Transportation: Albany, NY, USA, 2015. [Google Scholar]
- Pushka, A.; Regehr, J.D.; Fiorillo, G.; Mufti, A.; Algohi, B. Reliability analysis of typical highway bridges in Manitoba designed to the Modified HSS-25 live load model. Can. J. Civ. Eng. 2022, 49, 899–909. [Google Scholar] [CrossRef]
- USDOT. Traffic Monitoring Guide; Federal Highway Administration: Washington, DC, USA, 2022. [Google Scholar]
- Fiorillo, G. Reliability and Risk Analysis of Bridge Networks. Ph.D. Thesis, The City College of the City University of New York (CUNY), New York, NY, USA, 2016. [Google Scholar]
- Gere, J.M.; Timoshenko, S.P. Mechanics of Materials; International Thomson Publishing: Boston, MA, USA, 1990. [Google Scholar]
- McKenna, F.; Scott, M.H.; Fenves, G.L. Nonlinear Finite-Element Analysis Software Architecture Using Object Composition. J. Comput. Civ. Eng. 2010, 24, 95–107. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W. Description of Stress Strain Curves by Three Parameters; Techincal Note No. 902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Gaylord, E.H.; Gaylord, C.N. Structural Engineering Handbook; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Courbon, J. Design of Multi-Beam Bridges with Intermediate Diaphragms (Calcul des Ponts a Poutres Multiples Solidarisees par des Entretoises). Ann. Des Ponts 1940, 17, 115–116. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 9th ed.; American Association of State Highway and Transportation Officials, Inc.: Washington, DC, USA, 2020. [Google Scholar]
- Caprani, C.C. Calibration of a congestion load model for highway bridges using traffic microsimulation. Struct. Eng. Int. 2012, 22, 342–348. [Google Scholar] [CrossRef]
- Schijve, J. A normal distribution or a Weibull distribution for fatigue lives. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 851–859. [Google Scholar] [CrossRef]
- Rackwitz, R.; Flessler, B. Structural reliability under combined random load sequences. Comput. Struct. 1978, 9, 489–494. [Google Scholar] [CrossRef]
- Bakht, B.; Jaeger, L.G. Ultimate load test of slab-on-girder bridge. J. Struct. Eng. 1992, 118, 1608–1624. [Google Scholar] [CrossRef]
- EDF. Electricité de France, Finite Element Code_Aster, Analysis of Structures and Thermomechanics for Studies and Research. 2024. Available online: www.code-aster.org (accessed on 1 February 2025).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- CSA S6:19; Canadian Highway Bridge Design Code. Canadian Standard Association: Toronto, ON, Canada, 2019.
- RSMeans. Heavy Construction Cost Data; R.S. Means Co.: Kingston, MA, USA, 2009. [Google Scholar]
- Irco, A. Bridge Girder Manufacturing. 2025. Available online: https://ircoautomation.com/bridge-girder-manufacturing/ (accessed on 25 March 2025).
- Sarivan, I.M.; Madsen, O.; Wæhrens, B.V. Automatic welding-robot programming based on product-process-resource models. Int. J. Adv. Manuf. Technol. 2024, 132, 1931–1950. [Google Scholar] [CrossRef]


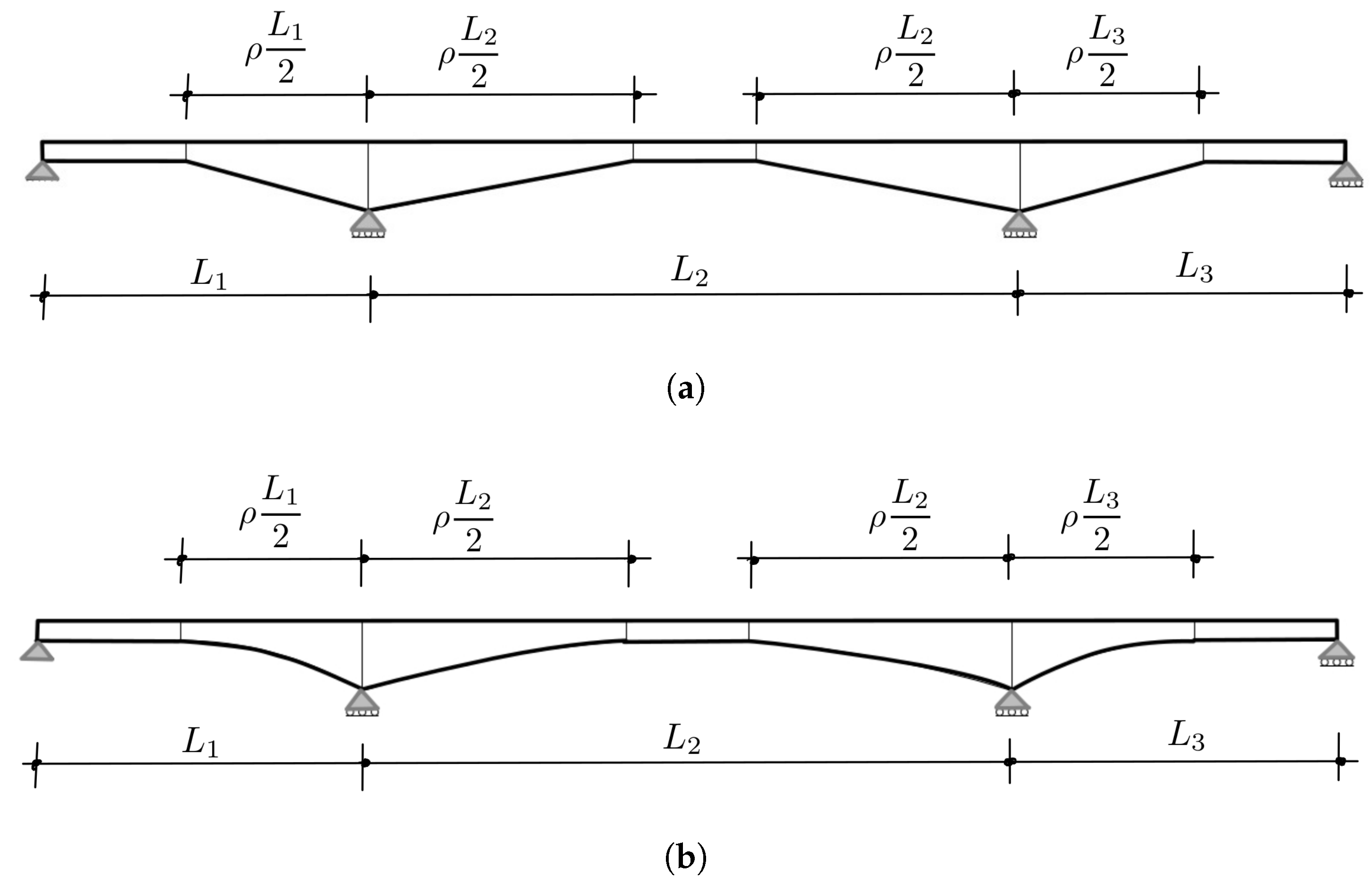



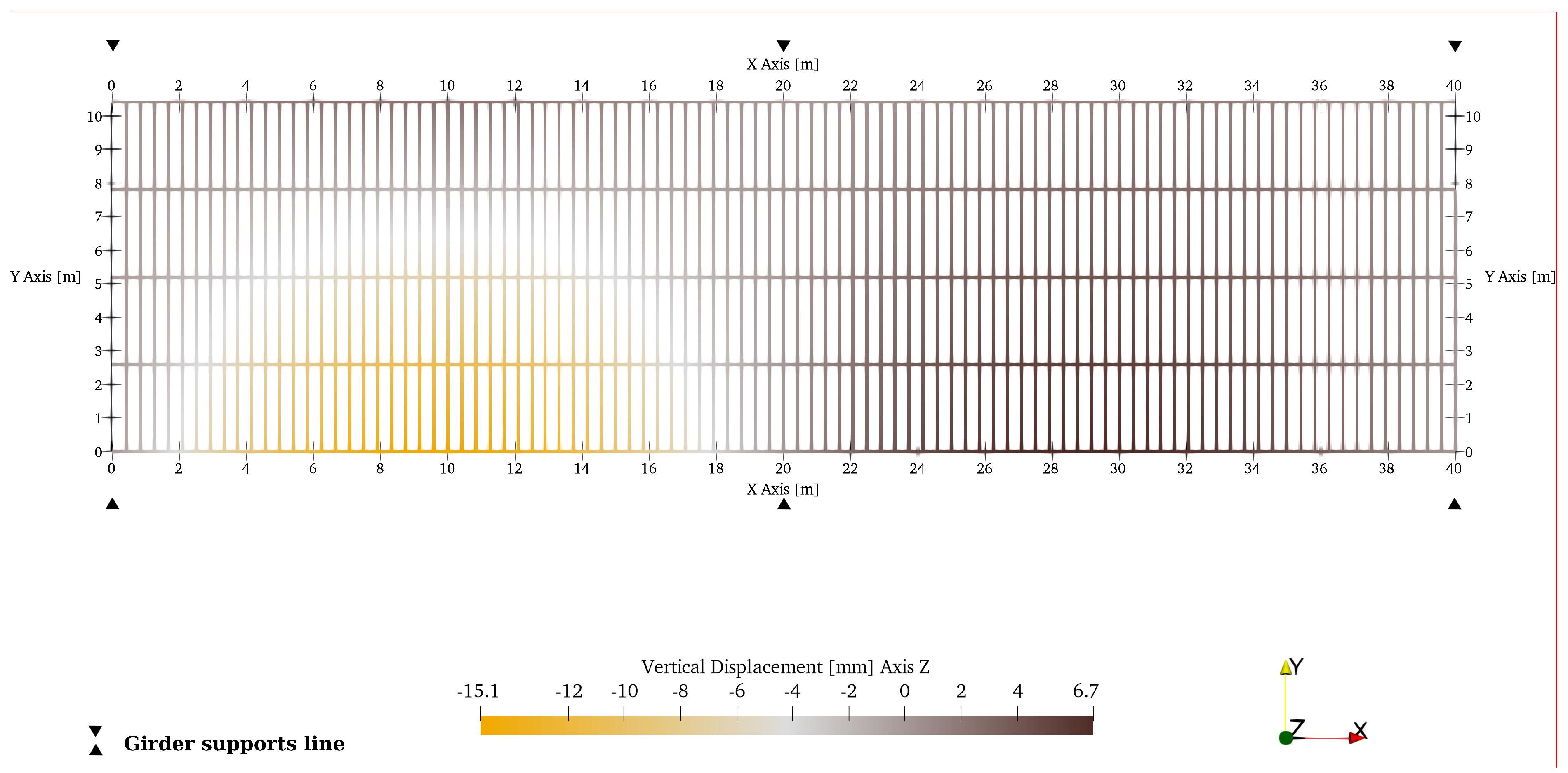
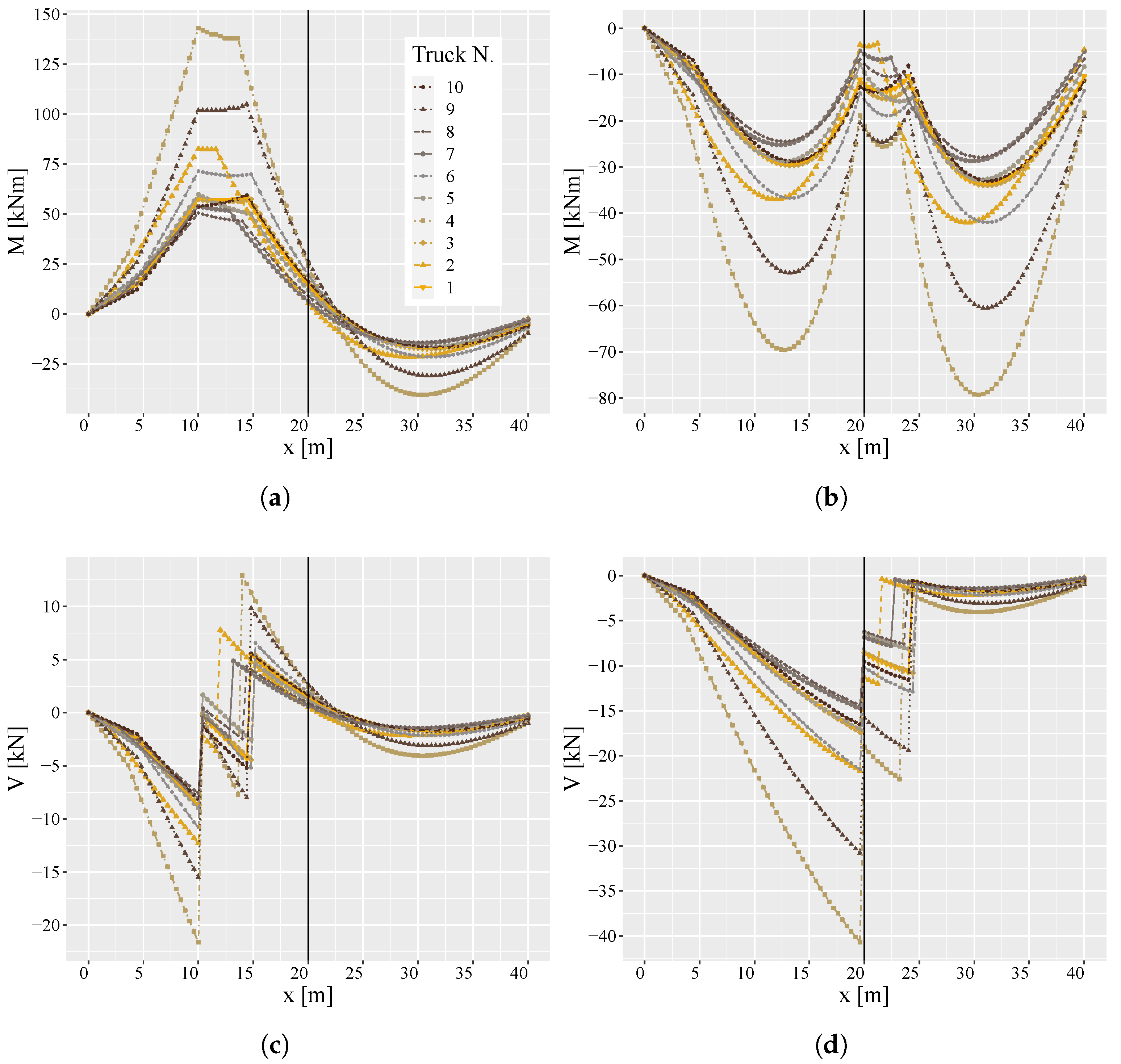
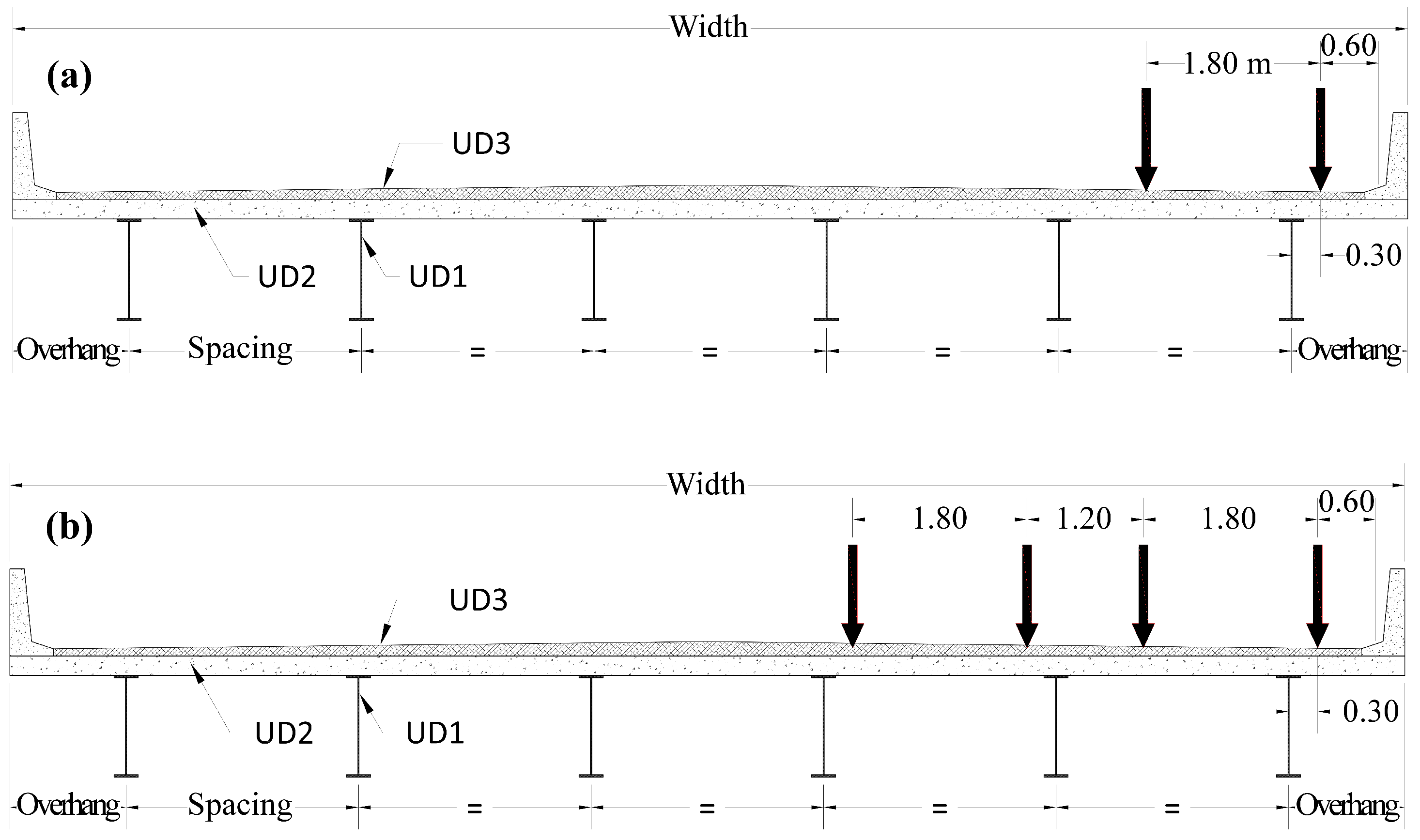





| Bridge N. | N. Spans | Shape | [%] | Spacing [m] | Spans [m] | Girder Flange | Girder Web | ||
|---|---|---|---|---|---|---|---|---|---|
| Width [mm] | Thickness [mm] | Variable Depth [mm] | Thickness [mm] | ||||||
| 1 | 2 | L, P | 25–100 | 2.4 | 10-10 | 550 | 30 | 400–640 | 4 |
| 2 | 10-17 | 440 | 25 | 680–1088 | 6 | ||||
| 3 | 20-20 | 470 | 25 | 800–1280 | 8 | ||||
| 4 | 20-33 | 550 | 26 | 1320–2110 | 10 | ||||
| 5 | 33-33 | 550 | 26 | 1320–2110 | 10 | ||||
| 6 | 50-30 | 750 | 40 | 2000–3200 | 15 | ||||
| 7 | 50-50 | 750 | 40 | 2000–3200 | 15 | ||||
| 8 | 3 | L, P | 25–100 | 2.4 | 10-10-10 | 550 | 29 | 400–640 | 4 |
| 9 | 10-17-10 | 440 | 24 | 680–1088 | 6 | ||||
| 10 | 33-33-33 | 530 | 27 | 1320–2110 | 10 | ||||
| 11 | 30-50-30 | 750 | 40 | 2000–3200 | 15 | ||||
| 12 | 50-50-50 | 750 | 40 | 2000–3200 | 15 | ||||
| 13 | 4 | L, P | 25–100 | 2.4 | 25-25-25-25 | 485 | 27 | 1000–1600 | 8 |
| 14 | 50-50-50-50 | 750 | 40 | 2000–3200 | 15 | ||||
| Class (1) | N. Axles (2) | Proportion [%] (3) | Distribution (4) | Parameters | Value (7) | |
|---|---|---|---|---|---|---|
(5) | (6) | |||||
| 5 | 2 | 15.2 | Log-normal | 4.2 | 0.3 | 31.37 |
| 6 | 3 | 5.0 | Log-normal | 4.8 | 0.4 | 8.70 |
| 8 | 4 | 4.0 | Log-normal | 4.9 | 0.3 | 23.75 |
| 9 | 5 | 71.2 | Truncated-normal | 243.4 | 77.3 | 73.96 |
| 10 | 6 | 2.2 | Log-normal | 5.45 | 0.36 | 82.97 |
| 13 | 8 | 1.3 | Truncated-normal | 426.6 | 123.5 | 541.21 |
| Class | Parameter | Truck Axle | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 5 | Mean | 0.42 | 0.58 | - | - | - | - | - | - |
| COV | 0.19 | 0.14 | - | - | - | - | - | - | |
| 6 | Mean | 0.41 | 0.30 | 0.29 | - | - | - | - | - |
| COV | 0.26 | 0.21 | 0.21 | - | - | - | - | - | |
| 8 | Mean | 0.25 | 0.35 | 0.20 | 0.20 | - | - | - | - |
| COV | 0.24 | 0.27 | 0.28 | 0.32 | - | - | - | - | |
| 9 | Mean | 0.21 | 0.21 | 0.20 | 0.19 | 0.19 | - | - | - |
| COV | 0.32 | 0.11 | 0.11 | 0.18 | 0.19 | - | - | - | |
| 10 | Mean | 0.20 | 0.19 | 0.19 | 0.14 | 0.14 | 0.14 | - | - |
| COV | 0.32 | 0.12 | 0.12 | 0.24 | 0.20 | 0.24 | - | - | |
| 13 | Mean | 0.12 | 0.11 | 0.15 | 0.14 | 0.12 | 0.13 | 0.12 | 0.11 |
| COV | 0.40 | 0.30 | 0.14 | 0.20 | 0.20 | 0.19 | 0.20 | 0.22 | |
| Class | Parameter | Axle Spacing | ||||||
|---|---|---|---|---|---|---|---|---|
| 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 6–7 | 7–8 | ||
| 5 | Mean [m] | 5.0 | - | - | - | - | - | - |
| COV | 0.22 | - | - | - | - | - | - | |
| 6 | Mean [m] | 5.3 | 1.3 | - | - | - | - | - |
| COV | 0.15 | 0.08 | - | - | - | - | - | |
| 8 | Mean [m] | 4.5 | 7.2 | 2.3 | - | - | - | - |
| COV | 0.20 | 0.44 | 1.17 | - | - | - | - | |
| 9 | Mean [m] | 5.1 | 1.3 | 9.8 | 1.4 | - | - | - |
| COV | 0.14 | 0.31 | 0.11 | 0.43 | - | - | - | |
| 10 | Mean [m] | 5.1 | 1.3 | 9.1 | 1.4 | 1.5 | - | - |
| COV | 0.14 | 0.08 | 0.18 | 0.21 | 0.20 | - | - | |
| 13 | Mean [m] | 4.2 | 1.6 | 3.7 | 5.3 | 2.4 | 3.5 | 1.7 |
| COV | 0.21 | 0.25 | 0.76 | 0.74 | 0.83 | 0.66 | 0.71 | |
| Detail Type | Mean | COV | Fatigue Threshold [MPa] |
|---|---|---|---|
| A | 1.37 | 0.09 | 165.0 |
| B | 1.22 | 0.10 | 110.0 |
| C | 1.29 | 0.12 | 69.0 |
| C′ | 1.29 | 0.12 | 82.7 |
| D | 1.18 | 0.07 | 48.3 |
| E | 1.19 | 0.07 | 17.9 |
| Position | Field Measurement | FEM | OpenBRAIN |
|---|---|---|---|
| Top Flange | 180 | 200 | 175 |
| Bottom Flange | 342 | 315 | 320 |
| Profile Shape | Bending Type | Adjusted R2 | ||
|---|---|---|---|---|
| P | Positive | 2.64 | 0.92 | |
| Negative | 2.16 | 0.80 | ||
| L | Positive | 2.62 | 0.76 | |
| Negative | 2.15 | 0.79 |
| Profile Shape | Bending Type | Detail | Reduction [%] | ||
|---|---|---|---|---|---|
| = 20% | = 100% | ||||
| Parabolic (P) | Positive | A | 2.11 | 2.20 | 25.4 |
| B | 1.80 | 1.90 | 25.1 | ||
| C, C′ | 1.91 | 2.01 | 26.3 | ||
| D | 1.74 | 1.84 | 24.5 | ||
| E | 1.76 | 1.86 | 24.7 | ||
| Negative | A | 2.18 | 2.26 | 22.8 | |
| B | 1.87 | 1.94 | 17.4 | ||
| C, C′ | 1.98 | 2.06 | 21.1 | ||
| D | 1.81 | 1.89 | 19.6 | ||
| E | 1.82 | 1.90 | 19.7 | ||
| Linear (L) | Positive | A | 2.11 | 2.20 | 25.4 |
| B | 1.80 | 1.90 | 25.1 | ||
| C, C′ | 1.91 | 2.00 | 23.4 | ||
| D | 1.74 | 1.84 | 24.5 | ||
| E | 1.76 | 1.86 | 24.7 | ||
| Negative | A | 2.18 | 2.23 | 13.6 | |
| B | 1.87 | 1.91 | 9.5 | ||
| C, C′ | 1.98 | 2.03 | 12.6 | ||
| D | 1.81 | 1.86 | 11.8 | ||
| E | 1.82 | 1.87 | 11.8 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiorillo, G.; Manouchehri, N. The Effect of Girder Profiles on the Probability of Fatigue Damage in Continuous I-Multigirder Steel Bridges. Infrastructures 2025, 10, 92. https://doi.org/10.3390/infrastructures10040092
Fiorillo G, Manouchehri N. The Effect of Girder Profiles on the Probability of Fatigue Damage in Continuous I-Multigirder Steel Bridges. Infrastructures. 2025; 10(4):92. https://doi.org/10.3390/infrastructures10040092
Chicago/Turabian StyleFiorillo, Graziano, and Navid Manouchehri. 2025. "The Effect of Girder Profiles on the Probability of Fatigue Damage in Continuous I-Multigirder Steel Bridges" Infrastructures 10, no. 4: 92. https://doi.org/10.3390/infrastructures10040092
APA StyleFiorillo, G., & Manouchehri, N. (2025). The Effect of Girder Profiles on the Probability of Fatigue Damage in Continuous I-Multigirder Steel Bridges. Infrastructures, 10(4), 92. https://doi.org/10.3390/infrastructures10040092






