Multiple Regression and Neural Network-Based Models for the Prediction of the Ultimate Strength of CFRP-Confined Columns

Abstract

Carbon Fiber-Reinforced Polymers (CFRPs) are gaining popularity as a reliable strengthening technique for reinforced concrete (RC) columns. Several efficient models were developed to predict the stress–strain (σ-ε) curve of CFRP-confined concrete based on experiment findings. The ultimate strength is a crucial parameter for accurate (σ-ε) behavior prediction, since it constitutes an initial step in estimating the corresponding axial strain, as it provides a direct indication of the desired increase in strength. Literature analytical models often produce inconsistent results due to errors in estimating the confinement pressure or effectively confined area or the lack of a strong and stable correlation between ultimate strength and confinement parameters. This study looked at a large collection of experimental results from existing research. It used a statistical method (Pearson’s coefficient) to see how well ultimate strength correlated with various confinement factors. For normal-strength concrete columns with circular sections, there was a strong linear correlation between ultimate strength and the thickness of the CFRP jacket. This correlation weakened for high-strength concrete (HSC) and for rectangular columns. A sensitivity analysis was performed to identify the most influential confinement parameters, showing that the number of CFRP layers (n $\times$ t) is the most dominant factor, particularly with normal-strength concrete (NSC) in circular columns, accounting for the vast majority of the variance in ultimate strength. Using multiple linear regression equations to predict ultimate strength was also explored; this method demonstrated the best performance with HSC in circular sections, but the results were less promising with NSC. Artificial Neural Networks (ANNs) were developed and trained on the built database, and four statistical metrics were computed for evaluation (R², RMSE, MAE, MRAE), proving highly accurate and superior to linear regression equations, with mean relative absolute errors MRAEs between 2.4–7.2% for ultimate strength prediction, opening new avenues for optimizing CFRP-strengthened element designs.

1. Introduction

Recently, Carbon Fiber-Reinforced Polymer (CFRP) has proven to be one of the most effective and widely used techniques for strengthening structural elements. Its distinctive mechanical properties—combined with advantages such as low weight, ease of application, corrosion resistance, and superior durability compared to traditional construction materials—have contributed to its growing popularity. As a result, numerous models have been developed to predict the stress–strain (σ–ε) behavior of CFRP-confined concrete.

Design-oriented models, such as those proposed by Youssef et al. [1] and Lam and Teng [2], are typically expressed as equations derived from experimental data. These models treat CFRP-confined concrete as a homogeneous material, simplifying their application in structural design. Among them, the model by Lam and Teng [3] is considered one of the most accurate and reliable—provided that the actual values of its parameters are known [4]. In particular, the ultimate strength at the peak (collapse surface) of the confined concrete is a key parameter, as it directly reflects the expected gain in strength from CFRP confinement. However, accurately estimating this value requires a thorough understanding of the confinement pressure exerted by the CFRP jacket.

While most previous studies have focused on circular columns, square and rectangular columns are more commonly found in real-world engineering applications. It is therefore essential to investigate these column types to better estimate the strength enhancement provided by CFRP composites. In non-circular sections, the confinement pressure is not uniformly distributed; the concrete enclosed by the four curved regions (parabolas) experiences greater confinement. As shown by Oliveira and Carrazedo [5], the distribution of stresses within the confined section reveals that the effectively confined area varies depending on the shape and aspect ratio of the cross-section (see Figure 1).

Despite the extensive literature addressing the behavior of CFRP-confined concrete, there remains a lack of consensus regarding the accurate prediction of its ultimate strength, particularly when considering the combined effects of confinement parameters, concrete strength, and cross-sectional geometry. Accordingly, this study aims to: (i) statistically investigate the relationship between confinement parameters and the ultimate strength of CFRP-confined concrete; (ii) determine, through sensitivity analysis, the most influential factors governing this strength for various concrete grades and geometries; and (iii) develop and validate predictive models using both multiple linear regression and artificial neural networks (ANNs).

In this study, an extensive experimental database comprising approximately 183 CFRP-confined concrete columns was compiled from previous research. The dataset includes key parameters such as unconfined concrete strength, CFRP jacket thickness, and the mechanical properties of the CFRP—particularly the fiber strain at rupture. Geometric characteristics, including the diameter (D) of circular columns and the cross-sectional dimensions (b × h) of rectangular and square columns, were also incorporated. Based on this dataset, the study (i) quantitatively evaluates the influence of each confinement parameter through Pearson correlation and Sobol sensitivity analyses, and (ii) develops predictive models using multiple linear regression and artificial neural networks (ANNs). The results demonstrate the superior predictive capability of ANN-based models, providing a reliable framework for the design and optimization of CFRP confinement systems.

2. Literature Review

2.1. Behavior of CFRP-Confined Concrete

When reinforced concrete (RC) columns are confined with Carbon Fiber-Reinforced Polymer (CFRP), they are subjected to a triaxial state of compressive stress. This includes a principal compressive stress applied vertically (due to axial loading) and a lateral confining pressure provided passively by the CFRP jacket. Unlike steel confinement, CFRP behaves elastically up to failure, and the confining pressure it exerts increases progressively as the concrete undergoes lateral expansion. Therefore, the confining pressure in CFRP-confined columns cannot be considered constant, in contrast to the relatively stable confinement provided by steel.

Table 1. Definition of main symbols and variables used in the analytical formulations.

Symbol	Description
$A_g$	Gross Area
$A_u$	Area of Unconfined Concrete (Parabolas)
$b$	Rectangle Width
$c$	Cohesion
$D$	Diameter
$E_f$	Tensile Modulus of Elasticity of CFRP
$f_{co}^{\prime }$	Unconfined concrete strength
$f_{cc}^{\prime }$	Strength of the confined concrete (Ultimate Strength)
$f_{frp}$	Ultimate Tensile Strength of CFRP
$f_l$	Confinement Pressure due to CFRP Jacket
$H$	Specimen height
$k_e$	Confinement Effectiveness Coefficient
$n$	Number of CFRP Layers
$p_f$	FRP Reinforcement Ratio
${\rho }_g$	Longitudinal Reinforcement Ratio
$r$	Rotating Radius
$t$	Nominal Ply Thickness of CFRP
εf or ${\epsilon }_{f,rup}$	Tensile Rupture Strain of the Fiber
${\sigma }_1$	Major Principal Stress (Ultimate Strength)
${\sigma }_3$	Minor Principal Stress (Confining Pressure)

shows the definition of the main symbols and variables used in the analytical formulations.

The maximum confinement pressure is reached when the circumferential strain in the CFRP jacket attains the ultimate tensile strain of the carbon fibers, leading to fiber rupture and a brittle failure of the confined concrete [6]. For circular sections, this confining pressure can be calculated using a force equilibrium approach, as illustrated in Figure 2.

$$f_l={\sigma }_3={\displaystyle \frac{2f_{frp}\times n\times t}{D}}={\displaystyle \frac{2E_f\times {\epsilon }_{f,rup}\times n\times t}{D}}={\displaystyle \frac{1}{2}}{\times p}_f\times f_{frp}$$

(1)

where f_l: confinement pressure due to CFRP jacket,

D: diameter of confined circular columns, f_frp: ultimate tensile strength of CFRP, E_f: tensile modulus of elasticity of CFRP, εf or ε_f,rup: tensile rupture strain of the fiber, n: number of CFRP plies composing the jacket, t: nominal ply thickness of CFRP, pf: FRP reinforcement ratio.

$$p_f={\displaystyle \frac{\pi .D\times n\times t}{\pi D^2/4}}={\displaystyle \frac{4\times n\times t}{D}}$$

(2)

It is well established that confinement efficiency is lower in square sections compared to circular ones, as illustrated in Figure 3. However, experimental studies [7,8,9] have shown that failure in CFRP-confined square concrete columns can also result from rupture of the CFRP jacket—particularly when the corners are rounded to reduce stress concentrations. In such cases, the confinement mechanism becomes more effective, and the jacket is more likely to reach its ultimate strain.

In the expression for confinement pressure (Equation (1)), the diameter (D) used for circular sections is replaced by an equivalent diameter that accounts for the geometry of square sections with rounded corners:

$$D=\sqrt{2}b-2r\left(\sqrt{2}-1\right)$$

(3)

2.2. Effective Confining Pressure

In square sections, due to the irregular distribution of the confining pressure, the value of the effective confining pressure is given by:

$$f_{le}=k_e{f}_l$$

(4)

$k_e$: confinement effectiveness factor:

$$A_u=4\left({\displaystyle \frac{b^2}{6}}\right)=2{\displaystyle \frac{b^2}{3}}$$

(5)

$A_u:$ area of parabolas that are not affected by confinement, $r:$ rotating radius, $A_e:$ effectively confined area

$$k_e={\displaystyle \frac{A_e}{A_c}}={\displaystyle \frac{(A_c-A_u)}{A_c}}=1-{\displaystyle \frac{A_u}{\left(A_g-A_s\right)}}=1-{\displaystyle \frac{A_u}{A_g\left(1-{\rho }_g\right)}}$$

(6)

$$k_e=1-{\displaystyle \frac{2b^2}{{3A}_g\left(1-{\rho }_g\right)}}$$

(7)

$b$ is replaced by $b^{\prime }$ in the previous relationship, if the cross-section is square with rounded corners

$${\displaystyle \frac{A_e}{A_c}}=1-{\displaystyle \frac{\frac{{2\left(b-2r\right)}^2}{{3A}_g}}{1-{\rho }_g}}$$

(8)

$A_c:$ area of Concrete cross-section, $A_g:$ gross area, ${\rho }_g:$ Reinforcement ratio.

Increasing the aspect ratio (h/b) of a rectangular section can lead to a reduction in the required confining pressure, resulting in diminished confinement efficiency [3].

$${\displaystyle \frac{A_e}{A_c}}=1-{\displaystyle \frac{\frac{\left(\frac{b}{h}\right){\left(h-2r\right)}^2+\left(\frac{h}{b}\right){\left(b-2r\right)}^2}{{3A}_g}}{1-{\rho }_g}}$$

(9)

Lam and Teng [3] proposed the parameter $k_a$ instead of $k_e$ in Equation (4), where an additional effect of the ratio (b/h) was introduced when predicting the ultimate strength $f_{\mathrm{c}\mathrm{c}}$:

$$k_a= {\displaystyle \frac{A_e}{A_c}}{\left({\displaystyle \frac{b}{h}}\right)}^2$$

(10)

2.3. A Review of Models That Predict the Ultimate Strength of CFRP-Confined Concrete

The Mohr-Coulomb failure criterion is often used to describe confined concrete based on soil data under triaxial compression

$${\sigma }_1={\displaystyle \frac{2c cos\mathrm{\varnothing }}{1-sin\mathrm{\varnothing }}}+{\displaystyle \frac{1+sin\mathrm{\varnothing }}{1-sin\mathrm{\varnothing }}}{\sigma }_3$$

(11)

${\sigma }_1$: major principal stress (ultimate strength), ${\sigma }_3$: minor principal stress (confining pressure), $\mathrm{\varnothing }$: friction angle, $c$: cohesive of soil, for unconfined concrete when ${\sigma }_3=0$:

$$f_{co}={\sigma }_1={\displaystyle \frac{2ccos\mathrm{\varnothing }}{1-sin\mathrm{\varnothing }}}$$

(12)

Richart et al. [10] were initially noted that confinement has a favorable effect on concrete, it was modeled by defining a value for the angle of internal friction $\mathrm{\varnothing }={37}^{°}$. Next, according to Goodman [11] for the majority of concrete strengths, the angle of friction should range between $\mathrm{\varnothing }={37}^{°}-{45}^{°}$, and the confinement effectiveness coefficient k is calculated based on the angle of friction:

$$k={\displaystyle \frac{1+sin\mathrm{\varnothing }}{1-sin\mathrm{\varnothing }}}$$

(13)

Therefore, the ultimate strength of confined concrete can be expressed by the following formula if a confinement ratio is applied that achieves the ascending branch of the (σ-ε) curve:

$$f_{\mathrm{c}\mathrm{c}}=f_{co}+k f_l$$

(14)

A value of k = 4.1 was originally proposed by Richart et al. [10] to represent a friction angle of approximately ∅ = 37°. However, subsequent research by Razvi and Saatcioglu [12,13] revealed that the confinement coefficient k tends to decrease as the confining pressure increases. In their experiments on high-strength concrete, Candappa et al. [14] suggested a higher value of k at low levels of confinement.

As a result, while some researchers [15,16,17,18,19,20] proposed a fixed value for k, others [21,22,23,24] argued that k should be modeled as a decreasing function of the confinement ratio.

Table 2. The most reliable models for ultimate strength prediction of CFRP- confined concrete.

Authors	Ultimate Strength of CFRP-Confined Concrete
Richart et al. [10], Fardis and Khalili [25]. ($f_{co}^{\prime }:20-55 \mathrm{MPa})$	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+4.1{\displaystyle \frac{f_l}{f_{co}^{\prime } }} (15)$
Mirmiran and Shahawy [9], Harries and Kharel [26].	$f_{cc}^{\prime }=f_{co}^{\prime }+4.269f_l^{0.587} (16)$
Razvi and Saatcioglu [27].	$f_{cc}^{\prime }=f_{co}^{\prime }+6.7f_l^{0.83} \left(17\right)$
Teng et al. [28].	$f_{cc}^{\prime }=f_{co}^{\prime }+3.3f_l \left(18\right)$
Campione and Miraglia [15]. $f_{co}^{\prime }:20-44 \mathrm{MPa}$	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+2{\displaystyle \frac{f_l}{f_{co}^{\prime } }} (19)$
Lim and Ozbakkaloglu [29]	$f_{cc}^{\prime }=f_{co}^{\prime }+5.2f_{co}^{\prime 0.91}{\left({\displaystyle \frac{f_l}{f_{co}^{\prime }}}\right)}^a a=f_{co}^{\prime -0.06} (20)$
Fahmy and Wu [21].	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+k_1{\displaystyle \frac{{f_l}^{0.7}}{f_{co}^{\prime } }} (21)$ $k_1=4.5 ,k_1=3.75$ $f_{co}^{\prime }\le 40 \mathrm{MPa}, f_{co}^{\prime }>40 \mathrm{MPa}$
Mohamad and Masmoudi [30].	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=0.7+2.7{({\displaystyle \frac{f_l}{f_{co}^{\prime } }})}^{0.7} (22)$
Samaan et al. [7].	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+6{{\displaystyle \frac{f_l}{f_{co}^{\prime } }}}^{0.7} (23)$
Girgin [31]. $7 {\le f}_{co}^{\prime }< 25$ $25 {\le f}_{co}^{\prime }\le 108$	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}={\left[1+{\displaystyle \frac{M}{B}}{\displaystyle \frac{f_l}{f_{co}^{\prime } }}\right]}^B (24)$ $B=1-0.0172{\left(log{f}_{co}^{\prime }\right)}^2$ $M=0.0035{f_{co}^{\prime }}^2-0.056f_{co}^{\prime }+2.83$ $M=0.0003{f_{co}^{\prime }}^2-0.076f_{co}^{\prime }+5.46$

summarizes the most significant and reliable models from previous studies that have been developed to predict the ultimate strength of CFRP-confined concrete.

To date, research continues to evolve, with increasingly sophisticated mathematical models being developed to predict the behavior of confined concrete across a wide range of material properties—including ultra-high-performance concrete [32,33] and various cross-sectional geometries [34].

Numerous significant experimental tests on CFRP-confined columns have been compiled to evaluate the effectiveness of these models. The mean relative absolute error (MRAE) was calculated, with values ranging from 13% to 37%. The accuracy of these models in predicting the ultimate strength of confined concrete varies depending on the cross-sectional shape and the initial strength of the concrete. As a result, research in this area remains active, with new models continually being proposed. However, many of these newer models still fall short when compared to more established ones—such as Equation (18) by Lam and Teng [2,3]—which has demonstrated consistent reliability and has been adopted by several design codes, including ACI 440.2R-2002 [35].

On the other hand, Berradia et al. [36] employed artificial neural networks (ANNs), demonstrating that these models offer greater accuracy, efficiency, and precision than traditional empirical equations in predicting the axial load-carrying capacity of circular columns confined with various FRP composites (carbon FRP, glass FRP, and aramid FRP). Similarly, Ali et al. [37] compared the performance of experimental models and ANNs, concluding that deep neural networks (DNNs) and convolutional neural networks (CNNs) show strong potential for future applications. Nistico et al. [38] compiled and compared data for square and circular columns reinforced with different types and configurations of fiber-reinforced polymers (e.g., strips, wraps, tubes), considering the influence of cross-sectional shape and FRP type on performance outcomes.

The present study statistically investigates the influence of cross-sectional shape and initial concrete strength on the ultimate strength of CFRP-confined columns. It also examines the correlation between confinement parameters and ultimate strength and evaluates the use of multiple linear regression and neural networks as alternative predictive methods.

3. Analytical Study

3.1. Database

Experimental data were collected from previous studies that investigated columns with circular cross-sections [1,2,4,18,19,29,39,40,41,42,43,44,45,46,47,48,49,50,51]. Additional studies focused on rectangular sections [52,53,54,55].

The selection of models and relationships was based on those most widely adopted and recognized for their reliability by practitioners, regardless of their publication date, due to their foundational significance in the field. Given the inherent complexity of the relationships between confinement parameters and ultimate strength, the proposed models in this study were derived from a limited yet robust dataset. This methodological approach supports the objectivity and impartiality of the findings. The compilation of the experimental database followed a rigorous, systematic framework prioritizing three fundamental principles to ensure model reliability and generalizability. Material Homogeneity was maintained by exclusively curating data from studies on Carbon Fiber-Reinforced Polymer (CFRP)-confined columns, systematically excluding other composites to guarantee unambiguous material behavior. Empirical Rigor mandated that all data be sourced solely from peer-reviewed publications, with mandatory reporting of all essential CFRP properties and raw experimental results. Finally, for Model Generalizability, the database intentionally incorporated a diverse range of structural shapes (circular and rectangular) and concrete strengths (from normal to high strength). Furthermore, in selecting input variables, we note that the ultimate tensile strength was not used as an independent variable, as it is a direct product of the two properties already selected: the stiffness and the tensile rupture strain, providing a more comprehensive material representation. Crucially, the potential influence of the polymeric matrix was deemed negligible, as analysis of the selected studies confirmed that none reported failure modes associated with fiber debonding or delamination, indicating that the polymer systems effectively ensured full composite action and stress transfer.

A. Descriptive Statistics:

In this study, a total of 183 cases were analyzed. The independent variables included: the total CFRP confinement thickness (calculated as the number of layers multiplied by the thickness per layer, n × t), the unconfined concrete strength (${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$), the tensile modulus of elasticity of the fibers (E_f), and the tensile rupture strain of the fibers (${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$). The dependent variable was the strength of the confined concrete (${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$).

Table 3. Descriptive statistics for variables in all data.

	Minimum	Maximum	Mean	Std. Deviation
$\mathit{n} \times \mathit{t}$(mm)	0.089	1.752	0.357	0.287
${\mathit{E}}_{\mathit{f}}$(MPa)	103,800	291,000	221,379	40,345.84
${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$	0.0019	0.0184	0.0131	0.0042
${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$(MPa)	17.03	169.37	38.07	19.95
${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$(MPa)	23.42	303.85	69.42	39.54

presents the descriptive statistics for each variable. As shown, the unconfined concrete strength (${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$) ranges from 17.03 MPa to 169.37 MPa, with a mean value of 38.07 MPa. The confined concrete strength (${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$) ranges from 23.42 MPa to 303.85 MPa, with an average of 69.42 MPa. The CFRP confinement thickness varies between 0.089 mm and 1.752 mm, with a mean value of 0.357 mm.

B. Linear correlations between the studied variables and the strength of confined concrete, results discussion:

Pearson’s correlation coefficient was used to assess the strength and direction of the linear relationship between the confined concrete strength and the selected variables. This coefficient quantifies how strongly two variables are linearly related. Additionally, the significance value (Sig. 2-tailed), also known as the p-value, indicates the probability of observing a correlation as extreme as the one calculated—assuming the null hypothesis of no correlation is true.

Table 4. Pearson Correlation between the strength of confined concrete and the independent studied variables.

		$\mathit{n}\times \mathit{t}$	${\mathit{E}}_{\mathit{f}}$	${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$	${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$
${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$	Pearson Correlation	0.447 **	−0.075	−0.403 **	0.744 **
	Sig. (2-tailed)	0.000	0.308	0.000	0.000
	N	189	189	189	189

**. Correlation is significant at the 0.01 level (2-tailed).

presents the correlation analysis results, revealing a strong and statistically significant linear relationship between the strength of concrete before and after confinement, with a Pearson correlation coefficient of 0.744. This correlation is significant at the α = 0.05 level, as indicated by a p-value (2-tailed) less than 0.05.

A moderate positive correlation was observed between the strength of confined concrete and the CFRP jacket thickness (Pearson correlation = 0.447). Additionally, a significant negative correlation was found between the confined concrete strength ($f_{cc}^{\prime })$ and the rupture strain (${\epsilon }_{f,rup}$), with a Pearson correlation of −0.403. This inverse relationship can be physically explained by the intrinsic mechanical behavior of CFRP materials and the confinement mechanism. Generally, CFRP systems exhibiting higher rupture strains correspond to fibers with lower elastic modulus, which are more deformable but develop lower confining pressures at a given strain level. Conversely, CFRP jackets with higher stiffness (lower rupture strain) generate greater lateral confinement pressure before failure, resulting in higher confined concrete strength. Furthermore, in high-strength concrete, the lateral expansion at failure is limited, restricting the strain mobilization in the CFRP jacket. As a result, systems with high rupture strain do not necessarily provide stronger confinement, leading to the observed negative correlation. This highlights the complex interaction between CFRP mechanical properties and concrete strength, emphasizing the need to account for material stiffness when analyzing confinement efficiency.

C. Variation in the correlation between ${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$ and ${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$ according to initial concrete strength (${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime } > 39 \mathbf{MPa}, {\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime } < 39 \mathbf{MPa}$):

The linear relationship between the strength of concrete before and after confinement was further examined by segmenting the data based on unconfined concrete strength. When the unconfined strength was below 39 MPa, the correlation was very weak, with a Pearson coefficient of 0.264. In contrast, for samples with unconfined strength above 39 MPa, a strong and statistically significant linear relationship was observed, with a Pearson coefficient of 0.73.

This marked difference suggests that the behavior of confined concrete varies significantly depending on the initial strength of the material. Therefore, it is advisable to divide the dataset into two groups: one with unconfined strength less than 39 MPa and another with strength greater than 39 MPa. Notably, this threshold is close to the mean value of $f_{co}^{\prime }$ for the collected data, as indicated in Table 3.

D. Effect of section shape (circular-rectangular) on the strength of confined concrete (t-test for two independent samples):

The data was divided into two independent groups based on the cross-sectional shape of the specimens (circular vs. rectangular). The average strength of the confined concrete was calculated separately for each group. An Independent Samples Test was then conducted, revealing a Sig. (2-tailed) value of 0.000, which is less than the significance level α = 0.05. This result indicates that the cross-sectional shape has a statistically significant effect on the strength of confined concrete.

E. Sort data:

To enhance the precision and accuracy of the predictions, the experimental test results were categorized based on key behavioral differences between rectangular and circular sections, as well as between normal-strength and high-strength concrete. The data was analyzed according to the following classification:

• Normal-strength circular columns (59 cases)
• High-strength circular columns (60 cases)
• Normal-strength rectangular columns (56 cases)
• High-strength rectangular columns (8 cases).

Given the limited sample size, this subset was excluded from the main statistical and predictive analyses to maintain the robustness and reliability of the results. Consequently, the findings and developed models presented in this study primarily apply to circular and rectangular columns made with normal-strength concrete, and to circular columns with high-strength concrete. Future research should focus on expanding the experimental database for rectangular HSC specimens to validate and generalize the conclusions drawn herein. This limitation does not affect the validity of the conclusions for the studied configurations but restricts their generalization to rectangular HSC columns.

3.2. Columns with Circular Sections and Normal-Strength Concrete NSC

A. Description of the sample and the studied independent variables:

The following variables were considered in the analysis: diameter of the cross-section $\left(\mathit{D}\right),$ specimen height $\left(\mathit{H}\right),$ CFRP layer thickness $(\mathit{n}\times \mathit{t}),$ concrete strength prior to confinement (${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$), tensile modulus of elasticity of CFRP $\left({\mathit{E}}_{\mathit{f}}\right),$ and tensile rupture strain of the fiber (${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$). The strength of confined concrete (${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$) was treated as the dependent variable.

Table 5. Descriptive statistics for variables in circular columns with NSC.

	Minimum	Maximum	Mean	Std. Deviation
D (mm)	76.00	508.00	153.6271	66.70
H (mm)	200.00	1824.00	350.6271	248.04
$\mathit{n}\times \mathit{t}$(mm)	0.1100	1.7520	0.297254	0.27077
${\mathit{E}}_{\mathit{f}}$(MPa)	103,800	291,000	232,598	19,636.95
${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$	0.0026	0.0180	0.011456	0.0031
${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$(MPa)	17.39	38.90	28.6093	7.44
${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$(MPa)	31.40	161.30	69.0032	22.85

presents the descriptive statistics for each of these variables.

As shown in

Table 6. Linear correlation between $f_{cc}^{\prime }$ of circular columns with NSC and the independent variables (Pearson Correlation).

		D	H	$\mathit{n}\times \mathit{t}$	${\mathit{E}}_{\mathit{f}}$	${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$	${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$
${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$	Pearson Correlation	−0.234	−0.154	0.533 **	0.022	0.001	0.176
	Sig. (2-tailed)	0.074	0.245	0.000	0.869	0.995	0.182
	N	59	59	59	59	59	59

**. Correlation is significant at the 0.01 level (2-tailed).

, the sample includes 59 cases. The unconfined concrete strength ranges from 17.39 MPa to 38.9 MPa, with an average value of 28.6 MPa. The confined concrete strength varies between 31.4 MPa and 161.3 MPa, with a mean of 69 MPa. The CFRP confinement thickness ranges from 0.11 mm to 1.75 mm, with an average thickness of 0.3 mm.

B. Correlation between the strength of confined concrete and the studied variables:

A Pearson correlation coefficient, which quantifies the strength and direction of a linear relationship between two variables, was used to analyze the association between the independent variables and the strength of confined concrete. The Pearson correlation between the confined concrete strength (f_cc’) and the CFRP layer thickness (n × t) was 0.533, with a significance level of 0.001, indicating a strong and statistically significant relationship (see Table 6).

Furthermore, the analysis revealed a direct relationship between confined concrete strength and CFRP jacket specifications, and an inverse relationship with the diameter of the cross-section. These findings are consistent with the confining pressure relationship described by Equation (1).

C. Multiple linear regression model:

The statistical software SPSS 27 was used to develop a multiple linear regression model, leading to the following findings:

-

The model’s correlation coefficient (R) is 0.878, which indicates a strong relationship between the predicted and actual values.

-

The coefficient of determination (R²) is 0.772, suggesting that approximately 77.2% of the variance in the dependent variable is explained by the model. This reflects moderate model efficiency.

The model’s error metrics are as follows: Root Mean Squared Error (RMSE) = 10.83,

Mean Absolute Error (MAE) = 8.89, Mean Relative Absolute Error (MRAE) = 14.6%. Given these results, the proposed multiple regression model was not considered sufficiently reliable for predictive purposes.

D. Structure of ANNs

Artificial Neural Networks (ANNs) are computational models that simulate data for purposes such as analysis, classification, and prediction—without requiring a predefined mathematical model. Due to their flexibility and adaptability, ANNs have attracted significant interest from researchers, offering advantages over traditional mathematical approaches. They are particularly valued for their dynamic and parallel processing capabilities.

In this study, a feedforward backpropagation ANN was employed. The network consists of multiple layers of interconnected processing units (neurons). Each network includes a single output neuron, which represents the predicted ultimate strength used during training. The connections between neurons are governed by weights, which determines the strength of signal transmission between layers.

The input layer receives the experimental data, while the output layer produces the predicted value (target). Between them, hidden layers process the input data to extract relevant features. The optimal number of hidden layers and neurons per layer is not known a priori and must be determined experimentally, as suggested by Jung and Ghaboussi [56] and Yousif [57].

Each neuron uses an activation function to process and transmit signals to the next layer. One of the most commonly used functions in this context is the tan-sigmoid function. During training, weight adjustments are made using the gradient descent algorithm, where the error is propagated backward through the network. This process systematically updates the weights to minimize the squared error within an acceptable range.

Figure 4 displays the trained ANN1’s structures: input (6 parameters), 3 hidden layers, one output layer, and the number of neurons in each layer 8:6:6:1).

In this study, 70% of the available experimental data was used to train the neural network, while the remaining 30% was split equally for testing (15%) and validation (15%). After training, the network’s output was compared to the actual experimental data. Training was terminated once the error between the predicted and target values reached a minimal threshold. This widely adopted ratio was strategically chosen to balance the need for sufficient data volume for Training (70%) with the requirements for validation (15%) which is essential for real-time performance monitoring, hyperparameter tuning, and preventing overfitting via early stopping and testing (15%) which ensures a final, unbiased evaluation of the model’s generalizability on a completely unseen dataset. This convention is supported by authoritative machine learning literature, including works by Hastie et al. [58].

The neural network was constructed, trained, and tested using MATLAB. R2014a The correlation coefficient (R) from linear regression was used to evaluate the network’s performance. The R values were 0.995 for the training set and 0.976 for the validation set, indicating excellent predictive accuracy.

Additional performance metrics included:

-

Root Mean Squared Error (RMSE) = 2.92

-

Mean Absolute Error (MAE) = 1.36

-

Mean Relative Absolute Error (MRAE) = 2.4%

These results demonstrate the high accuracy and reliability of the ANN model. Figure 5 illustrates the ANN1 output compared to the experimental data.

3.3. Columns with Circular Sections and High-Strength Concrete HSC

A. Description of the sample and the studied independent variables:

Table 7. Descriptive statistics for variables in circular columns with HSC.

	Minimum	Maximum	Mean	Std. Deviation
D (mm)	51.00	406.00	142.53	48.903
H (mm)	102.00	813.00	285.50	97.98
$\mathit{n}\times \mathit{t}$(mm)	0.08900	1.75200	0.49388	0.3748
${\mathit{E}}_{\mathit{f}}$(MPa)	103,800	260,000	196,713	60,873
${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$	0.001900	0.018000	0.0107448	0.0045
${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$(MPa)	40.00	169.37	54.337	23.527
${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$(MPa)	48.10	303.85	97.475	50.009

presents the descriptive statistics for the study variables. The sample size consisted of 60 cases. The unconfined concrete strength ranged from 40 MPa to 169.37 MPa, with an average value of 54.337 MPa. After confinement, the concrete strength ranged from 48.10 MPa to 303.85 MPa, with an average of 97.475 MPa.

B. correlation between the strength of confined concrete and the studied variables:

The strength of confined concrete is influenced by both the geometric dimensions of the column and the initial (unconfined) concrete strength, as indicated by the Pearson correlation coefficient. Consequently, whether the concrete is initially normal-strength or high-strength, its behavior after confinement may differ significantly.

For instance, in normal-strength concrete, the post-confinement strength is closely related to the confinement ratio, which is determined by the thickness and mechanical properties of the CFRP jacket. However, as shown in

Table 8. Linear correlation between $f_{cc}^{\prime }$ of circular columns with HSC and the independent variables (Pearson Correlation).

		D	H	$\mathit{n}\times \mathit{t}$	${\mathit{E}}_{\mathit{f}}$	${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$	${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$
${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$	Pearson Correlation	−0.523	−0.524	0.320	0.241	0.176	0.731 **
	Sig. (2-tailed)	0.000	0.000	0.013	0.063	0.179	0.000
	N		60	60	60	60	60

**. Correlation is significant at the 0.01 level (2-tailed).

, the effectiveness of confinement decreases when applied to high-strength concrete, indicating a diminishing return in strength enhancement as the initial concrete strength increases.

C. Multiple linear regression model:

The statistical software SPSS was used to develop a multiple linear regression model, yielding several key findings. The model demonstrated a strong correlation coefficient (R = 0.922), indicating a robust linear relationship between predicted and actual values. The coefficient of determination (R² = 0.85) suggests that 85% of the variance in the dependent variable is explained by the model, reflecting good predictive efficiency. Error metrics further support the model’s performance, with a Root Mean Squared Error (RMSE) of 19.23, a Mean Absolute Error (MAE) of 14, and a Mean Relative Absolute Error (MRAE) of 15.1%. Based on these results, the proposed multiple regression model is considered reasonably accurate and reliable for predictive purposes.

$$f_{cc}^{\prime } = 1.026 - 0.486 \ast \mathrm{D} + 96.327 \ast \left(\mathrm{n} \times \mathrm{t}\right) + 0.00 \ast E_f + 214.765 \ast {\epsilon }_{f,rup} + 0.763 f_{co}^{\prime }$$

(25)

D. Structure of artificial neural network:

The structure and performance of ANN2 are illustrated in Figure 6 and Figure 7. The model achieved a Root Mean Squared Error (RMSE) of 8.72, a Mean Absolute Error (MAE) of 6.64, and a Mean Relative Absolute Error (MRAE) of 7.2%.

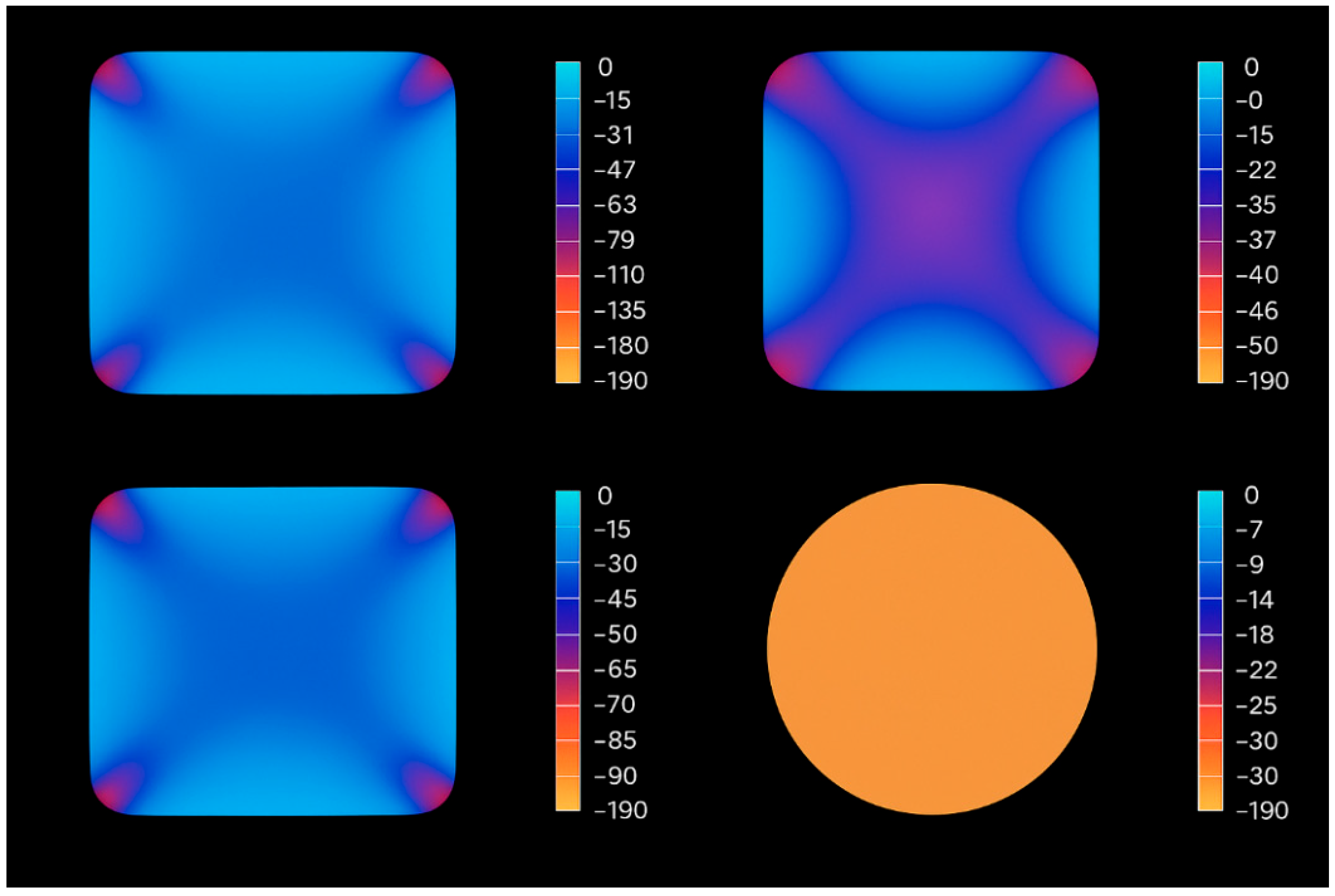
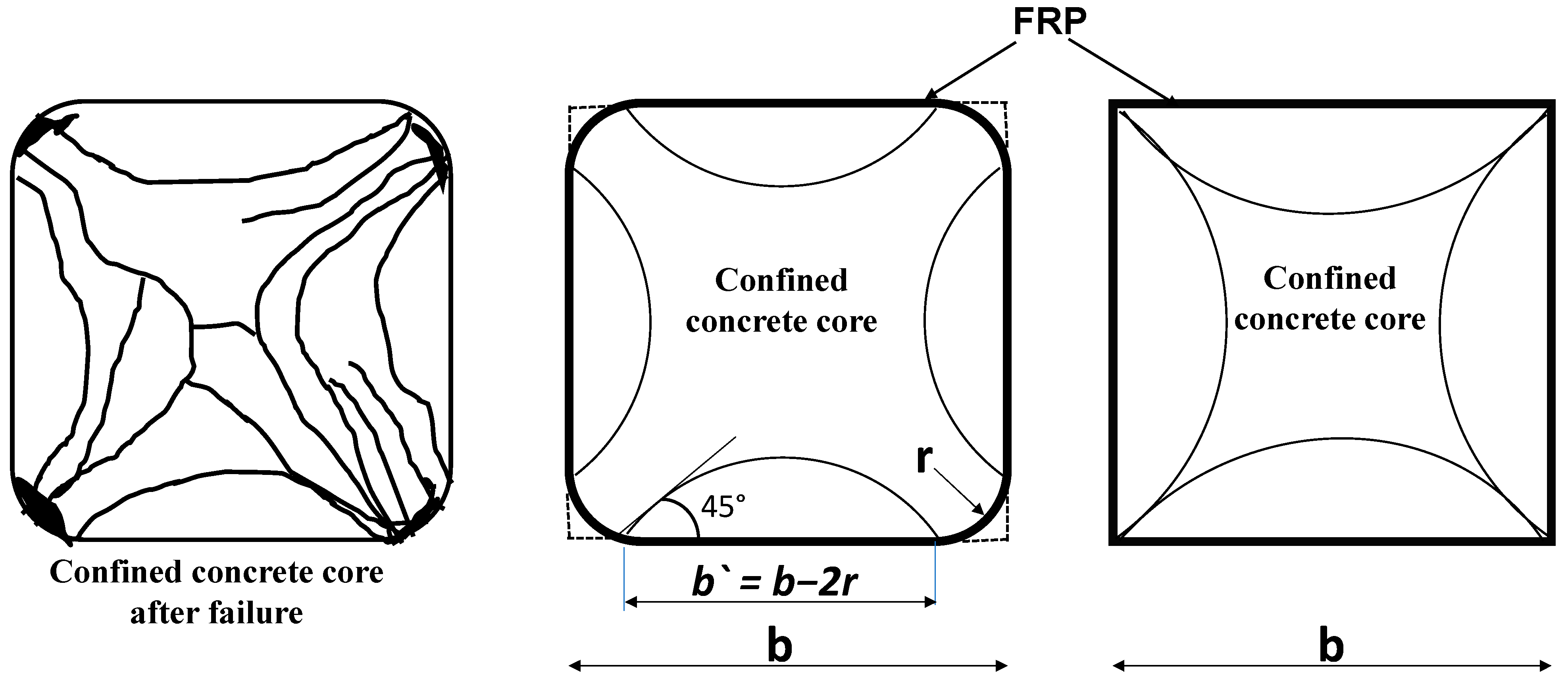
3.4. Columns with Rectangular Sections and Normal-Strength Concrete NSC

When developing a neural network to predict the strength of confined concrete in rectangular columns—without classifying the data based on concrete strength (i.e., normal or high)—significant result dispersion and training instability were observed. To address this, the data was sorted, and the network was trained specifically on specimens with unconfined concrete strengths not exceeding 39 MPa. The specifications of this sample are as follows:

A. Description of the sample and the studied independent variables:

The sample size consists of 56 cases, all with rectangular cross-sections. The aspect ratio of these sections ranges from 1.0 (square) to 2.7, with an average value of 1.55.

Table 9. Descriptive statistics for variables in rectangular columns with NSC.

	Minimum	Maximum	Mean	Std. Deviation
b	79	150	133.8393	24.2329
h	131.50	300	200.4643	59.2259
$\mathit{n}\times \mathit{t}$	0.1290	0.5160	0.2898	0.1115
${\mathit{E}}_{\mathit{f}}$	230,000	238,000	233,613.5714	3662.9153
${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$	0.0150	0.01840	0.0167	0.0013
${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$	17.03	37.30	26.8834	7.1751
${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$	23.42	78.10	38.8920	10.9448
h/b	1.00	2.70	1.5518	0.5515

presents the descriptive statistics for the variables. Height data was not available for some of the rectangular specimens. However, all included tests were conducted on short columns, where the influence of height is generally considered less critical. Moreover, as shown in Table 6, the analysis revealed no significant correlation between column height and confined concrete strength among short specimens, further justifying its exclusion as a primary input parameter in this study.

B. correlation between the strength of confined concrete and the studied variables in rectangular sections:

The results were generally consistent with those observed for circular sections, with one key difference: there was a moderate linear correlation between the concrete strength before and after confinement, and a nearly strong inverse relationship between the confined concrete strength and the aspect ratio of the rectangular section, as shown in

Table 10. Linear correlation between $f_{cc}^{\prime }$ of rectangular columns with NSC and the independent variables(Pearson Correlation).

		b	h	$\mathit{n}\times \mathit{t}$	${\mathit{E}}_{\mathit{f}}$	${\mathit{\epsilon }}_{\mathit{f},\mathit{r}\mathit{u}\mathit{p}}$	h/b	${\mathit{f}}_{\mathit{c}\mathit{o}}^{\prime }$
${\mathit{f}}_{\mathit{c}\mathit{c}}^{\prime }$	Pearson Correlation	0.393	−0.330	0.324 *	0.135	0.268	−0.510 **	0.469 **
	Sig. (2-tailed)	0.003	0.013	0.015	0.323	0.046	0.000	0.000
	N	56	56	56	56	56	56	56

**. Correlation is significant at the 0.01 level (2-tailed). *. Correlation is significant at the 0.05 level (2-tailed).

.

C. Multiple linear regression model:

The statistical software SPSS was used to develop a multiple linear regression model, which yielded a correlation coefficient (R) of 0.838, indicating a strong linear relationship between predicted and actual values. The coefficient of determination (R²) was 0.703, meaning that approximately 70.3% of the variance in the dependent variable was explained by the model, reflecting moderate predictive efficiency. The model’s error metrics included a Root Mean Squared Error (RMSE) of 5.9, a Mean Absolute Error (MAE) of 4.46, and a Mean Relative Absolute Error (MRAE) of 11.2%. Despite the relatively strong correlation, the magnitude of the error values suggests limited reliability, and as a result, the proposed multiple regression model was not adopted for further use.

D. Structure of artificial neural network:

Figure 8 shows the structure of ANN3 which consists of inputs (6 parameters), 7 hidden layers; each layer contains 15 neurons, and an output layer with one neuron.

Correlation coefficient R was calculated between the target and the trained network’s outputs and the values were 0.966 and 0.992 for training and validation databases, respectively. The root mean squared error RMSE was 2.56, and the mean relative absolute error MRAE was 3.8%, mean absolute error MAE= 1.42. Figure 9 shows ANN3 outputs via the target (experimental data).

The network structure was determined through an iterative trial-and-error process, in which various configurations were tested to achieve the lowest mean absolute error, thereby optimizing the model’s performance for each specific case study.

Table 11. Data for trained artificial neural networks.

ANN Structure Number of Neurons in Each Layer	Inputs	Target	Artificial Neural Network
8:6:6:1	D, H, $n\times t$, $f_{co}^{\prime }$, $E_f$, ${\epsilon }_{f,rup}$	$f_{cc}^{\prime }$: strength of confined-NSC in circular section	ANN1
6:6:6:1	D, H, $n\times t$ $f_{co}^{\prime }$, $E_f$, ${\epsilon }_{f,rup}$	$f_{cc}^{\prime }$: strength of confined-HSC in circular section	ANN2
15:15:15:15:15:15:15:1	h, b, $n\times t$ $f_{co}^{\prime }$, $E_f$, ${\epsilon }_{f,rup}$	$f_{cc}^{\prime }$: strength of confined-NSC in rectangular section	ANN3

presents the structure of all designed neural networks, including the number of hidden layers and the number of neurons in each layer, based on the dataset each network was trained on.

Figure 10 illustrates the mean relative absolute error (MRAE) obtained in predicting the ultimate strength for different models and cross-sectional configurations, namely circular_NSC, circular_HSC) and rectangular_NSC.

For Circular_NSC specimens, existing theoretical models and multiple regression analyses exhibited considerably higher error values, reaching up to 31.97% (PBH1), whereas the artificial neural network (ANN) model substantially reduced the error to as low as 2.4%. A similar trend was observed for Circular_HSC sections, where traditional approaches produced errors ranging between 13.17% and 22.97%, while the ANN achieved a significantly lower error of 7.2%. Likewise, for Rectangular_NSC sections, empirical and regression-based models showed errors up to 19.68%, while the ANN provided highly accurate predictions with an error as low as 3.8%.

These findings clearly demonstrate the superior predictive performance of the ANN compared to conventional regression and previously established theoretical models. The ANN effectively captures the nonlinear interactions among geometric, mechanical, and structural parameters, leading to far more precise predictions of ultimate strength. The substantial reduction in error values highlights the potential of neural network models as a powerful and reliable tool for improving strength prediction.

3.5. Ultimate Axial Strain Prediction

Most existing models employed for predicting the ultimate axial strain have utilized the relationship proposed by Richart et al. [10], in which he suggested that the effectiveness of confinement in increasing strain is approximately five times the increase in ultimate strength:

$${\epsilon }_{cc}={\epsilon }_{co}\left[1+5\left({\displaystyle \frac{f_{cc}^{\prime }}{f_{co}}}-1\right)\right]$$

(26)

where ${\epsilon }_{co}$ and ${\epsilon }_{cc}$ represent the axial strain at $f_{co}$ and $f_{cc}^{\prime }$, respectively. This indicates that the ultimate strength may serve as a preliminary step for predicting the corresponding axial strain εcc, as it can be employed as a fundamental input alongside other parameters when developing a customized model for its estimation. Consequently, the present model not only predicts the ultimate strength but also leverages these predictions to infer the corresponding strain in subsequent stages, thereby achieving the overarching objective of comprehensively modeling the (σ-ε) behavior.

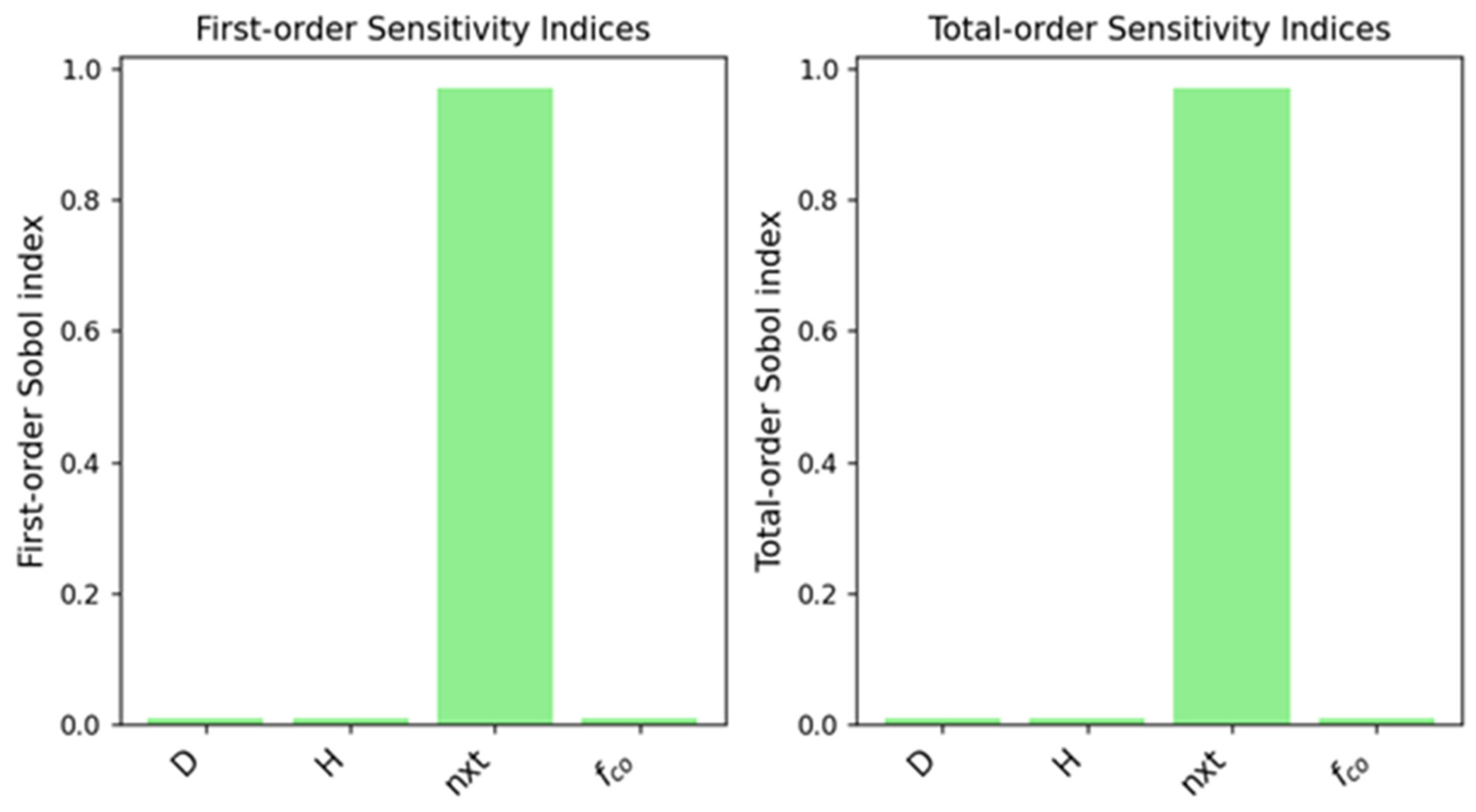
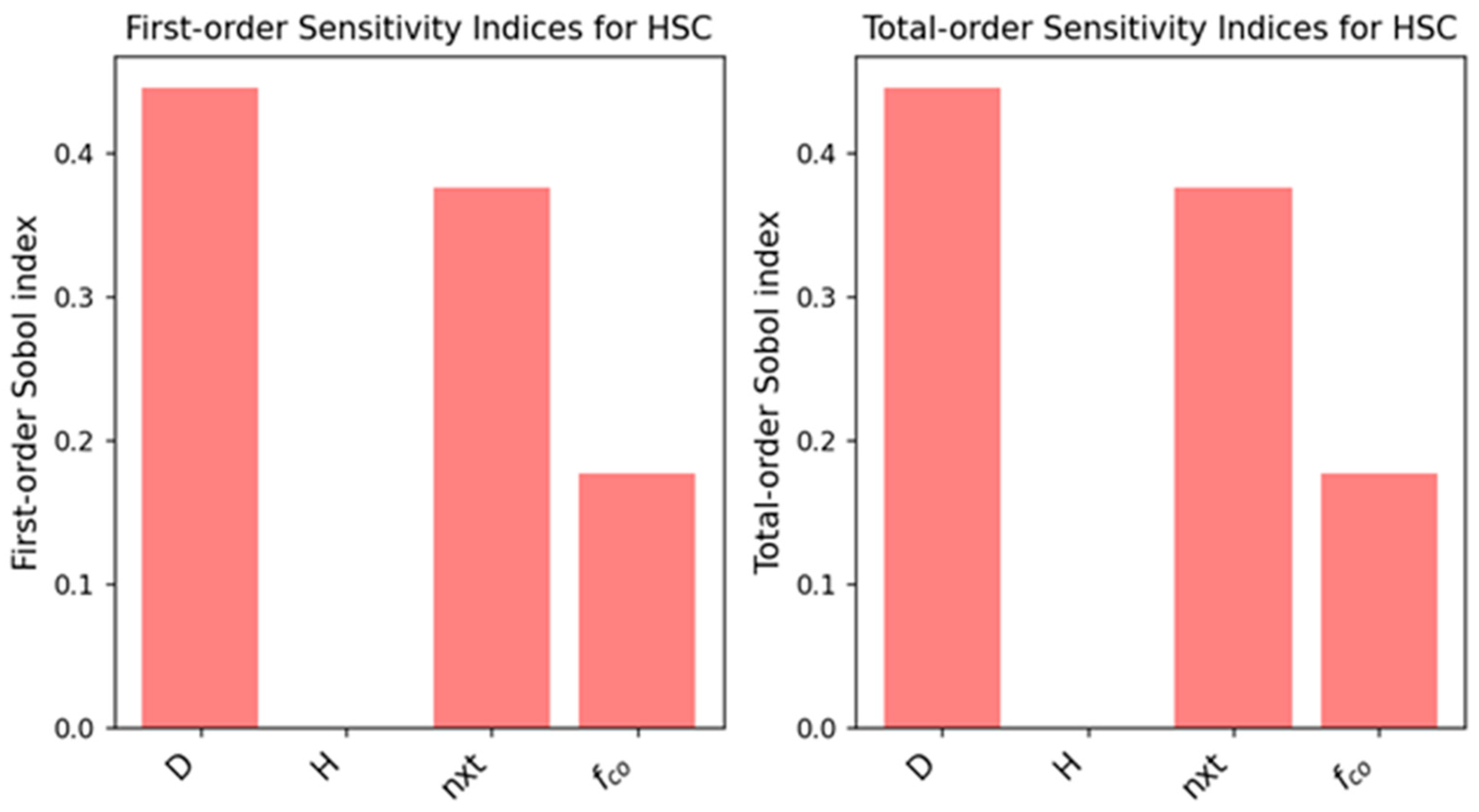
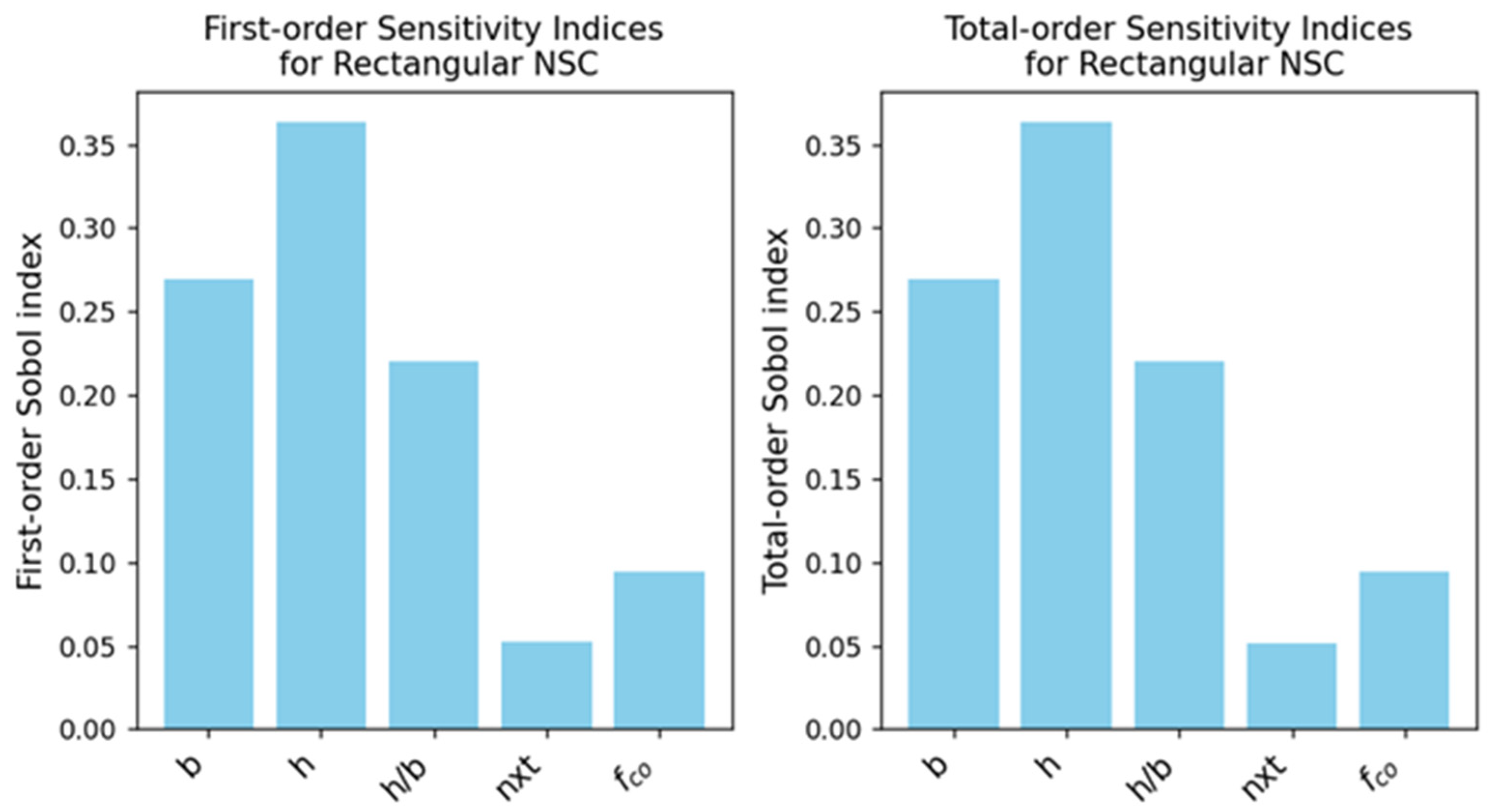
3.6. Sensitivity Analysis

Sobol analysis is a global sensitivity method that quantifies how uncertainties in a model’s input parameters contribute to variations in its output. Unlike local methods, it explores the entire parameter space using variance decomposition to provide a comprehensive importance ranking. It calculates first-order indices (S₁), which measure each parameter’s individual contribution to output variance, and total-order indices (ST), which include interaction effects with other parameters. A large difference between these indices reveals significant parameter interactions. This method is particularly valuable for complex systems like CFRP-confined concrete columns, as it identifies which design parameters—such as CFRP thickness, concrete strength, or geometry—most significantly influence the confined strength prediction.

A. Normal-strength concrete with circular cross-section:

The analysis performed on a database of normal-strength concrete (NSC) circular columns (Figure 11) shows that the number of CFRP layers ($\mathit{n}\times \mathit{t}$) overwhelmingly dominates the contribution to the variance in ultimate strength. In contrast, the diameter (D), height (H), and concrete strength ($f_{co}$) have comparatively negligible indices. Experimentally, this is consistent with observed trends: for specimens with identical geometry and $f_{co}$, the ultimate strength increases almost proportionally with $\mathit{n}\times \mathit{t}$, demonstrating that CFRP confinement is the primary driver of strength gain. The limited impact of D, H, and $f_{co}$ can be attributed to their narrow ranges in the dataset and the inherently linear response governed by the confinement mechanism. Nevertheless, these do not undermine the experimental reality that, in NSC circular columns, the number of CFRP layers is the critical determinant of enhanced strength, while geometry and unconfined strength play secondary roles within the tested ranges.

B. High-strength concrete with circular cross-section:

For high-strength concrete (HSC) circular columns (Figure 12), the column diameter (D) and the number of CFRP layers ($\mathit{n}\times \mathit{t}$) are the most critical parameters. D has the highest first-order Sobol index (approximately 0.48), as a larger cross-sectional area directly increases load-bearing capacity. nt is the second most influential parameter (S₁ ≈ 0.40), with additional layers increasing the confining pressure. The total-order indices for both are nearly identical to their first-order indices, indicating their effects are predominantly direct. The concrete compressive strength ($f_{co}$) has a more moderate influence (S₁ ≈ 0.14), while the column height (H) has a negligible effect. These findings highlight those geometric properties and FRP confinement are the most important factors for engineers to consider in the design of such structures.

C. Normal-strength concrete with rectangular cross-section:

For rectangular columns (Figure 13), geometric properties are the most influential factors. The section length (h) has the highest first-order index (S₁ ≈ 0.37), directly impacting the cross-sectional area and stability. The section width (b) is the second most influential parameter (S₁ ≈ 0.27), and the aspect ratio (h/b) is also significant (S₁ ≈ 0.22) because deviating from a more regular section shape makes the column more vulnerable to the “arching effect.” The total-order indices for these geometric parameters are nearly identical to their first-order indices, indicating minimal interaction with other variables. Conversely, the concrete compressive strength (fco) and the number of CFRP layers ($\mathit{n}\times \mathit{t}$) have a much lower impact (S₁ ≈ 0.09 and 0.05, respectively). The low sensitivity of $(\mathit{n}\times \mathit{t})$ contrasts with circular columns and is due to the “arching effect” in rectangular sections, where confinement is highly effective at the corners but provides diminishing returns on the flat sides.

4. Conclusions

This study successfully investigated the complex relationship between confinement parameters and the ultimate strength of CFRP-confined columns, yielding several key findings that can be summarized as follows:

• Predicting the ultimate strength using neural networks has proven to be more robust than available empirical relationships, as they can accommodate the varying non-linear correlations of parameters with the ultimate strength across different confined column properties.
• Statistical analysis confirmed that the effectiveness of confinement is significantly influenced by both the concrete’s strength and the shape of the cross-section.
• For normal-strength concrete in circular columns, a strong linear correlation was observed between the ultimate strength and the thickness of the CFRP jacket, indicating effective confinement. However, this correlation was weaker for high-strength concrete and rectangular columns.
• CFRP confinement is more feasible and effective when applied to normal-strength concrete.
• Artificial Neural Networks (ANNs) offer a highly effective way to model concrete behavior, with the potential to replace traditional mathematical models.
• When using ANNs with normal-strength concrete in circular columns, error metrics such as RMSE (2.92), MRAE (2.4%), and MAE (1.36) were low, indicating high predictive accuracy. Similar performance was observed for rectangular columns.
• For high-strength concrete in circular columns, the multiple linear regression model also showed good predictive accuracy, with a correlation coefficient (R) of 0.922 and a coefficient of determination (R²) of 0.85.
• The sensitivity analysis revealed a marked dominance of the number of CFRP layers (n × t) on the behavior of circular sections, irrespective of the concrete strength grade, despite the notably pronounced role of its initial strength in high-strength concrete specimens. Conversely, the dominance of this factor diminishes markedly in rectangular sections, giving way to geometric dimensions and elongation ratios as decisive criteria governing the ultimate strength.