The Importance of Structural Configuration in the Seismic Performance and Reliability of Buildings
Abstract
1. Introduction
2. Buildings Description and Modeling Considerations
2.1. Nonlinear Dynamic Analysis
2.2. Geometric Nonlinearity (P-Delta Effects)
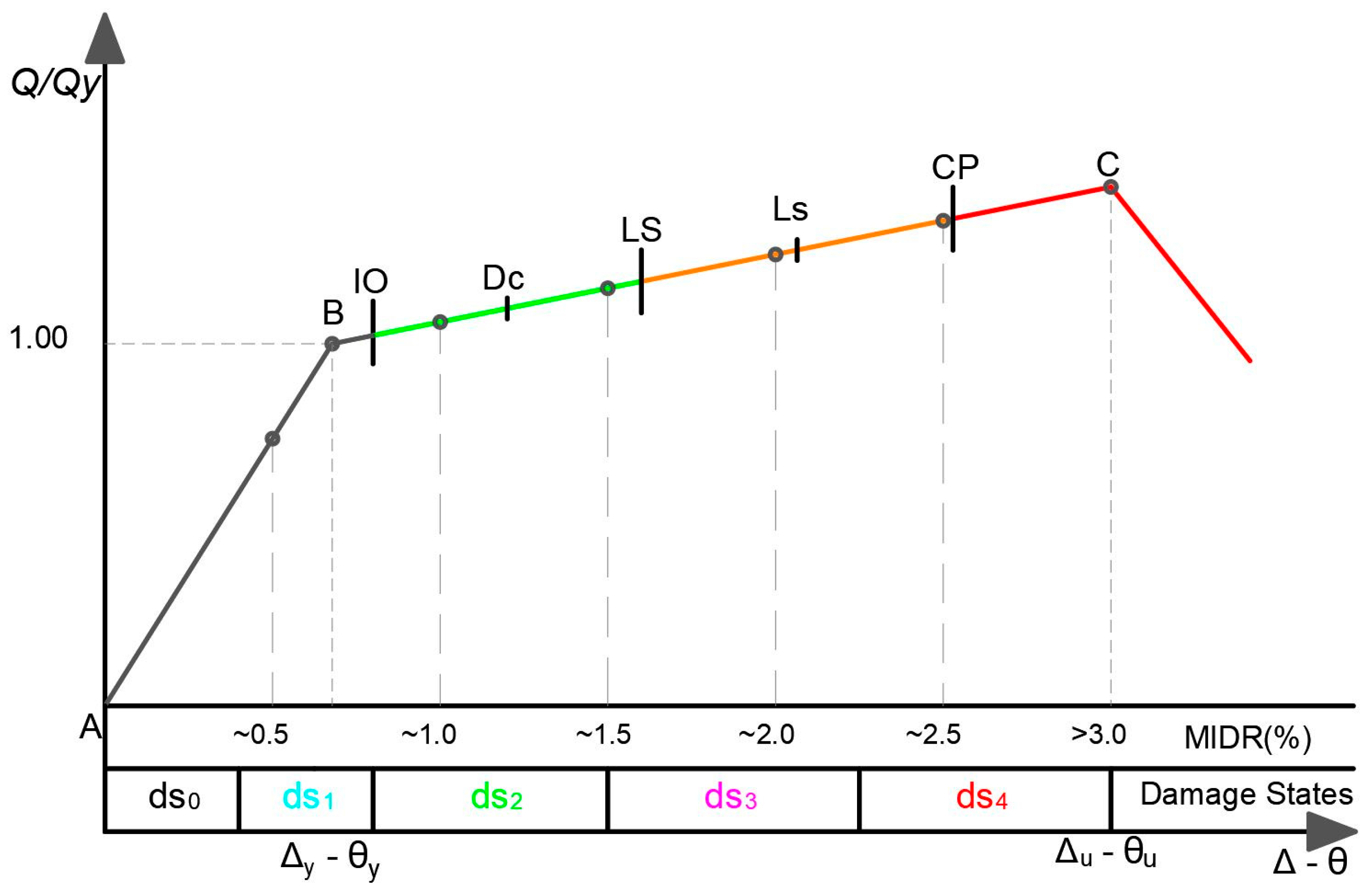
2.3. Performance Levels
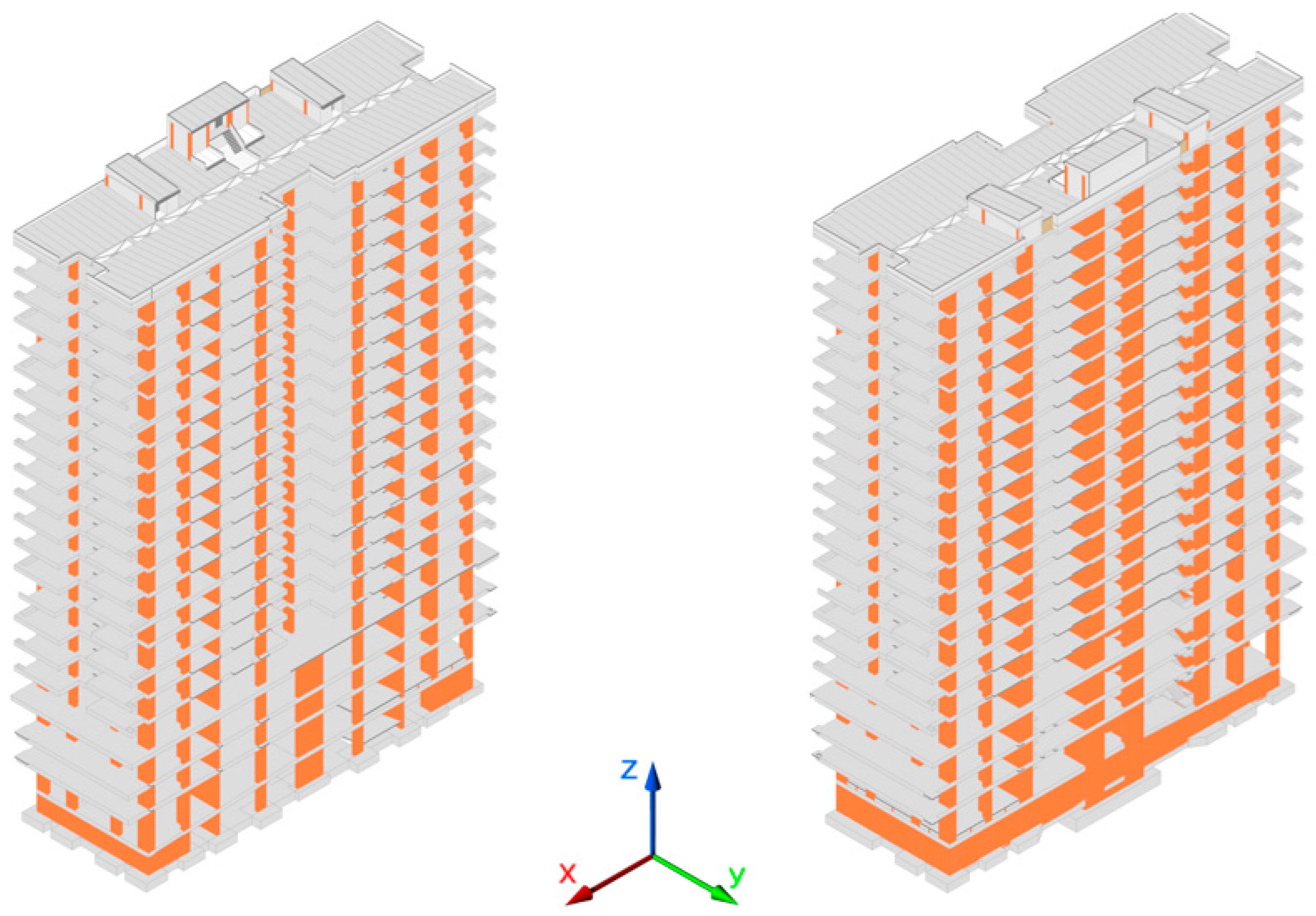
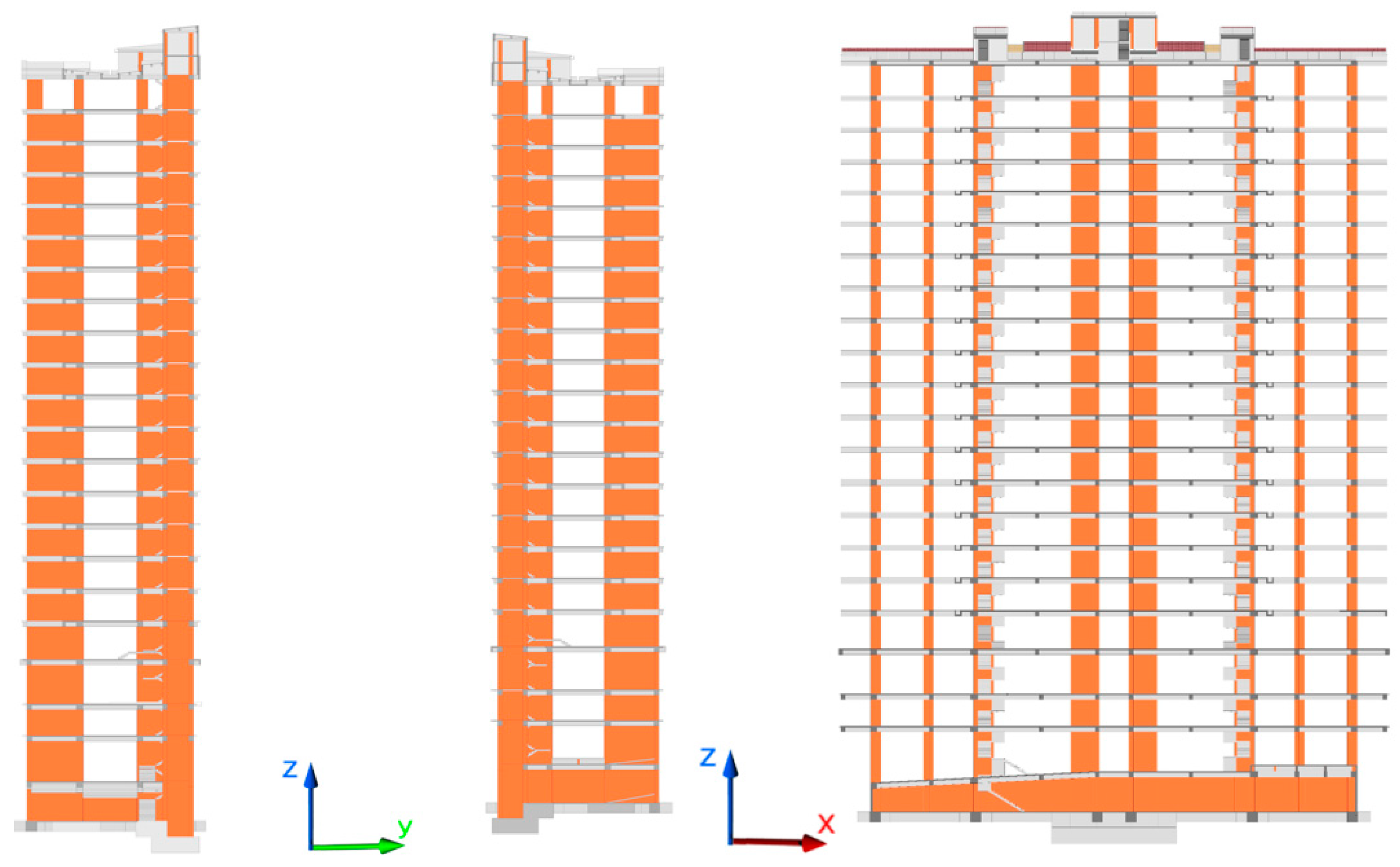
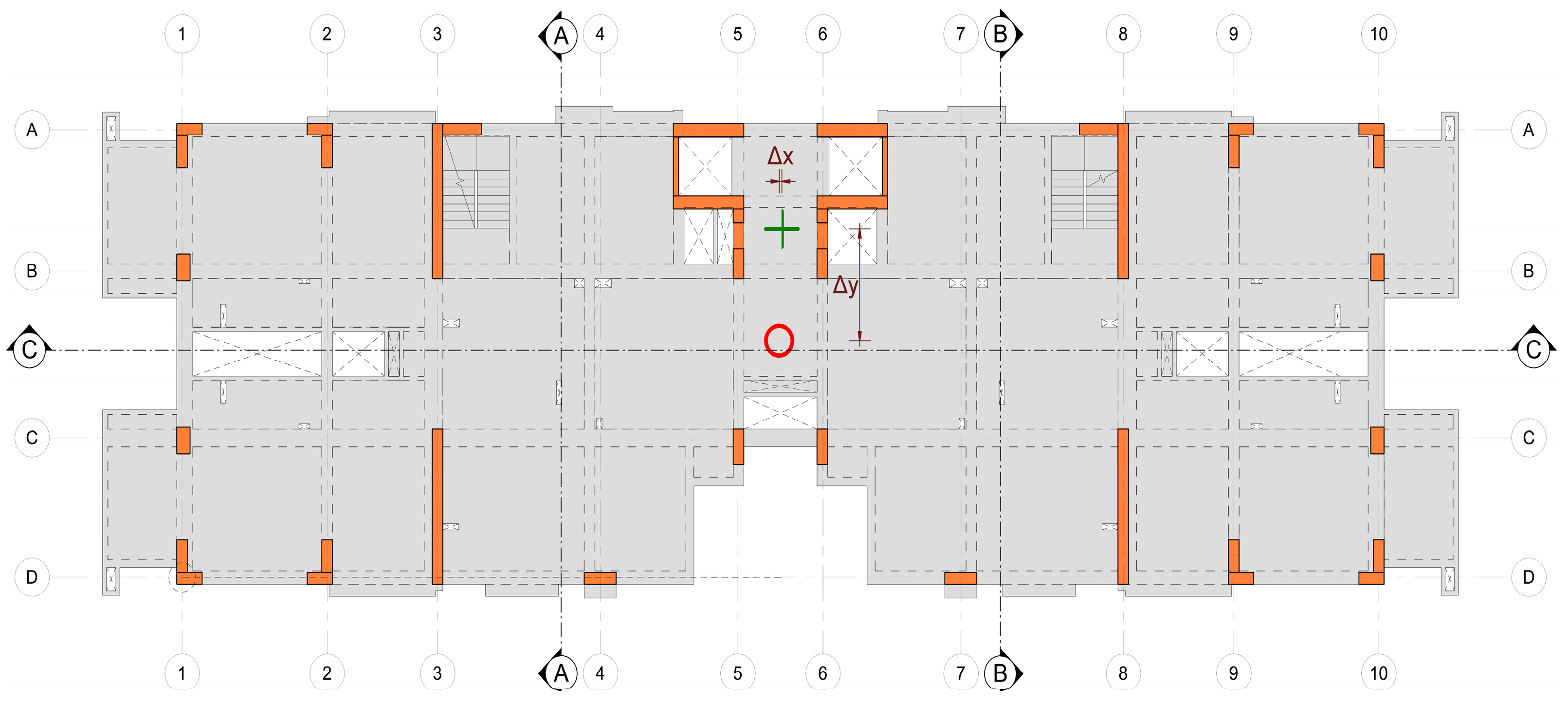
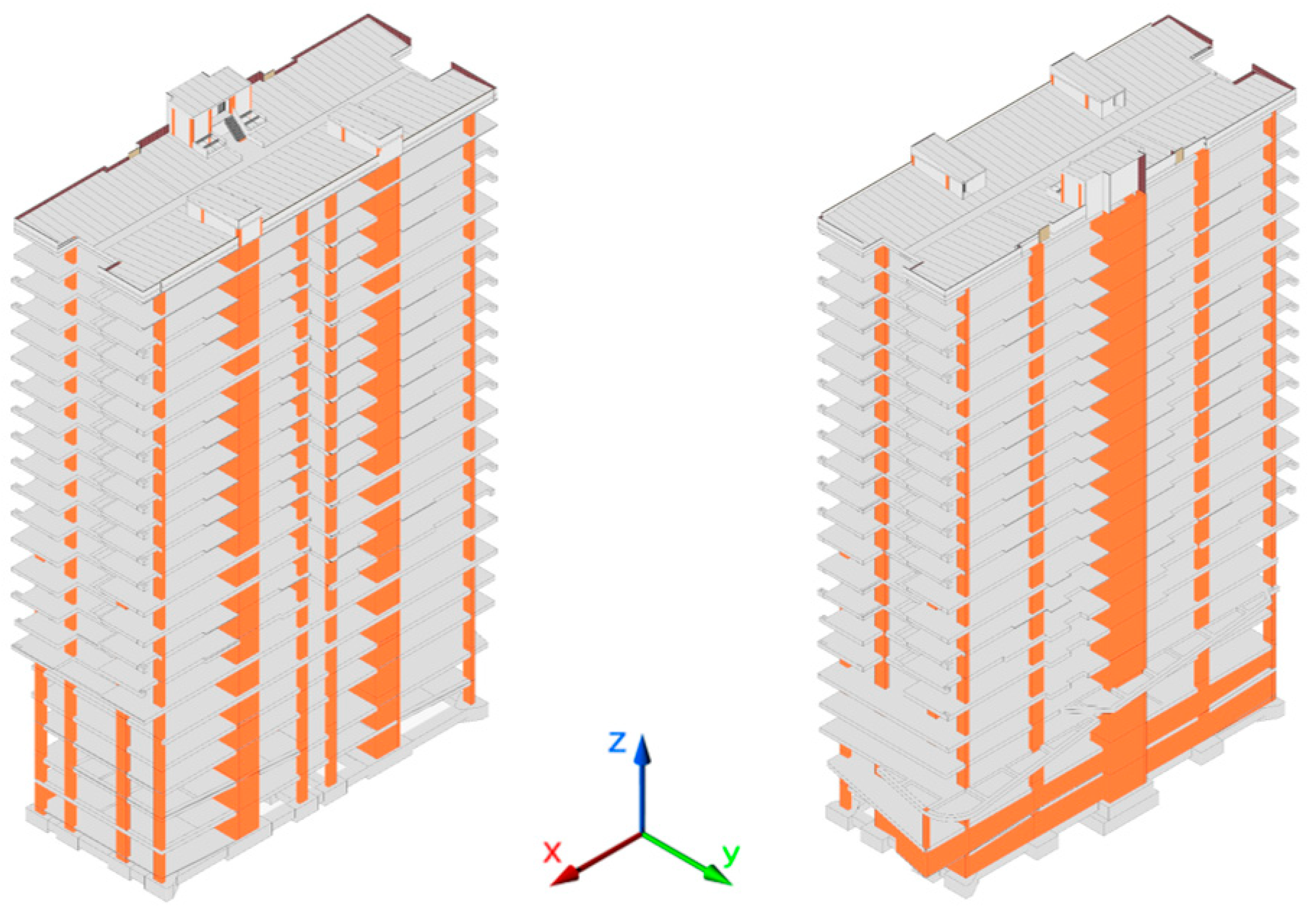
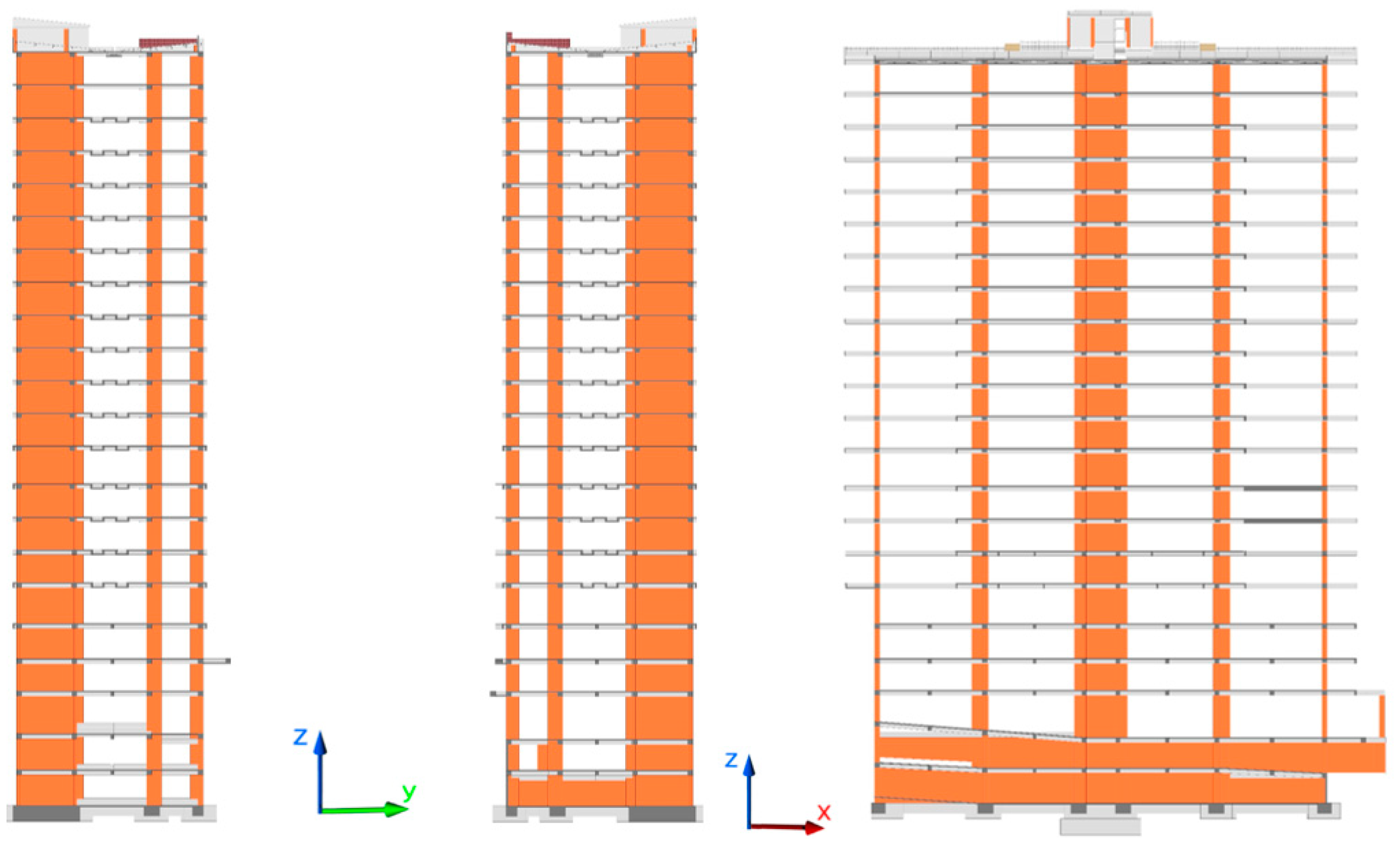
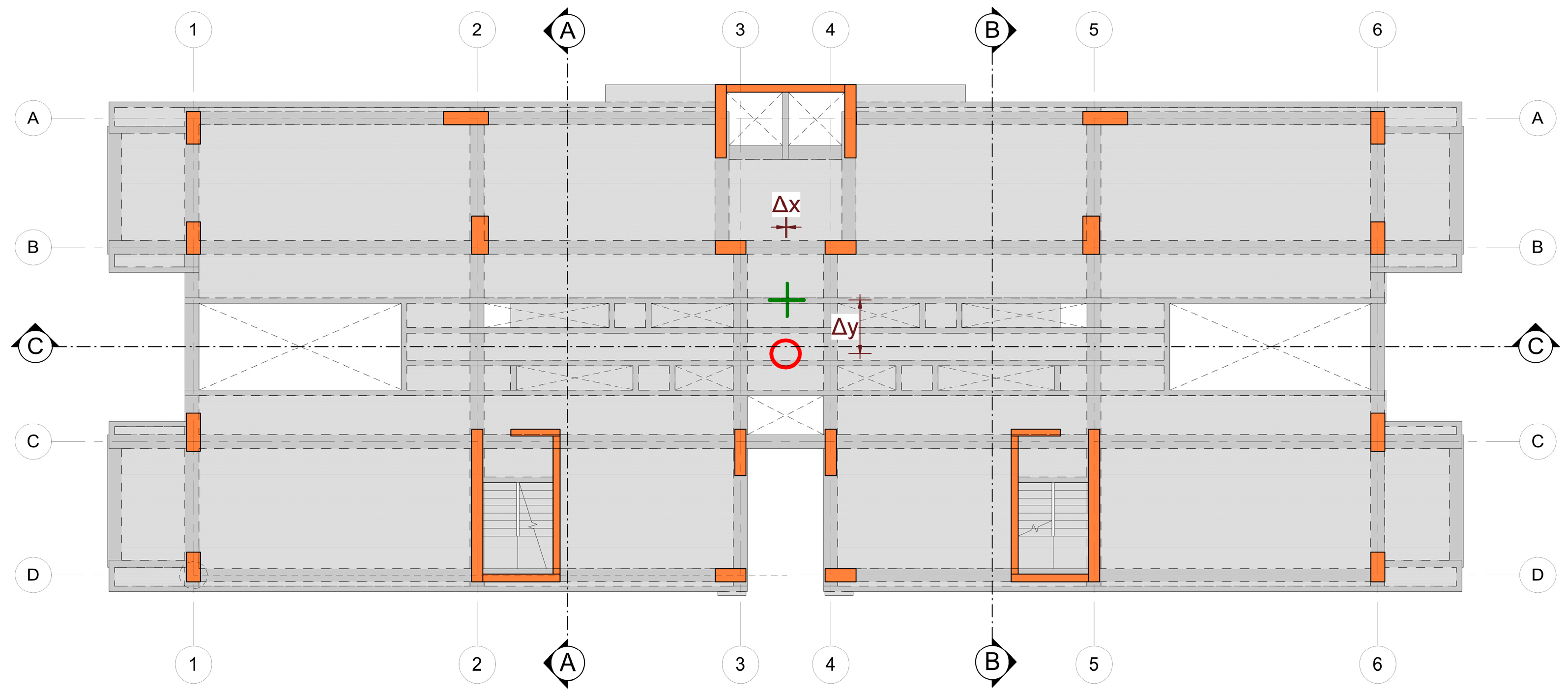
2.4. Building 1 (B1)
2.5. Building 2 (B2)
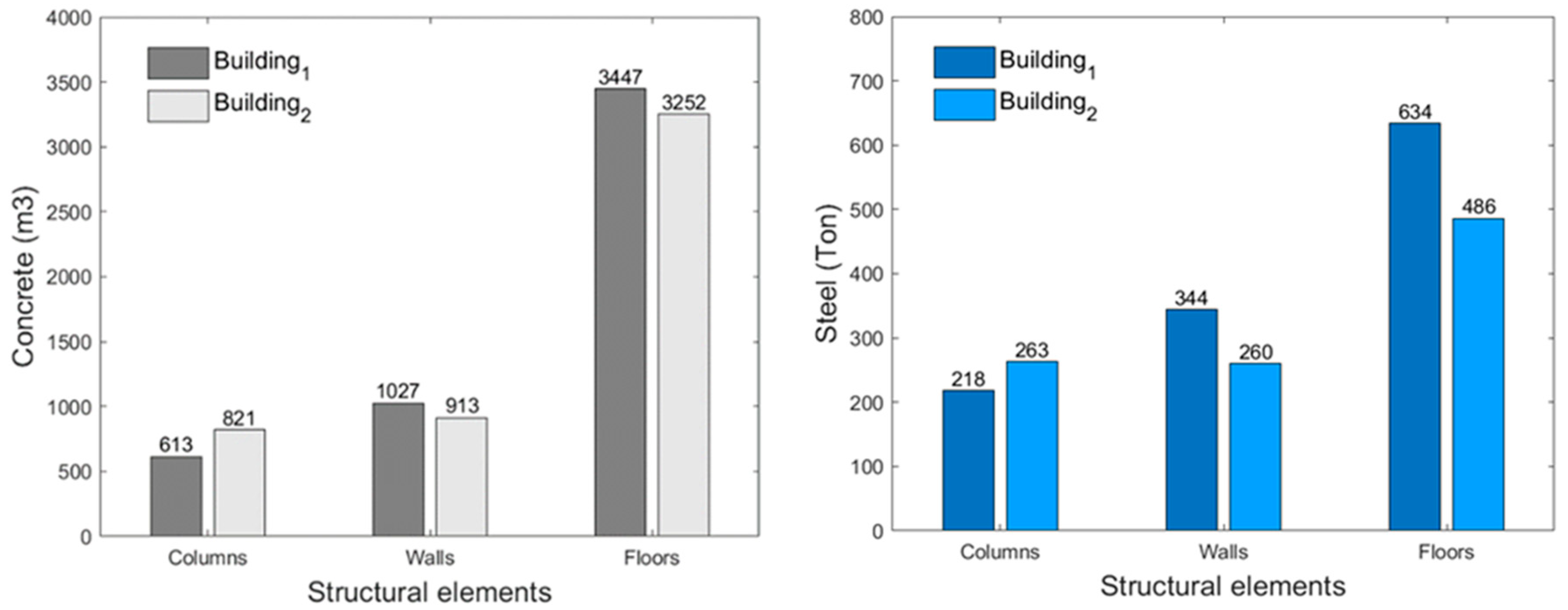
2.6. Construction Material Quantities
3. Seismic Hazard
- -
- Identify the IM to scale. In this case, the average spectral acceleration around the fundamental period of the building, AvSa, has been used.
- -
- Define the maximum value of the IM in order to select the scaling bands (ten in this case). This maximum value depends on the level of intensity used for the building design.
- -
- Select one hundred ground motion records from a database, which have been previously sorted with respect to AvSa. This average acceleration has been taken between 0.1 T and 1.8 T (T is the fundamental period of the structure) as lower and upper limits, respectively. The purpose is to include the contribution of higher modes as well as the softening of the structure due to the accumulation of damage [17].
- -
- After the sorting performed in the previous step, the ground motion record with the highest IM was scaled so that its new IM value belongs to the highest scaling interval. If the IM naturally fulfills the interval condition, no scale factor is considered. This step is repeated with the subsequent records, according to the sorted list, until the desirable number of records (ten) belonging to the highest interval is obtained.
- -
- The previous step is repeated for all intervals. Note that the scale factor in step 4 is calculated having in mind that the IM values are uniformly distributed within each interval.
4. Comparison Between Structural Configurations
4.1. Fragility Functions
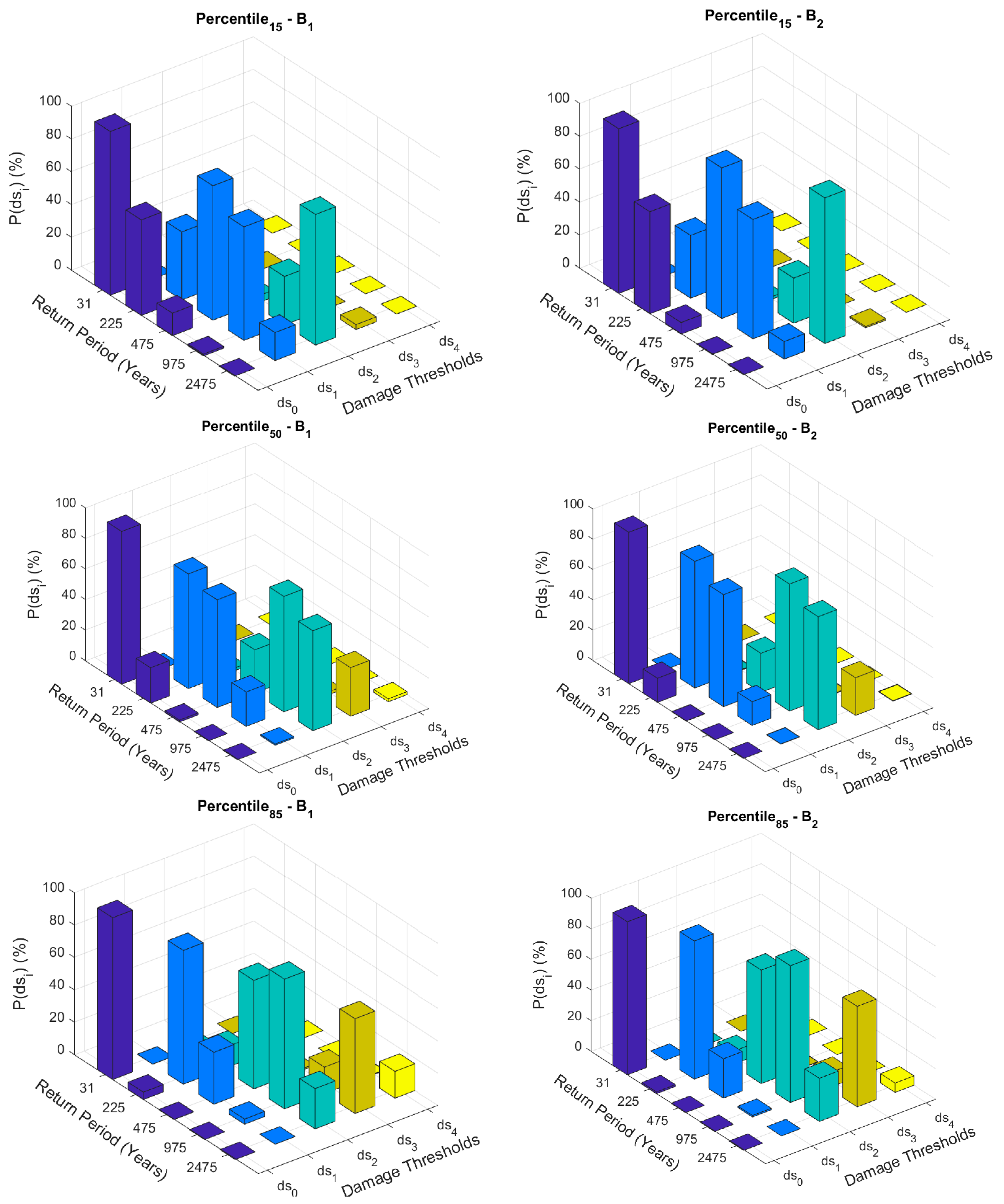
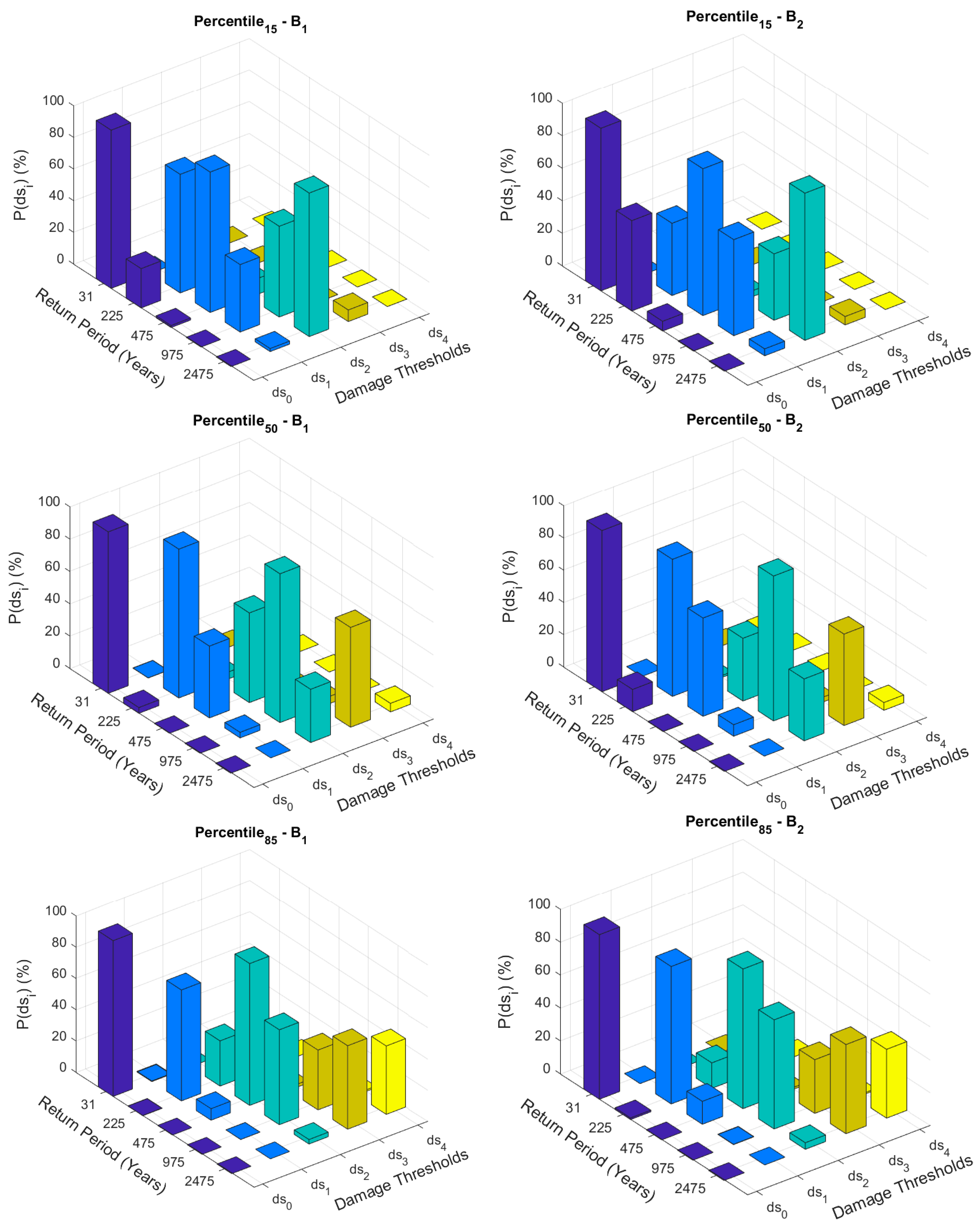
4.2. Probabilities of Occurrence of the Damage States
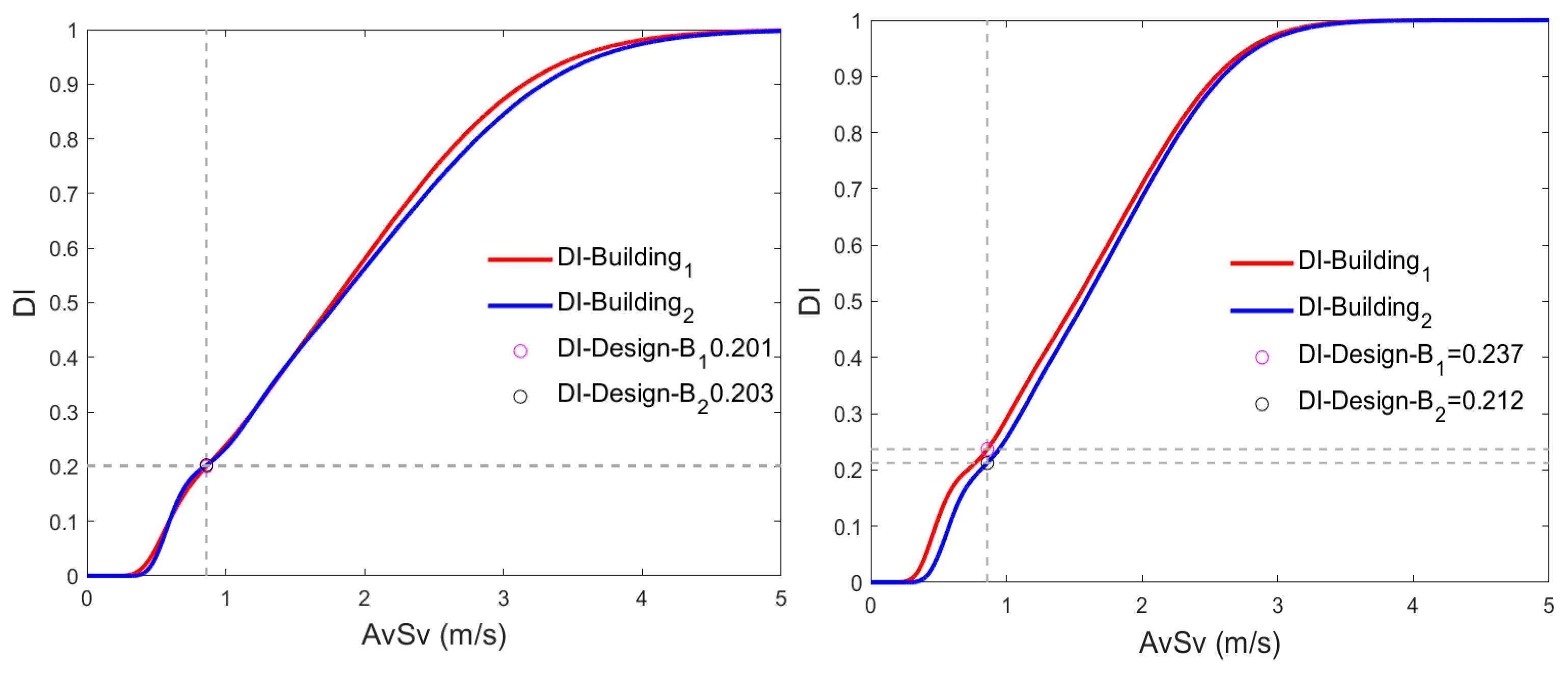
4.3. Global Damage Index
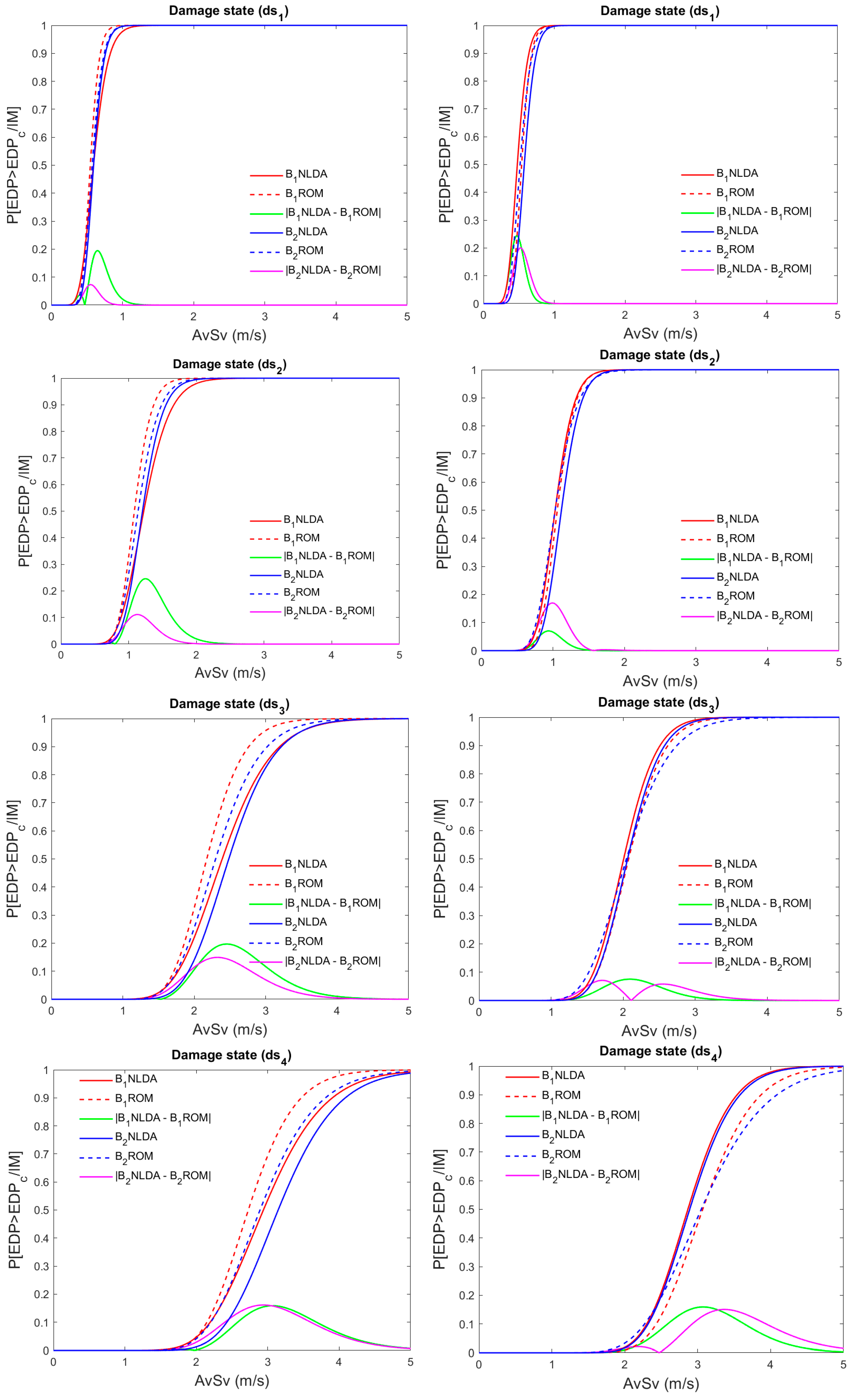
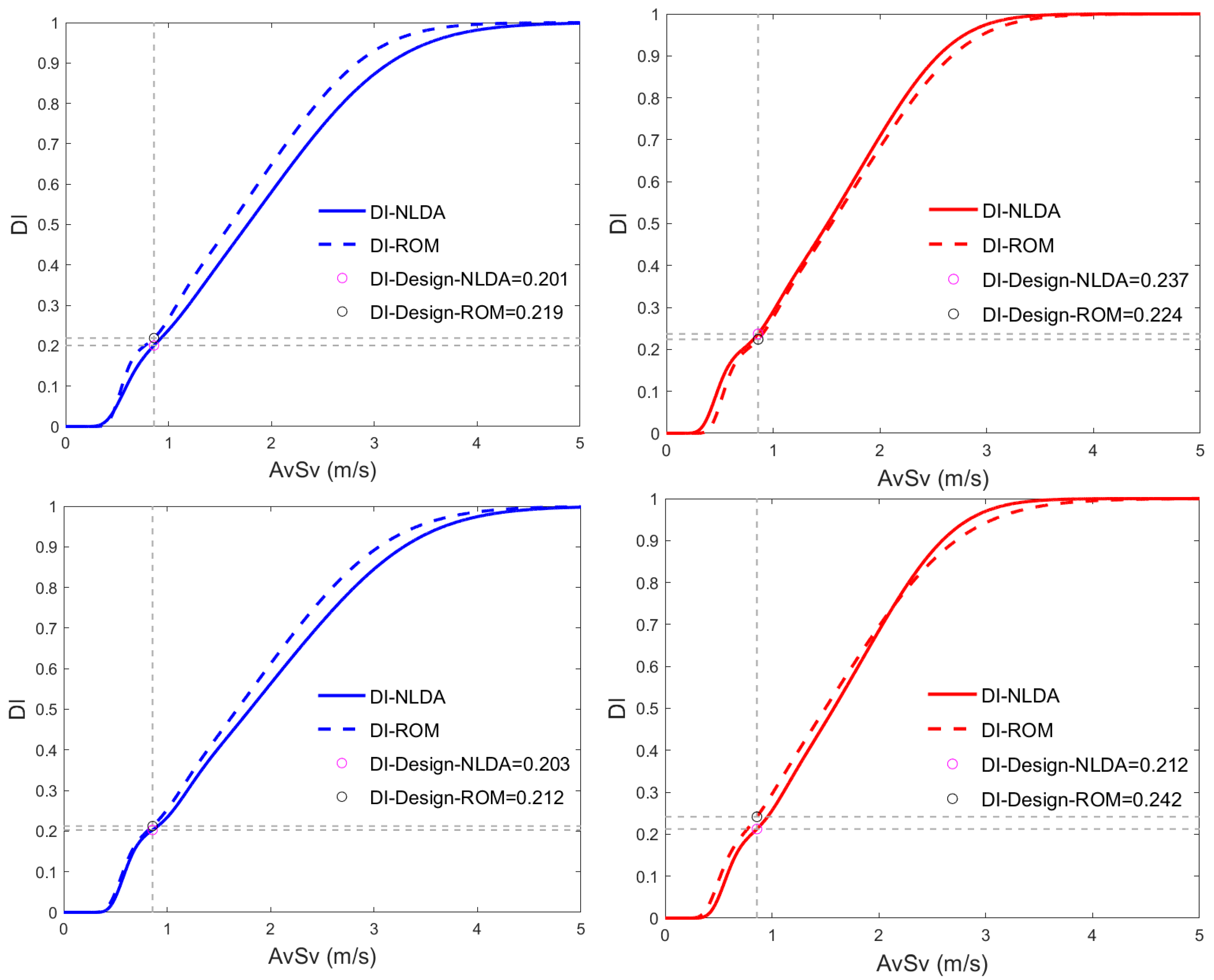
5. Comparison Between NLDA and ROM
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Millward-Hopkins, J.; Steinberger, J.K.; Rao, N.D.; Oswald, Y. Providing decent living with minimum energy: A global scenario. Glob. Environ. Change 2020, 65, 102168. [Google Scholar] [CrossRef]
- Storm, S. Inflation in the Time of Corona and War; Institute for New Economic Thinking Working Paper Series; Institute for New Economic Thinking: New York, NY, USA, 2022. [Google Scholar]
- Melchers, R.E. Structural reliability theory in the context of structural safety. Civ. Eng. Environ. Syst. 2007, 24, 55–69. [Google Scholar] [CrossRef]
- Rackwitz, R. Structural Reliability—Analysis and Prediction. Struct. Saf. 2001, 23, 194–195. [Google Scholar] [CrossRef]
- Ramli, A.; Akasah, Z.A.; Masirin, M.I.M. Factors Contributing Building Safety and Health Performance of Low Cost Housing in Malaysia. J. Saf. Eng. 2013, 2, 1–9. [Google Scholar]
- Moon, K. Optimal structural configurations for tall buildings. In Proceedings of the 13th East Asia-Pacific Conference on Structural Engineering and Construction, EASEC 2013, Sapporo, Japan, 11–13 September 2013. [Google Scholar]
- Mishra, A.K. Role of Reliability Analysis in Structural Design. Hydro Nepal J. Water Energy Environ. 2019, 24, 6–9. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Kumar, R.; Pruncu, C.I. Recent progress of reinforcement materials: A comprehensive overview of composite materials. J. Mater. Res. Technol. 2019, 8, 6354–6374. [Google Scholar] [CrossRef]
- Chiaia, B.; Barchiesi, E.; De Biagi, V.; Placidi, L. A novel structural resilience index: Definition and applications to frame structures. Mech. Res. Commun. 2019, 99, 52–57. [Google Scholar] [CrossRef]
- van de Lindt, J.W.; Sasani, M.; Warn, G.; Esteghamati, M.Z. (Eds) Resilient and Sustainable Buildings; American Society of Civil Engineers: Reston, VA, USA, 2023. [Google Scholar] [CrossRef]
- Fajfar, P. Analysis in seismic provisions for buildings: Past, present and future. In Geotechnical, Geological and Earthquake Engineering; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Wilson, E.L. Three Dimensional Static and Dynamic Analysis of Structures: A Physical Approach with Emphasis on Earthquake Engineering; Computers & Structures, Inc.: Berkeley, CA, USA, 2002. [Google Scholar]
- Vargas-Alzate, Y.F. Análisis Estructural Estático y Dinámico Probabilista de Edificios de Hormigón Armado. Aspectos Metodológicos y Aplicaciones a la Evaluación del Daño. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2013. (In Spanish). [Google Scholar]
- Deierlein, G.; Reinhorn, A.; Willford, M. Nonlinear Structural Analysis For Seismic Design. NEHRP Seism. Des. Tech. Brief 2010, 4, 1–36. [Google Scholar]
- de Almeida, N.M.; Silva, M.J.F.; Salvado, F.; Rodrigues, H.; Maletič, D. Risk-informed performance-based metrics for evaluating the structural safety and serviceability of constructed assets against natural disasters. Sustainability 2021, 13, 5925. [Google Scholar] [CrossRef]
- Asociación Colombiana de Ingeniería Sismica (AIS). Reglamento Colombiano de Construcción Sismo Resitente NSR-10; AIS: Bogotá, Colombia, 2010. (In Spanish) [Google Scholar]
- Tirado-Gutiérrez, R.J.; Vargas-Alzate, Y.F.; González-Drigo, R. Probabilistic estimation of the dynamic response of high-rise buildings via transfer functions. Eng. Struct. 2024, 302, 117299. [Google Scholar] [CrossRef]
- Cooley, J.W.; Lewis, P.A.W.; Welch, P.D. Application of the Fast Fourier Transform to Computation of Fourier Integrals, Fourier Series, and Convolution Integrals. IEEE Trans. Audio Electroacoust. 1967, 15, 79–84. [Google Scholar] [CrossRef]
- Vielma, J. Damage Trhesholds for Limit States of Reinforced Concrete Framed Buildings Designed According To Aci- 318/Ibc-2006. Rev. Int. De Desastres Nat. Accid. E Infraestruct. Civ. 2008, 8, 119–134. (In Spanish) [Google Scholar]
- Correa-Martínez, A.M.; Martens, U.; Rodríguez, G. Collage of tectonic slivers abutting the eastern Romeral Fault System in central Colombia. J. South Am. Earth Sci. 2020, 104, 102794. [Google Scholar] [CrossRef]
- ASCE 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2017. [CrossRef]
- ACI 318; Building Code Requeriments for Reinforced Concrete. American Concrete Institute: Detroit, MI, USA, 2019.
- Moehle, J.; Bozorgnia, Y.; Yang, T.Y. The Tall Buildings Initiative. In Proceedings of the SEAOC Convention, Squaw Creek, CA, USA, 26–29 September 2007. [Google Scholar]
- CSI Computers & Structural, INC. Structural and Earthquake Engineering Software. 2017. Available online: www.csiamerica.com (accessed on 27 November 2023).
- Aguiar, R. Análisis Sísmico por Desempeño; Centro de Investigaciones Científicas, Escuela Politécnica del Ejército: Quito, Ecuador, 2003. (In Spanish) [Google Scholar]
- ASCE 41-17; Seismic Evaluation and Retrofit of Existing Buildings: ASCE/SEI, 41-17. American Society of Civil Engineers Institute, Structural Engineering: Reston, VA, USA, 2017.
- FEMA. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; FEMA 356; Federal Emergency Management Agency: Washington, DC, USA, 2000. [Google Scholar]
- Dowell, R.K.; Seible, F.; Wilson, E.L. Pivot Hysteresis Model -Dowell, Seible & Wilson ACI 1998. ACI Struct. J. 1988, 95, 607–617. [Google Scholar]
- Charney, F.; Lopez-Garcia, D.; Hardyniec, A.; Ugalde, D. Modeling inherent damping in nonlinear dynamic analysis. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Asimakopoulos, A.V.; Karabalis, D.L.; Beskos, D.E. Inclusion of P-Δ effect in displacement-based seismic design of steel moment resisting frames. Earthq. Eng. Struct. Dyn. 2007, 36, 2171–2188. [Google Scholar] [CrossRef]
- Akhter, R.; Prakash, S.; Baig, M.A. P-Delta Effect on High Rise Building Subjected to Earthquake and Wind Load. Int. J. Eng. Sci. Comput. 2017, 7, 14441–14446. [Google Scholar]
- Taranath, B.S. Tall Building Design; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Charney, F.A. Seismic Loads-Guide to the Seismic Provisions of ASCE 7-10; American Society of Civil Engineers: Reston, VA, USA, 2015. [Google Scholar]
- Charney, F.A. Use of nonlinear analysis in the context of the ASCE 7 seismic load provisions. In Structures Congress 2011—Proceedings of the 2011 Structures Congress; American Society of Civil Engineers: Reston, VA, USA, 2011. [Google Scholar] [CrossRef]
- ATC-40; Seismic Evaluation and Retrofit of Concrete Buildings. Applied Technology Council: Redwood City, CA, USA, 1996.
- Fragiadakis, M.; Papadrakakis, M. Performance-based optimum seismic design of reinforced concrete structures. Earthq. Eng. Struct. Dyn. 2008, 37, 825–844. [Google Scholar] [CrossRef]
- Hanganu, A.D.; Oñate, E.; Barbat, A.H. A finite element methodology for local/global damage evaluation in civil engineering structures. Comput. Struct. 2002, 80, 1667–1687. [Google Scholar] [CrossRef]
- Haselton, C.B.; Whittaker, A.S.; Hortascu, A.; Baker, J.W.; Bray, J.; Grant, D.N. Selecting and scaling ground motions for performing response-history analyses. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Shedlock, K.M. California Earthquakes: Science, Risks, and the Politics of Hazard Mitigation. Eos Trans. Am. Geophys. Union 2002, 83, 39–40. [Google Scholar] [CrossRef]
- Servicio Geológico Colombiano. SGC. Sistema de Consulta de la Amenaza Sísmica de Colombia. 2020. Available online: https://amenazasismica.sgc.gov.co/ (accessed on 20 November 2025).
- Vargas-Alzate, Y.F.; Silva, V.; Vamvatsikos, D.; Pujades, L.G. A simplified approach for including the incidence angle effect in seismic risk assessment. Earthq. Eng. Struct. Dyn. 2022, 51, 191–212. [Google Scholar] [CrossRef]
- Martins, L.; Silva, V. Development of a fragility and vulnerability model for global seismic risk analyses. Bull. Earthq. Eng. 2021, 19, 6719–6745. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F.; Hurtado, J.E.; Pujades, L.G. New Insights into the Relationship Between Seismic Intensity Measures and Nonlinear Structural Response; Springer: Dordrecht, The Netherlands, 2022. [Google Scholar] [CrossRef]
- Mayes, R.L. Interstory drift design and damage control issues. Struct. Des. Tall Build. 1995, 4, 15–25. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F.; Pujades, L.G.; Barbat, A.H.; Hurtado, J.E. An Efficient Methodology to Estimate Probabilistic Seismic Damage Curves. J. Struct. Eng. 2019, 145, 04019010. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Jalayer, F. Selection of seismic intensity measures for prescribed limit states using alternative nonlinear dynamic analysis methods. Earthq. Eng. Struct. Dyn. 2021, 50, 1235–1250. [Google Scholar] [CrossRef]
- Bakalis, K.; Vamvatsikos, D. Seismic Fragility Functions via Nonlinear Response History Analysis. J. Struct. Eng. 2018, 144, 04018181. [Google Scholar] [CrossRef]
- Sokolov, V.Y. Hazard-Consistent Ground Motions: Generation on the Basis of Uniform Hazard Fourier Spectra. Bull. Seismol. Soc. Am. 2000, 90, 1010–1027. [Google Scholar] [CrossRef]
- Park, Y.; Ang, A.H.-S. Mechanistic Seismic Damage Model for Reinforced Concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- Surana, M.; Singh, Y.; Lang, D.H. Effect of irregular structural configuration on floor acceleration demand in hill-side buildings. Earthq. Eng. Struct. Dyn. 2018, 47, 2032–2054. [Google Scholar] [CrossRef]
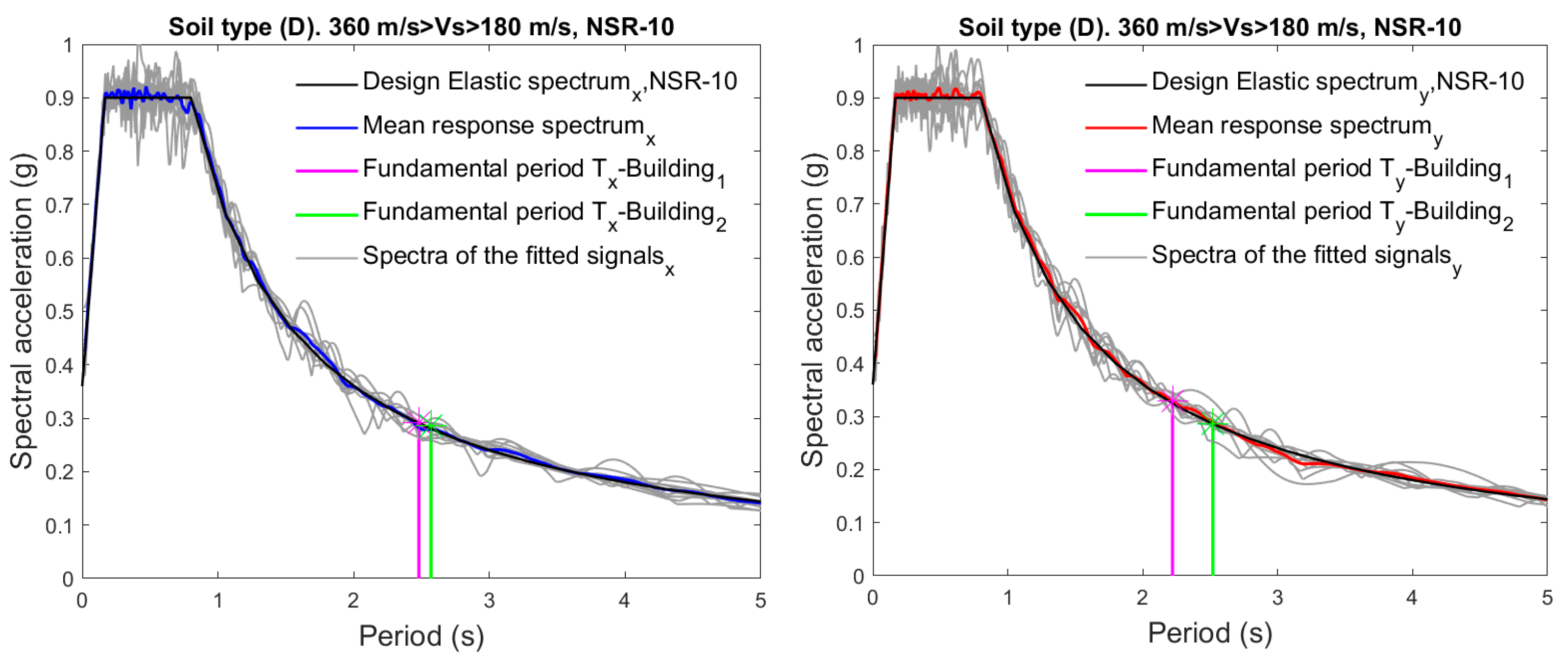
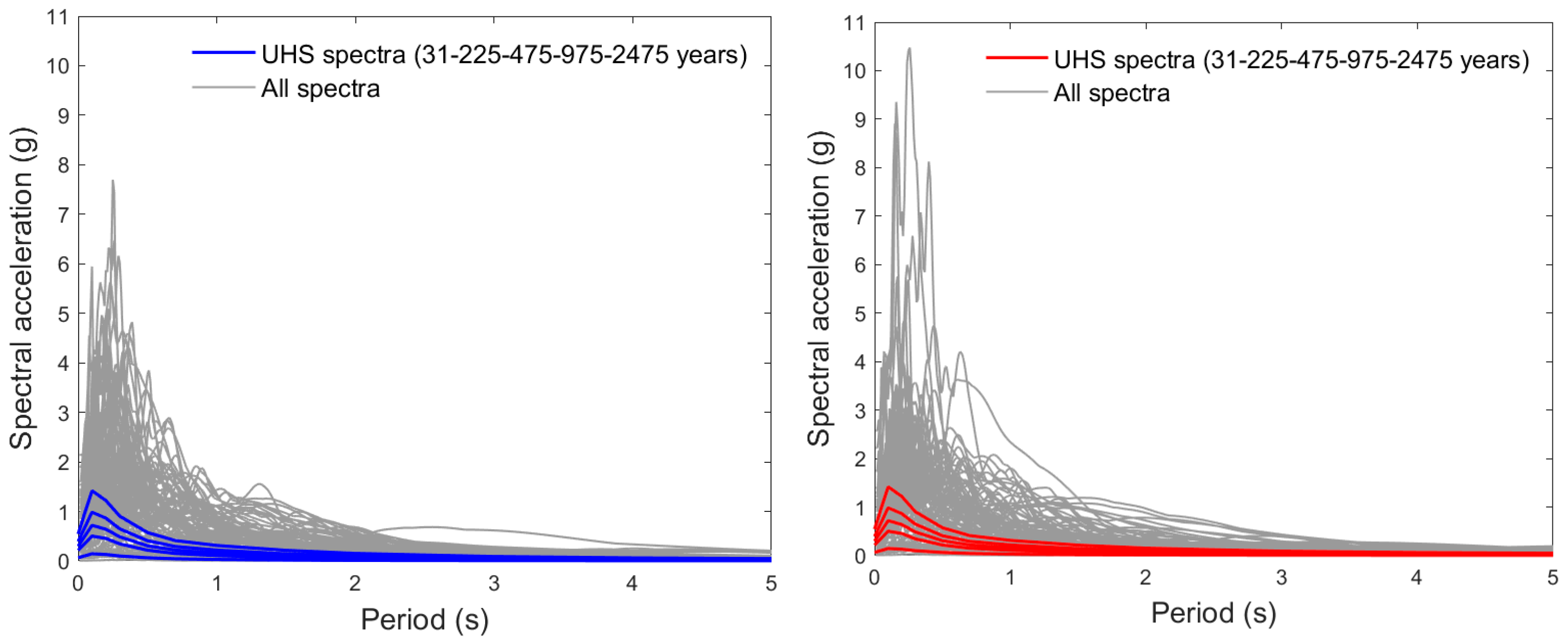
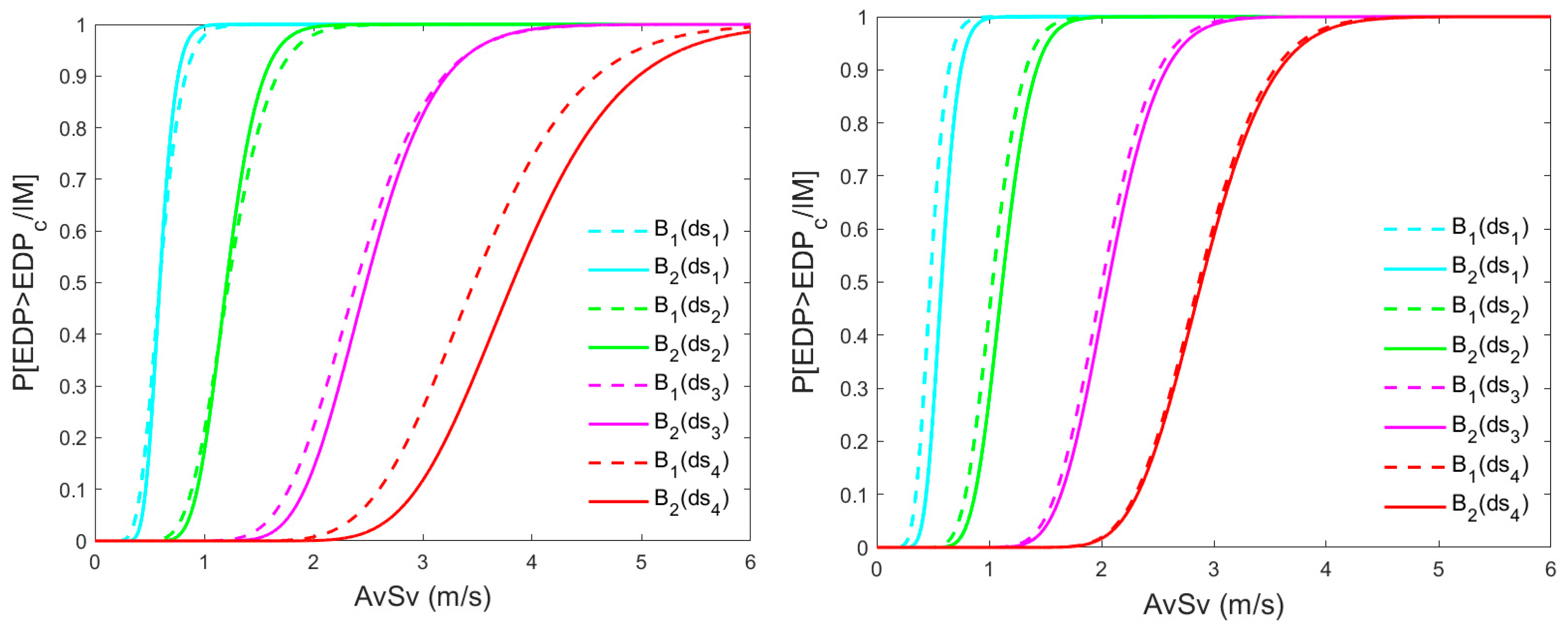
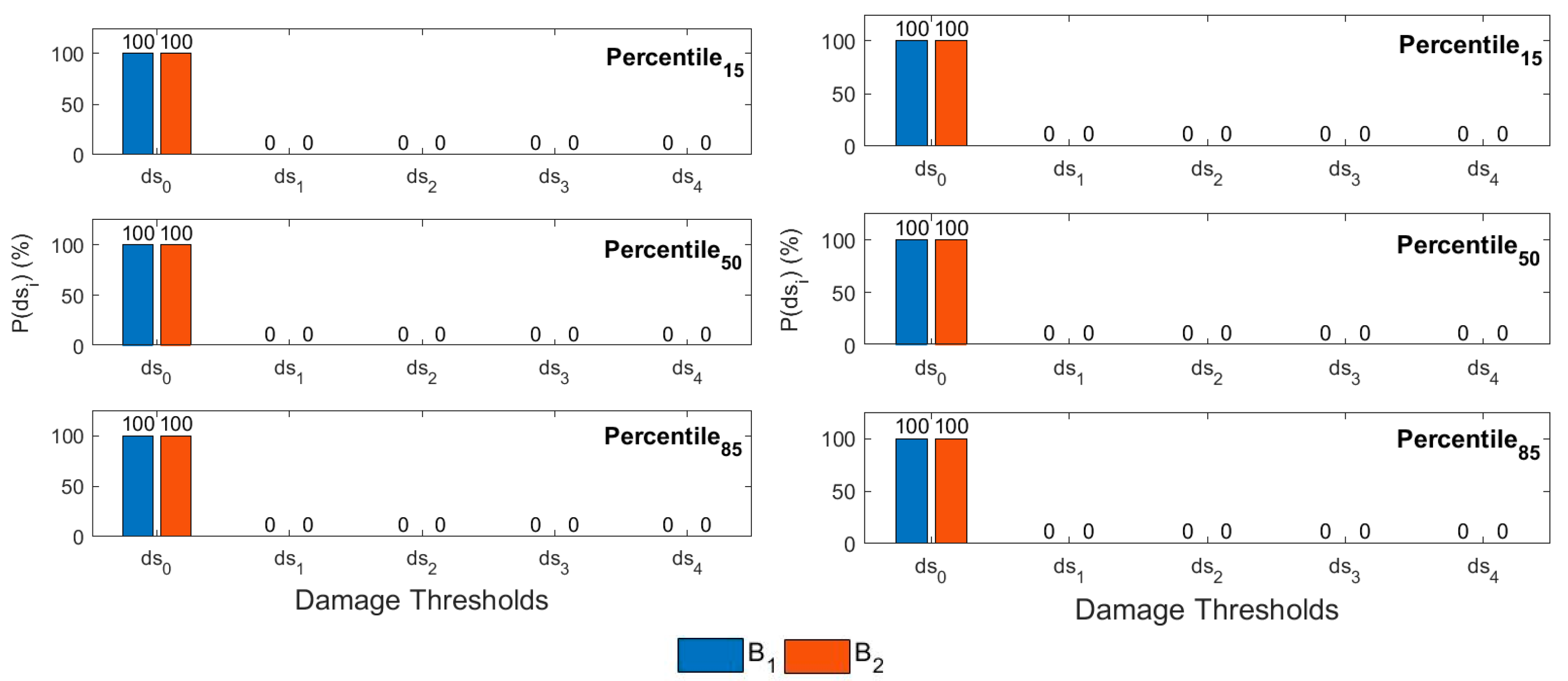
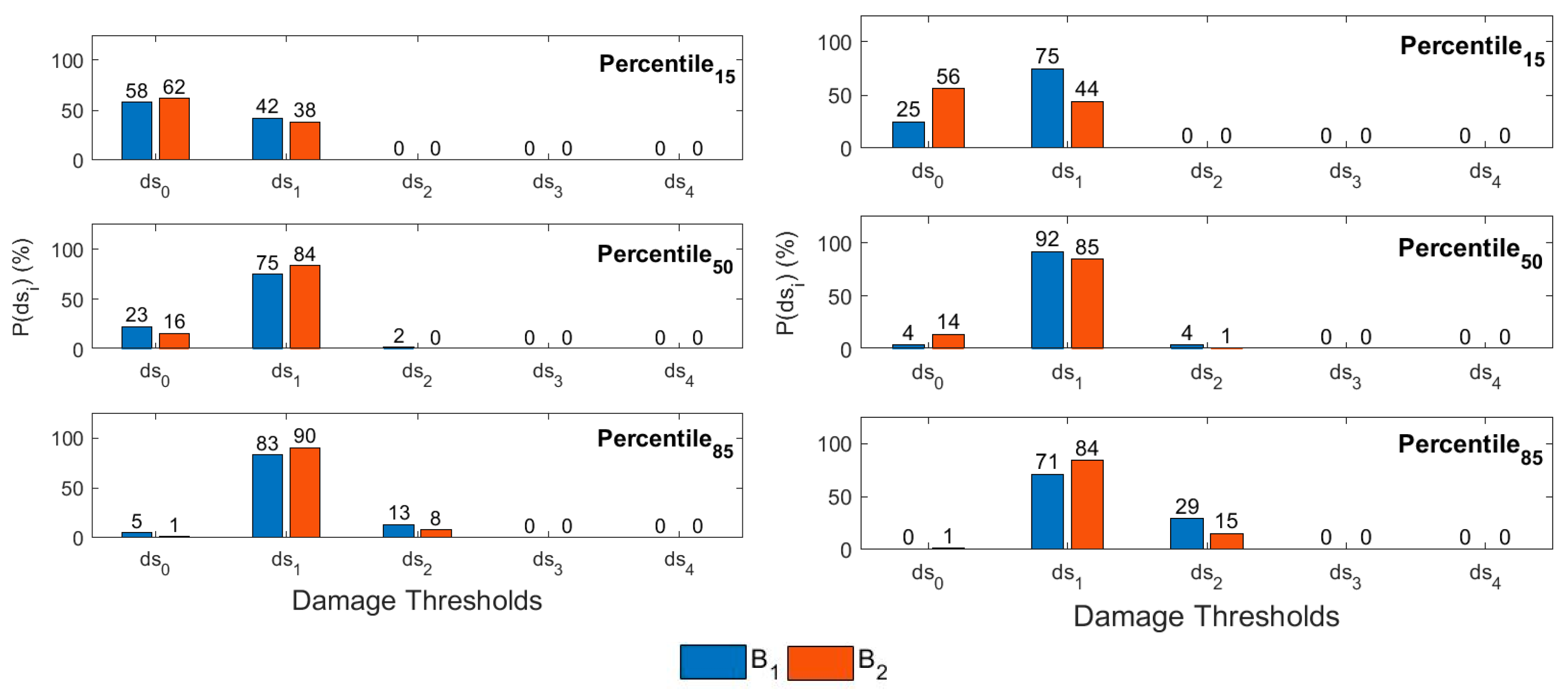
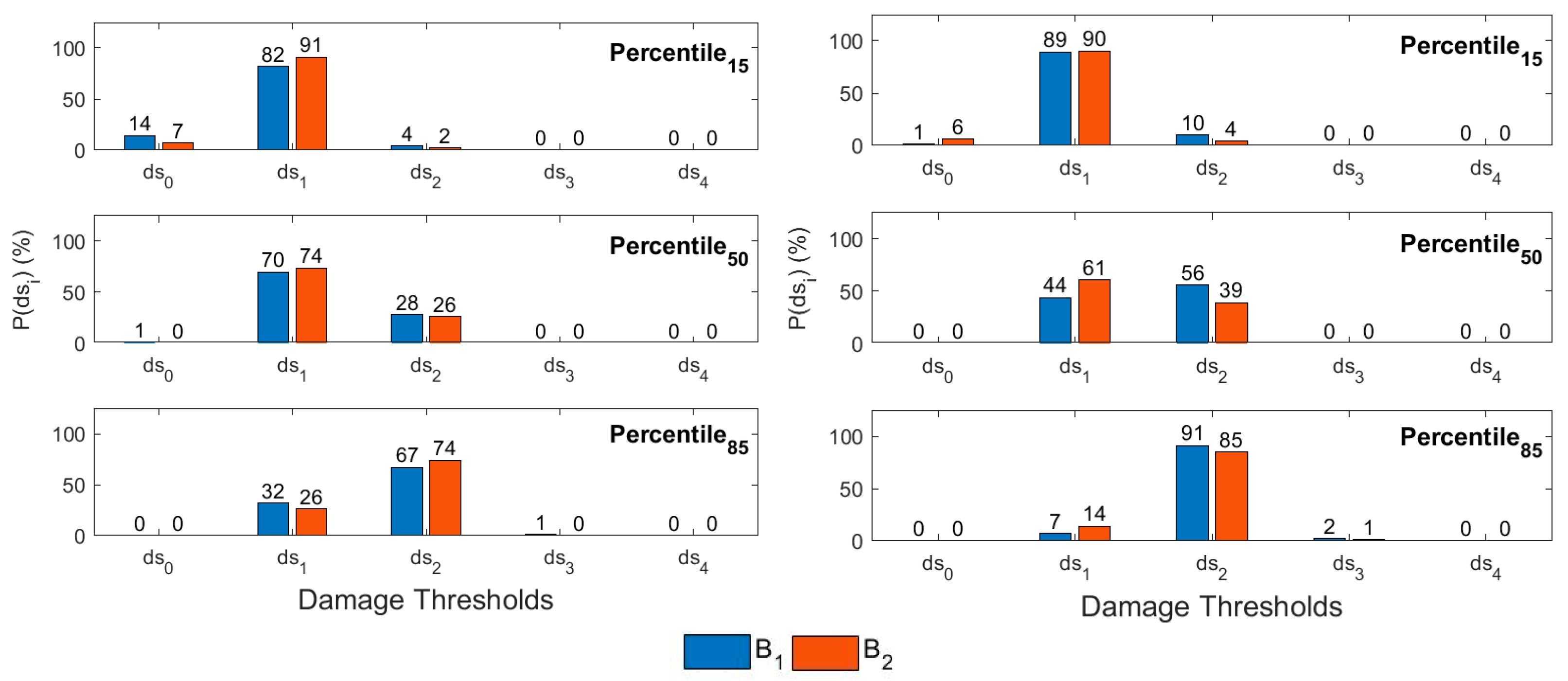
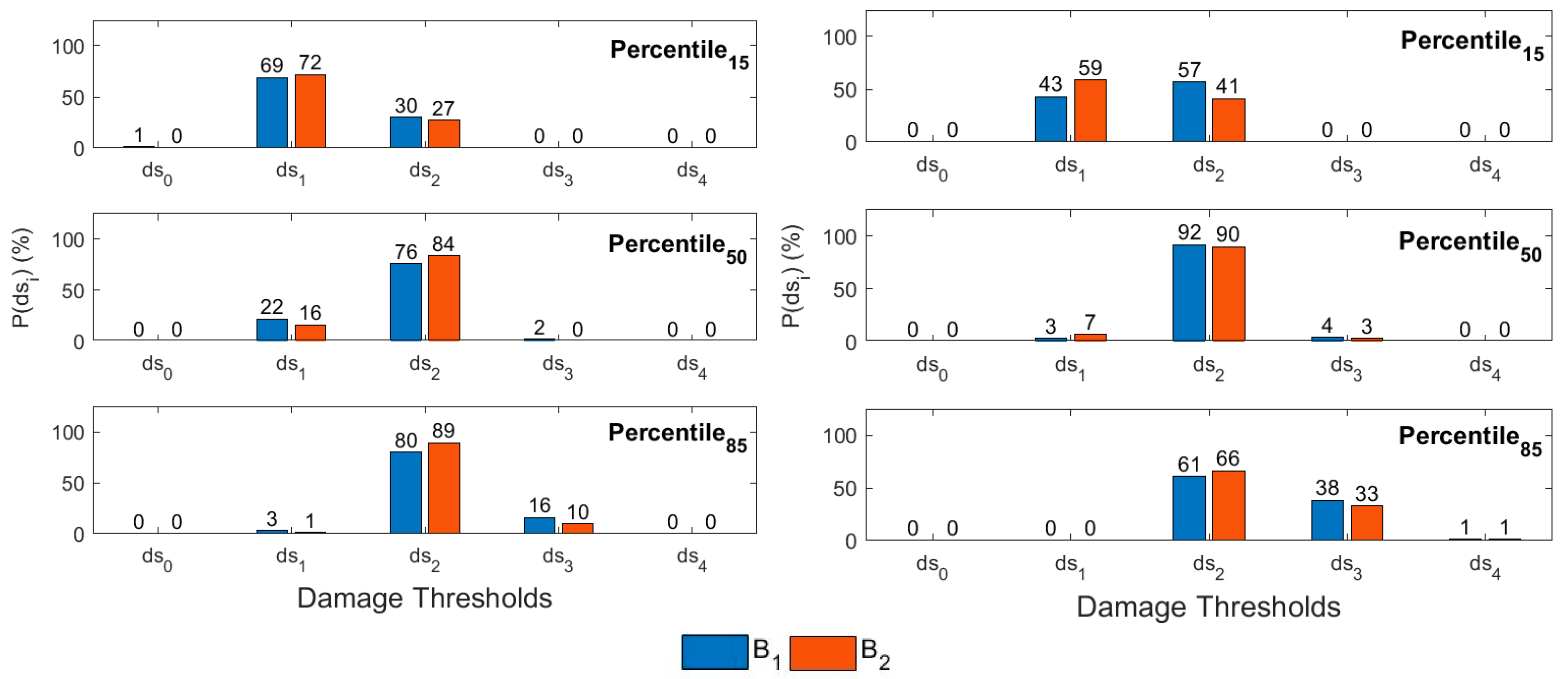
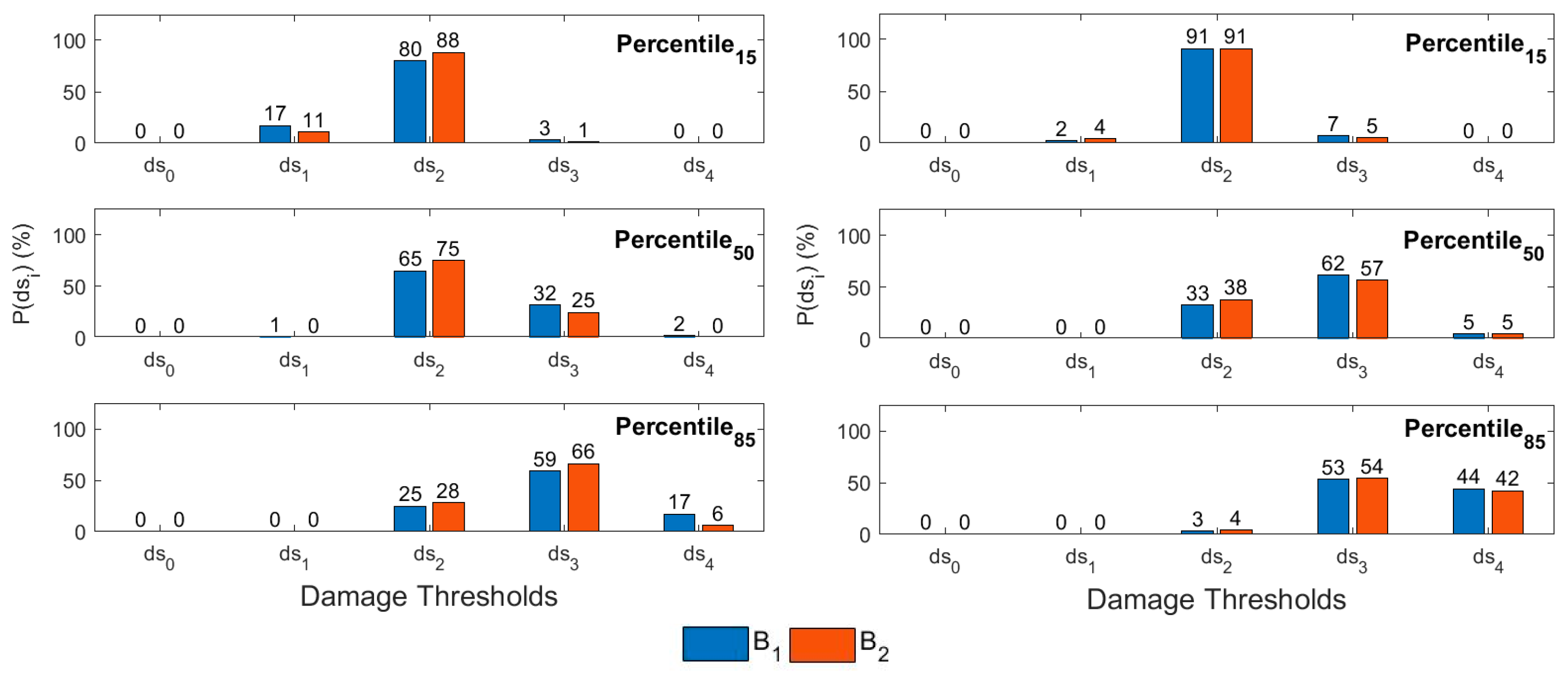
| Building | Stories | H (m) | W (Ton) | Vsx (Ton) | Vsy (Ton) | (s) | (s) | (s) | Mass (Ton/g) | % | % | % |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 23 | 72.10 | 19,574.5 | 4587.4 | 5452.7 | 2.45 | 2.19 | 1.95 | 1995.4 | 65 | 69 | 65 |
| 2 | 23 | 71.10 | 19,156.1 | 4244.6 | 5522.7 | 2.57 | 2.52 | 2.09 | 1952.7 | 67 | 69 | 72 |
| Beams | Columns | Walls | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Level | fc (MPa) | (m) | b (cm) | h (cm) | ρ (%) | b (cm) | h (cm) | ρ (%) | b (cm) | h (cm) | ρ (%) |
| 1–2 | 35 | 4.25 | 40–60 | 55 | >0.33 | 40–50 | Variable | 1–3 | 40 | Variable | 1–2 |
| 3 | 35 | 3.00 | 40–60 | 55 | >0.33 | 40–50 | Variable | 1–3 | 40 | Variable | 1–2 |
| 4 | 35 | 4.20 | 40–60 | 55 | >0.33 | 40–50 | Variable | 1–3 | 40 | Variable | 1–2 |
| 5 | 35 | 3.60 | 40–60 | 55 | >0.33 | 40–50 | Variable | 1–3 | 40 | Variable | 1–2 |
| 6–10 | 35 | 3.05 | 40–60 | 55 | >0.33 | 40–50 | Variable | 1–3 | 40 | Variable | 1–2 |
| 11–16 | 28–35 | 3.00 | 40–60 | 50 | >0.33 | 40–50 | Variable | 1–2 | 40 | Variable | 1–2 |
| 17–22 | 28 | 2.95 | 40–60 | 45 | >0.33 | 40–50 | Variable | 1 | 40 | Variable | 1 |
| Beams | Columns | Walls | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Level | fc (MPa) | (m) | b (cm) | h (cm) | ρ (%) | b (cm) | h (cm) | ρ (%) | b (cm) | h (cm) | ρ (%) |
| 1–2 | 35 | 3.85 | 40–60 | 50 | >0.33 | 40–60 | Variable | 1–3 | 25–40 | Variable | 1–2 |
| 3 | 35 | 4.45 | 40–60 | 50 | >0.33 | 40–60 | Variable | 1–3 | 25–40 | Variable | 1–2 |
| 4 | 35 | 3.00 | 40–60 | 50 | >0.33 | 40–60 | Variable | 1–3 | 25–40 | Variable | 1–2 |
| 5 | 35 | 3.30 | 40–60 | 50 | >0.33 | 40–60 | Variable | 1–3 | 25–40 | Variable | 1–2 |
| 6 | 35 | 3.80 | 40–60 | 50 | >0.33 | 40–60 | Variable | 1–3 | 25–40 | Variable | 1–2 |
| 7–15 | 35 | 3.05 | 40–60 | 50 | >0.33 | 40–50 | Variable | 1–3 | 25–40 | Variable | 1–2 |
| 16–22 | 28 | 3.05 | 40–50 | 50 | >0.33 | 40–50 | Variable | 1–2 | 25–40 | Variable | 1 |
| Building | ||
|---|---|---|
| B1 | 0.0079 | 0.0067 |
| B2 | 0.0072 | 0.0067 |
| Percentile 15 | |||||
| RP (years) | 31 | 225 | 475 | 975 | 2475 |
| DI_B1_x | 0.00 | 0.08 | 0.20 | 0.26 | 0.42 |
| DI_B1_y | 0.00 | 0.15 | 0.24 | 0.32 | 0.51 |
| DI_B2_x | 0.00 | 0.08 | 0.20 | 0.26 | 0.42 |
| DI_B2_y | 0.00 | 0.09 | 0.21 | 0.28 | 0.48 |
| Percentile 50 | |||||
| RP (years) | 31 | 225 | 475 | 975 | 2475 |
| DI_B1_x | 0.00 | 0.16 | 0.26 | 0.40 | 0.64 |
| DI_B1_y | 0.00 | 0.20 | 0.32 | 0.48 | 0.78 |
| DI_B2_x | 0.00 | 0.17 | 0.25 | 0.40 | 0.61 |
| DI_B2_y | 0.00 | 0.18 | 0.28 | 0.45 | 0.76 |
| Percentile 85 | |||||
| RP (years) | 31 | 225 | 475 | 975 | 2475 |
| DI_B1_x | 0.00 | 0.22 | 0.36 | 0.55 | 0.82 |
| DI_B1_y | 0.00 | 0.26 | 0.44 | 0.67 | 0.95 |
| DI_B2_x | 0.00 | 0.22 | 0.36 | 0.54 | 0.79 |
| DI_B2_y | 0.00 | 0.23 | 0.41 | 0.65 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tirado-Gutiérrez, R.J.; González-Drigo, R.; Vargas-Alzate, Y.F. The Importance of Structural Configuration in the Seismic Performance and Reliability of Buildings. Infrastructures 2025, 10, 325. https://doi.org/10.3390/infrastructures10120325
Tirado-Gutiérrez RJ, González-Drigo R, Vargas-Alzate YF. The Importance of Structural Configuration in the Seismic Performance and Reliability of Buildings. Infrastructures. 2025; 10(12):325. https://doi.org/10.3390/infrastructures10120325
Chicago/Turabian StyleTirado-Gutiérrez, Rodolfo J., Ramón González-Drigo, and Yeudy F. Vargas-Alzate. 2025. "The Importance of Structural Configuration in the Seismic Performance and Reliability of Buildings" Infrastructures 10, no. 12: 325. https://doi.org/10.3390/infrastructures10120325
APA StyleTirado-Gutiérrez, R. J., González-Drigo, R., & Vargas-Alzate, Y. F. (2025). The Importance of Structural Configuration in the Seismic Performance and Reliability of Buildings. Infrastructures, 10(12), 325. https://doi.org/10.3390/infrastructures10120325









