Numerical Analysis Research on Tunnel Damage Under the Action of Oblique Slip Faults Based on Multiple Slip Surfaces
Abstract
1. Introduction
2. Numerical Simulation
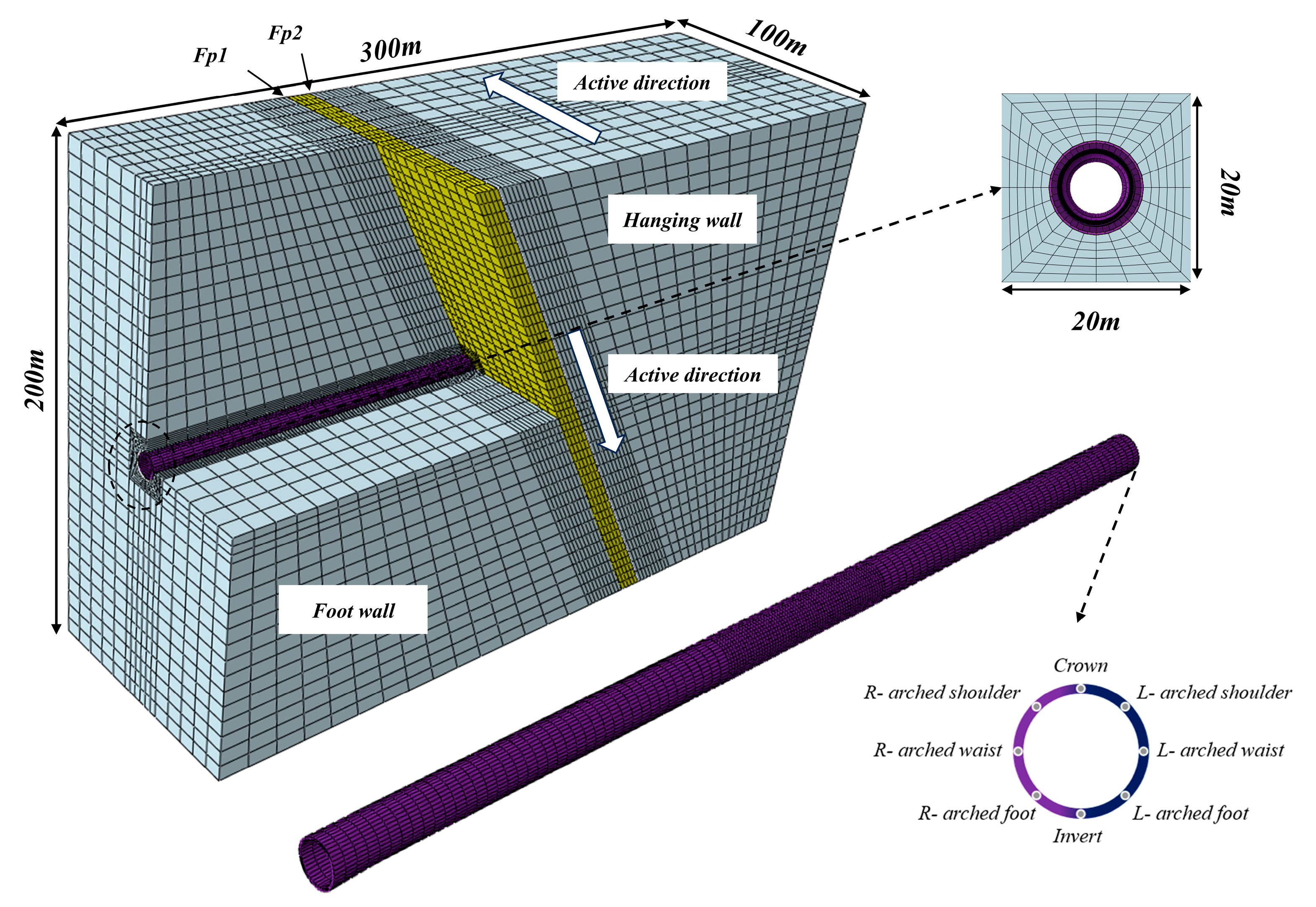
2.1. Project Background
2.2. Model Establishment
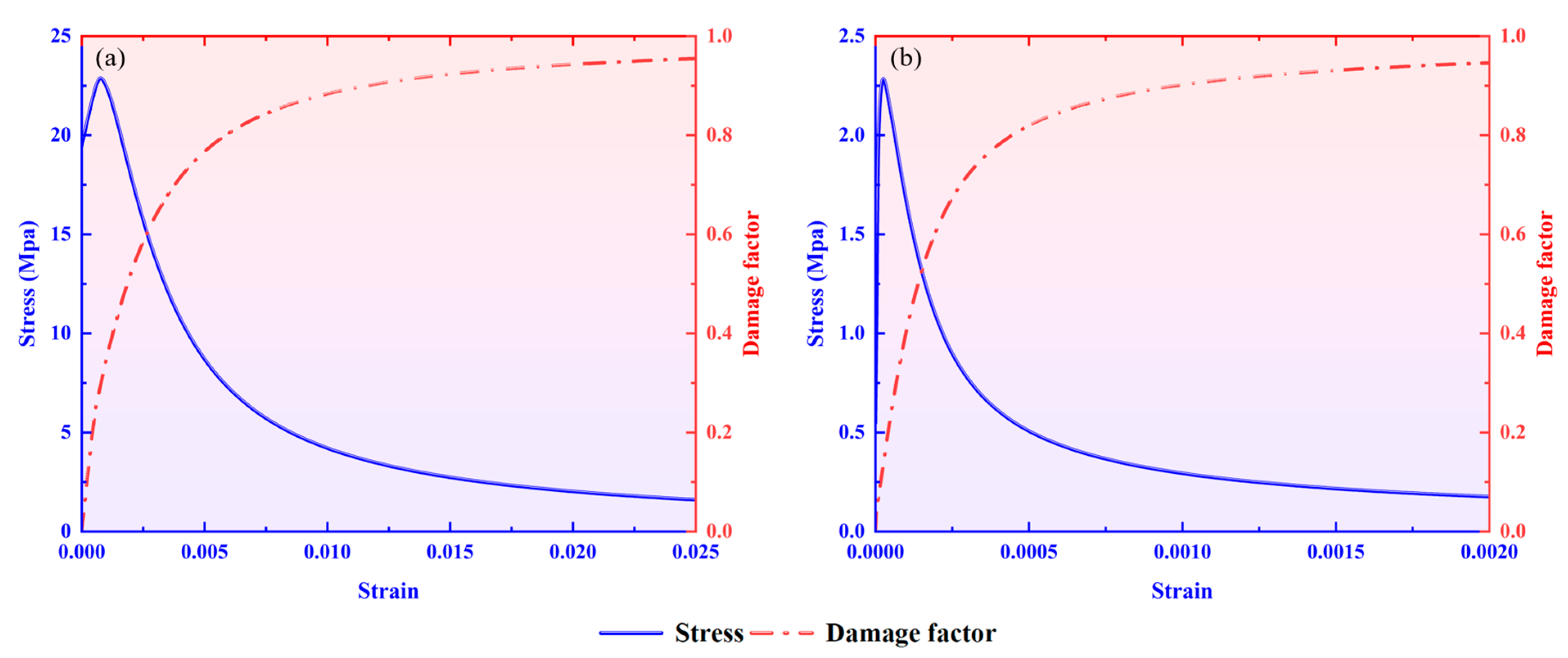
2.3. Simulation Process
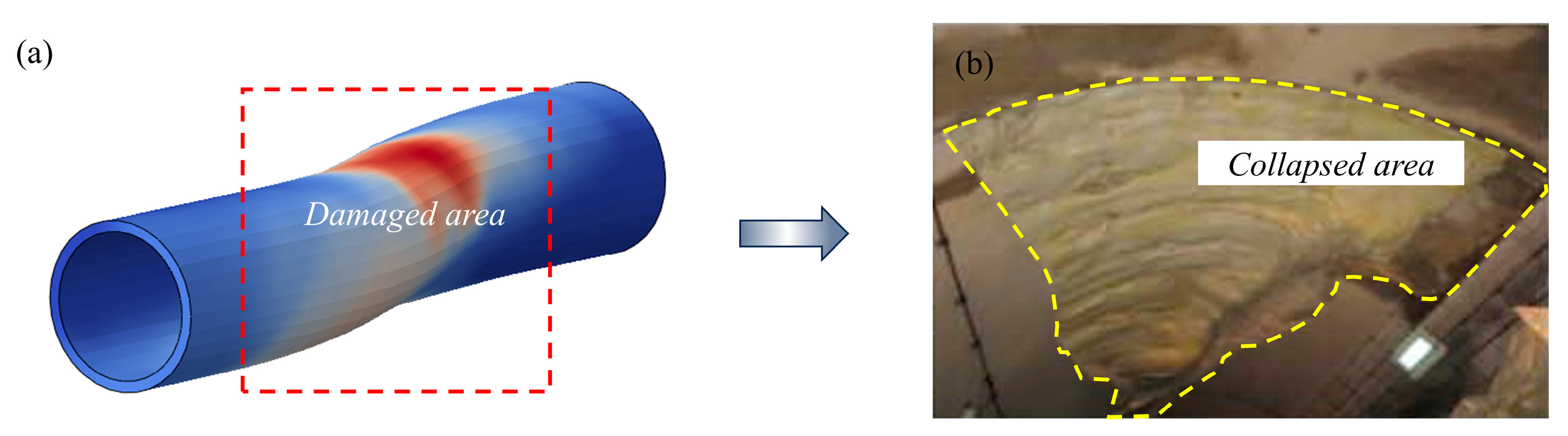
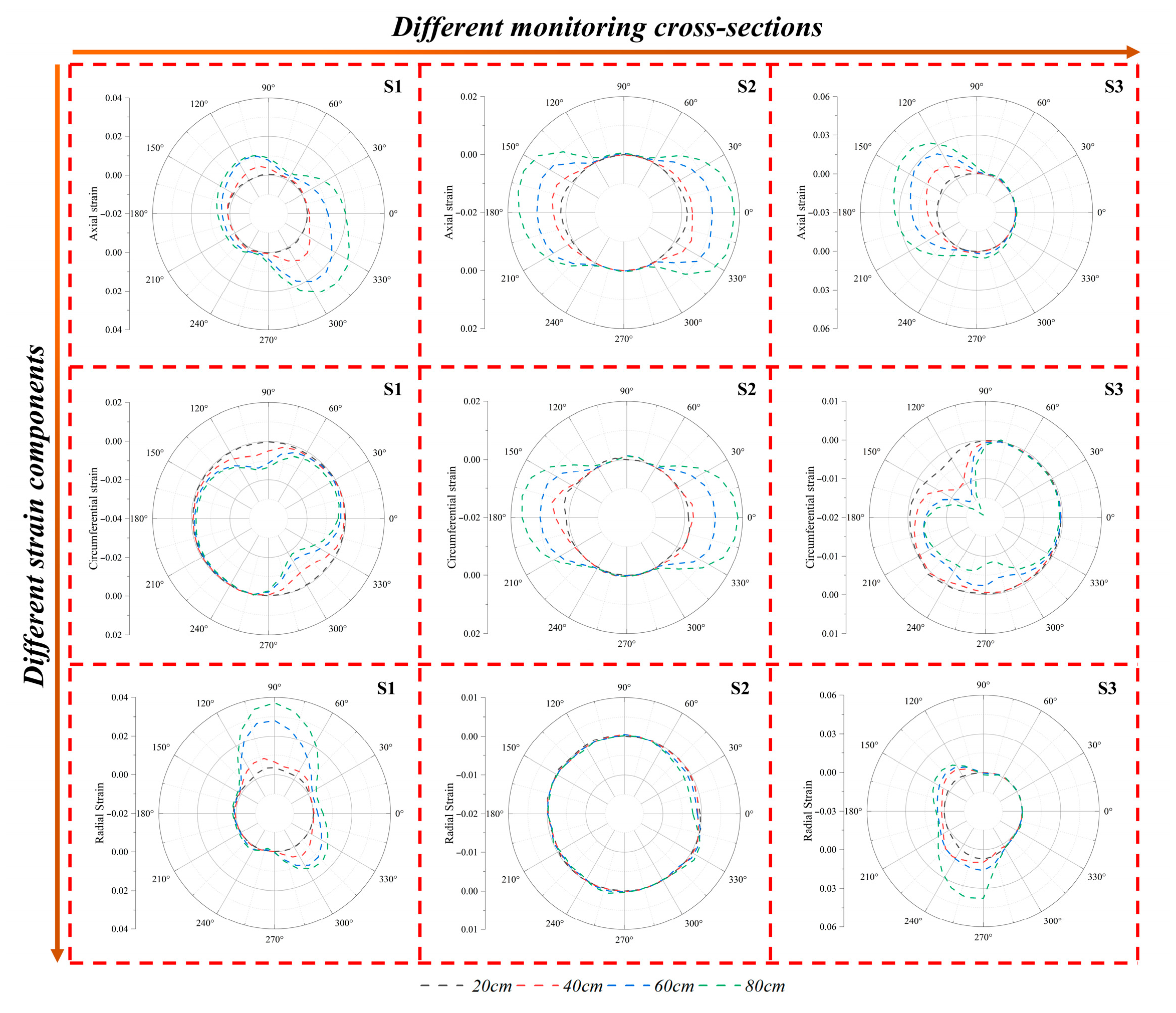
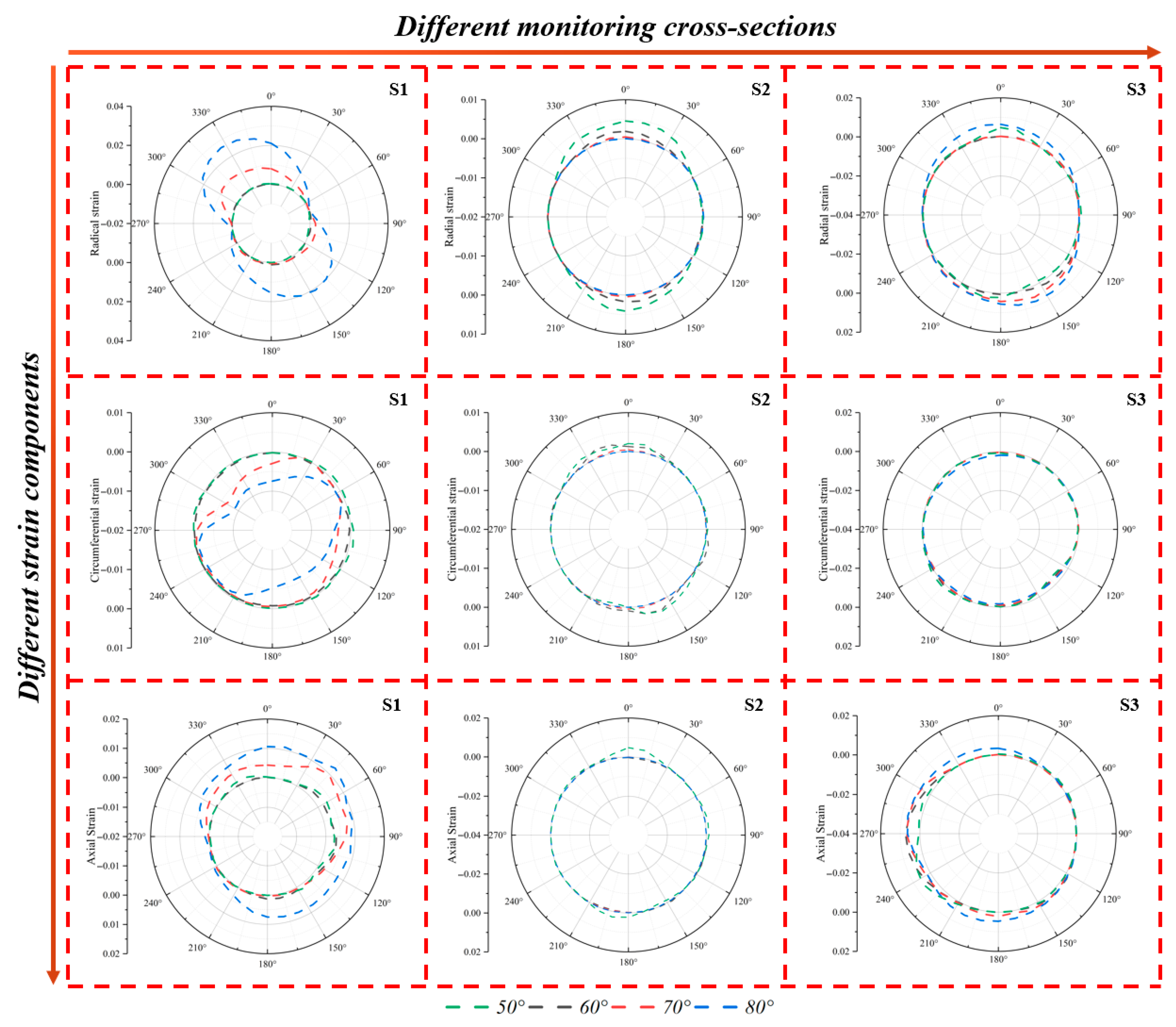
2.4. Verification
3. Result Analysis
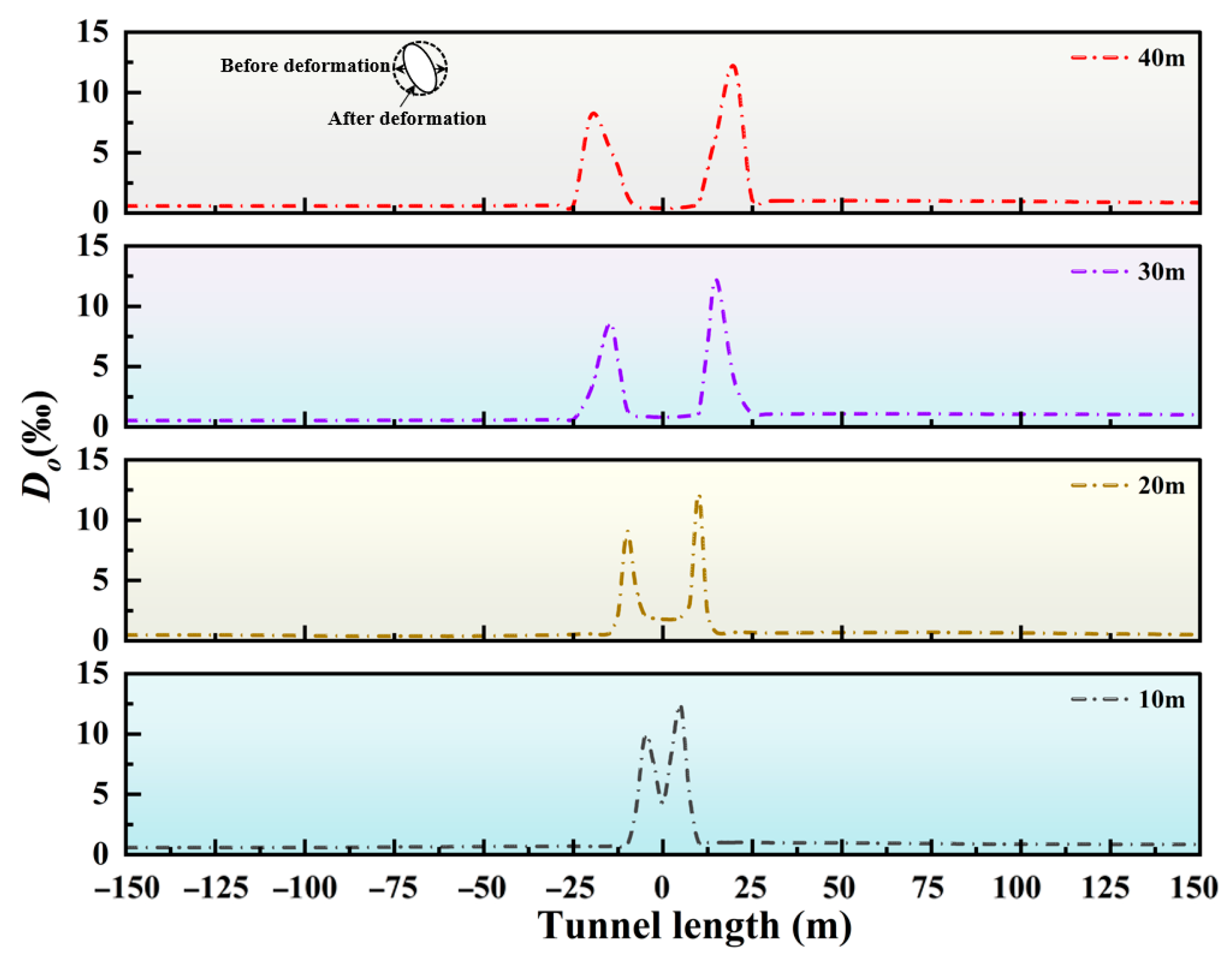
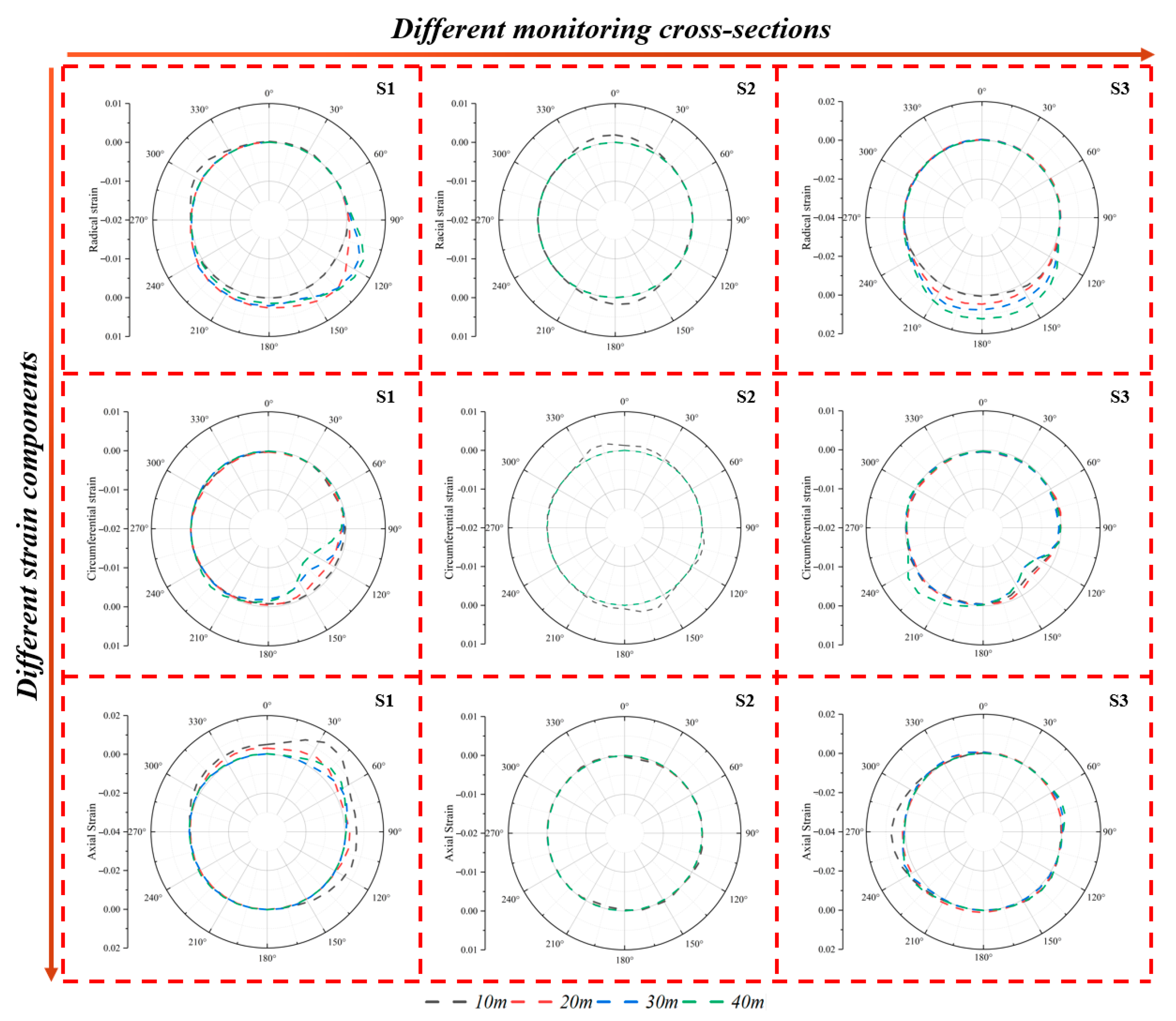
3.1. The Deformation Response Mechanism of Tunnels to the Displacement of Oblique-Slip Faults
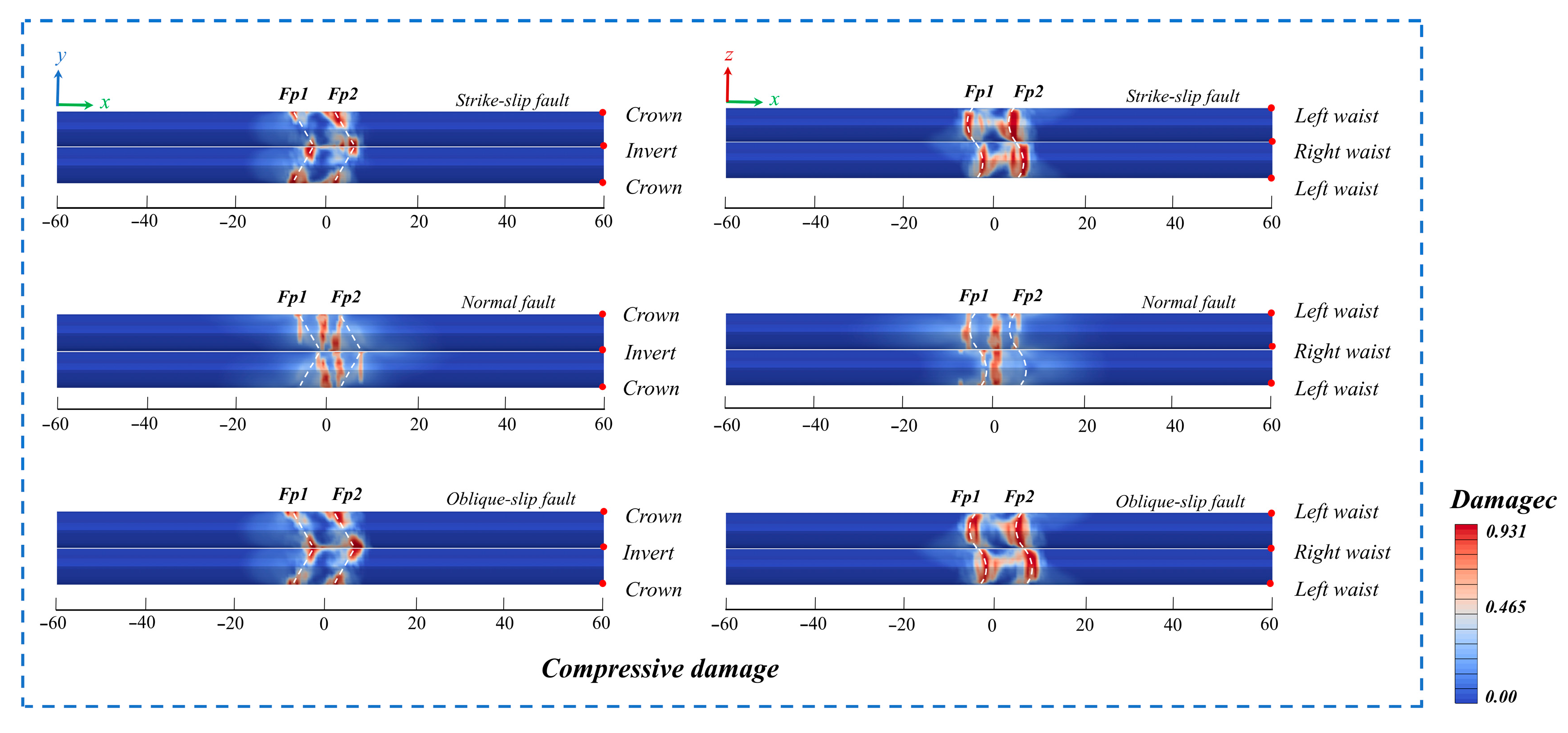
3.2. Influence of Different Fault Displacement Forms on Tunnels
4. Parameter Sensitivity Analysis
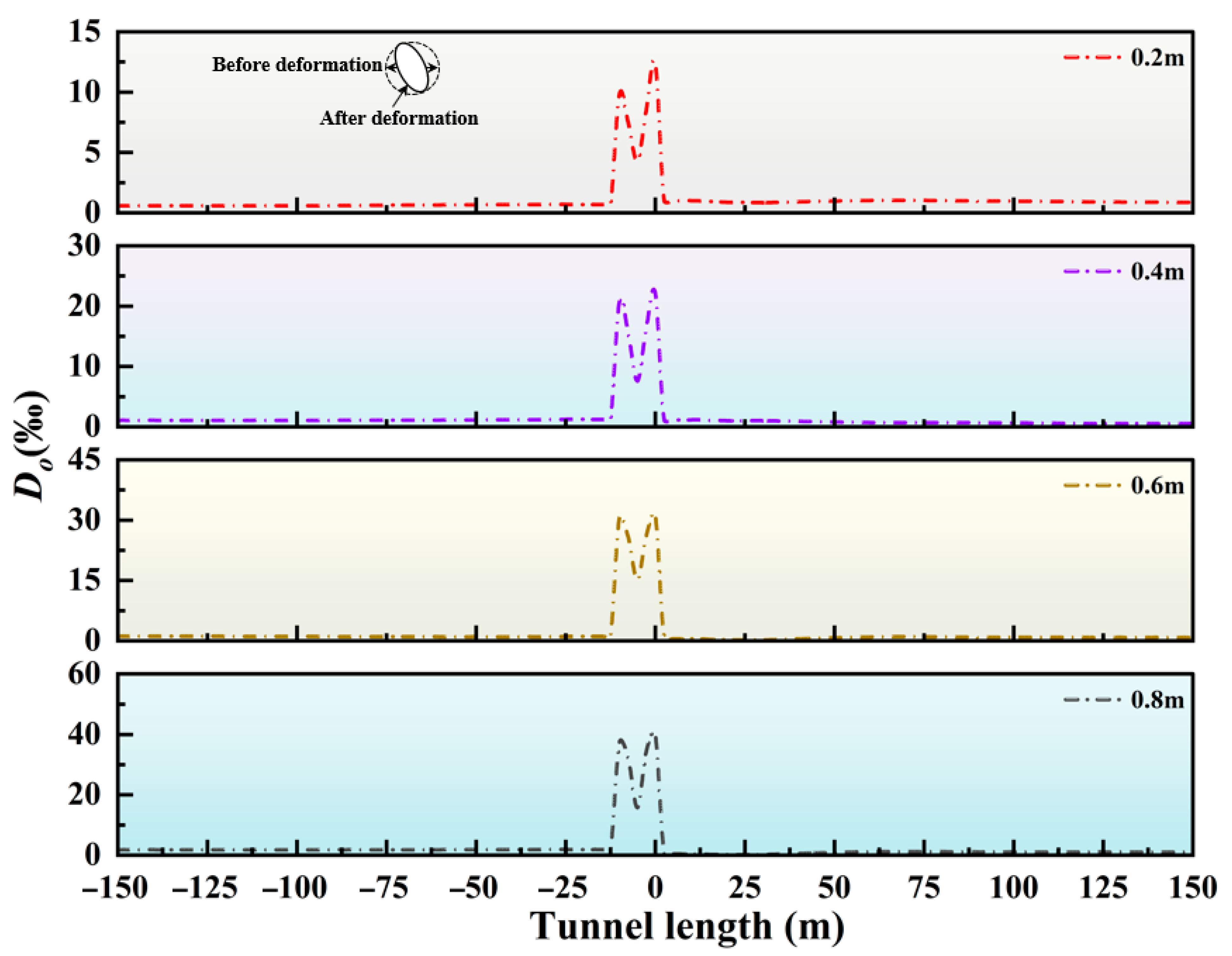
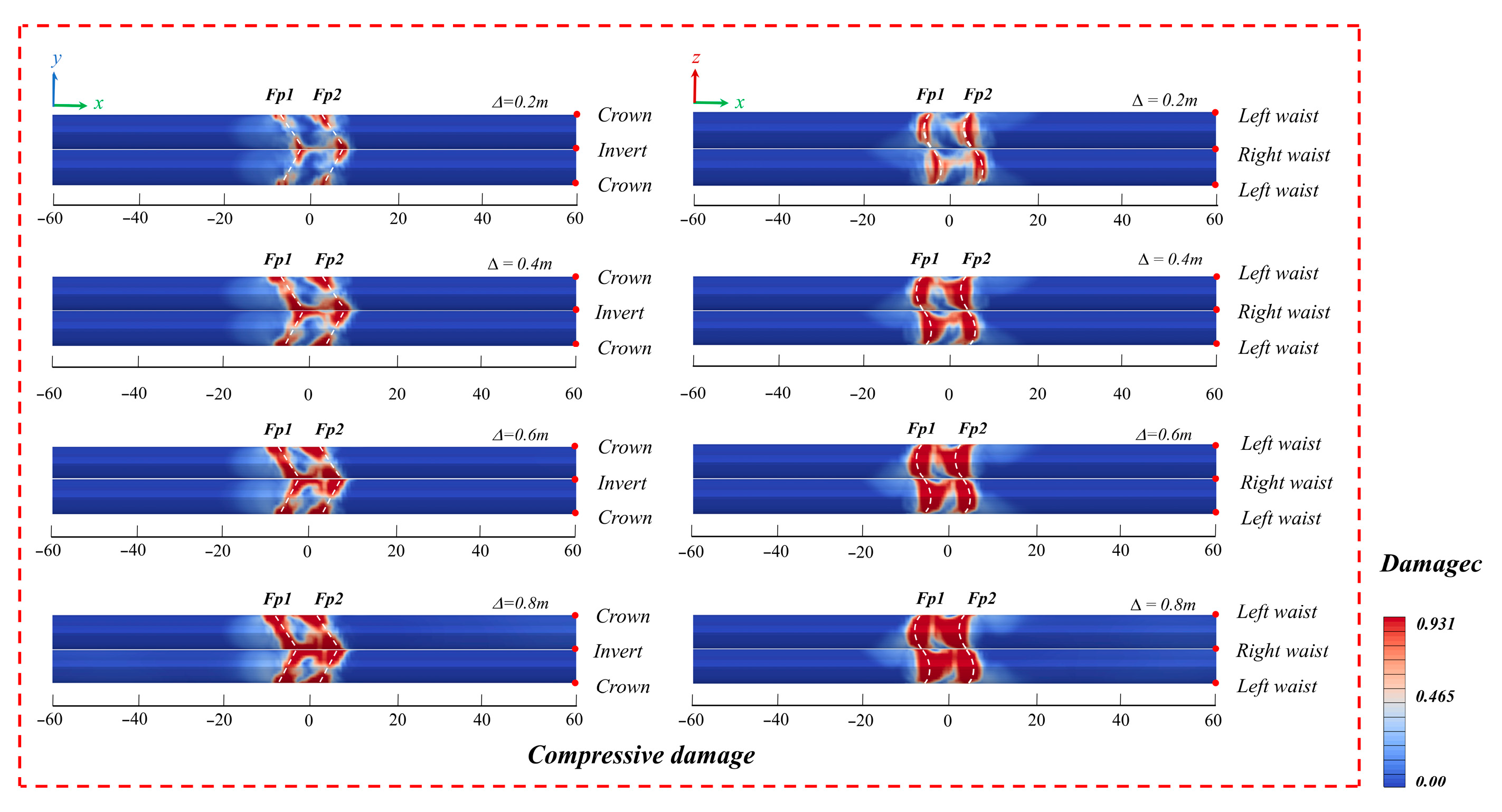
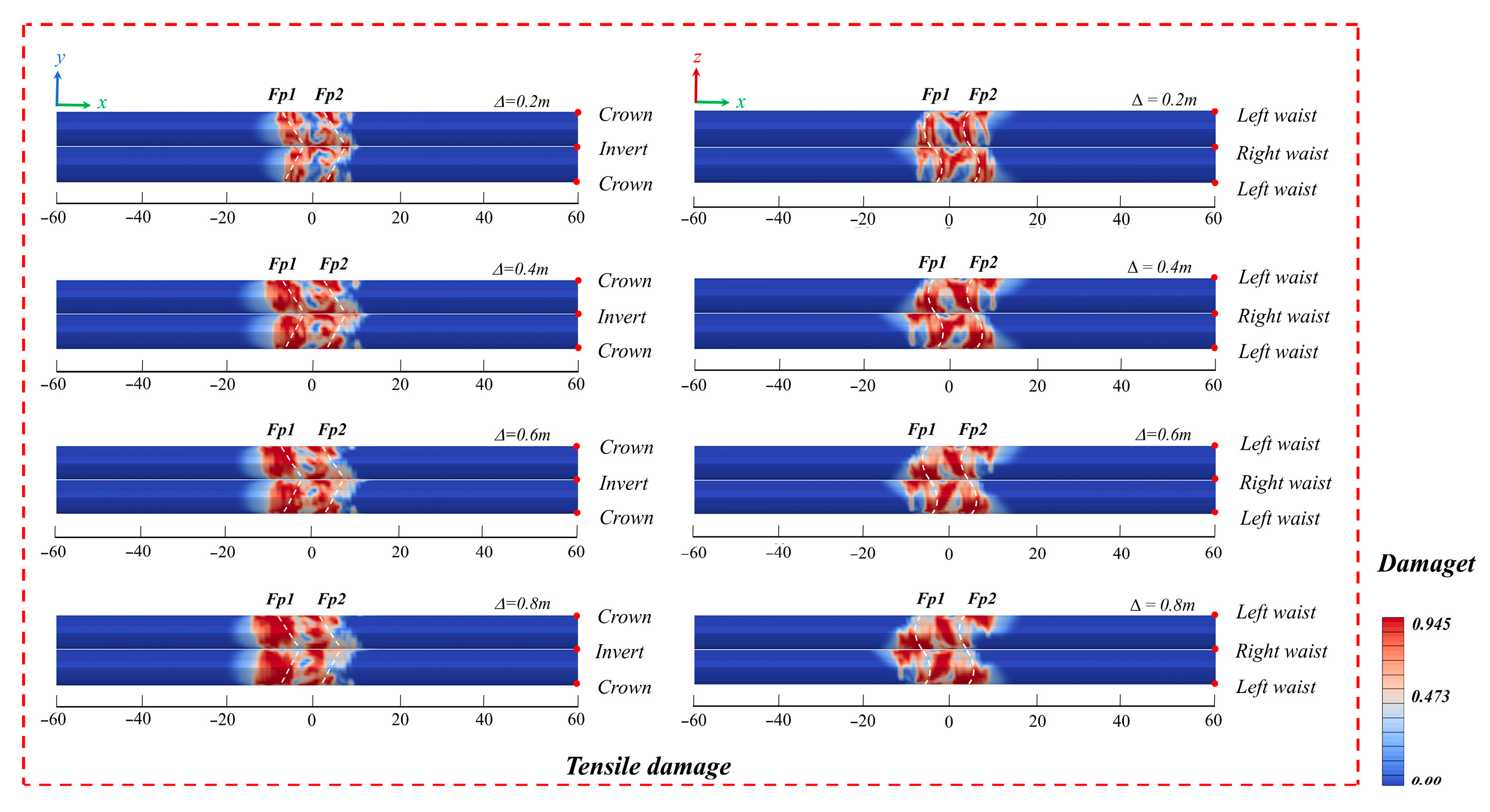
4.1. Influence of Fault Dislocation Distance
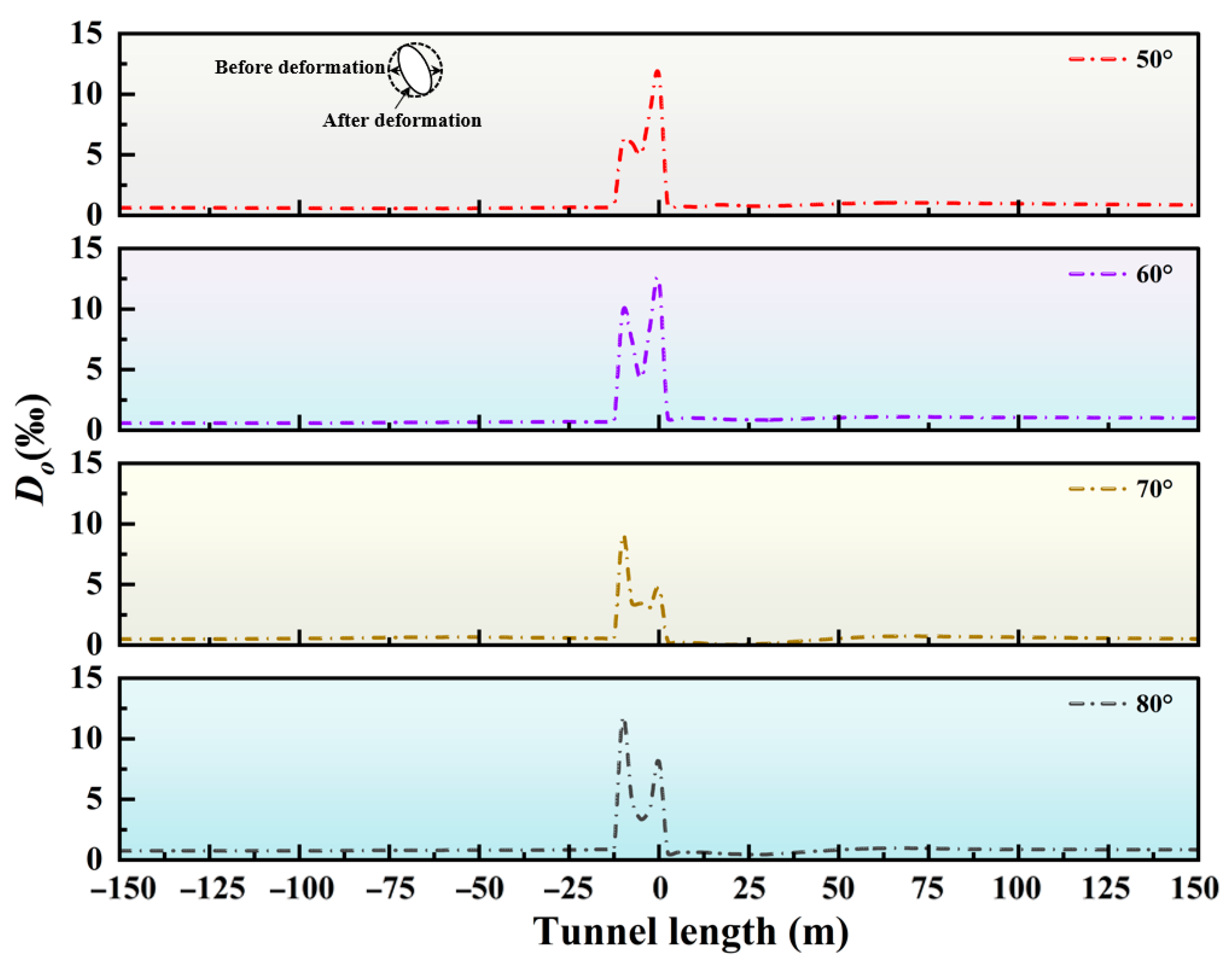
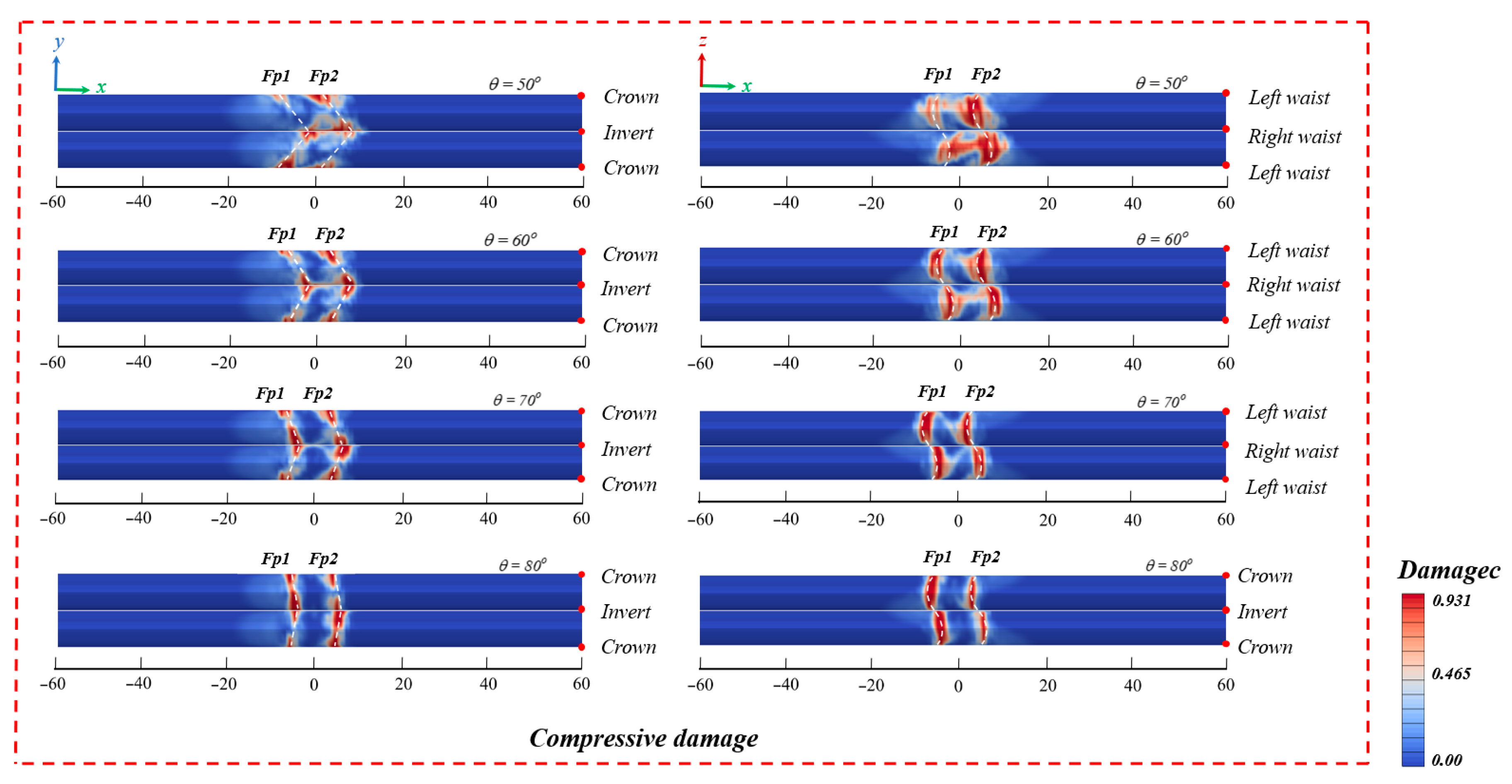
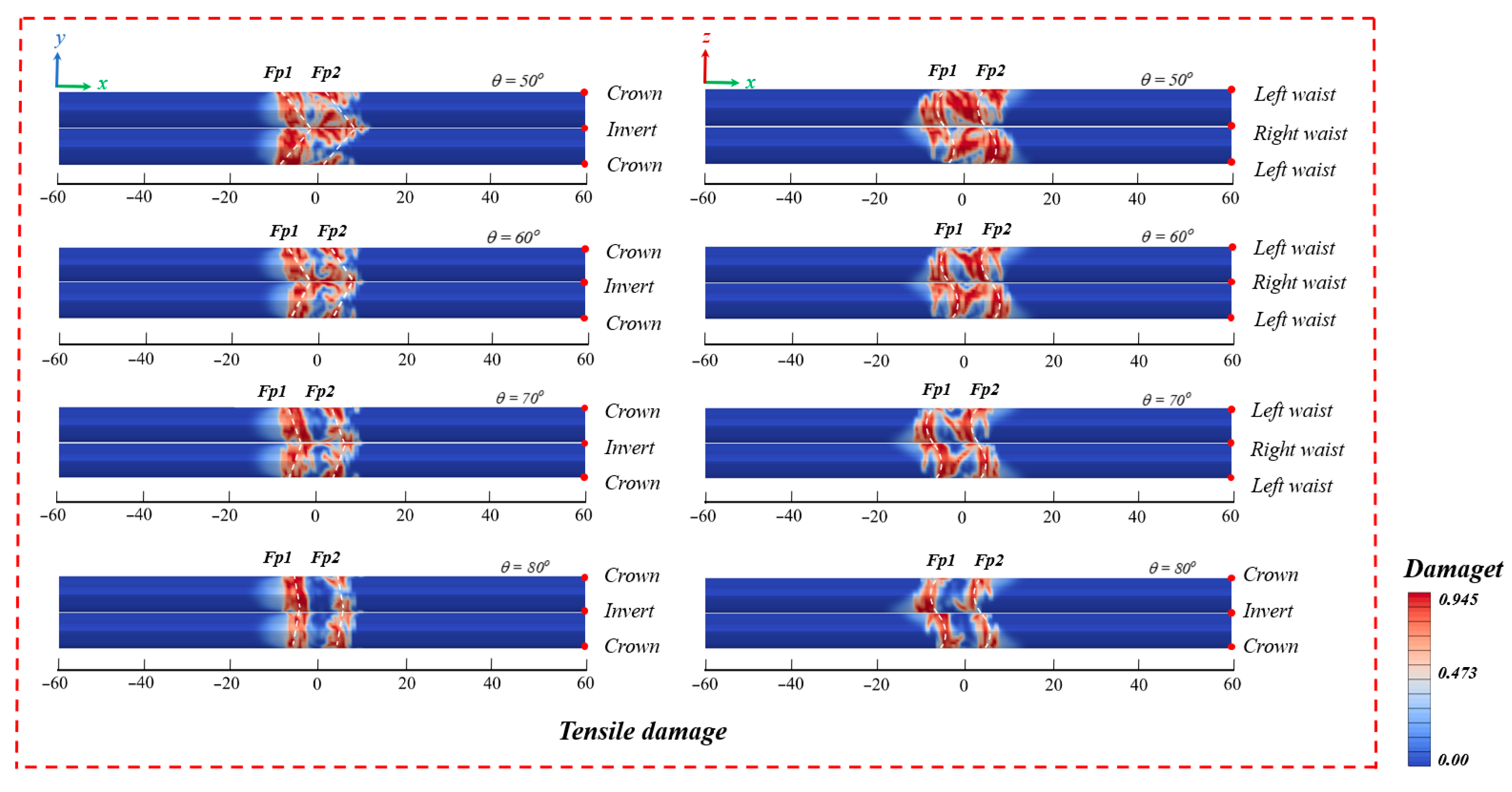
4.2. Influence of Fault Dip Angle
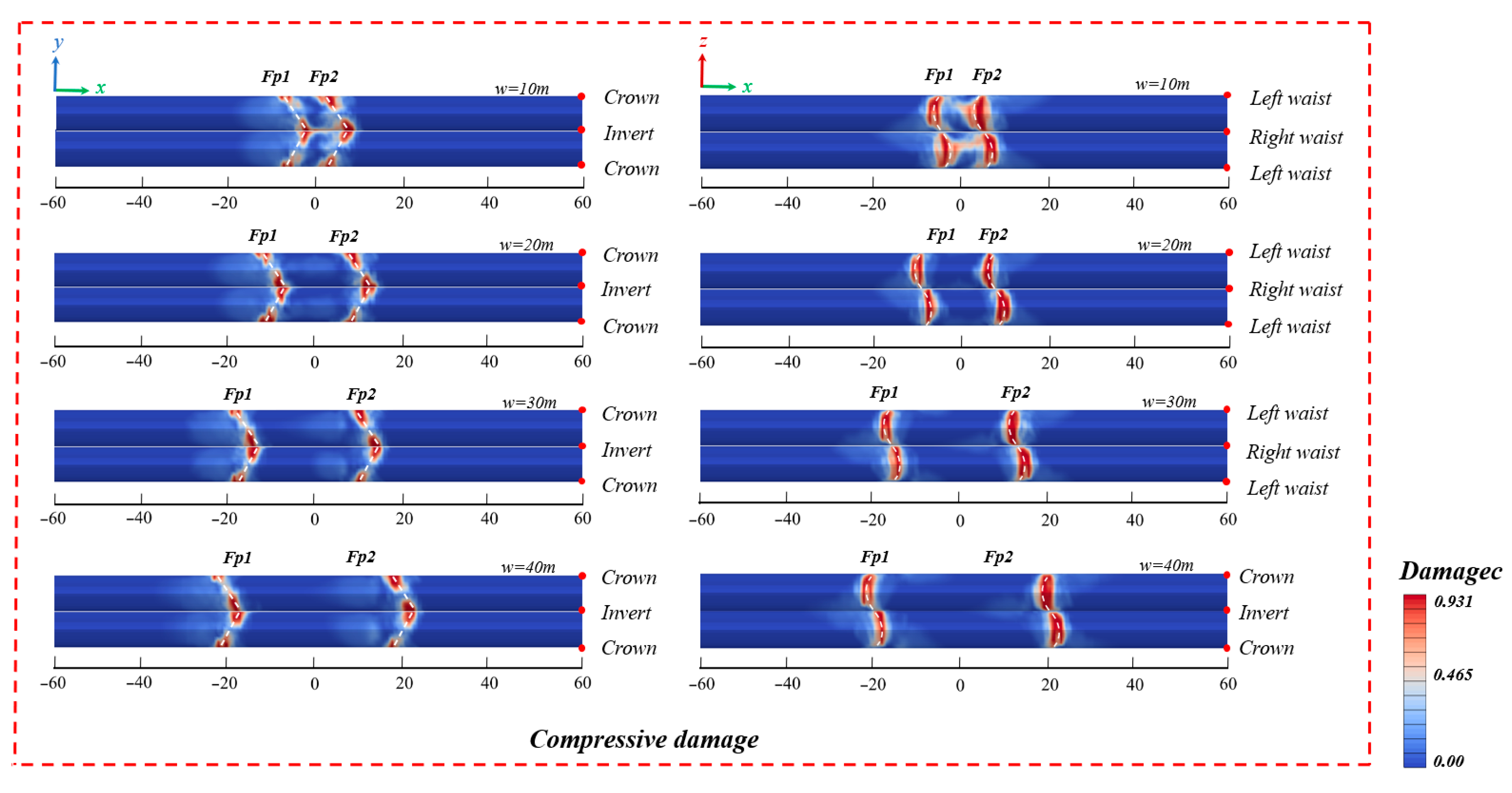
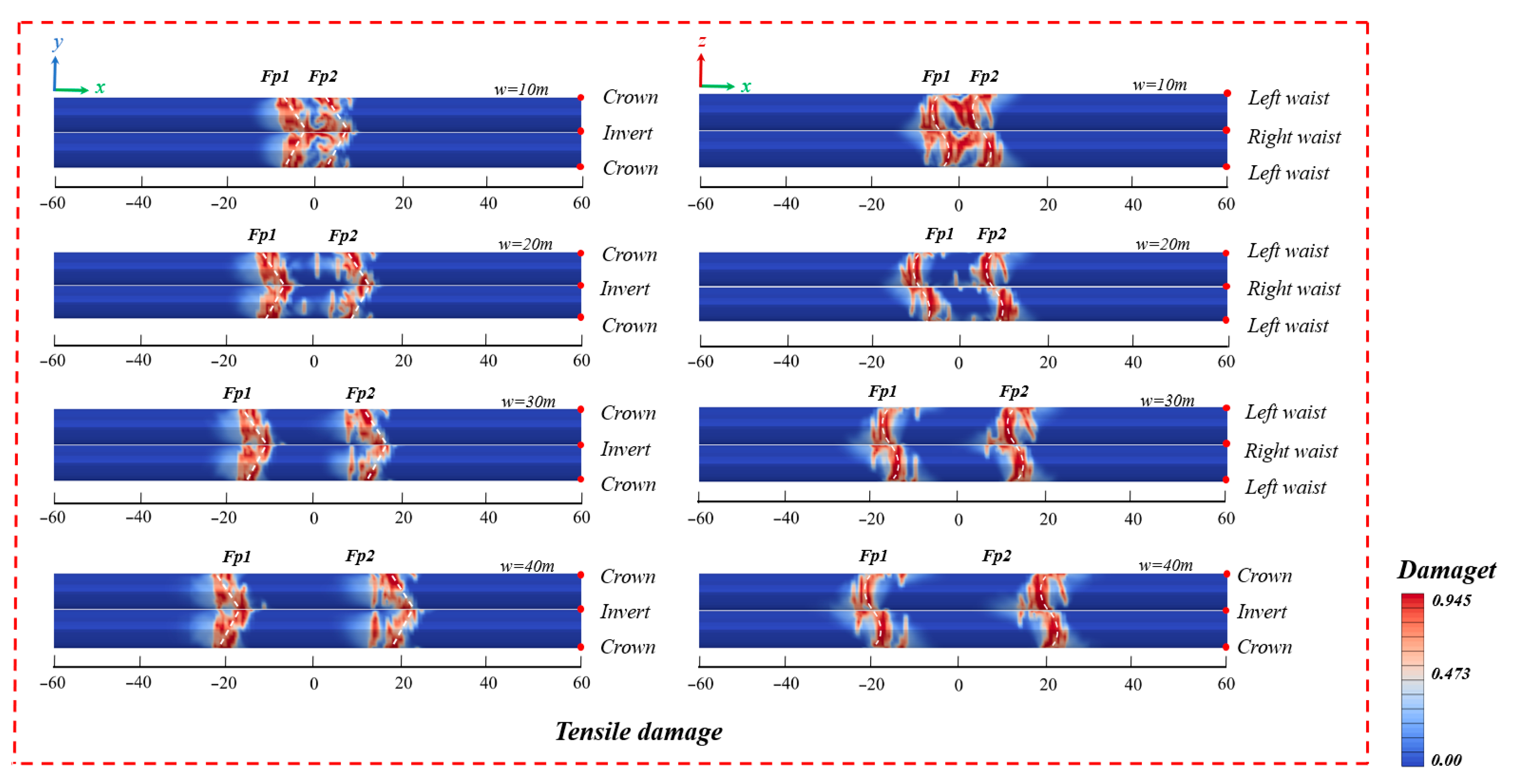
4.3. Influence of the Width of the Fault Fracture Zone
5. Conclusions and Discussions
- Tunnel damage is more severe under strike-slip faulting than under oblique-slip faulting. This is evidenced by a maximum Mises stress of 12.21 MPa under strike-slip motion, which is 30–40% greater than the 11.91 MPa observed under oblique-slip conditions.
- In the damage resulting from the activity of oblique-slip faults, displacement is the dominant factor. When the fault displacement reaches 80 cm, the failure rate of the vault and the invert within the fault zone is nearly 95%. Hence, when designing cross-fault tunnels, special attention should be paid to measures to resist tunnel faulting.
- Impact of fault dip angle: With the increase in the dip angle, the failure mode of the tunnel shifts from a tension–compression composite form to a tension–shear composite form. When the dip angle is small, the horizontal component of the fault displacement is significant, and the affected area is extensive. When the dip angle is large, the tension–shear coupling effect becomes more prominent. The deformation becomes more concentrated, resulting in a reduction of approximately 40% in the damaged area of the slip surface, and the propagation of damage towards the center of the fault zone is attenuated. Thus, in practical engineering, it is preferable for the tunnel to cross the fault at a large angle.
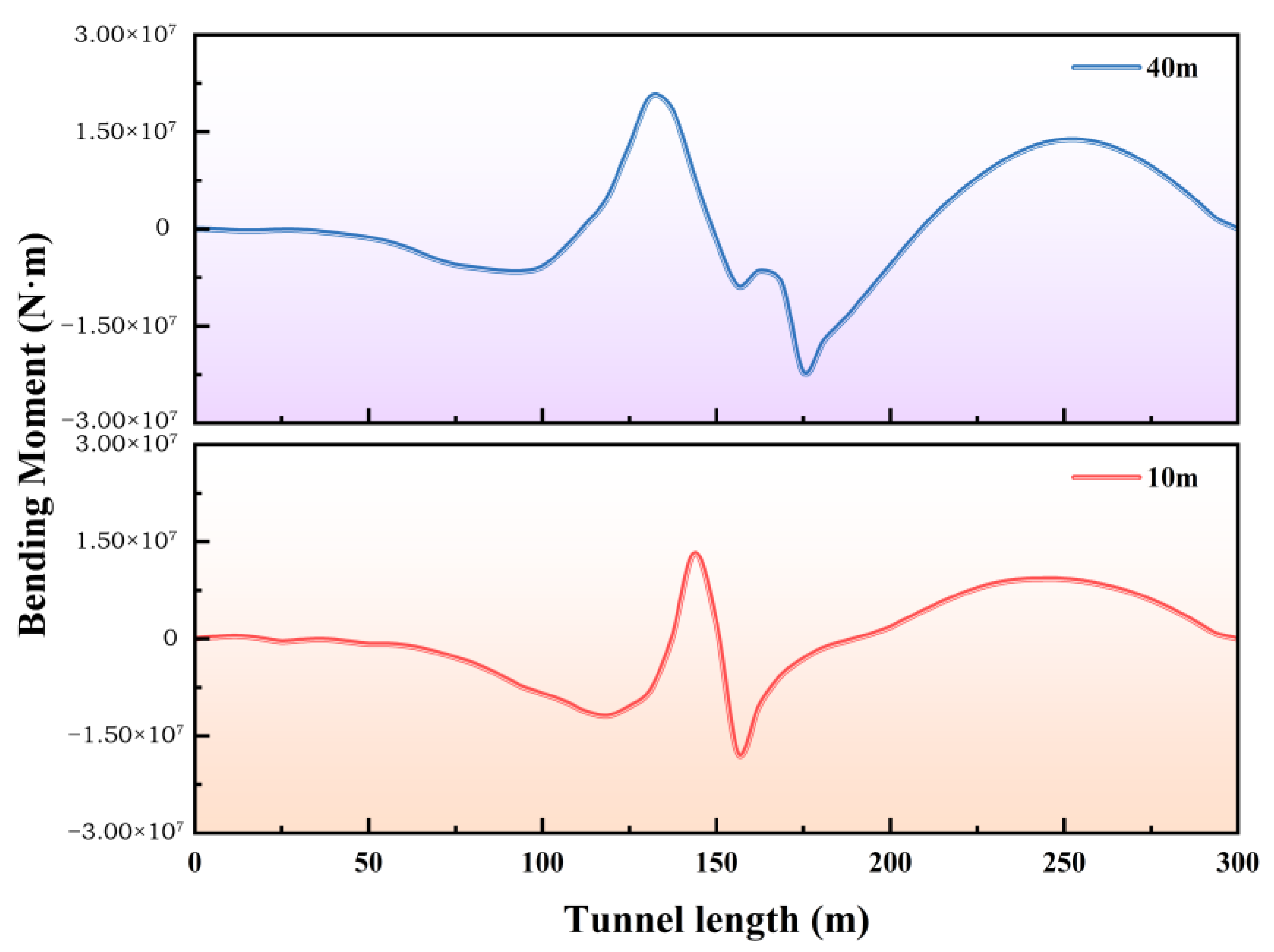
- Influence of the fault zone width: A relatively narrow fault zone (10 m) leads to local concentrated damage, while a relatively wide fault zone (40 m) makes the damage distribution more scattered. When crossing a 40 m wide fault zone, the degree of influence on the center of the fault zone is decreased by 30% compared to the case of a 10 m fault zone, and the damage path is longer. In engineering applications, it is recommended to prioritize the crossing plan of a relatively wide fault zone to realize the transformation from “concentrated shearing” to “distributed bending”, which is in line with the design concept of “using softness to counter hardness”.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, J.F.; Wang, W.; Wang, F.; Yuan, Y. Statistics of China’s Railway Tunnels by the End of 2023 and Overview of Tunnels of Key New Projects in 2023. Tunn. Constr. 2024, 44, 377–392. [Google Scholar]
- Yu, H.T.; Chen, J.T.; Bobet, A.; Yuan, Y. Damage observation and assessment of the Longxi tunnel during the Wenchuan earthquake. Tunn. Undergr. Space Technol. 2016, 54, 102–116. [Google Scholar] [CrossRef]
- Yu, H.T.; Yan, X.; Bobet, A.; Yuan, Y.; Xu, G.P.; Su, Q.K. Multi-point shaking table test of a long tunnel subjected to non-uniform seismic loadings. Bull. Earthq. Eng. 2018, 16, 1041–1059. [Google Scholar] [CrossRef]
- Yu, H.T.; Yuan, Y.; Liu, X.; Li, Y.W.; Ji, S.W. Damages of the Shaohuoping road tunnel near the epicentre. Struct. Infrastruct. Eng. 2013, 9, 935–951. [Google Scholar] [CrossRef]
- Yu, H.T.; Yuan, Y.; Xu, G.P.; Su, Q.K.; Yan, X.; Li, C. Multi-point shaking table test for long tunnels subjected to non-uniform seismic loadings—part II: Application to the HZM immersed tunnel. Soil Dyn. Earthq. Eng. 2018, 108, 187–195. [Google Scholar] [CrossRef]
- Zhong, Z.; Wang, Z.; Zhao, M.; Du, X. Structural damage assessment of mountain tunnels in fault fracture zone subjected to multiple strike-slip fault movement. Tunn. Undergr. Space Technol. 2020, 104, 103527. [Google Scholar] [CrossRef]
- Wang, W.L.; Wang, T.T.; Su, J.J.; Lin, C.H.; Seng, C.R.; Huang, T.H. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Hikima, K.; Koketsu, K. Rupture processes of the 2004 Chuetsu (mid-Niigata prefecture) earthquake, Japan: A series of events in a complex fault system. Geophys. Res. Lett. 2005, 32, L18305. [Google Scholar] [CrossRef]
- Lai, J.; He, S.; Qiu, J.; Chen, J.; Wang, L.; Wang, K.; Wang, J. Characteristics of seismic disasters and aseismic measures of tunnels in Wenchuan earthquake. Environ. Earth Sci. 2017, 76, 76–94. [Google Scholar] [CrossRef]
- Ishibe, T.; Shimazaki, K.; Tsuruoka, H.; Yamanaka, Y.; Satake, K. Correlation between Coulomb stress changes imparted by large historical strike-slip earthquakes and current seismicity in Japan. Earth Planets Space 2011, 63, 301–314. [Google Scholar] [CrossRef]
- Blanchard, F.; Laverty, G. Displacements in the Claremont water tunnel at the intersection with the Hayward fault. Bull. Seismol. Soc. Am. 1966, 56, 291–294. [Google Scholar] [CrossRef]
- He, C.; Li, L.; Zhang, J.; Geng, P.; Yan, Q.X. Seismic damage mechanism of tunnels through fault zones. Chin. J. Geotech. Eng. 2014, 36, 427–434. [Google Scholar]
- Cui, G.Y.; Wang, M.N.; Yu, L.; Lin, G. Study on the characteristics and mechanism of seismic damage for tunnel structures on fault rupture zone in Wenchuan seismic disastrous area. China Civ. Eng. J. 2013, 46, 122–127. (In Chinese) [Google Scholar]
- Wang, T.; Geng, P.; Li, P.; Wang, Q.; Wang, L. Deformation and failure of overburden soil subjected to normal fault dislocation and its impact on tunnel. Eng. Fail. Anal. 2022, 142, 106747. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, G.Z.; Jiang, L.W. Engineering effect of active fault and geological alignment of Chengdu to Kangding in Sichuan–Tibet Railway. J. Railw. Eng. Soc. 2015, 32, 6–11. [Google Scholar]
- Vazouras, P.; Karamanos, S.A.; Dakoulas, P. Finite element analysis of buried steel pipelines under strike-slip fault displacements. Soil Dyn. Earthq. Eng. 2010, 30, 1361–1376. [Google Scholar] [CrossRef]
- Cui, Z.; Li, J.H.; Fu, X.W.; Shen, Q.; Zhou, G.X.; Ma, Y.; Wang, T.Q. Evaluating the response of a tunnel subjected to strike-slip fault rupture in conjunction with model test and hybrid discrete–continuous numerical modeling. Rock. Mech. Rock. Eng. 2022, 55, 4743–4764. [Google Scholar]
- Yang, H.H.; Wang, M.N.; Luo, X.; Yu, L.; Zhang, X.; Tang, L.Z. Longitudinal and cross-sectional partitioned failure mechanism of tunnels subjected to stick-slip action of strike-slip faults. J. Cent. South Univ. 2024, 31, 250–271. [Google Scholar] [CrossRef]
- Du, X.L.; Wang, Z.; Zhao, M.; Zhong, Z.L.; Wang, H.R.; Sheng, Q. Experimental study on articulated design of mountain tunnel crossing strike-slip fault zones. China Civ. Eng. J. 2022, 55, 97–106. [Google Scholar]
- Zhang, X.; Wang, M.N.; Li, Z.J.; Yu, L.; Yang, H.H. Mechanical response of tunnels crossing active fault zones under normal or reverse faulting: A refined nonlinear analytical approximate solution. Comput. Geotech. 2024, 167, 106028. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, L.; Wang, M.N.; Yang, H.H. Mechanical response and failure characteristics of tunnels subjected to reverse faulting with nonuniform displacement: Theoretical and numerical investigation. Eng. Fail. Anal. 2024, 156, 107809. [Google Scholar] [CrossRef]
- Yang, H.H.; Wang, M.N.; Yu, L.; Zhang, X. Analytical and numerical analysis on the mechanical response and damage characteristics of tunnels subjected to multiple normal faulting. Comput. Geotech. 2024, 169, 106254. [Google Scholar] [CrossRef]
- Sabagh, M.; Ghalandarzadeh, A. Centrifugal modeling of continuous shallow tunnels at active normal faults intersection. Transp. Geotech. 2020, 22, 100325. [Google Scholar] [CrossRef]
- Liu, X.Z.; Li, X.F.; Lin, L.L.; Sang, Y.L. Experimental study on normal fault rupture propagation in loose strata and its impact on mountain tunnels. Tunn. Undergr. Space Technol. 2015, 49, 417–425. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, W.; Cui, Z. Study of mechanical response of tunnels crossing active faults in different burial depths. Buildings 2023, 13, 2723. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, Z.; Sheng, Q.; Zhao, W.; Song, L. Experimental study on the effect of flexible joints of a deep-buried tunnel across an active fault under high in-situ stress conditions. Undergr. Space 2024, 19, 189–207. [Google Scholar] [CrossRef]
- Zhang, N.; Zhou, H.; Gao, Y.; Zhu, Y.; Lu, J.; Zhao, C.; Cheng, G. Deformation and failure mechanism of deep-buried tunnel under the action of fault dislocation and application of nonlocal model in numerical simulation research. Eng. Fail. Anal. 2025, 174, 109496. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, X.; Alsahly, A.; Yuan, Y.; Meschke, G. Mechanics of longitudinal joints in segmental tunnel linings: A semi-analytical approach. Tunn. Undergr. Space Technol. 2025, 163, 106696. [Google Scholar] [CrossRef]
- Liu, Z.; Cao, B.T.; Xu, C.; Liu, X.; Yuan, Y.; Meschke, G. Mechanics of longitudinal joints in segmental tunnel linings: Role of connecting bolts. Tunn. Undergr. Space Technol. 2025, 161, 106601. [Google Scholar] [CrossRef]
- Liu, X.; Hong, J.; Liu, Z. Investigations on mechanical behavior of longitudinal joints in segmental tunnel linings reinforced with epoxy bonded-bolted steel plates. Tunn. Undergr. Space Technol. 2025, 163, 106724. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, Y.; Liu, Z.; Liu, X. Experimental and analytical investigation of the mechanical behavior of deformed segmental tunnel linings strengthened by stainless steel corrugated plate. Tunn. Undergr. Space Technol. 2025, 157, 106355. [Google Scholar] [CrossRef]
- Zhang, D.M.; Guo, L.; Huang, Z.K.; Shen, Y.Y.; Pitilakis, K. Failure mechanism of rock tunnels subjected to combined reversed fault dislocation and subsequent seismic excitation. Comput. Geotech. 2025, 187, 107485. [Google Scholar] [CrossRef]
- Wang, T.; Geng, P. Quantitative damage evaluation of tunnel subjected to a subsequent strong seismic after a quasi-static reverse faulting. Eng. Fail. Anal. 2024, 157, 107886. [Google Scholar] [CrossRef]
- Xin, C.; Feng, W.; Song, D.; Huang, S.; Liu, X. Seismic damage to non-fault-crossing and fault-crossing tunnels: Comparative study of the 2008 Wenchuan earthquake (Mw 7.9) and the 2022 Menyuan earthquake (Mw 6.7). Eng. Fail. Anal. 2024, 166, 108843. [Google Scholar] [CrossRef]
- Wang, H.R.; Zhong, Z.L.; Zhao, M.; Wang, Z.; Zhao, X.; Du, X.L. Model Experimental Study of the Influence of Strike-slip Fault Dislocation on Tunnel. J. Beijing Univ. Technol. 2021, 47, 691–701. [Google Scholar]
- Shen, Y.; Gao, B.; Yang, X.; Tao, S. Seismic damage mechanism and dynamic deformation characteristic analysis of mountain tunnel after Wenchuan earthquake. Eng. Geol. 2014, 180, 85–98. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, Z.L.; Zhao, M.; Du, X.-L. Research on simulation of normal faults and their influence on mountain tunnels. Chin. J. Geotech. Eng. 2020, 42, 1876–1884. [Google Scholar]
- Halabian, A.M.; Hokmabadi, T. A new hybrid model for rigorous analysis of buried pipelines under general faulting accounting for material and geometrical non-linearities with focusing on corrugated HDPE pipelines. Soil Dyn. Earthq. Eng. 2018, 115, 1–17. [Google Scholar] [CrossRef]
- British Standards Institution. Code of Practice for Temporary Works Procedures and the Permissible Stress Design of Falsework: BS5975; British Standards Institution: London, UK, 2008. [Google Scholar]
- Zhao, K.; Chen, W.Z.; Zhao, W.S.; Yang, D.S.; Song, W.P. Study on parameters of articulated design of tunnel lining under reverse fault dislocation. Chin. J. Rock Mech. Eng. 2018, 37, 3411–3421. (In Chinese) [Google Scholar]
- Byerlee, J. Friction of rocks. Pure Appl. Geophys. 1978, 116, 615–626. [Google Scholar] [CrossRef]
- Panet, M.; Guenot, A. Analysis of convergence behind the face of a tunnel. In Proceedings of the 3rd International Symposium, Brighton, UK, 7–11 June 1982. [Google Scholar]
- Andreotti, G.; Lai, C.G. Use of fragility curves to assess the seismic vulnerability in the risk analysis of mountain tunnels. Tunn. Undergr. Space Technol. 2019, 91, 103008. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China (MTPRC). Guidelines for Design of Highway Tunnel (JTG/T D70); China Communications Press: Beijing, China, 2010. [Google Scholar]
- Billen, M.; Cowgill, E.; Buer, E. Determination of fault friction from reactivation of abyssal-hill faults in subduction zones. Geology 2007, 35, 819–822. [Google Scholar] [CrossRef]
- Zhang, X.P.; Jiang, Y.J.; Sugimoto, S. Seismic damage assessment of mountain tunnel: A case study on the Tawarayama tunnel due to the 2016 Kumamoto Earthquake. Tunn. Undergr. Space Technol. 2018, 71, 138–148. [Google Scholar] [CrossRef]
- Wei, Y.M.; Wei, X.H.; Li, D.W.; Chen, Y.; Shen, X.; Sun, C. Remote sensing image characteristics and activity analysis of the Heqing-Eryuan fault zone in northwest Yunnan. Quat. Sci. 2017, 37, 234–249. (In Chinese) [Google Scholar]
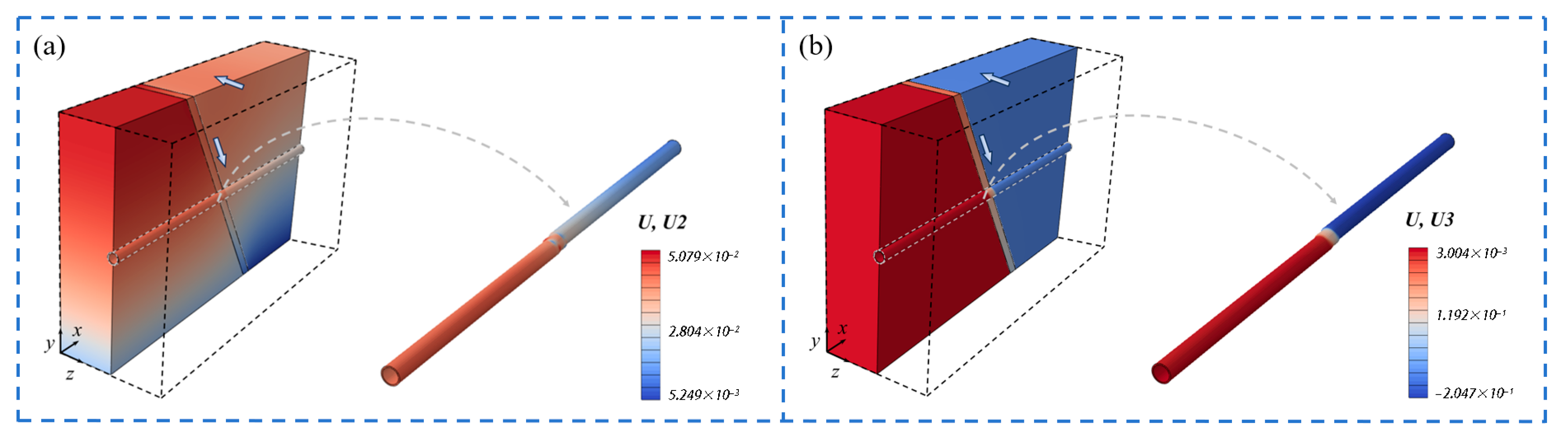
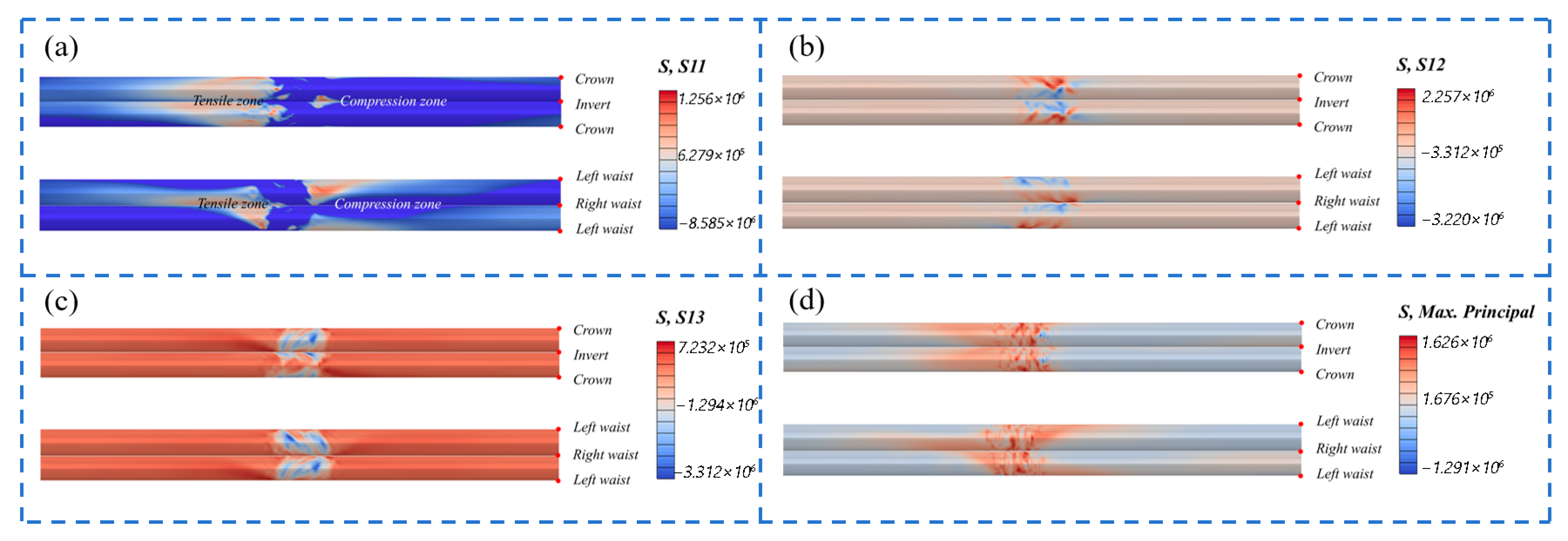
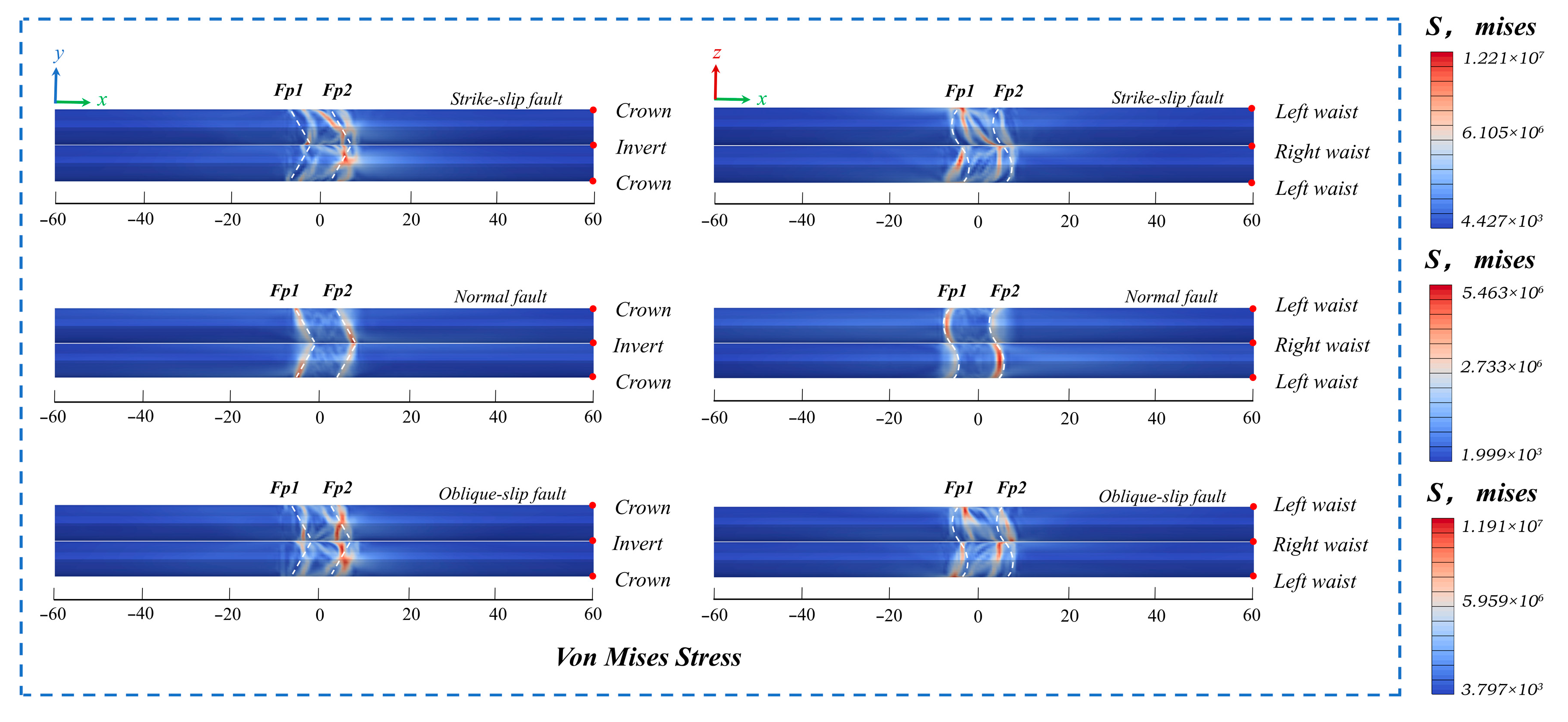
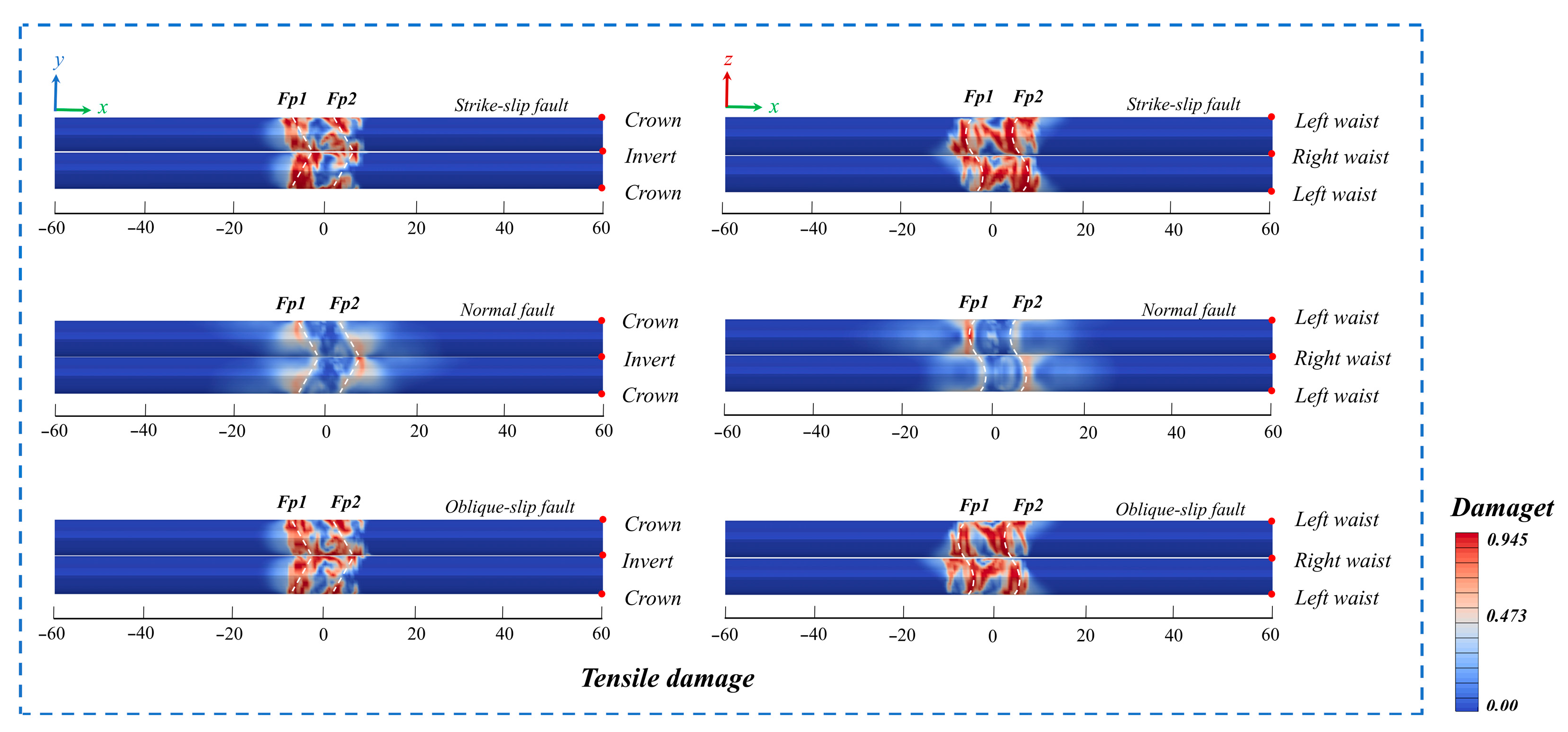

| Type | Density ρ/103 kg⋅m−3 | Elastic Modulus E/Gpa | Poisson’s Ratio ν | Internal Friction Angle φ/(°) | Cohesion Force c/Mpa |
|---|---|---|---|---|---|
| Intact rock | 2.9 | 7.5 | 0.28 | 45 | 1.1 |
| Fault fracture zone | 2.1 | 1.5 | 0.33 | 29 | 0.15 |
| Type | Density ρ/103 kg⋅m−3 | Elastic Modulus E/Gpa | Poisson’s Ratio ν | Dilation Angle φ/(°) | Compressive Yield Stress fc/Mpa | Tensile Yield Stress ft/Mpa |
|---|---|---|---|---|---|---|
| Concrete | 2.5 × 103 | 30 | 0.2 | 36.31 | 20.1 | 2.01 |
| Case | Horizontal Displacement Distance (m) | Fault Dip Angle (°) | Fault Width (m) | Tendency Dislocation Distance (m) |
|---|---|---|---|---|
| 1 | 0.2 | 50/60/70/80 | 10 | 0.04 |
| 2 | 0.2 | 60 | 10/20/30/40 | 0.04 |
| 3 | 0.2/0.4/0.6/0.8 | 60 | 10 | 0.04/0.08/0.12/0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Hua, X.; Liu, X.; Ge, J.; Xiang, C. Numerical Analysis Research on Tunnel Damage Under the Action of Oblique Slip Faults Based on Multiple Slip Surfaces. Infrastructures 2025, 10, 314. https://doi.org/10.3390/infrastructures10110314
Gao C, Hua X, Liu X, Ge J, Xiang C. Numerical Analysis Research on Tunnel Damage Under the Action of Oblique Slip Faults Based on Multiple Slip Surfaces. Infrastructures. 2025; 10(11):314. https://doi.org/10.3390/infrastructures10110314
Chicago/Turabian StyleGao, Chunhua, Xuyang Hua, Xule Liu, Jingyu Ge, and Cong Xiang. 2025. "Numerical Analysis Research on Tunnel Damage Under the Action of Oblique Slip Faults Based on Multiple Slip Surfaces" Infrastructures 10, no. 11: 314. https://doi.org/10.3390/infrastructures10110314
APA StyleGao, C., Hua, X., Liu, X., Ge, J., & Xiang, C. (2025). Numerical Analysis Research on Tunnel Damage Under the Action of Oblique Slip Faults Based on Multiple Slip Surfaces. Infrastructures, 10(11), 314. https://doi.org/10.3390/infrastructures10110314





