Three-Dimensional Refined Modeling and Mechanical Response Analysis of Tunnel Structure Safety in Karst Areas
Abstract
1. Introduction
2. Project Overview
2.1. Introduction to the Project
2.2. Geological Conditions
3. Numerical Modeling
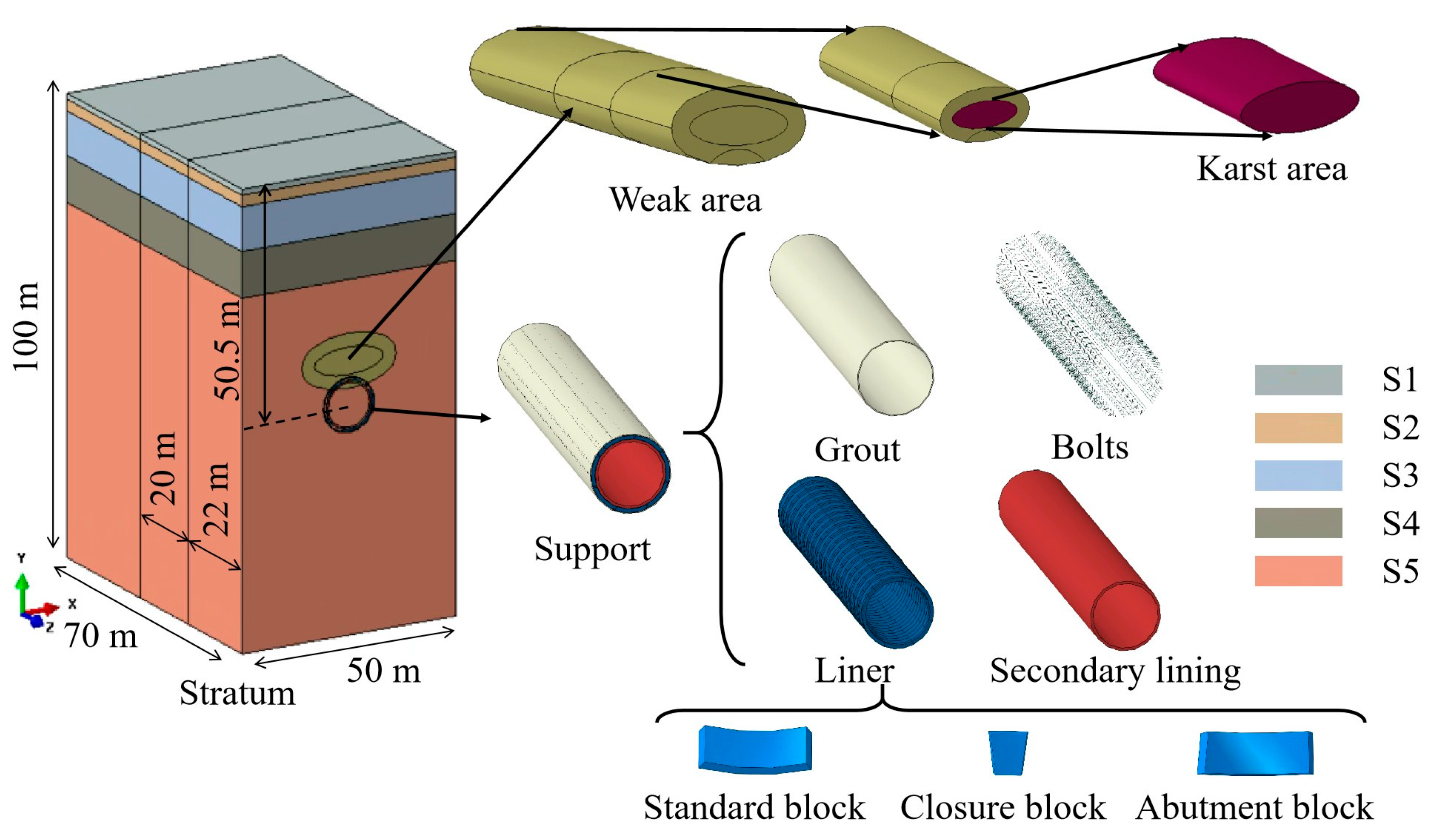
3.1. Geometric Modeling
3.2. Constitutive Model
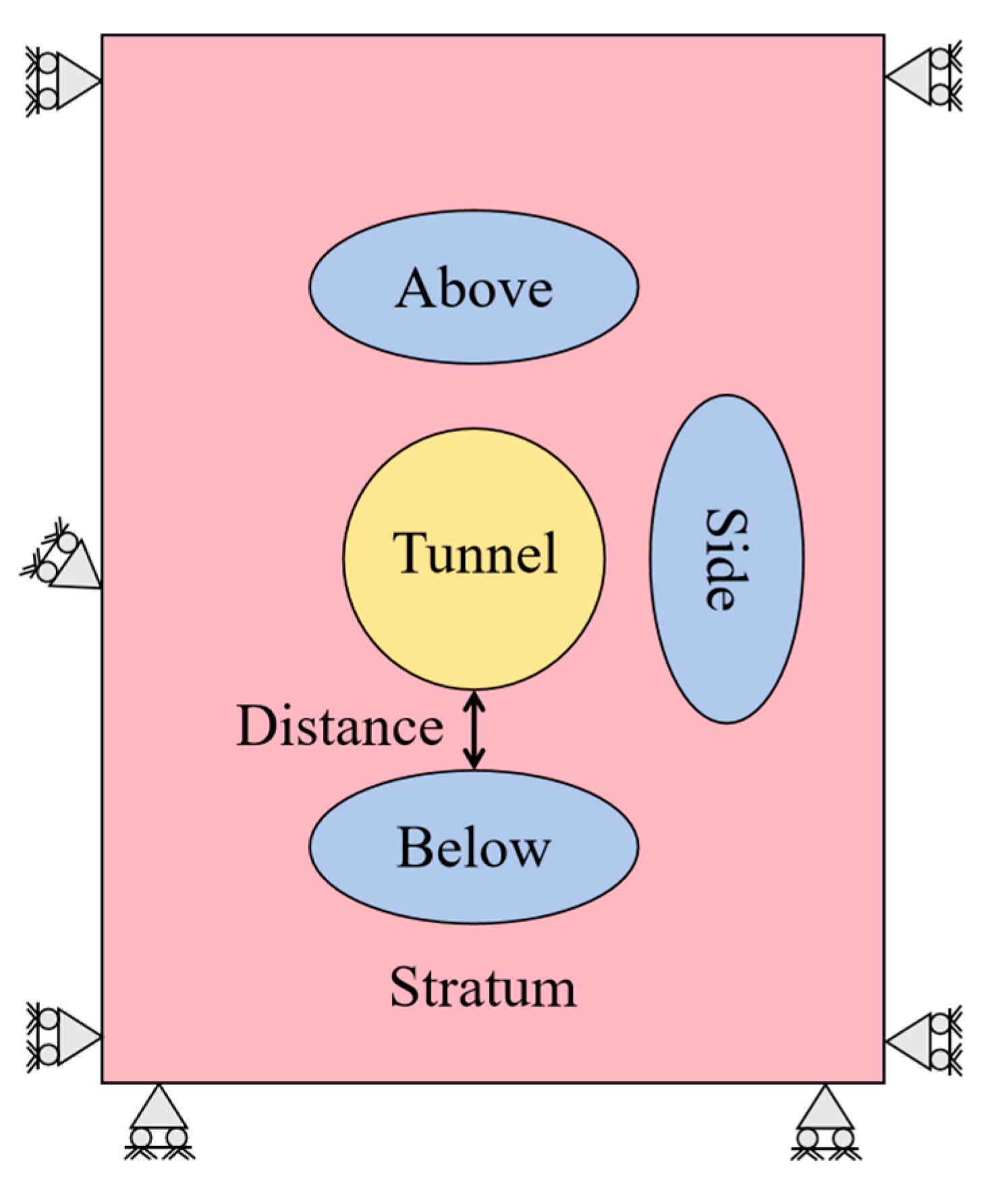
3.3. Loads, Steps and Boundary Conditions
- (a)
- Initial Geostress Equilibrium. Under karst conditions, an initial geostress equilibrium analysis is performed to establish the in situ stress field of the entire geological domain.
- (b)
- Stress Release of Surrounding Rock. According to the New Austrian Tunneling Method (NATM), immediate support is not applied after tunnel excavation, leading to partial stress release in the surrounding rock. Two common approaches can be used to simulate this stress release: (1) Extract the nodal geostress values around the tunnel contour, reduce them by a specified ratio, and reapply the reduced stresses in the opposite direction to achieve a new geostress equilibrium; Or (2) Reduce the elastic modulus of the rock mass within the tunnel contour and re-establish geostress equilibrium to obtain the updated stress field.
- (c)
- Excavation and Installation of Primary Lining (Including Backfill Grouting and Bolts). Excavate the rock and soil within the tunnel contour and activate the lining segments, backfill grout, and connecting bolts using the model change technique.
- (d)
- Installation of Secondary Lining. When considering the working condition with a secondary lining, this structural layer is activated. Generally, two types of contact relationships are possible between the primary and secondary linings. If surface roughening of the segmental lining is considered, the bonding strength between the two linings is high, and they can be modeled as an integrated system using tie contact. If no roughening is considered, the bonding strength is relatively weak, and slip may occur at the interface. In this case, a frictional contact model is more appropriate. In this study, the latter approach is adopted: tangential behavior is defined as frictional contact with a friction coefficient of 0.8, while normal behavior is modeled as hard contact, meaning the interface can transmit compressive stresses but not tension.
- (e)
- Application of Internal Water Pressure. After construction, the operational condition of the tunnel is analyzed to assess the stability of the supporting structure. Internal water pressure is applied in this step, and the mechanical responses of the primary lining, secondary lining, and other structural components are obtained. Water pressure was applied as an external static load to emphasize the structural mechanical response rather than a full fluid–structure coupling process.

4. Results
5. Discussion
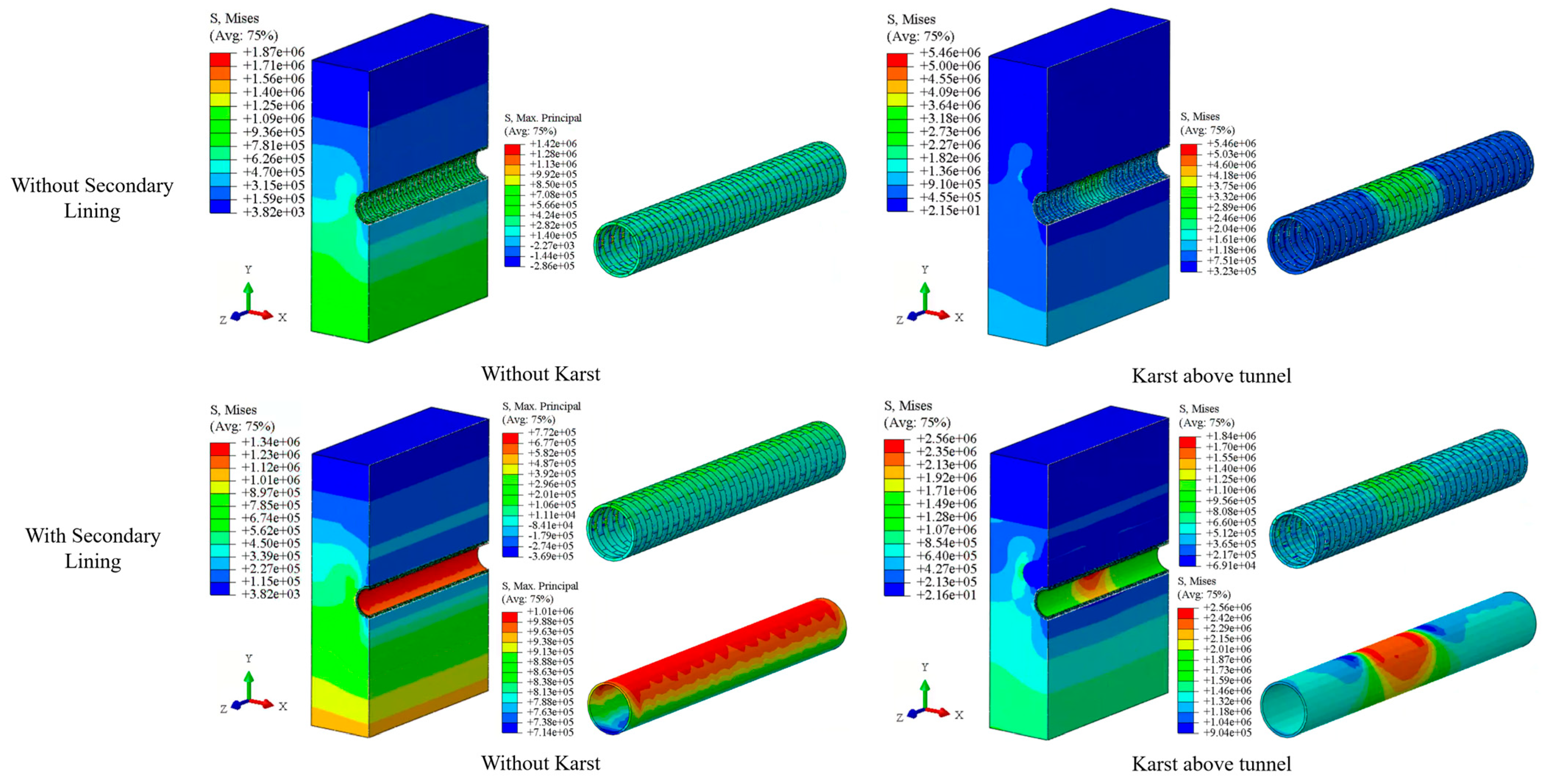
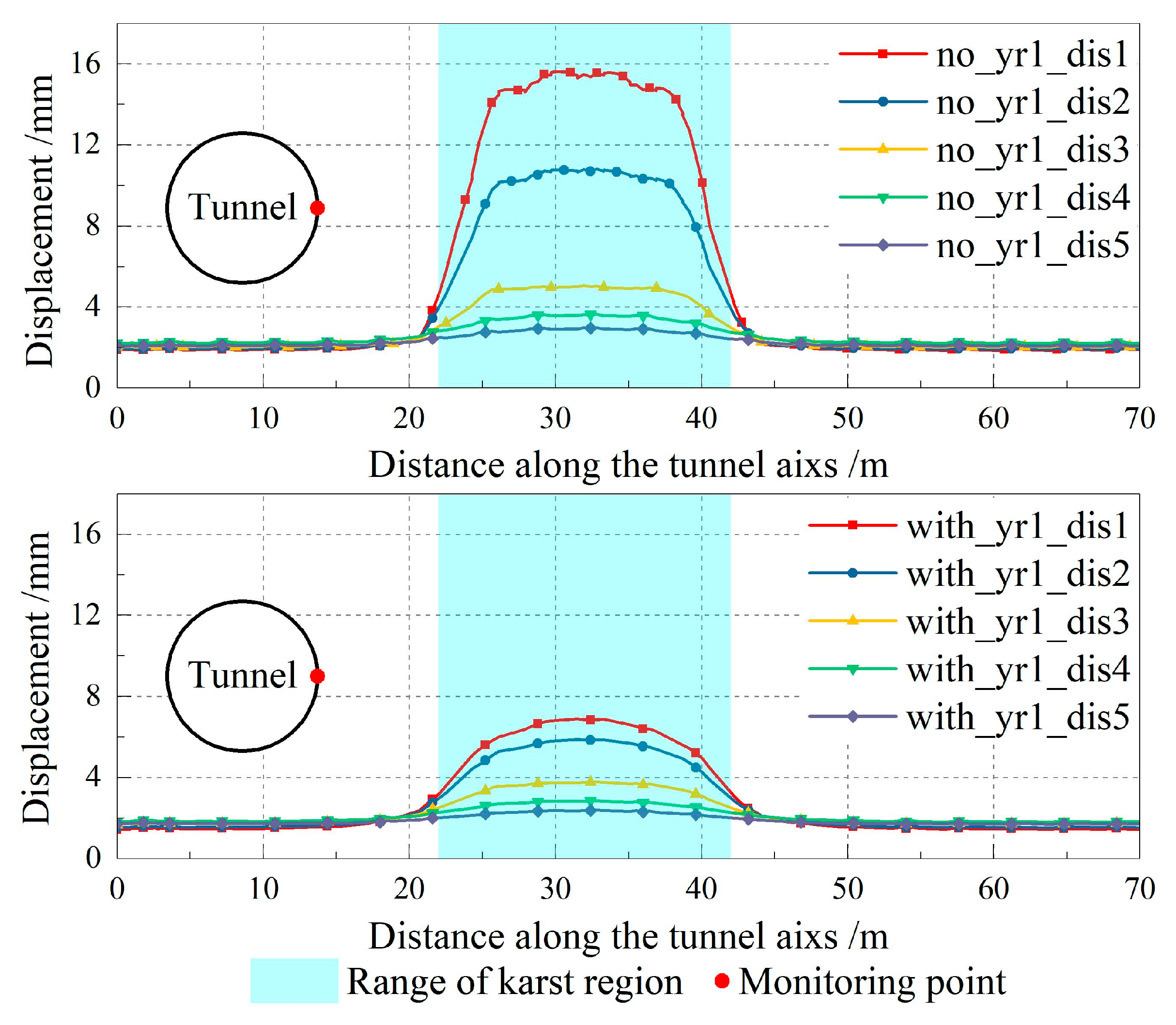
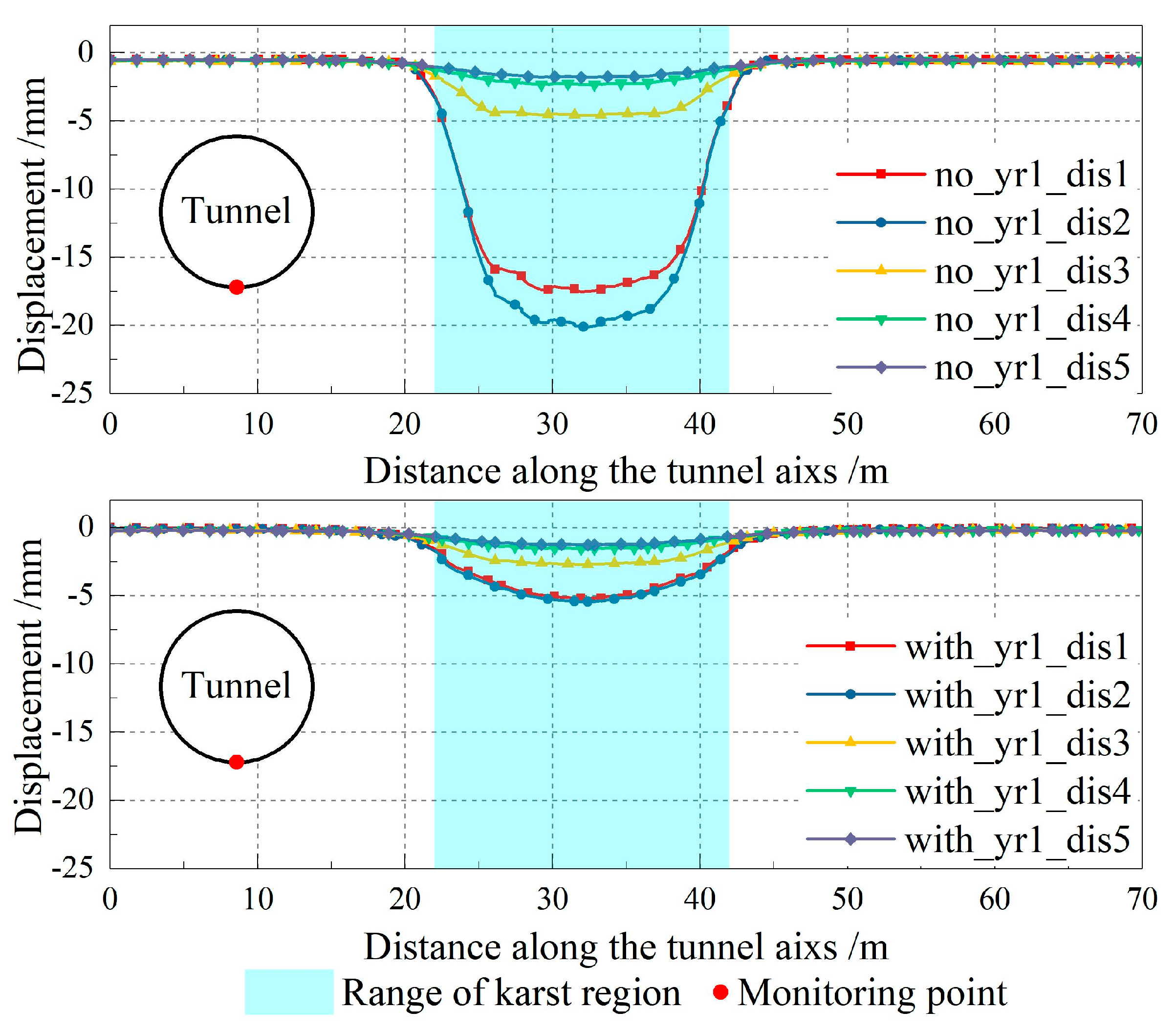
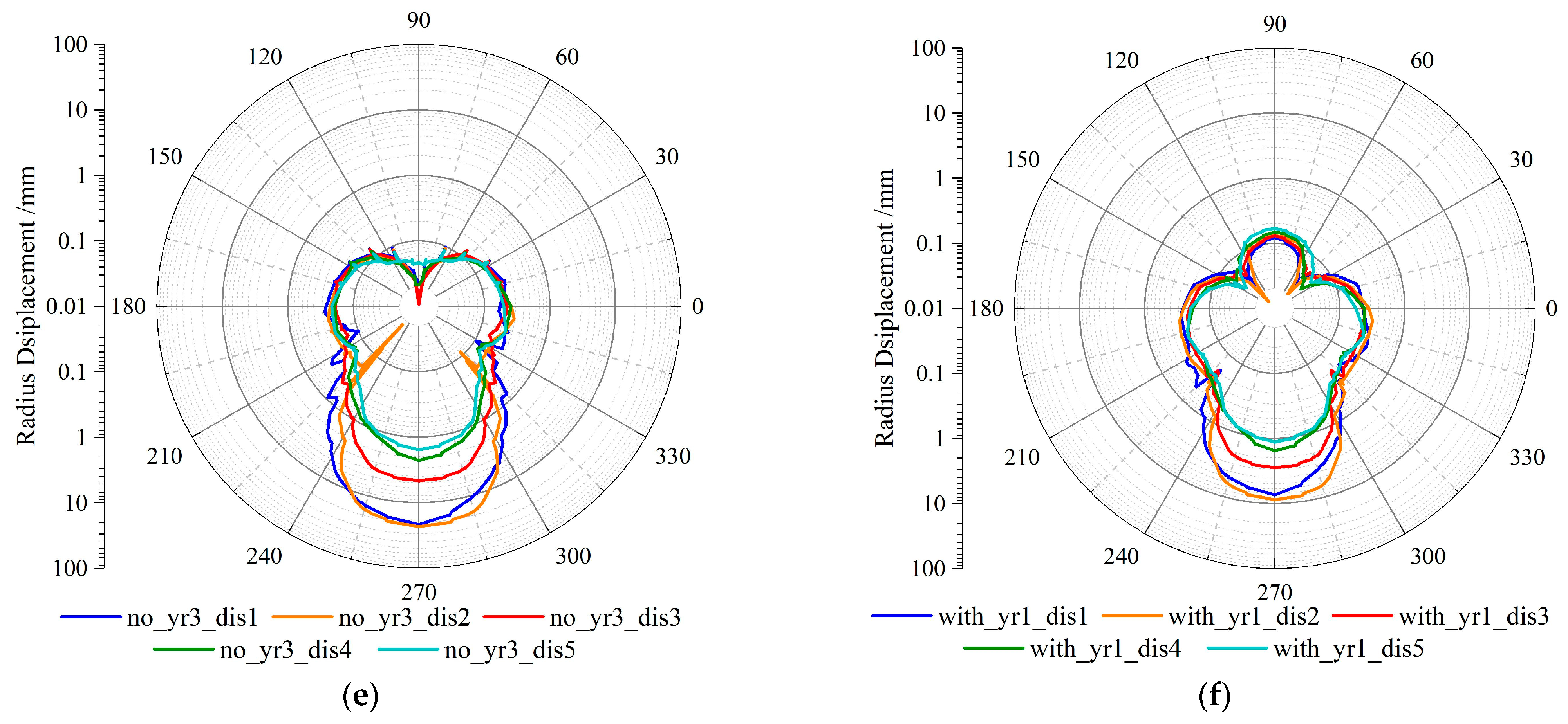
5.1. The Influence on Stress Field
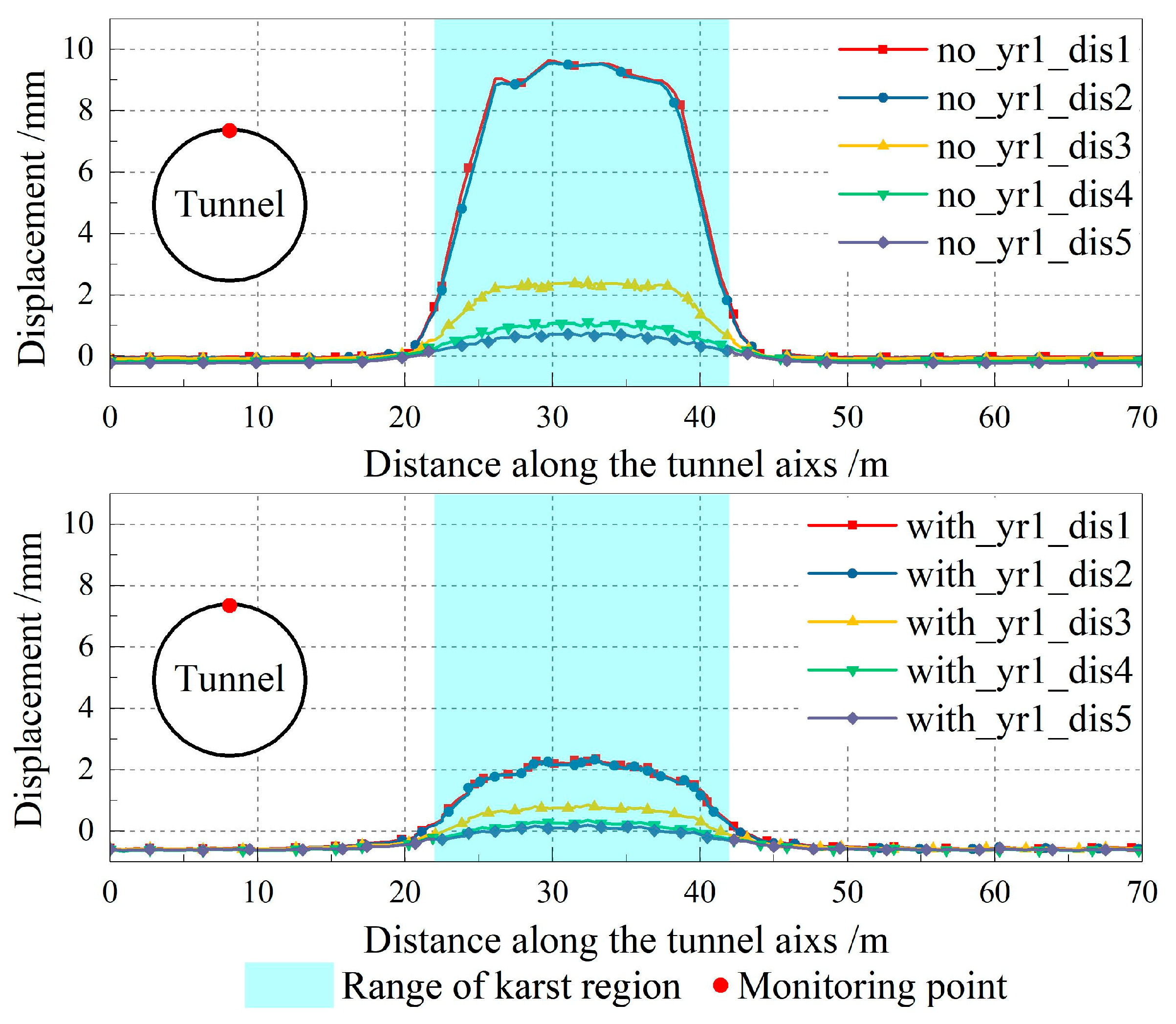
5.2. The Influence on Displacement Field
6. Conclusions
- (1)
- Effects of Karst Position and Distance: The spatial arrangement of karst cavities significantly affects the stress distribution and deformation of the tunnel lining. Cavities located closer to the lining or asymmetrically induce higher local stresses and radial displacements. Critical distances were identified, which can serve as reference values for construction safety assessments.
- (2)
- Deformation and Stress Features of the Lining: The tunnel lining exhibits asymmetric stress concentrations and localized radial displacements. Observed singularities in the stress and displacement fields may indicate precursory behaviors, emphasizing the need for monitoring and proactive management during tunneling.
- (3)
- Strengthening Influence and Design Implications of the Secondary Lining: The secondary lining significantly reduces peak stresses and limits radial deformation, enhancing overall structural stability. Quantitatively, it reduces peak stress by approximately 70–75% and radial deformation by up to 60% in high-risk zones near cavities (within 5 m from the lining). Therefore, a secondary lining thickness of about 0.4 m is recommended as a design reference for such areas.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, Q.; Ng, S.-T.T.; Peng, F.-L.; Dong, Y.-H. A Bottom-up Approach of Knowledge Graph Modelling for Urban Underground Public Spaces: Insights into Public Cognition. Tunn. Undergr. Space Technol. 2025, 163, 106710. [Google Scholar] [CrossRef]
- Dong, Y.-H.; Peng, F.-L.; Guo, T.-F. Quantitative Assessment Method on Urban Vitality of Metro-Led Underground Space Based on Multi-Source Data: A Case Study of Shanghai Inner Ring Area. Tunn. Undergr. Space Technol. 2021, 116, 104108. [Google Scholar] [CrossRef]
- Peng, F.-L.; Wang, W.-X.; Qiao, Y.-K.; Ma, C.-X.; Dong, Y.-H. Review on Data-Informed Planning for Underground Space. Undergr. Space 2025, S2467967425000789. [Google Scholar] [CrossRef]
- Lv, Y.; Jiang, Y.; Hu, W.; Cao, M.; Mao, Y. A Review of the Effects of Tunnel Excavation on the Hydrology, Ecology, and Environment in Karst Areas: Current Status, Challenges, and Perspectives. J. Hydrol. 2020, 586, 124891. [Google Scholar] [CrossRef]
- Gutiérrez, F.; Parise, M.; De Waele, J.; Jourde, H. A Review on Natural and Human-Induced Geohazards and Impacts in Karst. Earth-Sci. Rev. 2014, 138, 61–88. [Google Scholar] [CrossRef]
- Jeannin, P.-Y.; Malard, A.; Rickerl, D.; Weber, E. Assessing Karst-Hydraulic Hazards in Tunneling—The Brunnmühle Spring System—Bernese Jura, Switzerland. Environ. Earth Sci 2015, 74, 7655–7670. [Google Scholar] [CrossRef]
- Alija, S.; Torrijo, F.J.; Quinta-Ferreira, M. Geological Engineering Problems Associated with Tunnel Construction in Karst Rock Masses: The Case of Gavarres Tunnel (Spain). Eng. Geol. 2013, 157, 103–111. [Google Scholar] [CrossRef]
- Song, K.-I.; Cho, G.-C.; Chang, S.-B. Identification, Remediation, and Analysis of Karst Sinkholes in the Longest Railroad Tunnel in South Korea. Eng. Geol. 2012, 135–136, 92–105. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, Z.; Wang, S.; Chen, Y.-F.; Hu, R.; Zhao, X.-J.; Wu, X.-L.; Yang, X.-L. Evaluation of Hydrogeological Impact of Tunnel Engineering in a Karst Aquifer by Coupled Discrete-Continuum Numerical Simulations. J. Hydrol. 2021, 597, 125765. [Google Scholar] [CrossRef]
- Jiang, C.; Xie, H.; He, J.; Wu, W.; Zhang, Z. Analytical Solution of Seepage Field in Karst Tunnel. Adv. Civ. Eng. 2018, 2018, 9215472. [Google Scholar] [CrossRef]
- Song, X.; Cen, C.; Liu, K.; Zhang, C.; Zhou, A.; Wang, Y.; Peng, Q.; Na, J. Numerical Simulation Analysis of the Impact of Tunnel Construction on Aquifers in the Karst Regions of Southwestern China. Water 2025, 17, 619. [Google Scholar] [CrossRef]
- Wang, W.; Gao, S.; Min, Y.; Liu, L.; Chen, J. Three-Dimensional Fluid–Solid Coupling Numerical Simulation of Effects of Underlying Karst Cave on Shield Tunnel Through Sand Stratum. Geotech. Geol. Eng. 2019, 37, 4825–4836. [Google Scholar] [CrossRef]
- Pan, X.; Fang, Y.; Lai, Y.; Sun, H.; Cai, Y.; Shi, L.; Geng, X. Three-Dimensional Numerical Modeling of Water Distribution Tunnels in Karst Area. Arab. J. Geosci. 2020, 13, 1242. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, J.; Yang, J.; Ou, X.; Ye, X.; Zhang, Y. Formulation and Performance of Grouting Materials for Underwater Shield Tunnel Construction in Karst Ground. Constr. Build. Mater. 2018, 187, 327–338. [Google Scholar] [CrossRef]
- He, X.; Wang, S.; Lai, M.; Peng, X.; Chen, B. Mechanical Characterization of Subway Tunnel Construction in Urban Shallow Distributed Karst Stratums. Transp. Geotech. 2023, 43, 101139. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, B.; Zuo, Y.; Zhang, C.; Wang, Y.; Guo, Z. The Mechanism and Numerical Simulation Analysis of Water Bursting in Filling Karst Tunnel. Geotech. Geol. Eng. 2017, 36, 1197–1205. [Google Scholar] [CrossRef]
- Macek, R.W.; Silling, S.A. Peridynamics via Finite Element Analysis. Finite Elem. Anal. Des. 2007, 43, 1169–1178. [Google Scholar] [CrossRef]
- Javili, A.; Morasata, R.; Oterkus, E.; Oterkus, S. Peridynamics Review. Math. Mech. Solids 2019, 24, 3714–3739. [Google Scholar] [CrossRef]
- Shi, S.; Bu, L.; Li, S.; Xiong, Z.; Xie, X.; Li, L.; Zhou, Z.; Xu, Z.; Ma, D. Application of Comprehensive Prediction Method of Water Inrush Hazards Induced by Unfavourable Geological Body in High Risk Karst Tunnel: A Case Study. Geomat. Nat. Hazards Risk 2017, 8, 1407–1423. [Google Scholar] [CrossRef]
- Yang, X.; Xiao, H. Safety Thickness Analysis of Tunnel Floor in Karst Region Based on Catastrophe Theory. J. Cent. South Univ. 2016, 23, 2364–2372. [Google Scholar] [CrossRef]
- Tian, Q.; Zhang, J.; Zhang, Y. Similar Simulation Experiment of Expressway Tunnel in Karst Area. Constr. Build. Mater. 2018, 176, 1–13. [Google Scholar] [CrossRef]
- Wilding, M.; Benmore, C.; Weber, R.; Parise, J.; Lazareva, L.; Skinner, L.; Alderman, O.; Tamalonis, A. Exploring the Structure of High Temperature, Iron-Bearing Liquids. Mater. Today Proc. 2015, 2, S358–S363. [Google Scholar] [CrossRef]
- Wu, W.; Liu, X.; Guo, J.; Sun, F.; Huang, X.; Zhu, Z. Upper Limit Analysis of Stability of the Water-Resistant Rock Mass of a Karst Tunnel Face Considering the Seepage Force. Bull. Eng. Geol. Environ. 2021, 80, 5813–5830. [Google Scholar] [CrossRef]
- Onyango, J.A.; Sasaoka, T.; Shimada, H.; Hamanaka, A.; Moses, D. Equivalent Porous Medium (EPM) Modeling of Karst Features for Slope Stability Analysis in Karst-Prone Weak Rock Masses. Modelling 2025, 6, 81. [Google Scholar] [CrossRef]
- Lin, C.; Xia, C.; Zhang, H.; Liu, Z.; Zhou, C. Simulated Short- and Long-Term Deformation in Coastal Karst Caves. J. Mar. Sci. Eng. 2022, 10, 1315. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, S.; Zhang, L.; Guan, S.; Li, Z.; Cheng, L.; Liu, J.; Chen, J. Study on the Influence of Crystal Plugging on the Mechanical Behavior of Karst Tunnel Lining Structure. Processes 2025, 13, 568. [Google Scholar] [CrossRef]
- Li, G.; Zhou, W. Impact of Karst Water on Coal Mining in North China. Environ. Geol. 2006, 49, 449–457. [Google Scholar] [CrossRef]
- Mo, C.; Zhao, J.; Zhang, D. Mode I Microscopic Cracking Process of Granite Considering the Criticality of Failure. JGR Solid Earth 2023, 128, e2023JB027040. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, X. Forecasting Catastrophic Rupture in Brittle Rocks Using Precursory AE Time Series. JGR Solid Earth 2020, 125, e2019JB019276. [Google Scholar] [CrossRef]


| Layer Number | Stratum Category | Depth (m) | Water Content (%) | Natural Unit Weight (kN/m3) | Dry Unit Weight (kN/m3) | Cohesive (kPa) | Internal Friction Angle (°) | Compression Modulus (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|---|---|---|---|---|---|
| ①—2 (S1) | Plain fill | 1.3 | 32.2 | 18.3 | 12.4 | 10 | 10.0 | 3.0 | — |
| ②—1 (S2) | Silty clay | 2.5 | 32.9 | 18.4 | 12.3 | 20 | 14.0 | 3.5 | — |
| ⑮—1 (S3) | Gravelly silty clay | 9.6 | 29.0 | 18.8 | 13.3 | 30 | 18.0 | 5.0 | — |
| ㉝b—1 (S4) | Completely weathered limestone | 10.1 | 39.9 | 17.7 | 10.6 | 35 | 14.2 | 5.6 | — |
| ㉝a—3 (S5) | Moderately weathered carbonaceous limestone | 76.5 | — | 25.0 | — | 900 | 40.0 | Incompressible | 10.0 |
| Cavity Location | Above (Distance = 0.5 m) | Side (Distance = 0.5 m) | Below (Distance = 0.5 m) |
|---|---|---|---|
| Maximum principal stress distribution | 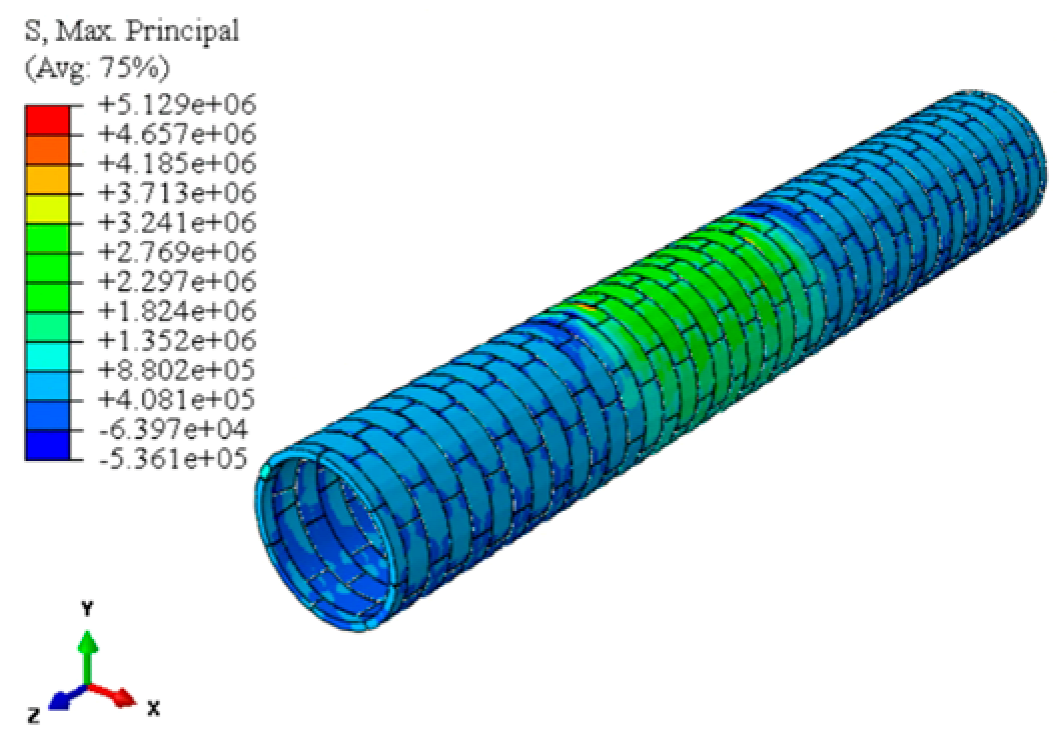 |  |  |
| Maximum tensile stress/MPa | 5.13 | 5.88 | 7.37 |
| Minimum principal stress distribution |  | 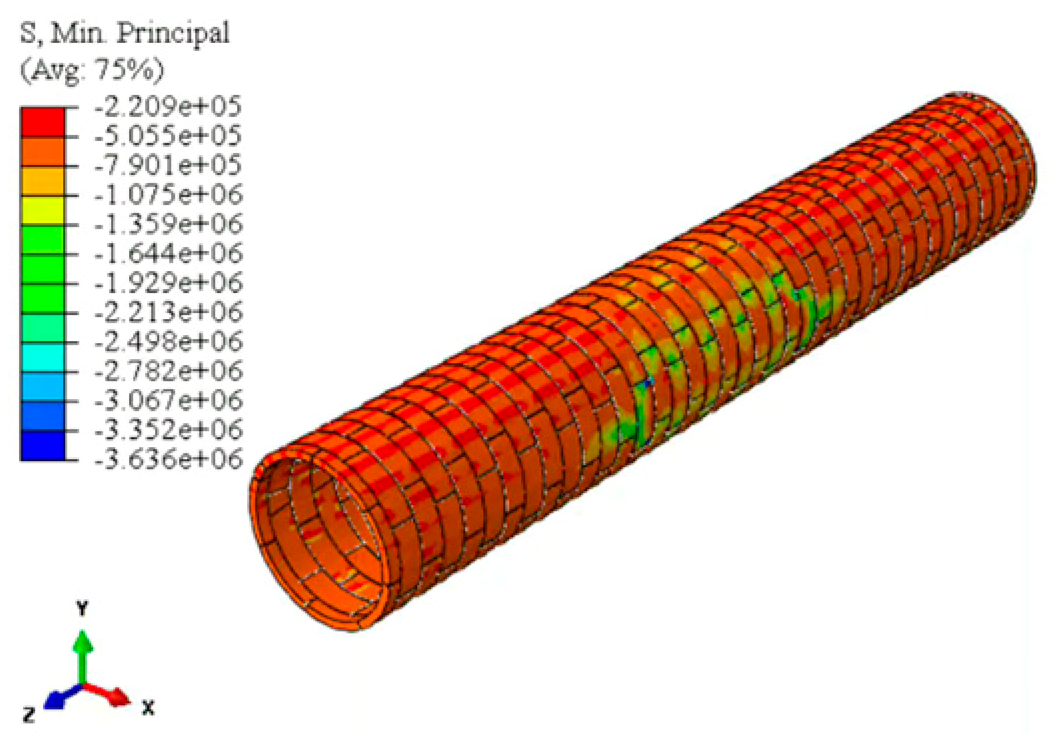 |  |
| Maximum compressive stress/MPa | 2.76 | 3.64 | 4.96 |
| Cavity Location | Above (Distance = 0.5 m) | Side (Distance = 0.5 m) | Below (Distance = 0.5 m) |
|---|---|---|---|
| Maximum principal stress distribution |  |  |  |
| Maximum tensile stress/MPa | 1.62 | 1.47 | 1.79 |
| Minimum principal stress distribution | 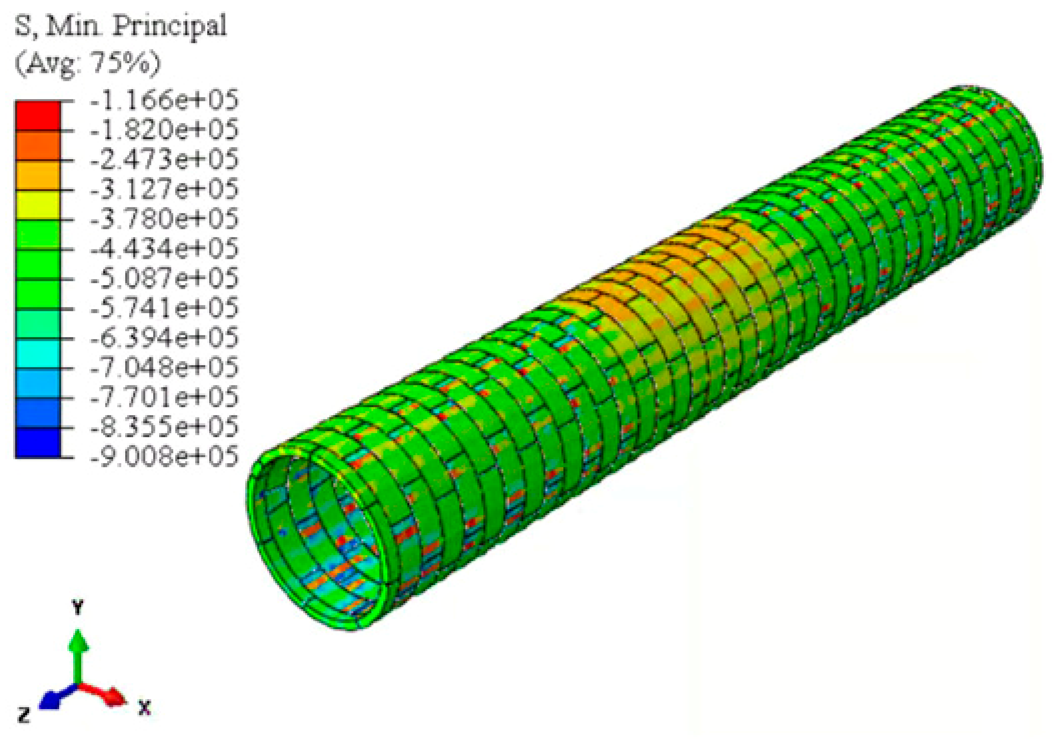 |  |  |
| Maximum compressive stress/MPa | 0.901 | 1.19 | 1.12 |
| Cavity Location | Above (Distance = 0.5 m) | Side (Distance = 0.5 m) | Below (Distance = 0.5 m) |
|---|---|---|---|
| Maximum principal stress distribution | 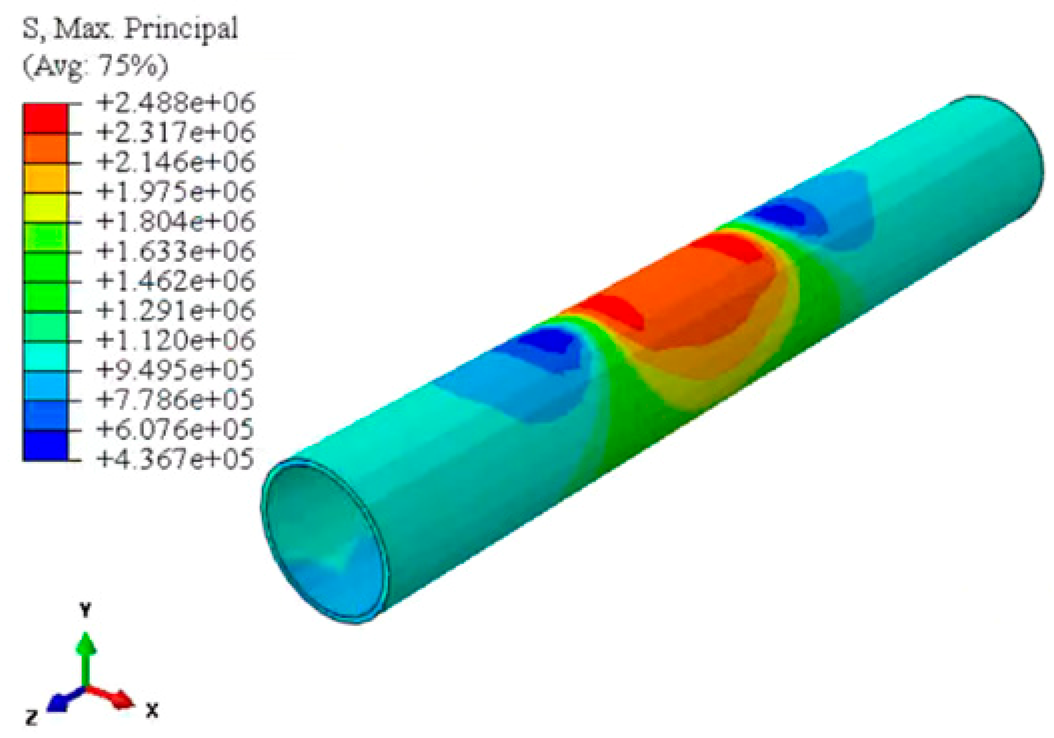 | 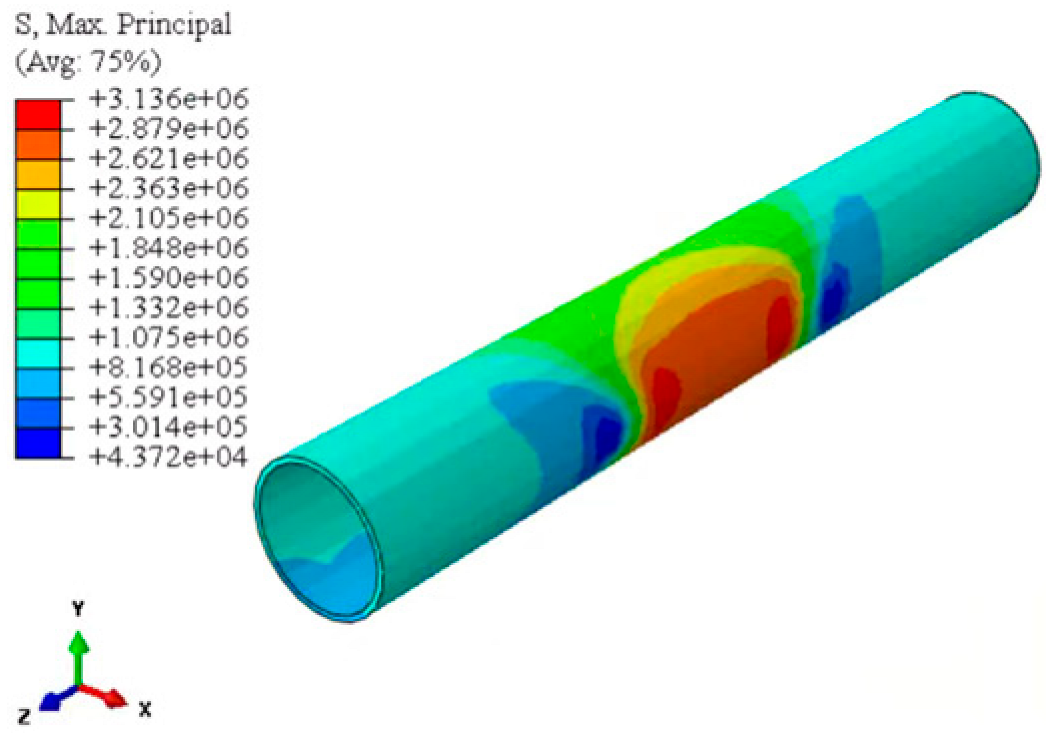 | 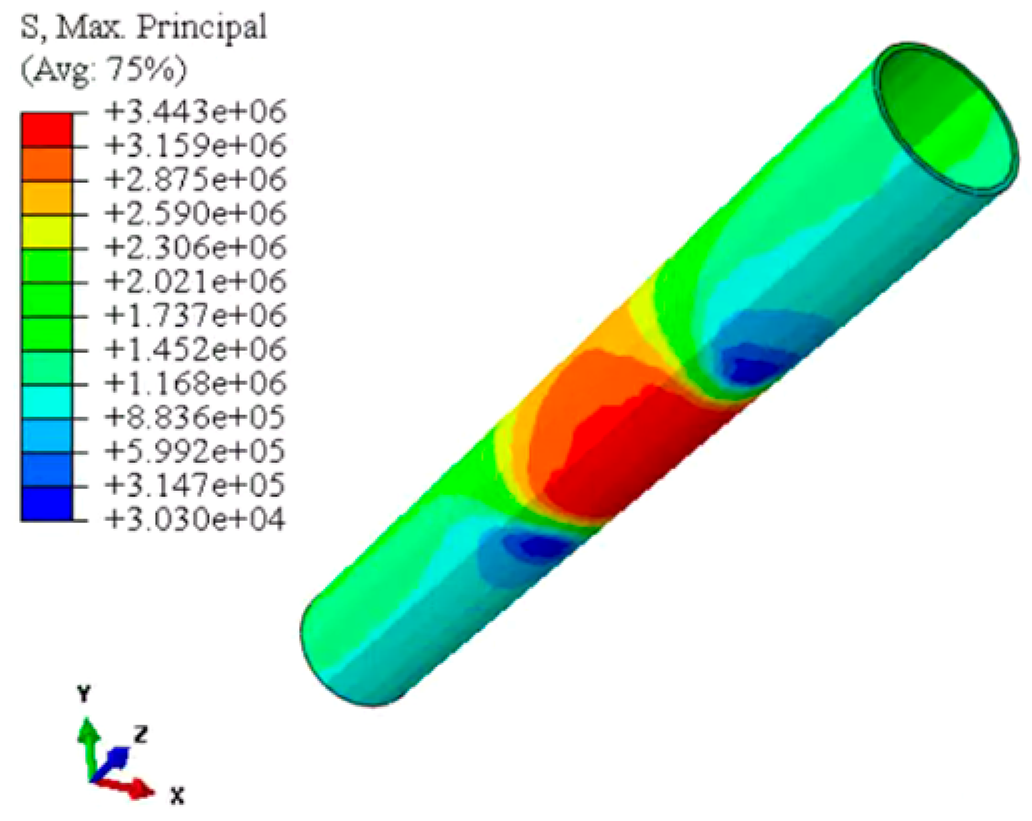 |
| Maximum tensile stress/MPa | 2.49 | 3.14 | 3.44 |
| Minimum principal stress distribution | 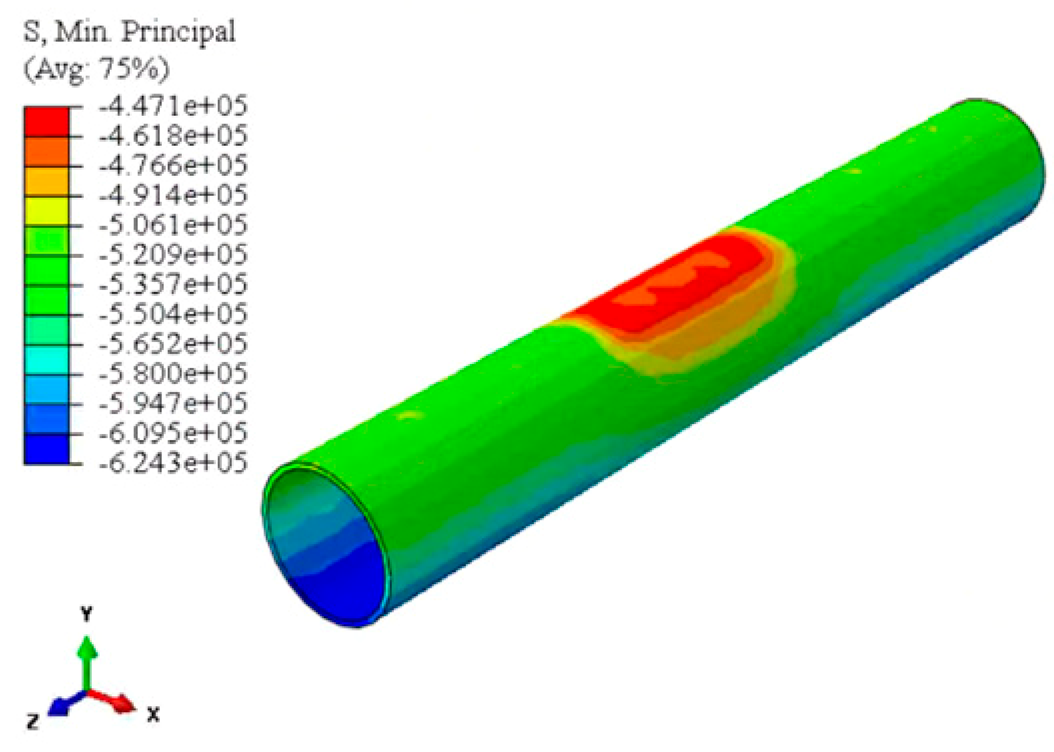 | 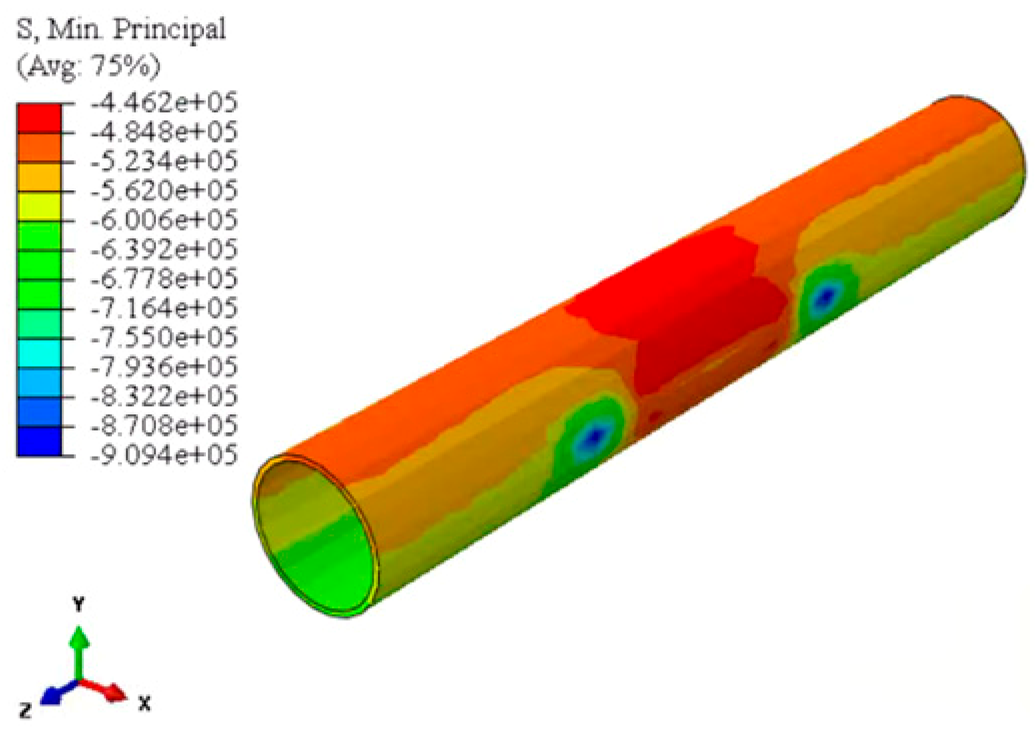 |  |
| Maximum compressive stress/MPa | 0.624 | 0.909 | 0.870 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, G.; Yang, F.; Dong, Y.; Liu, W.; Xu, M. Three-Dimensional Refined Modeling and Mechanical Response Analysis of Tunnel Structure Safety in Karst Areas. Infrastructures 2025, 10, 315. https://doi.org/10.3390/infrastructures10110315
Gu G, Yang F, Dong Y, Liu W, Xu M. Three-Dimensional Refined Modeling and Mechanical Response Analysis of Tunnel Structure Safety in Karst Areas. Infrastructures. 2025; 10(11):315. https://doi.org/10.3390/infrastructures10110315
Chicago/Turabian StyleGu, Guansi, Fei Yang, Yunhao Dong, Wei Liu, and Mingze Xu. 2025. "Three-Dimensional Refined Modeling and Mechanical Response Analysis of Tunnel Structure Safety in Karst Areas" Infrastructures 10, no. 11: 315. https://doi.org/10.3390/infrastructures10110315
APA StyleGu, G., Yang, F., Dong, Y., Liu, W., & Xu, M. (2025). Three-Dimensional Refined Modeling and Mechanical Response Analysis of Tunnel Structure Safety in Karst Areas. Infrastructures, 10(11), 315. https://doi.org/10.3390/infrastructures10110315






