A Numerical Simulation Study on Vertical Vibration Response for Rail Squat Detection with a Train in Regular Traffic
Abstract
1. Introduction
- (1)
- While train-mounted accelerometers have proven effective in detecting wear on rail switches and are strongly correlated with specific installation positions, it remains unclear whether these positions are equally effective for detecting the development of rail squats.
- (2)
- Train speed plays a crucial role in track condition monitoring. However, there has been insufficient research to identify the recommended train speed for accelerometer placement, particularly concerning the detection of rail squat features.
- (3)
- Although some squat cases have been mentioned in previous studies, there has been limited investigation into the sensitivity of squat features, such as length, width, and depth, to accelerometer responses. A systematic analysis of how these geometric characteristics influence acceleration signals is vital for optimizing squat-specific monitoring.
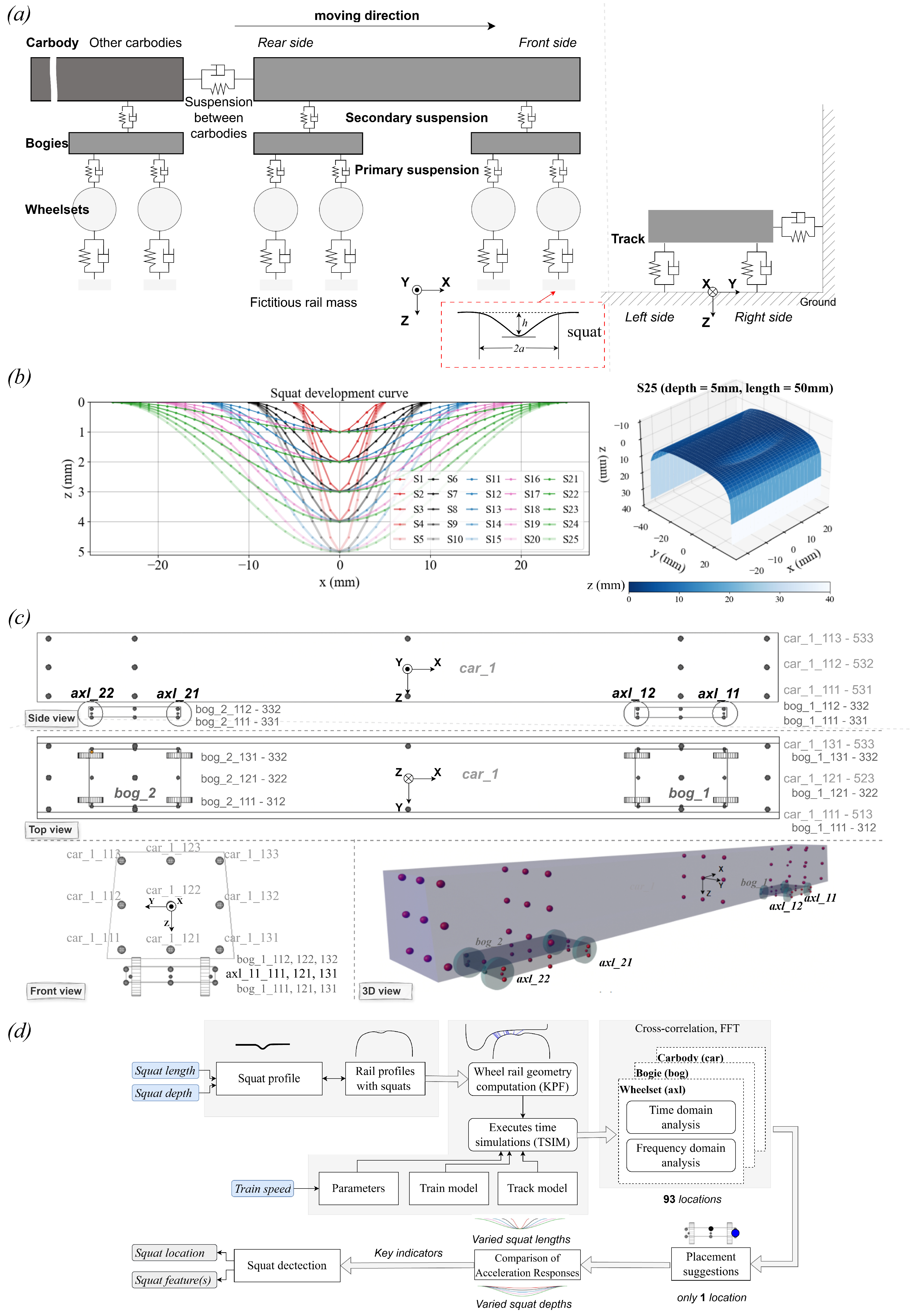
2. Methods
2.1. Train-Track Model
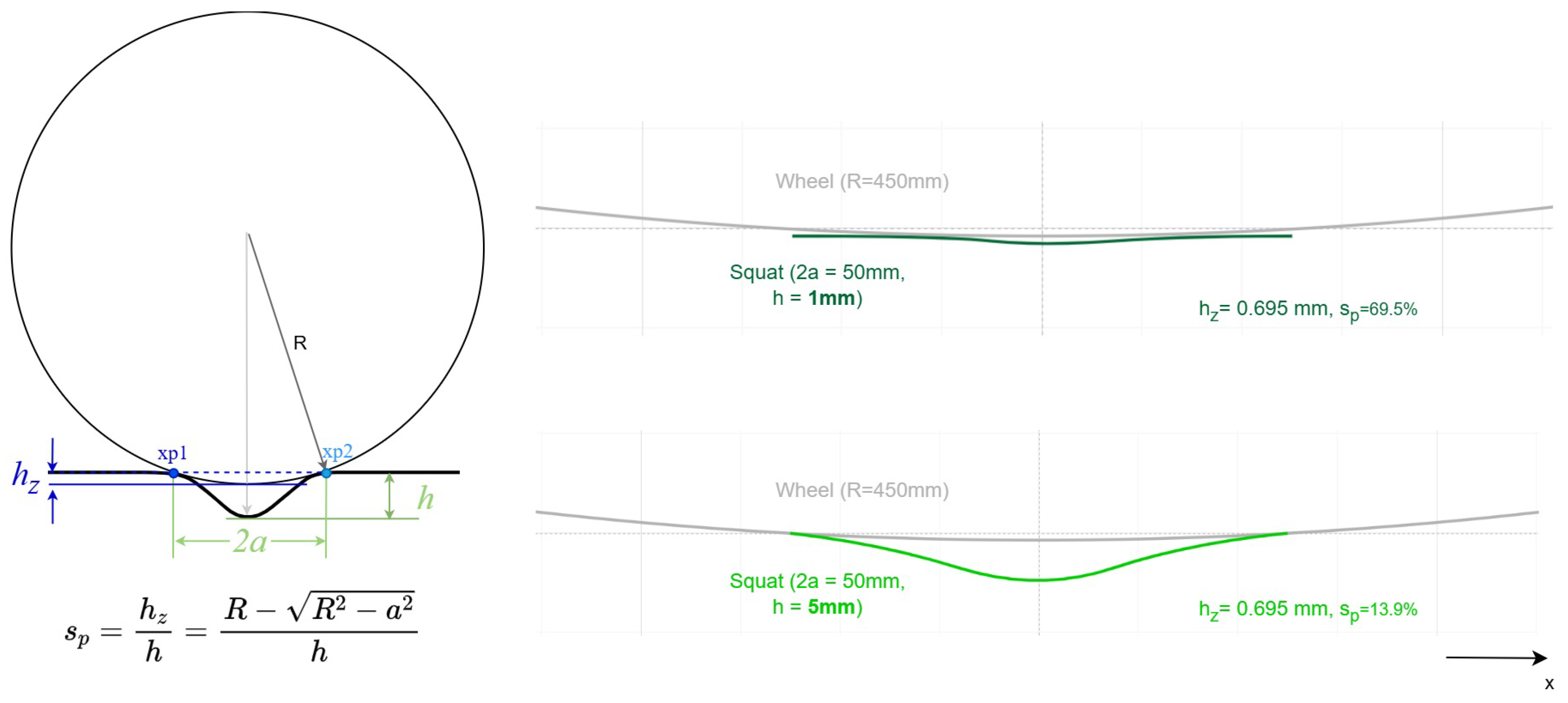
2.2. Squat Model
2.3. Analysis
3. Results
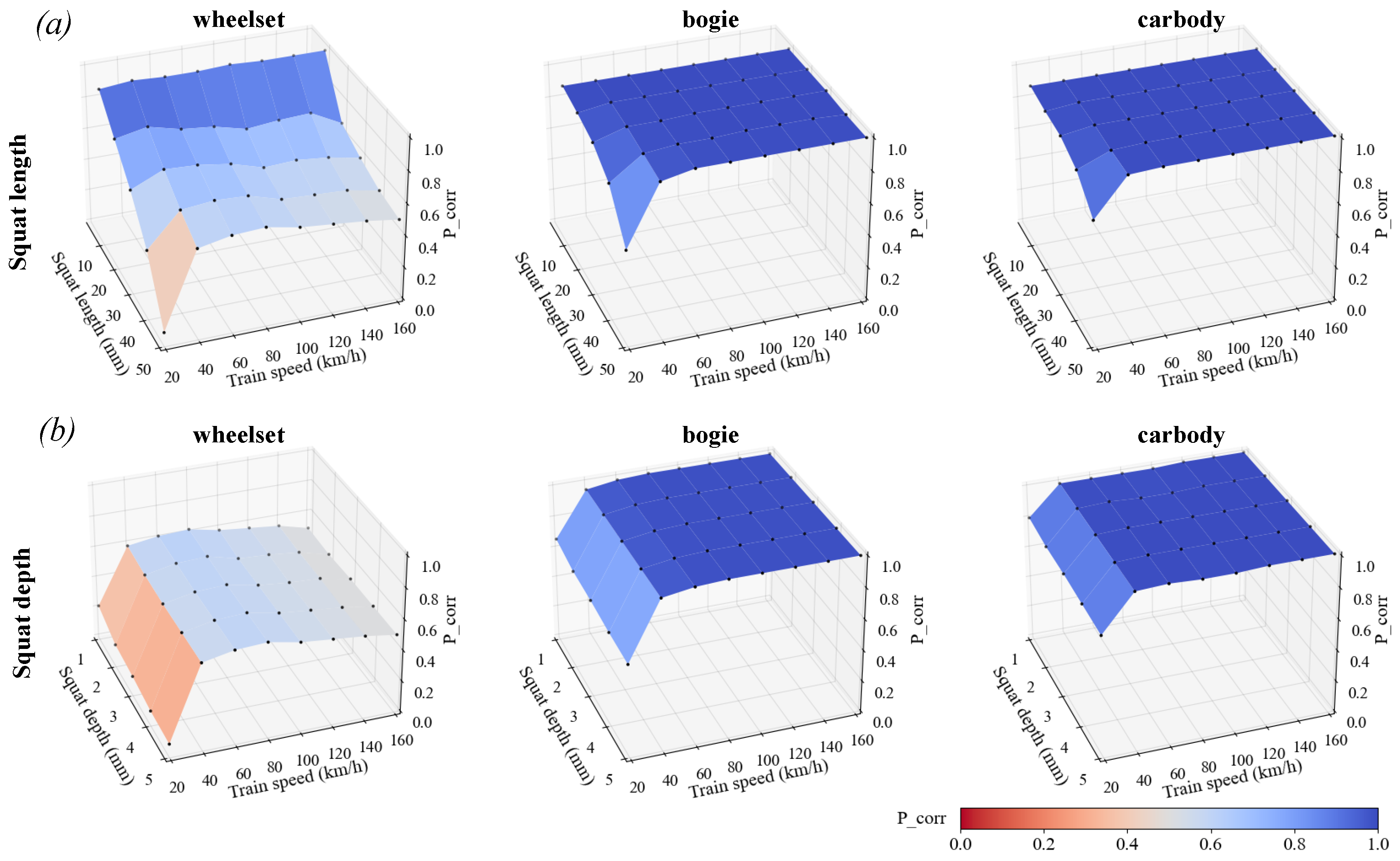
3.1. Optimal Accelerometer Placement
Train Speed Variation
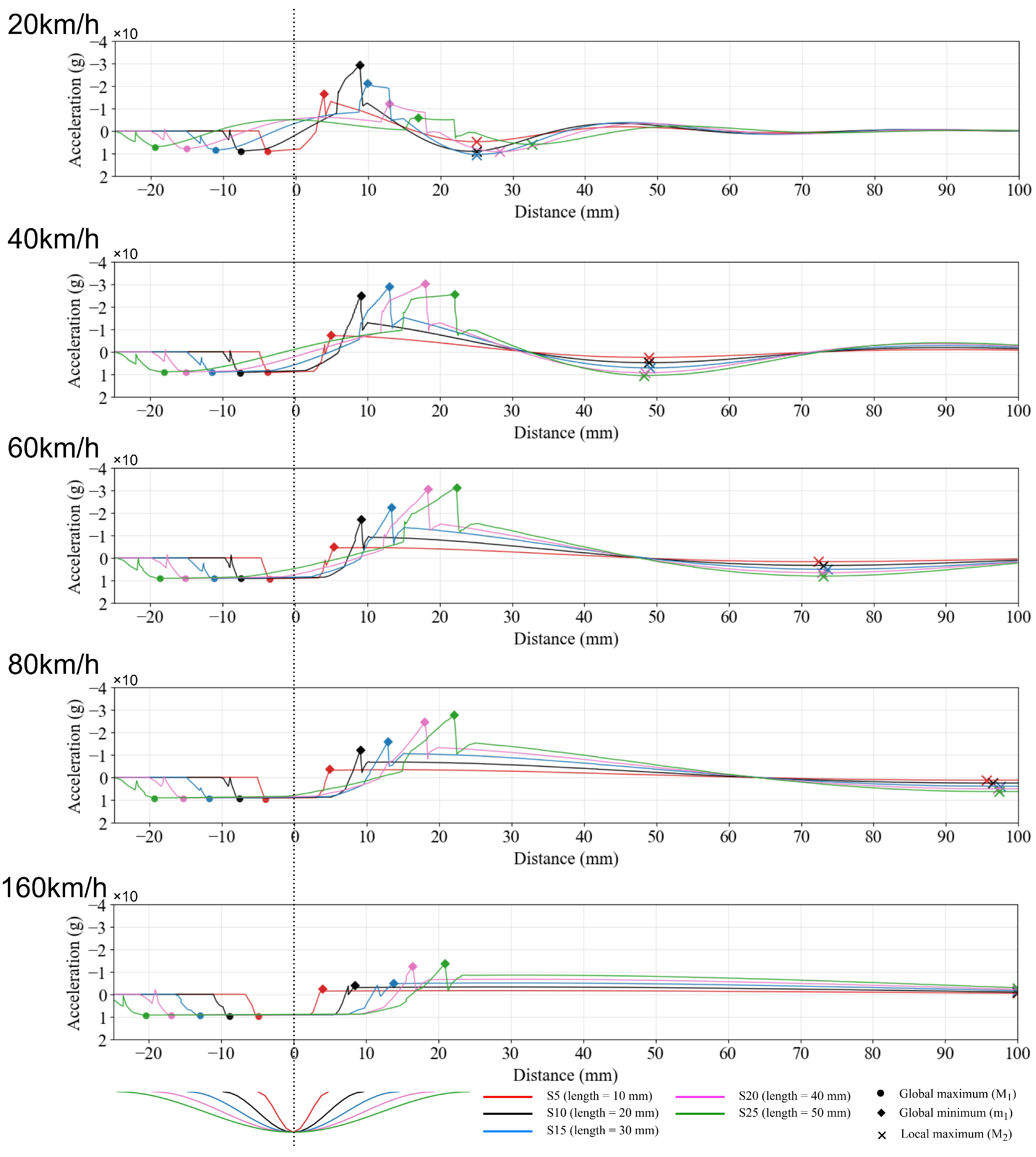
3.2. Acceleration
3.2.1. Squat Length
3.2.2. Squat Depth
4. Discussion
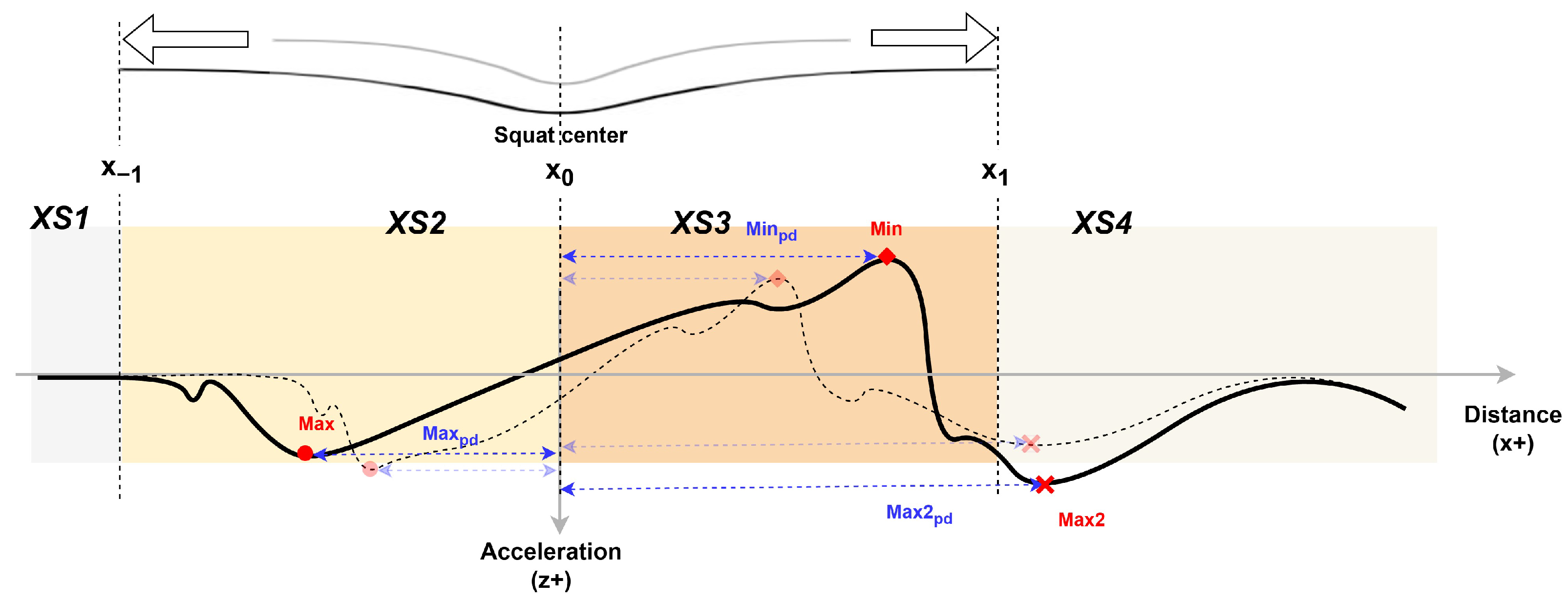
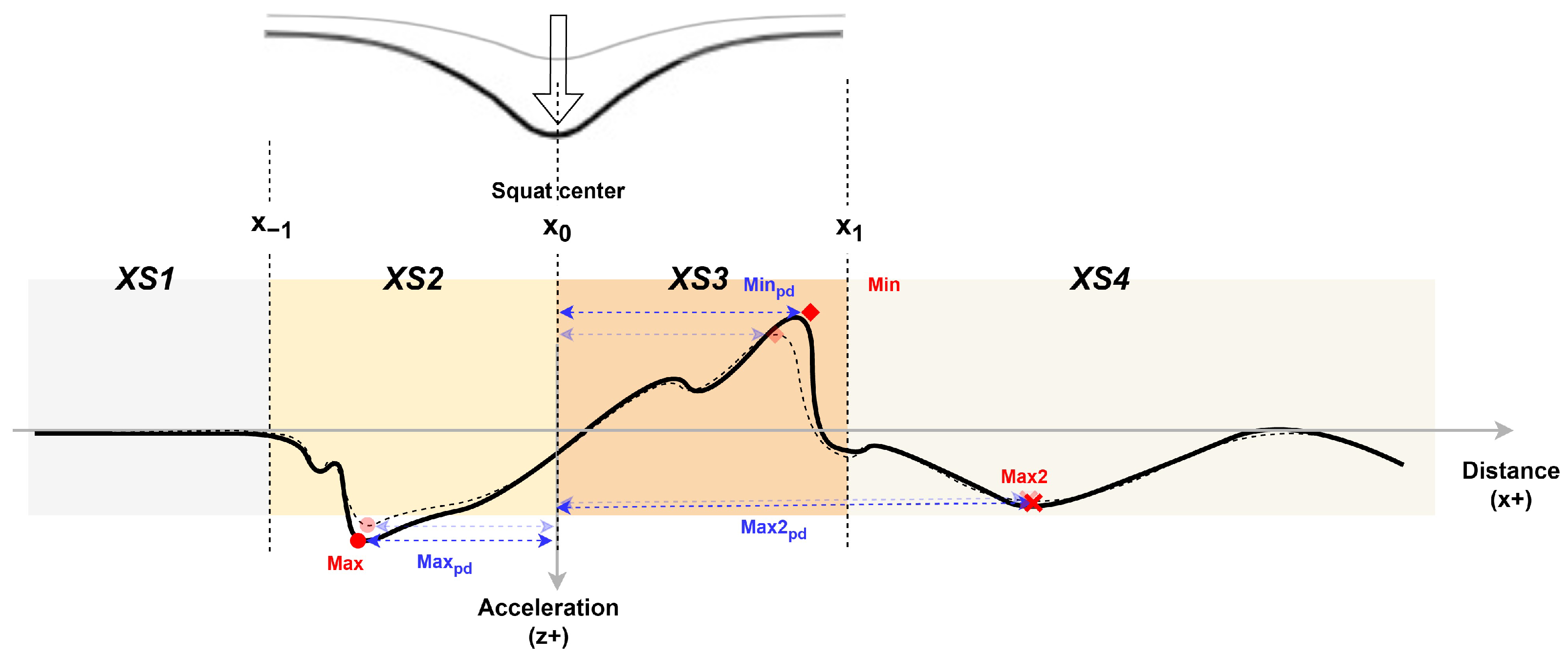
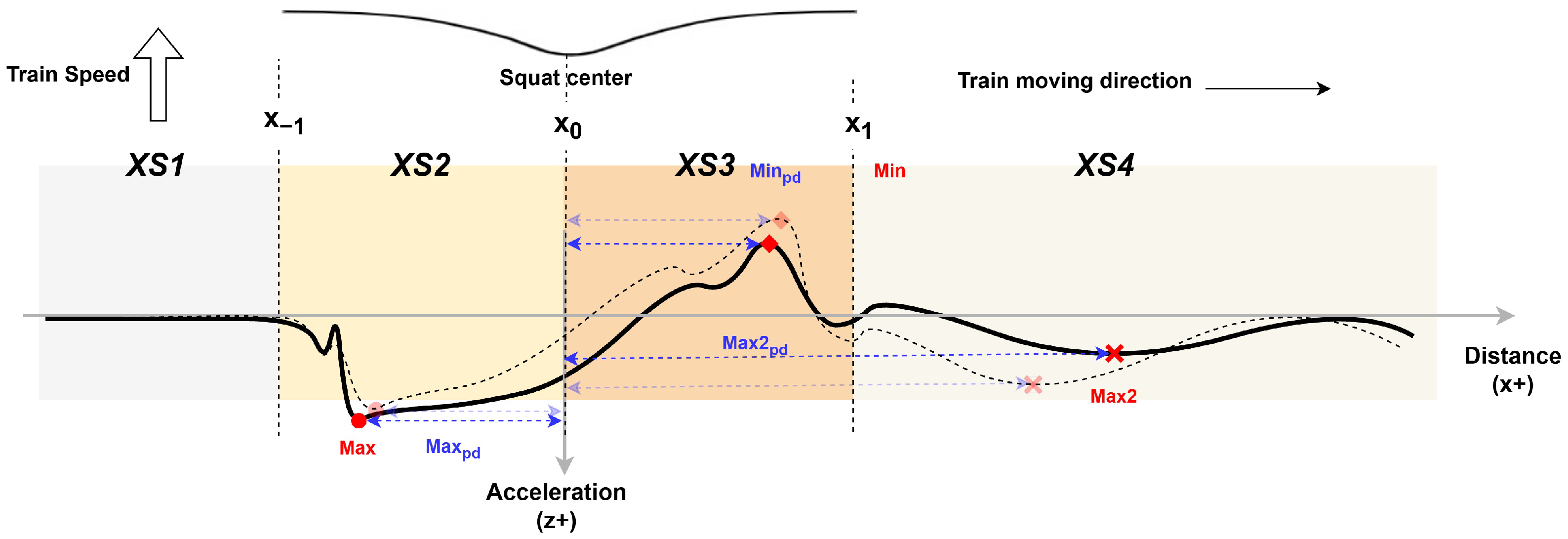
4.1. Mechanism
4.1.1. Acceleration Response
4.1.2. Influencing Factors
- Squat Length
- Squat Depth
- Train Speed
4.2. Squat Detection
4.2.1. Qualitative Analysis
4.2.2. Squat Center
4.2.3. Squat Length
4.3. Suggestions
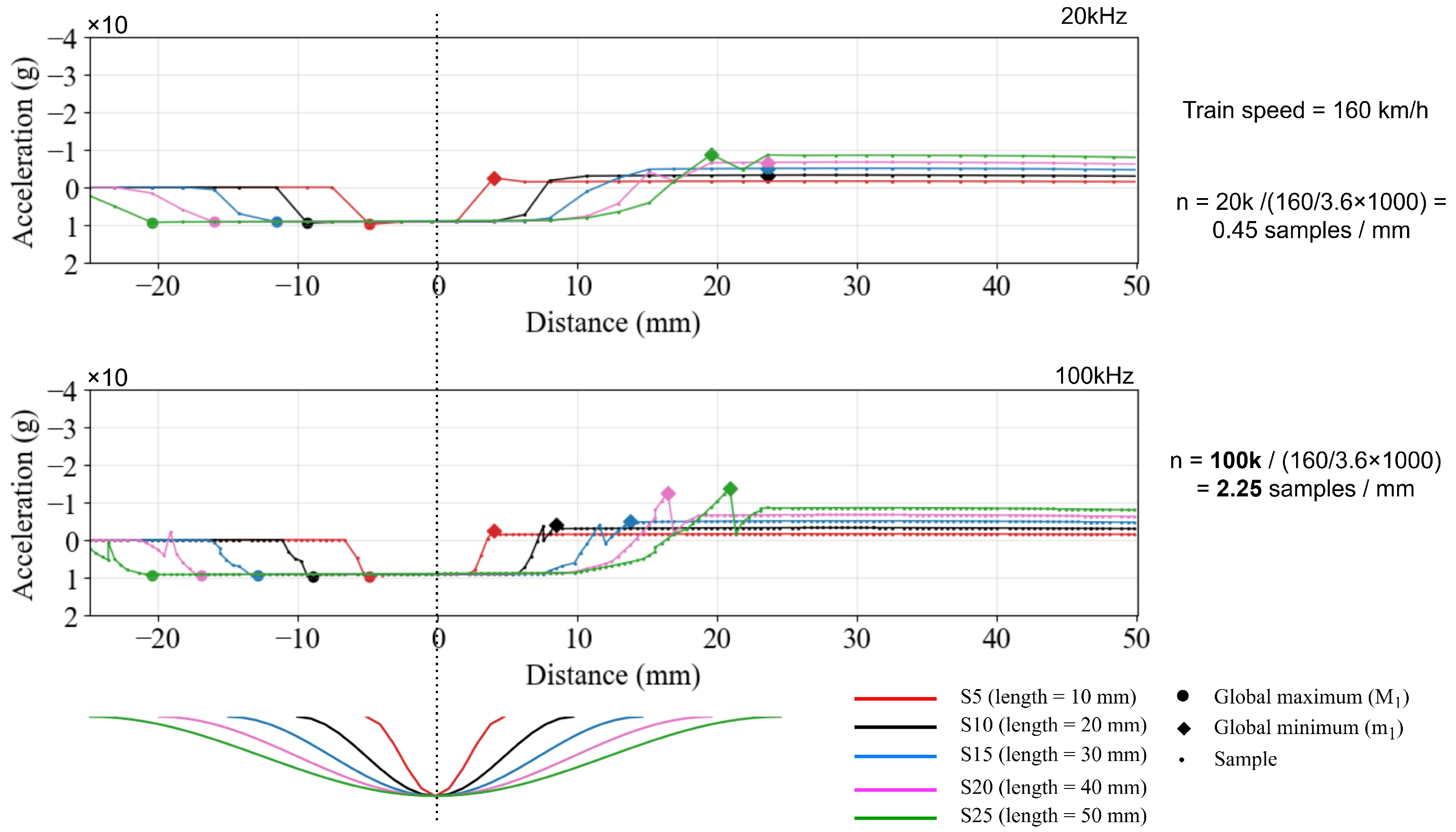
4.3.1. Squat Width Detection
4.3.2. Sensor Selection
4.3.3. Optimal Train Speeds
4.4. Limitations
5. Conclusions
- Sensor Placement and Train Speed: Accelerometers positioned on the first wheel set near the wheel–rail contact points exhibited the highest sensitivity to squat features. This supports the widely accepted principle in current research that sensor placement near the wheel–rail interface enhances detection accuracy. The analysis of results showed lower train speeds such as 20 km/h can induce a more pronounced correlation between squat features and vertical acceleration, especially when sensors were installed on the car body.
- Correlation Mechanism: A generalized mechanism linking squat geometry (length and depth) to vertical acceleration responses was established, despite variations in patterns due to changes in train speed and squat geometry. This mechanism, including three critical instants and four distinct response segments, concluded six evaluative indicators. These indicators are correlated with the train speed and squat geometry parameters to different degrees.
- Squat Detection Performance: Squat length exhibited the highest sensitivity compared to depth and width in defect identification. Leveraging two of the six evaluative indicators defined in the correlation mechanism, the proposed method successfully localized squats and quantified squat length in case studies, achieving 90% accuracy across all tested train speeds. This speed-invariant reliability underscores the found mechanism and the introduced method’s robustness and practical applicability for real-world rail maintenance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NDT | Non-Destructive Testing |
| RCF | Rolling Contact Fatigue |
| S&C | Switches and Crossings |
| ABA | Axle Box Acceleration |
| KPF | Kontaktpunktsfunktion (Swedish), Contact Point Function |
| DOF | Degree of Freedom |
| TSIM | Time simulation |
| OSN | Object and Serial Number |
| FFT | Fast Fourier Transform |
| DAQ | Data Acquisition |
Appendix A
| OSN | Coordinates (X,Y,Z) Unit: Meter | OSN | Coordinates (X,Y,Z) Unit: Meter |
|---|---|---|---|
| car_1_111 | bog_1_111 | ||
| car_1_121 | bog_1_121 | ||
| car_1_131 | bog_1_131 | ||
| car_1_112 | bog_1_112 | ||
| car_1_122 | bog_1_122 | ||
| car_1_132 | bog_1_132 | ||
| car_1_113 | bog_1_211 | ||
| car_1_123 | bog_1_221 | ||
| car_1_133 | bog_1_231 | ||
| car_1_211 | bog_1_212 | ||
| car_1_221 | bog_1_222 | ||
| car_1_231 | bog_1_232 | ||
| car_1_212 | bog_1_311 | ||
| car_1_222 | bog_1_321 | ||
| car_1_232 | bog_1_331 | ||
| car_1_213 | bog_1_312 | ||
| car_1_223 | bog_1_322 | ||
| car_1_233 | bog_1_332 | ||
| car_1_311 | bog_2_111 | ||
| car_1_321 | bog_2_121 | ||
| car_1_331 | bog_2_131 | ||
| car_1_312 | bog_2_112 | ||
| car_1_322 | bog_2_122 | ||
| car_1_332 | bog_2_132 | ||
| car_1_313 | bog_2_211 | ||
| car_1_323 | bog_2_221 | ||
| car_1_333 | bog_2_231 | ||
| car_1_411 | bog_2_212 | ||
| car_1_421 | bog_2_222 | ||
| car_1_431 | bog_2_232 | ||
| car_1_412 | bog_2_211 | ||
| car_1_422 | bog_2_221 | ||
| car_1_432 | bog_2_231 | ||
| car_1_413 | bog_2_212 | ||
| car_1_423 | bog_2_222 | ||
| car_1_433 | bog_2_232 | ||
| car_1_511 | axl_11_111 | ||
| car_1_521 | axl_11_121 | ||
| car_1_531 | axl_11_131 | ||
| car_1_512 | axl_12_111 | ||
| car_1_522 | axl_12_121 | ||
| car_1_532 | axl_12_131 | ||
| car_1_513 | axl_21_111 | ||
| car_1_523 | axl_21_121 | ||
| car_1_533 | axl_21_131 | ||
| axl_22_111 | |||
| axl_22_121 | |||
| axl_22_131 |


References
- The Organisation for Economic Co-operation and Development (OECD). Rail infrastructure maintenance spending. In Proceedings of the International Transport Forum, Leipzig, Germany, 21–24 May 2024. [Google Scholar]
- Mićić, M.; Brajović, L.; Lazarević, L.; Popović, Z. Inspection of RCF rail defects–Review of NDT methods. Mech. Syst. Signal Process. 2023, 182, 109568. [Google Scholar] [CrossRef]
- Kou, L. A review of research on detection and evaluation of the rail surface defects. Acta Polytech. Hung. 2022, 19, 167–186. [Google Scholar] [CrossRef]
- Popović, Z.; Lazarević, L.; Mićić, M.; Brajović, L. Critical analysis of RCF rail defects classification. Transp. Res. Procedia 2022, 63, 2550–2561. [Google Scholar] [CrossRef]
- Cannon, D.; Edel, K.O.; Grassie, S.; Sawley, K. Rail defects: An overview. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 865–886. [Google Scholar] [CrossRef]
- Magel, E.; Mutton, P.; Ekberg, A.; Kapoor, A. Rolling contact fatigue, wear and broken rail derailments. Wear 2016, 366, 249–257. [Google Scholar] [CrossRef]
- Palli, S.; Koona, R. Derailment causes of railway vehicle and its prevention. Int. J. Technol. Res. Eng. 2018, 5, 3735–3740. [Google Scholar]
- Gong, W.; Akbar, M.F.; Jawad, G.N.; Mohamed, M.F.P.; Wahab, M.N.A. Nondestructive testing technologies for rail inspection: A review. Coatings 2022, 12, 1790. [Google Scholar] [CrossRef]
- Xiong, L.; Jing, G.; Wang, J.; Liu, X.; Zhang, Y. Detection of rail defects using NDT methods. Sensors 2023, 23, 4627. [Google Scholar] [CrossRef]
- Komarasamy, D.; Iyapparaja, M.; Mohana, S.S.; Cibi, C.M.; Tibba, F.; Gayathri, R. Detailed Study on Various Techniques for Detecting Railway Track Anomaly. In Proceedings of the 2024 Second International Conference on Emerging Trends in Information Technology and Engineering (ICETITE), Ordos, China, 21–23 June 2024; pp. 1–10. [Google Scholar]
- Mićić, M.; Brajović, L.; Pustovgar, A. Methodology for statistical analysis of squat rail defects. In Proceedings of the XVIII Scientific-Expert Conference on Railways-RAILCON 18, Niš, Serbia, 11–12 October 2018; pp. 157–160. [Google Scholar]
- Al-Juboori, A.A.A. Mechanisms of Squat Initiation and Propagation on Rail Surfaces. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 2020. [Google Scholar]
- Popović, Z.; Radović, V. Analysis of cracking on running surface of rails. Gradevinar 2013, 65, 251–259. [Google Scholar]
- International Union of Railways (UIC). UIC Code 712; International Union of Railways: Paris, France, 2002. [Google Scholar]
- Bane NOR. Catalogue of Rail Faults; Bane NOR: Oslo, Norway, 2023. [Google Scholar]
- Li, Z.; Molodova, M.; Núñez, A.; Dollevoet, R. Improvements in axle box acceleration measurements for the detection of light squats in railway infrastructure. IEEE Trans. Ind. Electron. 2015, 62, 4385–4397. [Google Scholar] [CrossRef]
- Li, Z.; Dollevoet, R.; Molodova, M.; Zhao, X. Squat growth—Some observations and the validation of numerical predictions. Wear 2011, 271, 148–157. [Google Scholar] [CrossRef]
- Zuo, Y.; Lundberg, J.; Najeh, T.; Rantatalo, M.; Odelius, J. Squat Detection of Railway Switches and Crossings Using Point Machine Vibration Measurements. Sensors 2023, 23, 3666. [Google Scholar] [CrossRef]
- Reetz, S.; Najeh, T.; Lundberg, J.; Groos, J. Analysis of local track discontinuities and defects in railway switches based on track-side accelerations. Sensors 2024, 24, 477. [Google Scholar] [CrossRef]
- Hoelzl, C.; Arcieri, G.; Ancu, L.; Banaszak, S.; Kollros, A.; Dertimanis, V.; Chatzi, E. Fusing expert knowledge with monitoring data for condition assessment of railway welds. Sensors 2023, 23, 2672. [Google Scholar] [CrossRef] [PubMed]
- Pieringer, A.; Stangl, M.; Rothhämel, J.; Tielkes, T. Acoustic monitoring of rail faults in the German railway network. In Noise and Vibration Mitigation for Rail Transportation Systems, Proceedings of the 13th International Workshop on Railway Noise, Ghent, Belgium, 16–20 September 2019; Springer: Berlin/Heidelberg, Germany, 2021; pp. 242–250. [Google Scholar]
- Cho, H.; Park, J. Study of rail squat characteristics through analysis of train axle box acceleration frequency. Appl. Sci. 2021, 11, 7022. [Google Scholar] [CrossRef]
- Wei, X.; Yin, X.; Hu, Y.; He, Y.; Jia, L. Squats and corrugation detection of railway track based on time-frequency analysis by using bogie acceleration measurements. Veh. Syst. Dyn. 2020, 58, 1167–1188. [Google Scholar] [CrossRef]
- Jamshidi, A.; Núñez, A.; Dollevoet, R.; Li, Z. Robust and predictive fuzzy key performance indicators for condition-based treatment of squats in railway infrastructures. J. Infrastruct. Syst. 2017, 23, 04017006. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Ishida, M. Rail squats: Understand its causes, severity, and non-destructive evaluation techniques. In Proceedings of the 20th National Convention on Civil Engineering, Pattaya, Thailand, 8–10 July 2015; pp. 8–10. [Google Scholar]
- Zhu, H.; Li, H.; Al-Juboori, A.; Wexler, D.; Lu, C.; McCusker, A.; McLeod, J.; Pannila, S.; Barnes, J. Understanding and treatment of squat defects in a railway network. Wear 2020, 442, 203139. [Google Scholar] [CrossRef]
- Bedoya-Zapata, Á.; Rojas-Parra, S.; Díaz-Mazo, J.; García-Jiménez, J.; López-Londoño, J.; Vergara-Puello, R.; Molina, L.; Santa-Marín, J.; Toro, A.; Mesaritis, M.; et al. Case study: Understanding the formation of squat-type defects in a metropolitan railway. Eng. Fail. Anal. 2021, 123, 105325. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Soman, R.; Malinowski, P. Optimization of sensor placement for structural health monitoring: A review. Struct. Health Monit. 2019, 18, 963–988. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, L. Computational methodologies for optimal sensor placement in structural health monitoring: A review. Struct. Health Monit. 2020, 19, 1287–1308. [Google Scholar] [CrossRef]
- Dumitriu, M. Fault detection of damper in railway vehicle suspension based on the cross-correlation analysis of bogie accelerations. Mech. Ind. 2019, 20, 102. [Google Scholar] [CrossRef]
- Zhang, C.; Shen, S.; Huang, H.; Wang, L. Estimation of the vehicle speed using cross-correlation algorithms and MEMS wireless sensors. Sensors 2021, 21, 1721. [Google Scholar] [CrossRef]
- Hu, Z.; Lau, A.; Dai, J.; Frøseth, G.T. Identification of optimal accelerometer placement on trains for railway switch wear monitoring via multibody simulation. Front. Built Environ. 2024, 10, 1396578. [Google Scholar] [CrossRef]
- Persson, I. GENSYS Manual; GENSYS: Stockholm, Sweden, 2024. [Google Scholar]
- Pålsson, B.A. Optimisation of Railway Switches and Crossings. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2014. [Google Scholar]
- Andersson, E.; Berg, M.; Stichel, S. Rail Vehicle Dynamics; Centre for Research and Education in Railway Engineering, Railway Group KTH: Stockholm, Sweden, 2007. [Google Scholar]
- Andersson, R.; Torstensson, P.T.; Kabo, E.; Larsson, F. The influence of rail surface irregularities on contact forces and local stresses. Veh. Syst. Dyn. 2015, 53, 68–87. [Google Scholar] [CrossRef]
- Real, T.; Montrós, J.; Montalbán, L.; Zamorano, C.; Real, J. Design and validation of a railway inspection system to detect lateral track geometry defects based on axle-box accelerations registered from in-service trains. J. Vibroeng. 2014, 16, 210–224. [Google Scholar]
- Chudzikiewicz, A.; Bogacz, R.; Kostrzewski, M.; Konowrocki, R. Condition monitoring of railway track systems by using acceleration signals on wheel set axle-boxes. Transport 2018, 33, 555–566. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, H.; Gong, D.; Zhou, J.; Xiao, Z. Quantitative detection of vertical track irregularities under non-stationary conditions with variable vehicle speed. Sensors 2024, 24, 3804. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Sun, S.; Fei, Y.; Niu, L.; Tian, X.; Ke, Z.; Dai, P.; Liang, Z. An approach for the estimation of lateral track irregularity using axle-box acceleration. Eng. Comput. 2023, 40, 3036–3054. [Google Scholar] [CrossRef]
- Sun, X.; Yang, F.; Shi, J.; Ke, Z.; Zhou, Y. On-board detection of longitudinal track irregularity via axle box acceleration in HSR. IEEE Access 2021, 9, 14025–14037. [Google Scholar] [CrossRef]




| Parameter | Values | Units |
|---|---|---|
| car body mass | 36,467 | kg |
| Bogie mass | 5192 | kg |
| wheel set mass | 1599 | kg |
| Primary suspension, vertical springs | N/m | |
| Primary suspension, vertical dampers | Ns/m | |
| Secondary suspension, vertical springs | N/m | |
| Secondary suspension, vertical dampers | Ns/m | |
| Secondary suspension, air suspensions | Ns/m | |
| Secondary suspension, bump stops | N/m | |
| car body-bogie mass center distance | 9.5 | m |
| Bogie-wheel set mass center distance | 1.35 | m |
| wheel set radius | 0.45 | m |
| Wagon coupling, longitudinal springs | N/m | |
| Wagon coupling, longitudinal dampers | Ns/m | |
| Track-ground coupling, vertical springs | N/m | |
| Track-ground coupling, vertical damping | Ns/m | |
| Track-ground coupling, lateral springs | N/m | |
| Track-ground coupling, lateral damping | Ns/m | |
| wheel–rail model | wr_coupl_pe4; fasim lookup table | |
| Eigen frequency (vertical bending motion mode) | 9.9 | Hz |
| Eigen frequency (lateral bending motion mode) | 9.8 | Hz |
| Eigen frequency (cross-sectional shear motion mode) | 12.2 | Hz |
| Eigen frequency (longitudinal bending motion mode) | 12.7 | Hz |
| Train Speed (km/h) | ||||||
|---|---|---|---|---|---|---|
| 20 | O | △ | △ | O | O | × |
| 40 | △ | △ | O | O | O | × |
| 60 | △ | O | O | O | O | × |
| 80 | O | O | O | O | O | × |
| 100 | O | O | O | O | O | × |
| 120 | O | △ | O | O | O | × |
| 140 | O | △ | O | O | O | × |
| 160 | O | △ | O | O | O | × |
| Train Speed (km/h) | ||||||
|---|---|---|---|---|---|---|
| 20 | × | × | △ | △ | △ | × |
| 40 | × | × | △ | △ | △ | × |
| 60 | × | △ | O | △ | △ | × |
| 80 | × | △ | O | △ | △ | × |
| 100 | × | △ | O | △ | △ | × |
| 120 | × | △ | O | △ | △ | × |
| 140 | × | △ | O | △ | △ | × |
| 160 | × | △ | O | △ | △ | × |
| Squat Length (mm) (Case) | |||||||
|---|---|---|---|---|---|---|---|
|
10
(S5) |
20
(S10) |
30
(S15) |
40
(S20) |
50
(S25) | |||
| Train Speed (km/h) | |||||||
| 20 | 0.00 (100.00%) | 0.84 (95.83%) | −0.56 (98.15%) | −1.11 (97.23%) | −1.11 (97.78%) | ||
| 40 | 0.61 (93.90%) | 0.78 (96.13%) | 0.78 (97.40%) | 1.45 (96.39%) | 2.00 (96.00%) | ||
| 60 | 0.92 (90.85%) | 0.84 (95.83%) | 1.08 (96.40%) | 1.58 (96.05%) | 1.83 (96.34%) | ||
| 80 | 0.45 (95.55%) | 0.78 (96.13%) | 0.56 (98.15%) | 1.34 (96.66%) | 1.34 (97.33%) | ||
| 100 | 0.28 (97.25%) | 0.14 (99.33%) | 0.42 (98.60%) | 0.84 (97.91%) | 1.12 (97.77%) | ||
| 120 | −0.17 (98.30%) | 0.00 (100.00%) | −0.17 (99.45%) | 0.50 (98.75%) | 0.66 (98.67%) | ||
| 140 | −0.31 (96.95%) | −0.31 (98.48%) | −0.31 (98.97%) | 0.08 (99.79%) | 0.28 (99.44%) | ||
| 160 | −0.45 (97.78%) | −0.23 (98.88%) | 0.44 (98.52%) | −0.23 (99.44%) | 0.23 (99.55%) | ||
| Squat Length (mm) (Case) | |||||||
|---|---|---|---|---|---|---|---|
|
10
(S5) |
20
(S10) |
30
(S15) |
40
(S20) |
50
(S25) | |||
| Train Speed (km/h) | |||||||
| 20 | 7.78 (77.80%) | 16.11 (80.55%) | 21.11 (70.37%) | 27.78 (69.45%) | 36.66 (73.32%) | ||
| 40 | 8.78 (87.80%) | 16.67 (83.35%) | 24.44 (81.47%) | 33.11 (82.78%) | 40.22 (80.44%) | ||
| 60 | 8.83 (88.30%) | 16.67 (83.35%) | 24.50 (81.67%) | 33.50 (83.75%) | 41.00 (82.00%) | ||
| 80 | 8.89 (88.90%) | 16.67 (83.35%) | 24.67 (82.23%) | 33.33 (83.33%) | 41.33 (82.66%) | ||
| 100 | 8.89 (88.90%) | 16.39 (81.95%) | 24.72 (82.40%) | 33.89 (84.73%) | 41.11 (82.22%) | ||
| 120 | 9.00 (90.00%) | 16.66 (83.30%) | 24.33 (81.10%) | 33.66 (84.15%) | 41.33 (82.66%) | ||
| 140 | 8.95 (89.50%) | 16.73 (83.65%) | 24.50 (81.67%) | 33.05 (82.63%) | 41.22 (82.44%) | ||
| 160 | 8.89 (88.90%) | 17.33 (86.65%) | 26.67 (88.90%) | 33.33 (83.33%) | 41.33 (82.66%) | ||
| Sensor Type | Measurement Range (g) | Sensitivity (mV/g) | Resolution (g) | Sample Frequency (kHz) | References |
|---|---|---|---|---|---|
| PCB 354C02 | ±500 | 10 mV/g | 0.0005 g | 20 kHz | [37] |
| VIS 311A | ±50 | 100 mV/g | 0.00035 g | 20 kHz | [38] |
| J1 3510 | ±250 | 20 mV/g | 0.005 g | 20 kHz | [39] |
| CARS CS01AC | ±200 | 25 mV/g | 0.0005 g | 5 kHz | [40,41] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Lau, A. A Numerical Simulation Study on Vertical Vibration Response for Rail Squat Detection with a Train in Regular Traffic. Infrastructures 2025, 10, 313. https://doi.org/10.3390/infrastructures10110313
Hu Z, Lau A. A Numerical Simulation Study on Vertical Vibration Response for Rail Squat Detection with a Train in Regular Traffic. Infrastructures. 2025; 10(11):313. https://doi.org/10.3390/infrastructures10110313
Chicago/Turabian StyleHu, Zhicheng, and Albert Lau. 2025. "A Numerical Simulation Study on Vertical Vibration Response for Rail Squat Detection with a Train in Regular Traffic" Infrastructures 10, no. 11: 313. https://doi.org/10.3390/infrastructures10110313
APA StyleHu, Z., & Lau, A. (2025). A Numerical Simulation Study on Vertical Vibration Response for Rail Squat Detection with a Train in Regular Traffic. Infrastructures, 10(11), 313. https://doi.org/10.3390/infrastructures10110313







