Effect of Ground Motion Duration and Frequency Characteristics on the Probabilistic Risk Assessment of a Concrete Gravity Dam
Abstract
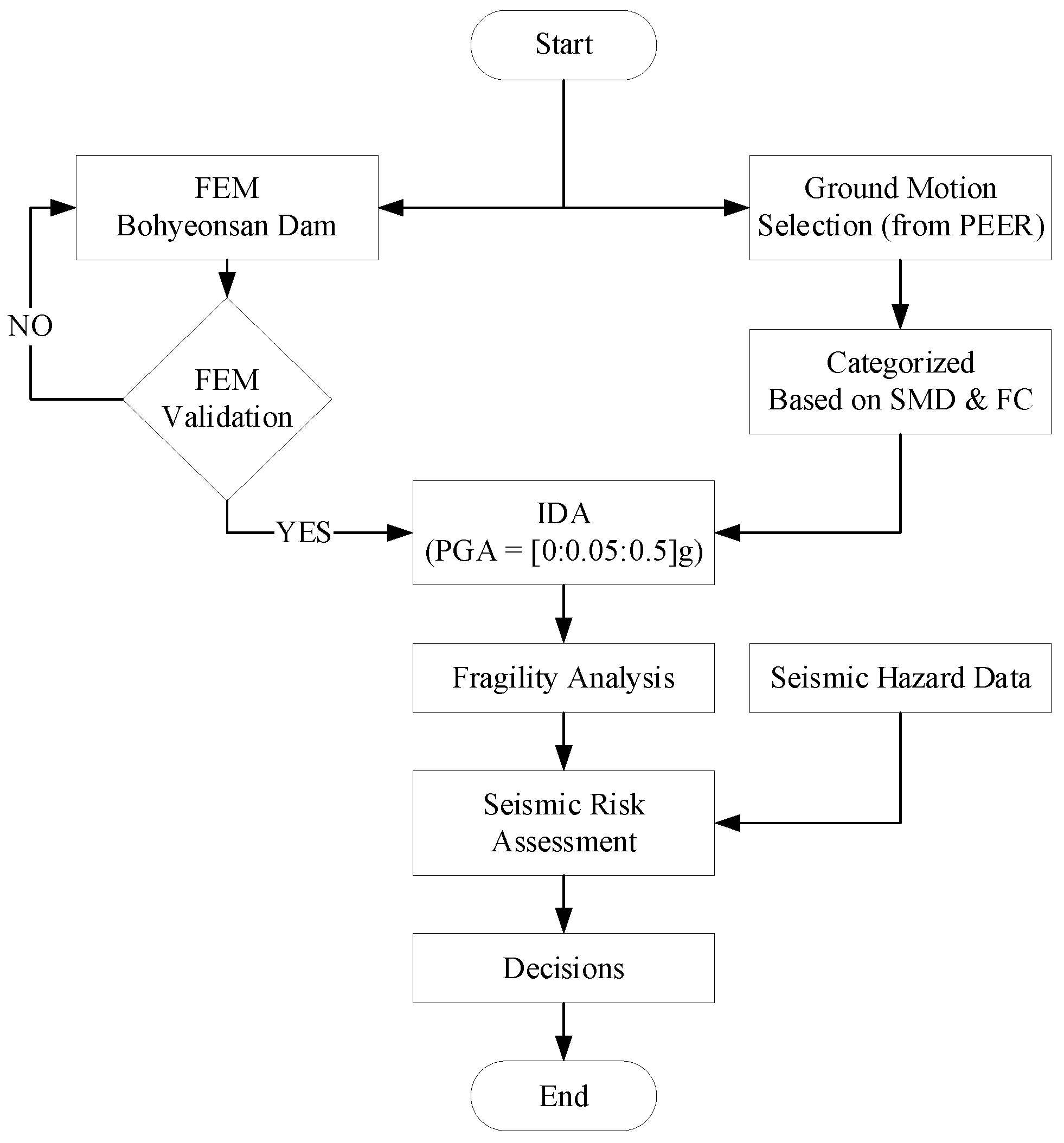
1. Introduction
2. Numerical Modeling of CGDs
2.1. Bohyeonsan Dam Detailing
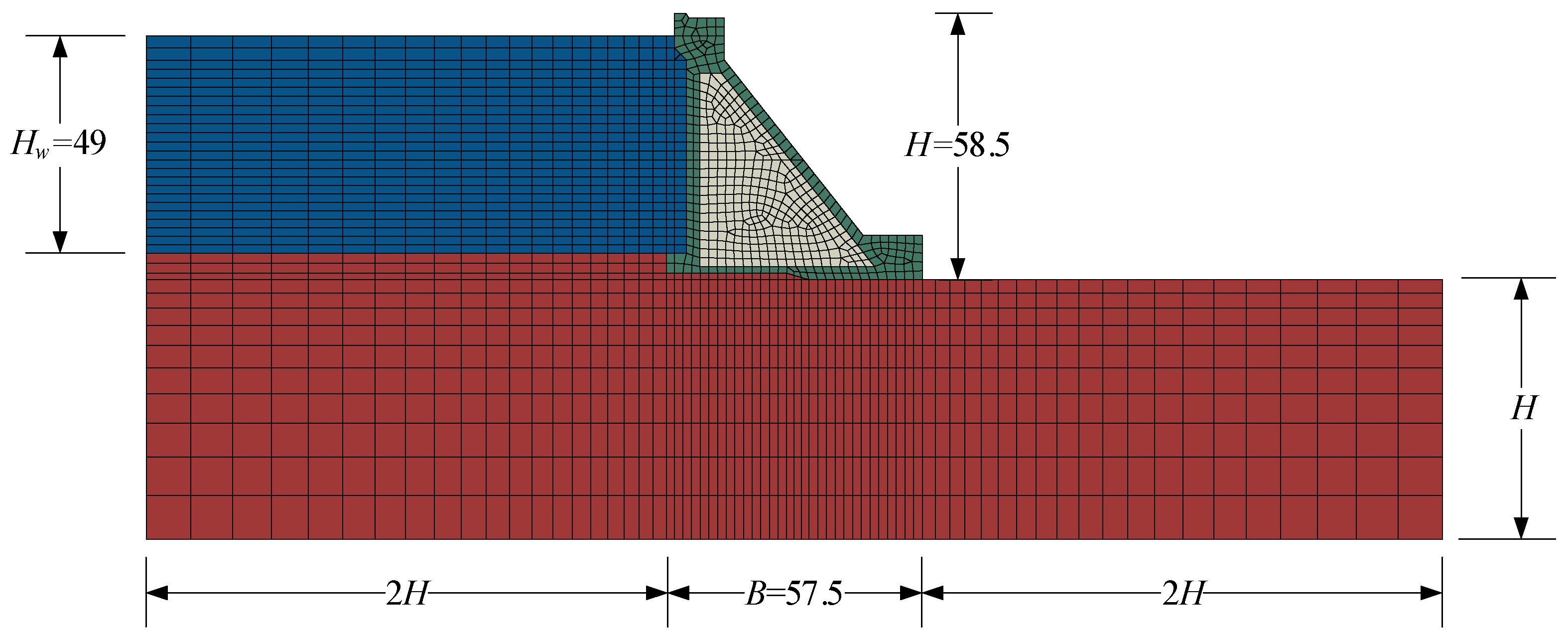
2.2. Finite Element Modeling and Analysis
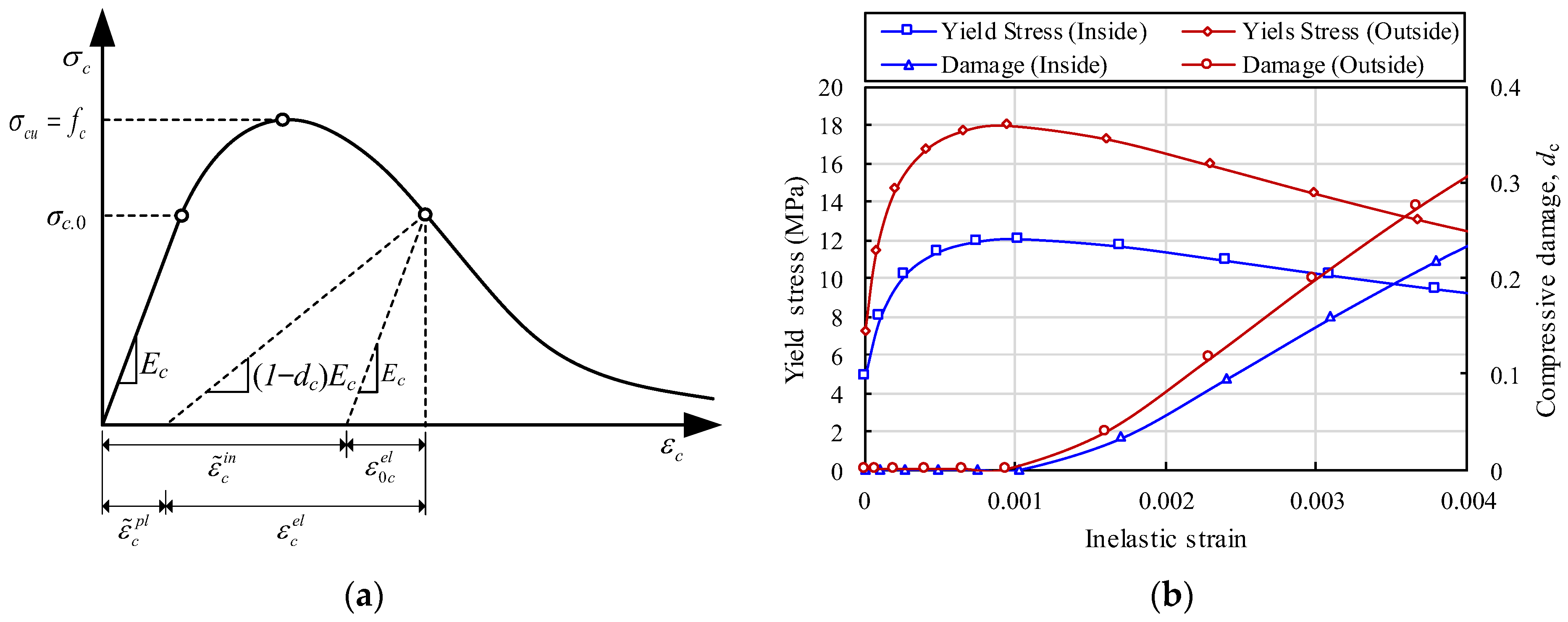
2.3. Material Modeling
2.4. FEM Evaluation
- FSI sign and coupling sanity check: Code/algorithm verification is used, where static hydrostatic preload recovers on the wet face, and dynamic reservoir uses acoustic elements with a non-reflecting boundary (impedance ), confirming pressure-to-traction transfer and normal-acceleration compatibility.
- Ground motion scaling loader: Ground motion scaling uses applied via amplitude and prescribed base acceleration; pre-checks confirm target PGA at each IDA level. Energy outputs (ALLIE/ALLKE/ALLAE) are physical.
- Mesh/time-step convergence: Mesh is graded (≤2 m near heel/toe and wet interface); automatic time-stepping resolves dominant periods. Stability under halved was confirmed on representative records.
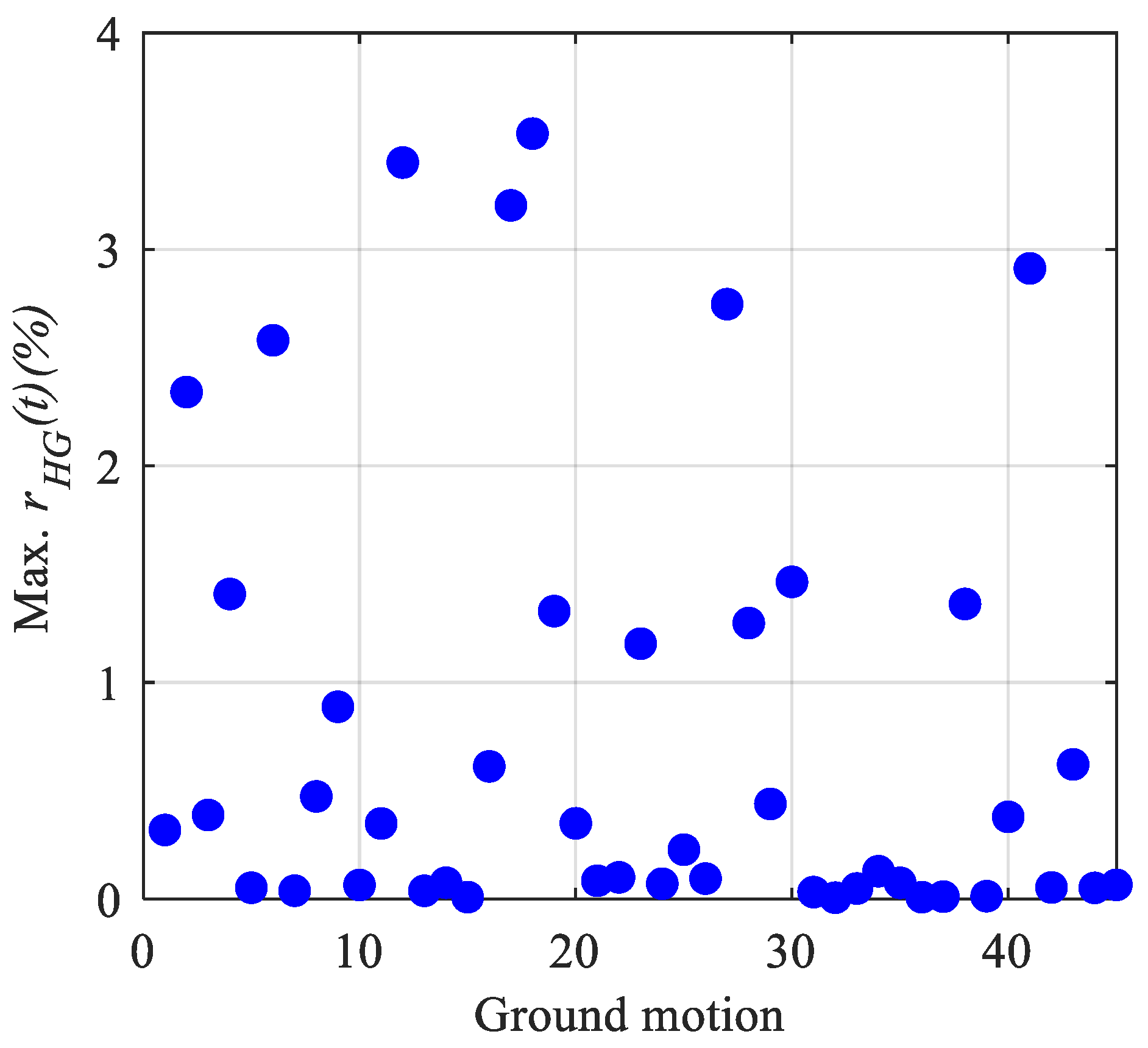
- Hourglass control: The hourglass-to-mechanical-energy ratio stayed below 5% (max 3.53% at 0.5 g), indicating negligible spurious modes.
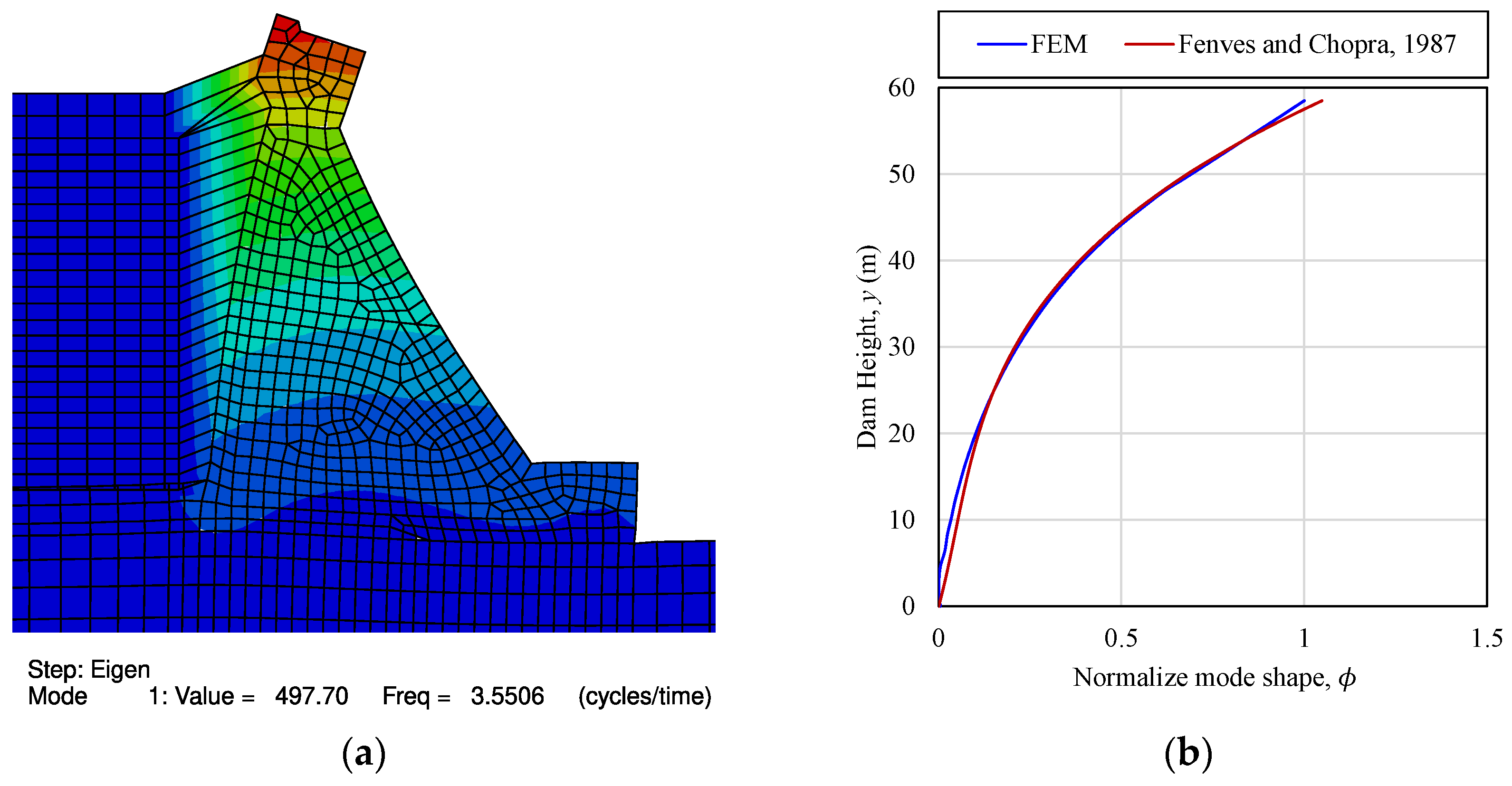
- Modal reasonableness: Finite element eigen frequency = 3.551 Hz agrees within ~10% with the Fenves and Chopra [46] analytical estimate of = 3.98 Hz; the first-mode shape matches the canonical profile.
- Model-form justification: A two-dimensional plane-strain DRF with acoustic reservoir and a foundation domain to ±2H (base fixed) is used; lateral , free represents stiff canyon confinement; far-reservoir impedance boundary emulates radiation damping. This captures global DRF coupling while omitting explicit contraction/lift–joint contact and vertical input; interpretation is bounded accordingly within the 0.05–0.50 g pre-collapse window.
- Due to the lack of original responses recorded from experimental data of the Bohyeonsan Dam, here, analytical/benchmark comparisons are carried out: fundamental frequency and mode-shape benchmarks are examined via the Fenves and Chopra method.
- Sources and classification: Aleatory record-to-record variability within duration/frequency bins was captured in fragility dispersion . Epistemic CDP parameters, foundation/boundary idealization, model form (2D), and hazard curve were used.
- Estimation (fragility): Binary exceedances from IDA are fit to a well-established lognormal fragility.
- Sensitivity: Group contrasts (LD/MD/SD; LF/MF/HF) quantify sensitivity to duration/frequency; qualitative checks note potential influence of lateral-boundary idealization and reservoir radiation modeling.
- Propagation to risk: Fragilities are convolved with the site hazard curve; crack propagation of fragility and hazard uncertainty is noted as a straightforward extension.
- Credibility statement: Comparative duration/frequency effects on drift-based fragility and risk for the Bohyeonsan monolith under 2D DRF are examined. Mesh/time-step/energy diagnostics are used, with an max of 3.53% (<5%); frequency and mode-shape benchmarks (~10% agreement); transparent fragility fitting with lognormal distribution; and a documented record of metadata and scaling. Applicability within the range for IM of 0.05–0.50 g was examined, with horizontal input, no joints/vertical, and 2D DRF with lateral confinement idealization.
3. Selection of Ground Motion
4. Results and Discussion
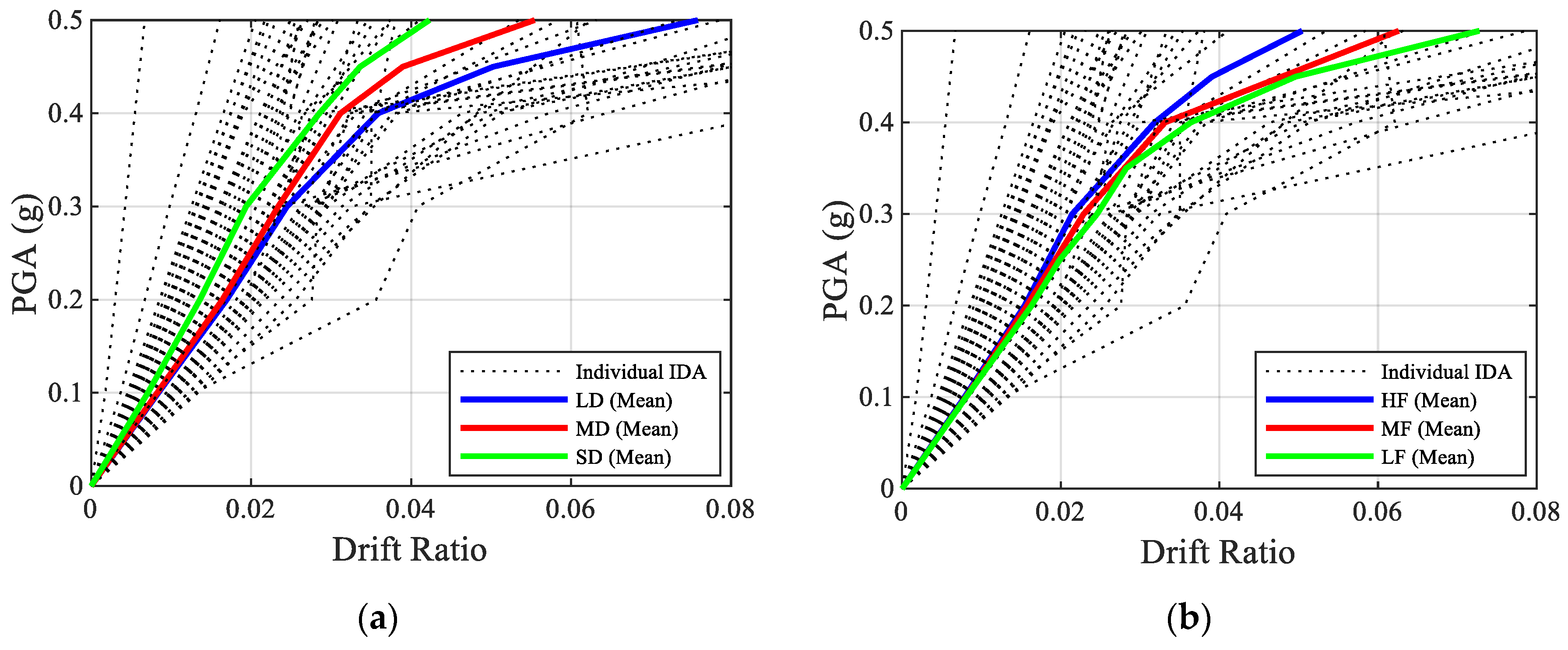
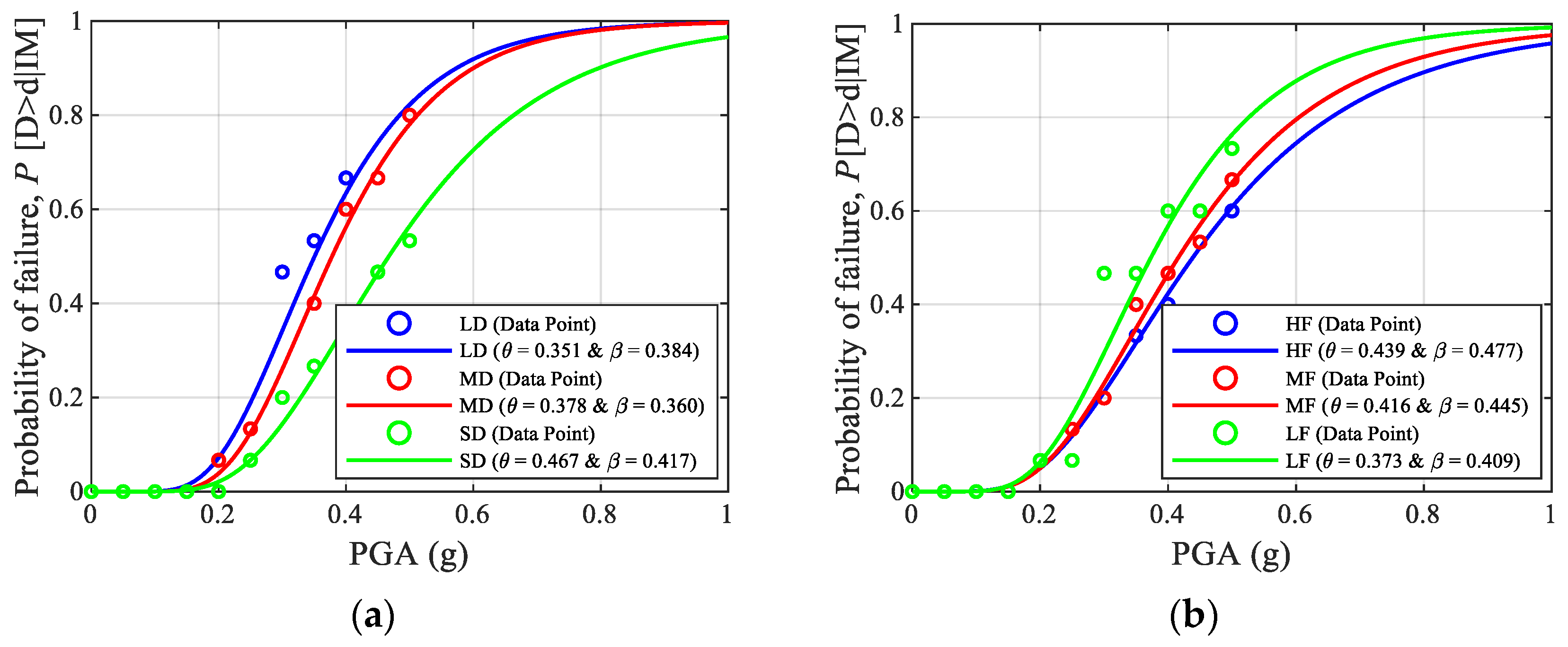
4.1. Fragility Analysis
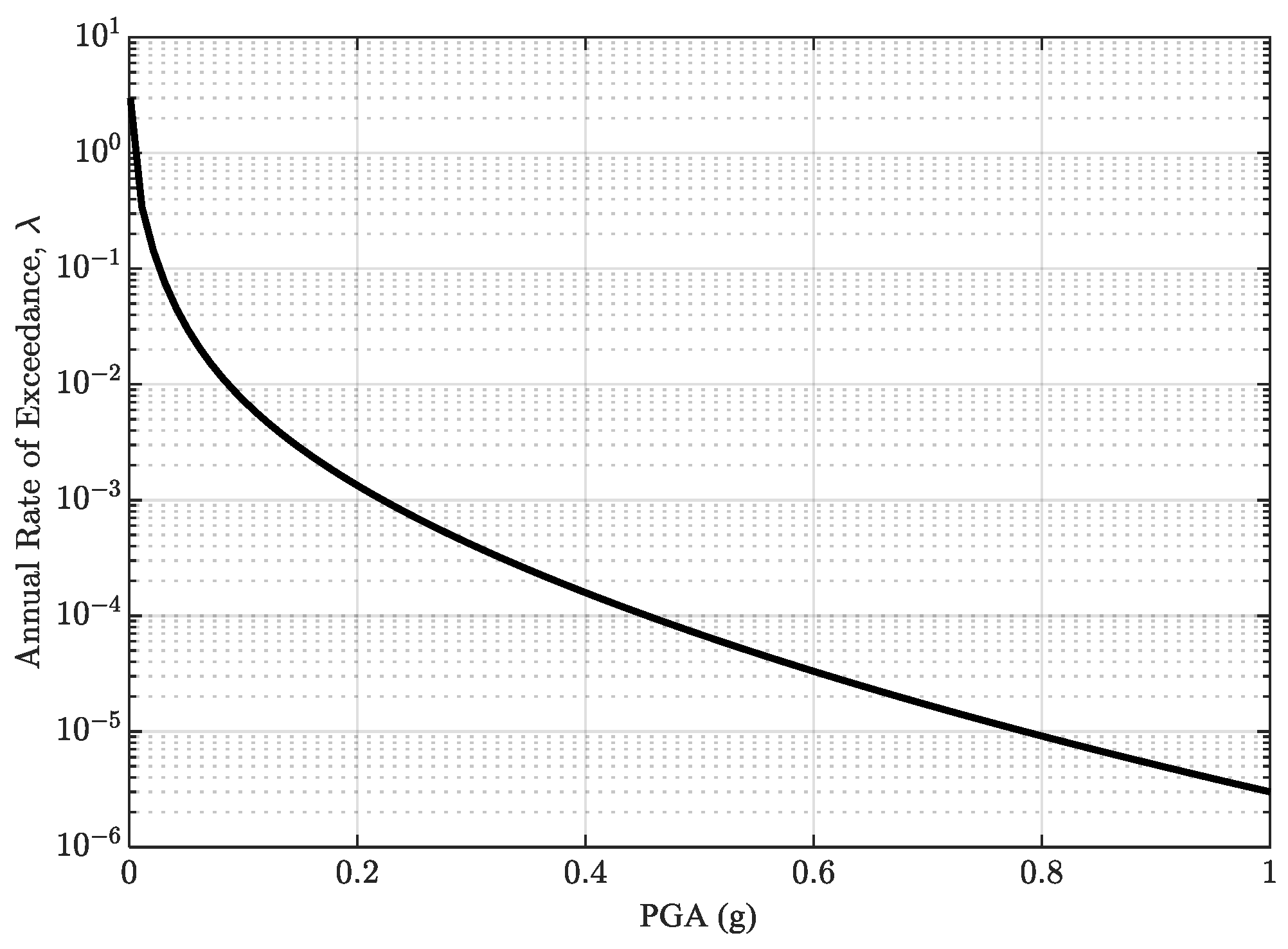
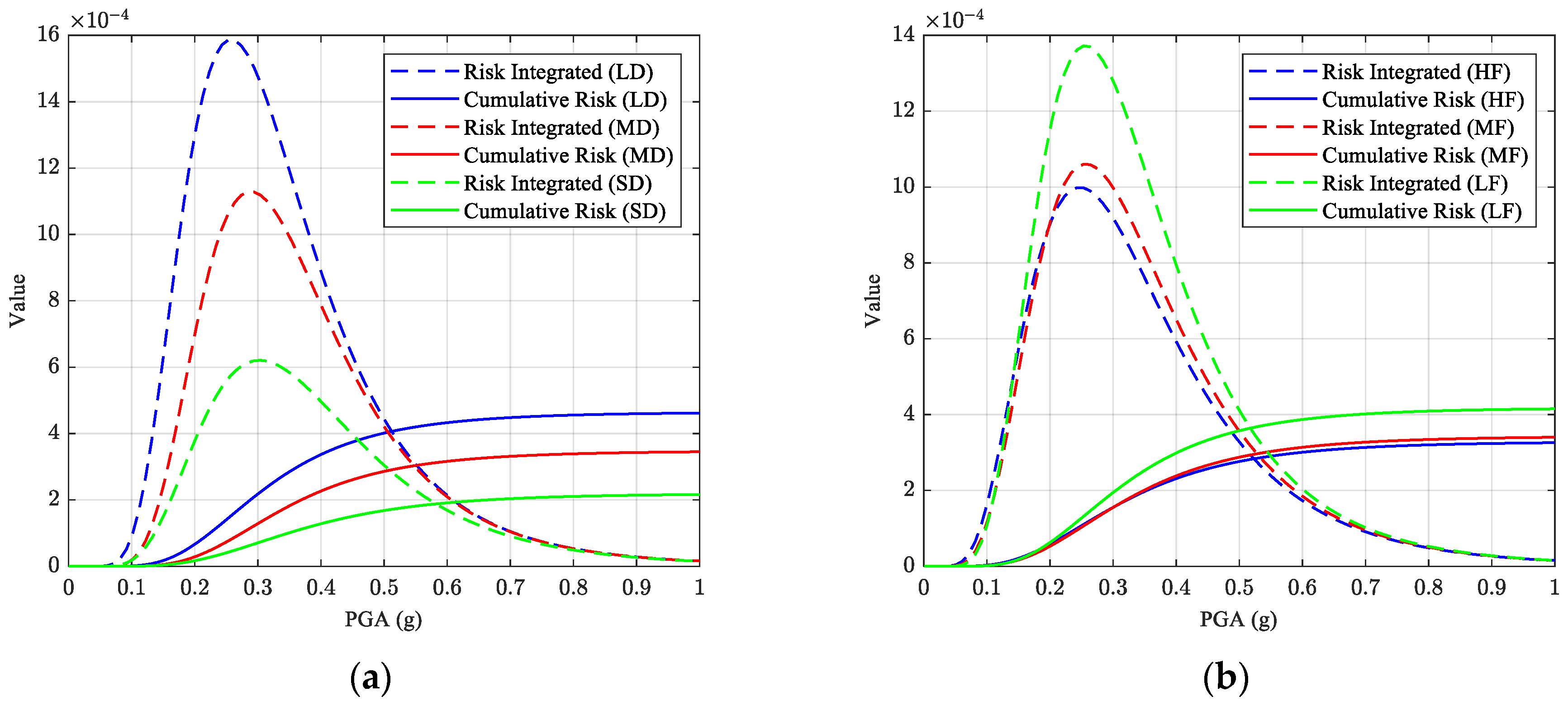
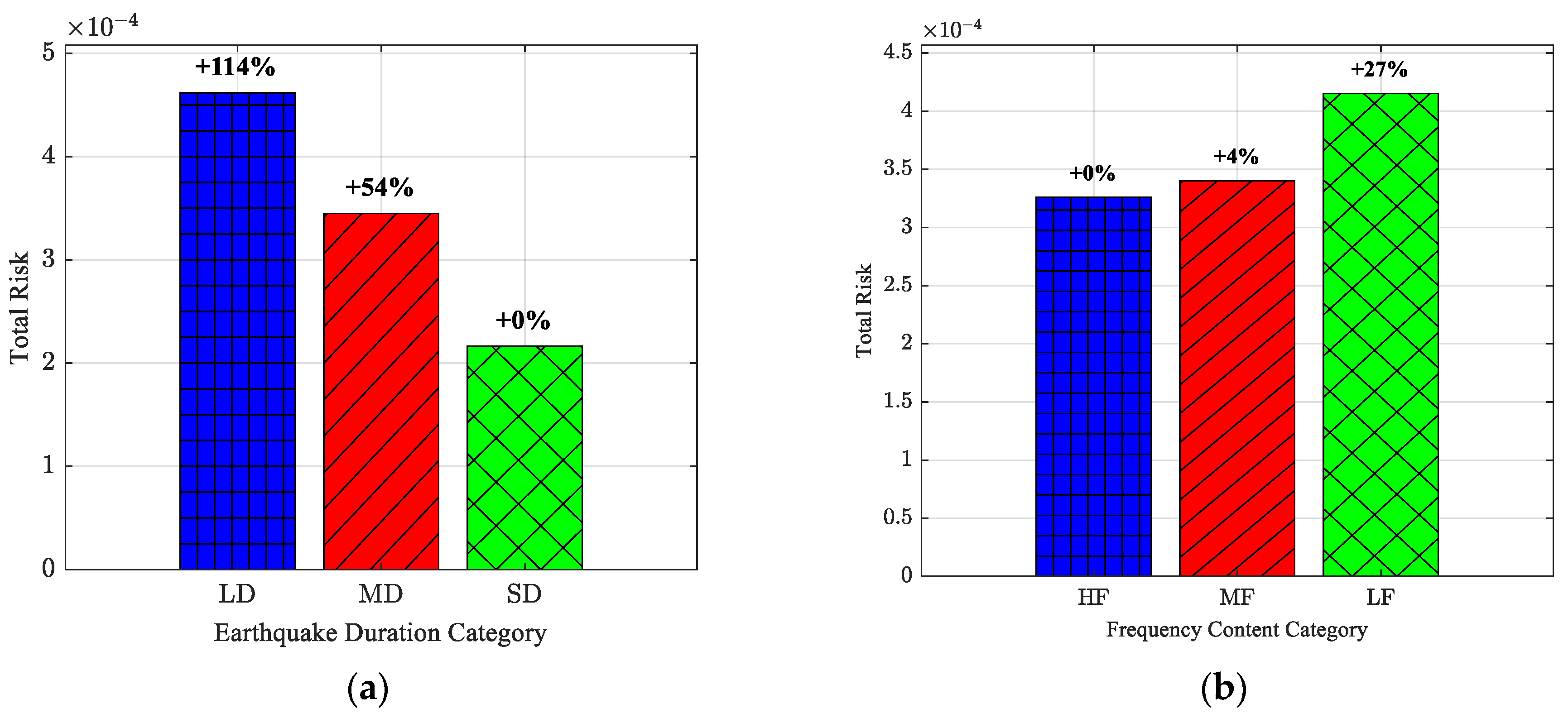
4.2. Seismic Risk Assessment
5. Conclusions
- ○
- Build duration- and frequency-stratified fragilities: Construct separate fragility curves for duration bins ∈{SD, MD, LD} (and, when needed, frequency bins ∈{HF, MF, LF}). Combine them with the site-specific hazard via , where is the annual frequency of exceeding the limit state and is the incremental hazard for motions in bin . When only the total hazard is available, use bin weights from PSHA deaggregation combined with a duration model to partition the hazard among SD/MD/LD. This “analyze once, reweight many” approach lets agencies reuse the same structural results under evolving PSHA inputs.
- ○
- IMs and reporting: Use PGA (or PGV where appropriate) as the primary IM and report it together with and PGA/PGV for each record group. Publish (median capacity) and (dispersion) per group (as in Figure 10), and provide risk computed by hazard convolution (Figure 12 and Figure 13). This makes the influence of duration/frequency explicit, not hidden inside a pooled curve.
- ○
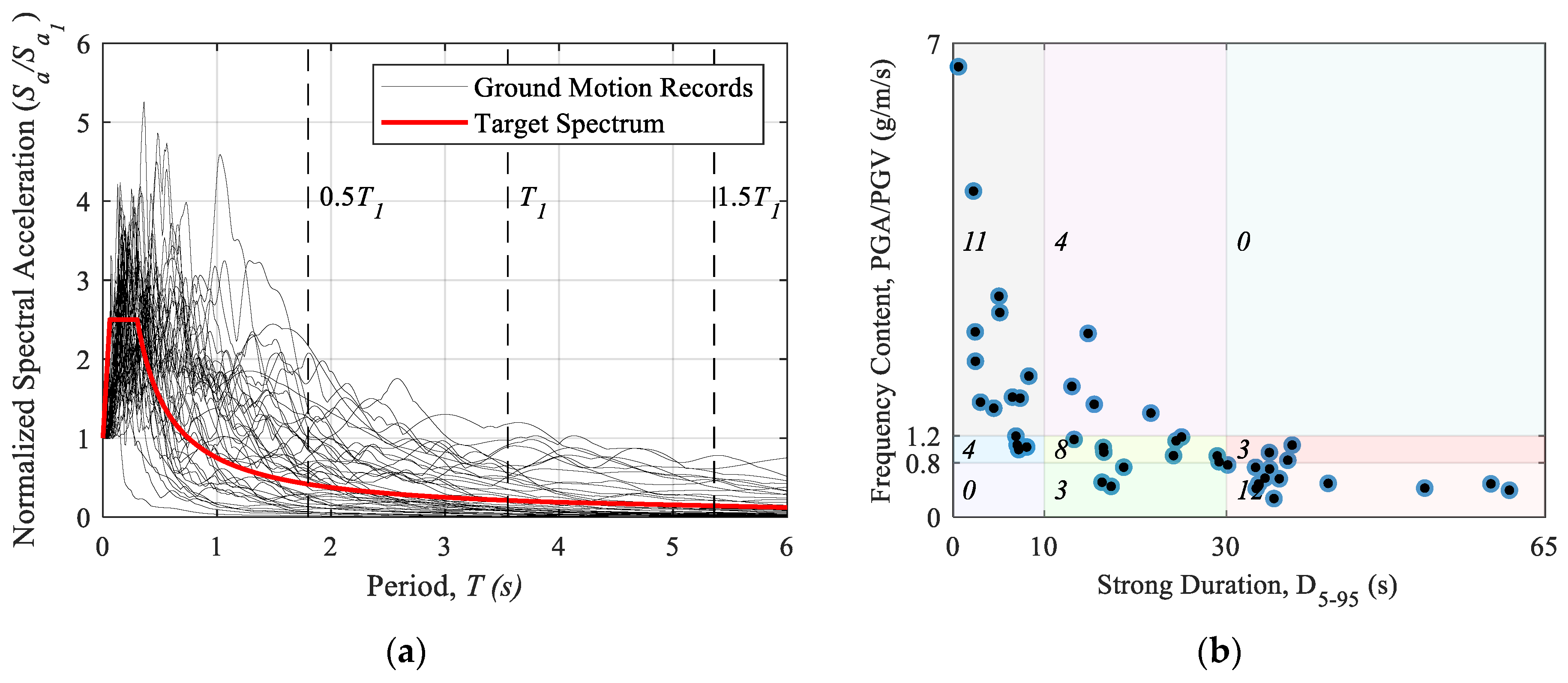
- Record selection for NLTHA: Curate recorded motions from the appropriate tectonic regime and site class; check spectral representativeness near against the code/site target (here, KDS 41 rock) without spectral matching so that duration and phase are preserved. Control the mix of SD/MD/LD and HF/MF/LF so the analysis set reflects the site-expected composition (see Table 3 and ).
- ○
- Dual design/assessment checks when long duration is non-negligible: If site deaggregation or regional knowledge indicates a non-trivial LD share (e.g., subduction-influenced or large-magnitude sources), verify performance against (i) the overall hazard-weighted fragility/risk and (ii) the LD-conditioned fragility/risk. Where the LD-conditioned check governs, prioritize mitigation that addresses cumulative-damage mechanisms.
- ○
- Communicate risk with clarity: In addition to a single annual exceedance value, report the contributions by group (e.g., LD vs. SD; LF vs. HF) so decision-makers see what portion of risk is driven by duration or low-frequency content. This facilitates targeted risk reduction and monitoring.
- ○
- Priorities for future work: Incorporate explicit contraction/lift–joint contact, vertical excitation, and selected 3D DRF effects to define a collapse limit state consistent with collapse-fragility frameworks; explore foundation heterogeneity (random-field properties and stratigraphic dip) and near-fault directivity when relevant. The comparative trends documented here—LD > MD > SD and LF > MF > HF—are expected to remain because they arise from cumulative-damage and quasi-resonance mechanisms identified in our results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nahar, T.T.; Cao, A.-T.; Kim, D. Risk assessment of aged concrete gravity dam subjected to material deterioration under seismic excitation. Int. J. Concr. Struct. Mater. 2020, 14, 53. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E. Seismic fragility analysis of concrete dams: A state-of-the-art review. Eng. Struct. 2016, 128, 374–399. [Google Scholar] [CrossRef]
- Yilmazturk, S.M.; Arici, Y.; Binici, B. Seismic assessment of a monolithic RCC gravity dam including three dimensional dam–foundation–reservoir interaction. Eng. Struct. 2015, 100, 137–148. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Zhang, Y.; Guo, L.; Wang, Y.; Thira Htun, T.T. Influences on the seismic response of a gravity dam with different foundation and reservoir modeling assumptions. Water 2021, 13, 3072. [Google Scholar] [CrossRef]
- Raghunandan, M.; Liel, A.B. Effect of ground motion duration on earthquake-induced structural collapse. Struct. Saf. 2013, 41, 119–133. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Brady, A.G. A study on the duration of strong earthquake ground motion. Bull. Seismol. Soc. Am. 1975, 65, 581–626. [Google Scholar] [CrossRef]
- Bommer, J.J.; MartÍNez-Pereira, A. The effective duration of earthquake strong motion. J. Earthq. Eng. 1999, 3, 127–172. [Google Scholar] [CrossRef]
- Chandramohan, R.; Baker, J.W.; Deierlein, G.G. Impact of hazard-consistent ground motion duration in structural collapse risk assessment. Earthq. Eng. Struct. Dyn. 2016, 45, 1357–1379. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, G.; Pang, B.; Du, C. The effects of strong motion duration on the dynamic response and accumulated damage of concrete gravity dams. Soil Dyn. Earthq. Eng. 2013, 45, 112–124. [Google Scholar] [CrossRef]
- Mohammadnezhad, H.; Saeednejad, N.; Mashayekhi, M. Statistical investigation of the influence of ground motion duration on concrete gravity dam responses by proposing a quantitative index. Structures 2023, 57, 105221. [Google Scholar] [CrossRef]
- Akköse, M.; Şimşek, E. Non-linear seismic response of concrete gravity dams to near-fault ground motions including dam-water-sediment-foundation interaction. Appl. Math. Model. 2010, 34, 3685–3700. [Google Scholar] [CrossRef]
- Ayati Ahmadi, A.; Noorzad, A.; MohammadNezhad, H.; Mirghasemi, A.A. Seismic fragility of rockfill dams with asphaltic concrete core. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 1585–1598. [Google Scholar] [CrossRef]
- Wang, C.; Hong, H.; Sherong, Z.; Wang, G. Influence of ground motion duration on responses of concrete gravity dams. J. Earthq. Eng. 2020, 24, 1156–1180. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Y.; Lu, W.; Yan, P.; Zhou, W.; Chen, M. A general definition of integrated strong motion duration and its effect on seismic demands of concrete gravity dams. Eng. Struct. 2016, 125, 481–493. [Google Scholar] [CrossRef]
- Rathje, E.M.; Abrahamson, N.A.; Bray, J.D. Simplified Frequency Content Estimates of Earthquake Ground Motions. J. Geotech. Geoenviron. Eng. 1998, 124, 150–159. [Google Scholar] [CrossRef]
- Zhu, T.J.; Heidebrecht, A.C.; Tso, W.K. Effect of peak ground acceleration to velocity ratio on ductility demand of inelastic systems. Earthq. Eng. Struct. Dyn. 1988, 16, 63–79. [Google Scholar] [CrossRef]
- Mavroeidis, G.P.; Papageorgiou, A.S. A mathematical representation of Near-Fault ground motions. Bull. Seismol. Soc. Am. 2003, 93, 1099–1131. [Google Scholar] [CrossRef]
- Bayraktar, A.; Altunişik, A.C.; Sevim, B.; Kartal, M.E.; Türker, T.; Bilici, Y. Comparison of near- and far-fault ground motion effect on the nonlinear response of dam–reservoir–foundation systems. Nonlinear Dyn. 2009, 58, 655–673. [Google Scholar] [CrossRef]
- Xu, S.; Xu, Q.; Chen, J.; Li, J. Improved endurance time analysis for seismic responses of concrete dam under near-fault pulse-like ground motions. Eng. Struct. 2022, 270, 114912. [Google Scholar] [CrossRef]
- Wang, G.; Yan, S.-D.; Li, D.-Q.; Du, W. Seismic performance assessment of high arch dams considering the pulse-like and directionality effects of near-fault ground motions. Eng. Struct. 2024, 321, 119010. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, S.; Wang, C.; Yu, M. Seismic performance evaluation of dam-reservoir-foundation systems to near-fault ground motions. Nat. Hazards 2014, 72, 651–674. [Google Scholar] [CrossRef]
- Wang, X.; Xue, B.; Xu, B.; Pang, R. Role of strong motion duration on seismic responses of high concrete faced rockfill dams. Structures 2021, 32, 1092–1102. [Google Scholar] [CrossRef]
- Ren, S.-P.; Chen, X.-J.; Ren, Z.-L.; Cheng, P.; Liu, Y. Large-deformation modelling of earthquake-triggered landslides considering non-uniform soils with a stratigraphic dip. Comput. Geotech. 2023, 159, 105492. [Google Scholar] [CrossRef]
- Ren, S.-P.; Li, Y.; Chen, X.-J.; Cheng, P.; Liu, F.; Yao, K. Large-deformation analyses of seismic landslide runout considering spatially random soils and stochastic ground motions. Bull. Eng. Geol. Environ. 2025, 84, 136. [Google Scholar] [CrossRef]
- Sevieri, G.; De Falco, A.; Marmo, G. Shedding light on the effect of uncertainties in the seismic fragility analysis of existing concrete dams. Infrastructures 2020, 5, 22. [Google Scholar] [CrossRef]
- Chen, D.-H.; Yang, Z.-H.; Wang, M.; Xie, J.-H. Seismic performance and failure modes of the Jin’anqiao concrete gravity dam based on incremental dynamic analysis. Eng. Fail. Anal. 2019, 100, 227–244. [Google Scholar] [CrossRef]
- Bernier, C.; Padgett, J.E.; Proulx, J.; Paultre, P. Seismic fragility of concrete gravity dams with spatial variation of angle of friction: Case study. J. Struct. Eng. 2016, 142, 05015002. [Google Scholar] [CrossRef]
- Ganji, H.T.; Alembagheri, M.; Khaneghahi, M.H. Evaluation of seismic reliability of gravity dam-reservoirinhomogeneous foundation coupled system. Front. Struct. Civ. Eng. 2019, 13, 701–715. [Google Scholar] [CrossRef]
- Pasbani Khiavi, M. Investigation of the effect of reservoir bottom absorption on seismic performance of concrete gravity dams using sensitivity analysis. KSCE J. Civ. Eng. 2016, 20, 1977–1986. [Google Scholar] [CrossRef]
- Tidke, A.R.; Adhikary, S. Seismic fragility analysis of the Koyna gravity dam with layered rock foundation considering tensile crack failure. Eng. Fail. Anal. 2021, 125, 105361. [Google Scholar] [CrossRef]
- Cao, A.-T.; Nahar, T.T.; Kim, D.; Choi, B. Earthquake risk assessment of concrete gravity dam by cumulative absolute velocity and response surface methodology. Earthq. Struct. 2019, 17, 511–519. [Google Scholar] [CrossRef]
- ABAQUS. 6.14 Documentation; Dassault Systemes Simulia Corporation: Johnston, RI, USA, 2014. [Google Scholar]
- Nahar, T.T.; Rahman, M.M.; Kim, D. Damage index based seismic risk generalization for concrete gravity dams considering FFDI. Struct. Eng. Mech. 2021, 78, 53–66. [Google Scholar] [CrossRef]
- Westergaard, H.M. Water pressures on dams during earthquakes. Trans. Am. Soc. Civ. Eng. 1933, 98, 418–433. [Google Scholar] [CrossRef]
- Van Nguyen, D.; Kim, D.; Duy Nguyen, D. Nonlinear seismic soil-structure interaction analysis of nuclear reactor building considering the effect of earthquake frequency content. Structures 2020, 26, 901–914. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Q.; Shi, L.; Wang, H.; Li, X. An integral numerical analysis of impact of a commercial aircraft on nuclear containment. Sci. Technol. Nucl. Install. 2019, 2019, 9417954. [Google Scholar] [CrossRef]
- Bao, X.; Zhai, C.-H.; Zhang, M.-H.; Xu, L.-J. Seismic capacity assessment of postmainshock damaged containment structures using nonlinear incremental dynamic analysis. Struct. Des. Tall Spec. Build. 2020, 29, e1706. [Google Scholar] [CrossRef]
- Nahar, T.T.; Rahman, M.M.; Kim, D. Effective safety assessment of aged concrete gravity dam based on the reliability index in a seismically induced site. Appl. Sci. 2021, 11, 1987. [Google Scholar] [CrossRef]
- Ansari, M.I.; Agarwal, P. Damage index evaluation of concrete gravity dam based on hysteresis behavior and stiffness degradation under cyclic loading. Int. J. Struct. Stab. Dyn. 2017, 17, 1750009. [Google Scholar] [CrossRef]
- Nguyen, D.V.; Dookie, K.; Chunse, P.; Choi, B. Seismic soil–structure interaction analysis of concrete gravity dam using perfectly matched discrete layers with analytical wavelengths. J. Earthq. Eng. 2021, 25, 1657–1678. [Google Scholar] [CrossRef]
- Oyguc, E.; Hayır, A.; Oyguc, R. Structural modeling and dynamic analysis of a nuclear reactor building. In Structural Integrity and Failure; Oyguc, R., Tahmasebinia, F., Eds.; IntechOpen: London, UK, 2020; pp. 1–19. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Shamass, R.; Zhou, X.; Alfano, G. Finite-element analysis of shear-off failure of keyed dry joints in precast concrete segmental bridges. J. Bridge Eng. 2015, 20, 04014084. [Google Scholar] [CrossRef]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G. Analysis of residual flexural stiffness of steel fiber-reinforced concrete beams with steel reinforcement. Materials 2020, 13, 2698. [Google Scholar] [CrossRef]
- Allam, S.M.; Shoukry, M.S.; Rashad, G.E.; Hassan, A.S. Evaluation of tension stiffening effect on the crack width calculation of flexural RC members. Alex. Eng. J. 2013, 52, 163–173. [Google Scholar] [CrossRef]
- Fenves, G.L.; Chopra, A.K. Simplified Analysis for Earthquake Resistant Design of Concrete Gravity Dams; University of California, Earthquake Engineering Research Center: Berkeley, CA, USA, 1986. [Google Scholar]
- Fenves, G.; Chopra, A.K. Simplified Earthquake Analysis of Concrete Gravity Dams. J. Struct. Eng. 1987, 113, 1688–1708. [Google Scholar] [CrossRef]
- Zhao, W.; Ji, S. Mesh convergence behavior and the effect of element integration of a human head injury model. Ann. Biomed. Eng 2019, 47, 475–486. [Google Scholar] [CrossRef] [PubMed]
- PEER. PEER Ground Motion Database. Available online: https://ngawest2.berkeley.edu/ (accessed on 1 January 2025).
- KCSC. Standard for Seismic Design of Buildings (건축물 내진설계기준); KCSC: Annandale, VA, USA, 2022. [Google Scholar]
- Moon, D.-S.; Lee, Y.-J.; Lee, S. Fragility analysis of space reinforced concrete frame structures with structural irregularity in plan. J. Struct. Eng. 2018, 144, 04018096. [Google Scholar] [CrossRef]
- Bommer, J.J.; Elnashai, A.S.; Weir, A.G. Compatible acceleration and displacement spectra for seismic design codes. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Kennedy, R.; Ravindra, M. Seismic fragilities for nuclear power plant risk studies. Nucl. Eng. Des. 1984, 79, 47–68. [Google Scholar] [CrossRef]
- Ellingwood, B.; Tekie, P.B. Fragility analysis of concrete gravity dams. J. Infrastruct. Syst. 2001, 7, 41–48. [Google Scholar] [CrossRef]
- Shinozuka, M.; Feng, M.Q.; Lee, J.; Naganuma, T. Statistical analysis of fragility curves. J. Eng. Mech. 2000, 126, 1224–1231. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E. Collapse Fragility Curves for Concrete Dams: Comprehensive Study. J. Struct. Eng. 2016, 142, 04016075. [Google Scholar] [CrossRef]


| Property | Concrete | |
|---|---|---|
| Inside | Outside | |
| Compressive strength, (MPa) | 12 | 18 |
| Modulus of elasticity, (MPa) | 13,767 | 16,861 |
| Tensile strength, (MPa) | 1.3 | 1.6 |
| Poisson’s ratio (ν) | 0.18 | 0.18 |
| Density, ρ (kg/m3) | 2300 | 2300 |
| Dilation angle () (°) | 36 | 36 |
| Flow potential eccentricity, | 0.1 | 0.1 |
| Biaxial-to-uniaxial-strength ratio, | 1.16 | 1.16 |
| Ratio of the second stress invariant on the tensile meridian, | 0.667 | 0.667 |
| EQ No. | EQ Name | Station | Year | M | (s) | Duration Category | PGA/PGV (g/m/s) | Freq. Content |
|---|---|---|---|---|---|---|---|---|
| 1 | Borrego | El Centro Array #9 | 1942 | 6.5 | 37.22 | LD | 1.06 | MF |
| 2 | Kern County | LA—Hollywood Stor FF | 1952 | 7.36 | 33.54 | LD | 0.49 | LF |
| 3 | El Alamo | El Centro Array #9 | 1956 | 6.8 | 36.74 | LD | 0.84 | MF |
| 4 | Central Calif-02 | Hollister City Hall | 1960 | 5 | 34.72 | LD | 0.95 | MF |
| 5 | Borrego Mtn | El Centro Array #9 | 1968 | 6.63 | 41.18 | LD | 0.50 | LF |
| 6 | San Fernando | 2516 Via Tejon PV | 1971 | 6.61 | 51.78 | LD | 0.43 | LF |
| 7 | Tabas_Iran | Sedeh | 1978 | 7.35 | 30.14 | LD | 0.77 | LF |
| 8 | Taiwan SMART1(45) | SMART1 O08 | 1986 | 7.3 | 34.24 | LD | 0.57 | LF |
| 9 | Superstition Hills-02 | Imperial Valley Wildlife Liquefaction Array | 1987 | 6.54 | 35.81 | LD | 0.57 | LF |
| 10 | Landers | Arcadia—Arcadia Av | 1992 | 7.28 | 35.22 | LD | 0.27 | LF |
| 11 | Big Bear-01 | LA—Temple & Hope | 1992 | 6.46 | 34.74 | LD | 0.71 | LF |
| 12 | Northridge-01 | LB—City Hall | 1994 | 6.69 | 33.2 | LD | 0.73 | LF |
| 13 | Dinar_Turkey | Denizli | 1995 | 6.4 | 59.05 | LD | 0.49 | LF |
| 14 | Gulf of Aqaba | Hadera | 1995 | 7.2 | 33.27 | LD | 0.42 | LF |
| 15 | Kocaeli_Turkey | Afyon Bay | 1999 | 7.51 | 61.08 | LD | 0.40 | LF |
| 16 | Humbolt Bay | Ferndale City Hall | 1937 | 5.8 | 21.7 | MD | 1.54 | HF |
| 17 | Imperial Valley-01 | El Centro Array #9 | 1938 | 5 | 14.81 | MD | 2.71 | HF |
| 18 | Imperial Valley-02 | El Centro Array #9 | 1940 | 6.95 | 24.19 | MD | 0.91 | MF |
| 19 | Northwest Calif-02 | Ferndale City Hall | 1941 | 6.6 | 15.48 | MD | 1.67 | HF |
| 20 | Northern Calif-01 | Ferndale City Hall | 1941 | 6.4 | 13.03 | MD | 1.93 | HF |
| 21 | Imperial Valley-03 | El Centro Array #9 | 1951 | 5.6 | 24.47 | MD | 1.13 | MF |
| 22 | Kern County | Pasadena—CIT Athenaeum | 1952 | 7.36 | 29.19 | MD | 0.82 | MF |
| 23 | Northern Calif-02 | Ferndale City Hall | 1952 | 5.2 | 16.54 | MD | 0.96 | MF |
| 24 | Southern Calif | San Luis Obispo | 1952 | 6 | 13.27 | MD | 1.15 | MF |
| 25 | Central Calif-01 | Hollister City Hall | 1954 | 5.3 | 25.07 | MD | 1.18 | MF |
| 26 | Northern Calif-03 | Ferndale City Hall | 1954 | 6.5 | 17.34 | MD | 0.45 | LF |
| 27 | Hollister-01 | Hollister City Hall | 1961 | 5.6 | 18.72 | MD | 0.74 | LF |
| 28 | Hollister-02 | Hollister City Hall | 1961 | 5.5 | 16.48 | MD | 1.03 | MF |
| 29 | Parkfield | Cholame—Shandon Array #12 | 1966 | 6.19 | 28.99 | MD | 0.90 | MF |
| 30 | San Fernando | Borrego Springs Fire Sta | 1971 | 6.61 | 16.34 | MD | 0.51 | LF |
| 31 | Helena_Montana-01 | Carroll College | 1935 | 6 | 2.41 | SD | 2.74 | HF |
| 32 | Helena_Montana-02 | Helena Fed Bldg | 1935 | 6 | 0.57 | SD | 6.65 | HF |
| 33 | San Francisco | Golden Gate Park | 1957 | 5.28 | 5.02 | SD | 3.26 | HF |
| 34 | Parkfield | Cholame—Shandon Array #5 | 1966 | 6.19 | 6.5 | SD | 1.77 | HF |
| 35 | Parkfield | Temblor pre-1969 | 1966 | 6.19 | 4.45 | SD | 1.61 | HF |
| 36 | Lytle Creek | Cedar Springs Pumphouse | 1970 | 5.33 | 2.43 | SD | 2.30 | HF |
| 37 | Lytle Creek | Devil’s Canyon | 1970 | 5.33 | 2.22 | SD | 4.82 | HF |
| 38 | Lytle Creek | Lake Hughes #1 | 1970 | 5.33 | 6.88 | SD | 1.20 | MF |
| 39 | Lytle Creek | Santa Anita Dam | 1970 | 5.33 | 5.11 | SD | 3.02 | HF |
| 40 | Lytle Creek | Wrightwood—6074 Park Dr | 1970 | 5.33 | 2.99 | SD | 1.70 | HF |
| 41 | San Fernando | Colton—So Cal Edison | 1971 | 6.61 | 7.34 | SD | 1.76 | HF |
| 42 | San Fernando | Fort Tejon | 1971 | 6.61 | 8.3 | SD | 2.08 | HF |
| 43 | San Fernando | Gormon—Oso Pump Plant | 1971 | 6.61 | 7.19 | SD | 1.00 | MF |
| 44 | San Fernando | Pacoima Dam (upper left abut) | 1971 | 6.61 | 7.02 | SD | 1.06 | MF |
| 45 | Managua_Nicaragua-02 | Managua_ESSO | 1972 | 5.2 | 8.06 | SD | 1.03 | MF |
| EQ Group | n | M (Median [IQR]) | (km, Median [IQR]) | (m/s, Median [IQR]) | (s, Median [IQR]) | PGA/PGV (s, Median [IQR]) | |
|---|---|---|---|---|---|---|---|
| LD | 15 | 6.69 [0.77] | 86.31 [74.54] | 280.56 [129] | 35.22 [5.31] | 0.57 [0.29] | 0.14 |
| MD | 15 | 6 [1] | 34.98 [50.09] | 219.31 [65.49] | 17.34 [8.42] | 1.03 [0.5] | 0.11 |
| SD | 15 | 6 [1.07] | 15.96 [37.37] | 486 [278.98] | 5.11 [4.4] | 1.77 [1.48] | 0.18 |
| HF | 15 | 6 [0.97] | 22.94 [41.58] | 477.22 [318.15] | 5.11 [7.96] | 2.08 [1.15] | 0.14 |
| MF | 15 | 6 [1.3] | 25.81 [51.82] | 219.31 [198.59] | 24.19 [18.43] | 1.03 [0.17] | 0.13 |
| LF | 15 | 6.63 [0.77] | 86.31 [93.98] | 316.46 [124] | 34.24 [6.83] | 0.5 [0.2] | 0.17 |
| Limit State (LS) | Crest-Drift Ratio Threshold |
|---|---|
| Slight | 0.0128 |
| Moderate | 0.0343 |
| Extensive (used for fragility in this study) | 0.0477 |
| Collapse | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nahar, T.T.; Rahman, M.M.; Kim, D. Effect of Ground Motion Duration and Frequency Characteristics on the Probabilistic Risk Assessment of a Concrete Gravity Dam. Infrastructures 2025, 10, 259. https://doi.org/10.3390/infrastructures10100259
Nahar TT, Rahman MM, Kim D. Effect of Ground Motion Duration and Frequency Characteristics on the Probabilistic Risk Assessment of a Concrete Gravity Dam. Infrastructures. 2025; 10(10):259. https://doi.org/10.3390/infrastructures10100259
Chicago/Turabian StyleNahar, Tahmina Tasnim, Md Motiur Rahman, and Dookie Kim. 2025. "Effect of Ground Motion Duration and Frequency Characteristics on the Probabilistic Risk Assessment of a Concrete Gravity Dam" Infrastructures 10, no. 10: 259. https://doi.org/10.3390/infrastructures10100259
APA StyleNahar, T. T., Rahman, M. M., & Kim, D. (2025). Effect of Ground Motion Duration and Frequency Characteristics on the Probabilistic Risk Assessment of a Concrete Gravity Dam. Infrastructures, 10(10), 259. https://doi.org/10.3390/infrastructures10100259










