A Finite Element Formulation for True Coupled Modal Analysis and Nonlinear Seismic Modeling of Dam–Reservoir–Foundation Systems: Application to an Arch Dam and Validation
Abstract
1. Introduction
2. Coupled Model: Dam–Reservoir Interaction
2.1. Governing Equations
2.2. Finite Element Formulation
3. Proposed Coupled Finite Element Formulation
3.1. Coupled Approach with Generalized Damping
3.2. State–Space Formulation: Coupled Modal Analysis
3.3. Time-Stepping Formulation for Linear Seismic Analysis
3.4. Time-Stepping Formulation with Stress–Transfer for Nonlinear Seismic Analysis
3.4.1. Joint Constitutive Model
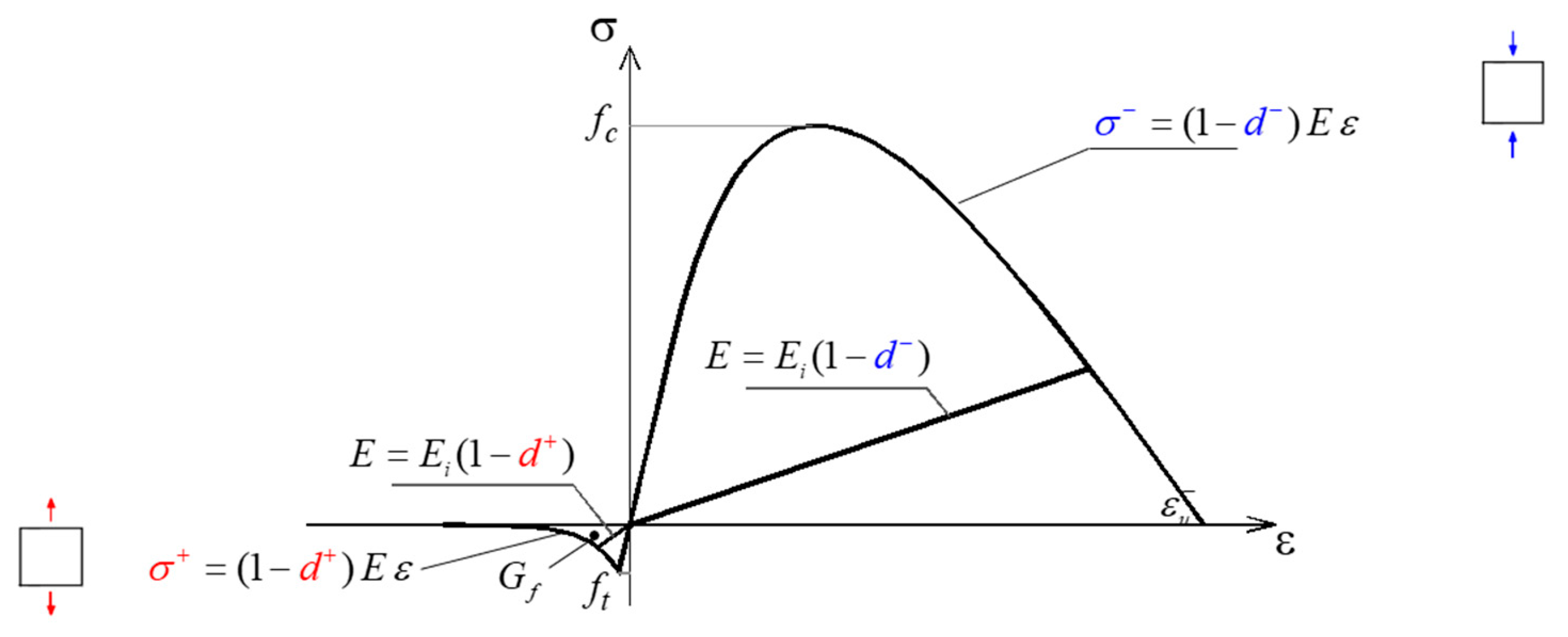
3.4.2. Concrete Constitutive Damage Model
3.5. The Computer Program DamDySSA5.0
Verification and Validation Tests
4. Application to a Real Large Arch Dam
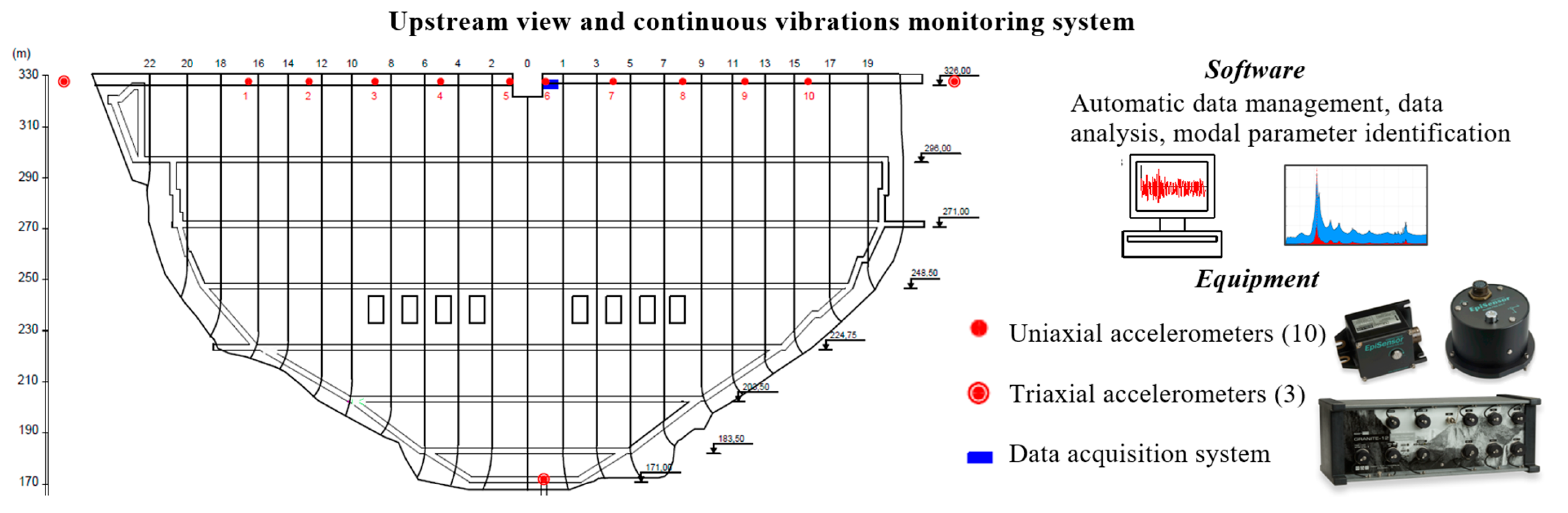
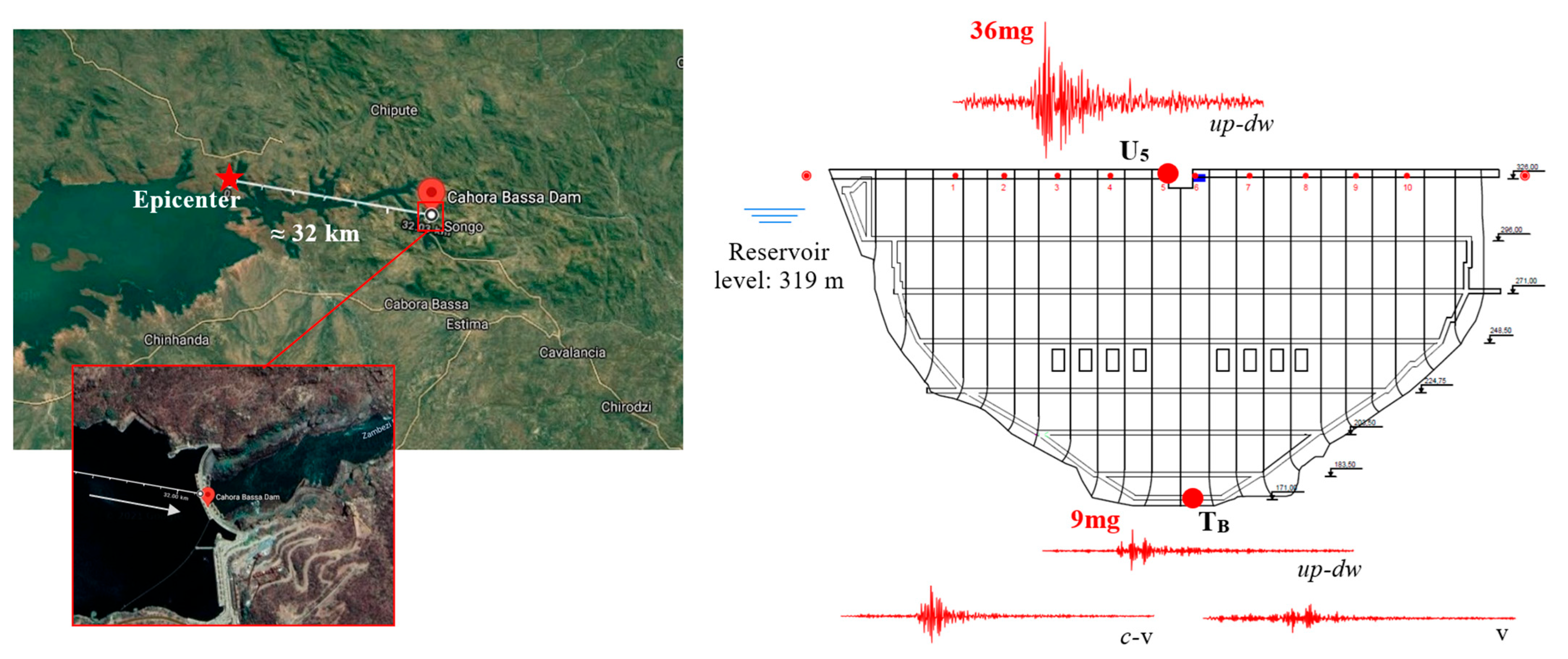
4.1. Case Study: Cahora Bassa Dam
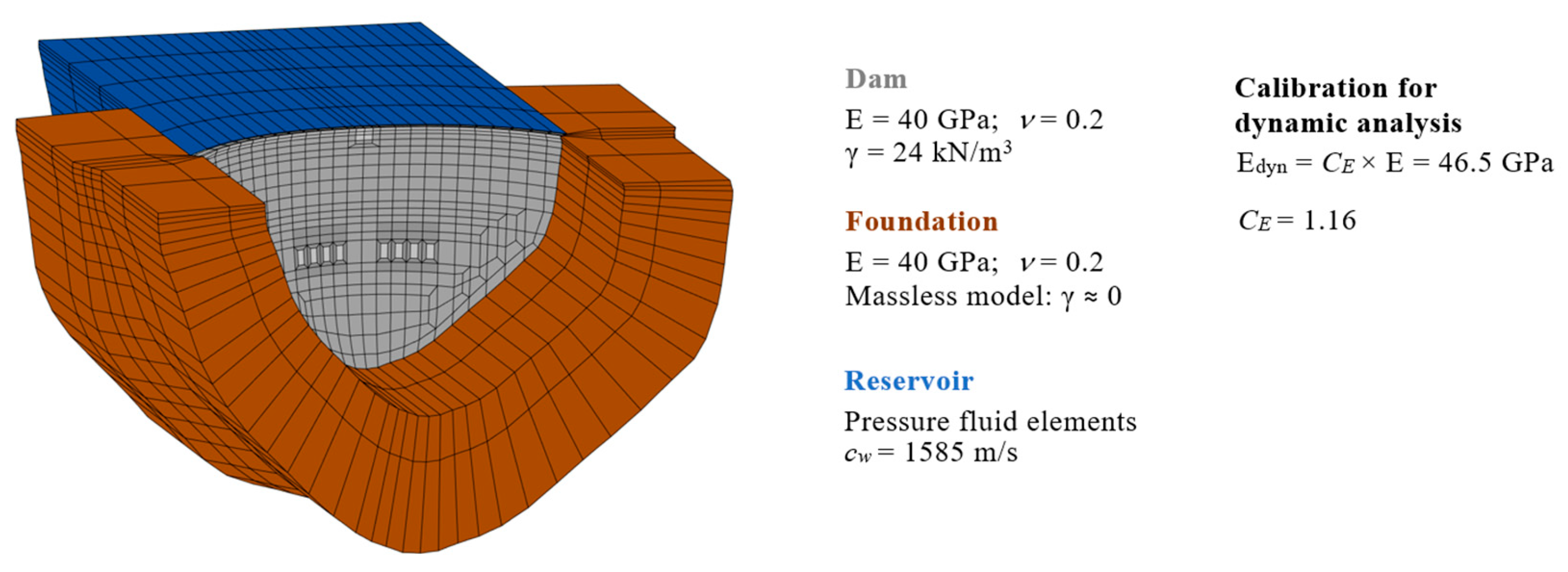
4.2. Numerical Model: Dam–Reservoir–Foundation System and Main Properties
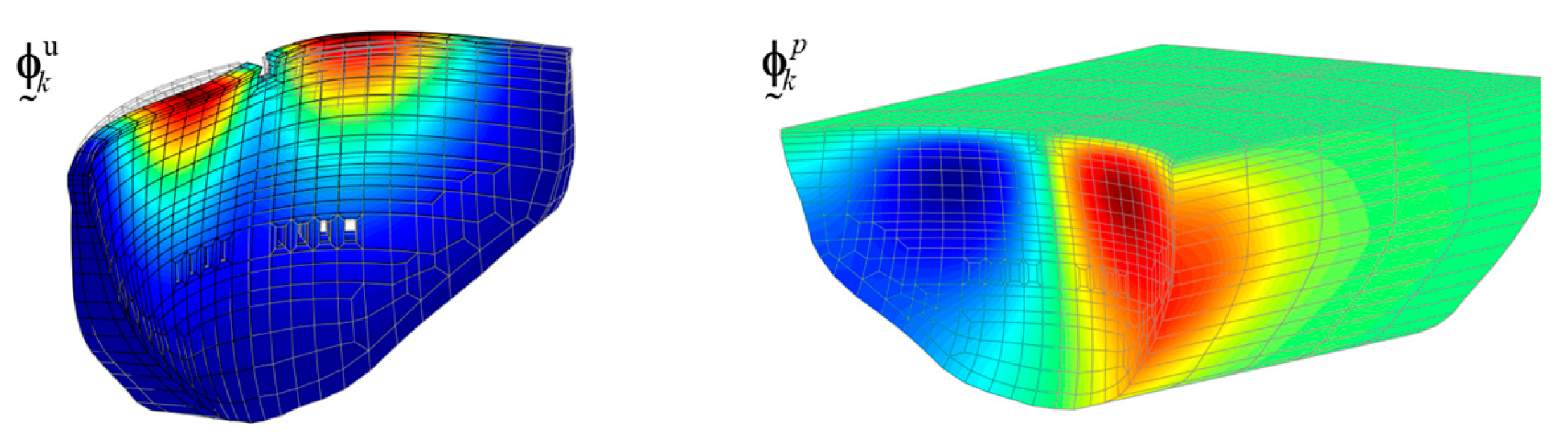
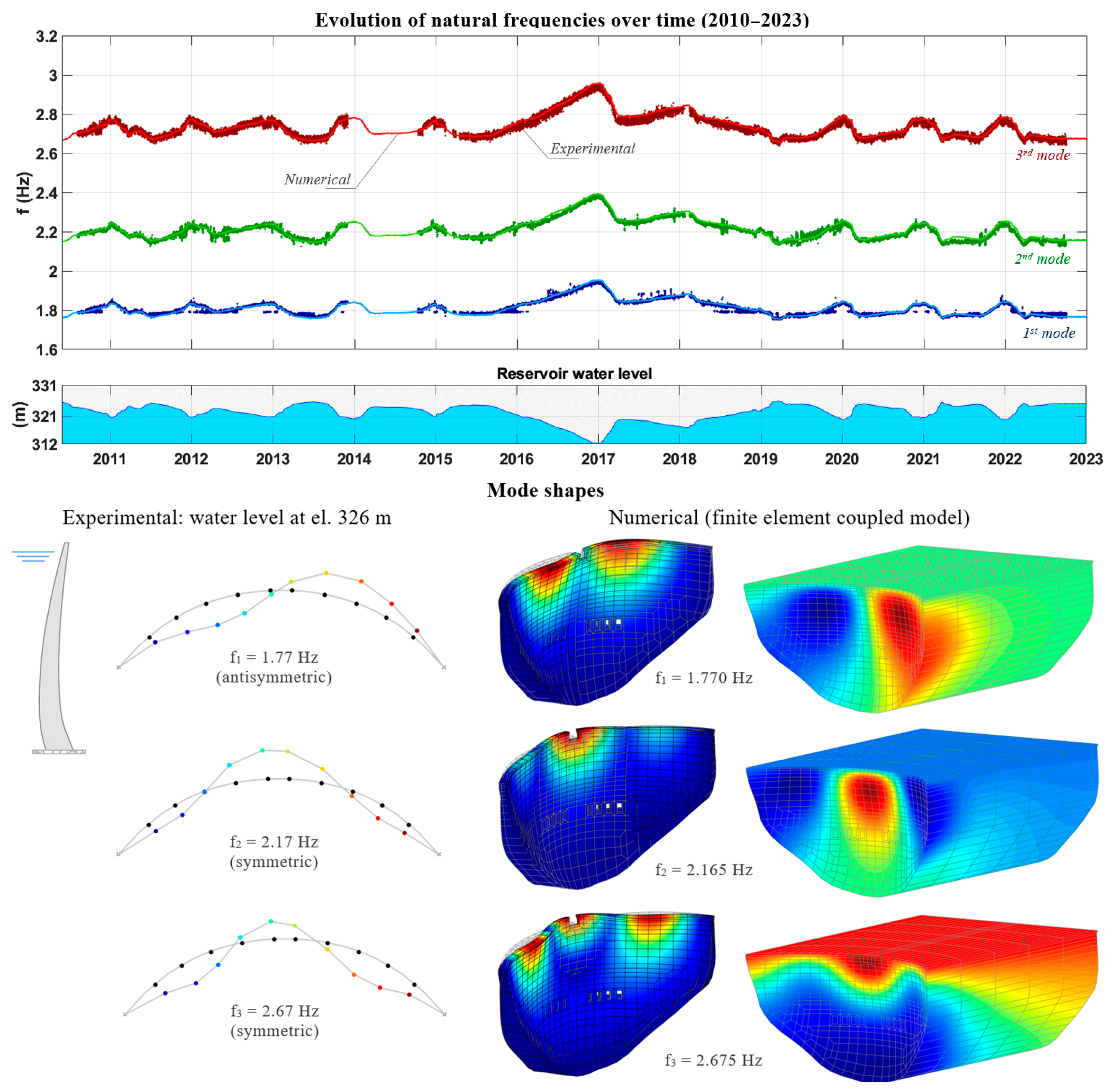
4.3. Modal Response: Natural Frequencies and Mode Shapes
4.4. Seismic Response Under a Low-Intensity Earthquake
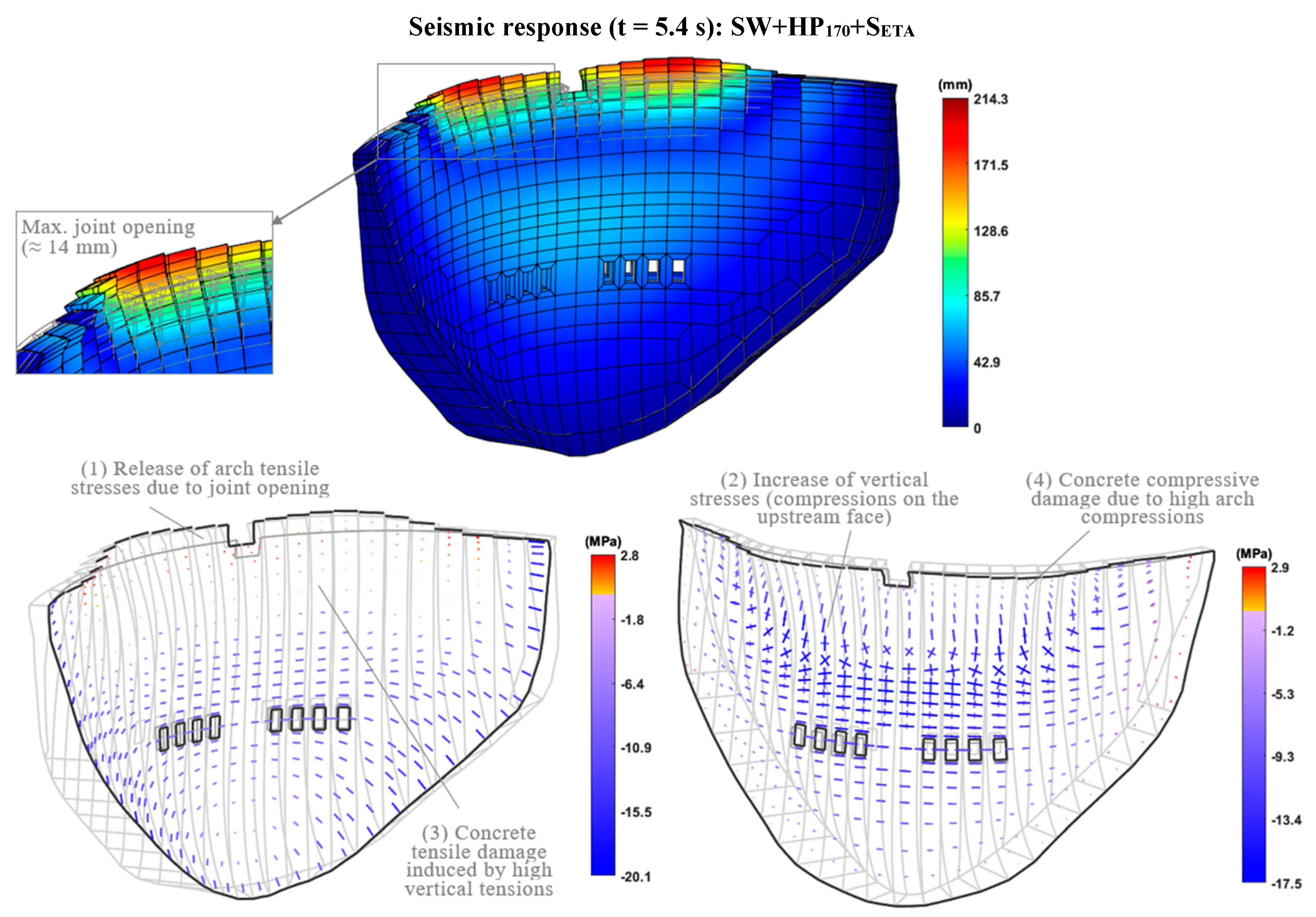
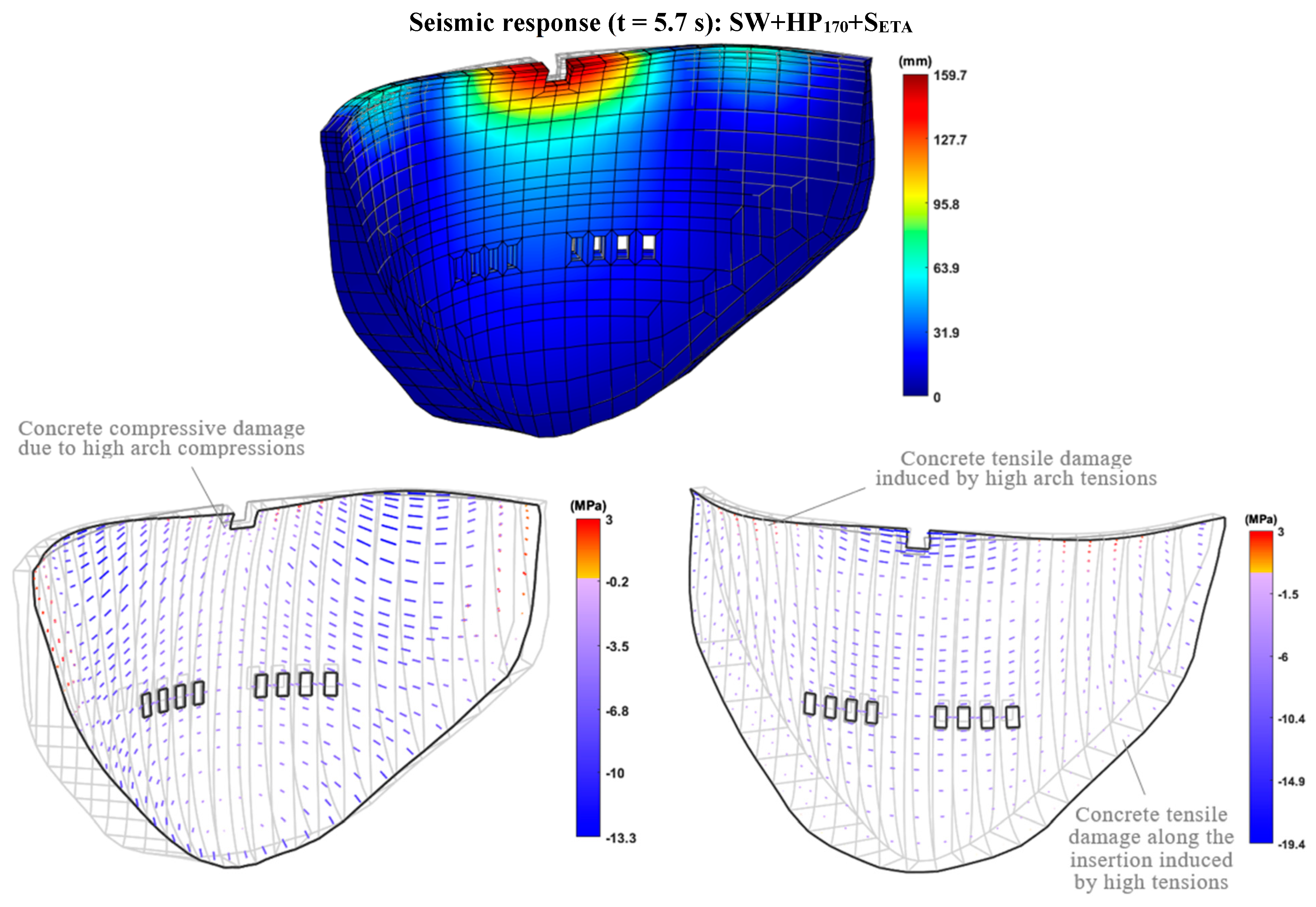
4.5. Nonlinear Seismic Analysis: Study on the Effects of Contraction Joint Movements and Concrete Damage
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| HCB | Hidroelétrica de Cahora Bassa |
| SSHM | Seismic and structural health monitoring |
| ETA | Endurance Time Analysis |
| OBE | Operating Basis Earthquake |
| MDE | Maximum Design Earthquake |
References
- Chopra, A.K. Earthquake Analysis of Arch Dams: Factors to Be Considered. J. Struct. Eng. 2012, 138, 205–214. [Google Scholar] [CrossRef]
- Chen, H. Seismic Safety of High Concrete Dams. Earthq. Eng. Eng. Vib. 2014, 13, 1–16. [Google Scholar] [CrossRef]
- Fenves, G.L.; Chopra, A.K. Effects of Reservoir Bottom Absorption on Earthquake Response of Concrete Gravity Dams. Earthq. Eng. Struct. Dyn. 1983, 11, 809–829. [Google Scholar] [CrossRef]
- Pedro, J.O.; Câmara, R. Coupled Models for Dynamic Analysis of Arch Dams. In Proceedings of the 8th European Conference on Earthquake Engineering, LNEC, Lisbon, Portugal, 7–12 September 1986. [Google Scholar]
- Fok, K.L.; Chopra, A.K. Earthquake Analysis of Arch Dams Including Dam-Water Interaction, Reservoir Boundary Absorption and Foundation Flexibility. Earthq. Eng. Struct. Dyn. 1986, 14, 155–184. [Google Scholar] [CrossRef]
- Tiliouine, B.; Seghir, A. Fluid-Structure Models for Dynamic Studies of Dam-Water Systems. In Proceedings of the 11th European Conference on Earthquake Engineering, Paris, France, 6–11 September 1998. [Google Scholar]
- Küçükarslan, S.; Coşkun, S.B.; Taşkın, B. Transient Analysis of Dam–Reservoir Interaction Including the Reservoir Bottom Effects. J. Fluids Struct. 2005, 20, 1073–1084. [Google Scholar] [CrossRef]
- Bouaanani, N.; Lu, F.Y. Assessment of Potential-Based Fluid Finite Elements for Seismic Analysis of Dam-Reservoir Systems. Comput. Struct. 2009, 87, 206–224. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, J.; Wang, J.-T. Influence of Seismic Input Mechanisms and Radiation Damping on Arch Dam Response. Soil Dyn. Earthq. Eng. 2009, 29, 1282–1293. [Google Scholar] [CrossRef]
- Oliveira, S.; Silvestre, A.; Espada, M.; Câmara, R. Modeling the Dynamic Behavior of Dam-Reservoir-Foundation Systems Considering Generalized Damping. Development of a 3DFEM State Formulation. In Proceedings of the International Conference on Structural Dynamic EURODYN, Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- Lokke, A.; Chopra, A.K. Direct Finite Element Method for Nonlinear Earthquake Analysis of 3-Dimensional Semi-Unbounded Dam–Water-Foundation Rock Systems. Earthq. Eng. Struct. Dyn. 2018, 47, 1309–1328. [Google Scholar] [CrossRef]
- Daniell, W.E.; Taylor, C.A. Effective Ambient Vibration Testing for Validating Numerical Models of Concrete Dams. Earthq. Eng. Struct. Dyn. 1999, 28, 1327–1344. [Google Scholar] [CrossRef]
- Darbre, G.R.; de Smet, C.A.M.; Kraemer, C. Natural Frequencies Measured from Ambient Vibration Response of the Arch Dam of Mauvoisin. Earthq. Eng. Struct. Dyn. 2000, 29, 577–586. [Google Scholar] [CrossRef]
- Proulx, J.; Paultre, P.; Rheault, J.; Robert, Y. An Experimental Investigation of Water Level Effects on the Dynamic Behaviour of a Large Arch Dam. Earthq. Eng. Struct. Dyn. 2001, 30, 1147–1166. [Google Scholar] [CrossRef]
- Sevim, B.; Bayraktar, A.; Altunışık, A.C.; Adanur, S.; Akköse, M. Determination of Water Level Effects on the Dynamic Characteristics of a Prototype Arch Dam Model Using Ambient Vibration Testing. Exp. Tech. 2012, 36, 72–82. [Google Scholar] [CrossRef]
- Alegre, A.; Carvalho, E.; Matsinhe, B.; Mendes, P.; Oliveira, S.; Proença, J. Monitoring Vibrations in Large Dams. In Proceedings of the HYDRO 2019—Concept to Closure: Practical Steps, Porto, Portugal, 14–16 October 2019. [Google Scholar]
- Guo, X.; Dufour, F.; Humbert, N. Modal Analysis of an Arch Dam Combining Ambient Vibration Measurements, Advanced Fluid-element Method and Modified Engineering Approach. Earthq. Eng. Struct. Dyn. 2022, 51, 1321–1342. [Google Scholar] [CrossRef]
- Proulx, J.; Darbre, G.R. Earthquake Response of Large Arch Dams. Observational Evidence and Numerical Modelling. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Chopra, A.K.; Wang, J.-T. Earthquake Response of Arch Dams to Spatially Varying Ground Motion. Earthq. Eng. Struct. Dyn. 2010, 39, 887–906. [Google Scholar] [CrossRef]
- Robbe, E.; Kashiwayanagi, M.; Yamane, Y. Seismic Analyses of Concrete Dam, Comparison between Finite-Element Analyses and Seismic Records. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–17 January 2017. [Google Scholar]
- Koufoudi, E.; Chaljub, E.; Dufour, F.; Bard, P.Y.; Humbert, N.; Robbe, E. Spatial Variability of Earthquake Ground Motions at the Dam–Foundation Rock Interface of Saint Guérin: Experimental and Numerical Investigations. Bull. Earthq. Eng. 2018, 16, 1751–1777. [Google Scholar] [CrossRef]
- Alegre, A.; Robbe, E.; Oliveira, S. Seismic Analysis of Cabril Dam. Measured Response and Comparison with Numerical Results from Code_Aster and DamDySSA. In Proceedings of the 4th Dam World Conference, LNEC, Lisboa, Portugal, 22–24 September 2020. [Google Scholar]
- Oliveira, S.; Alegre, A.; Carvalho, E.; Mendes, P.; Proença, J. Seismic and Structural Health Monitoring Systems for Large Dams: Theoretical, Computational and Practical Innovations. Bull. Earthq. Eng. 2022, 20, 4483–4512. [Google Scholar] [CrossRef]
- Wang, J.-T.; Zhang, C.; Jin, F. Nonlinear Earthquake Analysis of High Arch Dam-Water-Foundation Rock Systems. Earthq. Eng. Struct. Dyn. 2012, 41, 1157–1176. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Mirzabozorg, H. Seismic Performance Evaluation and Analysis of Major Arch Dams Considering Material and Joint Nonlinearity Effects. ISRN Civ. Eng. 2012, 2012, 681350. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Mirzabozorg, H.; Estekanchi, H.E. Nonlinear Seismic Assessment of Arch Dams and Investigation of Joint Behavior Using Endurance Time Analysis Method. Arab. J. Sci. Eng. 2014, 39, 3599–3615. [Google Scholar] [CrossRef]
- Goldgruber, M. Non-Linear Seismic Modelling of Concrete Dams. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2015. [Google Scholar]
- Wang, R.; Chen, L.; Zhang, C. Seismic Design of Xiluodu Ultra-High Arch Dam. Water Sci. Eng. 2018, 11, 288–301. [Google Scholar] [CrossRef]
- Alegre, A. Modelling and Monitoring the Dynamic Behaviour of Concrete Dams. Modal Analysis and Seismic Response. Ph.D. Thesis, Instituto Superior Técnico, University of Lisbon, Lisbon, Portugal, 2021. [Google Scholar]
- Niwa, A.; Clough, R.W. Non-Linear Seismic Response of Arch Dams. Earthq. Eng. Struct. Dyn. 1982, 10, 267–281. [Google Scholar] [CrossRef]
- Fenves, G.L.; Mojtahedi, S.; Reimer, R.B. Effect of Contraction Joints on Earthquake Response of an Arch Dam. J. Struct. Eng. 1992, 118, 1039–1055. [Google Scholar] [CrossRef]
- Lau, D.T.; Boruziaan, B.; Razaqpur, A.G. Modelling of Contraction Joint and Shear Sliding Effects on Earthquake Response of Arch Dams. Earthq. Eng. Struct. Dyn. 1998, 27, 1013–1029. [Google Scholar] [CrossRef]
- Câmara, R. A Method for Coupled Arch Dam-Foundation-Reservoir Seismic Behaviour Analysis. Earthq. Eng. Struct. Dyn. 2000, 29, 441–460. [Google Scholar] [CrossRef]
- Faria, R.; Oliver, J.; Cervera, M. A Strain-Based Plastic Viscous-Damage Model for Massive Concrete Structures. Int. J. Solids Struct. 1998, 35, 1533–1558. [Google Scholar] [CrossRef]
- Valliappan, S.; Yazdchi, M.; Khalili, N. Seismic Analysis of Arch Dams—A Continuum Damage Mechanics Approach. Int. J. Numer. Methods Eng. 1999, 45, 1695–1724. [Google Scholar] [CrossRef]
- Oliveira, S.; Faria, R. Numerical Simulation of Collapse Scenarios in Reduced Scale Tests of Arch Dams. Eng. Struct. 2006, 28, 1430–1439. [Google Scholar] [CrossRef]
- Pan, J.; Zhang, C.; Xu, Y.; Jin, F. A Comparative Study of the Different Procedures for Seismic Cracking Analysis of Concrete Dams. Soil Dyn. Earthq. Eng. 2011, 31, 1594–1606. [Google Scholar] [CrossRef]
- Omidi, O.; Lotfi, V. Earthquake Response of Concrete Arch Dams: A Plastic–Damage Approach. Earthq. Eng. Struct. Dyn. 2013, 42, 2129–2149. [Google Scholar] [CrossRef]
- Westergaard, H.M. Water Pressures on Dams during Earthquakes. Trans. Am. Soc. Civ. Eng. 1933, 98, 418–472. [Google Scholar] [CrossRef]
- Kuo, J.S.H. Fluid-Structure Interactions: Added Mass Computations for Incompressible Fluid; Report No. UCB/EERC-82/09; University of California: Berkeley, CA, USA, 1982. [Google Scholar]
- Miquel, B.; Bouaanani, N. Simplified Evaluation of the Vibration Period and Seismic Response of Gravity Dam–Water Systems. Eng. Struct. 2010, 32, 2488–2502. [Google Scholar] [CrossRef]
- Altunisik, A.C.; Sesli, H. Dynamic Response of Concrete Gravity Dams Using Different Water Modelling Approaches: Westergaard, Lagrange and Euler. Comput. Concr. 2015, 16, 429–448. [Google Scholar] [CrossRef]
- Xu, H.; Zou, D.; Kong, X.; Su, X. Error Study of Westergaard’s Approximation in Seismic Analysis of High Concrete-Faced Rockfill Dams Based on SBFEM. Soil Dyn. Earthq. Eng. 2017, 94, 88–91. [Google Scholar] [CrossRef]
- Wang, M.; Chen, J.; Wu, L.; Song, B. Hydrodynamic Pressure on Gravity Dams with Different Heights and the Westergaard Correction Formula. Int. J. Geomech. 2018, 18, 04018134. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Bettess, P. Fluid-Structure Dynamic Interaction and Wave ForcesAn Introduction to Numerical Treatment. Int. J. Numer. Methods Eng. 1978, 13, 1–16. [Google Scholar] [CrossRef]
- Sani, A.A.; Lotfi, V. Dynamic Analysis of Concrete Arch Dams by Ideal-Coupled Modal Approach. Eng. Struct. 2010, 32, 1377–1383. [Google Scholar] [CrossRef]
- Oliveira, S.; Alegre, A.; Silvestre, A.; Espada, M.; Câmara, R. Seismic Safety Evaluation of Luzzone Dam. Use of a 3DFEM State Formulation in Pressures and Displacements. In Proceedings of the 13th ICOLD International Benchmark Workshop on Numerical Analysis of Dams, Lausanne, Switzerland, 9–11 September 2015. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Elsevier Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Ohayon, R. Symmetric Variational Formulations for Harmonic Vibration Problems Coupling Primal and Dual Variables—Application to Fluid-Structure Coupled Systems. La Rechereche Aerosp. 1979, 3, 69–77. [Google Scholar]
- Daniel, W.J. Modal Methods in Finite Element Fluid-Structure Problems with Mixed Variables. Int. J. Numer. Methods Eng. 1980, 15, 1161–1175. [Google Scholar] [CrossRef]
- Ohayon, R.; Valid, R. True Symmetric Formulation of Free Vibrations for Fluid-Structure Interaction in Bounded Media—Finite Element Results. In Numerical Methods in Coupled Systems; Lewis, R.W., Bettess, P., Hinton, E., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- Felippa, C.A. Symmetrization of Coupled Eigenproblems by Eigenvector Augmentation. Commun. Appl. Numer. Methods 1988, 4, 561–563. [Google Scholar] [CrossRef]
- Lotfi, V. Frequency Domain Analysis of Concrete Arch Dams by Decoupled Modal Approach. Struct. Eng. Mech. 2005, 21, 423–435. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. Coupled Problems—A Simple Time-Stepping Procedure. Commun. Appl. Numer. Methods 1985, 1, 233–239. [Google Scholar] [CrossRef]
- Veletsos, A.; Ventura, C. Modal Analysis of Non-Classically Damped Linear Systems. Earthq. Eng. Struct. Dyn. 1986, 14, 217–243. [Google Scholar] [CrossRef]
- Oliveira, S.; Alegre, A. Vibrations in Large Dams. Monitoring and Modelling. In Proceedings of the 26th ICOLD Congress on Large Dams, Vienna, Austria, 1–7 July 2018. [Google Scholar]
- Alegre, A.; Oliveira, S.; Espada, M.; Câmara, R.; Lemos, J. Hydrodynamic Pressures on Dams. Numerical and Experimental Results for Non-Vertical Upstream Faces. In Proceedings of the 10 °Congresso Nacional de Mecânica Experimental, LNEC, Lisboa, Portugal, 12–14 October 2016. [Google Scholar]
- Oliveira, S.; Alegre, A. Seismic and Structural Health Monitoring of Dams in Portugal. In Seismic Structural Health Monitoring; Limongelli, M.P., Çelebi, M., Eds.; Springer Tracts in Civil Engineering; Springer International Publishing: Cham, Switzerland, 2019; pp. 87–113. ISBN 978-3-030-13975-9. [Google Scholar]
- Newmark, N. A Method of Computation for Structural Dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Alegre, A.; Oliveira, S. Non-Linear Seismic Analysis of Arch Dams Considering Joint Movements and a Concrete Damage Model. In Proceedings of the 4th Dam World Conference, LNEC, Lisboa, Portugal, 21–25 September 2020. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures, 3rd ed.; Computers & Structures, Inc: Berkeley, CA, USA, 2003. [Google Scholar]
- de Borst, R.; Sluys, L.J. Computational Methods in Non-Linear Solid Mechanics; Faculty of Civil Engineering and Geosciences, Delft University of Technology: Delft, The Netherlands, 1999. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Fox, D.D. The Finite Element Method for Solid and Structural Mechanics, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 9781856176347. [Google Scholar]
- Alegre, A.; Oliveira, S.; Mendes, P.; Proença, J.; Carvalho, E.; Matsinhe, B. Numerical Models for Seismic Analysis of Arch Dams. In Proceedings of the Congreso de Métodos Numéricos en Ingeniería (CMNE2022), Las Palmas de Gran Canaria, Spain, 12–14 September 2022; pp. 411–430. [Google Scholar]
- Alegre, A.; Oliveira, S.; Mendes, P.; Proença, J.; Ramos, R.; Carvalho, E. Seismic Safety Assessment of Arch Dams Using an ETA-Based Method with Control of Tensile and Compressive Damage. Water 2022, 14, 3835. [Google Scholar] [CrossRef]
- Lemaitre, J. How to Use Damage Mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Simo, J.C.; Ju, J.W. Strain- and Stress-Based Continuum Damage Models—I. Formulation. Int. J. Solids Struct. 1987, 23, 821–840. [Google Scholar] [CrossRef]
- Simo, J.C.; Ju, J.W. Strain- and Stress-Based Continuum Damage Models—II. Computational Aspects. Int. J. Solids Struct. 1987, 23, 841–869. [Google Scholar] [CrossRef]
- Faria, R.; Oliver, J. A Rate-Dependent Plastic-Damage Constitutive Model for Large Scale Computations in Concrete Structures. Monogr. Cent. Int. Metod. Numer. Ing. 1993, 17, 78. [Google Scholar]
- Bažant, Z.P.; Oh, B.H. Crack Band Theory for Fracture of Concrete. Mater. Struct. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Clough, R.W. Non-Linear Mechanisms in the Seismic Response of Arch Dams. In Proceedings of the International Research Conference on Earthquake Engineering, Skopje, Yugoslavia, 30 June–3 July 1980. [Google Scholar]
- Fenves, G.L.; Mojtahedi, S.; Reimer, R.B. ADAP-88: A Computer Program for Non-Linear Earthquake Analysis of Concrete Arch Dams; University of California: Berkeley, CA, USA, 1989. [Google Scholar]
- Fok, K.L.; Hall, J.F.; Chopra, A.K. EACD-3D: A Computer Program for Three-Dimensional Earthquake Analysis of Concrete Dams; University of California: Berkeley, CA, USA, 1986. [Google Scholar]
- Zangar, C.N. Hydrodynamic Pressures on Dams Due to Horizontal Earthquake Effects; Engineering Monograph, No. 11; Bureau of Reclamation: Washington, DC, USA, 1952.
- Oliveira, S.; Mendes, P.; Rodrigues, M.; Alegre, A.; Proença, J.; Carvalho, E.; Matsinhe, B. Cahora Bassa Vibrations Monitoring between 2010–2022. Analysis of Frequencies Using HST Statistical Models for Effects Separation. In Proceedings of the XII International Conference on Structural Dynamics (EURODYN 2023), TU Delft, Delft, The Netherlands, 2–5 July 2023. [Google Scholar]
- Carvalho, E.; Matsinhe, B. First Steps on Automatic Data Acquisition and Analysis System in Cahora Bassa Dam. In Proceedings of the HYDRO 2014, Como, Italy, 13–15 October 2014. [Google Scholar]
- Alegre, A.; Mendes, P.; Carvalho, E.; Matsinhe, B.; Oliveira, S.; Proença, J. Use of SSHM Data for Dynamic Behavior Analysis and Damage Detection on Large Dams. The Cases of Cabril Dam and Cahora Bassa Dam. In Proceedings of the 10th International Conference on Structural Health Monitoring of Intelligent Infrastructure (SHMII-10), Porto, Portugal, 30 June–2 July 2021; Álvaro, C., Caetano, E., Eds.; International Society for Structural Health Monitoring of Intelligent Infrastructure (ISHMII): Winnipeg, MB, Canada, 2021. [Google Scholar]
- Carvalho, E.; Matsinhe, B.; Mendes, P.; Oliveira, S.; Alegre, A.; Ciudad-Real, M.; Skolnik, D.; El-Idrissi, M. SSHM Systems for Dams: 12 Years’ Experience in Cahora Bassa Dam. Equipment, Software, and Main Results. In Experimental Vibration Analysis for Civil Engineering Structures (EVACES 2023); Limongelli, M.P., Giordano, P.F., Quqa, S., Gentile, C., Cigada, A., Eds.; Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2023; pp. 273–282. [Google Scholar]
- Brincker, R.; Zhang, L.; Andersen, P. Modal Identification from Ambient Responses Using Frequency Domain Decomposition. In Proceedings of the IMAC18: International Modal Analysis Conference, San Antonio, TX, USA, 7–10 February 2000. [Google Scholar]
- Peeters, B. System Identification and Damage Detection in Civil Engineering. Ph.D. Thesis, Faculteit Toegepaste Wetenschapen, Katholieke Universiteir Leuven, Leuven, Belgium, 2000. [Google Scholar]
- Proulx, J.; Darbre, G.R.; Kamileris, N. Analytical and Experimental Investigation of Damping in Arch Dams Based on Recorded Earthquakes. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Wang, J.-T.; Chopra, A.K. Linear Analysis of Concrete Arch Dams Including Dam-Water-Foundation Rock Interaction Considering Spatially Varying Ground Motions. Earthq. Eng. Struct. Dyn. 2010, 39, 731–750. [Google Scholar] [CrossRef]
- Robbe, E. Seismic Back Analysis of Monticello Arch Dam—Blind Prediction Workshop and Additional Analyses. In Proceedings of the USSD 2017 Annual Conference and Exhibition, Anaheim, CA, USA, 3–7 April 2017. [Google Scholar]
- Salamon, J.; Hariri-Ardebili, M.A.; Malm, R.; Wood, C.; Faggiani, G. Theme A: Seismic Analysis of Pine Flat Concrete Dam. In Numerical Analysis of Dams, Proceedings of the 15th ICOLD International Benchmark Workshop; Bolzon, G., Sterpi, D., Mazzà, G., Frigerio, A., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 91. [Google Scholar]
- Estekanchi, H.E.; Vafai, H.; Sadeghazar, M. Endurance Time Method for Seismic Analysis and Design of Structures. Sci. Iran. 2004, 11, 361–370. [Google Scholar]
- Meghella, M.; Furgani, L. Application of Endurance Time Analysis Method to the NonLinear Seismic Analysis of Dams: Potentialities and Limitations. In Proceedings of the ICOLD 82nd Annual Meeting, Banff, AB, Canada, 4–5 October 2014. [Google Scholar]
- Furgani, L.; Hariri-Ardebili, M.A.; Meghella, M.; Seyed-Kolbadi, S.M. On the Dynamic Capacity of Concrete Dams. Infrastructures 2019, 4, 57. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Furgani, L.; Meghella, M.; Saouma, V.E. A New Class of Seismic Damage and Performance Indices for Arch Dams via ETA Method. Eng. Struct. 2016, 110, 145–160. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alegre, A.; Oliveira, S.; Proença, J.; Mendes, P.; Carvalho, E. A Finite Element Formulation for True Coupled Modal Analysis and Nonlinear Seismic Modeling of Dam–Reservoir–Foundation Systems: Application to an Arch Dam and Validation. Infrastructures 2025, 10, 193. https://doi.org/10.3390/infrastructures10080193
Alegre A, Oliveira S, Proença J, Mendes P, Carvalho E. A Finite Element Formulation for True Coupled Modal Analysis and Nonlinear Seismic Modeling of Dam–Reservoir–Foundation Systems: Application to an Arch Dam and Validation. Infrastructures. 2025; 10(8):193. https://doi.org/10.3390/infrastructures10080193
Chicago/Turabian StyleAlegre, André, Sérgio Oliveira, Jorge Proença, Paulo Mendes, and Ezequiel Carvalho. 2025. "A Finite Element Formulation for True Coupled Modal Analysis and Nonlinear Seismic Modeling of Dam–Reservoir–Foundation Systems: Application to an Arch Dam and Validation" Infrastructures 10, no. 8: 193. https://doi.org/10.3390/infrastructures10080193
APA StyleAlegre, A., Oliveira, S., Proença, J., Mendes, P., & Carvalho, E. (2025). A Finite Element Formulation for True Coupled Modal Analysis and Nonlinear Seismic Modeling of Dam–Reservoir–Foundation Systems: Application to an Arch Dam and Validation. Infrastructures, 10(8), 193. https://doi.org/10.3390/infrastructures10080193









