Effect of Design on Human Injury and Fatality Due to Impacts by Small UAS
Abstract
1. Introduction
2. MBS Model Development to Simulate UAS Interactions with Human Body
2.1. MBS Model Development Activities
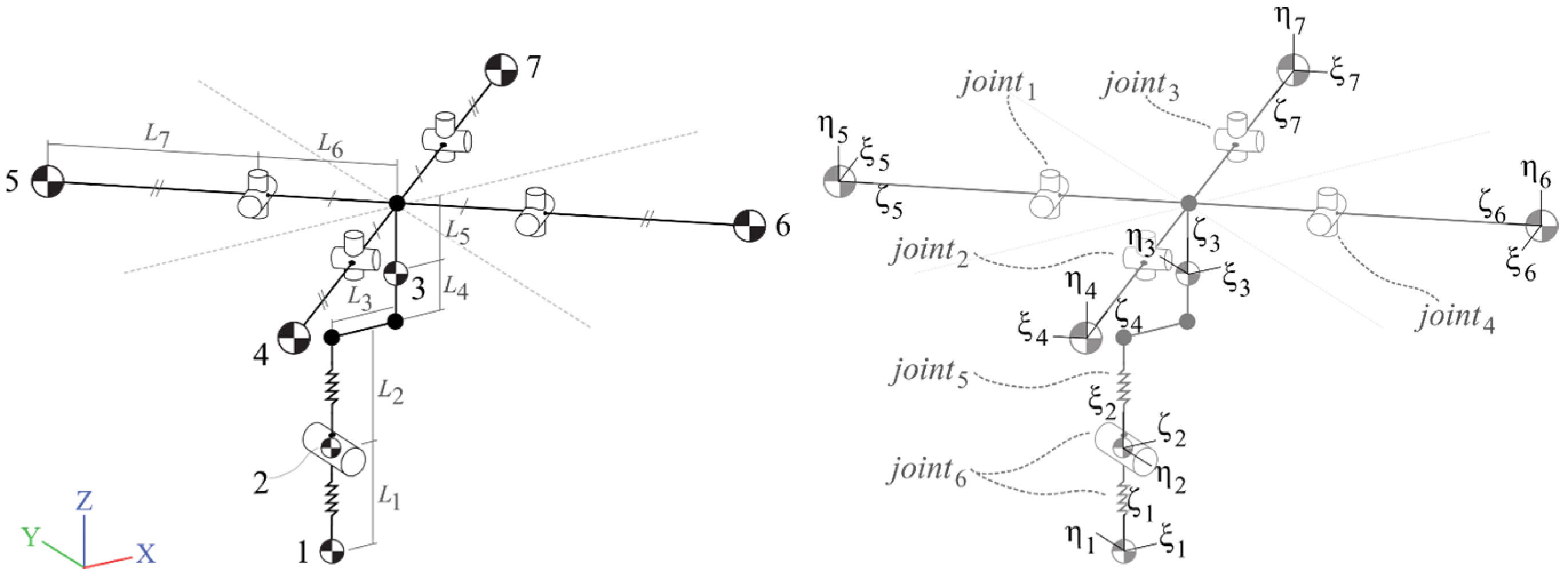
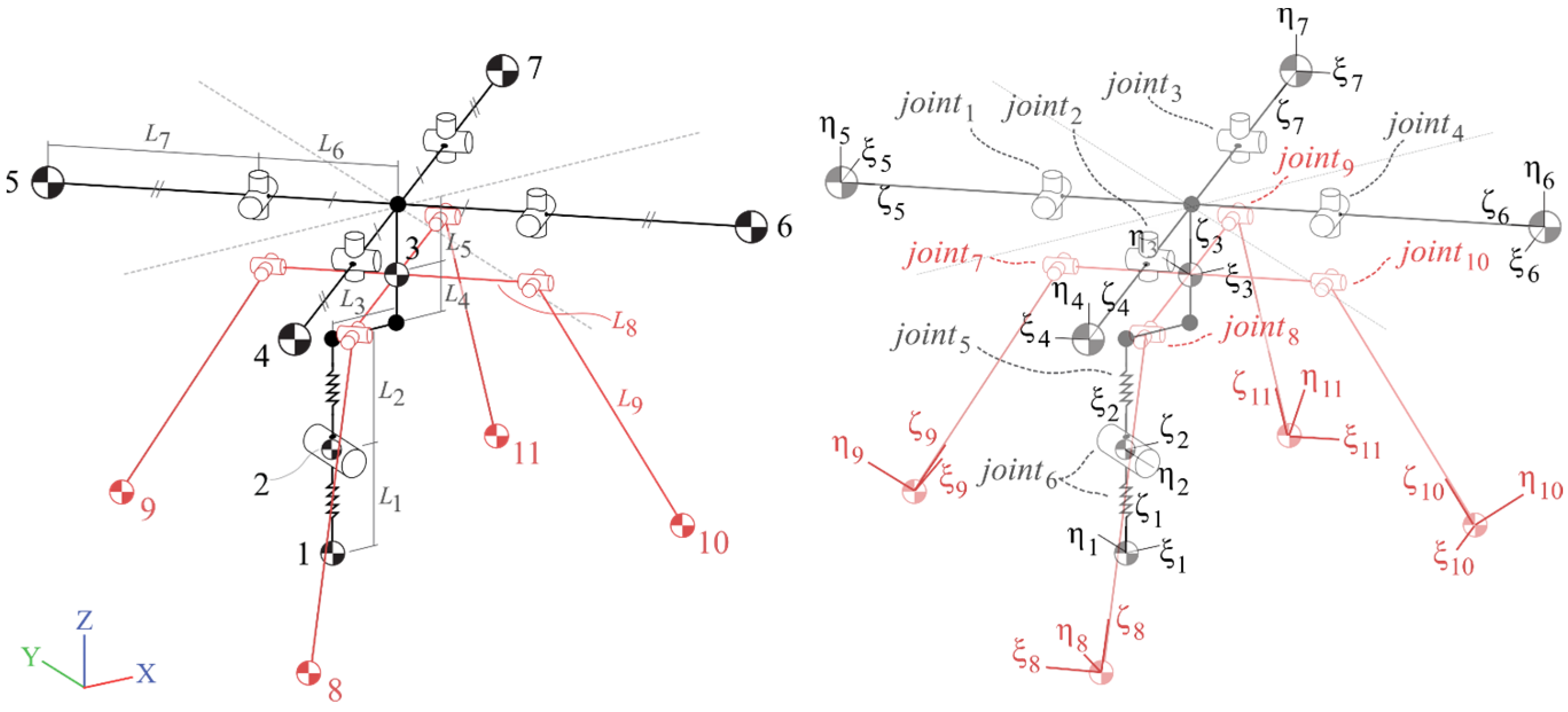
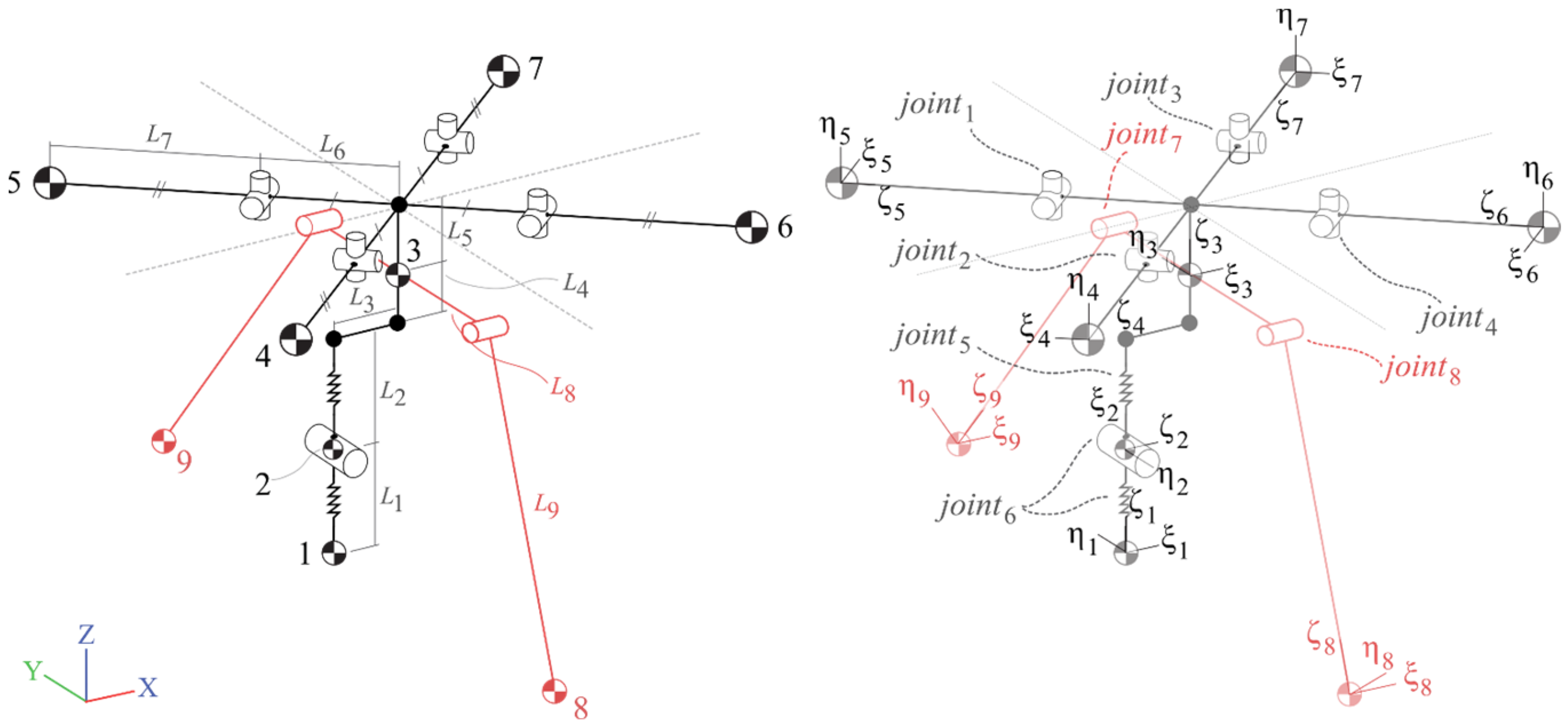
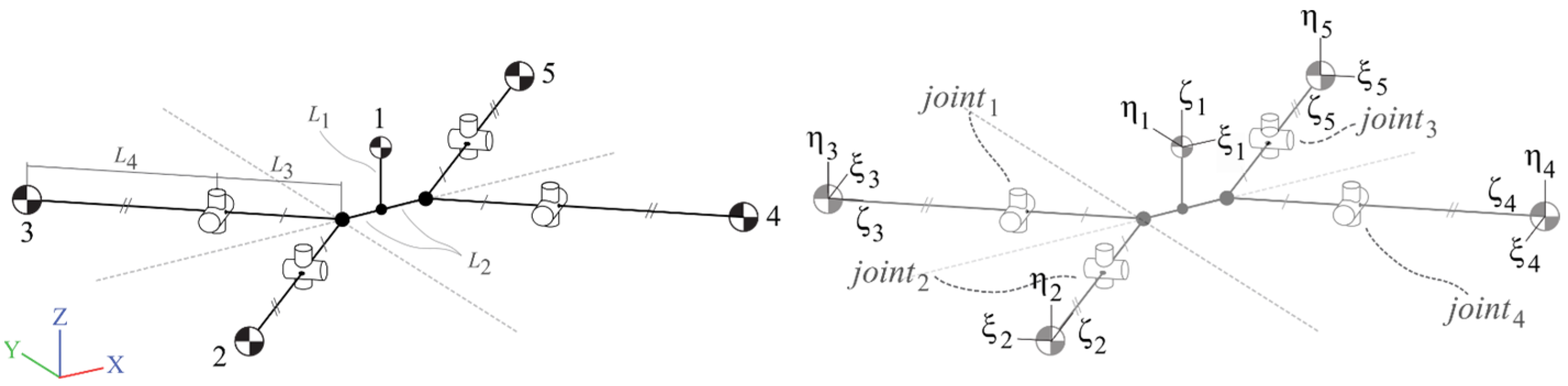
2.2. UAS Multibody System Models
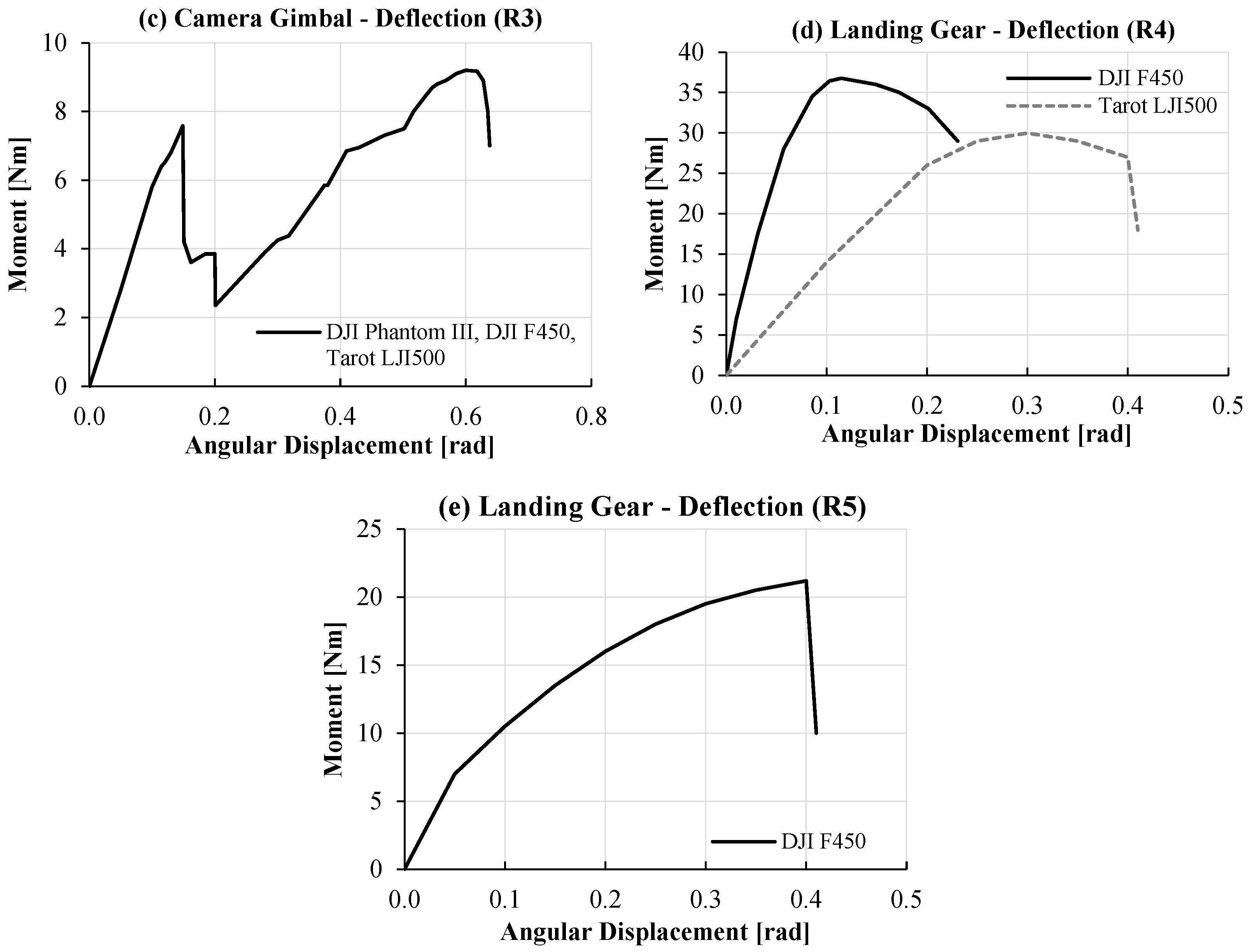
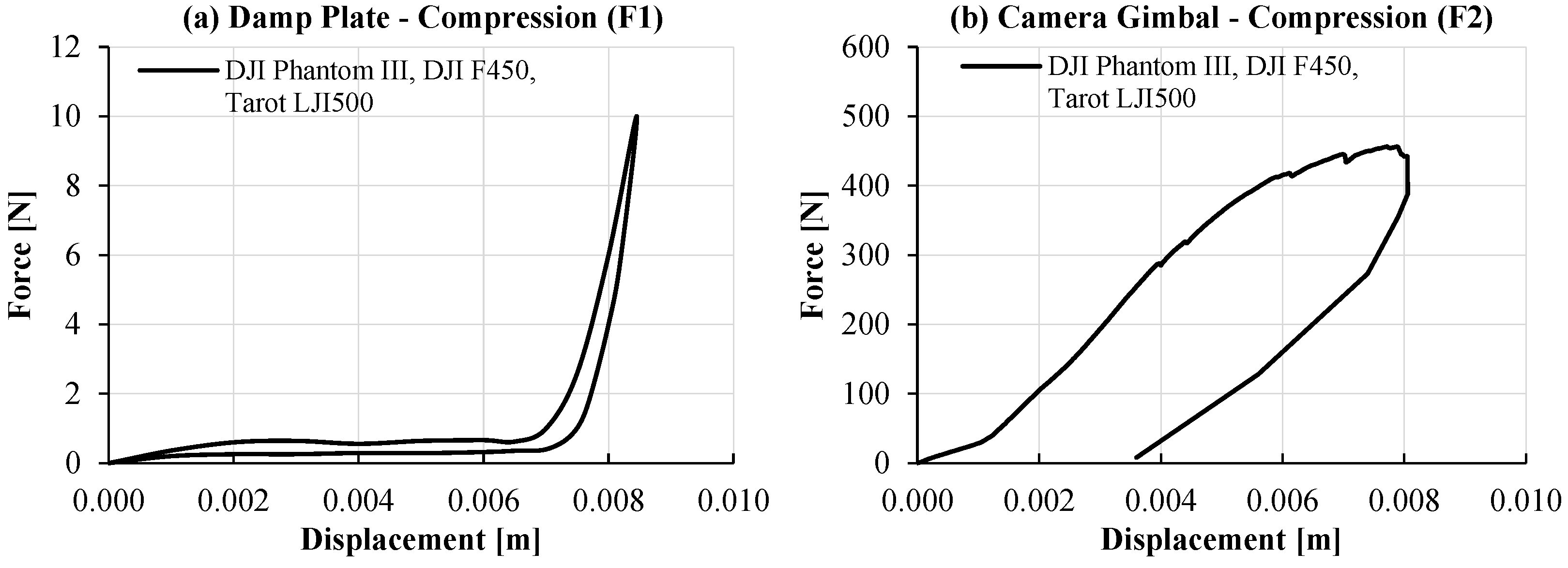
2.3. Joint Types and Force/Moment Characteristics
2.4. Contact Characteristics
2.5. MBS Model of Human Body and Head Injury
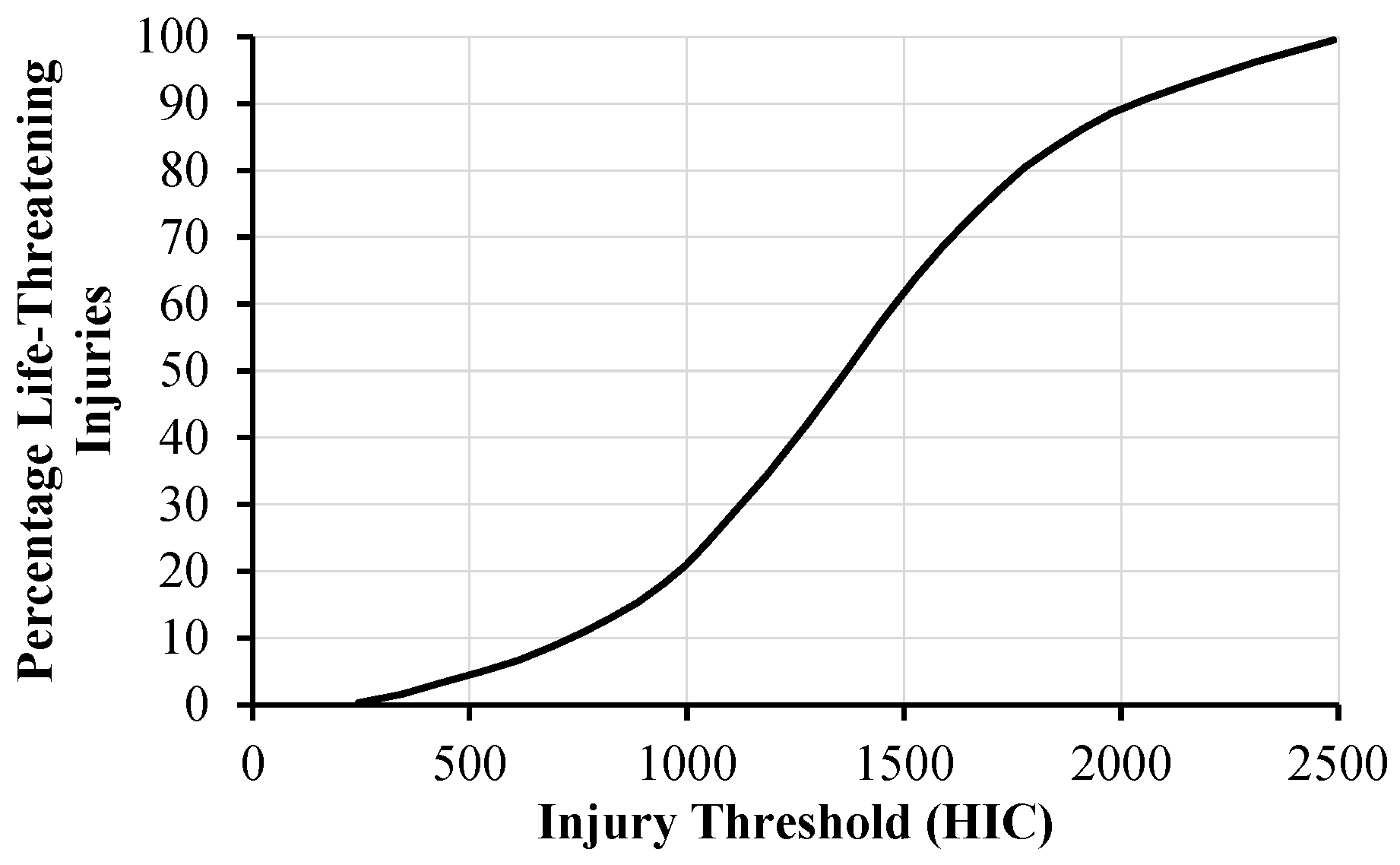
2.6. Conversion into Probability of Fatality
3. Impact Scenario Selection and Simulation Setup
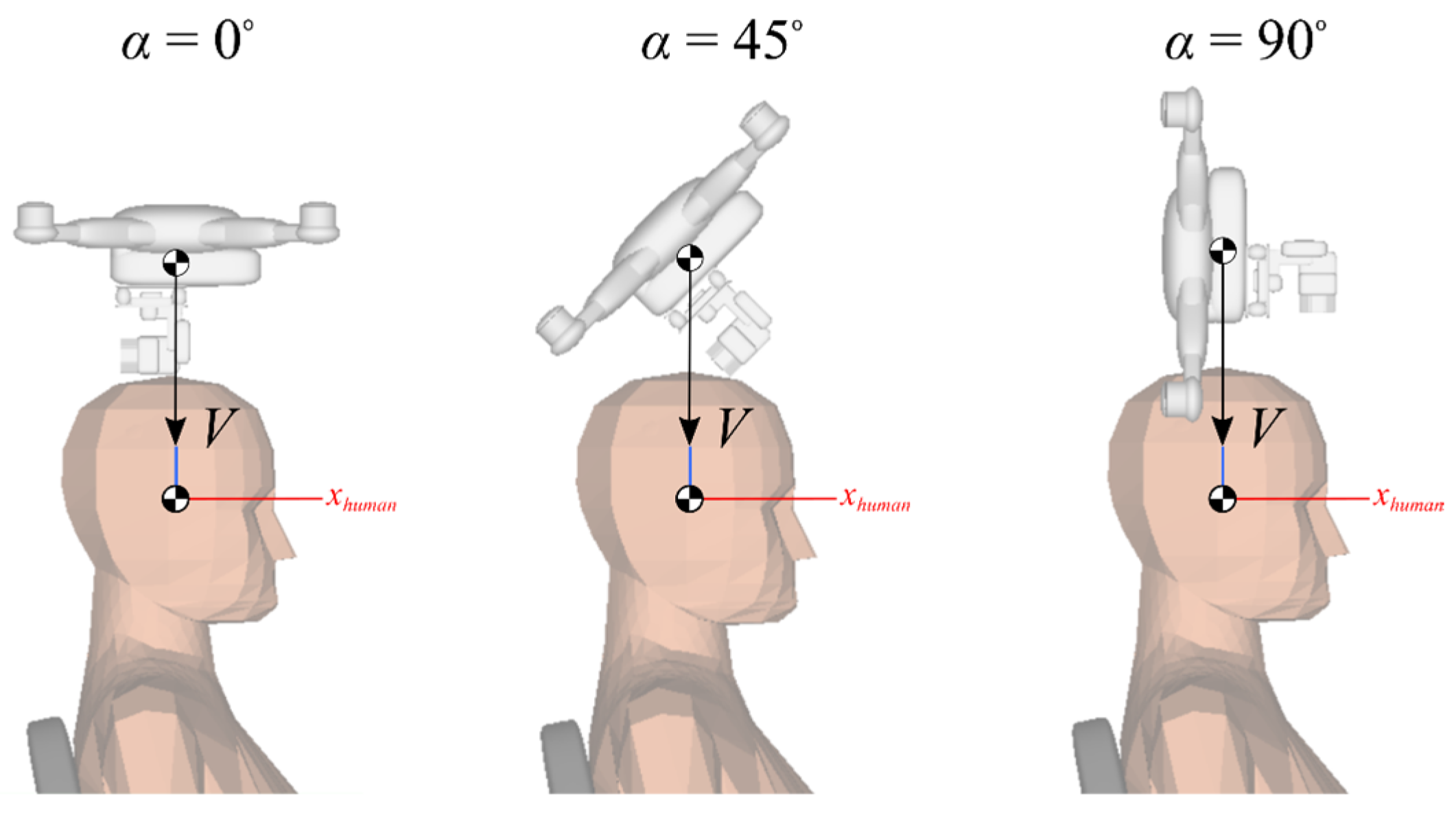
3.1. Controlled Horizontal Flight Impact
3.2. Uncontrolled Vertical Drop Impact
4. Simulation Results for Controlled Horizontal Flight Impact
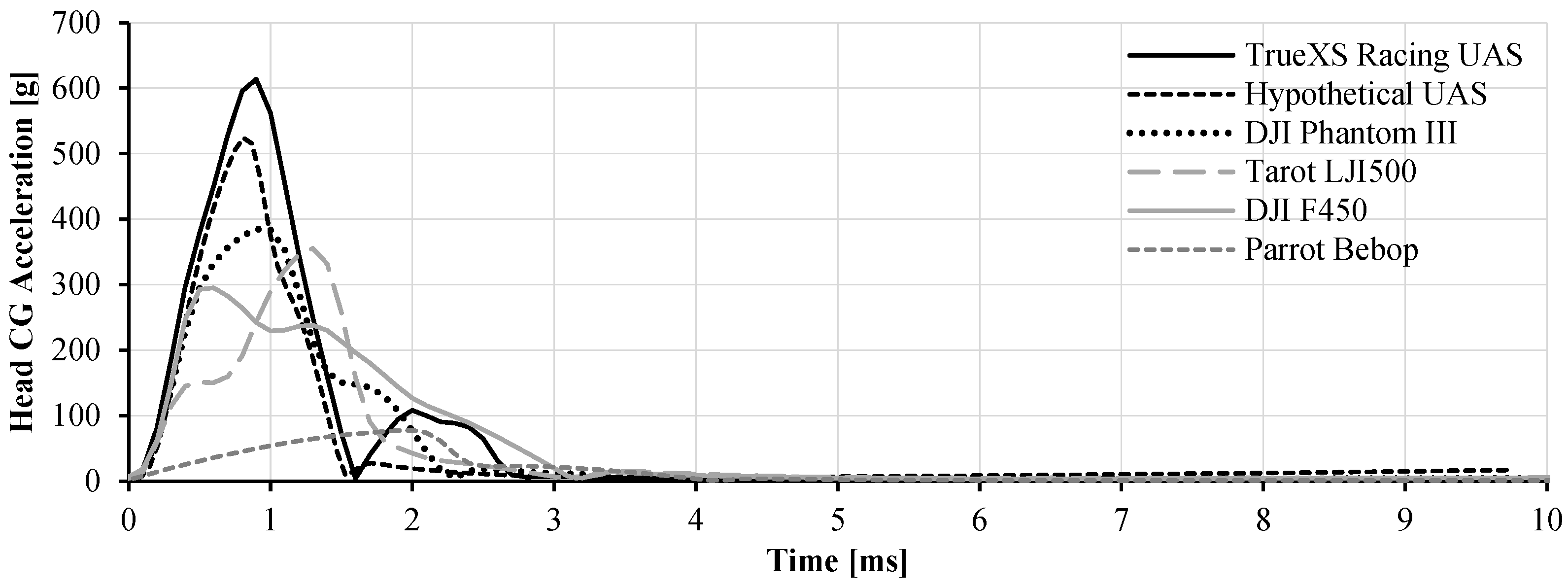
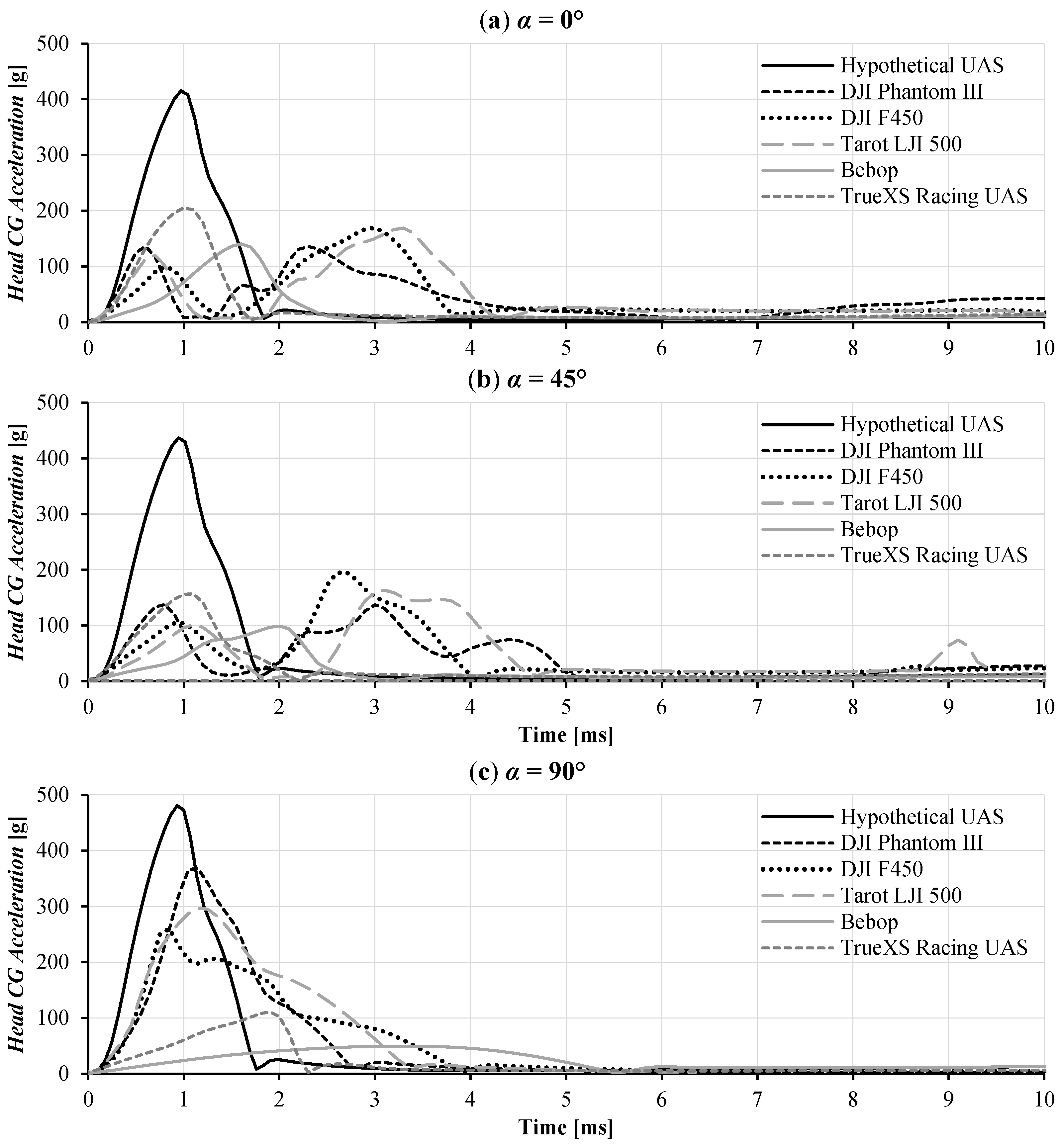
4.1. Head CG Acceleration–Time History
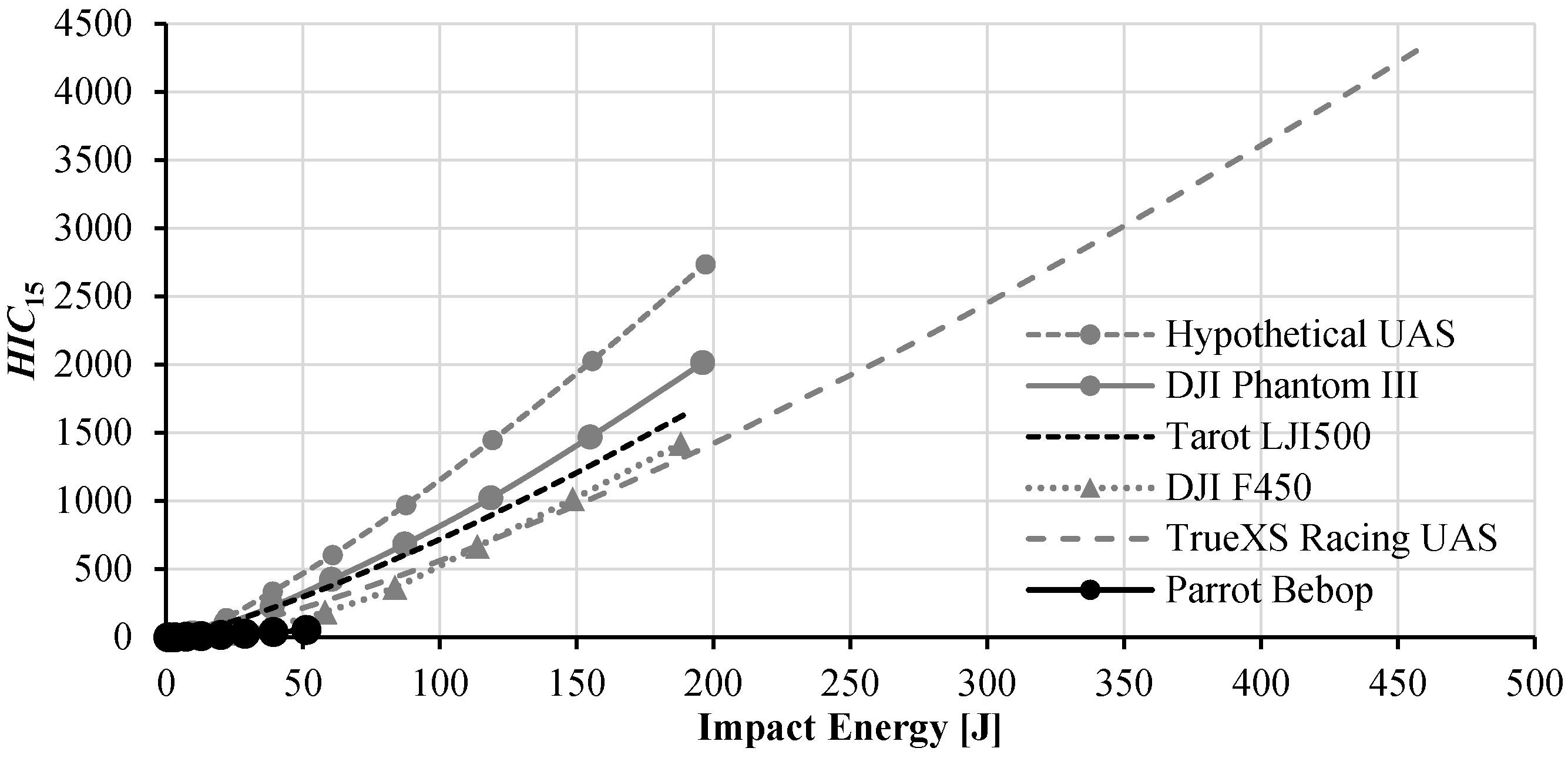
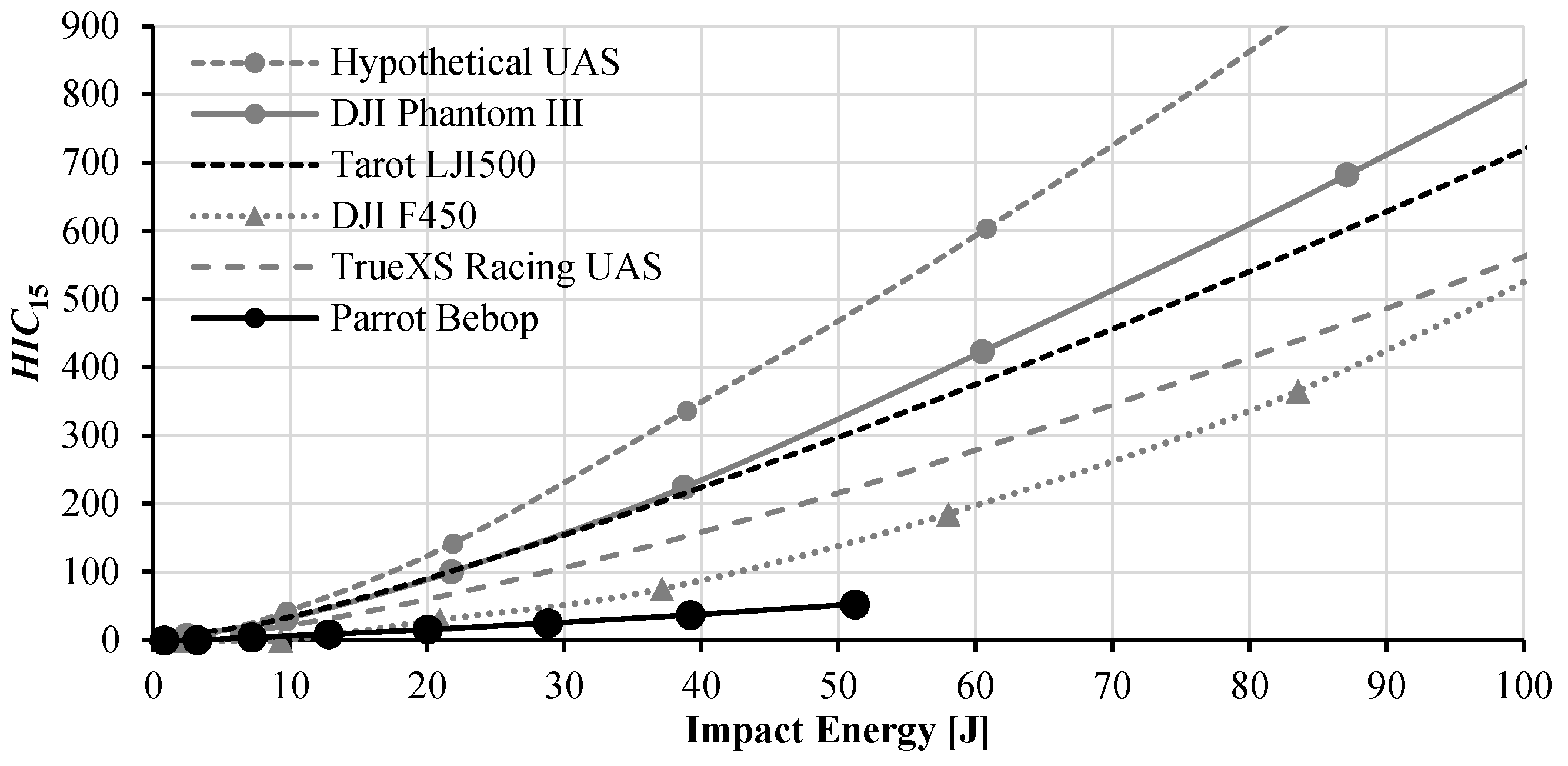
4.2. Head Injury Criterion (HIC15)
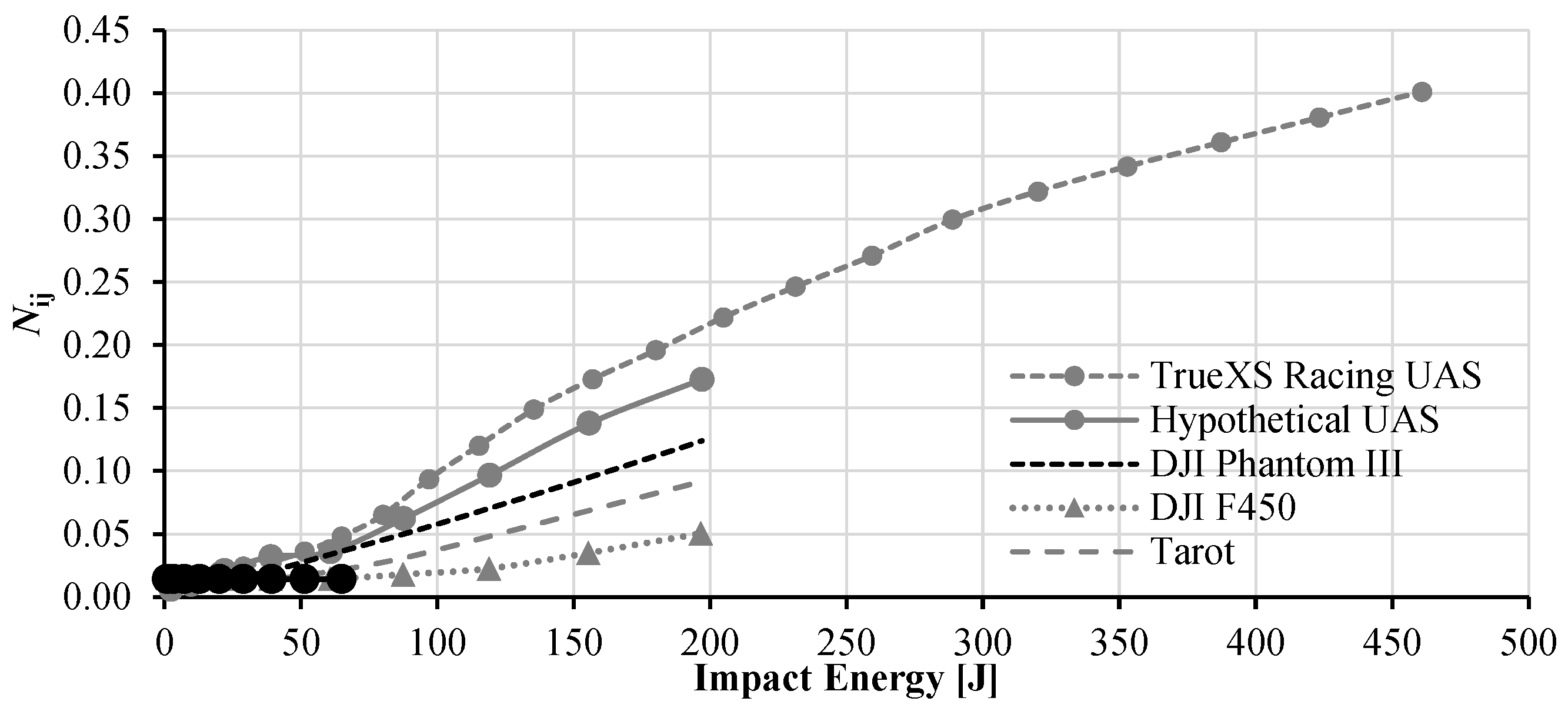
4.3. Neck Injury (Nij)
4.4. Probability of Fatality (PoF)
4.5. Discussion of Results Relative to UAS Design
5. Simulation Results for Uncontrolled Vertical Drop Impact
5.1. Head CG Acceleration–Time History
5.2. Head Injury Criterion (HIC15) and Probability of Fatality (PoF) for UAS Measuring 1.2 Kg
5.3. Head Injury Criterion (HIC15) and Probability of Fatality (PoF) for UAS Measuring 0.4 Kg
5.4. Discussion of Results Relative to UAS Design
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Male Body | PMHS #1 | PMHS #2 | PMHS #3 | PMHS Mean | MBS Male Model [13,25] | Difference |
|---|---|---|---|---|---|---|
| Height | 178 cm | 168 cm | 180 cm | 175.3 cm | 174 cm | −0.8% |
| Weight | 77.1 kg | 73.9 kg | 64.9 kg | 72.0 kg | 75.7 kg | +5.1% |
| Impact Case No. | OSU Test | PMHS # | Impact Direction ψ [°] | Impact Elevation θ [°] | UAS Pitch α [°] | Impact Speed, V [m/s] | Eccentricity [mm] | HIC15 | Differ. % | Point of Contact | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Test | MBS | ||||||||||
| 1 | #2 | 1 | 90 | 0 | 0 | 17 | 28.2 | 866 | 689 | −22.8 | Motor Arm |
| 2 | #3 | 1 | 90 | 0 | 0 | 18.5 | 17.7 | 1076 | 886 | −19.4 | Motor Arm |
| 3 | #4 | 1 | 90 | 0 | 0 | 21.5 | 6.0 | 2892 | 2656 | −8.5 | Fuselage |
| 4 | #10 | 2 | 90 | 0 | 0 | 18.5 | 43.4 | 500 | 527 | +5.3 | Motor Arm |
| 5 | #11a | 2 | 90 | 58 | 58 | 21.5 | 42.1 | 929 | 828 | −11.5 | Motor Arm |
| 6 | #16a | 3 | 90 | 58 | 58 | 18.5 | 43.4 | 412 | 381 | −7.8 | Motor Arm |
| 7 | #17 | 3 | 90 | 58 | 58 | 21.5 | 20.7 | 2527 | 2251 | −11.5 | Fuselage |
References
- End, A.; Barzantny, C.; Stolz, M.; Grupe, P.; Schmidt, R.; Papenfuß, A.; Eißfeldt, H. Public Acceptance of Civilian Drones and Air Taxis in Germany: A Comprehensive Overview. CEAS Aeronaut. J. 2025, 16, 665–676. [Google Scholar] [CrossRef]
- Glick, T.B.; Figliozzi, M.A.; Unnikrishnan, A. Case Study of Drone Delivery Reliability for Time-Sensitive Medical Supplies with Stochastic Demand and Meteorological Conditions. Transp. Res. Rec. J. Transp. Res. Board 2022, 2676, 242–255. [Google Scholar] [CrossRef]
- El-Adle, A.M.; Ghoniem, A.; Haouari, M. Parcel Delivery by Vehicle and Drone. J. Oper. Res. Soc. 2021, 72, 398–416. [Google Scholar] [CrossRef]
- Benarbia, T.; Kyamakya, K.A. Literature Review of Drone-Based Package Delivery Logistics Systems and Their Implementation Feasibility. Sustainability 2021, 14, 360. [Google Scholar] [CrossRef]
- Mohd Daud, S.M.S.; Mohd Yusof, M.Y.P.; Heo, C.C.; Khoo, L.S.; Chainchel Singh, M.K.; Mahmood, M.S.; Nawawi, H. Applications of Drone in Disaster Management: A Scoping Review. Sci. Justice 2022, 62, 30–42. [Google Scholar] [CrossRef] [PubMed]
- Mogili, U.R.; Deepak, B.B.V.L. Review on Application of Drone Systems in Precision Agriculture. Procedia Comput. Sci. 2018, 133, 502–509. [Google Scholar] [CrossRef]
- Aljalaud, F.; Kurdi, H.; Youcef-Toumi, K. Bio-Inspired Multi-UAV Path Planning Heuristics: A Review. Mathematics 2023, 11, 2356. [Google Scholar] [CrossRef]
- Meng, W.; Zhang, X.; Zhou, L.; Guo, H.; Hu, X. Advances in UAV Path Planning: A Comprehensive Review of Methods, Challenges, and Future Directions. Drones 2025, 9, 376. [Google Scholar] [CrossRef]
- Tutsoy, O.; Asadi, D.; Ahmadi, K.; Nabavi-Chashmi, S.Y.; Iqbal, J. Minimum Distance and Minimum Time Optimal Path Planning with Bioinspired Machine Learning Algorithms for Faulty Unmanned Air Vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9069–9077. [Google Scholar] [CrossRef]
- JARUS. SORA v2.0 to v2.5—Summary of Changes for External Consultation. EASA Workshop Presentation Slides; JARUS: Online, 2023; Available online: https://www.easa.europa.eu/sites/default/files/dfu/sora_workshop_feb_2023_-_4_summary_of_changes_sora.pdf (accessed on 23 July 2025).
- FAA. Operation and Certification of Small Unmanned Aircraft Systems; FAA: Washington, DC, USA, 2016. Available online: https://www.govinfo.gov/content/pkg/FR-2016-06-28/pdf/2016-15079.pdf (accessed on 23 July 2025).
- JARUS. Theoretical Basis for Ground Risk Classification and Mitigation, Annex F to Guidelines on SORA; JARUS: Online, 2024; Available online: http://jarus-rpas.org/wp-content/uploads/2024/06/SORA-v2.5-Annex-F-Release.JAR_doc_29pdf.pdf (accessed on 10 June 2025).
- RCC (Range Commanders Council). Range Safety Criteria for Unmanned Air Vehicles, Rationale and Methodology Supplement. Supplement to Document 323-99. 2001. Available online: https://www.trmc.osd.mil/wiki/download/attachments/113019905/323-99Sup.pdf?version=1&modificationDate=1623181167646&api=v2 (accessed on 15 June 2025).
- Magister, T. The Small Unmanned Aircraft Blunt Criterion Based Injury Potential Estimation. Saf. Sci. 2010, 48, 1313–1320. [Google Scholar] [CrossRef]
- Toyota Motor Corporation. Documentation THUMS, AM50 Occupant Model Academic Version 5.0_20150527. 2015. Available online: https://www.toyota.co.jp/thums/about/ (accessed on 15 June 2025).
- Happee, R.; Ridella, S. Mathematical Human Body Models Representing a Mid Size Male and a Small Female for Frontal, Lateral and Rearward Impact Loading. In Proceedings of the IRCOBI Conference Proceedings, Montpellier, France, 20–22 September 2000; pp. 1–18. [Google Scholar]
- Arterburn, D.; Olivares, G.; Bolte, J.; Prabhu, R.; Duma, S. Task A14: UAS Ground Collision Severity Evaluation, 2017–2019; NTIS: Springfield, VA, USA, 2019; Available online: https://assureuas.com/wp-content/uploads/2021/06/A14-Final-Report.pdf (accessed on 23 February 2025).
- Svatý, Z.; Vrtal, P.; Mičunek, T.; Kohout, T.; Nouzovský, L.; Frydrýn, M.; Blodek, T.; Kocián, K. Impact Analysis Assessment of UAS Collision with a Human Body. PLoS ONE 2025, 20, e0320073. [Google Scholar] [CrossRef]
- Rattanagraikanakorn, B.; Schuurman, M.; Gransden, D.I.; Happee, R.; De Wagter, C.; Sharpanskykh, A.; Blom, H.A.P. Modelling Head Injury Due to Unmanned Aircraft Systems Collision: Crash Dummy vs Human Body. Int. J. Crashworthiness 2022, 27, 400–413. [Google Scholar] [CrossRef]
- Weng, Y.; Bian, K.; Gunasekaran, K.; Gholipour, J.; Vidal, C.; Mao, H. Modeling Small Remotely Piloted Aircraft System to Head Impact for Investigating Craniocerebral Response. J. Biomech. 2021, 128, 110748. [Google Scholar] [CrossRef] [PubMed]
- Toyota Motor Corporation. Documentation: Total Human Model for Safety AM50 Pedestrian/Occupant Model Academic Version 4.02. 2018. Available online: https://www.toyota.co.jp/thums/about/ (accessed on 15 June 2025).
- Stark, D.B.; Willis, A.K.; Eshelman, Z.; Kang, Y.S.; Ramachandra, R.; Bolte, J.H.; McCrink, M. Human Response and Injury Resulting from Head Impacts with Unmanned Aircraft Systems. Stapp Car Crash J. 2019, 63, 29–64. [Google Scholar] [CrossRef] [PubMed]
- Ohio State University. Annex C: Task A14 UAS Ground Collision Severity Evaluation, Ohio State University Final Report; NTIS: Springfield, VA, USA, 2019; Available online: https://assureuas.com/wp-content/uploads/2021/06/A14-Annex-C.pdf (accessed on 5 April 2025).
- Jiang, C.; Blom, H.; Rattanagraikanakorn, B. Enhancing Safety Feedback to the Design of Small, Unmanned Aircraft by Joint Assessment of Impact Area and Human Fatality. Risk Anal. 2025, 45, 1115–1131. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, Z.; Lan, H.; Cao, L.; Guo, D.; Hao, Z.; Bai, C.; Yang, Z. Study of the Head and Neck Injury Risk under Impact Conditions of the Light UAV with a Medium Weight. Arch. Civ. Mech. Eng. 2023, 23, 226. [Google Scholar] [CrossRef]
- Li, R.; Li, Z.; Lan, H.; Bai, C.; Guo, Y.; Wang, Y.; Wang, J.; Liu, X.; Yang, Z. Study on the Head and Neck Injury Risk Impacted by UAV: Effect of Impact Velocity, Angle, Location, and Mass. Int. J. Crashworthiness 2024, 29, 482–494. [Google Scholar] [CrossRef]
- Rattanagraikanakorn, B.; Gransden, D.I.; Schuurman, M.; De Wagter, C.; Happee, R.; Sharpanskykh, A.; Blom, H.A.P. Multi-Body System Modelling of Unmanned Aircraft System Collisions with the Human Head. Int. J. Crashworthiness 2020, 25, 689–707. [Google Scholar] [CrossRef]
- Rattanagraikanakorn, B. Modelling Collisionconsequences of Unmanned Aircraft Systems on Human. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2021. [Google Scholar]
- Brake, M.R. An Analytical Elastic-Perfectly Plastic Contact Model. Int. J. Solids Struct. 2012, 49, 3129–3141. [Google Scholar] [CrossRef]
- TASS International. MADYMO Theory Manual, Version 7.7; TASS International: Helmond, The Netherlands, 2017. [Google Scholar]
- TASS International. MADYMO Human Body Models Manual, Release 7.7; TASS International: Helmond, The Netherlands, 2017. [Google Scholar]
- Klinich, K.; Saul, R.; Auguste, G.; Backaitis, S.; Kleinberger, M. Techniques for Developing Child Dummy Protection Reference Values. Measurement. 1996. Available online: https://rosap.ntl.bts.gov/view/dot/14741/dot_14741_DS1.pdf (accessed on 15 June 2025).
- Seacrist, T.; Balasubramanian, S.; García-España, J.F.; Maltese, M.R.; Arbogast, K.B.; Lopez-Valdes, F.J.; Kent, R.W.; Tanji, H.; Higuchi, K. Kinematic Comparison of Pediatric Human Volunteers and the Hybrid III 6-Year-Old Anthropomorphic Test Device. Ann. Adv. Automot. Med. 2010, 54, 97–108. [Google Scholar] [CrossRef]
- Seacrist, T.; Samuels, M.; García-España, J.F.; Arbogast, K.B.; Mathews, E.A.; Balasubramanian, S.; Maltese, M.R.; Longhitano, D.; St. Lawrence, S. Kinematic Comparison of the Hybrid III and Q-Series Pediatric ATDs to Pediatric Volunteers in Low-Speed Frontal Crashes. Ann. Adv. Automot. Med. 2012, 56, 285–298. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Lv, W.; Hynčík, L.; Zhou, B.; Zhao, H.; Cui, S.; He, L.; Ruan, S. Injury Study of the 6-Year-Old Pediatric Thorax and Abdomen in Frontal Sled Tests Using Different Computational Models. Front. Future Transp. 2022, 3, 890776. [Google Scholar] [CrossRef]
- Parr, M.J.C.; Miller, M.E.; Bridges, N.R.; Buhrman, J.R.; Perry, C.E.; Wright, N.L. Evaluation of the Nij Neck Injury Criteria with Human Response Data for Use in Future Research on Helmet Mounted Display Mass Properties. In Proceedings of the 56th Human Factors and Ergonomics Society Annual Meeting, Boston, MA, USA, 22–26 October 2012; pp. 2070–2074. [Google Scholar] [CrossRef]
- Schmitt, K.-U.; Niederer, P.F.; Cronin, D.S.; Morrison, B., III; Muser, M.H.; Walz, F. Trauma Biomechanics; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Tyrell, D.C.; Severson, K.J.; Marquis, B.P. Analysis of Occupant Protection Strategies in Train Collisions. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition; San Francisco, CA, USA, 12–17 November 1995. Available online: https://rosap.ntl.bts.gov/view/dot/8520 (accessed on 11 November 2024).
- Prasad, P.; Mertz, H.J. The Position of the United States Delegation to the ISO Working Group 6 on the Use of HIC in the Automotive Environment; SAE Technical Paper; SAE: Warrendale, PA, USA, 1985. [Google Scholar]
- Rattanagraikanakorn, B.; Blom, H.A.P.; Sharpanskykh, A.; de Wagter, C.; Jiang, C.; Schuurman, M.J.; Gransden, D.I.; Happee, R. Modeling and Simulating Human Fatality Due to Quadrotor UAS Impact. In Proceedings of the AIAA AVIATION 2020 FORUM, Online, 15–19 June 2020. [Google Scholar] [CrossRef]
- Parrot Drones SAS. All-In-One Drone Solution for 3D Modeling (Parrot Bebop-Pro 3D Modeling Product Sheet). Online. 2018. Available online: https://www.parrot.com/assets/s3fs-public/2021-09/bat_parrot_productsheet_power_bb-3d-modelling_a4_2018-01-08_en.pdf (accessed on 10 October 2019).
- FPV Drone Reviews. Top 5 Fastest Racing Drones of 2018—Buying Guide. Online. 2018. Available online: https://fpvdronereviews.com/guides/fastest-racing-drones/ (accessed on 10 October 2019).
- Belcastro, C.M.; Newman, R.L.; Evans, J.; Klyde, D.H.; Barr, L.C.; Ancel, E. Hazards Identification and Analysis for Unmanned Aircraft System Operations. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Foster, J.V.; Hartman, D.C. High-Fidelity Multirotor Unmanned Aircraft System Simulation Development for Trajectory Prediction under off-Nominal Flight Dynamics. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Arterburn, D.; Ewing, M.; Prabhu, R.; Zhu, F.; Francis, D. FAA UAS Center of Excellence Task A4: UAS Ground Collision Severity Evaluation; ASSURE: Huntsville, AL, USA, 2017; Available online: https://assureuas.com/wp-content/uploads/2021/06/A4-Final-Report.pdf (accessed on 17 May 2025).
- Bernard, E.; Johnston, A. Explosions and Blast Injuries—A Primer for Clinicians. N. Engl. J. Med. 2013, 368, 1045. [Google Scholar] [CrossRef]
- Fahlstedt, M.; Halldin, P.; Kleiven, S. Comparison of Multibody and Finite Element Human Body Models in Pedestrian Accidents with the Focus on Head Kinematics. Traffic Inj. Prev. 2016, 17, 320–327. [Google Scholar] [CrossRef] [PubMed]
- ASSURE. Annex B: NIAR Final Report—Task A14: UAS Ground Collision Severity Evaluation 2017–2018; NTIS: Springfield, VA, USA, 2019; Available online: https://assureuas.com/wp-content/uploads/2021/06/A14-Annex-B.pdf (accessed on 23 July 2025).







| UAS Type | Total Weight [kg] | Max. Speed [m/s] | Configuration | Airframe Materials | Airframe Design | Estimated Cost |
|---|---|---|---|---|---|---|
| DJI Phantom III (Baseline) | 1.21 | 18 | Quadcopter with camera gimbal system | ABS Plastic | Sandwich shell structure | ~USD 00 |
| DJI F450 | 1.16 | 18 | ABS Plastic | Sandwich plate structure with moulded plastic motor arm | ~USD 500 (kit estimate) * | |
| Tarot LJI500 | 1.18 | 18 | Carbon Fibre | Sandwich plate structure with carbon fibre rod as motor arm | ~USD 450 (kit estimate) * | |
| Parrot Bebop | 0.40 | 16 | Quadcopter with front camera cover with polystyrene foam | ABS Plastic | Moulded ABS plastic structure | ~USD 500 |
| TrueXS Racing UAS | 0.40 | 48 | Racing quadcopter with onboard camera | Carbon Fibre | Sandwich plate structure of thick laminates, including motor arm | USD 200–500 (custom build) * |
| Weight Class | UAS Type | Real-World View | Multibody System View |
|---|---|---|---|
| Mid-size UAS () | DJI Phantom III (Baseline) |  |  |
| Hypothetical UAS | N/A | 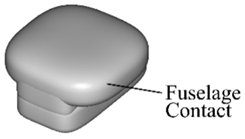 | |
| Tarot LJI500 |  | 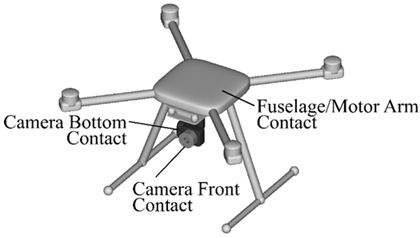 | |
| DJI F450 |  | 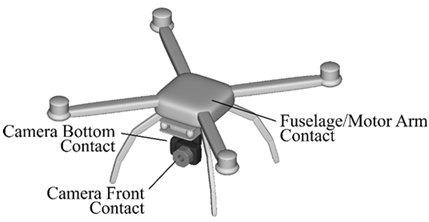 | |
| Micro UAS () | Parrot Bebop |  |  |
| TrueXS Racing UAS |  | 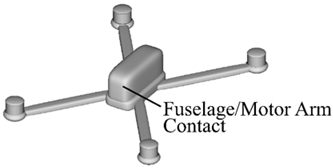 |
| UAS Model | Segment Body Masses [kg] | Segment Lengths [m] |
|---|---|---|
| DJI Phantom III (Baseline) | W1 = 0.101, W2 = 0.056, W3 = 0.839, W4–7 = 0.055 | l1 = 0.040, l2 = 0.020, l3 = 0.023, l4 = 0.016, l5 = 0.030, l6 = 0.014, l7 = 0.165 |
| Hypothetical UAS (Rigid) | W1 = 1.21 | - |
| DJI F450 | W1 = 0.101, W2 = 0.056, W3 = 0.640, W4–7 = 0.087, W8–11 = 0.017 | l1 = 0.040, l2 = 0.020, l3 = 0.023, l4 = 0.020, l5 = 0.008, l6 = 0.030, l7 = 0.170, l8 = 0.049, l9 = 0.100 |
| TarotLJI500 | W1 = 0.101, W2 = 0.056, W3 = 0.621, W4–7 = 0.090, W8–9 = 0.040 | l1 = 0.040, l2 = 0.020, l3 = 0.023, l4 = 0.020, l5 = 0.008, l6 = 0.030, l7 = 0.170, l8 = 0.060, l9 = 0.200 |
| Parrot Bebop | W1 = 0.360, W2–5 = 0.010 | l1 = 0.015, l2 = 0.025, l3 = 0.055, l4 = 0.080 |
| TrueXS Racing UAS | W1 = 0.360, W2–5 = 0.010 | l1 = 0.012, l2 = 0.032, l3 = 0.080 |
| UAS Type | Joint Type | Moment Characteristics | Force Characteristics |
|---|---|---|---|
| DJI Phantom III | Joint 1–4 (Universal) | R1, R2 | - |
| Joint 5 (Translational) | - | F1 | |
| Joint 6 (Translational–Revolute) | R3 | F2 | |
| Hypothetical UAS | - | - | - |
| DJI F450 | Joint 1–4 (Universal) | R1, R2 | - |
| Joint 5 (Translational) | - | F1 | |
| Joint 6 (Translational–Revolute) | R3 | F2 | |
| Joint 7–10 (Universal) | R4, R5 | - | |
| Tarot LJI500 | Joint 1–4 (Universal) | R1, R2 | - |
| Joint 5 (Translational) | - | F1 | |
| Joint 6 (Translational–Revolute) | R3 | F2 | |
| Joint 7–8 (Revolute) | R4 | - | |
| Parrot Bebop | Joint 1–4 (Universal) | R1, R2 | - |
| TrueXS Racing UAS | Joint 1–4 (Universal) | R1, R2 | - |
| Kinetic Energy | 151 J (Case a) | 51 J (Case b) | ||||
|---|---|---|---|---|---|---|
| Speed [m/s] | HIC15 | PoF | Speed [m/s] | HIC15 | PoF | |
| RCC [13] | n.a. | n.a. | 0.99 | n.a. | n.a. | 0.089 |
| Hypothetical | 15.8 | 1950 | 0.91 | 9.2 | 481 | 0.022 |
| DJI Phantom III | 15.8 | 1572 | 0.66 | 9.2 | 374 | 0.022 |
| Tarot LJI500 | 16.0 | 1354 | 0.48 | 9.3 | 340 | 0.011 |
| DJI F450 | 16.1 | 1152 | 0.32 | 9.4 | 161 | 0.010 |
| True XS Racing | 27.5 | 1060 | 0.30 | 16 | 247 | 0.011 |
| Parrot Bebop | 27.5 | n.a. | n.a. | 16 | 58 | 0.001 |
| Pitch Angle | 0° (Case a) | 45° (Case b) | 90° (Case c) | |||
|---|---|---|---|---|---|---|
| Unit | HIC15 | PoF | HIC15 | PoF | HIC15 | PoF |
| RCC [13] 195 J | n.a. | 1.0 | n.a. | 1.0 | n.a. | 1.0 |
| Hypothetical | 1502 | 0.720 | 1521 | 0.734 | 1584 | 0.778 |
| DJI Ph. III | 296 | 0.013 | 335 | 0.014 | 1239 | 0.505 |
| Tarot LJI500 | 272 | 0.012 | 291 | 0.013 | 982 | 0.290 |
| DJI F450 | 173 | 0.011 | 201 | 0.011 | 800 | 0.162 |
| Pitch Angle | 0° (Case a) | 45° (Case b) | 90° (Case c) | |||
|---|---|---|---|---|---|---|
| Unit | HIC15 | PoF | HIC15 | PoF | HIC15 | PoF |
| RCC [13] 65 J | n.a. | 0.32 | n.a. | 0.32 | n.a. | 0.32 |
| True XS Rac. | 312 | 0.013 | 160 | 0.010 | 83 | 0.005 |
| Parrot Bebop | 128 | 0.009 | 71 | 0.003 | 42 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rattanagraikanakorn, B.; Blom, H.A.P.; Gransden, D.I.; Schuurman, M.; De Wagter, C.; Sharpanskykh, A.; Happee, R. Effect of Design on Human Injury and Fatality Due to Impacts by Small UAS. Designs 2025, 9, 88. https://doi.org/10.3390/designs9040088
Rattanagraikanakorn B, Blom HAP, Gransden DI, Schuurman M, De Wagter C, Sharpanskykh A, Happee R. Effect of Design on Human Injury and Fatality Due to Impacts by Small UAS. Designs. 2025; 9(4):88. https://doi.org/10.3390/designs9040088
Chicago/Turabian StyleRattanagraikanakorn, Borrdephong, Henk A. P. Blom, Derek I. Gransden, Michiel Schuurman, Christophe De Wagter, Alexei Sharpanskykh, and Riender Happee. 2025. "Effect of Design on Human Injury and Fatality Due to Impacts by Small UAS" Designs 9, no. 4: 88. https://doi.org/10.3390/designs9040088
APA StyleRattanagraikanakorn, B., Blom, H. A. P., Gransden, D. I., Schuurman, M., De Wagter, C., Sharpanskykh, A., & Happee, R. (2025). Effect of Design on Human Injury and Fatality Due to Impacts by Small UAS. Designs, 9(4), 88. https://doi.org/10.3390/designs9040088








