Emulation of Variational Quantum Circuits on Embedded Systems for Real-Time Quantum Machine Learning Applications

Abstract

This paper presents an engineering design framework for integrating Variational Quantum Circuits (VQCs) into industrial control systems via real-time quantum emulation on embedded hardware. In this work, we present a novel framework for fully embedded real-time quantum machine learning (QML), in which a four-qubit, four-layer VQC is both emulated and trained in situ on an FPGA-based embedded platform (dSPACE MicroLabBox 1202). The system achieves deterministic microsecond-scale response at a closed-loop frequency of 100 kHz, enabling its application in latency-critical control tasks. We demonstrate the feasibility of online VQC training within this architecture by approximating nonlinear functions in real time, thereby validating the potential of embedded QML for advanced signal processing and control applications. This approach provides a scalable and practical path toward real-time Quantum Reinforcement Learning (QRL) and other quantum-enhanced embedded controllers. The results validate the feasibility of real-time quantum emulation and establish a structured engineering design methodology for implementing trainable quantum machine learning (QML) models on embedded platforms, thereby enabling the development of deployable quantum-enhanced controllers.

1. Introduction

Quantum computing is emerging as a transformative computational paradigm with the potential to revolutionize design optimization and machine learning-based automation across a wide range of scientific and engineering disciplines [1,2]. Among the most versatile techniques in this emerging field are Variational Quantum Circuits (VQCs), which enable hybrid quantum–classical learning by embedding trainable parameters into quantum gate operations [3]. VQCs serve as the core building blocks of many quantum machine learning (QML) models, facilitating expressive representations that are particularly well suited to supervised learning, reinforcement learning, and quantum-enhanced optimization [4]. Due to their adaptive and parameterized structure, QML models—particularly Quantum Reinforcement Learning (QRL)—hold significant potential for latency-sensitive applications, such as industrial control, robotics, and multi-agent energy systems, in which real-time decision-making is critical [5,6,7,8].

When implemented on classical hardware, QRL offers a deterministic and accessible platform for small-scale quantum-inspired learning, albeit with architectural limitations compared to true quantum devices. Cost-effective classical platforms enable quantum-inspired algorithm prototyping for industrial control without the need for quantum infrastructure, thereby ensuring microsecond-scale responses. However, they lack quantum’s exponential speedup and entanglement, limiting scalability and necessitating hybrid approaches for more advanced QML tasks. While experimental progress continues, current noisy intermediate-scale quantum (NISQ) devices remain constrained in terms of qubit count, gate fidelity, and accessibility, often requiring remote execution via cloud services, which introduces latency and temporal variability [9]. For time-critical applications, such as feedback control or high-bandwidth signal processing, this latency is prohibitive. Conventional CPU- and GPU-based simulators, though effective for algorithmic studies, are generally unsuitable for real-time control tasks that demand control cycles in the order of tens to hundreds of microseconds. Their lack of deterministic execution and poor scalability under embedded constraints present fundamental barriers to integration within control-oriented system architectures [10].

From an engineering design perspective, these limitations underscore the urgent need for dedicated hardware–software co-design strategies that enable real-time inference, in situ learning, and tight integration with physical control loops. Achieving such functionality requires embedded architectures that are not only computationally efficient but also architected to meet strict timing, resource, and energy constraints. Furthermore, the practical deployment of QML models in embedded contexts demands the careful design of data encoding pipelines, interpretable parameter update mechanisms, and modular, scalable circuit representations, each of which forms a distinct layer within a structured QML system design framework [11,12,13].

To address these limitations, the field-programmable gate array (FPGA)-based emulation of quantum circuits has emerged as a promising engineering approach, offering deterministic timing behavior, energy-efficient execution, and tight integration with control hardware for time-critical applications [14]. Unlike noisy intermediate-scale quantum (NISQ) devices, which are constrained by limited qubit counts and cloud-induced latencies, or CPU/GPU simulators, which are hindered by exponential computational costs, FPGAs have enabled high-speed emulation since early efforts, achieving 16-qubit processing [15]. Their configurability and real-time responsiveness make them particularly well suited for control systems with modest qubit requirements, such as those in industrial automation and robotics. In this context, FPGA-based emulation provides a practical design platform for bridging classical control systems with future quantum-enhanced architectures, supporting both algorithm development and physical prototyping [7,16].

Recent advancements in FPGA-based emulation have primarily targeted simple circuits with limited entanglement, such as Clifford + T and rotational gate sets, or basic algorithms like Grover’s search and Shor’s factoring, achieving high-throughput for up to 32 qubits [17,18,19,20,21]. For instance, low-tier FPGAs accelerate circuit verification, and others emulate protocols like B92 quantum key distribution, yet most prioritize scalability and precision over microsecond-scale latency, which is essential for real-time applications [22,23]. Architectures that leverage pipelined execution show promise for throughput optimization but generally rely on static computation kernels or external training, which limits adaptability. Such designs are insufficient for emulating fully entangled and trainable VQCs, which form the computational backbone of QML models [12,13,24]. A fully embedded, real-time framework that simultaneously emulates and trains parameterized VQCs in situ within a high-frequency control loop remains absent, representing a critical gap for dynamic QML tasks in latency-sensitive domains like industrial control [16].

While significant advancements have been made in FPGA-based quantum circuit emulation, most existing works focus on either specific quantum algorithms (e.g., QFT, Grover’s, and QAOA) or large-scale offline simulation frameworks designed for throughput rather than latency [25,26,27]. These implementations, though efficient for verifying quantum protocols or accelerating quantum key distribution, often lack the adaptability needed for dynamic learning tasks. For example, simulators like Qulacs and decision diagram-based engines [28,29] achieve high efficiency for circuit verification and sampling but are unsuitable for microsecond-scale, real-time inference. Moreover, FPGA-based emulators, such as those designed by Mahmud [20,25,27] and Pilch [30], emphasize fixed-pipeline architectures and parallelism, with limited support for in situ learning. These limitations underscore the absence of a comprehensive design methodology for embedded QML systems that integrates real-time learning capabilities with tight computational and hardware constraints.

No existing study has presented a fully embedded framework that enables both the real-time emulation and in situ training of a Variational Quantum Circuit (VQC) on FPGA hardware with microsecond-scale latency. Existing implementations, such as those by Choi et al. [31], propose standalone FPGA-based emulators for algorithms like Grover’s and QAOA but do not incorporate trainable parameters or adaptive feedback mechanisms. Similarly, architectures such as Qu-Trefoil [32] and HPRC-based simulators [27] emphasize large-scale quantum circuit emulation, yet are limited by latency, energy consumption, or the lack of an embedded real-time control functionality. These constraints indicate a critical gap in realizing adaptive, trainable QML models that are suitable for deployment in embedded real-time control applications, where inference and learning must be performed within strict timing requirements.

To address this need, we present a fully embedded design framework for the real-time emulation and online training of a Variational Quantum Circuit (VQC) on an FPGA-based platform (dSPACE MicroLabBox 1202). Our system implements a four-qubit, four-layer VQC with 48 trainable parameters that is entirely mapped onto the FPGA fabric. It operates deterministically at a closed-loop frequency of 100 kHz, without reliance on external processors, making it well suited for latency-critical applications in control, robotics, and signal processing. Crucially, the system supports full in situ training using the parameter shift rule, allowing the VQC to adapt its parameters during live operation. As a proof of concept, we train the circuit in real time to approximate a nonlinear function, demonstrating both the feasibility and potential of embedded quantum machine learning (QML) in real-time control environments. This architecture provides a practical and scalable bridge between classical embedded platforms and future quantum-enhanced controllers, with applications in power electronics, industrial automation, and multi-agent energy systems [16].

This work addresses a critical engineering design problem: how to emulate and train Variational Quantum Circuits (VQCs) within the strict timing, memory, and computational constraints of embedded real-time systems. Our approach provides a structured methodology—including architectural design, algorithm mapping, and optimization criteria—that enables VQC-based controllers to be deployed in latency-sensitive environments, such as robotics, power systems, and industrial automation.

The rest of this paper is organized as follows: Section 2 reviews matrix-based quantum simulation techniques that motivate the chosen real-time implementation. Section 3 details the encoding, evolution, and decoding stages executed on the FPGA platform. Section 4 presents the in situ training algorithm based on the parameter-shift rule. Section 5 reports the experimental results obtained at a 100 kHz sampling rate, and Section 6 draws conclusions and outlines future research directions.

2. Analytical Simulation of Quantum Computing

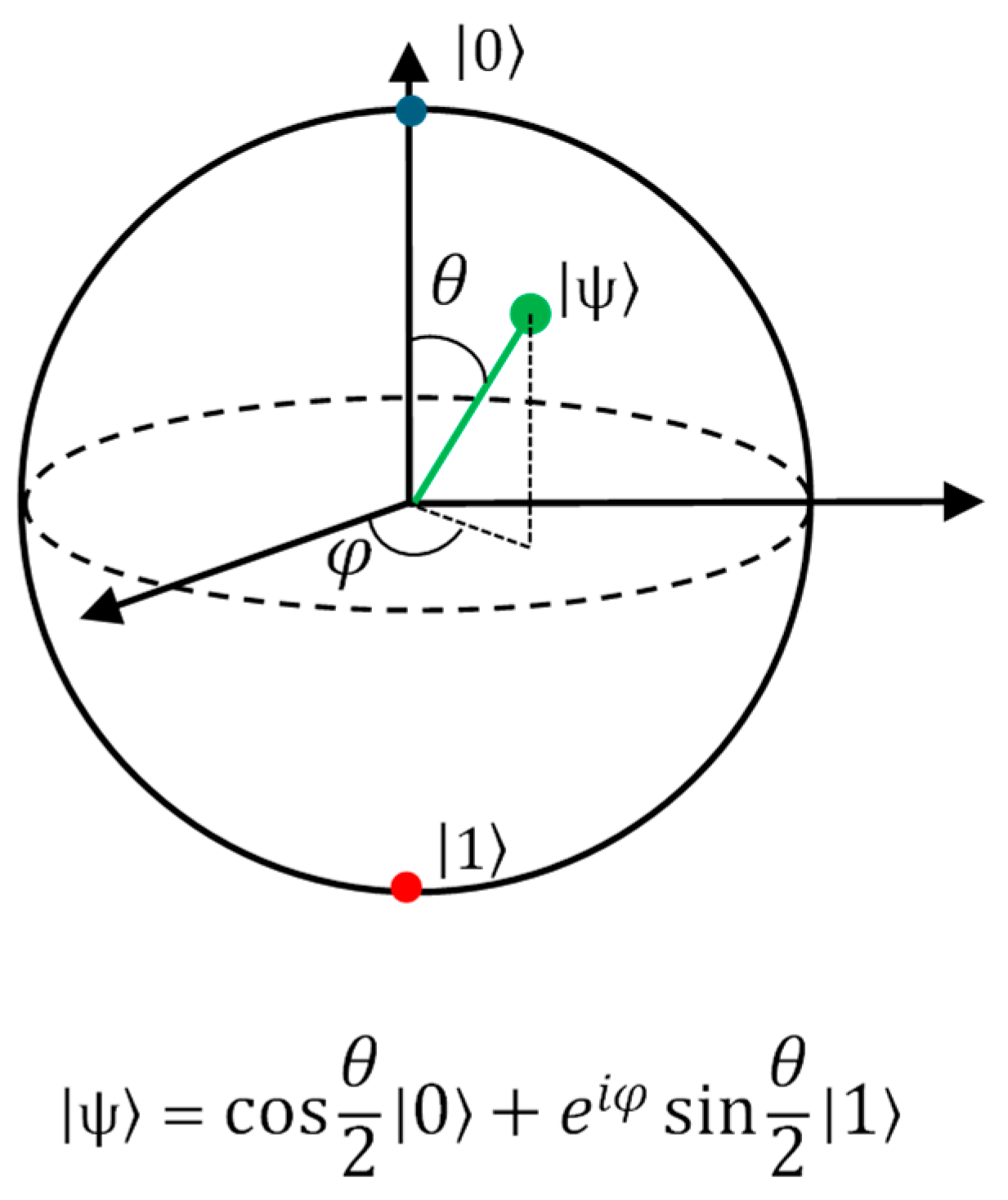
2.1. Quantum Computing Basics

Quantum computing signifies a groundbreaking shift in computational capabilities, utilizing quantum mechanics to handle information in ways that classical computers cannot. This introduction presents essential concepts of quantum computing, such as qubits, quantum circuits, entanglement, and the process of quantum computation, while emphasizing their potential impact on ML applications. As an emerging field, quantum computing harnesses the principles of quantum mechanics to conduct calculations and address problems. Unlike classical computers, which rely on bits (binary digits) for information processing, quantum computers utilize qubits (quantum bits) [33]. This key distinction enables quantum computers to process information in ways that are exponentially more powerful than classical computers for certain specific tasks.

The fundamental unit of quantum computing is the qubit, the quantum counterpart to the classical bit. Unlike classical bits, which can only be in a state of 0 or 1, qubits can be in a superposition, representing both 0 and 1 at the same time [34]. This characteristic, combined with entanglement and quantum interference principles, enables quantum computers to handle large amounts of information simultaneously. This parallel processing capability is described mathematically in (1) and is key to the potential speed and efficiency of quantum computing.

$$\left|\psi \right.⟩=\alpha \left|0\right.⟩+\beta \left|1\right.⟩$$

(1)

In quantum computing, qubits are represented by complex numbers $\alpha$ and $\beta$, which must adhere to the normalization condition ${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$. This condition ensures that the probabilities of the qubit being in either state $\left|0\right.⟩$ or $\left|1\right.⟩$ sum to 1.

The ability of qubits to exist in superposition states, where α and $\beta$ are non-zero, allows them to perform multiple calculations simultaneously, leading to a substantial increase in computational power. The state of a qubit can be graphically represented on the Bloch sphere, as shown in Figure 1, with the north and south poles corresponding to the basis states $\left|0\right.⟩$ and $\left|1\right.⟩$, respectively. Any point on the surface of the Bloch sphere represents a valid superposition state of the qubit.

The systems with multiple qubits are expressed as the Kronecker product of individual qubit states as follows:

$$\left|\phi \right.⟩=\left|{\psi }_1\right.⟩⨂\left|{\psi }_2\right.⟩⨂\dots ⨂\left|{\psi }_n\right.⟩={\sum }_{x=00\dots 0}^{11\dots 1}{C}_x\left|x\right.⟩$$

(2)

where $n$ is the number of qubits, and $C_x$ represents complex coefficients, as follows:

$${\sum }_{x=00\dots 0}^{11\dots 1}{\left|C_x\right|}^2=1$$

(3)

2.2. Quantum Gates

Quantum gates are the building blocks of quantum circuits and are similar to classical logic gates. They are represented by unitary matrices that operate on qubits. Rotation gates, which perform rotations around the X, Y, and Z axes of the Bloch sphere representation of a qubit, can be represented as (8).

The Controlled-NOT (CNOT) gate, shown in (9), is a two-qubit gate that flips the second qubit (target qubit) if and only if the first qubit (control qubit) is in the state $\left|1\right.⟩$. The CNOT gate is particularly important because, together with single-qubit gates, it forms a universal set of quantum gates, meaning any quantum operation can be approximated to arbitrary precision using only these gates.

$$\begin{gathered} {\mathrm{R}}_{\mathrm{X}}\left(\theta \right)=\left[\begin{array}{cc}\cos \left({\displaystyle \frac{\theta }{2}}\right)& -i\sin \left({\displaystyle \frac{\theta }{2}}\right)\\ -i\sin \left({\displaystyle \frac{\theta }{2}}\right)& \cos \left({\displaystyle \frac{\theta }{2}}\right)\end{array}\right] \\ {\mathrm{R}}_{\mathrm{Y}}\left(\theta \right)=\left[\begin{array}{cc}\cos \left({\displaystyle \frac{\theta }{2}}\right)& -\sin \left({\displaystyle \frac{\theta }{2}}\right)\\ -\sin \left({\displaystyle \frac{\theta }{2}}\right)& \cos \left({\displaystyle \frac{\theta }{2}}\right)\end{array}\right] \\ {\mathrm{R}}_{\mathrm{Z}}\left(\theta \right)=\left[\begin{array}{cc}{e}^{-i{\displaystyle \frac{\theta }{2}}}& 0\\ 0& e^{-i{\displaystyle \frac{\theta }{2}}}\end{array}\right] \end{gathered}$$

(4)

$$\mathrm{C}\mathrm{N}\mathrm{O}\mathrm{T}=\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}0& 1\\ 1& 0\end{array}\end{array}\right]$$

(5)

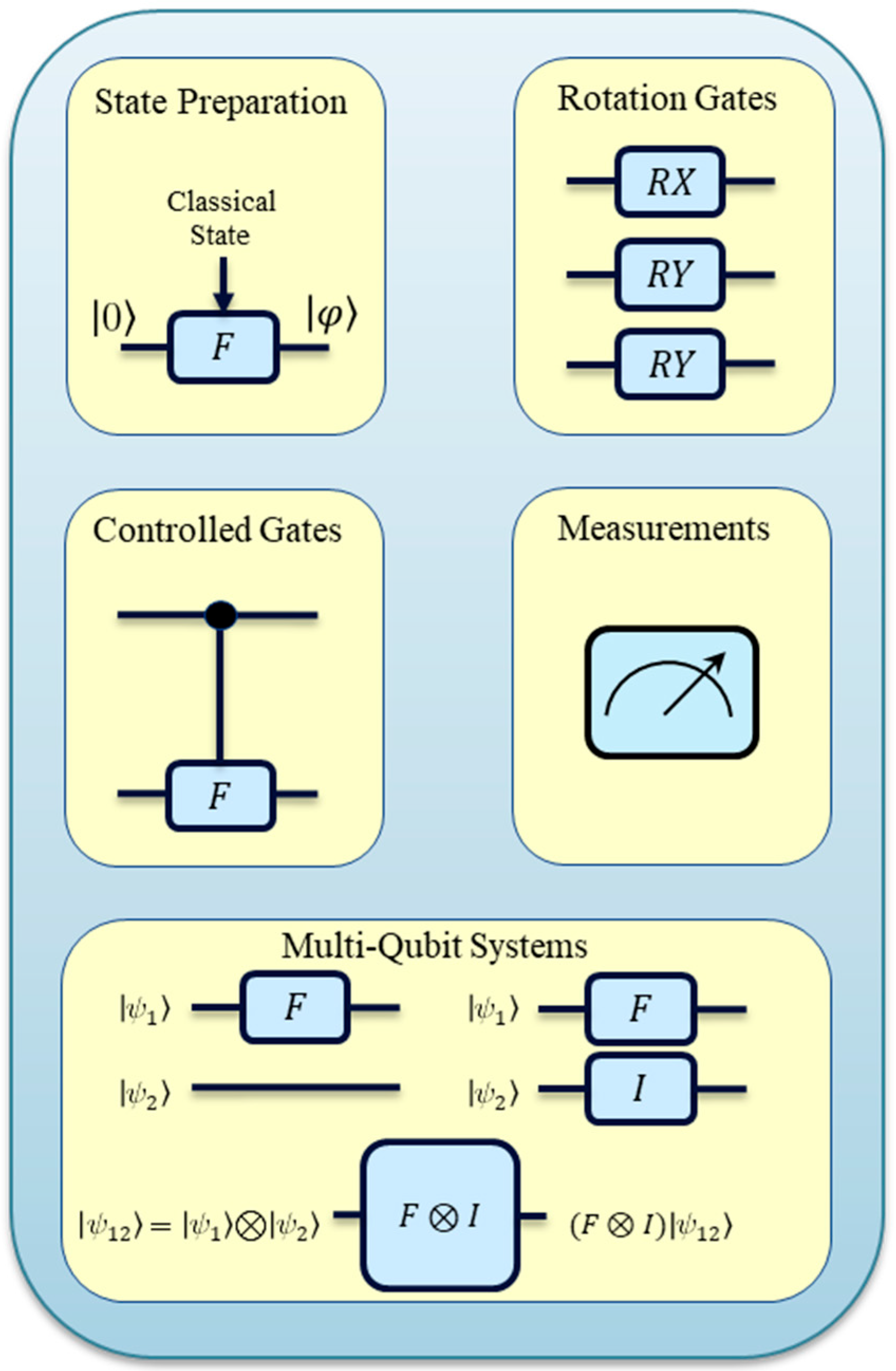
2.3. Multiple-Qubit Systems

Applying a quantum gate to a single qubit can be extended to the entire system using the tensor product formalism in a multi-qubit quantum system. This approach is essential for defining localized quantum operations within multi-qubit systems, whether the system’s state is separable or entangled. Specifically, to apply a quantum gate, $F$, to a single qubit while leaving the other qubits unchanged, the operator, $F$, is combined with identity matrices, $I$, which correspond to the unaffected qubits, via the tensor product. The resulting operator acts on the entire system, ensuring that the gate, $F$, modifies only the target qubit without altering the states of the others.

For an $N$-qubit system, the operator, $F$, is applied to the $k$-th qubit by constructing the composite operator $F_k=I\otimes \cdots \otimes F\otimes \cdots \otimes I$, where $F_k$ occupies the $k$-th position in the tensor product. This framework allows for the precise targeting of individual qubits, thereby facilitating operations in both separable and entangled states.

Figure 2 provides a modular gate-level toolbox for VQC construction, enabling system designers to select, configure, and cascade quantum-inspired blocks based on application needs. The figure exemplifies this with an $N$-qubit system, where a single-qubit gate, $F$, is extended to a two-qubit system using the tensor product, $F\otimes I$. This operation applies $F$ exclusively to the first qubit, leaving the second qubit unchanged. This preserves the integrity of the multi-qubit system while achieving localized control.

2.4. Quantum State Measurement

Quantum measurement in quantum mechanics involves projecting a quantum system’s state onto an eigenstate of the measured observable, with outcomes determined probabilistically. The expectation value of an observable A $A$, denoted $⟨A⟩$, is the average result over many measurements on identical states, defined as $⟨A⟩=⟨\psi \left|A\right|\psi ⟩$ for a state $|\psi ⟩$. Expectation values reveal properties like the probability of measuring specific basis states for qubits, making them essential for quantum computations.

The Pauli Z operator, which is used for measurements on a computational basis, is defined as follows:

$$Z=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$$

(6)

For a qubit state $\left|\psi \right.⟩=\alpha |0⟩+\beta |1⟩$, represented as the column vector $\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]$, the expectation value $⟨Z⟩$ is computed as follows:

$$⟨Z⟩=\left[\begin{array}{cc}{\alpha }^{*}& {\beta }^{*}\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]={\left|\alpha \right|}^2-{\left|\beta \right|}^2$$

(7)

In multi-qubit systems, $Z_i$ acts on the $i$-th qubit, with $⟨Z_i⟩$ depending on its reduced state.

3. Emulation of VQCs

Quantum Neural Networks (QNNs) integrate the principles of quantum computing with artificial neural networks, utilizing superposition, interference, and entanglement to create more efficient algorithms. A key element of QNNs is Variational Quantum Circuits (VQCs), which use parameterized quantum gates tailored for distinct tasks. VQCs can be trained through gradient-based optimization [35] or metaheuristic approaches [36], enabling the development of quantum machine learning models for various applications, such as reinforcement learning.

In real-time quantum machine learning, embedded systems like Speedgoat and dSPACE outperform offline simulators such as PennyLane, which face latency issues. These embedded platforms run simulations directly on hardware, providing the low latency and high reliability that are crucial for real-time applications.

Real-time applications, particularly in control systems, often involve a limited number of inputs and typically only one or two outputs. Since each input is encoded into a qubit, the number of required qubits in such applications remains modest. This constraint enables embedded systems to effectively and analytically simulate quantum circuits in real time. Consequently, embedded platforms present a promising opportunity to test and evaluate the performance of quantum algorithms in real-time scenarios.

Our approach demonstrates precise, real-time simulation without delays or network integration issues, enhancing responsiveness to dynamic control needs. The adaptable nature of embedded systems allows for quick reconfiguration to accommodate changing VQC setups, providing unmatched versatility compared to remote simulators.

3.1. Matrix-Based VQCs

Figure 3 outlines the configurable VQC design procedure, including the selection of qubit size, layer depth, and entanglement scheme, forming the basis for rapid prototyping of QML architectures in embedded environments. As can be seen in this figure, in order to emulate a VQC based on the real-time analytical simulation of quantum computing, the embedded system executes the quantum circuit, with all quantum gates implemented using their matrix representations, as detailed in Section 3, to generate a quantum-driven signal as follows:

• State Preparation: The input states, including the input voltage, inductor current, and output voltage, are processed through functions $f_{in}\left(x\right)$ to generate parameter angles $\theta$. These angles are then encoded into quantum states using parameterized rotation gates within the encoding layer.
• Tensor Product and Parameterization Layers: The encoded states undergo tensor product operations and pass through multiple parameterization layers. Each layer consists of CNOT and rotation gates that manipulate the qubit states according to the trained VQC model. This structure ensures that the qubits capture nonlinear relationships within the input data.
• Measurement and Output: After passing through the parameterization layers, the qubit states are measured to generate expectation values, $E{V}_i$, which are transformed into control actions, $a_i=f_{out}\left(E{V}_i\right)$. These control actions determine the quantum-derived action.
• Closed-Loop Feedback: The system integrates real-time feedback, where the plant’s output is continuously monitored and fed back into the VQC, ensuring dynamic adjustments to maintain optimal performance.

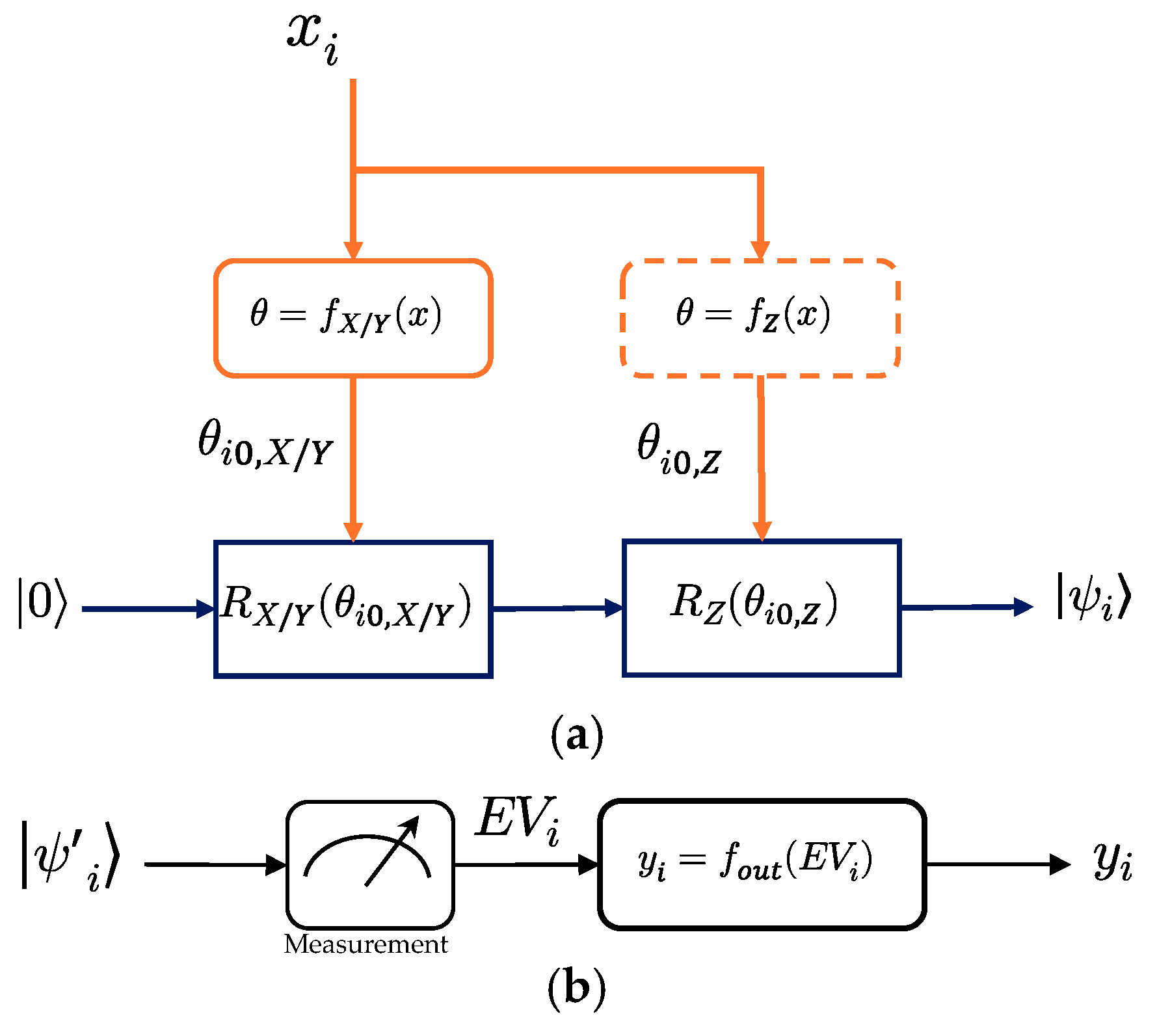
3.2. Quantum State Encoding Procedure

The encoding layer of a VQC typically includes rotation gates that prepare qubits to match the states of input data. Figure 4a illustrates quantum state encoding. As can be seen in this figure, classical input data is transformed into quantum states by an X or Y rotation gate, where the angle corresponds to the input data. A Z-axis rotation also eliminates the global phase effect, preserving relative phase information [37,38].

3.3. Quantum State Decoding Procedure

In the final stage of the VQC, the expectation value (EV) of each qubit can be measured along the Z-axis. However, the output of the VQC can be decoded to map any desired function, as shown in Figure 4b.

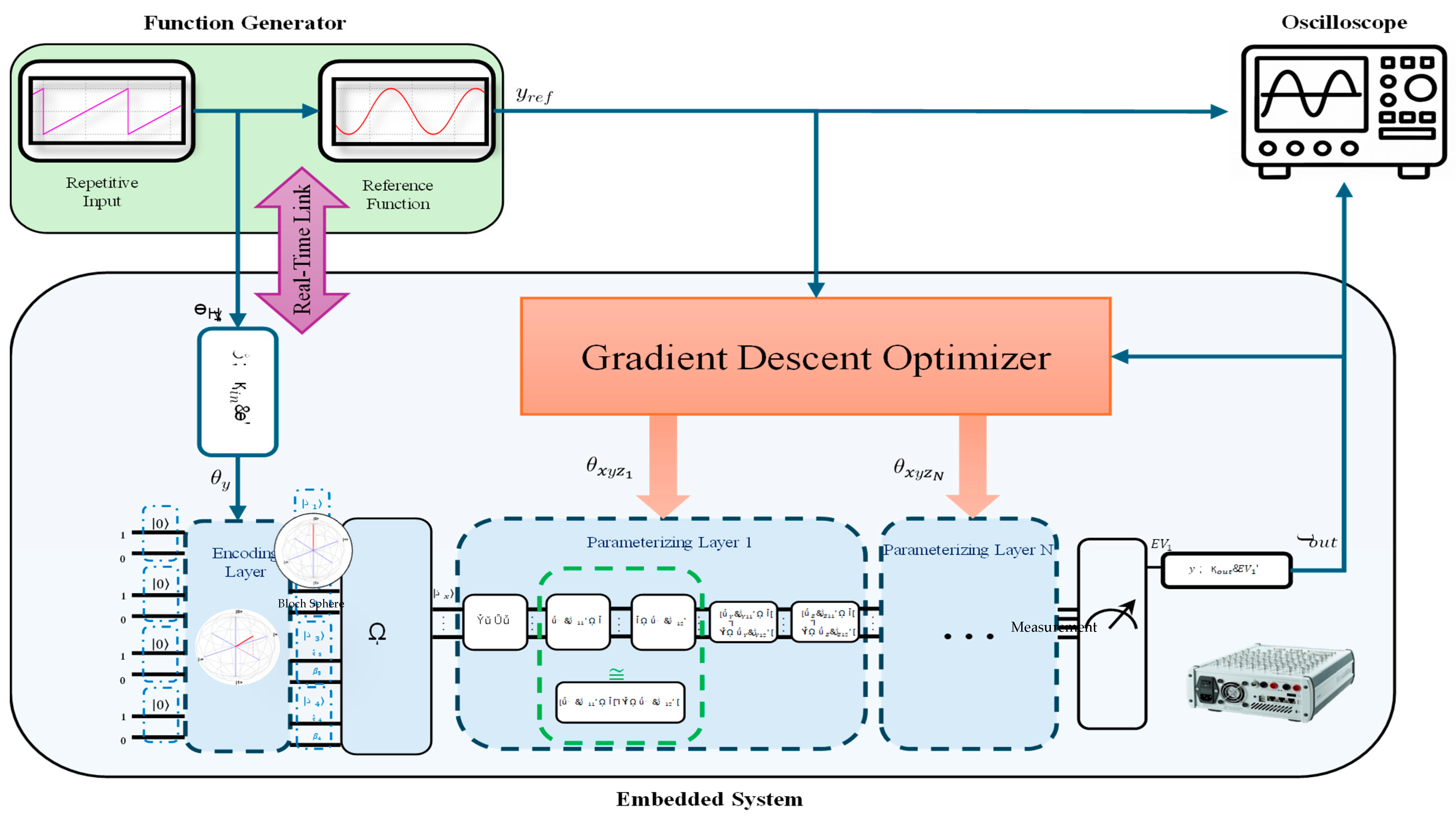
4. Real-Time Quantum Machine Learning Design and Deployment

Real-time quantum machine learning (RT-QML) involves the use of VQCs on embedded systems to enable fast, adaptive decision-making. This section presents the end-to-end pipeline: from data encoding to circuit optimization and real-time control signal decoding. In this work, we develop and demonstrate a real-time VQC approximator, which is shown in Figure 5 as a supervised quantum machine learning example—specifically, fitting a known target function $f\left(x\right)$—to showcase the feasibility and capabilities of our proposed real-time embedded simulation framework. While the methodology is general and can be extended to reinforcement learning or unsupervised tasks, the supervised case provides a clear, interpretable benchmark for evaluating performance, training efficiency, and hardware responsiveness.

4.1. Objective Function and Training Procedure

In this supervised learning setting, the quantum model, $y(x;\theta ,a)=a\cdot ⟨Z_1(x;\theta )⟩$, aims to approximate a known function, such as $f\left(x\right)$, by minimizing the mean squared error as follows:

$$J\left(\theta ,a\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(f\left(x_i\right)-a\cdot ⟨Z_1\left(x_i;\theta \right)⟩\right)}^2$$

(8)

where $\theta \in R^{N_Q{N}_L{N}_G}$ are the trainable VQC parameters, ($N_Q$ qubits × $N_L$ layers × $N_G$ gate angles), and $a$ is a learnable scaling factor. Training is performed using gradient descent [35].

4.2. Quantum State Encoding

Each input, $x\in \left[x_{min},x_{max}\right]$, is first normalized and then encoded using quantum rotation gates as follows:

$$x_n={\displaystyle \frac{x-x_{min}}{x_{max}-x_{min}}}$$

(9)

Then, the normalized input is mapped into rotation angles of the encoding layer using encoding functions as follows [35]:

$$\begin{gathered} {\theta }_{i0\mathrm{Y}}=Arcsin\left(x_n\right) \\ {\theta }_{i0\mathrm{Z}}=Arcsin\left({x_n}^2\right) \end{gathered}$$

(10)

These angles are applied across four qubits using RY and RZ gates, forming the input state for the quantum circuit.

4.3. VQC Architecture and Optimization

The encoded input state is processed through $N_L$ layers of the VQC. Each layer consists of a fixed pattern of entangling CNOT gates, followed by parameterized single-qubit rotations (RX, RY, and RZ). This structure enables the VQC to represent a broad class of complex functions.

To optimize the VQC, the parameters, ${\theta }_i$, associated with the rotation gates are updated based on the gradient descent method. Specifically, gradients with respect to each ${\theta }_i$ are computed using the parameter-shift rule as follows [35]:

$${\displaystyle \frac{\partial f\left(\theta \right)}{\partial {\theta }_i}}={\displaystyle \frac{f\left({\theta }_i+\frac{\pi }{2}\right)-f\left({\theta }_i-\frac{\pi }{2}\right)}{2}}$$

(11)

The computed gradients are then used to update the parameters as follows:

$${\theta }_i\leftarrow {\theta }_i-\eta \cdot {\displaystyle \frac{\partial J}{\partial {\theta }_i}}$$

(12)

where $\eta$ is the learning rate, and $J$ is the cost function defined to measure the difference between the VQC output and the target reference signal. Through this iterative optimization process, the VQC progressively improves its approximation of the desired function.

In this system, the entire optimization is performed in real time. The input and reference signals are streamed continuously, while the VQC parameters are updated on the fly using the gradient descent method. This enables the circuit to adapt its parameters dynamically and achieve optimal performance over time.

4.4. Output Decoding and Control Integration

After the final VQC layer, a quantum measurement is performed on the first qubit. The resulting expectation value, $⟨Z_1⟩$, is scaled by a and serves as the output, which is a real-time quantum-driven signal, as follows:

$$y=a\cdot ⟨Z_1⟩$$

(13)

4.5. Pseudocode

The real-time training procedure on the dSPACE MicroLabBox 1202 has been described in Algorithm 1, where $(\theta \in R^{48})$ represents the VQC rotation parameters, $(a\in R)$ is the scaling factor, and the objective is to minimize (8) with $(N=20)$. All operations are constrained to the 10 µs cycle. This algorithm can be interpreted as a generalized design procedure for training QML models in embedded systems, specifying the architectural steps and timing constraints necessary for online learning with VQCs.

Algorithm 1 Pseudocode for the design procedure of the real-time VQC training algorithm

001. 1. Initialization: 002.    - Randomly initialize $\theta \sim \mathcal{U}{\left(-\pi ,\pi \right)}^{48}$ , $a\sim \mathcal{U}\left(\mathrm{0,3}\right)$ , and $iteration=0$ on FPGA 003.    - Set $maxitter=100$ , $samplerate=100\mathrm{k}\mathrm{H}\mathrm{z}$ (10 µs cycle), $T=0.1s$ , $N_{\mathrm{samples}}=\mathrm{10,000}$ , $N=20$ 004. 2. Signal Sampling: 005.    - Initialize buffer $B$ in FPGA memory for current 100 ms period // 10 Hz, 2 Vpp sawtooth 006.    - Generate input samples within 10 µs cycle: 007.      - $x_t=2\cdot \left(t\cdot 10mod1\right)-1$ 008.      - $f_x=\cos \left(2\pi \cdot 10\cdot t\right)$ 009.    - If the new period starts at $(t\mathrm{m}\mathrm{o}\mathrm{d}T=0)$ : 010.      - $indices=linspace\left(0,(N_{\mathrm{samples}}-1),\left(N\right)\right)$ 011.      - $x=x_t\left[\mathrm{indices}\right]$ 012.      - $f_x=f_x\left[\mathrm{indices}\right]$ 013.      - Store $\left(x,f_x\right)$ in $B$ 014. 3. VQC Output Computation: 015.    - For $i=1$ to $N$ : 016.      - $x_{n,i}={\displaystyle \frac{x_i+1}{2}}$ 017.      - Encode State: 018.        - ${\theta }_{Y,i}=\arcsin \left(x_{n,i}\right)$ 019.        - ${\theta }_{Z,i}=\arccos \left(x_{n,i}^2\right)$ 020.        - Initialize $\left|{\psi }_i\right.⟩={\left|0\right.⟩}^{\otimes 4}$ 021.        - For $q=1$ to $4$ : 022.          - $\left|{\psi }_i\right.⟩\leftarrow R_Y\left({\theta }_{Y,i}\right)R_Z\left({\theta }_{Z,i}\right)\left|{\psi }_i\right.⟩$ on qubit $q$ 023.      - Apply VQC: 024.        - For $l=1$ to $4$ : 025.        - For $q=1$ to $3$ : 026.            - Apply CNOT on qubits $\left(q,q+1\right)$ to $\left|{\psi }_i\right.⟩$ 027.        - Apply CNOT on qubits $\left(\mathrm{4,1}\right)$ to $\left|{\psi }_i\right.⟩$ 028.          - Apply rotations: $\left|{\psi }_i\right.⟩\leftarrow R_X\left({\theta }_{l,q,1}\right)R_Y\left({\theta }_{l,q,2}\right)R_Z\left({\theta }_{l,q,3}\right)\left|{\psi }_i\right.⟩$ for all $q=1$ to $4$ 029.      - ${⟨Z_1⟩}_i=\mathrm{Tr}(\left|{\psi }_i\right.⟩\left.⟨{\psi }_i|\cdot Z_1\right)$ 030.      - $y_i=a\cdot {⟨Z_1⟩}_i$ 031. 4. Error Computation: 032.    - Compute MSE: $J\left(\theta ,a\right)={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(f_x\left[i\right]-y_i\right)}^2$ 033. 5. Parameter Update: 034.    - If iteration < max_iterations: 035.      - For $j=1$ to $48$ : 036.        - ${\theta }^{+}=\theta ,{\theta }^{+}\left[j\right]=\theta \left[j\right]+{\displaystyle \frac{\pi }{2}}$ 037.        - ${\theta }^{-}=\theta ,{\theta }^{-}\left[j\right]=\theta \left[j\right]-{\displaystyle \frac{\pi }{2}}$ 038.        - $J^{+}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(f_x\left[i\right]-a\cdot ⟨Z_1\left(x_{n,i};{\theta }^{+}\right)⟩\right)}^2$ 039.        - $J^{-}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(f_x\left[i\right]-a\cdot ⟨Z_1\left(x_{n,i};{\theta }^{-}\right)⟩\right)}^2$ 040.        - ${\displaystyle \frac{\partial J}{\partial {\theta }_j}}={\displaystyle \frac{J^{+}-J^{-}}{2}}$ 041.      - Update $\theta :\theta \leftarrow \theta -\eta \cdot {\nabla }_{\theta }J$ , where $\eta =0.01$ 042.      - Update $a$ : 043.        - $\delta =0.01$ 044.        - $J_a^{+}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(f_x\left[i\right]-\left(a+\delta \right)\cdot ⟨Z_1\left(x_{n,i};\theta \right)⟩\right)}^2$ 045.        - $J_a^{-}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(f_x\left[i\right]-\left(a-\delta \right)\cdot ⟨Z_1\left(x_{n,i};\theta \right)⟩\right)}^2$ 046.        - ${\displaystyle \frac{\partial J}{\partial a}}={\displaystyle \frac{J_a^{+}-J_a^{-}}{2\delta }}$ 047.        - $a\leftarrow a-\eta \cdot {\displaystyle \frac{\partial J}{\partial a}}$ 048.      - $iteration\leftarrow iteration+1$ 049.    - Else: 050.      - Output Generation: 051.        - For $i=1toN$ : 052.          - $x_{n,i}={\displaystyle \frac{x_i+1}{2}}$ 053.          - ${\theta }_{Y,i}=\arcsin \left(x_{n,i}\right),{\theta }_{Z,i}=\arccos \left(x_{n,i}^2\right)$ 054.          - Initialize $\left|{\psi }_i\right.⟩={\left|0\right.⟩}^{\otimes 4}$ 055.          - For $q=1to4$ : 056.             $\left|{\psi }_i\right.⟩\leftarrow R_Y\left({\theta }_{Y,i}\right)R_Z\left({\theta }_{Z,i}\right)\left|{\psi }_i\right.⟩$ on qubit $q$ 057.          - For $l=1$ to $4$ : 058.            - For $q=1$ to $3$ : 059.              - Apply CNOT on qubits $\left(q,q+1\right)$ to $\left|{\psi }_i\right.⟩$ 060.            - Apply CNOT on qubits $\left(\mathrm{4,1}\right)$ to $\left|{\psi }_i\right.⟩$ 061.            - Apply rotations$:\left|{\psi }_i\right.⟩\leftarrow R_X\left({\theta }_{l,q,1}\right)R_Y\left({\theta }_{l,q,2}\right)R_Z\left({\theta }_{l,q,3}\right)\left|{\psi }_i\right.⟩$ for all $q=1$ to $4$ 062.          - ${⟨Z_1⟩}_i=\mathrm{Tr}(\left|{\psi }_i\right.⟩\left.⟨{\psi }_i|\cdot Z_1\right)$ 063.          - $y_i=a\cdot {⟨Z_1⟩}_i$ 064.          - $\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{d}\hspace{1em}\mathrm{t}\mathrm{o}\hspace{1em}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}\mathrm{t}\hspace{1em}{y}_i$

// 10 Hz, 2 Vpp sawtooth // 10 Hz cosine reference // Select 20 samples // Uniform samples in $\left(\left[-1,1\right]\right)$ // Reference cosine samples // Within 10 µs cycle // Normalize to $\left[0,1\right]$ // Compute ${\theta }_{0Y}$ for encoding // Compute ${\theta }_{0Z}$ for encoding // 4-qubit state // Apply $R_Y$ and $R_Z$ to each qubit // Apply 4 layers // Measure expectation on qubit 1 // VQC output // Parallelized on FPGA // Parameter-shift rule // Gradient descent // Within 10 µs cycle // Apply encoding rotations // Apply VQC layers // Output real-time signal

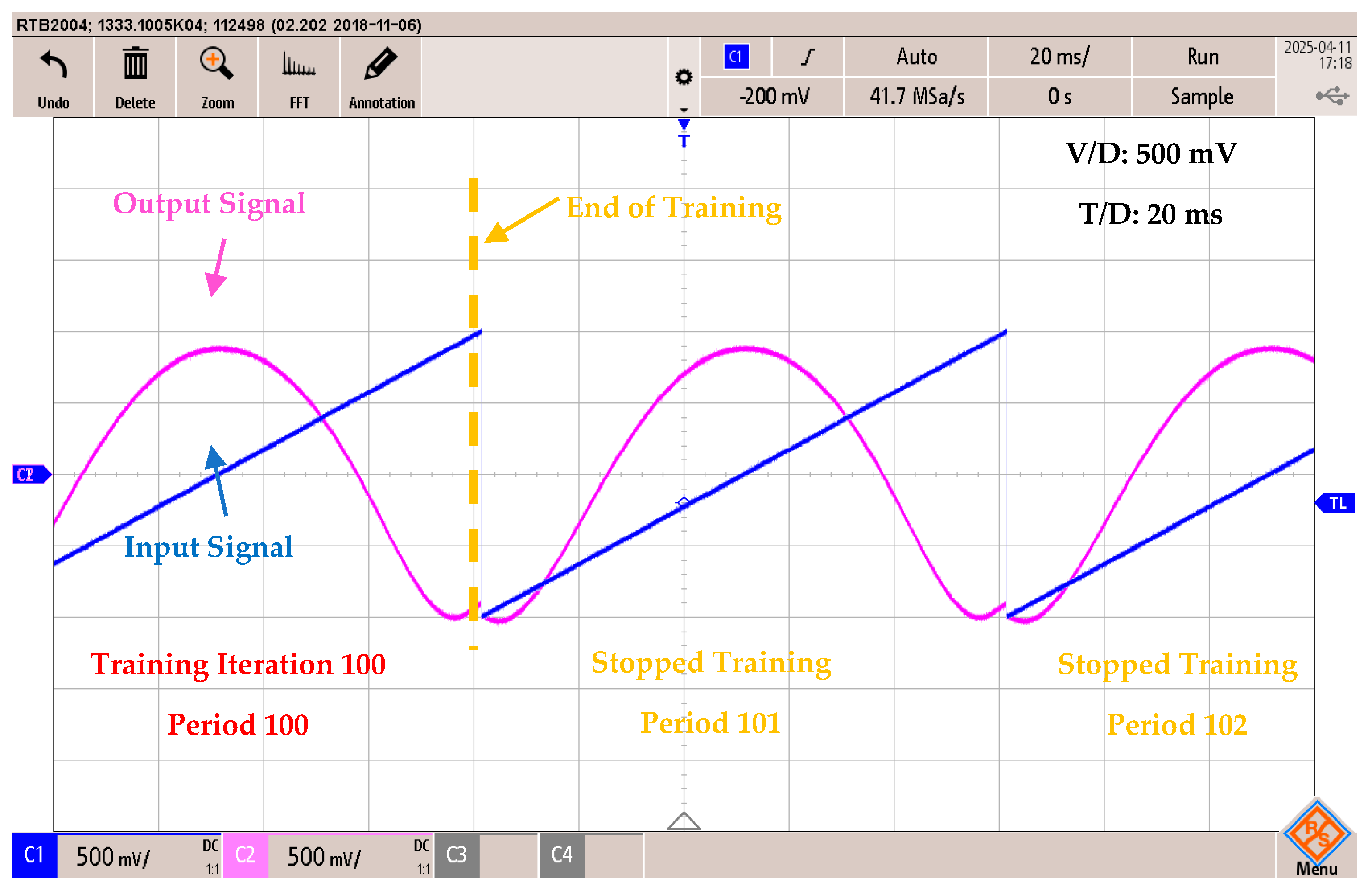
5. Experimental Results

This section validates the proposed VQC design framework in terms of latency, accuracy, and hardware resource efficiency, benchmarking the architecture against its design goals. To demonstrate the functionality of the proposed emulation method, a real-time VQC approximator, shown in Figure 5, has been implemented on an embedded system (dSPACE MicroLabBox 1202) as an RT-QML. For FPGA-level representation, an HDL Coder was used to generate VHDL code for the controller subsystem, providing a hardware-synthesizable logic design for high-speed operation. As shown in this figure, the system includes a function generator that produces a sawtooth signal as a repetitive input for the VQC and a reference function, which is a cosine function in this case. The emulated VQC, which is depicted in Figure 6, has 48 trainable parameters (4 qubits × 4 layers × 3 gate angles). The experimental setup is shown in Figure 7. The function generator generates a 10 Hz (100 ms period), 2 Vpp sawtooth waveform as the input of the VQC approximator implemented in MicroLabBox. The input waveform is sampled every 10 µs, and the corresponding output is emulated at the same rate in real time. The training was executed in real time, and to ensure that the approximated function is distinguishable from the exact function, deliberately limited precision was considered by setting the training iteration number to 100.

The real-time emulation was deployed on the dSPACE MicroLabBox 1202 platform, which integrates an FPGA and a real-time processor that are suitable for signal processing and embedded control tasks. The key specifications include:

• Processor: NXP QorlQ P5020, dual-core, 2 GHz;
• FPGA: Xilinx Kintex-7 (XC7K325T);
• I/O Interface: Analog inputs for signal injection and digital/PWM outputs for external device interfacing.

The real-time link between the function generator and the embedded system transmits input and reference function values at a 100 kHz sampling frequency. These values are used to encode the input into the VQC and to update its parameters through gradient descent. The VQC parameters are trained in real time using the block diagram shown in Figure 5 and the procedure outlined in Algorithm 1. After 100 periods of the input signal (corresponding to 100 optimization iterations, or $T=100\times {\displaystyle \frac{1}{10\mathrm{H}\mathrm{z}}}=10$ s), the resulting real-time output of the trained VQC is shown in Figure 8. This optimized result approximates the cosine function with the desired precision, which reflects a design trade-off between computational complexity and response time that guides design decisions for resource-limited deployments.

The rotation angles of the VQC approximator during each training epoch were extracted from the MICROLABBOX, and the corresponding VQC was simulated offline in MATLAB/Simulink 2024a for different rotation angle sets using the same functions employed in the real-time implementation, as shown in Figure 9a. In this figure, the gray markers indicate the training trajectory of the VQC, which gradually turn black as they approach the optimal solution. The blue curve represents the analytical target function, $cos\left(x\right)$, while the red curve depicts the final trained VQC output. To further validate the real-time training results, the optimally trained parameters, which are listed in

Table 1. Final trained rotation angles of the VQC (degrees).

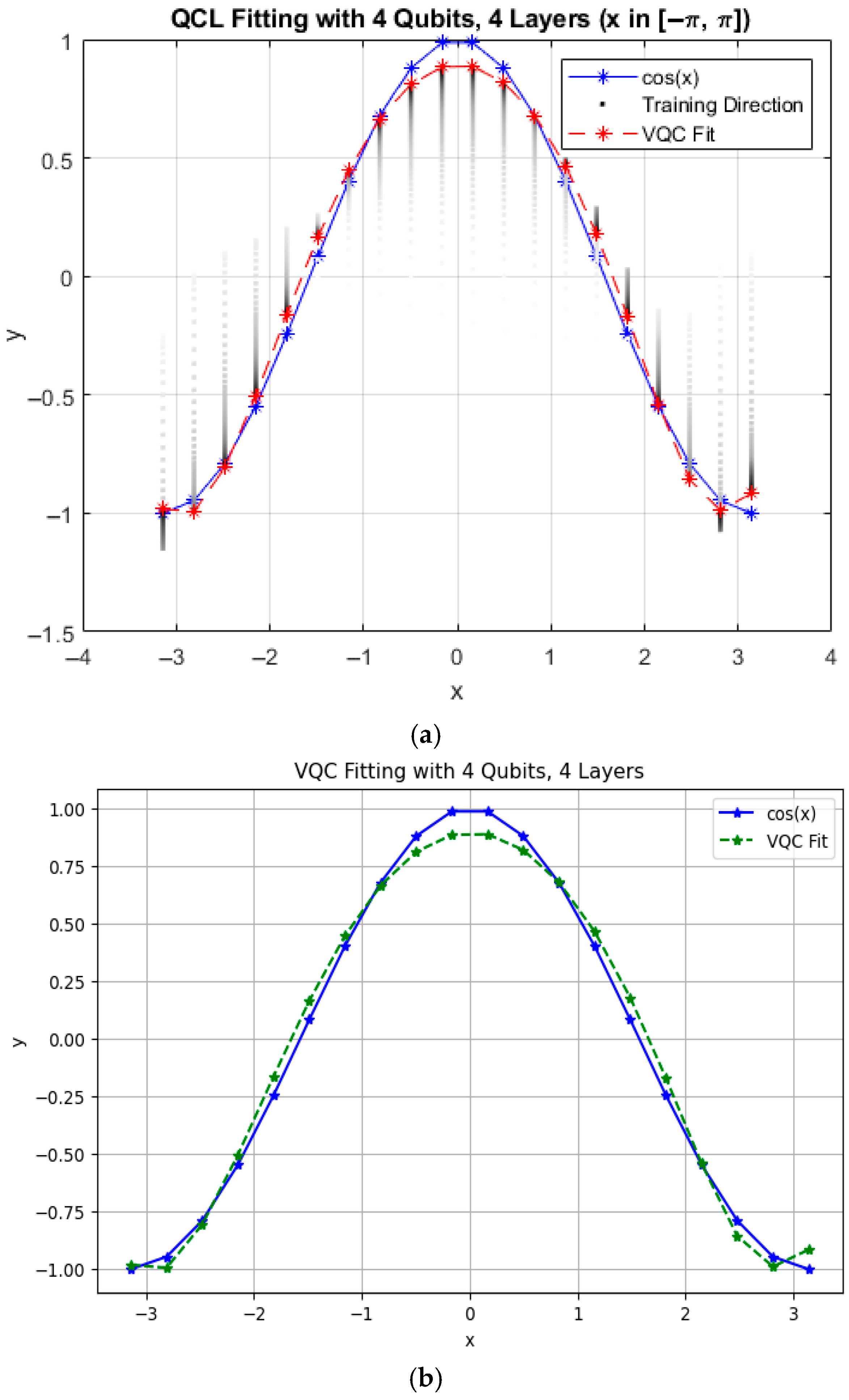
Layer	Qubit	RX (°)	RY (°)	RZ (°)
1	0	−9.958	−15.934	18.123
	1	−26.757	91.673	−43.934
	2	8.9381	108.18	84.763
	3	−79.383	105.83	22.701
2	0	−62.63	45.751	−7.4886
	1	168.51	43.482	−102.18
	2	116.4	−122.56	99.826
	3	33.988	−89.244	−99.064
3	0	−104.04	−108.13	138.78
	1	−107.76	148.22	180
	2	−108.62	−21.4	−22.007
	3	−10.863	−124	−140
4	0	−83.423	54.351	−73.195
	1	−32.859	76.037	−65.237
	2	34.16	−100.17	−27.301
	3	−85.606	−137.73	2.8304
Optimized scaling factor a = 2.1515

, were also used to simulate the optimal VQC approximator using the PENNYLANE Python library [39], as shown in Figure 9b. The close agreement between the MATLAB/Simulink 2024a and PENNYLANE 0.41.1 results confirms the accuracy of the proposed matrix-based real-time emulation framework and demonstrates the feasibility of embedded quantum emulators for real-time signal generation.

While a direct quantitative comparison to previous works is challenging due to the novelty of this approach, it is worth highlighting the key distinctions of our system. Most existing FPGA-based quantum circuit emulations have focused on fixed kernels or shallow circuits with limited entanglement, targeting algorithms such as Grover’s search or simple quantum arithmetic [8,9,10,11]. In contrast, our implementation realizes a fully parameterized, fully entangled four-qubit, four-layer Variational Quantum Circuit (VQC), achieving real-time closed-loop operation and in situ training entirely on embedded hardware. To our knowledge, this is the first demonstration of such a system running VQC-based control at 100 kHz with deterministic latency. Furthermore, our results showcase the practical potential of VQCs as real-time adaptive controllers—a role traditionally dominated by classical neural networks—thereby positioning VQCs as a competitive architecture for future industrial control and signal processing applications.

6. Conclusions

This study validates the feasibility of real-time quantum machine learning (QML) in embedded systems, demonstrating a fully embedded design framework for Variational Quantum Circuit (VQC) emulation and training on the dSPACE MicroLabBox 1202. Our architecture, which implements a four-qubit, four-layer VQC with 48 trainable parameters, achieves a 100 kHz closed-loop frequency with deterministic microsecond-scale responses. Real-time training to approximate a cosine waveform yields a root mean square error (RMSE) below 3% within 100 iterations (10 s). Unlike prior FPGA-based emulations focused on fixed kernels or external training [8,19], our in situ training supports dynamic QML tasks, positioning VQCs as viable real-time adaptive controllers.

This paper introduces and validates an engineering design framework for emulating and training Variational Quantum Circuits (VQCs) on embedded systems in real time. Our contributions include the specification of design steps, architectural integration, and timing validation, offering a scalable path toward the practical deployment of quantum machine learning in latency-critical control systems. Future directions include expanding the toolbox for larger-scale QML designs, transitioning from FPGA to ASIC-based quantum-inspired processors, and scaling up to larger qubit counts and deeper circuits, thereby optimizing computational pipelines for enhanced efficiency. Potential applications include real-time Quantum Reinforcement Learning (QRL) in multi-agent energy systems, optimizing profit distribution for equitable resource allocation [16], and risk-aware control in stochastic energy networks using thermodynamic models [40]. The coordinated optimization of electric and heating systems via balancing multi-domain constraints offers another promising avenue [41]. By bridging classical embedded platforms and quantum-inspired control, this framework lays the foundation for the industrial adoption of QML in latency-critical domains like robotics, power electronics, and energy systems.