1D Finite Element Modeling of Bond-Slip Behavior and Deflection in Reinforced Concrete Flexural Members
Abstract
1. Introduction
2. Material Models
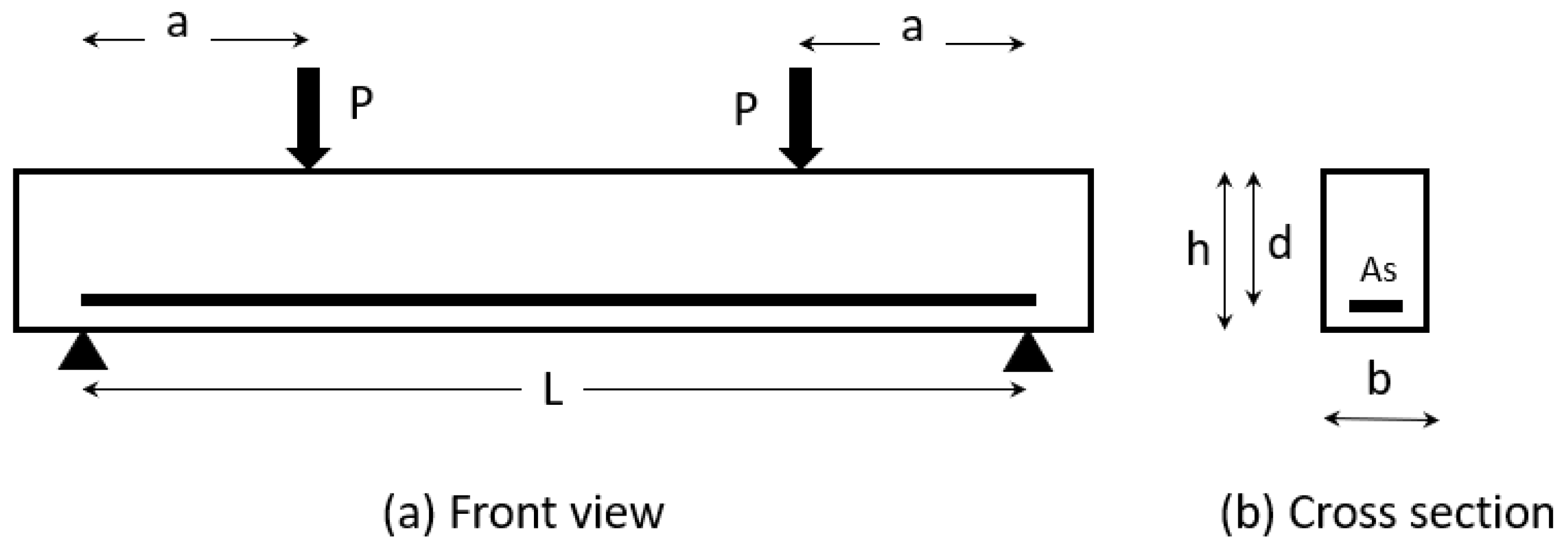
3. Database for Validation of Proposed Models
4. Deflection of Reinforced Concrete Beams
4.1. Short-Term Deflection Calculation According to EC2 [17]
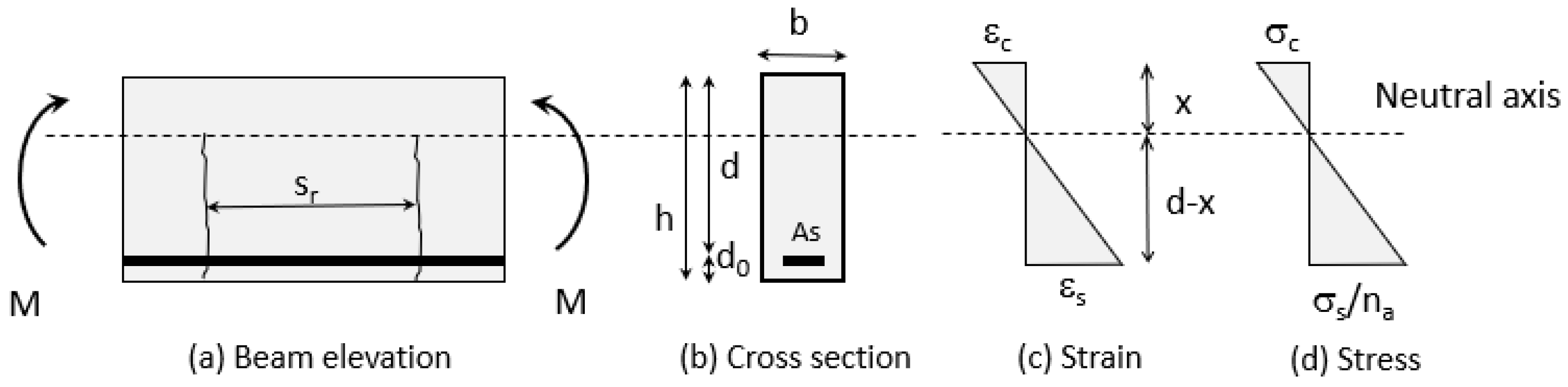
4.2. Fracture Mechanics-Based Sectional Model
4.3. Stress and Strain Distribution Between Two Cracks
4.4. 1D Finite Element Modeling of the Stress Distribution Between Two Cracks
4.5. 1D Finite Element Matrix System for RC Beam
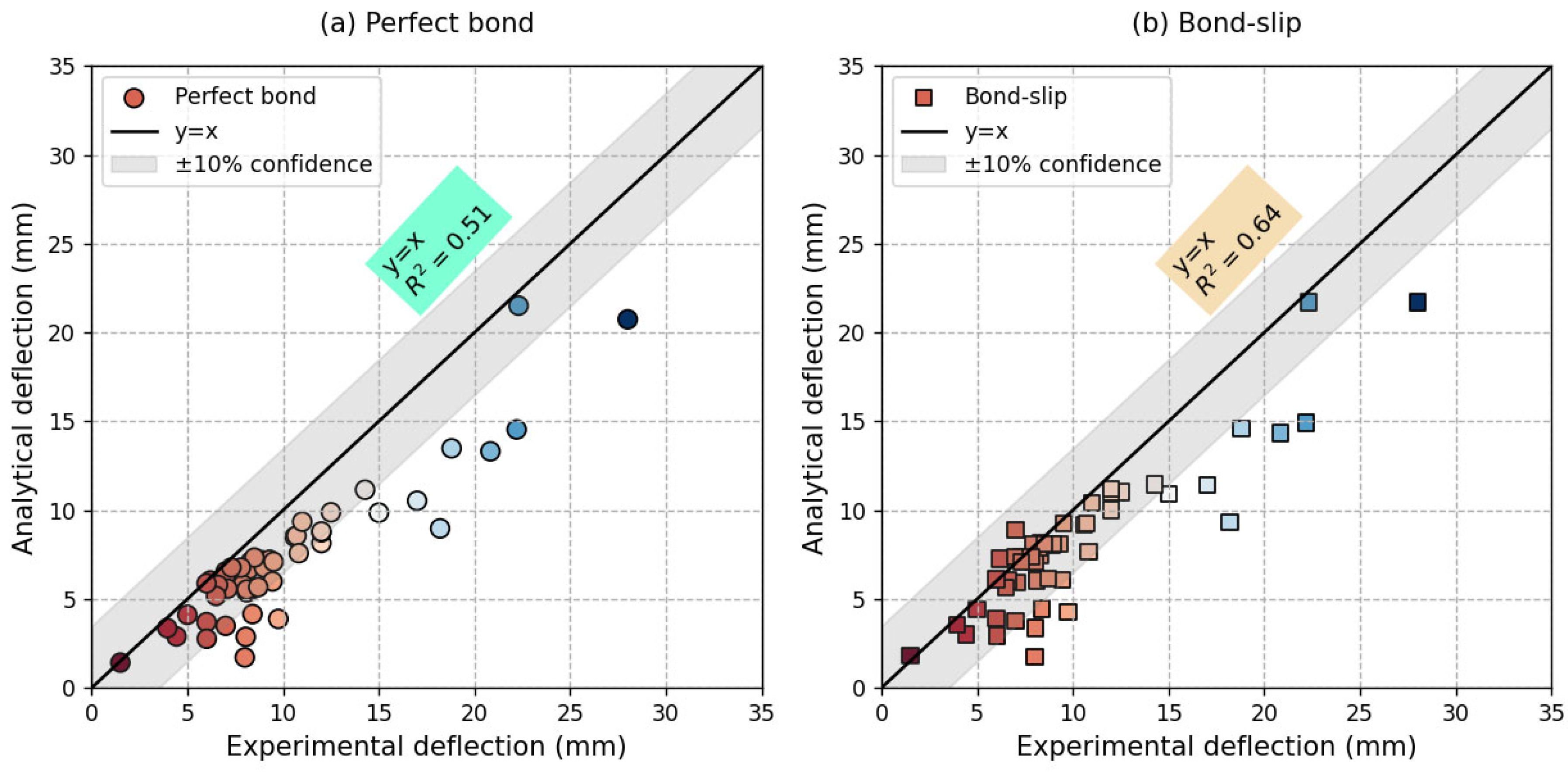
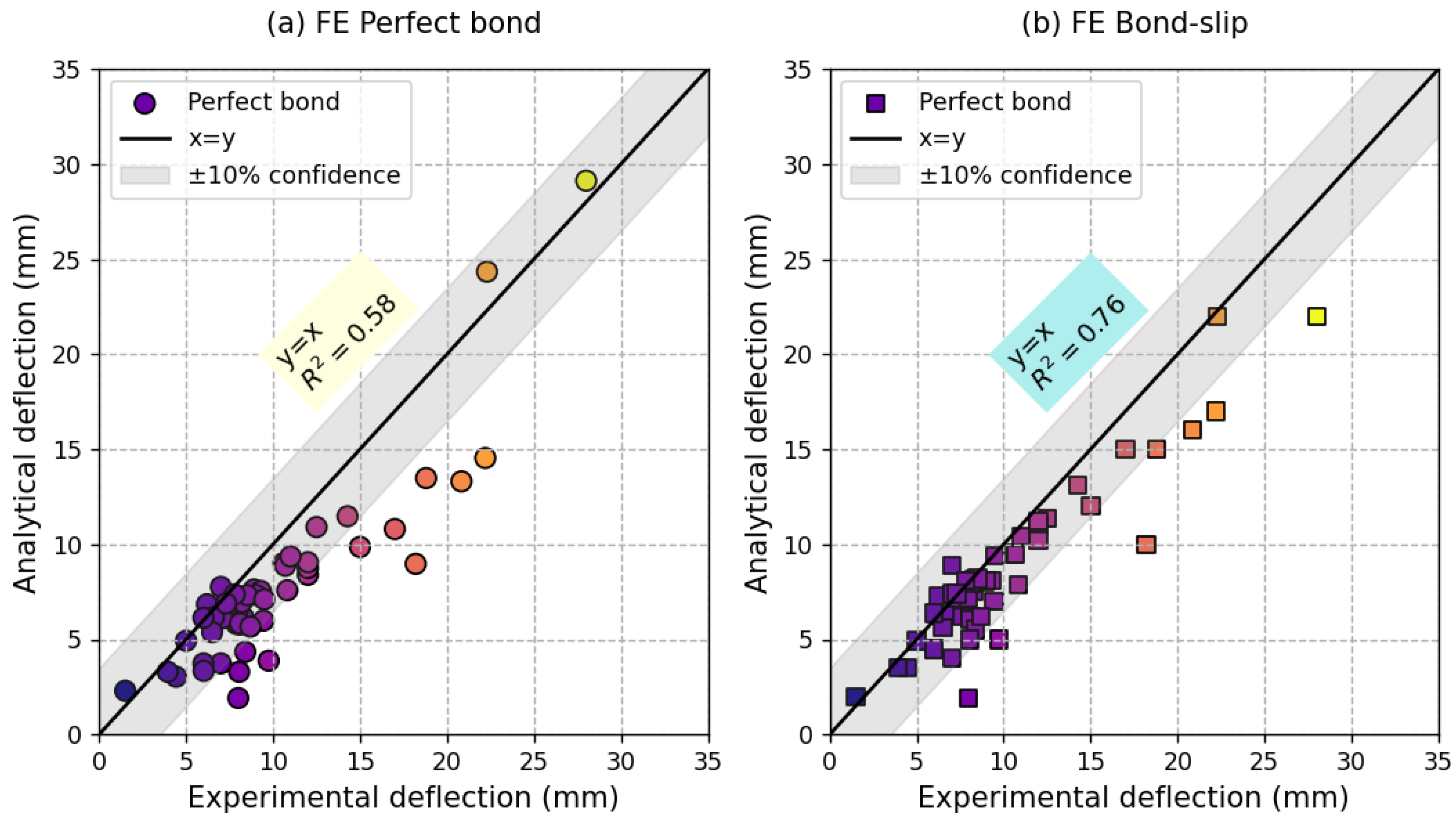
5. Results
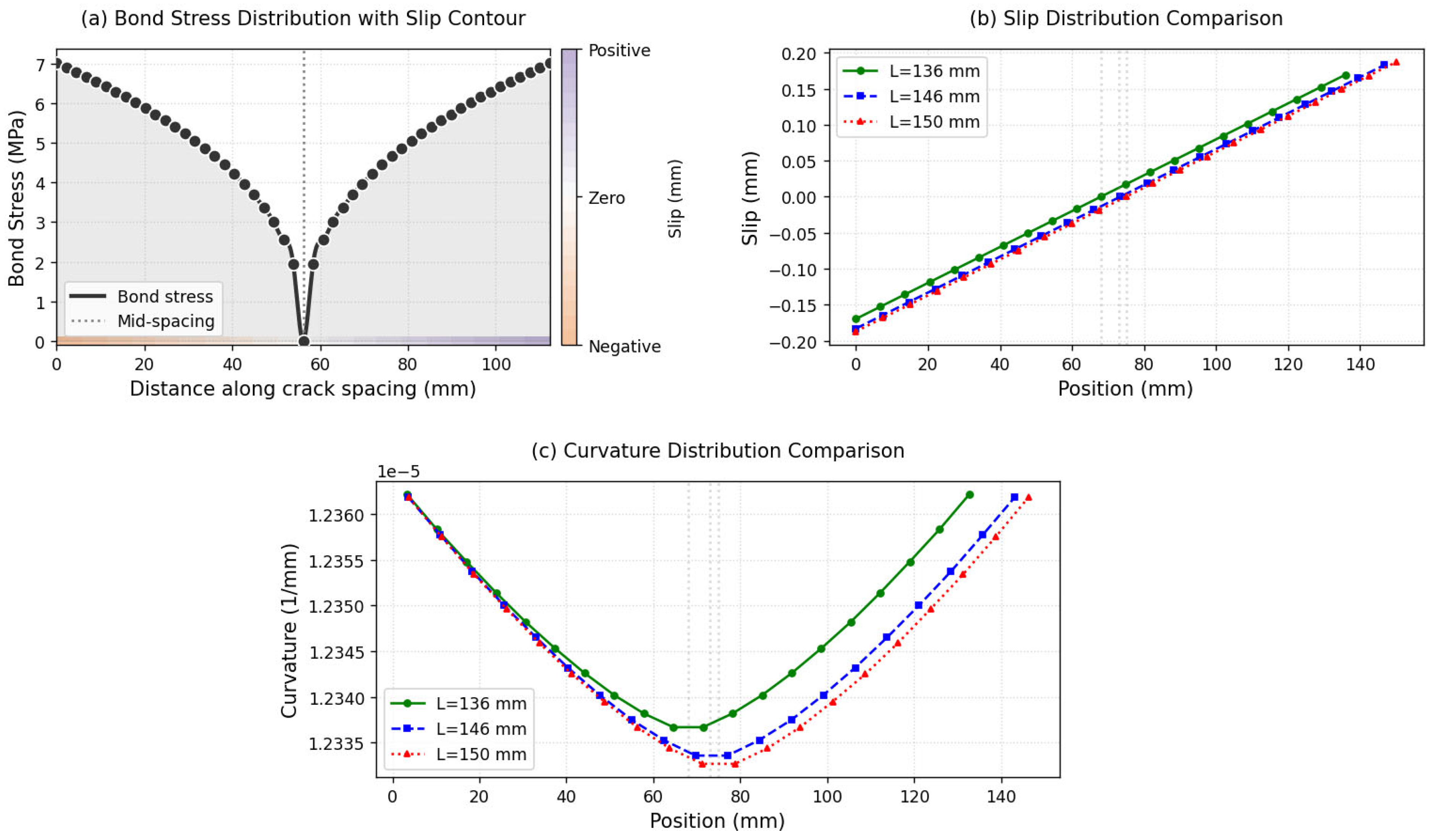
5.1. Bond Stress Distribution Between Two Flexural Cracks
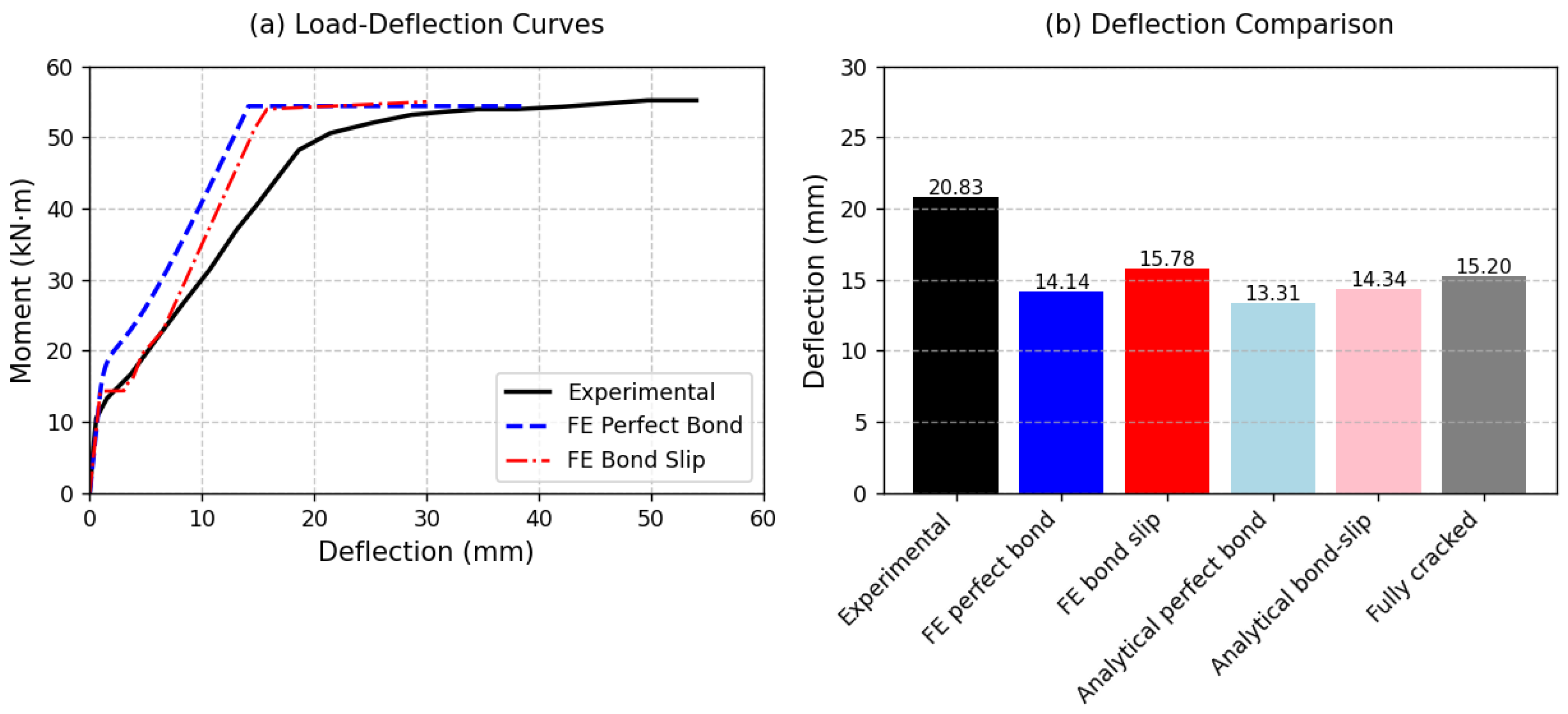
5.2. Validation of the Proposed FE Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| L | Beam span |
| b | Cross-section width |
| h | Cross-section height |
| d0 | Concrete cover height |
| d | Effective height, d = h − d0 |
| a | Distance between the applied load and the support |
| As | Reinforcement area |
| P | Applied load |
| fy | Steel yield strength |
| fcm | Concrete compressive strength |
| fck | Characteristic compressive strength equal to fcm-8 (MPa) |
| fctm | Concrete splitting tensile strength |
| Ec | Concrete elastic modulus |
| Es | Steel elastic modulus |
| x | Height of the compressive zone |
| εc | Concrete compressive strain |
| εct | Concrete tensile strain at the interface rebar-concrete |
| εc1 | Concrete compressive strain at peak stress |
| εcu1 | Concrete failure strain |
| εt | Concrete tensile strain |
| εs | Steel rebar tensile strain |
| σc | Concrete compressive stress |
| σt | Concrete tensile stress |
| σs | Steel tensile stress |
| na = Es/Ec | Modular ratio |
| sr | Cracks spacing |
| M | Applied bending moment |
| Curvature of cracked section | |
| Curvature of uncracked section | |
| Mcr | Cracking moment |
| ε0 | Mean normal strain |
| κ | Curvature |
| C = d0 | Concrete cover to the longitudinal reinforcement |
| ϕ | Bar diameter |
| ρp,eff | Effective reinforcement ratio |
| AC, eff | Effective tension area of concrete |
| k1 | Bond coefficient (0.8 for ribbed bars, 1.6 for plain bars) |
| k2 | Strain distribution coefficient (0.5 for pure tension, 1.0 for bending) |
| k3 | Empirical coefficient (recommended equal to 3.4) |
| k4 | Empirical coefficient (recommended equal to 0.425) |
| NC | Compressive force in the compression bloc |
| NT | Tensile force in the tension bloc |
| Ns | Tensile force in rebar |
| τb | Bond stress |
| τb,max | Maximum value of bond stress |
| τbf | Residual bond strength |
| s1 | Slip corresponding to the bond strength |
| s2 | Slip corresponding to the residual bond strength |
| KC | Concrete stiffness matrix |
| KS | Steel stiffness matrix |
| Kbond | Bond-slip stiffness matrix |
| BC | Concrete strain-displacement matrix |
| BS | Steel strain-displacement matrix |
| N | Shape functions for slip |
| κi | Curvature of the ith element in the FE model |
| xi | Position of the neutral axis for the ith element |
| B | Curvature-Displacement Matrix is the second derivative of the shape functions |
| wi | The weights associated with the Gauss-Lobatto quadrature rule at integration point i |
| J | J = Le is the Jacobian of the mapping from the natural coordinate to the physical coordinate |
| εslip | Steel strain due to slip |
| Lb | Bond transfer length |
Appendix A
| Paper | Beam | L (mm) | b (mm) | h (mm) | a (mm) | As (mm2) | fy (MPa) | fcm (MPa) | fctm (MPa) | Ec (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| Ajdukiewicz [31] | BNNm-b2 | 2400 | 200 | 300 | 800 | 452.4 | 410 | 61.8 | 4.5 | 41,900 |
| BNNh-b2 | 452.4 | 103 | 6.7 | 51,900 | ||||||
| BNNm-b1 | 804.2 | 60.8 | 4.2 | 41,500 | ||||||
| BNNh-b1 | 804.2 | 100.9 | 7.2 | 51,900 | ||||||
| Ignjatoviç [32] | NAC-1 | 3000 | 200 | 300 | 1000 | 150.8 | 555 | 43.7 | 3.1 | 26,600 |
| NAC-2 | 763.4 | |||||||||
| Kang [33] | H0-1.8 | 2700 | 135 | 270 | 900 | 576.1 | 410.8 | 64.5 | 4.2 | 37,700 |
| H0-1.5 | 402.1 | 389.1 | ||||||||
| H0-1 | 265.5 | 407.6 | ||||||||
| H0-0.5 | 157.1 | 377.0 | ||||||||
| N0-1.8 | 576.1 | 410.8 | 38.6 | 3.3 | 29,200 | |||||
| N0-1.5 | 402.1 | 389.1 | ||||||||
| N0-1 | 265.5 | 407.6 | ||||||||
| N0-0.5 | 157.1 | 377.0 | ||||||||
| Wardeh [34] | BN-1 | 1500 | 150 | 200 | 500 | 402.1 | 550 | 38.6 | 3.6 | 39,400 |
| BN-2 | 307.9 | |||||||||
| Sato [35] | v-01-10WB | 2200 | 150 | 200 | 700 | 157.1 | 332 | 30.6 | 2.9 | 30,342 |
| v-01-13WB | 265.5 | 353 | ||||||||
| v-01-16WB | 402.1 | 342 | ||||||||
| v-01-10WB-d | 157.1 | 332 | 32.5 | 3.0 | 29,200 | |||||
| v-01-13WB-d | 265.5 | 353 | ||||||||
| v-01-16WB-d | 402.1 | 342 | ||||||||
| hv-01-13WB | 265.5 | 331 | 68.7 | 3.0 | 31,854 | |||||
| v30-03-wb | 265.5 | 331 | 106.4 | 6.3 | 44,080 | |||||
| v45-03-wb | 265.5 | 331 | 57.0 | 3.0 | 31,854 | |||||
| v60-03-wb | 265.5 | 331 | 40.2 | 3.5 | 32,113 | |||||
| vex45-03-wb | 265.5 | 331 | 55.3 | 3.6 | 36,347 | |||||
| Seara-Paz [30] | H50-0 | 3400 | 200 | 300 | 1275.5 | 402.1 | 500 | 60.7 | 4.3 | 36,300 |
| H65-0 | 46.9 | 4.0 | 35,200 | |||||||
| Arezomandi [36] | CC-F-6-1 | 2700 | 300 | 460 | 900 | 567.1 | 568 | 37.2 | 3.5 | 34,500 |
| CC-F-7-1 | 760.3 | 517 | ||||||||
| CC-F-6-2 | 567.1 | 568 | 34.2 | 3.0 | 33,100 | |||||
| CC-F-7-2 | 760.3 | 517 | ||||||||
| Dar [37] | OB | 5000 | 300 | 500 | 1666 | 1885 | 561 | 19.2 | - | 21,300 |
| Shen [38] | B0 | 1600 | 150 | 300 | 550 | 226.2 | 548 | 42.1 | - | 33,200 |
| Choobbor [39] | US | 1690 | 120 | 240 | 563.3 | 157.1 | 540.1 | 38.78 | - | - |
| Wei [40] | Ref | 2250 | 200 | 300 | 975 | 258 | 400 | 40 | - | 39,000 |
| Song [41] | B-1 | 2800 | 200 | 300 | 1000 | 1140.4 | 455 | 39.1 | - | 32,100 |
| Zhang [42] | RC | 2100 | 150 | 250 | 900 | 628.4 | 410 | 45.2 | 2.26 | 34,500 |
| Nguyen [43] | RC | 2400 | 130 | 300 | 850 | 307.9 | 500 | 35 | 2.0 | 30,000 |
| Wu [44] | R | 2000 | 150 | 250 | 700 | 508.9 | 420 | 60.5 | - | 34,634 |
| Ahmed [45] | BM | 4550 | 190 | 340 | 1925 | 942.5 | 565 | 35 | - | 31,900 |
| Deng [46] | RC1 | 1600 | 150 | 250 | 550 | 157.1 | 435 | 37.4 | 3.35 | 35,000 |
| Ren [47] | NR | 1700 | 150 | 200 | 600 | 226.2 | 500 | 32.2 | - | - |
| Wang [48] | L0 | 1960 | 230 | 270 | 880 | 480.7 | 340 | 34.8 | - | - |
| Yoo [49] | RC-PI | 2222 | 125 | 250 | 743 | 567.06 | 479 | 45 | - | - |
| Zhang [50] | BO | 1600 | 150 | 300 | 500 | 265.5 | 440 | 30 | - | 30,000 |
| El-Emam [51] | CB1 | 2200 | 200 | 300 | 850 | 157.1 | 448 | 30.8 | 2.63 | - |
| Feng [52] | RCBS | 1800 | 200 | 300 | 600 | 157.1 | 300 | 32.7 | - | - |
| Karabulut [16] | SC20-1 | 1000 | 150 | 200 | 300 | 157.1 | 420 | 20.0 | - | - |
| Shi [53] | RC | 1400 | 150 | 200 | 500 | 265.5 | 400 | 37.8 | 2.66 | 31,100 |
Appendix B
Appendix B.1. Worked Example
| Parameter | Symbol | Value | Unit | Remark |
|---|---|---|---|---|
| Yielding moment | My | 126.1 | kN.m | Equation (A9) |
| Uncracked curvature | 1.22 × 10−6 | 1/mm | Equation (4) | |
| Cracked curvature | 7.05 × 10−6 | 1/mm | Equation (5) | |
| Effective curvature | 6.62 × 10−6 | 1/mm | Equation (3) | |
| Midspan deflection | 25.36 | mm | Equation (8) | |
| Transmission length | Lt | 476 | mm | |
| Average bond stress | 4.2 | MPa | Equation (A8) | |
| Slip | s | 0.05 | mm | Equation (A4) |
| Slip induced curvature | 2.74 × 10−7 | 1/mm | ||
| Total curvature | 6.89 × 10−6 | 1/mm | ||
| Total midspan deflection | 26.41 | mm | Equation (8) |
Appendix C
- 1.
- Initialization:
- -
- Define the initial displacement vector U⁰ (usually zero).
- -
- Set the external load increment ΔFext.
- -
- Choose a convergence tolerance (e.g., 10−6) and a relaxation factor (e.g., 0.8).
- 2.
- Iteration Loop (per load step):For each load increment, iterate until convergence:
- a.
- Compute Internal Forces:Fint = Fint(Uᵏ)Derived from the stress state in concrete, steel, and bond–slip interface.
- b.
- Compute Residual Vector:Rᵏ = Fext − Fint(Uᵏ)
- c.
- Assemble Tangent Stiffness Matrix:Kglobal = KC + KS + KbondContributions from
- -
- Concrete: KC = ∫ Act EC(ε) BCᵀ BC dx
- -
- Steel: KS = ∫ AS ES(ε) BSᵀ BS dx
- -
- Bond: Kbond = ∫ Nᵀ (dτb/ds) N dx
- d.
- Solve for Displacement Correction:ΔU = Kglobal−1 Rᵏ
- e.
- Update DisplacementsUᵏ⁺1 = Uᵏ + α ΔUα is the relaxation factor to improve convergence.
- f.
- Check Convergence:||Rᵏ⁺1|| ≤ toleranceIf not satisfied, repeat from step (a).
- 3.
- Post-Convergence:Once converged, compute derived quantities:
- -
- Curvature: κᵢ = εs,i/(d − xᵢ)
- -
- Slip and stress distributions
References
- D’Antino, T.; Pisani, M.A. A Proposal to Improve the Effectiveness of the Deflection Control Method Provided by Eurocodes for Concrete, Timber, and Composite Slabs. Materials 2021, 14, 7627. [Google Scholar] [CrossRef] [PubMed]
- El-Zeadani, M.; Rashid, R.S.M.; Amran, M.Y.H.; Hejazi, F.; Jaafar, M.S. Short-term deflection of RC beams using a discrete rotation approach. Int. J. Adv. Struct. Eng. 2019, 11, 473–490. [Google Scholar] [CrossRef]
- Beljkaš, Ž.; Baša, N. Neural Networks—Deflection Prediction of Continuous Beams with GFRP Reinforcement. Appl. Sci. 2021, 11, 3429. [Google Scholar] [CrossRef]
- Kim, S.-W.; Han, D.-S.; Kim, K.-H. Evaluation of Shear Effect on Deflection of RC Beams. Appl. Sci. 2021, 11, 7690. [Google Scholar] [CrossRef]
- Visintin, P.; Sturm, A.B.; Oehlers, D.J. Long- and short-term serviceability behavior of reinforced concrete beams: Mechanics models for deflections and crack widths. Struct. Concr. 2018, 19, 489–507. [Google Scholar] [CrossRef]
- Zakrzewski, M.; Domski, J. Cracking Behavior and Deflections in Recycled-Aggregate Beams Reinforced with Waste Fibers Subjected to Long-Term Constant Loading. Materials 2023, 16, 3622. [Google Scholar] [CrossRef]
- Kaklauskas, G.; Sokolov, A. A peculiar value of M to M ratio: Reconsidering assumptions of curvature analysis of reinforced concrete beams. Appl. Eng. Sci. 2021, 7, 100053. [Google Scholar] [CrossRef]
- Dancygier, A.N.; Berkover, E. Cracking localization and reduced ductility in fiber-reinforced concrete beams with low reinforcement ratios. Eng. Struct. 2016, 111, 411–424. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code (ACI 318-19) and Commentary on Building Code Requirements for Structural Concrete (ACI 318R-19). American Concrete Institute: Farmington Hills, MI, USA, 2019.
- Daud, R.A.; Daud, S.A.; Al-Azzawi, A.A. Tension stiffening evaluation of steel fibre concrete beams with smooth and deformed reinforcement. J. King Saud Univ.—Eng. Sci. 2021, 33, 147–152. [Google Scholar] [CrossRef]
- Teng, L.; Zhang, R.; Khayat, K.H. Tension-Stiffening Effect Consideration for Modeling Deflection of Cracked Reinforced UHPC Beams. Sustainability 2021, 14, 415. [Google Scholar] [CrossRef]
- Hasan, N.M.S.; Visintin, P.; Oehlers, D.J.; Bennett, T.; Sobuz, H.R. Time dependent deflection of RC beams allowing for partial interaction and non-linear shrinkage. Mater. Struct. 2019, 52, 52. [Google Scholar] [CrossRef]
- Fantilli, A.P.; Orfeo, B.; Caldentey, A.P. The deflection of reinforced concrete beams containing recycled steel fibers. Struct. Concr. 2021, 22, 2089–2104. [Google Scholar] [CrossRef]
- Amin, A.; Foster, S.J.; Kaufmann, W. Instantaneous deflection calculation for steel fibre reinforced concrete one way members. Eng. Struct. 2017, 131, 438–445. [Google Scholar] [CrossRef]
- Karabulut, M. Machine Learning-Driven Flexural Performance Prediction and Experimental Investigation of Glass Fiber-Reinforced Polymer Bar-Reinforced Concrete Beams. Polymers 2025, 17, 713. [Google Scholar] [CrossRef]
- Karabulut, M. Nonlinear Load-Deflection Analysis of Steel Rebar-Reinforced Concrete Beams: Experimental, Theoretical and Machine Learning Analysis. Buildings 2025, 15, 432. [Google Scholar] [CrossRef]
- Comité Européen de Normalisation. Eurocode 2. Design of Concrete Structures—Part 1: Common Rules for Building and Civil Engineering; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Mohamad, R.; Hammadeh, H.; Kousa, M.; Wardeh, G. Fracture Based Non Linear Model For Reinforced Concrete Beams. GEOMATE J. 2020, 18, 110–117. Available online: https://geomatejournal.com/geomate/article/view/408 (accessed on 1 January 2020). [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.-E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Wang, T.; Hsu, T.T.C. Nonlinear finite element analysis of concrete structures using new constitutive models. Comput. Struct. 2001, 79, 2781–2791. [Google Scholar] [CrossRef]
- Mosley, B.; Bungey, J.; Hulse, R. Reinforced Concrete Design: To Eurocode 2, 6th ed.; Palgrave Macmillan: New York, NY, USA, 2007. [Google Scholar]
- Bakleh, B.; Hasan, H.; Wardeh, G. Analytical Model for the Prediction of Instantaneous and Long-Term Behavior of RC Beams under Static Sustained Service. Appl. Mech. 2023, 4, 31–43. [Google Scholar] [CrossRef]
- Wardeh, G.; Ghorbel, E.; Gomart, H.; Fiorio, B. Experimental and analytical study of bond behavior between recycled aggregate concrete and steel bars using a pullout test. Struct. Concr. 2017, 18, 811–825. [Google Scholar] [CrossRef]
- CEB-FIP. Model Code 2010; International Federation for Structural Concrete: Lausanne, Switzerland, 2012. [Google Scholar]
- Manfredi, G.; Pecce, M. A refined R.C. beam element including bond–slip relationship for the analysis of continuous beams. Comput. Struct. 1998, 69, 53–62. [Google Scholar] [CrossRef]
- Oliveira, R.S.; Ramalho, M.A.; Corrêa, M.R.S. A layered finite element for reinforced concrete beams with bond–slip effects. Cem. Concr. Compos. 2008, 30, 245–252. [Google Scholar] [CrossRef]
- Jakubovskis, R.; Kaklauskas, G.; Gribniak, V.; Weber, A.; Juknys, M. Serviceability Analysis of Concrete Beams with Different Arrangements of GFRP Bars in the Tensile Zone. J. Compos. Constr. 2014, 18, 04014005. [Google Scholar] [CrossRef]
- Öchsner, A.; Merkel, M. One-Dimensional Finite Elements; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Oñate, E. Structural Analysis with the Finite Element Method Linear Statics; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Seara-paz, S.; González-fonteboa, B.; Martínez-abella, F.; Eiras-lópez, J. Flexural performance of reinforced concrete beams made with recycled concrete coarse aggregate. Eng. Struct. 2018, 156, 32–45. [Google Scholar] [CrossRef]
- Ajdukiewicz, A.B.; Kliszczewicz, A.T. Comparative Tests of Beams and Columns Made of Recycled Aggregate Concrete and Natural Aggregate Concrete. J. Adv. Concr. Technol. 2007, 5, 259–273. [Google Scholar] [CrossRef]
- Ignjatovic, I.S.; Marinkovic, S.B.; Miskovic, Z.; Savic, A.R. Flexural behavior of reinforced recycled aggregate concrete beams under short-term loading. Mater. Struct. 2013, 46, 1045–1059. [Google Scholar] [CrossRef]
- Kang, T.H.-K.; Kim, W.; Kwak, Y.-K.; Hong, S.-G. Flexural Testing of Reinforced Concrete Beams with Recycled Concrete Aggregates. ACI Struct. J. 2014, 111, 607–616. [Google Scholar] [CrossRef]
- Wardeh, G.; Ghorbel, E. Experimental Investigation and Analytical Study on the Flexural Behavior of Reinforced Recycled Aggregate Concrete Beams. J. Mod. Mech. Eng. Technol. 2018, 5, 1–23. [Google Scholar] [CrossRef]
- Sato, R.; Maruyama, I.; Sogabe, T.; Sogo, M. Flexural Behavior of Reinforced Recycled Concrete Beams. J. Adv. Concr. Technol. 2007, 5, 43–61. [Google Scholar] [CrossRef]
- Arezoumandi, M.; Smith, A.; Volz, J.S.; Khayat, K.H. An experimental study on flexural strength of reinforced concrete beams with 100% recycled concrete aggregate. Eng. Struct. 2015, 88, 154–162. [Google Scholar] [CrossRef]
- Dar, M.A.; Verma, A.; Malalasekara, P.; Kok, A.; Quek, J.; Pang, S.D. Hybrid strengthening scheme for reinforced concrete beams: Flexural behaviour and large-scale testing. Eng. Struct. 2024, 301, 117206. [Google Scholar] [CrossRef]
- Shen, J.; Dai, H.; Zhou, G.; Shi, J. Flexural behavior of pre-damaged RC beams strengthened with UHPFRC-CFRP grid layer. Eng. Struct. 2024, 317, 118669. [Google Scholar] [CrossRef]
- Choobbor, S.S.; Hawileh, R.A.; Abu-Obeidah, A.; Abdalla, J.A. Performance of hybrid carbon and basalt FRP sheets in strengthening concrete beams in flexure. Compos. Struct. 2019, 227, 111337. [Google Scholar] [CrossRef]
- Wei, J.; Teng, L.; Khayat, K.H. Coupled effect of fiber type and reinforcement ratio on flexural behavior of reinforced beams cast with super workable concrete. Constr. Build. Mater. 2024, 438, 137039. [Google Scholar] [CrossRef]
- Song, L.; Wei, M.; Zhang, X.; Li, C.; Dong, Z.; Wang, Y. Flexural performance of reinforced concrete beams repaired with BFRP grid-TSUHDC. Constr. Build. Mater. 2024, 443, 137748. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, D.; Abdalla, J.A.; Hawileh, R.A.; Qin, F.; Xu, X. Flexural behavior of reinforced concrete beams externally strengthened with ECC and FRP grid reinforcement. Constr. Build. Mater. 2024, 446, 137964. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Ho, M.H.; Tran, V.R.; Phan, H.N.; Nguyen, D.D.N.; Huynh, P.N. Flexural performance of reinforced concrete beams strengthened with prestressed FRP sheets: Experiments and numerical investigations. Case Stud. Constr. Mater. 2024, 21, e03475. [Google Scholar] [CrossRef]
- Wu, F.; Lei, S.; Liu, Z.; Cao, J.; Liu, L. Flexural behavior of RC beams strengthened with CFRP grid-reinforced engineering cementitious composite. Structures 2024, 67, 106978. [Google Scholar] [CrossRef]
- Ahmed, I.; Reichenbach, S.; Kromoser, B. Flexural behaviour of reinforced concrete beams with voids: Topology optimisation basis. Structures 2024, 67, 107037. [Google Scholar] [CrossRef]
- Deng, L.; Liu, Y.; Zhou, Z.; Zou, Y.; Shi, W.; Jin, Z.; Zhong, Q. Flexural performance of BFRP grid–ECC in strengthening damaged RC beams. Structures 2024, 69, 107420. [Google Scholar] [CrossRef]
- Ren, Y.; Guo, R.; Liu, A.; Xia, M.; Pan, Y. Study on flexural behaviour and analytical model of RC beams strengthened with FRP grid-ECC composite layers. Structures 2025, 73, 108445. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, H.; Chen, H.; Chen, Z.; Zhuang, N. Experimental and numerical study on the flexural properties of RC beams with different CFRP-strengthened schemes. J. Build. Eng. 2024, 97, 110734. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Chun, B.; Choi, J.; Min, K.-H.; Shin, H.-O. Enhancing the flexural capacity of RC beams under various loading rates through strengthening with ultra-high-performance fiber-reinforced concrete. Dev. Built Environ. 2024, 20, 100581. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H. Study on Flexural Performance of Reinforced Concrete Beams Strengthened with FRP Grid–PCM Composite Reinforcement. Appl. Sci. 2024, 14, 9013. [Google Scholar] [CrossRef]
- El-Emam, H.M.; Ata, B.; Ahmad, S.S.E.; Salim, H.A.; Reda, R.M. Enhancing Flexural Resistance in Pre-Damaged RC Beams with Near-Surface Mounted GFRP Bar and Bolt Anchoring System. Buildings 2024, 14, 723. [Google Scholar] [CrossRef]
- Feng, X.; Liu, D.; Long, X.; Duan, K.; Zuo, J.; Liu, W.; Dong, H. Flexural Capacity of the Normal Sections of Concrete Beams Strengthened with Corrugated Steel Plates. Buildings 2024, 14, 1398. [Google Scholar] [CrossRef]
- Shi, C.; Jin, S.; Wang, C.; Yang, Y. Enhancing Flexural Behavior of Reinforced Concrete Beams Strengthened with Basalt Fiber-Reinforced Polymer Sheets Using Carbon Nanotube-Modified Epoxy. Materials 2024, 17, 3250. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamad, R.; Wardeh, G.; Kousa, M.A.A.A.; Jahami, A. 1D Finite Element Modeling of Bond-Slip Behavior and Deflection in Reinforced Concrete Flexural Members. Designs 2025, 9, 75. https://doi.org/10.3390/designs9030075
Mohamad R, Wardeh G, Kousa MAAA, Jahami A. 1D Finite Element Modeling of Bond-Slip Behavior and Deflection in Reinforced Concrete Flexural Members. Designs. 2025; 9(3):75. https://doi.org/10.3390/designs9030075
Chicago/Turabian StyleMohamad, Rahaf, George Wardeh, Mayada Al Ahmad Al Kousa, and Ali Jahami. 2025. "1D Finite Element Modeling of Bond-Slip Behavior and Deflection in Reinforced Concrete Flexural Members" Designs 9, no. 3: 75. https://doi.org/10.3390/designs9030075
APA StyleMohamad, R., Wardeh, G., Kousa, M. A. A. A., & Jahami, A. (2025). 1D Finite Element Modeling of Bond-Slip Behavior and Deflection in Reinforced Concrete Flexural Members. Designs, 9(3), 75. https://doi.org/10.3390/designs9030075








