An Approach for Predicting the Lifetime of Lead-Free Soldered Electronic Components: Hitachi Rail STS Case Study

Abstract

Throughout much of the 20th century, Sn–Pb solder dominated electronics. However, environmental and health concerns have driven the adoption of lead-free alternatives. Since 2006, legislation such as the European Union’s RoHS Directive has mandated lead-free solder in most electronic devices, prompting extensive research into high-performance substitutes. Lead-free solders offer advantages such as reduced environmental impact and improved reliability but replacing Sn–Pb presents challenges in areas like melting point and wetting ability. This transition is primarily motivated by a focus on protecting environmental and human health, while ensuring equal or even improved reliability. Research has explored lead-free solder’s mechanical properties, microstructure, wettability, and reliability. However, there is a notable lack of studies on its long-term performance and lifetime influence. To address this gap, mathematical models are used to predict intermetallic bond evolution from process conditions, validated with experimental tests. This study contributes by extending these models to predict bond evolution under typical operating conditions of devices and comparing the predictions with actual intermetallic thickness values found through metallographic sections.

1. Introduction

For much of the 20th century, Sn–Pb solder was the industry standard for electronics. However, growing concerns about lead’s toxicity has led to a major swift towards lead-free alternatives in recent decades [1,2,3]. Since 2006, European legislation like the Restriction of Hazardous Substances Directive (RoHS) has banned lead in most electrical and electronic devices. This shift away from traditional Sn–Pb solder reflects a critical prioritization of public health and environmental protection. While Sn–Pb offered some performance benefits, its drawbacks ultimately made its continued use unacceptable. Lead exposure poses serious health risks, including neurological damage and reproductive problems [4]. Additionally, lead pollution harms ecosystems through air and water contamination. Concerns about lead’s health and environmental impacts led to legislation like the European Union’s Restriction of Hazardous Substances Directive (RoHS). Since 2006, this law has effectively banned lead-based solder (Sn–Pb) in most electronics. When Directive 2011/65/EU (RoHS 2) replaced Directive 2002/95/EC (RoHS 1), existing exemptions were transferred to Annex III of RoHS 2. The maximum validity for exemptions increased from four to five years for most categories of electrical and electronic equipment (EEE), except for categories 8 and 9, which have a seven-year validity. According to Article 5(2), exemptions listed in Annex III as of 21 July 2011 follow this maximum validity unless specified otherwise. Consequently, over 30 exemptions would have expired on 21 July 2016 if they were not extended by the industry. The European Commission contracted the Oeko-Institut and Fraunhofer IZM to review these exemption applications from June 2015 to July 2016 [5]. This triggered a surge in the research and development of high-performance, lead-free alternatives. Ideally, these new solders would be just as good or even better than Sn–Pb, but without the toxic risks. Lead-free solders offer some advantages. They allow for the use of less harmful “no-clean” or water-soluble fluxes, reducing heat stress during soldering. Additionally, they can be more resistant to electrical wear, oxidation, and corrosion, improving the overall reliability of the solder joint. However, replacing a well-understood material like Sn–Pb solder comes with challenges. Researchers are constantly working to improve the performance and reliability of lead-free solders, addressing issues like higher melting points, weaker wetting ability, and long-term stability. Overall, the shift to lead-free solders in the electronics industry reflects a critical focus on protecting human health and the environment. While challenges remain, ongoing research is making lead-free alternatives ever more effective, paving the way for a more sustainable future in electronics manufacturing. Several previous studies have explored different aspects of lead-free solder [6], including its mechanical properties [7], microstructure and intermetallic layers [8], wettability [9], and overall reliability [10]. While these studies provide valuable insights, none have specifically investigated the impact of lead-free solder on the lifespan of solder joints. This paper uses mathematical models to predict how intermetallic bonds change over time based on soldering conditions. These models are validated by testing boards made by Hitachi in collaboration with independent labs. Previously, researchers have proposed various formulas to estimate intermetallic thickness growth. These formulas, based on experiments and data from the literature, can provide somewhat accurate predictions. Our models focus on lead-free alloys, especially SAC (tin–silver–copper). However, they can be adapted to work with outdated lead-based alloys as well. These models predict both the initial intermetallic thickness after soldering and its growth during stress tests. These tests include high-temperature exposure, thermal shocks, and thermal cycles simulating real-world conditions (−40 °C to 125 °C). Our original contribution is extending these models to predict how bonds change under normal operating conditions. These predictions, conducted only for boards with SAC solder, were then compared to the actual intermetallic thickness measured in metallographic sections. The rest of this manuscript is organized as follows: Section 2 provides a literature review on lead-free solders. Section 3 describes the proposed model, while Section 4 presents the test trials and numerical results. Section 5 discusses the metallographic sections in comparison to the model estimations. Finally, conclusions and future developments are presented in Section 6.

2. Literature Review

Lead-free solders are becoming increasingly important in the electronics industry due to the environmental and health concerns associated with lead-based solders. Cheng et al. [6] reviewed the recent research on lead-free solders, focusing on their properties and performance. Lead-free solders have been shown to be reliable in a variety of applications. However, there are some challenges that need to be addressed, such as higher melting temperatures and reduced ductility.

Jung and Jung [9] focused on the importance of solder wettability for reliable microelectronic packaging and explored how the wetting balance test is used to assess it. They highlighted the wetting balance test (also known as Meniscograph) as the most common method for quantitatively measuring the wettability between molten solder and a substrate.

Fan et al. [11] investigated how the surface finish of electronic component pads (where the solder connects) affects the microstructure and intermetallic compound (IMC) growth in tin–bismuth (Sn–Bi) and tin–bismuth–silver (Sn–Bi–Ag) solders. They highlighted the importance of pad surface finish in influencing IMC growth in Sn–Bi and Sn–Bi–Ag solders. Their work suggests that Cu–OSP, or the addition of silver to the solder, is a possible strategy to mitigate excessive IMC growth and potentially improve the reliability of solder joints.

Dale et al. [12] studied the fatigue life (durability under repeated stress) of a specific lead-free solder alloy (Sn3.0Ag0.5Cu) under combined loading conditions. They underlined the importance of considering combined loading conditions when evaluating the reliability of solder joints in electronic devices. Their study suggests that solder joints may be more susceptible to fatigue failure in applications where they experience both shear and tensile stress.

Wang et al. [13] proposed a new analytical model to predict the growth of intermetallic compounds (IMCs) in Cu–Sn–Cu sandwich structures. This model offers a simpler yet effective tool for researchers and engineers to design reliable Cu–Sn–Cu structures for electronic applications.

Peng et al. [14] explored Cu–Sn intermetallic compounds (IMCs) growth kinetics for high-temperature resistant packaging in semiconductor power devices. They established a 3D kinetics model and equations for Cu₆Sn₅ and Cu₃Sn growth. Experimental validation shows temperature and Cu particle size affect growth kinetics, while Sn content impacts solidification time.

Ramli et al. [15] presented a review that summarizes factors impacting intermetallic compounds (IMCs) formation and growth, which are crucial for joint structure. Their key findings were: (1) Minor alloying elements significantly affect primary and interfacial IMCs, altering microstructure and IMC growth rates; (2) Surface finishes material heavily influences IMC layer thickness and composition via dissolution during soldering; (3) Higher aging temperatures and longer times increase IMC thickness; (4) Smaller solder volumes lead to thicker IMC layers due to faster copper concentration growth in smaller solder balls.

Ismail et al. [16] conducted a comprehensive review of 171 research articles and papers from Scopus, Google Scholar, and Dimensions databases to examine the impact of surface roughness on wettability and intermetallic compound (IMC) layer formation in lead-free solder joints. Their analysis revealed a predominant focus on soldering processes and materials, with limited attention to surface roughness effects. Future research could explore post-treatment methods, such as additives or reinforcement, to improve lead-free solder material properties. Understanding the correlation between soldering processes and surface roughness in lead-free solder materials is crucial for advancing knowledge in this field and optimizing solder joint performance.

The focus of the models is on lead-free alloys, particularly SAC (tin–silver–copper), but they can be adapted to leaded alloys, which are now obsolete. The predictions address both the intermetallic thickness achievable after the soldering process and its growth following testing through accelerated exposure to heat, thermal shocks, and thermal cycles simulating operating conditions from −40 °C to 125 °C. The original contribution of this work was to extend the use of these mathematical relationships to predict bond evolution under normal device operating conditions. These predictions, made exclusively for boards with SAC alloy soldering, were then compared with the intermetallic thickness values observed through metallographic sections.

3. Proposed Model

Solder joints in electronic components typically undergo two types of fatigue failure: ductile rupture, often due to creep, which involves localized fracture at the interface between the intermetallic layer and the solder, or brittle rupture with localized fracture within the intermetallic layer or along the surface finish. Ductile rupture for these solders is due to thermomechanical fatigue, as the operating temperatures of electronic assemblies range from a minimum of −40 °C to a maximum of 125 °C; ductile rupture is the result of progressive damage due to thermomechanical cycles that cause the formation of a crack. Tin-based solders such as SAC operate at relatively high temperatures compared to the melting temperature of the alloy, which means that yielding occurs at relatively low applied stress values, while creep and diffusion processes are quite rapid. The solder itself can exhibit strain rate-independent as well as plastic and strain rate-dependent behavior; therefore, the solder layer can be simplified as a combination of a spring and a viscous damper, while the intermetallic layer exhibits elastic behavior and is modeled as a spring. Brittle rupture also depends on the thickness of the intermetallic layer; in fact, it seems that the strain rate value at which the transition from ductile rupture to brittle rupture occurs becomes lower and lower as the intermetallic layer grows, until only brittle ruptures are observed as the life of the board increases. The intermetallic layer grows over time, especially with exposure to heat during the board’s working cycles.

At this point, it is clear that the thickness of the intermetallic layer is important for the reliability of the soldered joint: if it is an intrinsic quality of a solder joint made on electronic boards, and its presence in an adequate quantity denotes good quality of the solder joint under consideration, it is also important that there are no excessive thicknesses downstream of the soldering process, nor that their growth is excessive during operation, in order to avoid premature and sudden failures. It should be remembered that not only the thickness of the intermetallic layer affects the reliability of the soldered joint, but also its morphology; the microstructure of a soldered joint changes over time, with the grains of the solder growing larger and coarser. Furthermore, if the intermetallic layer becomes thicker, the intermetallic compound grains dispersed in the solder also become larger, thus losing the strengthening effect mentioned above.

It should be clarified that the initial intermetallic thickness after the soldering process is an unknown parameter; it has not been experimentally measured because metallographic sections were performed on tested electronic boards (which have already undergone accelerated aging cycles). However, as mentioned earlier, considering the soldering parameters, an initial intermetallic thickness X₀ (after the process) has been calculated, to which the thickness variation ΔX predicted through the test parameters will be added. The sum obtained will give the total predicted intermetallic thickness X_tot after the test, which will then be compared with the intermetallic thickness observed through metallographic sections of the tested boards. It should be noted that, since the intermetallic thickness of the secondary Cu₃Sn compound is not clearly visible in the metallographic sections and is negligible in size, it can be assumed that the calculated total intermetallic thickness is that of the primary Cu₆Sn₅ compound. In summary, once the process parameters, such as temperature and time, are defined, and once the modes, times, and temperatures of the accelerated tests are determined, all the necessary elements are available to use the formulas.

Regarding lead-free alloys used to solder component terminals to the copper base (or pad) with possible nickel surface finish, the following Formula (1) is used to calculate the intermetallic thickness in a generic manner [17].

$$X\left(t,T\right) = k{t}^n$$

(1)

This formula is expressed as a function of time and temperature and is a power law where the intermetallic thickness depends on the growth rate parameter k (which varies with temperature and is measured in μm/s) and the dimensionless growth exponent n. These two parameters vary based on temperature and the type of surface finish used (nickel or copper). Generally, the value of n is approximately 1/3 if the diffusion of the reactive species forming the intermetallic compounds is limited to grain boundaries, whereas the value of n is approximately 1/2 if the diffusion of the metallic species is volumetric, in which case the intermetallic thickness growth is faster [18]. In turn, k can be expanded as a further expression, which is referred to as Formula (2).

$$k = k_0{e}^{-{\displaystyle \frac{Q}{RT}}}$$

(2)

In this expression, k₀ represents the unit growth constant, Q is the apparent activation energy, R is the Boltzmann constant, and T is the absolute temperature. The value of k expressed in this extended form will be subsequently used in the intermetallic thickness prediction formula during testing. By combining Formulas (1) and (2), an extended expression for calculating the intermetallic thickness is obtained, as shown below in Formula (3).

$$X\left(t,T\right) = \left(k_0{e}^{-{\displaystyle \frac{Q}{RT}}}\right)t^n$$

(3)

In the case of the initial thickness calculation, the literature provides values of k and n, eliminating the need for using the extended formula for k.

Table 1. Values of k and n for Sn–Ag–Cu alloy on copper surface finish [19].

Temperature (°C)	k (μm/sn)	n
225	0.37	0.20
235	0.31	0.27
245	0.46	0.27
260	0.65	0.29
280	0.66	0.28

and

Table 2. Values of k and n for Sn–Ag–Cu alloy on copper coated with nickel [19].

Temperature (°C)	k (μm/sn)	n
225	0.09	0.40
235	0.15	0.51
245	0.21	0.50
260	0.37	0.50

below show the literature values of k and n for SAC alloys at various temperatures and surface finishes.

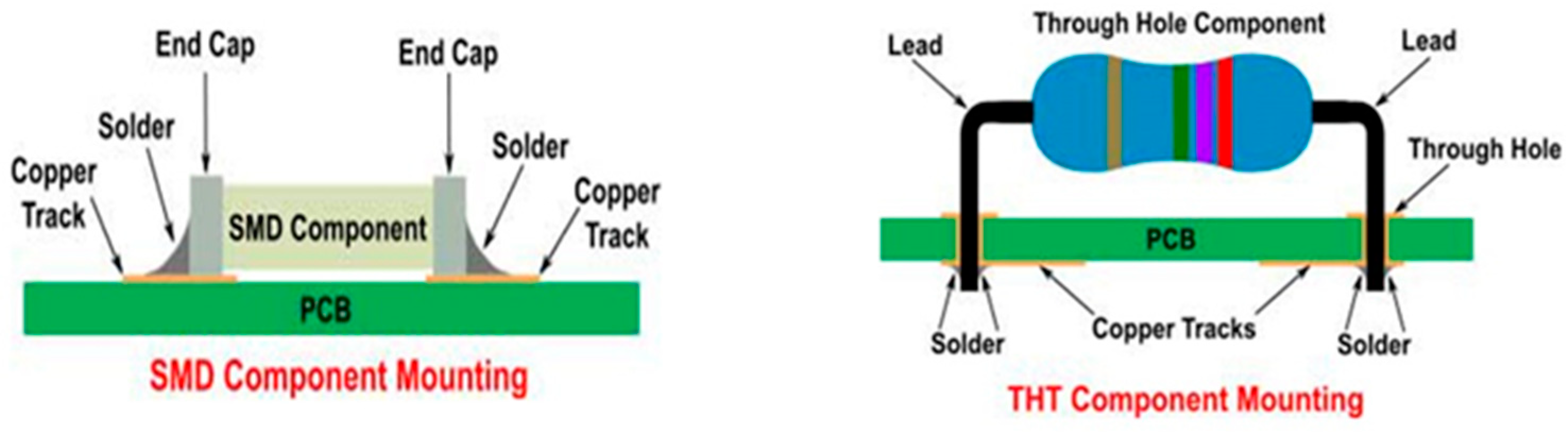
The process parameters are then defined for Surface Mount Devices (SMD) and Through-Hole Technology (THT) components (see Figure 1), with the former soldered in the oven using reflow soldering and the latter using wave soldering. Regarding the soldering of the analyzed components, an SMD component has copper terminals, with the base (or pad) it is soldered on being copper but presenting a nickel surface finish. The reflow soldering process occurs with a dwell time above the liquidus temperature around 65–70 s, while the peak temperature above the liquidus is approximately 235–245 °C. For Through-Hole Technology (THT) components, the terminal is again made of copper, while the through-hole is copper and is also coated with a nickel finish. The peak temperature reached by the hole in contact for 4–5 s with the molten alloy wave is approximately 250 °C.

With these parameters defined, a prediction of the intermetallic thickness X₀ downstream of the soldering process can be outlined. By then replacing the tabulated values of k and n with the process temperatures and substituting the time variable in Formula (1) with the available data, values of thickness X₀ in μm are obtained, as shown in

Table 3. Prediction of intermetallic layer thickness X₀ for SMD components after the soldering process.

	Surface Mount Device (SMD)
	Terminal in Cu				Pad in Cu/Ni
Temperature (°C)	235		245		235		245
Time (s)	65	70	65	70	65	70	65	70
X0 (µm)	0.96	0.98	1.42	1.45	1.26	1.31	1.69	1.76
- X0 maximum of 1.45 μm for the copper terminal. - X0 maximum of 1.76 μm for copper pads with a nickel finish.

and

Table 4. Prediction of intermetallic layer thickness X₀ for THT components after the soldering process.

THT (Through-Hole Component)
Terminal (Cu)		Hole (Cu/Ni)
X0	4.6 s	X0	4.6 s
245 °C	0.69 μm	245 °C	0.45 μm
260 °C	1.00 μm	260 °C	0.80 μm
X0 maximum of 1.45 μm for the copper terminal. X0 maximum of 0.80 μm for the copper hole with a nickel finish.

, from which the larger one will be taken to evaluate the worst-case scenario.

4. Estimation of the Growth Delta of the Intermetallic Thickness Following the Test Trials

Once the thickness X₀ downstream of the process is estimated, the growth ΔX of the intermetallic thickness can be evaluated using Formula (3). When using Formula (3) for ΔX, some considerations must be made regarding the constants used, which pertain to SAC-type alloys. The analyzed solder joints are composed of these alloys. For SAC alloys, values found in the literature will be used for n and k₀ [18], specifically, n = 0.52 and k₀ = 0.0178 m/s^0.52 (value to be converted to μm/s^0.52).

The other constants include the Boltzmann constant R (equal to 8.314 J/K mol) and the apparent activation energy Q. The apparent activation energy for diffusion and intermetallic thickness growth phenomena is not uniquely determined and depends on many factors, even at small scales. It is experimentally obtained by researchers in reverse, starting from the observed intermetallic thickness value, through graphs that plot ln(k) against 1/T [18]. It is also reported in the literature that the apparent activation energy can be calculated very approximately by multiplying the absolute melting temperature value of the intermetallic compound by 85. For example, considering the primary compound that melts at 415 °C, it results in a value of 58.5 kJ/mol [19]; another value reported in the literature is 57.7 kJ/mol [18]. However, since obtaining a precise value for each case is impossible, based on the many values found in the literature, the apparent activation energy generally ranges around 50–60 kJ/mol for the primary intermetallic compound Cu₆Sn₅ and more generally for the total intermetallic thickness, with extreme values that can exceed 80 kJ/mol [20] predictions. Given the exponential nature of Formula (3), the maximum ΔX that can be calculated is the one resulting from the minimum observed activation energy, which will therefore be set at 50 kJ/mol to assess the worst-case scenario. Regarding the test phases, after the soldering process, the boards undergo three stages of exposure to high and low temperatures:

(1)

The first phase involves constant temperature exposure in an oven at 125 °C for 12 h.

(2)

The second phase consists of thermal shock for 50 cycles, with rapid transitions from −40 °C to 85 °C at a heating/cooling rate of 41.66 °C/min (the transition between temperatures occurs in less than 3 min), with a constant stay of 15 min at each of the two temperatures, totaling 36 min per cycle.

(3)

The third phase spans 55 h in total, repeating a thermal cycle with a constant stay at −40 °C and 85 °C for 20 min at each of the two temperatures, with transitions between temperatures at a rate of 5 °C/min, which is gentler than that of the thermal shocks. A complete cycle lasts 90 min, so the total number of cycles in 55 h will be 36.666.

By calculating the total exposure times to the respective temperatures for each phase of the cycle, neglecting the transition phases between temperatures, we obtain:

• Total stay at 125 °C for 12 h (43,200 s).
• Thermal shock with a total stay of 12 h and 30 min (45,000 s) for each of the two temperatures (−40 °C and 85 °C).
• Thermal cycle with a total stay of 12 h, 13 min, and 20 s (44,000 s in total) for each of the two temperatures (−40 °C and 85 °C).

For completeness, the graphs related to thermal shocks and thermal cycles are provided in Figure 2.

Thermal cycling parameters are detailed in terms of duration and temperatures in

Table 5. Total exposure time (in seconds) and temperature for each test phase.

Steps	Cycles (n)	Temp (°C)	Minutes per Cycle (min)	Seconds per Cycle (s)	Total Time (s)
Phase 1 (Const Temp)	1	125	720	43,200	43,200
Phase 2 (Low Temp)	50	−40	15	900	45,000
Phase 2 (High Temp)	50	+85	15	900	45,000
Phase 3 (Low Temp)	36.66	−40	20	1200	44,000
Phase 3 (High Temp)	36.66	+85	20	1200	44,000

.

Referring back to Formula (3), the time parameters (in seconds) and absolute temperature are substituted into the equation to predict the maximum achievable ΔX, with Q set to 50 kJ/mol (this value will be converted to J/mol in the formula). It is reiterated that this apparent activation energy value determines the maximum observable delta; thus, we consider the worst-case scenario, which predicts the maximum growth of the intermetallic thickness. The predicted maximum thickness deltas are summarized in

Table 6. Intermetallic layer increase (prediction) for each acceptance test phase.

	Temperature (K)	Time (s)	ΔX Max (µm)
Industrial oven	398	43,200	1.254566946
Thermal shock	358	45,000	0.236857009
	233	45,000	0.0000288759
Thermal cycle	358	44,000	0.234105235
	233	44,000	0.0000285404
			1.725586605
			1.73

, detailing the individual thickness variations calculated for each test phase and temperature, then summed in the final row.

In this last table, it is worth noting that exposure to −40 °C does not generate significant variations in the intermetallic thickness, while exposure to the high temperatures of 125 °C and 85 °C largely influences it. Therefore, the expected maximum ΔX is the sum: 1.73 μm.

5. Comparison of the Estimates with the Values of Intermetallic Thickness Observed through Metallographic Sections

At this point, the maximum ΔX just obtained is added to the maximum initial thicknesses X₀ downstream of the previously calculated process (it is recalled that Xtot = X₀ + ΔX). This estimates an upper limit of prediction for the total thickness downstream of the accelerated test to which the board is subjected, to be compared with the thickness data found in the metallographic sections.

Table 7. Post-inspection intermetallic layer thickness values, estimates, and real results obtained from metallographic sections.

	Estimate Value	Response Value
	Xtot (Maximum Value)	Xtot (Maximum Value)
Terminal SMD	3.2 μm	2.5 μm
Pad SMD	3.5 μm	2 μm
Terminal THT	2.7 μm	1.2 μm
Hole THT	2.5 μm	1 μm

shows the comparison between the estimates and findings.

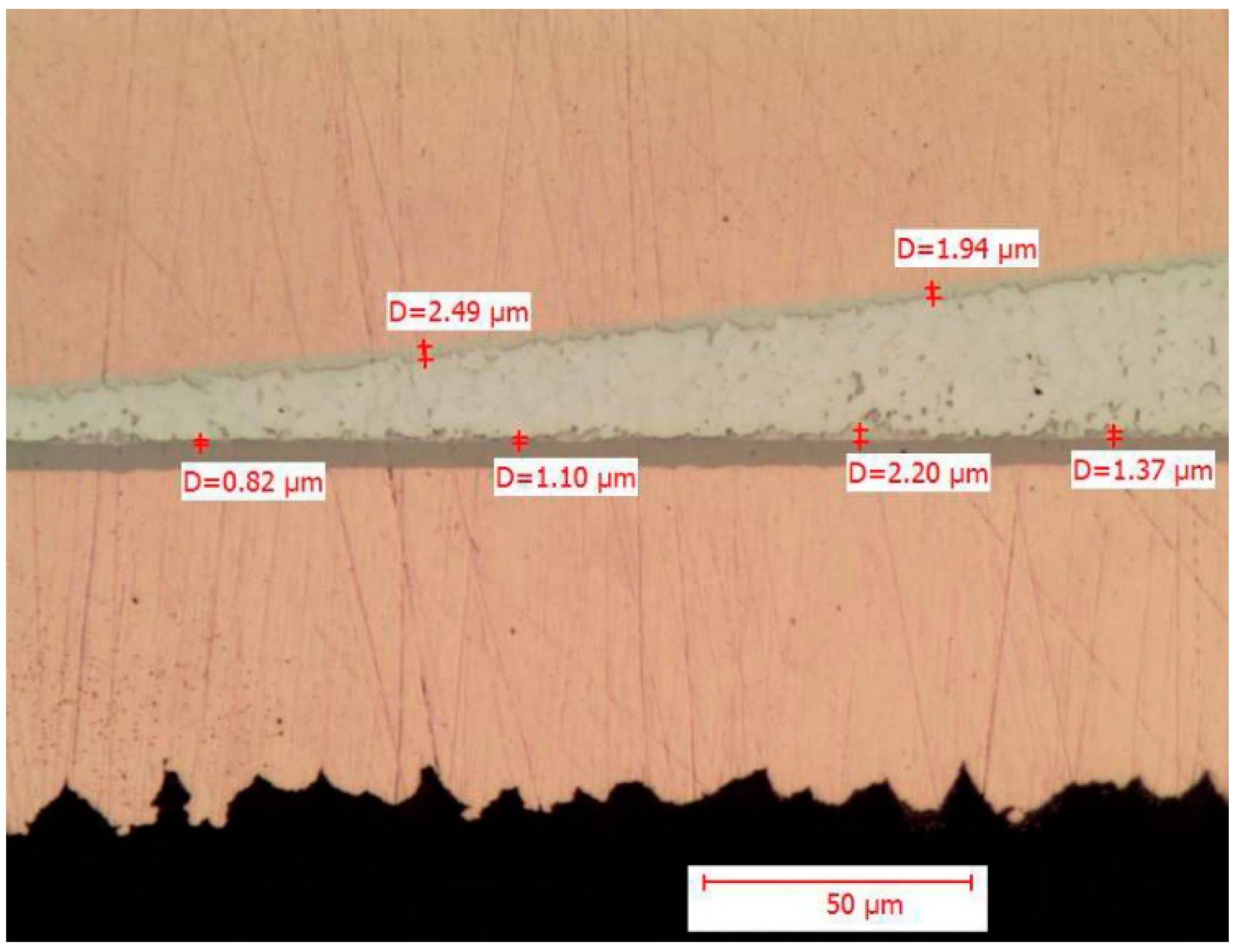
It can be observed that the maximum thickness values found in the metallographic sections fall below the upper limits estimated by the mathematical models. It is also interesting to note that the thickness values of intermetallic layers observed for THT components are lower than those observed for SMD components, which is consistent with the estimation. The upper limits observed in the tests are approximately 1 μm lower than those estimated, which is a positive result. However, the literature suggests that an intermetallic thickness of up to 4 μm is still acceptable. In the case at hand, even after the accelerated test conducted following the soldering process, the thickness remains below this 4 μm threshold. To provide an overview, some images of the metallographic sections are reported in Figure 3 and Figure 4, which contain the measurement of the intermetallic thickness downstream of the tests.

The above figure shows in detail the point measurement of the intermetallic thickness. The comb-like structure of the intermetallic layer is clearly evident, as well as how the solder matrix presents additives and dispersed intermetallic phases of Ag₃Sn (more elongated grains) and Cu₆Sn₅.

The above image shows both the pad/solder interface and the terminal/solder interface, detailing the point measurements of the intermetallic thickness.

An additional estimation of the intermetallic thickness delta during operation was made, involving the use of Formula (3) with years and ambient temperature as parameters, adapting the numerical model used to design aging test cycles. The results in the worst-case scenario, where the apparent activation energy Q is assumed to be 50 kJ/mol, are shown in

Table 8. Prediction of the intermetallic layer thickness growth delta (values expressed in µm) with exposure to various ambient temperatures.

T (°C)	1 Year	5 Years	10 Years	20 Years	30 Years
20	0.17	0.39	0.57	0.81	1.00
30	0.34	0.78	1.11	1.60	1.97
40	0.63	1.46	2.10	3.01	3.72
50	1.15	2.65	3.81	5.46	6.74
60	2.01	4.64	6.66	9.55	11.79
70	3.40	7.86	11.27	16.16	19.96
80	5.59	12.92	18.52	26.56	32.80
90	8.94	20.66	29.62	42.47	52.44
100	13.95	32.21	46.18	66.22	81.77
110	21.25	49.06	70.35	100.89	124.57
120	31.68	73.16	104.91	150.44	185.75
130	46.32	106.95	153.36	219.92	271.54
140	66.47	153.50	220.12	315.64	389.72
150	93.79	216.58	310.57	445.34	549.87
200	294.0	604.5	973.5	1243.0	1395.9

. This table presents the maximum delta obtainable (expressed in μm) once again.

This growth delta during operation, solely due to ambient temperature, needs to be added to the initial intermetallic thickness downstream of the soldering process. It is worth noting that the boards in use have not undergone any testing following the soldering processes, unlike the samples analyzed earlier. Growth deltas, stemming from operation or ambient temperature alone, are acceptable if the soldering process is of high quality and leaves an initial intermetallic thickness of a few micrometers. Conversely, if the process is not controlled, the growth delta could significantly affect joint integrity. From the results in Table 8, it is anticipated that a board operating at ambient temperatures of 20–30 °C will not experience excessive intermetallic thickness variation, with significant changes becoming apparent after 30 years. However, in the extreme range of 40–60 °C found in desert environments with intense sun exposure, noticeable variation is observed after just one year of operation, while excessively significant changes should arise after ten years or more. These effects theoretically compound with thermal effects related to current passages, although they consist of short, non-continuous electrical pulses that should not significantly alter the joint’s lifespan. Further investigation into this aspect could be worthwhile.

Finally, it is necessary to make a qualitative comparison between the data obtained from lead-free alloys and those obtainable through the use of a generic SnPb alloy, albeit obsolete for current environmental requirements. It is well known that in terms of performance, alloys that involve the use of lead have less pronounced intermetallic thicknesses downstream of the process and during operation compared to those found for lead-free alloys. However, the differences in thickness are minimal, and lead-free alloys have a greater tendency to form intermetallic compounds. This is partly because a SAC-type alloy has a tin (Sn) percentage of approximately 95%, and copper (Cu) is also present in the alloy, in addition to that of the base metal of the pad or hole. Both are the main reactants that will form Cu₆Sn₅ and Cu₃Sn. In contrast, a SnPb alloy has a tin content of 63% and reacts only with copper (Cu) from the base metal. Therefore, it is intuitive to conclude that, quantitatively, the formation of compounds and intermetallic thicknesses will be more pronounced for lead-free alloys, presenting ingredients in greater measure. However, from what we have observed, the differences still appear negligible [18]. Nevertheless, production processes, in accordance with the RoHS directive, have shifted towards the use of lead-free alloys for soldering, and it is appropriate to focus on these, as performed in the present work. Conducting a microscopic analysis on alloys that use lead is useful to predict the behavior of devices already installed or still on the market. In this regard, Hitachi provided us with some metallographic sections of SnPb solder joints present on electronic boards still in use. Three electronic boards were analyzed: a new board, a board that was used in an Italian environment (standard environment), and finally a board that was used in a different climate environment and in the presence of various corrosive agents (hostile environment). For each board, three solder joints of SMD components mounted in different areas were analyzed and, in this case, the copper pads have a nickel surface finish. The average intermetallic thickness values found are reported in

Table 9. Average intermetallic layer thicknesses in µm observed for SnPb alloy solders on various components and analyzed boards.

Component	1	2	3
New electronic board	1.04 μm	0.92 μm	0.74 μm
Electronic board in standard environment	1.18 μm	1.43 μm	2.33 μm
Electronic board in hostile environment	1.48 μm	1.32 μm	1.50 μm

and Figure 5, Figure 6 and Figure 7.

It can be observed that, concerning the new board, the intermetallic thickness values found downstream of the soldering process are consistent with those predicted by the estimates previously performed for a lead-free, SAC-type solder alloy. As expected for a SnPb-type alloy, used in this case, the intermetallic thickness is slightly lower compared to what is expected for the lead-free SAC alloy. Regarding the two boards used in standard and hostile environments, assuming an initial intermetallic thickness downstream of the soldering process equal to that found in the new board, a contained thickness variation during operation is evident, in line with what is also expected for a SAC alloy. However, applying the constants of SAC alloys to SnPb alloy solder joints for the prediction model of ΔX (Formula (3)) would lead to an overestimation of the thickness variation compared to the new board.

Similarly, the total intermetallic thickness observed in the exercised boards is contained and aligns with expectations, with no significant differences from the experimentally observed intermetallic thickness. It should be noted that although one of the two boards operated in a hostile environment and was exposed to a higher degree to chemical agents such as sulfur, it likely benefited from exposure to lower temperatures (Northern European railway route). Finally, the morphology of the intermetallic compound grains observed for SnPb alloy solder joints consistently appears comb-like, but the intermetallic thickness, particularly on the new board, exhibits more jagged edges and less smooth contours than those observed in the analysis conducted for SAC alloy solder joints.

To complete the discussion on predicting the thickness of the intermetallic layer, one can make a reverse reasoning, setting a limit value for ΔX beyond which the total intermetallic thickness becomes excessive and compromises the mechanical strength and reliability of the solder joint permanently. If, as previous stated, an intermetallic layer thickness of 4 μm is deemed acceptable, assuming an initial thickness X₀ downstream of the soldering process of 1 μm, a limit value of ΔX of 3 μm can be defined. Assuming again the same constants seen for the analysis of SAC alloy solder joints and fixing ΔX, the exposure and operational times at various temperatures that would lead to a 3 μm variation can be calculated from Formula (3), thus defining a useful life of the solder joint and therefore of the board. Estimates of useful life are reported in

Table 10. Expected lifetime of electronic boards under constant temperature exposure/use, based on intermetallic layer thickness (ΔX limit of 3 µm).

Temperature (°C)	Expected Lifetime in Years (ΔX = 3 μm)
10	984.1
20	244.0
30	66.3
40	19.6
50	6.2
60	2.1
70	0.8
80	0.3
90	0.1

.

As the reader can notice, exposure to room temperature ensures an “infinite life”. It is instead the temperatures reached by the soldering during operation that, if kept constant, lead to a rapid drift in the growth of the intermetallic thickness. Generally, temperatures up to 40 °C are not concerning. However, even though current flow and board usage may bring soldering temperatures up to 85 °C for very short periods, it must still be considered that at high temperatures the growth of intermetallic thickness is greatly facilitated. Consequently, the solder joints of an electronic board, if subjected to an excessive, repeated, and continuous number of work cycles, in terms of mechanical strength and reliability, could last less than desired and expected.

6. Conclusions

This research begins with a comprehensive overview of the intermetallic compounds present in the soft soldering processes of joints used in the assembly of electronic boards. The models proposed in the literature are used to estimate the intermetallic thickness.

The values obtained from the theoretical models are compared to experimental results of a new electronic board with an SbPb alloy solder and a SAC (lead-free) alloy solder joint on a board subjected to accelerated aging cycles.

Experimental results have shown intermetallic compound (IMC) values always below 3 µm, with a variation from a minimum value of 0.7 µm for a SnPb alloy solder joint on a new board to a maximum value of 2.7 µm observed on a SAC (lead-free) alloy solder joint on a board subjected to accelerated aging cycles. In both types of soldering processes, whether reflow soldering or wave soldering, no criticalities have emerged that lead to uncontrolled growth of IMCs. These phenomena could only materialize in an advanced stage of operation, where the electronic board approaches its end of life or in situations where the board is subjected to particular environmental stresses, without appropriate protection.

The original contribution of this work is the use of mathematical models, employing an inverse approach compared to what is described in the scientific literature.

The mathematical relationships referred to are those typically used to design aging tests for electronic boards. In this work, these relationships have been readapted to assess reliability during the operating period, up to the end of life; for this purpose, the test thermal parameters have been replaced by those imposed by the different installation environments. The use of mathematical models has allowed us to obtain a reliable estimate of the intermetallic layer thicknesses, both with reference to the initial ones, just after the process, and their evolution over time.

Utilizing the models, it has also been found that the intermetallic layer is sensitive to high temperatures, with thickness values that can grow exponentially (in relatively short times compared to a typical lifespan of 10–20 years) if the soldered joints are subjected frequently or constantly to operating temperatures well above 40 °C, with increasingly drastic thickness variations from 50 °C onwards.

From an industrial perspective, studies like this allow for the prediction of the reliability of printed circuit boards already at the design stage, minimizing the need for destructive (and/or aging) tests required to monitor the quality of processes/products and maintain greater control over a phenomenon as microscopic as it is relevant to that of intermetallic compounds. Moreover, the reduction of thermal aging tests and related destructive tests means a reduction in energy consumption and a lower environmental impact, in a context where manufacturing companies are devoting increasing attention with regard to life cycle assessment (LCA) of products and processes.

Future developments of this work will involve the use of models to explore the evolution of the intermetallic layer with a higher level of detail, by densifying the temporal observation points with varying temperatures, or even by artificially increasing the operating temperatures of the boards and their joints during testing through current passages. We aim to expand our study to include a broader range of lead-free solder alloys and conduct a more detailed analysis of discrepancies in subsequent projects. This will allow us to provide a more comprehensive understanding of the model’s predictive capabilities across different materials and conditions. A greater amount of data would, for example, enable interpolating the values of k and n at each temperature to predict the growth of the intermetallic layer by simulating the conditions and operating temperatures of the solder joints.