Electromagnetic Interaction Model between an Electric Motor and a Magnetorheological Brake
Abstract
1. Introduction
2. Electric Motor Representation
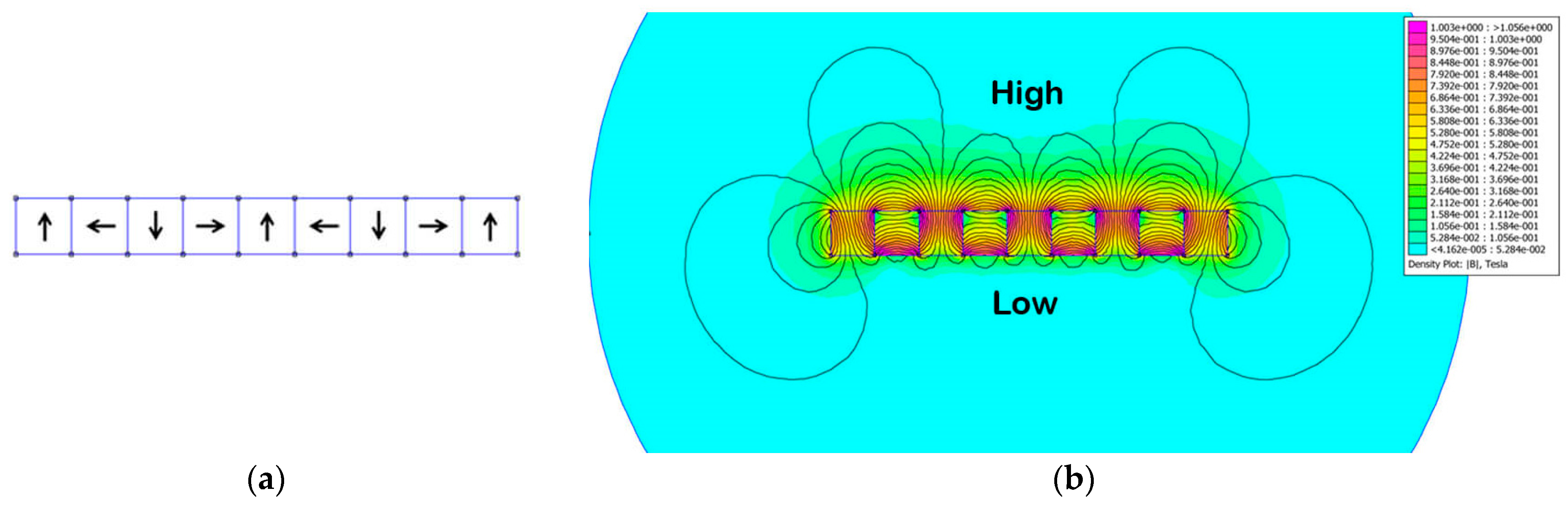
- (a)
- Halbach array.
- (b)
- Helmholtz coil.
2.1. The Halbach Array
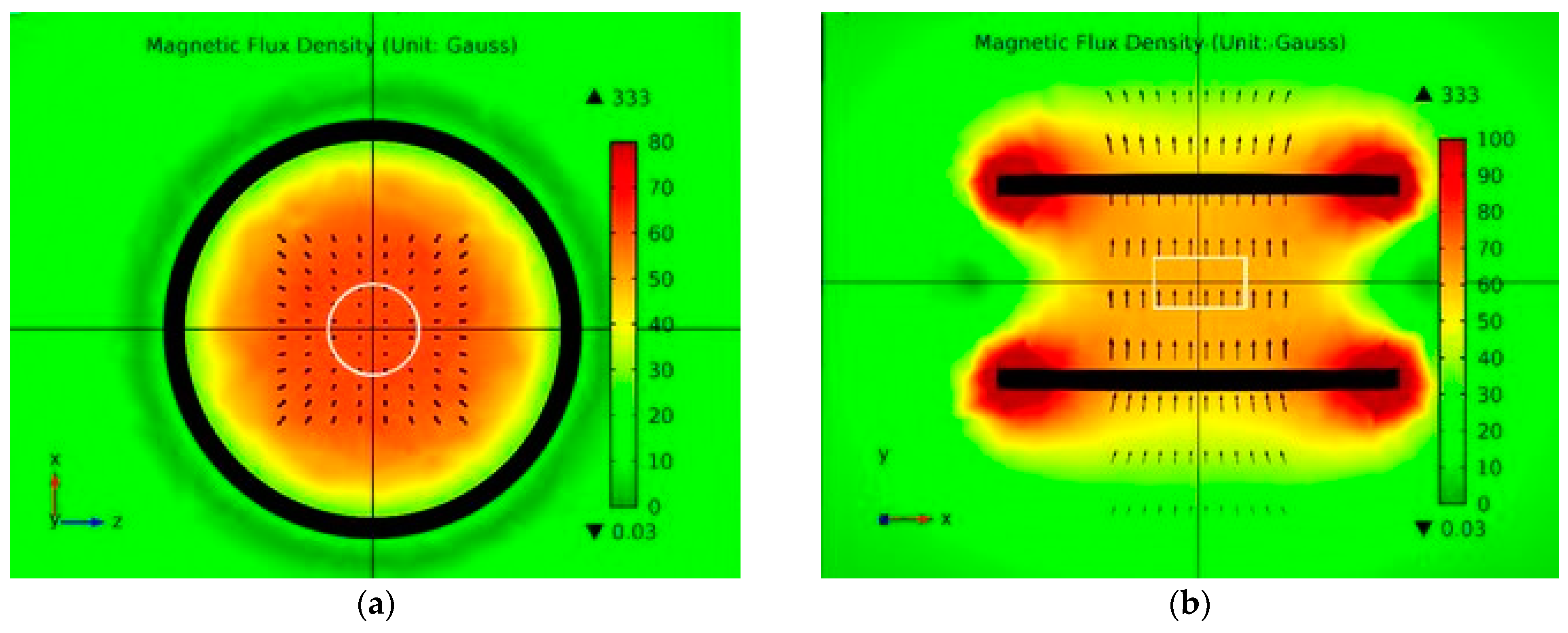
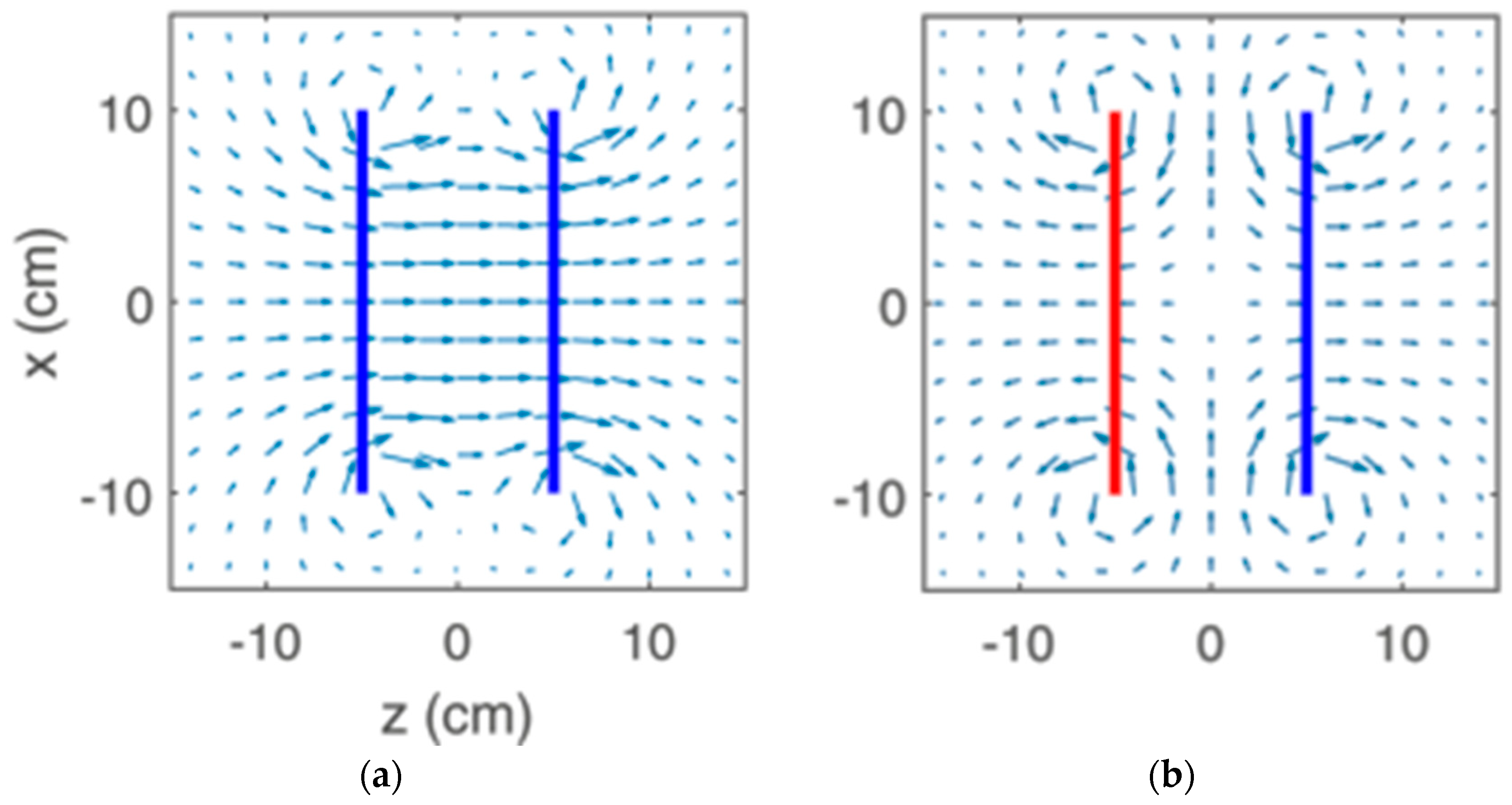
2.2. The Helmholtz Coil Configuration
- Same current direction.
- Opposite direction of current.
2.3. The Helmholtz Coil Geometry
3. Model Description
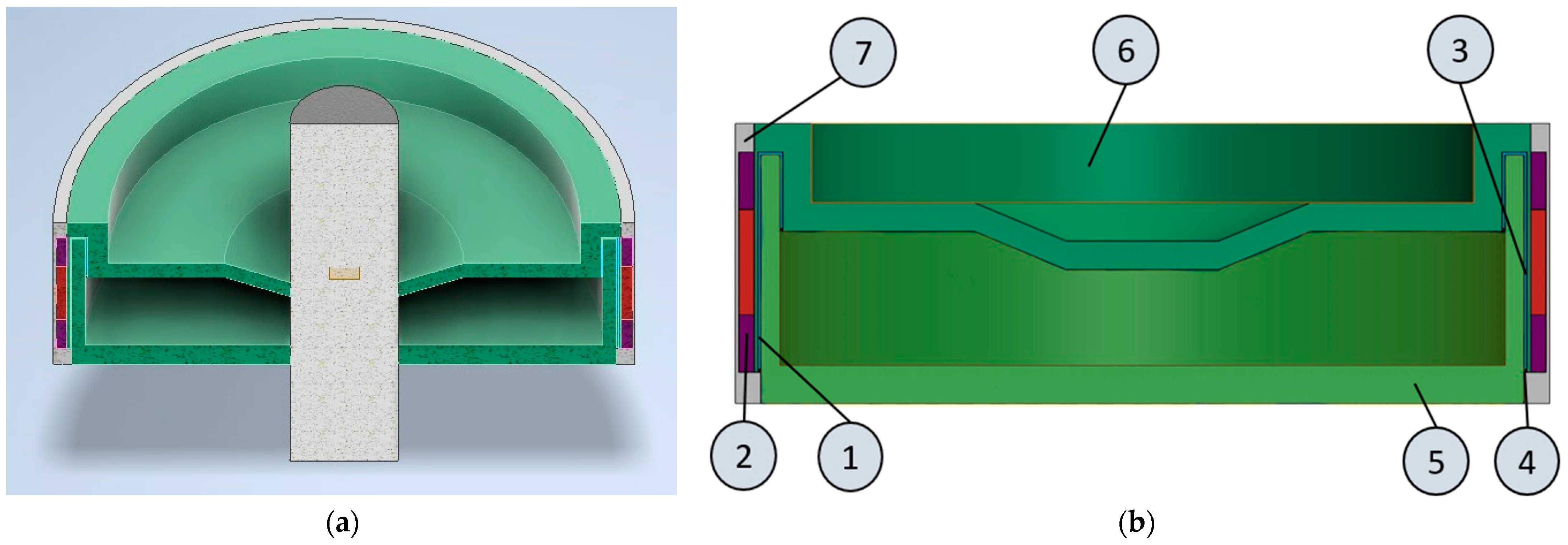
3.1. The Brake
3.1.1. Braking System Layout
3.1.2. The Fluid Selection
3.1.3. Material Selection
3.2. Simulation Methodology
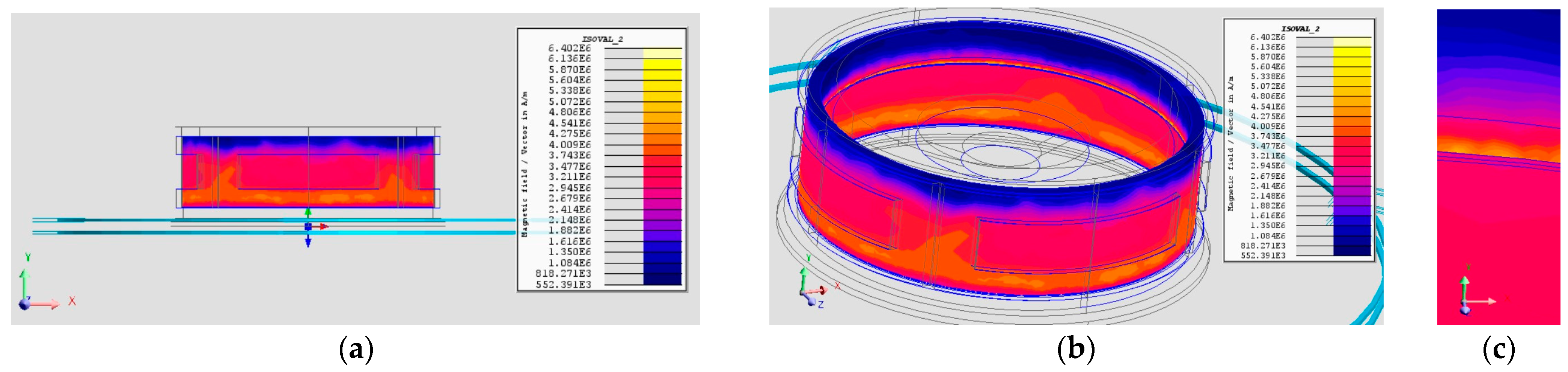
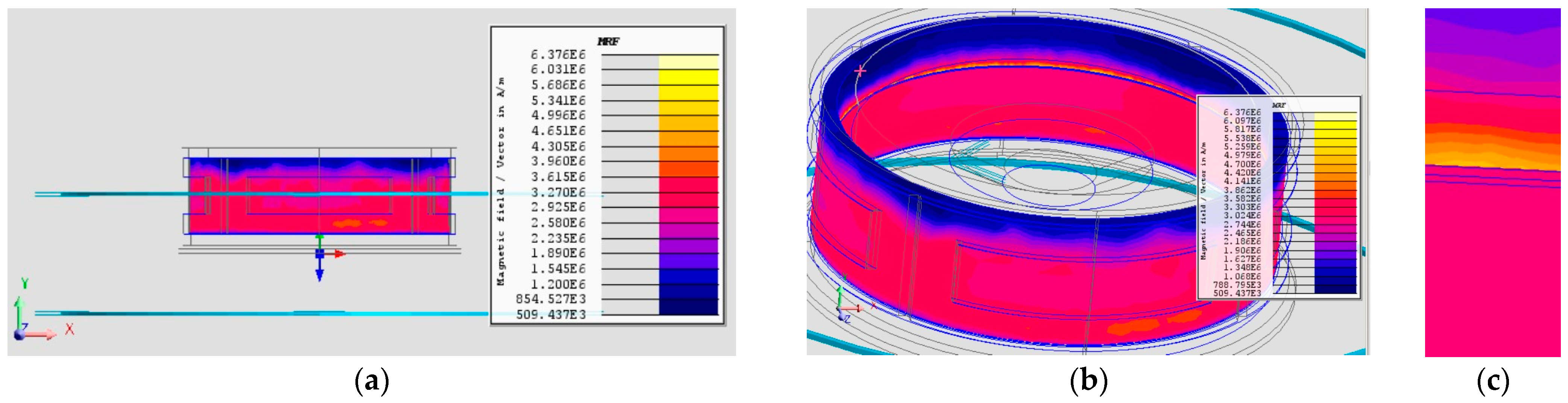
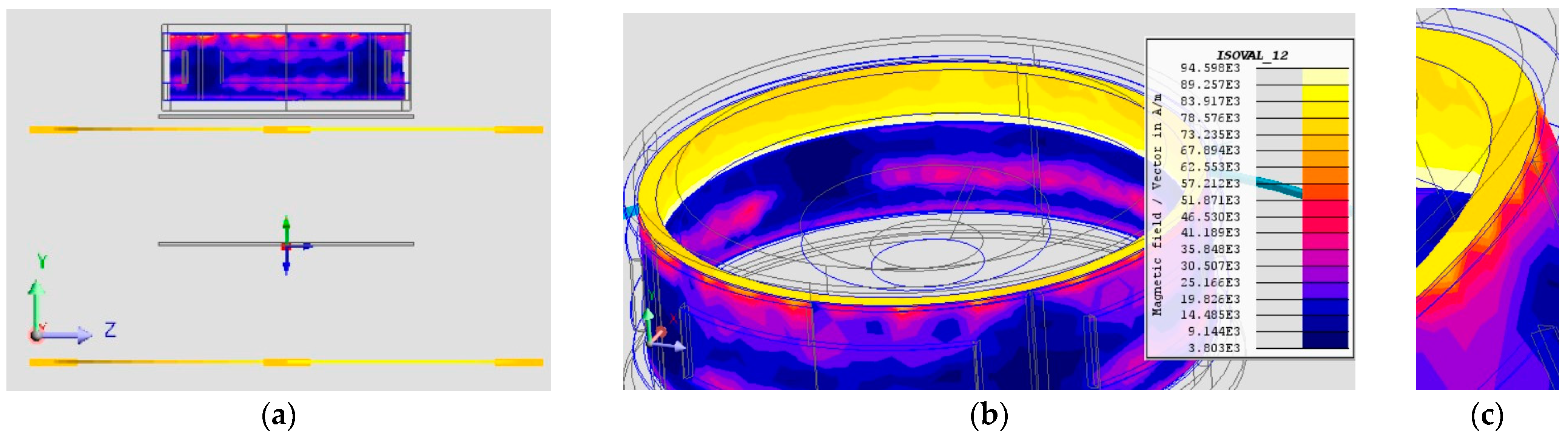
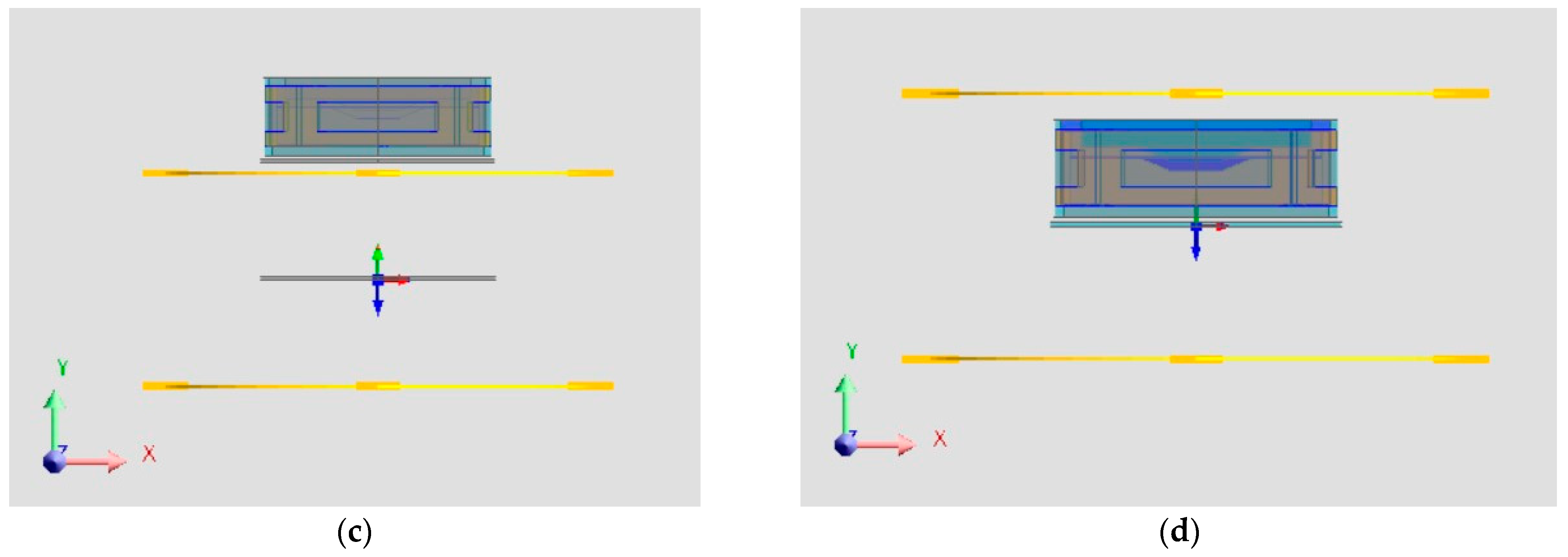
3.3. Simulation of Each Configuration
3.3.1. Configuration 1
3.3.2. Configuration 2
3.3.3. Configuration 3
3.3.4. Configuration 4
3.4. Brake Analysis Layout
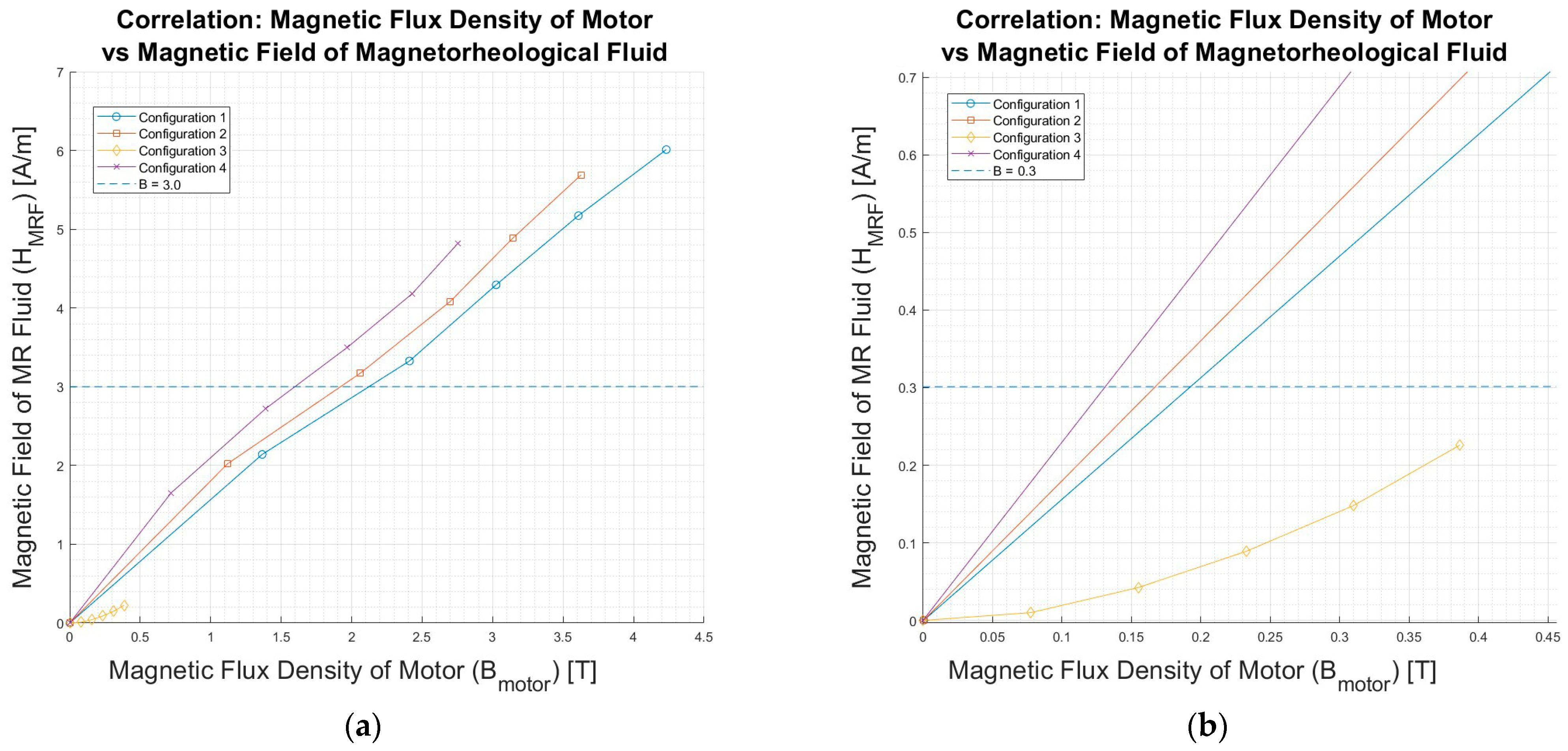
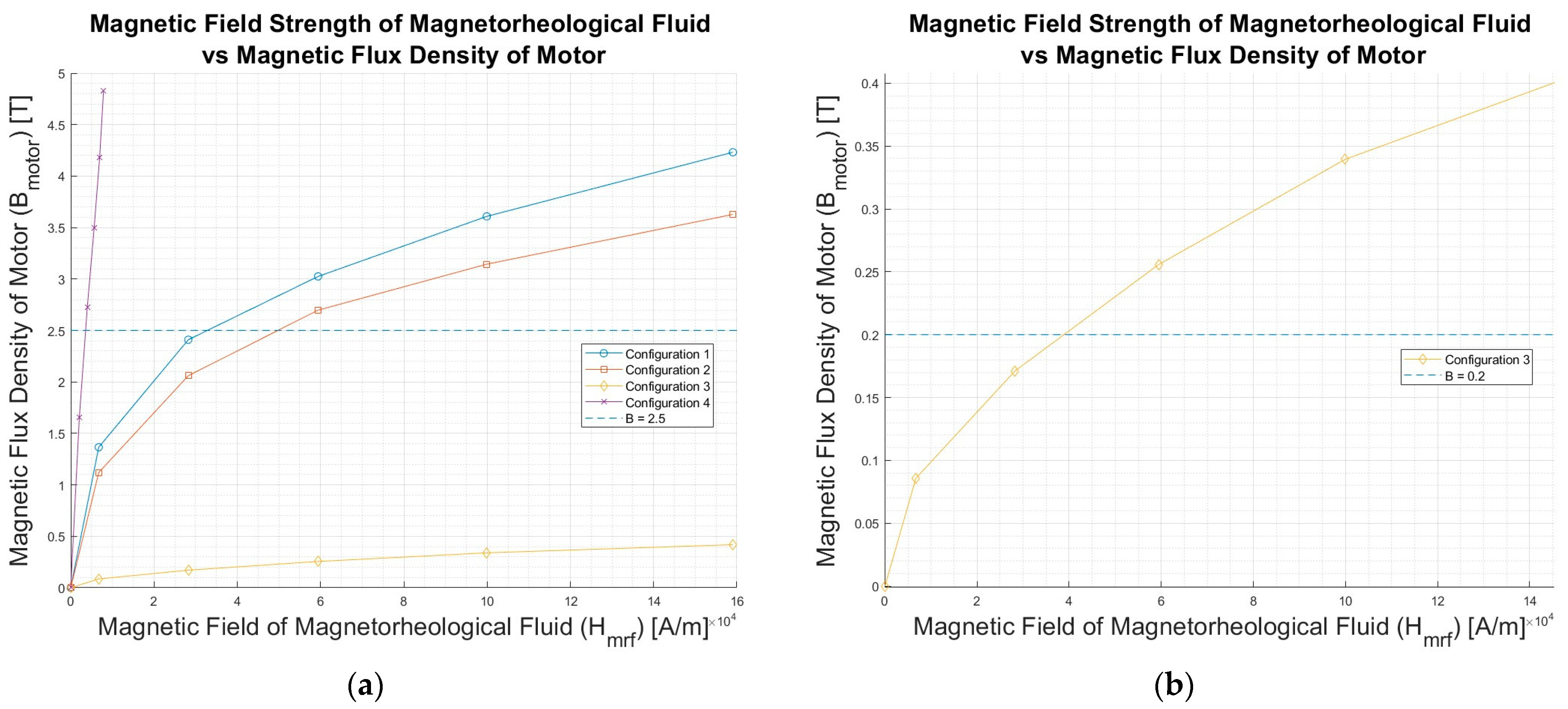
4. Analysis of the Results
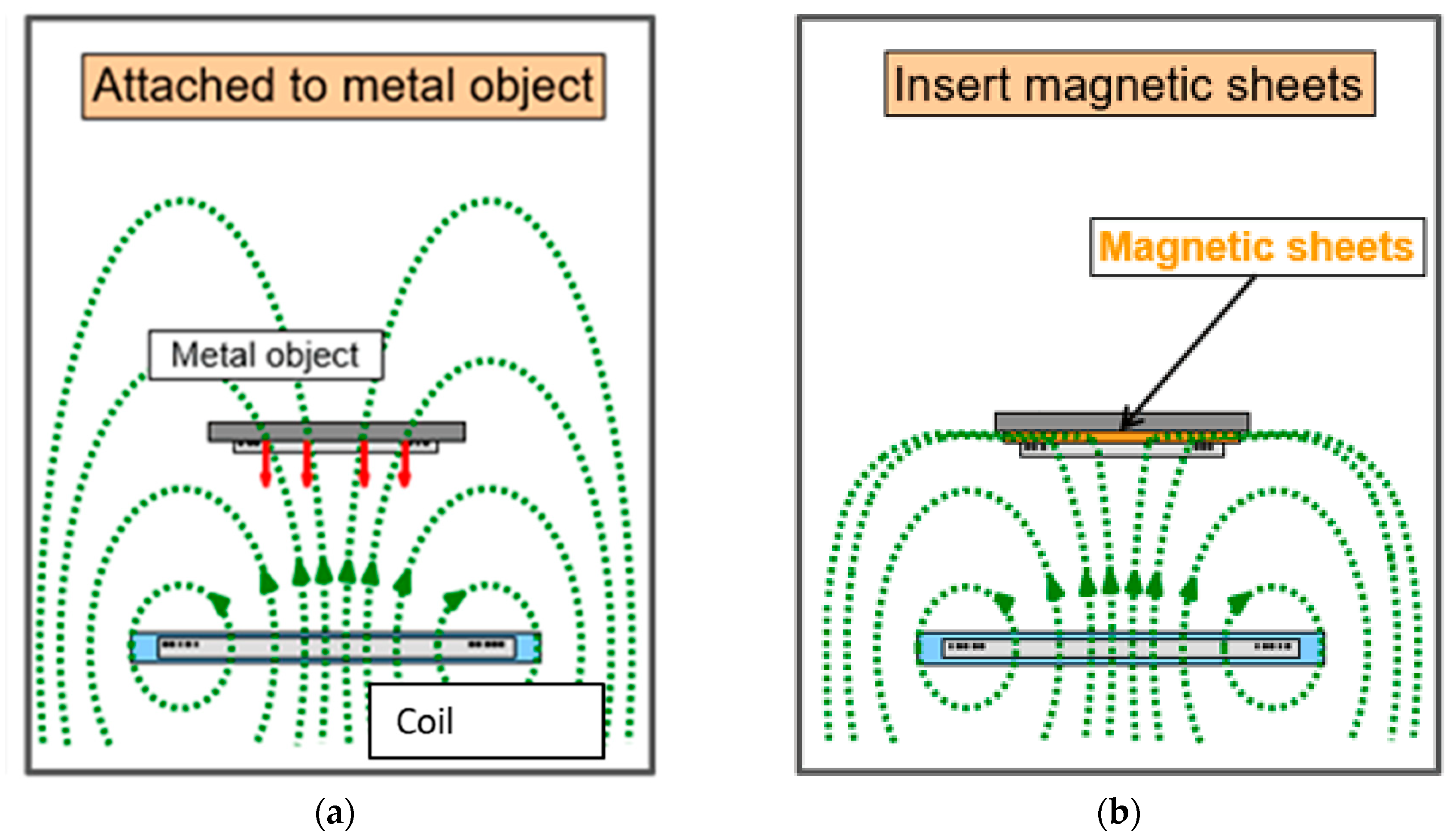
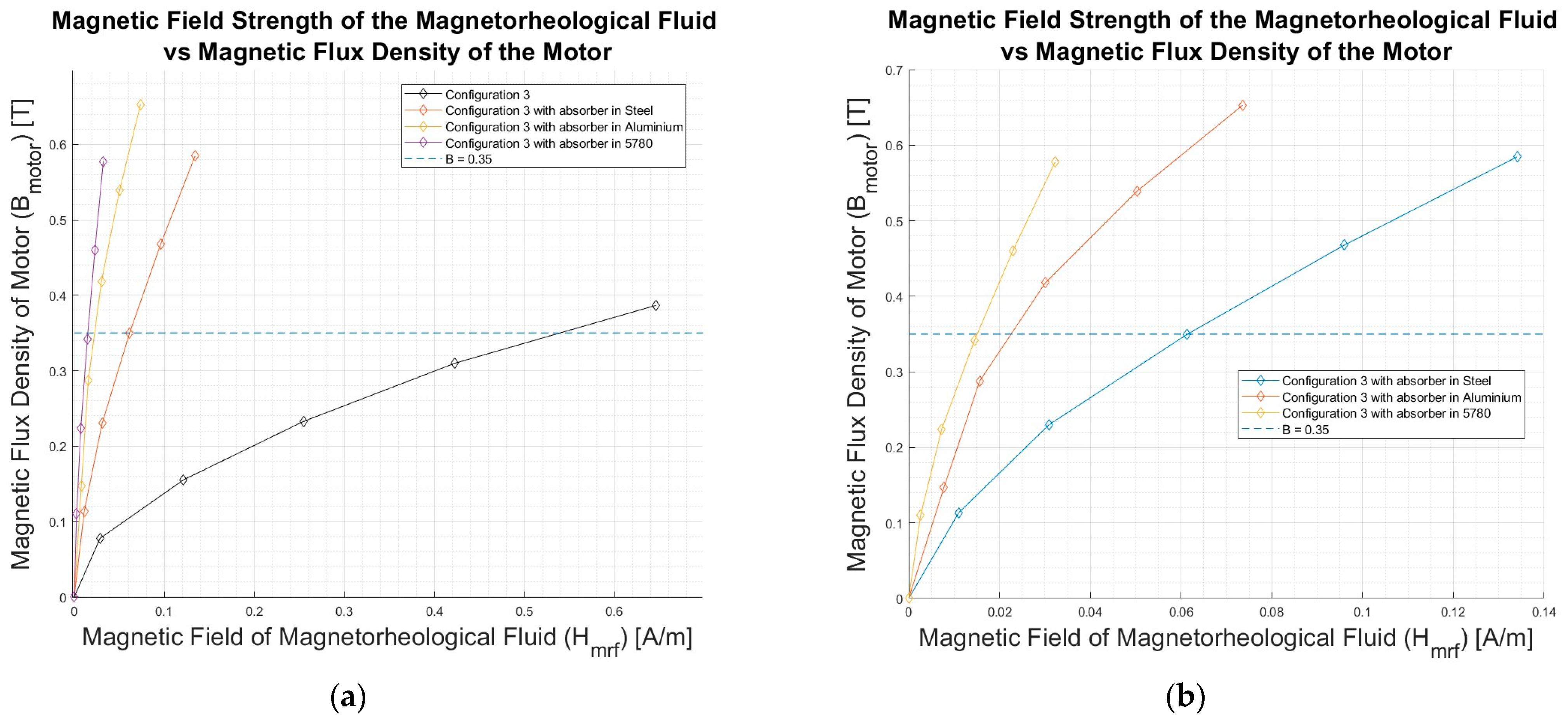
5. The Absorber Solution
5.1. Analysis of the Results
5.2. The Materials
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Carvalho Pinheiro, H.; Messana, A.; Carello, M. In-wheel and on-board motors in BEV: Lateral and vertical performance comparison. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Imberti, G.; de Carvalho Pinheiro, H.; Carello, M. Impact of the Braking System Generated Pollutants on the Global Vehicle Emissions: A Review. In Proceedings of the ICESE 2023, Leuven, Belgium, 8–10 September 2023; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Imberti, G. Regenerative Braking Effects on Pollutant Release and Zero-Emissions Brakes Technologies. Master’s Thesis, Politecnico di Torino, Turin, Italy, 2021. [Google Scholar]
- Dyke, S.J.; Spencer, B.F., Jr.; Sain, M.K.; Carlson, J.D. An experimental study of MR dampers for seismic protection. Smart Mater. Struct. 1998, 7, 693. [Google Scholar] [CrossRef]
- Brancati, R.; Di Massa, G.; Motta, C.; Pagano, S.; Petrillo, A.; Santini, S. A Test Rig for Experimental Investigation on a MRE Vibration Isolator. In The International Conference of IFToMM ITALY; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Imberti, G.; de Carvalho Pinheiro, H.; Carello, M. Design of an Innovative Zero-Emissions Braking System for Vehicles. In Proceedings of the 2022 International Conference on Electrical, Computer, Communications and Mechatronics Engineer-ing, ICECCME, Male, Maldives, 16–18 November 2022. [Google Scholar] [CrossRef]
- de Carvalho Pinheiro, H.; Imberti, G.; Carello, M. Pre-Design and Feasibility Analysis of a Magneto-Rheological Braking System for Electric Vehicles; SAE Technical Paper; SAE Publications: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Fahem, M.E. Axial and Radial Flux Permanent Magnet Machines—What Is the Difference? EMWORKS, 2020. Available online: https://www.emworks.com/blog/electromechanical/axial-and-radial-flux-permanent-magnet-machines-what-is-the-difference (accessed on 6 June 2023).
- Emrax. Emrax 348, Motor Installation and Maintenance Manual; EMRAX d.o.o: Kamnik, Slovenia, 2020. [Google Scholar]
- Woolmer, T.; McCulloch, M. Analysis of the Yokeless and Segmented Armature Machine. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007. [Google Scholar]
- European Union. Commission Communication in the Framework of the Implementation of Directive 2006/95/EC of the European Parliament and of the Council on the Harmonisation of the Laws of Member States Relating to Electrical Equipment Designed for Use within Certain Voltag; European Union: Brussels, Belgium, 2015. [Google Scholar]
- AIS-004; (Part 3): Automotive Vehicles–Requirements for Electromagnetic Compatibility, Central Motor Vehicle Rules—Technical Standing Committee. The Automotive Research Association of India: Pune, India, 2009.
- European Parliament. Directive 2014/30/EU of the European Parliament; European Union: Brussels, Belgium, 2014; Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32014L0030#d1e32-97-1 (accessed on 11 September 2018).
- Halbach, K. Design of permanent multipole magnets with oriented rare earth cobalt material. Nucl. Instrum. Methods 1980, 169, 1–10. [Google Scholar] [CrossRef]
- Halbach, K. Applications of Permanent Magnets in Accelerators and Electron Storage Rings. J. Appl. Phys. 1985, 57, 3605–3608. [Google Scholar] [CrossRef]
- SDM Magnetics. Brief Introduction to Halbach Array. Techtalk, 2022. Available online: https://www.magnet-sdm.com/2018/10/30/halbach-array/ (accessed on 12 March 2024).
- Abbott, J.J. Parametric design of tri-axial nested Helmholtz coils. Rev. Sci. Instrum. 2015, 86, 054701. [Google Scholar] [CrossRef] [PubMed]
- Sundarnath, J.K.; Resendiz, E.M.; Kuravi, S. Particle Arrangement using External Magnetic Field and its effect on Pressure Drop in a Tightly Packed Ferromagnetic Porous Bed. Powder Technol. 2020, 375, 275–283. [Google Scholar] [CrossRef]
- Butta, M.; Ripka, P.; Infante, G.; Badini-Confalonieri, G.A. Magnetic microwires with field induced helical anisotropy for coil-less fluxgate. IEEE Trans. Magn. 2010, 46, 2562–2565. [Google Scholar] [CrossRef]
- Sadiq, U.A.; Oluyombo, O.W. Optimization Design and Characterization of Helmholtz Coils. J. Inf. Eng. Appl. 2019, 9, 4. [Google Scholar]
- Daron, B.B.; Jonathan, E.; Madsen, M.J. Magnetic field mapping. Wabash J. Phys. 2015, 4, 1–13. [Google Scholar]
- Jiang, C.; Gao, P.; Yang, X.; Ji, D.; Sun, J.; Yang, Z. Helmholtz Coils Based WPT Coupling Analysis of Temporal Interference Electrical Stimulation System. Appl. Sci. 2022, 12, 9832. Available online: https://www.mdpi.com/2076-3417/12/19/9832 (accessed on 30 May 2023). [CrossRef]
- Scientific Instruments GmbH. Definitions Used for Helmholtz Coils; Scientific Instruments GmbH: Gilching, Germany, 2021; Available online: https://www.si-gmbh.de/wp-content/uploads/2021/06/DefinitionsUsedForHelmholtzCoils.pdf (accessed on 12 March 2024).
- Fufaev, A. Derivation, Magnetic Field of a Helmholtz Coil. 2021. Available online: https://en.universaldenker.org/arguments/326#calculate-the-magnetic-field-of-the-first-helmholtz-coil (accessed on 20 June 2023).
- Holmes, N.; Tierney, T.M.; Leggett, J.; Boto, E.; Mellor, S.; Roberts, G.; Hill, R.M.; Shah, V.; Barnes, G.R.; Brookes, M.J.; et al. Balanced, bi-planar magnetic field and field gradient coils for field compensation in wearable magnetoencephalography. Sci. Rep. 2019, 9, 14196. [Google Scholar] [CrossRef] [PubMed]
- Rajnak, M.; Wu, Z.; Dolnik, B.; Paulovicova, K.; Tothova, J.; Cimbala, R.; Kurimský, J. Magnetic Field Effect on Thermal, Dielectric, and Viscous Properties of a Transformer Oil-Based Magnetic Nanofluid, Peter Kopcansky, Lars Wadsö, Milan Timko. Energies 2019, 12, 4532. [Google Scholar] [CrossRef]
- Bruneel, J. Axial Flux Motor vs Radial Flux Motor: A Focus on Magnetic Field Orientation. TRAXIAL. 04 04 2022. Available online: https://traxial.com/blog/electric-motor-design-magnetic-field-orientation/ (accessed on 5 April 2023).
- Akatsu, K.; Wakui, S. A comparison between axial and radial flux PM motor by optimum design method from the required output NT characteristics. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2006, 25, 496–509. [Google Scholar] [CrossRef]
- Cary, N. Designing with MR Fluid; Lord Corporation Engineering: Cary, NC, USA, 1999. [Google Scholar]
- Özsoy, K.; Usal, M.R. A mathematical model for the magnetorheological materials and magneto reheological devices. Eng. Sci. Technol. Int. J. 2018, 21, 1143–1151. [Google Scholar] [CrossRef]
- Lord, C. MRF-132DG Magneto-Rheological Fluid; Lord Technical Data; Lord Corporation Engineering: Cary, NC, USA, 2023. [Google Scholar]
- Kumbhar, B.K.; Patil, S.R.; Sawant, S.M. Synthesis and characterization of magneto-rheological (MR) fluids. Eng. Sci. Technol. Int. J. 2015, 18, 432–438. [Google Scholar]
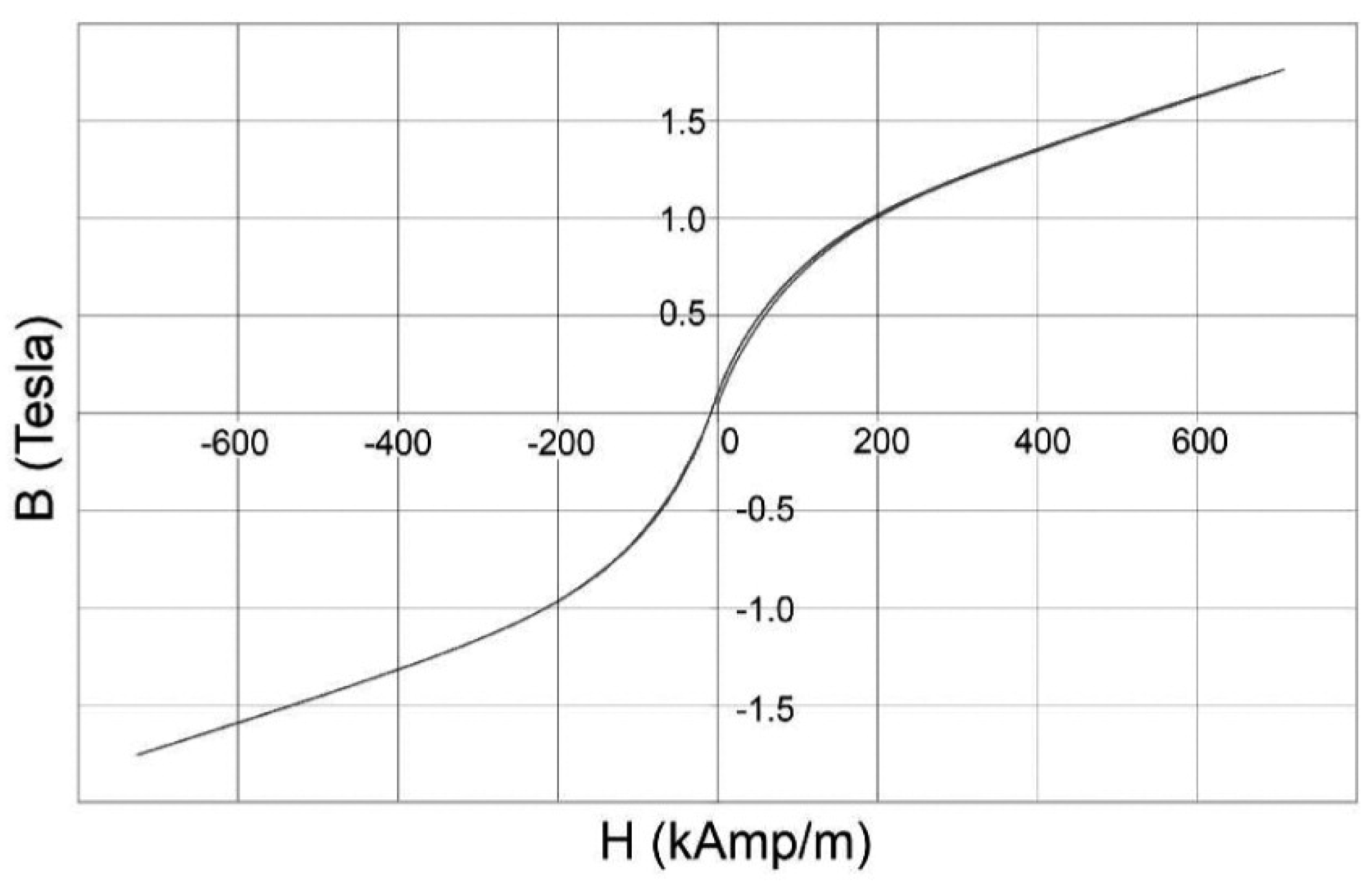
- AspenCore Inc. Magnetic Hysteresis. Electronics Tutorials 2023. Available online: https://www.electronics-tutorials.ws/electromagnetism/magnetic-hysteresis.html (accessed on 20 June 2023).
- ASTM International. Annual Book of ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Karakoc, K. Design of a Magnetorheological Brake System Based on Magnetic Circuit Optimization. Master’s Thesis, Bogazici University, Istanbul, Turkey, 2007. [Google Scholar]
- Taiyo. Radio Wave Absorber MICROSOBER® for a Clean Electromagnetic Environment. Taiyo Wire Cloth Co. 22 March 2022. Available online: https://www.twc-net.com/blog/2022/post-688.html (accessed on 30 June 2023).
- Kotsuka, Y. Electromagnetic Wave Absorbers: Detailed Theories and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019. [Google Scholar]
- Mušič, B.; Žnidaršič, A.; Venturini, P.; Domžale, H. Materials, electromagnetic absorbing. Inf. MIDEM 2011, 41, 86–91. [Google Scholar]
- Holland Shielding Systems, BV. 5780-C-EMI Flexible Absorber Sheets, Technical Datasheet. Lipsweg 124, Netherlands, 19-9-2017. Available online: https://hollandshielding.com/en/flexible-emi-absorber-sheets (accessed on 12 March 2024).
- Zhang, W.; Yang, S.-L. Analysis and verification of the Helmholtz field coil electromagnetic based on finite element method. Energy Mech. Eng. 2016, 702–711. [Google Scholar] [CrossRef]
- Tan, L.; Eldin, K.; Elnail, I.; Ju, M.; Huang, X. Comparative Analysis and Design of the Shielding Techniques in WPT Systems for Charging EVs. Energies 2019, 12, 2115. [Google Scholar] [CrossRef]



| Character | Name | Values | ||
|---|---|---|---|---|
| R | Coil radius [m] | 0.40 | ||
| d/2 | Half distance from the centre [m] | 0.01 | 0.09 | 0.20 |
| d | Distance from the centre [m] | 0.02 | 0.18 | 0.40 |
| A | Rectangular coil section area [] | |||
| N | Number of turns per coil | 100 | ||
| ρ | Resistivity [Wm] | |||
| FF | Fill factor [0 < Sf < 1] | 0.71 | ||
| V | Volume of the coil [] | |||
| Req | Equivalent resistance [W] | 24.07 | ||
| k | Helmholtz coil constant | |||
| MRF-132-DG | |
|---|---|
| Initial viscosity [Pa s] (at 25 °C) | 0.2–0.5 |
| Density [g/] | 2.95–3.15 |
| Magnetic field strength [kA/m] | 150–250 |
| Yield point [kPa] | 50–100 |
| Reaction time [ms] | 15–25 |
| Operating temperature [°C] | −40 to +130 |
| Typical supply voltage [V] | 2–25 |
| Typical current intensity [A] | 1–2 |
| Magnetic Properties | Aluminium | Copper | Steel | MRF-132-DG |
|---|---|---|---|---|
| Initial relative permeability | 1 | 1 | 2500 | 3.798 |
| Saturation magnetization [T] | - | - | 2.5 | 2.1 |
| Knee adjusting coefficient | - | - | 0.5 | 0.4 |
| Thermal conductivity [Wm−1K−1] | 0.52 | 0.92 | - | - |
| Saturation flux density [T] | - | - | 1.55 | 1.65 |
| MRF-132-DG | Motor (Steel) | |
|---|---|---|
| Permeability [h/m] | 3.798 | 2500 |
| Cross sectional area A [] | 0.00042 | 0.0012 |
| Average magnetic flux density B [T] | - | 0.1932 |
| Average magnetic field H [A/m] | - |
| Magnetic Field of the MRF [A/m] | ||||
|---|---|---|---|---|
| k | Configuration 1 | Configuration 2 | Configuration 3 | Configuration 4 |
| 0.03 | ||||
| 2.14 | 2.02 | 0.01 | ||
| 3.32 | 3.17 | 0.04 | ||
| 4.29 | 4.08 | 0.09 | ||
| 5.17 | 4.89 | 0.15 | ||
| 6.01 | 5.69 | 0.23 | ||
| Magnetic Flux density of the Motor [T] | ||||
|---|---|---|---|---|
| k | Configuration 1 | Configuration 2 | Configuration 3 | Configuration 4 |
| 6.19 | ||||
| 1.37 | 1.12 | 0.08 | 1.65 | |
| 2.41 | 2.06 | 0.16 | 2.72 | |
| 4.29 | 2.70 | 0.23 | 3.50 | |
| 3.02 | 3.14 | 0.31 | 4.18 | |
| 3.61 | 3.63 | 0.39 | 4.83 | |
| 5780-C5B Absorber | |
|---|---|
| Material | Magnetic powder + rubber |
| Initial relative permeability | 250 |
| Saturation magnetization [T] | Around 2 |
| Knee adjusting coefficient | 0.5 |
| Mass density [kg/] | 4.4 |
| Surface resistance |
| Configuration 3—Magnetic Flux Densities on the Motor B [T] | ||||
|---|---|---|---|---|
| Coefficient k | Without Absorber | With Absorber in | ||
| Steel | Aluminium | 5780-C5B | ||
| 0.08 | 0.11 | 0.15 | 0.11 | |
| 0.16 | 0.23 | 0.29 | 0.22 | |
| 0.23 | 0.35 | 0.42 | 0.34 | |
| 0.31 | 0.47 | 0.54 | 0.46 | |
| 0.39 | 0.58 | 0.65 | 0.58 | |
| Configuration 3—Magnetic Field on the MRF-132-DG H [A/m] | ||||
|---|---|---|---|---|
| Coefficient k | Without Absorber | With Absorber in: | ||
| Steel | Aluminium | 5780-C5B | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caushaj, S.; Imberti, G.; de Carvalho Pinheiro, H.; Carello, M. Electromagnetic Interaction Model between an Electric Motor and a Magnetorheological Brake. Designs 2024, 8, 25. https://doi.org/10.3390/designs8020025
Caushaj S, Imberti G, de Carvalho Pinheiro H, Carello M. Electromagnetic Interaction Model between an Electric Motor and a Magnetorheological Brake. Designs. 2024; 8(2):25. https://doi.org/10.3390/designs8020025
Chicago/Turabian StyleCaushaj, Sidorela, Giovanni Imberti, Henrique de Carvalho Pinheiro, and Massimiliana Carello. 2024. "Electromagnetic Interaction Model between an Electric Motor and a Magnetorheological Brake" Designs 8, no. 2: 25. https://doi.org/10.3390/designs8020025
APA StyleCaushaj, S., Imberti, G., de Carvalho Pinheiro, H., & Carello, M. (2024). Electromagnetic Interaction Model between an Electric Motor and a Magnetorheological Brake. Designs, 8(2), 25. https://doi.org/10.3390/designs8020025






