Load-Settlement Curve and Subgrade Reaction of Strip Footing on Bi-Layered Soil Using Constitutive FEM-AI Coupled Techniques
Abstract
1. Introduction
2. Artificial Intelligence (AI) Techniques
2.1. Genetic Algorithm GA
2.2. Genetic Programming (GP)
2.3. Evolutionary Polynomial Regression EPR
2.4. Artificial Neural Network (ANN)
3. Methodology
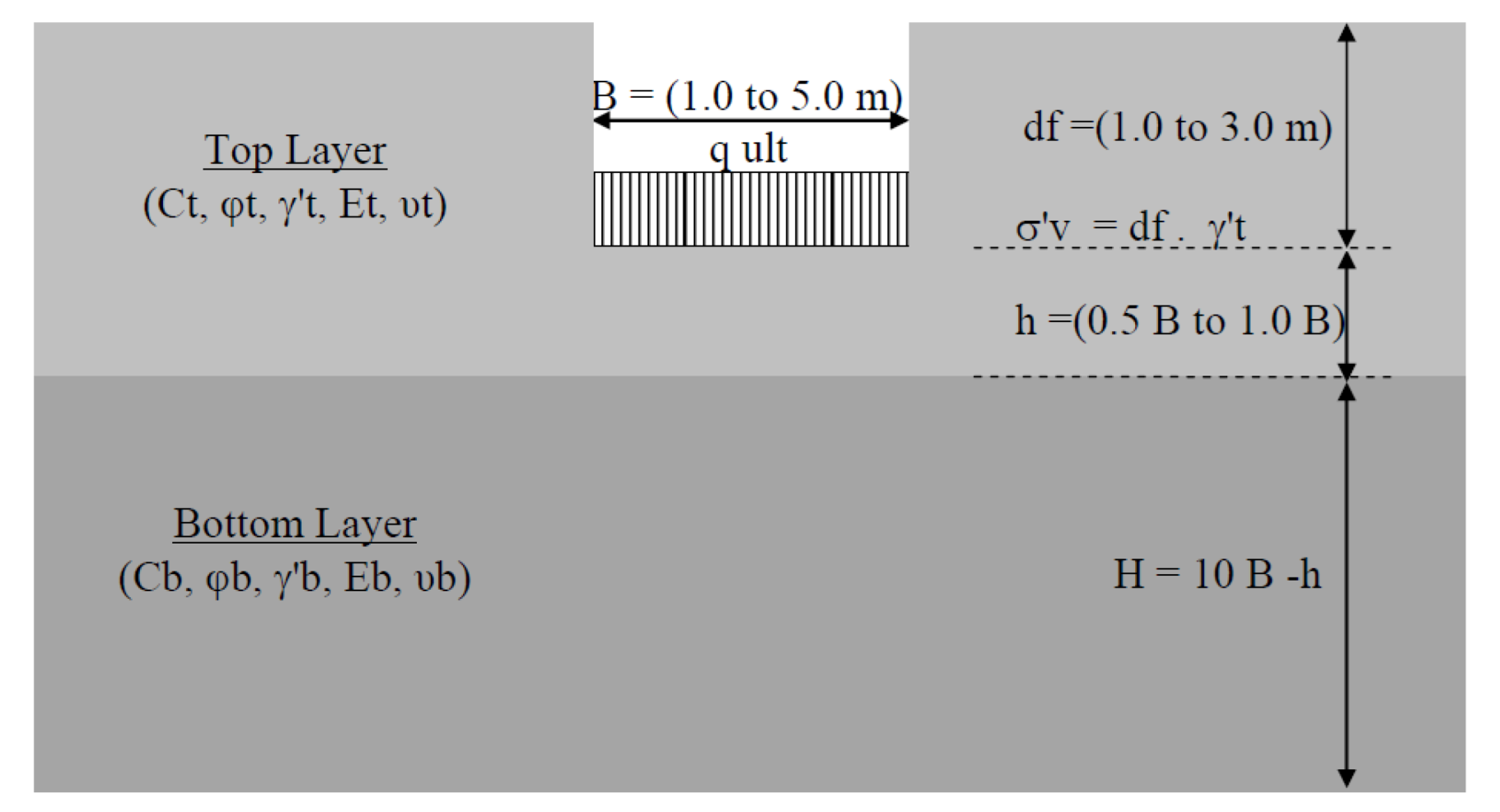
3.1. Research Program
3.1.1. Phase 1: Constitutive FEM Models
- Top layer (soil type S1 to soil type S6)
- Bottom layer (soil type S1 to soil type S6)
- Width of strip footing (B) (1.0 m to 5.0 m)
- Top layer thickness (h) (0.5 B to 1.0 B)
- Overburden stress (σ′v) (1.0 m to 3.0 m by the top density γ′t)
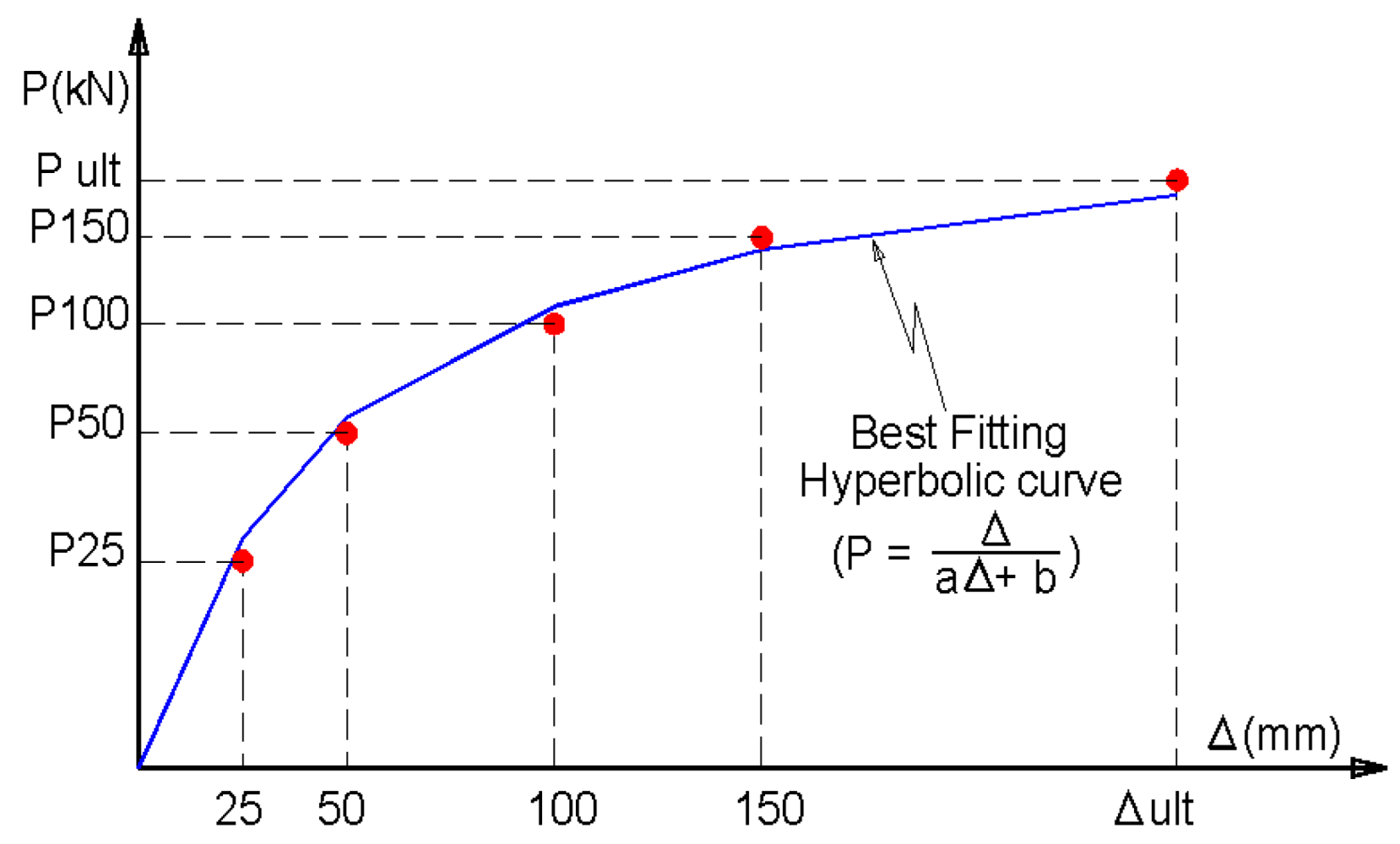
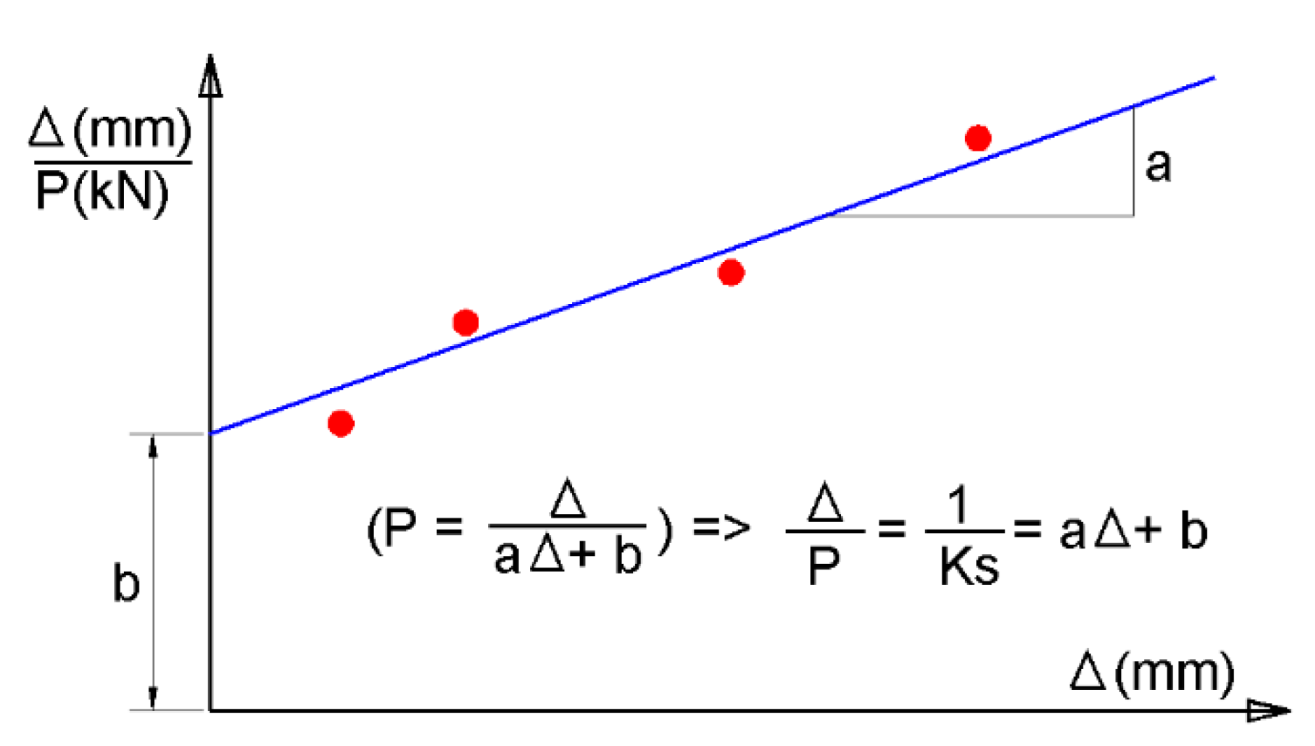
3.1.2. Phase 2: Evaluate (a and b) Factors, Generate the Database and Conduct Statistical Analysis
- Cohesion, tangent of friction angle and effective density of top layer (Ct) kN/m2, tan (φt) and (γ′t) kN/m3, respectively.
- Top layer thickness (h) m,
- Cohesion, tangent of friction angle and effective density of bottom layer (Cb) kN/m2, tan (φb) and (γ′b) kN/m3, respectively.
- Strip footing width (B) m,
- Effective over burden stress at foundation depth (σ′v) kN/m2,
- 1000 × hyperbolic factor (a),
- 1000 × hyperbolic factor (b).
3.1.3. Phase 3: Predicting (a and b) Values Using AI Techniques
4. Results and Discussion of the Predictive Models
4.1. Results Presentation
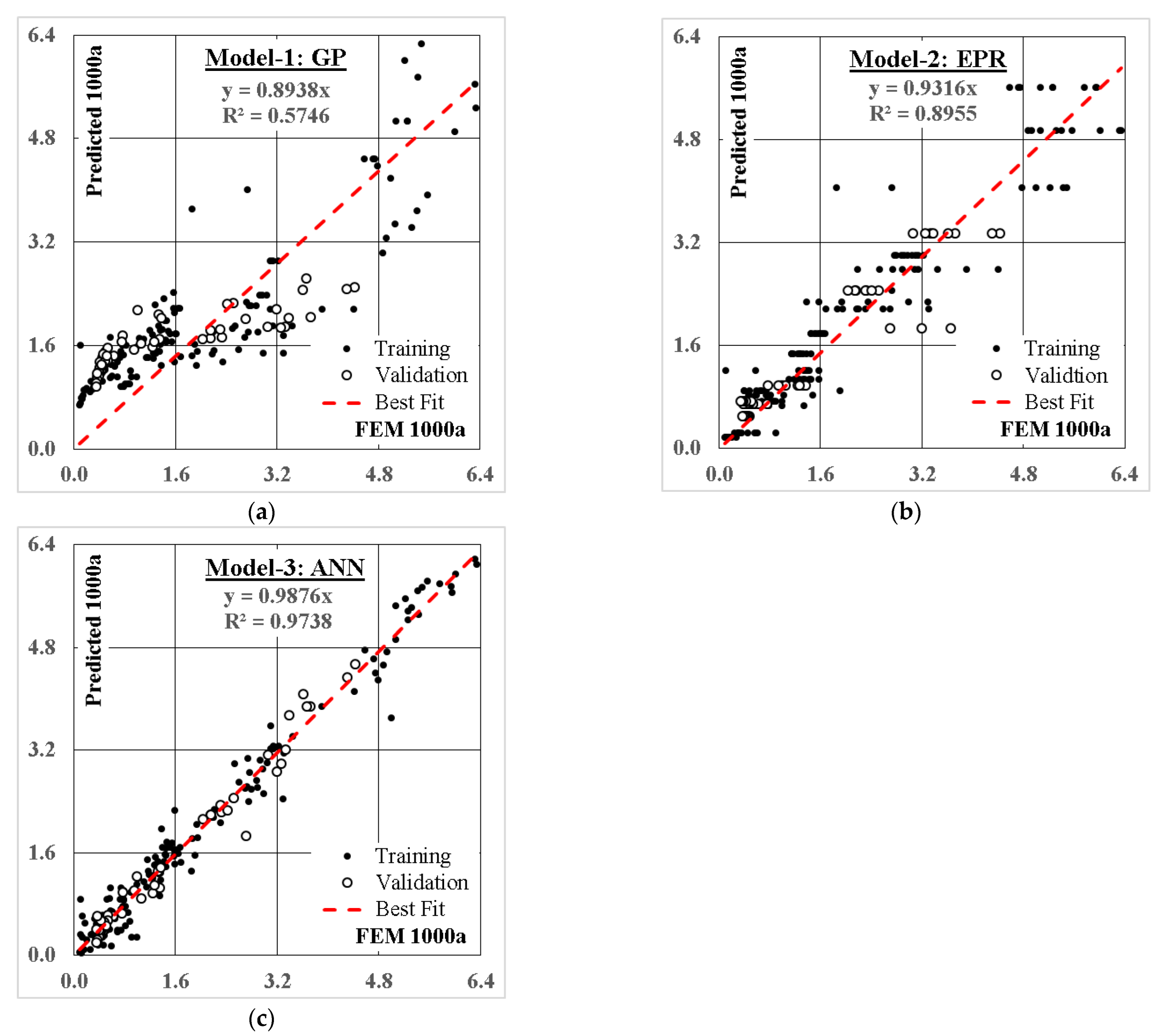
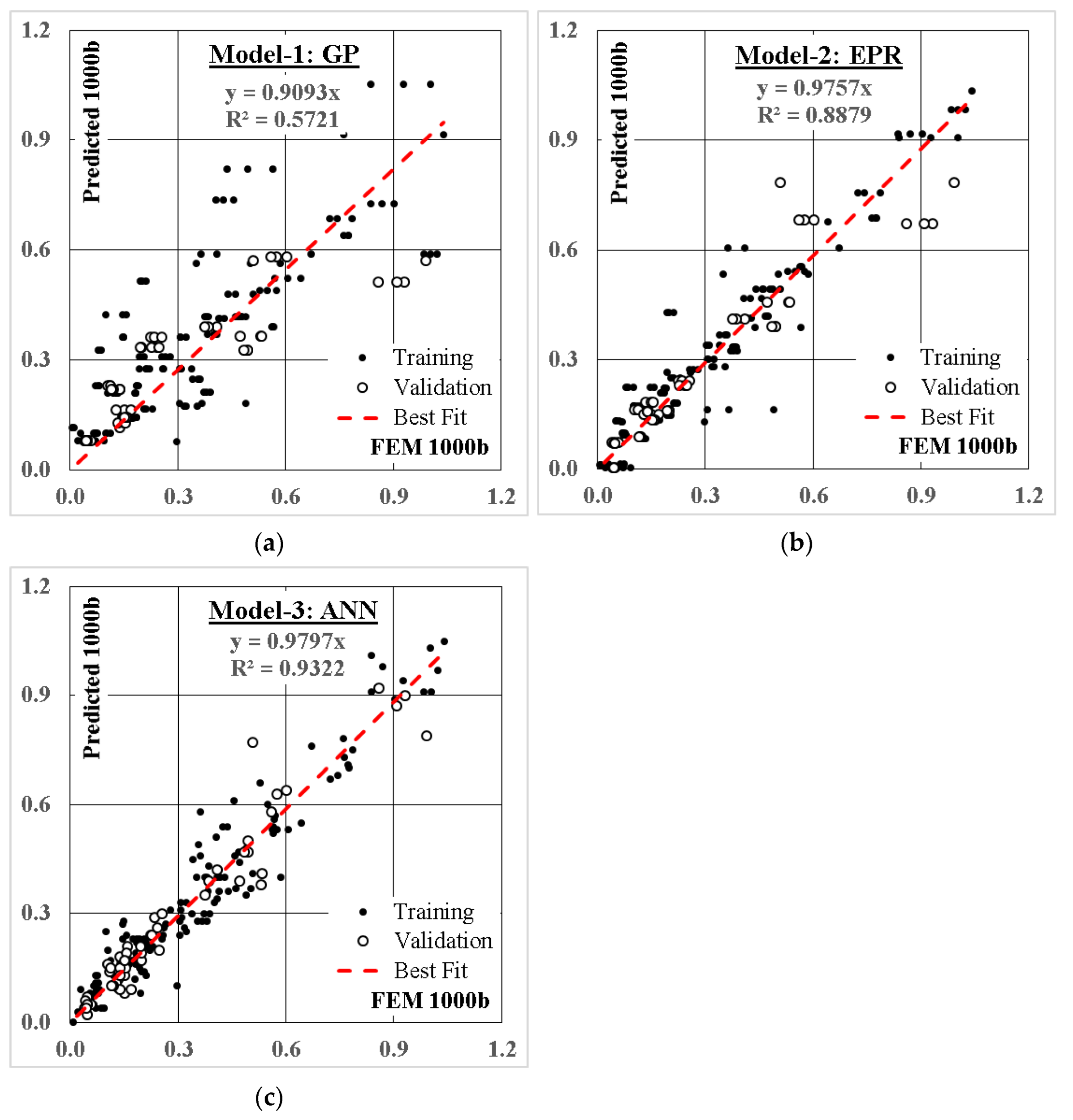
4.1.1. Model (1)—Using (ANN) Technique
4.1.2. Model (2)—Using GP Technique
4.1.3. Model (3)—Using EPR Technique
4.2. Results Discussion
5. Conclusions
- The developed formulas using the GP technique showed a limited accuracy of 50%. All input factors were utilized, except the cohesion of both top and bottom soils (Ct), (Cb).
- EPR technique generated two seven term polynomials out of 1287 possible terms. The accuracy is better than the GP models (65%). In addition, all input factors except the overburden pressure (σ′v) and the cohesion of both the top and bottom soils (Ct), (Cb) were generated.
- Finally, ANN technique presents the best accuracy of 80% and used all the input factors. The relative importance of each factor is indicated by the size of the blocks in Figure 5, and, accordingly, all factors have almost the same effect on the load-settlement curve except (B), tan (φt) and tan (φb), which have a slightly higher effect.
- Both GP and EPR could not capture the influence of soil cohesion on the load-settlement curve, which gives the advantage to the ANN model.
- The developed GP model is not recommended because of its limited accuracy.
- Although the ANN model showed the best accuracy and utilised all input factors, its model is too complicated to be manually handled.
- The developed EPR model could be used for manual calculations, while the ANN model is suitable for computerized calculations
- The developed models should be used within the factor values considered in the study. The prediction accuracy must be verified beyond this range.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Biswas, T.; Saran, S.; Shanker, D. Analysis of a strip footing using constitutive law. Geosciences 2016, 6, 41–44. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Mojtahedi, F.F.; Azizi, S.; Mahdi, H.A.; Sujatha, E.R.; Ebid, A.M.; Darzi, A.G.; Aneke, F.I. Innovative overview of SWRC application in modeling geotechnical engineering problems. Designs 2022, 6, 69. [Google Scholar] [CrossRef]
- Ebid, A.M.; Onyelowe, K.C.; Salah, M. Estimation of bearing capacity of strip footing rested on bilayered soil profile using FEM-AI-coupled techniques. Adv. Civ. Eng. 2022, 2022, 8047559. [Google Scholar] [CrossRef]
- Manisana, R.; Patil, N.N.; Swamy, H.M.R.; Shivashankar, R. Load-settlement characteristics of reinforced and unreinforced foundation soil. Int. J. Eng. Res. Technol. 2014, 3, 888–892. [Google Scholar]
- Nwokediuko, N.M.; Ogirigbo, O.R.; Inerhunwa, I. Load-settlement characteristics of tropical red soils of Southern Nigeria. Eur. J. Eng. Technol. Res. 2019, 4, 107–113. [Google Scholar] [CrossRef]
- Van Baars, S. Numerical check of the Meyerhof bearing capacity equation for shallow foundations. Innov. Infrastruct. Solutions 2017, 3, 9. [Google Scholar] [CrossRef]
- Ebid, A.M.; Onyelowe, K.C.; Arinze, E.E. Estimating the ultimate bearing capacity for strip footing near and within slopes using AI (GP, ANN, and EPR) techniques. J. Eng. 2021, 2021, 3267018. [Google Scholar] [CrossRef]
- Gazetas, G. Analysis of machine foundation vibrations: State of the art. Int. J. Soil Dyn. Earthq. Eng. 1983, 2, 2–42. [Google Scholar] [CrossRef]
- Elsamee, W.N.A. An experimental study on the effect of foundation depth, size and shape on subgrade reaction of cohessionless soil. Engineering 2013, 5, 785–795. [Google Scholar] [CrossRef]
- Iancu, B.T.; Ionut, O.T. Numerical Analyses of Plate Loading Test Numerical Analyses of Plate Loading Test; Buletinul Institutului Politehnic: Iasi, Romania, 2009; pp. 57–65. [Google Scholar]
- Mughieda, O.; Mehana, M.S.; Hazirbaba, K. Effect of soil subgrade modulus on raft foundation behavior. MATEC Web Conf. 2017, 120, 06010. [Google Scholar] [CrossRef]
- Ziaie-Moay, R.; Janbaz, M. Effective parameters on modulus of subgrade reaction in clayey soils. J. Appl. Sci. 2009, 9, 4006–4012. [Google Scholar] [CrossRef]
- Mahdi, H.A.; Ebid, A.M.; Onyelowe, K.C.; Nwobia, L.I. Predicting the behaviour of laterally loaded flexible free head pile in layered soil using different AI (EPR, ANN and GP) techniques. Multiscale Multidiscip. Model. Exp. Des. 2022, 5, 225–242. [Google Scholar] [CrossRef]
- Ebid, A.M. 35 Years of (AI) in geotechnical engineering: State of the art. Geotech. Geol. Eng. 2020, 39, 637–690. [Google Scholar] [CrossRef]
- Wang, C.X.; Carter, J.P. Deep penetration of strip and circular footings into layered clays. Int. J. Géoméch. 2002, 2, 205–232. [Google Scholar] [CrossRef]
- Carter, J.P. Solving boundary value problems in geotechnical engineering. In Pre-Failure Deformation Characteristics of Geomaterials; Jamiolkowski, M., Lancellotta, R., Lo Presti, D., Eds.; Swets & Zeitlinger: Lisse, The Netherlands, 2001. [Google Scholar]
- Merifield, R.S.; Nguyen, V.Q. Two- and three-dimensional bearing-capacity solutions for footings on two-layered clays. Géoméch. Geoengin. 2006, 1, 151–162. [Google Scholar] [CrossRef]
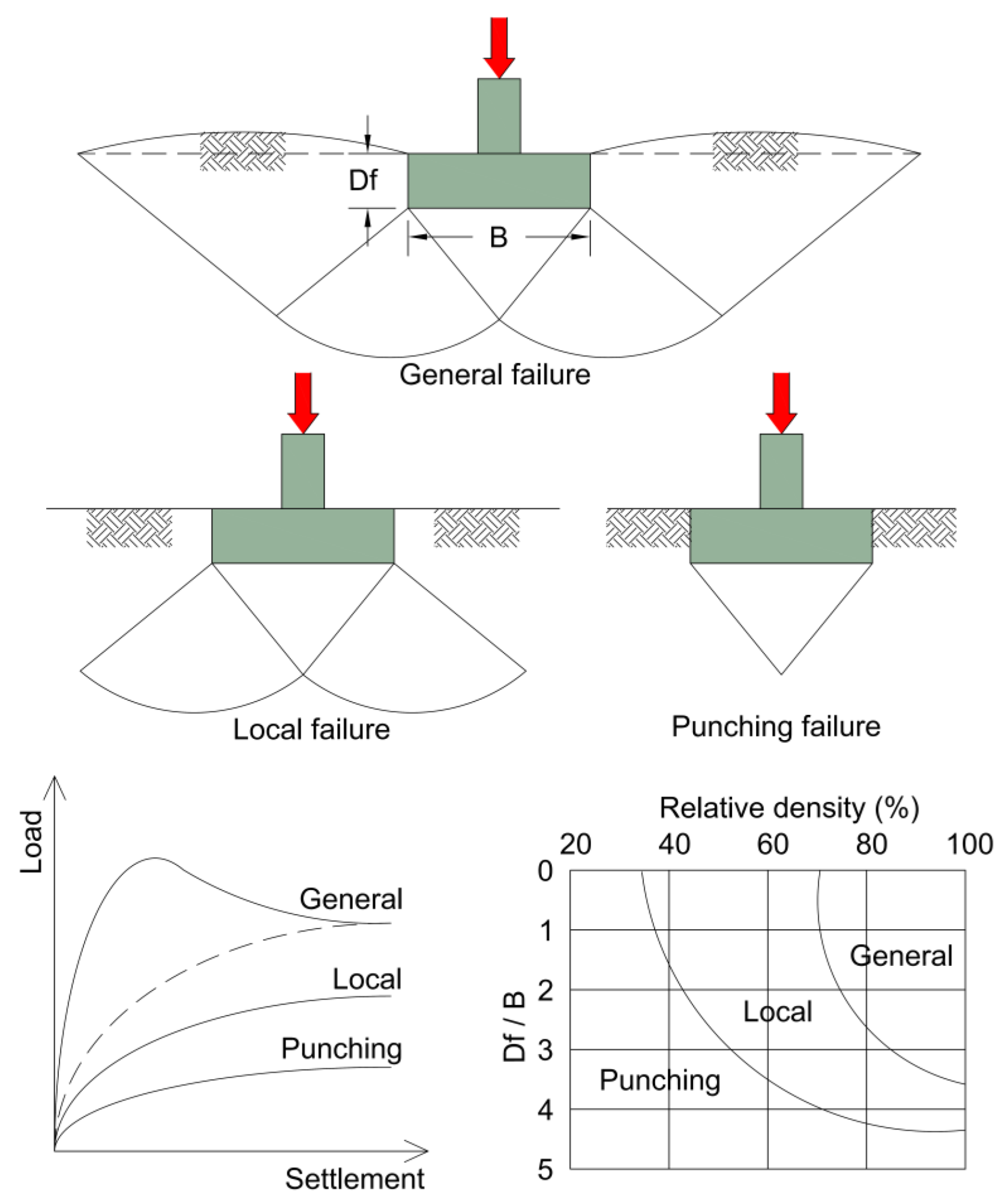



| No | Investigator | Year | Suggested Formula |
|---|---|---|---|
| 1 | Winkler | 1867 | |
| 2 | Biot | 1937 | |
| 3 | Terzaghi | 1955 | |
| 4 | Vesic | 1961 | |
| 5 | Meyerhof and Baike | 1965 | |
| 6 | Selvadurai | 1984 | |
| 7 | Bowles | 1988 |
| Soil Type | Soil Description | C (kN/m2) | φ (°) | γ (kN/m3) | E (MN/m2) | υ |
|---|---|---|---|---|---|---|
| S 1 | loose Sand | 0.0 | 29 | 16 | 9.0 | 0.350 |
| S 2 | Dense Sand | 0.0 | 38 | 20 | 50.0 | 0.300 |
| S 3 | Soft Clay | 25 | 0.0 | 14 | 1.5 | 0.450 |
| S 4 | Stiff Clay | 100 | 0.0 | 20 | 10.0 | 0.350 |
| S 5 | Soft Silt | 25 | 5 | 18 | 6.0 | 0.400 |
| S 6 | Stiff Silt | 100 | 20 | 20 | 30.0 | 0.330 |
| Ct | tan (φt) | γ′t | h | Cb | tan (φb) | γ′b | B | σ′v | 1000a | 1000b | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| kN/m2 | - | kN/m3 | m | kN/m2 | - | kN/m3 | m | kN/m2 | kN/m2 | kN/m2 | |
| Training set | |||||||||||
| Min. | 0.1 | 0.0 | 14.0 | 0.5 | 0.1 | 0.0 | 14.0 | 1.0 | 18.0 | 0.343 | 0.086 |
| Max. | 100 | 1 | 20 | 5 | 100 | 1 | 20 | 5 | 54 | 6.340 | 1.880 |
| Avg. | 35.6 | 0.4 | 18.1 | 2.1 | 37.4 | 0.3 | 17.8 | 3.0 | 35.0 | 1.850 | 0.327 |
| SD | 46.0 | 0.3 | 2.2 | 1.3 | 41.2 | 0.3 | 2.4 | 1.6 | 14.7 | 1.610 | 0.272 |
| VAR | 1.29 | 0.87 | 0.12 | 0.61 | 1.10 | 1.02 | 0.13 | 0.54 | 0.42 | 0.870 | 0.832 |
| Validation set | |||||||||||
| Min. | 0.1 | 0.0 | 14.0 | 0.5 | 0.1 | 0.0 | 14.0 | 1.0 | 18.0 | 0.372 | 0.094 |
| Max. | 100 | 1 | 20 | 5 | 100 | 1 | 20 | 5 | 54 | 6.450 | 1.920 |
| Avg. | 40.6 | 0.3 | 18.4 | 1.8 | 39.5 | 0.3 | 17.6 | 2.7 | 38.4 | 1.880 | 0.347 |
| SD | 46.9 | 0.3 | 2.0 | 1.2 | 39.9 | 0.3 | 2.5 | 1.5 | 14.5 | 1.540 | 0.263 |
| VAR | 1.15 | 0.97 | 0.11 | 0.67 | 1.01 | 1.18 | 0.14 | 0.56 | 0.38 | 0.819 | 0.758 |
| Ct | tan (φt) | γ′t | h | Cb | tan (φb) | γ′b | B | σ′v | 1000a | 1000b | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ct | 1.00 | ||||||||||
| tan (φt) | −0.66 | 1.00 | |||||||||
| γ′t | 0.59 | 0.05 | 1.00 | ||||||||
| h | −0.21 | 0.40 | 0.07 | 1.00 | |||||||
| Cb | 0.06 | 0.08 | 0.13 | 0.04 | 1.00 | ||||||
| tan (φb) | 0.09 | 0.02 | 0.02 | 0.05 | −0.55 | 1.00 | |||||
| γ′b | 0.09 | 0.08 | 0.15 | 0.08 | 0.43 | 0.32 | 1.00 | ||||
| B | 0.02 | −0.01 | −0.01 | 0.88 | 0.02 | 0.01 | 0.04 | 1.00 | |||
| σ′v | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | ||
| 1000a | −0.12 | −0.50 | −0.55 | −0.30 | −0.20 | −0.29 | −0.38 | −0.07 | −0.18 | 1.00 | |
| 1000b | −0.15 | −0.08 | −0.30 | 0.41 | −0.19 | −0.25 | −0.47 | 0.56 | 0.01 | 0.13 | 1.00 |
| Hidden | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | H10 | |||
| Input Layer | (Bias) | −0.96 | 1.31 | −0.01 | −1.42 | −0.34 | 0.29 | −0.39 | 0.17 | −0.59 | −1.54 | |
| Ct | −0.27 | 0.63 | 0.75 | −0.07 | 0.12 | 0.22 | −0.15 | −0.41 | 0.00 | −0.1 | ||
| tan (φt) | 0.31 | 0.36 | 0.41 | 1.16 | 0.17 | −0.03 | −0.45 | 0 | −0.3 | −0.36 | ||
| γ′t | −0.74 | 0.51 | −0.16 | −0.63 | 0.00 | −0.28 | −0.09 | 0.41 | −0.34 | −0.49 | ||
| h | 0.15 | −0.65 | 0.23 | 0.02 | −0.04 | −0.22 | −0.11 | 0.4 | −0.35 | −0.15 | ||
| Cb | 0.32 | −0.4 | 0.44 | 0.33 | −0.78 | 0.00 | 0.24 | −0.06 | 0.08 | −0.37 | ||
| tan (φb) | 1.24 | −0.94 | 0.56 | 0.47 | −0.8 | −0.32 | −0.9 | −0.71 | −0.49 | −0.27 | ||
| γ′b | −0.26 | −0.83 | 0.26 | 0.61 | −1.04 | 0.32 | −1.11 | −0.42 | 0.6 | −0.17 | ||
| B | 0.1 | 0.25 | −0.15 | 0.15 | 0.37 | 0.5 | 0.02 | −0.55 | 0.5 | −0.01 | ||
| σ′v | 0.45 | 0.26 | −0.21 | −0.26 | −0.01 | −0.24 | −0.6 | 0.37 | 0.02 | −0.27 | ||
| Hidden | ||||||||||||
| H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | H10 | (Bias) | ||
| Output | 1000a | −0.81 | −1.33 | −0.51 | −1.28 | −0.16 | 0.15 | 0.12 | 0.09 | 0.03 | 0.92 | −0.49 |
| 1000b | 0.33 | 0.73 | −0.07 | 0.78 | 0.62 | 0.04 | −0.15 | −0.33 | 0.46 | 0.06 | −0.18 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebid, A.M.; Onyelowe, K.C.; Salah, M. Load-Settlement Curve and Subgrade Reaction of Strip Footing on Bi-Layered Soil Using Constitutive FEM-AI Coupled Techniques. Designs 2022, 6, 104. https://doi.org/10.3390/designs6060104
Ebid AM, Onyelowe KC, Salah M. Load-Settlement Curve and Subgrade Reaction of Strip Footing on Bi-Layered Soil Using Constitutive FEM-AI Coupled Techniques. Designs. 2022; 6(6):104. https://doi.org/10.3390/designs6060104
Chicago/Turabian StyleEbid, Ahmed M., Kennedy C. Onyelowe, and Mohamed Salah. 2022. "Load-Settlement Curve and Subgrade Reaction of Strip Footing on Bi-Layered Soil Using Constitutive FEM-AI Coupled Techniques" Designs 6, no. 6: 104. https://doi.org/10.3390/designs6060104
APA StyleEbid, A. M., Onyelowe, K. C., & Salah, M. (2022). Load-Settlement Curve and Subgrade Reaction of Strip Footing on Bi-Layered Soil Using Constitutive FEM-AI Coupled Techniques. Designs, 6(6), 104. https://doi.org/10.3390/designs6060104







