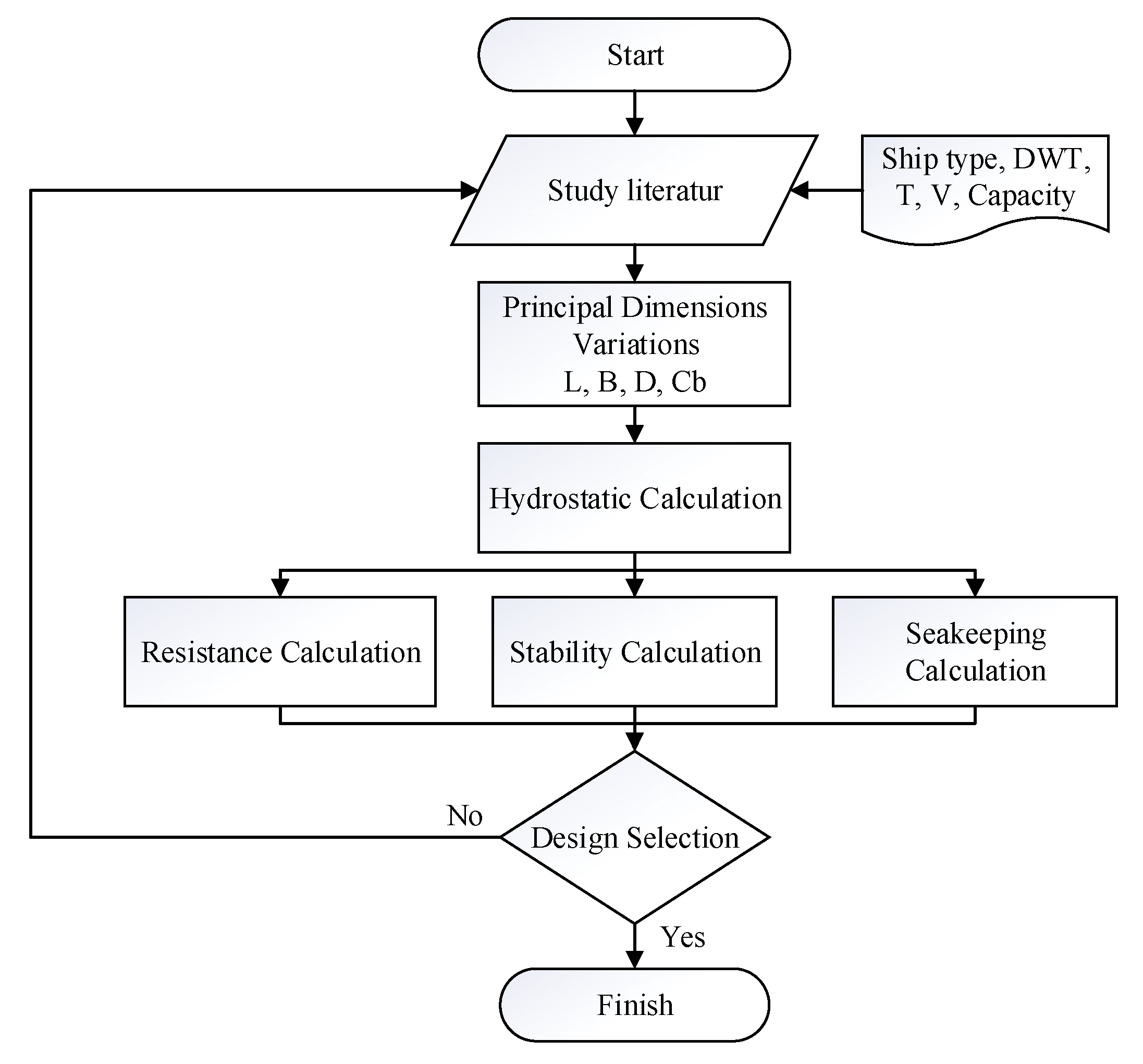
Figure 1.
Flowchart of the initial design of the ship.
Figure 1.
Flowchart of the initial design of the ship.
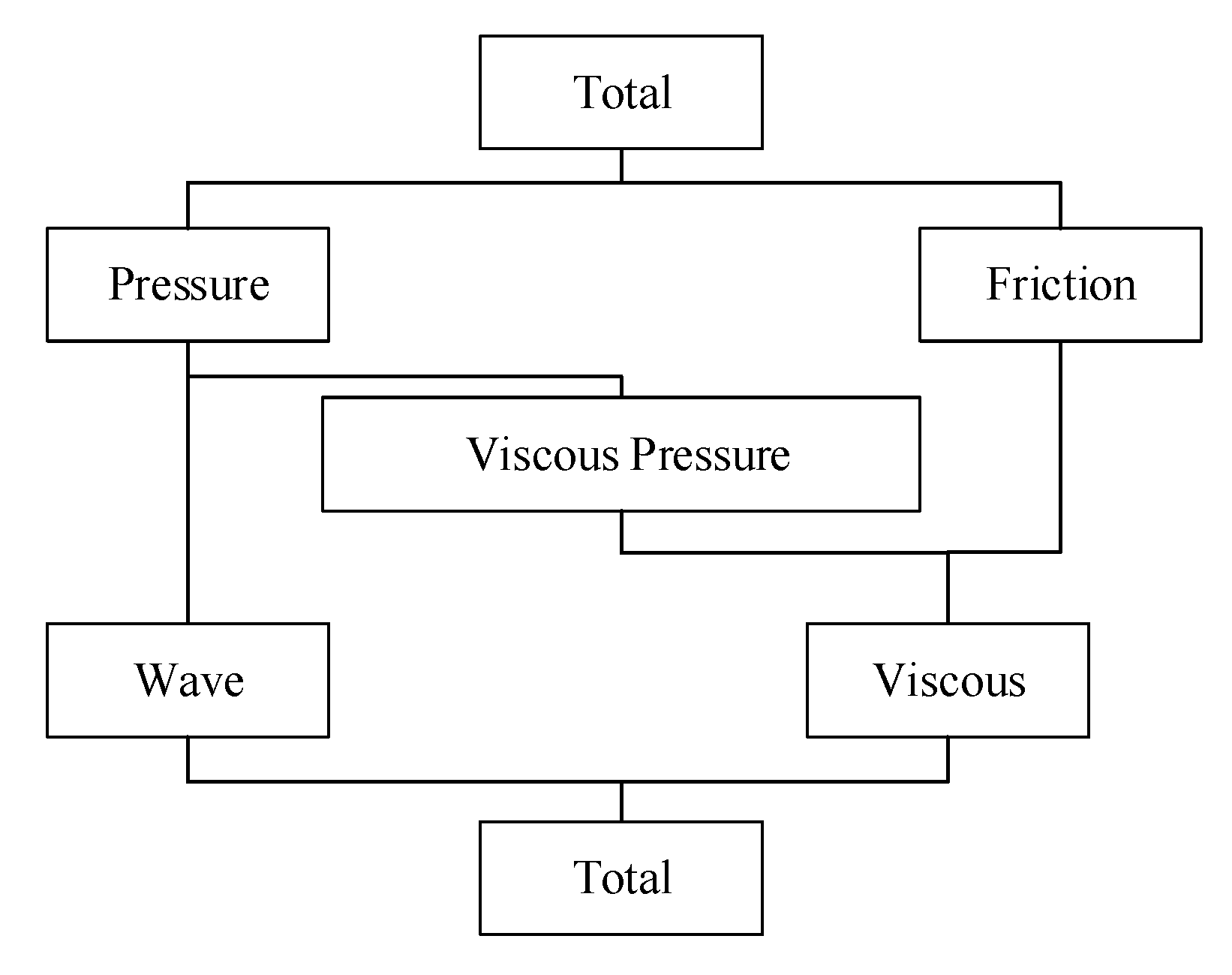
Figure 2.
Types of ship resistance.
Figure 2.
Types of ship resistance.
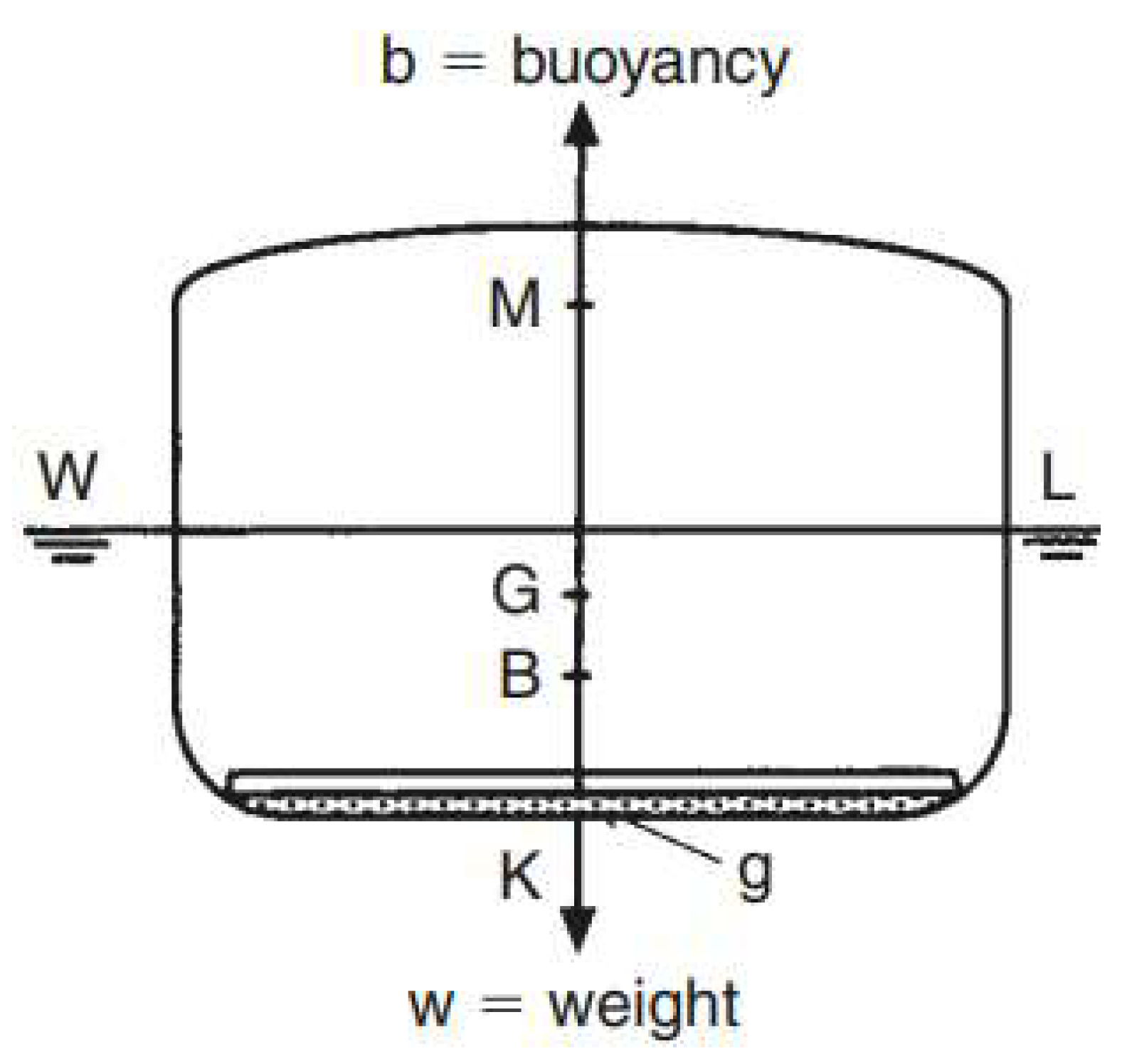
Figure 3.
Point of stability on the ship.
Figure 3.
Point of stability on the ship.
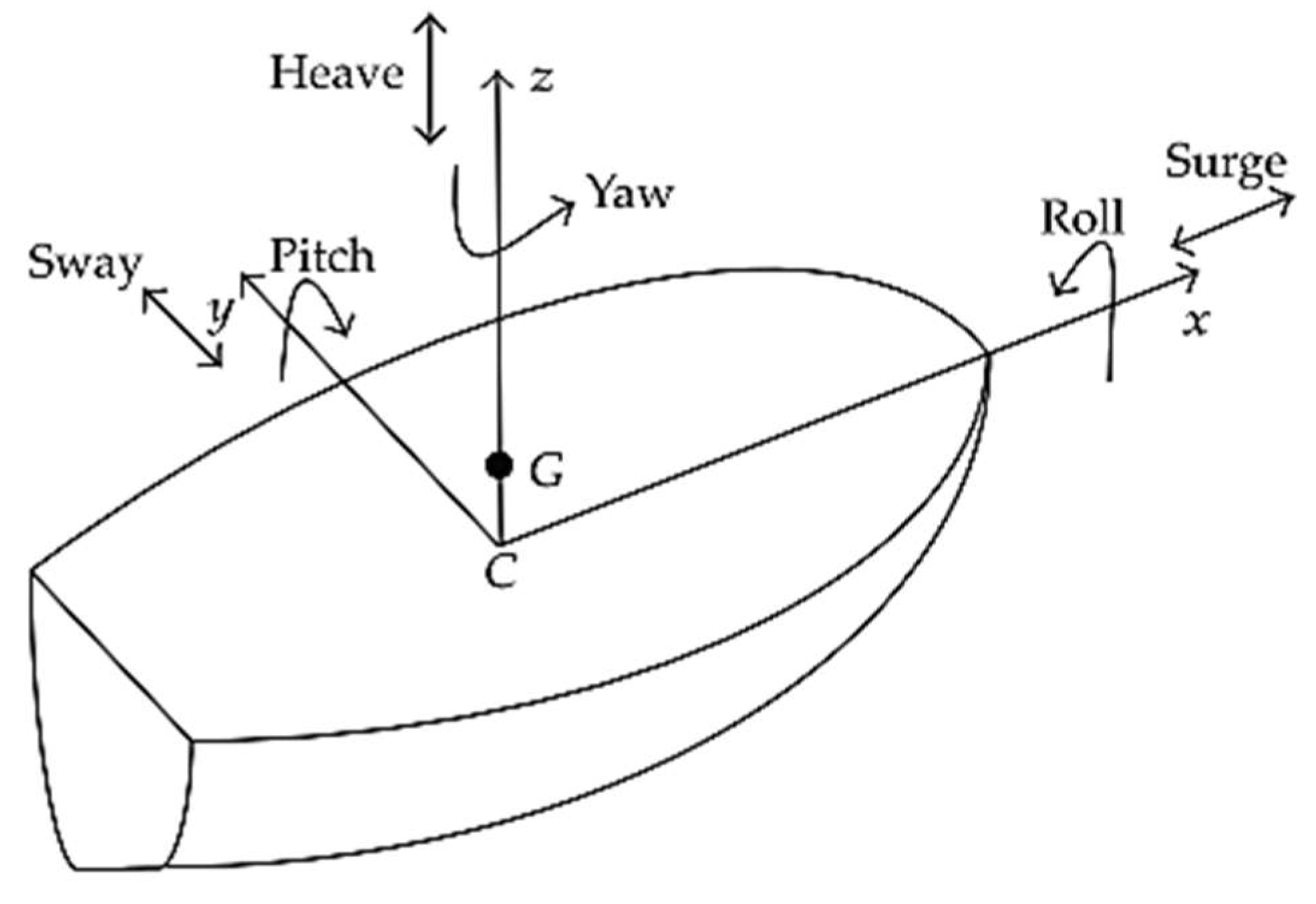
Figure 4.
Movement of the ship’s 6 degrees of freedom.
Figure 4.
Movement of the ship’s 6 degrees of freedom.
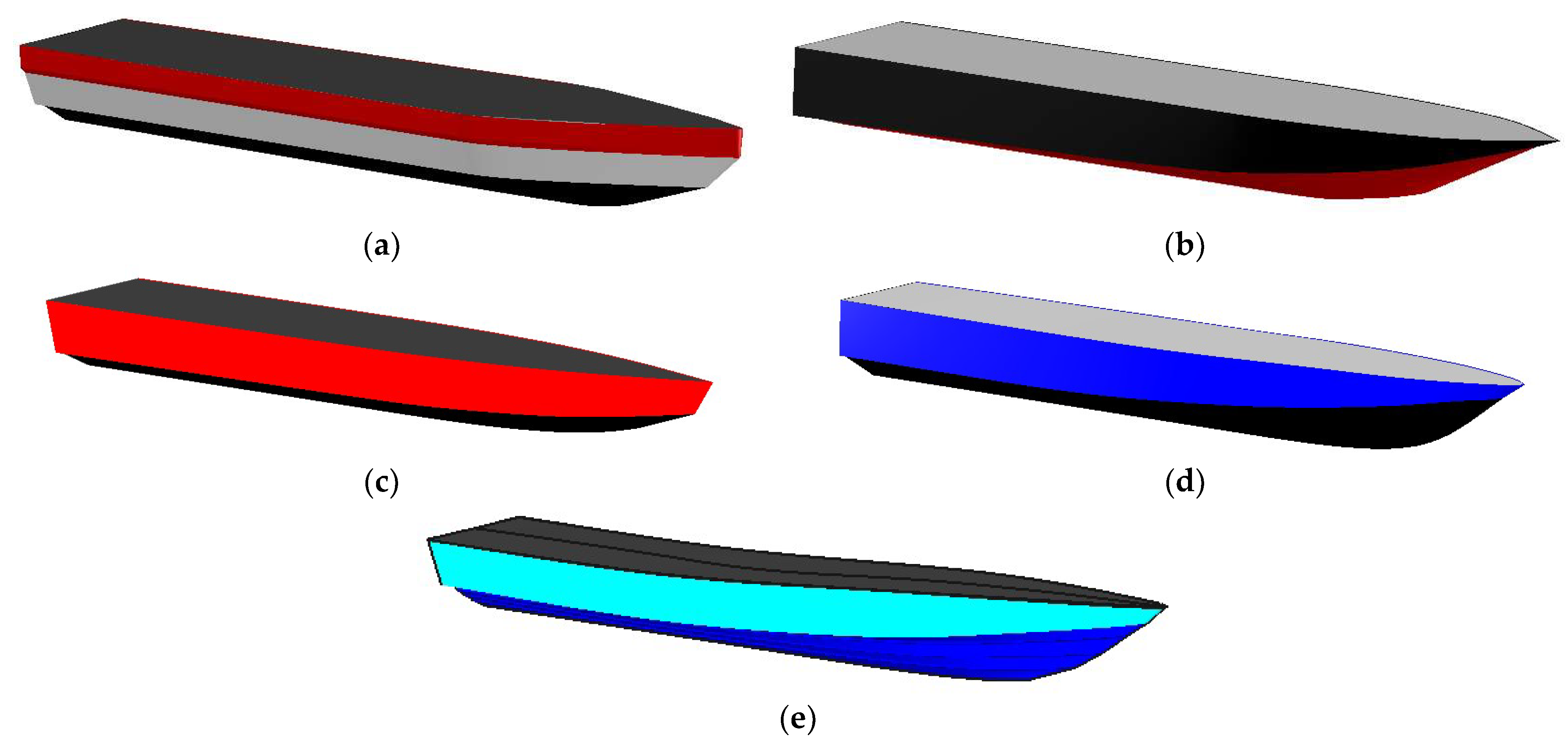
Figure 5.
Patrol boat 3D hull designs: (a) high-speed rescue craft (12 m); (b) SMIT patrol boat; (c) lightweight rescue craft (13 m); (d) fast police boat (15 m); (e) Aresa 1300 Sentinel RHIB.
Figure 5.
Patrol boat 3D hull designs: (a) high-speed rescue craft (12 m); (b) SMIT patrol boat; (c) lightweight rescue craft (13 m); (d) fast police boat (15 m); (e) Aresa 1300 Sentinel RHIB.
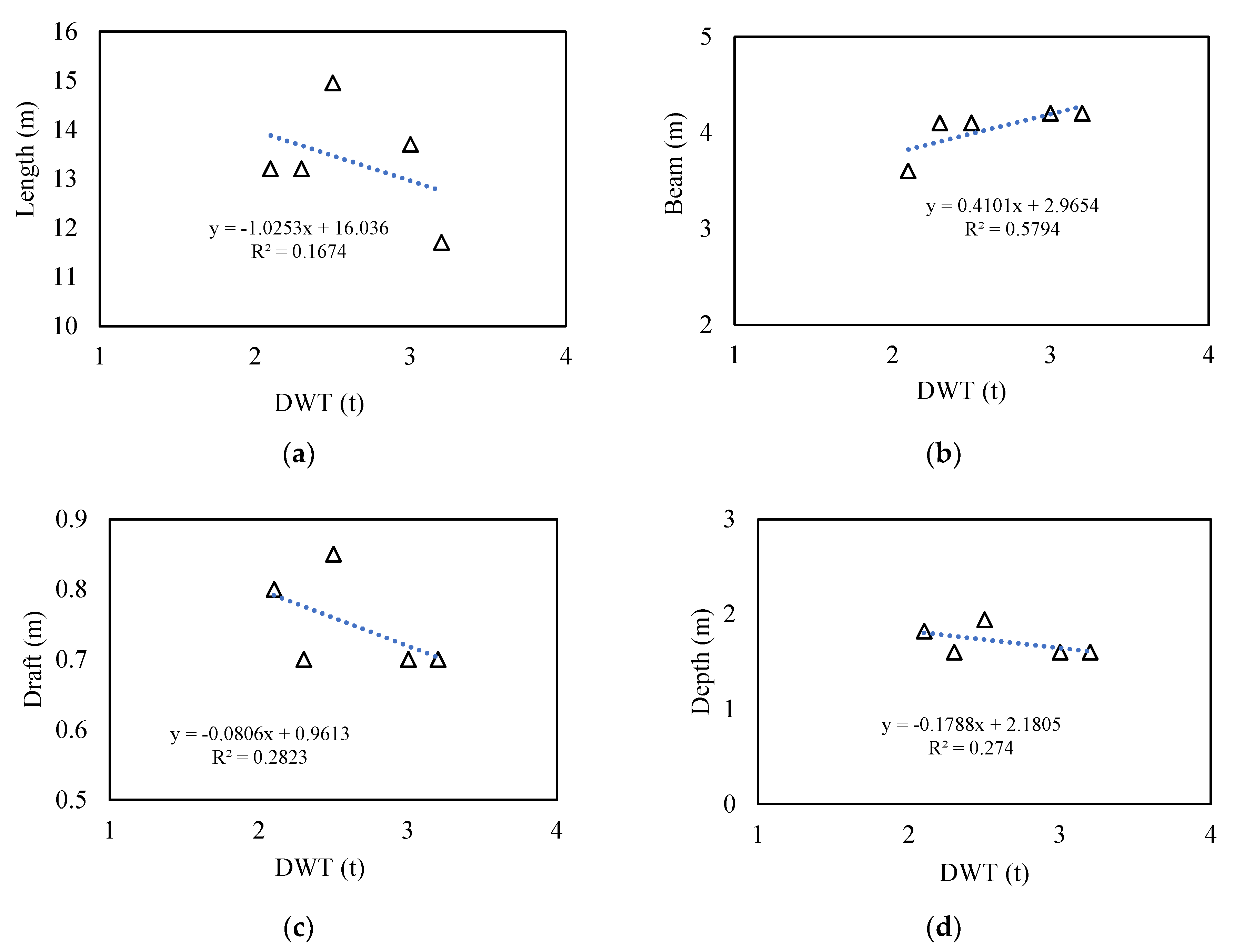
Figure 6.
Graphs of regression results: (a) length vs. DWT; (b) beam vs. DWT; (c) draft vs. DWT; (d) depth vs. DWT.
Figure 6.
Graphs of regression results: (a) length vs. DWT; (b) beam vs. DWT; (c) draft vs. DWT; (d) depth vs. DWT.
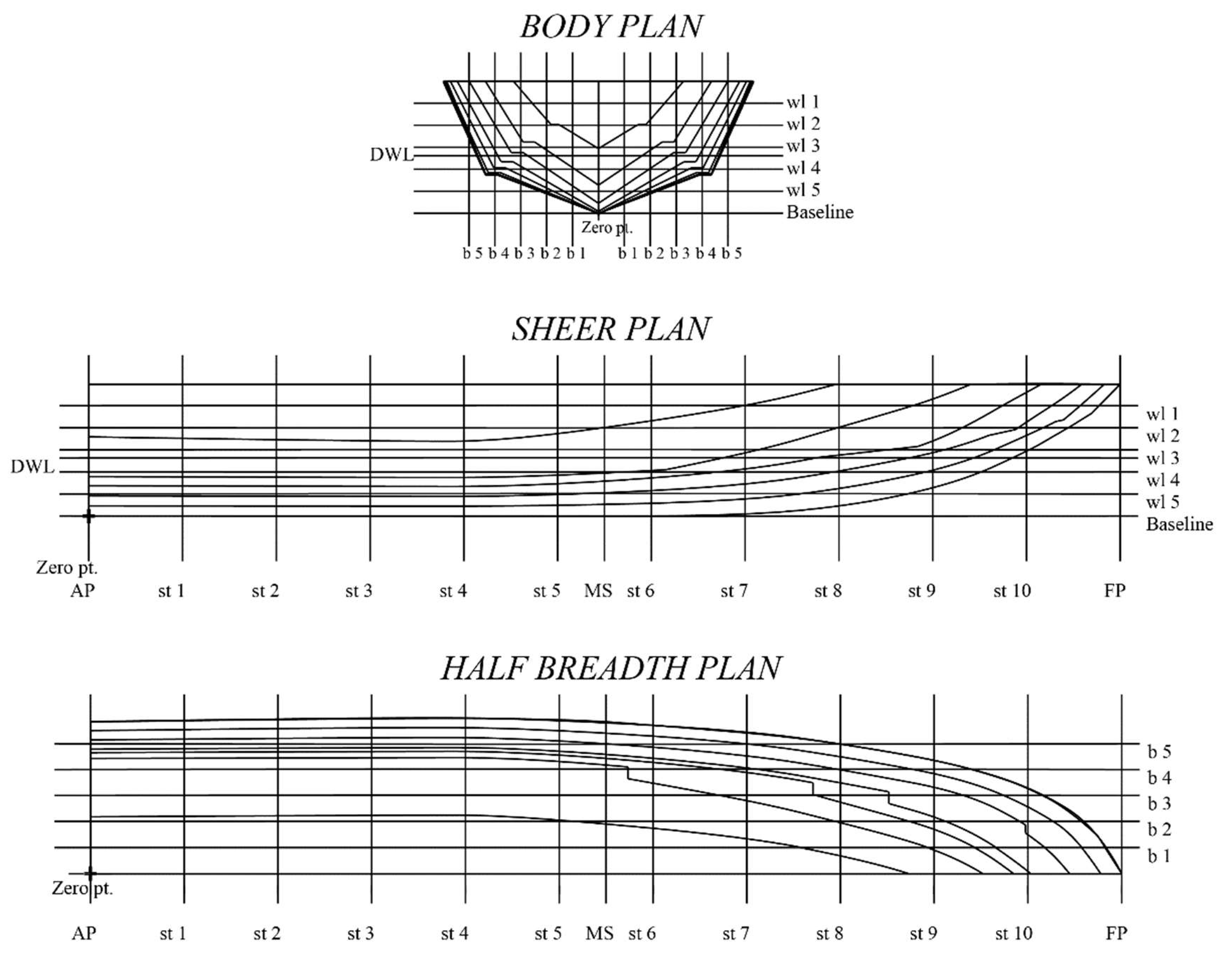
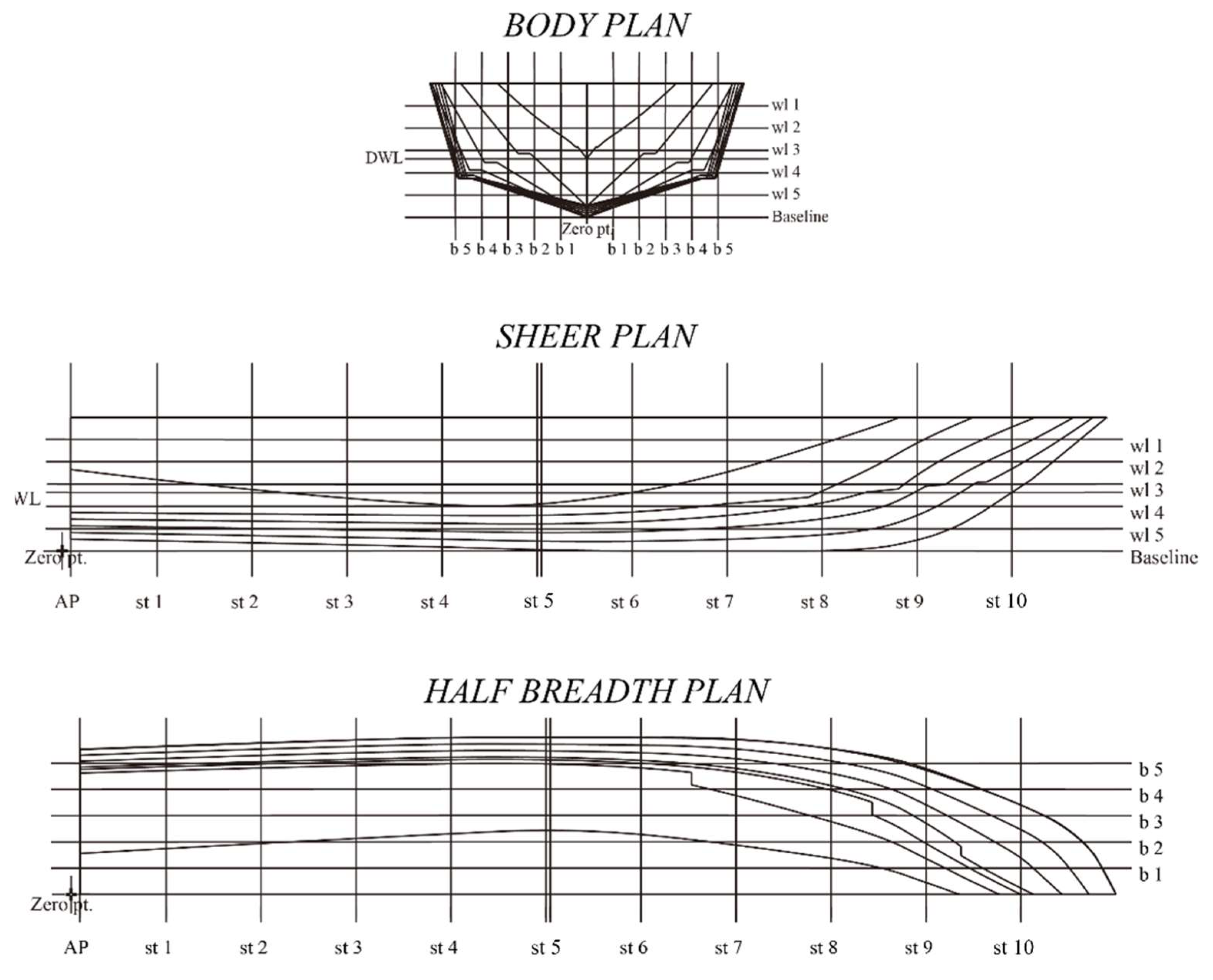
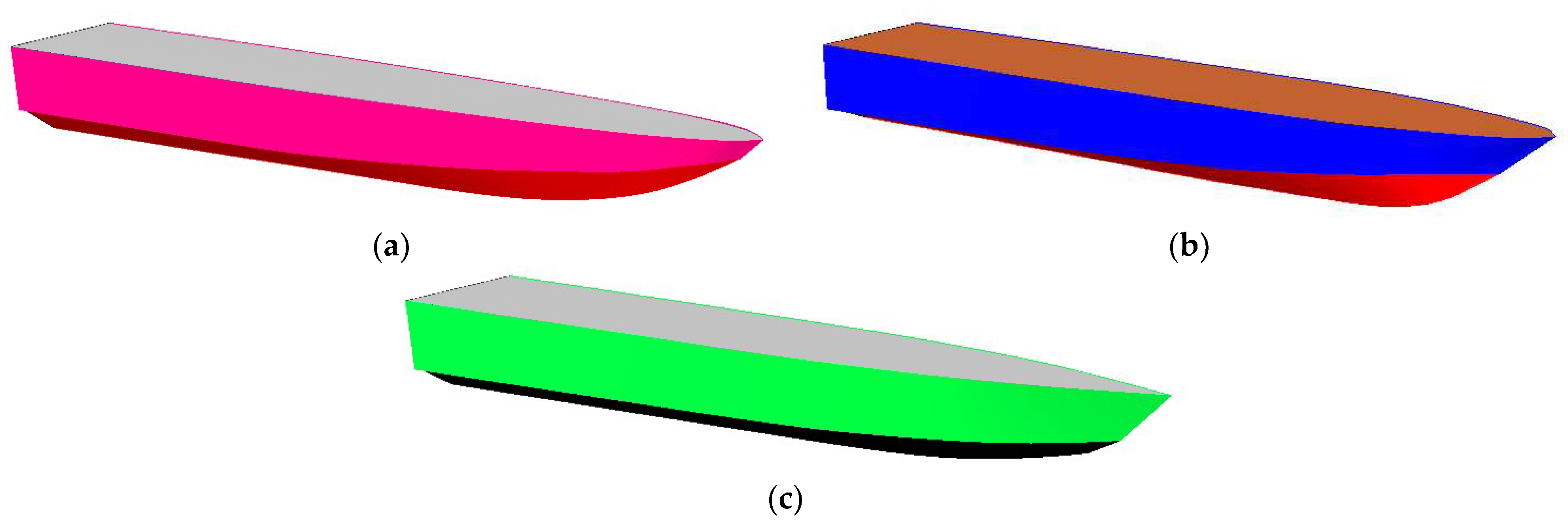
Figure 7.
3D hull designs from regression results: (
a) Regression I; (
b) Regression II; (
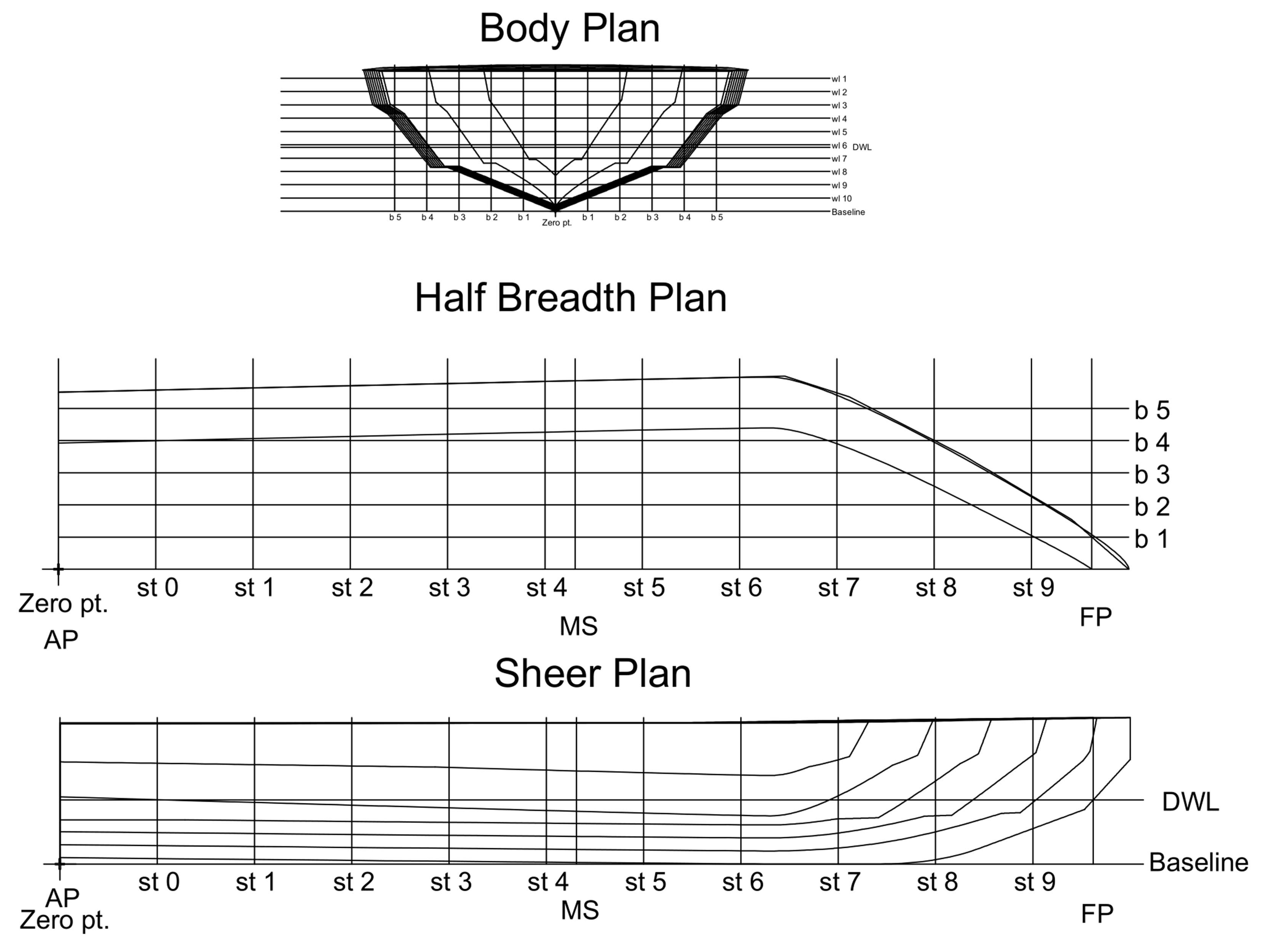
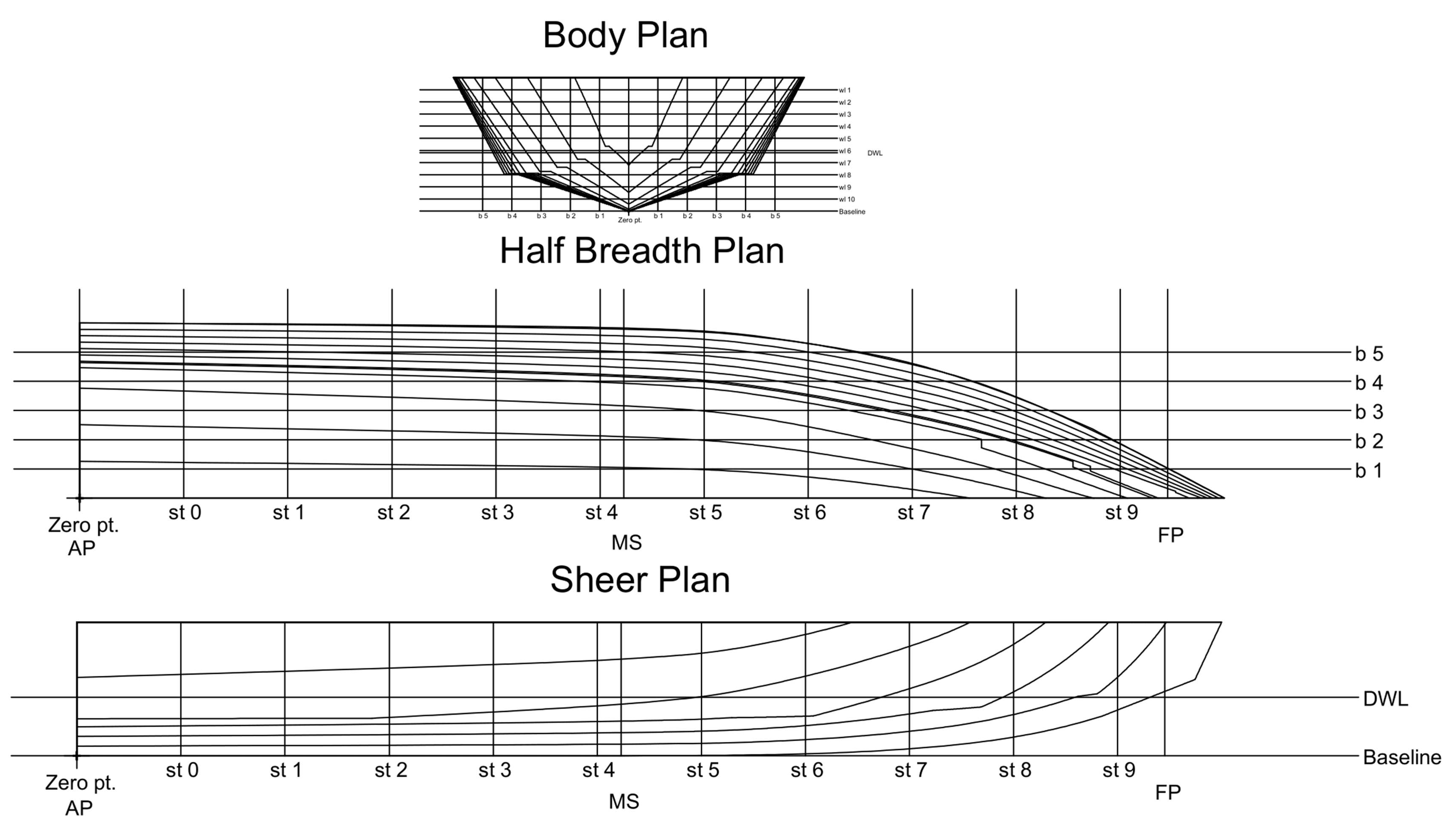
c) Regression III. The lines plan of regression-based hulls is given in
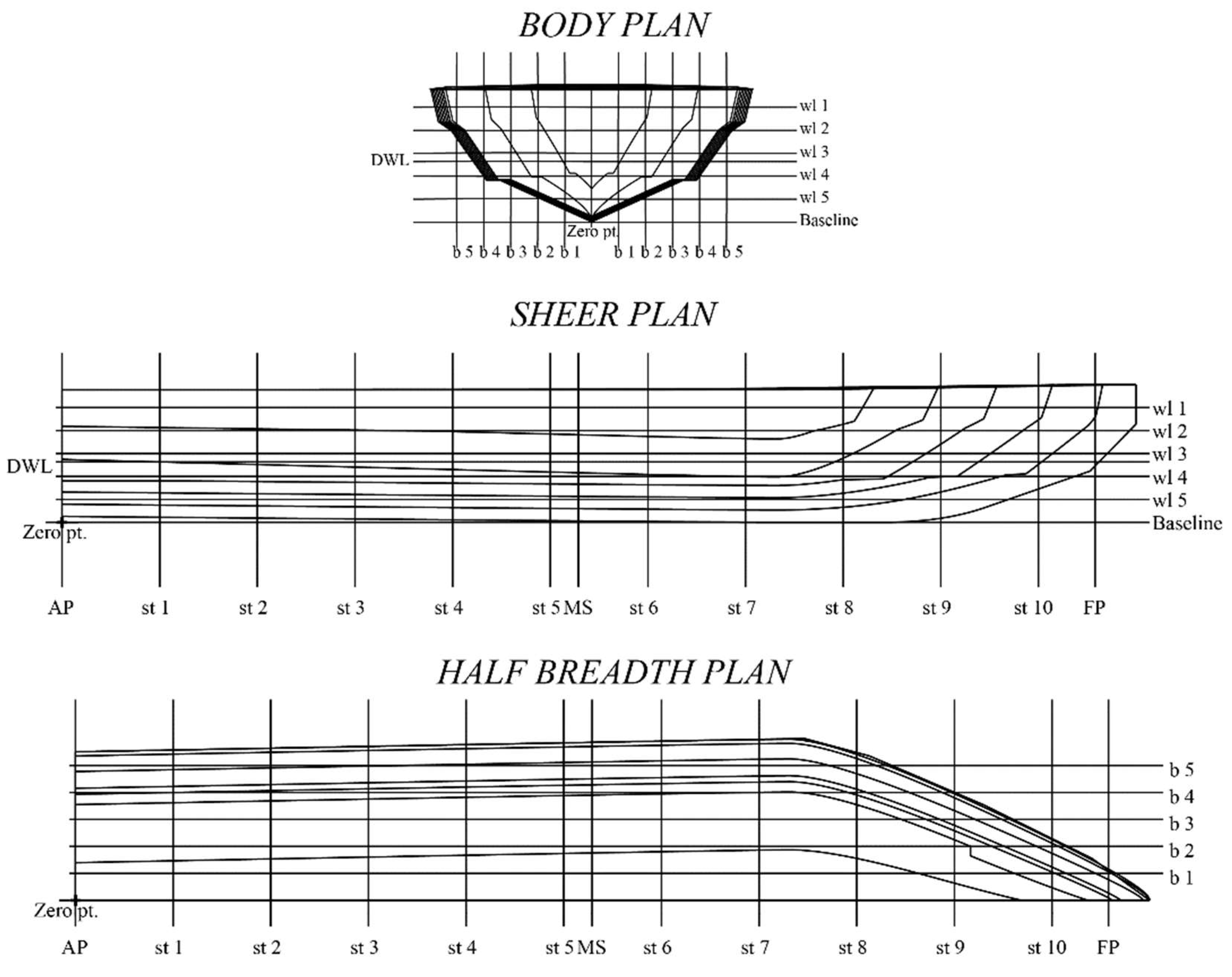
Appendix B.
Figure 7.
3D hull designs from regression results: (
a) Regression I; (
b) Regression II; (
c) Regression III. The lines plan of regression-based hulls is given in
Appendix B.
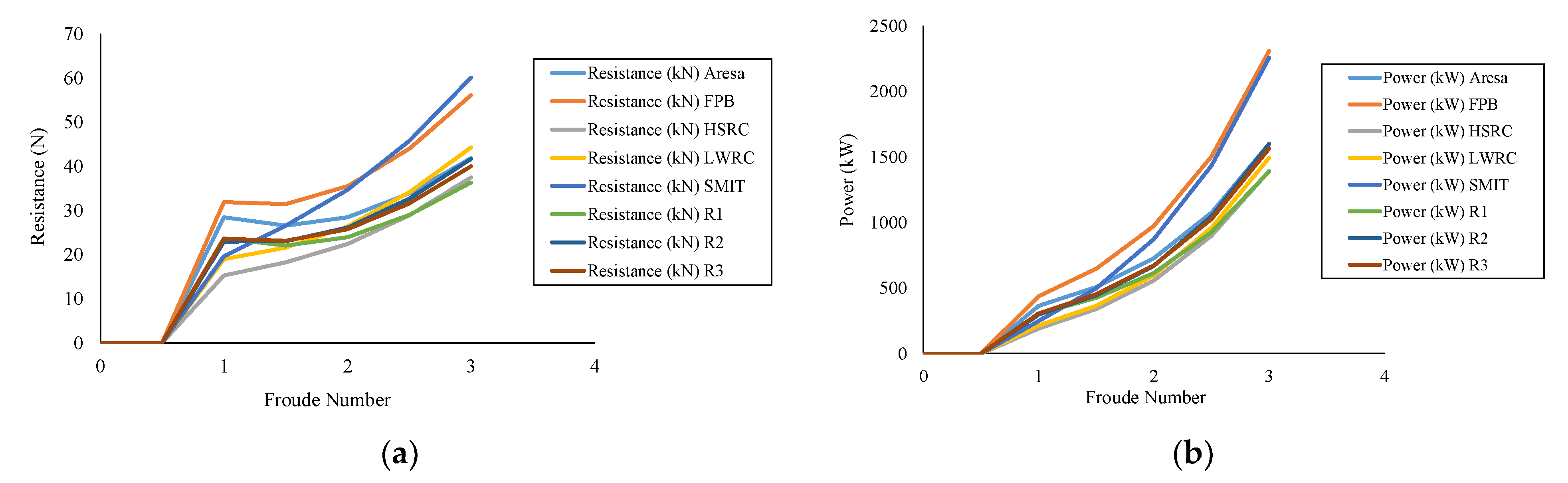
Figure 8.
Graphs of reference ship resistance assessment results: (a) speed vs. resistance; (b) speed vs. effective power.
Figure 8.
Graphs of reference ship resistance assessment results: (a) speed vs. resistance; (b) speed vs. effective power.
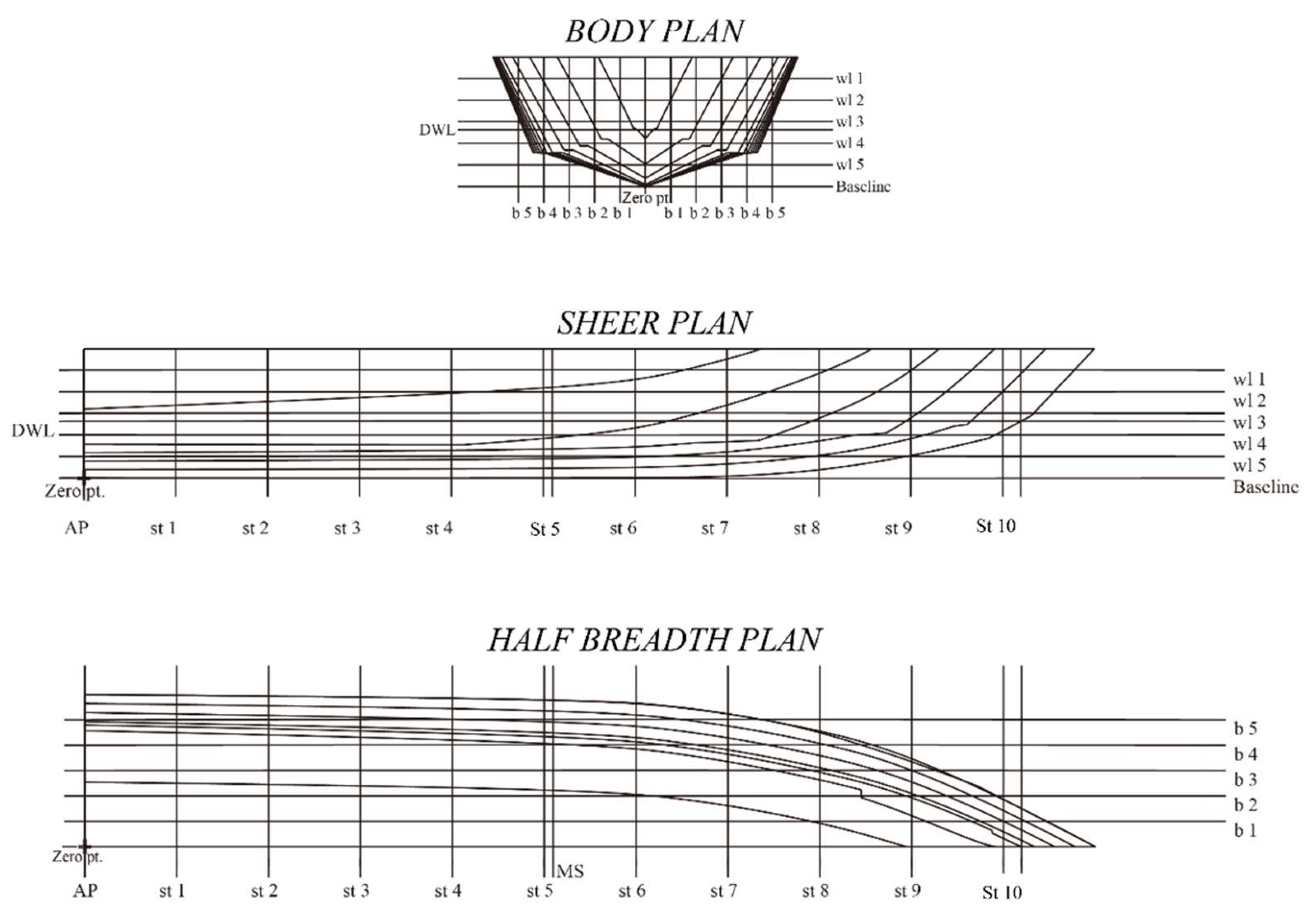
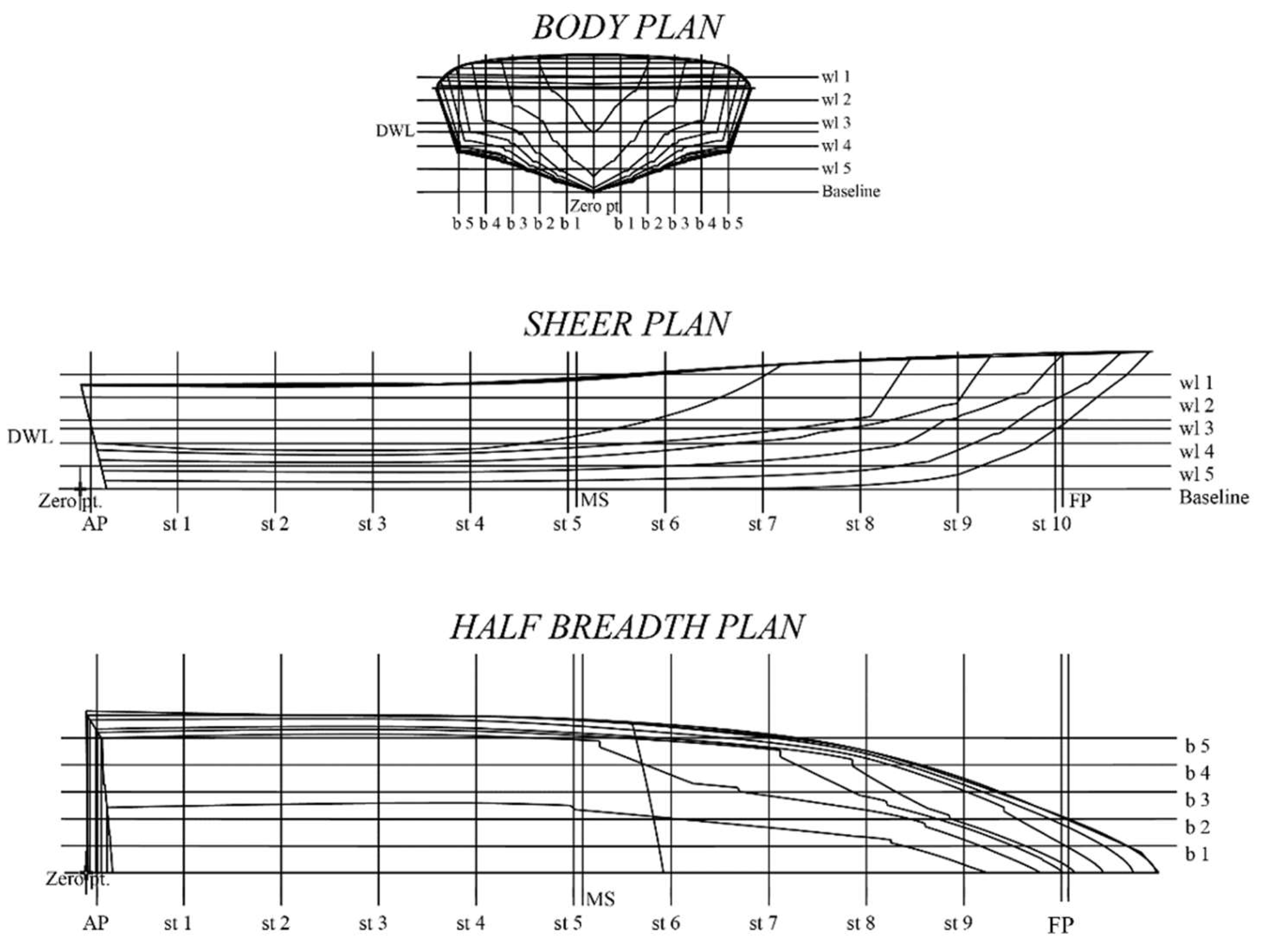
Figure 9.
3D hull designs that resulted from scaling: (
a) Scale I; (
b) Scale II; (
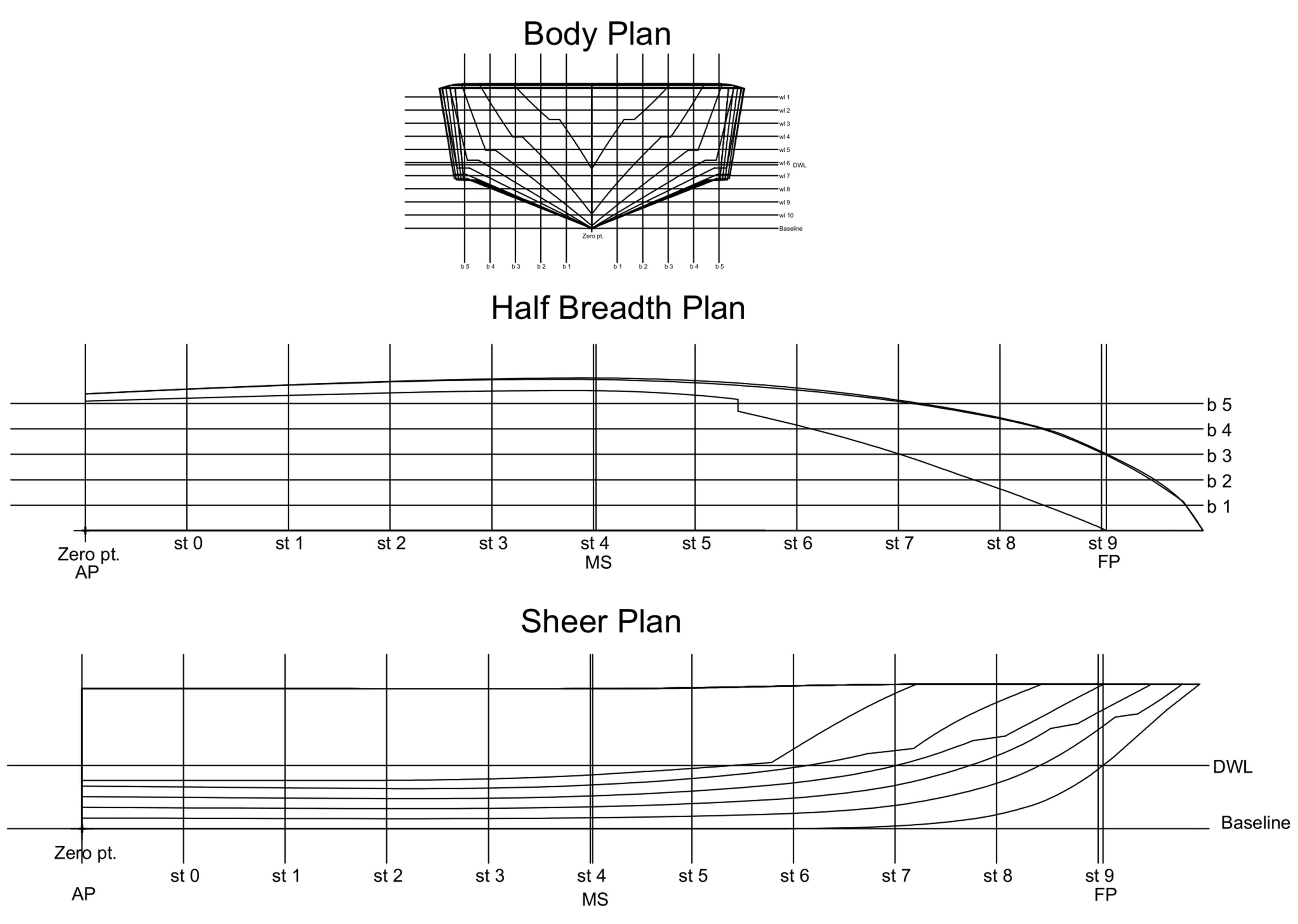
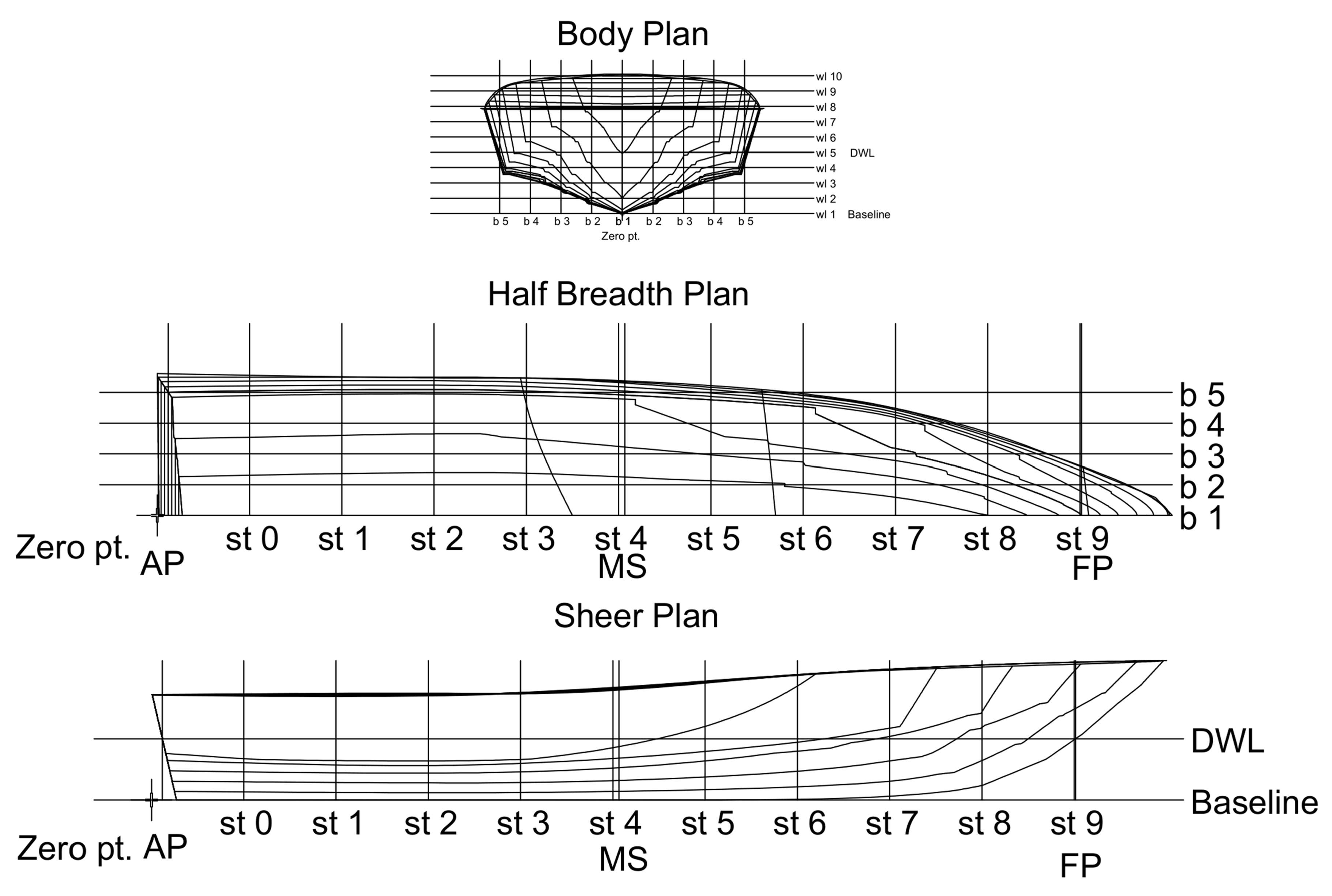
c) Scale III. The lines plan of scaling-based hulls is given in
Appendix C.
Figure 9.
3D hull designs that resulted from scaling: (
a) Scale I; (
b) Scale II; (
c) Scale III. The lines plan of scaling-based hulls is given in
Appendix C.
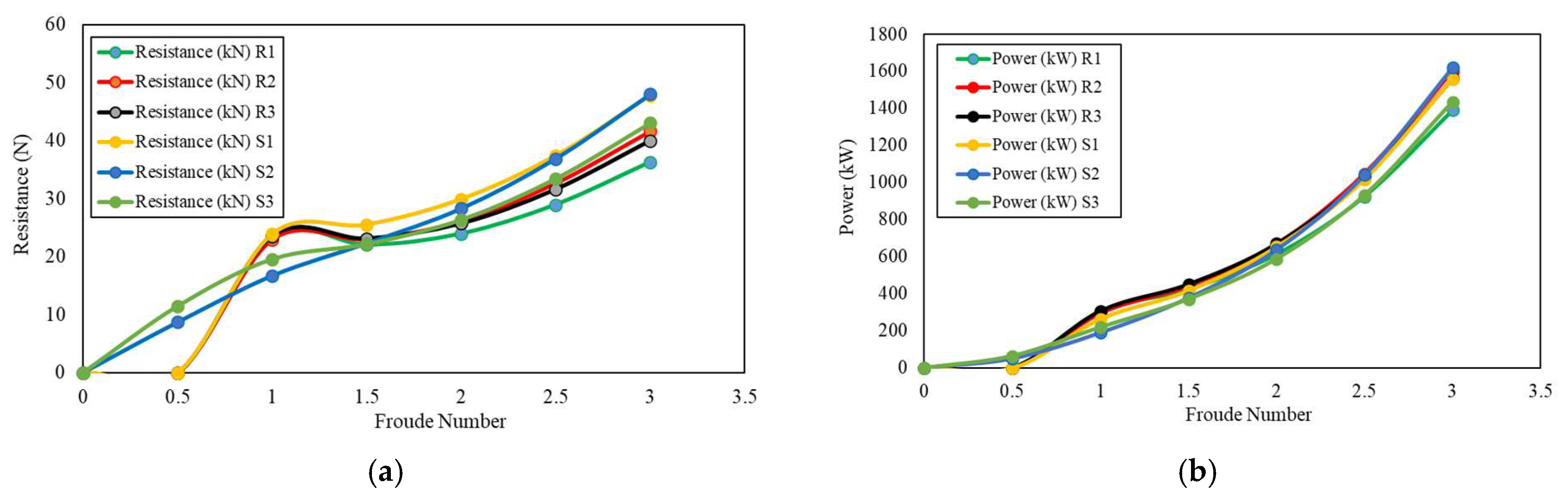
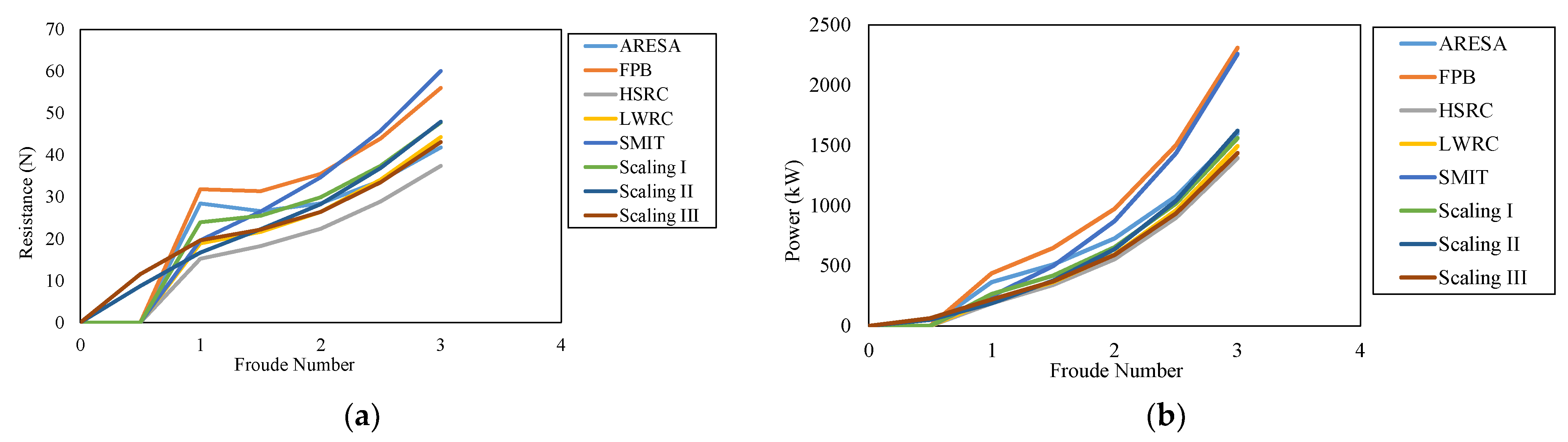
Figure 10.
Comparison between regression and scale models: (a) Froude number and resistance; (b) Froude number and power.
Figure 10.
Comparison between regression and scale models: (a) Froude number and resistance; (b) Froude number and power.
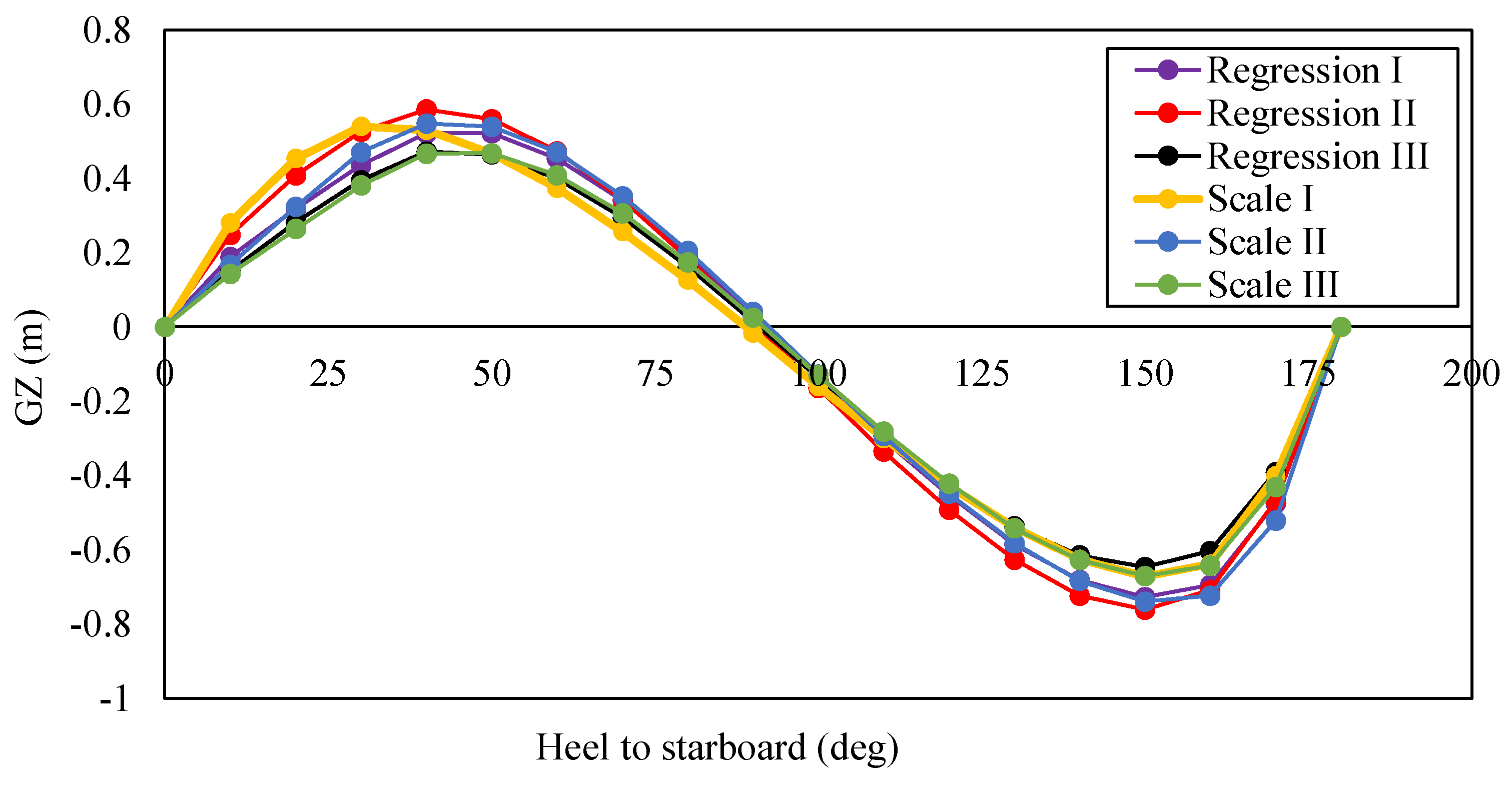
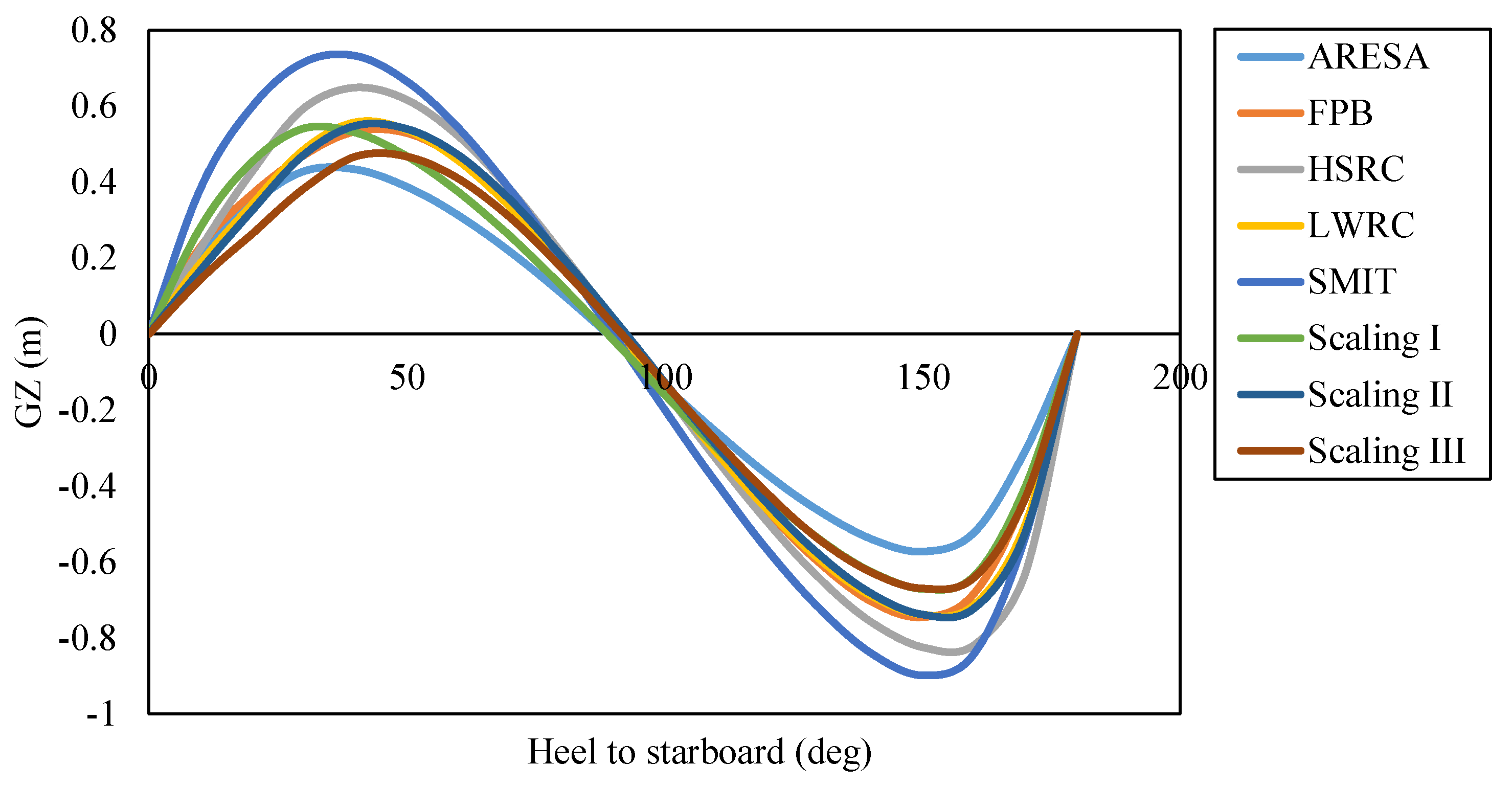
Figure 11.
Comparison of GZ values with ship’s tilt angle for regression and scaling models.
Figure 11.
Comparison of GZ values with ship’s tilt angle for regression and scaling models.
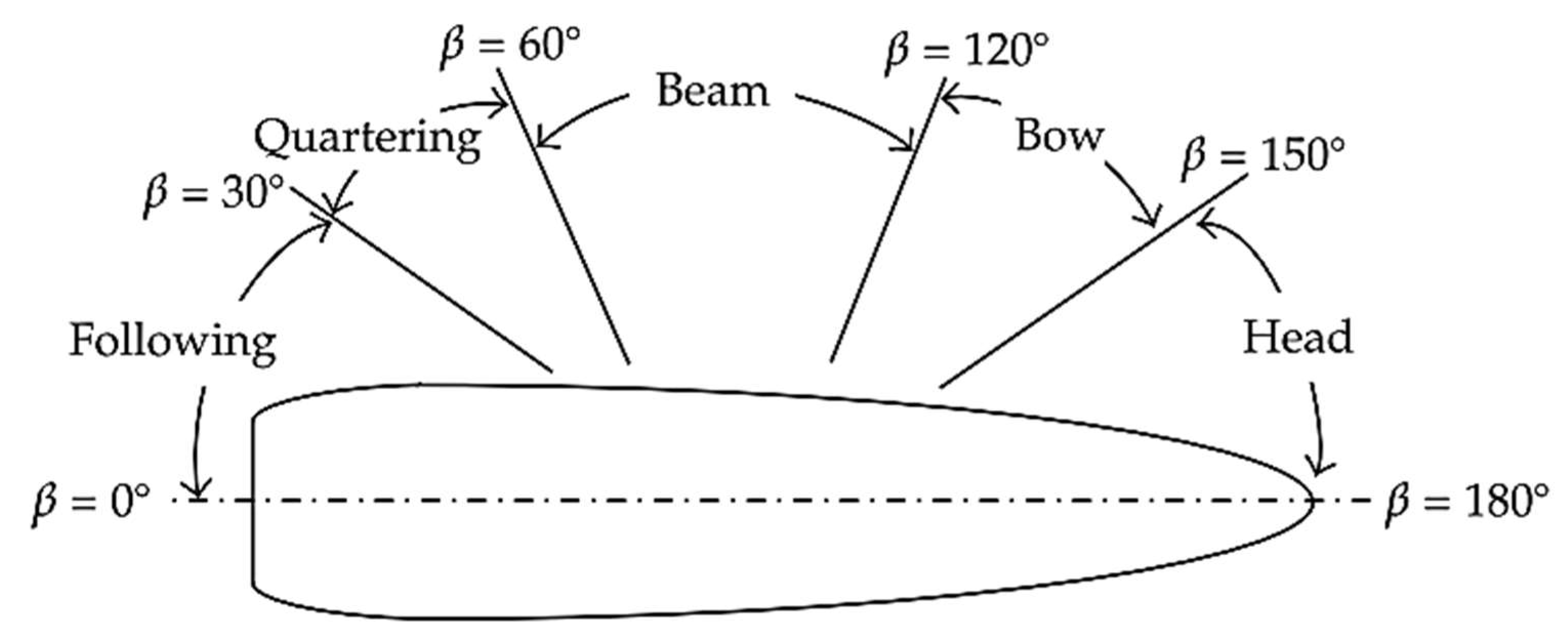
Figure 12.
Orientations of wave directions.
Figure 12.
Orientations of wave directions.
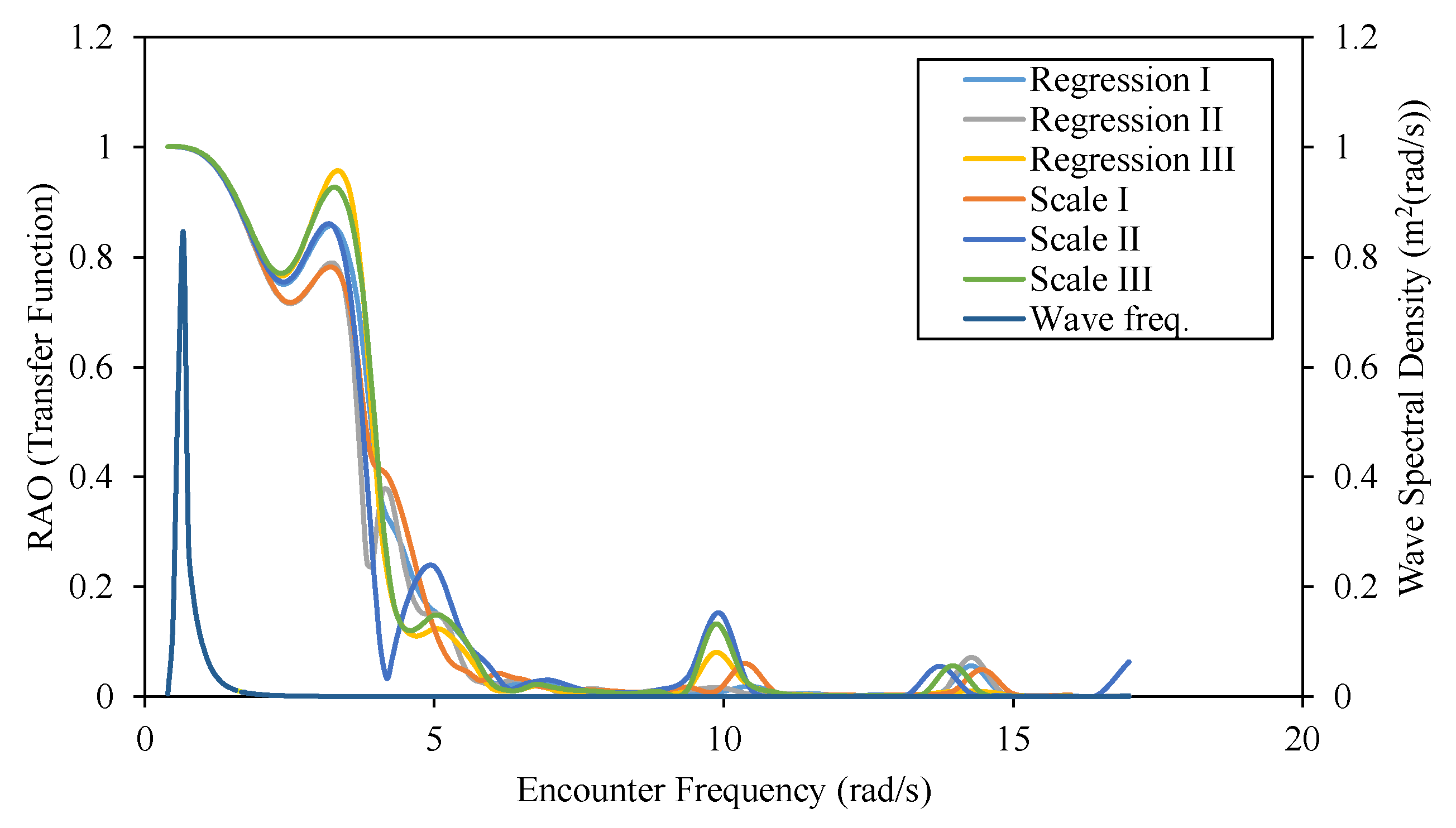
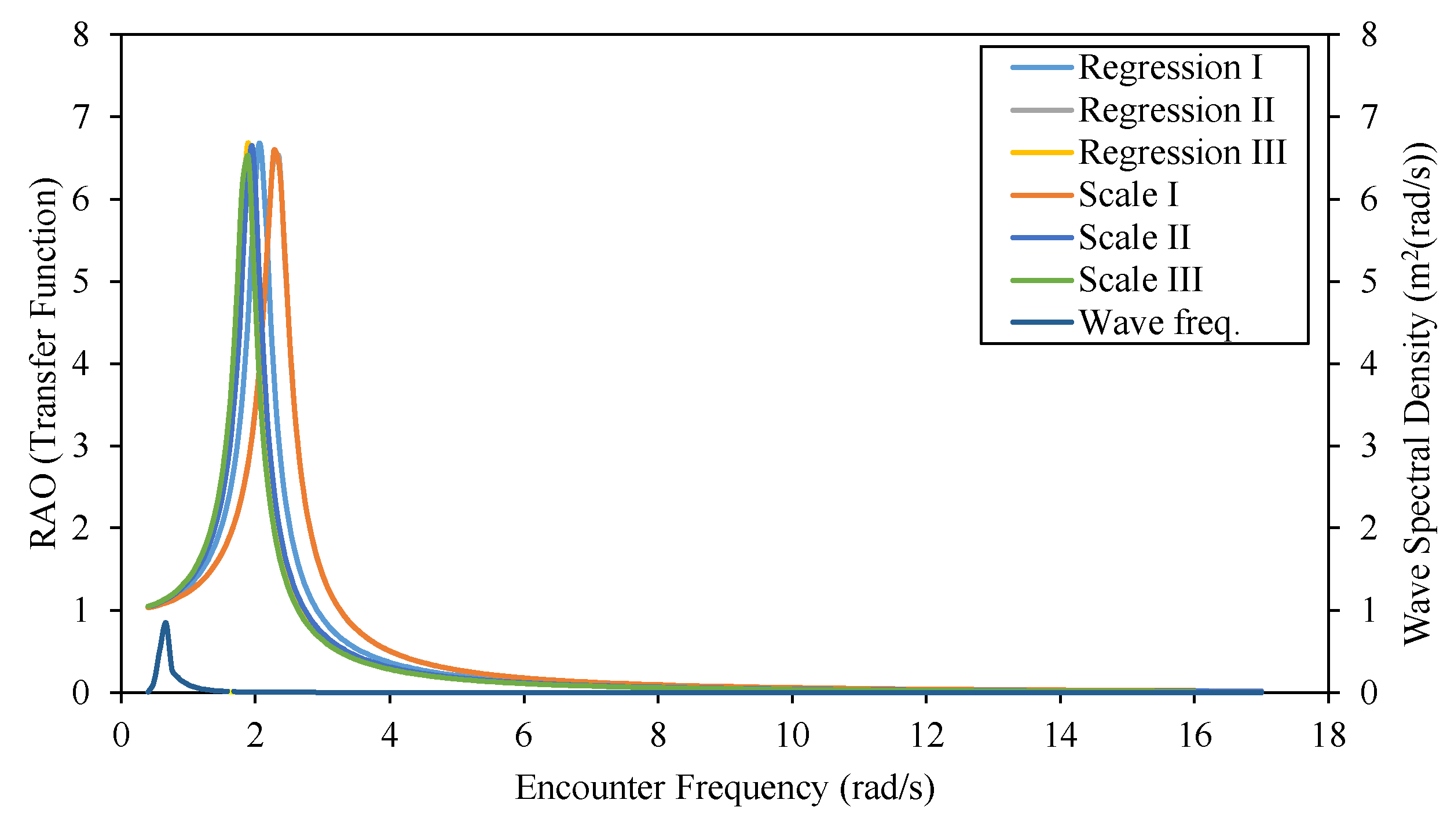
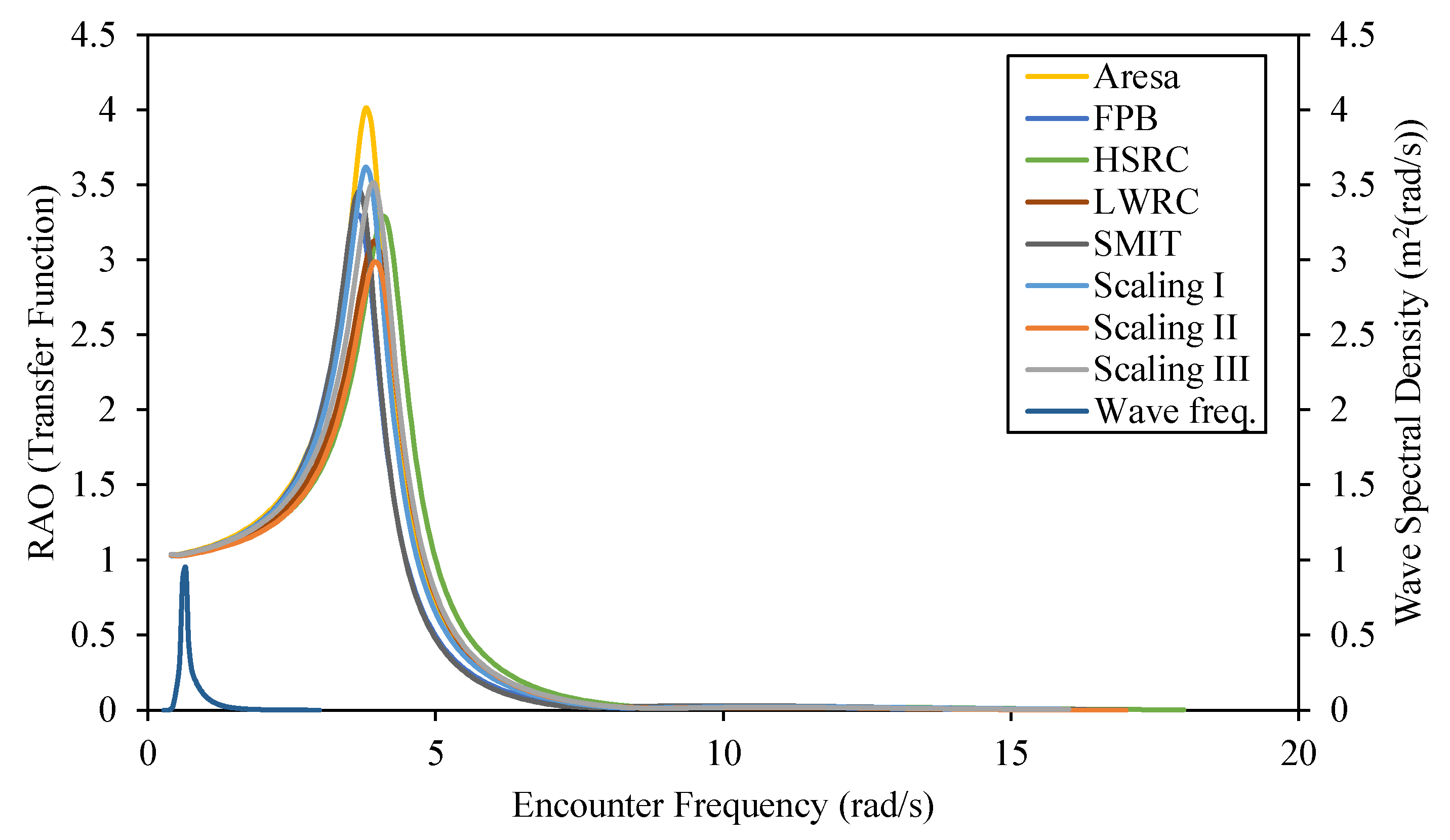
Figure 13.
RAO heaving motion graph for regression and scale models.
Figure 13.
RAO heaving motion graph for regression and scale models.
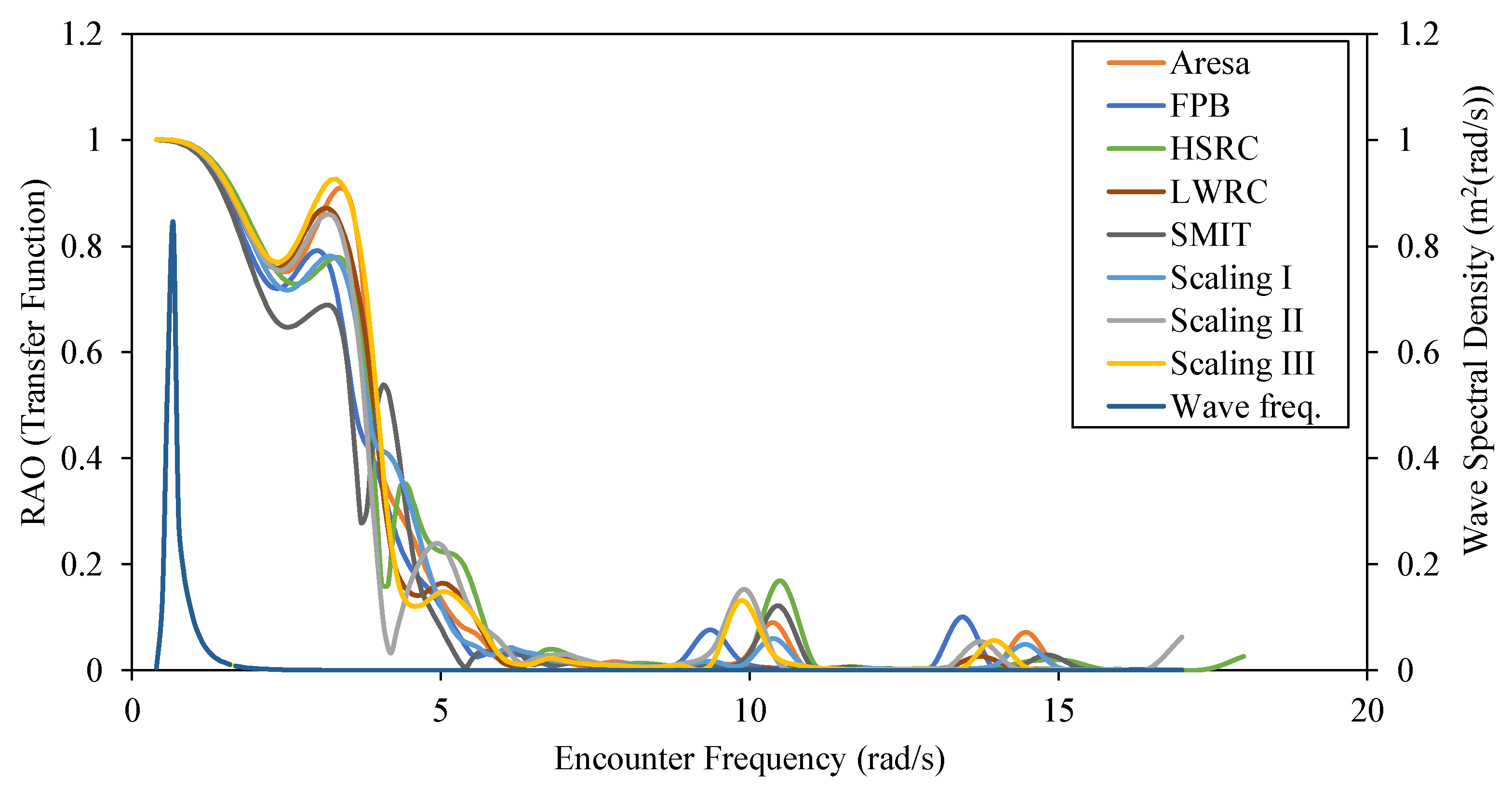
Figure 14.
RAO rolling motion graph for regression and scale models.
Figure 14.
RAO rolling motion graph for regression and scale models.
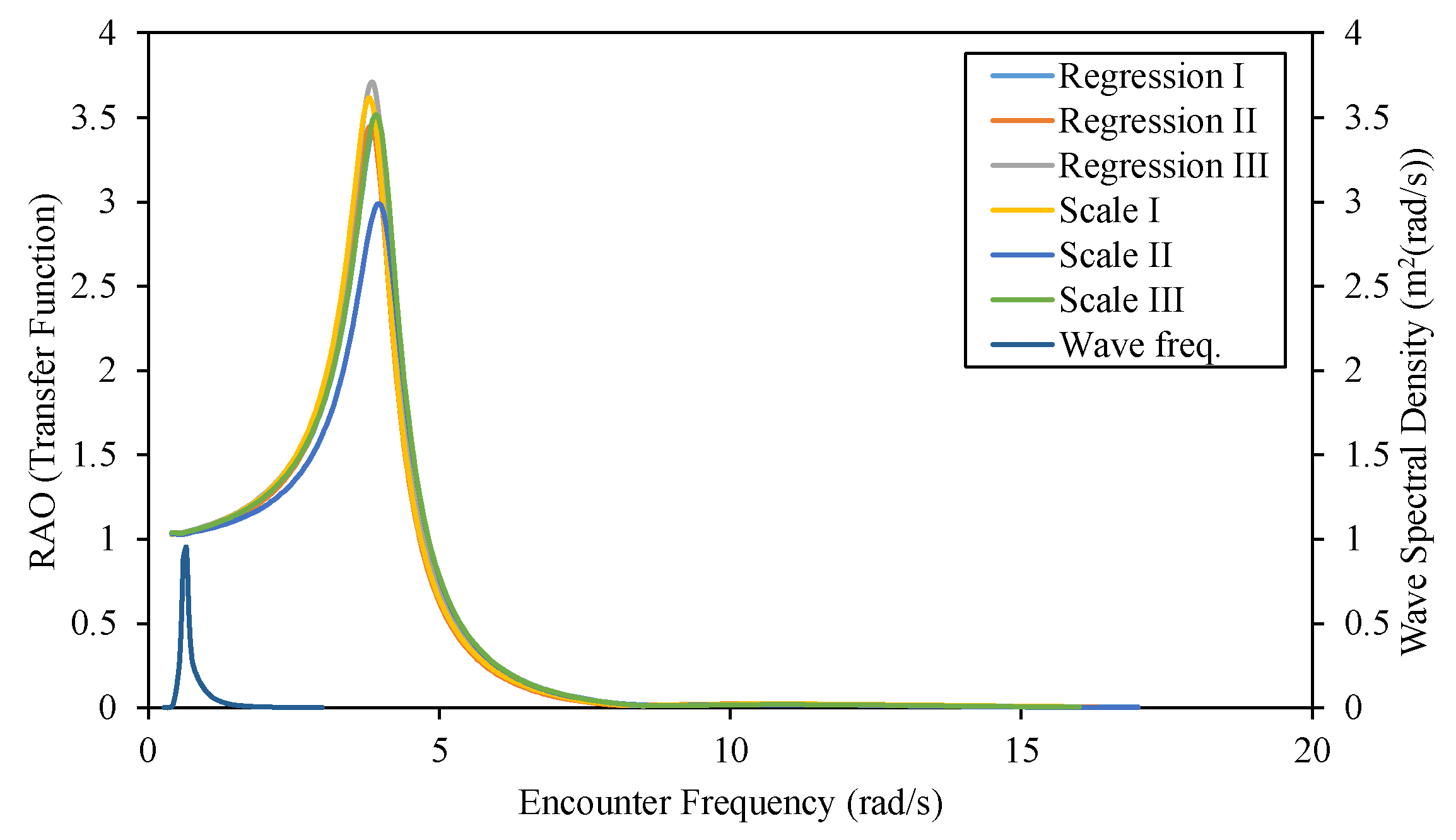
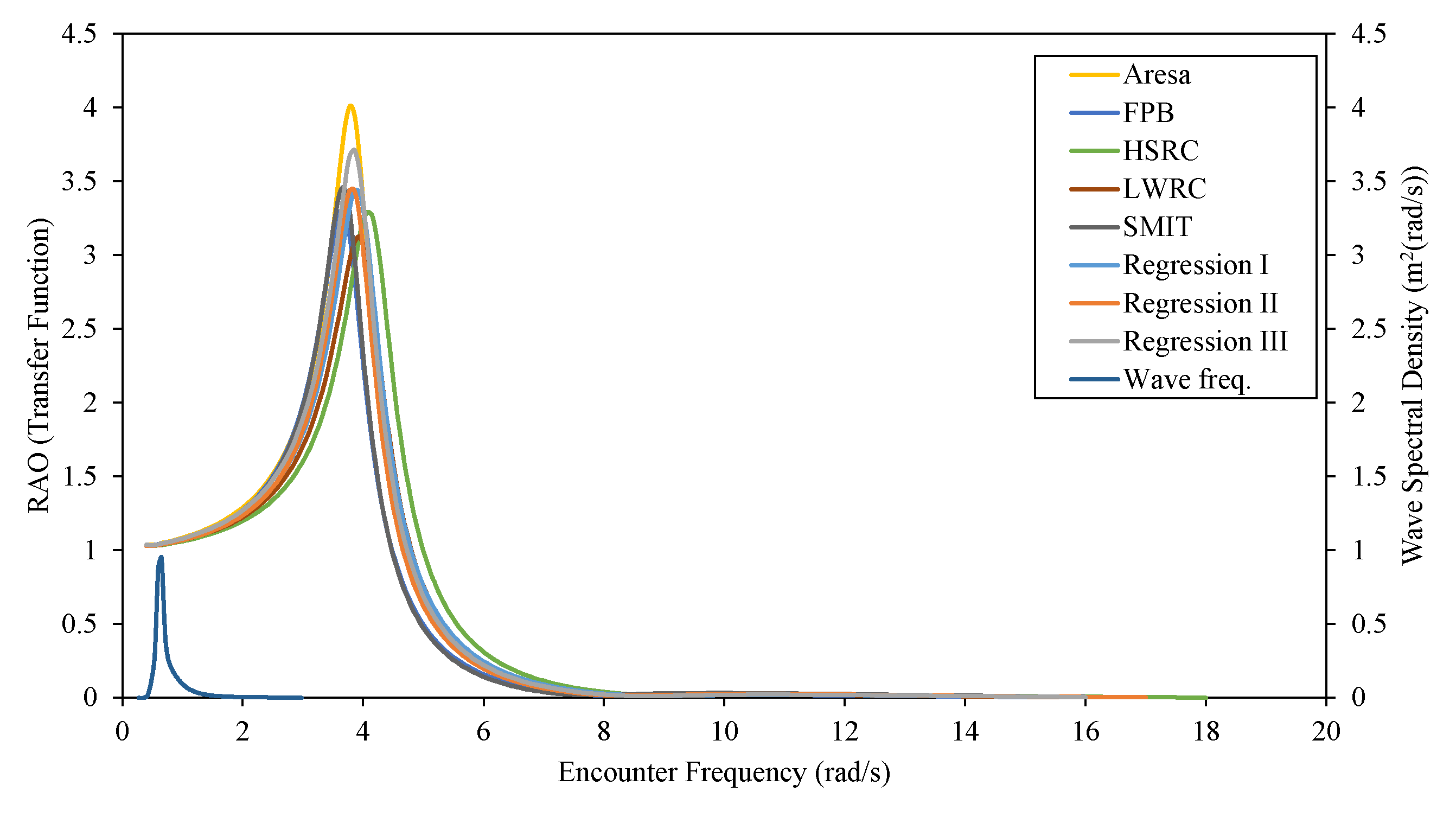
Figure 15.
Graph of RAO pitching motion for regression and scale models.
Figure 15.
Graph of RAO pitching motion for regression and scale models.
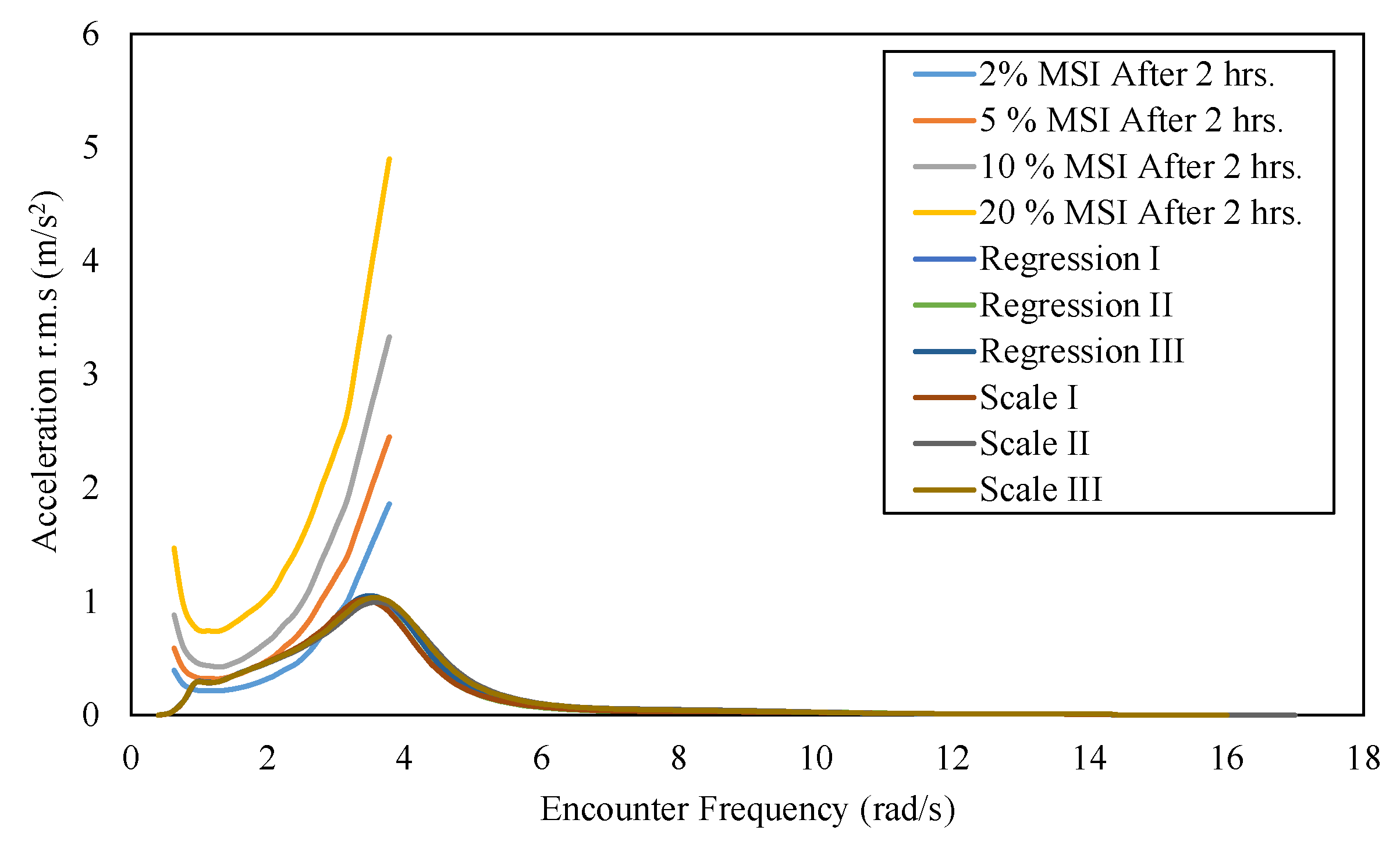
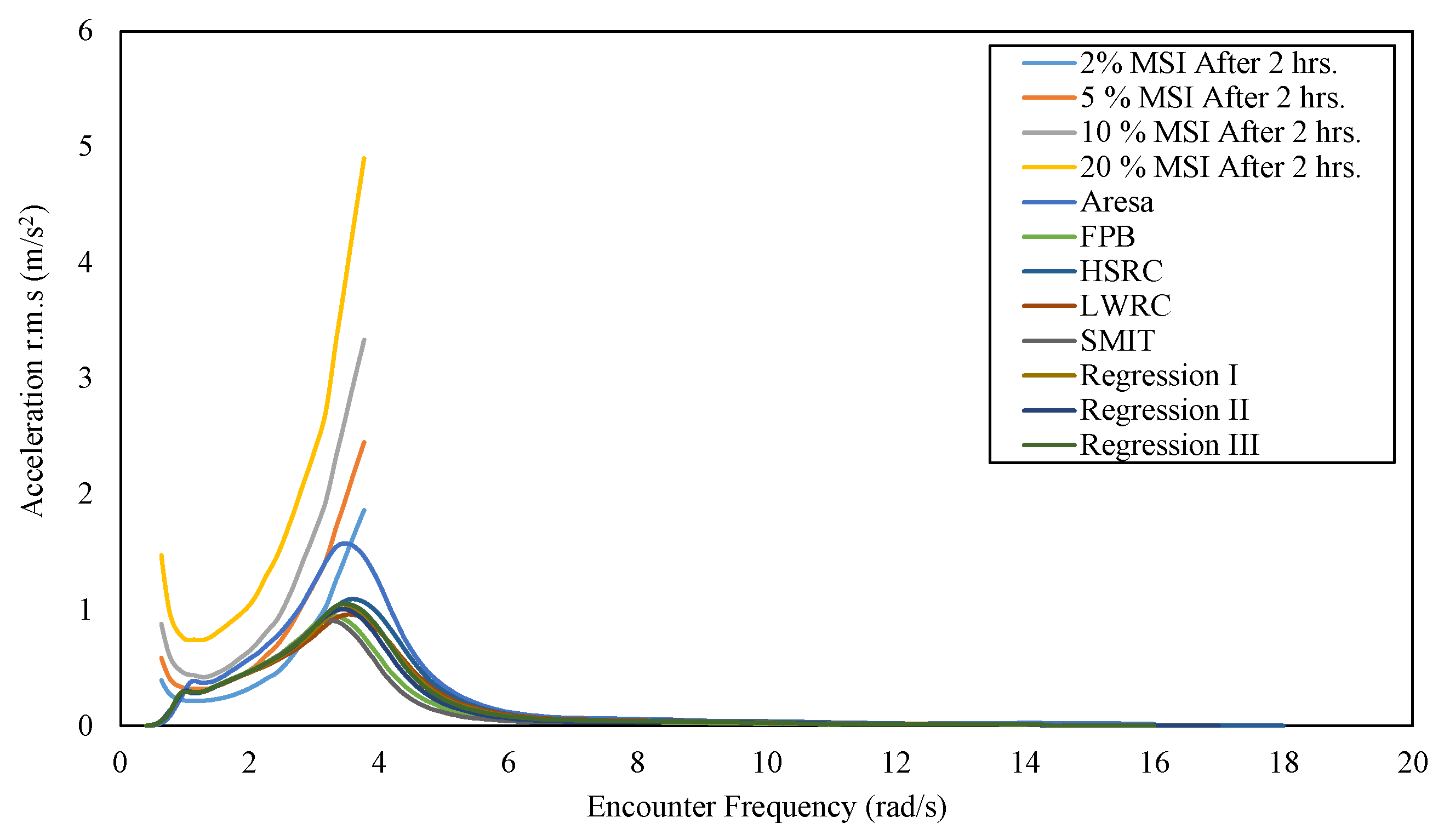
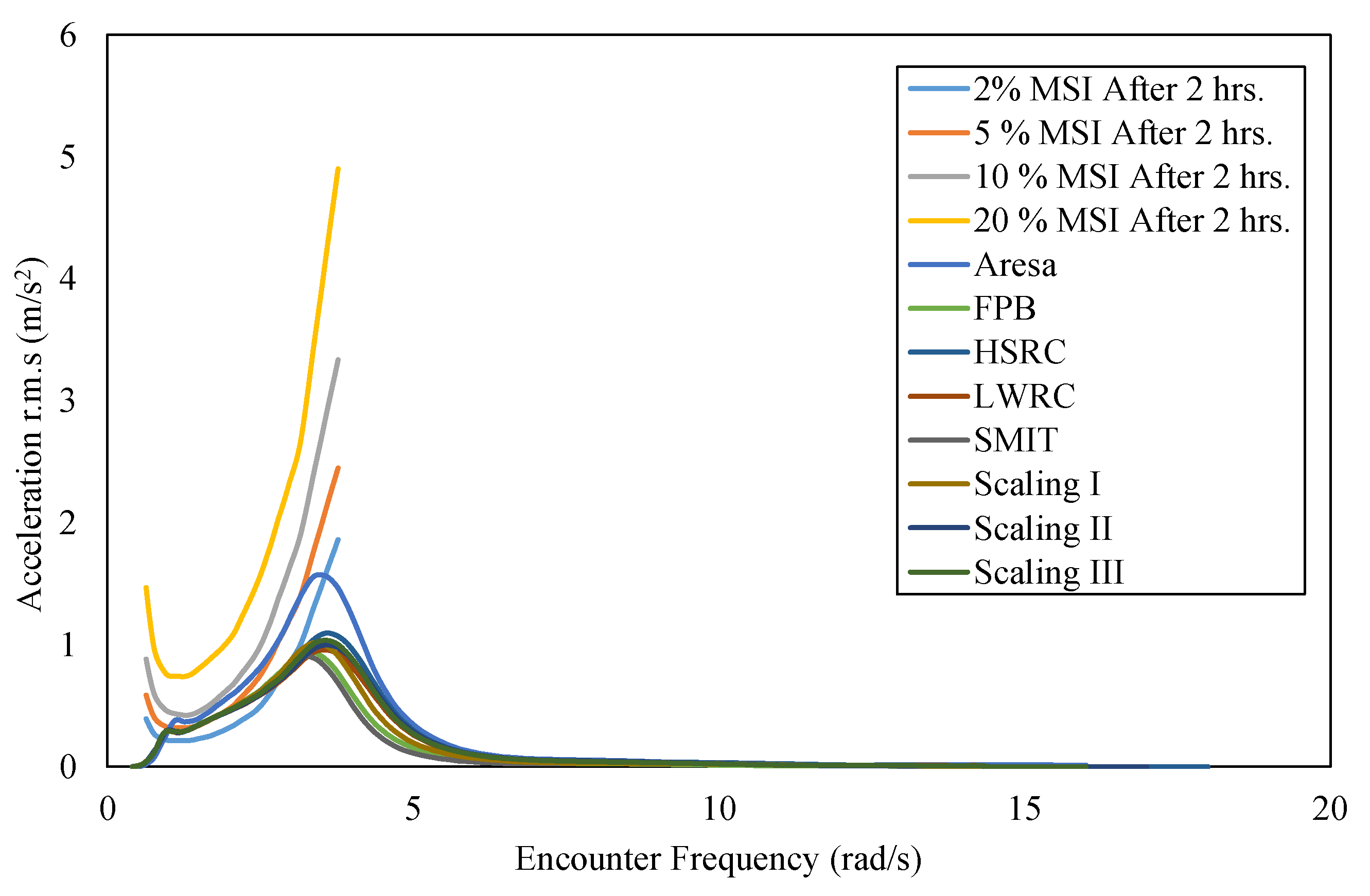
Figure 16.
MSI graph for regression and scale models.
Figure 16.
MSI graph for regression and scale models.
Figure 17.
Comparison between regression models and reference ships: (a) Froude number with resistance; (b) Froude number with power.
Figure 17.
Comparison between regression models and reference ships: (a) Froude number with resistance; (b) Froude number with power.
Figure 18.
Comparison of GZ values with the ship’s tilt angle between regression models and reference ships.
Figure 18.
Comparison of GZ values with the ship’s tilt angle between regression models and reference ships.
Figure 19.
RAO heaving motion graph for regression models and reference ships.
Figure 19.
RAO heaving motion graph for regression models and reference ships.
Figure 20.
RAO rolling motion graph for regression models and reference ships.
Figure 20.
RAO rolling motion graph for regression models and reference ships.
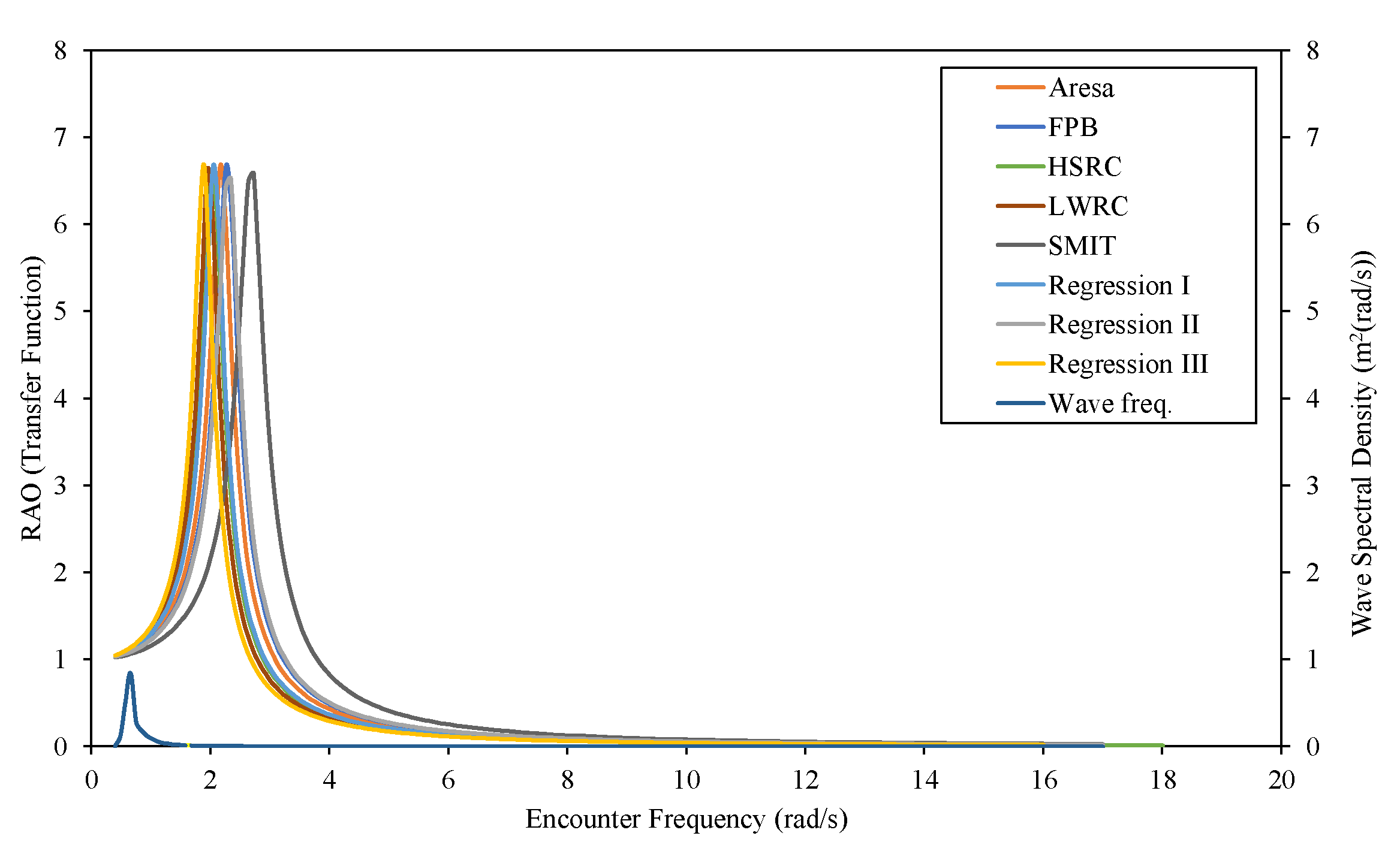
Figure 21.
RAO pitching motion graph for regression models and reference ships.
Figure 21.
RAO pitching motion graph for regression models and reference ships.
Figure 22.
MSI graph for regression models and reference ships.
Figure 22.
MSI graph for regression models and reference ships.
Figure 23.
Comparison between scaled and reference ship models: (a) Froude number with resistance; (b) Froude number with power.
Figure 23.
Comparison between scaled and reference ship models: (a) Froude number with resistance; (b) Froude number with power.
Figure 24.
Comparison of GZ values with ship’s tilt angle for scaling models and reference ships.
Figure 24.
Comparison of GZ values with ship’s tilt angle for scaling models and reference ships.
Figure 25.
RAO heaving motion graph for scaling models and reference ships.
Figure 25.
RAO heaving motion graph for scaling models and reference ships.
Figure 26.
RAO rolling motion graph for scaling models and reference ships.
Figure 26.
RAO rolling motion graph for scaling models and reference ships.
Figure 27.
RAO pitching motion graph for scaling models and reference ships.
Figure 27.
RAO pitching motion graph for scaling models and reference ships.
Figure 28.
MSI graph for scaling models and reference ships.
Figure 28.
MSI graph for scaling models and reference ships.
Table 1.
Primary data on reference patrol boats.
Table 1.
Primary data on reference patrol boats.
| Parameter | Type of Hull |
|---|
| High-Speed Rescue Craft (12 m) | SMIT Patrol Boat | Lightweight Rescue Craft (13 m) | Fast
Police Boat (15 m) | Aresa 1300 Sentinel RHIB |
|---|
| DWT (t) | 3.200 | 2.300 | 3.000 | 2.500 | 2.100 |
| LOA (m) | 11.700 | 13.200 | 13.700 | 14.950 | 13.200 |
| Beam (m) | 4.200 | 4.100 | 4.200 | 4.100 | 3.600 |
| Depth (m) | 1.600 | 1.600 | 1.600 | 1.940 | 1.820 |
| Draft (m) | 0.700 | 0.700 | 0.700 | 0.850 | 0.800 |
| LWL (m) | 11.296 | 11.490 | 12.840 | 13.702 | 11.921 |
| Cb (-) | 0.435 | 0.530 | 0.435 | 0.421 | 0.454 |
| Displacement (t) | 10.910 | 17.270 | 13.010 | 18.930 | 14.560 |
Table 2.
Primary data of new patrol boat designs.
Table 2.
Primary data of new patrol boat designs.
| Parameter | Value |
|---|
| DWT (t) | 2.60 |
| LOA (m) | 13.37 |
| Beam (m) | 4.032 |
| Depth (m) | 1.715 |
| Draft (m) | 0.751 |
Table 3.
Details of main dimensions of patrol boats from regression method.
Table 3.
Details of main dimensions of patrol boats from regression method.
| Parameter | Model |
|---|
| Regression I | Regression II | Regression III |
|---|
| DWT (t) | 2.600 | 2.600 | 2.600 |
| LOA (m) | 13.370 | 13.370 | 13.370 |
| Beam (m) | 4.031 | 4.031 | 4.031 |
| Depth (m) | 1.715 | 1.715 | 1.715 |
| Draft (m) | 0.751 | 0.751 | 0.751 |
| LWL (m) | 11.967 | 12.042 | 12.393 |
| Cb (-) | 0.451 | 0.459 | 0.461 |
| Displacement (t) | 13.120 | 14.700 | 14.170 |
Table 4.
Results of reference ship resistance analysis.
Table 4.
Results of reference ship resistance analysis.
| Froude Number | Resistance (kN) | Effective Power (kW) |
|---|
| Aresa | FPB | HSRC | LWRC | SMIT | Aresa | FPB | HSRC | LWRC | SMIT |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 28.44 | 31.86 | 15.26 | 18.90 | 19.60 | 363.65 | 436.30 | 189.30 | 214.15 | 249.07 |
| 1.5 | 26.59 | 31.38 | 18.22 | 21.60 | 26.52 | 507.71 | 645.75 | 339.06 | 363.24 | 497.49 |
| 2 | 28.44 | 35.49 | 22.39 | 26.40 | 34.65 | 725.00 | 971.91 | 555.61 | 593.96 | 870.22 |
| 2.5 | 33.82 | 43.95 | 28.93 | 34.10 | 45.80 | 1077.20 | 1502.97 | 897.49 | 959.23 | 1434.57 |
| 3 | 41.85 | 56.08 | 37.46 | 44.30 | 60.09 | 1598.98 | 2308.20 | 1391.57 | 1492.36 | 2254.81 |
Table 5.
Details of primary dimensions of patrol boats from scale method.
Table 5.
Details of primary dimensions of patrol boats from scale method.
| Parameter | Model |
|---|
| Scale I | Scale II | Scale III |
|---|
| DWT (t) | 2.600 | 2.600 | 2.600 |
| LOA (m) | 13.370 | 13.370 | 13.370 |
| Beam (m) | 4.031 | 4.031 | 4.031 |
| Depth (m) | 1.715 | 1.715 | 1.715 |
| Draft (m) | 0.751 | 0.751 | 0.751 |
| LWL (m) | 12.027 | 12.909 | 12.535 |
| Cb (-) | 0.454 | 0.436 | 0.435 |
| Displacement (t) | 15.040 | 12.810 | 13.120 |
Table 6.
Comparison of resistance values in regression method and scaling method.
Table 6.
Comparison of resistance values in regression method and scaling method.
| Froude Number | Resistance (kN) |
|---|
| Regression I | Regression II | Regression III | Scale I | Scale II | Scale III |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0 | 0 | 0 | 0 | 8.70 | 11.50 |
| 1 | 23.62 | 22.96 | 23.57 | 23.90 | 16.70 | 19.60 |
| 1.5 | 22.05 | 23.02 | 23.10 | 25.50 | 22.30 | 22.20 |
| 2 | 23.96 | 26.13 | 25.73 | 29.90 | 28.30 | 26.40 |
| 2.5 | 28.97 | 32.67 | 31.60 | 37.40 | 36.90 | 33.50 |
| 3 | 36.29 | 41.63 | 39.98 | 47.80 | 48.00 | 43.10 |
Table 7.
Comparison of power values in regression method and scaling method.
Table 7.
Comparison of power values in regression method and scaling method.
| Froude Number | Power (kW) |
|---|
| Regression I | Regression II | Regression III | Scale I | Scale II | Scale III |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0 | 0 | 0 | 0 | 49.88 | 64.32 |
| 1 | 303.72 | 295.26 | 306.74 | 264.79 | 189.14 | 219.43 |
| 1.5 | 423.79 | 442.28 | 450.94 | 416.81 | 376.61 | 370.75 |
| 2 | 612.77 | 668.17 | 669.67 | 653.59 | 636.48 | 588,13 |
| 2.5 | 924.89 | 1048.07 | 1028.11 | 1018.44 | 1040.17 | 931.76 |
| 3 | 1389.25 | 1600.05 | 1560.83 | 1558.96 | 1619.79 | 1435.34 |
Table 8.
Values of ship stability in regression and scaling models.
Table 8.
Values of ship stability in regression and scaling models.
| Model | Stability |
|---|
| GZ (m) | Max Heel Angle (deg) | Area Under GZ Curve (m.deg) | Angle of Vanishing Point (deg) |
|---|
| Regression I | 0.533 | 44.500 | 30.280 | 91.834 |
| Regression II | 0.587 | 41.800 | 33.780 | 90.856 |
| Regression III | 0.479 | 43.600 | 26.590 | 90.978 |
| Scale I | 0.547 | 33.600 | 30.650 | 89.020 |
| Scale II | 0.554 | 43.600 | 31.350 | 92.549 |
| Scale III | 0.478 | 44.500 | 26.570 | 91.765 |
Table 9.
Probabilities of slamming and deck wetness in regression and scale models.
Table 9.
Probabilities of slamming and deck wetness in regression and scale models.
| No. | Criteria | Regression I | Regression II | Regression III | Scale I | Scale II | Scale III |
|---|
| 1 | Deck Wetness (MII/h) | 0.114 | 0.073 | 0.150 | 0.329 | 0.158 | 0.150 |
| 2 | Slamming (MII/h) | 0.536 | 0.426 | 0.570 | 0.455 | 0.502 | 0.450 |
Table 10.
Comparison of resistance values between regression method and reference ships.
Table 10.
Comparison of resistance values between regression method and reference ships.
| Froude Number | Resistance (kN) |
|---|
| Aresa | FPB | HSRC | LWRC | SMIT | Regression I | Regression II | Regression III |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 28.44 | 31.86 | 15.26 | 18.90 | 19.60 | 23.62 | 22.96 | 23.57 |
| 1.5 | 26.59 | 31.38 | 18.22 | 21.60 | 26.52 | 22.05 | 23.02 | 23.10 |
| 2 | 28.44 | 35.49 | 22.39 | 26.40 | 34.65 | 23.96 | 26.13 | 25.73 |
| 2.5 | 33.82 | 43.95 | 28.93 | 34.10 | 45.80 | 28.97 | 32.67 | 31.60 |
| 3 | 41.85 | 56.08 | 37.46 | 44.30 | 60.09 | 36.29 | 41.63 | 39.98 |
Table 11.
Comparison of power values between regression method and reference ships.
Table 11.
Comparison of power values between regression method and reference ships.
| Froude Number | Power (kW) |
|---|
| Aresa | FPB | HSRC | LWRC | SMIT | Regression I | Regression II | Regression III |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 363.65 | 436.30 | 189.30 | 214.15 | 249.07 | 303.72 | 295.26 | 306.74 |
| 1.5 | 507.71 | 645.75 | 339.06 | 363.244 | 497.49 | 423.79 | 442.28 | 450.94 |
| 2 | 725.00 | 971.91 | 555.61 | 593.962 | 870.22 | 612.77 | 668.17 | 669.67 |
| 2.5 | 1077.20 | 1502.97 | 897.49 | 959.234 | 1434.57 | 924.89 | 1048.07 | 1028.11 |
| 3 | 1598.98 | 2308.20 | 1391.57 | 1492.36 | 2254.81 | 1389.25 | 1600.05 | 1560.83 |
Table 12.
Values of ship stability for regression models and reference ships.
Table 12.
Values of ship stability for regression models and reference ships.
| Model | Stability |
|---|
| GZ (m) | Max Heel Angle (deg) | Area Under GZ Curve (m.deg) | Angle of Vanishing Point (deg) |
|---|
| ARESA | 0.441 | 35.500 | 24.650 | 89.216 |
| FPB | 0.540 | 44.500 | 31.960 | 92.048 |
| HSRC | 0.648 | 40.900 | 36.800 | 91.765 |
| LWRC | 0.561 | 42.700 | 31.300 | 91.373 |
| SMIT | 0.737 | 36.400 | 42.640 | 90.000 |
| Regression I | 0.533 | 44.500 | 30.280 | 91.834 |
| Regression II | 0.587 | 41.800 | 33.780 | 90.856 |
| Regression III | 0.479 | 43.600 | 26.590 | 90.978 |
Table 13.
Probabilities of slamming and deck wetness for regression models and reference ships.
Table 13.
Probabilities of slamming and deck wetness for regression models and reference ships.
| No | Criteria | Aresa | FPB | HSRC | LWRC | SMIT | Regression I | Regression II | Regression III |
|---|
| 1 | Deck Wetness (MII/h) | 0.362 | 0.046 | 0.178 | 0.124 | 0.426 | 0.114 | 0.073 | 0.15 |
| 2 | Slamming (MII/h) | 0.510 | 0.371 | 0.557 | 0.621 | 1.9 | 0.536 | 0.426 | 0.57 |
Table 14.
Comparison of resistance values between scaling methods and reference ships.
Table 14.
Comparison of resistance values between scaling methods and reference ships.
| Froude Number | Resistance (kN) |
|---|
| ARESA | FPB | HSRC | LWRC | SMIT | Scaling I | Scaling II | Scaling III |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 8.70 | 11.50 |
| 1 | 28.44 | 31.86 | 15.26 | 18.90 | 19.60 | 23.90 | 16.70 | 19.60 |
| 1.5 | 26.59 | 31.38 | 18.22 | 21.60 | 26.52 | 25.50 | 22.30 | 22.20 |
| 2 | 28.44 | 35.49 | 22.39 | 26.40 | 34.65 | 29.90 | 28.30 | 26.40 |
| 2.5 | 33.82 | 43.95 | 28.93 | 34.10 | 45.80 | 37.40 | 36.90 | 33.50 |
| 3 | 41.85 | 56.08 | 37.46 | 44.30 | 60.09 | 47.80 | 48.00 | 43.10 |
Table 15.
Comparison of power values between scaling methods and reference ships.
Table 15.
Comparison of power values between scaling methods and reference ships.
| Froude Number | Power (kW) |
|---|
| ARESA | FPB | HSRC | LWRC | SMIT | Scale I | Scale II | Scale III |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 49.88 | 64.32 |
| 1 | 363.65 | 436.30 | 189.30 | 214.15 | 249.07 | 264.79 | 189.14 | 219.43 |
| 1.5 | 507.71 | 645.75 | 339.06 | 363.24 | 497.49 | 416.81 | 376.61 | 370.75 |
| 2 | 725.00 | 971.91 | 555.61 | 593.96 | 870.22 | 653.59 | 636.48 | 588.13 |
| 2.5 | 1077.20 | 1502.97 | 897.49 | 959.23 | 1434.57 | 1018.44 | 1040.17 | 931.76 |
| 3 | 1598.98 | 2308. 20 | 1391.57 | 1492.36 | 2254.81 | 1558.96 | 1619.78 | 1435.34 |
Table 16.
Values of ship stability in scaling models and reference ships.
Table 16.
Values of ship stability in scaling models and reference ships.
| Model | Stability Parameter |
|---|
| Gz (m) | Max Heel Angle (deg) | Area Under GZ Curve (m.deg) | Angle of Vanishing Point (deg) |
|---|
| ARESA | 0.441 | 35.500 | 24.650 | 89.216 |
| FPB | 0.540 | 44.500 | 31.960 | 92.048 |
| HSRC | 0.648 | 40.900 | 36.800 | 91.765 |
| LWRC | 0.561 | 42.700 | 31.300 | 91.373 |
| SMIT | 0.737 | 36.400 | 42.640 | 90.000 |
| Scale I | 0.547 | 33.600 | 30.650 | 89.020 |
| Scale II | 0.554 | 43.600 | 31.350 | 92.549 |
| Scale III | 0.478 | 44.500 | 26.570 | 91.765 |
Table 17.
Probabilities of slamming and deck wetness for regression models and reference ships.
Table 17.
Probabilities of slamming and deck wetness for regression models and reference ships.
| Criteria | ARESA | FPB | HSRC | LWRC | SMIT | Scale I | Scale II | Scale III |
|---|
| Deck Wetness (MII/h) | 0.362 | 0.046 | 0.178 | 0.124 | 0.426 | 0.329 | 0.158 | 0.150 |
| Slamming (MII/h) | 0.510 | 0.371 | 0.557 | 0.621 | 1.900 | 0.455 | 0.502 | 0.450 |
Table 18.
Recapitulation of resistance analysis results.
Table 18.
Recapitulation of resistance analysis results.
| Method | Model | Resistance (Fn = 3) |
|---|
| Resistance (kN) | Power (kW) |
|---|
| Reference Ship | Aresa | 41.85 | 1598.98 |
| FPB | 56.08 | 2308.20 |
| HSRC | 37.46 | 1391.57 |
| LWRC | 44.30 | 1492.36 |
| SMIT | 60.09 | 2254.81 |
| Regression | Regression I | 36.29 | 1389.25 |
| Regression II | 41.63 | 1600.05 |
| Regression III | 39.98 | 1560.83 |
| Scaling | Scale I | 47.80 | 1558.97 |
| Scale II | 48.00 | 1619.79 |
| Scale III | 43.10 | 1435.34 |
Table 19.
Percentages of resistance similarities between regression models and reference models.
Table 19.
Percentages of resistance similarities between regression models and reference models.
| Model Comparison | Similarity (%) |
|---|
| Resistance |
|---|
| Regression I | Aresa | 86.714 |
| FPB | 64.711 |
| HSRC | 96.877 |
| LWRC | 81.919 |
| SMIT | 60.393 |
| Regression II | Aresa | 99.474 |
| FPB | 74.233 |
| HSRC | 89.983 |
| LWRC | 93.973 |
| SMIT | 69.279 |
| Regression III | Aresa | 95.532 |
| FPB | 71.291 |
| HSRC | 93.697 |
| LWRC | 90.248 |
| SMIT | 66.534 |
| MAX | 99.474 |
| MIN | 60.393 |
| AVERAGE | 82.324 |
Table 20.
Percentages of resistance similarities between scale models and reference models.
Table 20.
Percentages of resistance similarities between scale models and reference models.
| Model Comparison | Similarity (%) |
|---|
| Resistance |
|---|
| Scale I | Aresa | 87.552 |
| FPB | 85.235 |
| HSRC | 78.368 |
| LWRC | 92.678 |
| SMIT | 79.547 |
| Scale II | Aresa | 87.188 |
| FPB | 85.592 |
| HSRC | 78.042 |
| LWRC | 92.292 |
| SMIT | 79.880 |
| Scale III | Aresa | 97.100 |
| FPB | 76.854 |
| HSRC | 86.914 |
| LWRC | 97.291 |
| SMIT | 71.726 |
| MAX | 97.291 |
| MIN | 71.726 |
| AVERAGE | 85.084 |
Table 21.
Colour indicators in tables of similarity resistances between models.
Table 21.
Colour indicators in tables of similarity resistances between models.
| Colour | Description |
|---|
| | Larger scale model |
| | Larger regression model |
| | Larger reference model |
Table 22.
Recapitulation of stability analysis results.
Table 22.
Recapitulation of stability analysis results.
| Method | Model | Stability |
|---|
| Gz (m) | Max Heel Angle (deg) | Area Under GZ Curve (m.deg) | Angle of Vanishing Point (deg) |
|---|
| Reference Ship | Aresa | 0.441 | 35.5 | 24.65 | 89.216 |
| FPB | 0.540 | 44.5 | 31.96 | 92.048 |
| HSRC | 0.648 | 40.9 | 36.80 | 91.765 |
| LWRC | 0.561 | 42.7 | 31.30 | 91.373 |
| SMIT | 0.737 | 36.4 | 42.64 | 90.000 |
| Regression | Regression I | 0.533 | 44.5 | 30.28 | 91.834 |
| Regression II | 0.587 | 41.8 | 33.78 | 90.856 |
| Regression III | 0.479 | 43.6 | 26.59 | 90.978 |
| Scaling | Scale I | 0.547 | 33.6 | 30.65 | 89.020 |
| Scale II | 0.554 | 43.6 | 31.35 | 92.549 |
| Scale III | 0.478 | 44.5 | 26.57 | 91.765 |
Table 23.
Percentages of similarity stability between regression models and reference models.
Table 23.
Percentages of similarity stability between regression models and reference models.
| Model Comparison | Similarity (%) |
|---|
| Surface Area under Curve |
|---|
| Regression I | Aresa | 81.407 |
| FPB | 94.743 |
| HSRC | 82.283 |
| LWRC | 96.741 |
| SMIT | 71.013 |
| Regression II | Aresa | 72.972 |
| FPB | 94.612 |
| HSRC | 91.793 |
| LWRC | 92.658 |
| SMIT | 79.221 |
| Regression III | Aresa | 92.704 |
| FPB | 83.198 |
| HSRC | 72.255 |
| LWRC | 84.952 |
| SMIT | 62.359 |
| MAX | 96.741 |
| MIN | 62.359 |
| AVERAGE | 83.528 |
Table 24.
Percentages of similarity stability between scale models and reference models.
Table 24.
Percentages of similarity stability between scale models and reference models.
| Model Comparison | Similarity (%) |
|---|
| Surface Area under Curve |
|---|
| Scale I | Aresa | 80.424 |
| FPB | 95.901 |
| HSRC | 83.288 |
| LWRC | 97.923 |
| SMIT | 71.881 |
| Scale II | Aresa | 78.628 |
| FPB | 98.091 |
| HSRC | 85.190 |
| LWRC | 99.841 |
| SMIT | 73.523 |
| Scale III | Aresa | 92.774 |
| FPB | 83.135 |
| HSRC | 72.201 |
| LWRC | 84.888 |
| SMIT | 62.312 |
| MAX | 99.841 |
| MIN | 62.312 |
| AVERAGE | 84.000 |
Table 25.
Colour indicators in the stability similarity tables between models.
Table 25.
Colour indicators in the stability similarity tables between models.
| Colour | Description |
|---|
| | Larger scale model |
| | Larger regression model |
| | Larger reference model |
Table 26.
Recapitulation of seakeeping analysis results.
Table 26.
Recapitulation of seakeeping analysis results.
| Method | Model | Seakeeping |
|---|
Heaving
(m/m) | Rolling
(rad/rad) | Pitching
(rad/rad) | MSI
(%) | Deck Wetness
(MII/h) | Slamming
(MII/h) |
|---|
| Reference Ship | Aresa | 1.001 | 6.682 | 4.014 | 5.00 | 0.362 | 0.510 |
| FPB | 1.001 | 6.683 | 3.301 | 5.00 | 0.046 | 0.371 |
| HSRC | 1.001 | 6.562 | 3.288 | 5.00 | 0.178 | 0.557 |
| LWRC | 1.001 | 6.637 | 3.125 | 5.00 | 0.124 | 0.621 |
| SMIT | 1.000 | 6.576 | 3.460 | 5.00 | 0.426 | 1.900 |
| Regression | Regression I | 1.001 | 6.679 | 3.433 | 5.00 | 0.114 | 0.536 |
| Regression II | 1.001 | 6.516 | 3.440 | 5.00 | 0.073 | 0.426 |
| Regression III | 1.001 | 6.679 | 3.708 | 5.00 | 0.150 | 0.570 |
| Scaling | Scale I | 1.001 | 6.584 | 3.616 | 5.00 | 0.329 | 0.455 |
| Scale II | 1.001 | 6.629 | 2.984 | 5.00 | 0.158 | 0.502 |
| Scale III | 1.001 | 6.506 | 3.513 | 5.00 | 0.150 | 0.450 |
Table 27.
Percentages of seakeeping similarity between regression models and reference models.
Table 27.
Percentages of seakeeping similarity between regression models and reference models.
| Model Comparison | Similarity (%) |
|---|
| Heaving | Rolling | Pitching |
|---|
| Regression I | Aresa | 99.973 | 99.960 | 85.516 |
| FPB | 99.978 | 99.948 | 96.156 |
| HSRC | 99.994 | 98.237 | 95.798 |
| LWRC | 99.994 | 99.200 | 86.415 |
| SMIT | 99.971 | 98.448 | 99.200 |
| Regression II | Aresa | 99.976 | 97.513 | 85.707 |
| FPB | 99.981 | 97.501 | 95.941 |
| HSRC | 99.997 | 99.303 | 95.584 |
| LWRC | 99.986 | 98.169 | 90.841 |
| SMIT | 99.969 | 99.090 | 99.422 |
| Regression III | Aresa | 99.986 | 99.961 | 92.390 |
| FPB | 99.991 | 99.949 | 89.001 |
| HSRC | 99.994 | 98.236 | 88.670 |
| LWRC | 99.995 | 99.370 | 84.270 |
| SMIT | 99.959 | 98.447 | 93.306 |
| MAX | 99.997 | 99.961 | 99.422 |
| MIN | 99.959 | 97.501 | 84.270 |
| AVERAGE | 99.983 | 98.889 | 91.881 |
Table 28.
Percentages of seakeeping similarity between scale models and reference models.
Table 28.
Percentages of seakeeping similarity between scale models and reference models.
| Model Comparison | Similarity (%) |
|---|
| Heaving | Rolling | Pitching |
|---|
| Scale I | Aresa | 99.985 | 98.537 | 90.096 |
| FPB | 99.990 | 98.525 | 91.267 |
| HSRC | 99.995 | 99.655 | 90.927 |
| LWRC | 99.994 | 99.200 | 86.415 |
| SMIT | 99.960 | 99.870 | 95.681 |
| Scale II | Aresa | 99.997 | 99.210 | 74.337 |
| FPB | 99.992 | 99.198 | 90.403 |
| HSRC | 99.977 | 98.979 | 90.741 |
| LWRC | 99.988 | 99.878 | 95.479 |
| SMIT | 99.942 | 99.192 | 86.232 |
| Scale III | Aresa | 99.995 | 97.370 | 87.527 |
| FPB | 100.000 | 97.358 | 93.946 |
| HSRC | 99.985 | 99.157 | 93.596 |
| LWRC | 99.996 | 98.025 | 88.952 |
| SMIT | 99.950 | 98.944 | 98.490 |
| MAX | 100.000 | 99.878 | 98.490 |
| MIN | 99.942 | 97.358 | 74.337 |
| AVERAGE | 99.983 | 98.873 | 90.273 |
Table 29.
Colour indicators in seakeeping similarity tables between models.
Table 29.
Colour indicators in seakeeping similarity tables between models.
| Colour | Description |
|---|
| | Larger scale model |
| | Larger regression model |
| | Larger reference model |
| | Same value |
Table 30.
Percentages of similarity for regression and scaling models vs. reference model.
Table 30.
Percentages of similarity for regression and scaling models vs. reference model.
| Criteria | Similarity |
|---|
| Regression vs. Reference Ship | Scale vs. Reference Ship |
|---|
| Resistance | Stability | Seakeeping | Resistance | Stability | Seakeeping |
|---|
| MAX | 99.474 | 96.741 | 99.793 | 97.291 | 99.841 | 99.456 |
| MIN | 60.393 | 62.359 | 93.910 | 71.726 | 62.312 | 90.546 |
| AVERAGE | 82.324 | 83.528 | 96.918 | 85.084 | 84.000 | 96.376 |
Table 31.
Weights of primary criteria.
Table 31.
Weights of primary criteria.
| Criterion | Description | Weight |
|---|
| C1 | Resistance | 50% |
| C2 | Stability | 30% |
| C3 | Seakeeping | 20% |
Table 32.
Alternative design models.
Table 32.
Alternative design models.
| Alternative | Description |
|---|
| A1 | Aresa 1300 Sentinel |
| A2 | Fast Police Boat |
| A3 | High-Speed Rescue Craft |
| A4 | Lightweight Rescue Craft |
| A5 | SMIT Patrol Boat |
| A6 | Regression I |
| A7 | Regression II |
| A8 | Regression III |
| A9 | Scale I |
| A10 | Scale II |
| A11 | Scale III |
Table 33.
Data criteria for simulation results of design models.
Table 33.
Data criteria for simulation results of design models.
| Alternative Model | Criteria |
|---|
| C1 | C2 | C3 |
|---|
| A1 | 41.850 | 24.650 | 3.898 |
| A2 | 56.080 | 31.960 | 3.661 |
| A3 | 37.460 | 36.800 | 3.616 |
| A4 | 44.300 | 31.300 | 3.587 |
| A5 | 60.090 | 42.640 | 3.678 |
| A6 | 36.290 | 30.280 | 3.704 |
| A7 | 41.630 | 33.780 | 3.652 |
| A8 | 39.980 | 26.590 | 3.796 |
| A9 | 47.800 | 30.650 | 3.733 |
| A10 | 48.000 | 31.350 | 3.537 |
| A11 | 43.100 | 26.570 | 3.673 |
Table 34.
MADM normalised data.
Table 34.
MADM normalised data.
| Normalisation |
|---|
| Alternative | C1 | C2 | C3 |
|---|
| A1 | 0.867 | 0.578 | 0.907 |
| A2 | 0.647 | 0.750 | 0.966 |
| A3 | 0.969 | 0.863 | 0.978 |
| A4 | 0.819 | 0.734 | 0.986 |
| A5 | 0.604 | 1.000 | 0.962 |
| A6 | 1.000 | 0.710 | 0.955 |
| A7 | 0.872 | 0.792 | 0.969 |
| A8 | 0.908 | 0.624 | 0.932 |
| A9 | 0.759 | 0.719 | 0.947 |
| A10 | 0.756 | 0.735 | 1.000 |
| A11 | 0.842 | 0.623 | 0.963 |
Table 35.
MADM weighted data.
Table 35.
MADM weighted data.
| Alternative | Criterion | Total Weight |
|---|
| C1 | C2 | C3 |
|---|
| A1 | 0.434 | 0.173 | 0.181 | 0.788 |
| A2 | 0.324 | 0.225 | 0.193 | 0.742 |
| A3 | 0.484 | 0.259 | 0.196 | 0.939 |
| A4 | 0.410 | 0.220 | 0.197 | 0.827 |
| A5 | 0.302 | 0.300 | 0.192 | 0.794 |
| A6 | 0.500 | 0.213 | 0.191 | 0.904 |
| A7 | 0.436 | 0.238 | 0.194 | 0.867 |
| A8 | 0.454 | 0.187 | 0.186 | 0.827 |
| A9 | 0.380 | 0.216 | 0.189 | 0.785 |
| A10 | 0.378 | 0.221 | 0.200 | 0.799 |
| A11 | 0.421 | 0.187 | 0.193 | 0.801 |
Table 36.
MADM ranking results.
Table 36.
MADM ranking results.
| Alternative Design | Total Weight | Ranking |
|---|
| A3 | 0.939 | 1 |
| A6 | 0.904 | 2 |
| A7 | 0.867 | 3 |
| A8 | 0.827 | 4 |
| A4 | 0.827 | 5 |
| A11 | 0.801 | 6 |
| A10 | 0.799 | 7 |
| A5 | 0.794 | 8 |
| A1 | 0.788 | 9 |
| A9 | 0.785 | 10 |
| A2 | 0.742 | 11 |
Table 37.
Details and time required for each method.
Table 37.
Details and time required for each method.
| Method | Process Details | Estimated Time (Minutes) |
|---|
| Reference Ship | Determining type of ship | 15 |
| Looking for primary data and shape of hull of five reference ships according to type of ship determined | 75 |
| Modelling five selected reference ships | 150 |
| Performing hydrodynamic analysis of entire hull of ship | 350 |
| Performing analysis results calculations | 200 |
| Total | 790 |
| Regression | Determining type of ship | 15 |
| Looking for primary data of five ships according to type of ship determined | 50 |
| Performing regression analysis calculations | 20 |
| Modelling three ships according to regression results with new geometry | 150 |
| Performing hydrodynamic analysis of three new hulls | 210 |
| Performing analysis results calculations | 120 |
| Total | 565 |
| Scaling | Determining type of ship | 15 |
| Looking for primary data and shape of hull of five reference ships according to type of ship determined | 75 |
| Modelling five selected reference ships | 150 |
| Analyzing resistance of entire hull until three hulls with lowest resistance values are selected | 100 |
| Defining new primary dimension | 20 |
| Performing scaling process with help of 3D modelling software on three selected ships according to new size | 30 |
| Performing hydrodynamic analyses of three new hulls | 210 |
| Performing analysis results calculations | 120 |
| Total | 720 |