A New Off-Board Electrical Vehicle Battery Charger: Topology, Analysis and Design
Abstract
:1. Introduction
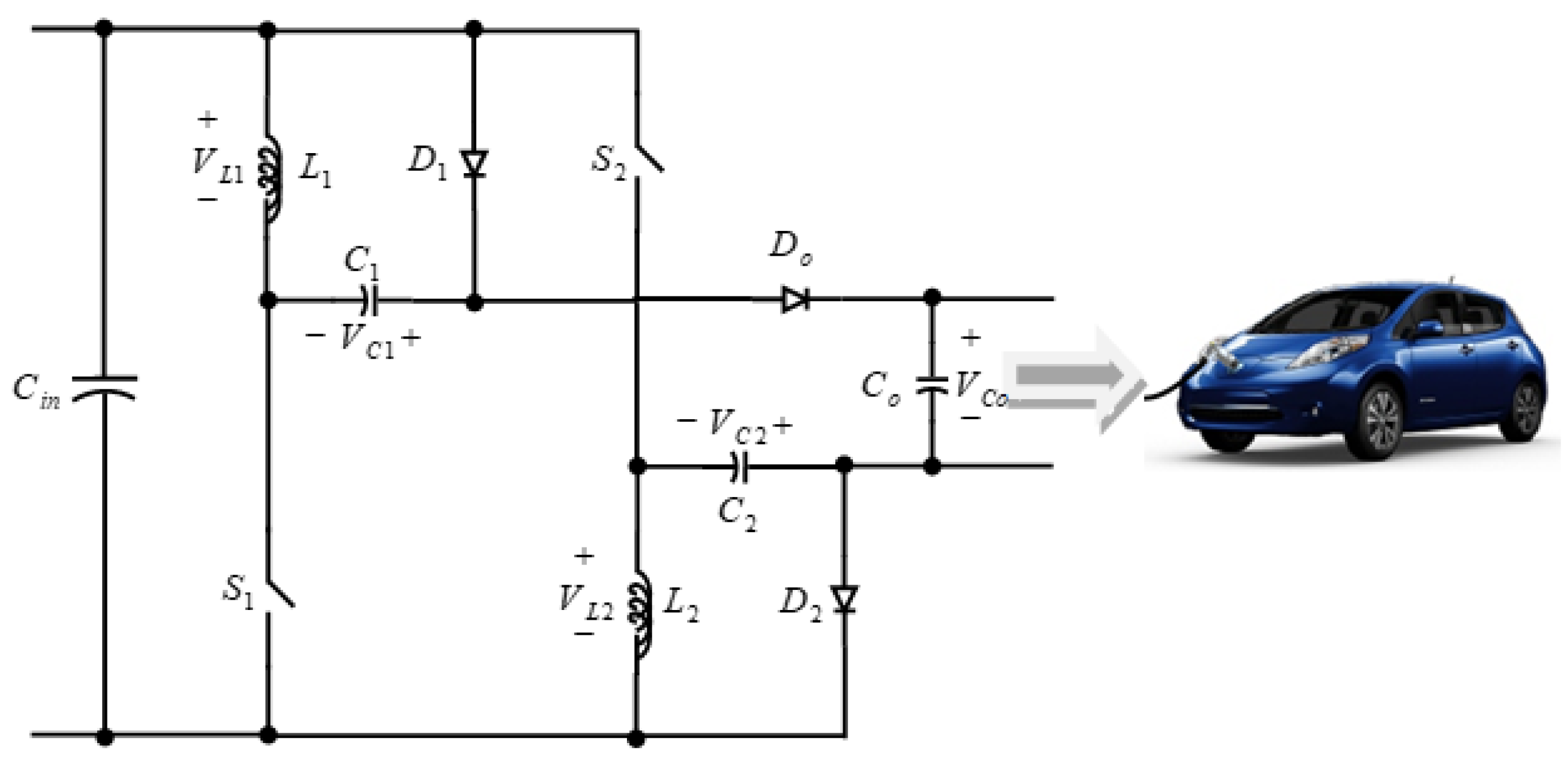
2. The Proposed Converter Topology Analysis
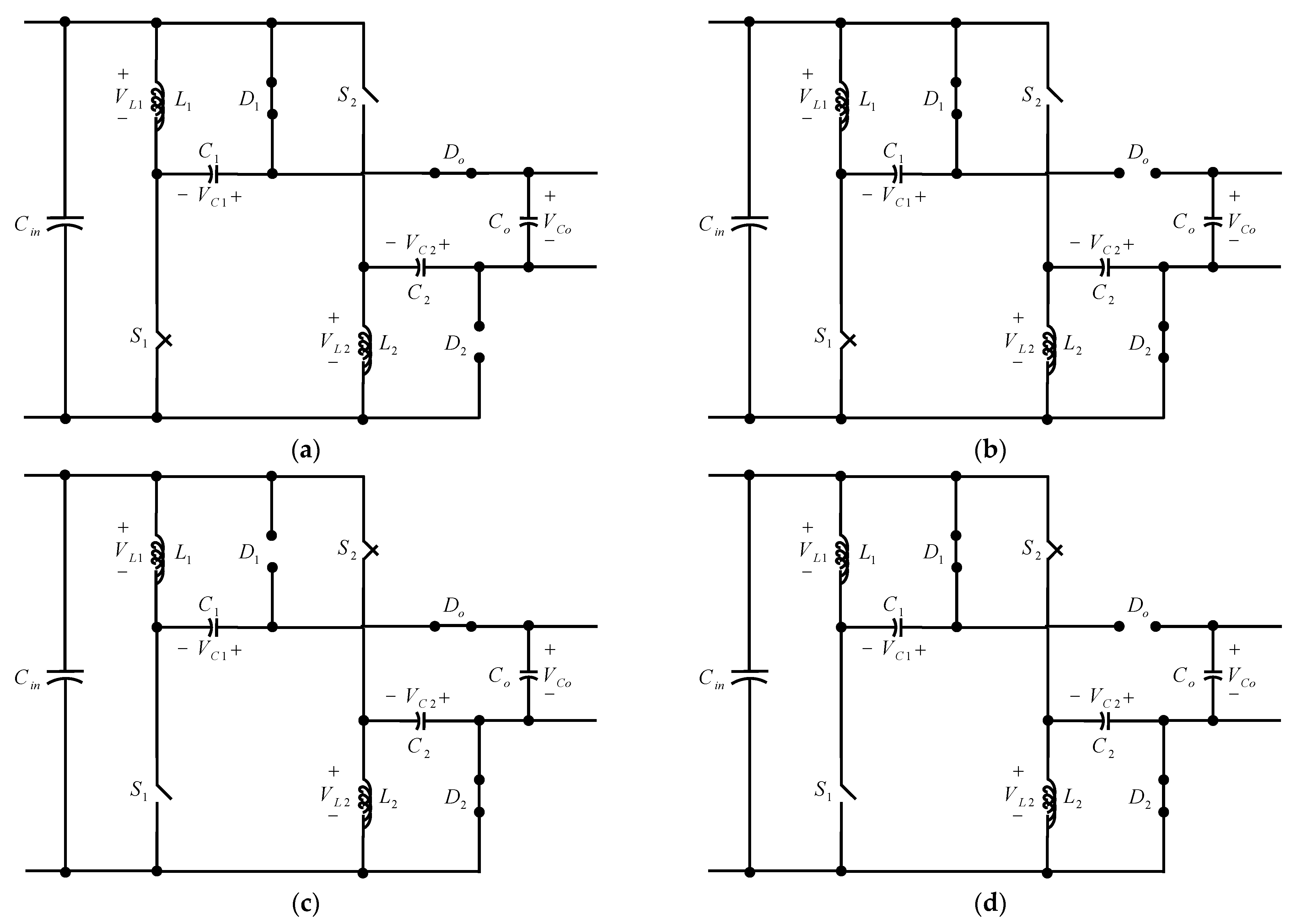
2.1. Analysis of the Proposed Converter in CCM
2.2. Analysis of the Proposed Converter in DCM
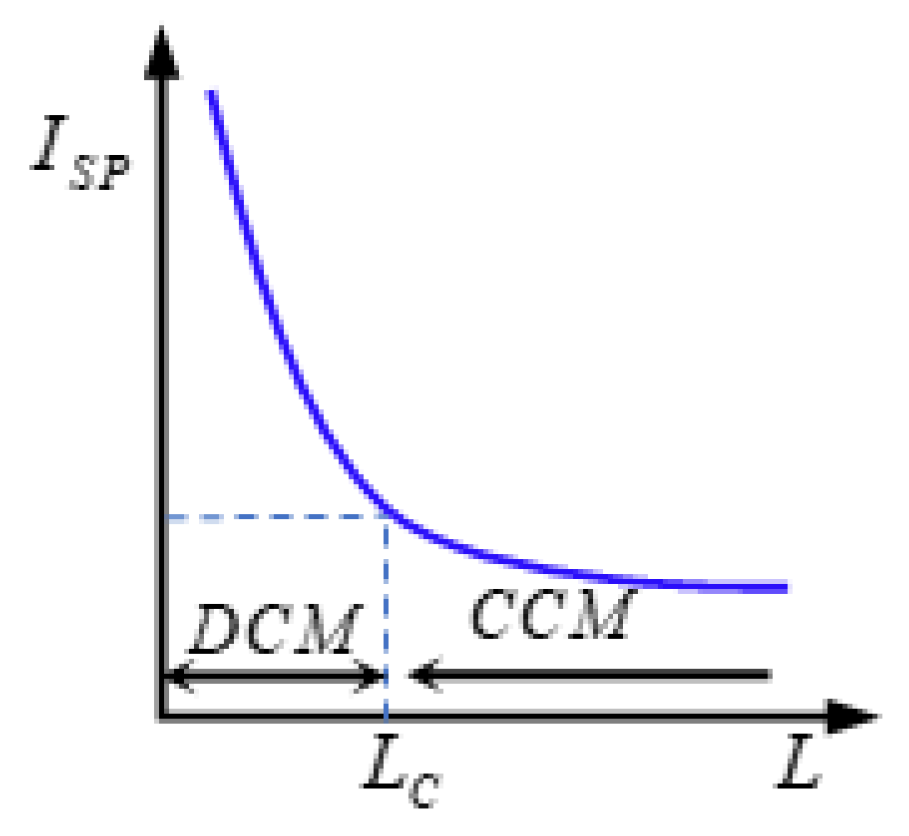
3. Critical Inductance Calculation
4. Design Considerations
4.1. Switches Current in CCM
4.2. Switches Current in DCM
4.3. Switches Voltage Stress
5. Efficiency Analysis
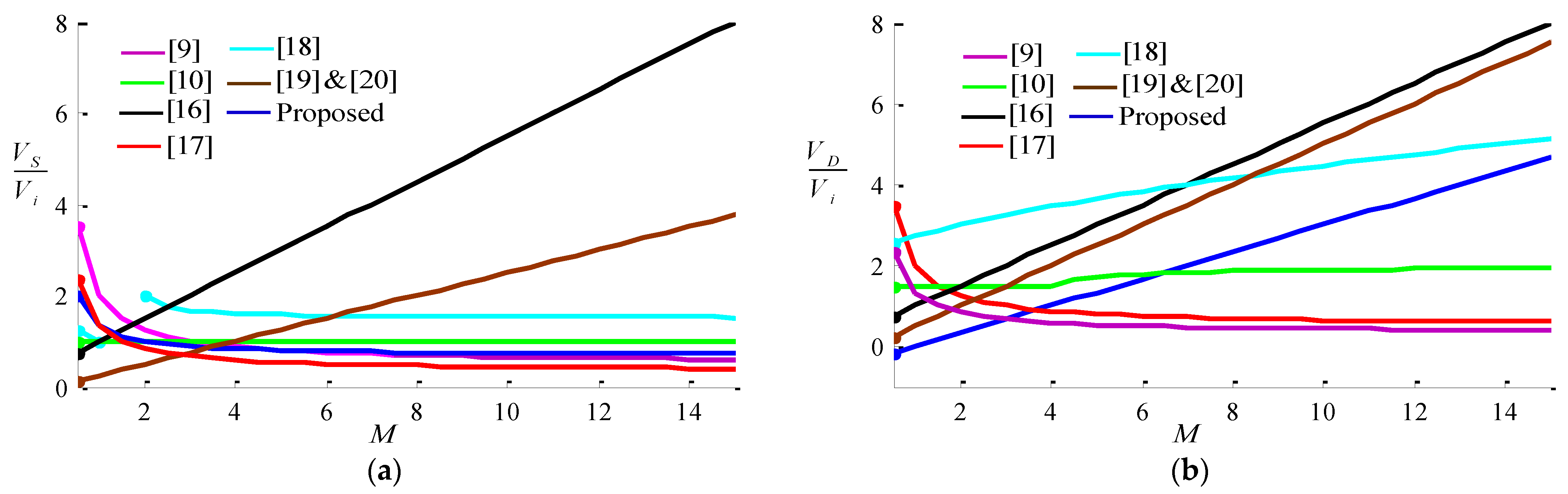
6. Comparison
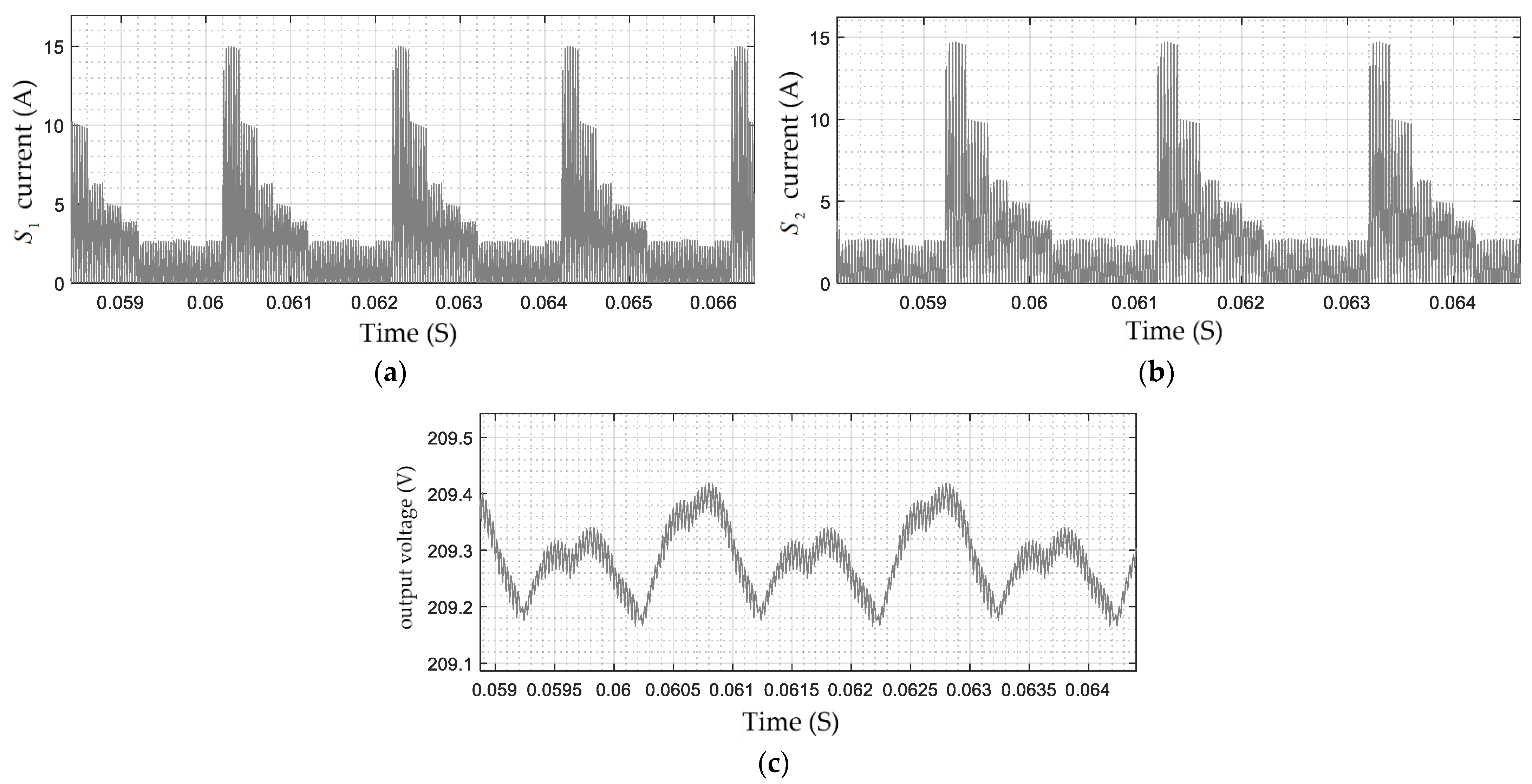
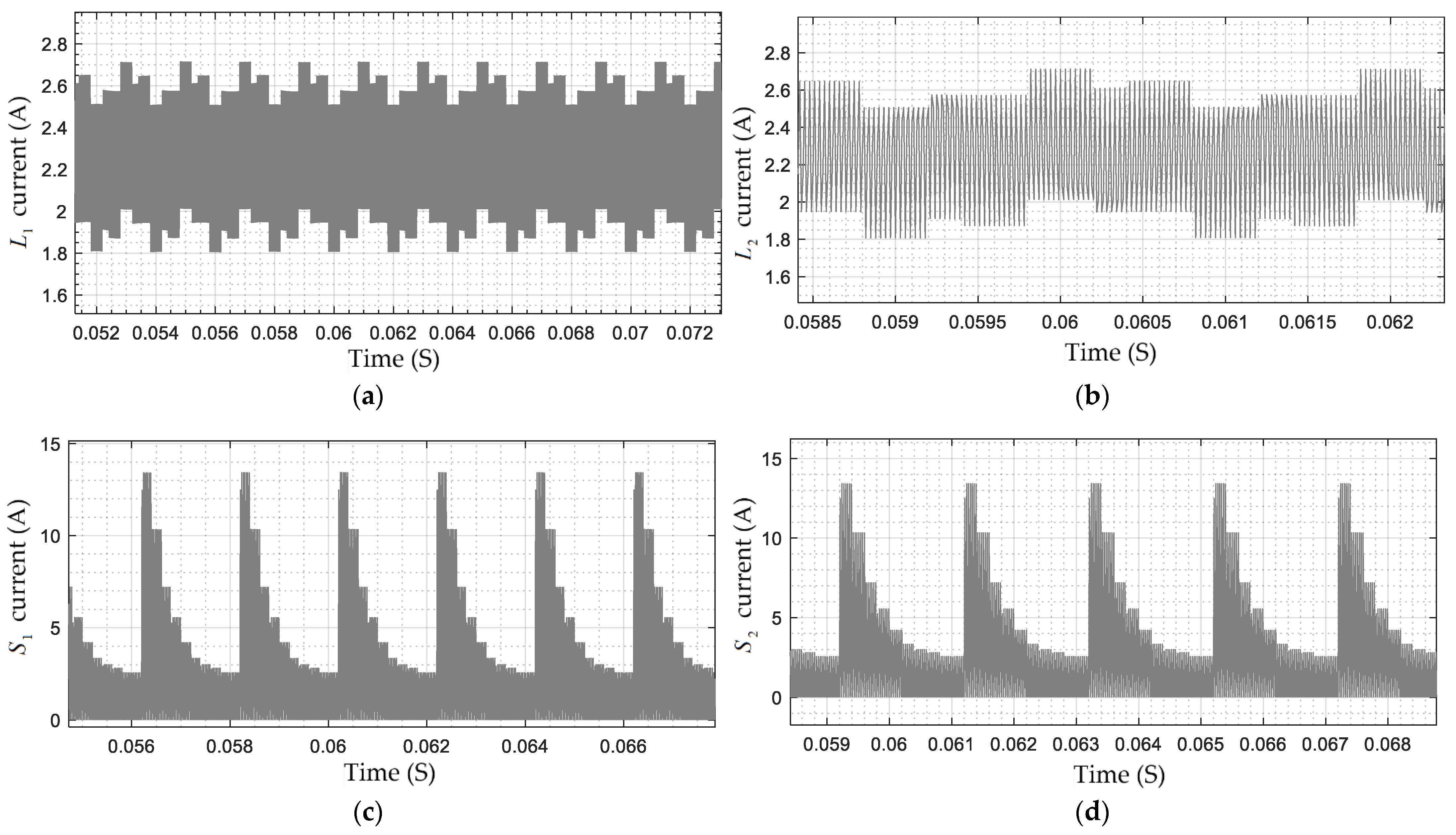
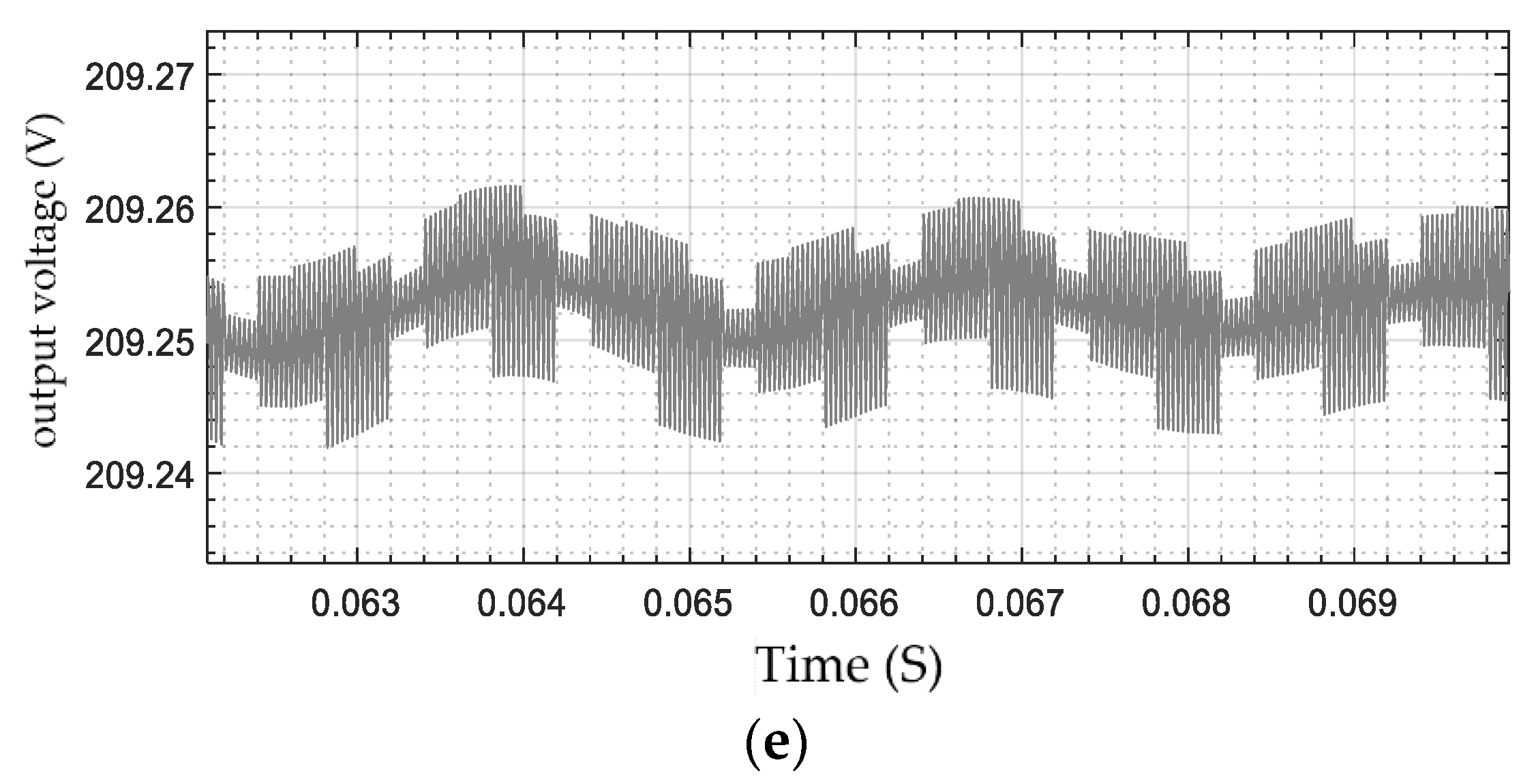
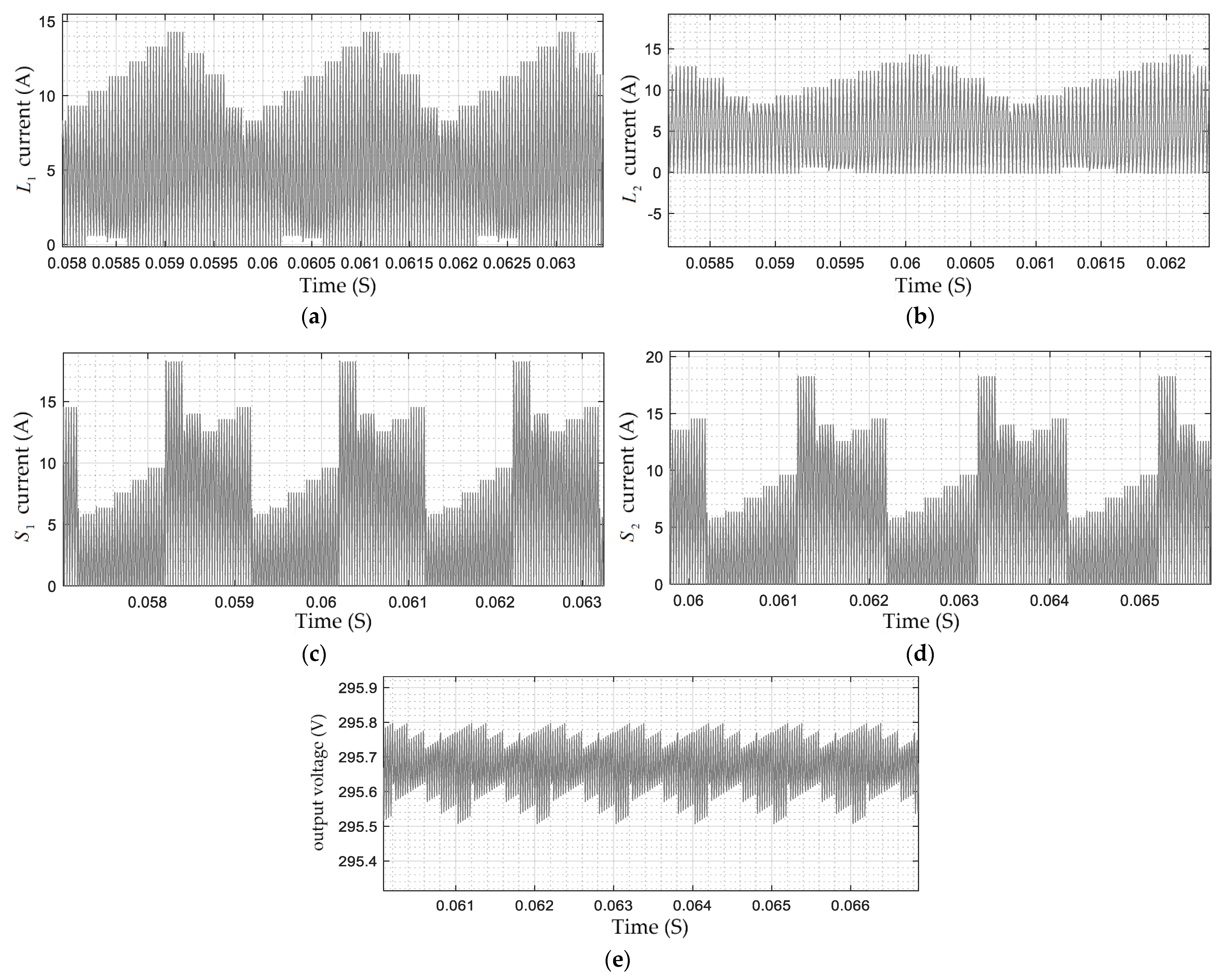
7. Experimental Results
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iyer, V.M.; Gulur, S.; Gohil, G.; Bhattacharya, S. An Approach Towards Extreme Fast Charging Station Power Delivery for Electric Vehicles with Partial Power Processing. IEEE Trans. Ind. Electron. 2019, 67, 8076–8087. [Google Scholar] [CrossRef]
- Ucer, E.; Koyuncu, I.; Kisacikoglu, M.C.; Yavuz, M.; Meintz, A.; Rames, C. Modeling and Analysis of a Fast Charging Station and Evaluation of Service Quality for Electric Vehicles. IEEE Trans. Transp. Electron. 2019, 5, 215–225. [Google Scholar] [CrossRef]
- Rafiei, M.; Boudjadar, J.; Khooban, M.-H. Energy Management of a Zero-Emission Ferry Boat With a Fuel-Cell-Based Hybrid Energy System: Feasibility Assessment. IEEE Trans. Ind. Electron. 2021, 68, 1739–1748. [Google Scholar] [CrossRef]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S. Extreme Fast Charging of Electric Vehicles: A Technology Overview. IEEE Trans. Transp. Electron. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- Khooban, M.-H. An Optimal Non-Integer Model Predictive Virtual Inertia Control in Inverter-Based Modern AC Power Grids-Based V2G Technology. IEEE Trans. Energy Convers. 2021, 36, 1336–1346. [Google Scholar] [CrossRef]
- Metwly, M.Y.; Abdel-Majeed, M.S.; Abdel-Khalik, A.S.; Hamdy, R.A.; Hamad, M.S.; Ahmed, S. A Review of Integrated On-Board EV Battery Chargers: Advanced Topologies, Recent Developments and Optimal Selection of FSCW Slot/Pole Combination. IEEE Access 2020, 8, 85216–85242. [Google Scholar] [CrossRef]
- Srdic, S.; Lukic, S. Toward extreme fast charging: Challenges and opportunities in directly connecting to medium-voltage line. IEEE Electrif. Mag. 2019, 7, 22–31. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of battery charger topologies, charging power levels, and infrastructure for plug-in electric and hybrid vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Banaei, M.R.; Sani, S.G. Analysis and implementation of a new sepic-based single-switch buck-boost dc-dc converter with continuous input current. IEEE Trans. Power Electron. 2018, 33, 10317–10325. [Google Scholar] [CrossRef]
- Shahir, F.M.; Babaei, E.; Farsadi, M. Extended topology for boost dc-dc converter. IEEE Trans. Power Electron. 2019, 34, 2375–2384. [Google Scholar] [CrossRef]
- Aggeler, D.; Canales, F.; Zelaya-De La Parra, H.; Coccia, A.; Butcher, N.; Apeldoorn, O. Ultra-Fast Dc-Charge Infrastructures for Ev-Mobility and Future smart Grids. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, Sweden, 11–13 October 2010; pp. 1–8. [Google Scholar]
- Garcia, O.; Zumel, P.; de Castro, A.; Cobos, A. Automotive dc-dc bidirectional converter made with many interleaved buck stages. IEEE Trans. Power Electron. 2006, 21, 578–586. [Google Scholar] [CrossRef]
- Kang, T.; Kim, C.; Suh, Y.; Park, H.; Kang, B.; Kim, D. A design and control of bi-directional non-isolated dc-dc converter for rapid electric vehicle charging system. In Proceedings of the Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 14–21. [Google Scholar]
- Zhang, J.; Lai, J.; Kim, R.; Yu, W. High-power density design of a soft-switching high-power bidirectional dc-dc converter. IEEE Trans. Power Electron. 2007, 22, 1145–1153. [Google Scholar] [CrossRef]
- Christen, D.; Jauch, F.; Biel, J. Ultra-fast charging station for electric vehicles with integrated split grid storage. In Proceedings of the 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–11. [Google Scholar]
- Shahir, F.M.; Babaei, E.; Farsadi, M. Voltage-lift technique based non-isolated boost dc-dc converter: Analysis and design. IEEE Trans. Power Electron. 2018, 33, 5917–5926. [Google Scholar] [CrossRef]
- Salvador, M.A.; Lazzarin, T.B.; Coelho, R.F. High step-up dc-dc converter with active switched-inductor and passive switched-capacitor networks. IEEE Trans. Ind. Electron. 2018, 65, 5644–5654. [Google Scholar] [CrossRef]
- Shahir, F.M.; Babaei, E.; Farsadi, M. Analysis and design of voltage-lift technique based non-isolated boost dc-dc converter. IET Power Electron. 2018, 11, 1083–1091. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, B.; Lou, Q.; Chen, S. Interleaved non-isolated high step-up dc/dc converter based on the diode-capacitor multiplier. IET Power Electron. 2014, 7, 390–397. [Google Scholar] [CrossRef]
- Pan, C.T.; Chuang, C.F.; Chu, C.C. A novel transformer-less adapt-able voltage quadrupler dc converter with low switch voltage stress. IEEE Trans. Power Electron. 2014, 29, 4787–4796. [Google Scholar] [CrossRef]

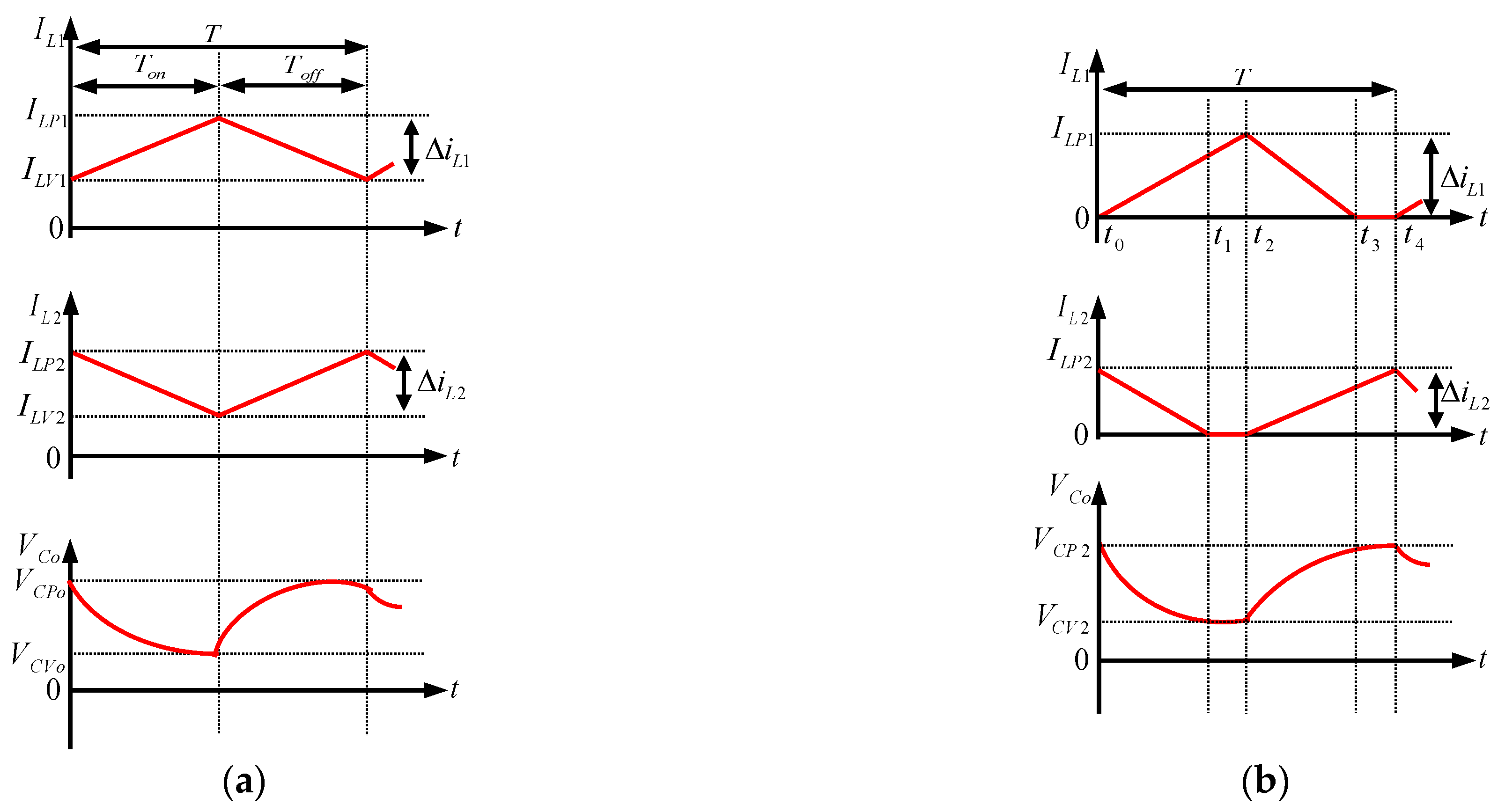

| Elements/Time Interval | CCM | DCM | ||||
|---|---|---|---|---|---|---|
| Elements/Ref. | [9] | [10] | [16] | [18] | [19] | [20] | [17] | Proposed |
|---|---|---|---|---|---|---|---|---|
| Switch | 2 | 2 | 1 | 2 | 2 | 2 | 1 | 2 |
| Inductor | 3 | 2 | 2 | 2 | 2 | 2 | 4 | 2 |
| Capacitor | 3 | 2 | 3 | 2 | 4 | 4 | 6 | 3 |
| Diode | 2 | 3 | 3 | 4 | 4 | 5 | 3 | 3 |
| Voltage gain in CCM | ||||||||
| Max. Nor. voltage of switch | 1 | |||||||
| Max. Nor. voltage of diode |
| Parameters | CCM | DCM |
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahir, F.M.; Gheisarnejad, M.; Sadabadi, M.S.; Khooban, M.-H. A New Off-Board Electrical Vehicle Battery Charger: Topology, Analysis and Design. Designs 2021, 5, 51. https://doi.org/10.3390/designs5030051
Shahir FM, Gheisarnejad M, Sadabadi MS, Khooban M-H. A New Off-Board Electrical Vehicle Battery Charger: Topology, Analysis and Design. Designs. 2021; 5(3):51. https://doi.org/10.3390/designs5030051
Chicago/Turabian StyleShahir, Farzad Mohammadzadeh, Meysam Gheisarnejad, Mahdieh S. Sadabadi, and Mohammad-Hassan Khooban. 2021. "A New Off-Board Electrical Vehicle Battery Charger: Topology, Analysis and Design" Designs 5, no. 3: 51. https://doi.org/10.3390/designs5030051
APA StyleShahir, F. M., Gheisarnejad, M., Sadabadi, M. S., & Khooban, M.-H. (2021). A New Off-Board Electrical Vehicle Battery Charger: Topology, Analysis and Design. Designs, 5(3), 51. https://doi.org/10.3390/designs5030051








