High-Accuracy Gaze Estimation for Interpolation-Based Eye-Tracking Methods
Abstract
1. Introduction
- A novel method to compensate for the influence of eye-camera location in gaze estimation based on virtual perspective camera alignment (Section 2.1). Contrary to traditional interpolation-based methods, the proposed method uses a normalized plane between the eye plane and the viewed plane to align the eye-camera in the center of the optical axis, and thus gains unrestricted eye-camera placement for uncalibrated and fully calibrated eye trackers.
- A novel method to undistort eye feature distribution on the eye plane (Section 2.2). After aligning the eye-camera onto the optical axis, the eye feature distribution will be symmetric and uniform centered in the eye feature distribution. However, due to the nonlinear projection of eyeball on the eye plane, the eye feature distribution presents a radial distortion. This method uses the distortion coefficients to reshape the eye feature distribution in an almost linear dispersion.
- This work introduces a new open-source dataset for eye-tracking studies called EyeInfo dataset (available on https://github.com/fabricionarcizo/eyeinfo, accessed on 17 August 2020). This dataset contains high-speed monocular eye-tracking data from an off-the-shelf remote eye tracker using active illumination. The data from each user has a text file with annotations concerning the eye feature, environment, viewed targets, and facial features. This dataset follows the basic principles of the General Data Protection Regulation (GDPR).
2. Materials and Methods
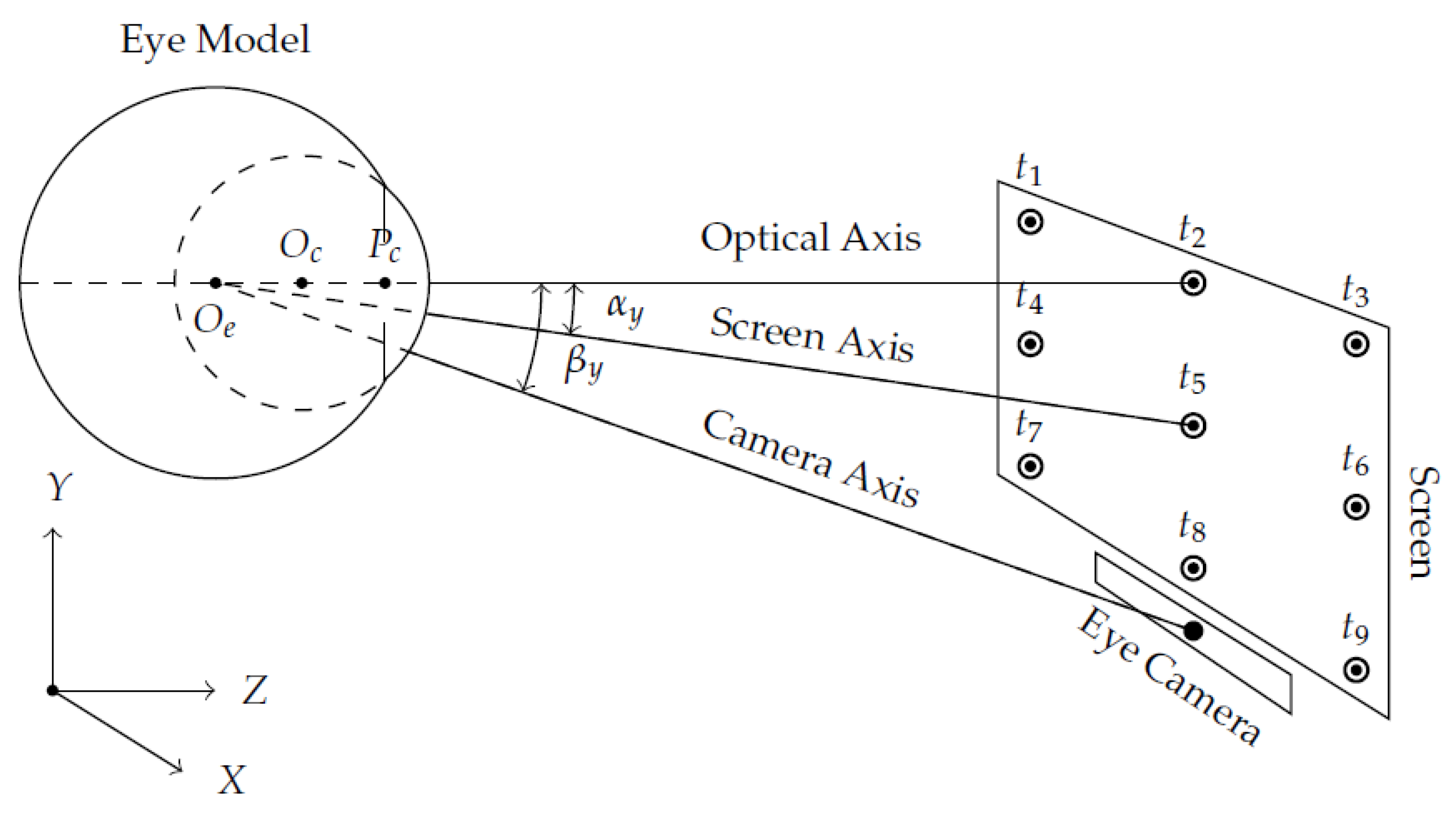
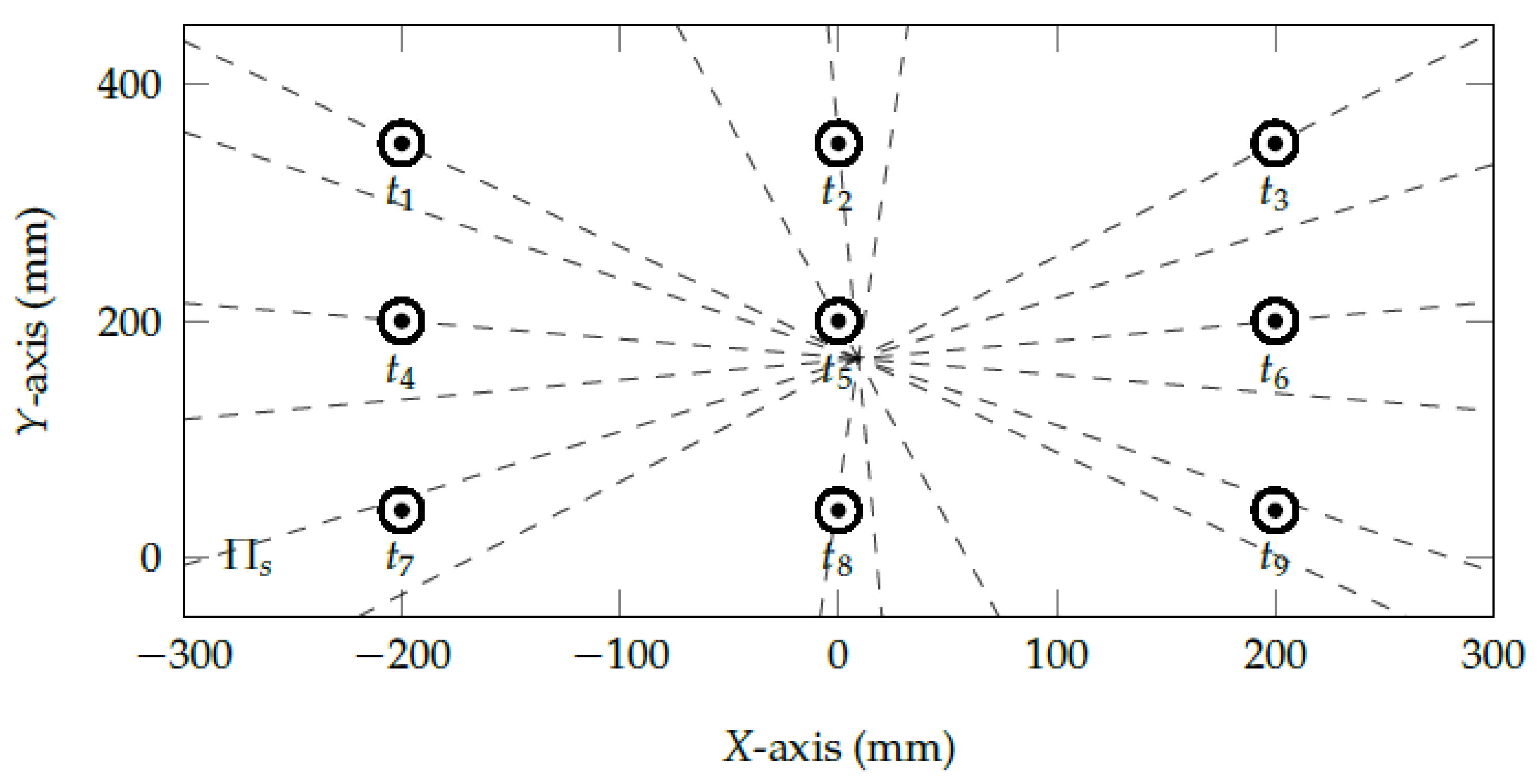
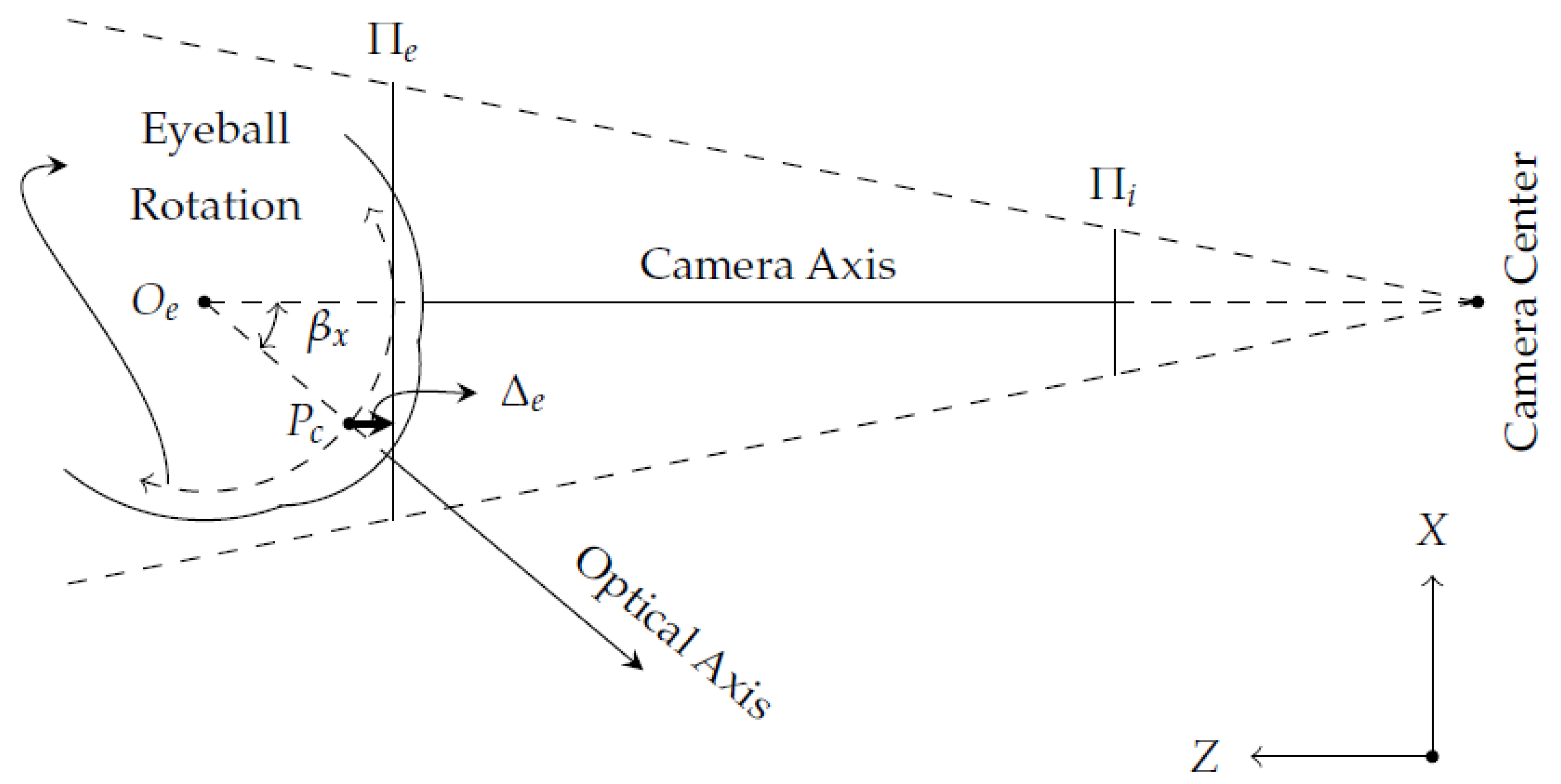
2.1. Eye-Camera Location Compensation Method
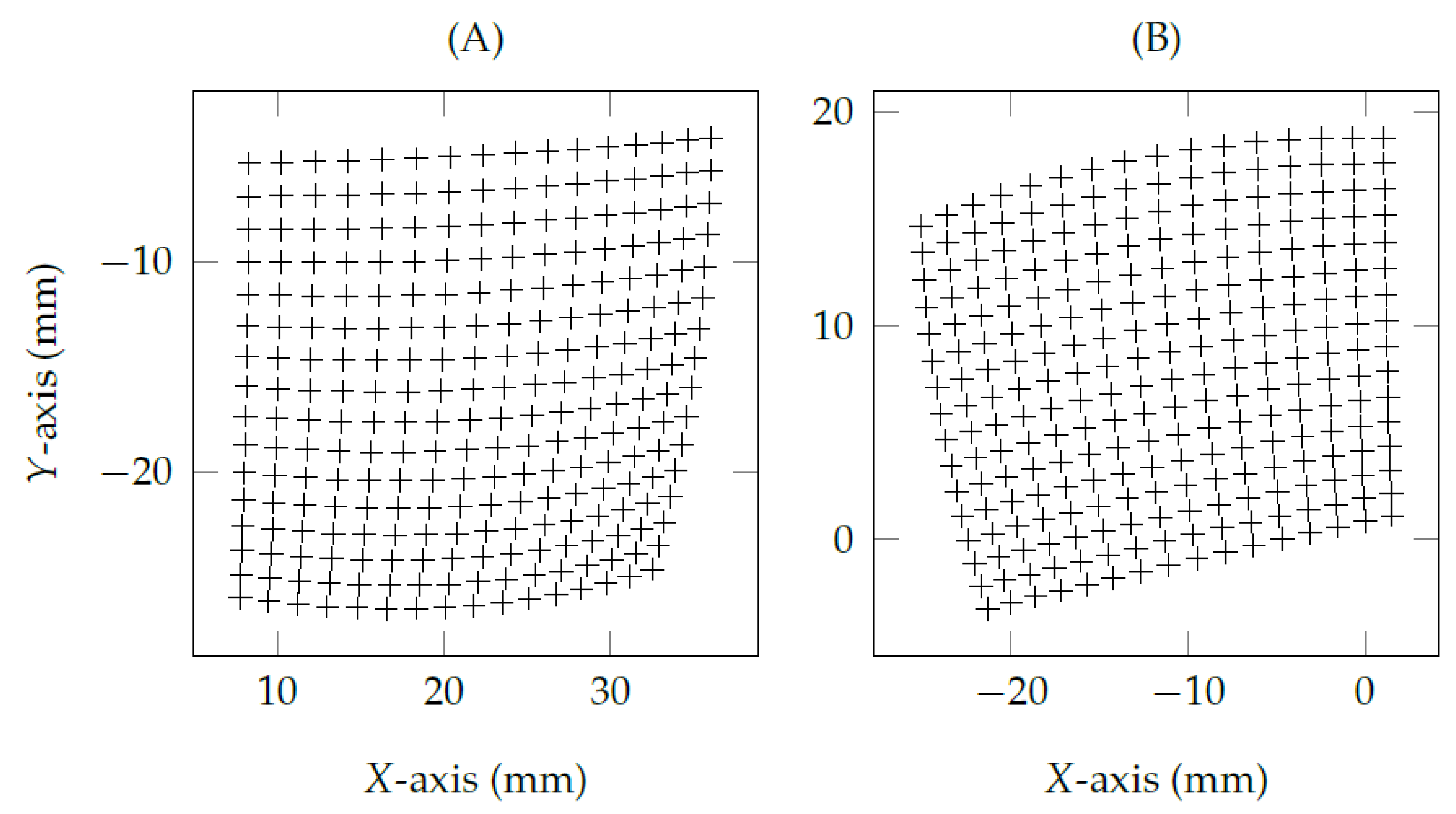
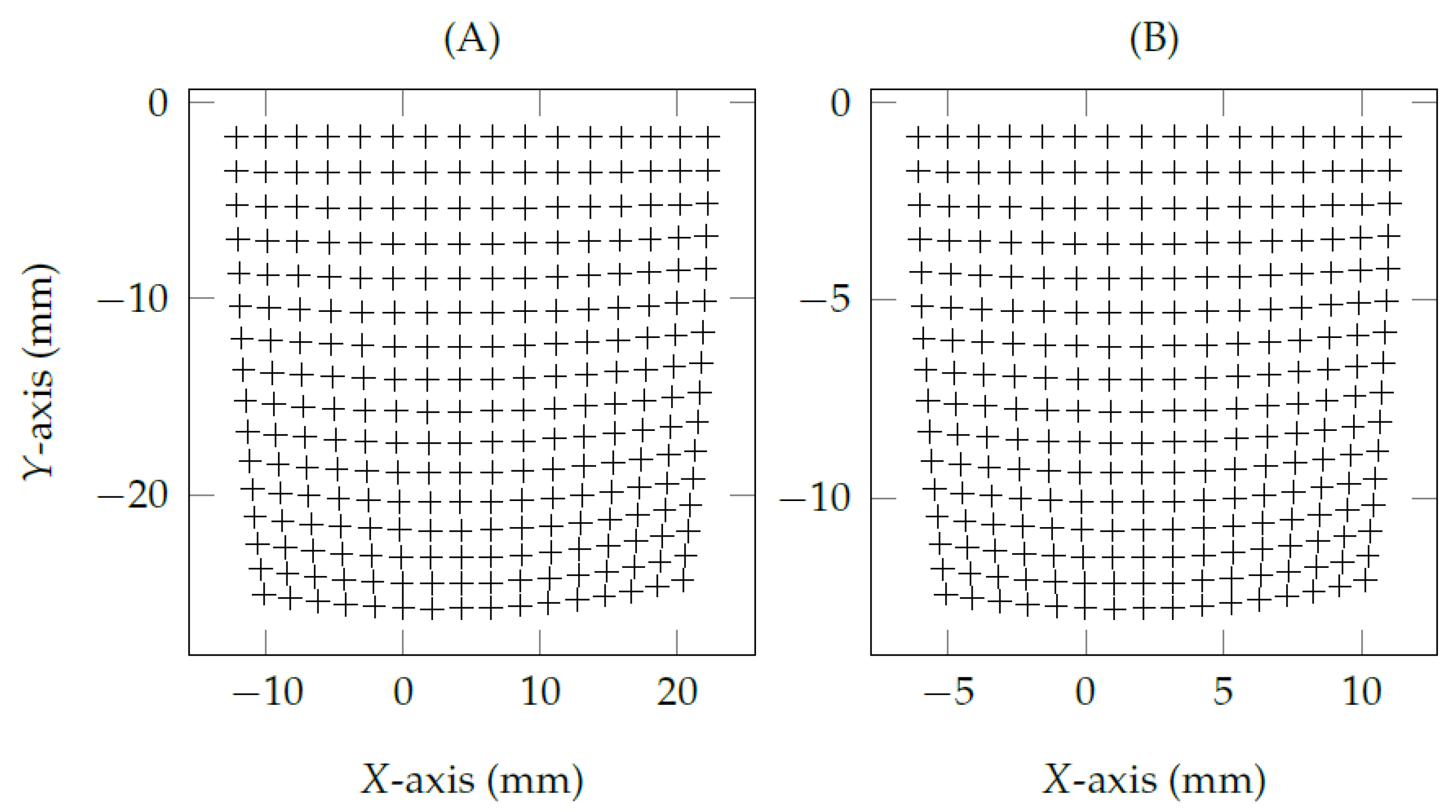
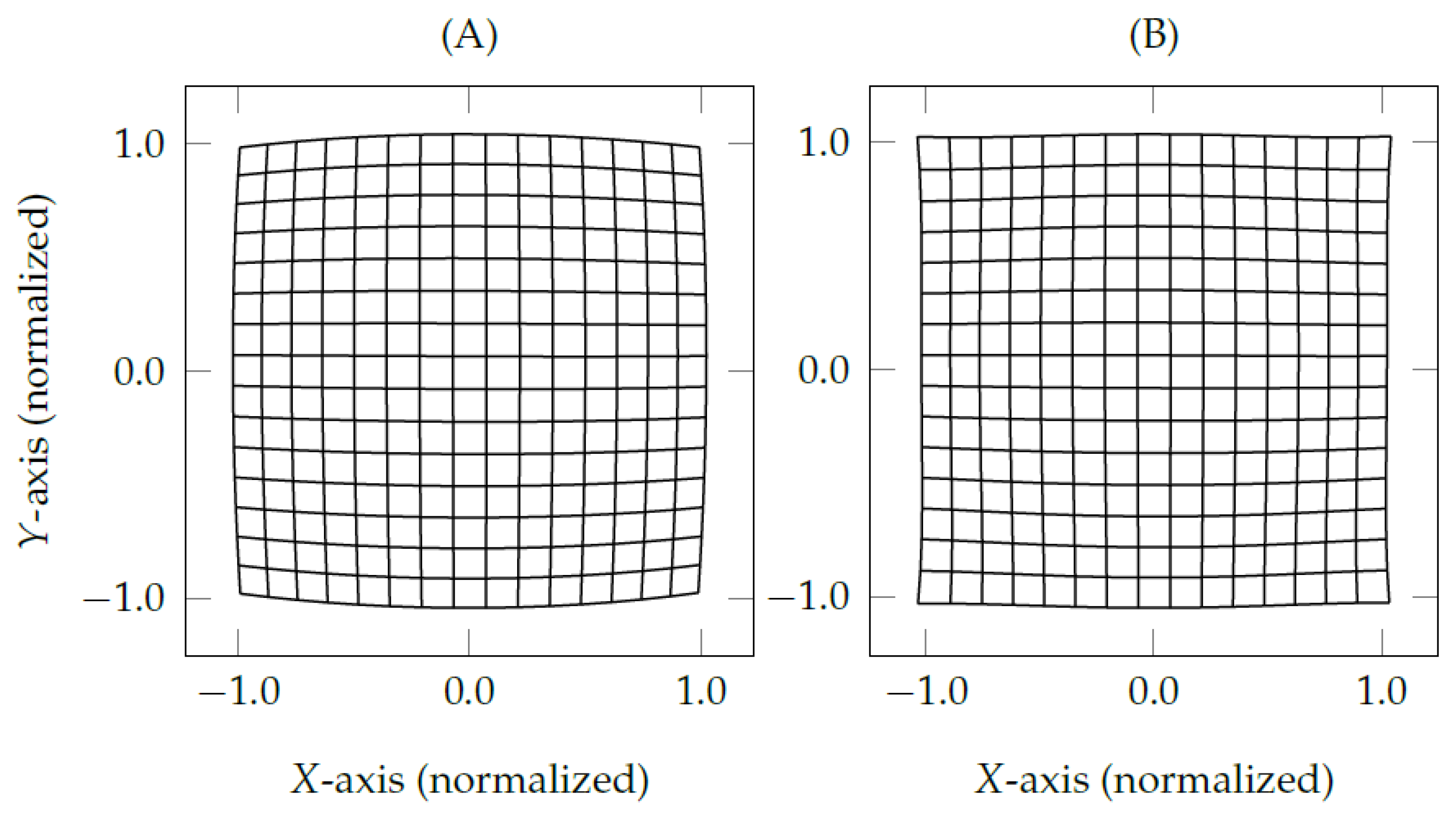
2.2. Eye Feature Distribution Undistortion Method
2.3. Simulated Study
2.4. User Study
2.4.1. Design
2.4.2. Eye-Tracking Data
2.4.3. Apparatus
2.4.4. Participants
2.4.5. Tasks
2.4.6. Experiment Protocol
2.4.7. Independent and Dependent Variables
2.4.8. Measures
2.4.9. Hypotheses
3. Results
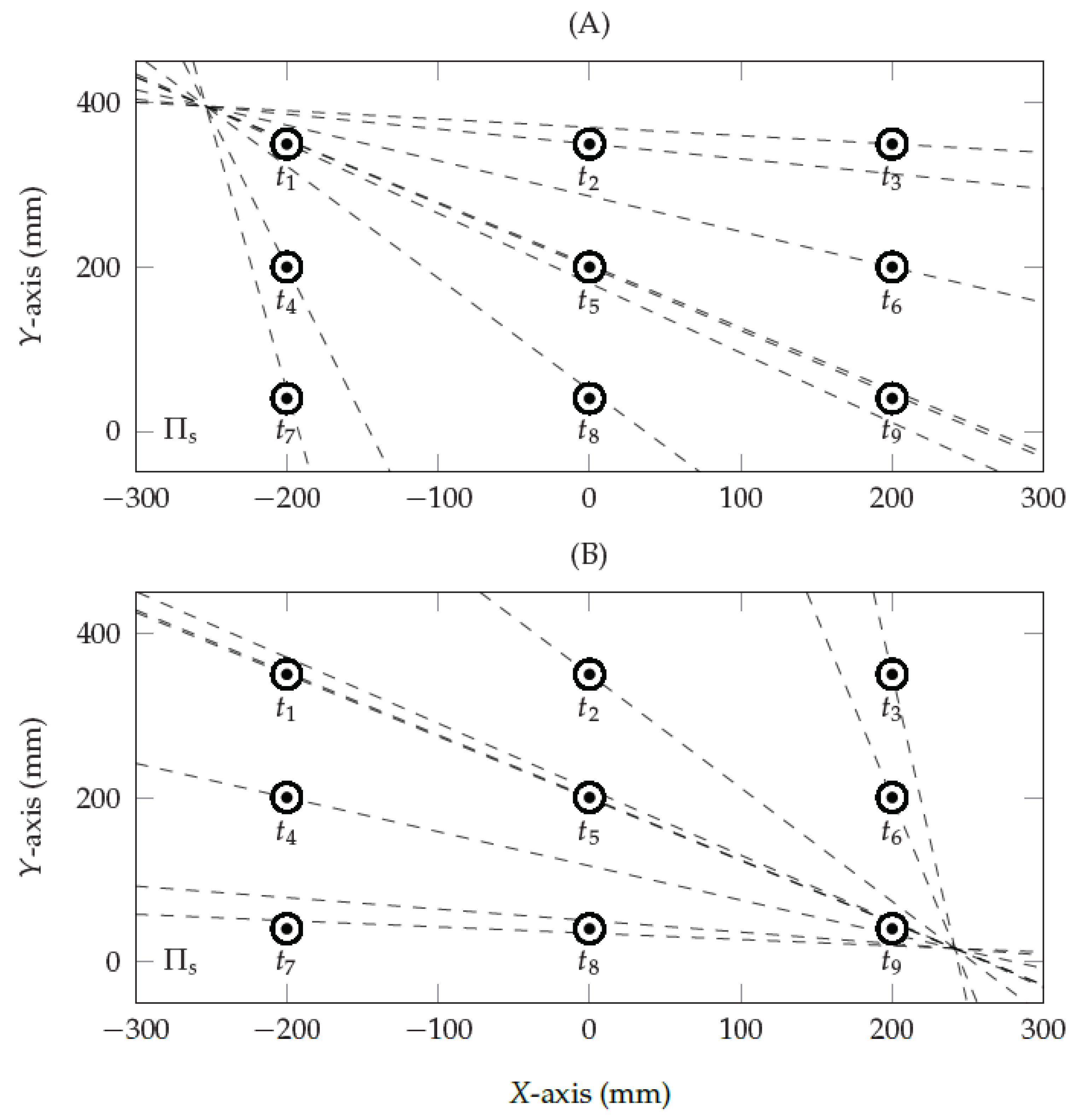
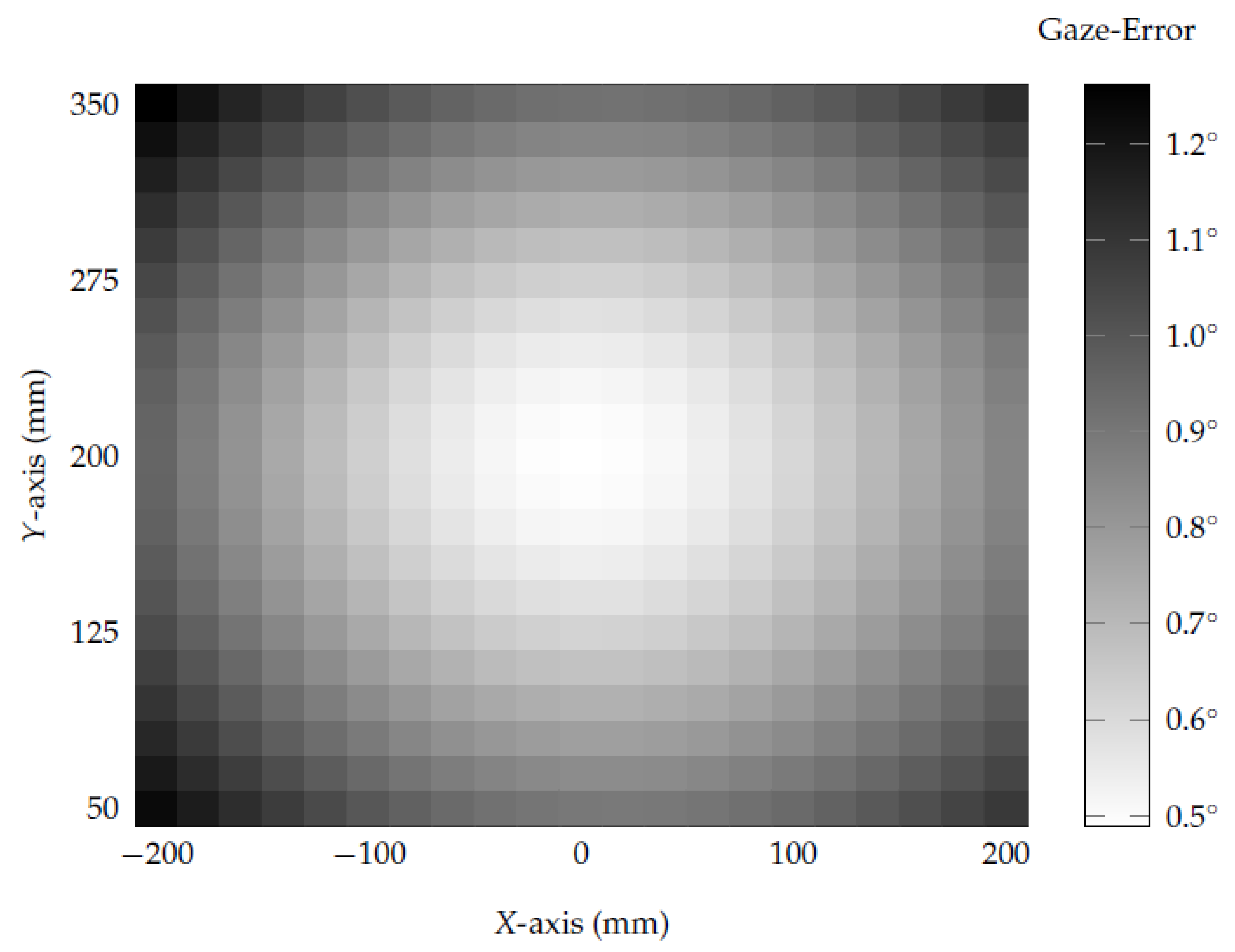
3.1. Evaluation of Eye-Camera Location
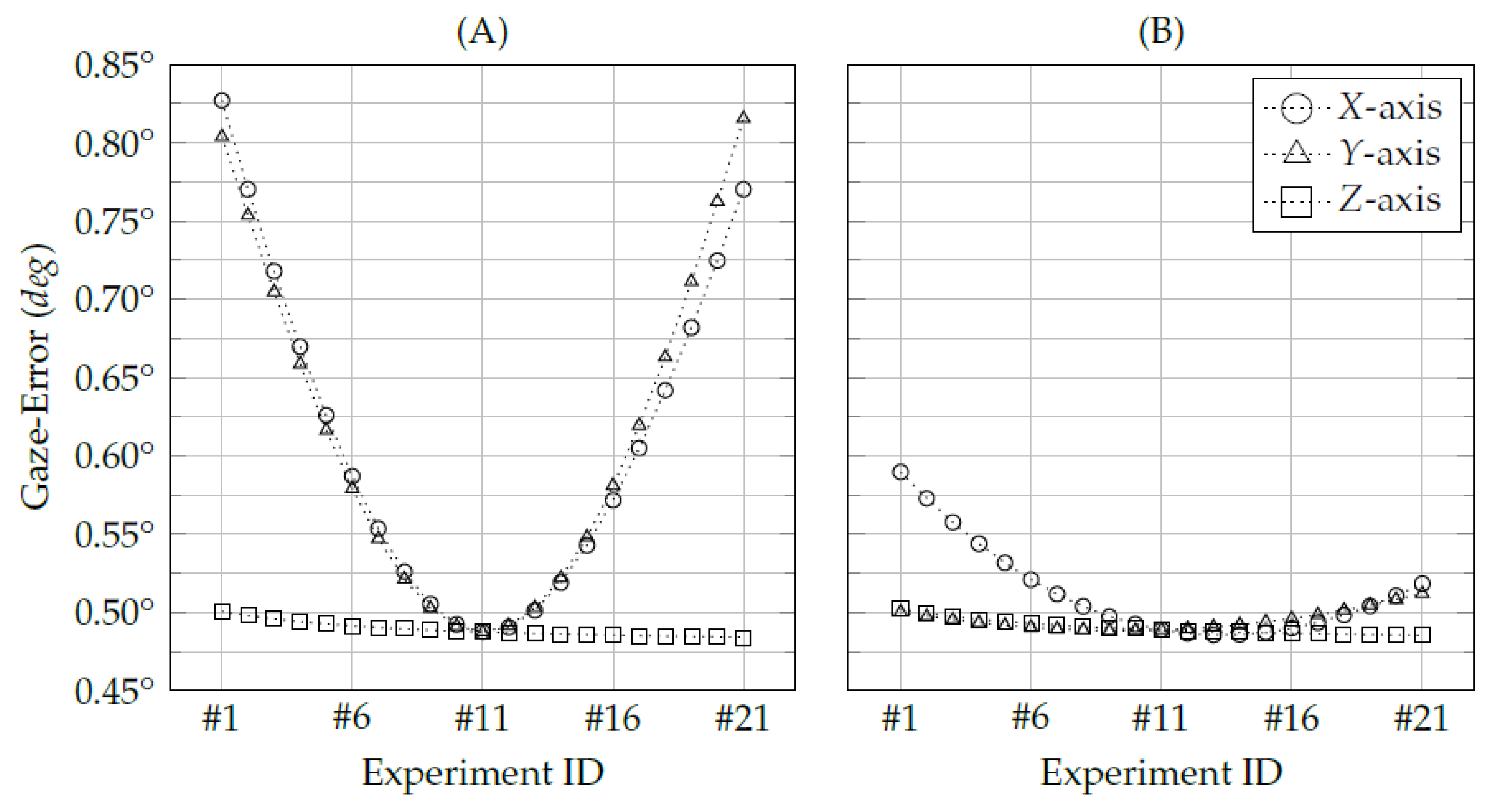
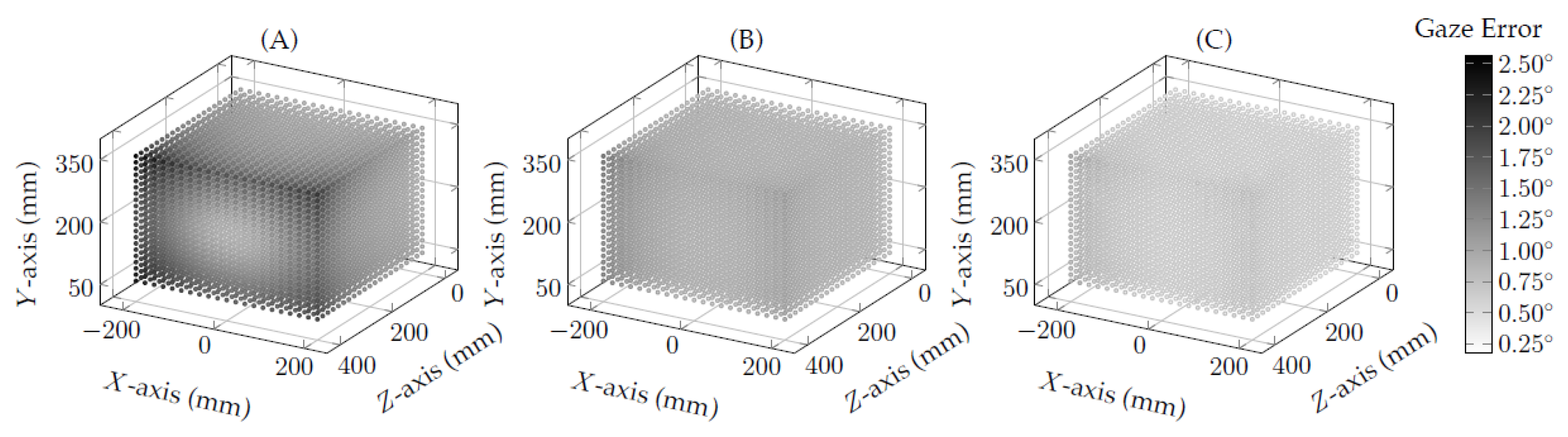
3.2. Evaluation of Proposed Methods Using Simulated Data
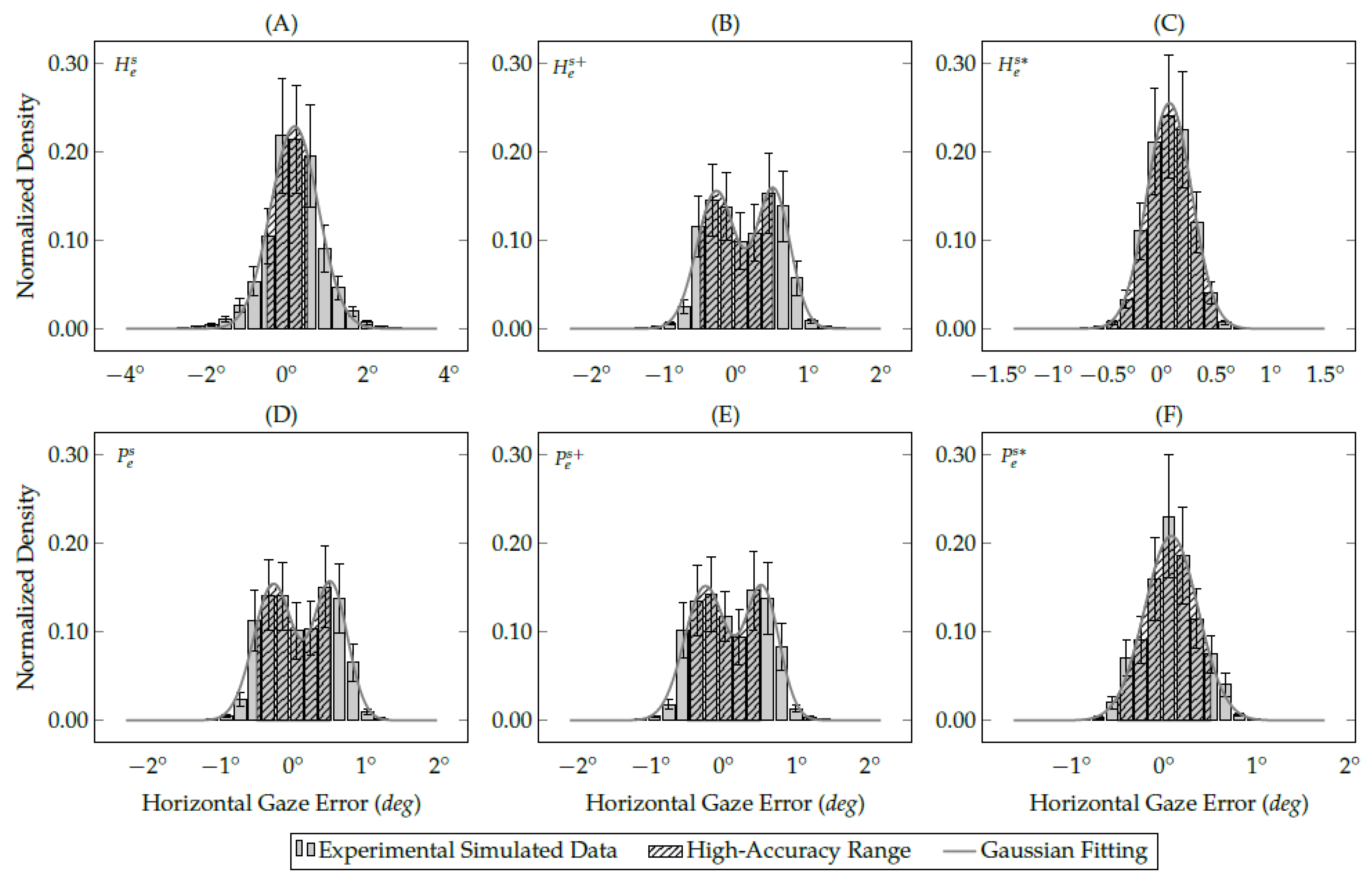
3.3. Evaluation of Proposed Methods Using Real Data
4. Discussion
- Assuming the eye plane and the viewed plane as a stereo vision system, it is possible to use the epipolar geometry to estimate the eye-camera location in an uncalibrated setup.
- The second-order polynomial was the one that best compensates for the eye-camera location. We have tested high-order polynomials as well; however, they overfit the model and take the epipole (that represents the virtual eye-camera location) to the infinity, i.e., the epipolar lines become parallel.
- When the eye-camera is on the eye’s optical axis and moves in depth (z-axis), the shape of the eye feature distribution keeps the same while changing its scales on both x- and y-axes. It means the eye-camera location compensation method must realign the camera only on x- and y-coordinates in the three-dimensional space.
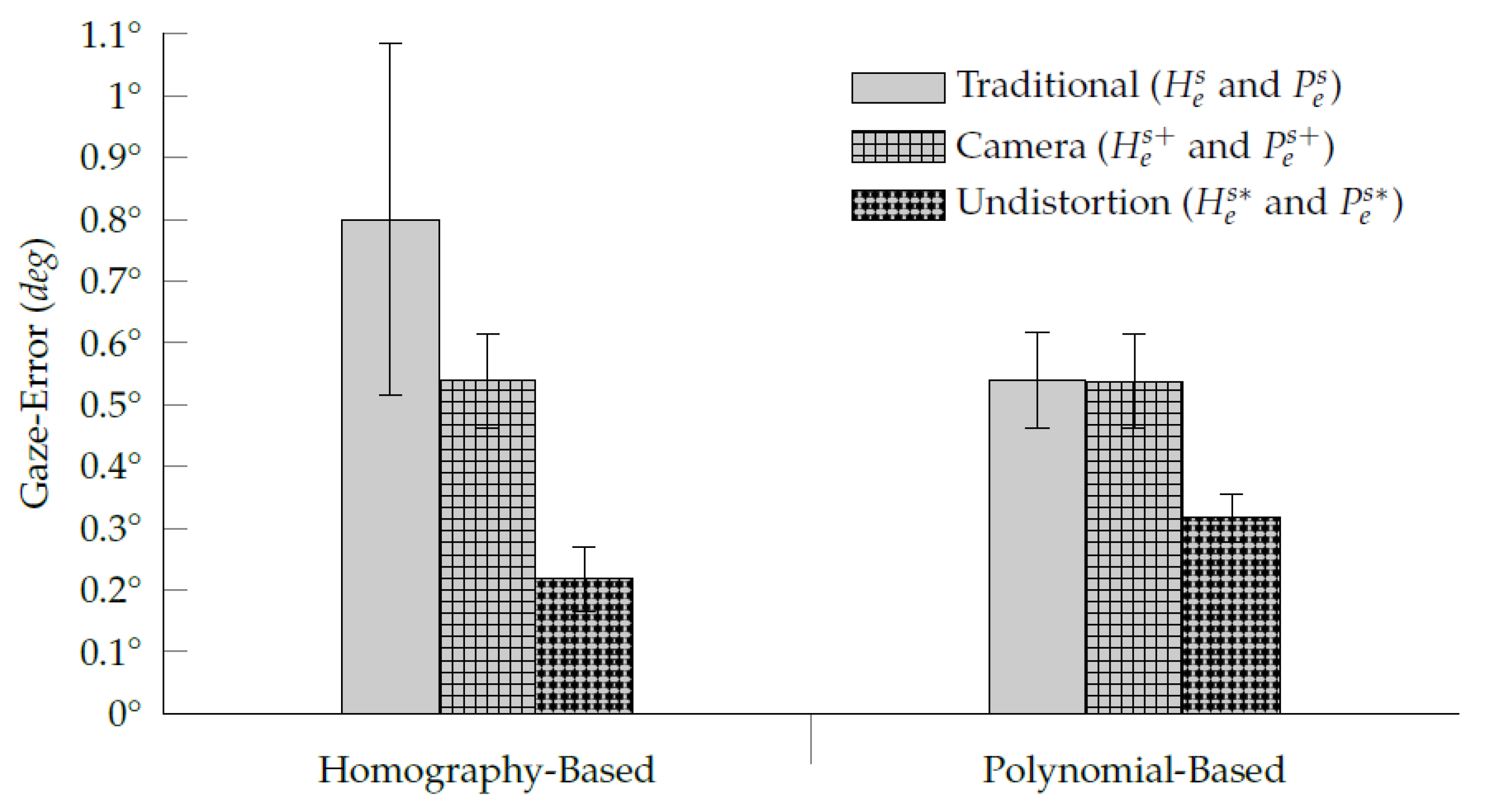
- Due to the eye-camera location, the homography-based methods have gaze-error magnitudes more significant than the interpolation-based methods.
- The proposed methods most benefit uncalibrated setups because it is not required to understand the geometry and the locations of the eye tracker components to reduce the negative influence of large and angles of the eye-camera’s optical axis into the gaze estimation.
- Both proposed methods improve the accuracy of interpolation-based eye-tracking methods using the same eye-tracking data from the gaze-mapping calibration. However, the proposed eye feature distribution undistortion method would benefit from gaining further user data, such as using more calibration data or combining with a recalibration procedure.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PoR | Point-of-Regard |
| RET | Remote Eye Trackers |
| HMET | Head-Mounted Eye Trackers |
| GDPR | Data Protection Regulation |
| PCCR | Pupil Center-Corneal Reflection |
| KDE | Kernel Density Estimation |
| WCS | World Coordinate System |
| Gaussian Probability Density Function | |
| HMD | Head-Mounted Displays |
| CNN | Convolutional Neural Networks |
| DLM | Deep Learning Models |
| LoS | Line of Sight |
| DoF | Degrees of Freedom |
| OLS | Ordinary Least Squares |
Appendix A. Gaze Estimation Methods
Appendix A.1. Appearance-Based Gaze Estimation Methods
Appendix A.2. Feature-Based Gaze Estimation Methods
| Method | Description | Accuracy | Calibration | Advantages | Disadvantages |
|---|---|---|---|---|---|
| Homography | A planar projective mapping between the eye plane and viewed plane | – | 4 targets | It requires only four pieces of calibration data | It is more sensitive to noise, such as camera location |
| Second-Order Polynomial | A regression which minimizes the sum of squared residuals | – | 9 targets | It is simple to implement and presents good accuracy | It is less accurate than homography-based methods |
| Camera Compensation | A method to reshape the eye feature distribution in a normalized space | – | 9 targets | It increases the number of high-accuracy gaze estimations | The use of high-order polynomials overfits the model |
| Distortion Compensation | A method to compensate for the non-coplanarity of | – | 9 targets | It presents the lowest error in real and simulated scenarios | It can blow up the estimations around the boundaries |
References
- Hansen, D.W.; Ji, Q. In the Eye of the Beholder: A Survey of Models for Eyes and Gaze. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 478–500. [Google Scholar] [CrossRef]
- Tonsen, M.; Steil, J.; Sugano, Y.; Bulling, A. InvisibleEye: Mobile Eye Tracking Using Multiple Low-Resolution Cameras and Learning-Based Gaze Estimation. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2017, 1, 106:1–106:21. [Google Scholar] [CrossRef]
- Larumbe, A.; Cabeza, R.; Villanueva, A. Supervised Descent Method (SDM) Applied to Accurate Pupil Detection in off-the-Shelf Eye Tracking Systems. In Proceedings of the 2018 Symposium on Eye Tracking Research & Applications (ETRA ’18), Warsaw, Poland, 14–17 June 2018; ACM: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Hansen, D.W.; Agustin, J.S.; Villanueva, A. Homography normalization for robust gaze estimation in uncalibrated setups. In Proceedings of the 2010 Symposium on Eye Tracking Research & Applications (ETRA ’10), Austin, TX, USA, 22–24 March 2010; ACM: New York, NY, USA, 2010; pp. 13–20. [Google Scholar] [CrossRef]
- Hansen, D.W.; Roholm, L.; Ferreiros, I.G. Robust Glint Detection through Homography Normalization. In Proceedings of the 2014 Symposium on Eye Tracking Research & Applications (ETRA ’14), Safety Harbor, FL, USA, 26–28 March 2014; ACM: New York, NY, USA, 2014; pp. 91–94. [Google Scholar] [CrossRef]
- Rattarom, S.; Aunsri, N.; Uttama, S. Interpolation based polynomial regression for eye gazing estimation: A comparative study. In Proceedings of the 2015 12th International Conference on Electrical Engineering, Electronics, Computer, Telecommunications and Information Technology (ECTI-CON ’15), Hua Hin, Thailand, 24–27 June 2015; IEEE Computer Society: Washington, DC, USA, 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Rattarom, S.; Aunsri, N.; Uttama, S. A Framework for Polynomial Model with Head Pose in Low Cost Gaze Estimation. In Proceedings of the 2017 International Conference on Digital Arts, Media and Technology (ICDAMT ’17), Chiang Mai, Thailand, 1–4 March 2017; IEEE Computer Society: Washington, DC, USA, 2017; pp. 24–27. [Google Scholar] [CrossRef]
- Setiawan, M.T.; Wibirama, S.; Setiawan, N.A. Robust Pupil Localization Algorithm Based on Circular Hough Transform for Extreme Pupil Occlusion. In Proceedings of the 2018 4th International Conference on Sensing Technology (ICST ’18), Yogyakarta, Indonesia, 7–8 August 2018; IEEE Computer Society: Washington, DC, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Dewi, D.A.S.; Wibirama, S.; Ardiyanto, I. Robust Pupil Localization Algorithm under Off-axial Pupil Occlusion. In Proceedings of the 2019 2nd International Conference on Bioinformatics, Biotechnology and Biomedical Engineering (BIoMIC ’19), Yogyakarta, Indonesia, 12–13 September 2019; IEEE Computer Society: Washington, DC, USA, 2019; Volume 1, pp. 1–6. [Google Scholar] [CrossRef]
- Narcizo, F.B.; Hansen, D.W. Depth Compensation Model for Gaze Estimation in Sport Analysis. In Proceedings of the 2015 IEEE International Conference on Computer Vision Workshop (ICCVW ’15), Santiago, Chile, 7–13 December 2015; IEEE Computer Society: Washington, DC, USA, 2015; pp. 788–795. [Google Scholar] [CrossRef]
- Konrad, R.; Angelopoulos, A.; Wetzstein, G. Gaze-Contingent Ocular Parallax Rendering for Virtual Reality. ACM Trans. Graph. 2020, 39, 1–12. [Google Scholar] [CrossRef]
- Coutinho, F.L.; Morimoto, C.H. Augmenting the robustness of cross-ratio gaze tracking methods to head movement. In Proceedings of the 2012 Symposium on Eye Tracking Research & Applications (ETRA ’12), Santa Barbara, CA, USA, 28–30 March 2012; ACM: New York, NY, USA, 2012; pp. 59–66. [Google Scholar] [CrossRef]
- Kar, A.; Corcoran, P. A Review and Analysis of Eye-Gaze Estimation Systems, Algorithms and Performance Evaluation Methods in Consumer Platforms. IEEE Access 2017, 5, 16495–16519. [Google Scholar] [CrossRef]
- Morimoto, C.H.; Mimica, M.R.M. Eye gaze tracking techniques for interactive applications. Comput. Vis. Image Underst. 2005, 98, 4–24. [Google Scholar] [CrossRef]
- Li, F.; Munn, S.M.; Pelz, J.B. A model-based approach to video-based eye tracking. J. Mod. Opt. 2008, 55, 503–531. [Google Scholar] [CrossRef]
- Cerrolaza, J.J.; Villanueva, A.; Cabeza, R. Study of polynomial mapping functions in video-oculography eye trackers. ACM Trans. Comput.-Hum. Interact. 2012, 19, 10:1–10:25. [Google Scholar] [CrossRef]
- Torricelli, D.; Conforto, S.; Schmid, M.; D’Alessio, T. A neural-based remote eye gaze tracker under natural head motion. Comput. Methods Programs Biomed. 2008, 92, 66–78. [Google Scholar] [CrossRef]
- Hennessey, C.; Lawrence, P.D. Improving the accuracy and reliability of remote system-calibration-free eye-gaze tracking. IEEE Trans. Biomed. Eng. 2009, 56, 1891–1900. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Z.; Ping, A. Non-contact gaze tracking with head movement adaptation based on single camera. World Acad. Sci. Eng. Technol. 2009, 59, 395–398. [Google Scholar] [CrossRef]
- Nagamatsu, T.; Sugano, R.; Iwamoto, Y.; Kamahara, J.; Tanaka, N. User-calibration-free gaze tracking with estimation of the horizontal angles between the visual and the optical axes of both eyes. In Proceedings of the 2010 Symposium on Eye Tracking Research & Applications (ETRA ’10), Austin, TX, USA, 22–24 March 2010; ACM: New York, NY, USA, 2010; pp. 251–254. [Google Scholar] [CrossRef]
- Su, D.; Li, Y.F. Toward flexible calibration of head-mounted gaze trackers with parallax error compensation. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO ’16), Qingdao, China, 3–7 December 2016; IEEE Computer Society: Washington, DC, USA, 2016; pp. 491–496. [Google Scholar] [CrossRef]
- Zhu, Z.; Ji, Q. Novel eye gaze tracking techniques under natural head movement. IEEE Trans. Biomed. Eng. 2007, 54, 2246–2260. [Google Scholar] [CrossRef]
- Chen, J.; Tong, Y.; Gray, W.D.; Ji, Q. A robust 3D eye gaze tracking system using noise reduction. In Proceedings of the 2008 Symposium on Eye Tracking Research & Applications (ETRA ’08), Savannah, GA, USA, 26–28 March 2008; ACM: New York, NY, USA, 2008; pp. 189–196. [Google Scholar] [CrossRef]
- Hartley, R.I.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; p. 670. [Google Scholar]
- Blignaut, P. A new mapping function to improve the accuracy of a video-based eye tracker. In Proceedings of the of South African Institute for Computer Scientists and Information Technologists Conference (SAICSIT ’13), East London, South Africa, 7–9 October 2013; ACM: New York, NY, USA, 2013; pp. 56–59. [Google Scholar] [CrossRef]
- Coutinho, F.L.; Morimoto, C.H. Improving Head Movement Tolerance of Cross-Ratio Based Eye Trackers. Int. J. Comput. Vis. 2012, 101, 1–23. [Google Scholar] [CrossRef]
- Morimoto, C.H.; Koons, D.; Amir, A.; Flickner, M. Frame-rate pupil detector and gaze tracker. In Proceedings of the 7th IEEE International Conference on Computer Vision (ICCV ’99), Kerkyra, Greece, 20–27 September 1999; IEEE Computer Society: Washington, DC, USA, 1999. [Google Scholar]
- Li, D.; Winfield, D.; Parkhurst, D.J. Starburst: A Hybrid Algorithm for Video-Based Eye Tracking Combining Feature-Based and Model-Based Approaches. In Proceedings of the 2005 IEEE Computer Vision and Pattern Recognition–Workshops (CVPR ’05), San Diego, CA, USA, 21–23 September 2005; IEEE Computer Society: Washington, DC, USA, 2005; pp. 1–8. [Google Scholar] [CrossRef]
- Yoo, D.H.; Chung, M.J. A novel non-intrusive eye gaze estimation using cross-ratio under large head motion. Comput. Vis. Image Underst. 2005, 98, 25–51. [Google Scholar] [CrossRef]
- Zhang, C.; Chi, J.N.; Zhang, Z.; Gao, X.; Hu, T.; Wang, Z. Gaze estimation in a gaze tracking system. Sci. China Inf. Sci. 2011, 54, 2295–2306. [Google Scholar] [CrossRef]
- Panero, J.; Zelnik, M. Human Dimension & Interior Space: A Source Book of Design Reference Standards; Watson-Guptill: New York, NY, USA, 1979; p. 320. [Google Scholar]
- Tilley, A.R. The Measure of Man and Woman: Human Factors in Design; Wiley: New York, NY, USA, 2001; p. 112. [Google Scholar]
- Weng, J.; Cohen, P.; Herniou, M. Camera calibration with distortion models and accuracy evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 965–980. [Google Scholar] [CrossRef]
- Böhme, M.; Dorr, M.; Graw, M.; Martinetz, T.; Barth, E. A software framework for simulating eye trackers. In Proceedings of the 2008 Symposium on Eye Tracking Research & Applications (ETRA ’08), Savannah, GA, USA, 26–28 March 2008; ACM: New York, NY, USA, 2008; pp. 251–258. [Google Scholar] [CrossRef]
- Skovsgaard, H.; Agustin, J.S.; Johansen, S.A.; Hansen, J.P.; Tall, M. Evaluation of a remote webcam-based eye tracker. In Proceedings of the 1st Conference on Novel Gaze-Controlled Applications (NGCA ’11), Karlskrona, Sweden, 26–27 May 2011; ACM: New York, NY, USA, 2011; pp. 7:1–7:4. [Google Scholar] [CrossRef]
- Johansen, S.A.; Agustin, J.S.; Skovsgaard, H.; Hansen, J.P.; Tall, M. Low cost vs. high-end eye tracking for usability testing. In Proceedings of the 2011 CHI Extended Abstracts on Human Factors in Computing Systems (CHI EA ’11), Vancouver, BC, Canada, 7–12 May 2011; ACM: New York, NY, USA, 2011; pp. 1177–1182. [Google Scholar] [CrossRef]
- Cattini, S.; Rovati, L. A Simple Calibration Method to Quantify the Effects of Head Movements on Vision-Based Eye-Tracking Systems. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference Proceedings (I2MTC ’16), Taipei, Taiwan, 23–26 May 2016; IEEE Computer Society: Washington, DC, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Brousseau, B.; Rose, J.; Eizenman, M. SmartEye: An Accurate Infrared Eye Tracking System for Smartphones. In Proceedings of the 2018 9th IEEE Annual Ubiquitous Computing, Electronics Mobile Communication Conference (UEMCON ’18), New York, NY, USA, 8–10 November 2018; IEEE Computer Society: Washington, DC, USA, 2018; pp. 951–959. [Google Scholar] [CrossRef]
- Su, D.; Li, Y.F.; Xiong, C. Parallax error compensation for head-mounted gaze trackers based on binocular data. In Proceedings of the 2016 IEEE International Conference on Real-time Computing and Robotics (RCAR ’16), Angkor Wat, Cambodia, 6–10 June 2016; IEEE Computer Society: Washington, DC, USA, 2016; pp. 76–81. [Google Scholar] [CrossRef]
- Li, J.; Li, S.; Chen, T.; Liu, Y. A Geometry-Appearance-Based Pupil Detection Method for Near-Infrared Head-Mounted Cameras. IEEE Access 2018, 6, 23242–23252. [Google Scholar] [CrossRef]
- Hua, H.; Krishnaswamy, P.; Rolland, J.P. Video-based eye tracking methods and algorithms in head-mounted displays. Opt. Express 2006, 14, 4328–4350. [Google Scholar] [CrossRef]
- Pfeuffer, K.; Vidal, M.; Turner, J.; Bulling, A.; Gellersen, H. Pursuit Calibration: Making Gaze Calibration Less Tedious and More Flexible. In Proceedings of the 26th Annual ACM Symposium on User Interface Software and Technology (UIST ’13), St. Andrews, UK, 8–11 October 2013; ACM: New York, NY, USA, 2013; pp. 261–270. [Google Scholar] [CrossRef]
- Blignaut, P. Using smooth pursuit calibration for difficult-to-calibrate participants. J. Eye Mov. Res. 2017, 10, 1–13. [Google Scholar] [CrossRef]
- Bernet, S.; Cudel, C.; Lefloch, D.; Basset, M. Autocalibration-based partioning relationship and parallax relation for head-mounted eye trackers. Mach. Vis. Appl. 2013, 24, 393–406. [Google Scholar] [CrossRef][Green Version]
- Cesqui, B.; van de Langenberg, R.; Lacquaniti, F.; d’Avella, A. A novel method for measuring gaze orientation in space in unrestrained head conditions. J. Vis. 2013, 13, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Kassner, M.; Patera, W.; Bulling, A. Pupil: An Open Source Platform for Pervasive Eye Tracking and Mobile Gaze-Based Interaction. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing (UbiComp ’14), Seattle, WA, USA, 13–17 September 2014; ACM: New York, NY, USA, 2014; pp. 1151–1160. [Google Scholar] [CrossRef]
- Fuhl, W.; Santini, T.C.; Kübler, T.; Kasneci, E. ElSe: Ellipse selection for robust pupil detection in real-world environments. In Proceedings of the 2016 Symposium on Eye Tracking Research & Applications (ETRA ’16), Charleston, SC, USA, 14–17 March 2016; ACM: New York, NY, USA, 2016; pp. 123–130. [Google Scholar] [CrossRef]
- Santini, T.; Fuhl, W.; Kasneci, E. PuReST: Robust Pupil Tracking for Real-Time Pervasive Eye Tracking. In Proceedings of the 2018 Symposium on Eye Tracking Research & Applications (ETRA ’18), Warsaw, Poland, 14–17 June 2018; ACM: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Zhang, X.; Sugano, Y.; Fritz, M.; Bulling, A. Appearance-based gaze estimation in the wild. In Proceedings of the 2015 IEEE Computer Vision and Pattern Recognition (CVPR ’15), Boston, MA, USA, 7–12 June 2015; IEEE Computer Society: Washington, DC, USA, 2015; pp. 4511–4520. [Google Scholar] [CrossRef]
- Krafka, K.; Khosla, A.; Kellnhofer, P.; Kannan, H.; Bhandarkar, S.; Matusik, W.; Torralba, A. Eye Tracking for Everyone. In Proceedings of the 2016 IEEE Computer Vision and Pattern Recognition (CVPR ’16), Las Vegas, NV, USA, 27–30 June 2016; IEEE Computer Society: Washington, DC, USA, 2016; pp. 2176–2184. [Google Scholar] [CrossRef]
- Kellnhofer, P.; Recasens, A.; Stent, S.; Matusik, W.; Torralba, A. Gaze360: Physically Unconstrained Gaze Estimation in the Wild. In Proceedings of the 2019 IEEE International Conference on Computer Vision (ICCV ’19), Seoul, Korea, 27 October–2 November 2019; IEEE Computer Society: Washington, DC, USA, 2019; pp. 6911–6920. [Google Scholar] [CrossRef]
- Xia, Y.; Liang, B. Gaze Estimation Based on Deep Learning Method. In Proceedings of the 4th International Conference on Computer Science and Application Engineering (CSAE ’20), Sanya, China, 20–22 October 2020; ACM: New York, NY, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, H.; Bao, Y.; Lu, F. Appearance-based Gaze Estimation With Deep Learning: A Review and Benchmark. arXiv 2021, arXiv:2104.12668. [Google Scholar]
- Prince, S.J.D. Computer Vision: Models, Learning, and Inference; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Bušta, M.; Drtina, T.; Helekal, D.; Neumann, L.; Matas, J. Efficient Character Skew Rectification in Scene Text Images. In Proceedings of the of Asian Conference on Computer Vision–Workshops (ACCV ’15), Singapore, 1–2 November 2014; Jawahar, C.V., Shan, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 134–146. [Google Scholar] [CrossRef]
- Sigut, J.; Sidha, S.A. Iris center corneal reflection method for gaze tracking using visible light. IEEE Trans. Biomed. Eng. 2011, 58, 411–419. [Google Scholar] [CrossRef] [PubMed]
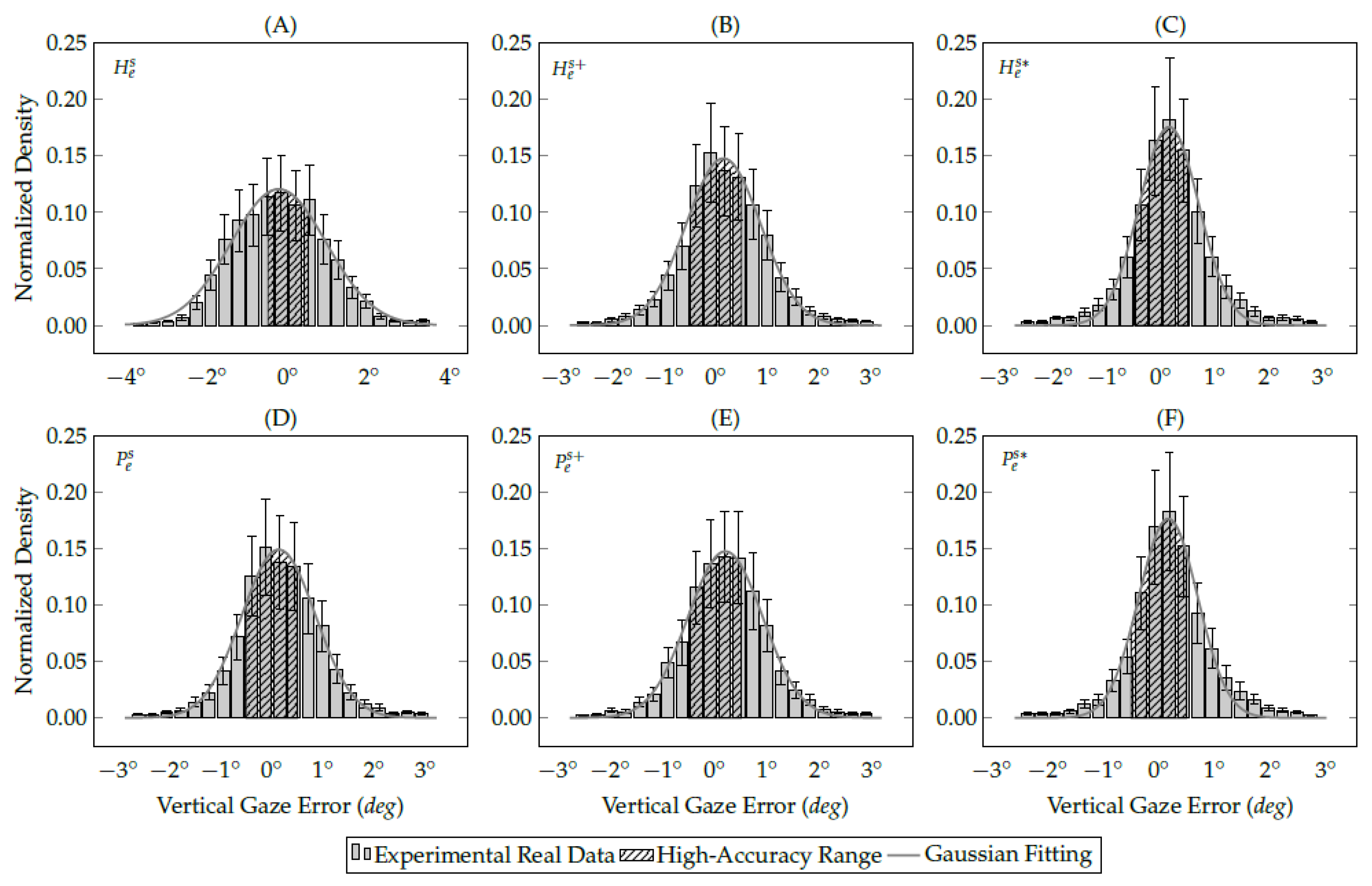
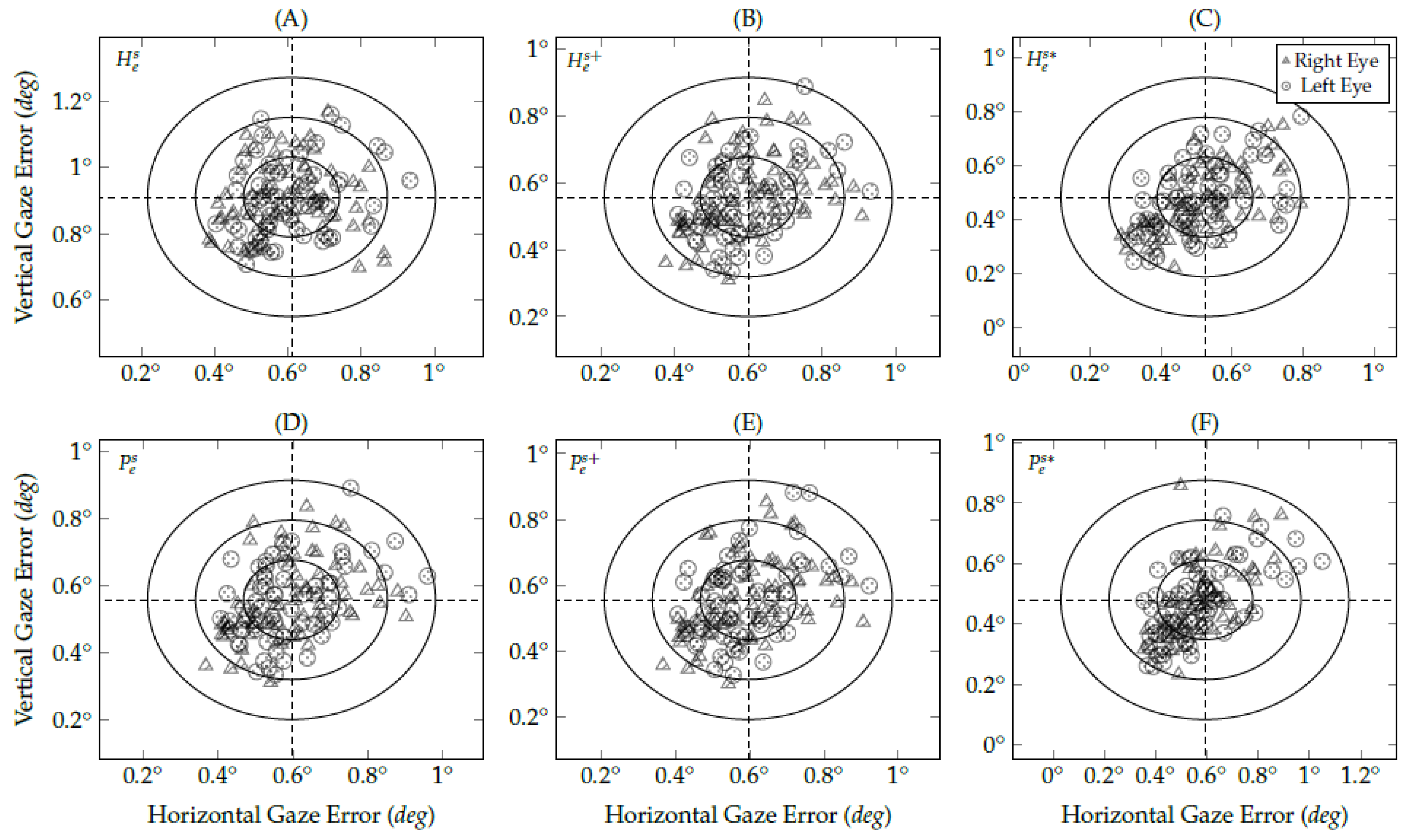
| Methods | Gaze | Gaze | Gaze | Average |
|---|---|---|---|---|
| 0.58 | 0.63 | 1.00 | 0.74 | |
| 0.64 | 0.84 | 1.00 | 0.83 | |
| 0.98 | 1.00 | 1.00 | 0.99 | |
| 0.64 | 0.83 | 1.00 | 0.82 | |
| 0.63 | 0.84 | 1.00 | 0.82 | |
| 0.91 | 0.98 | 1.00 | 0.96 |
| Methods | Gaze | Gaze | Average |
|---|---|---|---|
| 0.50 | 0.32 | 0.41 | |
| 0.50 | 0.50 | 0.50 | |
| 0.51 | 0.62 | 0.57 | |
| 0.47 | 0.50 | 0.49 | |
| 0.49 | 0.50 | 0.50 | |
| 0.55 | 0.63 | 0.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narcizo, F.B.; dos Santos, F.E.D.; Hansen, D.W. High-Accuracy Gaze Estimation for Interpolation-Based Eye-Tracking Methods. Vision 2021, 5, 41. https://doi.org/10.3390/vision5030041
Narcizo FB, dos Santos FED, Hansen DW. High-Accuracy Gaze Estimation for Interpolation-Based Eye-Tracking Methods. Vision. 2021; 5(3):41. https://doi.org/10.3390/vision5030041
Chicago/Turabian StyleNarcizo, Fabricio Batista, Fernando Eustáquio Dantas dos Santos, and Dan Witzner Hansen. 2021. "High-Accuracy Gaze Estimation for Interpolation-Based Eye-Tracking Methods" Vision 5, no. 3: 41. https://doi.org/10.3390/vision5030041
APA StyleNarcizo, F. B., dos Santos, F. E. D., & Hansen, D. W. (2021). High-Accuracy Gaze Estimation for Interpolation-Based Eye-Tracking Methods. Vision, 5(3), 41. https://doi.org/10.3390/vision5030041






