Does Vergence Affect Perceived Size?
Abstract
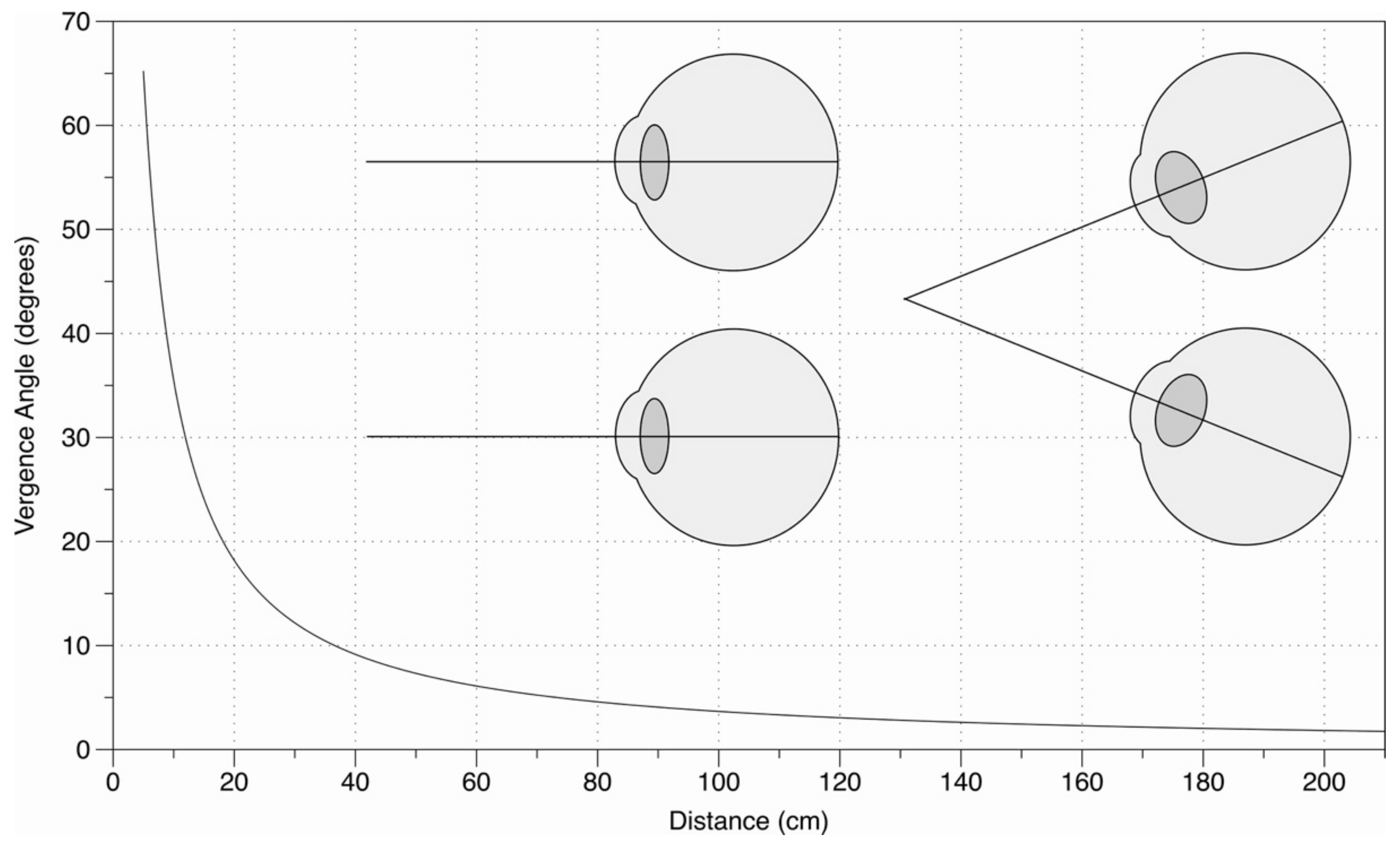
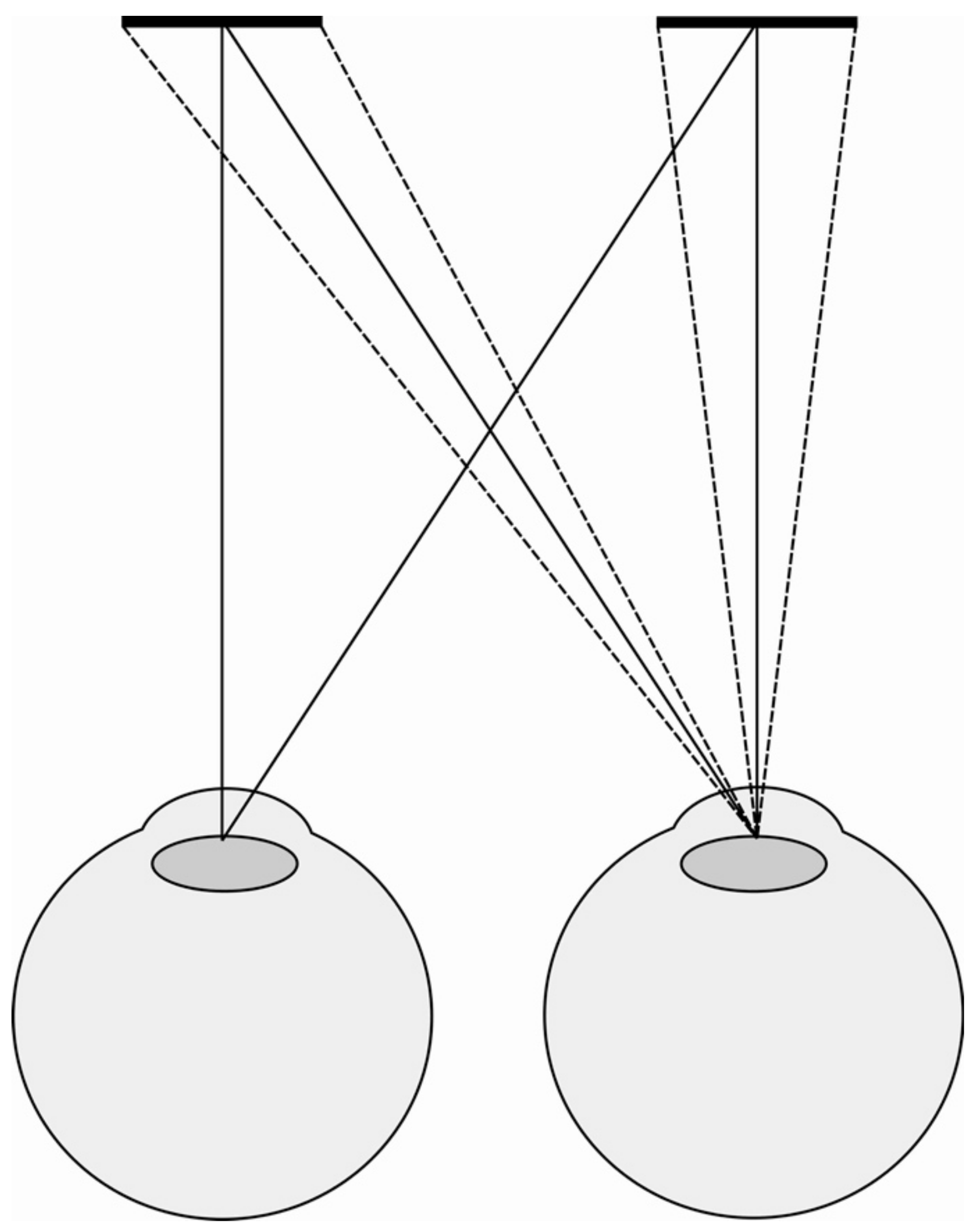
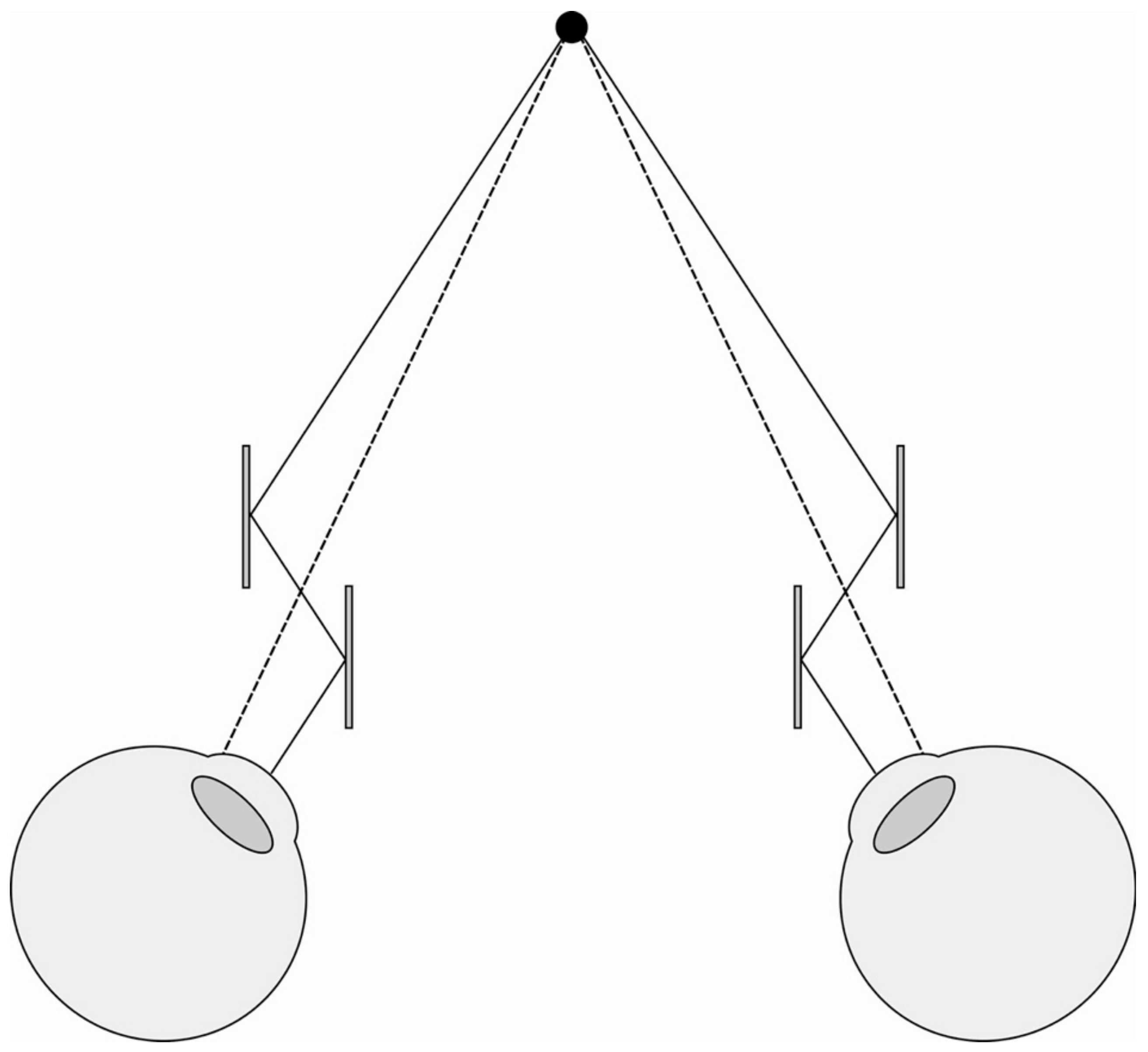
1. Introduction
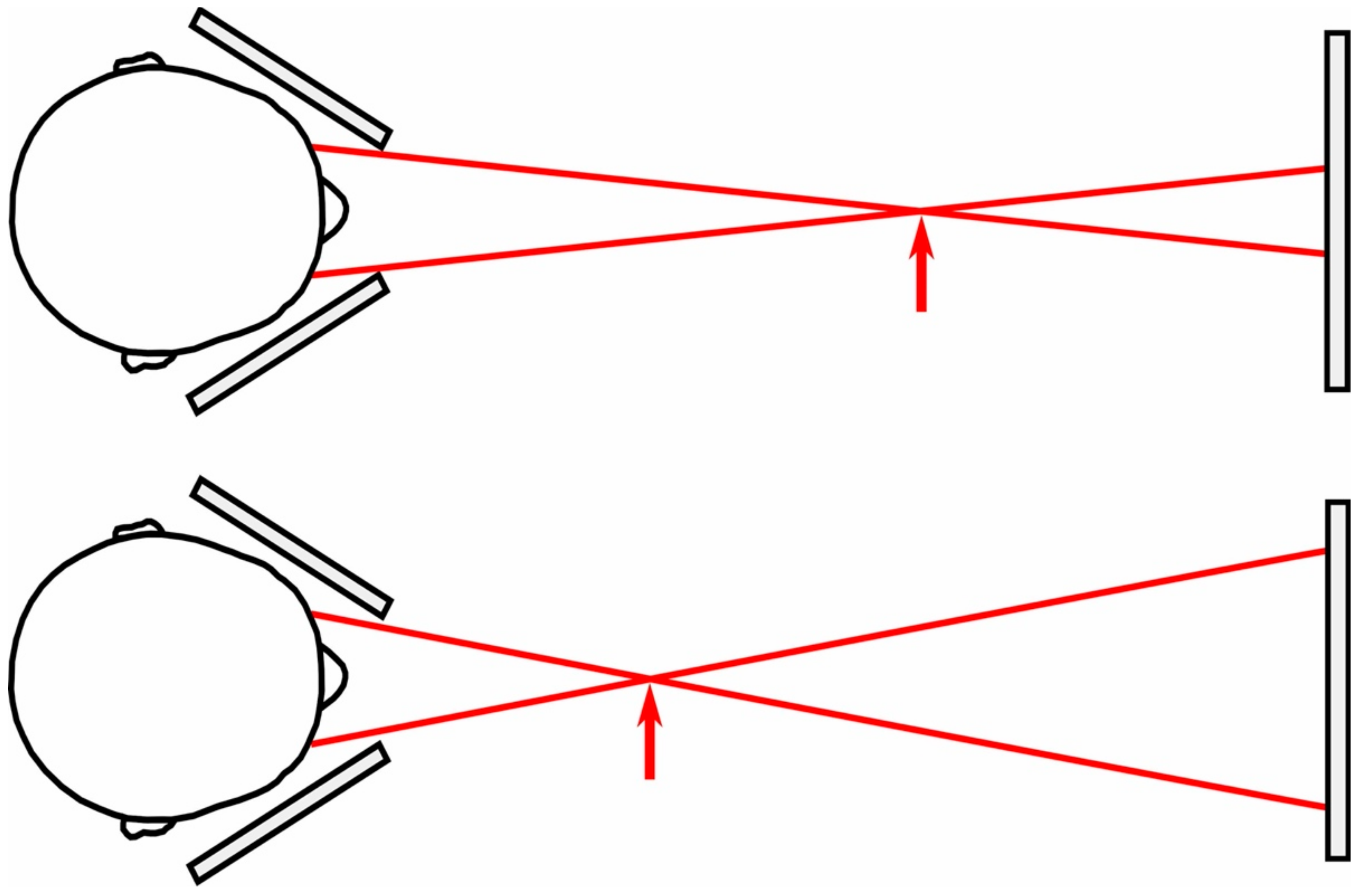
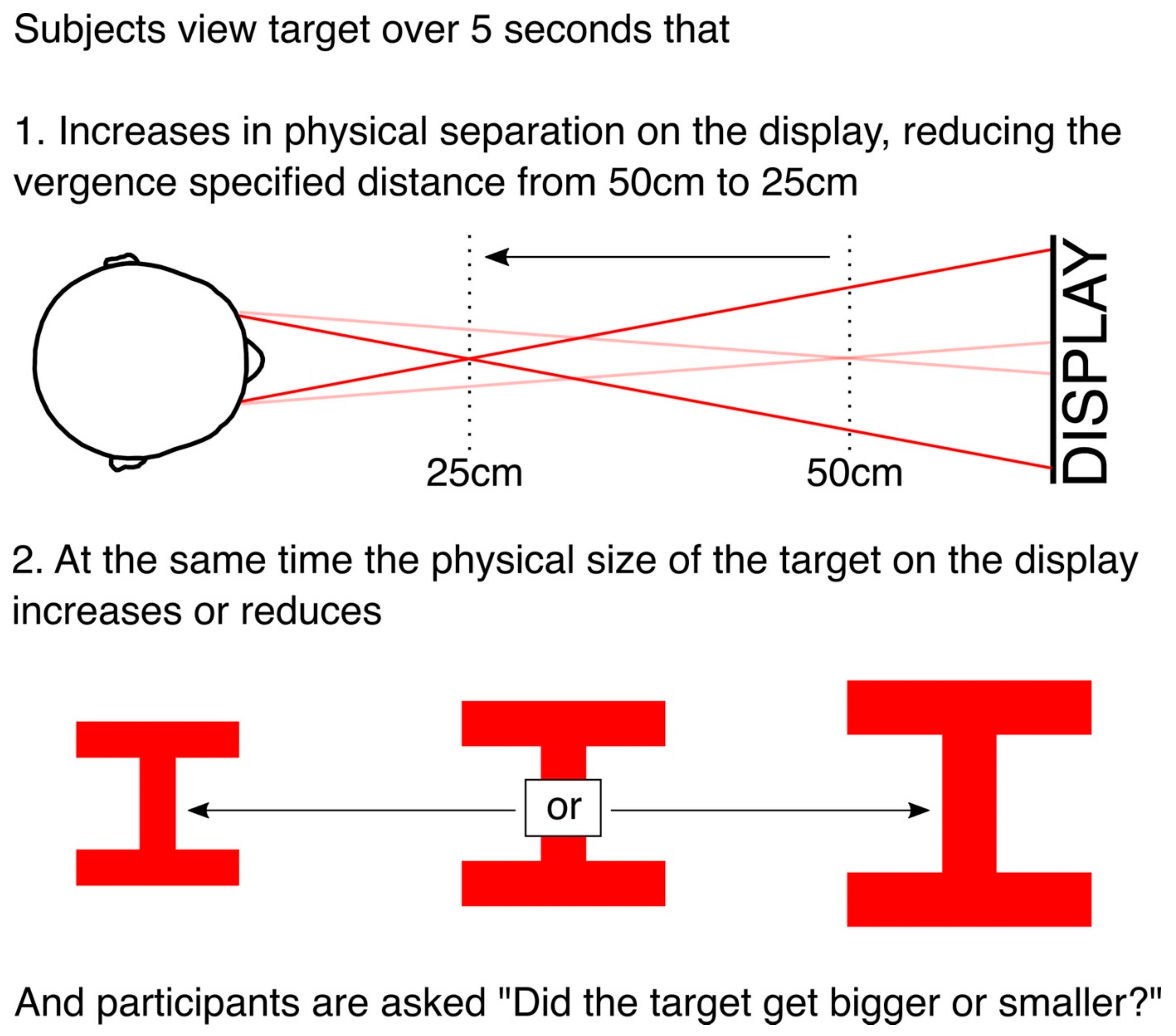
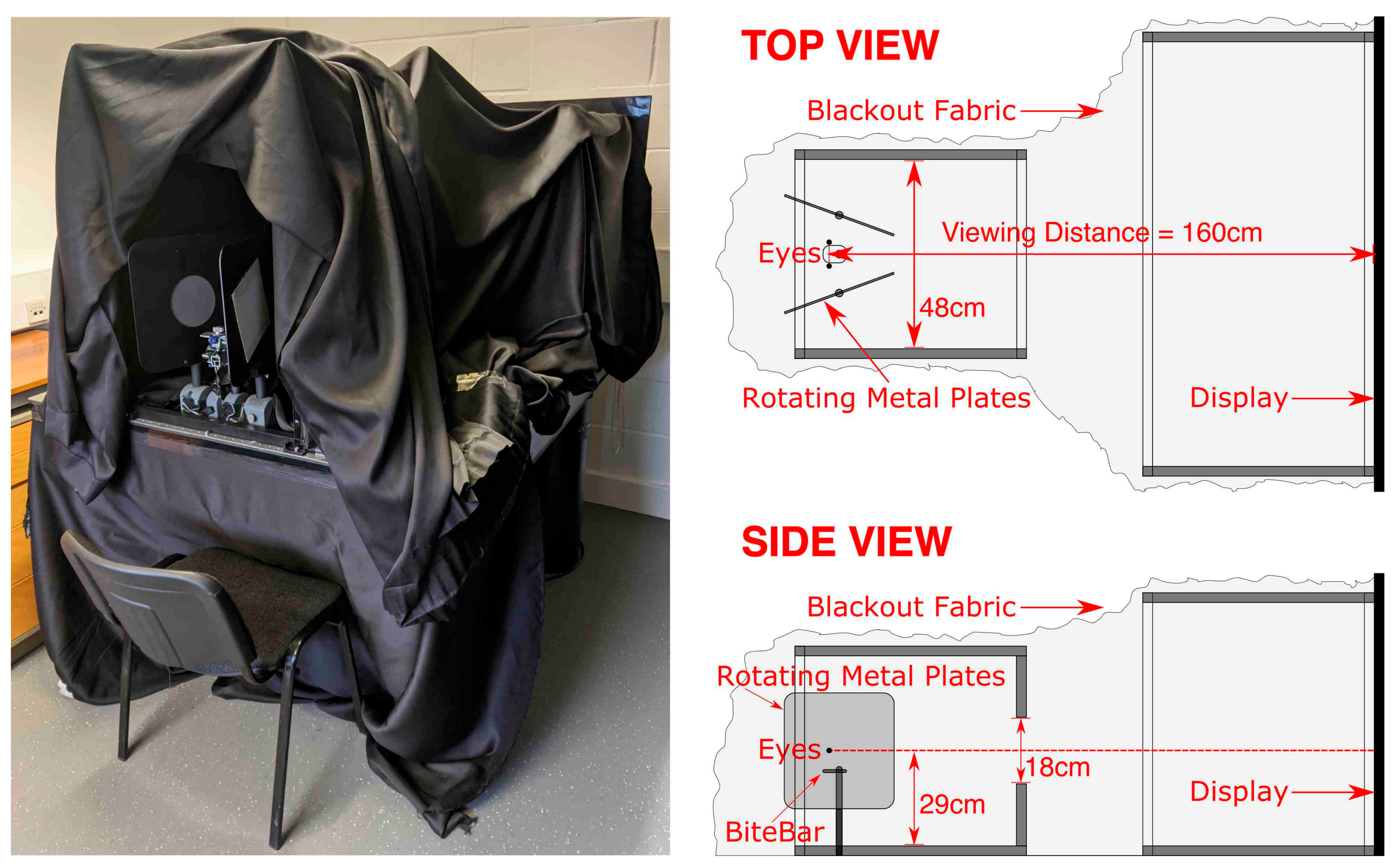
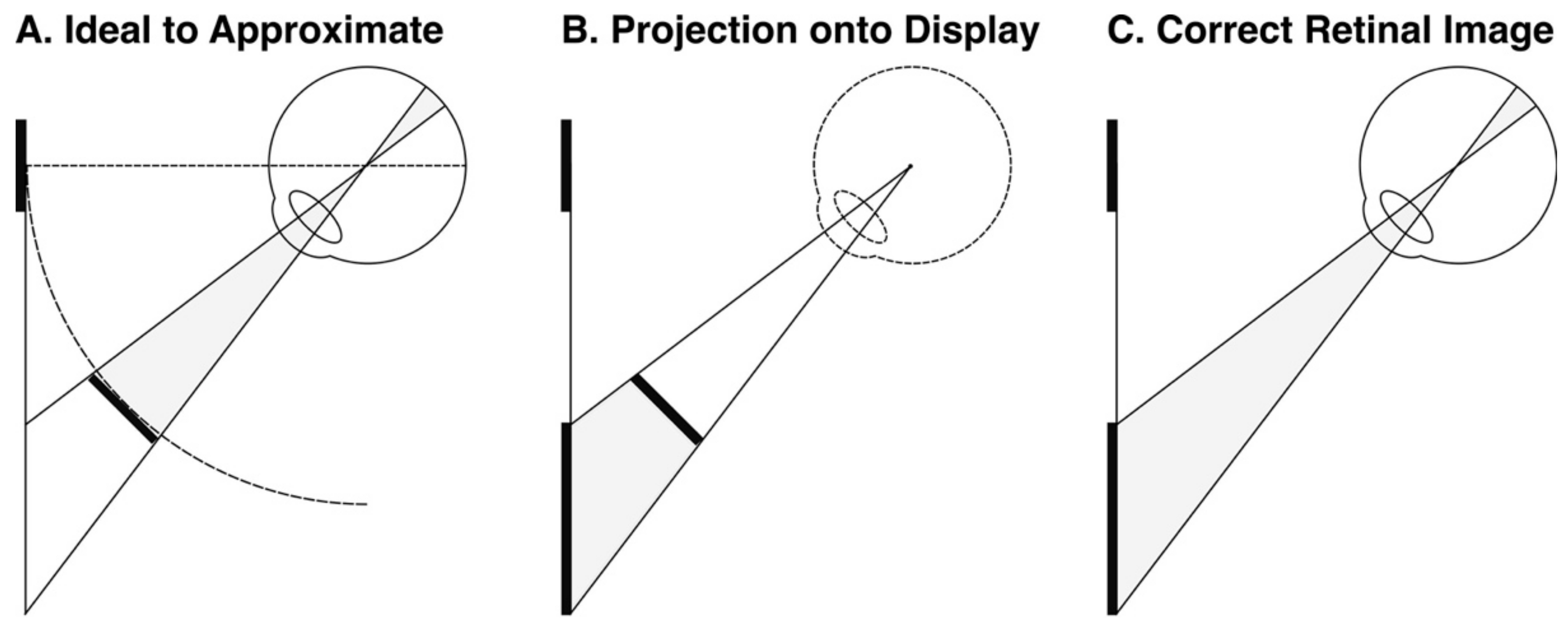
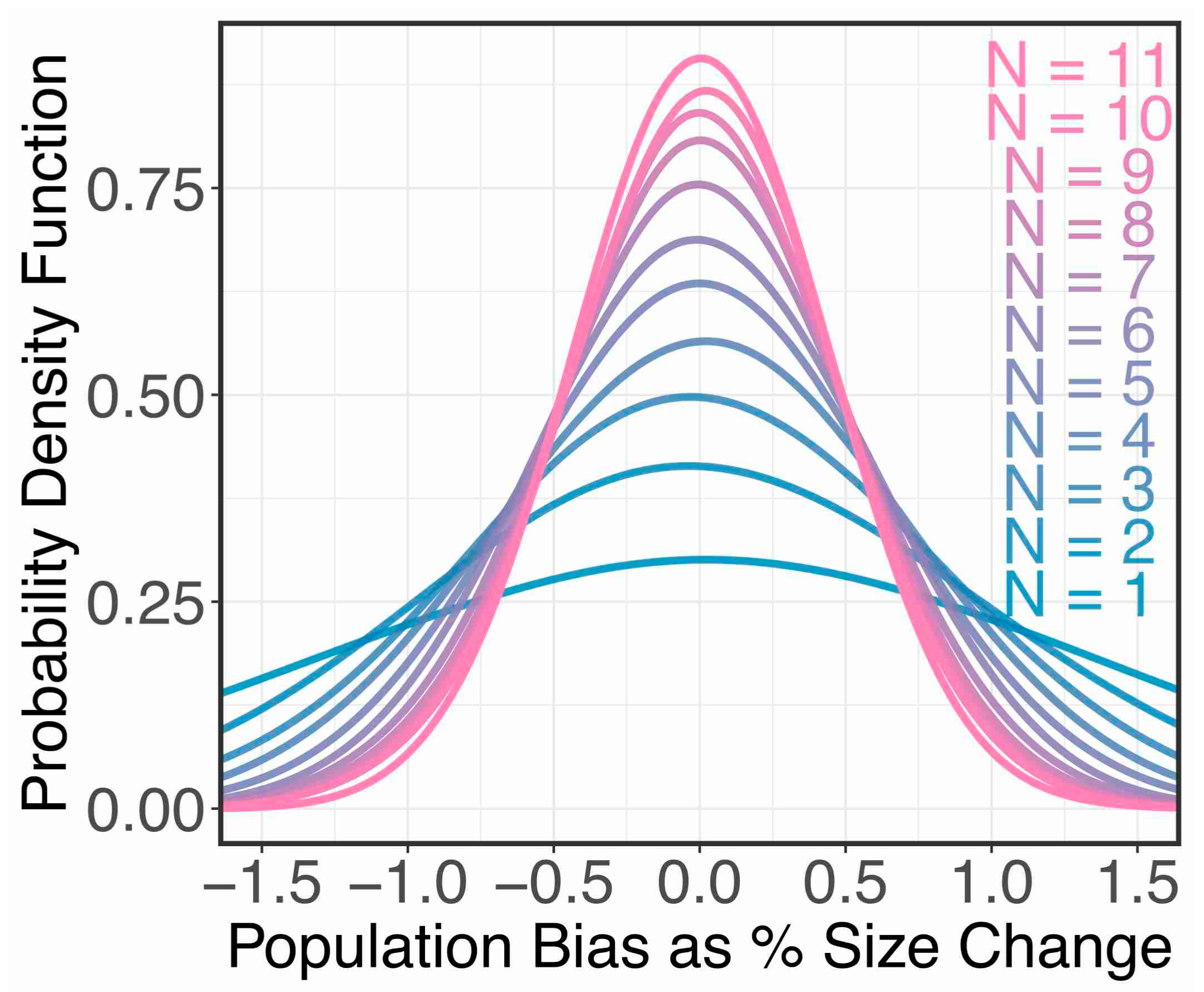
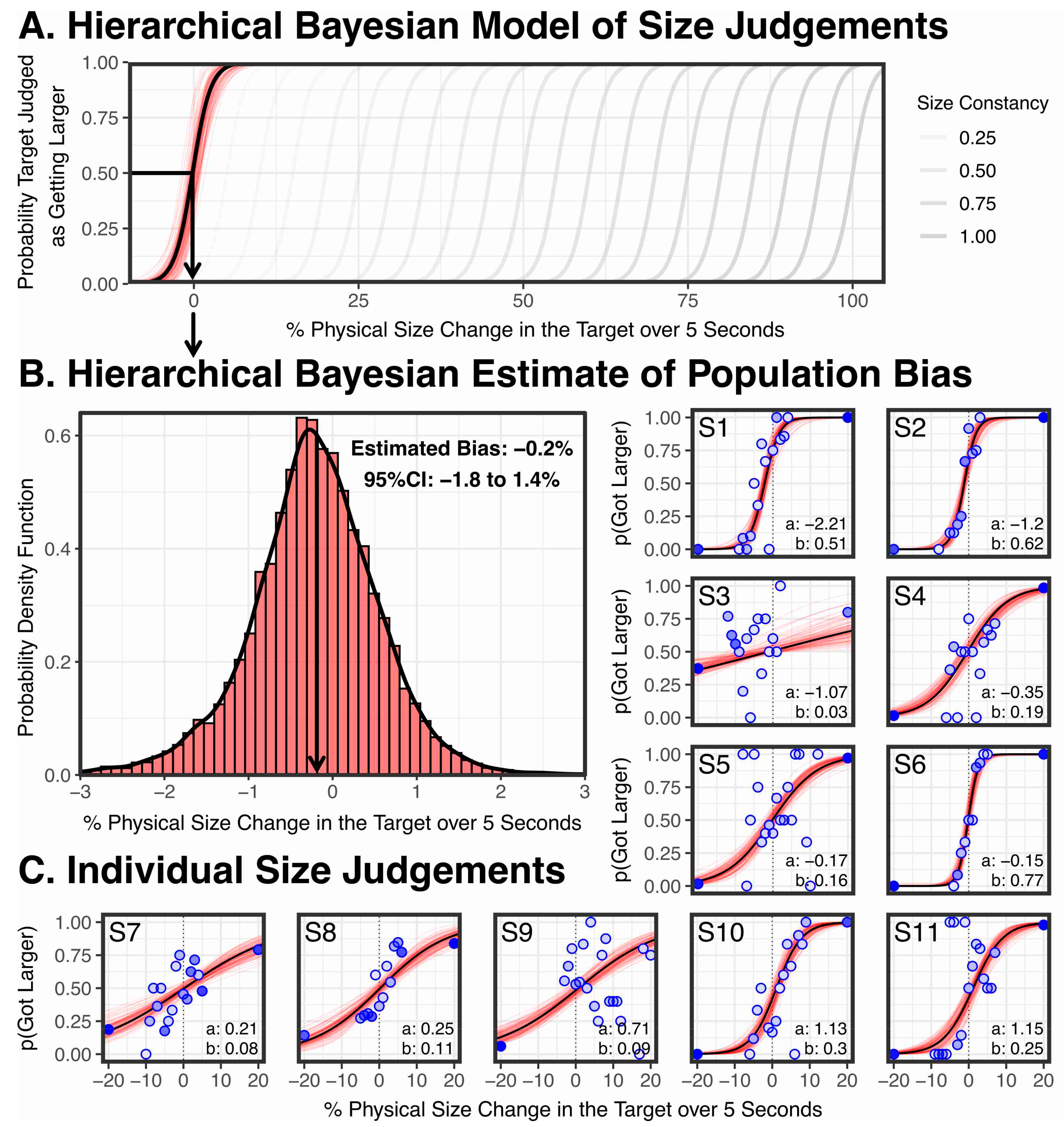
2. Materials and Methods
3. Results
4. Discussion
4.1. Eye Tracking
4.2. Vergence–Accommodation Conflict
4.3. Vergence vs. Looming
4.4. Gradual Changes in Vergence
4.5. Limited Changes in Vergence
4.6. Convergent vs. Divergent Eye Movements
4.7. Vergence Micropsia
4.8. Cognitive Explanation of Vergence Size Constancy
4.9. Multisensory Integration
4.10. Vergence Modulation of V1
4.11. Telestereoscopic Viewing
4.12. Development of Size Constancy
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sperandio, I.; Chouinard, P.A. The Mechanisms of Size Constancy. Multisens. Res. 2015, 28, 253–283. [Google Scholar] [CrossRef] [PubMed]
- Murray, S.O.; Boyaci, H.; Kersten, D. The representation of perceived angular size in human primary visual cortex. Nat. Neurosci. 2006, 9, 429–434. [Google Scholar] [CrossRef] [PubMed]
- Sperandio, I.; Chouinard, P.A.; Goodale, M.A. Retinotopic activity in V1 reflects the perceived and not the retinal size of an afterimage. Nat. Neurosci. 2012, 15, 540–542. [Google Scholar] [CrossRef] [PubMed]
- Leibowitz, H.; Brislin, R.; Perlmutrer, L.; Hennessy, R. Ponzo Perspective Illusion as a Manifestation of Space Perception. Science 1969, 166, 1174–1176. [Google Scholar] [CrossRef]
- Goodale, M.A. How Big is that Banana? Differences in Size Constancy for Perception and Action. 2020. Available online: https://www.youtube.com/watch?v=EbFkPk7Q3Z8 (accessed on 30 September 2020).
- Millard, A.S.; Sperandio, I.; Chouinard, P.A. The contribution of stereopsis in Emmert’s law. Exp. Brain Res. 2020, 238, 1061–1072. [Google Scholar] [CrossRef]
- Emmert, E. Größenverhältnisse der Nachbilder. Klinische Monatsblätter Für Augenheilkunde Und Für Augenärztliche Fortbildung 1881, 19, 443–450. [Google Scholar]
- Combe, E.; Wexler, M. Observer Movement and Size Constancy. Psychol. Sci. 2010, 21, 667–675. [Google Scholar] [CrossRef]
- Brenner, E.; van Damme, W.J. Judging distance from ocular convergence. Vis. Res. 1998, 38, 493–498. [Google Scholar] [CrossRef]
- Linton, P. The Perception and Cognition of Visual Space; Palgrave: London, UK, 2017. [Google Scholar]
- Linton, P. Do We See Scale? 2018. BioRxiv 2018. [Google Scholar] [CrossRef]
- Rogers, B.J.; Bradshaw, M.F. Disparity Scaling and the Perception of Frontoparallel Surfaces. Perception 1995, 24, 155–179. [Google Scholar] [CrossRef]
- Mon-Williams, M.; Tresilian, J.R. Some Recent Studies on the Extraretinal Contribution to Distance Perception. Perception 1999, 28, 167–181. [Google Scholar] [CrossRef]
- Viguier, A.; Clément, G.; Trotter, Y. Distance perception within near visual space. Perception 2001, 30, 115–124. [Google Scholar] [CrossRef]
- Linton, P. Does vision extract absolute distance from vergence? Atten. Percept. Psychophys. 2020, 82, 3176–3195. [Google Scholar] [CrossRef]
- Kepler, J. Paralipomena to Witelo. In Optics: Paralipomena to Witelo and Optical Part of Astronomy; Donahue, W.H., Ed.; Green Lion Press: Santa Fe, Mexico, 2000. [Google Scholar]
- Descartes, R. Dioptrique (Optics). In The Philosophical Writings of Descartes; Cottingham, J., Stoothoff, R., Murdoch, D., Eds.; Cambridge University Press: Cambridge, UK, 1985; Volume 1. [Google Scholar]
- Wheatstone, C. XVIII Contributions to the physiology of vision—Part the first. On some remarkable, and hitherto unobserved, phenomena of binocular vision. Philos. Trans. R. Soc. Lond. 1838, 128, 371–394. [Google Scholar] [CrossRef]
- Smith, R. A Compleat System of Opticks in Four Books, Viz. A Popular, a Mathematical, a Mechanical, and a Philosophical Treatise. To Which Are Added Remarks Upon the Whole; Robert, S., Ed.; Cornelius Crownfield: Cambridge, UK, 1738. [Google Scholar]
- Priestley, J. The History and Present State of Discoveries Relating to Vision, Light, and Colours; J. Johnson: London, UK, 1772. [Google Scholar]
- Von Goethe, J.W. Zur Farbenlehre; Cotta’schen Buchhandlung: Tübingen, Germany, 1810. [Google Scholar]
- Meyer, H. Ueber einige Täuschungen in der Entfernung u. Grösse der Gesichtsobjecte. Arch. Physiol. Heilkd. 1842, 316. [Google Scholar]
- Meyer, H. Ueber die Schätzung der Grösse und der Entfernung der Gesichtsobjecte aus der Convergenz der Augenaxen. Ann. Phys. 1852, 161, 198–207. [Google Scholar] [CrossRef]
- Brewster, D. On the knowledge of distance given by binocular vision. Trans. R. Soc. Edinb. 1844, 15, 663–674. [Google Scholar] [CrossRef]
- Locke, J. XXV. On single and double vision produced by viewing objects with both eyes; and on an optical illusion with regard to the distance of objects. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1849, 34, 195–201. [Google Scholar] [CrossRef]
- Kohly, R.P.; Ono, H. Fixating on the wallpaper illusion: A commentary on “The role of vergence in the perception of distance: A fair test of Bishop Berkeley’s claim” by Logvinenko et al. Spat. Vis. 2001, 15, 377–386. [Google Scholar] [CrossRef]
- Lie, I. Convergence as a cue to perceived size and distance. Scand. J. Psychol. 1965, 6, 109–116. [Google Scholar] [CrossRef]
- Ono, H.; Mitson, L.; Seabrook, K. Change in convergence and retinal disparities as an explanation for the wallpaper phenomenon. J. Exp. Psychol. 1971, 91, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Howard, I.P. Perceiving in Depth, Volume 3: Other Mechanisms of Depth Perception; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Wheatstone, C.I. The Bakerian Lecture.—Contributions to the physiology of vision.—Part the second. On some remarkable, and hitherto unobserved, phenomena of binocular vision (continued). Philos. Trans. R. Soc. Lond. 1852, 142, 1–17. [Google Scholar] [CrossRef]
- Helmholtz, H. Handbuch der Physiologischen Optik, Vol. III; L. Voss: Leipzig, Germany, 1866. [Google Scholar]
- Adams, O.S. Stereogram decentration and stereo-base as factors influencing the apparent size of stereoscopic pictures. Am. J. Psychol. 1955, 68, 54–68. [Google Scholar] [CrossRef] [PubMed]
- Biersdorf, W.R.; Ohwaki, S.; Kozil, D.J. The Effect of Instructions and Oculomotor Adjustments on Apparent Size. Am. J. Psychol. 1963, 76, 1–17. [Google Scholar] [CrossRef]
- Enright, J.T. The eye, the brain and the size of the moon: Toward a unified oculomotor hypothesis for the moon illusion. In The Moon Illusion; Hershenson, M., Ed.; Erlbaum Associates: Mahwah, NJ, USA, 1989; pp. 59–121. [Google Scholar]
- Frank, H. Ueber den Einfluss inadaquater Konvergenz und Akkommodation auf die Sehgrosse. Psychol. Forsch. 1930, 13, 135–144. [Google Scholar] [CrossRef]
- Gogel, W.C. The Effect of Convergence on Perceived Size and Distance. J. Psychol. 1962, 53, 475–489. [Google Scholar] [CrossRef]
- Heinemann, E.G.; Tulving, E.; Nachmias, J. The effect of oculomotor adjustments on apparent size. Am. J. Psychol. 1959, 72, 32–45. [Google Scholar] [CrossRef]
- Hermans, T.G. Visual size constancy as a function of convergence. J. Exp. Psychol. 1937, 21, 145–161. [Google Scholar] [CrossRef]
- Hermans, T.G. The relationship of convergence and elevation changes to judgments of size. J. Exp. Psychol. 1954, 48, 204–208. [Google Scholar] [CrossRef]
- Judd, C.H. Some facts of binocular vision. Psychol. Rev. 1897, 4, 374–389. [Google Scholar] [CrossRef]
- Komoda, M.K.; Ono, H. Oculomotor adjustments and size-distance perception. Percept. Psychophys. 1974, 15, 353–360. [Google Scholar] [CrossRef][Green Version]
- Leibowitz, H.; Moore, D. Role of changes in accommodation and convergence in the perception of size. J. Opt. Soc. Am. 1966, 56, 1120–1129. [Google Scholar] [CrossRef]
- Leibowitz, H.W.; Shiina, K.; Hennessy, R.T. Oculomotor adjustments and size constancy. Percept. Psychophys. 1972, 12, 497–500. [Google Scholar] [CrossRef][Green Version]
- Locke, N.M. Some Factors in Size-Constancy. Am. J. Psychol. 1938, 51, 514–520. [Google Scholar] [CrossRef]
- McCready, D.W. Size-distance perception and accommodation-convergence micropsia—A critique. Vis. Res. 1965, 5, 189–206. [Google Scholar] [CrossRef]
- Regan, D.; Erkelens, C.J.; Collewijn, H. Necessary conditions for the perception of motion in depth. Investig. Ophthalmol. Visual Sci. 1986, 27, 584–597. [Google Scholar]
- Von Holst, E. Aktive Leistungen der menschlichen Gesichtswahrnemung. Stud. General. 1957, 10, 231–243. [Google Scholar]
- Von Holst, E. 1st der Einfluss der Akkommodation auf die gesehene Dinggrijsse ein “reflektorischer” Vorgang? Naturwissenschaften 1955, 42, 445–446. [Google Scholar] [CrossRef]
- Von Holst, E. Die Beteiligung von Konvergenz und Akkommodation an der wahrgenommenen Grossenkonstanz. Naturwissenschaften 1955, 42, 444–445. [Google Scholar] [CrossRef]
- Wallach, H.; Zuckerman, C. The constancy of stereoscopic depth. Am. J. Psychol. 1963, 76, 404–412. [Google Scholar] [CrossRef]
- Helmholtz, H. Das Telestereoskop. Annalen Physik 1857, 178, 167–175. [Google Scholar] [CrossRef]
- Helmholtz, P.H. II. On the telestereoscope. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1858, 15, 19–24. [Google Scholar] [CrossRef]
- Rogers, B. Are stereoscopic cues ignored in telestereoscopic viewing? J. Vis. 2009, 9, 288. [Google Scholar] [CrossRef]
- Rogers, B.J. Information, illusion, and constancy in telestereoscopic viewing. In Vision in 3D Environments; Harris, L.R., Jenkin, M.R.M., Eds.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Newman, D.G.; Ostler, D. Hyperstereopsis Associated with Helmet-Mounted Sighting and Display Systems for Helicopter Pilots. Aerosp. Med. Assoc. 2009. [Google Scholar] [CrossRef]
- Priot, A.E.; Neveu, P.; Philippe, M.; Roumes, C. Adaptation to alterations of apparent distance in stereoscopic displays: From lab to hyperstereopsis. In Proceedings of the 2012 International Conference on 3D Imaging (IC3D), Liege, Belgium, 3–5 December 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Priot, A.-E.; Laboissière, R.; Plantier, J.; Prablanc, C.; Roumes, C. Partitioning the components of visuomotor adaptation to prism-altered distance. Neuropsychologia 2011, 49, 498–506. [Google Scholar] [CrossRef]
- Priot, A.-E.; Laboissière, R.; Sillan, O.; Roumes, C.; Prablanc, C. Adaptation of egocentric distance perception under telestereoscopic viewing within reaching space. Exp. Brain Res. 2010, 202, 825–836. [Google Scholar] [CrossRef][Green Version]
- Priot, A.-E.; Vacher, A.; Vienne, C.; Neveu, P.; Roumes, C. The initial effects of hyperstereopsis on visual perception in helicopter pilots flying with see-through helmet-mounted displays. Displays 2018, 51, 1–8. [Google Scholar] [CrossRef]
- Stuart, G.; Jennings, S.; Kalich, M.; Rash, C.; Harding, T.; Craig, G. Flight performance using a hyperstereo helmet-mounted display: Adaptation to hyperstereopsis. Proc. SPIE Int. Soc. Opt. Eng. 2009, 7326. [Google Scholar] [CrossRef]
- Taylor, F.V. Change in size of the afterimage induced in total darkness. J. Exp. Psychol. 1941, 29, 75–80. [Google Scholar] [CrossRef]
- Mon-Williams, M.; Tresilian, J.R.; Plooy, A.; Wann, J.P.; Broerse, J. Looking at the task in hand: Vergence eye movements and perceived size. Exp. Brain Res. 1997, 117, 501–506. [Google Scholar] [CrossRef] [PubMed]
- Morrison, J.D.; Whiteside, T.C. Binocular cues in the perception of distance of a point source of light. Perception 1984, 13, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Sperandio, I.; Kaderali, S.; Chouinard, P.A.; Frey, J.; Goodale, M.A. Perceived size change induced by nonvisual signals in darkness: The relative contribution of vergence and proprioception. J. Neurosci. Off. J. Soc. Neurosci. 2013, 33, 16915–16923. [Google Scholar] [CrossRef] [PubMed]
- Bross, M. Emmert’s law in the dark: Active and passive proprioceptive effects on positive visual afterimages. Perception 2000, 29, 1385–1391. [Google Scholar] [CrossRef] [PubMed]
- Carey, D.P.; Allan, K. A motor signal and “visual” size perception. Exp. Brain Res. 1996, 110, 482–486. [Google Scholar] [CrossRef]
- Faivre, N.; Dönz, J.; Scandola, M.; Dhanis, H.; Ruiz, J.B.; Bernasconi, F.; Salomon, R.; Blanke, O. Self-Grounded Vision: Hand Ownership Modulates Visual Location through Cortical β and γ Oscillations. J. Neurosci. 2017, 37, 11–22. [Google Scholar] [CrossRef]
- Gregory, R.L.; Wallace, J.G.; Campbell, F.W. Changes in the size and shape of visual after-images observed in complete darkness during changes of position in space. Q. J. Exp. Psychol. 1959, 11, 54–55. [Google Scholar] [CrossRef]
- Ramsay, A.I.G.; Carey, D.P.; Jackson, S.R. Visual-proprioceptive mismatch and the Taylor illusion. Exp. Brain Res. 2007, 176, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Lou, L. Apparent Afterimage Size, Emmert’s Law, and Oculomotor Adjustment. Perception 2007, 36, 1214–1228. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, K. Effects of oculomotor cues on the apparent size of afterimages. Jpn. Psychol. Res. 1986, 28, 168–175. [Google Scholar] [CrossRef]
- Urist, M.J. Afterimages and ocular muscle proprioception. AMA Arch. Ophthalmol. 1959, 61, 230–232. [Google Scholar] [CrossRef] [PubMed]
- Zenkin, G.M.; Petrov, A.P. Transformation of the Visual Afterimage Under Subject’s Eye and Body Movements and the Visual Field Constancy Mechanisms. Perception 2015, 44, 973–985. [Google Scholar] [CrossRef] [PubMed]
- Marin, F.; Rohatgi, A.; Charlot, S. WebPlotDigitizer, a polyvalent and free software to extract spectra from old astronomical publications: Application to ultraviolet spectropolarimetry. arXiv 2017, arXiv:1708.02025. [Google Scholar]
- Ono, H.; Comerford, J. Stereoscopic depth constancy. In Stability and Constancy in Visual Perception: Mechanisms and Process; Epstein, W., Ed.; Wiley: Hoboken, NJ, USA, 1977. [Google Scholar]
- Bishop, P.O. Vertical Disparity, Egocentric Distance and Stereoscopic Depth Constancy: A New Interpretation. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1989, 237, 445–469. [Google Scholar]
- Konrad, R.; Angelopoulos, A.; Wetzstein, G. Gaze-Contingent Ocular Parallax Rendering for Virtual Reality. arXiv 2019, arXiv:1906.09740. [Google Scholar]
- Linton, P. Would Gaze-Contingent Rendering Improve Depth Perception in Virtual and Augmented Reality? arXiv 2019, arXiv:1905.10366v1. [Google Scholar]
- Hoffman, D.M.; Girshick, A.R.; Akeley, K.; Banks, M.S. Vergence–accommodation conflicts hinder visual performance and cause visual fatigue. J. Vis. 2008, 8, 33. [Google Scholar] [CrossRef]
- Brainard, D.H. mQUESTPlus: A Matlab Implementation of QUEST+. Available online: https://github.com/brainardlab/mQUESTPlus (accessed on 30 September 2020).
- Watson, A.B. QUEST+: A general multidimensional Bayesian adaptive psychometric method. J. Vis. 2017, 17, 10. [Google Scholar] [CrossRef]
- Lakens, D.; Scheel, A.M.; Isager, P.M. Equivalence Testing for Psychological Research: A Tutorial. Adv. Methods Pract. Psychol. Sci. 2018, 1, 259–269. [Google Scholar] [CrossRef]
- Kleiner, M.; Brainard, D.; Pelli, D. What’s new in Psychtoolbox-3?” Perception 36 ECVP Abstract Supplement. PLoS ONE 2007, 36. [Google Scholar]
- Prins, N.; Kingdom, F.A.A. Applying the Model-Comparison Approach to Test Specific Research Hypotheses in Psychophysical Research Using the Palamedes Toolbox. Front. Psychol. 2018, 9, 1250. [Google Scholar] [CrossRef]
- Prins, N.; Kingdom, F.A.A. Available online: http://www.palamedestoolbox.org/hierarchicalbayesian.html (accessed on 30 September 2020).
- Rouder, J.N.; Speckman, P.L.; Sun, D.; Morey, R.D.; Iverson, G. Bayesian t tests for accepting and rejecting the null hypothesis. Psychon. Bull. Rev. 2009, 16, 225–237. [Google Scholar] [CrossRef]
- Hooge, I.T.C.; Hessels, R.S.; Nyström, M. Do pupil-based binocular video eye trackers reliably measure vergence? Vis. Res. 2019, 156, 1–9. [Google Scholar] [CrossRef]
- Siegel, H.; Duncan, C.P. Retinal Disparity and Diplopia vs. Luminance and Size of Target. Am. J. Psychol. 1960, 73, 280–284. [Google Scholar] [CrossRef]
- Choe, K.W.; Blake, R.; Lee, S.-H. Pupil size dynamics during fixation impact the accuracy and precision of video-based gaze estimation. Vis. Res. 2016, 118, 48–59. [Google Scholar] [CrossRef]
- Drewes, J.; Zhu, W.; Hu, Y.; Hu, X. Smaller Is Better: Drift in Gaze Measurements due to Pupil Dynamics. PLoS ONE 2014, 9, e111197. [Google Scholar] [CrossRef]
- Wildenmann, U.; Schaeffel, F. Variations of pupil centration and their effects on video eye tracking. Ophthalmic Physiol. Opt. 2013, 33, 634–641. [Google Scholar] [CrossRef]
- Wyatt, H.J. The human pupil and the use of video-based eyetrackers. Vis. Res. 2010, 50, 1982–1988. [Google Scholar] [CrossRef]
- Balaban, C.D.; Kiderman, A.; Szczupak, M.; Ashmore, R.C.; Hoffer, M.E. Patterns of Pupillary Activity During Binocular Disparity Resolution. Front. Neurol. 2018, 9. [Google Scholar] [CrossRef]
- Naber, M.; Nakayama, K. Pupil responses to high-level image content. J. Vis. 2013, 13, 7. [Google Scholar] [CrossRef]
- González, E.G.; Allison, R.S.; Ono, H.; Vinnikov, M. Cue conflict between disparity change and looming in the perception of motion in depth. Vis. Res. 2010, 50, 136–143. [Google Scholar] [CrossRef]
- Faivre, N.; Arzi, A.; Lunghi, C.; Salomon, R. Consciousness is more than meets the eye: A call for a multisensory study of subjective experience. Neurosci. Conscious. 2017. [Google Scholar] [CrossRef] [PubMed]
- Grove, C.; Cardinali, L.; Sperandio, I. Does Tool-Use Modulate the Perceived Size of an Afterimage During the Taylor Illusion? Perception 2019, 48, 181. [Google Scholar]
- Firestone, C.; Scholl, B.J. Cognition does not affect perception: Evaluating the evidence for “top-down” effects. Behav. Brain Sci. 2016, 39, e229. [Google Scholar] [CrossRef] [PubMed]
- Fodor, J.A. The Modularity of Mind: An Essay on Faculty Psychology; MIT Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Pylyshyn, Z. Is vision continuous with cognition?: The case for cognitive impenetrability of visual perception. Behav. Brain Sci. 1999, 22, 341–365. [Google Scholar] [CrossRef]
- Chen, J.; Sperandio, I.; Goodale, M.A. Proprioceptive Distance Cues Restore Perfect Size Constancy in Grasping, but Not Perception, When Vision Is Limited. Curr. Biol. 2018, 28, 927–932.e4. [Google Scholar] [CrossRef]
- Faivre, N.; Salomon, R.; Blanke, O. Visual consciousness and bodily self-consciousness. Curr. Opin. Neurol. 2015, 28, 23–28. [Google Scholar] [CrossRef]
- Gepshtein, S.; Burge, J.; Ernst, M.O.; Banks, M.S. The combination of vision and touch depends on spatial proximity. J. Vis. 2005, 5, 7. [Google Scholar] [CrossRef]
- Hillis, J.M.; Ernst, M.O.; Banks, M.S.; Landy, M.S. Combining Sensory Information: Mandatory Fusion Within, but Not Between, Senses. Science 2002, 298, 1627–1630. [Google Scholar] [CrossRef]
- Ash, A.; Palmisano, S.; Kim, J. Vection in Depth during Consistent and Inconsistent Multisensory Stimulation. Perception 2011, 40, 155–174. [Google Scholar] [CrossRef]
- Fischer, M.H.; Kornmüller, A.E. Optokinetic-Induced Motion Perception and Optokinetic Nystagmus. J. Psychol. Neurol. 1930, 41, 273–308. [Google Scholar]
- Linton, P. V1 as an Egocentric Cognitive Map. PsyArXiv 2021. [Google Scholar] [CrossRef]
- Trotter, Y.; Celebrini, S.; Stricanne, B.; Thorpe, S.; Imbert, M. Modulation of neural stereoscopic processing in primate area V1 by the viewing distance. Science 1992, 257, 1279–1281. [Google Scholar] [CrossRef]
- Cottereau, B.; Durand, J.-B.; Vayssière, N.; Trotter, Y. The influence of eye vergence on retinotopic organization in human early visual cortex. Percept. ECVP Abstr. 2014, 81. [Google Scholar] [CrossRef]
- Cumming, B.G.; Parker, A.J. Binocular Neurons in V1 of Awake Monkeys Are Selective for Absolute, Not Relative, Disparity. J. Neurosci. 1999, 19, 5602–5618. [Google Scholar] [CrossRef]
- Dobbins, A.C.; Jeo, R.M.; Fiser, J.; Allman, J.M. Distance Modulation of Neural Activity in the Visual Cortex. Science 1998, 281, 552–555. [Google Scholar] [CrossRef]
- Trotter, Y.; Celebrini, S.; Stricanne, B.; Thorpe, S.; Imbert, M. Neural processing of stereopsis as a function of viewing distance in primate visual cortical area V1. J. Neurophysiol. 1996, 76, 2872–2885. [Google Scholar] [CrossRef]
- Trotter, Y.; Celebrini, S.; Trotter, Y.; Celebrini, S. Gaze direction controls response gain in primary visual-cortex neurons. Nature 1999, 398, 239–242. [Google Scholar] [CrossRef]
- Trotter, Y.; Celebrini, S.; Durand, J.B. Evidence for implication of primate area V1 in neural 3-D spatial localization processing. J. Physiol. Paris 2004, 98, 125–134. [Google Scholar] [CrossRef]
- Trotter, Y.; Stricanne, B.; Celebrini, S.; Thorpe, S.; Imbert, M. Neural Processing of Stereopsis as a Function of Viewing Distance; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Gnadt, J.W.; Mays, L.E. Depth tuning in area LIP by disparity and accommodative cues. Soc. Neurosci. Abs. 1991, 17, 1113. [Google Scholar]
- Gnadt, J.W.; Mays, L.E. Neurons in monkey parietal area LIP are tuned for eye-movement parameters in three-dimensional space. J. Neurophysiol. 1995, 73, 280–297. [Google Scholar] [CrossRef]
- Quinlan, D.J.; Culham, J.C. FMRI reveals a preference for near viewing in the human parieto-occipital cortex. NeuroImage 2007, 36, 167–187. [Google Scholar] [CrossRef]
- Culham, J.; Gallivan, J.; Cavina-Pratesi, C.; Quinlan, D. FMRI investigations of reaching and ego space in human superior parieto-occipital cortex. In Embodiment, Ego-Space and Action; Klatzky, R.L., MacWhinney, B., Behrman, M., Eds.; Psychology Press: New York, NY, USA, 2008; pp. 247–274. [Google Scholar]
- Richards, W. Spatial remapping in the primate visual system. Kybernetik 1968, 4, 146–156. [Google Scholar] [CrossRef]
- Lehky, S.; Pouget, A.; Sejnowski, T. Neural Models of Binocular Depth Perception. Cold Spring Harb. Symp. Quant. Biol. 1990, 55, 765–777. [Google Scholar] [CrossRef]
- Pouget, A.; Sejnowski, T.J. A neural model of the cortical representation of egocentric distance. Cereb. Cortex 1994, 4, 314–329. [Google Scholar] [CrossRef]
- Chen, J.; Sperandio, I.; Henry, M.J.; Goodale, M.A. Changing the Real Viewing Distance Reveals the Temporal Evolution of Size Constancy in Visual Cortex. Curr. Biol. 2019, 29, 2237–2243.e4. [Google Scholar] [CrossRef]
- Johnston, E.B. Systematic distortions of shape from stereopsis. Vis. Res. 1991, 31, 1351–1360. [Google Scholar] [CrossRef]
- Saleem, A.B.; Diamanti, E.M.; Fournier, J.; Harris, K.D.; Carandini, M. Coherent encoding of subjective spatial position in visual cortex and hippocampus. Nature 2018, 562, 124–127. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C. The Role of the Vertical Dimension in Stereoscopic Vision. Perception 1982, 11, 377–386. [Google Scholar] [CrossRef]
- Mayhew, J. The Interpretation of Stereo-Disparity Information: The Computation of Surface Orientation and Depth. Perception 1982, 11, 387–407. [Google Scholar] [CrossRef]
- Mayhew, J.E.W.; Longuet-Higgins, H.C. A computational model of binocular depth perception. Nature 1982, 297, 376–378. [Google Scholar] [CrossRef]
- Gillam, B.; Lawergren, B. The induced effect, vertical disparity, and stereoscopic theory. Percept. Psychophys. 1983, 34, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Rogers, B. Perception: A Very Short Introduction; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Cumming, B.G.; Johnston, E.B.; Parker, A.J. Vertical Disparities and Perception of Three-Dimensional Shape. Nat. Lond. 1991, 349, 411–413. [Google Scholar] [CrossRef] [PubMed]
- Sobel, E.C.; Collett, T.S. Does vertical disparity scale the perception of stereoscopic depth? Proc. R. Soc. Lond. Ser. B Biol. Sci. 1991, 244, 87–90. [Google Scholar] [CrossRef]
- Vienne, C.; Plantier, J.; Neveu, P.; Priot, A.-E. The Role of Vertical Disparity in Distance and Depth Perception as Revealed by Different Stereo-Camera Configurations. I-Perception 2016, 7. [Google Scholar] [CrossRef]
- Linton, P. Does Human Vision Triangulate Absolute Distance. British Machine Vision Association: 3D Worlds from 2D Images in Humans and Machines. 2020. Available online: https://www.youtube.com/watch?v=6P3EYCEn52A (accessed on 30 September 2020).
- Tehrani, M.A.; Majumder, A.; Gopi, M. Correcting perceived perspective distortions using object specific planar transformations. In Proceedings of the IEEE International Conference on Computational Photography (ICCP), Evanston, IL, USA, 13–15 May 2016. [Google Scholar] [CrossRef]
- Gogel, W.C. The Sensing of Retinal Size. Vis. Res. 1969, 9, 1079–1094. [Google Scholar] [CrossRef]
- Predebon, J. The role of instructions and familiar size in absolute judgments of size and distance. Percept. Psychophys. 1992, 51, 344–354. [Google Scholar] [CrossRef]
- Bower, T.G.R. Stimulus variables determining space perception in infants. Science 1965, 149, 88–89. [Google Scholar] [CrossRef]
- Granrud, C.E. Size constancy in newborn human infants [ARVO Abstract]. Investig. Ophthalmol. Visual Sci. 1987, 28, 5. [Google Scholar]
- Slater, A.; Mattock, A.; Brown, E. Size constancy at birth: Newborn infants’ responses to retinal and real size. J. Exp. Child. Psychol. 1990, 49, 314–322. [Google Scholar] [CrossRef]
- Gregory, R.L.; Wallace, J.G. Recovery from early blindness. Exp. Psychol. Soc. Monogr. 1963, 2, 65–129. [Google Scholar]
- Šikl, R.; Šimecček, M.; Porubanová-Norquist, M.; Bezdíček, O.; Kremláček, J.; Stodůlka, P.; Fine, I.; Ostrovsky, Y. Vision after 53 years of blindness. I-Perception 2013, 4, 498–507. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linton, P. Does Vergence Affect Perceived Size? Vision 2021, 5, 33. https://doi.org/10.3390/vision5030033
Linton P. Does Vergence Affect Perceived Size? Vision. 2021; 5(3):33. https://doi.org/10.3390/vision5030033
Chicago/Turabian StyleLinton, Paul. 2021. "Does Vergence Affect Perceived Size?" Vision 5, no. 3: 33. https://doi.org/10.3390/vision5030033
APA StyleLinton, P. (2021). Does Vergence Affect Perceived Size? Vision, 5(3), 33. https://doi.org/10.3390/vision5030033



