An Adaptive Homeostatic Algorithm for the Unsupervised Learning of Visual Features
Abstract
1. Introduction: Reconciling Competition and Cooperation
2. Unsupervised Learning and the Optimal Representation of Images
2.1. Algorithm: Sparse Coding with a Control Mechanism for the Selection of Atoms
| Algorithm 1 Generalized Matching Pursuit: |
|
2.2. Algorithm: Histogram Equalization Homeostasis
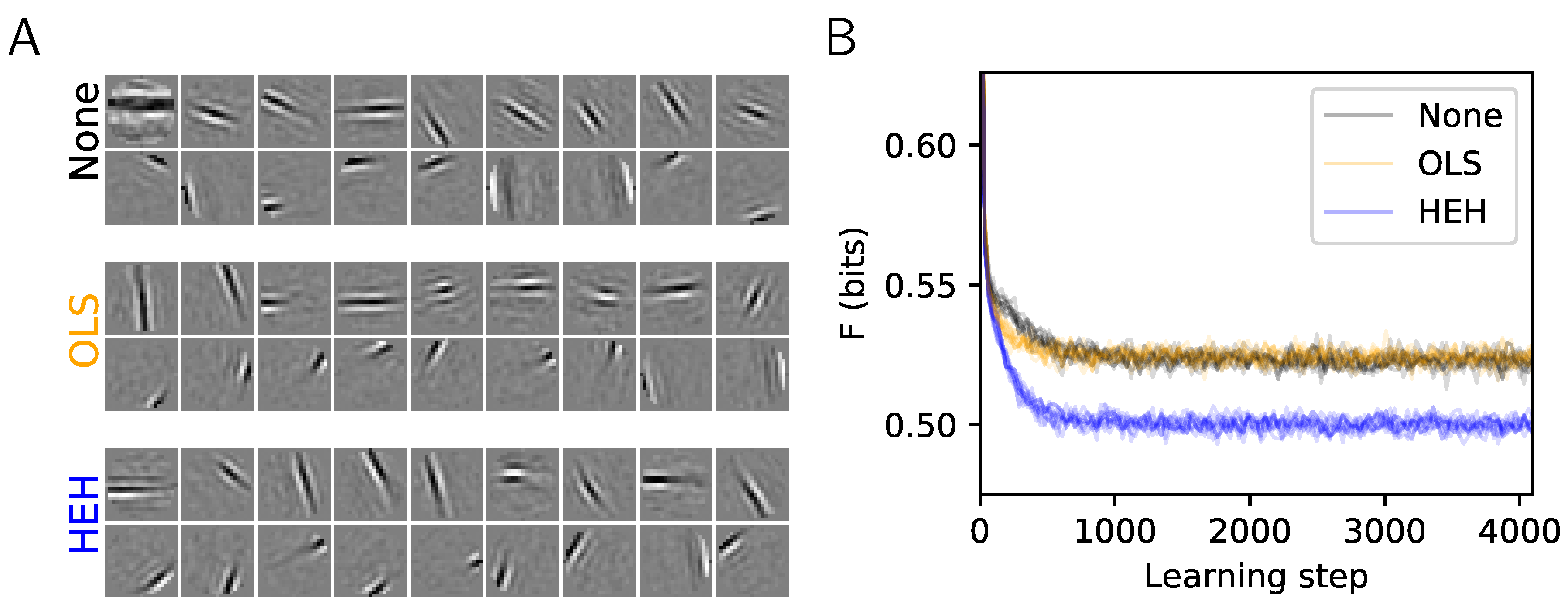
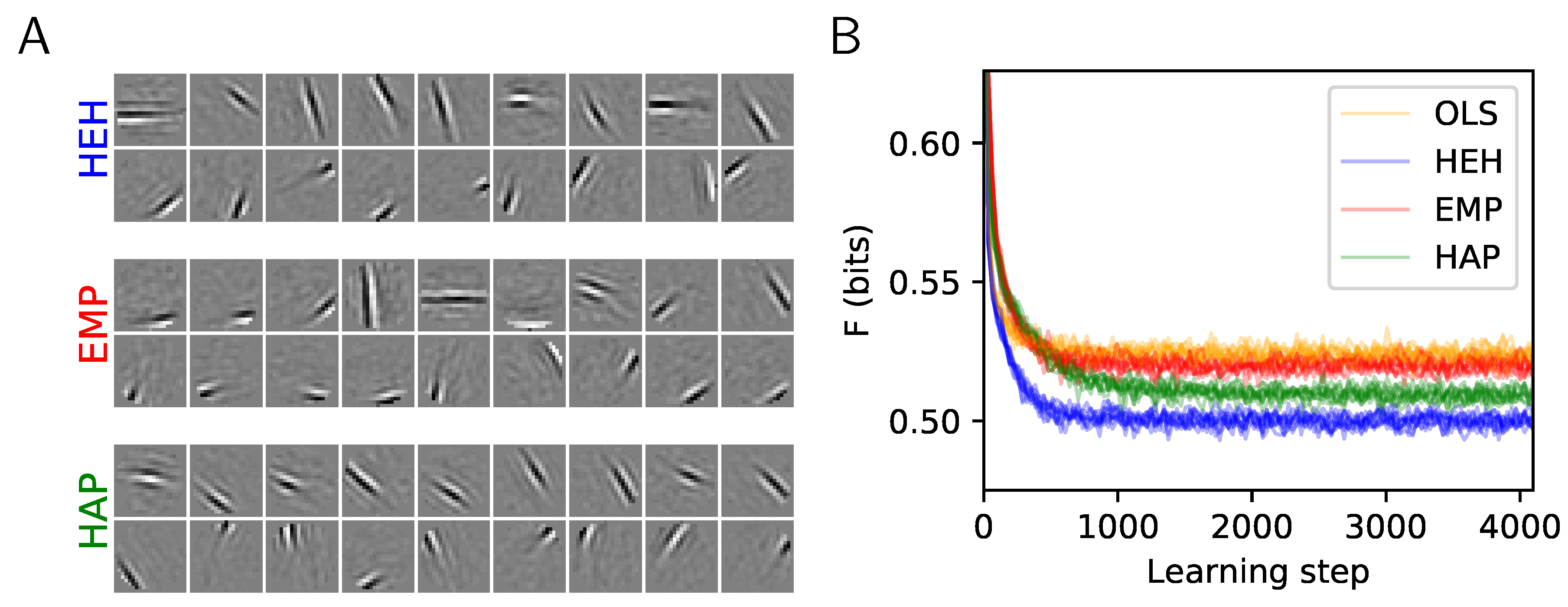
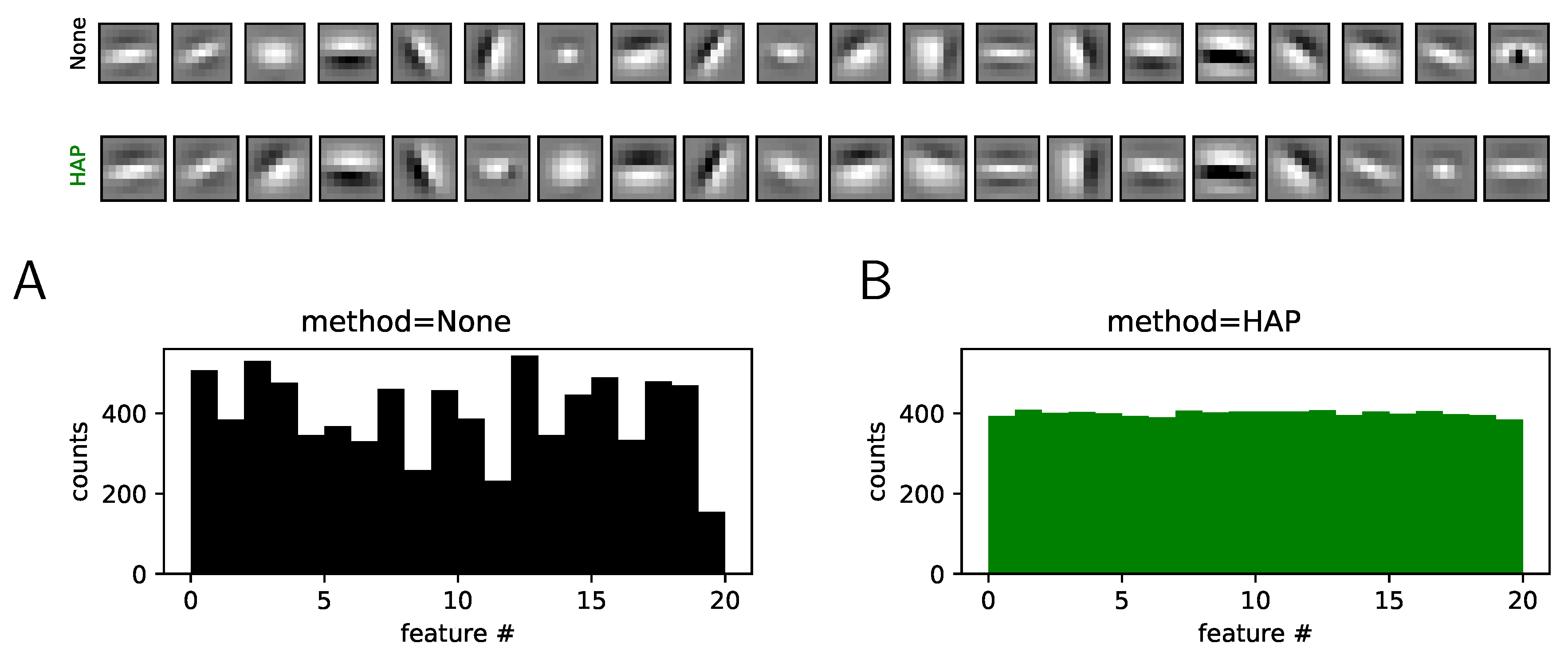
2.3. Results: A More Efficient Unsupervised Learning Using Homeostasis
| Algorithm 2 Homeostatic Unsupervised Learning of Kernels: |
|
3. Discussion and Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Hubel, D.H.; Wiesel, T.N. Receptive fields and functional architecture of monkey striate cortex. J. Physiol. 1968, 195, 215–243. [Google Scholar] [CrossRef]
- Perrinet, L.U. Sparse Models for Computer Vision. In Biologically Inspired Computer Vision; Cristóbal, G., Keil, M.S., Perrinet, L.U., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015; Chapter 14. [Google Scholar] [CrossRef]
- Olshausen, B.; Field, D.J. Natural image statistics and efficient coding. Netw. Comput. Neural Syst. 1996, 7, 333–339. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and Composing Robust Features with Denoising Autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Sulam, J.; Papyan, V.; Romano, Y.; Elad, M. Multi-Layer Convolutional Sparse Modeling: Pursuit and Dictionary Learning. arXiv, 2017; arXiv:1708.08705. [Google Scholar] [CrossRef]
- Perrinet, L.U.; Bednar, J.A. Edge co-occurrences can account for rapid categorization of natural versus animal images. Sci. Rep. 2015, 5, 11400. [Google Scholar] [CrossRef]
- Makhzani, A.; Frey, B.J. k-Sparse Autoencoders. arXiv, 2013; arXiv:1312.5663. [Google Scholar]
- Papyan, V.; Romano, Y.; Elad, M. Convolutional neural networks analyzed via convolutional sparse coding. Mach. Learn. 2016, 1050, 27. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv, 2013; arXiv:1312.6114. [Google Scholar]
- Olshausen, B.; Field, D.J. Sparse coding with an overcomplete basis set: A strategy employed by V1? Vis. Res. 1997, 37, 3311–3325. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J. Sparse modeling for image and vision processing. Found. Trends Comput. Graph. Vis. 2014, 8, 85–283. [Google Scholar] [CrossRef]
- Marder, E.; Goaillard, J.M. Variability, compensation and homeostasis in neuron and network function. Nat. Rev. Neurosci. 2006, 7, 563. [Google Scholar] [CrossRef]
- Hansel, D.; van Vreeswijk, C. The mechanism of orientation selectivity in primary visual cortex without a functional map. J. Neurosci. 2012, 32, 4049–4064. [Google Scholar] [CrossRef]
- Schwartz, O.; Simoncelli, E.P. Natural signal statistics and sensory gain control. Nat. Neurosci. 2001, 4, 819–825. [Google Scholar] [CrossRef]
- Carandini, M.; Heeger, D.J.D. Normalization as a canonical neural computation. Nat. Rev. Neurosci. 2012, 13, 1–12. [Google Scholar] [CrossRef]
- Ringach, D.L. Spatial structure and symmetry of simple-cell receptive fields in macaque primary visual cortex. J. Neurophysiol. 2002, 88, 455–463. [Google Scholar] [CrossRef]
- Rehn, M.; Sommer, F.T. A model that uses few active neurones to code visual input predicts the diverse shapes of cortical receptive fields. J. Comput. Neurosci. 2007, 22, 135–146. [Google Scholar] [CrossRef]
- Loxley, P.N. The Two-Dimensional Gabor Function Adapted to Natural Image Statistics: A Model of Simple-Cell Receptive Fields and Sparse Structure in Images. Neural Comput. 2017, 29, 2769–2799. [Google Scholar] [CrossRef]
- Brito, C.S.; Gerstner, W. Nonlinear Hebbian learning as a unifying principle in receptive field formation. PLoS Comput. Biol. 2016, 12, e1005070. [Google Scholar] [CrossRef]
- Perrinet, L.U.; Samuelides, M.; Thorpe, S.J. Emergence of filters from natural scenes in a sparse spike coding scheme. Neurocomputing 2003, 58–60, 821–826. [Google Scholar] [CrossRef]
- Rao, R.; Ballard, D. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef]
- Perrinet, L.U. Role of Homeostasis in Learning Sparse Representations. Neural Comput. 2010, 22, 1812–1836. [Google Scholar] [CrossRef]
- Sandin, F.; Martin-del Campo, S. Dictionary learning with equiprobable matching pursuit. arXiv, 2017; arXiv:1611.09333. [Google Scholar]
- Olshausen, B. Sparse Codes and Spikes. In Probabilistic Models of the Brain: Perception and Neural Function; Rao, R., Olshausen, B., Lewicki, M., Eds.; MIT Press: Cambridge, MA, USA, 2002; Chapter Sparse Codes and Spikes; pp. 257–272. [Google Scholar]
- Smith, E.C.; Lewicki, M.S. Efficient auditory coding. Nature 2006, 439, 978–982. [Google Scholar] [CrossRef]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; Wiley: New York, NY, USA, 1949. [Google Scholar]
- Oja, E. A Simplified Neuron Model as a Principal Component Analyzer. J. Math. Biol. 1982, 15, 267–273. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Solutions of Ill-Posed Problems; Winston & Sons: Washington, DC, USA, 1977. [Google Scholar]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- DeWeese, M.R.; Wehr, M.; Zador, A.M. Binary Spiking in Auditory Cortex. J. Neurosci. 2003, 23, 7940–7949. [Google Scholar] [CrossRef]
- Bethge, M.; Rotermund, D.; Pawelzik, K. Second Order Phase Transition in Neural Rate Coding: Binary Encoding is Optimal for Rapid Signal Transmission. Phys. Rev. Lett. 2003, 90, 088104. [Google Scholar] [CrossRef]
- Khoei, M.A.; Ieng, S.H.; Benosman, R. Asynchronous Event-Based Motion Processing: From Visual Events to Probabilistic Sensory Representation. Neural Comput. 2019, 31, 1–25. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing, 2nd ed.; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Perrinet, L.; Samuelides, M.; Thorpe, S. Coding Static Natural Images Using Spiking Event Times: Do Neurons Cooperate? IEEE Trans. Neural Netw. 2004, 15, 1164–1175. [Google Scholar] [CrossRef]
- Fischer, S.; Redondo, R.; Perrinet, L.U.; Cristóbal, G. Sparse Approximation of Images Inspired from the Functional Architecture of the Primary Visual Areas. EURASIP J. Adv. Signal Process. 2007, 2007, 122. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal Matching Pursuit: Recursive Function Approximation with Applications to Wavelet Decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Vallender, S. Calculation of the Wasserstein Distance between Probability Distributions on the Line. Theory Probab. Appl. 2006, 18, 784–786. [Google Scholar] [CrossRef]
- Doersch, C. Tutorial on Variational Autoencoders. arXiv, 2016; arXiv:1606.05908. [Google Scholar]
- Laughlin, S. A simple coding procedure enhances a neuron’s information capacity. Z. Naturforschung. Sect. C Biosci. 1981, 36, 910–912. [Google Scholar] [CrossRef]
- Simoncelli, E.P.; Olshausen, B. Natural Image Statistics and Neural Representation. Annu. Rev. Neurosci. 2001, 24, 1193–1216. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perrinet, L.U. An Adaptive Homeostatic Algorithm for the Unsupervised Learning of Visual Features. Vision 2019, 3, 47. https://doi.org/10.3390/vision3030047
Perrinet LU. An Adaptive Homeostatic Algorithm for the Unsupervised Learning of Visual Features. Vision. 2019; 3(3):47. https://doi.org/10.3390/vision3030047
Chicago/Turabian StylePerrinet, Laurent U. 2019. "An Adaptive Homeostatic Algorithm for the Unsupervised Learning of Visual Features" Vision 3, no. 3: 47. https://doi.org/10.3390/vision3030047
APA StylePerrinet, L. U. (2019). An Adaptive Homeostatic Algorithm for the Unsupervised Learning of Visual Features. Vision, 3(3), 47. https://doi.org/10.3390/vision3030047




