Multiple Photographs of a Perspective Scene Reveal the Principles of Picture Perception
Abstract
1. Introduction
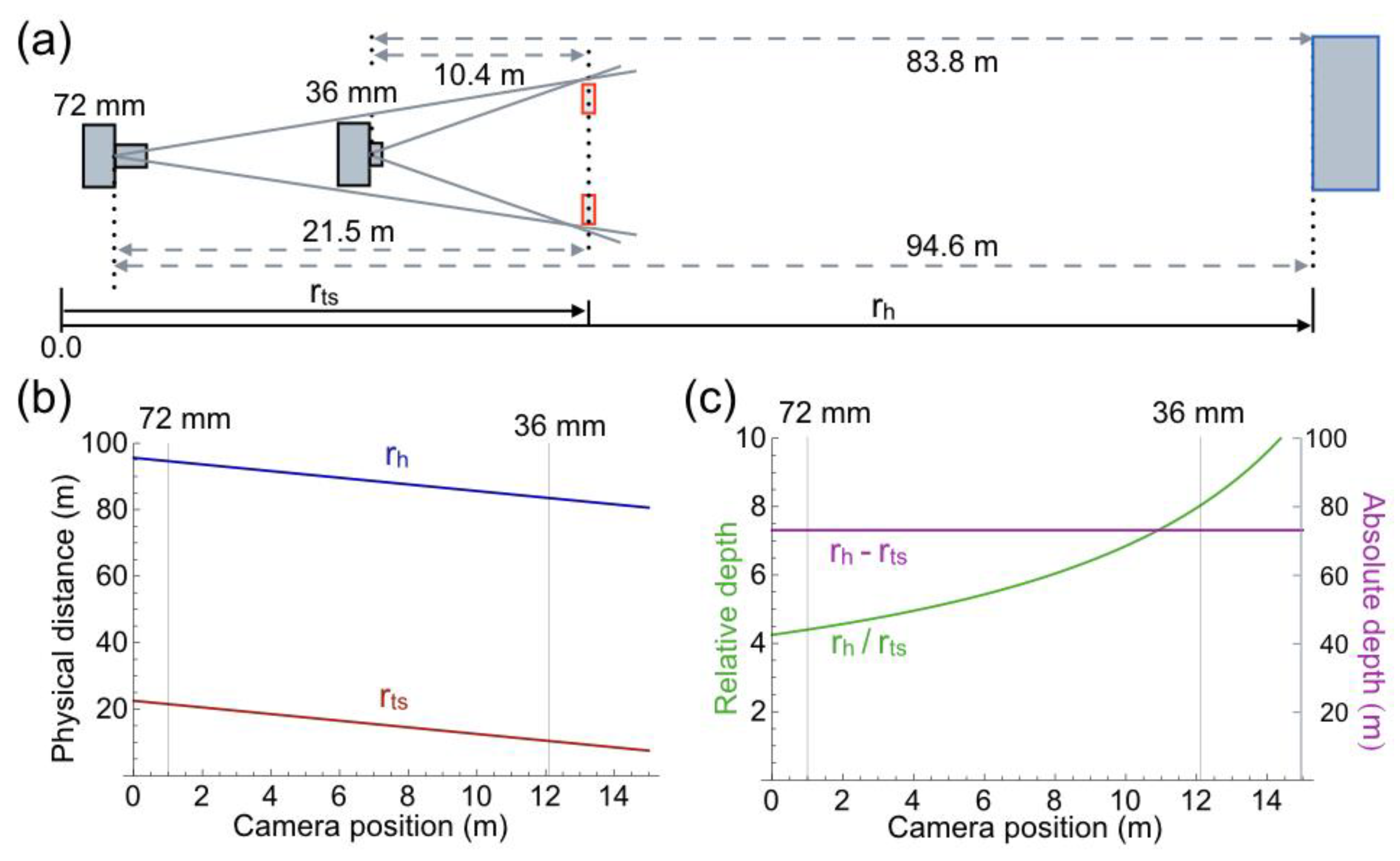
2. Comparison of Photographs Taken from Different Camera Positions
3. Geometry of the Physical Scene
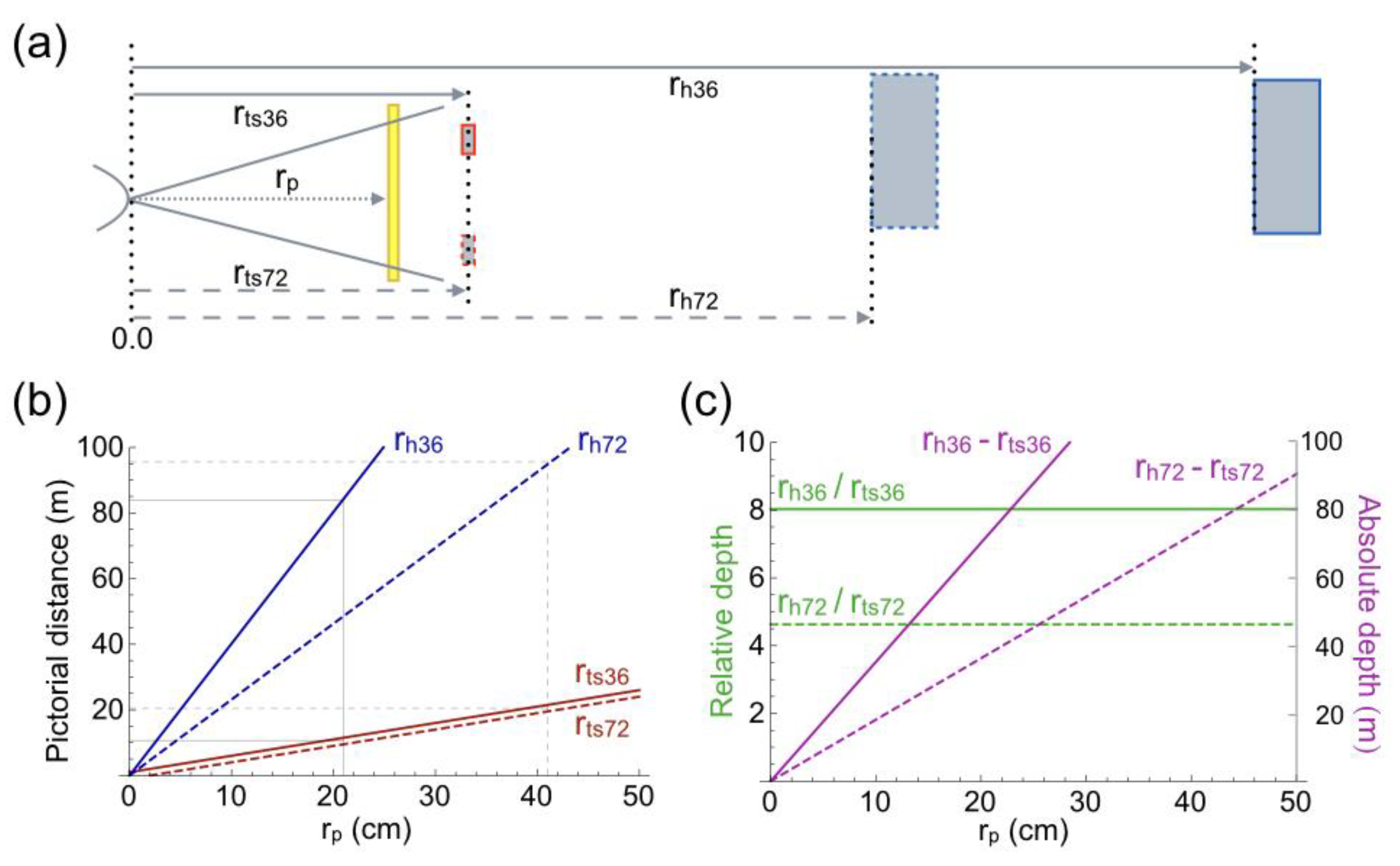
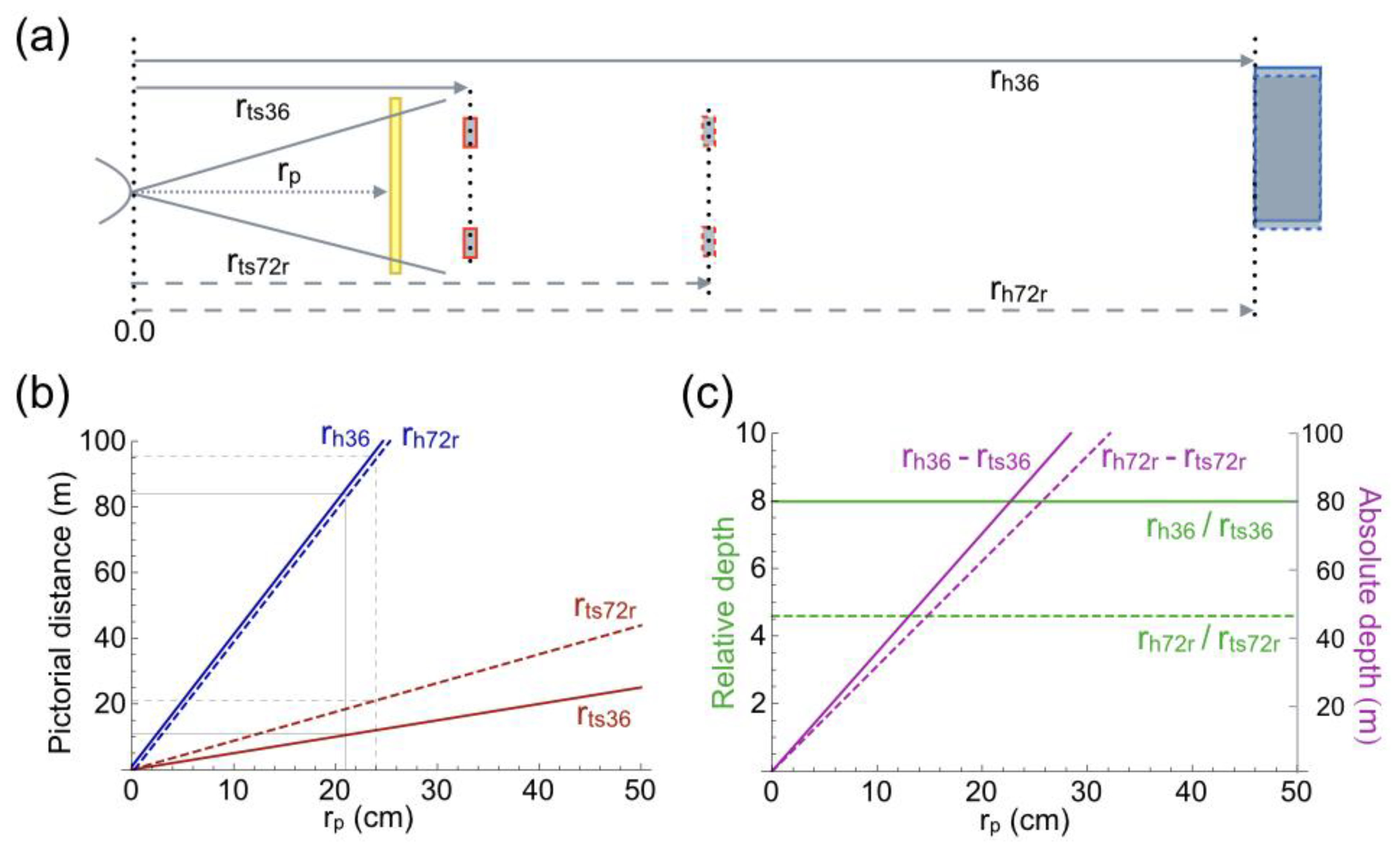
4. Geometry of the Pictorial Scene
4.1. Distance
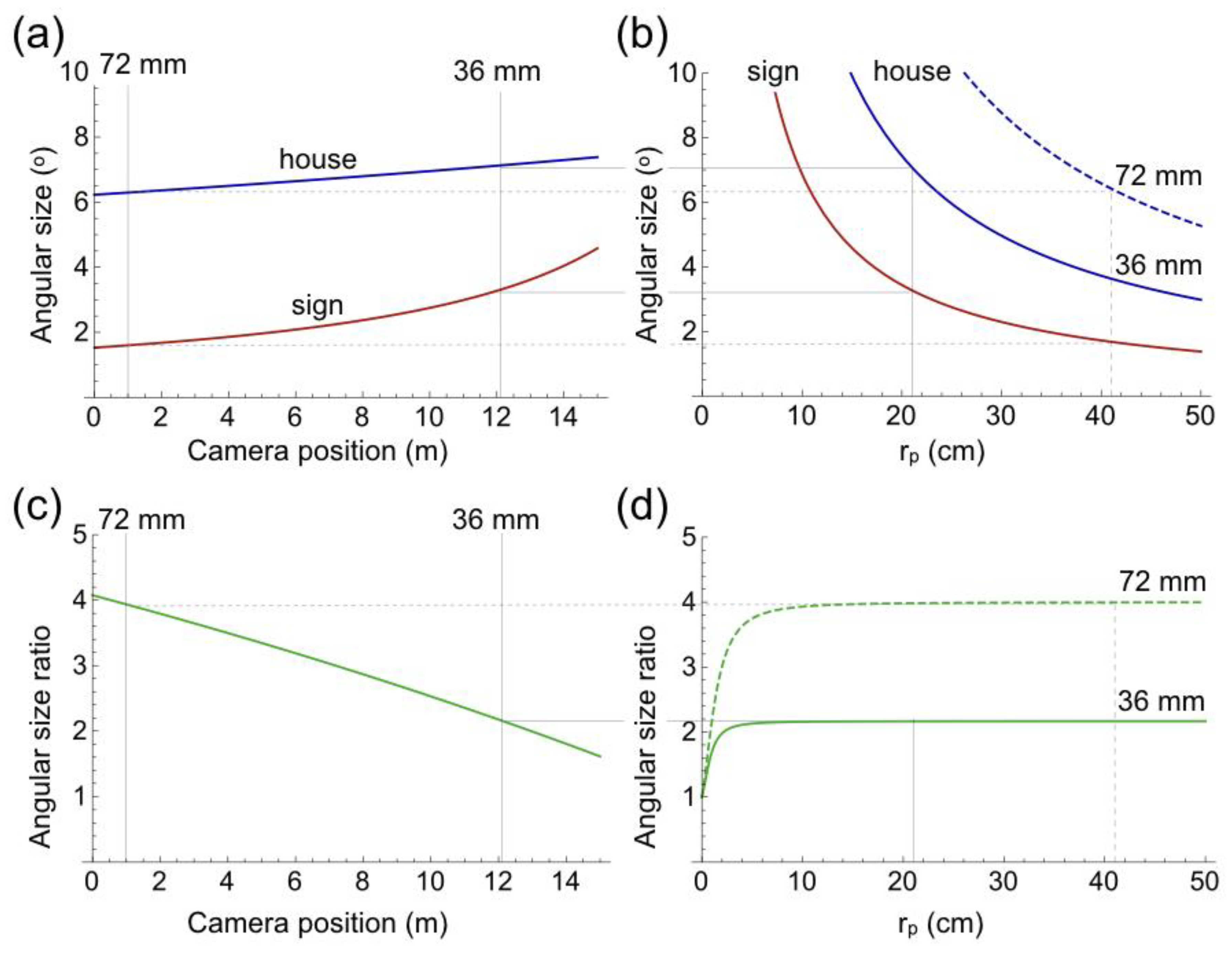
4.2. Angular Size
4.3. Visual Direction
5. Sizes, Distances, and Distortions in Pictures
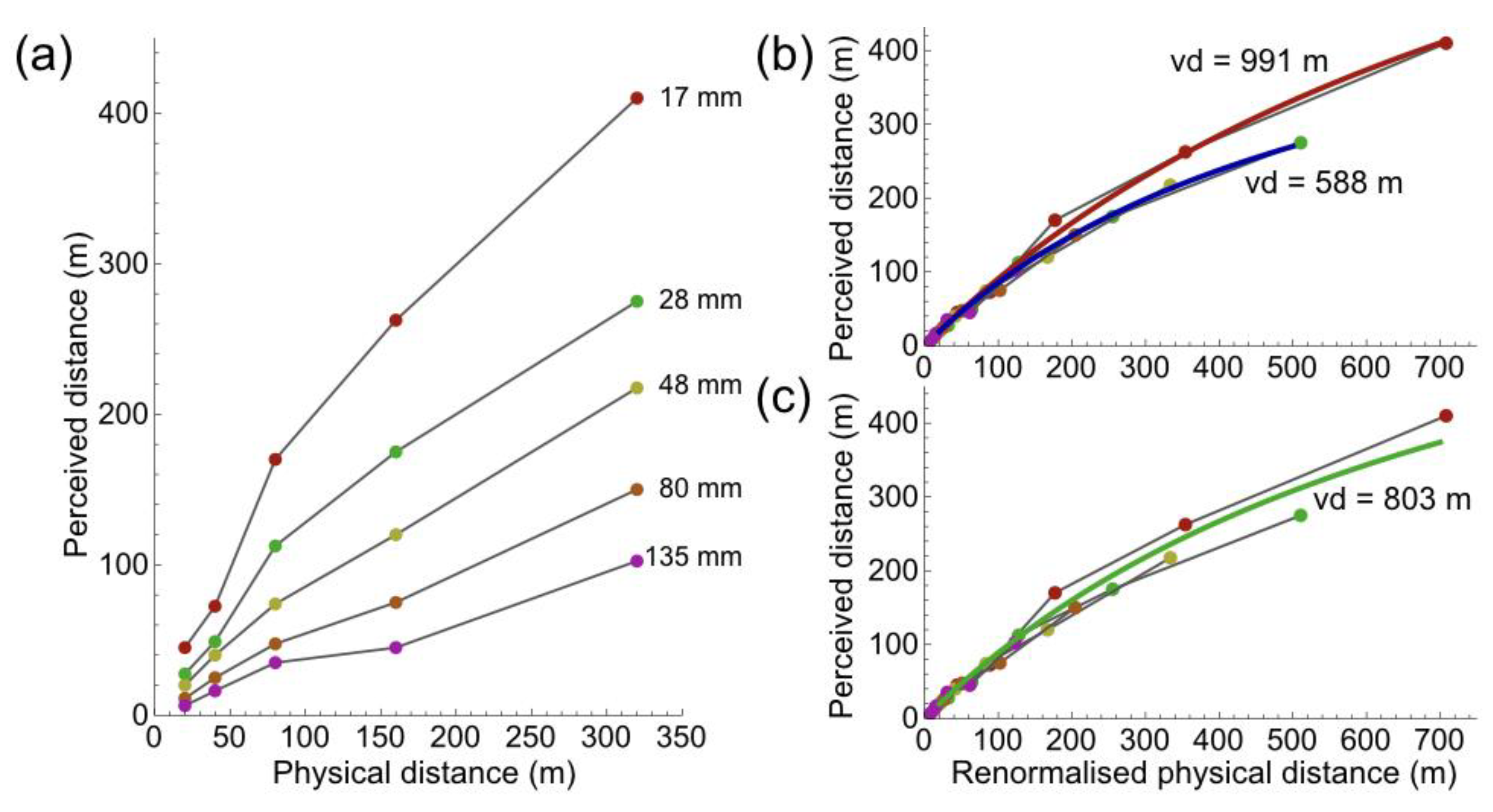
6. Distance in Pictorial Space Fitted with Perspective Distance Functions
7. Discussion
7.1. Invariance in Picture Perception
7.2. Misconceptions about Picture Perception
8. Conclusions
Funding
Conflicts of Interest
References
- Busey, T.A.; Brady, N.P.; Cutting, J.E. Compensation is unnecessary for the perception of faces in slanted pictures. Percept. Psychophys. 1990, 48, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, E.B. Spatial layout, orientation relative to the observer, and perceived projection in pictures viewed at an angle. J. Exp. Psychol. 1987, 13, 256–266. [Google Scholar] [CrossRef]
- Goldstein, E.B. Geometry or not geometry? Perceived orientation and spatial layout in pictures viewed at an angle. J. Exp. Psychol. Hum. Percept. Perf. 1988, 14, 312–314. [Google Scholar] [CrossRef]
- Halloran, T.O. The frame turns also: Factors in differential rotation in pictures. Percept. Psychophys. 1993, 54, 496–508. [Google Scholar] [CrossRef] [PubMed]
- Perkins, D.N. Compensating for distortion in viewing pictures obliquely. Percept. Psychophys. 1973, 14, 13–18. [Google Scholar] [CrossRef]
- Pirenne, M.H. Optics, Painting and Photography; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Rosinski, R.R.; Farber, J. Compensation for viewing point in the perception of pictured space. In The Perception of Pictures; Hagen, M.A., Ed.; Academic: New York, NY, USA, 1980; pp. 137–176. [Google Scholar]
- Rosinski, R.R.; Mulholland, T.; Degelman, D.; Farber, J. Picture perception: An analysis of visual compensation. Percept. Psychophys. 1980, 28, 521–526. [Google Scholar] [CrossRef] [PubMed]
- Wallach, H.; Marshall, F.J. Shape constancy in pictorial representation. Percept. Psychophys. 1986, 39, 233–235. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Kubovy, M. Weakening the robustness of perspective: Evidence for a modified theory of compensation in picture perception. Percept. Psychophys. 1999, 61, 456–467. [Google Scholar] [CrossRef] [PubMed]
- Vishwanath, D.; Girshick, A.R.; Banks, M.S. Why pictures look right when viewed from the wrong place. Nat. Neurosci. 2005, 8, 1401–1410. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, J.J.; van Doorn, A.J.; Kappers, A.M.L.; Todd, J.T. Pointing out of the picture. Perception 2004, 33, 513–530. [Google Scholar] [CrossRef] [PubMed]
- Rogers, B.; Gyani, A. Binocular disparities, motion parallax, and geometric perspective in Patrick Hughes’s “reverspectives”: Theoretical analysis and empirical findings. Perception 2010, 39, 330–348. [Google Scholar] [CrossRef] [PubMed]
- Todorovic, D. Is pictorial perception robust? The effect of the observer vantage point on the perceived depth structure of linear-perspective images. Perception 2008, 37, 106–125. [Google Scholar] [CrossRef] [PubMed]
- Gibson, J.J. The Ecological Approach to Visual Perception; Houghton Mifflin: Boston, MA, USA, 1979. [Google Scholar]
- Sedgwick, H. Relating direct and indirect perception of spatial layout. In Looking into Pictures: An Interdisciplinary Approach to Pictorial Space; Hecht, H., Schwartz, R., Atherton, M., Eds.; MIT Press: Cambridge, MA, USA, 2003; pp. 61–75. [Google Scholar]
- Costall, A.P. Seeing through pictures. Word Image 1990, 6, 273–277. [Google Scholar]
- Hagen, M.A. Varieties of Realism: Geometries of Representational Art; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Hochberg, J. The psychophysics of picture perception. Audio Vis. Commun. Rev. 1962, 10, 22–54. [Google Scholar]
- Hochberg, J. Art and perception. In Handbook of Perception: Vol. X. Perceptual Ecology; Carterette, E.C., Friedman, M.P., Eds.; Academic Press: New York, NY, USA, 1979; pp. 225–258. [Google Scholar]
- Kennedy, J. A Psychology of Picture Perception; Jossey-Bass: San Francisco, CA, USA, 1974. [Google Scholar]
- Kubovy, M. The Psychology of Perspective and Renaissance Art; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Rogers, S. Perceiving pictorial space. In Perception of Space and Motion; Epstein, W., Rogers, S., Eds.; Academic Press: San Diego, CA, USA, 1995; pp. 119–163. [Google Scholar]
- Willats, J. Art and Representation; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Koenderink, J.J.; van Doorn, A.J.; Wagemans, J. Depth. i-Perception 2011, 2, 541–564. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, J.J.; van Doorn, A.J. Gauge fields in pictorial space. SIAM J. Imaging Sci. 2012, 5, 1213–1233. [Google Scholar] [CrossRef]
- Koenderink, J.J.; van Doorn, A.J. The structure of visual spaces. J. Math. Imaging Vis. 2008, 31, 171–187. [Google Scholar] [CrossRef]
- Wagemans, J.; van Doorn, A.J.; Koenderink, J.J. Pictorial depth probed through relative sizes. i-Perception 2011, 2, 992–1013. [Google Scholar] [CrossRef] [PubMed]
- Baird, J.C.; Wagner, M. Transformation theory of size judgment. J. Exp. Psychol. Hum. Percept. Perf. 1991, 17, 852–864. [Google Scholar] [CrossRef]
- Bian, Z.; Braunstein, M.L.; Andersen, G.J. The ground dominance effect in the perception of 3-D layout. Percept. Psychophys. 2005, 67, 815–828. [Google Scholar] [CrossRef]
- Da Silva, J.A. Scales for perceived egocentric distance in a large open field: Comparison of three psychophysical methods. Am. J. Psychol. 1985, 98, 119–144. [Google Scholar] [CrossRef] [PubMed]
- Feria, C.S.; Braunstein, M.L.; Andersen, G.J. Judging distance across texture discontinuities. Perception 2003, 32, 1423–1440. [Google Scholar] [CrossRef] [PubMed]
- Foley, J.M.; Ribeiro-Filho, N.P.; Da Silva, J.A. Visual perception of extent and the geometry of visual space. Vis. Res. 2004, 44, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Gilinsky, A.S. Perceived size and distance in visual space. Psychol. Rev. 1951, 58, 460–482. [Google Scholar] [CrossRef] [PubMed]
- Haber, R.N. Toward a theory of the perceived spatial layout of scenes. Comput. Vis. Gr. Image Process. 1985, 31, 282–321. [Google Scholar] [CrossRef]
- He, Z.J.; Ooi, T.L. Perceiving binocular depth with reference to a common surface. Perception 2000, 29, 1313–1334. [Google Scholar] [CrossRef] [PubMed]
- He, Z.J.; Wu, B.; Ooi, T.L.; Yarbrough, G.; Wu, J. Judging egocentric distance on the ground: Occlusion and surface integration. Perception 2004, 33, 789–806. [Google Scholar] [CrossRef] [PubMed]
- Madison, C.; Thompson, W.; Kersten, D.; Shirley, P.; Smits, B. Use of inter-reflection and shadow for surface contact. Percept. Psychophys. 2001, 63, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Meng, J.C.; Sedgwick, H.A. Distance perception mediated through nested contact relations among surfaces. Percept. Psychophys. 2001, 63, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Meng, J.C.; Sedgwick, H.A. Distance perception across spatial discontinuities. Percept. Psychophys. 2002, 64, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Ni, R.; Braunstein, M.L.; Andersen, G.J. Perception of scene layout from optical contact, shadows, and motion. Perception 2004, 33, 1305–1318. [Google Scholar] [CrossRef] [PubMed]
- Ooi, T.L.; Wu, B.; He, Z.J. Distance determined by the angular declination below the horizon. Nature 2001, 414, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Ooi, T.L.; Wu, B.; He, Z.J. Perceptual space in the dark affected by the intrinsic bias of the visual system. Perception 2006, 35, 605–624. [Google Scholar] [CrossRef] [PubMed]
- Philbeck, J.W.; Loomis, J.M. Comparison of two indicators of perceived egocentric distance under full-cue and reduced-cue conditions. J. Exp. Psychol. Hum. Percept. Perf. 1997, 23, 72–85. [Google Scholar] [CrossRef]
- Sinai, M.J.; Ooi, T.L.; He, Z.J. Terrain influences the accurate judgment of distance. Nature 1998, 395, 497–500. [Google Scholar] [CrossRef] [PubMed]
- Toye, R.C. The effect of viewing position on the perceived layout of space. Percept. Psychophys. 1986, 40, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Wagner, M. The metric of visual space. Percept. Psychophys. 1985, 38, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Wagner, M. The Geometries of Visual Space; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2006. [Google Scholar]
- Wiest, W.M.; Bell, B. Stevens’s exponent for psychophysical scaling of perceived, remembered and inferred distance. Psychol. Bull. 1985, 98, 457–470. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Ooi, T.L.; He, Z.J. Perceiving distance accurately by a directional process of integrating ground information. Nature 2004, 428, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Erkelens, C.J. Virtual slant explains perceived slant, distortion and motion in pictorial scenes. Perception 2013, 42, 253–270. [Google Scholar] [CrossRef] [PubMed]
- Erkelens, C.J. Computation and measurement of slant specified by linear perspective. J. Vis. 2013, 13, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Erkelens, C.J. The extent of visual space inferred from perspective angles. i-Perception 2015, 6, 5–14. [Google Scholar] [CrossRef] [PubMed]
- Erkelens, C.J. Perception of perspective angles. i-Perception 2015, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Erkelens, C.J. The perspective structure of visual space. i-Perception 2015, 6, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Erkelens, C.J. Perspective space as a model for distance and size perception. i-Perception 2017, 8, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Kraft, R.; Green, J.S. Distance perception as a function of photographic area of view. Percept. Psychophys. 1989, 45, 459–466. [Google Scholar] [CrossRef] [PubMed]
- Cooper, E.A.; Piazza, E.A.; Banks, M.S. The perceptual basis of common photographic practice. J. Vis. 2012, 12, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Perona, P. A new perspective on portraiture. J. Vis. 2007, 7, 992. [Google Scholar] [CrossRef]
- Cutting, J.E. Reconceiving perceptual space. In Looking into Pictures: An Interdisciplinary Approach to Pictorial Space; Hecht, H., Schwartz, R., Atherton, M., Eds.; MIT Press: Cambridge, MA, USA, 2003; pp. 215–238. [Google Scholar]
- Banks, M.S.; Cooper, E.A.; Piazza, E.A. Camera focal length and the perception of pictures. Ecol. Psychol. 2014, 26, 30–46. [Google Scholar] [CrossRef] [PubMed]
- Bengston, J.K.; Stergios, J.C.; Ward, J.L.; Jester, R.E. Optic array determinants of apparent distance and size in pictures. J. Exp. Psychol. Hum. Percept. Perf. 1980, 6, 751–759. [Google Scholar] [CrossRef]
- Smith, O.W.; Gruber, H. Perception of depth in photographs. Percept. Mot. Skills 1958, 8, 307–313. [Google Scholar] [CrossRef]
- Todorovic, D. The effect of observer vantage point on perceived distortions in linear perspective images. Atten. Percept. Psychophys. 2009, 71, 183–193. [Google Scholar] [CrossRef] [PubMed]
- Gilinsky, A.S. The effect of attitude upon the perception of size. J. Psychol. 1955, 68, 173–192. [Google Scholar] [CrossRef]
- Cutting, J.E. Rigidity in cinema seen from the front row, side aisle. J. Exp. Psychol. Hum. Percept. Perf. 1987, 13, 323–334. [Google Scholar] [CrossRef]
- Hagen, M.A. Influence of picture surface and station point on the ability to compensate for oblique view in pictorial perception. Dev. Psychol. 1976, 12, 57–63. [Google Scholar] [CrossRef]
- Koenderink, J.J.; van Doorn, A.J.; de Ridder, H.; Oomes, S. Visual rays are parallel. Perception 2010, 39, 1163–1171. [Google Scholar] [CrossRef] [PubMed]





© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erkelens, C.J. Multiple Photographs of a Perspective Scene Reveal the Principles of Picture Perception. Vision 2018, 2, 26. https://doi.org/10.3390/vision2030026
Erkelens CJ. Multiple Photographs of a Perspective Scene Reveal the Principles of Picture Perception. Vision. 2018; 2(3):26. https://doi.org/10.3390/vision2030026
Chicago/Turabian StyleErkelens, Casper J. 2018. "Multiple Photographs of a Perspective Scene Reveal the Principles of Picture Perception" Vision 2, no. 3: 26. https://doi.org/10.3390/vision2030026
APA StyleErkelens, C. J. (2018). Multiple Photographs of a Perspective Scene Reveal the Principles of Picture Perception. Vision, 2(3), 26. https://doi.org/10.3390/vision2030026




