Short-Term Periodized Programming May Improve Strength, Power, Jump Kinetics, and Sprint Efficiency in Soccer
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Procedure
2.3. Statistical Analyses
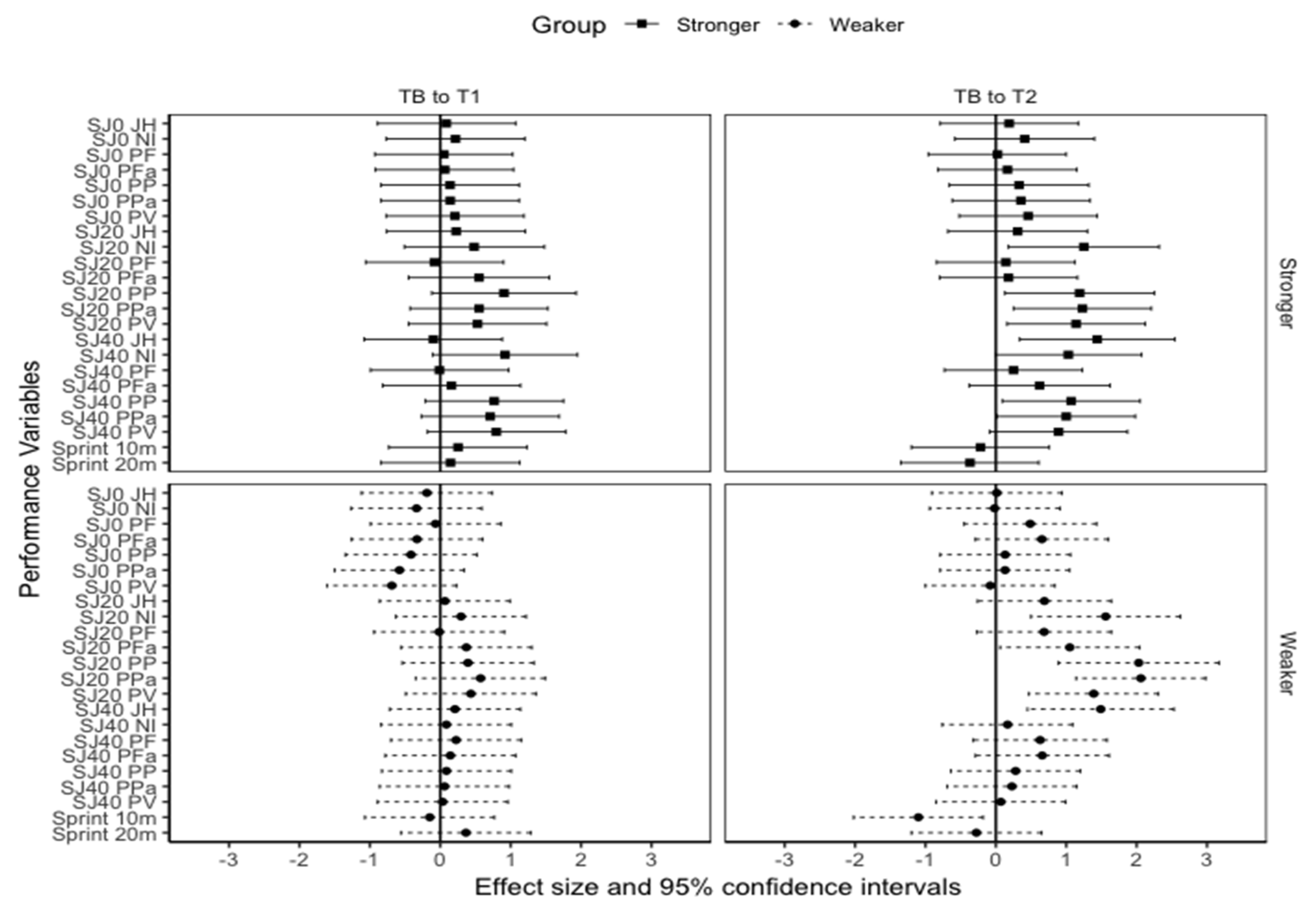
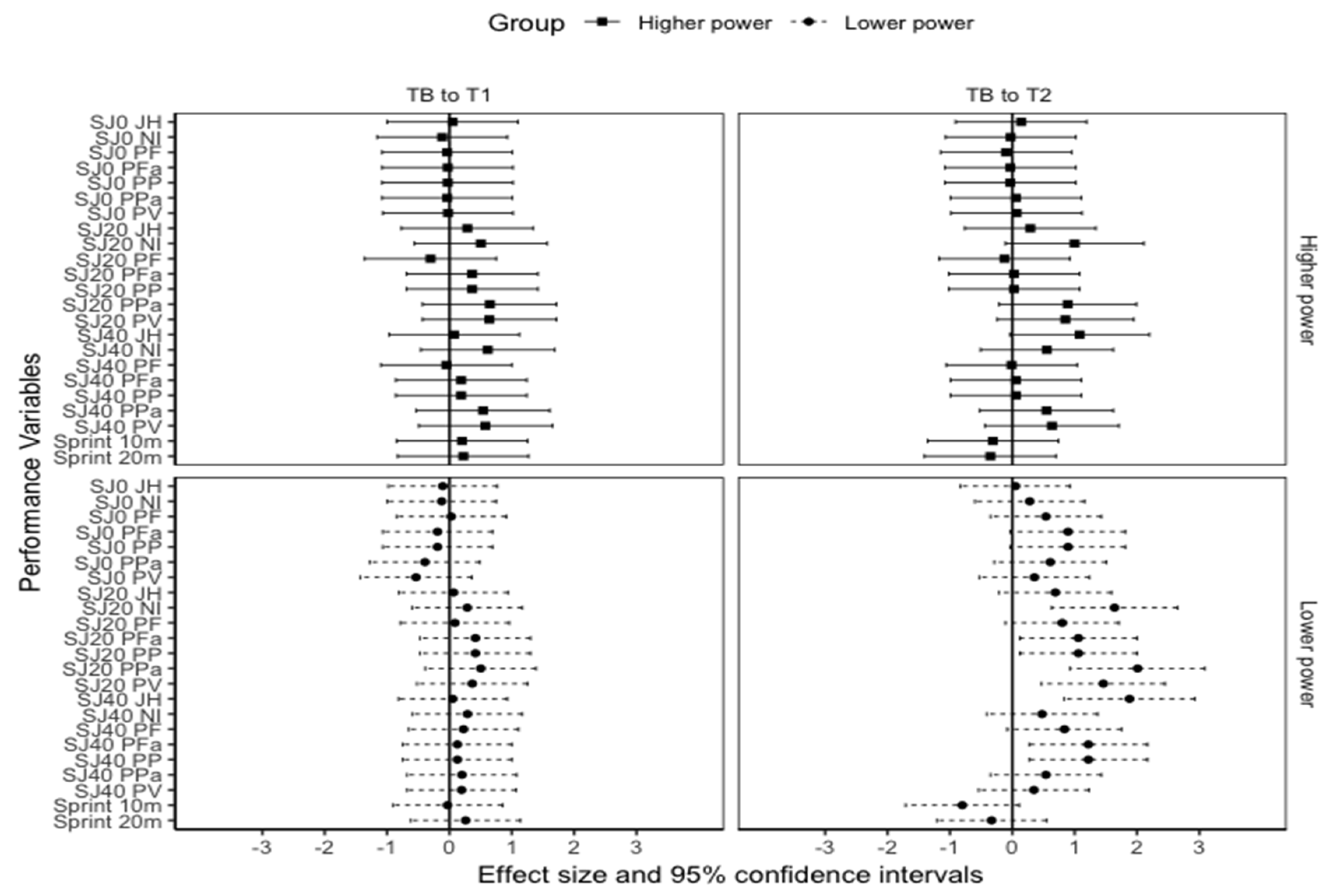
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stølen, T.; Chamari, K.; Castagna, C.; Wisløff, U. Physiology of Soccer: An Update. Sports Med. 2005, 35, 501–536. [Google Scholar] [CrossRef]
- Radzimiński, Ł.; Szwarc, A.; Padrón-Cabo, A.; Jastrzębski, Z. Correlations between Body Composition, Aerobic Capacity, Speed and Distance Covered among Professional Soccer Players during Official Matches. J. Sports Med. Phys. Fit. 2020, 60, 257–262. [Google Scholar] [CrossRef] [PubMed]
- Silvestre, R.; West, C.; Maresh, C.M.; Kraemer, W.J. Body Composition and Physical Performance in Men’s Soccer: A Study of a National Collegiate Athletic Association Division I Team. J. Strength Cond. Res. 2006, 20, 177–183. [Google Scholar] [CrossRef] [PubMed]
- Suarez-Arrones, L.; Lara-Lopez, P.; Torreno, N.; Saez de Villarreal, E.; Di Salvo, V.; Mendez-Villanueva, A. Effects of Strength Training on Body Composition in Young Male Professional Soccer Players. Sports 2019, 7, 104. [Google Scholar] [CrossRef]
- Wisløff, U.; Helgerud, J.; Hoff, J. Strength and Endurance of Elite Soccer Players. Med. Sci. Sports Exerc. 1998, 30, 462–467. [Google Scholar] [CrossRef] [PubMed]
- Zanini, D.; Kuipers, A.; Somensi, I.V.; Pasqualotto, J.F.; de Quevedo, J.G.; Teo, J.C.; Antes, D.L.; Zanini, D.; Kuipers, A.; Somensi, I.V.; et al. Relationship between Body Composition and Physical Capacities in Junior Soccer Players. Rev. Bras. Cineantropometria Desempenho Hum. 2020, 22, 1–7. [Google Scholar] [CrossRef]
- Carroll, K.M.; Bernards, J.R.; Bazyler, C.D.; Taber, C.B.; Stuart, C.A.; DeWeese, B.H.; Sato, K.; Stone, M.H. Divergent Performance Outcomes Following Resistance Training Using Repetition Maximums or Relative Intensity. Int. J. Sports Physiol. Perform. 2019, 14, 46–54. [Google Scholar] [CrossRef]
- DeWeese, B.H.; Hornsby, G.; Stone, M.; Stone, M.H. The Training Process: Planning for Strength–Power Training in Track and Field. Part 1: Theoretical Aspects. J. Sport Health Sci. 2015, 4, 308–317. [Google Scholar] [CrossRef]
- DeWeese, B.H.; Hornsby, G.; Stone, M.; Stone, M.H. The Training Process: Planning for Strength–Power Training in Track and Field. Part 2: Practical and Applied Aspects. J. Sport Health Sci. 2015, 4, 318–324. [Google Scholar] [CrossRef]
- Harris, G.R.; Stone, M.H.; O’bryant, H.S.; Proulx, C.M.; Johnson, R.L. Short-Term Performance Effects of High Power, High Force, or Combined Weight-Training Methods. J. Strength Cond. Res. 2000, 14, 14–20. [Google Scholar] [CrossRef]
- Issurin, V. Block Periodization versus Traditional Training Theory: A Review. J. Sports Med. Phys. Fit. 2008, 48, 65–75. [Google Scholar]
- Ahtiainen, J.P.; Pakarinen, A.; Alen, M.; Kraemer, W.J.; Häkkinen, K. Muscle Hypertrophy, Hormonal Adaptations and Strength Development during Strength Training in Strength-Trained and Untrained Men. Eur. J. Appl. Physiol. 2003, 89, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Cormie, P.; McGuigan, M.R.; Newton, R.U. Adaptations in Athletic Performance after Ballistic Power versus Strength Training. Med. Sci. Sports Exerc. 2010, 42, 1582–1598. [Google Scholar] [CrossRef]
- Ishida, A.; Rochau, K.; Findlay, K.P.; Devero, B.; Duca, M.; Stone, M.H. Effects of an Initial Muscle Strength Level on Sports Performance Changes in Collegiate Soccer Players. Sports 2020, 8, 127. [Google Scholar] [CrossRef] [PubMed]
- Suchomel, T.J.; Nimphius, S.; Stone, M.H. The Importance of Muscular Strength in Athletic Performance. Sports Med. 2016, 46, 19–26. [Google Scholar] [CrossRef]
- Dos’Santos, T.; Thomas, C.; Jones, P.A.; Comfort, P. Assessing Muscle-Strength Asymmetry via a Unilateral-Stance Isometric Midthigh Pull. Int. J. Sports Physiol. Perform. 2017, 12, 505–511. [Google Scholar] [CrossRef] [PubMed]
- Haun, C.T.; Martin, J.S.; Gleason, B.H.; Kavanaugh, A.A.; DeWeese, B.H.; Stone, M.H.; Mizuguchi, S. Static Jump Test Performance Is Related to Back Squat Strength in Athletes. Int. J. Sports Sci. Coach. 2017, 12, 653–660. [Google Scholar] [CrossRef]
- Kuki, S.; Sato, K.; Stone, M.H.; Okano, K.; Yoshida, T.; Tanigawa, S. The Relationship between Isometric Mid-Thigh Pull Variables, Jump Variables and Sprint Performance in Collegiate Soccer Players. J. Trainol. 2017, 6, 42–46. [Google Scholar] [CrossRef]
- Morris, R.O.; Jones, B.; Myers, T.; Lake, J.; Emmonds, S.; Clarke, N.D.; Singleton, D.; Ellis, M.; Till, K. Isometric Midthigh Pull Characteristics in Elite Youth Male Soccer Players: Comparisons by Age and Maturity Offset. J. Strength Cond. Res. 2018, 34, 2947–2955. [Google Scholar] [CrossRef]
- Brady, C.J.; Harrison, A.J.; Flanagan, E.P.; Haff, G.G.; Comyns, T.M. The Relationship between Isometric Strength and Sprint Acceleration in Sprinters. Int. J. Sports Physiol. Perform. 2019, 15, 38–45. [Google Scholar] [CrossRef]
- McGuigan, M.R.; Newton, M.J.; Winchester, J.B.; Nelson, A.G. Relationship between Isometric and Dynamic Strength in Recreationally Trained Men. J. Strength Cond. Res. 2010, 24, 2570–2573. [Google Scholar] [CrossRef] [PubMed]
- McGuigan, M.R.; Winchester, J.B. The Relationship between Isometric and Dynamic Strength in College Football Players. J. Sports Sci. Med. 2008, 7, 101–105. [Google Scholar] [CrossRef]
- Wang, R.; Hoffman, J.R.; Tanigawa, S.; Miramonti, A.A.; La Monica, M.B.; Beyer, K.S.; Church, D.D.; Fukuda, D.H.; Stout, J.R. Isometric Mid-Thigh Pull Correlates with Strength, Sprint, and Agility Performance in Collegiate Rugby Union Players. J. Strength Cond. Res. 2016, 30, 3051–3056. [Google Scholar] [CrossRef]
- Sams, M.L.; Sato, K.; DeWeese, B.H.; Sayers, A.L.; Stone, M.H. Quantifying Changes in Squat Jump Height across a Season of Men’s Collegiate Soccer. J. Strength Cond. Res. 2018, 32, 2324–2330. [Google Scholar] [CrossRef] [PubMed]
- Stone, M.H.; O’Bryant, H.S.; McCoy, L.; Coglianese, R.; Lehmkuhl, M.; Schilling, B. Power and Maximum Strength Relationships during Performance of Dynamic and Static Weighted Jumps. J. Strength Cond. Res. 2003, 17, 140–147. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W.G. Measures of Reliability in Sports Medicine and Science. Sports Med. 2000, 30, 1–15. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- James, L.P.; Gregory Haff, G.; Kelly, V.G.; Connick, M.J.; Hoffman, B.W.; Beckman, E.M. The Impact of Strength Level on Adaptations to Combined Weightlifting, Plyometric, and Ballistic Training. Scand. J. Med. Sci. Sports 2018, 28, 1494–1505. [Google Scholar] [CrossRef]
- Young, K.; Gabbett, T.; Haff, G.G.; Newton, R.U. The Effect of Initial Strength Levels on the Training Response to Heavy Resistance Training and Ballistic Training on Upper Body Pressing Strength. J. Aust. Strength Cond. 2013, 21, 85–87. [Google Scholar]
- Vescovi, J.D.; McGuigan, M.R. Relationships between Sprinting, Agility, and Jump Ability in Female Athletes. J. Sports Sci. 2008, 26, 97–107. [Google Scholar] [CrossRef]
- Cormie, P.; McBride, J.M.; McCaulley, G.O. Power-Time, Force-Time, and Velocity-Time Curve Analysis of the Countermovement Jump: Impact of Training. J. Strength Cond. Res. 2009, 23, 177–186. [Google Scholar] [CrossRef] [PubMed]
- McBride, J.M.; Triplett-McBride, T.; Davie, A.; Newton, R.U. The Effect of Heavy- vs. Light-Load Jump Squats on the Development of Strength, Power, and Speed. J. Strength Cond. Res. 2002, 16, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Young, W.B. Transfer of Strength and Power Training to Sports Performance. Int. J. Sports Physiol. Perform. 2006, 1, 74–83. [Google Scholar] [CrossRef] [PubMed]
- Stone, M.; Plisk, S.; Collins, D. Training Principles: Evaluation of Modes and Methods of Resistance Trainin—A Coaching Perspective. Sports Biomech. 2002, 1, 79–103. [Google Scholar] [CrossRef]
- Baker, D.; Nance, S. The Relation between Strength and Power in Professional Rugby League Players. J. Strength Cond. Res. 1999, 13, 224–229. [Google Scholar]
- Thomas, C.; Comfort, P.; Jones, P.A.; Dos’Santos, T. A Comparison of Isometric Midthigh-Pull Strength, Vertical Jump, Sprint Speed, and Change-of-Direction Speed in Academy Netball Players. Int. J. Sports Physiol. Perform. 2017, 12, 916–921. [Google Scholar] [CrossRef]
| Week | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|
| 1 | PT, Wt | OFF | Wt | OFF | Wt | OFF | OFF |
| 2, 3 | Tr, Wt | Tr | Tr, Wt | Tr | Tr, Wt | OFF | OFF |
| 4 | PT, Tr, Wt | Tr | Tr, Wt | Tr | Tr, Wt | OFF | OFF |
| 5, 6 | Tr, Wt | Tr | Tr, Wt | Tr | Tr, Wt | Match | OFF |
| 7 | Wt | Tr | Wt | Tr | PT, Wt | OFF | OFF |
| Phase | Week | Sets × Reps | Daily Relative Intensities (D1, D2, D3) | Volume Load (Kgs) |
|---|---|---|---|---|
| SE | 1 | 3 × 10 (3 × 5) | ML, ML, VL | 17,221 ± 2548 |
| SE | 2 | 3 × 10 (3 × 5) | M, M, L | 18,800 ± 2735 |
| SE | 3 | 3 × 10 (3 × 5) | H, H, L | 19,992 ± 2966 |
| MS | 4 | 5 × 5 (5 × 3) | ML, ML, VL | 16,333 ± 2145 |
| MS | 5 | 3 × 5 (3 × 3) | M, M, L | 12,159 ± 1486 |
| MS | 6 | 3 × 5 (3 × 3) | H, H, L | 12,664 ± 1670 |
| MS | 7 | 3 × 3 | VL, VL, VL | 8053 ± 1595 |
| Day | Strength Endurance | Muscle Strength |
|---|---|---|
| Day 1 and Day3 | Back Squat | Back Squat |
| BB Shoulder Press | BB CG Push Press | |
| DB Lunge | DB Step Up | |
| BB Bench Press | BB Bench Press | |
| DB Triceps Extension | ||
| Day 2 | Clean Pull | Pull from Knee |
| Straight-Leg Deadlift | Straight-Leg Deadlift | |
| Bent-Over Row | Bent-Over Row | |
| DB Pull Over | DB Pull Over | |
| DB Biceps Curl |
| Variables | Stronger (n = 8) | Weaker (n = 9) | ||||
|---|---|---|---|---|---|---|
| TB | T1 | T2 | TB | T1 | T2 | |
| SJ0 | ||||||
| JH (m) | 0.37 ± 0.06 | 0.38 ± 0.05 | 0.38 ± 0.05 | 0.28 ± 0.03 § | 0.28 ± 0.04 § | 0.28 ± 0.04 § |
| NI (N∙s−1) | 216.2 ± 16.4 | 219.7 ± 15.9 | 223.9 ± 20.5 | 177.3 ± 24.7 § | 170.0 ± 18.7 § | 176.9 ± 21.9 § |
| PF (N) | 1903.3 ± 164.0 | 1912.4 ± 192.2 | 1907.0 ± 152.6 | 1516.1 ± 157.5 § | 1506.9 ± 114.0 § | 1588.2 ± 137.2 § |
| PFa (N∙kg−0.67) | 101.8 ± 7.8 | 102.3 ± 83.2 | 103.0 ± 7.4 | 89.9 ± 6.5 § | 88.1 ± 3.7 § | 93.9 ± 5.9 § |
| PP (W) | 4693.5 ± 62.5 | 4783.9 ± 673.4 | 4929.4 ± 791.9 | 3621.9 ± 601.7 § | 3408.8 ± 402.4 § | 3696.2 ± 523.8 § |
| PPa (W∙kg−0.67) | 251.5 ± 37.5 | 257.3 ± 44.8 | 267.9 ± 53.1 | 214.7 ± 31.9 § | 199.3 ± 20.0 § | 218.8 ± 31.0 § |
| PV (m∙s−1) | 2.9 ± 0.2 | 3.0 ± 0.3 | 3.1 ± 0.4 | 2.8 ± 0.3 | 2.7 ± 0.2 § | 2.8 ± 0.3 |
| SJ20 | ||||||
| JH (m) | 0.28 ± 0.05 | 0.28 ± 0.05 | 0.28 ± 0.03 | 0.20 ± 0.03 § | 0.20 ± 0.02 § | 0.21 ± 0.02 § |
| NI (N∙s−1) | 232.4 ± 19.9 | 236.9 ± 19.5 | 242.6 ± 22.1 * | 184.1 ± 16.3 § | 189.4 ± 24.1 § | 202.4 ± 19.0 *¶§ |
| PF (N) | 2038.6 ± 186.2 | 2033.1 ± 189.3 | 2049.4 ± 173.3 | 1652.0 ± 122.0 § | 1650.2 ± 98.1 § | 1740.2 ± 114.5 ¶§ |
| PFa (N∙kg−0.67) | 93.9 ± 7.4 | 94.7 ± 7.3 | 94.4 ± 6.5 | 82.2 ± 3.8 § | 83.7 ± 3.1 § | 87.3 ± 2.5 *¶§ |
| PP (W) | 4519.4 ± 625.3 | 4596.2 ± 584.9 * | 4742.2 ± 687.0 * | 3340.7 ± 321.0 § | 3514.5 ± 582.2 § | 3823.4 ± 363.9 *¶§ |
| PPa (W∙kg−0.67) | 208.6 ± 30.6 | 217.8 ± 40.4 | 218.9 ± 34.0 * | 166.1 ± 12.7 § | 179.1 ± 28.7 § | 192.1 ± 17.1 *§ |
| PV (m∙s−1) | 2.6 ± 0.2 | 2.7 ± 0.3 | 2.7 ± 0.2 * | 2.3 ± 0.1 § | 2.5 ± 0.3 | 2.6 ± 0.2 *§ |
| SJ40 | ||||||
| JH (m) | 0.20 ± 0.04 | 0.20 ± 0.03 | 0.22 ± 0.03 *¶ | 0.12 ± 0.02 § | 0.13 ± 0.01 § | 0.14 ± 0.02 *¶§ |
| NI (N∙s−1) | 238.7 ± 24.2 | 259.3 ± 32.8 | 259.1 ± 28.2 | 192.6 ± 23.8 § | 194.7 ± 25.0 § | 196.8 ± 27.5 § |
| PF (N) | 2202.7 ± 183.4 | 2202.0 ± 180.8 | 2223.1 ± 178.4 | 1823.8 ± 123.1 § | 1843.6 ± 106.7 § | 1898.4 ± 109.6 § |
| PFa (N∙kg−0.67) | 89.5 ± 5.8 | 89.9 ± 6.6 | 90.9 ± 5.2 | 79.2 ± 3.7 § | 79.8 ± 3.3 § | 82.0 ± 2.6 § |
| PP (W) | 4316.1 ± 593.3 | 4703.9 ± 817.7 | 4728.4 ± 679.5 | 3323.2 ± 433.3 § | 3363.7 ± 458.8 § | 3447.0 ± 497.5 § |
| PPa (W∙kg−0.67) | 175.5 ± 23.7 | 192.6 ± 37.4 | 193.9 ± 30.2 | 144.4 ± 18.0 § | 145.8 ± 20.1 | 149.3 ± 23.1 § |
| PV (m∙s−1) | 2.2 ± 0.2 | 2.4 ± 0.3 | 2.4 ± 0.3 | 2.1 ± 0.2 | 2.1 ± 0.2 | 2.1 ± 0.3 § |
| Sprint | ||||||
| 10 m (s) | 1.81 ± 0.12 | 1.83 ± 0.06 | 1.79 ± 0.07 | 1.82 ± 0.06 | 1.81 ± 0.06 | 1.76 ± 0.05 |
| 20 m (s) | 3.07 ± 0.16 | 3.09 ± 0.09 | 3.03 ± 0.09 | 3.09 ± 0.09 | 3.12 ± 0.07 | 3.07 ± 0.09 |
| Higher Power (n = 7) | Lower Power (n = 10) | |||||
|---|---|---|---|---|---|---|
| Variables | TB | T1 | T2 | TB | T1 | T2 |
| SJ0 | ||||||
| JH (m) | 0.37 ± 0.08 | 0.37 ± 0.06 | 0.38 ± 0.06 | 0.29 ± 0.03 § | 0.29 ± 0.04 § | 0.29 ± 0.04 § |
| NI (N∙s−1) | 222.5 ± 11.4 | 220.6 ± 19.5 | 221.9 ± 29.2 | 176.9 ± 20.6 § | 174.3 ± 21.1 § | 183 ± 20.0 § |
| PF (N) | 1919.4 ± 178.2 | 1911.8 ± 241.9 | 1899.8 ± 211.8 | 1543.5 ± 166.3 § | 1547.8 ± 134.4 § | 1625.1 ± 135.0 § |
| PFa (N∙kg−0.67) | 102.8 ± 7.6 | 102.6 ± 10.0 | 102.6 ± 10.1 | 90.3 ± 6.3 § | 89.3 ± 3.7 § | 95.1 ± 4.3 § |
| PP (W) | 4892.1 ± 506.5 | 4850.6 ± 731.1 | 4903.8 ± 1011.4 | 3590.1 ± 471.0 § | 3499.6 ± 441.7 § | 3837.4 ± 494.9 ¶§ |
| PPa (W∙kg−0.67) | 263.4 ± 35.9 | 262.0 ± 46.5 | 266.5 ± 63.7 | 210.1 ± 21.8 § | 201.9 ± 20.0 § | 224.8 ± 26.2 ¶ |
| PV (m∙s−1) | 3.0 ± 0.3 | 3.0 ± 0.3 | 3.0 ± 0.5 | 2.8 ± 0.2 § | 2.7 ± 0.2 § | 2.8 ± 0.3 § |
| SJ20 | ||||||
| JH (m) | 0.28 ± 0.06 | 0.28 ± 0.05 | 0.28 ± 0.04 | 0.21 ± 0.03 § | 0.21 ± 0.03 § | 0.22 ± 0.03 § |
| NI (N∙s−1) | 233.2 ± 24.1 | 238.3 ± 20.6 | 246.1 ± 20.8 | 188.3 ± 18.2 § | 193.2 ± 25.7 § | 203.9 ± 18.8 *¶§ |
| PF (N) | 2074.7 ± 168.3 | 2052.6 ± 205.6 | 2065.8 ± 188.3 | 1665.4 ± 122.5 § | 1674.8 ± 109.5 § | 1759.6 ± 115.8 ¶§ |
| PFa (N∙kg−0.67) | 95.5 ± 6.5 | 96.1 ± 6.7 | 95.5 ± 6.0 § | 82.3 ± 3.6 § | 83.9 ± 3.1 § | 87.3 ± 2.8 *¶§ |
| PP (W) | 4594.7 ± 653.6 | 4806.4 ± 386.9 | 4864.3 ± 647.4 | 3405.9 ± 343.7 § | 3475.6 ± 456.0 § | 3829.8 ± 336.3 *¶§ |
| PPa (W∙kg−0.67) | 211.7 ± 32.0 | 223.6 ± 39.9 | 225.6 ± 32.4 | 168.1 ± 12.9 § | 178.8 ± 27.1 § | 190.1 ± 14.7 *§ |
| PV (m∙s−1) | 2.6 ± 0.2 | 2.7 ± 0.3 | 2.7 ± 0.3 | 2.3 ± 0.1 § | 2.5 ± 0.3 | 2.5 ± 0.2 * |
| SJ40 | ||||||
| JH (m) | 0.20 ± 0.05 | 0.20 ± 0.05 | 0.21 ± 0.05 | 0.13 ± 0.03 § | 0.13 ± 0.02 § | 0.15 ± 0.03 *¶§ |
| NI (N∙s−1) | 241.4 ± 25.1 | 257.9 ± 42.2 | 251.0 ± 39.8 | 195.3 ± 23.8 § | 202.1 ± 27.3 § | 208.7 ± 35.3 § |
| PF (N) | 2240.0 ± 162.1 | 2237.0 ± 162.6 | 2238.9 ± 196.9 | 1835.6 ± 122.0 § | 1855.0 ± 107.6 § | 1919.7 ± 112.2 ¶§ |
| PFa (N∙kg−0.67) | 90.8 ± 4.9 | 91.3 ± 5.5 | 91.0 ± 3.7 | 79.3 ± 3.4 § | 79.8 ± 3.2 § | 82.8 ± 2.4 *¶§ |
| PP (W) | 4408.4 ± 573.3 | 4740.8 ± 944.6 | 4608.2 ± 918.5 | 3357.9 ± 425.0 § | 3471.9 ± 470.1 § | 3659.2 ± 614.3 § |
| PPa (W∙kg−0.67) | 178.9 ± 23.4 | 194.1 ± 42.3 | 187.6 ± 38.2 | 145.1 ± 17.2 § | 149.4 ± 19.3 § | 158.2 ± 27.4 |
| PV (m∙s−1) | 2.3 ± 0.2 | 2.4 ± 0.4 | 2.3 ± 0.3 | 2.1 ± 0.2 | 2.1 ± 0.2 | 2.2 ± 0.3 |
| Sprint | ||||||
| 10 m (s) | 1.79 ± 0.12 | 1.81 ± 0.05 | 1.76 ± 0.05 | 1.83 ± 0.15 | 1.83 ± 0.09 | 1.78 ± 0.08 |
| 20 m (s) | 3.04 ± 0.06 | 3.07 ± 0.06 | 3 ± 0.07 | 3.11 ± 0.10 | 3.13 ± 0.07 | 3.08 ± 0.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishida, A.; Travis, S.K.; Stone, M.H. Short-Term Periodized Programming May Improve Strength, Power, Jump Kinetics, and Sprint Efficiency in Soccer. J. Funct. Morphol. Kinesiol. 2021, 6, 45. https://doi.org/10.3390/jfmk6020045
Ishida A, Travis SK, Stone MH. Short-Term Periodized Programming May Improve Strength, Power, Jump Kinetics, and Sprint Efficiency in Soccer. Journal of Functional Morphology and Kinesiology. 2021; 6(2):45. https://doi.org/10.3390/jfmk6020045
Chicago/Turabian StyleIshida, Ai, S. Kyle Travis, and Michael H. Stone. 2021. "Short-Term Periodized Programming May Improve Strength, Power, Jump Kinetics, and Sprint Efficiency in Soccer" Journal of Functional Morphology and Kinesiology 6, no. 2: 45. https://doi.org/10.3390/jfmk6020045
APA StyleIshida, A., Travis, S. K., & Stone, M. H. (2021). Short-Term Periodized Programming May Improve Strength, Power, Jump Kinetics, and Sprint Efficiency in Soccer. Journal of Functional Morphology and Kinesiology, 6(2), 45. https://doi.org/10.3390/jfmk6020045







