Predictive Validity of the Snatch Pull Force-Velocity Profile to Determine the Snatch One Repetition-Maximum in Male and Female Elite Weightlifters
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Data Collection
2.3. Data Processing
2.4. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bazyler, C.D.; Mizuguchi, S.; Zourdos, M.C.; Sato, K.; Kavanaugh, A.A.; DeWeese, B.H.; Breuel, K.F.; Stone, M.H. Characteristics of a National Level Female Weightlifter Peaking for Competition: A Case Study. J. Strength Cond. Res. 2018, 32, 3029–3038. [Google Scholar] [CrossRef]
- McGuigan, M.R.; Kane, M.K. Reliability of performance of elite Olympic weightlifters. J. Strength Cond. Res. 2004, 18, 650–653. [Google Scholar] [CrossRef] [PubMed]
- Travis, S.K.; Goodin, J.R.; Beckham, G.K.; Bazyler, C.D. Identifying a test to monitor weightlifting performance in competitive male and female weightlifters. Sports 2018, 46, 46. [Google Scholar] [CrossRef] [PubMed]
- Beckham, G.; Mizuguchi, S.; Carter, C.; Sato, K.; Ramsey, M.; Lamont, H.; Hornsby, G.; Haff, G.; Stone, M. Relationships of isometric mid-thigh pull variables to weightlifting performance. J. Sports Med. Phys. Fit. 2013, 53, 573–581. [Google Scholar]
- Shetty, A.B. Quantification of selected segmental strengths in weightlifting. J. Appl. Sport Sci. Res. 1990, 4, 37–41. [Google Scholar]
- Mokkink, L.B.; Terwee, C.B.; Patrick, D.L.; Alonso, J.; Stratford, P.W.; Knol, D.L.; Bouter, L.M.; de Vet, H.C. The COSMIN study reached international consensus on taxonomy, terminology, and definitions of measurement properties for health-related patient-reported outcomes. J. Clin. Epidemiol. 2010, 63, 737–745. [Google Scholar] [CrossRef]
- McGuigan, M. Monitoring Training and Performance in Athletes; Human Kinetics: Champaign, IL, USA, 2017. [Google Scholar]
- Joffe, S.A.; Tallent, J. Neuromuscular predictors of competition performance in advanced international female weightlifters: A cross-sectional and longitudinal analysis. J. Sports Sci. 2020, 38, 985–993. [Google Scholar] [CrossRef] [PubMed]
- Morin, J.B.; Jiménez-Reyes, P.; Brughelli, M.; Samozino, P. When Jump Height is not a Good Indicator of Lower Limb Maximal Power Output: Theoretical Demonstration, Experimental Evidence and Practical Solutions. Sports Med. 2019, 49, 999–1006. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.R.; Nelson, J.K.; Silverman, S.J. Research Methods in Physical Activity, 7th ed.; Thomas, J.R., Nelson, J.K., Silverman, S.J., Eds.; Human Kinetics: Champaign, IL, USA, 2015; pp. 359–401. [Google Scholar]
- Haff, G.G.; Garcia-Ramos, A.; James, L.P. Using Velocity to Predict the Maximum Dynamic Strength in the Power Clean. Sports 2020, 8, 129. [Google Scholar] [CrossRef]
- Benavides-Ubric, A.; Díez-Fernández, D.M.; Rodríguez-Pérez, M.A.; Ortega-Becerra, M.; Pareja-Blanco, F. Analysis of the load-velocity relationship in deadlift exercise. J. Sports Sci. Med. 2020, 19, 452–459. [Google Scholar]
- Caven, E.J.G.; Bryan, T.J.E.; Dingley, A.F.; Drury, B.; Garcia-Ramos, A.; Perez-Castilla, A.; Arede, J.; Fernandes, J.F.T. Group versus individualised minimum velocity thresholds in the prediction of maximal strength in trained female athletes. Int. J. Environ. Res. Public Health 2020, 17, 7811. [Google Scholar] [CrossRef] [PubMed]
- Picerno, P.; Iannetta, D.; Comotto, S.; Donati, M.; Pecoraro, F.; Zok, M.; Tollis, G.; Figura, M.; Varalda, C.; Di Muzio, D.; et al. 1RM prediction: A novel methodology based on the force-velocity and load-velocity relationships. Eur. J. Appl. Physiol. 2016, 116, 2035–2043. [Google Scholar] [CrossRef]
- Bosquet, L.; Porta-Benache, J.; Blais, J. Validity of a commercial linear encoder to estimate bench press 1 RM from the force-velocity relationship. J. Sports Sci. Med. 2010, 9, 459–463. [Google Scholar] [PubMed]
- Sandau, I.; Chaabene, H.; Granacher, U. Validity and reliability of a snatch pull test to model the force-velocity relationship in male elite weightlifters. J. Strength Cond. Res. 2021. [Google Scholar] [CrossRef]
- Sandau, I.; Jentsch, H.; Bunk, M. Realanalyzer HD—A real-time barbell tracking software for weightlifting. EWF Sci. Mag. 2019, 5, 14–23. [Google Scholar]
- Sandau, I.; Lippmann, J.; Jentsch, H.; Seidel, I. Reliabilität des Realanalyzer, ein 2-D-Messsystems zur Echtzeiterfassung der Hantelbewegung im Gewichtheben. In Proceedings of the “NeuroMotion” Aufmerksamkeit, Automatisierung, Adaptation, Münster, Germany, 21–23 March 2012; p. 126. [Google Scholar]
- Samozino, P.; Morin, J.B.; Hintzy, F.; Belli, A. A simple method for measuring force, velocity and power output during squat jump. J. Biomech. 2008, 41, 2940–2945. [Google Scholar] [CrossRef] [PubMed]
- Samozino, P.; Edouard, P.; Sangnier, S.; Brughelli, M.; Gimenez, P.; Morin, J.B. Force-velocity profile: Imbalance determination and effect on lower limb ballistic performance. Int. J. Sports Med. 2014, 35, 505–510. [Google Scholar] [CrossRef]
- Samozino, P.; Rejc, E.; Di Prampero, P.E.; Belli, A.; Morin, J.B. Optimal force-velocity profile in ballistic movements-altius: Citius or fortius? Med. Sci. Sports Exerc. 2012, 44, 313–322. [Google Scholar] [CrossRef]
- Hopkins, W.G. Spreadsheets for analysis of validity and reliability. Sportscience 2015, 19, 36–42. [Google Scholar]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive statistics for studies in sports medicine and exercise science. Med. Sci. Sports Exerc. 2009, 41, 3–13. [Google Scholar] [CrossRef]
- Payne, R.B. Method comparison: Evaluation of least squares, Deming and Passing/Bablok regression procedures using computer simulation. Ann. Clin. Biochem. 1997, 34 Pt 3, 319–320. [Google Scholar] [CrossRef]
- Jukic, I.; García-Ramos, A.; Malecek, J.; Omcirk, D.; Tufano, J.J. Validity of Load-Velocity Relationship to Predict 1 Repetition Maximum During Deadlifts Performed With and Without Lifting Straps: The Accuracy of Six Prediction Models. J. Strength Cond. Res. 2020. [Google Scholar] [CrossRef]
- Suchomel, T.J.; Comfort, P.; Stone, M.H. Weightlifting pulling derivatives: Rationale for implementation and application. Sports Med. 2015, 45, 823–839. [Google Scholar] [CrossRef] [PubMed]
- Rivière, J.R.; Rossi, J.; Jimenez-Reyes, P.; Morin, J.B.; Samozino, P. Where does the one-repetition maximum exist on the force-velocity relationship in squat? Int. J. Sports Med. 2017, 38, 1035–1043. [Google Scholar] [CrossRef] [PubMed]
- French, D.N. Advanced power techniques. In Developing Power; McGuigan, M., Ed.; Human Kinetics: Champaign, IL, USA, 2017; pp. 177–198. [Google Scholar]
- García-Ramos, A.; Haff, G.G.; Padial, P.; Feriche, B. Reliability of power and velocity variables collected during the traditional and ballistic bench press exercise. Sports Biomech. 2018, 17, 117–130. [Google Scholar] [CrossRef]
- Sandau, I.; Granacher, U. Effects of the barbell load on the acceleration phase during the snatch in elite Olympic weightlifting. Sports 2020, 8, 59. [Google Scholar] [CrossRef] [PubMed]
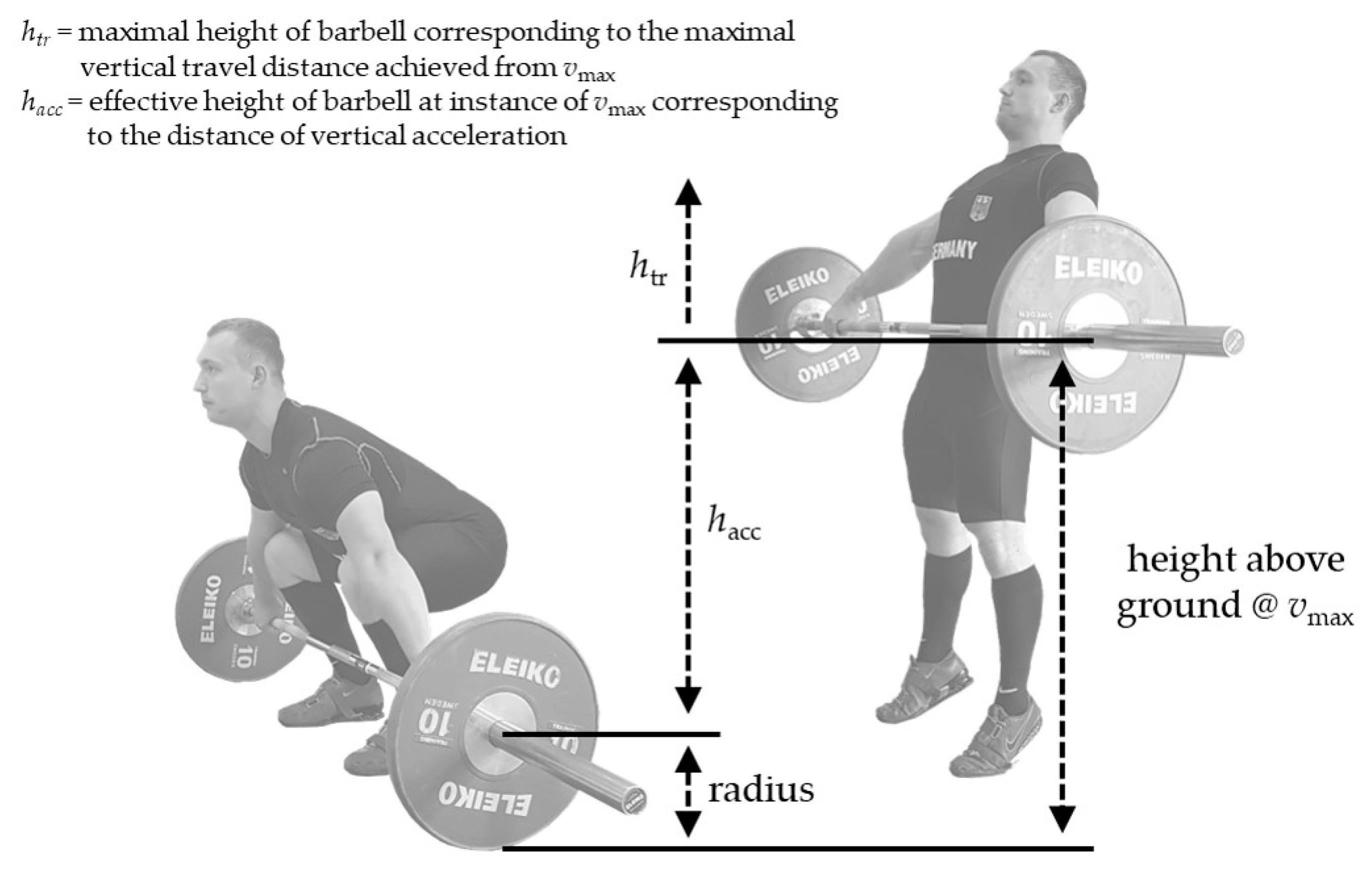
| Age (years) | Body Mass (kg) | 1RM Snatch (kg) | 1RM Clean and Jerk (kg) | |
|---|---|---|---|---|
| Overall | 23.3 ± 4.0 | 79.0 ± 16.6 | 124.8 ± 37.6 | 155.5 ± 41.7 |
| Male | 22.8 ± 3.3 | 87.4 ± 15.1 | 150.8 ± 11.5 | 184.2 ± 14.6 |
| Female | 24.0 ± 5.6 | 65.0 ± 6.0 | 81.3 ± 13.1 | 107.7 ± 12.9 |
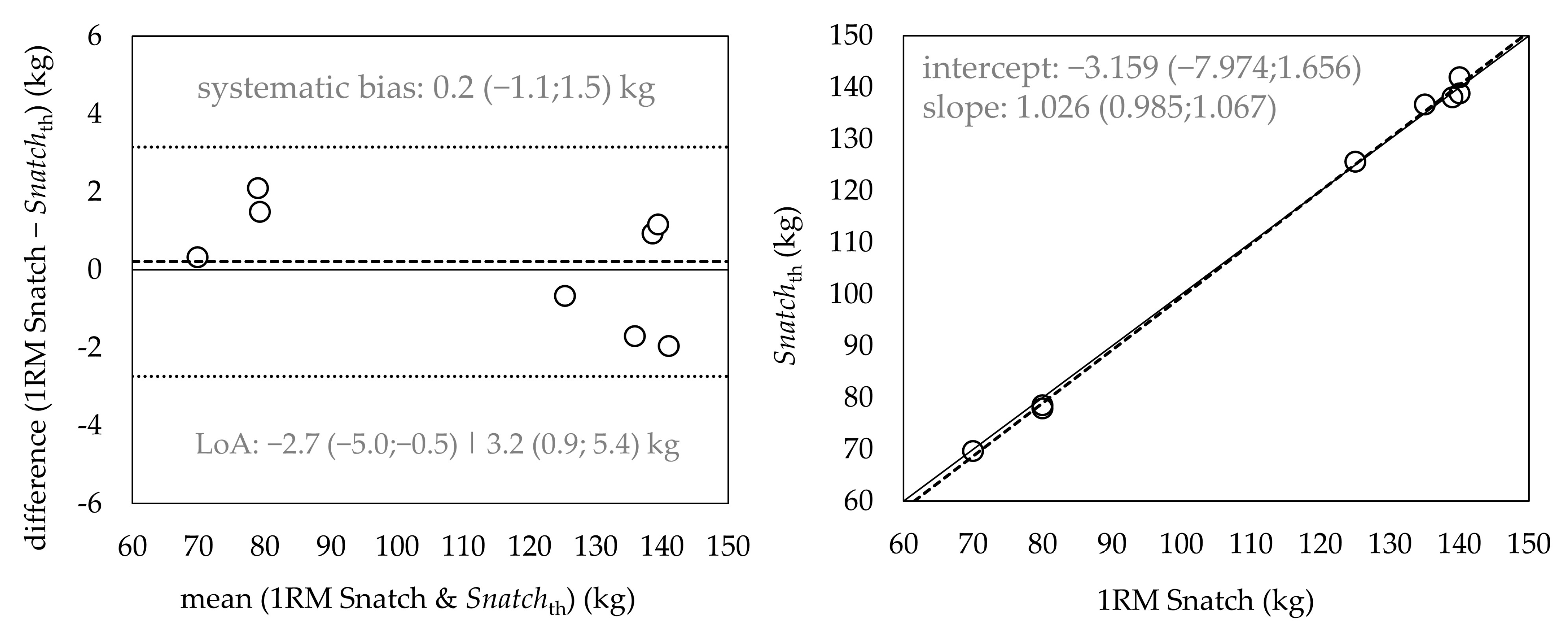
| 1RM Snatch | Snatchth | ||||||
|---|---|---|---|---|---|---|---|
| actual 1RM (kg) | vthre (m·s−1) | predicted 1RM (kg) | |||||
| 113.6 ± 31.1 | 1.97 ± 0.12 | 113.4 ± 32.0 | |||||
| Snatch Pull | Snatch Pull FvR2 | ||||||
| load @80% (kg) | load @110% (kg) | vmax @80% (m·s−1) | vmax @110% (m·s−1) | hacc @110% (m) | (m·s−1) | (N) | (W) |
| 91.3 ± 26.1 | 123.5 ± 33.7 | 2.30 ± 0.14 | 1.83 ± 0.15 | 0.80 ± 0.08 | 2.20 ± 0.32 | 2569.4 ± 613.2 | 1408.7 ± 377.2 |
| t(7) | p | d (95% CL) | r (95% CL) | Diff (%) | SDD (95% CL) (kg) | SDD% (%) |
|---|---|---|---|---|---|---|
| 0.393 | 0.706 | 0.01 (−0.02;0.04) | 0.99 (0.99;1.00) | 0.18 | 1.5 (1.0;3.1) | 1.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandau, I.; Chaabene, H.; Granacher, U. Predictive Validity of the Snatch Pull Force-Velocity Profile to Determine the Snatch One Repetition-Maximum in Male and Female Elite Weightlifters. J. Funct. Morphol. Kinesiol. 2021, 6, 35. https://doi.org/10.3390/jfmk6020035
Sandau I, Chaabene H, Granacher U. Predictive Validity of the Snatch Pull Force-Velocity Profile to Determine the Snatch One Repetition-Maximum in Male and Female Elite Weightlifters. Journal of Functional Morphology and Kinesiology. 2021; 6(2):35. https://doi.org/10.3390/jfmk6020035
Chicago/Turabian StyleSandau, Ingo, Helmi Chaabene, and Urs Granacher. 2021. "Predictive Validity of the Snatch Pull Force-Velocity Profile to Determine the Snatch One Repetition-Maximum in Male and Female Elite Weightlifters" Journal of Functional Morphology and Kinesiology 6, no. 2: 35. https://doi.org/10.3390/jfmk6020035
APA StyleSandau, I., Chaabene, H., & Granacher, U. (2021). Predictive Validity of the Snatch Pull Force-Velocity Profile to Determine the Snatch One Repetition-Maximum in Male and Female Elite Weightlifters. Journal of Functional Morphology and Kinesiology, 6(2), 35. https://doi.org/10.3390/jfmk6020035







