A Study on the Impact of Different PV Model Parameters and Various DC Faults on the Characteristics and Performance of the Photovoltaic Arrays
Abstract
1. Introduction
- Reviewing recent studies on how various parameters affect PV cells and modules’ behavior and efficiency.
- Identifying knowledge gaps by investigating the complex interdependencies among different parameters and their cumulative impact on PV arrays’ performance.
- Conducting a complete investigation of PV arrays’ dynamic characteristics by examining the effects of series resistance, shunt resistance, photocurrent, reverse saturation current, and the diode ideality factor through mathematical extractions, advanced simulations, and experimental methods.
- Investigating typical electrical faults in PV arrays, such as line-to-line, line-to-ground, partial shading, and complete shading, acquiring insights into fault detection and classification methodologies, ultimately boosting system reliability and efficiency.
2. PV Modelling and Parameters Extraction
2.1. Modelling of the PV System
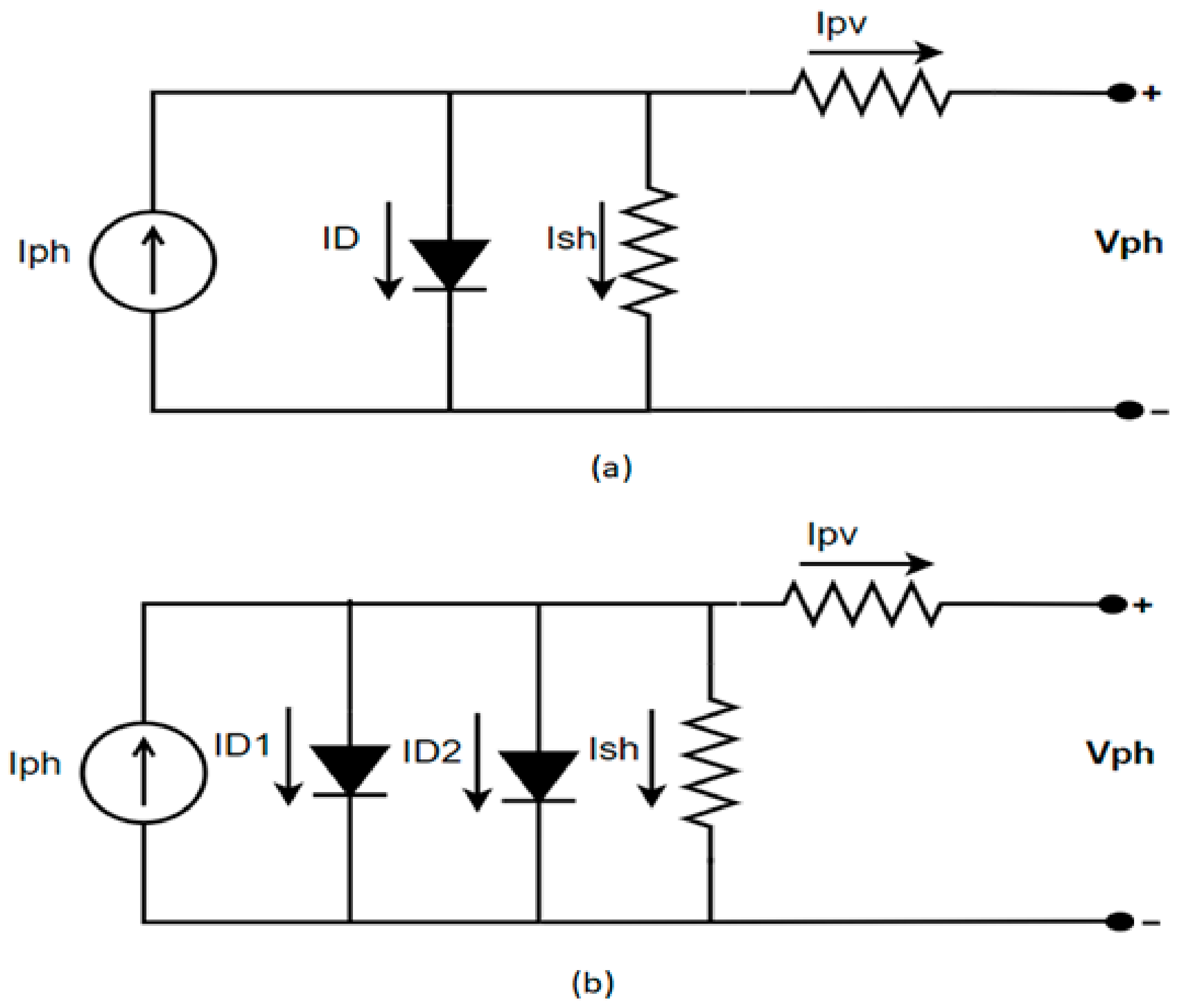
2.1.1. Equivalent Model of Series Connected PV Cells
2.1.2. Equivalent Model of the PV Module
2.2. PV Module Parameters Extraction
2.2.1. Extraction of the Photocurrent Parameter (Iph)
2.2.2. Extraction of the Shunt Resistance (Rsh)
2.2.3. Extraction of the Series Resistance (Rs)
2.2.4. Extraction of the Reverse Saturation Current (Io)
2.2.5. Extraction of the Diode Ideality Factor (α)
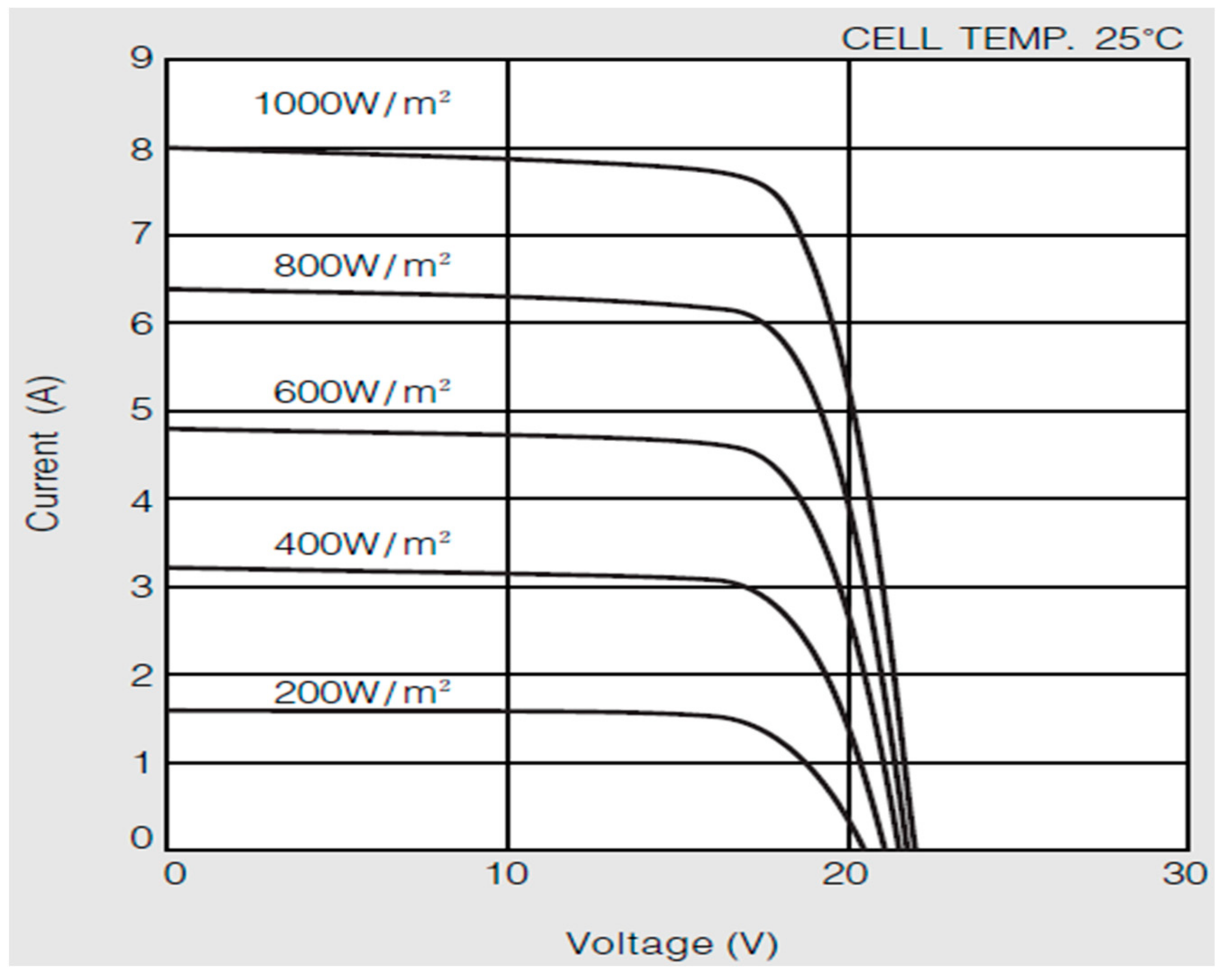
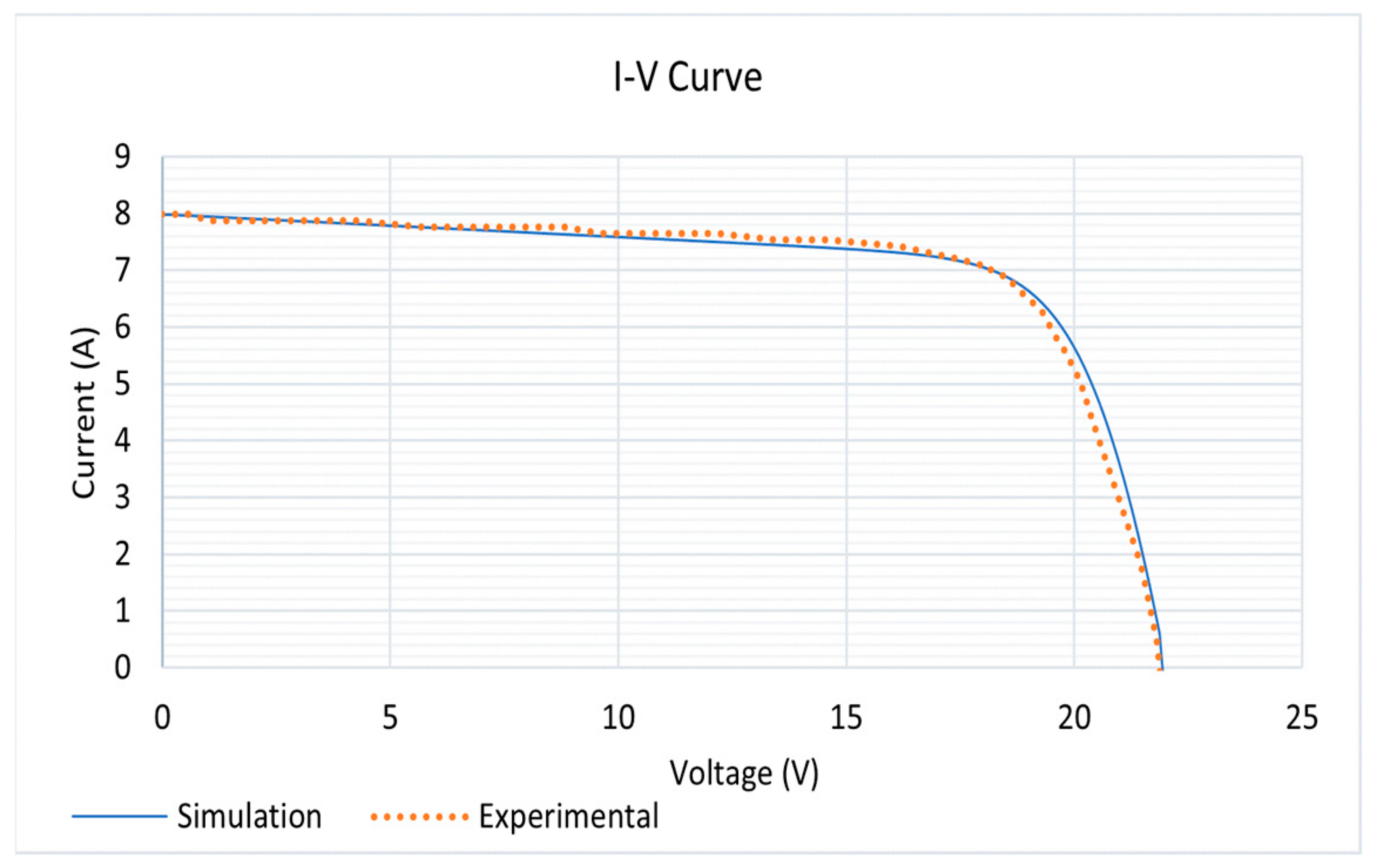
2.3. Parameters Extraction Implementation and Validation
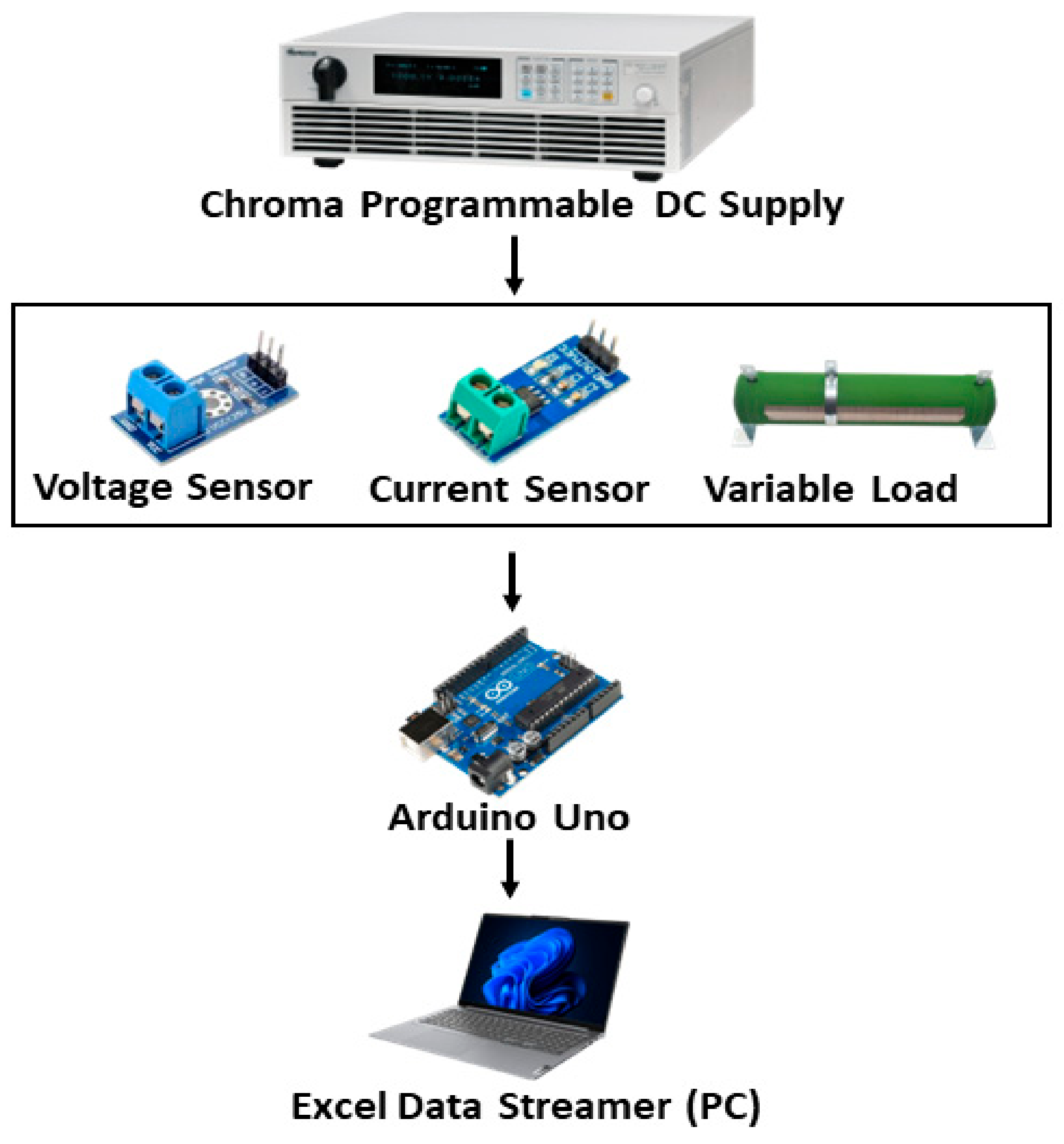
2.4. Experimental Setup Validation
3. The Effect of Different Parameters and Faults on the Performance of the PV Array
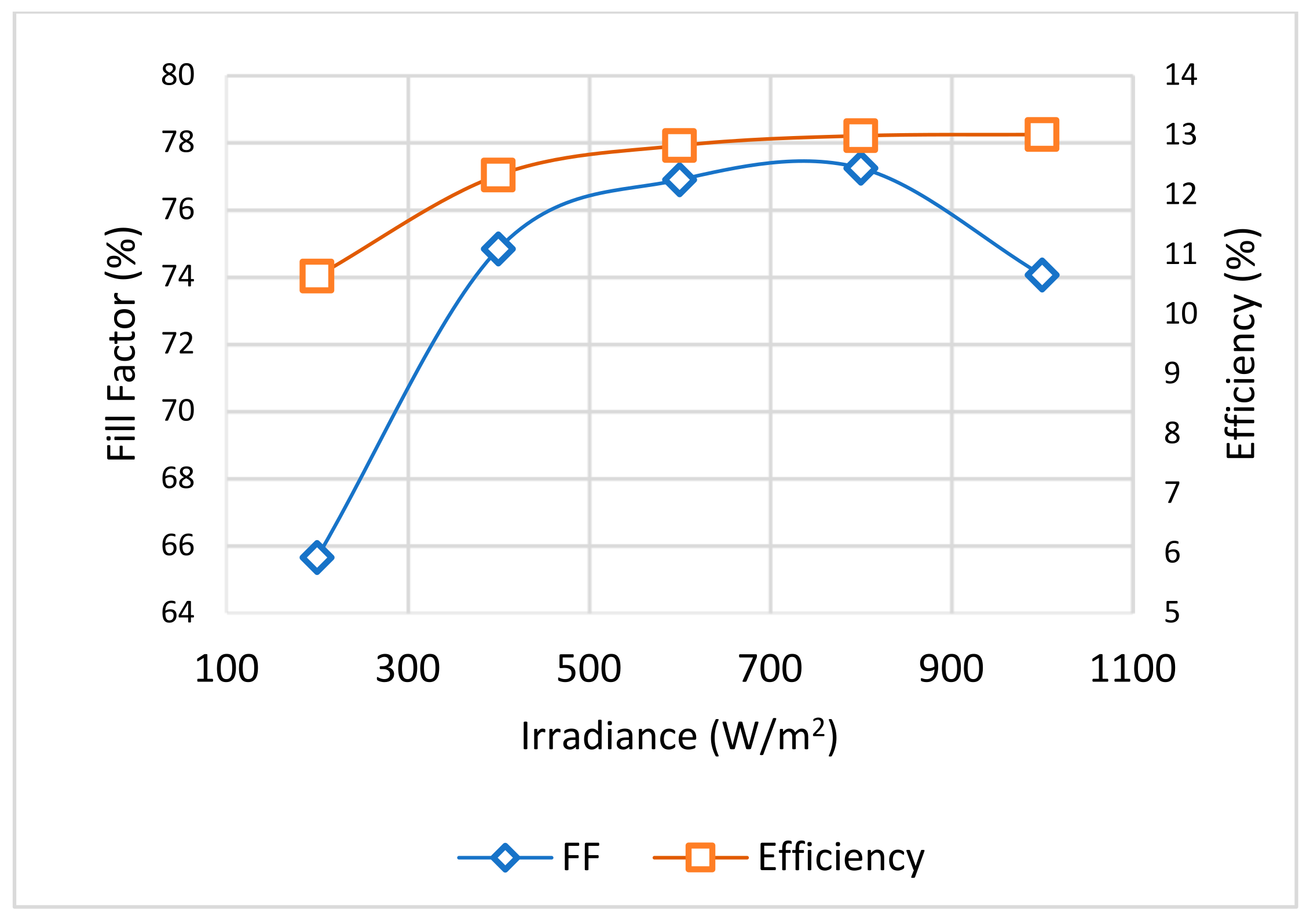
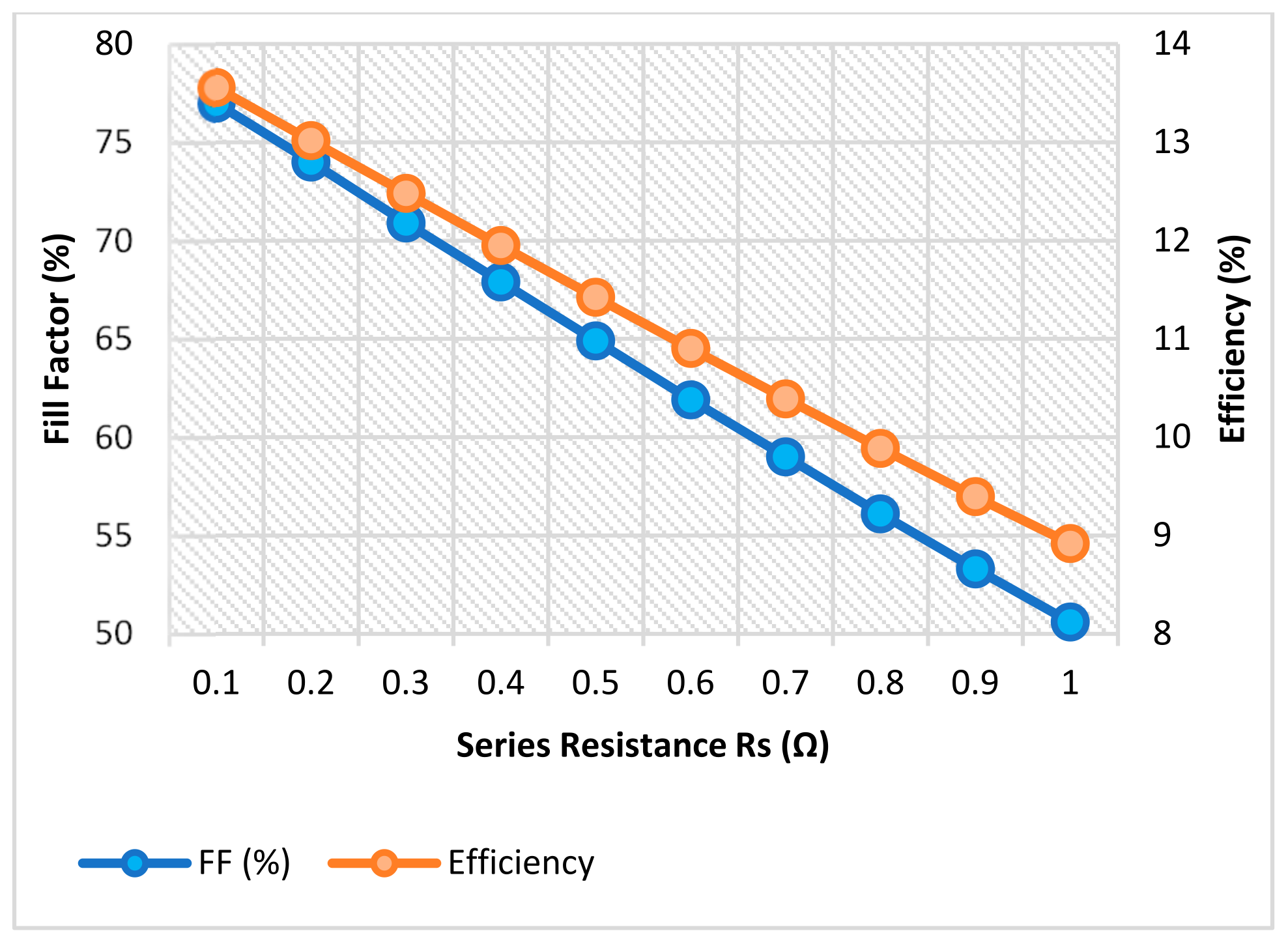
3.1. The Fill Factor (FF)
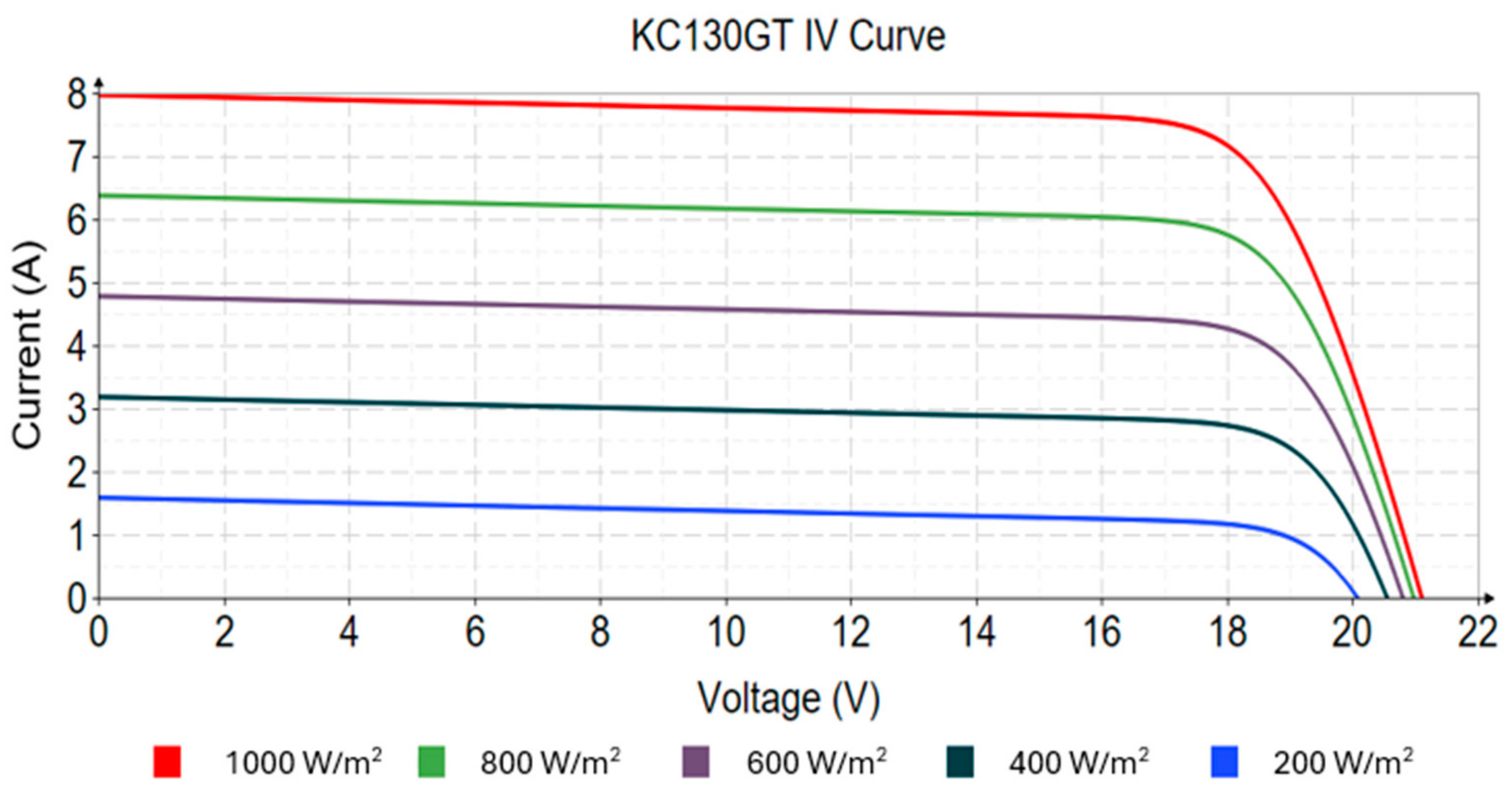
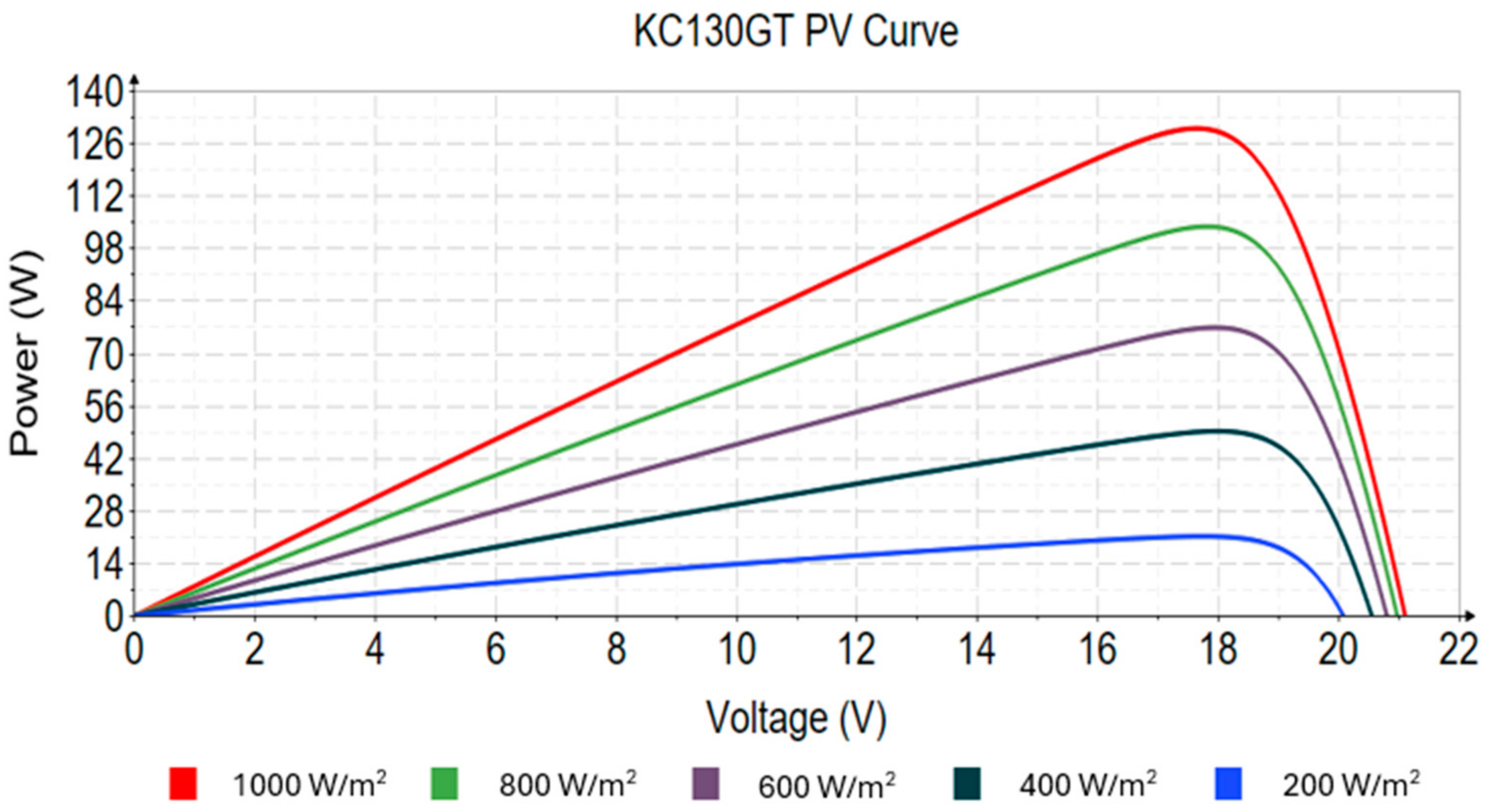
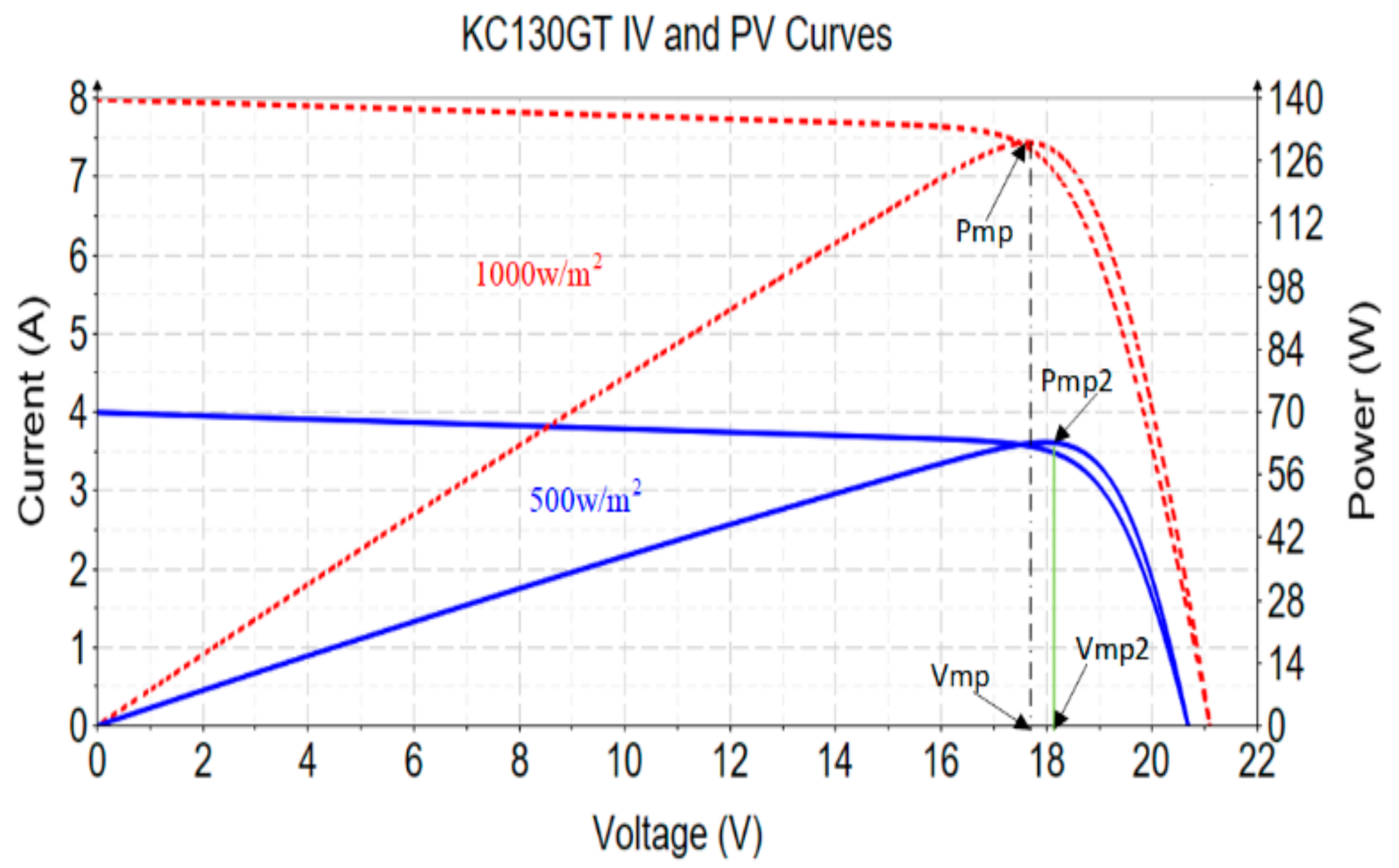
3.2. The Effect of the Irradiance Level (G)
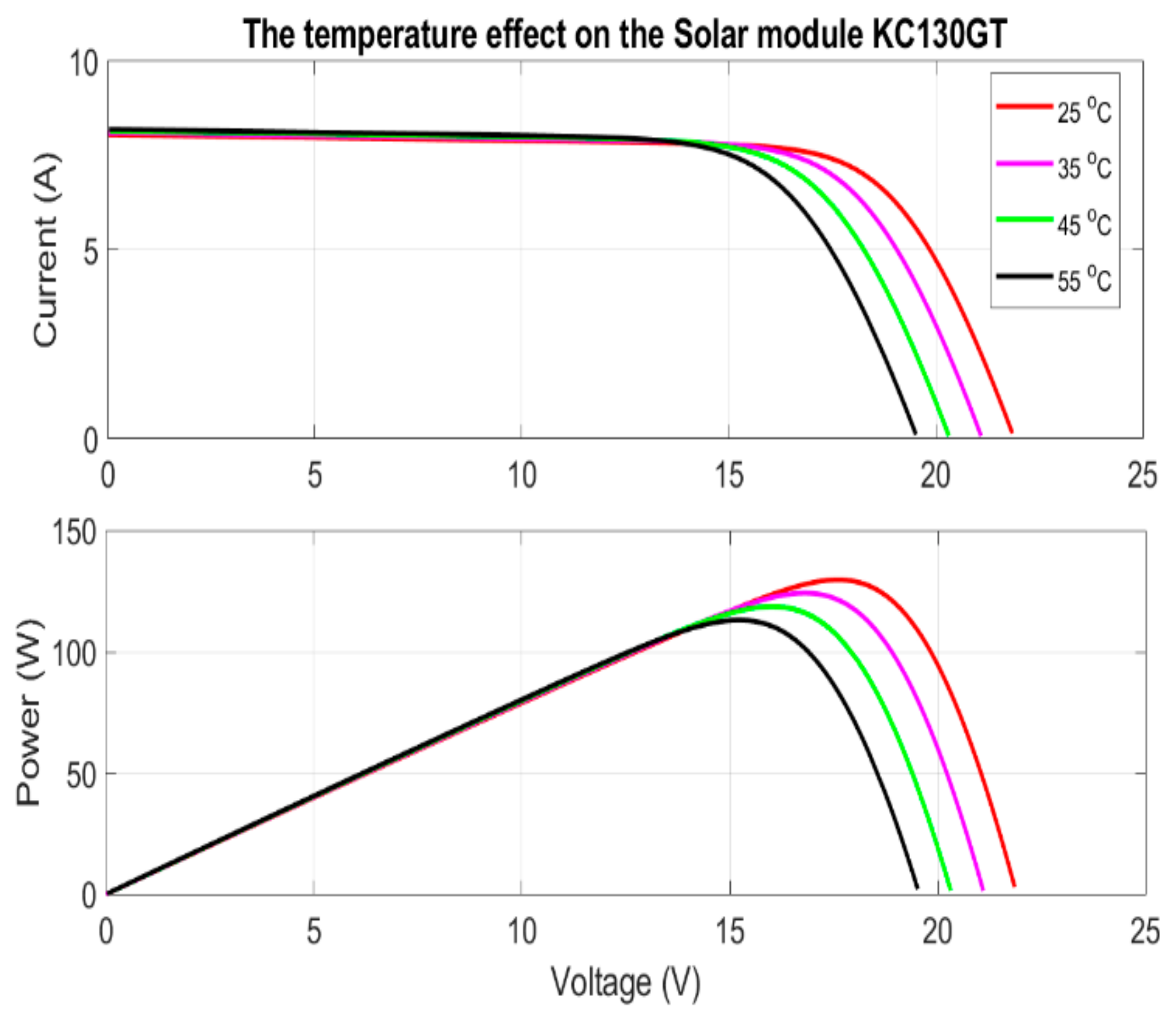
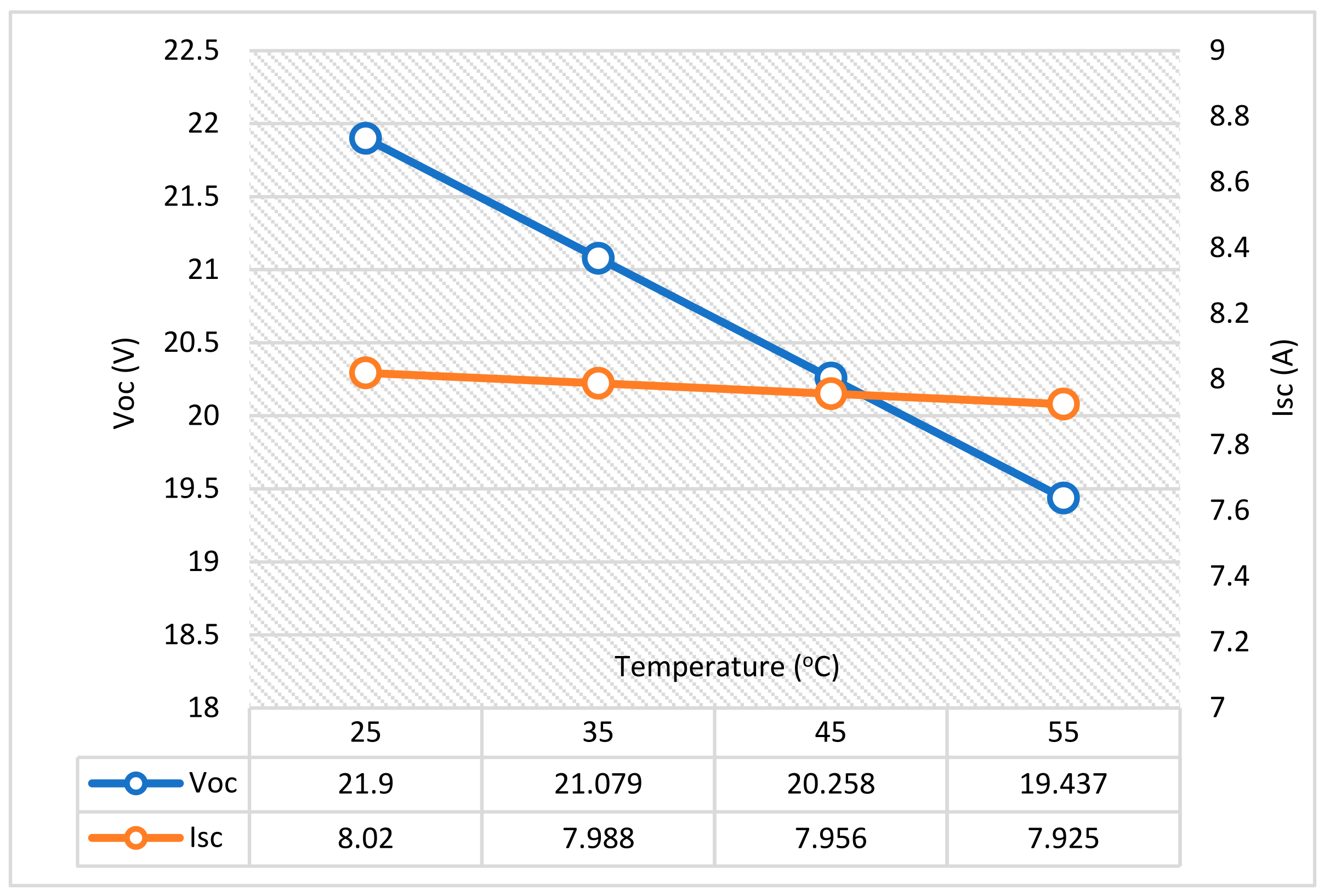
3.3. The Effect of Temperature (K)
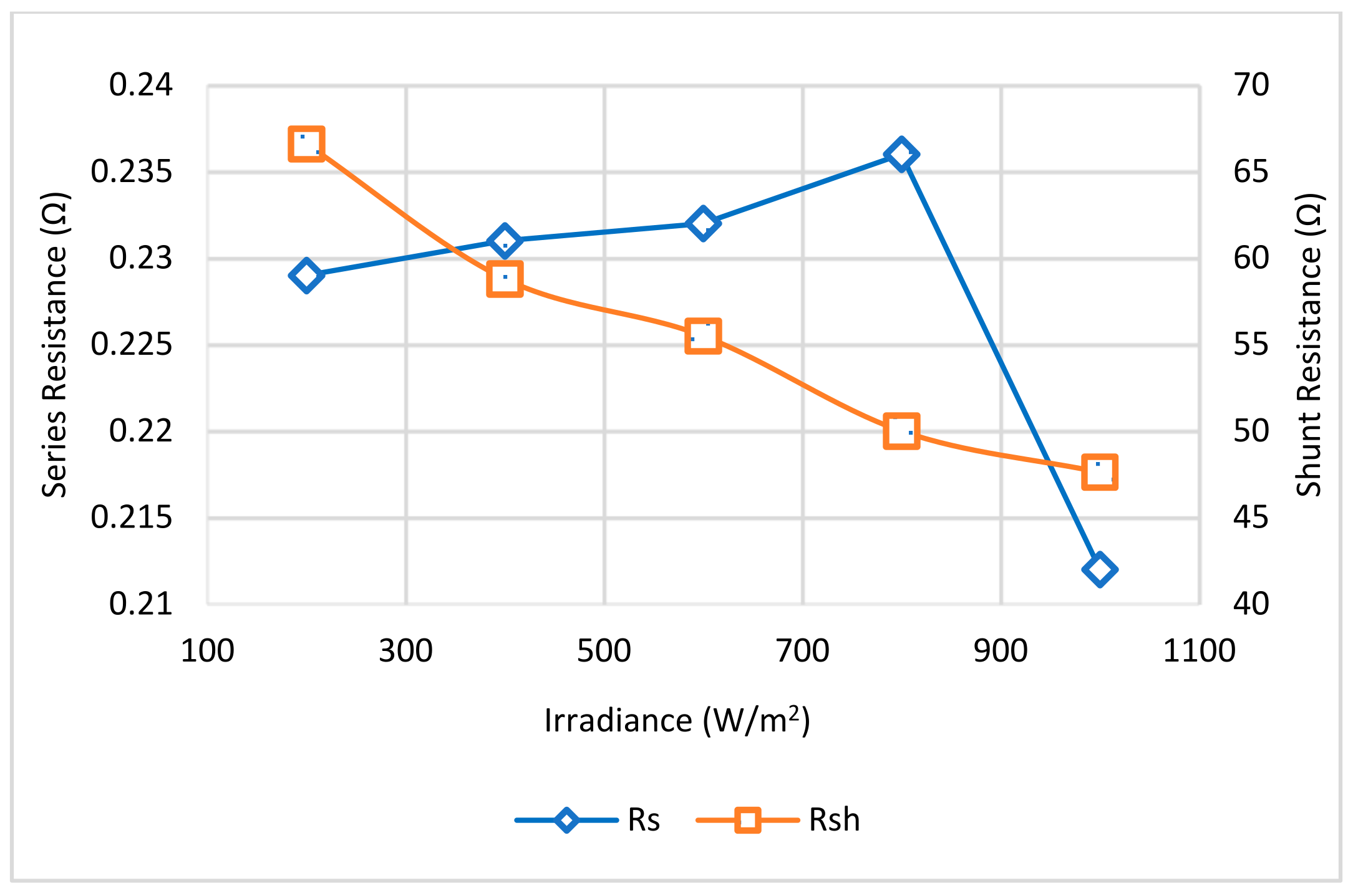
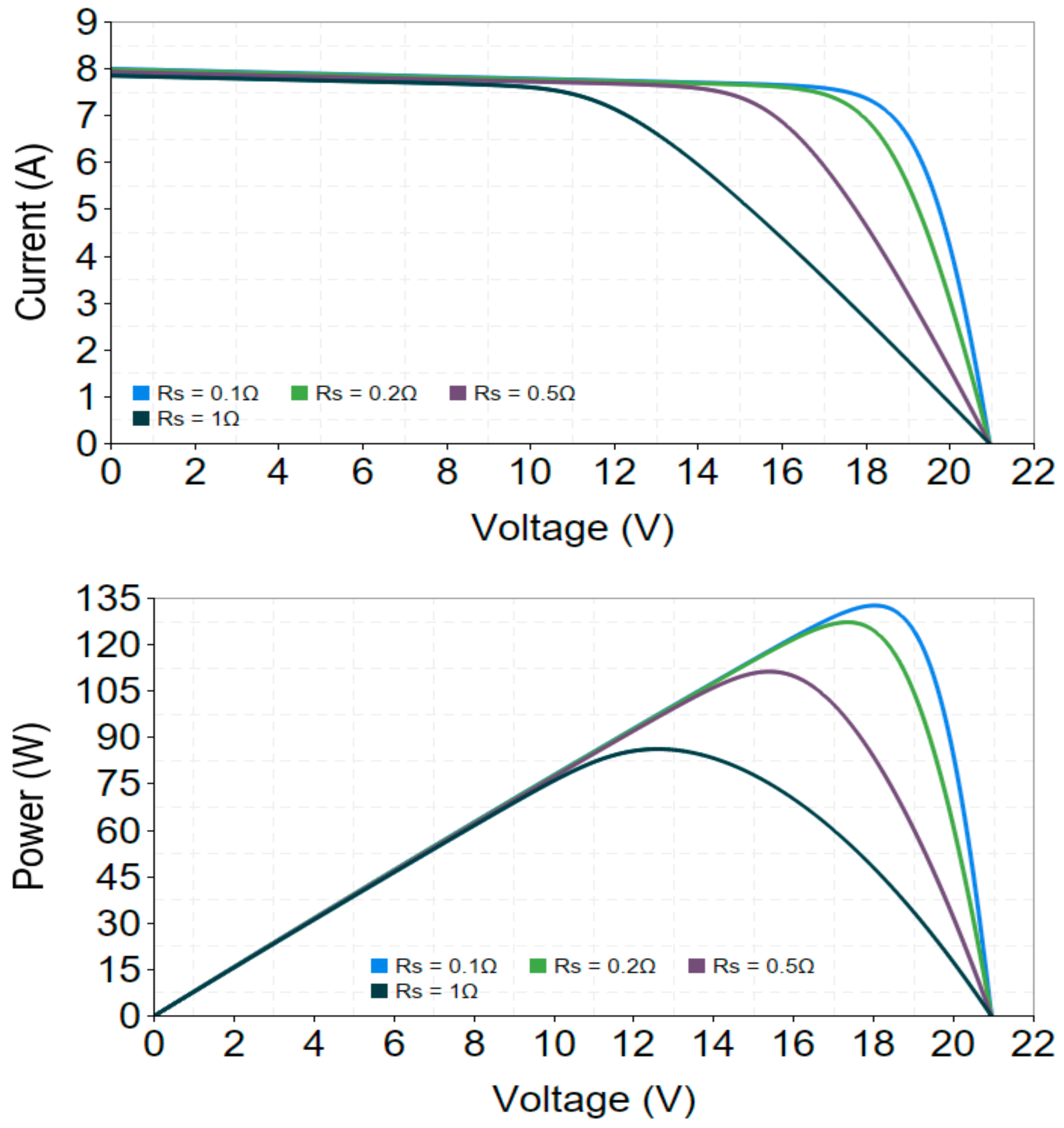
3.4. The Effect of Series Resistance (Rs)
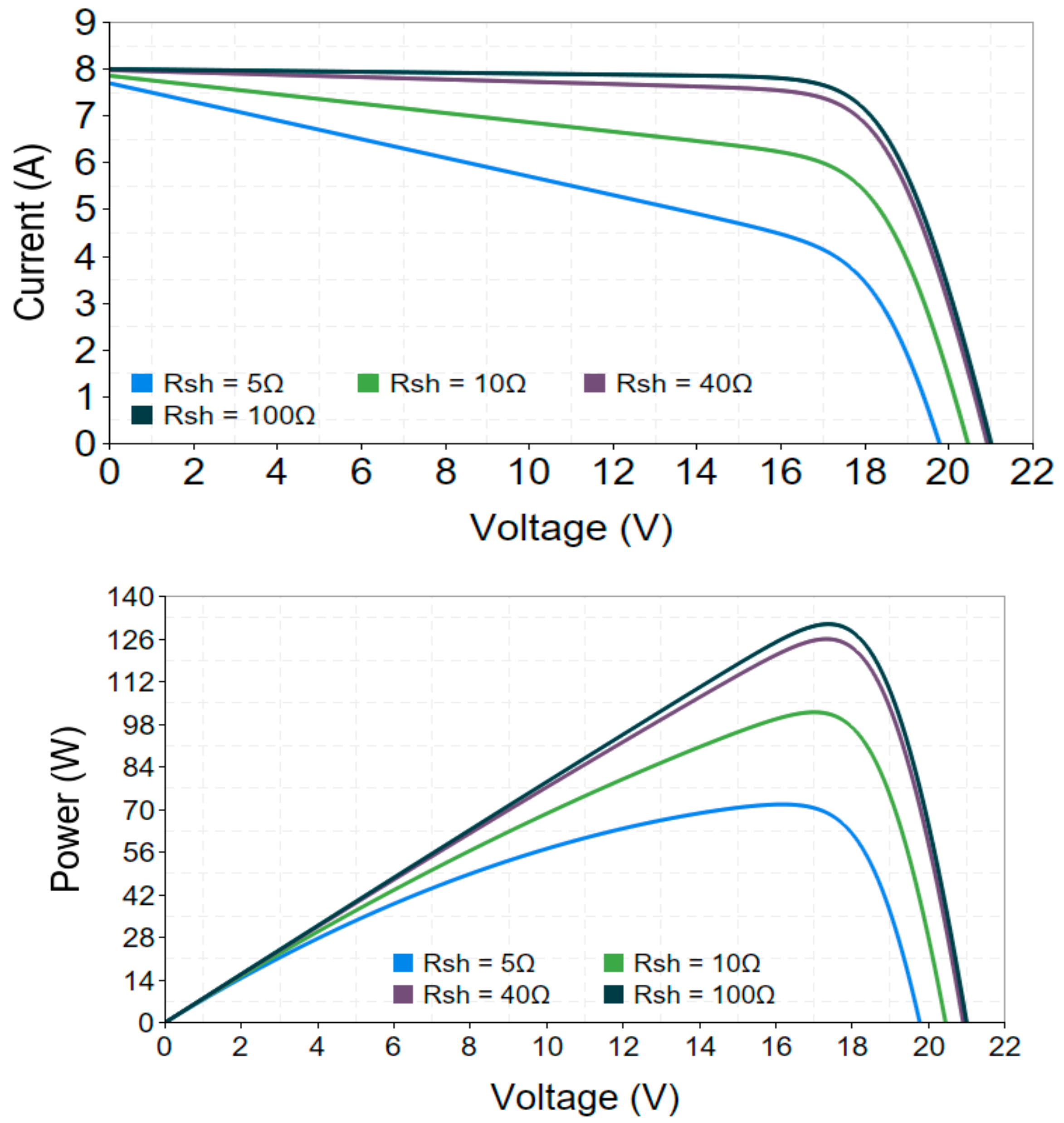
3.5. The Effect of the Shunt Resistance (Rsh)
3.6. The Effect of the Reverse Saturation Current (Io)
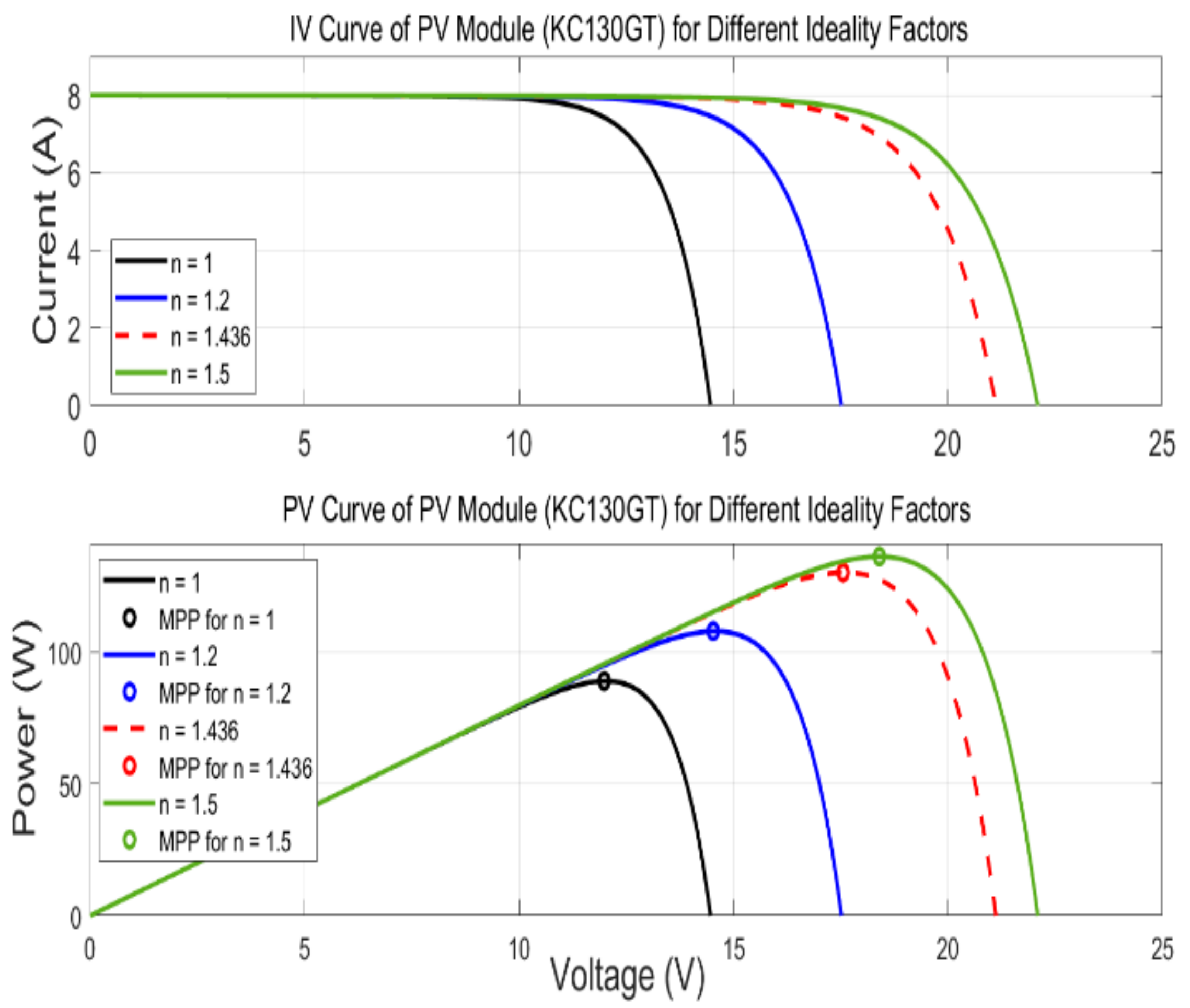
3.7. The Effect of the Diode Ideality Factor (α)
4. The Performance of the PV Arrays under the Effect of Different Electrical Faults
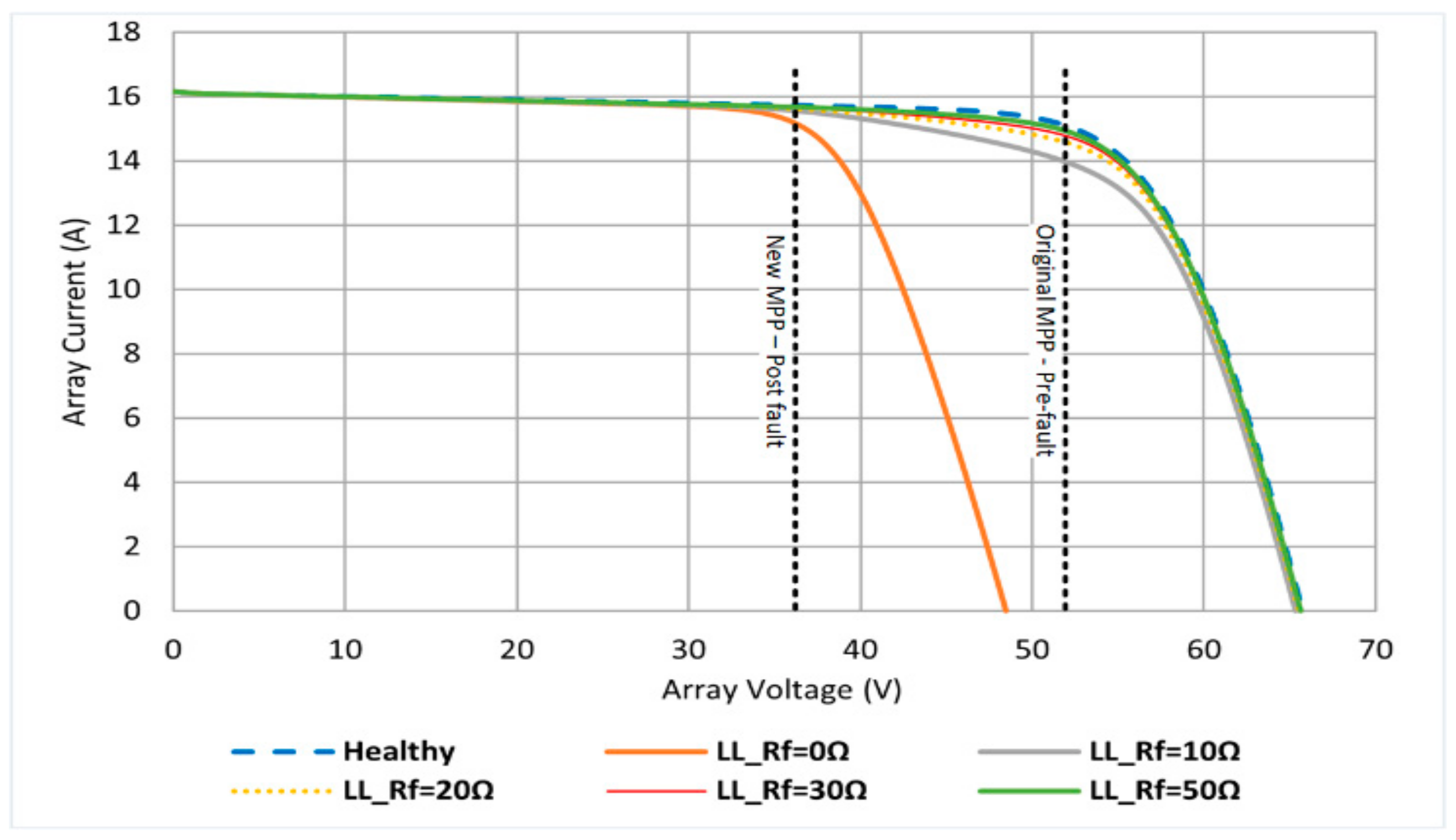
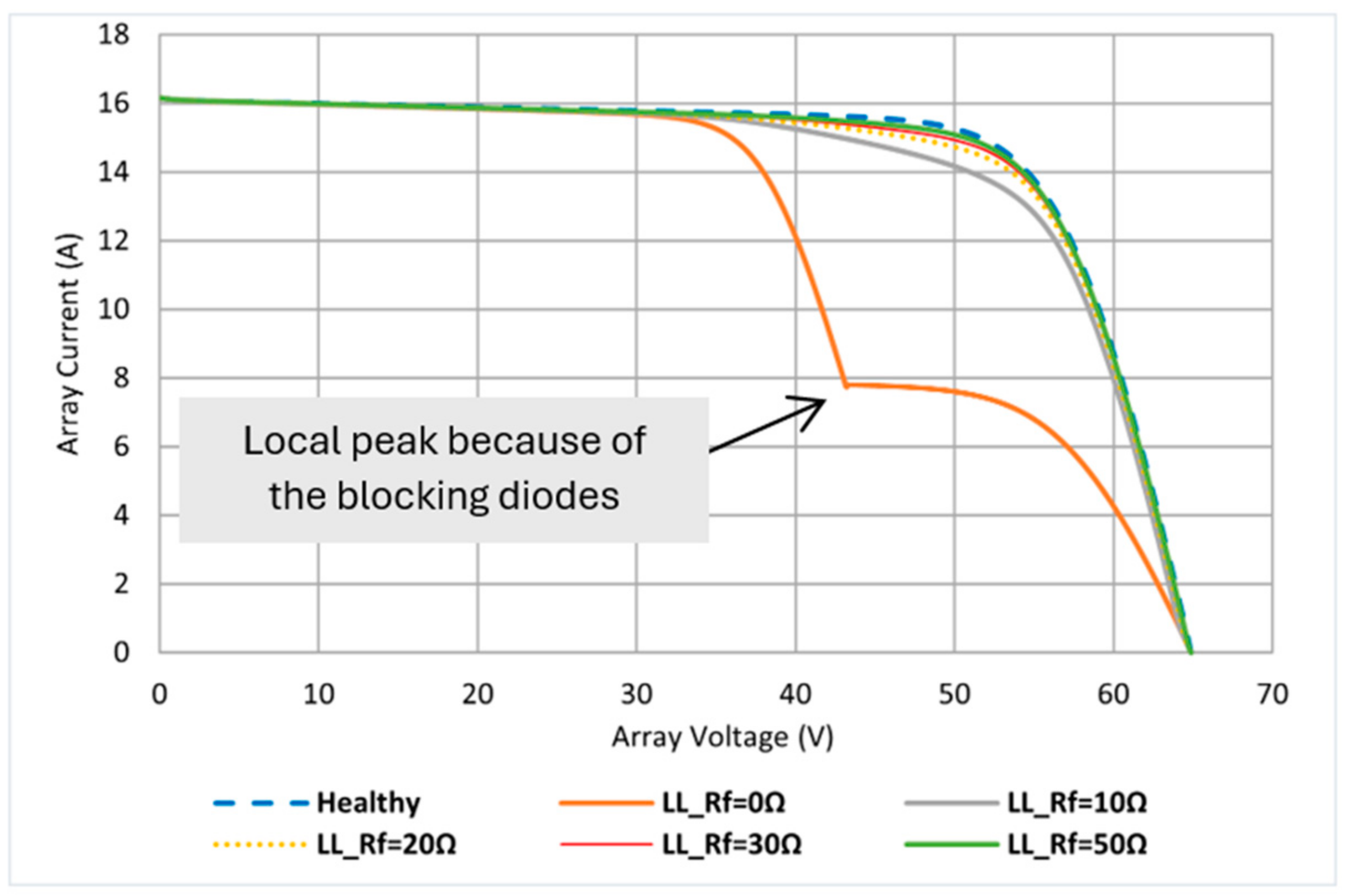
4.1. Line-to-Line Fault (LL)
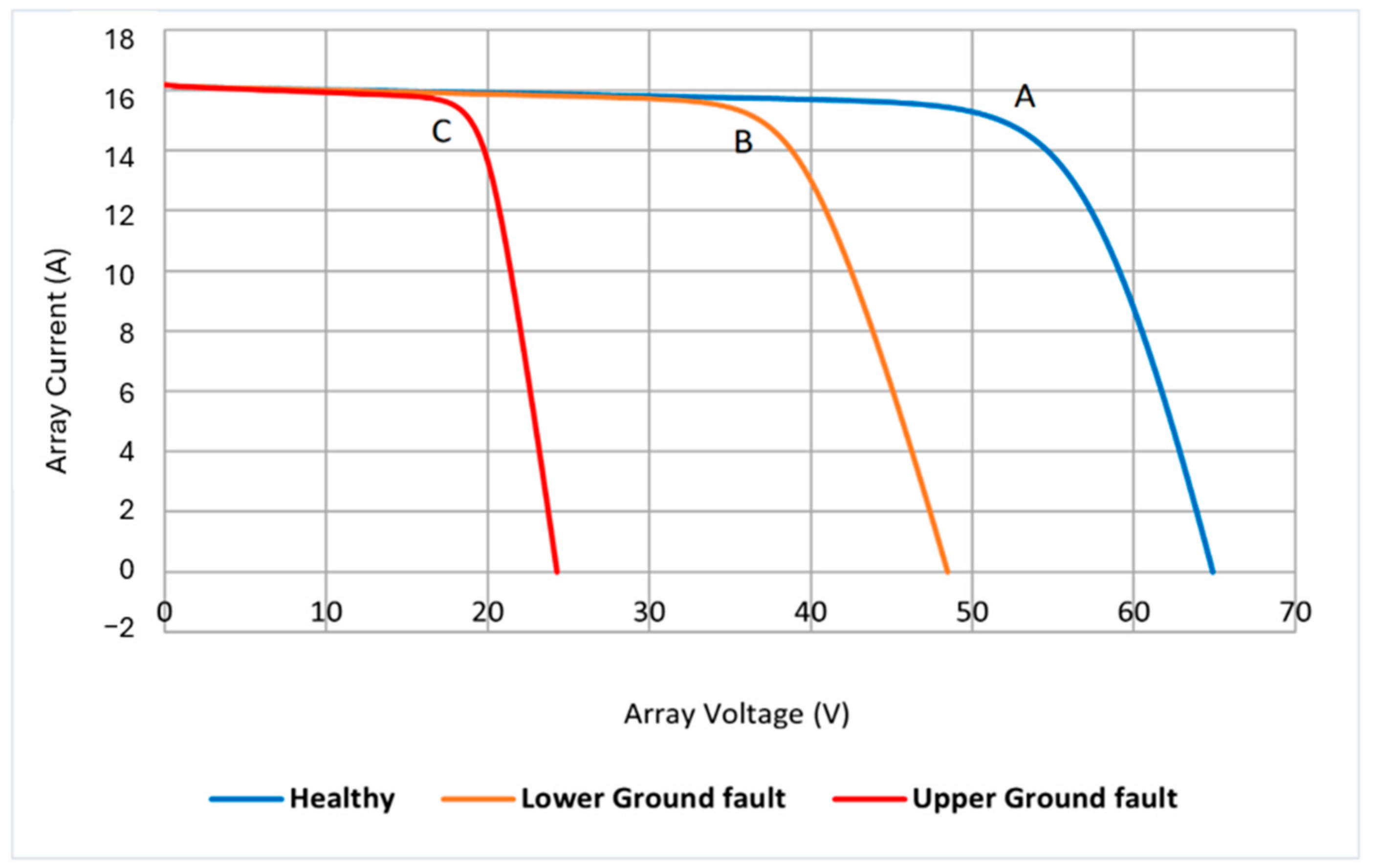
4.2. Line-To-Ground Fault
4.3. Partial Shading and Complete Shading Faults
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lorenzo, G.A.E. Solar Electricity: Engineering of Photovoltaic Systems; Institute of Solar Energy: Mendoza, Argentina; Polytechnic University of Madrid: Madrid, Spain, 1994. [Google Scholar]
- Tian, H.; Mancilla-david, F.; Ellis, K.; Jenkins, P.; Muljadi, E. A Detailed Performance Model for Photovoltaic Systems Preprint; NREL/JA-5500-54601; National Renewable Energy laboratory (NREL): Golden, CO, USA, 2012. Available online: http://www.osti.gov/bridge (accessed on 24 September 2023).
- Bhatia, S.C. Solar devices. Adv. Renew. Energy Syst. 2014, 68–93. [Google Scholar] [CrossRef]
- Al-Ezzi, A.S.; Ansari, M.N.M. Photovoltaic Solar Cells: A Review. Appl. Syst. Innov. 2022, 5, 67. [Google Scholar] [CrossRef]
- Oelhafen, P.; Schüler, A. Nanostructured materials for solar energy conversion. Sol. Energy 2005, 79, 110–121. [Google Scholar] [CrossRef]
- Blandford, R.; Watkins, M. This Month in Physics History: April 25, 1954: Bell Labs Demonstrates the First Practical Silicon Solar Cell. APS News 2009, 18, 2. [Google Scholar]
- Libra, M.; Kozelka, M.; Šafránková, J.; Belza, R.; Poulek, V.; Beránek, V.; Sedláček, J.; Zholobov, M.; Šubrt, T.; Severová, L. Agrivoltaics: Dual usage of agricultural land for sustainable development. Int. Agrophysics 2024, 38, 121–126. [Google Scholar] [CrossRef]
- Velasco, M.H. Enabling Year-round Cultivation in the Nordics-Agrivoltaics and Adaptive LED Lighting Control of Daily Light Integral. Agriculture 2021, 11, 1255. [Google Scholar] [CrossRef]
- Green, M.; Dunlop, E.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Hao, X. Solar cell efficiency tables (version 56). Prog. Photovolt. Res. Appl. 2020, 28, 629–638. [Google Scholar] [CrossRef]
- Suthar, M.; Singh, G.K.; Saini, R.P. Comparison of mathematical models of photo-voltaic (PV) module and effect of various parameters on its performance. In Proceedings of the 2013 International Conference on Energy Efficient Technologies for Sustainability (ICEETS), Nagercoil, India, 10–12 April 2013; pp. 1354–1359. [Google Scholar]
- Ahmed, T.; Goncalves, T.; Tlemcani, M. Single diode model parameters analysis of photovoltaic cell. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Bermigham, UK, 20–23 November 2016; Volume 017659, pp. 396–400. [Google Scholar] [CrossRef]
- Sarkar, N.I. Effect of various model parameters on solar photovoltaic cell simulation: A SPICE analysis. Renew. Wind. Water Sol. 2016, 3, 1. [Google Scholar] [CrossRef]
- Skoplaki, J.; Palyvos, E. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Seapan, M.; Limsakul, C.; Chayavanich, T.; Kirtikara, K.; Chayavanich, N.; Chenvidhya, D. Effects of dynamic parameters on measurements of IV curve. In Proceedings of the 2008 33rd IEEE Photovoltaic Specialists Conference, San Diego, CA, USA, 11–16 May 2008; pp. 1–3. [Google Scholar] [CrossRef]
- El-Khozondar, H.J.; El-Khozondar, R.J.; Matter, K. Parameters Influence on MPP Value of the Photo Voltaic Cell. Energy Procedia 2015, 74, 1142–1149. [Google Scholar] [CrossRef]
- Saloux, E.; Teyssedou, A.; Sorin, M. Explicit model of photovoltaic panels to determine voltages and currents at the maximum power point. Sol. Energy 2011, 85, 713–722. [Google Scholar] [CrossRef]
- Hamoodi, A.N.; Hamoodi, S.A.; Mohammed, R.A. Photovoltaic Modeling and Effecting of Temperature and Irradiation on I-V and P-V Characteristics. Int. J. Appl. Eng. Res. 2018, 13, 3123–3127. Available online: http://www.ripublication.com (accessed on 4 January 2024).
- Ukoima, K.; Agwu, E. Resistance, temperature and irradiance parameter analysis of a single diode photovoltaic cell model. Umudike J. Eng. Technol. 2019, 5, 97–107. [Google Scholar]
- Bouzguenda, M.; Salmi, T.; Gastli, A.; Masmoudi, A. Evaluating solar photovoltaic system performance using MATLAB. In Proceedings of the 2012 First International Conference on Renewable Energies and Vehicular Technology (REVET), Nabeul, Tunisia, 26–28 March 2012; pp. 55–59. [Google Scholar]
- Tayagaki, T.; Sasaki, A.; Ishizuka, S.; Yoshita, M. Impact of Shunt Resistance on the Performance of Curved Thin-Film Photovoltaic Modules With Series-Connected Solar Cells. IEEE J. Photovolt. 2022, 12, 1527–1532. [Google Scholar] [CrossRef]
- McMahon, T.; Basso, T.; Rummel, S. Cell shunt resistance and photovoltaic module performance. In Proceedings of the Conference Record of the Twenty Fifth IEEE Photovoltaic Specialists Conference, Washington, DC, USA, 13–17 May 1996; pp. 1291–1294. [Google Scholar]
- Al Abdullah, K.; Al Alloush, F.; Jaafar, A.; Salame, C. Study of the Effects Related to the Electric Reverse Stress Currents on the Mono-Si Solar Cell Electrical Parameters. Energy Procedia 2013, 36, 104–113. [Google Scholar] [CrossRef]
- Ramos-hernanz, J.; Lopez-guede, J.M.; Zulueta, E. Reverse Saturation Current Analysis in Photovoltaic Cell Models. WSEAS Trans. Power Syst. 2017, 12, 231–237. [Google Scholar]
- Chegaar, M.; Hamzaoui, A.; Namoda, A.; Petit, P.; Aillerie, M.; Herguth, A. Effect of Illumination Intensity on Solar Cells Parameters. Energy Procedia 2013, 36, 722–729. [Google Scholar] [CrossRef]
- Silva, E.A.; Bradaschia, F.; Cavalcanti, M.C.; Nascimento, A.J. Parameter Estimation Method to Improve the Accuracy of Photovoltaic Electrical Model. IEEE J. Photovolt. 2015, 6, 278–285. [Google Scholar] [CrossRef]
- Silva, E.A.; Bradaschia, F.; Cavalcanti, M.C.; Nascimento, A.J. Renewable Energy-Utilisation and System Integration. IEEE J. Photovolt. 2016, 6, 278–285. [Google Scholar] [CrossRef]
- Nayak, B.; Mohapatra, A.; Misra, B. Non Linear IV Curve of PV Module: Impacts on MPPT and Parameters Estimation. Int. J. Eng. Res. Technol. 2012, 1, 1–8. [Google Scholar]
- Baradieh, K.; Zainuri, M.A.A.B.M.; Kamari, N.A.M.; Yusof, Y.; Abdullah, H.; Zaman, M.H.B.M. Fault Detection and Classification in the Photovoltaic Arrays using Machine Learning. In Proceedings of the 2023 IEEE Industrial Electronics and Applications Conference (IEACon), Penang, Malaysia, 6–7 November 2023; pp. 177–182. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Diantoro, M.; Suprayogi, T.; Hidayat, A.; Taufiq, A.; Fuad, A.; Suryana, R. Shockley’s Equation Fit Analyses for Solar Cell Parameters from I-V Curves. Int. J. Photoenergy 2018, 2018, 9214820. [Google Scholar] [CrossRef]
- Stornelli, V.; Muttillo, M.; de Rubeis, T.; Nardi, I. A New Simplified Five-Parameter Estimation Method for Single-Diode Model of Photovoltaic Panels. Energies 2019, 12, 4271. [Google Scholar] [CrossRef]
- Md Tofael, A.; Teresa, G. Fault Analysis in Solar Photovoltaic Arrays. In Proceedings of the 5th International Conference on Renewable Energy Research and Applications, Bermigham, UK, 6–9 November 2016; pp. 20–23. [Google Scholar]
- Patil, S.R.; Burade, P.G.; Kadam, D.P. Five parameters extraction of single diode PV model by metaheuristic optimization method by identified built-up data. In Proceedings of the 5th International Conference on Renewable Energy Research and Applications, Bermigham, UK, 6–9 November 2016; Volume 12, pp. 20–23. [Google Scholar] [CrossRef]
- Quaschning, V.; Hanitsch, R. Numerical simulation of current-voltage characteristics of photovoltaic systems with shaded solar cells. Sol. Energy 1996, 56, 513–520. [Google Scholar] [CrossRef]
- Kumar, A.N.; Sameer, M.; Rasheed, M.M.; Balakrishna, A.; Venkat, S.N.; Manasa, V. A detailed modeling and simulation of photovoltaic module. In Proceedings of the 2020 International Conference on Smart Technologies in Computing, Electrical and Electronics (ICSTCEE), Bengaluru, India, 9–10 October 2020; pp. 39–43. [Google Scholar]
- Qi, C.; Ming, Z. Photovoltaic Module Simulink Model for a Stand-alone PV System. Phys. Procedia 2012, 24, 94–100. [Google Scholar] [CrossRef]
- Zainal, N.A.; Ajisman; Yusoff, A.R. Modelling of Photovoltaic Module Using Matlab Simulink. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 114, p. 012137. [Google Scholar] [CrossRef]
- Sharma, C.; Jain, A. Solar Panel Mathematical Modeling Using Simulink. J. Eng. Res. Appl. 2014, 4, 67–72. [Google Scholar]
- Mayfield, R. Photovoltaic Installation and Design for Dummies; Wiley Publishing, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bun, L. Detection and Localization of Faults in a System Photovoltaic Fault Detection and Localization for a PV System, Electric Energy; University of Grenoble: Grenoble, French, 2012. [Google Scholar]
- Zbib, B.; Al Sheikh, H. Fault Detection and Diagnosis of Photovoltaic Systems through I-V Curve Analysis. In Proceedings of the 2020 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Istanbul, Turkey, 12–13 June 2020; pp. 1–6. [Google Scholar]
- Diab, A.A.Z.; Sultan, H.M.; Do, T.D.; Kamel, O.M.; Mossa, M.A. Coyote Optimization Algorithm for Parameters Estimation of Various Models of Solar Cells and PV Modules. IEEE Access 2020, 8, 111102–111140. [Google Scholar] [CrossRef]
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear Minimization Algorithm for Determining the Solar Cell Parameters with Microcomputers. Int. J. Sol. Energy 1986, 4, 1–12. [Google Scholar] [CrossRef]
- Ortiz-Conde, J.M.A.; Sánchez, F.J.G. New method to extract the model parameters of solar cells from the explicit analytic solutions of their illuminated I-V characteristics. Sol. Energy Mater. Sol. Cells 2006, 90, 352–361. [Google Scholar] [CrossRef]
- Chan, J.C.H.P.D.S.H.; Phillips, J.R. A comparative study of extraction methods for solar cell model parameters. Solid-State Electron. 1986, 29, 329–337. [Google Scholar] [CrossRef]
- Ćalasan, M.; Aleem, S.H.; Zobaa, A.F. On the root mean square error (RMSE) calculation for parameter estimation of photovoltaic models: A novel exact analytical solution based on lambert w function. Energy Convers. Manag. 2020, 210, 112716. [Google Scholar] [CrossRef]
- Orioli, A.; Di Gangi, A. A procedure to calculate the five-parameter model of crystalline silicon photovoltaic modules on the basis of the tabular performance data. Appl. Energy 2013, 102, 1160–1177. [Google Scholar] [CrossRef]
- Appelbaum, J.; Peled, A. Parameters extraction of solar cells-A comparative examination of three methods. Sol. Energy Mater. Sol. Cells 2014, 122, 64–173. [Google Scholar] [CrossRef]
- Oliva, D.; Elaziz, M.A.; Elsheikh, A.H.; Ewees, A.A. A review on meta-heuristics methods for estimating parameters of solar cells. J. Power Sources 2019, 435, 126683. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X.; Xu, Y. Parameter extraction of solar cells using particle swarm optimization. J. Appl. Phys. 2009, 105, 094502. [Google Scholar] [CrossRef]
- El-Naggar, K.; AlRashidi, M.; AlHajri, M.; Al-Othman, A. Simulated Annealing algorithm for photovoltaic parameters identification. Sol. Energy 2012, 86, 266–274. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.; Ekoh, E.E. Evaluation of numerical algorithms used in extracting the parameters of a singlediode photovoltaic model. Sustain. Energy Technol. Assess. 2016, 13, 51–59. [Google Scholar]
- Ram, J.P.; Babu, T.S.; Dragicevic, T.; Rajasekar, N. A new hybrid bee pollinator follower pollination algorithm for solar PV parameter estimation. Energy Convers. Manag. 2017, 135, 463–476. [Google Scholar] [CrossRef]
- Kumari, P.A.; Geethanjali, P. Adaptive genetic algorithm based multiobjective optimization for photovoltaic cell design parameter extraction. Energy Procedia 2017, 117, 432–441. [Google Scholar] [CrossRef]
- Merchaoui, M.; Sakly, A.; Mimouni, M.F. Particle swarm optimisation with adaptive mutation strategy for photovoltaic solar cell/module parameter extraction. Energy Convers. Manag. 2018, 175, 151–163. [Google Scholar] [CrossRef]
- García-Ródenas, R.; Linares, L.J.; López-Gómez, J.A. A memetic chaotic gravitational search algorithm for unconstrained global optimization problems. Appl. Soft Comput. 2019, 79, 14–29. [Google Scholar] [CrossRef]
- Ji, J.; Gao, S.; Wang, S.; Tang, Y.; Yu, H.; Todo, Y. Self-adaptive gravitational search algorithm with a modified chaotic local search. IEEE Access 2017, 5, 7881–17895. [Google Scholar] [CrossRef]
- Skvarenina, T.L. Handbook for Solar Photovoltaic Systems; Purdue University: West Lafayette, IN, USA, 2018. [Google Scholar]
- Skvarenina, T.L. The Power Electronics Handbook; Purdue University: West Lafayette, IN, USA, 2018. [Google Scholar]
- Erhard, N.; Holleitner, A. 13-Semiconductor nanowires studied by photocurrent spectroscopy. In Semiconductor Nanowires; Arbiol, J., Xiong, Q., Eds.; Woodhead Publishing: Sawston, UK, 2015; pp. 365–391. [Google Scholar] [CrossRef]
- Ruschel, C.S.; Gasparin, F.P.; Costa, E.R.; Krenzinger, A. Assessment of PV modules shunt resistance dependence on solar irradiance. Sol. Energy 2016, 133, 35–43. [Google Scholar] [CrossRef]
- Piliougine, M.; Spagnuolo, G.; Sidrach-De-Cardona, M. Series resistance temperature sensitivity in degraded mono–crystalline silicon modules. Renew. Energy 2020, 162, 677–684. [Google Scholar] [CrossRef]
- Kabbani, A.; Honnurvali, M.S. PV Cell Parameters Modeling and Temperature Effect Analysis. Int. J. Renew. Energy Dev. 2021, 10, 563–571. [Google Scholar] [CrossRef]
- Meyer, E.L. Extraction of Saturation Current and Ideality Factor from Measuring Voc and Isc of Photovoltaic Modules. Int. J. Photoenergy 2017, 2017, 8479487. [Google Scholar] [CrossRef]
- Sabadus, A.; Paulescu, M. Extraction of the diode saturation current and ideality factor from the PV module datasheet. AIP Conf. Proc. 2023, 2843, 40004. [Google Scholar] [CrossRef]
- Corporation, K. “Model kc130gt” Kyocera s Advanced Cell Processing Technology; Kyocera Corporation: Kyoto, Japan. Available online: http://www.kyocera.com (accessed on 2 February 2024).
- Allegro Microsystems, Fully Integrated, Hall-Effect-Based Linear Current Sensor IC with 2.1 kVRMS Voltage Isolation and a Low-Resistance Current Conductor. Rev. 22. February 2024. pp. 1–16. Available online: https://www.allegromicro.com/-/media/files/datasheets/acs712-datasheet.pdf (accessed on 2 February 2024).
- El Hammoumi, A.; Motahhir, S.; Chalh, A.; El Ghzizal, A.; Derouich, A. Low-cost virtual instrumentation of PV panel characteristics using Excel and Arduino in comparison with traditional instrumentation. Renew. Wind. Water Sol. 2018, 5, 3. [Google Scholar] [CrossRef]
- Green, M.A. Accuracy of analytical expressions for solar cell fill factors. Sol. Cells 1982, 7, 337–340. [Google Scholar] [CrossRef]
- Libra, M.; Petrik, T.; Poulek, V.; Tyukhov, I.I.; Kourim, P. Changes in the Efficiency of Photovoltaic Energy Conversion in Temperature Range With Extreme Limits. IEEE J. Photovolt. 2021, 11, 1479–1484. [Google Scholar] [CrossRef]
- Ahmed, T.; Goncalves, T.; Albino, A.; Rashel, M.R.; Veiga, A.; Tlemcani, M. Different parameters variation analysis of a PV cell. In Proceedings of the 2016 International Conference for Students on Applied Engineering (ICSAE), Newcastle Upon Tyne, UK, 20–21 October 2016; pp. 176–180. [Google Scholar]
- Muhammad, F.F.; Yahya, M.Y.; Hameed, S.S.; Aziz, F.; Sulaiman, K.; Rasheed, M.A.; Ahmad, Z. Employment of single-diode model to elucidate the variations in photovoltaic parameters under different electrical and thermal conditions. PLoS ONE 2017, 12, e0182925. [Google Scholar] [CrossRef]
- Islam, A.; Chowdhury, I.B. A simulink based generalized model of PV cell/array. In Proceedings of the 2014 3rd International Conference on the Developments in Renewable Energy Technology (ICDRET), Dhaka, Bangladesh, 29–31 May 2014; pp. 1–5. [Google Scholar]
- Qi, B.; Wang, J. Fill factor in organic solar cells. Phys. Chem. Chem. Phys. 2013, 15, 8972–8982. [Google Scholar] [CrossRef]
- Street, R.A.; Schoendorf, M.; Roy, A.; Lee, J.H. Interface state recombination in organic solar cells. Phys. Rev. B 2010, 81, 205307. [Google Scholar] [CrossRef]
- Jain, P.; Xu, J.-X.; Panda, S.K.; Poon, J.; Spanos, C.; Sanders, S.R. Fault diagnosis via PV panel-integrated power electronics. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Baradieh, K.I.; Al-Hamouz, Z. Modelling and Simulation of Line Start Permanent Magnet Synchronous Motors with Broken Bars. J. Electr. Electron. Syst. 2018, 7, 2. [Google Scholar] [CrossRef]
- Baradieh, K.; Al-Hamouz, Z.; Abido, M. ANN Based Broken Rotor Bar Fault Detection in LSPMS Motors. J. Electr. Electron. Syst. 2018, 7, 2332–2796. [Google Scholar] [CrossRef]
- Nie, S.; Chen, Y.; Pei, X.; Wang, H.; Kang, Y. Fault diagnosis of a single-phase inverter using the magnetic field waveform near the output inductor. In Proceedings of the 2011 IEEE Applied Power Electronics Conference and Exposition (APEC 2011), Fort Worth, TX, USA, 6–11 March 2011; pp. 1648–1655. [Google Scholar] [CrossRef]
- Rakesh, N.; Banerjee, S.; Subramaniam, S.; Babu, N. A simplified method for fault detection and identification of mismatch modules and strings in a grid-tied solar photovoltaic system. Int. J. Emerg. Electr. Power Syst. 2020, 21, 20200001. [Google Scholar] [CrossRef]
- Alam, M.K.; Khan, F.; Johnson, J.; Flicker, J. A Comprehensive Review of Catastrophic Faults in PV Arrays: Types, Detection, and Mitigation Techniques. IEEE J. Photovolt. 2015, 5, 982–997. [Google Scholar] [CrossRef]
- Detection, F.; In, P.; Photovoltaic, S.; Presented, A.D. Protection in Solar Photovoltaic Arrays Acknowledgments. 2015. Available online: https://repository.library.northeastern.edu/downloads/neu:m039kr12f?datastream_id=content (accessed on 18 September 2023).
- Badr, M.M.; Hamad, M.S.; Abdel-Khalik, A.S.; Hamdy, R.A.; Ahmed, S.; Hamdan, E. Fault Identification of Photovoltaic Array Based on Machine Learning Classifiers. IEEE Access 2021, 9, 159113–159132. [Google Scholar] [CrossRef]
- Wang, G.; Youn, C.C.; Stankovic, A.M. DC-side high impedance ground fault detection for transformerless single-phase PV systems. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; pp. 1–6. [Google Scholar]
- Chine, W.; Mellit, A.; Pavan, A.M.; Lughi, V. Fault diagnosis in photovoltaic arrays. In Proceedings of the 2015 International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 67–72. [Google Scholar]
- Restrepo-Cuestas, B.J.; Durango-Flórez, M.; Trejos-Grisales, L.A.; Ramos-Paja, C.A. Analysis of Electrical Models for Photovoltaic Cells under Uniform and Partial Shading Conditions. Computation 2022, 10, 111. [Google Scholar] [CrossRef]
- Khalil, I.U.; Ul-Haq, A.; Mahmoud, Y.; Jalal, M.; Aamir, M.; Ahsan, M.U.; Mehmood, K. Comparative Analysis of Photovoltaic Faults and Performance Evaluation of its Detection Techniques. IEEE Access 2020, 8, 26676–26700. [Google Scholar] [CrossRef]
- Grisales, L.A.T.; Ramos-Paja, A.J.S.-M.C.A. Fault Detection and Performance Analysis of Photovoltaic Installations. Tecnura 2016, 20, 171–184. Available online: http://eprints.hud.ac.uk/id/eprint/34576/ (accessed on 11 April 2024).
- Grisales, L.A.T.; Ramos-Paja, A.J.S.-M.C.A. Techniques for modeling photovoltaic systems under partial shading. Tecnura 2016, 20, 171–184. [Google Scholar]
- Kim, K.A.; Seo, G.-S.; Cho, B.-H.; Krein, P.T. Photovoltaic Hot-Spot Detection for Solar Panel Substrings Using AC Parameter Characterization. IEEE Trans. Power Electron. 2015, 31, 1121–1130. [Google Scholar] [CrossRef]













| Parameter | Description | Unit |
|---|---|---|
| Iph | Photocurrent | A |
| Id | Diode current | A |
| Ish | Shunt current | A |
| Io | Reverse saturation current | A |
| Vd | Diode voltage | V |
| G | Solar irradiation under a given condition | W/m2 |
| Gref | Illumination reference (1000 W/m2) | W/m2 |
| Tcell | Temperature of the cell | (°K) |
| Tref | Reference temperature | (°K) |
| KI | Short circuit current temperature coefficient | (A/°K) |
| Kv | Open circuit temperature coefficient | (V/°K) |
| a | The ideality factor of the diode | - |
| Rs | Series resistance | Ω |
| Rsh | Shunt resistance | Ω |
| Vt | Thermal voltage = | V |
| K | Boltzmann’s constant = × | J/K |
| q | Electron Charge = | C |
| Parameter under STC | Value |
|---|---|
| Maximum power (Pmax) | 130 W |
| Voltage at maximum power point (Vmp) | 17.6 V |
| Current at maximum power point (Imp) | 7.39 A |
| Open-circuit voltage (Voc) | 21.9 V |
| Short-circuit current (Isc) | 8.02 A |
| Temperature coefficient of Voc | −8.21 × 10−2 V/°C |
| Temperature coefficient of Isc | 3.18 × 10−3 A/°C |
| Ns | 36 |
| Parameter | Estimated Value |
|---|---|
| −0.021 A/V | |
| −0.2291 A/V | |
| Iph | 8.02 A |
| Io | 1.648 × 10−16 A |
| Rsh | 47.619 Ω |
| Rs | 0.212 Ω |
| α | 1.436 |
| Irradiance (W/m2) | Isc (A) | Voc (V) | Pmp (W) | FF |
|---|---|---|---|---|
| 1000 | 8.02 | 21.9 | 130.071 | 0.741 |
| 800 | 6.416 | 20.966 | 103.891 | 0.7726 |
| 600 | 4.812 | 20.794 | 76.938 | 0.767 |
| 400 | 3.208 | 20.544 | 49.314 | 0.748 |
| 200 | 1.604 | 20.205 | 21.274 | 0.656 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baradieh, K.I.; Zainuri, M.A.A.M.; Mohamed Kamari, N.A.; Abdullah, H.; Yusof, Y.; Zulkifley, M.A.; Koondhar, M.A. A Study on the Impact of Different PV Model Parameters and Various DC Faults on the Characteristics and Performance of the Photovoltaic Arrays. Inventions 2024, 9, 93. https://doi.org/10.3390/inventions9050093
Baradieh KI, Zainuri MAAM, Mohamed Kamari NA, Abdullah H, Yusof Y, Zulkifley MA, Koondhar MA. A Study on the Impact of Different PV Model Parameters and Various DC Faults on the Characteristics and Performance of the Photovoltaic Arrays. Inventions. 2024; 9(5):93. https://doi.org/10.3390/inventions9050093
Chicago/Turabian StyleBaradieh, Khaled Ibrahim, Muhammad Ammirrul Atiqi Mohd Zainuri, Nor Azwan Mohamed Kamari, Huda Abdullah, Yushaizad Yusof, Mohd Asyraf Zulkifley, and Mohsin Ali Koondhar. 2024. "A Study on the Impact of Different PV Model Parameters and Various DC Faults on the Characteristics and Performance of the Photovoltaic Arrays" Inventions 9, no. 5: 93. https://doi.org/10.3390/inventions9050093
APA StyleBaradieh, K. I., Zainuri, M. A. A. M., Mohamed Kamari, N. A., Abdullah, H., Yusof, Y., Zulkifley, M. A., & Koondhar, M. A. (2024). A Study on the Impact of Different PV Model Parameters and Various DC Faults on the Characteristics and Performance of the Photovoltaic Arrays. Inventions, 9(5), 93. https://doi.org/10.3390/inventions9050093








