Abstract
This study aims to propose a central composite design (CCD) combined with response surface methodology (RSM) to create a statistical experimental design. A new parametric optimization of entropy generation is presented. The flow behavior of magnetohydrodynamic hybrid nanofluid (HNF) flow through two flat contracting expanding plates of channel alongside radiative heat transmission was considered. The lower fixed plate was externally heated whereas the upper porous plate was cooled by injecting a coolant fluid with a uniform velocity inside the channel. The resulting equations were solved by the Homotopic Analysis Method using MATHEMATICA 10 and Minitab 17.1. The design consists of several input factors, namely a magnetic field parameter (), radiation parameter () and group parameter (). To obtain the values of flow response parameters, numerical experiments were used. Variables, especially the entropy generation (), were considered for each combination of design. The resulting RSM empirical model obtained a high coefficient of determination, reaching 99.97% for the entropy generation number (). These values show an excellent fit of the model to the data.
1. Introduction
Entropy generation is a measure of the irreversibility of thermal energy. This plays a crucial part in engineering applications, especially in design and heat transfer optimization. It is defined as a measure of thermal disorder or randomness. Entropy generation is frequently related to irreversible processes in thermodynamics, where energy is lost to heat or other forms of energy that cannot fully be transformed back to useful work. The second law of thermodynamics, which states that the total entropy of an isolated system either rises or stays constant but never falls, governs this idea. Entropy generation is the process by which a closed system’s overall dissipation is calculated over time [1,2,3,4,5]. Every physical process and every thermodynamic operation involve some energy dissipation, an increase in disorder and an increase in entropy. Also, to analyze the charter of important parameters, such as entropy, changes may occur with some parameters and may not change with some other parameters. Sensitivity analysis is a valuable method for calculating this effect in fluid dynamics. With this methodology, an empirical quadratic order providing a correlation between input parameters and entropy generation is called for when performing numerical simulation and experimental analysis [6,7,8,9]. Methods based on modern AI techniques, such as Artificial Neural Networks (ANNs) and Response Surface Methodology (RSM), are used to obtain empirical models [10]. RSM is the most commonly used statistical technique when many input factors affect a particular performance index or quality attribute. Statistical experimental methods are important in industrial and engineering design and simulation works. Sensitivity analysis is an important method in science and engineering, especially for complex system engineering issues. It identifies areas of emphasis for system design to ensure robustness and correctness across multiple inputs by conducting diagnostic modeling and simulations. Sensitivity analysis has been employed to study the effects of changing viscosity and thermal conductivity on flow performance metrics [11], including the Nusselt number and skin friction coefficient over a permeable wedge. Here, the author concluded that skin friction was the most sensitive to the suction parameter among the others involved. Whereas, the Nusselt number shows variation in thermal conductivity. In Ref. [12], the authors investigated the sensitivity analysis of nanofluids including nanoparticles and motile bacteria. The results depicted that skin friction was more sensitive towards the Brownian motion parameter and the Sherwood parameter showed high sensitivity due to the Lewis number. Meanwhile, Ref. [13] investigated the sensitivity analysis of Cu–water nanofluid-forced convection over a wedge. The author confirmed from the results that optimal conditions for skin friction and the Nusselt number arose for M = 0.62, a wedge angle of 166.72 and a nanoparticle concentration of 0.052. Also, Ref. [14] delved into the sensitivity analysis of various physical input quantities in solar heat exchangers and concluded that the Richardson number, diameter of nanoparticles and wall surface emissivity positively influenced the Nusselt number in a solar heat exchanger. In Ref. [15], the sensitivity and optimization of hybrid nanofluid heat transfer was investigated. Parametric optimization using RSM for the boundary layer flow of ethylene glycol-based ZnO nanoliquid over a moving wedge was investigated in [16]. Meanwhile, Ref. [17] conducted numerical and sensitivity analyses of three-dimensional flow and heat transfer of a nanoliquid over a wedge and concluded that a higher pressure gradient and shear-to-strain rate but lower Lewis number were found to be the best conditions in which the heat transfer rate was maximized. A vast amount of the literature exists on the sensitivity analysis of boundary value problems [18,19,20,21]. By conducting a sensitivity analysis, it is possible to determine what variables, such as the skin friction coefficient, Nusselt number and Sherwood number, have a significant impact on flow performance metrics. This information can be used to focus on these critical aspects and analyze the stability of corresponding effective parameters on flow behavior.
Furthermore, nanofluids exhibit significantly higher thermal conductivity than regular fluids due to the effective suspension of metallic nanoparticles in the base fluid. Since then, several mathematical models have been developed to better understand and enhance the thermal conductivity of nanofluids [22,23,24,25,26,27,28,29,30].
The aim of this study is to provide a central composite design combined with Response Surface Methodology to create a statistical experimental design. A new parametric optimization of entropy generation is presented. The flow behavior of magnetohydrodynamic hybrid nanofluid flow in an expanding/constricting channel alongside radiative heat transmission was taken into account. The sensitivity of variables related to the flow is presented by means of Response Surface Methodology (RSM) and the statistical method called Analysis of Variance (ANOVA). This study is not yet available in the existing literature.
2. Mathematical Modelling
The flow geometry is shown in Figure 1. The forces applied on the flow were the uniform and transverse magnetic field. An externally heated lower wall (T0) of the channel is represented along the x-axis. In order to cool down the upper wall to temperature (T1), a coolant fluid through the upper wall with a uniform velocity was injected. The channel expanded and contracted with respect to the time function b(t).
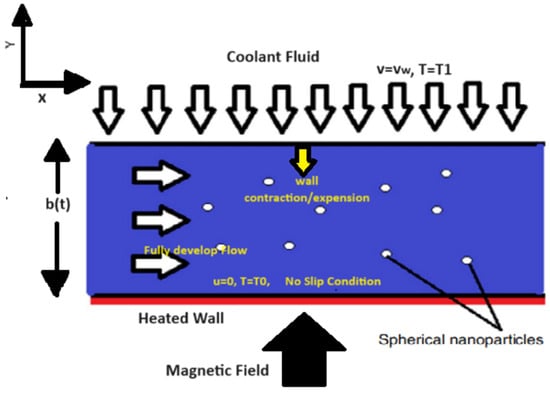
Figure 1.
Flow geometry of the problem.
Both the fluid phase and nanoparticles were considered to be in a thermally stable state, exhibiting no velocity for sliding along the wall.
2.1. Governing Equations
The momentum and energy equations can be written in vector form as the following:
where is the enthalpy and represents dissipation. The respective boundary conditions are
The stream function is introduced as
where .
The non-dimensional resulting equations [31] take the following forms:
where = is the radiation parameter. The coefficient of the terms was equated including with and without of Equation (7).
The associated boundary conditions are
The mathematical Equations (6) and (7) subject to boundary conditions (8) and (9) were solved with the help of the Homotopic Analysis Method [32,33,34,35] and the series solutions were obtained as
2.2. Entropy Generation
In this section, a comprehensive research study of the parametric optimization for flow performance, and specifically the entropy generation number for the flow of hybrid nanofluid in an expanding/contracting channel, is presented.
The equation of entropy of the hybrid nanofluid [31] is written as
where . The total energy of the system described in (12) can also be written as
Here, constitutes the entropy generated by heat transfer, constitutes the entropy generated by fluid friction and constitutes the entropy generated by the magnetic field force.
3. Results
In this section, the sensitivity analysis results are presented. To explore the flow of a hybrid nanofluid across a channel, the statistical method known as Analysis of Variance (ANOVA) will be used to compare the means of two or more groups or treatments.
3.1. Response Surface Methodology (RSM)
In order to manage enormous datasets in research and engineering, statistical experimental design is crucial. Using the entropy generation number and other output reactions to establish empirical correlations between input parameters is essential.
We used the Central Composite Design (CCD) to build our experimental design since it is efficient at tolerating three input factors. To obtain the corresponding output values for each response variable, namely the magnetic field parameter (), radiation parameter () and group parameter (), we utilized the bvp4c routine in MATLAB (Version with bvp4c solver). The input parameters A, B and C were represented using symbolic notation, while the coefficients of the entropy generation number () were also used. The general quadratic functions of based on principles of the RSM are defined in [36]. With the use of these functions, we were able to create mathematical representations by using input parameters and the intended result variables, providing a useful tool for additional analysis and optimization.
where are coefficients of .
3.2. ANOVA
ANOVA partitions the total variation in a dataset into variation between groups and variation within groups. It is used to determine what terms in an empirical correlation have a significant effect on the output quantities. The sequential F-test was applied with twenty-one runs to construct the regression model’s fit, and the selection and rejection of terms in the model were based on large values of F and small values of p (p < 0.05). It can be conducted as a one-way ANOVA when comparing multiple independent groups or as a two-way ANOVA when studying the effects of two independent factors. Assumptions of ANOVA include the normal distribution of data within groups, equal variances and the independence of observations. To improve the estimated regression and statistical analysis of experimental models, simulation studies were conducted using various experimental substances, and residual plots were formed using ANOVA. It is widely employed in research fields such as psychology, biology, economics and social sciences. It provides a powerful tool for hypothesis testing and investigating differences between groups, allowing researchers to draw meaningful conclusions from their data.
3.3. Development of Empirical Correlation
The reliability of Response Surface Methodology (RSM) in determining the input variables on response quantities such as the entropy generation number were investigated. During the sensitivity analysis, residual error and lack of fit were considered, with a residual error indicating the regression lines of unexplained data points and lack of fit occurring when the model failed to capture the relationship between the input variables and response quantities. A three-level face-centered CCD-RSM was taken into consideration. Design input variables with their CCD levels are presented in Table 1.

Table 1.
Design input parameters and their levels.
A three-level face-centered CCD-RSM was used with minimum, central and maximum values of −1, 0 and 1, respectively. Nineteen degrees of freedom (DOFs) with twenty runs were suitable for constructing the design as shown in Table 2. The table was drawn using Minitab.

Table 2.
Design of experiments and response results.
The p-value evaluates a model’s accuracy, the F-value measures the range of values around the average value. The F-values in Table 3 display that the model was statistically significant for the entropy generation number.

Table 3.
Analysis of variance (ANOVA).
The RSM model’s coefficient of determination () was 99.98% for . The adjusted coefficient of determination () for was 99.97%. These statistics () also give the surety of the fit goodness. Table 4 presents the entropy generation regression coefficient. A large p-value is not statistically significant and represents that altering the input value will not affect the output results. Meanwhile, a low p-value () is considered statistically significant and those values that obtained this criterion were retained in the model, while those that did not were eliminated.

Table 4.
Regression analysis for .
3.4. Sensitivity Analysis of the Pertained Parameter
The use of sensitivity analysis in engineering problems is a common technique to determine how changing parametric values affects the desired outcomes. This approach particularly gives suitable results when trying to identify the impact of multiple influential factors. Sensitivity analysis predicts the outcome of a decision by analyzing a relevant set of parameters. To analyze the sensitivity of the pertained parameters, the derivatives of Equation (15) were taken and the tabulated form of empirical correlation was obtained.
Figure 2 indicates that the data were continuous with the frequency focused on zero which represents the numerical data following the normal probability distributions of a bell-shaped plot. Figure 3 shows that the empirical correlation was more symmetrical and less distorted. Figure 4 indicates that as the number of observations increased, the residual decreased, which showed a strong connection between the fitted and original values. To estimate the goodness of fit also discussed by and which data had high numerical values, as shown in Table 4, a strong correlation between the input variables and was observed.
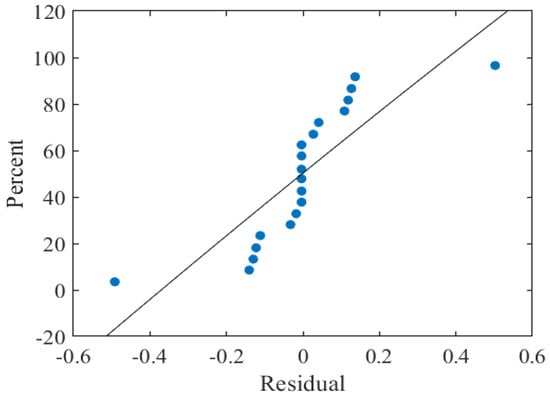
Figure 2.
Normal probability graph of the total energy of .
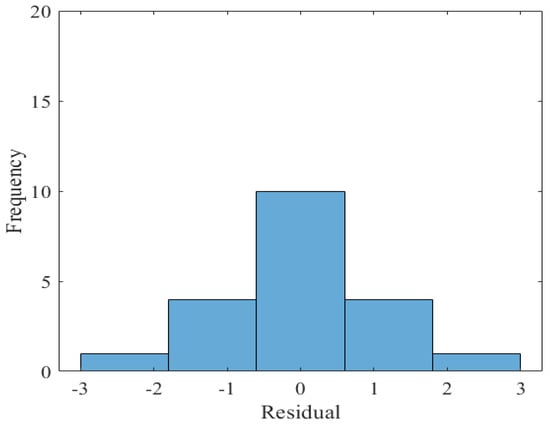
Figure 3.
Histogram of the empirical correlation of .
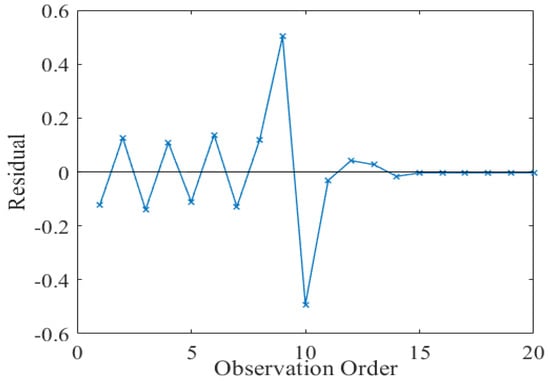
Figure 4.
Observation order against standardized residual plot of .
Table 5 outlines the variations in output response quantities. The sensitivity of entropy generation at , with symbols and varying according to Table 5, was observed. Figure 5, Figure 6 and Figure 7 provide a graphical view of the sensitivity analysis of the output response parameters of with bar charts indicating the response. The effects of the input variables’ magnetic field , radiation parameter and group parameter are indicated in Figure 5, Figure 6 and Figure 7. In Figure 5, Figure 6 and Figure 7, the effects of input variables on entropy generation (), where A and B are dominant parameters, are also represented. Furthermore, Ne was positively sensitive to all three parameters. This means that increasing the radiation parameter () enhanced the response of entropy generation (), as discussed in Table 5. Also, it means that entropy increased with a change in all the parameters, but the change was rapid with the rise in radiation parameters, and minimum variation was observed with the change in a magnetic field. Entropy also showed sensitivity to the group parameters.

Table 5.
Sensitivity of .
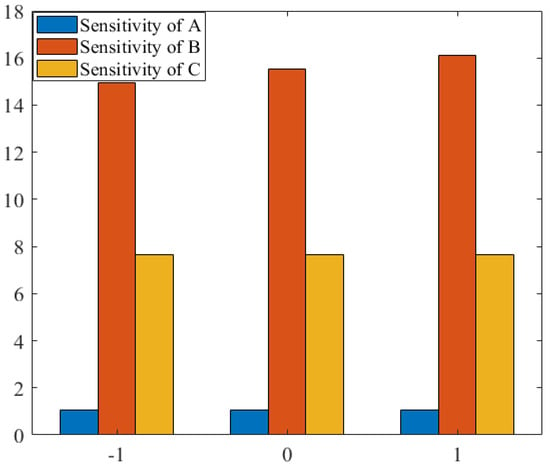
Figure 5.
Sensitivity analysis at at the central level and at the lower level for .
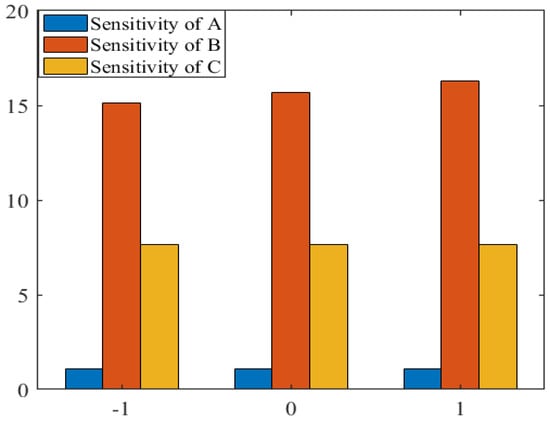
Figure 6.
Sensitivity analysis at at the central level and at the central level for .
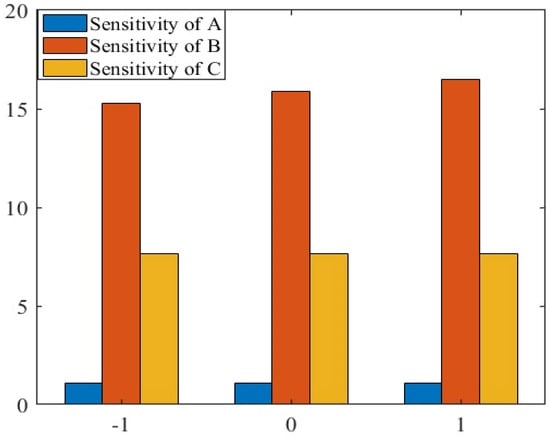
Figure 7.
Sensitivity analysis at at the central level and at the upper level for .
Sensitivity analysis is useful in limiting the discussion of the non-uniqueness of a solution to changing the sensitivity parameters only.
4. Conclusions
This study provides a comprehensive sensitivity analysis of the entropy generation of nanofluid flow on expanding/contracting channels. Sensitivity analysis is an engineering tool that helps to improve the understanding of input parameters with respect to output response, leading to effective decision-making. The effects of factors such as magnetic field parameters, radiation parameters and group parameters were investigated. To obtain a deeper understanding of the flow dynamic, an empirical correlation was developed by using response surface methodology to examine the sensitivity of the flow response parameters. The critical observations of this study are listed as the following:
- The sensitivity analysis identified that the radiation parameter was the most influential in the flow.
- It was found that by increasing radiation parameters, entropy generation increased.
- It was noted that the group parameter had a significant role in determining the flow behavior.
Author Contributions
Conceptualization, A.Z.; supervision, R.E.; investigation, M.A.R.; validation, N.S.; formal analysis, S.M.S.; writing—original draft, M.A.R.; writing—review and editing, S.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| b(t) | Expand or contract function |
| b0 | Initial channel height |
| Bi, i = 1, 2, 3, 4, 5 | Constant parameters in hybrid nanofluids |
| α | Expansion ratio |
| f (η), g(η) | Compositional form of temperature |
| k*nf | Mean absorption coefficient of the hybrid nanofluid |
| M | Magnetic parameter |
| N | Radiation parameter |
| σ* | Stefan Boltzmann constant |
| Λ | Wall permeability |
| Pr | Prandtl number |
| p* | Dimensional pressure |
| p | Non-dimensional pressure |
| Re | Reynold number |
| Br | Brinkman number |
| Ec | Eckert number |
| t | Time |
| T | Temperature |
| T1 | Temperature at the lower plate |
| T2 | Temperature at the upper plate |
| u¯ | Dimensional velocity in the x direction |
| u | Non-dimensional velocity in the x direction |
| Dimensional velocity in the y direction | |
| V | Non-dimensional velocity in the y direction |
| F | Stream function variable |
| θ | Temperature |
| A1 | Temperature difference |
| Nanoparticle volume fractions | |
| Entropy generation | |
| Ne | Non-dimensional total entropy generation |
| Br/A1 | Group parameter |
| NH | Entropy generated by heat transfer |
| Nf | Entropy generated by fluid friction |
| Nm | Entropy generated by the magnetic field force |
| A, B, C | Regression parameters |
| βi, i = 0, 1, 2,3, 11, 22, 33, 12, 13, 23 | Regression coefficient for Ne |
| Subscripts | |
| F | Host fluid |
| hnf | Hybrid nanofluid |
| P | Particle |
References
- Zhang, L.; Bhatti, M.M.; Marin, M.; Mekheimer, K.S. Entropy analysis on the blood flow through anisotropically tapered arteries filled with magnetic zinc-oxide (ZnO) nanoparticles. Entropy 2020, 22, 1070. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A.; Safaei, M.R.; Alrashed, A.A.A.A.; Nguyen, T.K.; Filho, E.P.B. Entropy generation in thermal radiative loading of structures with distinct heaters. Entropy 2017, 19, 506. [Google Scholar] [CrossRef]
- Ellahi, R.; Alamri, S.Z.; Basit, A.; Majeed, A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. J. Taibah Univ. Sci. 2018, 12, 476. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.-S. Numerical simulation of entropy generation with thermal radiation on MHD carreau nanofluid towards a shrinking sheet. Entropy 2016, 18, 200. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.-S.; Yang, Z. Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Alidoust, S.; Mohammadnejad Ardeshiri, E.; Kamyab, M.H.; Toghraie, D. Experimental study of rheological behavior of MWCNT-Al2O3/SAE50 hybrid nanofluid to provide the best nano-lubrication conditions. Nanoscale Res. Lett. 2022, 17, 4. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Esfandeh, S. Improving engine oil lubrication in light-duty vehicles by using of dispersing MWCNT and ZnO nanoparticles in 5W50 as viscosity index improvers (VII). Appl. Therm. Eng. 2018, 143, 493–506. [Google Scholar] [CrossRef]
- Abdulrahman, A. Modeling and optimization of dynamic viscosity of copper nanoparticles dispersed in gear oil using response surface methodology. Mater. Today Proc. 2021, 42, 771–775. [Google Scholar] [CrossRef]
- Kole, M.; Dey, T.K. Role of interfacial layer and clustering on the effective thermal conductivity of CuO–gear oil nanofluids. Exp. Therm. Fluid Sci. 2011, 35, 1490–1495. [Google Scholar] [CrossRef]
- Gürel, A.E.; Ağbulut, Ü.; Biçen, Y. Assessment of machine learning, time series, response surface methodology and empirical models in prediction of global solar radiation. J. Clean. Prod. 2020, 277, 122353. [Google Scholar] [CrossRef]
- Hussain, D.; Asghar, Z.; Zeeshan, A.; Alsulami, H. Analysis of sensitivity of thermal conductivity and variable viscosity on wall heat flux in flow of viscous fluid over a porous wedge. Int. Commun. Heat Mass Transf. 2022, 135, 106104. [Google Scholar] [CrossRef]
- Chan, S.Q.; Aman, F.; Mansur, S. Sensitivity analysis on thermal conductivity characteristics of a water-based bionanofluid flow past a wedge surface. Math. Probl. Eng. 2018, 2018, 9410167. [Google Scholar] [CrossRef]
- Vahedi, S.M.; Pordanjani, A.H.; Raisi, A.; Chamkha, A.J. Sensitivity analysis and optimization of MHD forced convection of a Cu-water nanofluid flow past a wedge. Eur. Phys. J. Plus 2019, 134, 124. [Google Scholar] [CrossRef]
- Shirvan, K.M.; Mamourian, M.; Mirzakhanlari, S.; Ellahi, R. Two phase simulation and sensitivity analysis of effective parameters on combined heat transfer and pressure drop in a solar heat exchanger filled with nanofluid by RSM. J. Mol. Liq. 2016, 220, 888–901. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Shehzad, S.A.; Mackolil, J.; Shashikumar, N.S. Heat transfer optimization of hybrid nanomaterial using modified Buongiorno model: A sensitivity analysis. Int. J. Heat Mass Transf. 2021, 171, 121081. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Mackolil, J.; Mallikarjunaiah, S.M. Response surface optimization of heat transfer rate in Falkner-Skan flow of ZnO−EG nanoliquid over a moving wedge: Sensitivity analysis. Int. Commun. Heat Mass Transf. 2021, 125, 105348. [Google Scholar] [CrossRef]
- Rana, P.; Gupta, G. Numerical and sensitivity computations of three-dimensional flow and heat transfer of nanoliquid over a wedge using modified Buongiorno model. Comput. Math. Appl. 2021, 101, 51–62. [Google Scholar] [CrossRef]
- Darbari, B.; Rashidi, S.; Abolfazli Esfahani, J. Sensitivity analysis of entropy generation in nanofluid flow inside a channel by response surface methodology. Entropy 2016, 18, 52. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Grosan, T.; Pop, I. Natural convection and entropy generation in a square cavity with variable temperature side walls filled with a nanofluid: Buongiorno’s mathematical model. Entropy 2017, 19, 337. [Google Scholar] [CrossRef]
- Safaei, M.R.; Ahmadi, G.; Goodarzi, M.S.; Shadloo, M.S.; Goshayeshi, H.R.; Dahari, M. Heat transfer and pressure drop in fully developed turbulent flows of graphene nanoplatelets–silver/water nanofluids. Fluids 2016, 1, 20. [Google Scholar] [CrossRef]
- Goodarzi, M.; Tlili, I.; Tian, Z.; Safaei, M.R. Efficiency assessment of using graphene nanoplatelets-silver/water nanofluids in microchannel heat sinks with different cross-sections for electronics cooling. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 347–372. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An analytical treatment for the exact solutions of MHD flow and heat over two–three dimensional deforming bodies. Int. J. Heat Mass Transf. 2015, 90, 781–789. [Google Scholar]
- Kanwal, A.; Khan, A.A.; Sait, S.M.; Ellahi, R. Heat transfer analysis of magnetohydrodynamics peristaltic fluid with inhomogeneous solid particles and variable thermal conductivity through curved passageway. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 1884. [Google Scholar] [CrossRef]
- Ellahi, R.; Hussain, F.; Abbas, S.A.; Sarafraz, M.M.; Goodarzi, M.; Shadloo, M.S. Study of two-phase newtonian nanofluid flow hybrid with hafnium particles under the effects of slip. Inventions 2020, 5, 6. [Google Scholar] [CrossRef]
- Zeeshan, A.; Hussain, D.; Asghar, Z.; Bhatti, M.M.; Duraihem, F.Z. Thermal optimization of MHD nanofluid over a wedge by using response surface methodology: Sensitivity analysis. Propuls. Power Res. 2023, 12, 556–567. [Google Scholar]
- Chamkha, A.J.; Jena, S.K.; Mahapatra, S.K. MHD convection of nanofluids: A review. J. Nanofluids 2015, 4, 271–292. [Google Scholar]
- Bhatti, M.M.; Bég, O.A.; Ellahi, R.; Doranehgard, M.H.; Rabiei, F. Electro-magnetohydrodynamics hybrid nanofluid flow with gold and magnesium oxide nanoparticles through vertical parallel plates. J. Magn. Magn. Mater. 2022, 564, 170136. [Google Scholar]
- Gibanov, N.S.; Sheremet, M.A.; Oztop, H.F.; Al-Salem, K. MHD natural convection and entropy generation in an open cavity having different horizontal porous blocks saturated with a ferrofluid. J. Magn. Magn. Mater. 2018, 452, 193–204. [Google Scholar]
- Zafar, S.; Khan, A.A.; Sait, S.M.; Ellahi, R. Numerical investigation on unsteady compressible flow of viscous fluid with convection under the effect of Joule heating. J. Comput. Appl. Mech. 2024, 55, 423–439. [Google Scholar]
- Rizwan, M.; Hassan, M.; Makinde, O.D.; Bhatti, M.M.; Marin, M. Rheological modeling of metallic oxide nanoparticles containing non-newtonian nanofluids and potential investigation of heat and mass flow characteristics. Nanomaterials 2022, 12, 1237. [Google Scholar] [CrossRef]
- Zeeshan, A.; Khan, M.I.; Ellahi, R.; Asghar, A.Z. Artificial neural network simulation and sensitivity analysis for optimal thermal transport of magnetic viscous fluid over shrinking wedge via RSM. Int. J. Numer. Methods Heat Fluid Flow 2023, 33, 3492–3518. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Shahzad, N.; Hussain, A.; Sait, S.M. Mixed convection of two layers with radiative electro-magnetohydrodynamics nanofluid flow in vertical enclosure. Nanotechnology 2024, 35, 095402. [Google Scholar] [CrossRef]
- Liao, S.J. An analytic approximate technique for free oscillations of positively damped systems with algebraically decaying amplitude. Int. J. Non-Linear Mech. 2003, 38, 1173–1183. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1457. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A. Mathematical models of electro magnetohydrodynamic multiphase flows synthesis with nanosized Hafniump particles. Appl. Sci. 2018, 8, 275. [Google Scholar] [CrossRef]
- Srinivas, S.; Reddy, A.S.; Ramamohan, T.R. A study on thermal-diffusion and diffusion-thermo effects in a two-dimensional viscous flow between slowly expanding or contracting walls with weak permeability. Int. J. Heat Mass Transf. 2012, 55, 3008–3020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).