The Basic k-ϵ Model and a New Model Based on General Statistical Descriptions of Anisotropic Inhomogeneous Turbulence Compared with DNS of Channel Flow at High Reynolds Number

Abstract

Predictions are presented of mean values of statistical variables of large-scale turbulent flow of the widely used basic k-$ϵ$ model, and of a new model, which is based on general statistical descriptions of turbulence. The predictions are verified against published results of direct numerical simulations (DNSs) of Navier–Stokes equations. The verification concerns turbulent channel flow at shear Reynolds numbers of 950, 2000, and ${10}^4$. The basic k-$ϵ$ model is largely based on empirical formulations accompanied by calibration constants. This contrasts with the new model, where descriptions of leading statistical quantities are based on the general principles of statistical turbulence at a large Reynolds number and stochastic theory. Predicted values of major output variables such as turbulent viscosity, diffusivity of passive admixture, temperature, and fluid velocities compare well with DNS for the new model. Significant differences are seen for the basic k-$ϵ$ model.

1. Introduction

The description of turbulence has been an issue right from the beginning. A solid starting point for analysis is the Navier–Stokes equations, which describe the flow. These can be time-averaged, resulting in equations for mean values of velocity, pressure, and temperature. The problem arises with the average values of the products of fluctuating quantities within the non-linear convection terms in the equations. They describe the effect of fluctuations on mean flow quantities. The proposed representations of average nonlinear convective fluctuations are of a hypothetical nature, drawing analogies with molecular chaos. Boussinesq [1] was the first to follow this line of thinking by introducing the gradient hypothesis: the averaged nonlinear fluxes are proportional to the derivative of the mean flow quantity, preceded by a constant termed the turbulent viscosity or turbulent diffusion coefficient. Several versions and extensions based on the same idea have since been put forward by the pioneers of turbulence theory: Taylor [2], Prandtl [3], and von Karman [4], among others. They also form the basis of many of today’s computer models used in engineering and environmental analyses; for example, see the books of Hanjalic and Launder [5] and Bernard and Wallace [6].

An offspring of the aforementioned concept is the basic k-$ϵ$ model, which is widely used in engineering and environmental analyses [5,6]. This model describes the average value of momentum fluxes through the gradient of the mean velocity. Fluctuations are isotropic and the coefficient proceeding the gradient equals $c_{\mu }\frac{k^2}{ϵ}$, where k is the mean kinetic energy of fluctuations, $ϵ$ is the mean energy dissipation rate, and $c_{\mu }$ is a calibration constant. The model is completed by equations for k and $ϵ$. The gradient hypothesis is also applied to several other flux terms in equations with different values of calibration constants.

The problems with gradient-based models include their hypothetical origin and lack of uniqueness. Starting from a sketchy analogy with laminar diffusion, almost limitless forms of gradient representations and proceeding functional dependencies can be devised. A new development that surpasses these limitations is the statistical description of anisotropic inhomogeneous turbulence; see Brouwers [7,8,9]. Turbulence at a high Reynolds number is featured by unstable eddies of whirling irregular fluid velocities whose behaviors are governed by the domination of the inertial forces in the momentum balance; see Monin and Yaglom, Vol. II, Ch.8 [10]. The eddies start at sizes of the configuration and then break down to smaller ones until the point where viscous forces come into play at sizes of a few millimeters. Here, Kolmogorov’s theory of small viscous scales comes into play [10]. Building on this framework of high Reynolds turbulence and using the methods of the stochastic theory of Van Kampen [11] and Stratonovich [12], explicit statistical descriptions of governing variables are obtained. They are the leading terms of asymptotic expansions based on the small value of the inverse of the universal Lagrangian Kolmogorov constant. The results represent unique descriptions of turbulent flow statistics, subject to deviations due to truncated higher-order terms.

The results of direct numerical simulation (DNS) of the Navier–Stokes equations offer an opportunity for testing the outcomes of turbulence models. With the evolution of modern computing power, it has become possible to generate a wealth of accurate data on turbulent flow at high Reynolds numbers. The recent DNS data of the turbulent channel flow of Hoyas et al. [13,14] and Kuerten et al. [15] are particularly noteworthy. Fluctuating channel velocities are strongly anisotropic and averages of flow quantities vary strongly with distance from the wall. Inhomogeneity and anisotropy are characteristics of turbulence, in practice. The DNS data provide a meaningful test case for models. In this paper, a detailed comparison is presented of the DNS data, along with predictions of the basic k-$ϵ$ model and the new model based on general statistical descriptions, referred to as the fundamental model.

2. The Basic $\mathit{k}$-$\mathit{ϵ}$ Model and the New Fundamental Model

The turbulent flow of an incompressible or nearly incompressible fluid, e.g., a liquid or gas flowing at speeds where the square of the Mach number is minimal, is considered. The density $\rho$ is assumed to be constant. Turbulent fluctuations measured at a fixed point in space are treated as a statistical process that is stationary or almost stationary in time compared to the time of velocity fluctuations. Statistical averages follow from time-averaging over sufficiently long time intervals. The time-averaged representation of the Navier–Stokes equations is given by the following:

• Conservation of mass:

$$\frac{\partial u_i}{\partial x_i}=0$$

(1)

• Conservation of momentum:

$$\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}+\frac{\partial <u_i^{\prime }{u}_j^{\prime }>}{\partial x_j}=-\frac{\partial p}{\partial x_i}$$

(2)

• Conservation of energy:

$$\frac{\partial \theta }{\partial t}+u_j\frac{\partial \theta }{\partial x_j}+\frac{\partial <u_j^{\prime }{\theta }^{\prime }>}{\partial x_j}=0$$

(3)

where angled brackets represent statistical averaging, t and x are time and space coordinates, u, p, and $\theta$ are the mean or time-averaged values of fluid velocity, pressure, and temperature, and $u’$ and $\theta ’$ represent fluctuations of velocity and temperature, referring to velocity and temperature minus their mean value. As we are concerned with the flow at a high Reynolds number, the contributions of the viscous forces and heat conductivity present in the Navier–Stokes equations have been dropped. Their effect can be disregarded when considering the main flow governed by the instability of the inviscid flow outside small boundary layers. The average temperature in energy Equation (3) can also be used to describe the average distribution of passive or almost passive admixture in the fluid. Restricting the formulation of the conservation equations to an incompressible or almost incompressible fluid implies that the solutions to (1) and (2) are not affected by the value of the conservative scalar temperature. The representation holds as long as the changes in temperature or admixture imposed at external boundary conditions are of limited magnitude.

2.1. Turbulent Diffusion in the Basic k-$ϵ$ Model

The appearance of turbulent fluxes—in the convection terms of the averaged conservation equations—results in an unclosed set of equations for mean flow variables. It is known as the closure problem. To resolve this issue, a diffusion hypothesis has been introduced in the basic k-$ϵ$ model. In this hypothesis, turbulent fluxes are treated as isotropic and are described by [5,6].

$$<u_j^{\prime }{u}_i^{\prime }>=\frac{2}{3}k{\delta }_{ij}-{\nu }_t(\frac{\partial u_j}{\partial x_i}+\frac{\partial u_i}{\partial x_j})$$

(4)

$$<u_j^{\prime }{\theta }^{\prime }>=-{\nu }_t\frac{\partial \theta }{\partial x_j}$$

(5)

where ${\nu }_t$ is a scalar that represents diffusivity or turbulent viscosity, which is defined by the following:

$${\nu }_t=c_{\mu }\frac{k^2}{ϵ}$$

(6)

where k is the average kinetic energy of fluctuations, $k=\frac{1}{2}<u_i{’}^2>$, and ${\displaystyle ϵ=\frac{1}{2}\nu <{(\frac{\partial u_i’}{\partial x_j}+\frac{\partial u_j’}{\partial x_i})}^2>}$ denotes the average energy dissipation rate, with $\nu$ being kinematic viscosity; $c_{\mu }$ in (4) and (5) is a calibration constant whose value is usually taken as $0.09$ [5,6]. In Equation (5), correction factors are sometimes added to the diffusion constant, i.e., a turbulent Prandtl number and a turbulent Schmidt number for temperature and admixture, respectively. But these numbers are generally close to unity and are omitted here.

2.2. Turbulent Diffusion in the Fundamental Model

The derivation of the fundamental model starts from a Langevin equation for fluid particle velocity [8,9,10]. In this equation, the limiting form of Kolmogorov’s theory of small scales is implemented, i.e., where the characteristic times for velocity fluctuations are much larger than the times of viscous scales. This is the case when the Reynolds number is large; see Kolmogorov [16]. One further step involves an expansion, in terms of the inverse of the Kolmogorov constant $C_0$. Matching predictions with measurements and DNS data reveal values of $C_0$ at around 6–7; in the present analysis, a value of 7 is adopted. Furthermore, the area where the Lagrangian description applies can be reduced to a point in the Eulerian flow description in the limit of small ${C_0}^{-1}$. In this way, Lagrangian-based descriptions are connected to Eulerian ones. The following descriptions for the flux terms are obtained [8,9]

$$<u_j^{\prime }{u}_i^{\prime }>=\frac{2}{3}(k+D_{nk}\frac{\partial u_n}{\partial x_k}){\delta }_{ij}-D_{ik}\frac{\partial u_j}{\partial x_k}-D_{jk}\frac{\partial u_i}{\partial x_k}$$

(7)

$$<u_j^{\prime }{\theta }^{\prime }>=-D_{ik}\frac{\partial \theta }{\partial x_k}$$

(8)

where the fundamentally based diffusion tensor, $D_{ij}$, is described by the following:

$$D_{iJ}=2C_0^{-1}{ϵ}^{-1}{\sigma }_{in}{\sigma }_{nj}+2C_0^{-2}{ϵ}^{-2}{\sigma }_{li}{\sigma }_{jk}{u}_n\frac{\partial {\sigma }_{lk}}{\partial x_n}-4C_0^{-2}{ϵ}^{-1}{\sigma }_{kj}{u}_n\frac{\partial }{\partial x_n}\left({ϵ}^{-1}{\sigma }_{im}{\sigma }_{mk}\right)$$

(9)

and

$${\sigma }_{in}=<u_i^{\prime }{u}_n^{\prime }>$$

(10)

is covariance or Reynolds stress. Relations (8)–(10) are part of the description, which holds in the entire flow configuration (except the thin viscous layers at walls) once they are coupled to conservation Equations (1)–(3). In this way, the turbulent flux change at each point, x, as described by (7) and (8), is connected to the kinetic energy and energy dissipation changes. Although the presence of $\nu$ in the expression for energy dissipation ${\displaystyle ϵ=\frac{1}{2}\nu <{(\frac{\partial u_i’}{\partial x_j}+\frac{\partial u_j’}{\partial x_i})}^2>}$ may suggest otherwise, $ϵ$ is a characteristic of the main inviscid flow outside the boundary layers [10]. The magnitude of velocity gradients in turbulence is governed by the small viscous scales. It scales as $1/\sqrt{\nu }$ and makes the magnitude of $ϵ$ independent of $\nu$. This independence is reflected in the equations for k and $ϵ$, presented in the next section.

The above expressions for the diffusion of the fundamental model reveal the dependency on mean gradients, which are of a more complex structure than those in the basic k-$ϵ$ model. This reflects the anisotropy of the fluctuating velocity field and reveals a more complex dependency on flow statistics.

The application of the fundamentally based diffusion approximation to a scalar, as conducted in Equation (8), is only justified if the scalar is conservative [8,9]. The value of the conservative scalar is constant when following a fluid particle and fluctuates in value in a fixed coordinate system due to fluid particle fluctuations. This is the case for temperature in an incompressible fluid such as liquids. It is approximately correct if the fluid is almost incompressible, as is the case in gases flowing at speeds where the square of the Mach number is small. The scalar representation can also be applied to passive or almost passive admixtures in fluids, such as aerosols in air [7,8,9]. It leads to errors when applied to non-conservative scalars such as kinetic energy and pressure; see Section 5.

3. Equations for $\mathit{k}$ and $\mathit{ϵ}$

Incorporating the expressions for turbulent diffusion from the basic k-$ϵ$ model and the fundamental model into the averaged conservation equations introduces two unknowns: the mean kinetic energy, k, and the mean energy dissipation rate, $ϵ$. Equations for k and $ϵ$ can be obtained from the Navier–Stokes equations [8,9]. Our aim is to describe flow away from the thin, viscous layers near walls, which are only a few millimeters. In line with this approach, the contributions in the equations for k and $ϵ$ from laminar viscosity will be disregarded (as was conducted in the conservation Equations (1)–(3)). To provide boundary conditions at the wall, the viscous layer is surpassed by applying the solutions of the log layer at $x=0$: [5,6].

The equation for k reads as follows [5,6]:

$$\frac{\partial k}{\partial t}+u_i\frac{\partial k}{\partial x_i}+\frac{\partial <u_i^{\prime }{k}^{\prime }>}{\partial x_i}+{\rho }^{-1}\frac{\partial <u_i^{\prime }{p}^{\prime }>}{\partial x_i}=P-ϵ$$

(11)

where P is the mean production of turbulent fluctuations, defined by the following:

$$P=-{\sigma }_{ij}\frac{\partial u_i}{\partial x_j}$$

(12)

and where $k^{\prime }$ and $p^{\prime }$ are the fluctuating parts of kinetic energy and pressure, respectively, which are the kinetic energy and dissipation rates minus their time-averaged values. There are two turbulent flux terms in Equation (11), i.e., the third and fourth terms on the LHS of (11), which need to be modeled. In the basic k-$ϵ$ model, both terms are lumped together [5,6] and are described by the following:

• Basic k-ϵ model

$$<u_i^{\prime }{k}^{\prime }>+{\rho }^{-1}<u_i^{\prime }{p}^{\prime }>=-\frac{{\nu }_t}{{\sigma }_k}\frac{\partial k}{\partial x_i}$$

(13)

where ${\sigma }_k$ is a calibration constant, which is usually taken unity: ${\sigma }_k=1$ [5,6].

• Fundamental model

The theory underlying the fundamental model provides general expressions for turbulent scalar fluxes, which are free from calibration factors. However, these expressions are only valid for conservative scalars and lead to disagreement with DNS results when applied to turbulent fluxes of kinetic energy and pressure [8]. A fallback to empirical construction is needed. It reads as follows:

$$<u_i^{\prime }{k}^{\prime }>+{\rho }^{-1}<u_i^{\prime }{p}^{\prime }>=-c_k{D}_{ij}\frac{\partial k}{\partial x_j}$$

(14)

where it is noted that if k was a conserved scalar, its diffusion should be described by $D_{ij}\frac{\partial k}{\partial x_j}$. Factor $c_k$ represents correction for non-conservative behavior and includes the relatively small contribution of pressure diffusion [8]. The above relations for the diffusion of kinetic energy and pressure will be compared and calibrated with the DNS results in Section 5.

The equation for $ϵ$, conventionally applied in CFD models, is largely an empirical construction [5,6]. Its basic form follows from the Navier–Stokes equations. It contains a number of terms that are governed by small viscous scales. These terms are generally replaced by expressions that meet the criteria of matching the results of decaying grid turbulence and the log layer of turbulent channel flow. The equation reads as follows:

• Basic k-ϵ model

$$\frac{\partial ϵ}{\partial t}+\frac{\partial u_iϵ}{\partial x_i}=\frac{\partial }{\partial x_i}\left(\frac{{\nu }_t}{{\sigma }_{ϵ}}\frac{\partial ϵ}{\partial x_i}\right)+(c_{ϵ1}P-c_{ϵ2}ϵ)\frac{ϵ}{k}$$

(15)

• Fundamental model

$$\frac{\partial ϵ}{\partial t}+\frac{\partial u_iϵ}{\partial x_i}=\frac{\partial }{\partial x_i}\left(\frac{D_{ij}}{{\sigma }_{ϵ}^{*}}\frac{\partial ϵ}{\partial x_j}\right)+(c_{ϵ1}P-c_{ϵ2}ϵ)\frac{ϵ}{k}$$

(16)

The constant $c_{ϵ2}$ ensures matching with the case of grid turbulence. Its value is usually taken to be $1.9$, which is somewhat less than the theoretical limit value of 2 for the infinite Reynolds number; see George [17]. The von Karman constant $\kappa$ is equal to $0.4$. For the basic k-$ϵ$ model, the calibration constant, ${\sigma }_{ϵ}$, is usually taken to be around $1.3$, and $c_{ϵ1}$ is specified by the equation (Equation (8.41) of [16]):

$$\frac{\sqrt{c_{\mu }}{\sigma }_{ϵ}}{{\kappa }^2}(c_{ϵ2}-c_{ϵ1})=1$$

(17)

The values appropriate for $c_{ϵ1}$ and ${\sigma }_{ϵ}^{*}$ for the fundamental model are determined in Section 6.

4. Channel Flow

The objective is to compare the results of the basic k-$ϵ$ model and the fundamental model with those of the DNS of the channel flow. The channel consists of parallel planes in between, where the mean velocity, $u_1$, is unidirectional in the direction, $x_1$, parallel to the planes. Its magnitude and the value of statistical averages related to velocity fluctuations only change in the direction, $x_2$, normal to the planes. For channel flow, there is an exact solution for the mean pressure [9], which reads as follows:

$$\frac{p}{\rho }=-u_{\tau }^2\frac{x_1}{H}-{\sigma }_{22}$$

(18)

where $u_{\tau }$ is shear velocity and $2H$ is channel height. The shear velocity is determined by the pressure drop in direction $x_1$ at a given $u_1$. There are theoretical and experimentally confirmed relations for the relationship determining $u_{\tau }$. Another exact result for the channel flow is the description of the covariance, ${\sigma }_{12}$ or $<u_1^{\prime }{u}_2^{\prime }>$.

$${\sigma }_{12}=-u_{\tau }^2(1-\frac{x_2}{H})$$

(19)

which is valid outside the thin viscous layer at the wall, [9].

In the subsequent analysis of channel flow, we shall make use of dimensionless formulations: $u_i$ is made dimensionless by $u_{\tau }$, ${\sigma }_{ij}$ and ${\displaystyle \frac{p}{\rho }}$ by $u_{\tau }^2$, $x_1$ and $x_2$ by H, and P and $ϵ$ by $\frac{u_{\tau }^3}{H}$; the subscript ₂ of $x_2$ will be dropped. In this new notation, Equations (18) and (19) are as follows:

$$\frac{p}{\rho }=-x_1-{\sigma }_{22}$$

(20)

which is valid outside the thin viscous layer at the wall.

$${\sigma }_{12}=-(1-x)$$

(21)

Furthermore, Equation (12) becomes

$$P=(1-x)\frac{d{u}_1}{dx}$$

(22)

The above solutions follow from the averaged momentum equations adapted to the case of channel flow [9]. A complete specification of all variables follows from the expressions for turbulent fluxes and the equations for k and $ϵ$. In the case of channel flow, these reduce to the following:

• Basic k-ϵ model

$$\begin{array}{cc}\hfill {\sigma }_{11}={\sigma }_{22}={\sigma }_{33}& =\frac{2}{3}k\hfill \end{array}$$

(23a)

$$\begin{array}{cc}\hfill {\sigma }_{12}& =-{\nu }_t\frac{d{u}_1}{dx}\hfill \end{array}$$

(23b)

$$\begin{array}{cc}\hfill <{\theta }^{\prime }{u}_2^{\prime }>& =-{\nu }_t\frac{d\theta }{dx}\hfill \end{array}$$

(23c)

$$\begin{array}{cc}\hfill {\nu }_t& =c_{\mu }\frac{k^2}{ϵ}\hfill \end{array}$$

(23d)

$$\begin{array}{cc}\hfill \frac{d}{dx}\left(\frac{{\nu }_t}{{\sigma }_k}\frac{dk}{dx}\right)+P-ϵ& =0\hfill \end{array}$$

(23e)

$$\begin{array}{cc}\hfill \frac{d}{dx}\left(\frac{{\nu }_t}{{\sigma }_{ϵ}}\frac{dϵ}{dx}\right)+(c_{ϵ1}P-c_{ϵ2}ϵ)\frac{ϵ}{k}& =0\hfill \end{array}$$

(23f)

• Fundamental model:

$$\begin{array}{cc}\hfill {\sigma }_{22}& =\frac{2}{3}(k+D_{12}\frac{d{u}_1}{dx})\hfill \end{array}$$

(24a)

$$\begin{array}{cc}\hfill {\sigma }_{33}& ={\sigma }_{22}\hfill \end{array}$$

(24b)

$$\begin{array}{cc}\hfill {\sigma }_{11}& =\frac{2}{3}(k-2D_{12}\frac{d{u}_1}{dx})\hfill \end{array}$$

(24c)

$$\begin{array}{cc}\hfill {\sigma }_{12}& =-D_{22}\frac{d{u}_1}{dx}\hfill \end{array}$$

(24d)

$$\begin{array}{cc}\hfill <{\theta }^{\prime }{u}_2^{\prime }>& =-D_{22}\frac{d\theta }{dx}\hfill \end{array}$$

(24e)

$$\begin{array}{cc}\hfill D_{12}& =\frac{2}{ϵC_0}{\sigma }_{12}({\sigma }_{11}+{\sigma }_{22})\hfill \end{array}$$

(24f)

$$\begin{array}{cc}\hfill D_{22}& =\frac{2}{ϵC_0}({\sigma }_{12}^2+{\sigma }_{22}^2)\hfill \end{array}$$

(24g)

$$\begin{array}{cc}\hfill c_k\frac{d}{dx}\left(D_{22}\frac{dk}{dx}\right)+P-ϵ& =0\hfill \end{array}$$

(24h)

$$\begin{array}{cc}\hfill \frac{1}{{\sigma }_{ϵ}^{*}}\frac{d}{dx}\left(D_{22}\frac{dϵ}{dx}\right)+(c_{ϵ1}P-c_{ϵ2}ϵ)\frac{ϵ}{k}& =0\hfill \end{array}$$

(24i)

In the subsequent sections, we shall compare the above descriptions with the results of DNS.

5. Testing the Diffusion Representations by DNS

In deriving equations for the mean values of flow quantities, the diffusion representation of mean fluxes has been used, i.e., the mean value of products of fluctuating quantities. Their correctness and accuracy will be assessed by comparing with the DNS results published for friction Reynolds numbers, $R{e}_{\tau }=u_{\tau }\frac{H}{\nu }$ of 950 [15], 2000 [13], and ${10}^4$ [14]. The comparison focuses on the flow in the main region—the region outside the thin boundary layer at the wall. In the main region, flow statistics are governed by unstable large eddies governed by inertia forces, while the effect of viscosity in this region is negligibly small. The presented basic k-$ϵ$ as well as the fundamental model intend to describe these statistics. The boundary layer is governed by viscous forces and is situated in the region $x<\frac{100}{R{e}_{\tau }}$; that is, $x<0.1,0.05$ and $0.01$ for $R{e}_{\tau }=950,2000,$ and ${10}^4$, respectively. The DNS results of the boundary layer near $x=0$ are omitted in this analysis.

5.1. Diffusion of Momentum

In the case of channel flow, turbulent momentum transport is apparent in the equation, as follows:

$$<u_1^{\prime }{u}_2^{\prime }>=-v_{DNS}\frac{d{u}_1}{dx}$$

(25)

where ${\nu }_{DNS}$ is turbulent viscosity according to the DNS results, which is the value calculated from Equation (25) when substituting the values of $<u_2^{\prime }{u}_1^{\prime }>$ and ${\displaystyle \frac{d}{dx}{u}_1}$ obtained from DNS data. The value according to the basic k-$ϵ$ model ${\nu }_t$ is given by Equation (6) and the value according to the fundamental model $D_{22}$ is given by Equation (24g), where the RHSs of these equations are evaluated from the DNS data. The DNS data used are those of $R{e}_{\tau }={10}^4$ [14]. The three calculated turbulent viscosities are shown as functions of x in Figure 1. The ratios $\frac{{\nu }_t}{{\nu }_{DNS}}$ and $\frac{D_{22}}{{\nu }_{DNS}}$ versus x are shown in Figure 2. Disregarding the thin viscous layer at the wall, the fundamental model gives satisfactory agreement over the entire x range without the use of calibration factors. Deviations are less than $10\%$ from the DNS results. They can be ascribed to the truncation of higher-order terms in the expansions in powers of $C_0^{-1}$, which were used in the theory that led to the presented expressions [8,9]. The same conclusion was arrived at when using the DNS data of $R{e}_{\tau }=2000$ [9,13]. The basic k-$ϵ$ model, on the other hand, disagrees quite a lot with DNS. The disagreement is the largest at small x values and gradually becomes smaller when approaching the central axis of the channel: $x=1$. The dependency on x is apparently not well captured by representation (23d), in contrast with (24g), which shows satisfactory agreement over the entire range.

5.2. Diffusion of Temperature

Temperature is considered a conservative quantity in incompressible flow at high Reynolds numbers, where heat conductivity through molecular vibration is negligibly small outside thin layers at the walls. From the theory underlying the fundamental model, it follows that the thermal diffusion constant equals $D_{ik}$: cf. Equation (8). In the case of channel flow, it becomes $D_{22}$ and becomes equal to that of turbulent viscosity: cf. Equations (24d) and (24e). This result is confirmed by the Lagrangian-based DNS of channel flow at $R{e}_{\tau }=950$ [15], where the thermal diffusion coefficient, according to DNS, $\frac{<u_2^{\prime }{\theta }^{\prime }>}{{\displaystyle \frac{d\theta }{dx}}}$ is compared to that of the fundamentally based model, $D_{22}$. The agreement closely resembles that shown in Figure 1 and Figure 2, c.q., $\frac{<u_2^{\prime }{u}_1^{\prime }>}{\frac{d{u}_1}{dx}}$ and $D_{22}$. Deviations of the predictions of the basic k-$ϵ$ model are likely as equally large as those shown in Figure 1 and Figure 2.

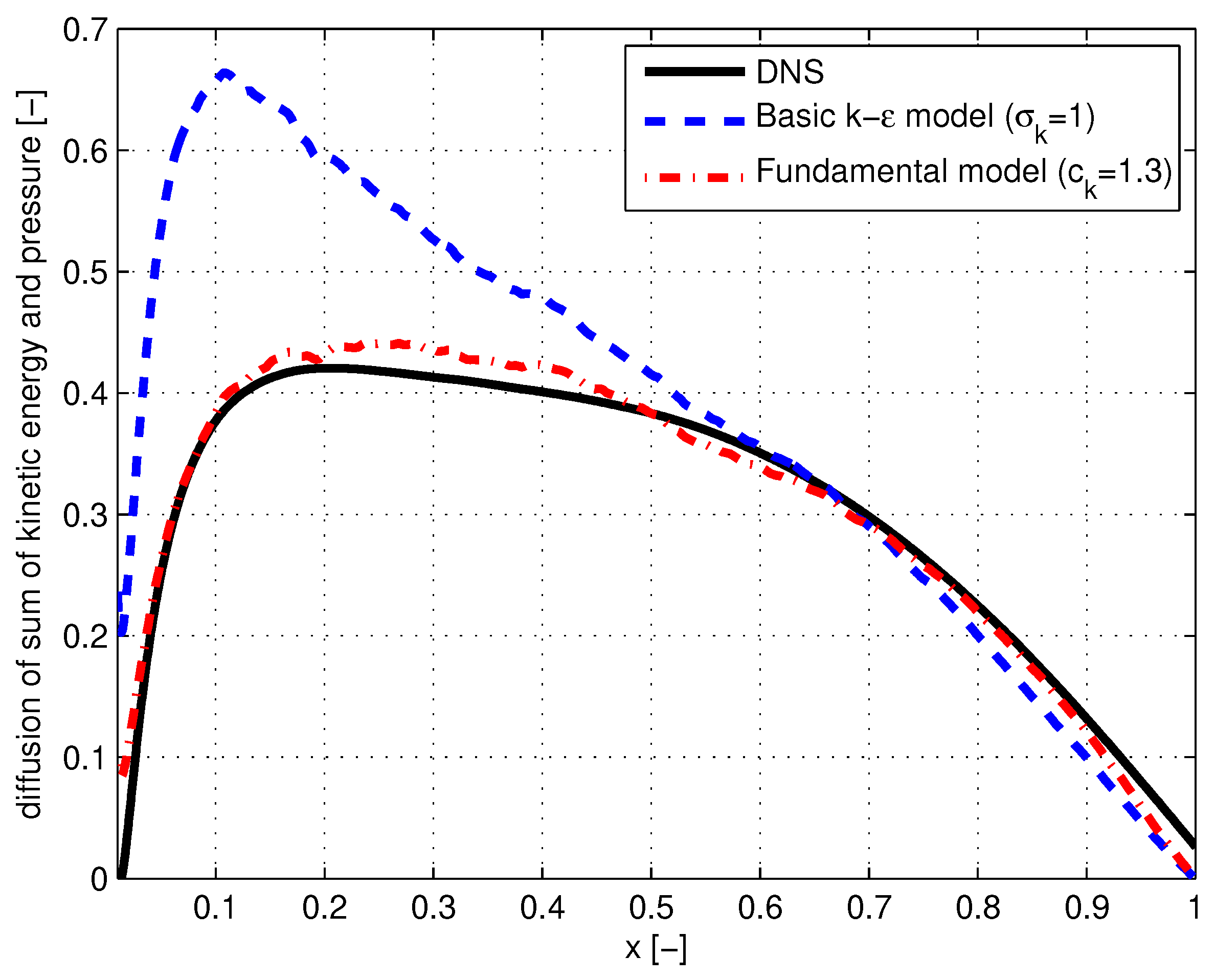
5.3. Diffusion of Kinetic Energy and Pressure

In the basic k-$ϵ$ model, fluxes of kinetic energy and pressure are lumped together, as shown in Equation (13). For channel flow, these terms become the following:

$$<k^{\prime }{u}_2^{\prime }>+<p^{\prime }{u}_2^{\prime }>=-\frac{{\nu }_t}{{\sigma }_k}\frac{dk}{dx}$$

(26)

From Equation (14), we have the following for the fundamental model:

$$<k^{\prime }{u}_2^{\prime }>+<p^{\prime }{u}_2^{\prime }>=-c_k{D}_{22}\frac{dk}{dx}$$

(27)

The description is used in the numerical solution of the equation for k in Section 6.

In Figure 3, we show the sum of both fluxes versus x, when the RHSs of (26) and (27) are evaluated by the DNS data. Values for the calibration constants ${\sigma }_k$ and $c_k$ of 1 and $1.3$ were taken. Also, the value of the sums is obtained by the direct calculation of their values using the DNS of $R{e}_{\tau }={10}^4$. The empirical construction of Equation (27), based on the fundamental model, offers surprisingly good agreement. The agreement extends over the entire x range and is obtained with the calibration constant, $c_k=1.3$.

5.4. Diffusion of Energy Dissipation

DNS data do not provide information on the average values of products of velocity fluctuations and dissipation fluctuations. Direct verification of the diffusion representation is, thus, not possible. Further, the differential equation for mean energy dissipation in both models is largely an empirical construction. What remains possible is to verify the values of quantities derived from the solutions of the coupled differential equations for mean kinetic energy and mean energy dissipation rate against DNS data. This is the subject of the next section.

6. Solutions of $\mathit{k}$ and $\mathit{ϵ}$ Compared with DNS

In the previous section, predictions of individual components of the models were verified by DNS. Further testing is executed by comparing numerically obtained solutions of the model equations as a whole with DNS.

6.1. Equations and Boundary Conditions

Model equations are given by coupled differential equations for mean kinetic energy and mean energy dissipation. For mean energy dissipation, the variable G is introduced, which is defined by the following:

$$G=\kappa ϵx$$

(28)

Near the wall, outside the viscous layer, solutions should comply with the solutions of the log layer. Inertial subrange asymptotics [18] reveal that production, P, and dissipation, $ϵ$, are equal in this region: $P=ϵ$. Furthermore, $\kappa \frac{d{u}_1}{dx}=1$, so that $G=1$. DNS results show values of G in the log layer, which are between $0.9$ and 1 [13,14]. In the present analysis, the theoretical value of 1 is taken. Making use of relations (21), (23b), (23d), and (28), differential Equations (23e) and (23f) can be transformed into the following coupled equations for k and G, which are appropriate for the basic k-$ϵ$ model.

• Basic k-ϵ model equations:

$$\frac{{\kappa }^2}{{\sigma }_k}\frac{x}{G}\frac{d}{dx}\left(\frac{Ax}{G}\frac{dk}{dx}\right)+\frac{{(1-x)}^2}{A}-1=0$$

(29)

$$\frac{{\kappa }^2}{{\sigma }_{ϵ}}\frac{x^2}{G^2}\frac{d}{dx}\left(\frac{Ax}{G}\frac{d}{dx}\left(\frac{G}{x}\right)\right)+\frac{1}{k}(\frac{c_{ϵ1}{(1-x)}^2}{A}-c_{ϵ2})=0$$

(30)

where

$$A=c_{\mu }{k}^2$$

(31)

where values of the empirical constants will be taken in agreement with [5,6]: $\kappa =0.4$, $c_{\mu }=0.09$, ${\sigma }_k=1$, ${\sigma }_{ϵ}=1.3$, $c_{ϵ1}=1.49$, $c_{ϵ2}=1.9$. The boundary conditions are as follows:

$$x=0;k=\frac{1}{\sqrt{c_{\mu }}};G=1$$

(32)

$$x=1;\frac{dk}{dx}=0;\frac{dG}{dx}=G$$

(33)

The boundary condition for k at $x=0$ follows from relations (21), (23b), and (23d), with ${\displaystyle ϵ=\frac{d{u}_1}{dx}}$ in the log layer. The boundary condition for G at $x=1$ corresponds to the zero slope of $ϵ$ at $x=1$.

The equations appropriate for the fundamental model follow from (24h) and (24i) upon using (28), (21), (24a)–(24g).

• Fundamental model equations:

$$\frac{c_k{\kappa }^{2}x}{G}\frac{d}{dx}\left(B\frac{x}{G}\frac{dk}{dx}\right)+\frac{{(1-x)}^2}{B}-1=0$$

(34)

$$\frac{{\kappa }^2{x}^{2}k}{G^2{\sigma }_{ϵ}^{*}}\frac{d}{dx}\left(B\frac{x}{G}\frac{d\frac{G}{x}}{dx}\right)+\frac{c_{ϵ1}{(1-x)}^2}{B}-c_{ϵ2}=0$$

(35)

and

$$B=\frac{2}{C_0}({\sigma }_{12}^2+{\sigma }_{22}^2)=\frac{2}{C_0}({(1-x)}^2+{\sigma }_{22}^2)$$

(36)

In these equations, k and ${\sigma }_{22}$ are related to each other by an algebraic relation, which is obtained by the systematic elimination of ${ϵ}^{-1}\frac{d{u}_1}{dx}$, ${\sigma }_{12}$, ${\sigma }_{11}$, ${\sigma }_{33}$, $D_{12}$, $D_{22}$ from Equations (21), (24a), and (24g), as follows:

$$k={\sigma }_{22}\frac{3{\sigma }_{22}^2+{(1-x)}^2}{2({\sigma }_{22}^2-{(1-x)}^2)}$$

(37)

The relation can be used to eliminate ${\sigma }_{22}$ from (34) and (35), resulting in two differential equations for k and G. However, the analysis of the above relation for k shows that in an area close to $x=0$, according to (37), ${\sigma }_{22}$ can have two values for one value of k. The verification of (37) using the results of DNS confirms the correctness of the equation and the double dependency in this area. The other way around is not the case: For each value of ${\sigma }_{22}$, there is only one value of k possible. The easiest approach is then to substitute the k relation (37) into the two differential equations, i.e., Equations (34) and (35), and solve for ${\sigma }_{22}$ and G. The value of k is subsequently obtained from (37). The boundary conditions are as follows:

$$x=0;G=1;{\sigma }_{22}=\sqrt{\frac{C_0}{2}-1}$$

(38)

$$x=1;\frac{d{\sigma }_{22}}{dx}=0;\frac{dG}{dx}=G$$

(39)

where the boundary condition for ${\sigma }_{22}$ at $x=0$ follows from Equations (21), (24d), and (24g), with $ϵ=\frac{d{u}_1}{dx}$ in the log layer, as in the basic k-$ϵ$ model, $c_{ϵ2}=1.9$. A value of $c_k$ of $1.3$ was established in Section 5.3 (Figure 3). A value of ${\sigma }_{ϵ}^{*}$ of $0.2$ is found to lead to the best agreement with DNS.

The value of $c_{ϵ1}$ follows from Equation (35) by letting x approach $x=0$. It yields the following relation:

$$c_{ϵ1}=c_{ϵ2}-\frac{k_0{\kappa }^2}{{\sigma }_{ϵ}^{*}}$$

(40)

which is analogous to Equation (17) for the basic k-$ϵ$ model; $k_0$ is the value of k at $x=0$ obtained from Equation (37). For $c_{ϵ2}=1.9$, $C_0=7$, ${\sigma }_{ϵ}^{*}=0.2$ and $k_0=4.48$, $c_{ϵ1}=-1.68$. This suggests negative production. However, for the first term on the LHS of Equation (35), one can write the following:

$$x^2\frac{d}{dx}\left(B\frac{x}{G}\frac{d\frac{G}{x}}{dx}\right)=x^2\frac{d}{dx}\left(\frac{B}{G}\frac{dG}{dx}\right)-x\frac{dB}{dx}+B$$

(41)

where the last two terms have the same character as that of production, making the total of production-like terms positive.

6.2. Numerical Solution

Numerical instability is encountered when solving Equations (29), (30), (34), and (35), a feature not uncommon for k-$ϵ$ equations; see Lew et al. [19]. The way out is to convert the equations into a diffusion problem by adding the terms ${\displaystyle \frac{dk}{dt}}$ and ${\displaystyle \frac{dG}{dt}}$ on the RHS of (29) and (30), ${\displaystyle \frac{d{\sigma }_{22}}{dt}}$ and ${\displaystyle \frac{dG}{dt}}$ on the RHS of (34) and (35). This requires starting from a suitably chosen initial solution at $t=0$; see Borse [20]. After sufficient time, the solution converges to the desired stationary result.

Another difficulty encountered in the execution of the numerical calculations concerns the boundary condition for G at $x=1$: cf. Equations (33) and (39). These are replaced by $(d/dx)G=0$ at $x=1$. The effect of this simplification is limited to a small region near $x=1$.

Figure 4 and Figure 5, respectively, show the distributions of kinetic energy, k, and the energy dissipation rate, G, versus x, according to DNS, the basic k-$ϵ$ model (calculated from Equations (29) and (30)), and the fundamental model (calculated from Equations (34) and (35)).

6.3. Analytical Solution

The distinction is made between the area near the wall referred to as the outer region and the area near the center of the channel referred to as the inner region. The outer region is the area where the production and dissipation of energy are dominant. Turbulent diffusion of kinetic energy and pressure and turbulent diffusion of dissipation are negligibly small. It is the area where the log layer description for mean flow applies and where production equals dissipation [21]. In the inner region, turbulent diffusion of kinetic energy and pressure, as well as turbulent diffusion of dissipation, are important and in balance with energy dissipation, while production is negligibly small. For each region, analytical solutions can be derived, which are subsequently matched to arrive at a complete solution.

6.3.1. Solutions for k and G in the Outer Region

Solutions valid in the outer region are obtained by retaining the second and third terms in Equations (28) and (33), yielding $A={(1-x)}^2$ and $B={(1-x)}^2$, or in terms of k and ${\sigma }_{22}$

• Basic k-ϵ model:

$$k=\frac{1}{\sqrt{c_{\mu }}}(1-x)$$

(42)

• Fundamental model:

$${\sigma }_{22}=\sqrt{(\frac{C_0}{2}-1)}(1-x)$$

(43)

Using the relation between k and ${\sigma }_{22}$, according to the fundamental model, cf. Equation (37), we have the following:

• Fundamental model:

$$k=k_0(1-x)$$

(44)

where $k_0$ is the value of k at $x=0$,

$$k_0=\frac{1}{2}\sqrt{(\frac{C_0}{2}-1)}\left(\frac{3C_0-4}{C_0-4}\right)$$

(45)

which amounts to $k_0=4.48$ for $C_0=7$.

To derive the equations for G, which are applicable in the outer region, the second and third terms of Equation (41) need to be taken into account (and replacing B with A in Equation (41), for the basic k-$ϵ$ model). Noting that in the outer region $A={(1-x)}^2$ and $B={(1-x)}^2$ one obtains for G from Equation (30) using relation (17) and from Equation (35) using relation (40), the result:

• Basic k-ϵ model and fundamental model:

$$G=(1-x)\sqrt{(1+x)}$$

(46)

The above descriptions for k and G are rather simple. They compare well with the numerical results for values of x, up to about $0.5$. At greater distances from the wall, they start to deviate and fail to meet the conditions of the zero slope at $x=1$. To overcome this deficiency, solutions valid for the inner region are developed.

6.3.2. Solutions for k in the Inner Region

Solutions for k are developed by describing k by a series of successive powers of $\eta =1-x$. The linear term in $\eta$ is omitted in order to satisfy the zero-slope condition at $\eta =0$. Disregarding terms of $O\left({\eta }^3\right)$ and higher, we write the following for k:

$$k=k_1+a{\eta }^2$$

(47)

where $k_1$ is the value of k at $x=1$; and $k_1$ and a are to be determined. Substituting expression (47) in Equations (29) and (34), and equating the leading terms of $O\left({\eta }^0\right)$ for a in the basic k-$ϵ$ and fundamental models, respectively, we obtain the following relations:

$$2a\frac{c_{\mu }{\kappa }^2{k}_1^2}{{\sigma }_k}=G_1^2$$

(48)

and

$$\frac{16a{c}_k{\kappa }^2{k}_1^2}{9C_0}=G_1^2$$

(49)

where $G_1$ is the value of G at $\eta =0$. In deriving result (49), we take for ${\sigma }_{22}$ at $\eta =0$ the value $\frac{2}{3}{k}_1$ in accordance with Equation (37). The boundary between the inner and outer region is defined by ${\eta }_0=1-x_0$. At this boundary, the value of k and its slope should match the values of the outer region. This yields the following relations:

$$k_1+a{\eta }_0^2=\frac{{\eta }_0}{\sqrt{c_{\mu }}};k_1+a{\eta }_0^2={\eta }_0{k}_0$$

(50)

$$2a{\eta }_0=\frac{1}{\sqrt{c_{\mu }}};2a{\eta }_0=k_0$$

(51)

for basic k-$ϵ$ and the fundamental model, respectively. From Equations (47)–(51), the following solutions are obtained:

• For the basic k-$ϵ$ model:

$${\eta }_0=4{\sigma }_k{G}_1^2\frac{\sqrt{c_{\mu }}}{{\kappa }^2};k_1=\frac{{\eta }_0}{2\sqrt{c_{\mu }}};a=\frac{1}{2\sqrt{c_{\mu }}{\eta }_0}$$

(52)

• and for the fundamental model:

$${\eta }_0=\frac{9G_1^2{C}_0}{2{\kappa }^2{k}_0^3{c}_k};k_1=\frac{k_0{\eta }_0}{2};a=\frac{k_0}{2{\eta }_0}$$

(53)

The above solution parameters can be determined by implementing the values of the system parameters, ${\sigma }_k,c_{\mu },\kappa ,C_0,k_0$, and $c_k$. The value of $G_1$ is taken from the numerical results: $G_1=0.25$ in the case of the basic k-$ϵ$ model and $G_1=0.44$ in the case of the fundamental model. An alternative approach to determine $G_1$ is to couple the above analytical solution of k to that of G presented in Section 6.3.3 below. It yields values for $G_1$ without recourse to the numerical results. The values are practically equal to those of the numerical results.

A complete analytical description of k for the outer and inner regions is obtained from Equations (41) and (44) when $x\le x_0$, and Equations (47) and (52) when $x\ge x_0$, where $x_0=0.47$ in the basic k-$ϵ$ model, and $x_0=0.33$ in the fundamental model. The results are shown in Figure 4 with solid blue and red lines.

6.3.3. Solutions for G in the Inner Region

For G in the inner region, the following expansion is used:

$$G=G_1(1-\eta )+a{\eta }^2.$$

(54)

where the linear term, $G_1\eta$, is introduced to satisfy the boundary condition at $x=1$: cf. Equations (33) and (39). The values of $G_1$ and a are to be determined. Substituting description (54) into Equations (30) and (35) and equating the leading terms of $O\left({\eta }^0\right)$ yield the following:

$$a=\alpha G_1^3$$

(55)

where

$$\alpha =\frac{{\sigma }_{ϵ}{c}_{ϵ2}}{2{\kappa }^2{c}_{\mu }{k}_1^3}$$

(56)

and

$$\alpha =\frac{9C_0{\sigma }_{ϵ}^{*}{c}_{ϵ2}}{16{\kappa }^2{k}_1^3}$$

(57)

for the basic k-$ϵ$ model and fundamental model, respectively. At the boundary of the inner and outer regions, $\eta ={\eta }_1$, the values of G and its slope, according to the outer and inner regions, should become equal. This yields the following relations:

$${\eta }_1\sqrt{(2-{\eta }_1)}=(1-{\eta }_1)G_1+\alpha G_1^2{\eta }_1^2$$

(58)

$$\frac{(2-\frac{3}{2}{\eta }_1)}{\sqrt{2-{\eta }_1}}=-G_1+2\alpha G_1^2{\eta }_1$$

(59)

Eliminating $G_1$ from the above equations yields the following irreducible equation for ${\eta }_1$:

$$\alpha =\frac{2}{{\eta }_1^4}\frac{{(1-\frac{{\eta }_1}{2})}^3}{{(1-\frac{{\eta }_1}{4})}^3}(1-\frac{3{\eta }_1}{4}+\frac{{\eta }_1^2}{4})$$

(60)

The value of $\alpha$ follows from Equation (56) by using the system’s values for the various parameters and taking for $k_1$ the value of the numerical calculations, i.e., $k_1=0.8$. Consequently, $\alpha =134$ and $\alpha =18$ for the basic k-$ϵ$ model and the fundamental model, respectively. Iteratively, one finds from Equation (60) that for the basic k-$ϵ$ model ${\eta }_1=0.31$ $(x_1=0.69)$ and the fundamental model, ${\eta }_1=0.47$$(x_1=0.53)$. A complete analytical description of G for the outer and inner regions is obtained from Equation (46) when $x\le x_1$ and Equations (54)–(56) when $x\ge x_1$. The results are shown in Figure 5 with solid blue and red lines.

6.4. Discussion of Results

Numerical and analytical solutions for kinetic energy, k, and energy dissipation, $ϵ$, with the latter in terms of $G=\kappa xϵ$, have been developed for the basic k-$ϵ$ model and a new fundamental model. The solutions are compared with DNS results and are shown in Figure 4 and Figure 5. Our conclusions are as follows:

• Analytical solutions agree in a satisfactory manner with numerical solutions. The analytical solutions reveal the relative contributions of turbulent diffusion, energy production, and energy dissipation in the outer and inner regions of the channel. They show to what extent the descriptions are empirically or fundamentally based and depend on calibration factors.
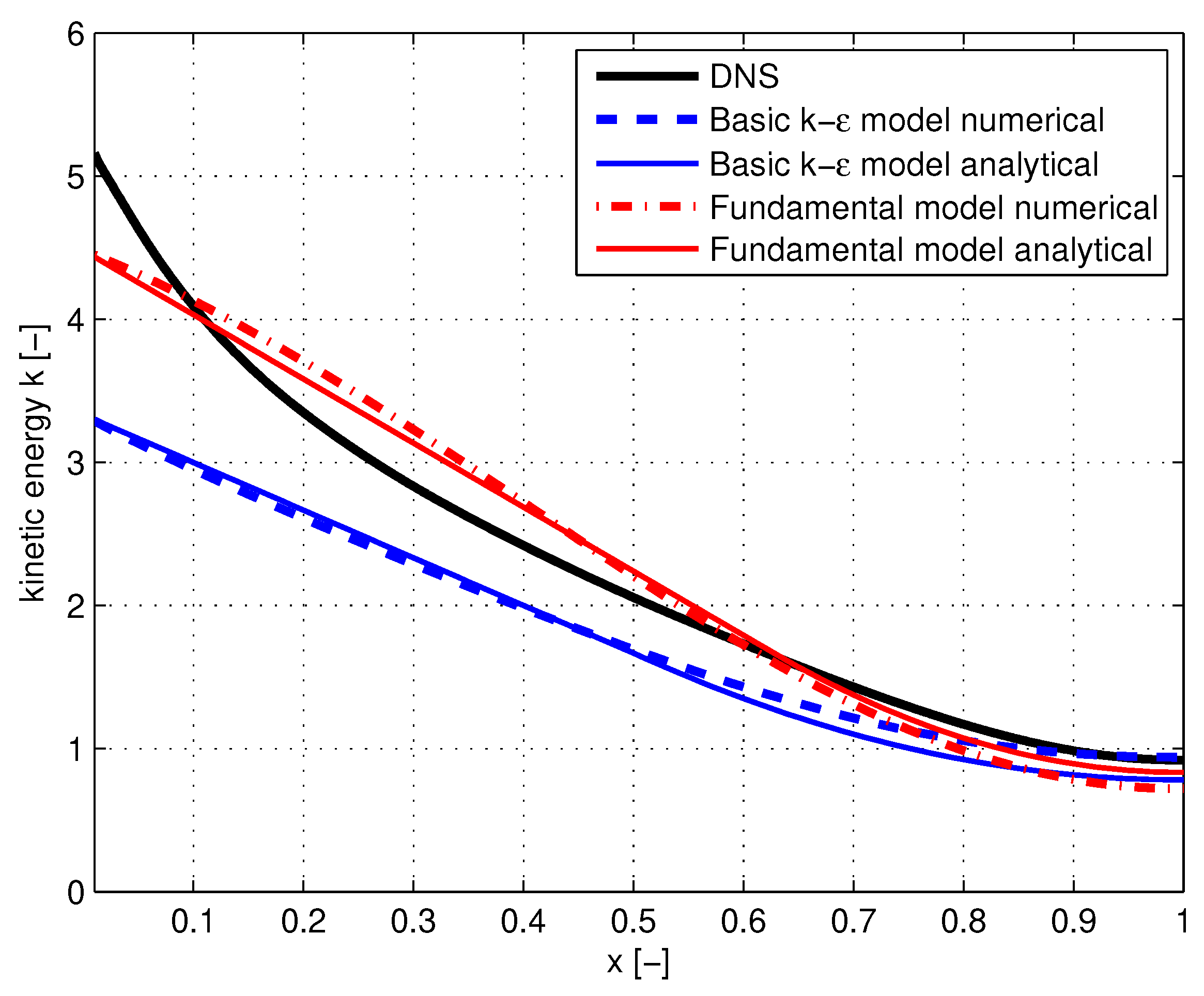
• Solutions for k in the outer region $(x\le 0.33)$ according to the fundamental model do not depend on calibration constants. They have a fundamental basis. The differences with DNS can be ascribed to errors as a result of truncation in the expansion with respect to $C_0^{-1}$, which underlies the fundamental model.
• Solutions for k in the inner region $(x\ge 0.33)$ according to the fundamental model depend on the calibration factor, $c_k$.
• Solutions for k in both the outer and inner regions, according to the basic k-$ϵ$ model, depend on the calibration factors $c_{\mu }$ and ${\sigma }_k$.
• Solutions for G in the outer region, according to the fundamental model and the basic k-$ϵ$ model, $(x\le 0.53)$ and $(x\le 0.69)$, do not depend on calibration factors. Differences with DNS are due to some deviation between the value of production and dissipation in this area.
• Solutions for G in the inner region, according to the fundamental model and the basic k-$ϵ$ model, $(x\ge 0.69)$ and $(x\ge 0.53)$, respectively, depend on the calibration factors ${\sigma }_{ϵ}^{*}$ and ${\sigma }_{ϵ}$.
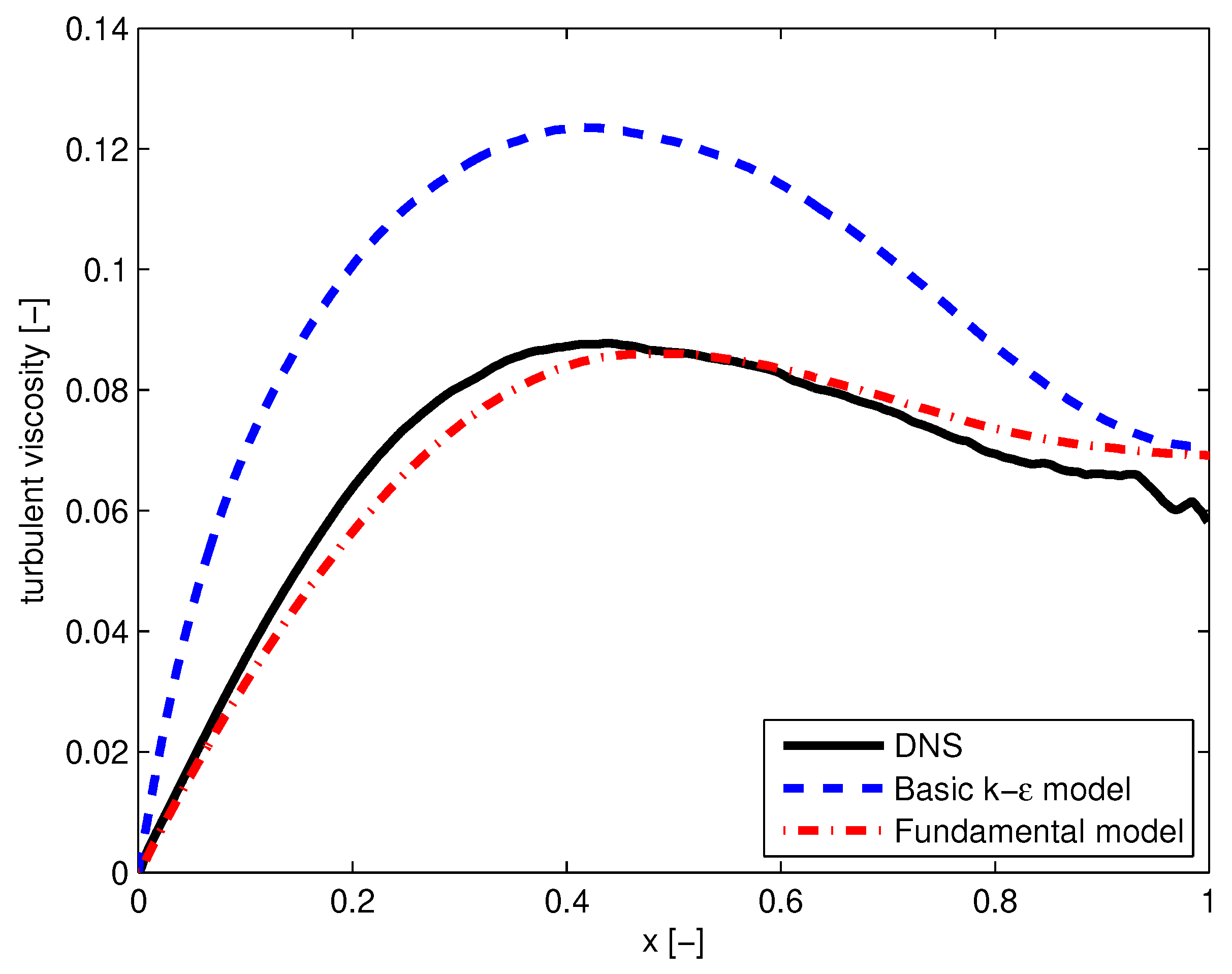
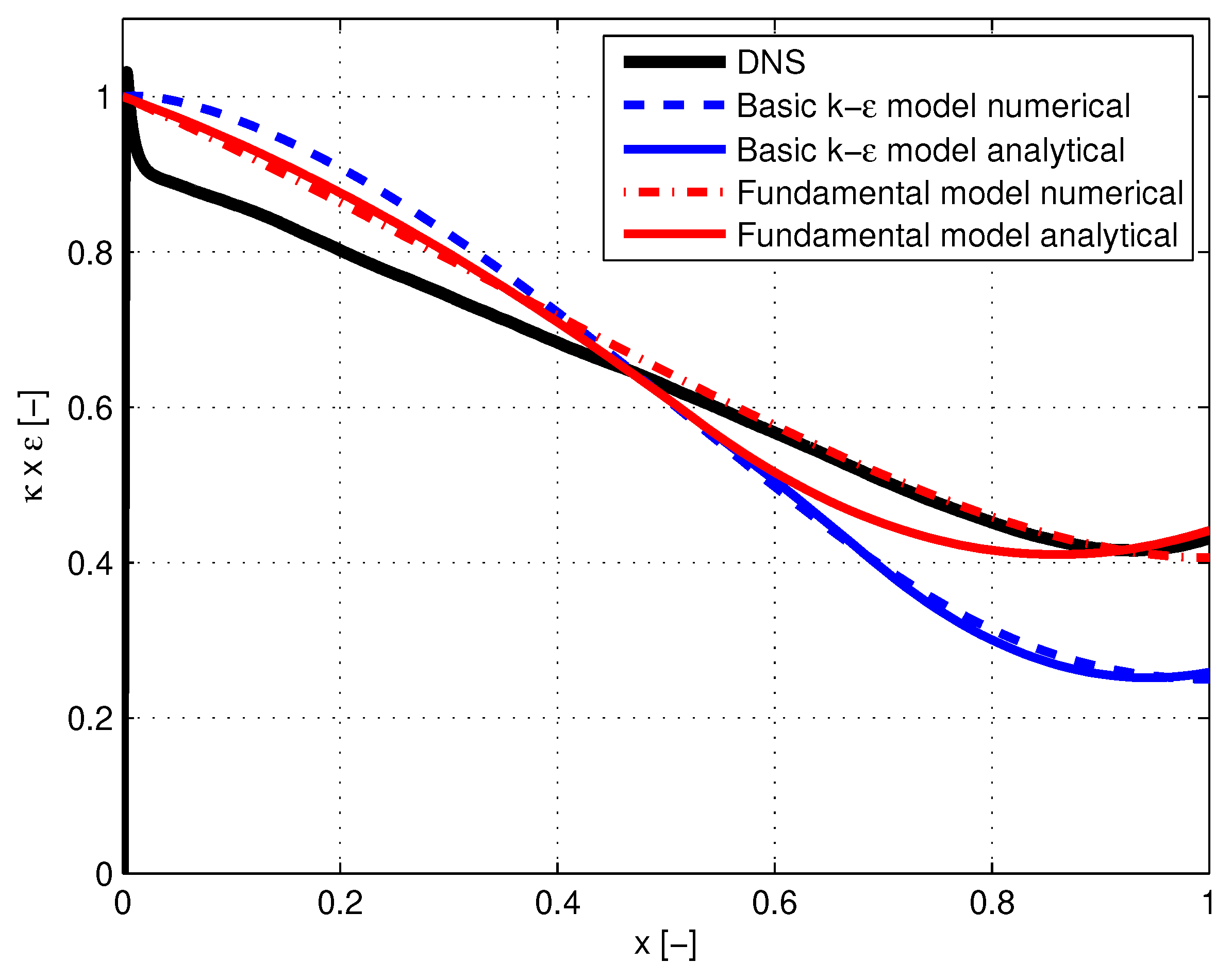
• Using standard calibration constants in the solutions of the basic k-$ϵ$ model results in notable deviations compared to DNS data. The deviations can be reduced by recalibrating ${\sigma }_{ϵ}$, $c_{\mu }$ and ${\sigma }_k$. Deviations between diffusion constants remain significant because of different functional dependencies; see Figure 1, Figure 2 and Figure 3.

7. Velocity Distributions

The basic k-$ϵ$ model is based on the assumption of an isotropic turbulence field. It cannot predict the anisotropic behavior of covariances or turbulent stresses. For the fundamental model, the distribution of ${\sigma }_{22}$ follows from the solution of Equation (34). According to Equation (24b) ${\sigma }_{33}={\sigma }_{22}$, while ${\sigma }_{11}=\frac{1}{2}k-{\sigma }_{22}$, where k is given by Equation (37). In Figure 6, the distribution, versus x, of the calculated values of the standard deviations of the fluctuations $\sqrt{{\sigma }_{11}}$, $\sqrt{{\sigma }_{22}}$, and $\sqrt{{\sigma }_{33}}$, is shown, according to the fundamental model and the results of DNS. Deviations are similar to those shown in [9] and are ascribed to the truncation of the expansions of $C_0^{-1}$, underlying the theory of the fundamental model. Deviations of the three variances, ${\sigma }_{11},{\sigma }_{22},{\sigma }_{33}$ from k, which describe anisotropy, are next to the leading order in the $C_0^{-1}$ expansion (cf. Equations (24a)–(24c)), and are, therefore, more sensitive to the truncation error.

For the gradient of the mean flow, the following relations can be derived. For the basic k-$ϵ$ model from Equations (21) and (23b), we have the following:

$$\frac{d{u}_1}{dx}=\frac{1-x}{{\nu }_t}$$

(61)

For the fundamental model from Equations (21) and (24d), we have the following:

$$\frac{d{u}_1}{dx}=\frac{1-x}{D_{22}}$$

(62)

In Figure 7, the distributions are shown of $\kappa x\frac{d{u}_1}{dx}$ versus x, according to DNS, the basic k-$ϵ$ model, and the fundamental model. The deviations between DNS and the basic k-$ϵ$ model are similar to those shown for ${\nu }_{DNS}$ and ${\nu }_t$ in Figure 1 and Figure 2. Similarly, the agreement between ${\nu }_{DNS}$ and $D_{22}$ is shown in Figure 1 and Figure 2. According to (21), ${\displaystyle P=(1-x)\frac{d{u}_1}{dx}}$, indicating that the disagreement of production with DNS in the case of the basic k-$ϵ$ model is similar to that shown in Figure 7, and that the agreement of production with DNS for the fundamental model is similar to that shown in Figure 7.

The distribution of mean velocity $u_1$ predicted by the basic k-$ϵ$ model and the fundamental model is obtained by integrating the RHSs of Equations (61) and (62). Because the models do not describe the velocity in the viscous layer at the wall, the integration starts at some distance from the wall for which the position $x=\frac{100}{R{e}_{\tau }}$ is taken. The value of $u_1$ at this point, according to the DNS results of $R{e}_{\tau }={10}^4$, is 17.2, which agrees with the values obtained from the measurements; see Monin and Yaglom, Vol. I, Figure 25 [21]. The results of the integration are shown in Figure 8, where the distributions of the mean velocity of the two models and DNS are presented. It is seen that for equal shear velocity (i.e., for equal longitudinal pressure gradient in the channel), the fundamental model somewhat overestimates mean velocity (by $5\%$), while the basic k-$ϵ$ model underestimates it by $18\%$.

8. Discussion

An analysis is presented of two models to determine the mean values of turbulent flow variables, i.e., velocity, $u_i$, pressure, p, turbulent diffusion, $D_{ij}$, kinetic energy, k, and energy dissipation, $ϵ$. The two models are the basic k-$ϵ$ model widely used in engineering applications and environmental analysis [5,6], as well as a new fundamentally based model, which is derived from recently published statistical descriptions of inhomogeneous anisotropic turbulence [7,8,9]. The analysis focused on turbulent channel flow, which is highly anisotropic and inhomogeneous. It is of direct relevance to duct flow applications, turbulent boundary layers around bodies, and the atmospheric surface layer around the earth. Model predictions were verified against the published results of direct numerical simulations (DNS) for shear Reynolds numbers of 950 [15], 2000 [13], and ${10}^4$ [14]. The comparison focused on the regions outside the thin viscous boundary layers, which are a few millimeters at the wall. The development status of DNS is mature; its results can serve as a reliable source for verifying model predictions.

The basic k-$ϵ$ model is built on an empirical isentropic representation of the turbulence field. It contains a gradient hypothesis for turbulent diffusion, which is supplemented by calibration constants. Using conventionally proposed values for the calibration constants [5,6], model predictions of several variables are found to deviate remarkably from the results of DNS. A summary is presented in

Table 1. The predictions of the basic k-$ϵ$ model and the new fundamental model, compared with the DNS of turbulent channel flow.

Variable	Basic k-$\mathit{ϵ}$ Model	New Fundamental Model
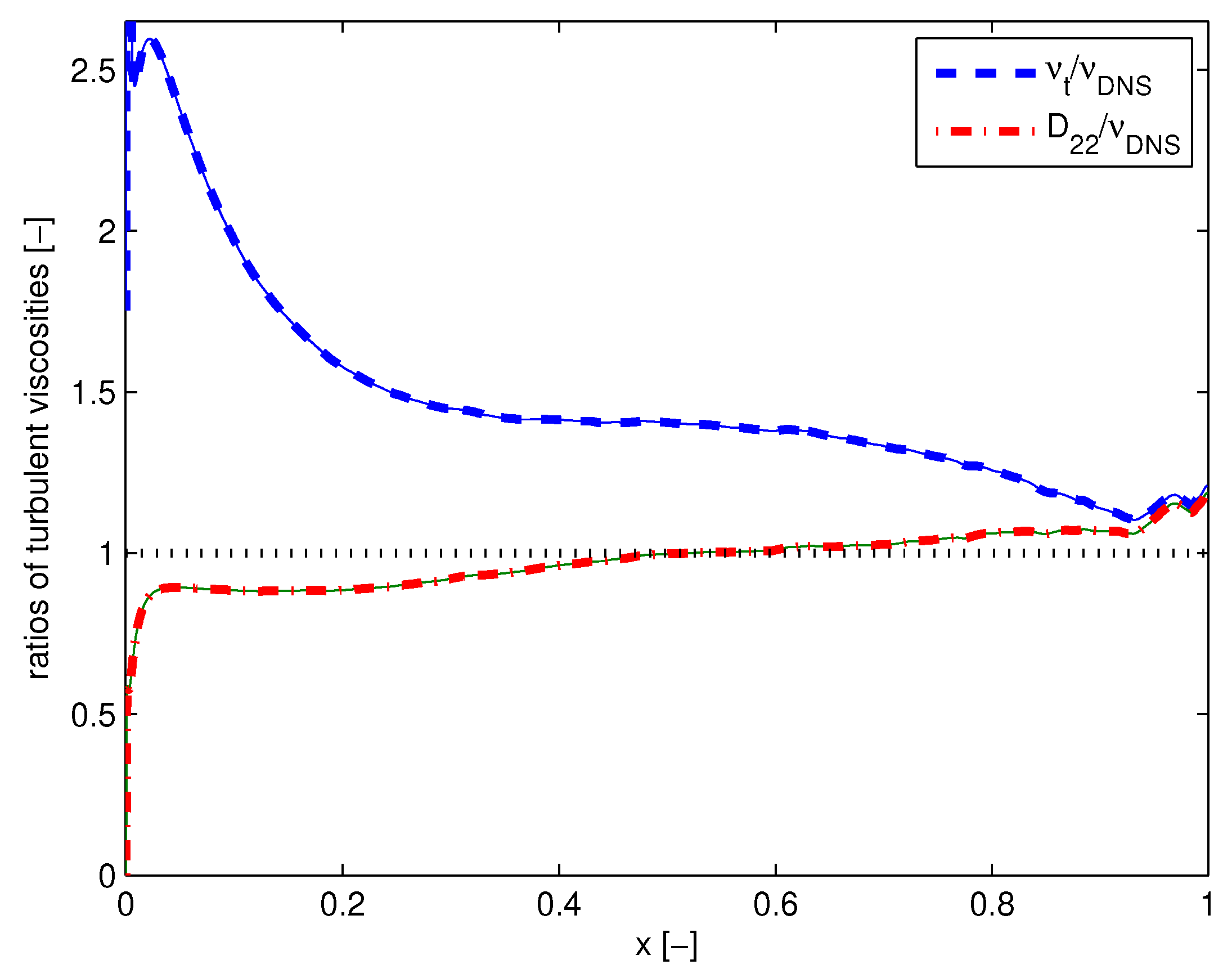
Turbulent viscosity	Empirical Equation (23d). Significant deviations: Figure 1 and Figure 2	Fundamentally based Equation (24d). Satisfactory agreement: Figure 1 and Figure 2
Turbulent diffusion of temperature, smoke, aerosol	Empirical Equation (23c). Significant deviations similar to Figure 1 and Figure 2	Fundamentally based Equation (24e). Satisfactory agreement similar to Figure 1 and Figure 2
Turbulent diffusion of kinetic energy and pressure	Empirical Equation (26). Deviation: Figure 3	Empirical Equation (27). Satisfactory agreement Figure 3
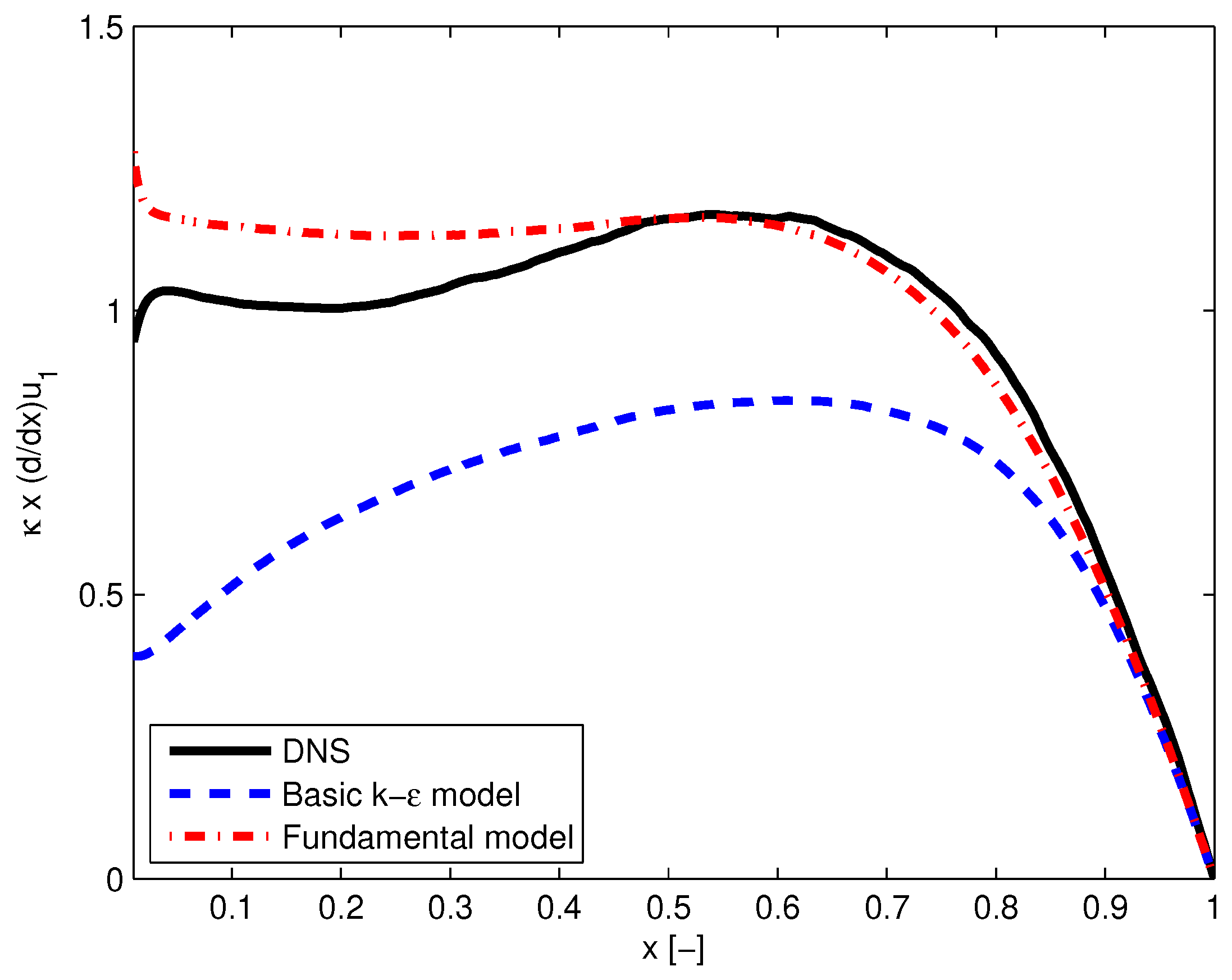
Mean value of kinetic energy	Empirical Equation (29). Deviation: Figure 4	In the outer half of the channel: Fundamentally based Equation (55). In the inner half: Empirical Equation (55). Satisfactory agreement Figure 4
Mean value of energy dissipation rate	In the outer half of the channel: fundamentally based Equation (46). In the inner half: empirical  Equation (55). Deviation: Figure 5	In the outer half of the channel: fundamentally based Equation (46). In the inner half: Empirical Equation (55). Satisfactory agreement: Figure 5
RMS values of fluctuations	No prediction	Qualitative agreement: Figure 6
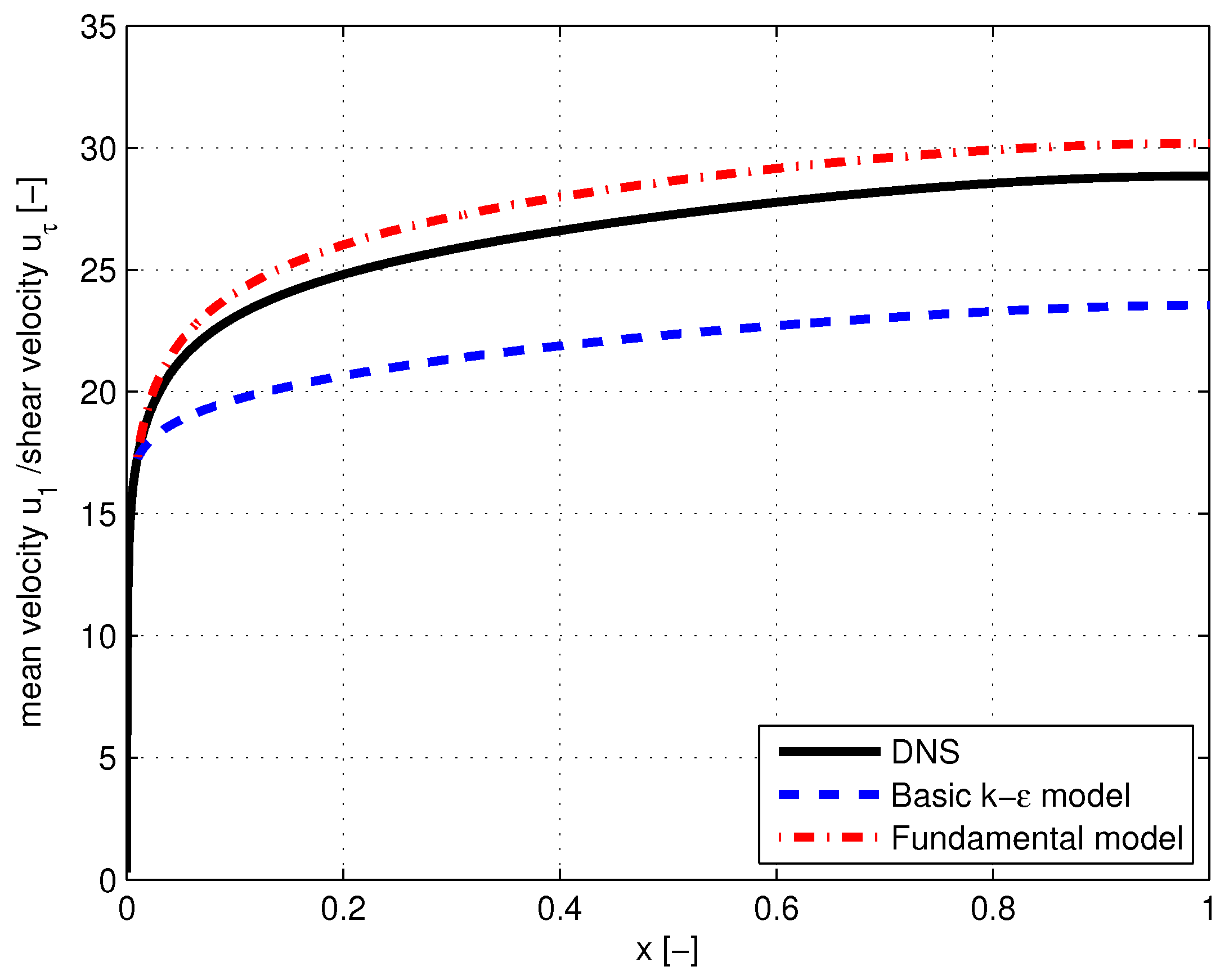
Mean value of velocity	Empirical Equation (61). Deviations: Figure 7 and Figure 8	Fundamentally based Equation (62). Satisfactory agreement Figure 7 and Figure 8

.

The fundamental model is derived from a theory that has a theoretical basis [7,8,9]. Expressions for the turbulent diffusion of momentum and of conservative scalars, such as temperature and passive admixture (smoke, aerosols), are of a general nature. They are free from calibration constants. They are found to agree in a satisfactory manner with DNS results at all distances, x, from the wall (outside the thin boundary layer at the wall). The theory underlying the fundamental model does not provide generally valid expressions for the turbulent diffusion of non-conservative scalar kinetic energy, pressure, and energy dissipation. The non-conservative diffusion terms are only important for the determination of k and $ϵ$ in the inner half of the channel. Here, non-conservative behavior has been modeled by using the diffusion expressions of conservative scalars provided with calibration factors. A summary is presented in Table 1.

9. Conclusions

CFD codes are generally based on empirical propositions for diffusion by turbulent fluctuations. This includes the basic k-$ϵ$ model widely used in engineering and environmental analyses. The limitation of these models is that they lack generality. It is uncertain whether the constituting variables are truly and accurately represented by the proposed expressions, both in magnitude and spatial dependency. The addition of calibration factors tempers the prediction inaccuracies to some extent. At the same time, they need to be specified for each new case. However, calibration predictions can still deviate markedly from the correct results at different positions in the flow field.

Models that are derived from generally valid principles do not suffer from these limitations. The presented new model contains descriptions of important diffusion terms, which satisfy this criterion. Calibration factors are absent, and because of their generality, applicability exceeds that of channel flow. Points for improvement of the new model are as follows:

(i)

The agreements between the new model and DNS are satisfactory but not perfect, due to the truncation of the expansion in powers of the inverse of the universal Kolmogorov constant that underpins the theoretical foundation of the model. Extending the expansion will reduce the truncation error significantly.

(ii)

What is missing is a general description of the turbulent dispersion of non-conservative scalars. Their impact is limited to the description of k and $ϵ$ in the interior part of the channel, or more generally, substantially away from walls where shear is imposed. The development of well-based descriptions for the diffusion of k and $ϵ$ will eliminate the remaining empiricism of the model.