Abstract
A new area of underwater equipment research focus is the use of underwater unmanned vehicles (UUVs) with launch mechanisms to deploy lightweight and small-sized robots for functions including communication, exploration, and detection. The internal ballistic mathematical model of the underwater launch system for small robots is established in this paper. The internal ballistic parameters and the robot displacement and velocity change rule over time are obtained. The optimization calculation of the crucial parameters to be determined by the particle swarm algorithm is completed. Following optimization, the gas cylinder’s initial pressure is 2 MPa, its capacity is 30 L, its opening area is 9.683 × 10−5 m2, and its opening time is 0.02 s. A numerical simulation is performed for the small robot’s underwater launch process, based on the mathematical and physical model supplied by Fluent 2020 software. The results yield the robot’s motion law and the properties of the flow field during the launch process. The purpose of the underwater launcher experiment is to determine the robot’s motion characteristics. The accuracy of the theoretical model is confirmed by comparing and analyzing the numerical simulation results with the actual data.
1. Introductions
Unmanned underwater vehicles (UUVs) have been an increasingly important area of attention for underwater equipment development globally because of their compact size, low weight, extended operating range, and affordable use [1,2]. UUVs with autonomous attack capabilities outperform current underwater combat gear and can be used with an existing underwater assault armament. The challenge of launching a small, light UUV to perform detection and communication duties has emerged as a barrier to the creation of novel UUVs [3], necessitating launcher optimization.
Using a multiphase VOF model and a conventional k-epsilon turbulence model, Liu, HJ et al. [4] examined the gravitational impact of launch velocity on the hydrodynamic properties of a vertically launched underwater vehicle using an air curtain. Numerical simulations were used to examine the link between the undersea vehicle’s form and launch velocity. Zhang, JH et al. [5] employed a visual experimental platform and a two-dimensional (2D) transient model to forecast the multiphase flow field during an underwater launch. Researchers studied how the flow field was affected by the muzzle velocity. The findings indicate that while the length of the pressure oscillations shortens, the highest peak pressure of the oscillations rises with increasing muzzle velocity. Gao, S. et al. [6] investigated the vortex structure and trajectory parameters of the wake of an underwater launch vehicle using an enhanced delayed separation vortex simulation, a VOF multiphase flow model, and an overlapping grid approach. A three-dimensional unsteady multiphase flow numerical model was established by Zhang, X. et al. [7] for the sealed firing of an underwater gun. The VOF multiphase flow model was chosen and integrated with the Schnerr–Sauer cavitation model. The flow field at the muzzle of a 30 mm underwater gun with two tubes fired in parallel was numerically calculated, and the results were compared with those of a single-tube firing. Li, WN et al. [8] created a two-way fluid–structure-linked numerical simulation technique to examine the launch tube’s flow properties and dynamic response. There has been additional discussion of the impact of launch depth and lateral flow. Three sample turbulence models—the Reynolds stress model (RSM), the large eddy simulation (LES) model, and the normalized group (RNG) k-epsilon model—were examined by Wang, YN et al. [9] in conjunction with VOF simulations. The volume of fluid (VOF) multiphase model was chosen to investigate bubble flow hydrodynamics in a top-submerged gunboat. In order to study the hydrodynamic characteristics and launch parameters during the whole launch process, Zhang, WQ et al. [10] created a computational fluid dynamics (CFD) model of the AUV launch tube system. The outcomes show how an underwater vehicle launch tube with a turbopump as the power input may operate with great efficiency. A platform for underwater air curtain firing simulation experiments has been built by Zhang, XW et al. [11], a mathematical–physical model of underwater air curtain launching was constructed, and the underwater artillery launching process was anticipated, based on the theory of gas jets in water and internal ballistics. Jayaprakash et al. [12] used a combination of experiments and CFD to study the evolution law of underwater bubble generation, expansion and contraction. For the study of launchers, Wei et al. [13] developed a scalable underwater launching system based on stress wave theory and split Hopkinson pressure rod technology, which can be used to study the cavitation phenomena and hydrodynamic properties of high-speed underwater objects.
As can be seen from the above, a majority of the study of underwater launching by academics has been on heavier weapons, including submarine-launched missiles and torpedoes, with very little research done on the process of micro-robotic underwater launching and associated launch systems. The majority of the present research includes the launch of missiles and torpedoes with dimensions typically between 500 and 2000 mm in diameter, 3500 and 13,000 mm in length, and 160 to 1500 kg in mass. This study’s item is 400 mm in length and 100 mm in diameter. In light of the variables influencing internal ballistic performance, this work will create an internal ballistic model of a tiny robotic launcher and optimize the launcher parameters using the particle swarm technique.
2. Materials and Methods
The mini-robot model is displayed in Figure 1 in order to create the ballistic model and optimize the launch parameters within the pneumatic mini-robot launcher. It is around 400 mm in length and 100 mm in diameter.
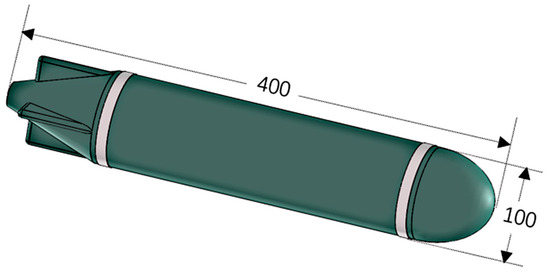
Figure 1.
Schematic diagram of the small robot model.
Figure 2 illustrates the components and workings of the pneumatic launcher. The launch tube has a length of 800 mm and a radial clearance of 1 mm between its inner diameter and the robot’s outer diameter. High-pressure gas from a gas cylinder is poured into the launch tube of the robot prior to launch. The launch command triggers the program-controlled launch valve, which opens progressively as soon as the robot is launched. Through the launch valve, compressed gas from the high-pressure gas cylinder enters the launch tube. The gas expands and works to create thrust, which propels the robot and allows it to exit the tube at a fast enough speed.
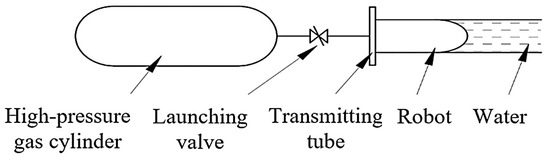
Figure 2.
Structure and principle diagram of the pneumatic launcher.
It is assumed that there is no heat exchange between the emission device and the outside world because the physical and chemical properties of the working medium change very little, meaning that the pressure-specific heat capacity is constant. As a result, the emission process can be simplified to an adiabatic process, ignoring the effects of gas leakage, gas viscosity, and the gas potential and kinetic energy.
2.1. Numerical Model Study
2.1.1. High-Pressure Gas Source Deflation Model
The high-pressure cylinder model, based on fundamental assumptions, is comparable to the adiabatic outgassing of a high-pressure cylinder at a constant capacity during the mini-robot’s launch. Assume that the high-pressure cylinder’s starting values are for the volume, for the pressure, for the temperature, and for the mass of the gas. Since it is believed that the entire launch process is adiabatic, , the launch valve is opened at that point. Since the high-pressure air bottle contains only the exhaust flux, there is no change in the flux entering, so , is the mass flow through the release valve [14]. Because the air bottle is in a fixed state, it does not work on the outside, so . In this case, the first law of thermodynamics can be written as:
The enthalpy of the gas in the instantaneous high-pressure cylinder is in the equation above. Equation (1) can be expressed for an ideal gas as
Rectification leads to the temperature differential equation:
Differentiating both sides of the equation of state for an ideal gas simultaneously to time yields:
Since the gas cylinder is in a constant volume state,, connected to (1), (3), (4), the differential equation of pressure change can be obtained:
2.1.2. Launch Valve Model
According to the gas dynamics theory, the flow rate at the valve port can be expressed as follows [15]:
where is the upstream pressure of the launch valve, is the density of the gas at the launch valve inlet, and is the downstream pressure of the launch valve.
The mass flow rate from the high-pressure gas cylinder through the launch valve can be written as [16]:
where is the flow coefficient of the launch valve, which can be taken as 0.6~0.65 according to the empirical value, is the instantaneous opening area of the launch valve, is the gas density at the exit section of the launch valve, and is the gas flow rate at the exit section of the launch valve.
Since the launching process is isentropic, the mass flows through the launching valve can be obtained from (6) and (7):
where represents the absolute temperature of the gas at the inlet of the launch valve.
According to the energy equation of an ideal gas adiabatic process, the critical pressure ratio can be obtained:
Bringing Equation (9) into (8), the mass flow rate of the sound velocity flow can be obtained as:
2.1.3. Launching Tube Model
The robot is propelled to move when the launch valve is opened, allowing high-pressure gas to enter the launch tube. The thermal process of the gas in the launch tube can be represented by the first law of thermodynamics in the following way, assuming that there is no heat exchange between the gas and the tube during the launch process:
where represents the internal energy of the gas in the launch tube of the launch process species, represents the internal energy of the gas in the launch tube before launch, represents the enthalpy of the gas flowing into the launch tube through the launch valve, W represents the work done to propel the robot motion and represents the work done to push the seawater between the launch tubes of the robot.
The temperature equation and pressure equation for the gas in the launch tube are:
where represents the mass of the gas in the launch tube; represents the instantaneous volume of gas in the launch tube.
The enthalpy equation of the gas entering the tube through the launch valve is
The rate of change of the gas mass in the launch tube is
The volume flow rate of seawater out of the annular gap between the robot and the wall of the launch tube is
where represents the flow coefficient of seawater through the annular gap; represents the annular clearance area between the launching tube and the robot; stands for seawater density; stands for seawater pressure at the launch tube port.
To propel the robot forward, the launch valve is opened, allowing gas to flow through it and into the launch tube. The launch tube’s gas volume is continuously growing, and the rate at which this volume changes is as follows:
where S represents the cross-section area of the robot; represents the motion speed of the robot.
2.1.4. Robot Motion Model in the Launch Tube
Five forces act on the mini-robot during the ejection process: the mini-robot’s own gravity, the thrust of the gas inside the launch tube, the resistance of the water to the mini-robot’s motion, the friction between the mini-robot and the launch tube, and the static pressure of the surrounding water environment. When the seawater flowing within the launch tube and the robot are examined collectively in accordance with Newton’s second rule, the robot’s equation of motion may be written as follows:
where represents the total mass of the robot and the seawater moving in the tube; represents the cross-sectional area of the inner diameter of the launching tube; represents the resistance of the robot; represents the resistance coefficient of the underwater movement of the robot; represents the friction coefficient between the robot and the launching tube; stands for the buoyancy force on the robot.
During the motion, the power of the work done by the gas thrust on the robot is
During the motion, the work done by extruding the seawater in the annular gap between the robot and the tube wall is
2.2. Optimization Design
2.2.1. Optimization Objective Determination
The performance of the ejection system is mainly determined by the cylinder’s initial pressure, volume, opening time, and opening area for a small robotic underwater launch system where the robot dimensions, the diameter of the launch cylinder, and the depth of the launch water are all essentially known. Consequently, the four aforementioned parameters have been selected for optimization.
2.2.2. Optimization Parameters’ Determination
The chosen range of the optimization parameters will have a greater influence on the optimization process. A selection range that is too short may restrict the local optimum and yield less than ideal outcomes. A selection range that is too big can readily create an excessive number of incorrect solutions, leading to a low optimization efficiency. The range of parameters that need to be optimized for this inquiry is shown in Table 1.

Table 1.
Value ranges of parameters to be optimized.
2.2.3. Objective Function Determination
To maximize the ballistic parameters in this research, the little robot has to escape the launch tube at a high exit velocity with the least amount of acceleration possible. As a result, the objective function is as follows:
where represents the robot’s moving speed; represents the correction coefficient, which is set to 0.1.
2.2.4. Optimization Process
The particles in the particle swarm algorithm are influenced by themselves and other particles in the population in the optimization process to complete the search for the optimal solution, and the specific steps can be carried out as follows:
- Initialize the particle swarm, and the parameters to be set are the learning factors and , the maximum evolutionary generation G and the current evolutionary generation g. Randomly generate size particles, the initial population position and motion speed; in the solution space, the population size is denoted by size, each particle is a solution in the space, the position of the i-th particle in the space is denoted by , and the velocity of the particle is denoted by . The individual extreme value of the i-th particle from the beginning to the current iteration search is denoted by , and the optimal solution of the whole population is denoted by bests;
- The initial position of each particle in the population is treated as an individual extreme value, and the fitness value of each particle is calculated according to the objective function, in which the current optimal position of the population is found;
- To prevent the particles from falling into a local optimum, the velocity and position of the particles are updated using the equation
The inertia weight , which is non-negative in the equation, is primarily responsible for modifying the query range of the solution space; for the two stochastic functions and , the range of values is [0,1], , , and the learning factor is and .
- 4.
- Compare the fitness value of the particle at this moment with the previous extreme value of the particle, and if is better than , replace with the current value as the new individual extreme value and update the position of the particle. Compare the fitness value of the particle at this moment with the optimal value bests of the population, and if is better than bests, then replace the current bests with the optimal value of the population to become the new fitness value and update the global optimal solution of the population;
- 5.
- To judge whether the algorithm satisfies the termination condition, if it does, it stops running and also outputs the optimal result; if it does not satisfy the termination condition, it takes and returns to step (3) to continue its iteration; the final termination condition of the algorithm is to reach the set maximum number of evolutionary generations or the result of the evaluation is lower than the set accuracy.
The computational flow of the particle swarm algorithm is shown in Figure 3.
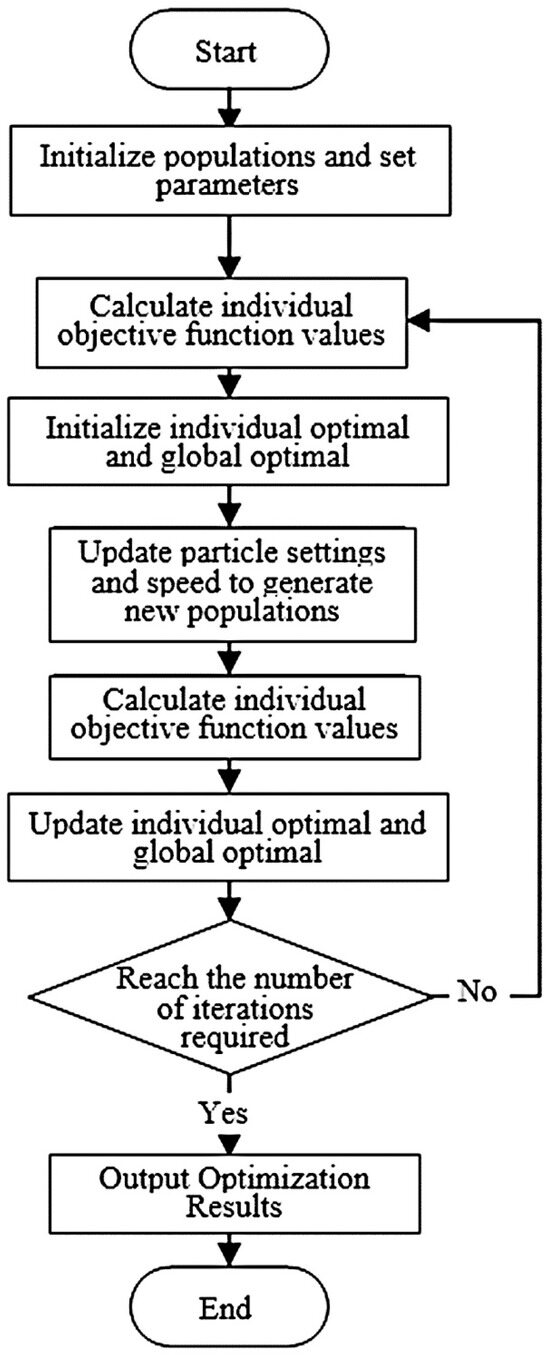
Figure 3.
Flow chart of particle swarm optimization.
2.3. Simulation and Experimentation
2.3.1. VOF Method
A two-dimensional axisymmetric internal ballistic model was developed in order to precisely ascertain the changes in the flow field and velocity of the tiny robotic underwater launcher during horizontal launching. The computational fluid dynamics (CFD) analysis software Fluent 2020 was utilized to simulate the robot’s exit from the cylinder. Due to the combined flow of high-pressure gas and water during the underwater launch process, there is a significant interaction between both phases, resulting in a strongly coupled nonlinear process. This work chooses the realizable turbulence model and the VOF multiphase flow model to represent the relative motion and development of the free interface between the gas and water phases, taking into account the flow characteristics in underwater launches. Furthermore, a six-degrees-of-freedom model and dynamic grid technology are used to characterize the different types of motion displayed by tiny robots.
The VOF approach tracks the interface in the simplified tiny robot underwater launch issue, which is a gas–liquid two-phase flow problem. The following is the governing volume fraction equation:
The VOF model tracks the interface between the gas–liquid phase by solving the continuous equation of the volume fraction of the liquid phase. Without considering the phase transition, there is no mass source term in the liquid phase, the right end of the equation is zero, and the calculation of the volume fraction should follow the following restrictions:
where is the gas phase volume fraction; is the liquid phase volume fraction.
The continuity equation is
Regarding the momentum equation, the VOF model computes a single momentum equation for the entire basin, the results of which are shared by the phases:
where is the density of the mixed phase; is the material parameter, and is obtained by the weighted average of the volume fraction ( can be , , etc.)
The energy equation is as follows:
where: E is the mass average energy of each phase; T is the mass average temperature of each phase, ( is E or T); is the mass average energy effective thermal conductivity of each phase (); is the turbulence thermal conductivity, defined by the turbulence model used.
The equation of state can be shown as
The VOF model allows only one phase to be defined as compressible: the gas phase as compressible, and the liquid phase as incompressible.
Regarding interpolation near the interface: By calculating the relative flow and diffusion flux of the flow over the control volume’s surface, the fluid software balances the source term of the control volume itself. In the VOF model, the surface flow may be computed using four different methods: geometric reconstruction, material acceptance, the Euler explicit, and the Euler implicit. The first two approaches employ distinct techniques to address the interpolation problem of elements surrounding various intersecting interfaces, whereas the remaining two approaches handle the same interpolation method for single-phase or polyphase elements, i.e., by utilizing the conventional first-order upwind, second-order upwind, or QUICK format. The most precise geo-metric reconstruction technique, appropriate for any unstructured mesh, is used in this research.
Regarding surface tension and avoid adhesion: The interphase surface tension may be reproduced when utilizing the VOF model to simulate multiphase flow problems by adjusting the contact angle that the fluid and the wall generate. It is caused by the surface-only gravitational force between the fluid microclusters, which reduces free energy by shrinking the interface’s area. The source term in the momentum equation of the continuum surface force (CSF) model is produced by the extra surface tension encountered during the VOF model’s simulation. This equation is as follows:
where: is the surface curvature.
The effect of surface tension is determined by Reynolds number and capillary number or Weber number . The use of the capillary number and the Weber number depends on the size of the Reynolds number, when , the capillary number needs to be used, and vice versa. The two are defined as follows:
where U is the free flow speed, when or , the surface tension can be ignored.
The VOF model is limited by the boundary condition of the wall itself, and the normal direction of the unit near the wall can be adjusted by setting the proper contact angle of the wall, so as to reduce the boundary limit. The surface normal of the actual element near the wall is:
where: is the wall contact angle; is the unit normal vector of the wall surface; is the unit tangent vector of the wall.
2.3.2. Turbulence Model
There is a lot of turbulent flow when a little robot is being launched underwater out of the tube. Currently, direct numerical simulation (DNS), large eddy simulation (LES), and Reynolds time mean numerical simulation (RANS) are the three most widely utilized numerical simulation techniques for turbulence.
By referring to the relevant literature in the field of underwater launching and combining with previous calculation experience, this paper adopts the realizable model of the vortex viscosity model in the RANS method for numerical calculation. The two transport equations that constitute the realizable model are as follows:
where: is the turbulence’s kinetic energy generated by the laminar flow velocity gradient; is the turbulence’s kinetic energy caused by buoyancy; is the fluctuation caused by turbulent pulsation; is the turbulent Prandtl number of the equation; is the turbulent Prandtl number of the equation; and are the source items.
, , and usually , , , and .
The turbulent viscosity is expressed as follows:
In the formula, , , , , and , .
2.3.3. Dynamic Grid Technology
In this research, we examine a tiny robot’s underwater launch procedure. For the purpose of computation, a simple static grid technique is not appropriate since the grid form in the model calculation domain varies as the robot moves. We can opt to employ the moving grid approach to solve this type of flow problem since the geometry of the grid in the computational domain varies as the boundary moves. In order to use the dynamic grid model, we must first define the moving boundary’s motion mode and the grid area that it is connected to. The boundary function and UDF are included in the definition of the boundary’s motion mode. The motion mode of the boundary is determined by the Fluent program based on the robot’s motion law in the flow field and the size of the selected time step; therefore, the model used in this work does not need to specify it beforehand. Based on the computation, Fluent anticipates where the motion boundary will be at the next instant and checks to see if the grid height barrier has been met. The mesh close to the moving border is either merged or divided based on the decision conditions.
For dynamic mesh models, Fluent offers three mesh-updating techniques: local remeshing, dynamic layering, and spring-based smoothing. Only the axial motion of the robot—which can be thought of as the impact of the grid boundary change on the flow field of the multiphase flow—is taken into account for the modeling of the unsteady flow field of the tiny robot in the underwater extraction process covered in this work. Thus, in order to achieve the robot movement, the dynamic stratification approach and the local reconstruction method are used.
Regarding the dynamic stratification method: The dynamic layering method is used to merge or split the grid layers according to the change in the height of the grid layers near the moving boundary. The relationship between stretching and compression is as follows:
where: is the height of the ideal mesh cell; is the splitting factor; is the merge factor.
Regarding the local reconstruction method: The fairing approach may be used to update unstructured mesh. The fairing approach may lower the mesh quality and cause a negative volume and simulation error termination if the moving boundary advances too far during the mesh updating procedure. A mesh reconstruction method is created to increase the dynamic mesh’s application span. When the dynamic mesh’s moving border extends beyond a certain point, causing significant distortion to the mesh, Fluent 2020 software will regenerate both the highly deformed and the surrounding mesh. The freshly produced mesh will be utilized if the regenerated mesh can satisfy the calculation’s quality and size criteria. The freshly created grid is abandoned if it does not match the specifications.
2.3.4. Multiphase Flow Field Modeling
The model has to be suitably streamlined in order to account for the computation time while still guaranteeing calculation accuracy. Figure 4 depicts the simplified calculation model.
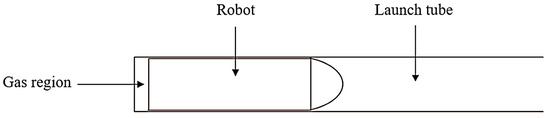
Figure 4.
Simplified calculation model.
The independence of the meshes must be investigated to eliminate the meshes’ impact on the simulation results and minimize the mistakes brought about by meshes in numerical simulations. Three grid numbers—Grid A (270,000), Grid B (390,000), and Grid C (550,000)—have their respective outcomes chosen for comparative study in this work. The findings displayed in Figure 5a,b are the consequence of choosing the first three outcomes for simulation till convergence and post-processing analysis. The data demonstrate the significant discrepancy of around 8% between the computed outcomes of Grid A and Grid B. Between Grid B and Grid C, the highest error is negligible—it is not greater than 3%. Grid B can be used in the final numerical computation to increase the calculation speed and produce numerical results that are precise enough.
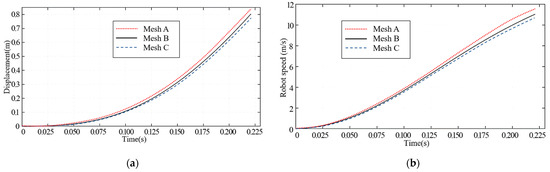
Figure 5.
Grid independence verification. (a) Displacement–time curves for the different meshes; (b) Velocity–time curves for the meshes.
Both the robot and the launch tube exhibit symmetry, as shown by the simplified computational model in Figure 4. A two-dimensional axisymmetric model may be utilized to decrease the amount of computation and increase computational efficiency. The simulation in this study disregards gravity, and the robot’s head, tail, and the launch tube wall are all set as wall boundaries, with the walls being adopted as adiabatic and non-slip walls; the external boundary of the launch tube and the boundary of the water area are all set as pressure outlets; the head and tail of the robot are designated as the motion limits, and the software’s 6DOF model is used to determine the robot’s axis’ direction. Since this study uses the sub-regional grid division approach, in order to achieve data exchange between the nodes, the boundaries of the moving and stationary waters must be specified as interface pairs. Figure 6 illustrates the specific boundary conditions that are specified.
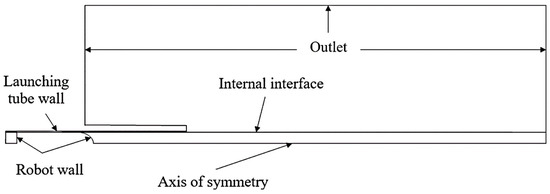
Figure 6.
Boundary condition setting.
2.3.5. Experimental System
A robot, a gas supply system, a launch support system, a valve control system, and a high-speed camera image capture system make up the robotic underwater ejection experiment system. Figure 7 displays the schematic diagram of the launch’s experimental setup.
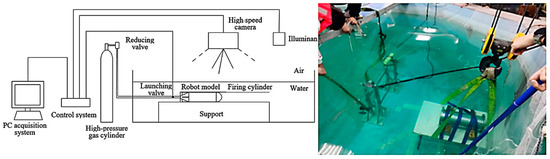
Figure 7.
Schematic layout of the launcher experiment.
3. Results and Discussion
3.1. Optimization Results and Analysis
Numerical solution software is used to program the particle swarm method’s mathematical model and the goal function. In order to determine the ideal settings for the robot ejection mechanism, the particle swarm method is applied, setting the primary parameters of the algorithm. Examples include the particle population size N, the inertia weight w, the maximum velocity vmax, learning factors c1 and c2, and the maximum number of evolutionary generations G. While N often is a number between 20 and 100, this study uses N = 50. The inertia weight w in the particle swarm algorithm primarily regulates the algorithm’s development and exploration; its value’s magnitude signifies the extent to which the speed of the preceding particle generation influenced the current speed; thus, the inertia weight’s magnitude should be selected judiciously. The method may enter a local optimum during runtime if the numbers are irrational, which would impair the search function. This study uses w = 0.8 as the inertia weight. The method’s search capabilities may be impacted if the value is not acceptable and causes the algorithm to run into a local optimum. The particle’s step duration is primarily restricted to an individual optimum search by the learning factor c1, and to a global optimal search by the learning factor c2, both of which typically take values between 0 and 4. In this investigation, c1 = c2 = 2 is used. The value of the particle’s moving velocity spans between -vmax and vmax, and the maximum velocity vmax = 0.2 is used in this study. vmax shows the maximum velocity of the particles in the population traveling in space. The program is said to finish after a certain number of iterations, denoted by the maximum number of iterations G, and the optimal answer in the final computation result is produced. The particle swarm optimization algorithm’s maximum evolutionary algebra, G = 500, is chosen for this work. Table 2 displays the optimum parameters that were determined by applying the particle swarm technique.

Table 2.
Parameter values after optimization.
The robot ejection system’s mathematical model of ballistic trajectory is fitted with the parameters optimized by the particle swarm algorithm, as illustrated in Figure 8. The optimized initial pressure of the gas cylinder is altered from the initial assumption of 2.5 MPa to 2 MPa, and the cylinder’s residual pressures at the conclusion of the launch are 2.36 MPa and 1.80 MPa, respectively. Following optimization, the launch time is down to 0.2 s, which is a little faster than the pre-optimization of 0.202 s. The pre-optimization of 0.202 s is somewhat longer than the launching time of 0.2 s, which is also significantly shorter. The launch time is 0.2 s after optimization, which is somewhat less than the 0.202 s before optimization. Simultaneously, the pressure change curve of the cylinder experiences a numerical decline sooner than before the optimization due to the launch valve’s opening time being 0.02 s after optimization. Due to the shortened launch valve opening time, the optimized launch cylinder chamber pressure curve is higher than the pre-optimization one in the early stage and reaches the peak value more quickly. The peak launch tube chamber pressure after optimization has a slight decrease, with the peak value changing from 0.5 MPa to 0.48 MPa, the decrease being 4%. Because of the launch valve’s quicker opening after optimization, the optimized robot starts up earlier than the pre-optimized robot did. The improved robot’s exit velocity marginally drops from 12.33 m/s before optimization to 12 m/s as a result of the gas cylinder’s starting pressure being reduced, and its internal ballistic performance improves when compared to the pre-optimization.
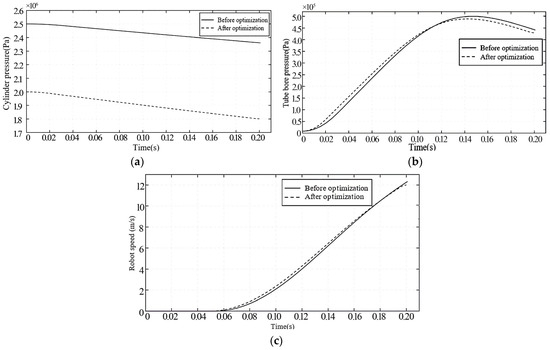
Figure 8.
Simulation curve. (a) Pressure curve of high pressure cylinder with time; (b) Pressure curve of firing tube chamber with time; (c) Robot velocity curve with time.
3.2. Simulation Analysis
3.2.1. Flow Field Characteristic Analysis
The gas–water phase diagram of the robot exit tube section is shown in Figure 9, and the flow field parameters for the robot’s underwater horizontal launch were obtained using numerical simulation.
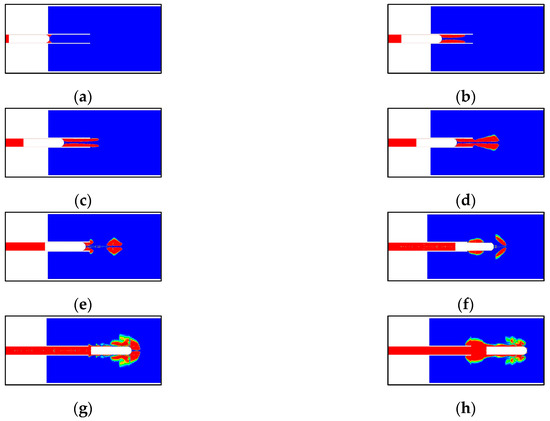
Figure 9.
Phase diagram of the robot-piping process. (a) Pre-launch period; (b) Pre-launch period; (c) Pre-launch period; (d) Mid-launch period; (e) Mid-launch period; (f) Mid-launch period; (g) Post-launch period; (h) Post-launch period.
As the robot emerges from the tube underwater, the sealing ring at its tail limits the flow of high-pressure gas at the rear of the launch tube. In order to accomplish its task, the high-pressure gas expands, applying a propulsive force to the robot and forcing it to exit the tube. The high-pressure gas at the bottom flows out of the gap between the robot and the launch tube before the robot does because of the gap, and because the high-pressure gas is moving faster than the robot, it exits the launch tube before the robot does, creating the gas jet phenomenon at the mouth of the launch tube barrel. As seen in Figure 9, from (a) to (c), the jets are expelled in two distinct gas stream forms rather than being collected together as would be expected for a three-dimensional structure, which would be ejected in the shape of a ring. The annular jet that first emerges from the launch tube progressively separates from the rear gas as time goes on due to the combined effects of the robot’s motion and the external water pressure. The robot squeezes the gas passing through the gap just before it leaves the tube, creating vortices to the sides and back of the launch tube mouth, as shown in Figure 9d–f. The gas mass has symmetry since the simulation is predicated based on the robot being in an environment with a uniform flow field. As seen in Figure 9g,h, when the robot emerges fully from the tube, high-pressure gas pours out of the tube, causing the gas mass to rapidly expand and be stretched by the robot. The gas mass also wraps around the robot together to the front during the robot’s escape from the tube.
3.2.2. Internal Ballistic Characteristics Analysis
The software was used to organize and analyze the two-dimensional axisymmetric numerical simulation data of the robot’s underwater launch. The values of the robot’s motion displacement and velocity at each moment were then derived using UDF, and the aforementioned values were plotted against time.
It is evident from the robot displacement graphs in Figure 10 that the robot’s displacement with respect to time is roughly quadratic. The robot’s displacement increases more slowly in the beginning and faster in the later stages. This is because the robot moves more slowly in the first stage and faster in the later stages, which causes the displacement to increase more largely. It takes the robot 0.22 s to exit the launch tube. When the robot initially starts moving, its velocity is almost linear. After an acceleration duration of 0.22 s, the robot may emerge from the tube at 11 m/s. The robot may smoothly leave the tube under these operating conditions since the velocity value is somewhat less than that found by solving the internal ballistic equation but still larger than the design velocity.
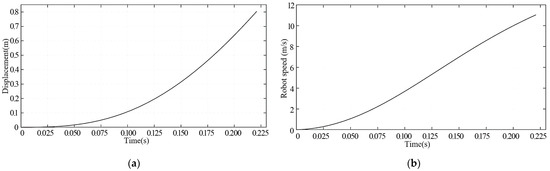
Figure 10.
Simulation curve. (a) Robot displacement curve; (b) Robot velocity curve.
3.3. Experimental Analysis
3.3.1. Multi-Phase Flow Field Characterization Analysis
This experiment primarily aims to investigate the properties of the robot after it emerges from the tube during the horizontal launch process. Two robots are launched for the test, and each robot is subjected to a different gas source pressure. The high-speed camera used in this experiment is the VE0710L. The full frame is 1280 × 800 pixels with 1500 frames. Figure 11 shows the flow field change characteristics of the robot’s out-of-the-tube process taken by the high-speed camera. The pressure of the cylinder outlet is set to 2 MPa by utilizing the pressure reducer.

Figure 11.
Phase diagram of the robot-piping process. (a) Pre-launch period; (b) Pre-launch period; (c) Pre-launch period; (d) Mid-launch period; (e) Mid-launch period; (f) Mid-launch period; (g) Mid-launch period; (h) Post-launch period; (i) Post-launch period; (j) Post-launch period.
When the launch valve is opened, high-pressure gas from the cylinder enters the launch tube through the gas tube and propels the robot into the water. At the start of the launch, as shown in Figure 11, from (a) to (c), the robot and the water in front of its head work together to push forward in the wake of the gas. Figure 11d,e show how the gas exits the launch tube before the robot and forms bubbles at the barrel’s mouth location. Because there is not much jet flow at this time, the bubbles are mostly small and their morphology is changing very little; the early bubbles are primarily axial in development; as time goes on, the rear gas continues to flow out, and the bubbles start to develop radially due to the influence of buoyancy and the blocking effect of the water. The robot’s initial seal ring movement out of the launch tube is shown in Figure 11e,f, where the number of bubbles greatly increased and a portion of the bubbles moved with the robot ahead; the robot’s second seal ring movement is shown in Figure 11g–j. The robot’s second seal ring moves out of the launch tube, causing a massive amount of gas to shoot out in the form of a cylindrical jet. The bubbles continue to expand and increase in volume, and the buoyancy force causes the bubbles’ position to rise. At the same time, the water flow disturbs the bubbles and deflects them. The robot’s forward speed causes the bubble to constantly elongate, drastically alter its shape, and cause the phenomena known as neck shrinkage. It is also evident in Figure 11j that when the launch valve is closed and the gas in the launch tube exits, a tiny quantity of water rushes backward into the launch tube.
3.3.2. Robot Motion Characteristic Analysis
The high-resolution picture acquisition system’s data is processed by numerical computation software to ascertain the hydrodynamic characteristics of the robot’s horizontal launch.
Figure 12 shows that when the launch valve is opened, the robot initially stays motionless. After that, its velocity progressively increases from 0 to a peak that is reached when it exits the launch tube. In the first phase, the pressure within the launch tube is low, and the velocity grows more slowly. In the second phase, the pressure inside the launch tube is steady, and the velocity increases almost linearly, peaking at 7.3 m/s in 0.305 s. The robot displacement is parabolic when the launch valve is opened; it first stays constant, increases gradually, and then steadily increases after a certain amount of time. This is due to the launch tube’s initially low and unstable pressure, which causes the robot to move as soon as it overcomes its resistance and accelerate as the pressure inside the tube rises.
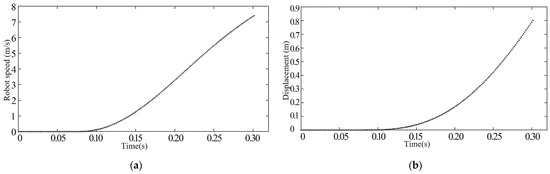
Figure 12.
Experimental curve. (a) Robot speed-time graph; (b) Robot displacement-time graph.
3.4. Comparative Analysis of Numerical Simulation Results and Experimental Results
The underwater horizontal robot launching process is numerically simulated and compared to the experimental launching procedure. While the actual annular bubbles occur together with some tiny bubbles, the numerical simulation displays the appearance of annular bubbles sooner than the experiment and with a consistent form. The annular bubbles all separate from the back gas when the robot head is ready to depart the tube; however, the axial movement of the annular bubbles predicted by the numerical simulation is significantly more than that of the actual data, and the bubble scale is bigger. The high-pressure gas inside the tube all forms a columnar jet at the tube’s mouth after the robot’s tail exits it. Bubbles form in both axial and radial directions, and the gas cloud expands and necks. However, the radial scale of the gas cloud that forms during the experimental process is larger than the results of the numerical simulation.
The underwater horizontal launch of the robot out of the tube procedure was compared in terms of its hydrodynamic properties. The results are compared as shown in Figure 13. When the launch valve is opened, it takes some time to build up the launch tube’s chamber pressure. The robot begins to move when the chamber pressure inside the tube is greater than its resistance. These are the hydrodynamic characteristics of the robot during the underwater horizontal launch out of the tube. There are some discrepancies between the two hydrodynamic data because the experimental launch procedure is more complicated than the numerical simulation, which is configured for perfect launch circumstances.
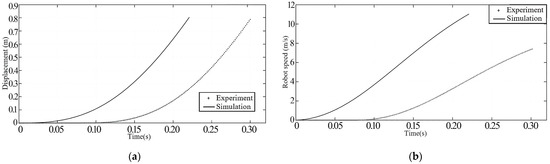
Figure 13.
Comparative curves. (a) Comparison of displacement between experimental and numerical simulation; (b) Comparison of experimental and numerical simulation speeds.
The displacement–time and velocity–time change laws of the numerical simulation results and the experimental findings are essentially the same, as can be inferred from Figure 13. The primary variations between the two are the robot’s speed as it exits the tube and the duration of time that each uses. The robot emerges from the launching tube in 0.305 s in the experiment, but it takes 0.22 s in the simulation—a 39% mistake. Moreover, the robot’s exit velocity from the tube is 7.3 m/s in the experiment, but it exits the tube at 11 m/s in the simulation—a 34% inaccuracy. The high-pressure gas in the robot’s tail in the simulation can fully act on the robotic tail, despite the fact that the simulation model and the actual model have the same cross-sectional area and a flat tail, respectively. However, the real model experiences a phenomenon known as partial push compensation, which causes the numerical simulation emission pipe to rise more quickly, resulting in a robot that operates in less time and at a higher output speed.
4. Conclusions
This paper optimizes the cylinder pressure, cylinder volume, launch valve opening area, and launch valve opening time using the particle swarm approach. Establishing a complex two-phase flow field computational model of a small robot’s underwater horizontal launch-out-of-the-tube process, setting up an underwater launch experiment system, and conducting underwater launch experiments are all accomplished with the use of Fluent 2020 software, which is based on the VOF model, realizable turbulence model, and dynamic mesh technology. This research can serve as a guide for the development of underwater launching systems for these robots, enabling the more accurate and convenient performance of tasks including detection, exploration, and communication underwater by small, lightweight robots.
- Following optimization, the gas cylinder’s initial pressure is 2 MPa, its capacity is 30 L, its opening area is 9.683, its opening time is 0.02 s, and its opening time is 0.02 s. Following optimization, there is a modest reduction in the launching time, a peak pressure decrease in the launching tube rifling, and a slight decrease in the robot’s exit velocity from the tube.
- The analysis of the evolution of bubble expansion and contraction at the cylinder’s mouth during the robot-launching process yielded the following results: the robot moved out of the launching tube in 0.22 s, and its top speed was 11 m/s. These results confirmed the viability of the optimized launching device.
- The robot’s underwater launching bubbles’ evolution process is identified. The robot needs 0.305 s to travel out of the launching tube, and its exit velocity from the tube may reach 7.3 m/s. The robot’s launch time results in an error of 39%, and the tube’s exit velocity results in an error of 34%, according to a comparison and analysis of the simulation and experimental data. This is because the experimental model’s tail is conical and has a tail, but the simulation model’s tail is flat. There is a situation in the real model where certain thrusts cancel each other out.
Author Contributions
Conceptualization, H.G. and Z.P.; methodology, F.M.; software, F.M.; validation, H.G. and S.H.; formal analysis, Z.P.; investigation, H.G.; resources, S.H.; data curation, F.M.; writing—original draft preparation, H.G. and Z.P.; writing—review and editing, F.M. and S.H.; visualization, Z.P.; supervision, S.H.; project administration, F.M.; funding acquisition, H.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key R&D Program of Shandong Province of China, grant number 2021JMR0302, and the National Natural Science Foundation of China, grant number 5207110396.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The authors gratefully acknowledge the financial support from the Key R&D Program of Shandong Province of China, and the National Natural Science Foundation of China.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| The volume of high-pressure cylinders | |
| The pressure of the gas in a high-pressure cylinder | |
| Temperature | |
| Quality of gas in high-pressure cylinders | |
| Q | Heat |
| Work | |
| Energy input | |
| Energy output | |
| The enthalpy value of the gas in a transient high-pressure cylinder | |
| The specific heat capacity at a constant volume | |
| The specific heat capacity at a constant pressure | |
| t | Time |
| Specific heat capacity ratio | |
| R | Universal constant |
| Upstream pressure of the launch valve | |
| Density of gas at the inlet of the launch valve | |
| Downstream pressure of the launch valve | |
| Flow coefficient of the launch valve | |
| Instantaneous opening area of the launch valve | |
| Gas density at the exit section of the launch valve | |
| Gas flow rate at the exit section of the launch valve | |
| Critical pressure ratio | |
| The internal energy of the gas in the tube during emission | |
| The internal energy of the gas in the tube before launch | |
| The enthalpy of the gas flowing through the launch valve into the launch tube | |
| The work done to move the robot | |
| The work that pushes the water between the robot’s launch tubes | |
| The mass of the gas in the tube | |
| The instantaneous gas volume in the launch tube | |
| The flow coefficient of seawater through an annular gap | |
| Area of annular clearance between the launch tube and the robot | |
| Seawater density | |
| Seawater pressure at the launch tube’s mouth | |
| S | The cross-sectional area of the robot |
| The speed of the robot | |
| The robot and the total mass of the moving seawater in the tube | |
| Tube diameter of a cross-sectional area | |
| The resistance of the robot | |
| The resistance coefficient of the robot’s underwater movement | |
| The friction coefficient between the robot and the launching tube | |
| The buoyancy of the robot | |
| Correction factor | |
| Gas phase’s volume fraction | |
| Liquid phase’s volume fraction | |
| Density of the mixed phase | |
| Material parameter | |
| The mass average energy of each phase | |
| T | Mass mean temperature of each phase |
| Mass average energy effective thermal conductivity of each phase’s conductivity | |
| Turbulent heat conductivity | |
| Surface curvature | |
| Free flow velocity | |
| Wall contact angle | |
| Unit normal vector of the wall | |
| Unit tangent vector of the wall | |
| Turbulent kinetic energy | |
| Turbulent energy dissipation rate | |
| Turbulent kinetic energy generated by the laminar velocity gradient | |
| Turbulent kinetic energy caused by buoyancy | |
| Turbulence caused by pulsation | |
| Equation turbulence Prandtl number | |
| Equation turbulence Prandtl number | |
| , | Source item |
| Turbulent viscosity | |
| Ideal height of grid cells | |
| Fission factor | |
| Merge factor |
References
- Chen, Y.L.; Wang, J.T.; Zhu, S.T.; Gu, Y.; Dai, H.Y.; Xu, J.Y.; Zhu, Y.P.; Wu, T.X. Knowledge Graph Construction for Foreign Military Unmanned Systems. In Proceedings of the 7th China Conference on Knowledge Graph and Semantic Computing (CCKS), Qinhuangdao, China, 24–27 August 2022; pp. 127–137. [Google Scholar]
- He, Y.; Wang, D.B.; Ali, Z.A. A review of different designs and control models of remotely operated underwater vehicle. Meas. Control 2020, 53, 1561–1570. [Google Scholar] [CrossRef]
- Huang, M.; Jiang, Y.; Wang, B. Research on Interior Ballistic of a Gas Multi-stage Cylinder Ejection. MATEC Web Conf. 2018, 179, 03005. [Google Scholar] [CrossRef][Green Version]
- Liu, H.J.; Peng, X.Z.; Zou, Z.Z. Effects of the launch speed on hydrodynamic force of the underwater vehicle vertical launch with the gas curtain. In Proceedings of the International Conference on Mechanics, Dynamic Systems and Materials Engineering (MDSME 2012), Guangzhou, China, 24–25 November 2012; pp. 84–87. [Google Scholar]
- Zhang, J.H.; Yu, Y.G.; Zhang, X.W. Numerical investigation on the multiphase flow field at various muzzle velocities. J. Mech. Sci. Technol. 2022, 36, 4021–4032. [Google Scholar] [CrossRef]
- Gao, S.; Shi, Y.; Pan, G.; Quan, X.B.; Yu, Y.L. An investigation on the wake vortex structure and trajectory characteristics of the vehicle launched underwater. Ships Offshore Struct. 2023. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, Y.G.; Zhang, X.W. Research on multiphase flow field characteristics of underwater gun double-tube parallel firing. Propellants Explos. Pyrotech. 2023, 48, e202300068. [Google Scholar] [CrossRef]
- Li, W.N.; Zhang, Z.Y.; Lu, J.X.; Li, Z.S.; Wang, C. Investigations on the flow characteristics and the structural response of the launch tube during the underwater launching process. Ocean. Eng. 2023, 279, 114603. [Google Scholar] [CrossRef]
- Wang, Y.N.; Vanierschot, M.; Cao, L.L.; Cheng, Z.F.; Blanpain, B.; Guo, M.X. Hydrodynamics study of bubbly flow in a top-submerged lance vessel. Chem. Eng. Sci. 2018, 192, 1091–1104. [Google Scholar] [CrossRef]
- Zhang, W.Q.; Jia, G.T.; Wu, P.; Yang, S.; Huang, B.; Wu, D.Z. Study on hydrodynamic characteristics of AUV launch process from a launch tube. Ocean. Eng. 2021, 232, 109171. [Google Scholar] [CrossRef]
- Zhang, X.W.; Yu, Y.G.; Zhou, L.L. Numerical study on the multiphase flow characteristics of gas curtain launch for underwater gun. Int. J. Heat Mass Transf. 2019, 134, 250–261. [Google Scholar] [CrossRef]
- Jayaprakash, A.; Singh, S.; Chahine, G. Experimental and Numerical Investigation of Single Bubble Dynamics in a Two-Phase Bubbly Medium. J. Fluids Eng.-Trans. ASME 2011, 133, 121305. [Google Scholar] [CrossRef]
- Wei, Y.P.; Wang, Y.W.; Fang, X.; Huang, C.G.; Duan, Z.P. A Scaled Underwater Launch System Accomplished by Stress Wave Propagation Technique. Chin. Phys. Lett. 2011, 28, 024601. [Google Scholar] [CrossRef][Green Version]
- Lu, H.T.; Li, W.B.; Cui, B. The Performance of Pneumatic Gun Launching Spherical Projectile. In Proceedings of the 32nd International Symposium on Ballistics, Reno, NV, USA, 8–13 May 2022. [Google Scholar]
- Yuan, R.B.; Sun, C.G.; Lee, Q.; Yang, H.F. Dynamic Simulation of Position Servo System of Pneumatic Manipulator Based on AMESim and Simulink. In Proceedings of the International Conference on Manufacturing Science and Engineering (ICMSE 2009), Zhuhai, China, 26–28 December 2009; pp. 2580–2584. [Google Scholar]
- Bing, T. Optimization of Structure Parameters for Hydraulic Energy Accumulated Torpedo Launching Device. Mater. Sci. Forum 2011, 704–705, 612–618. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).