Harnessing Deep Convolutional Neural Networks Detecting Synthetic Cannabinoids: A Hybrid Learning Strategy for Handling Class Imbalances in Limited Datasets
Abstract
:1. Introduction
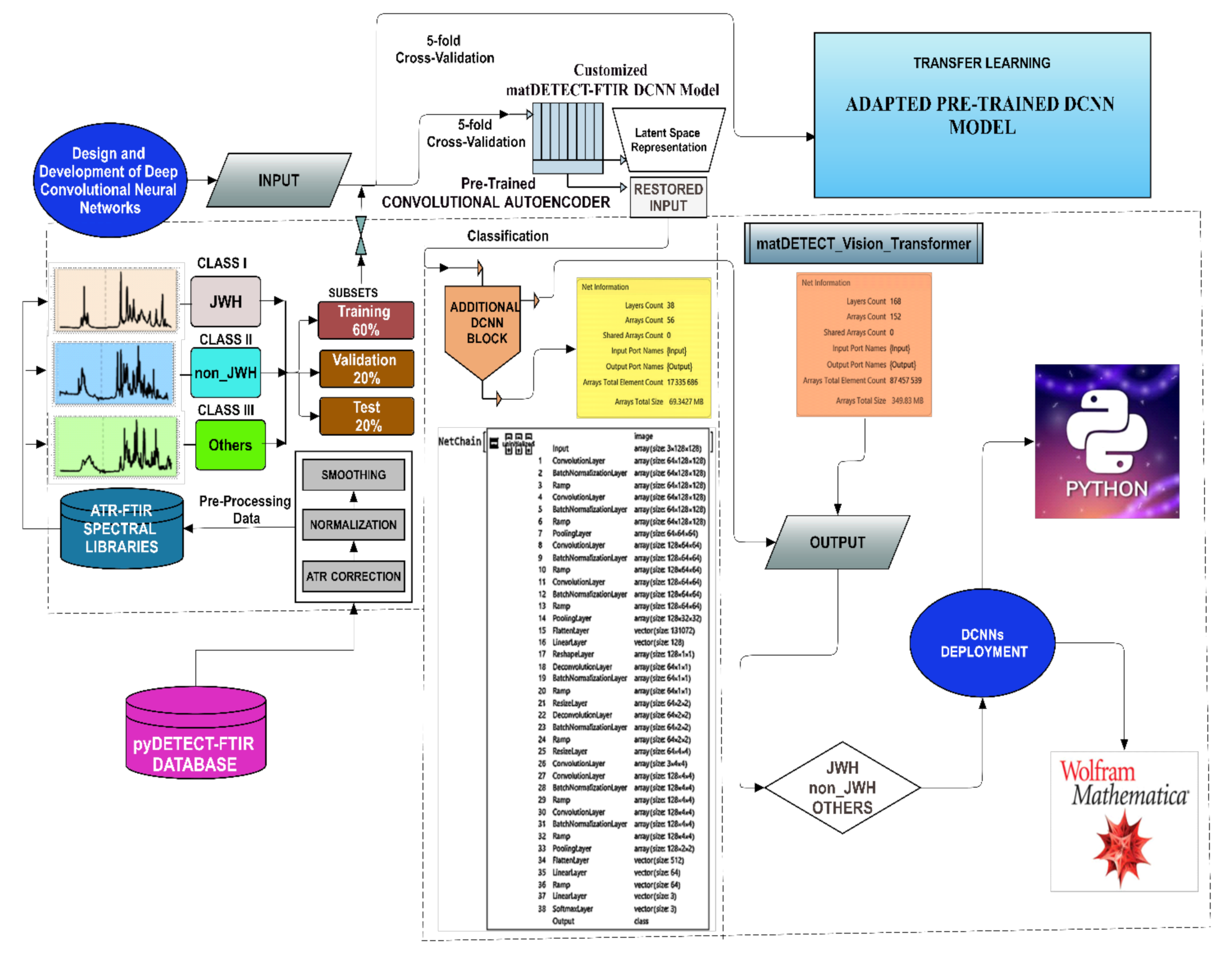
2. Materials and Methods
2.1. Related Work
2.2. Computational Platform
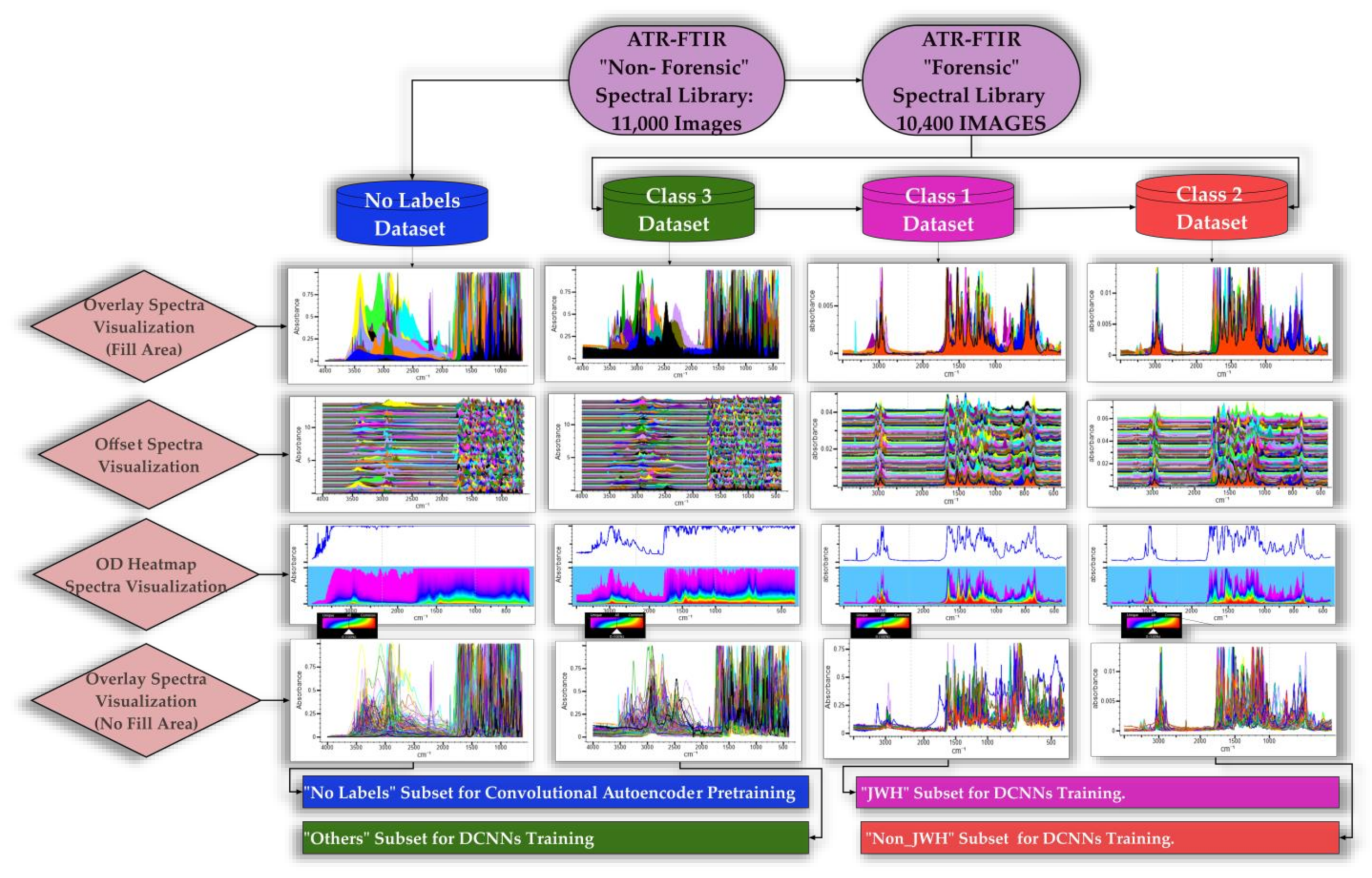
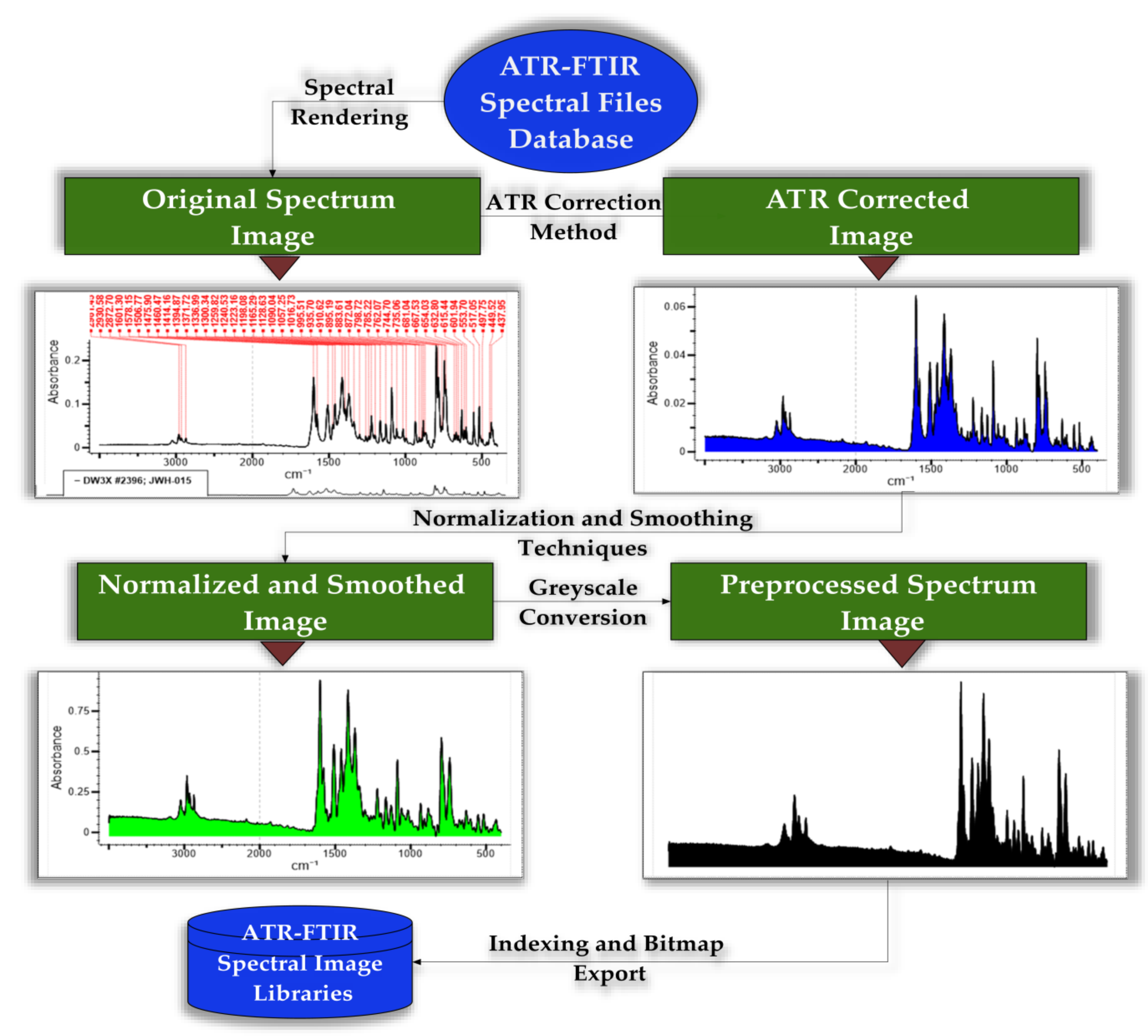
2.3. The Spectral Database
- Class 1 comprises 125 images of JWH synthetic cannabinoids (which were first synthesized by Dr. John W. Huffman), falling into 11 structural subclasses such as Naphthoylindoles (e.g., JWH-018, JWH-073); Alkylated Naphthoylindoles (e.g., JWH-122 8-Methylnaphthyl isomer, JWH-018 2’-Naphthyl isomer); Cyclohexylphenols (e.g., JWH-015, JWH-133); Fluorinated Naphthoylindoles (e.g., FUB-JWH-018, JWH-210 N-[5-Fluoropentyl] analog); Hydroxylated Naphthoylindoles (e.g., JWH-018-4, JWH-019 N-[6-Hydroxyhexyl] metabolite); Chlorinated Naphthoylindoles (e.g., JWH-398 6-Chloronaphthyl isomer, JWH-398 2-Chloronaphthyl isomer); Benzoylindoles (e.g., JWH-302, JWH-307); Phenylacetylindoles (e.g., JWH-250, JWH-251); Naphthylmethylindenes (e.g., JWH-081, JWH-210); Adamantoylindoles (e.g., JWH-018 Adamantyl analog, JWH-018 Adamantyl carboxamide); and Naphthoylpyrroles (e.g., JWH-147, JWH-370).
- Class 2 houses 250 images of non-JWH synthetic cannabinoids, covering several distinct groups such as Classical Cannabinoids (e.g., HU-210, synthesized by Dr. Raphael Mechoulam and his colleagues from Hebrew University, Tetrahydrocannabinol, Cannabidiol, Cannabinol, Cannabichromene, Cannabigerol); Hybrid Cannabinoids (e.g., AM 251 developed by Alexandros Makriyannis at Northeastern University, URB-447 from the University of Rome “La Sapienza Biomedical”); Aminoalkylindoles (e.g., WIN 55,212-2, RCS-8, CHMINACA, Cumyl-PICA, APINACA); Aminoalkylindazoles (e.g., AB-FUBINACA, AB-PINACA), etc.
- Class 3 encompasses a broad spectrum of other designer drugs, totaling 10,050 images. This third heterogeneous class, substantial in its diversity, not only broadens the classification spectrum but also enhances the comparative dimension of the machine learning process. These originate mainly from categories such as psychedelics, piperazines, dissociatives, empathogens, stimulants, sedatives, abused prescription medications, and other drugs of similar importance (e.g., Lysergic Acid Alpha-Hydroxy-Ethylamide, α-Ethyltryptamine, Scaline, 25B-NBOMe, 25C-NBOH, Fentanyl-Furanyl, Testosterone, Flubromazepam, Cocaine, Diazepam, Heroin, Morphine, Scopolamine, Strychnine, Pheniramine, etc.).
- Duplicating Existing Samples: involves replicating some of the minority class instances to balance the class distribution;
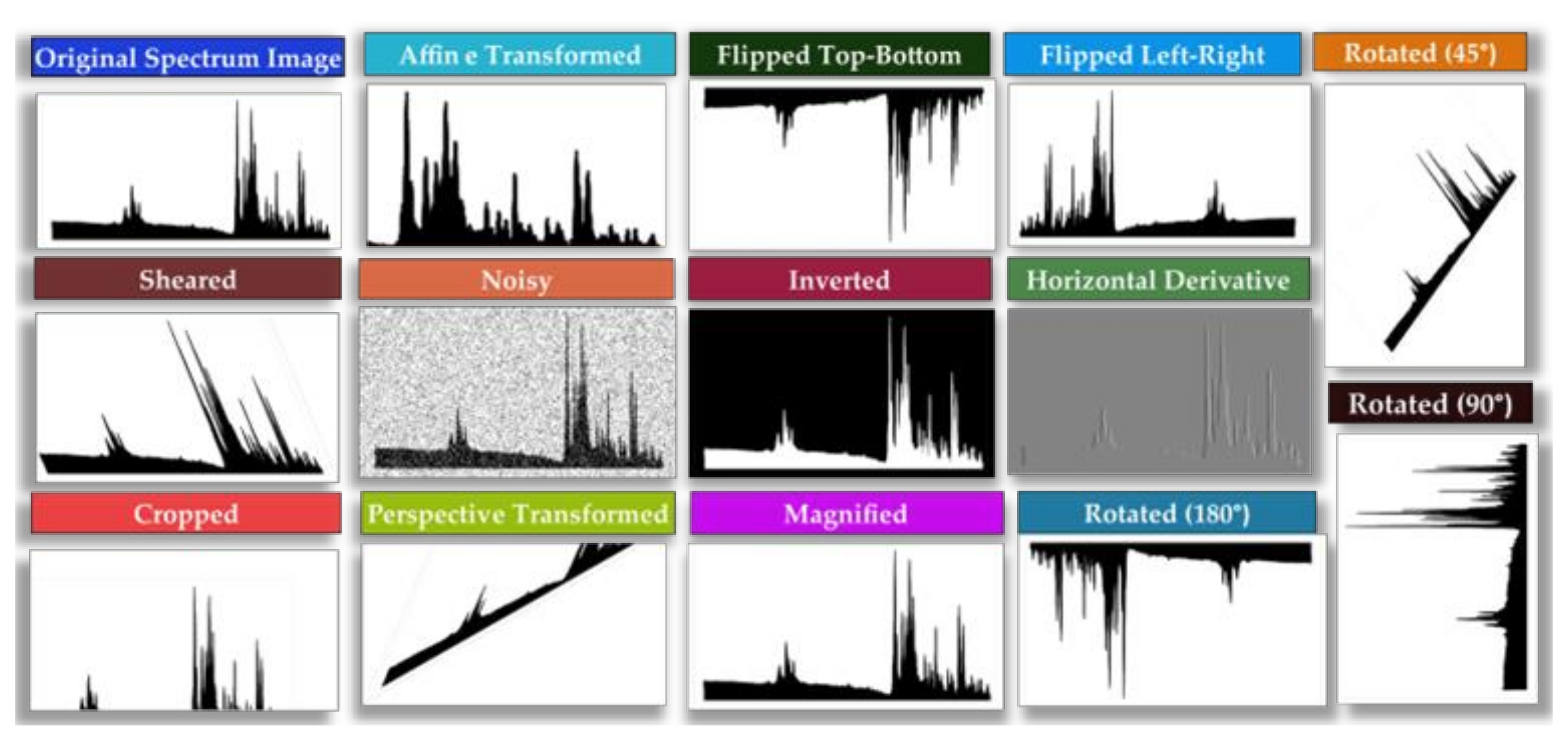
- Data Augmentation: involves augmenting the data through techniques, such as random rotations, shifts, and zooms, in order to generate additional synthetic samples.
- Total number of samples (total_samples) = 125 + 250 + 10,050 = 10,425;
- Number of classes (num_classes) = 3.
- Class 1 (JWH): 125;
- Class 2 (non-JWH): 250;
- Class 3 (other designer drugs): 10,050.
- weight_class_1 = 10,425/3 × 125 ≈ 27.80;
- weight_class_2 = 10,425/3 × 250 ≈ 13.90;
- weight_class_3 = 10,425/3 × 10,425 ≈ 0.33.
2.4. Core Components of the Developed DCNNs
- Convolution (Convolution Layers)
- b.
- Pooling (Pooling Layers)
- c.
- Full Connection (Fully Connected Layer)
2.5. Loss Functions, Activation Algorithms, Optimization, Regularization, and Fine-Tuning in the Developed DCNNs
- d.
- Focal Loss Function
- e.
- Activation Algorithms
- f.
- Rectified Linear Unit (ReLU)
- g.
- Softmax
- h.
- Optimization techniques
- i.
- ADAM optimization algorithm
- Compute the gradient gt of the focal loss for the three-class problem at step t.
- Update the moment estimates:
- 3.
- Correct bias in moment estimates:
- 4.
- Update the parameters of the DCNN:
- j.
- Regularization and Fine-tuning
- k.
- Learning Rate Scheduling
- l.
- Early Stopping
- m.
- L2 Regularization
2.6. Architectures of the Proposed Deep Convolutional Neural Networks
2.6.1. The matDETECT_FTIR DCNN Model
- Convolutional Autoencoder Block
- Encoder Unit
- Input Layer.
- Convolution Layer_1 (1792 parameters);
- Batch Normalization Layer_1 (256 parameters);
- ReLU Activation_1 (0 parameters);
- Convolution Layer_2 (36,928 parameters);
- Batch Normalization Layer_2 (256 parameters);
- ReLU Activation_2 (0 parameters);
- Pooling Layer_1 (0 parameters);
- Convolution Layer_3 (73,856 parameters);
- Batch Normalization Layer_3 (512 parameters);
- ReLU Activation_3 (0 parameters);
- Convolution Layer_4 (147,584 parameters);
- Batch Normalization Layer_4 (512 parameters);
- ReLU Activation_4 (0 parameters);
- Pooling Layer_2 (0 parameters);
- Flatten Layer_1 (0 parameters);
- Linear Layer_1 with 128 nodes (16,777,344 parameters).
- Decoder Unit
- Reshape layer to dimensions (0 parameters);
- Deconvolution Layer_1 (73,792 parameters);
- Batch Normalization Layer_5 (256 parameters);
- ReLU Activation_5 (0 parameters);
- Resize layer with a scaling factor of 2 in both dimensions (0 parameters);
- Deconvolution Layer_2 (36,928 parameters);
- Batch Normalization Layer_6 (256 parameters);
- ReLU Activation_6 (0 parameters);
- Resize layer with a scaling factor of 2 in both dimensions (0 parameters);
- Convolution Layer_5 (195 parameters).
- Additional Classification Block
- Convolution Layer_6 (3584 parameters);
- Batch Normalization Layer_7 (512 parameters);
- ReLU Activation_7 (0 parameters);
- Convolution Layer_7 (147,584 parameters);
- Batch Normalization Layer_8 (512 parameters);
- ReLU Activation_8 (0 parameters);
- Pooling Layer_3 (0 parameters);
- Flatten Layer_2 (0 parameters);
- Linear Layer_2 with 64 nodes (32,832 parameters);
- ReLU Activation_9 (0 parameters);
- Linear Layer_3 with 3 nodes (195 parameters);
- Softmax Layer (0 parameters).
- Output Layer.
- Layer count = 38;
- Array count = 56;
- Array total element count= 17,335,686;
- Trainable parameters = 17,334,150;
- Non-trainable parameters = 1536;
- Array total size = 69.3427 MB;
- GFLOP/S = 3.126450246.
2.6.2. The matDETECT Vision Transformer DCNN model
- A balance between model size and performance: while the ViT-B/32 offers slightly lower accuracy rates compared to its ViT-B/16 counterpart, it presents a reduced computational burden, making it more feasible for real-time or on-device applications;
- Optimal resource allocation: the ViT-B/32 model offers a good balance between the number of parameters and the Top-1 and Top-5 accuracy scores on ImageNet-1k. This ensures efficient utilization of resources without significantly compromising performance;
- Dataset characteristics: depending on the nature and diversity of our dataset, the ViT-B/32 might have offered certain advantages in feature extraction and representation over other configurations.
- a.
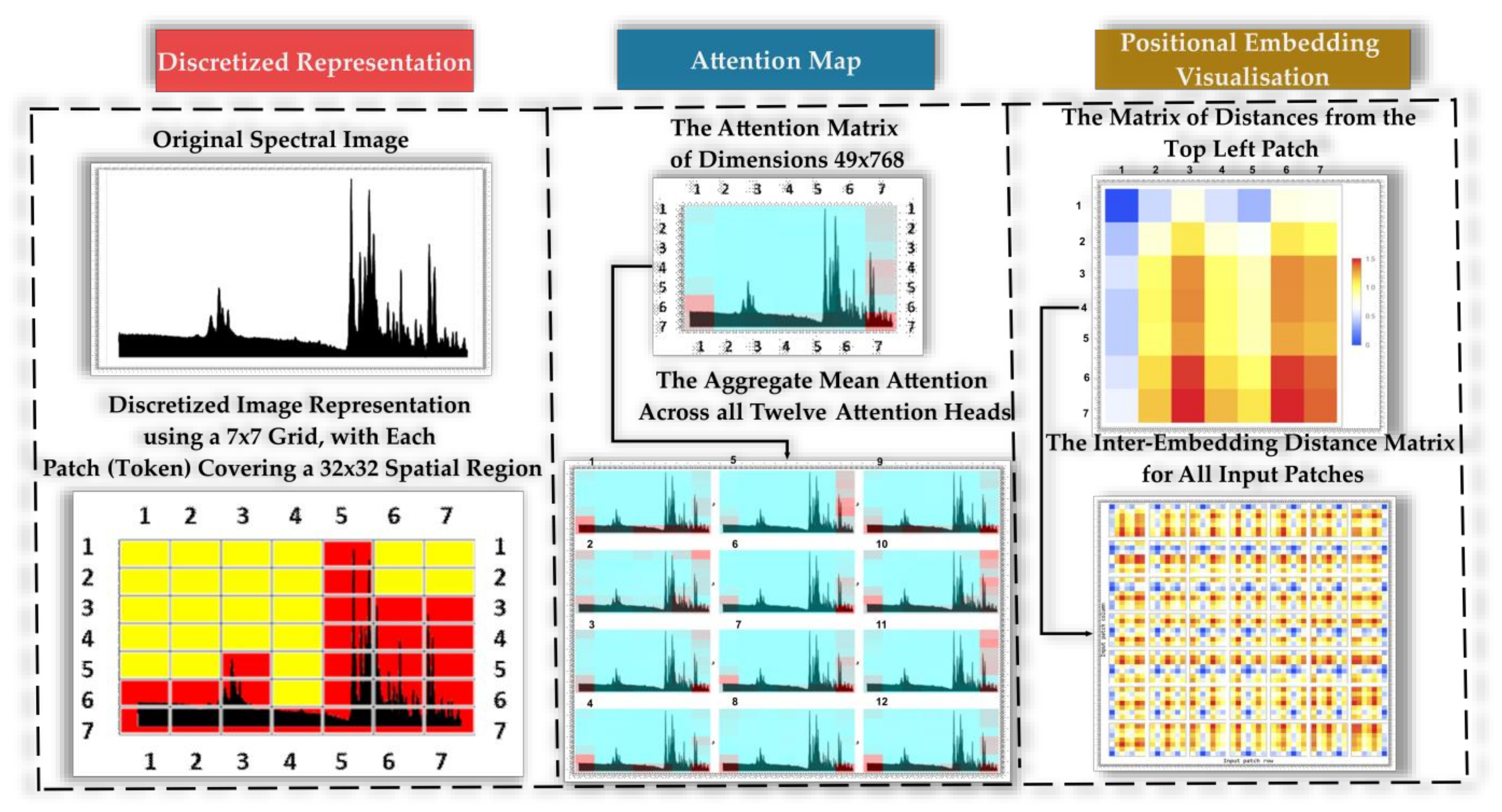
- Self-attention, attention matrix, positional embedding, attention matrix, and distance mechanisms.
Training, Optimization, and Fine-Tuning
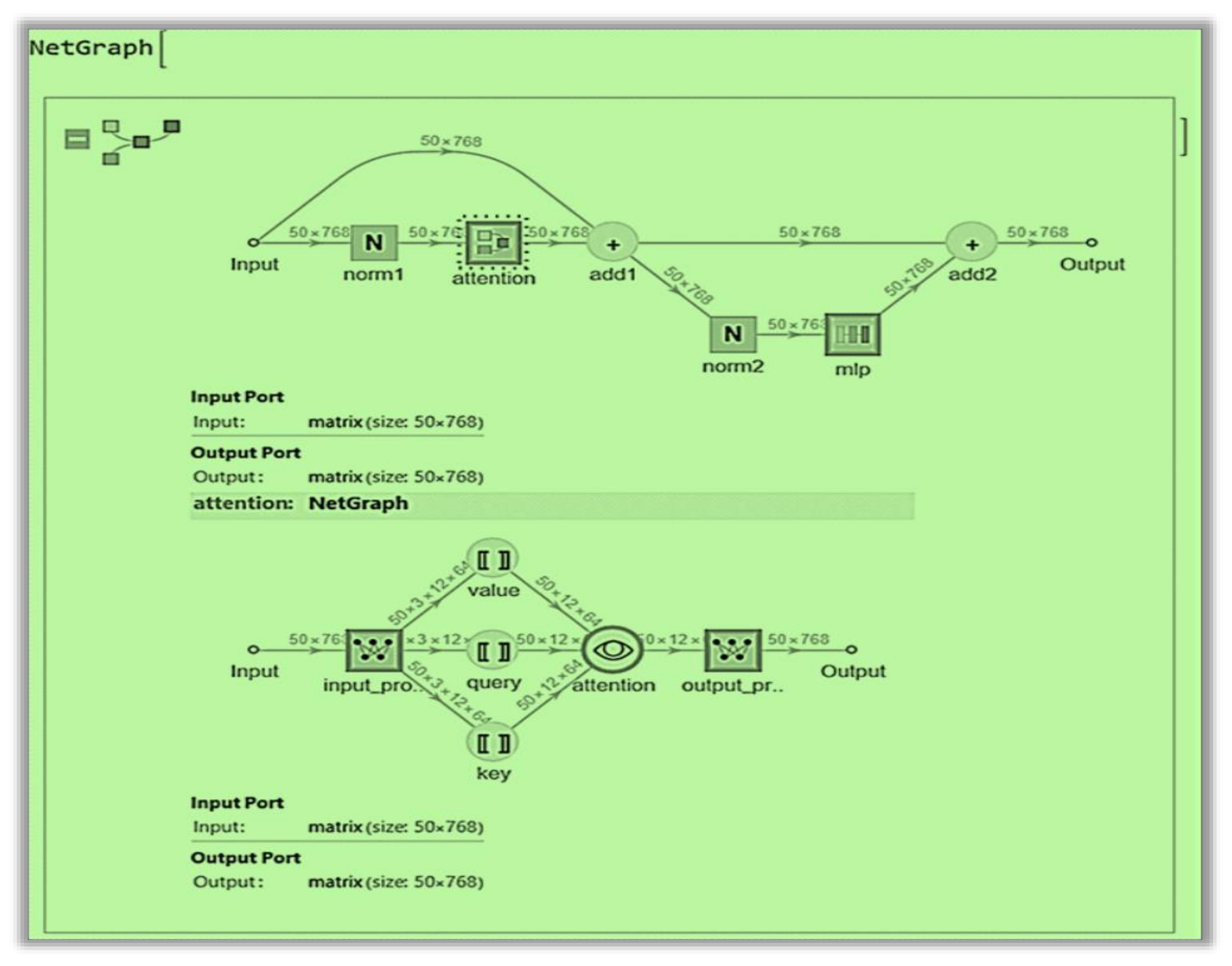
- Model Preparation: The pre-trained model was loaded, and the last linear (fully connected or dense) layer was excised to pave the way for the subsequent integration of new layers.
- Network Assembly: A new linear layer and a Softmax layer were added to the altered ViT-B/32 model to mitigate overfitting, calibrate output values facilitating their interpretation as probabilities, and predict the three specified classes (Figure 8).
- Network Training: A 5-fold cross-validation approach was used, which involved partitioning the data into training, validation, and testing sets, thereby facilitating a robust evaluation of the model throughout the training phase (Table 6).
- Model Evaluation: A rigorous assessment was performed to gauge the performance of the model, ensuring its reliability and precision in discerning the classes of synthetic cannabinoids.
- Model Preservation: The trained network was secured for future utilization and deployment by exporting it as a “.mx” file.
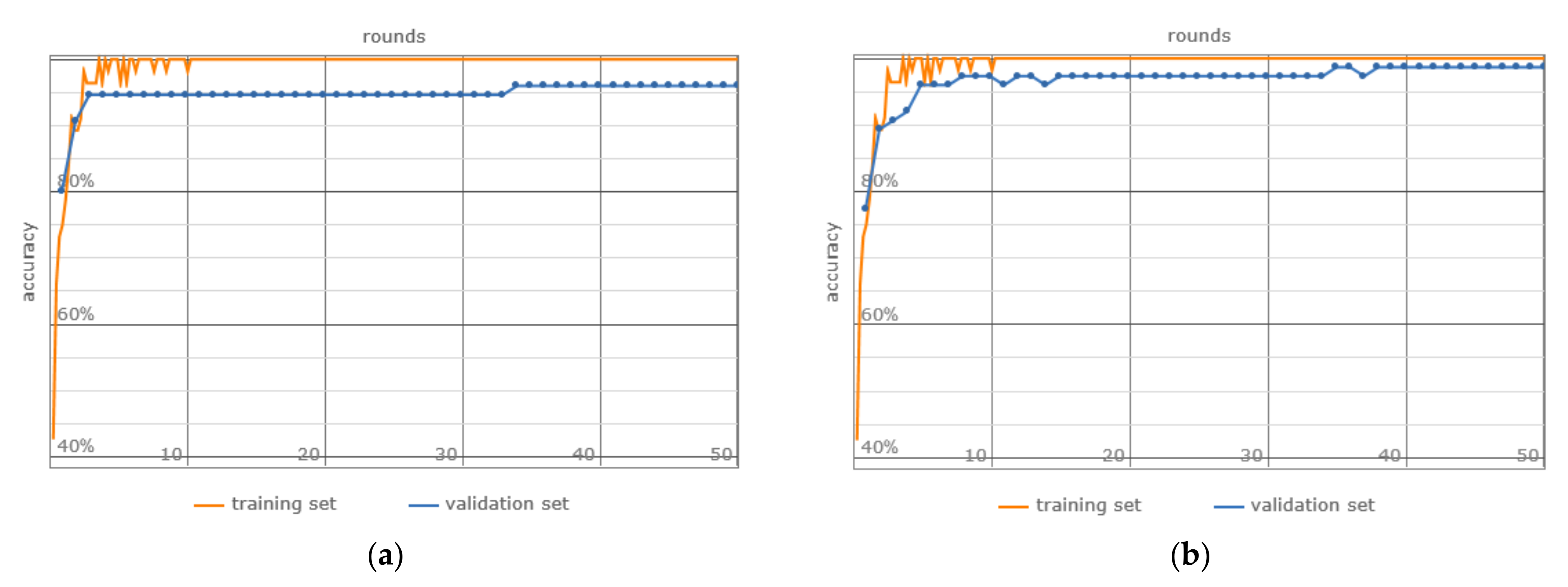
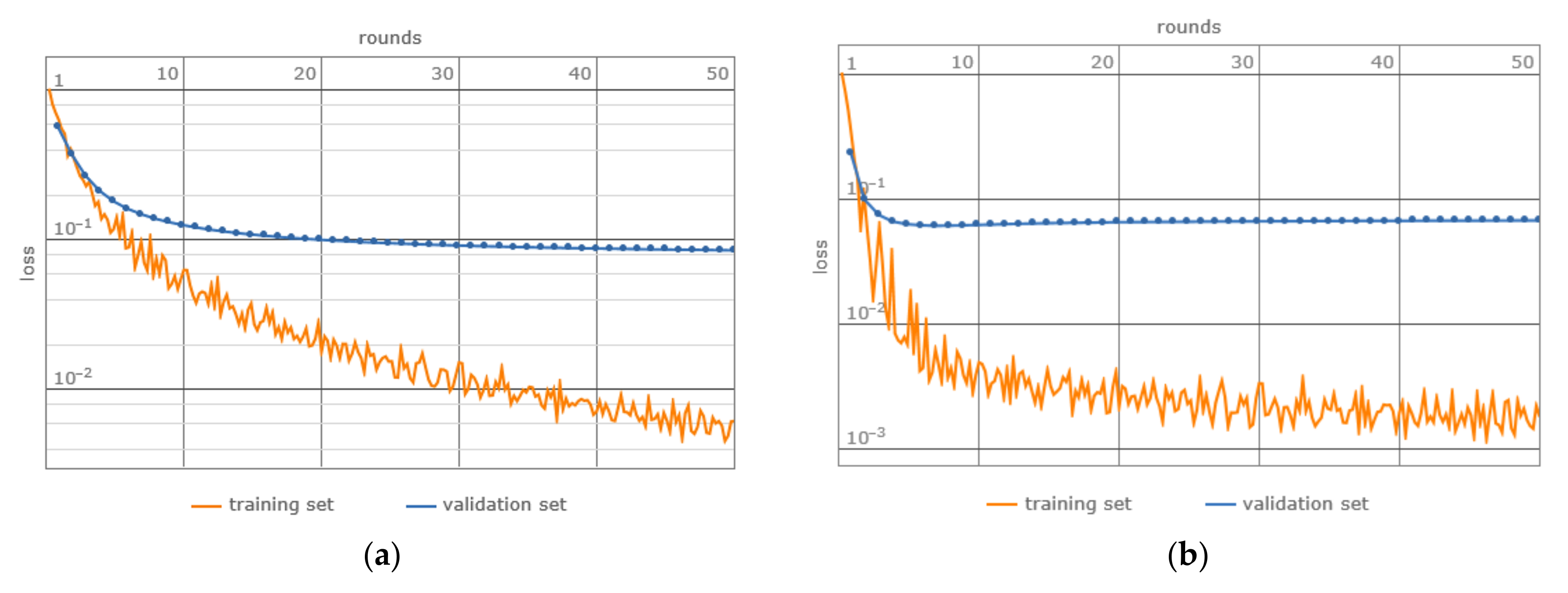
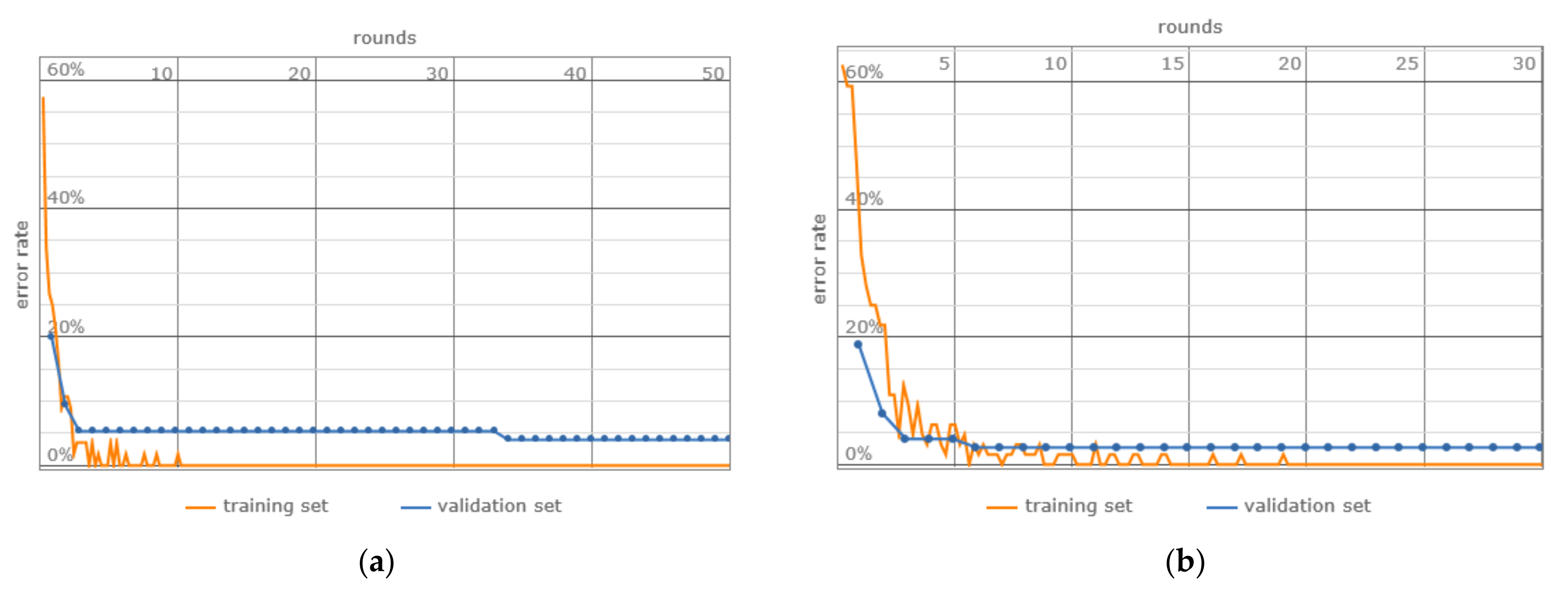
3. Results
4. Discussion
- Accuracy: The matDETECT Vision Transformer model exhibits marginally superior accuracy compared to the matDETECT_FTIR model.
- Precision: Notably, the matDETECT_FTIR model demonstrates elevated precision, suggesting a diminished incidence of false positives.
- Specificity: The matDETECT Vision Transformer model boasts enhanced specificity, implying a more effective detection of true negatives.
- Sensitivity (Recall): Furthermore, the matDETECT Vision Transformer showcases superior sensitivity, indicating a heightened capacity to detect true positives.
- Error Rate: Although both models present analogous error rates, the matDETECT Vision Transformer registers a marginally reduced rate.
- Kappa Coefficient: Additionally, the matDETECT Vision Transformer evidences an elevated kappa coefficient, signifying an enhanced model concordance.
- Macro-F1 Score: Both models possess comparable macro-F1 scores, insinuating a harmonized equilibrium between precision and recall.
- Loss: The matDETECT Vision Transformer model records a lesser loss, hinting at a potentially superior data fit.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alkhuder, K. Attenuated total reflection-Fourier transform infrared spectroscopy: A universal analytical technique with promising applications in forensic analyses. Int. J. Leg. Med. 2022, 136, 1718–1729. [Google Scholar] [CrossRef] [PubMed]
- Blanco-González, A.; Cabezón, A.; Seco-González, A.; Conde-Torres, D.; Antelo-Riveiro, P.; Piñeiro, Á.; Garcia-Fandino, R. The Role of AI in Drug Discovery: Challenges, Opportunities, and Strategies. Pharmaceuticals 2023, 16, 891. [Google Scholar] [CrossRef]
- Gupta, R.; Srivastava, D.; Sahu, M.; Tiwari, S.; Ambasta, R.K.; Kumar, P. Artificial intelligence to deep learning: Machine intelligence approach for drug discovery. Mol. Divers. 2021, 25, 1315–1360. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Parallel Distributed Processing: Explorations in the Microstructure of Cognition; Learning Internal Representations by Error Propagation; MIT Press: Cambridge, MA, USA, 1986; Volume 1, pp. 318–362. [Google Scholar]
- Pu, Y.; Gan, Z.; Henao, R.; Yuan, X.; Li, C.; Stevens, A.; Carin, L. Variational autoencoder for deep learning of images, labels and captions. Adv. Neural Inf. Process. Syst. 2016, 29, 2352–2360. [Google Scholar]
- Ilesanmi, A.E.; Ilesanmi, T.O. Methods for image denoising using convolutional neural network: A review. Complex Intell. Syst. 2021, 7, 2179–2198. [Google Scholar] [CrossRef]
- Arai, H.; Chayama, Y.; Iyatomi, H.; Oishi, K. Significant dimension reduction of 3D brain MRI using 3D convolutional autoencoders. In Proceedings of the 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018; pp. 5162–5165. [Google Scholar]
- Guo, X.; Liu, X.; Zhu, E.; Yin, J. Deep clustering with convolutional autoencoders. In Proceedings of the International Conference on Neural Information Processing 2017, Guangzhou, China, 14–18 November 2017; pp. 373–382. [Google Scholar]
- Kucharski, D.; Kleczek, P.; Jaworek-Korjakowska, J.; Dyduch, G.; Gorgon, M. Semi-supervised nests of melanocytes segmentation method using convolutional autoencoders. Sensors 2020, 20, 1546. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Luong, T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-based Neural Machine Translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (ACL) 2015, Lisbon, Portugal, 17–21 September 2015; pp. 1412–1421. [Google Scholar]
- Islam, S.; Elmekki, H.; Elsebai, A.; Bentahar, J.; Drawel, N.; Rjoub, G.; Pedrycz, W. A Comprehensive Survey on Applications of Transformers for Deep Learning Tasks. arXiv 2023, arXiv:2306.07303 2023. [Google Scholar]
- Maray, N.; Ngu, A.H.; Ni, J.; Debnath, M.; Wang, L. Transfer Learning on Small Datasets for Improved Fall Detection. Sensors 2023, 23, 1105. [Google Scholar] [CrossRef]
- Burlacu, C.M.; Gosav, S.; Burlacu, B.A.; Praisler, M. Convolutional Neural Network Detecting Synthetic Cannabinoids. In Proceedings of the International Conference on e-Health and Bioengineering (EHB), Iasi, Romania, 18–19 November 2021. [Google Scholar]
- Google Research. Vision_Transformer. Available online: https://github.com/google-research/vision_transformer (accessed on 16 March 2023).
- Wolfram Neural Net Repository. Available online: https://resources.wolframcloud.com/NeuralNetRepository/resources/Vision-Transformer-Trained-on-ImageNet-Competition-Data/ (accessed on 2 June 2023).
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929v2. [Google Scholar]
- Wolfram Research, I. Mathematica Version 13.3; Wolfram Research, Inc.: Champaign, IL, USA, 2023. [Google Scholar]
- Hellmann, D. The Python 3 Standard Library by Example, 2nd ed.; Addison-Wesley Professional: Boston, NA, USA, 2017. [Google Scholar]
- Pereira, L.S.; Lisboa, F.L.; Neto, J.C.; Valladão, F.; Sena, M.M. Direct classification of new psychoactive substances in seized blotter papers by ATR-FTIR and multivariate discriminant analysis. Microchem. J. 2017, 133, 96–103. [Google Scholar] [CrossRef]
- Pereira, L.S.; Lisboa, F.L.; Neto, J.C.; Valladão, F.N.; Sena, M.M. Screening method for rapid classification of psychoactive substances in illicit tablets using mid infrared spectroscopy and PLS-DA. Forensic Sci. Int. 2018, 288, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Hua, Z.; Liu, C.; Lv, R.; Jia, W.; Su, M. ATR-FTIR combined with machine learning for the fast non-targeted screening of new psychoactive substances. Forensic Sci. Int. 2023, 349, 111761. [Google Scholar] [CrossRef] [PubMed]
- Tsujikawa, K.; Yamamuro, T.; Kuwayama, K.; Kanamori, T.; Iwata, Y.T.; Miyamoto, K.; Kasuya, F.; Inoue, H. Application of a portable near infrared spectrometer for presumptive identification of psychoactive drugs. Forensic Sci. Int. 2014, 242, 162–171. [Google Scholar] [CrossRef]
- Radhakrishnan, A.; Damodaran, K.; Soylemezoglu, A.C.; Uhler, C.; Shivashankar, G.V. Machine Learning for Nuclear Mechano-Morphometric Biomarkers in Cancer Diagnosis. Sci. Rep. 2017, 7, 17946. [Google Scholar] [CrossRef]
- Koutsoukas, A.; Monaghan, K.; Li, X.; Huan, J. Deep-learning: Investigating deep neural networks hyper-parameters and comparison of performance to shallow methods for modeling bioactivity data. J. Cheminform. 2017, 9, 42. [Google Scholar] [CrossRef]
- Mendenhall, J.; Meiler, J. Improving quantitative structure-activity relationship models using Artificial Neural Networks trained with dropout. J. Comput.-Aided Mol. Des. 2016, 30, 177–189. [Google Scholar]
- Wallach, I.; Dzamba, M.; Heifets, A. AtomNet: A Deep Convolutional Neural Network for Bioactivity Prediction in Structure-based Drug Discovery. arXiv 2015, arXiv:1510.02855. [Google Scholar]
- Shi, W.; Singha, M.; Srivastava, G.; Pu, L.; Ramanujam, J.; Brylinski, M. Pocket2Drug: An Encoder-Decoder Deep Neural Network for the Target-Based Drug Design. Front. Pharmacol. 2022, 13, 837715. [Google Scholar] [CrossRef]
- Sun, C.; Cao, Y.; Wei, J.M.; Liu, J. Autoencoder-based drug-target interaction prediction by preserving the consistency of chemical properties and functions of drugs. J. Bioinform. 2021, 37, 3618–3625. [Google Scholar] [CrossRef]
- Pintelas, E.; Livieris, I.E.; Pintelas, P.E. A Convolutional Autoencoder Topology for Classification in High-Dimensional Noisy Image Datasets. Sensors 2021, 21, 7731. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z.B. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; Volume 1 (Long and Short Papers), pp. 4171–4186. [Google Scholar]
- Chen, H.; Wang, Y.; Guo, T.; Xu, C.; Deng, Y.; Liu, Z.; Ma, S.; Xu, C.; Xu, C.; Gao, W. Pre-trained image processing transformer. arXiv 2021, arXiv:2012.00364. [Google Scholar]
- Ali, L.; Alnajjar, F.; Jassmi, H.A.; Gocho, M.; Khan, W.; Serhani, M.A. Performance Evaluation of Deep CNN-Based Crack Detection and Localization Techniques for Concrete Structures. Sensors 2021, 21, 1688. [Google Scholar] [CrossRef]
- Alshammari, H.; Gasmi, K.; Ben Ltaifa, I.; Krichen, M.; Ben Ammar, L.; Mahmood, M.A. Olive Disease Classification Based on Vision Transformer and CNN Models. Comput. Intell. Neurosci. 2022, 2022, 3998193. [Google Scholar] [CrossRef]
- Liu, W.; Li, C.; Xu, N.; Jiang, T.; Rahaman, M.M.; Sun, H.; Wu, X.; Hu, W.; Chen, H.; Sun, C.; et al. CVM-Cervix: A Hybrid Cervical Pap-Smear Image Classification Framework Using CNN, Visual Transformer and Multilayer Perceptron. arXiv 2022, arXiv:2206.00971. [Google Scholar] [CrossRef]
- Gheflati, B.; Rivaz, H. Vision Transformers for Classification of Breast Ultrasound Images. In Proceedings of the Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, UK, 11–15 July 2022; pp. 480–483. [Google Scholar]
- Liu, Y.; Yao, W.; Qin, F.; Zhou, L.; Zheng, Y. Spectral Classification of Large-Scale Blended (Micro)Plastics Using FT-IR Raw Spectra and Image-Based Machine Learning. Environ. Sci. Technol. 2023, 57, 6656–6663. [Google Scholar] [CrossRef]
- Zhou, W.; Qian, Z.; Ni, X.; Tang, Y.; Guo, H.; Zhuang, S. Dense Convolutional Neural Network for Identification of Raman Spectra. Sensors 2023, 23, 7433. [Google Scholar] [CrossRef]
- Intel. Available online: https://www.intel.com/content/www/us/en/docs/onemkl/developer-guide-windows/2023-0/overview-intel-distribution-for-linpack-benchmark.html (accessed on 26 September 2023).
- Dongarra, J.; Bunch, J.; Moler, C.; Stewart, G.W. LINPACK Users Guide; SIAM: Philadelphia, PA, USA, 1979. [Google Scholar]
- Dongarra, J. Performance of Various Computers Using Standard Linear Equations Software; Computer Science Technical Report Number CS-89-85, TN 37996-1301; University of Tennessee: Knoxville, TN, USA, 2014; Available online: http://www.netlib.org/benchmark/performance.ps (accessed on 25 September 2023).
- TOP500. Available online: https://www.top500.org/statistics/list/ (accessed on 27 September 2023).
- Burlacu, C.M.; Burlacu, A.C.; Praisler, M. Physico-chemical analysis, systematic benchmarking, and toxicological aspects of the JWH aminoalkylindole class-derived synthetic JWH cannabinoids. Ann. Univ. Dunarea Jos Galati Fascicle II Math. Phys. Theor. Mech. 2021, 44, 34–45. [Google Scholar] [CrossRef]
- Elreedy, D.; Atiya, A. A Comprehensive Analysis of Synthetic Minority Oversampling Technique (SMOTE) for Handling Class Imbalance. Inf. Sci. 2019, 505, 32–64. [Google Scholar] [CrossRef]
- Menges, F. Spectragryph—Optical Spectroscopy Software, Version 1.2.16.1. 2022. Available online: http://www.effemm2.de/spectragryph/ (accessed on 5 September 2023).
- Wenig, P.; Odermatt, J. OpenChrom: A cross-platform open-source software for the mass spectrometric analysis of chromatographic data. BMC Bioinform. 2010, 11, 405. [Google Scholar] [CrossRef] [PubMed]
- Alomar, K.; Aysel, H.I.; Cai, X. Data Augmentation in Classification and Segmentation: A Survey and New Strategies. J. Imaging 2023, 9, 46. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Adv. Neural Inf. Process. Syst. 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Lee, M. Recent Advances in Generative Adversarial Networks for Gene Expression Data: A Comprehensive Review. Mathematics 2023, 11, 3055. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- An, Q.; Rahman, S.; Zhou, J.; Kang, J.J. A Comprehensive Review on Machine Learning in Healthcare Industry: Classification, Restrictions, Opportunities and Challenges. Sensors 2023, 23, 4178. [Google Scholar] [CrossRef]
- van Engelen, J.E.; Hoos, H.H. A survey on semi-supervised learning. Mach. Learn. 2020, 109, 373–440. [Google Scholar] [CrossRef]
- Machine Learning Mastery. Available online: https://machinelearningmastery.com/the-transformer-attention-mechanism/ (accessed on 6 September 2023).

| Tests | Number of Equations to Solve (Problem Size) | Leading Dimension of Array (LDA) | Number of Trials to Run | Data Alignment Value (in Kbytes) |
|---|---|---|---|---|
| 1 | 1000 | 1000 | 8 | 4 |
| 2 | 2000 | 2000 | 6 | 4 |
| 3 | 5000 | 5008 | 4 | 4 |
| 4 | 10,000 | 10,000 | 4 | 4 |
| 5 | 15,000 | 15,000 | 3 | 4 |
| 6 | 18,000 | 18,008 | 3 | 4 |
| 7 | 20,000 | 20,016 | 3 | 4 |
| 8 | 22,000 | 22,008 | 3 | 4 |
| 9 | 25,000 | 25,000 | 3 | 4 |
| 10 | 26,000 | 26,000 | 3 | 4 |
| 11 | 27,000 | 27,000 | 2 | 4 |
| 12 | 30,000 | 30,000 | 1 | 1 |
| 13 | 35,000 | 35,000 | 1 | 1 |
| 14 | 40,000 | 40,000 | 1 | 1 |
| 15 | 45,000 | 45,000 | 1 | 1 |
| Floating Point Operations per Second Average (GFlop/s) | |||||
|---|---|---|---|---|---|
| Test | Average | Maximal | Residual | Residual Norm | Check |
| 1 | 173.7785 | 202.8784 | 1.30 × 10−6 | 3.94 × 10−4 | pass |
| 2 | 229.6025 | 253.6362 | 1.30 × 10−6 | 3.94 × 10−4 | pass |
| 3 | 276.6376 | 293.3389 | 1.30 × 10−6 | 3.94 × 10−4 | pass |
| 4 | 270.1227 | 275.2453 | 1.30 × 10−6 | 3.94 × 10−4 | pass |
| 5 | 254.1475 | 258.5500 | 1.30 × 10−6 | 3.94 × 10−4 | pass |
| 6 | 253.9643 | 255.3168 | 1.30 × 10−6 | 3.94 × 10−4 | pass |
| 7 | 259.4283 | 261.4543 | 1.30 × 10−6 | 3.94 × 10−4 | pass |
| 8 | 253.8448 | 256.6712 | 1.30 × 10−6 | 3.94 × 10−4 | pass |
| 9 | 256.9164 | 257.9535 | 4.17 × 10−6 | 3.29 × 10−4 | pass |
| 10 | 255.6003 | 259.7284 | 4.17 × 10−6 | 3.29 × 10−4 | pass |
| 11 | 258.8156 | 313.4706 | 4.17 × 10−6 | 3.29 × 10−4 | pass |
| 12 | 255.3485 | 255.3485 | 4.17 × 10−6 | 3.29 × 10−4 | pass |
| 13 | 254.7538 | 254.7538 | 4.17 × 10−6 | 3.29 × 10−4 | pass |
| 14 | 257.2128 | 312.2128 | 4.17 × 10−6 | 3.29 × 10−4 | pass |
| 15 | 133.0238 | 133.0238 | 2.33 × 10−5 | 3.07 × 10−4 | pass |
| Spectral Library | Training Set | Validation Set | Test Set |
|---|---|---|---|
| Non-Forensic | 6600 | 2200 | 2200 |
| Forensic | 6255 | 2085 | 2085 |
| Component or Layer Ablated | Effect on Classification (Macro-F1 Score) | Effect on Detection (Specificity) | Overall Accuracy (%) |
|---|---|---|---|
| Full Network (matDETECT) | 0.9037 | 0.9728 | 96.16 |
| Without Convolutional Autoencoder | 0.8832 (−0.0205) | 0.9625 (−0.0103) | 93.8 (−2.36) |
| Omitted 1 to 3 Convolution Layers | 0.8652–0.8832 (−0.0385 to −0.0205) | 0.9555–0.9605 (−0.0173 to −0.0123) | 92.2–93.6 (−3.96 to −2.56) |
| Omitted 1 to 4 Batch Normalization Layers | 0.8800–0.8910 (−0.0237 to −0.0127) | 0.9610–0.9645 (−0.0118 to −0.0083) | 93.7–94.9 (−2.46 to −1.27) |
| Omitted 1 to 3 Max Pooling Layers | 0.8880–0.8980 (−0.0157 to −0.0057) | 0.9630–0.9675 (−0.0098 to −0.0053) | 94.5–95.5 (−1.66 to −0.66) |
| Omitted 1 Flatten Layer | 0.8971–0.9021 (−0.0066 to −0.0016) | 0.9700–0.9715 (−0.0028 to −0.0013) | 95.7–96.0 (−0.46 to −0.16) |
| Omitted 1 Fully Connected Layer | 0.9002–0.9042 (−0.0035 to −0.0005) | 0.9718–0.9733 (−0.0010 to −0.0005) | 96.0–96.3 (−0.16 to −0.14) |
| Parameters | Statistics | Top-5 Accuracy | Top-1 Accuracy | |||
|---|---|---|---|---|---|---|
| Model Size | Pach Size | Number of Layers | Total Number of Weights | File Seize (MB) | ImageNet-1k (%) | ImageNet-1k (%) |
| Base (ViT-B/16) | 16 | 168 | 86,567,656 | 346.354 | 95.318 | 81.072 |
| Base (ViT-B/32) | 32 | 168 | 88,224,232 | 352.981 | 92.466 | 75.912 |
| Large (ViT-L/16) | 16 | 324 | 304,326,632 | 1217.44 | 94.638 | 79.662 |
| Large (ViT-L/32) | 32 | 324 | 306,535,400 | 1226.28 | 93.070 | 76.972 |
| Classifier Measurements * | New matDETECT Vision Transformer |
|---|---|
| Batches Per Round (Epoch) | 8 |
| Batch Size | 32 |
| Batches Per Second | 6.59536 |
| Mean Batches Per Second | 5.8947 |
| Total Batches | 400 |
| Examples Processed | 12800 |
| Initial Learning Rate | 0.001 |
| Final Learning Rate | 0.000574294 |
| Mean Examples Per Second | 188.63 |
| Total Rounds (Epochs) | 50 |
| Total Training Time (s) | 67.8575 |
| Parameters | Statistics | ||||
|---|---|---|---|---|---|
| Model Size | Pach Size | Number of Layers | Total Number of Weights | File Seize (MB) | Gflop/s |
| New matDETECT Vision Transformer | 32 | 168 | 87,457,539 | 345.83 MB | 8.23 |
| Base (ViT-B/32) | 32 | 168 | 88,224,232 | 352.981 | 8.56 |
| Forensic ATR-FTIR Spectral Library (10,425 Images) Macro-Averaged Metrics (Test Set) | |||
|---|---|---|---|
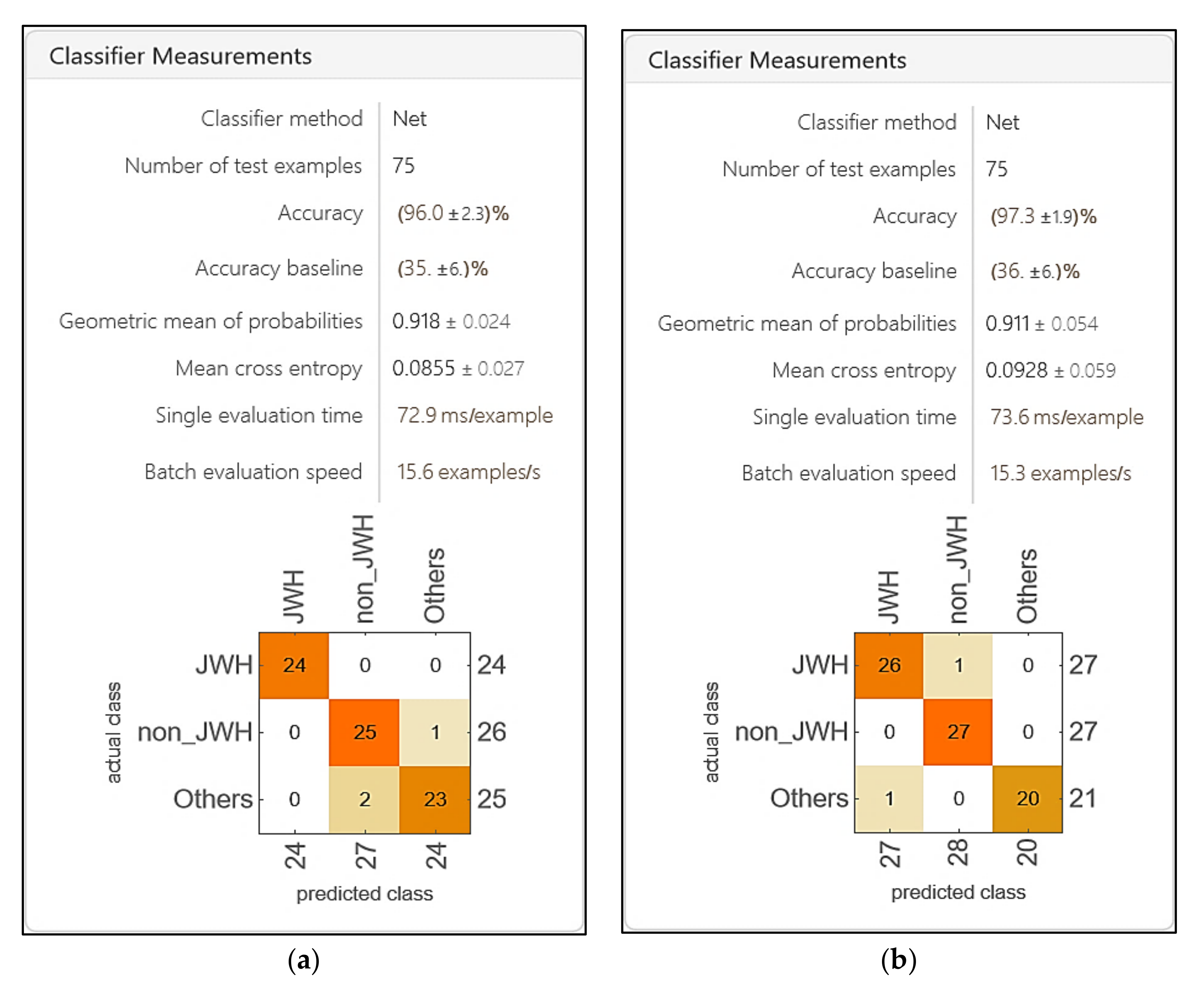
| DCNN | Accuracy | Precision | 1-Precision |
| matDETECT_FTIR | 0.9616 | 0.8658 | 0.1341 |
| matDETECT Vision Transformer | 0.9738 | 0.8485 | 0.1514 |
| Forensic ATR-FTIR Spectral Library (10,425 Images) Macro-Averaged Metrics (Test Set) | |||
|---|---|---|---|
| DCNN | Specificity | Sensitivity (Recall) | 1-Recall |
| matDETECT_FTIR | 0.9728 | 0.9616 | 0.0383 |
| matDETECT Vision Transformer | 0.9954 | 0.9758 | 0.0241 |
| Forensic ATR-FTIR Spectral Library (10,425 Images) Macro-Averaged Metrics (Test Set) | ||
|---|---|---|
| DCNN | Error Rate | Kappa Coefficient |
| matDETECT_FTIR | 0.2391 | 0.7930 |
| matDETECT Vision Transformer | 0.2308 | 0.8350 |
| Forensic ATR-FTIR Spectral Library (10,425 Images) Macro-Averaged Metrics (Test Set) | ||
|---|---|---|
| DCNN | Macro-F1 Score | Loss |
| matDETECT_FTIR | 0.9037 | 0.1342 |
| matDETECT Vision Transformer | 0.9025 | 0.0979 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burlacu, C.M.; Burlacu, A.C.; Praisler, M.; Paraschiv, C. Harnessing Deep Convolutional Neural Networks Detecting Synthetic Cannabinoids: A Hybrid Learning Strategy for Handling Class Imbalances in Limited Datasets. Inventions 2023, 8, 129. https://doi.org/10.3390/inventions8050129
Burlacu CM, Burlacu AC, Praisler M, Paraschiv C. Harnessing Deep Convolutional Neural Networks Detecting Synthetic Cannabinoids: A Hybrid Learning Strategy for Handling Class Imbalances in Limited Datasets. Inventions. 2023; 8(5):129. https://doi.org/10.3390/inventions8050129
Chicago/Turabian StyleBurlacu, Catalina Mercedes, Adrian Constantin Burlacu, Mirela Praisler, and Cristina Paraschiv. 2023. "Harnessing Deep Convolutional Neural Networks Detecting Synthetic Cannabinoids: A Hybrid Learning Strategy for Handling Class Imbalances in Limited Datasets" Inventions 8, no. 5: 129. https://doi.org/10.3390/inventions8050129
APA StyleBurlacu, C. M., Burlacu, A. C., Praisler, M., & Paraschiv, C. (2023). Harnessing Deep Convolutional Neural Networks Detecting Synthetic Cannabinoids: A Hybrid Learning Strategy for Handling Class Imbalances in Limited Datasets. Inventions, 8(5), 129. https://doi.org/10.3390/inventions8050129






