FEA Assessment of Contact Pressure and Von Mises Stress in Gasket Material Suitability for PEMFCs in Electric Vehicles
Abstract
:1. Introduction
- The study addresses the research gap by providing a comprehensive and direct comparison between two widely used gasket materials, LSR and EPDM, specifically in PEMFC applications.
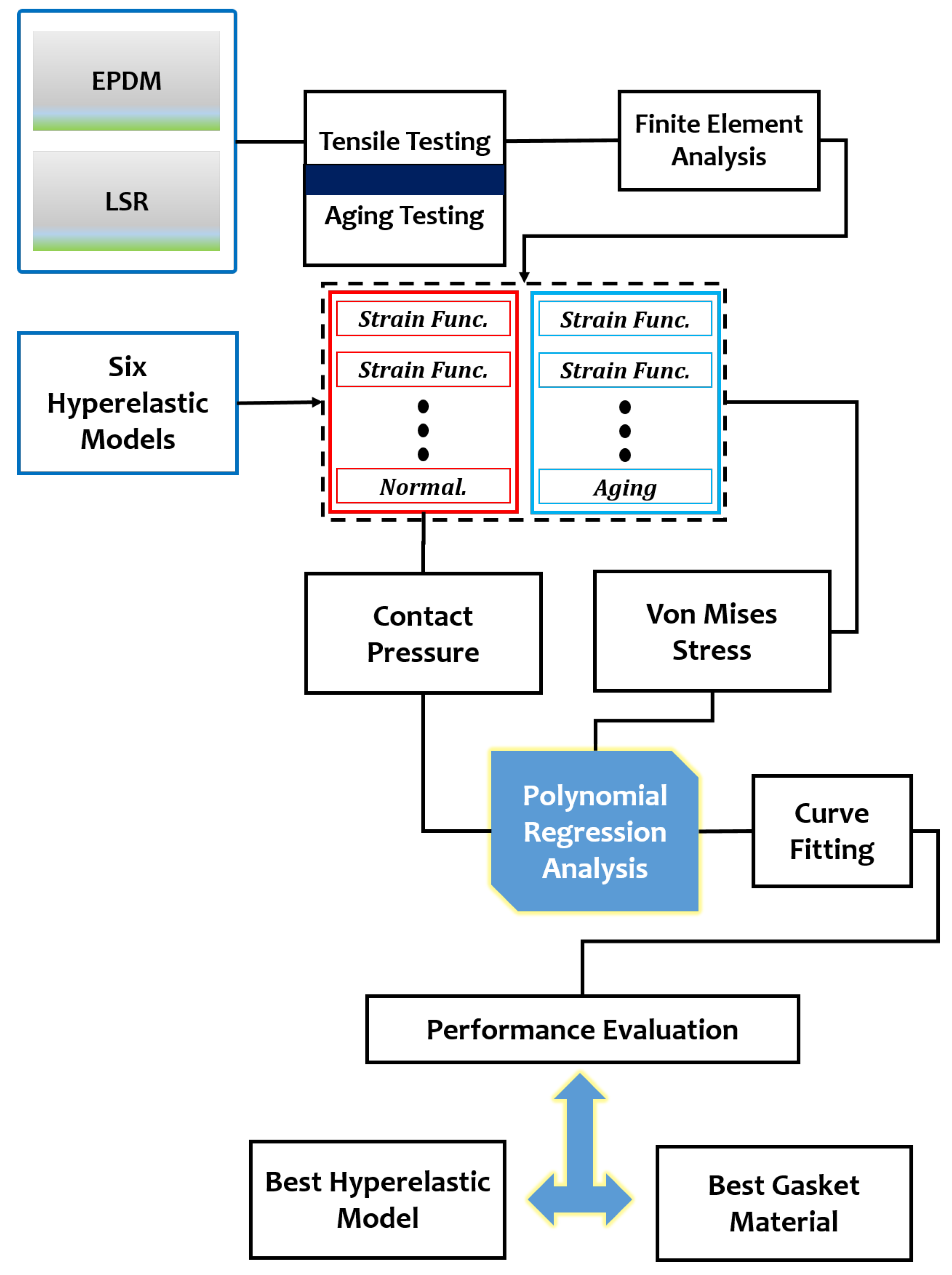
- The study generates experimental data for LSR and EPDM gasket materials under tensile tests (uniaxial and biaxial) and ageing tests. This experimental data is essential for validating the subsequent Finite Element Analysis (FEA) models using contact pressure and von Mises stress and enhancing the accuracy and reliability of the study’s findings.
- By employing advanced FEA using the Marc software, the study extracts strain functions for both LSR and EPDM gaskets. This approach is significant as it enables researchers to understand how each material responds to different contact pressures and von Mises stress, providing valuable information on their mechanical behaviour and deformation characteristics.
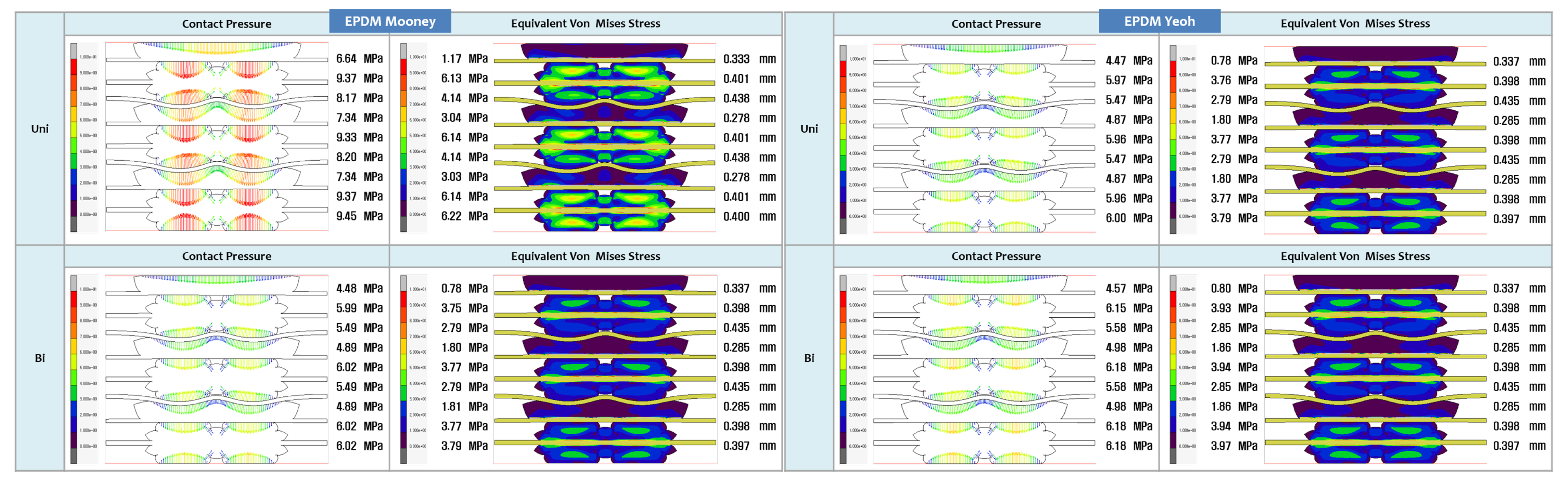
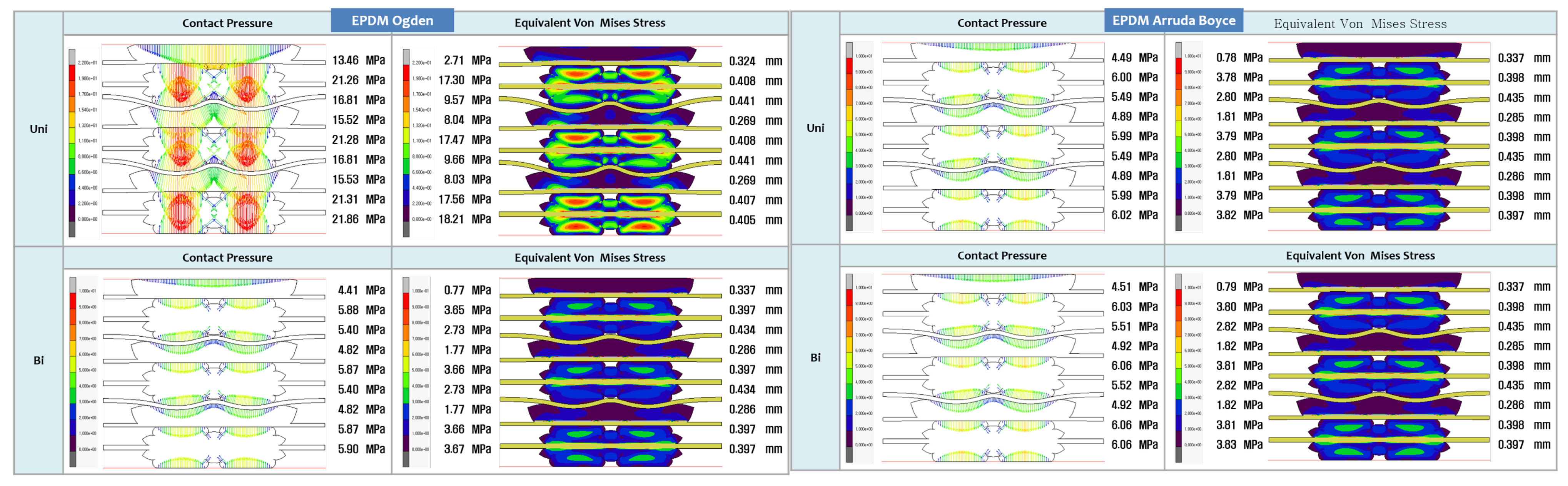
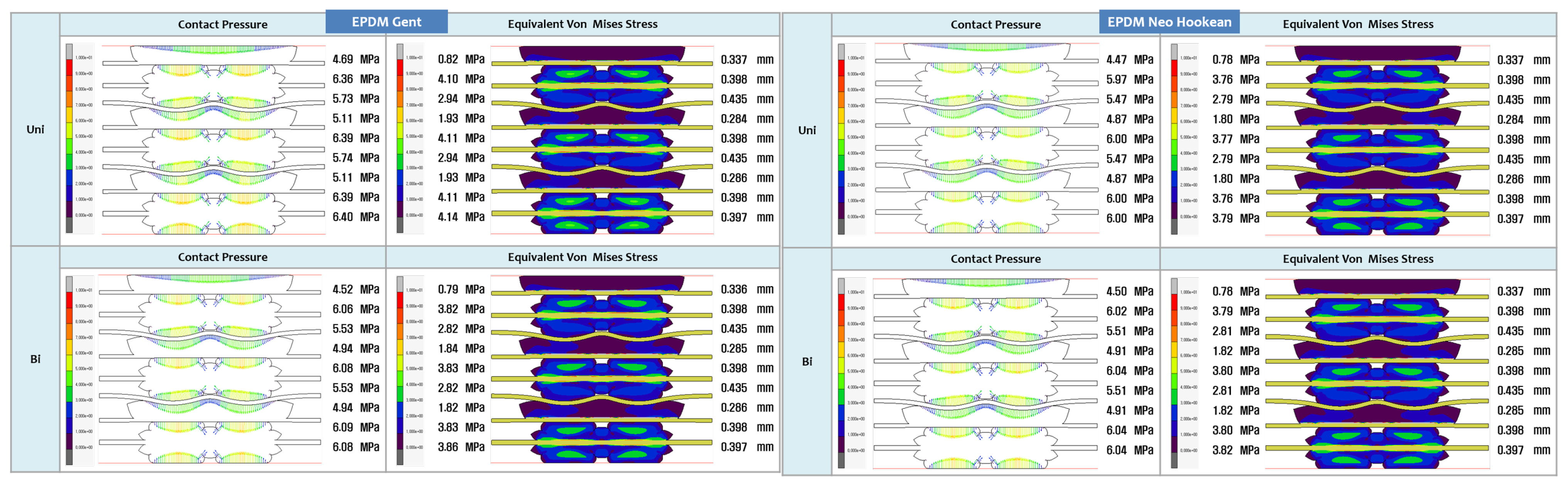
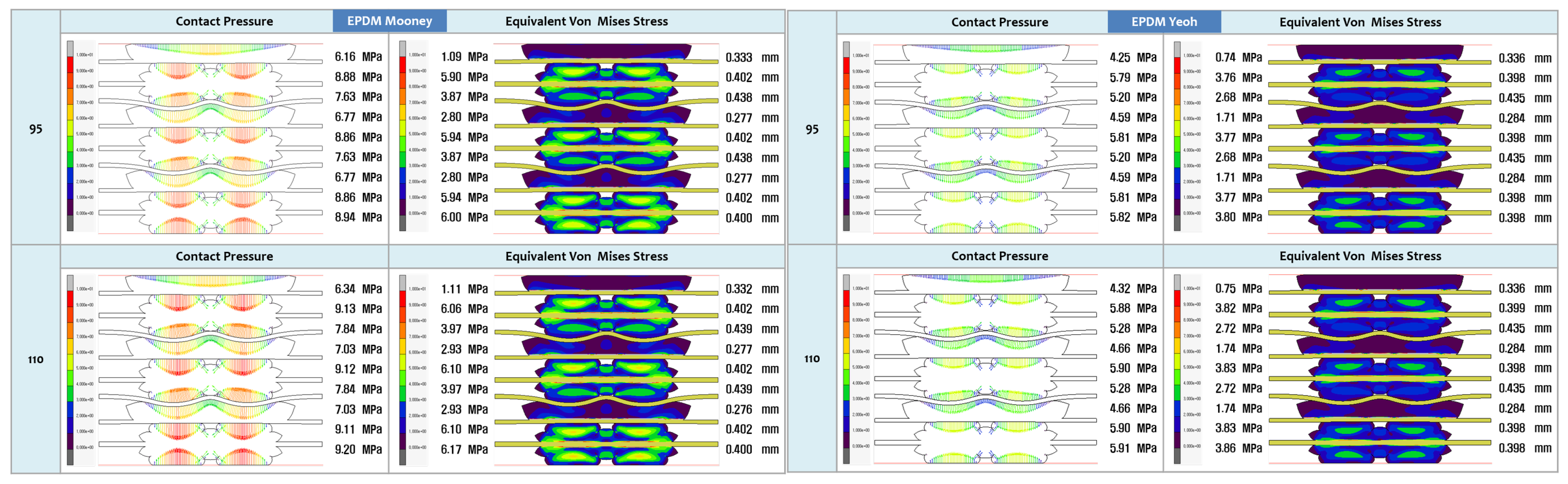
- The study’s focus is on evaluating the contact pressure distribution and Von Mises stress distribution for LSR and EPDM gaskets. These analyses shed light on each material’s sealing efficiency and mechanical stability under varying tensile and ageing tests, directly addressing the research gap concerning the structural integrity and long-term reliability of PEMFC gasket materials.
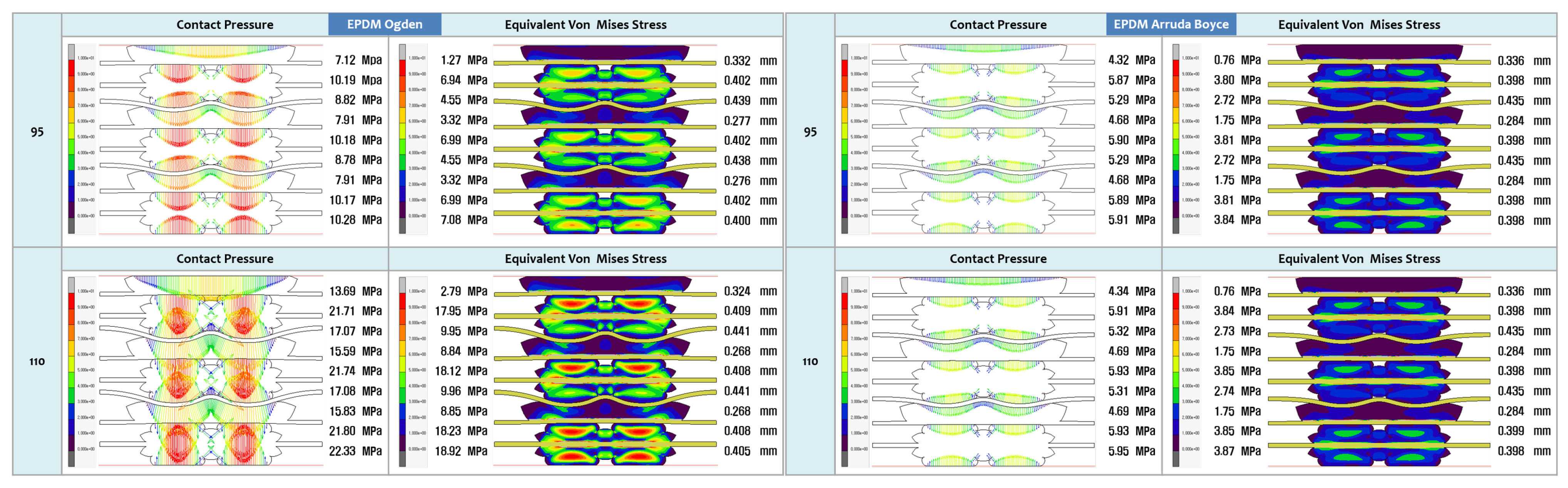
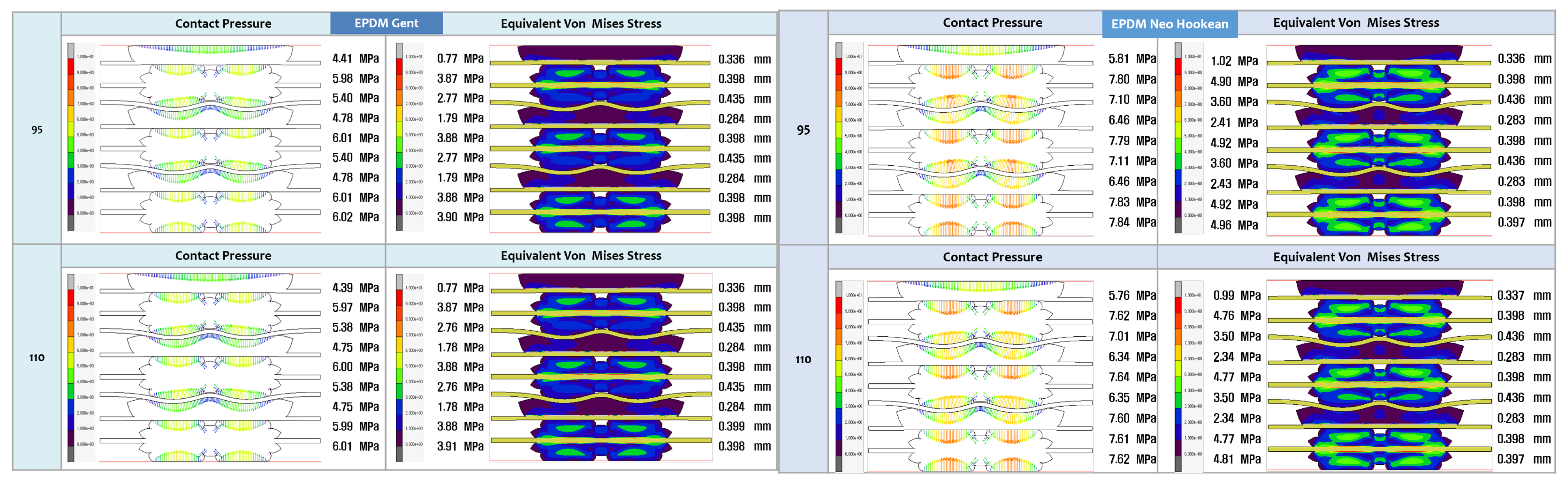
- The study aims to assess the accuracy of various hyperelastic models, such as Ogden, Gent, Mooney-Rivlin, Yeoh, Neo-Hookean, and Arruda-Boyce, in representing the mechanical behaviour of LSR and EPDM gasket materials. By evaluating these models and their predictions against experimental and FEA data, this research will provide valuable insights into the most appropriate hyperelastic model for accurately simulating the behaviour of gaskets in PEMFC applications.
2. Materials and Methods
2.1. Overview of Gasket Material Selection
2.2. Overview of Hyper-Elastic Constitutive Models
- Neo-Hookean model parameters:
- represents the strain energy density.
- is the shear modulus (also known as the material’s Lamé parameter), which characterises the material’s resistance to shear deformation.
- is the bulk modulus, which characterises the material’s resistance to volume change.
- is the first invariant of the modified deformation tensor.
- J is the volume ratio of the deformed state to the undeformed state, known as the Jacobian.
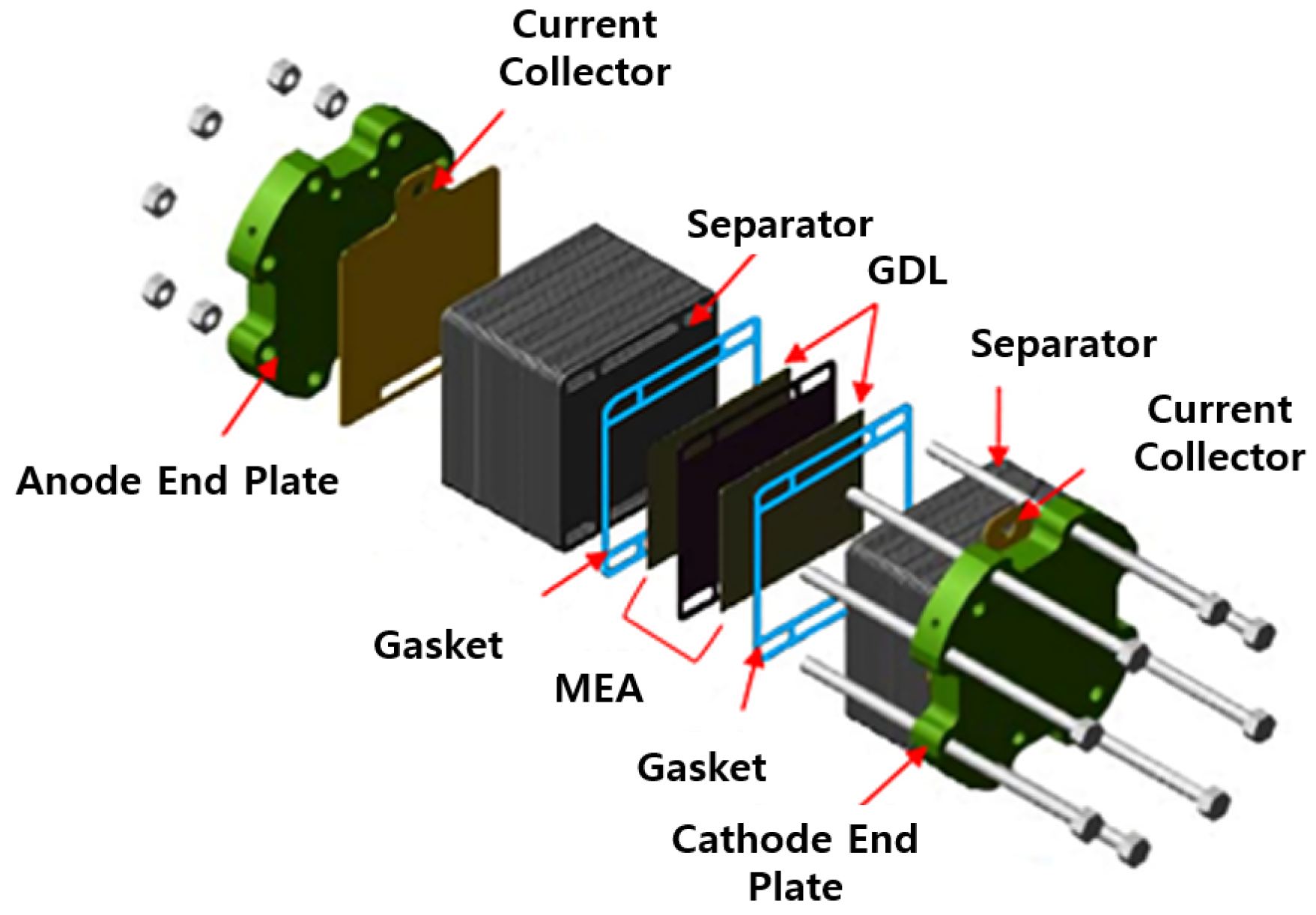
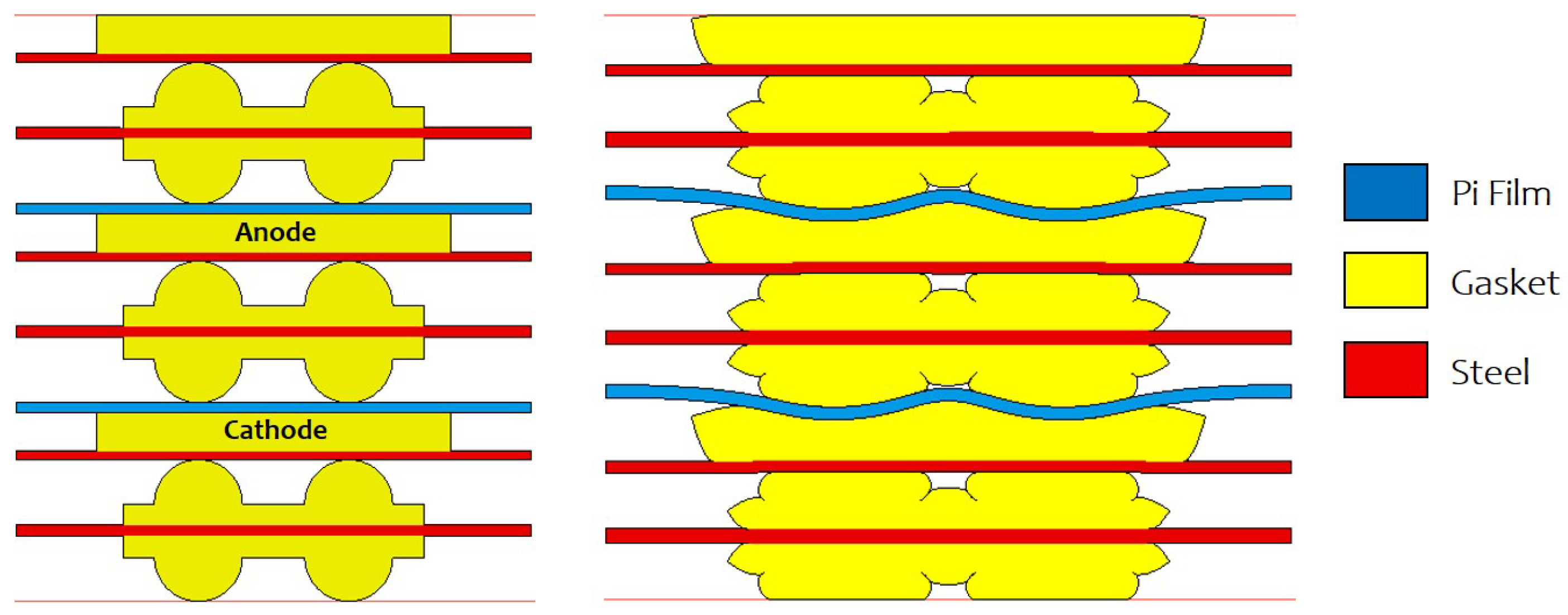
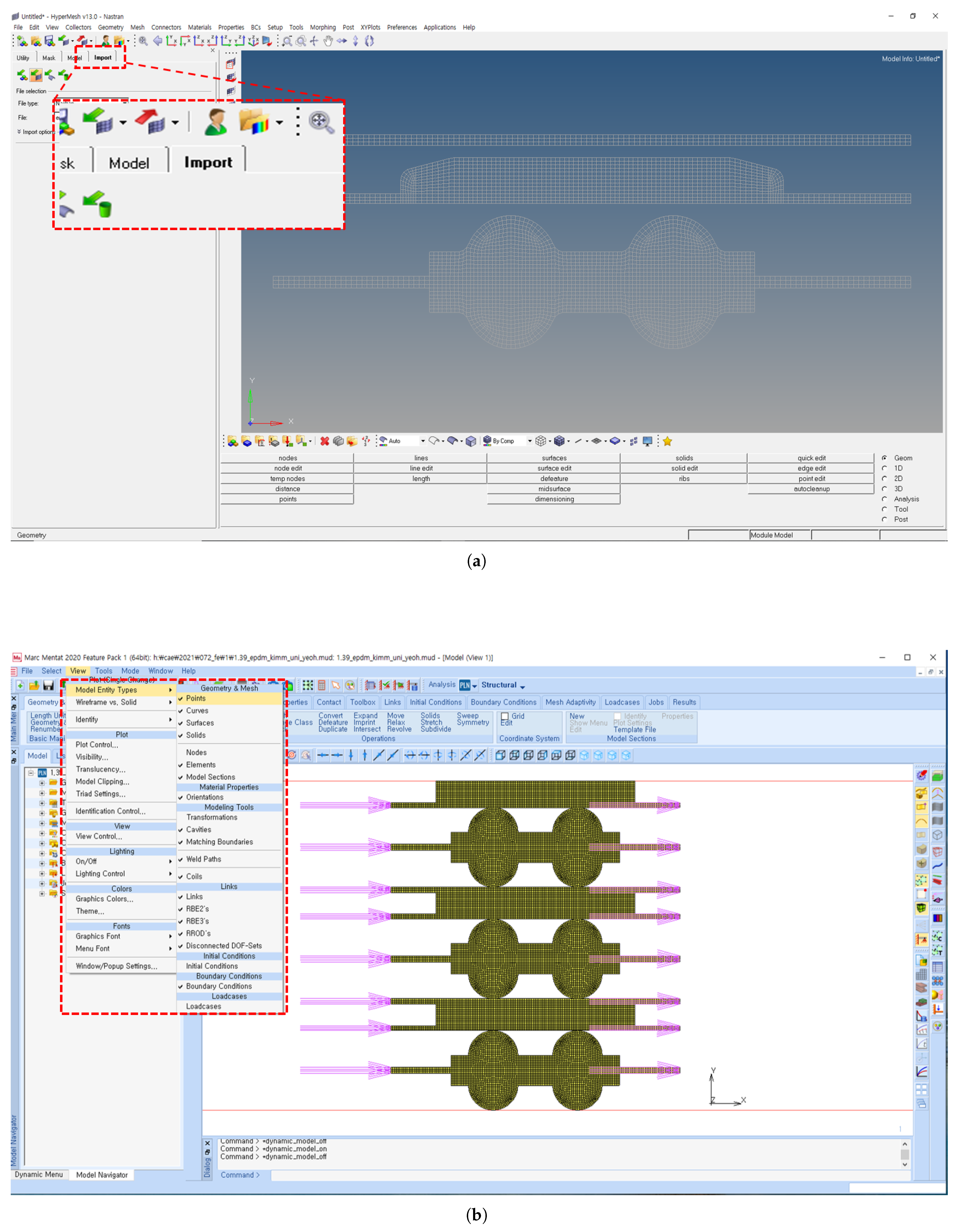
2.3. Proposed Gasket Material FEA Model
- Geometry and Mesh Generation: Create a detailed 3D geometry of the gasket and its sealing components. Generate a finite element mesh for the entire assembly, including the gasket, mating surfaces, and bolts or fasteners.
- Material Properties: Define the material properties of the gasket using a suitable hyperelastic model (e.g., Neo-Hookean, Mooney-Rivlin, etc.). Input the material parameters derived from experimental data.
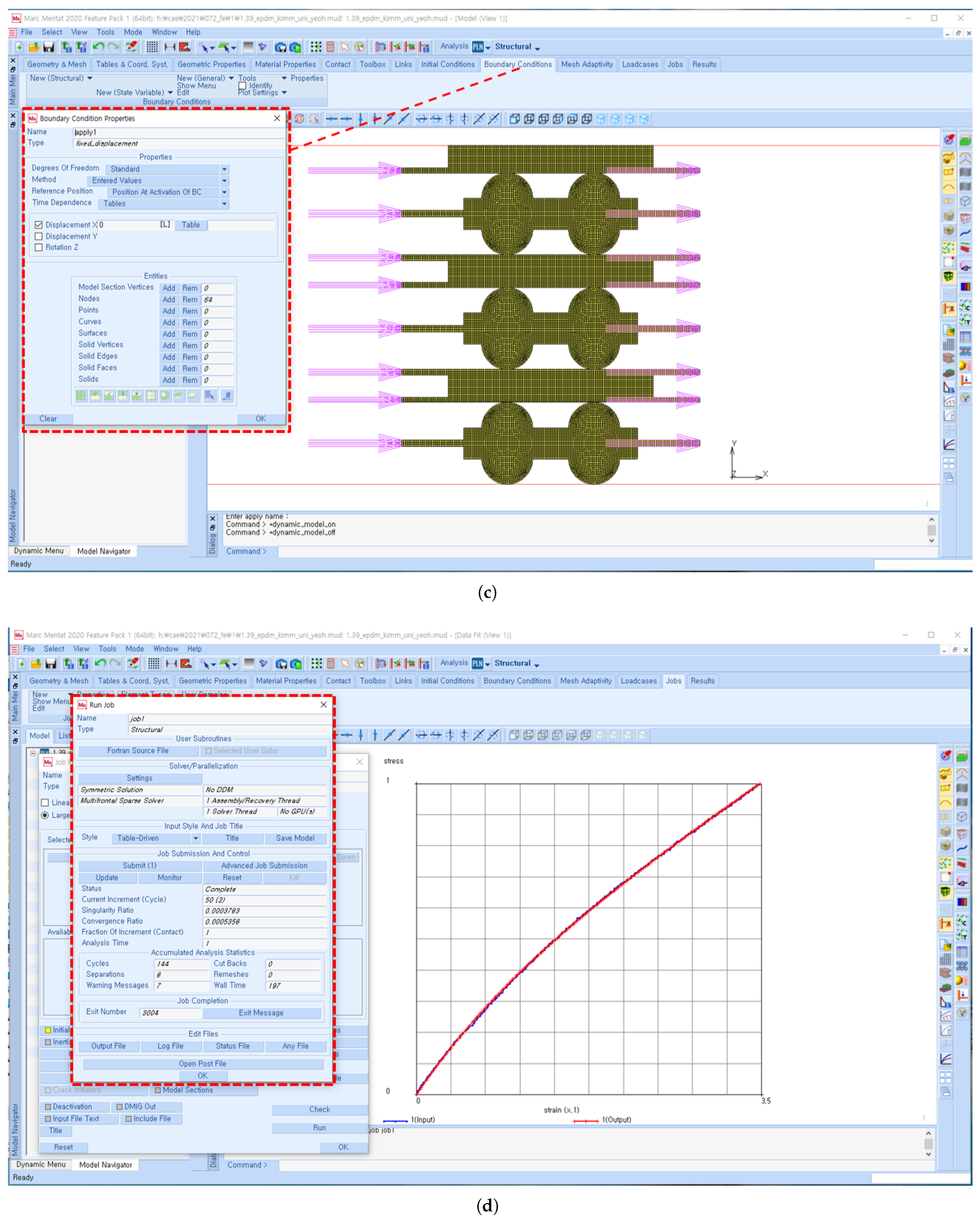
- Boundary Conditions: Apply appropriate boundary conditions to simulate the actual operating conditions of the gasket assembly.
- Contact Modelling: Define the contact interactions between the gasket and the mating surfaces. This step is crucial to accurately simulate how the gasket deforms and interacts with the surrounding components. Choose an appropriate contact algorithm, such as penalty-based or augmented Lagrange, and specify friction coefficients if friction plays a role in sealing.
- Load Application: Apply loads or pressures that mimic the operational conditions of the gasket. These loads might include internal or external forces, thermal expansion, mechanical loading, or a combination.
- Analysis and Solution: Perform a nonlinear static analysis to simulate the deformation and stress distribution in the gasket and the surrounding components. Solve the FEA problem iteratively, considering the nonlinearities introduced by the hyperelastic material behaviour and contact interactions.
- Results Interpretation: Extract and analyse the results, which include:
- Displacements and deformations of the gasket and other components.
- Strains and stresses, including von Mises stress, throughout the assembly.
- Contact pressures at the gasket’s sealing surface.
- Focus on areas of interest, such as the gasket-contacting regions and regions prone to stress concentrations.
- Validation and Comparison: Validate the FEA model by comparing the predicted results to experimental data or known analytical solutions. Assess the model’s accuracy and reliability in capturing the behaviour of the gasket assembly under different loading conditions.
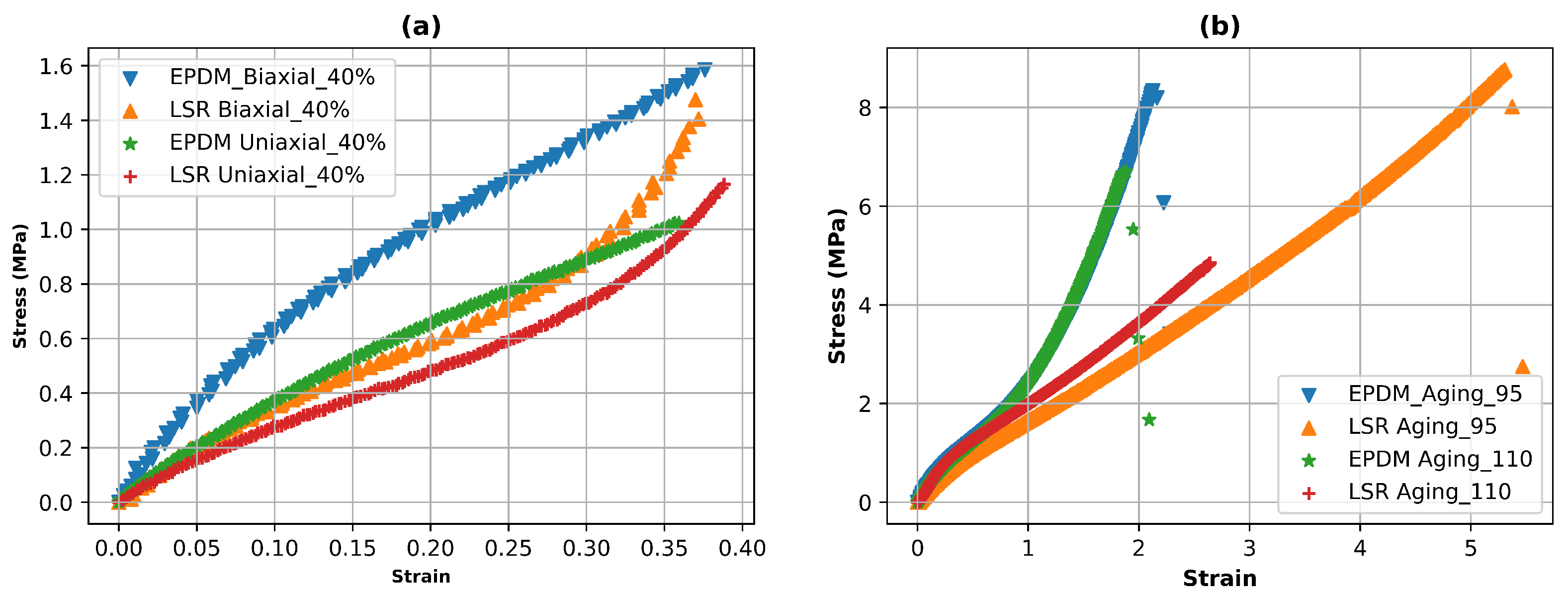
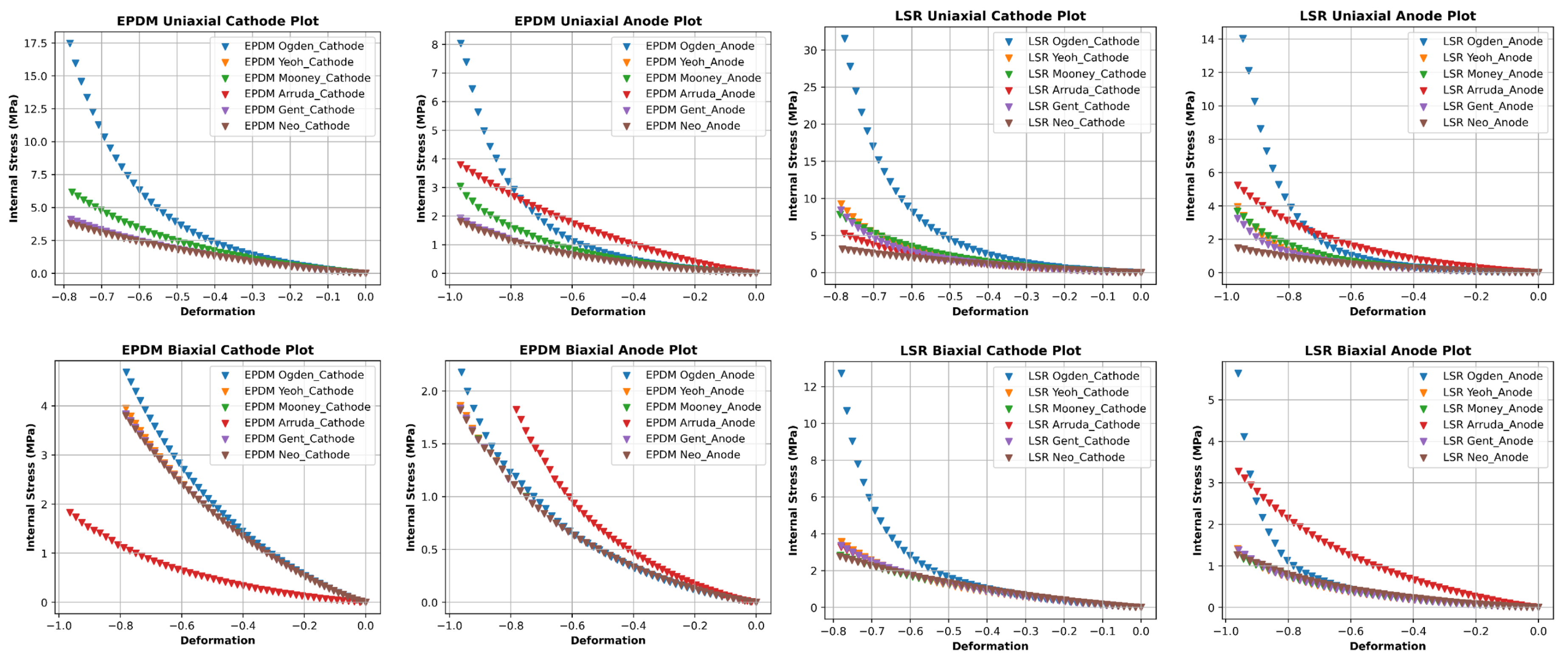
2.4. Experimental Testing for the Gasket Materials
3. Results and Discussion
3.1. Gasket Material FEA Modelling Characterization
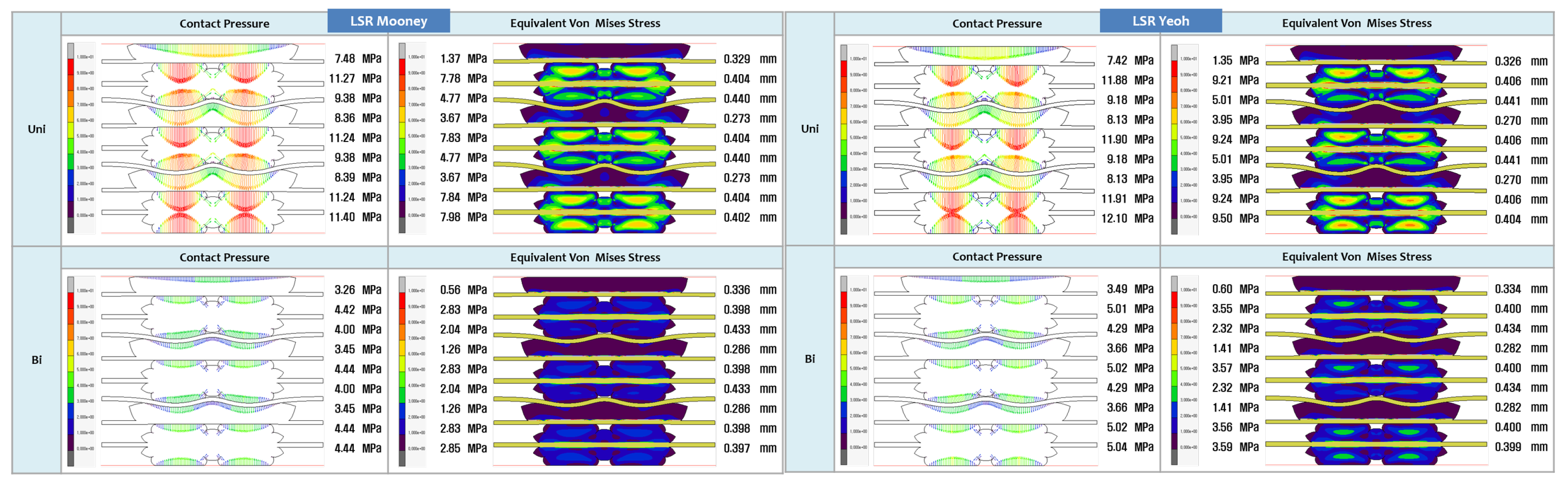
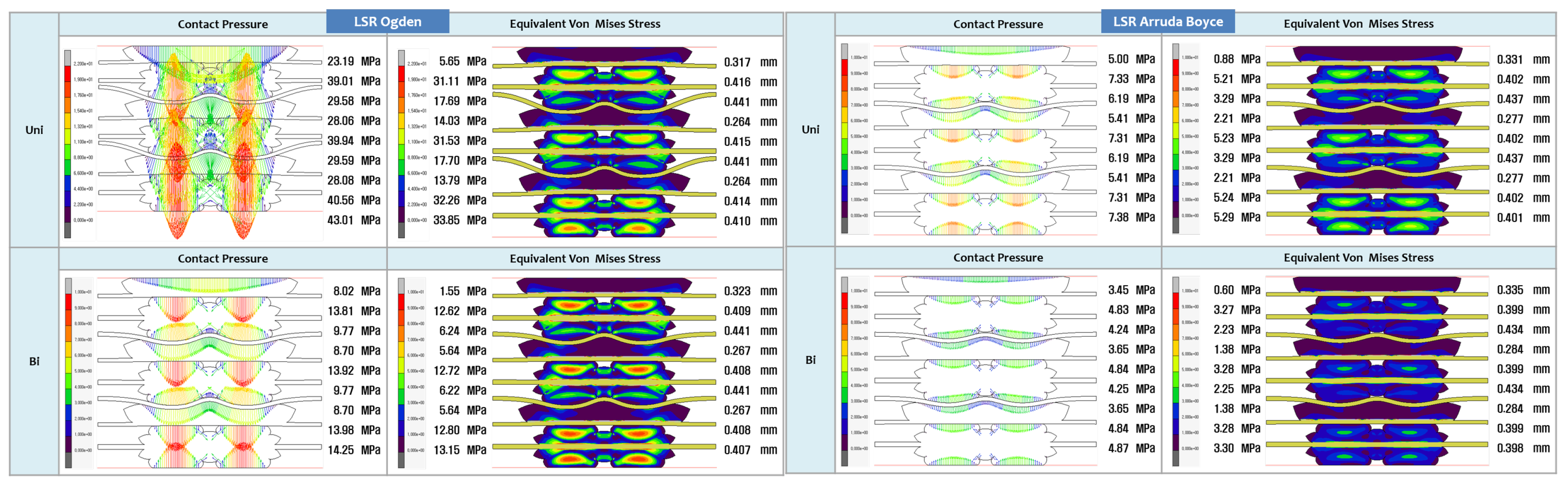
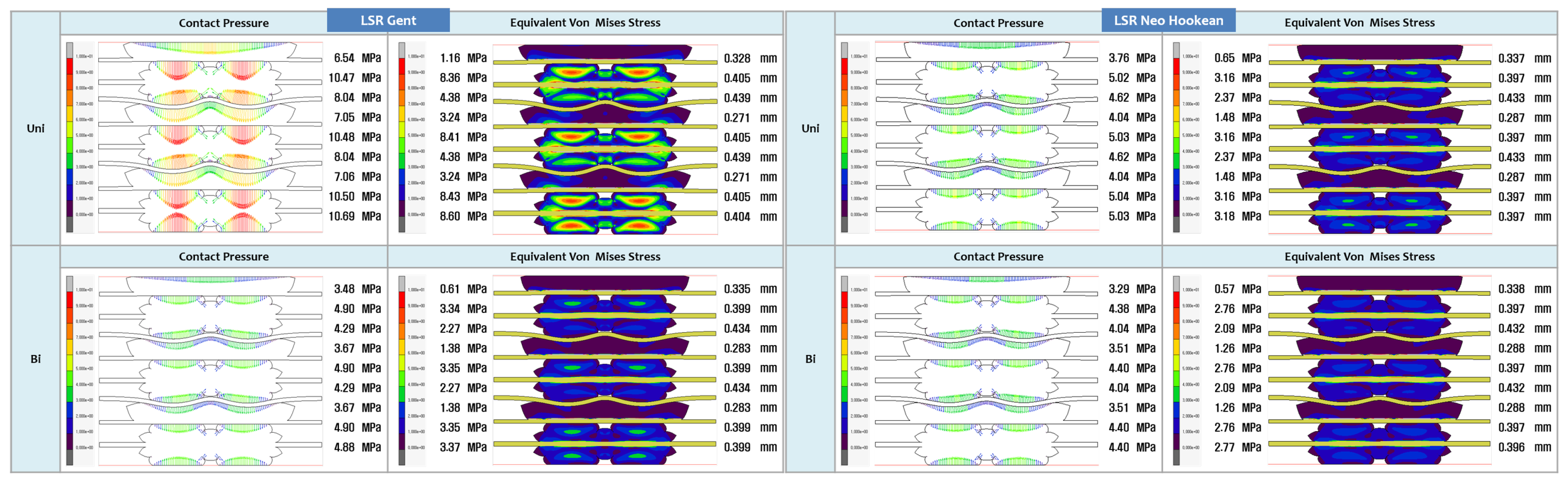
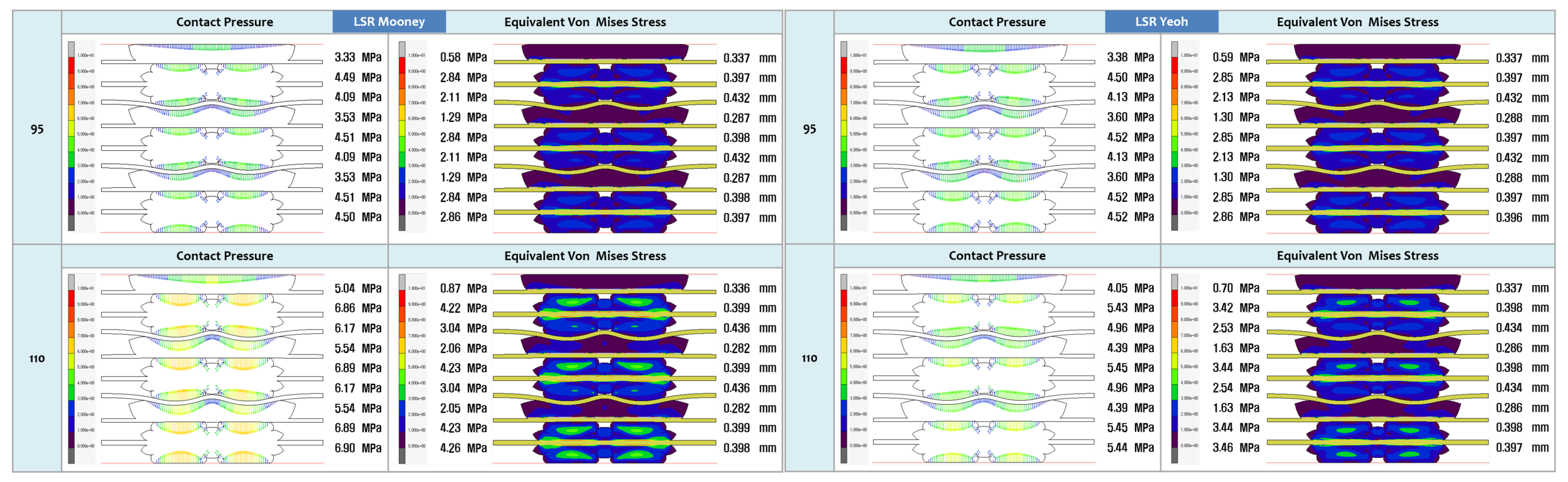
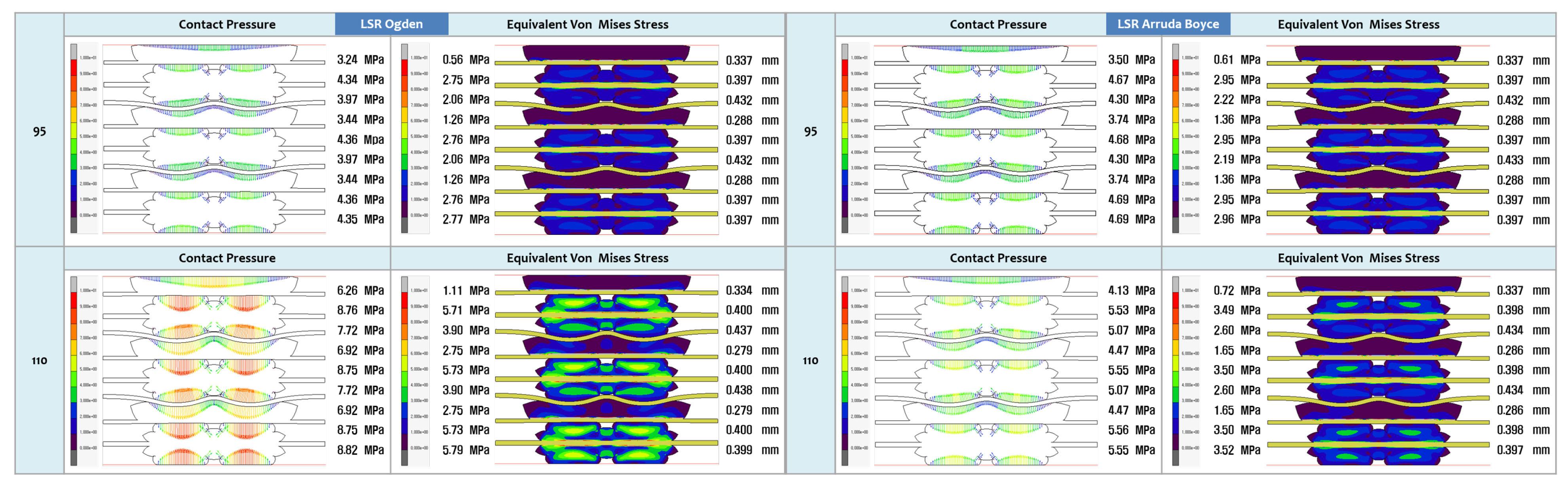
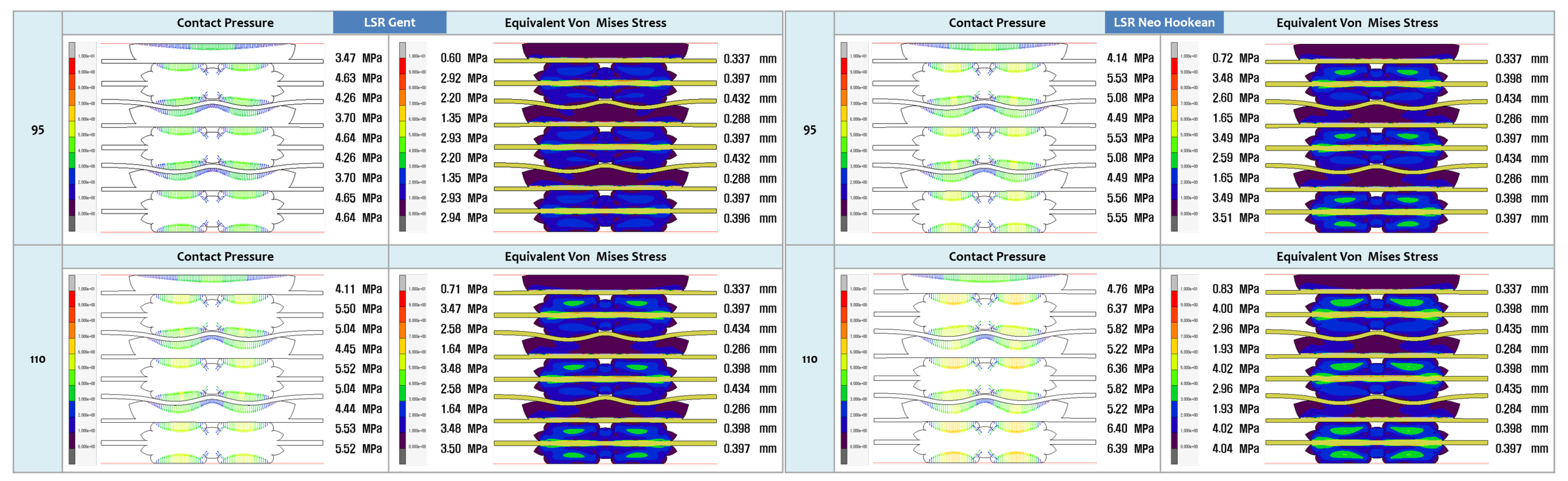
3.2. FEA Modelling Visualization
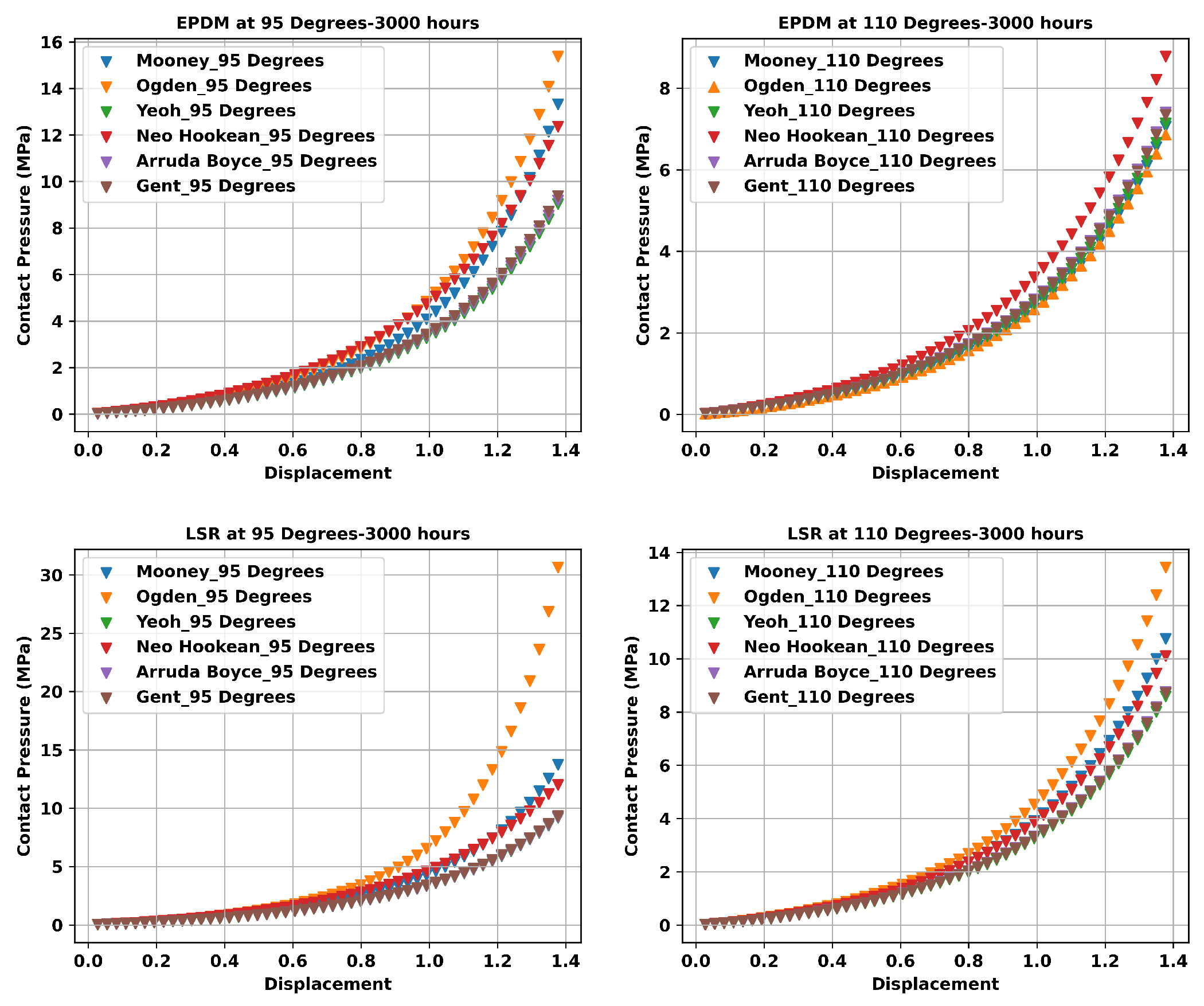
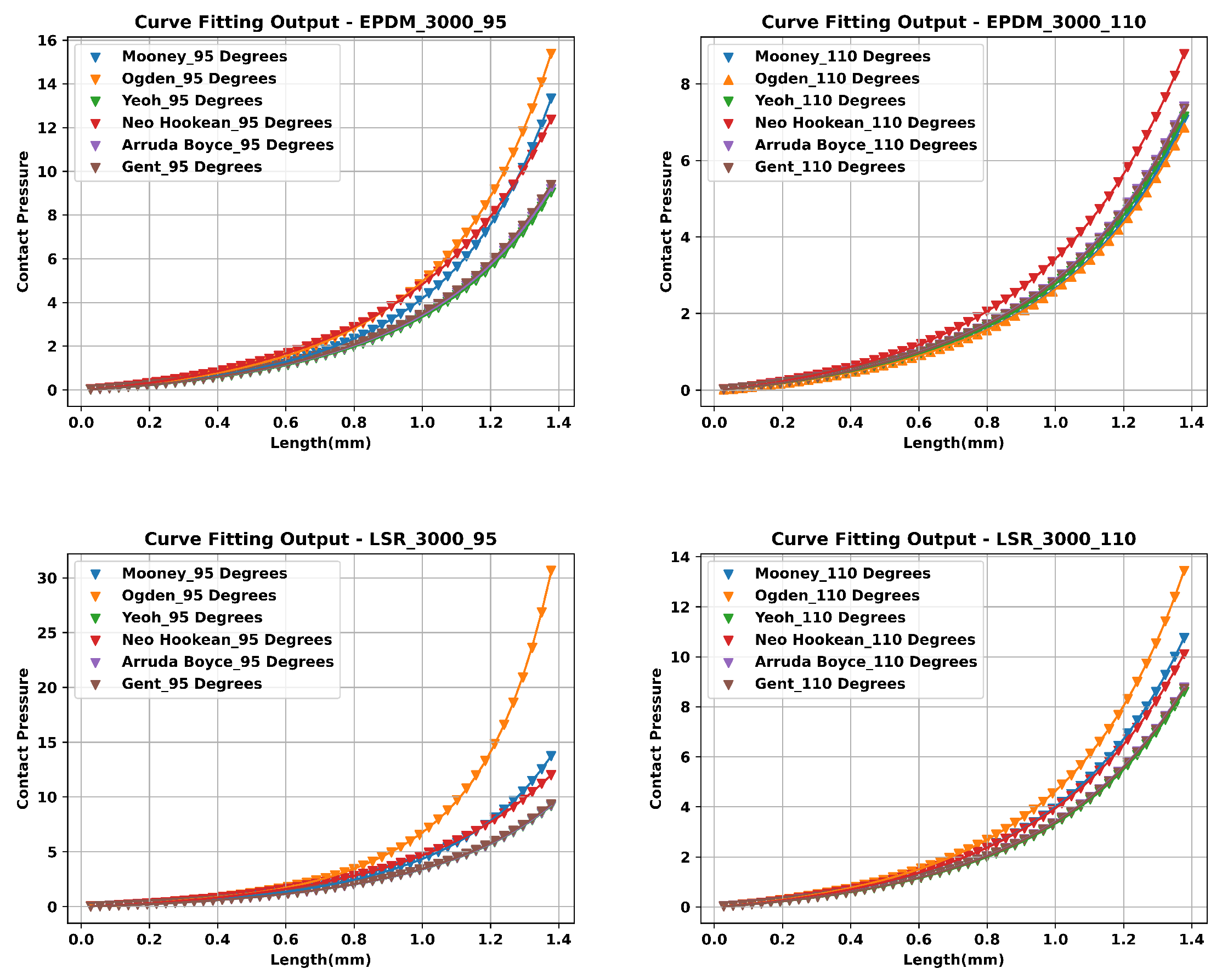
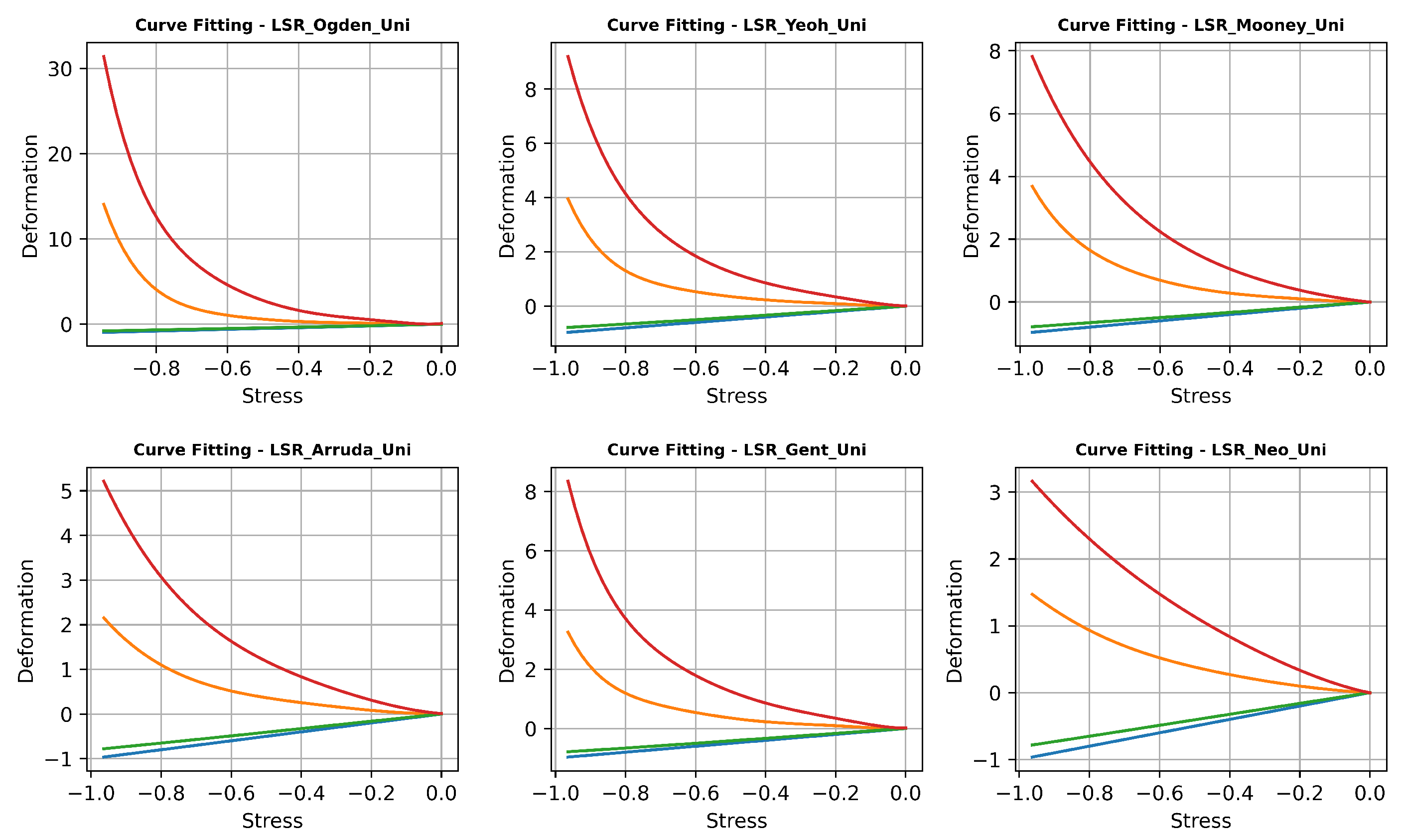
3.3. FEA Modelling Output and Curve Fitting Assessment
3.4. Proposed Non-Linear Regression Analysis
- where y is the dependent variable,
- x is the independent variable and
- a0, a1, a2, ⋯ are the coefficients that need to be estimated.
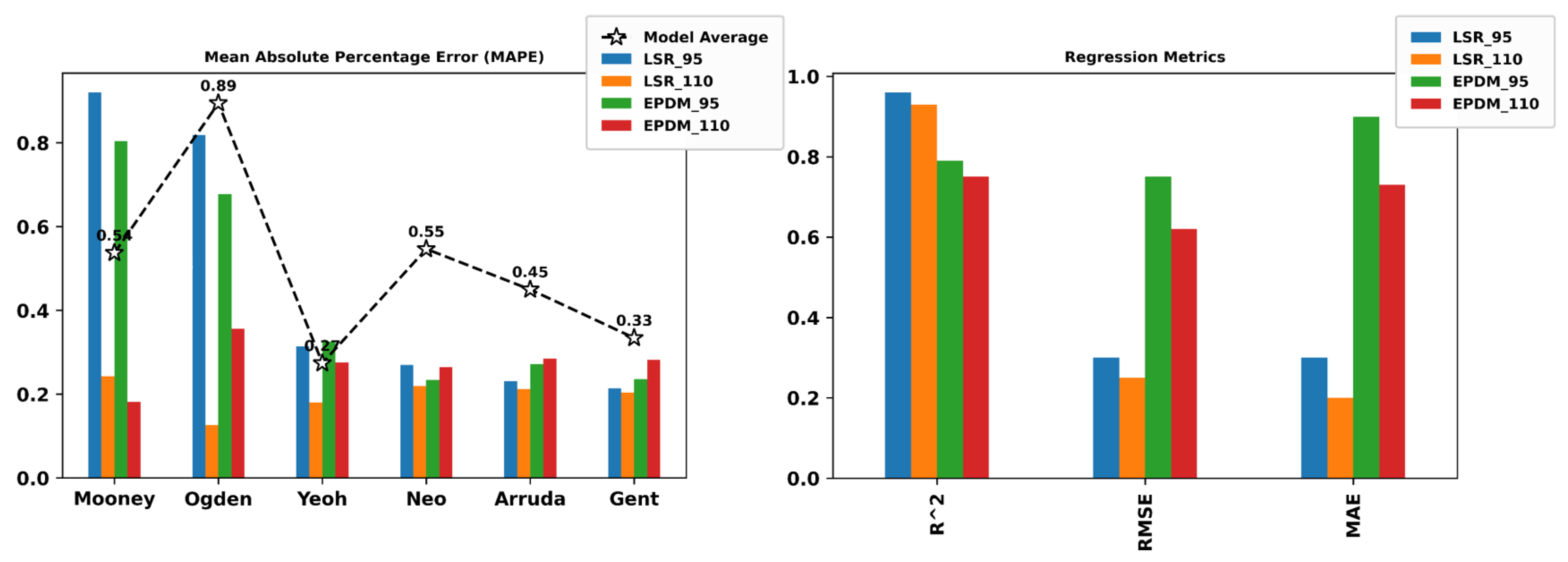
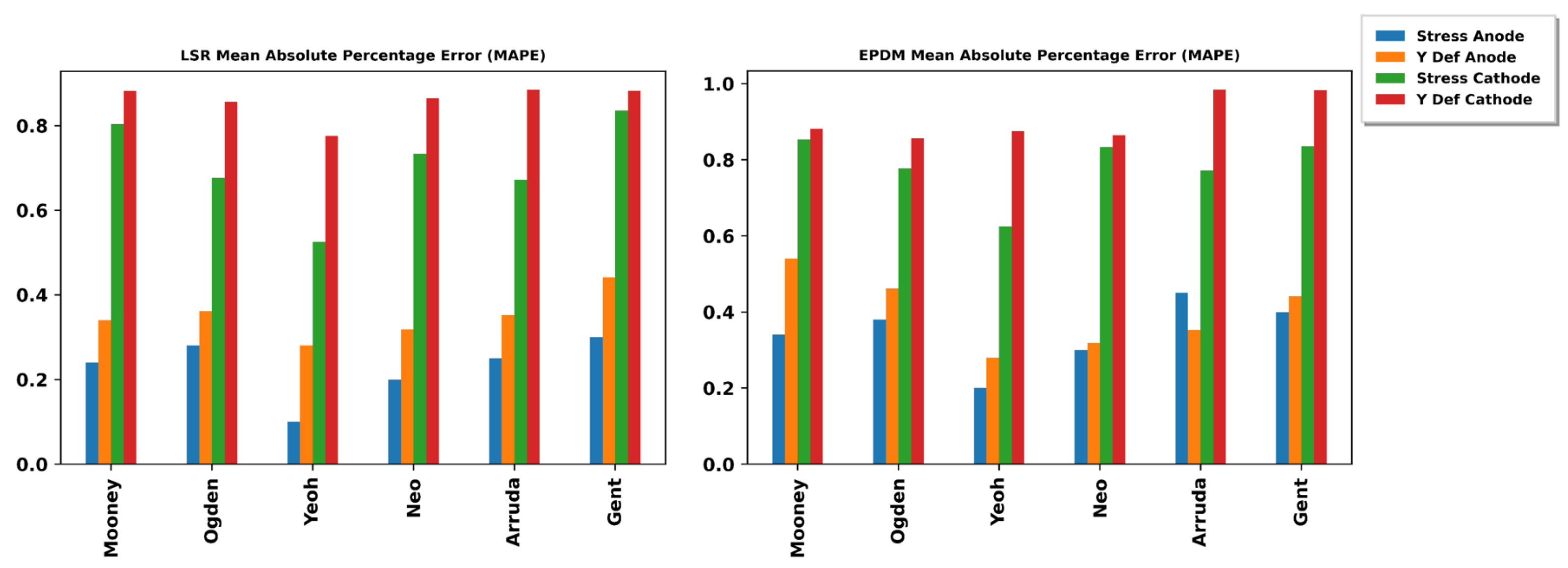
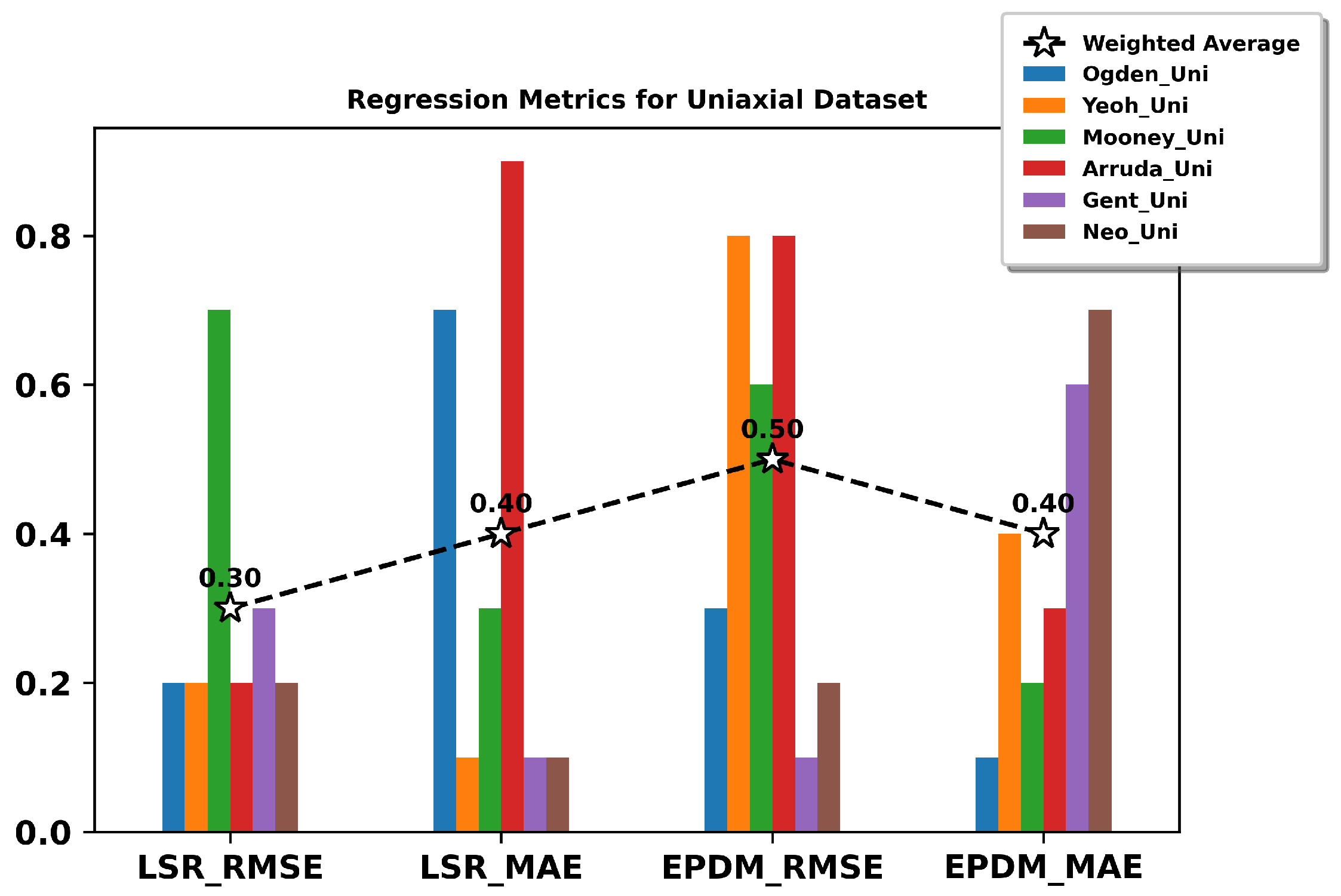
3.5. Non-Linear Regression Performance Metrics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ATIR-FTIR | Attenuated Total Reflectance Fourier Transform Infrared Spectroscopy |
| CR | Cluoropene Rubber |
| DMA | Dynamic Mechanical Analysis |
| EPDM | Ethylene Propylene Diene Monomer |
| FEA | Finite Element Analysis |
| FEP | Fluorinated Ethylene Propylene |
| LSR | Liquid Silicon Rubber |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MEA | Membrane Electrode Assembly |
| MSE | Mean Square Error |
| NBR | Nitrite Butadiene Rubber |
| PEMFC | Proton-exchange membrane fuel cell |
| PFSA | Perfluoro Sulfonic Acid |
| PTFE | Polytetrafluoroethylene |
| R2 | R-Squared |
| RMSE | Root Mean Square Error |
| STC | Sensors, Test and Calibration |
| TFA | Trifluoroacetic acid |
| VMQ | Silicone Rubber Vinyl Methyl |
| XPS | X-ray Photoelectron Spectroscopy |
Appendix A
References
- Singla, M.K.; Nijhawan, P.; Oberoi, A.S. Hydrogen fuel and fuel cell technology for cleaner future: A review. Environ. Sci. Pollut. Res. 2021, 28, 15607–15626. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, Y.; Hosseini, S.E.; Butler, B.; Alzhahrani, H.; Senior, B.T.F.; Ashuri, T.; Krohn, J. Hydrogen Fuel Cell Vehicles; Current Status and Future Prospect. Appl. Sci. 2019, 9, 2296. [Google Scholar] [CrossRef]
- John, M.T.; Peter, P.E.; Peter, J.D.; Gari, P.O. Decarbonising energy: The developing international activity in hydrogen technologies and fuel cells. J. Energy Chem. 2020, 51, 405–415. [Google Scholar] [CrossRef]
- Jamil, A.; Rafiq, S.; Iqbal, T.; Khan, H.A.A.; Khan, H.M.; Azeem, B.; Mustafa, M.Z.; Hanbazazah, A.S. Current status and future perspectives of proton exchange membranes for hydrogen fuel cells. Chemosphere 2022, 303 Pt 3, 135204. [Google Scholar] [CrossRef]
- Pourrahmani, H.; Siavashi, M.; Yavarinasab, A.; Matian, M.; Chitgar, N.; Wang, L.; Van herle, J. A Review on the Long-Term Performance of Proton Exchange Membrane Fuel Cells: From Degradation Modeling to the Effects of Bipolar Plates, Sealings, and Contaminants. Energies 2022, 15, 5081. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Alanazi, A.; Vichare, P.; Sayed, E.T.; Maghrabie, H.M.; Elsaid, K.; Abdelkareem, M.A. Novel Trends in Proton Exchange Membrane Fuel Cells. Energies 2022, 15, 4949. [Google Scholar] [CrossRef]
- Vikas, K.; Poornesh, K.; Koorata, U.S.; Pranav, P.; Soney, C.G. Review on physical and chemical properties of low and high-temperature polymer electrolyte membrane fuel cell (PEFC) sealants. Polym. Degrad. Stab. 2022, 205, 110151. [Google Scholar] [CrossRef]
- Yiqing, W.; Tahrizi, A.; Yilin, W.; Ying, C.; Eric, D.W.; Mark, H.E.; Kenneth, G.R.; Yong, W.; Feng, G.; Unmesh, M.; et al. A comparative study between real-world and laboratory accelerated ageing of Cu/SSZ-13 SCR catalysts. Appl. Catal. B Environ. 2022, 318, 121807. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Al Khattab, R. Fresh Properties and Sulfuric Acid Resistance of Sustainable Mortar Using Alkali-Activated GGBS/Fly Ash Binder. Polymers 2022, 14, 591. [Google Scholar] [CrossRef]
- Winter, L.; Lampke, T. Influence of Hydrothermal Sealing on the High Cycle Fatigue Behavior of the Anodized 6082 Aluminum Alloy. Coatings 2022, 12, 1070. [Google Scholar] [CrossRef]
- Yang, D.; Tan, Y.; Li, B.; Ming, P.; Xiao, Q.; Zhang, C. A Review of the Transition Region of Membrane Electrode Assembly of Proton Exchange Membrane Fuel Cells: Design, Degradation, and Mitigation. Membranes 2022, 12, 306. [Google Scholar] [CrossRef] [PubMed]
- Ke, S.; Yimin, W.; Yuhang, D.; Hongjie, X.; Philip, M.; Tobias, S.; Katharina, B.; Christopher, E.; Hannes, W.W.; Jens, S.; et al. Assembly techniques for proton exchange membrane fuel cell stack: A literature review. Renew. Sustain. Energy Rev. 2022, 153, 111777. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, Y.K.; Kim, D.H. Mechanical properties of gasket elastomers for sealing applications. J. Appl. Polym. Sci. 2016, 133, 43873. [Google Scholar] [CrossRef]
- Kurniawan, A.; Shim, Y. Tensile behaviour of silicone rubber gaskets under different temperature conditions. J. Appl. Polym. Sci. 2017, 134, 44635. [Google Scholar] [CrossRef]
- Kang, J.; Lee, C.; Kim, J. Tensile and compression properties of soft rubber gaskets used in automotive applications. Polym. Test. 2015, 42, 42–47. [Google Scholar] [CrossRef]
- Wang, X.; Li, X. Influence of filler type on the mechanical properties of nitrile rubber gaskets for sealing applications. J. Appl. Polym. Sci. 2017, 134, 45217. [Google Scholar] [CrossRef]
- Chen, J.; Yang, J.; Li, Y. Tensile properties and stress relaxation behaviour of silicone rubber gaskets for automotive applications. Polym. Test. 2015, 47, 90–95. [Google Scholar] [CrossRef]
- Pehlivan-Davis, S. Polymer Electrolyte Membrane (PEM) Fuel Cell Seals Durability. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2016. Available online: https://hdl.handle.net/2134/21749 (accessed on 8 April 2023).
- Wu, F.; Chen, B.; Yan, Y.; Chen, Y.; Pan, M. Degradation of Silicone Rubbers as Sealing Materials for Proton Exchange Membrane Fuel Cells under Temperature Cycling. Polymers 2018, 10, 522. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, Q.; Tu, Z.; Tu, W.; Wan, Z.; Pan, M.; Zhang, H. Degradation of silicone rubbers with different hardness in various aqueous solutions. Polym. Degrad. Stab. 2014, 109, 122–128. [Google Scholar] [CrossRef]
- Lin, C.W.; Chien, C.H.; Tan, J.; Chao, Y.J.; Van Zee, J.W. Dynamic mechanical characteristics of five elastomeric gasket materials aged in a simulated and accelerated PEM fuel cell environment. Int. J. Hydrogen Energy 2011, 36, 6756–6767. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Y. Sealing performance and mechanical behaviour of PEMFCs sealing system based on thermodynamic coupling. Int. J. Hydrogen Energy 2020, 45, 23480–23489. [Google Scholar] [CrossRef]
- Shen, L.; Xia, L.; Han, T.; Wu, H.; Guo, S. Improvement of hardness and compression set properties of EPDM seals with alternating multilayered structure for PEM fuel cells. Int. J. Hydrog. Energy 2016, 41, 23164–23172. [Google Scholar] [CrossRef]
- Hu, G.; Zhang, P.; Wang, G.; Zhang, M.; Li, M. The influence of rubber material on sealing performance of packing element in compression packer. J. Nat. Gas Sci. Eng. 2017, 38, 120–138. [Google Scholar] [CrossRef]
- Lin, C.W.; Chien, C.H.; Tan, J.; Chao, Y.J.; Van Zee, J.W. Chemical degradation of five elastomeric seal materials in a simulated and accelerated PEM fuel cell environment. J. Power Sources 2011, 196, 1955–1966. [Google Scholar] [CrossRef]
- Pehlivan-Davis, S.; Clarke, J.; Armour, S. Comparison of accelerated ageing of silicone rubber gasket material with ageing in a fuel cell environment. J. Appl. Polym. Sci. 2013, 129, 1446–1454. [Google Scholar] [CrossRef]
- Wang, Z.; Tan, J.; Wang, Y.; Liu, Z.; Feng, Q. Chemical and mechanical degradation of silicone rubber under two compression loads in simulated proton-exchange membrane fuel-cell environments. J. Appl. Polym. Sci. 2019, 136, 47855. [Google Scholar] [CrossRef]
- Chang, H.; Wan, Z.; Chen, X.; Wan, J.; Luo, L.; Zhang, H.; Tu, Z. Temperature and humidity effect on ageing of silicone rubbers as sealing materials for proton exchange membrane fuel cell applications. Appl. Therm. Eng. 2016, 104, 472–478. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, C.; Fan, P.; Kuang, Y.; Dong, Z. The Sealing Effect Improvement Prediction of Flat Rubber Ring in Roller Bit Based on Yeoh-Revised Model. Materials 2022, 15, 5529. [Google Scholar] [CrossRef]
- Lin, A.; Wu, J.; Li, H.; Li, Z.; Su, B.; Wang, Y. Effect of Geometric Error on Friction Behavior of Cylinder Seals. Polymers 2021, 13, 3438. [Google Scholar] [CrossRef]
- Vieira, J.C.; Mendes, A.d.O.; Ribeiro, M.L.; Vieira, A.C.; Carta, A.M.; Fiadeiro, P.T.; Costa, A.P. FEM Analysis Validation of Rubber Hardness Impact on Mechanical and Softness Properties of Embossed Industrial Base Tissue Papers. Polymers 2022, 14, 2485. [Google Scholar] [CrossRef]
- Latif, R.F.; Khan, N.S. Comparative Analysis of Various Hyperelastic Models for Neoprene Gasket at Ranging Strains. In Proceedings of the 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 8–12 January 2019; pp. 179–188. [Google Scholar] [CrossRef]
- Cheon, K.-M.; Akpudo, U.E.; Kareem, A.B.; Nwabufo, O.C.; Jeon, H.-R.; Hur, J.-W. An FEA-Assisted Decision-Making Framework for PEMFC Gasket Material Selection. Energies 2022, 15, 2580. [Google Scholar] [CrossRef]
- Olayinka, A.; Emblom, W.J. Surface roughness of AISI 1010 and AISI 304 of PEMFC bipolar plates with microscale hydroformed capillary channels. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2022, 236, 1332–1340. [Google Scholar] [CrossRef]
- Kim, Y.K.; Kim, Y.H.; Kim, J.Y. Development of silicone-based gasket material for PEMFCs. J. Power Sources 2018, 284, 289–298. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, Y.; Wang, J.; Liu, Q. A review on proton exchange membrane fuel cell (PEMFC) gasket materials. J. Power Sources 2016, 308, 101–119. [Google Scholar] [CrossRef]
- Haque, M.E.; Danquah, M.K. A review on the design, selection and optimization of gasket materials for proton exchange membrane fuel cell (PEMFC). Renew. Sustain. Energy Rev. 2015, 47, 766–776. [Google Scholar] [CrossRef]
- Rau, N.; Spiess, W. Fluorinated Ethylene Propylene (FEP) gaskets for proton exchange membrane fuel cells (PEMFCs): An overview. J. Appl. Polym. Sci. 2016, 133, 43189. [Google Scholar]
- Lee, H.J.; Kim, J.Y. Performance comparison of silicone and fluoropolymer gaskets for proton exchange membrane fuel cells (PEMFCs). J. Power Sources 2018, 389, 157–166. [Google Scholar] [CrossRef]
- Baker, J.M.; Kim, Y. Dynamic mechanical analysis of an EPDM rubber. J. Appl. Polym. Sci. 2013, 130, 378–384. [Google Scholar] [CrossRef]
- Dubey, N.C.; Bose, S.K. Studies on the thermal and mechanical properties of EPDM and its composites. Polym. Compos. 2015, 36, 631–637. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, J.; Han, X. Preparation and properties of EPDM/organic silica hybrid nanocomposites. J. Appl. Polym. Sci. 2015, 132, 42076. [Google Scholar] [CrossRef]
- Hiltunen, M.; Nurminen, J.; Ahola, S. Effect of filler type and content on the properties of EPDM rubber compounds. Rubber Chem. Technol. 2015, 88, 564–576. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Han, X. Synthesis and properties of EPDM/organoclay nanocomposites. J. Appl. Polym. Sci. 2013, 128, 4117–4123. [Google Scholar] [CrossRef]
- Fang, Y.; Xu, L.; Du, Y. Recent advances in liquid silicone rubber (LSR) materials and applications. J. Appl. Polym. Sci. 2020, 137, 48180. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, H.J.; Kim, K.H. Preparation and mechanical properties of liquid silicone rubber/silicone rubber composite materials. J. Appl. Polym. Sci. 2019, 136, 47758. [Google Scholar] [CrossRef]
- Chiu, H.W.; Li, J.H. Application of liquid silicone rubber (LSR) materials in medical and healthcare products. Polymers 2020, 12, 1019. [Google Scholar]
- Li, L.; Li, Q.; Li, H.; Qiu, Q. A review of liquid silicone rubber (LSR) material and its processing technologies. Polymers 2019, 11, 2288. [Google Scholar]
- Sun, X.; Li, C.; Li, S.; Zhang, X. Properties and applications of liquid silicone rubber (LSR) in 3D printing. Polymers 2020, 12, 1866. [Google Scholar]
- Chen, X.; Lin, T. The research progress of liquid silicone rubber (LSR) materials in the field of soft-touch consumer electronics. J. Appl. Polym. Sci. 2019, 136, 48005. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Y.; Liu, Y. Study on the thermal stability and mechanical properties of liquid silicone rubber (LSR) under high-temperature conditions. J. Appl. Polym. Sci. 2019, 136, 46936. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Lu, J. The research progress of liquid silicone rubber (LSR) materials in the field of aerospace. J. Appl. Polym. Sci. 2019, 136, 46580. [Google Scholar] [CrossRef]
- Kang, S.K.; Kim, Y.J.; Jeong, J.S. Characterization of FKM and VQM elastomers used in various sealing applications. J. Appl. Polym. Sci. 2019, 136, 46699. [Google Scholar] [CrossRef]
- Lee, J.Y.; Lee, Y.J. Performance comparison of FKM and VQM elastomers in high-temperature sealing applications. J. Polym. Eng. 2017, 37, 831–839. [Google Scholar] [CrossRef]
- Kim, H.J.; Lee, S.H. Evaluation of mechanical and dynamic mechanical properties of FKM and VQM elastomers. J. Elastomers Plast. 2015, 47, 165–173. [Google Scholar]
- Zhang, J.; Liu, Y.; Chen, X. FKM and VQM elastomers as dynamic seal materials: A review. J. Polym. Eng. 2019, 39, 901–913. [Google Scholar]
- Oh, J.H.; Kim, J.H. Chemical and thermal stability of FKM and VQM elastomers in high-temperature applications. J. Polym. Sci. Technol. 2017, 27, 145–152. [Google Scholar] [CrossRef]
- Murea, C.M. Updated Lagrangian for Compressible Hyperelastic Material with Frictionless Contact. Appl. Mech. 2022, 3, 533–543. [Google Scholar] [CrossRef]
- Ogden, R.; Saccomandi, G.; Sgura, I. Fitting hyperelastic models to experimental data. Comput. Mech. 2004, 34, 484–502. [Google Scholar] [CrossRef]
- Kim, B.; Lee, S.B.; Lee, J.; Cho, S.; Park, H.; Yeom, S.; Park, S.H. A comparison among Neo-Hookean model, Mooney-Rivlin model, and Ogden model for chloroprene rubber. Int. J. Precis. Eng. Manuf. 2012, 13, 759–764. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Ghayesh, M.H.; Chin, R.; Amabili, M. A review on the nonlinear dynamics of hyperelastic structures. Nonlinear Dyn. 2022, 110, 963–994. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Niu, S. A viscoelastic constitutive model for gasket materials under dynamic loading. J. Appl. Mech. Tech. Phys. 2019, 60, 763–771. [Google Scholar]
- Wang, X.; Su, J.; Hu, X. A constitutive model for gasket material based on the logarithmic strain rate. J. Appl. Mech. Tech. Phys. 2017, 58, 244–252. [Google Scholar]
- Chen, X.; Liu, Y. Constitutive models for gasket materials considering the nonlinear behaviour of fibre-reinforced rubber composites. Int. J. Non-Linear Mech. 2015, 77, 16–25. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, H. A new hyperelastic constitutive model for gasket materials under large deformation. J. Mech. 2017, 33, 797–807. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Niu, S. An improved constitutive model for gasket materials considering the nonlinear behaviour of rubber composites. Int. J. Mech. Mater. Des. 2018, 14, 53–65. [Google Scholar]


| EPDM | LSR | |||
|---|---|---|---|---|
| Material | Uniaxial | Biaxial | Uniaxial | Biaxial |
| Mooney Rivlin | = 4.72729 | = 0.646931 | = 4.38303 | = 0.421825 |
| = 0.749213 | = 6.03391 | = 0.50852 | = 6.03424 | |
| = 0.143837 | = 0.00225633 | = 0.422279 | = 0.0257173 | |
| Yeoh | = 0.643052 | = 0.644965 | = 0.479358 | = 0.3965 |
| = 4.30289 | = 5.07886 | = 9.36578 | = 5.4214 | |
| = 2.56582 | = 0.00478875 | = 0.379155 | = 0.0479549 | |
| Ogden | M = −0.209622 E = −8.3336 | M = −2.14506 E = −0.0658951 | M = −0.256473 E = −9.15496 | M = −2.31696 E = −22.8029 |
| M = 0.0826136 E = 0.462419 | M = −1.27328 E = −0.0417977 | M = −0.0108753 E = −9.06697 | M = 0.35083 E = 4.46914 | |
| M = 2.69067 E = 0.493692 | M = 0.939258 E = 2.81305 | M = 0.000119912 E = 24.9996 | M = 5.80656 E = 24.9999 | |
| Neo-Hookean | = 0.643045 | = 0.647817 | = 0.538368 | = 0.468658 |
| Arruda Boyce | = 1.26113 | = 1.27561 | = 0.336706 | = 0.492217 |
| = 33.1881 | = 44.4993 | = 1.1 | = 1.84821 | |
| Gent | = 3.80574 | = 3.86915 | = 2.79158 | = 2.39144 |
| = 16.5941 | = 93.0439 | = 4.52345 | = 7.1634 | |
| EPDM | LSR | |||
|---|---|---|---|---|
| Material | 95 °C | 110 °C | 95 °C | 110 °C |
| Mooney Rivlin | = 1.89472 | = 2.69426 | = 0.430276 | = 0.3454 |
| = 0.609227 | = 0.639308 | = 0.0162594 | = 0.33012 | |
| = 0.194325 | = 0.193217 | = 0.016835 | = 0.0323504 | |
| Yeoh | = 0.559296 | = 0.571377 | = 0.475585 | = 0.573542 |
| = 0.026558 | = 0.0237455 | = 0.00318065 | = 0.00468581 | |
| = 0.00294048 | = 0.00393118 | = 2.74909 | = 2.83474 | |
| Ogden | M = −0.664004 E = −3.93474 | M = −0.146388 E = −9.04283 | M = −0.402385 E = −0.686773 | M = −0.563078 E = −3.63278 |
| M = − E = −0.0664976 | M = −0.913931 E = −1.97932 | M = 0.626279 E = 2.41526 | M = −0.000248025 E = −0.0898954 | |
| M = 0.0757264 E = 4.91726 | M = −0.000730606 E = −0.0493021 | M = 7.91621 E = 15.2995 | M = 0.328036 E = 2.76844 | |
| Neo-Hookean | = 0.843536 | = 0.817821 | = 0.594852 | = 0.685988 |
| Arruda Boyce | = 0.942321 | = 0.917499 | = 0.972442 | = 1.1427 |
| = 3.61357 | = 3.33084 | = 28.6273 | = 20.9499 | |
| Gent | = 3.54155 | = 3.49077 | = 2.95009 | = 3.50546 |
| = 15.1266 | = 13.6892 | = 119.115 | = 88.4981 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-H.; Kareem, A.B.; Joo, W.J.; Hur, J.-W. FEA Assessment of Contact Pressure and Von Mises Stress in Gasket Material Suitability for PEMFCs in Electric Vehicles. Inventions 2023, 8, 116. https://doi.org/10.3390/inventions8050116
Park S-H, Kareem AB, Joo WJ, Hur J-W. FEA Assessment of Contact Pressure and Von Mises Stress in Gasket Material Suitability for PEMFCs in Electric Vehicles. Inventions. 2023; 8(5):116. https://doi.org/10.3390/inventions8050116
Chicago/Turabian StylePark, Soo-Hyun, Akeem Bayo Kareem, Woo Jeong Joo, and Jang-Wook Hur. 2023. "FEA Assessment of Contact Pressure and Von Mises Stress in Gasket Material Suitability for PEMFCs in Electric Vehicles" Inventions 8, no. 5: 116. https://doi.org/10.3390/inventions8050116
APA StylePark, S.-H., Kareem, A. B., Joo, W. J., & Hur, J.-W. (2023). FEA Assessment of Contact Pressure and Von Mises Stress in Gasket Material Suitability for PEMFCs in Electric Vehicles. Inventions, 8(5), 116. https://doi.org/10.3390/inventions8050116









