Research and Development of Criterial Correlations for the Optimal Grid Element Size Used for RANS Flow Simulation in Single and Compound Channels
Abstract
1. Introduction
- Non-stationarity;
- Irregularity, lack of strict order in time;
- Randomness;
- Three-dimensionality;
- Viscous and vortex nature of the flow;
- Coherence of large vortex structures.
- —characteristic size, m.
- —characteristic velocity, m/s;
- —viscosity, m2/s. There are currently several main approaches to modeling turbulence:
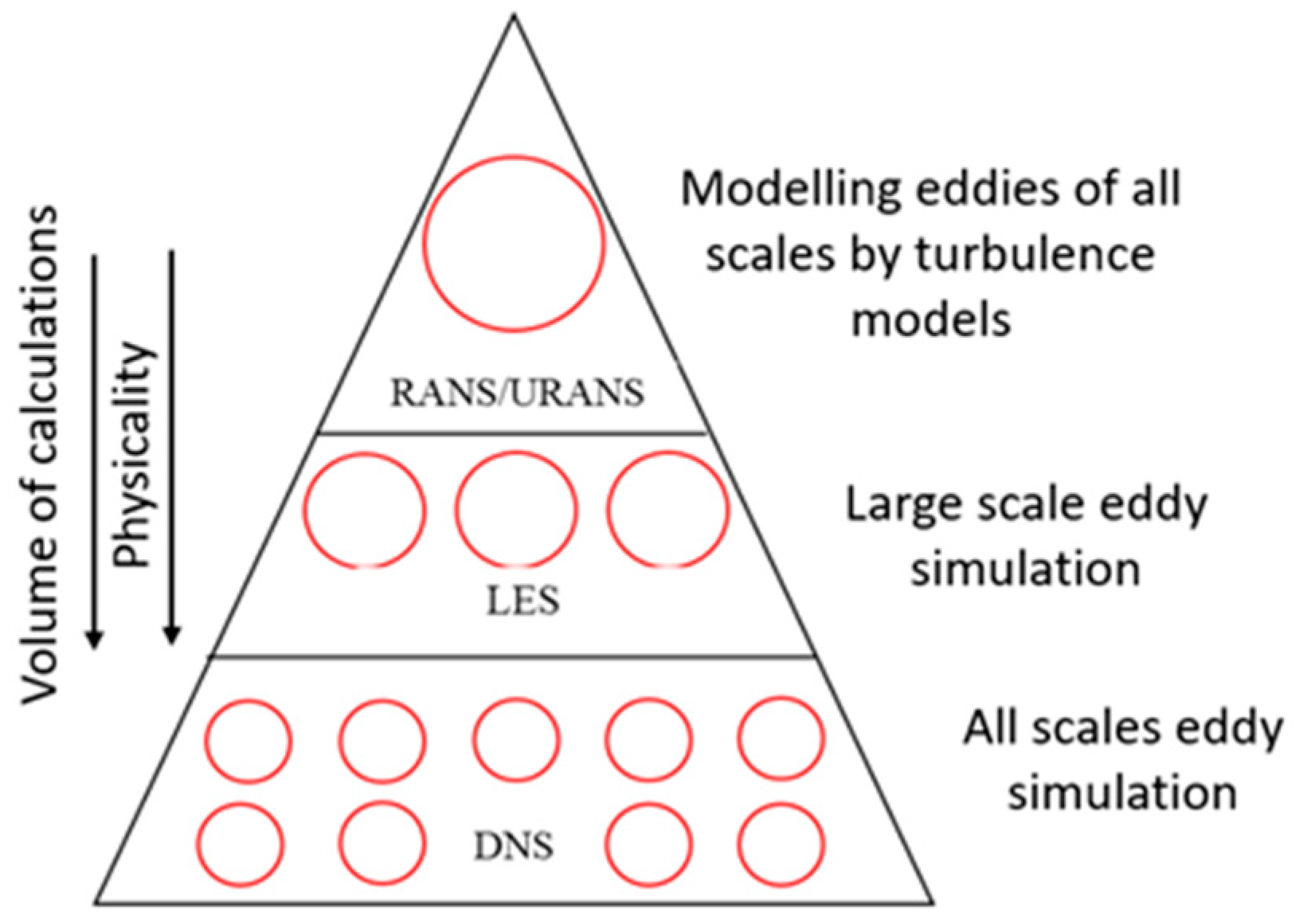
- Direct numerical simulation (DNS) [1] calculates the Navier–Stokes equations for eddies of all scales up to the Kolmogorov scale. With an increase in the size of the computational cell, the system of equations for DNS, as a rule, does not converge. At present, the DNS is used mainly for research purposes and in modeling low-Re currents.
- Large eddy modeling (LES) [2] uses the separation of eddies by scale: large eddies are directly resolved, small eddies are modeled using subgrid models. LES methods require a grid of the order of the scale of large eddies. Currently, LES is used in scientific research and technical applications as a highly accurate method.
- Modeling of Reynolds-averaged Navier-Stokes equations or unsteady Reynolds-averaged Navier-Stokes equations (RANS, URANS) [3]. Modeling is done by closing the equations through Boussinesq hypothesis and semi-empirical turbulence models over the entire energy spectrum.
- y—wall distance, m.
- —shear velocity, m/s.
- —viscosity, m2/s.
- The size of the grid element in correlations should be associated with characteristic hydrodynamic quantities that have a length scale and characterize the flow regime.
- The nature of the quantities used should allow one to estimate the scale of the element a priori, before conducting numerical studies.
- Correlations should take into account the results of empirical and analytical studies of turbulent flows in channels.
2. Research Object
3. Research Method
- —channel characteristic size, m;
- —optimal linear size of the global element of the grid model, m;
- —dimensionless distance from the wall corresponding to the transition to the flow core, [19];
- —the Reynolds number in the characteristic cross section of the channel, ; where is the characteristic flow velocity.
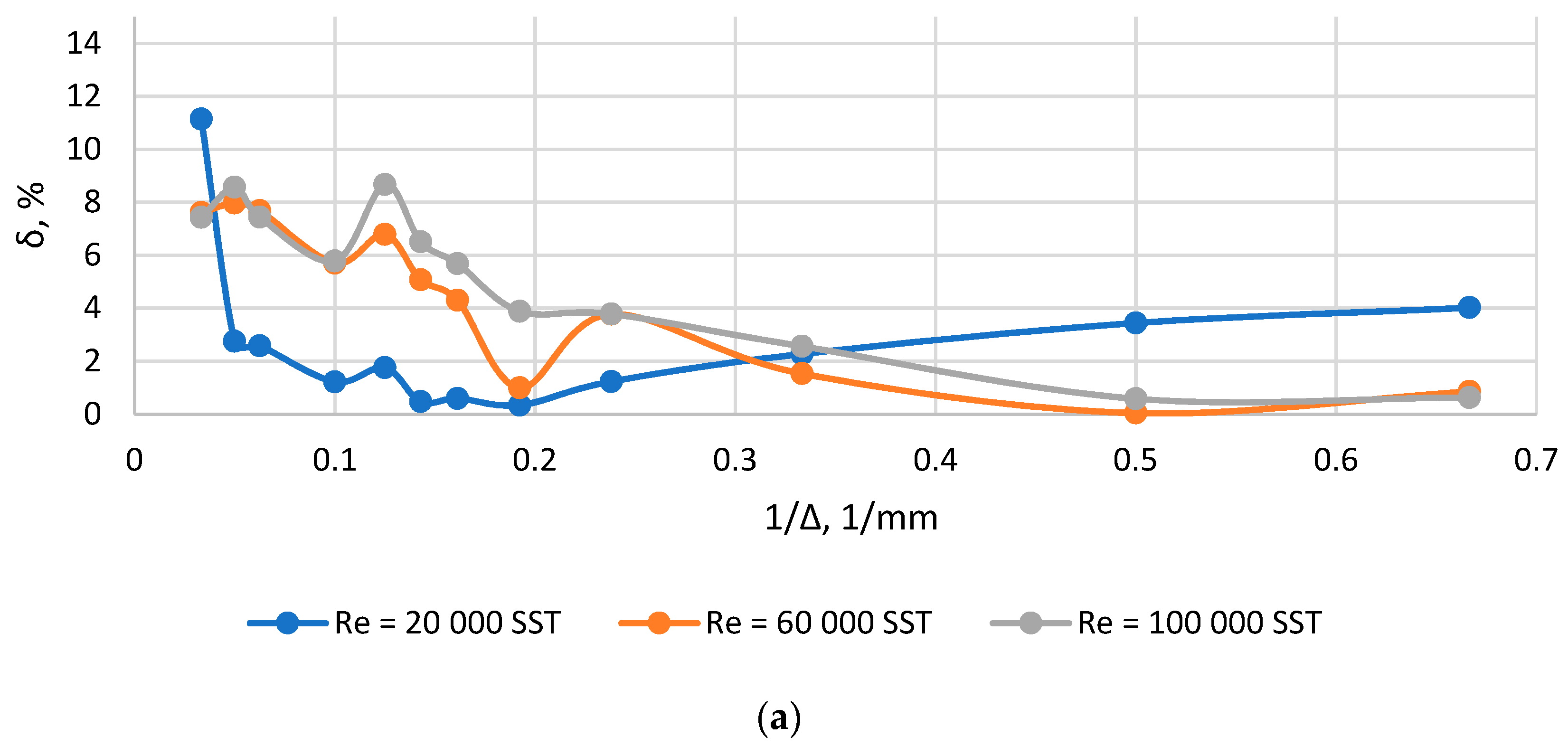
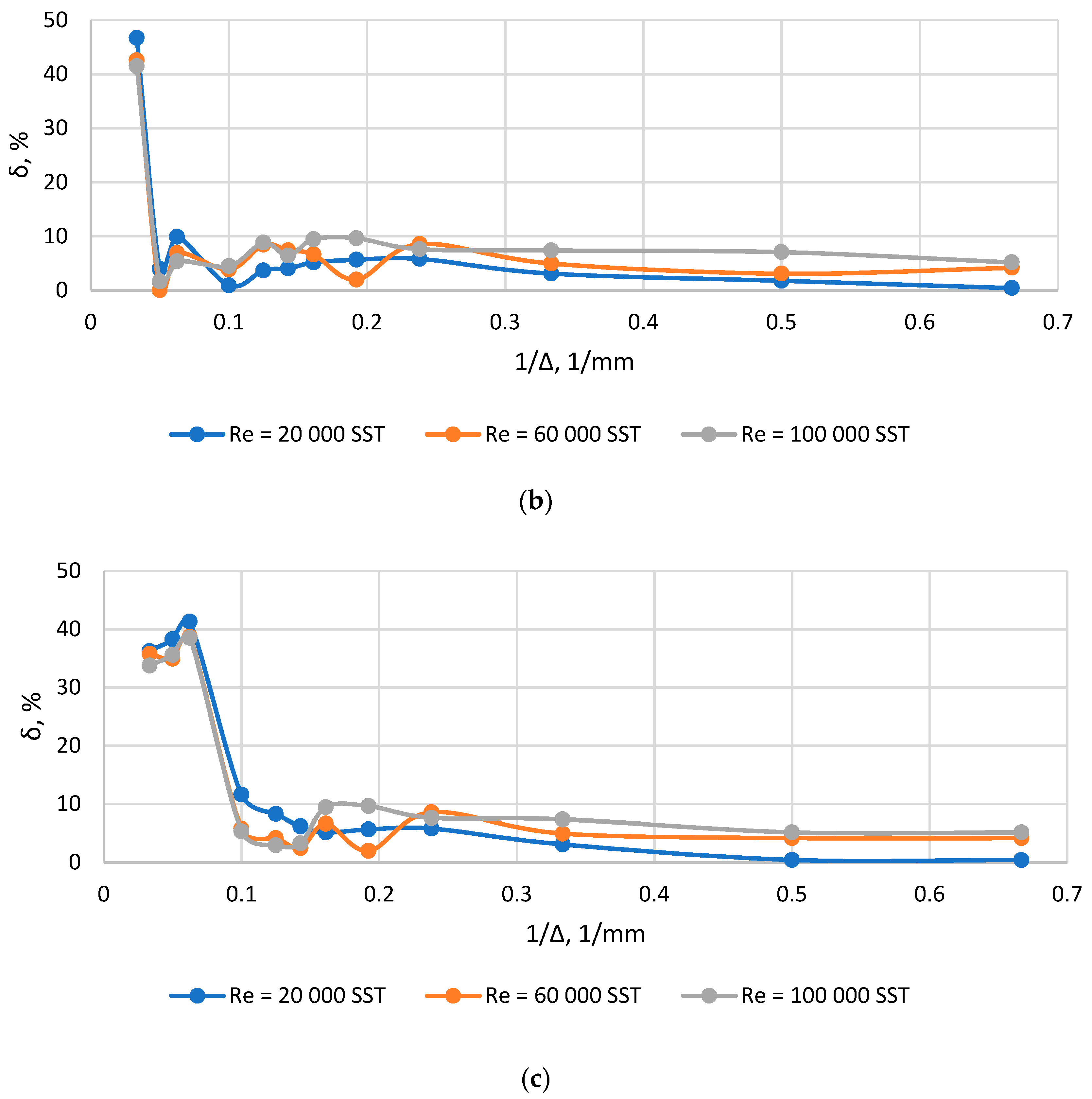
- Conducting research on grid convergence for single channels with various regime and geometric characteristics.
- Revealing transition points to grid convergence using approximation power expressions.
- Reducing the values of the size of the element corresponding to the transition to the grid convergence to the dimensionless form Ko by dividing by the thickness of the turbulent boundary layer.
- Formation of correlations Ko(Re’) for individual channels with a test of statistical significance.
- Formation of the overall correlation Ko(Re’) with a test of statistical significance.
- Verification of the obtained general correlation dependence on the compound channel.
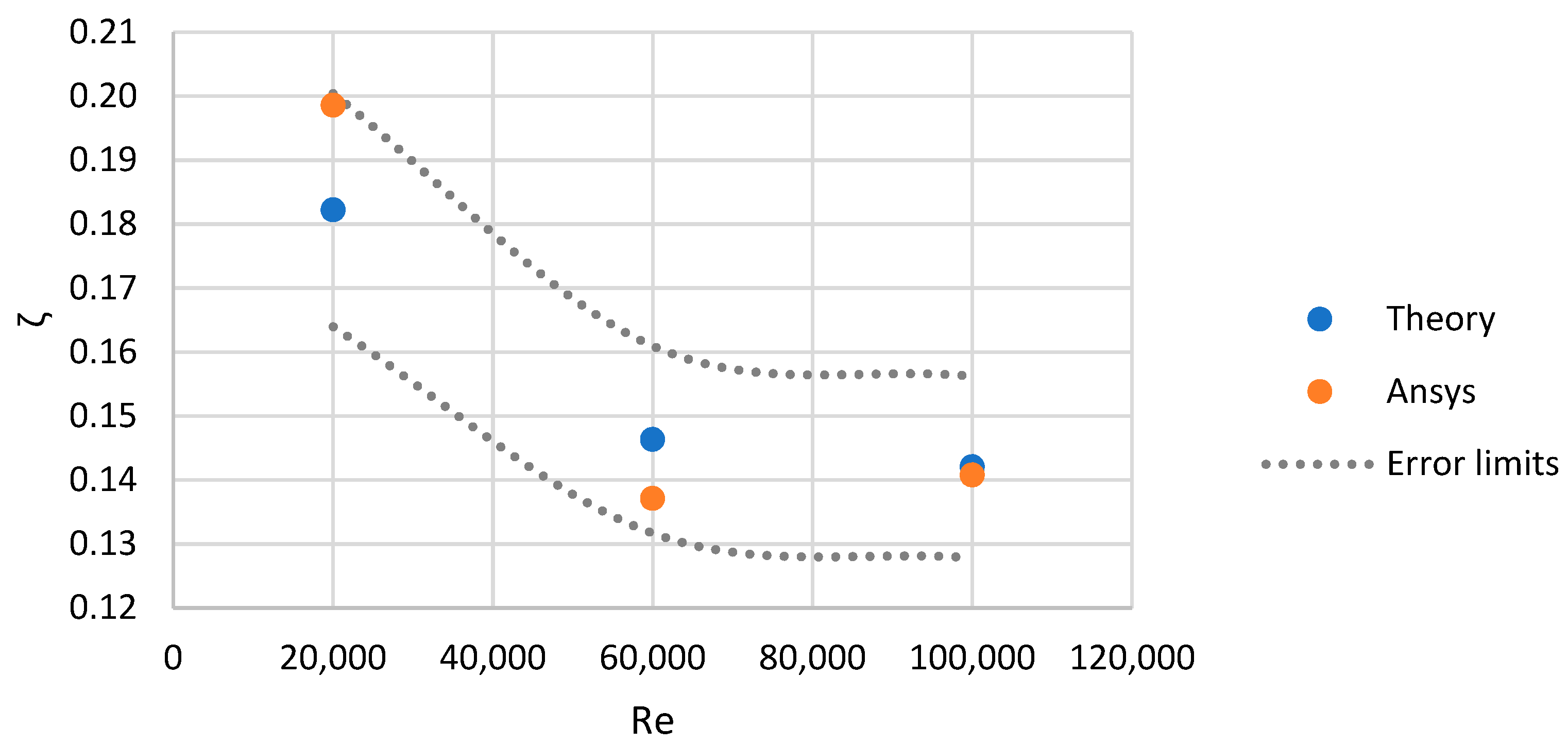
4. Results and Discussion
5. Conclusions
- There are regularities that relate the size of the grid model element, which ensures convergence along the grid, with the regime and geometric parameters of the flow in the channel;
- As a dimensionless similarity criterion, one can introduce the coefficient Ko, the ratio of the size of the grid model element that ensures grid convergence to the thickness of the turbulent boundary layer;
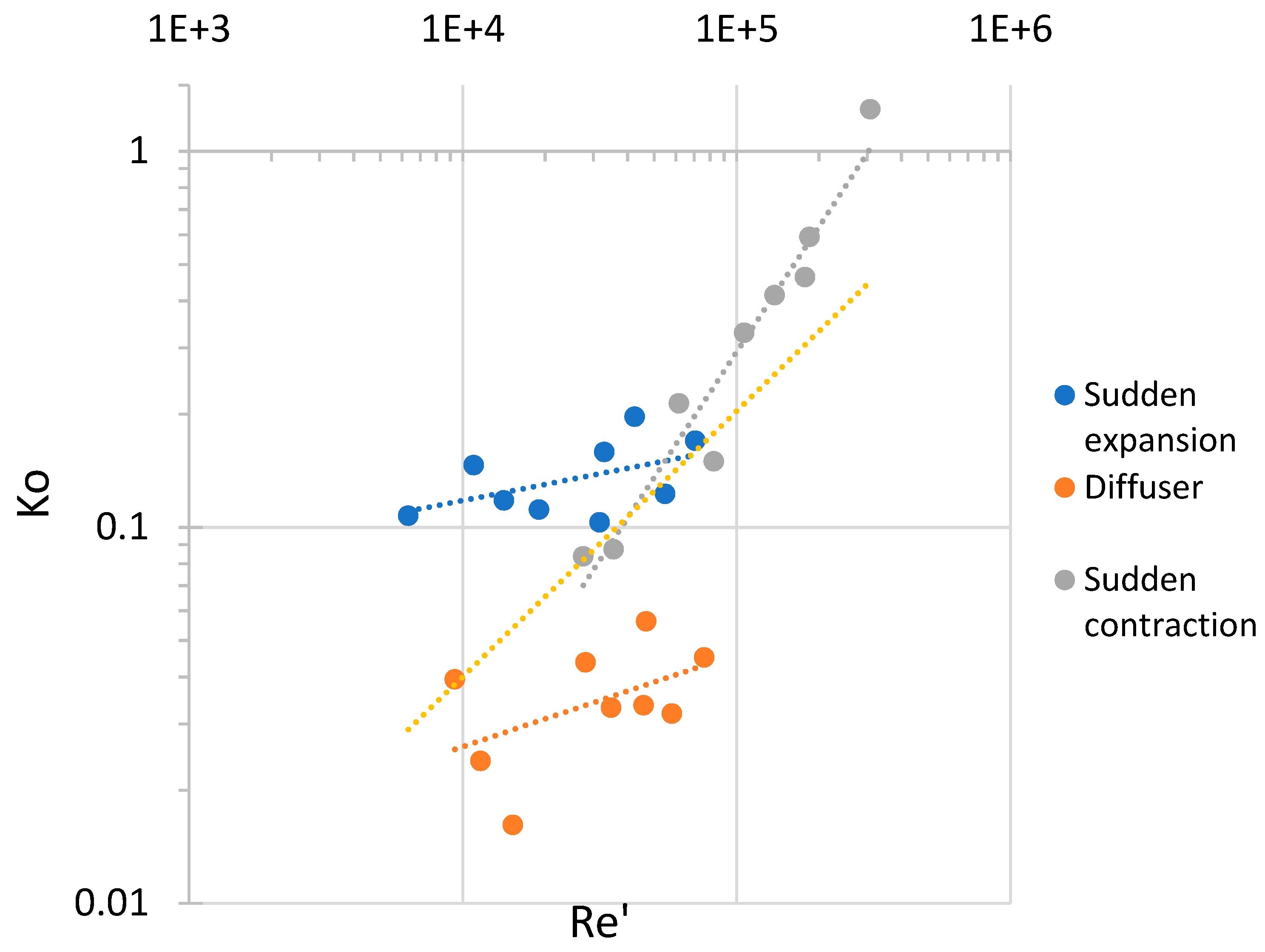
- There are statistically significant correlations Ko(Re’) for channels with sudden expansion, sudden contraction and diffusers, and there is also an overall statistically significant correlation Ko(Re’);
- This correlation makes it possible to a priori estimate the required size of the grid model element, including for compound channels, the simulation results using the obtained grid settings are within acceptable limits compared to the literature data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moin, P.; Mahesh, K. DIRECT NUMERICAL SIMULATION: A Tool in Turbulence Research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Fransen, R.; Morata, E.C.; Duchaine, F.; Gourdain, N.; Gicquel, L.Y.M.; Vial, L.; Bonneau, G. Comparison of RANS and LES in High Pressure Turbines. In Proceedings of the 3Me Colloque INCA, ONERA, Toulouse, France, 17–18 November 2011; pp. 1–15. [Google Scholar]
- Che Sidik, N.A.; Yusuf, S.N.A.; Asako, Y.; Mohamed, S.B.; Aziz Japa, W.M.A. A Short Review on RANS Turbulence Models. CFDL 2020, 12, 83–96. [Google Scholar] [CrossRef]
- Spalart, P. Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Goldberg, U.; Peroomian, O.; Chakravarthy, S. Application of the K-Epsilon-R Turbulence Model to Wall-Bounded Compressive Flows. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit; American Institute of Aeronautics and Astronautics, Reno, NV, USA, 12 January 1998. [Google Scholar]
- Wilcox, D.C. Formulation of the K-w Turbulence Model Revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Zhiyin, Y. Large-Eddy Simulation: Past, Present and the Future. Chin. J. Aeronaut. 2015, 28, 11–24. [Google Scholar] [CrossRef]
- Popov, G.; Matveev, V.; Baturin, O.; Novikova, Y.; Volkov, A. Selection of Parameters for Blade-to-Blade Finite-Volume Mesh for CFD Simulation of Axial Turbines. MATEC Web Conf. 2018, 220, 03003. [Google Scholar] [CrossRef][Green Version]
- Lu, Z.; Piro, M.H.A.; Christon, M.A. Mesh and Turbulence Model Sensitivity Analyses of Computational Fluid Dynamic Simulations of a 37M CANDU Fuel Bundle. Nucl. Eng. Technol. 2022, 54, 4296–4309. [Google Scholar] [CrossRef]
- Osipov, S.; Shcherbatov, I.; Vegera, A.; Bryzgunov, P.; Makhmutov, B. Computer Flow Simulation and Verification for Turbine Blade Channel Formed by the C-90-22 A Profile. Inventions 2022, 7, 68. [Google Scholar] [CrossRef]
- Sadrehaghighi, I. Mesh Sensitivity & Mesh Independence Study; CFD Open Series: Annapolis, MD, USA, 2021; p. 56. [Google Scholar]
- Balduzzi, F.; Bianchini, A.; Ferrara, G.; Ferrari, L. Dimensionless Numbers for the Assessment of Mesh and Timestep Requirements in CFD Simulations of Darrieus Wind Turbines. Energy 2016, 97, 246–261. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Al-Hadhrami, L. Effect of Reynolds Number and Property Variation on Fluid Flow and Heat Transfer in the Entrance Region of a Turbine Blade Internal-Cooling Channel. Int. J. Rotating Mach. 2005, 2005, 36–44. [Google Scholar] [CrossRef]
- Komarov, I.; Osipov, S.; Vegera, A.; Kharlamova, D.; Zonov, A. Verification of Computer Flow Simulation in Confuser and Diffuser Channels. In Proceedings of the International Symposium on Sustainable Energy and Power Engineering 2021, Singapore, 18–21 December 2021; Irina, A., Zunino, P., Eds.; Lecture Notes in Mechanical Engineering. Springer Nature Singapore: Singapore, 2022; pp. 343–352, ISBN 9789811693755. [Google Scholar]
- Rogalev, A.N.; Kindra, V.O.; Osipov, S.K.; Makhmutov, B.A.; Zonov, A.S. Numerical Research of the Influence of the Geometric Parameters of Shadowing Fins on the Intensity of Jet Cooling by Supercritical Carbon Dioxide. J. Phys.: Conf. Ser. 2020, 1683, 022050. [Google Scholar] [CrossRef]
- Salim, S.M.; Cheah, S.C. Wall Y+ Strategy for Dealing with Wall-Bounded Turbulent Flows. In Proceedings of the International MultiConference of Engineers and Computer Scientists 2009 Vol IIIMECS 2009, Hong Kong, 18–20 March 2009; pp. 1–6. [Google Scholar]
- Nagib, H.M.; Chauhan, K.A.; Monkewitz, P.A. Approach to an Asymptotic State for Zero Pressure Gradient Turbulent Boundary Layers. Phil. Trans. R. Soc. A. 2007, 365, 755–770. [Google Scholar] [CrossRef] [PubMed]
- Kline, S.J.; Reynolds, W.C.; Schraub, F.A.; Runstadler, P.W. The Structure of Turbulent Boundary Layers. J. Fluid Mech. 1967, 30, 741–773. [Google Scholar] [CrossRef]
- Handbook of Hydraulic Resistance; The National Science Foundation: Washington, DC, USA, 2008; p. 526.
- Rodgers, J.L.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]


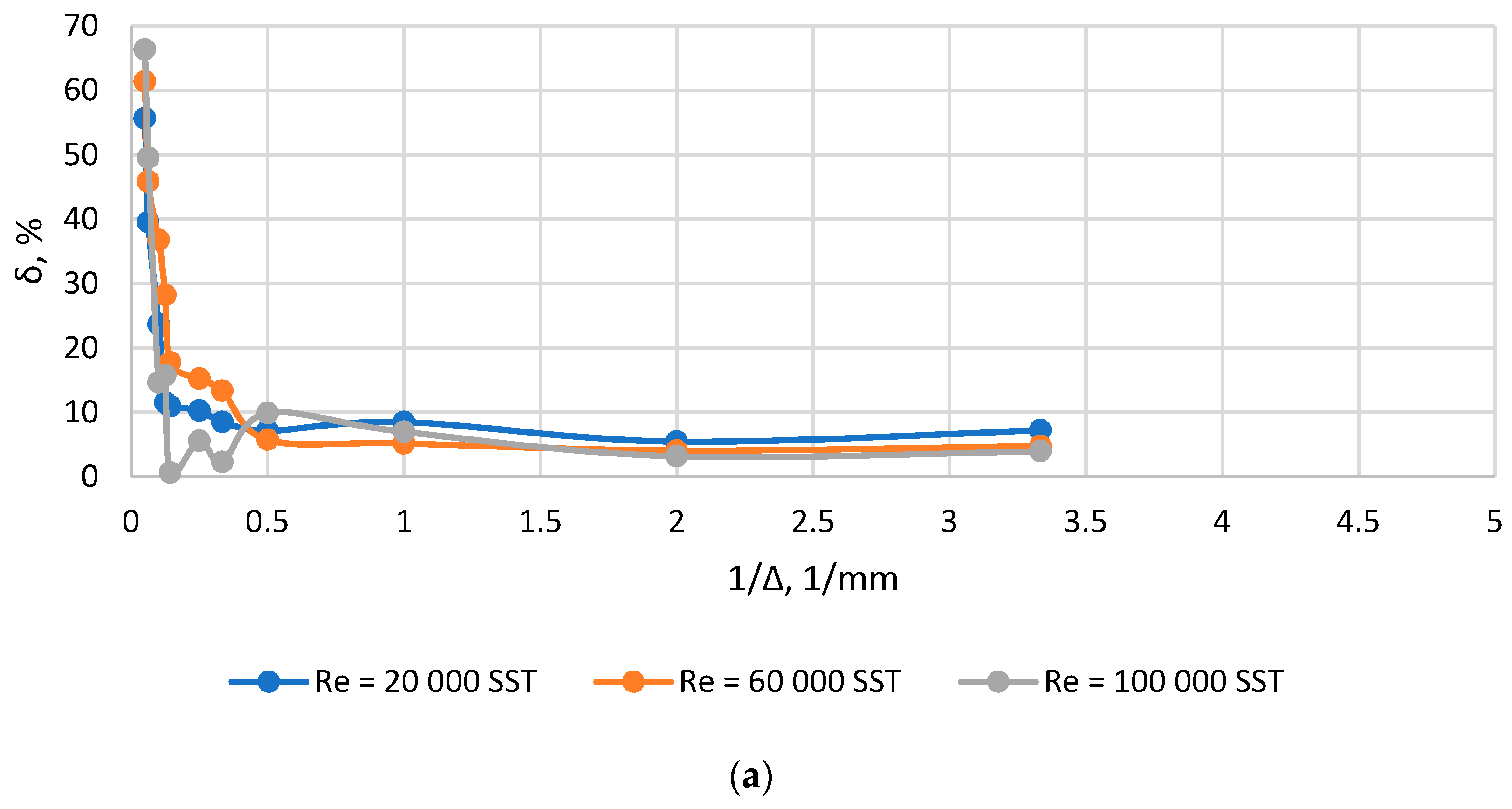
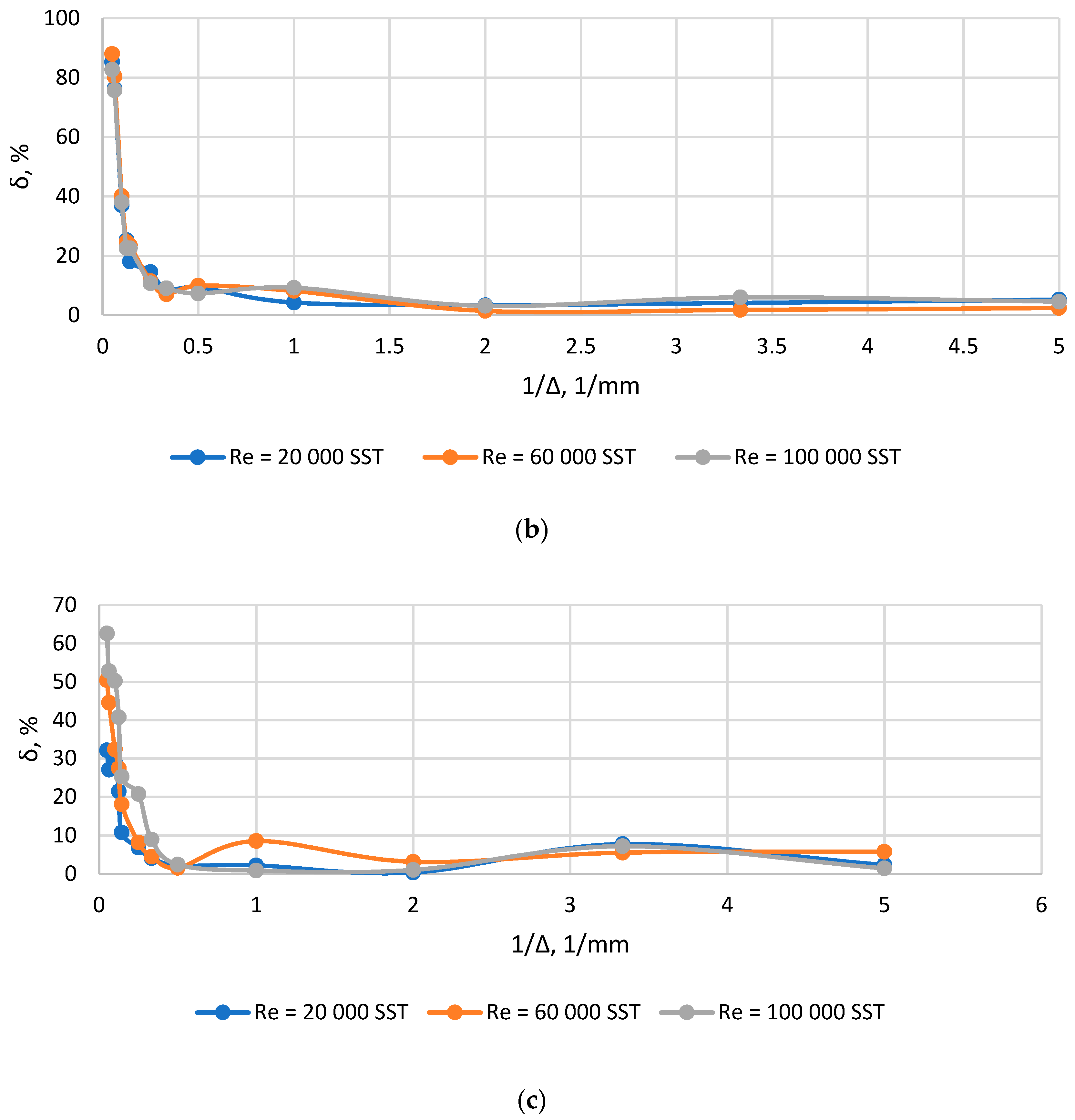

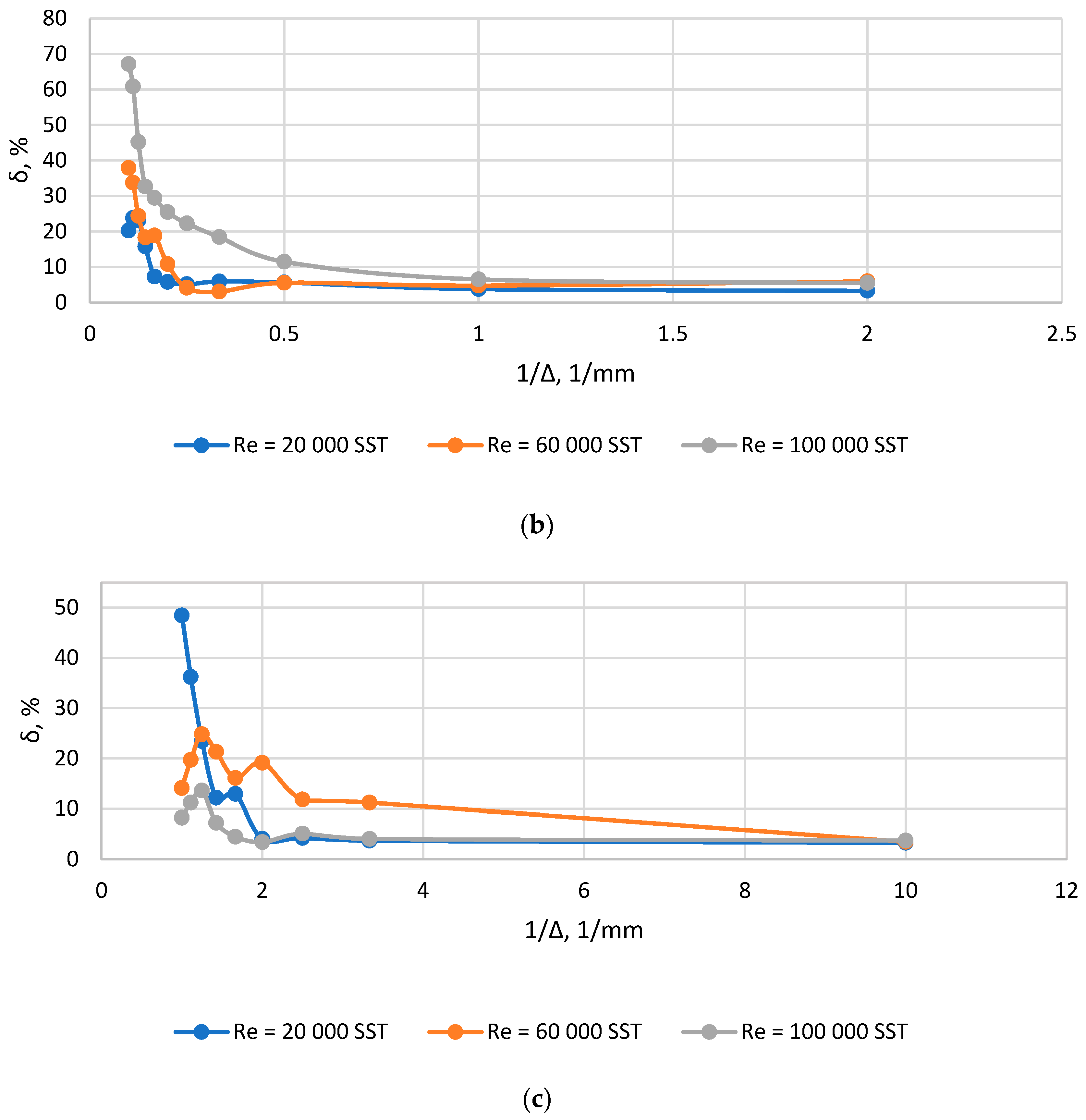
| Channel with a Sudden Expansion | |||
|---|---|---|---|
| 0.1 | 0.3 | 0.5 | |
| , mm | 84 | 84 | 84 |
| , mm | 265.6 | 153.4 | 118.8 |
| , mm | 50 | 50 | 50 |
| , mm | 1400 | 700 | 700 |
| 20,000; 60,000; 100,000 | 20,000; 60,000; 100,000 | 20,000; 60,000; 100,000 | |
| Channel with a sudden contraction | |||
| 0.1 | 0.3 | 0.5 | |
| , mm | 84 | 84 | 84 |
| , mm | 48.1 | 83.3 | 107.5 |
| , mm | 50 | 50 | 50 |
| , mm | 700 | 700 | 700 |
| 20,000 60,000 100,000 | 20,000 60,000 100,000 | 20,000 60,000 100,000 | |
| Diffuser channel | |||
| 10 | 15 | 20 | |
| , mm | 84 | 84 | 84 |
| , mm | 220.4 | 289.32 | 359 |
| , mm | 168 | 168 | 168 |
| , mm | 700 | 700 | 1078 |
| 20,000; 60,000; 100,000 | 20,000; 60,000; 100,000 | 20,000; 60,000; 100,000 | |
| 84 | 100 | 150 | 100 | 120 | 189 | 150 | 250 |
|---|---|---|---|---|---|---|---|
| 14 | |||||||
| 20,000 60,000 100,000 | |||||||
| General | Steady State RANS, 2D Axisymmetric | Turbulence Model | k-ω SST |
|---|---|---|---|
| Velocity inlet, m/s | 3.478 10.434 17.39 | Gauge pressure outlet, Pa | 0 |
| Fluid | First near-wall prismatic layer y+ | 1 | |
| , kg/m3 | 1.225 | Number of prismatic layers | 10 |
| , M2/c | 1.46 ·10−5 | Growth coefficient | 1.1 |
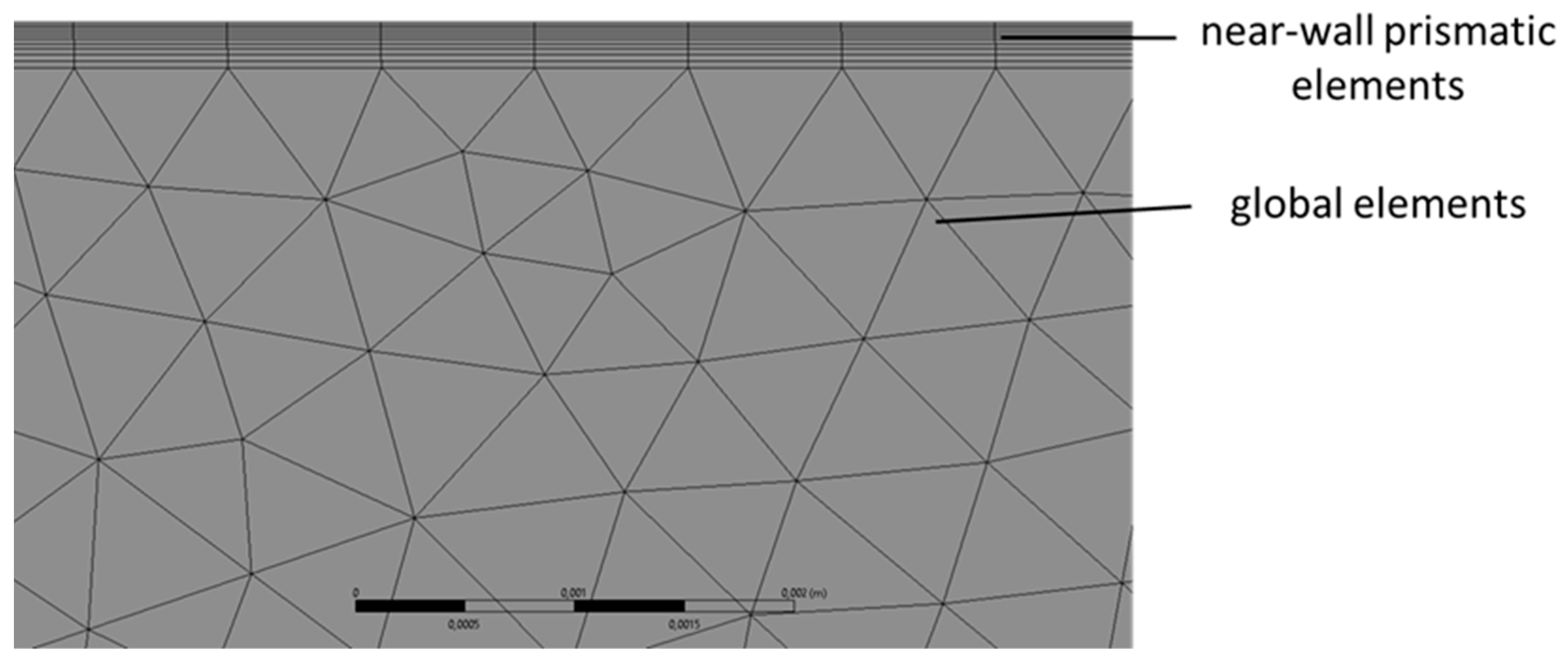
| Meshing method | Unstructured, triangles | Global element size, mm | 0.2–40 |
| Sudden Expansion | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Re | 20,000 | 60,000 | 100,000 | 20,000 | 60,000 | 100,000 | 20,000 | 60,000 | 100,000 |
| 0.1 | 0.1 | 0.1 | 0.3 | 0.1 | 0.1 | 0.5 | 0.5 | 0.5 | |
| Re′ | 6324 | 18,973 | 31,622 | 10,959 | 32,879 | 54,799 | 14,142 | 42,426 | 70,710 |
| , mm | 14.48 | 5.4 | 3.1 | 6.8 | 2.67 | 1.28 | 3.37 | 2.02 | 1.09 |
| Ko | 0.107 | 0.111 | 0.103 | 0.146 | 0.158 | 0.122 | 0.117 | 0.196 | 0.169 |
| Sudden contraction | |||||||||
| Re | 20,000 | 60,000 | 100,000 | 20,000 | 60,000 | 100,000 | 20,000 | 60,000 | 100,000 |
| 0.1 | 0.1 | 0.1 | 0.3 | 0.1 | 0.1 | 0.5 | 0.5 | 0.5 | |
| Re′ | 61,632 | 184,704 | 308,160 | 106,735 | 319,872 | 533,675 | 137,743 | 412,800 | 688,716 |
| , MM | 0.63 | 0.40 | 0.85 | 0.74 | 1.01 | 0.88 | 1.16 | 0.75 | 0.89 |
| Ko | 0.213 | 0.591 | 1.294 | 0.087 | 0.329 | 0.462 | 0.083 | 0.149 | 0.414 |
| Diffuser | |||||||||
| Re | 20,000 | 60,000 | 100,000 | 20,000 | 60,000 | 100,000 | 20,000 | 60,000 | 100,000 |
| 10 | 10 | 10 | 15 | 15 | 15 | 20 | 20 | 20 | |
| Re′ | 15,245 | 45,735 | 76,225 | 11,613 | 34,840 | 58,067 | 9,359 | 28,077 | 46,796 |
| , mm | 0.4 | 0.3 | 0.25 | 1 | 0.5 | 0.3 | 2.5 | 1 | 0.8 |
| Ko | 0.016 | 0.033 | 0.045 | 0.023 | 0.033 | 0.031 | 0.039 | 0.043 | 0.056 |
| Geometry | Correlation | cp | ||
|---|---|---|---|---|
| Sudden expansion | 0.497 | 2.29 | 1.74 | |
| Sudden contraction | 0.97 | 16.06 | 1.74 | |
| Diffuser | 0.492 | 2.26 | 1.74 | |
| General | 0.652 | 3.44 | 1.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bryzgunov, P.; Osipov, S.; Komarov, I.; Rogalev, A.; Rogalev, N. Research and Development of Criterial Correlations for the Optimal Grid Element Size Used for RANS Flow Simulation in Single and Compound Channels. Inventions 2023, 8, 4. https://doi.org/10.3390/inventions8010004
Bryzgunov P, Osipov S, Komarov I, Rogalev A, Rogalev N. Research and Development of Criterial Correlations for the Optimal Grid Element Size Used for RANS Flow Simulation in Single and Compound Channels. Inventions. 2023; 8(1):4. https://doi.org/10.3390/inventions8010004
Chicago/Turabian StyleBryzgunov, Pavel, Sergey Osipov, Ivan Komarov, Andrey Rogalev, and Nikolay Rogalev. 2023. "Research and Development of Criterial Correlations for the Optimal Grid Element Size Used for RANS Flow Simulation in Single and Compound Channels" Inventions 8, no. 1: 4. https://doi.org/10.3390/inventions8010004
APA StyleBryzgunov, P., Osipov, S., Komarov, I., Rogalev, A., & Rogalev, N. (2023). Research and Development of Criterial Correlations for the Optimal Grid Element Size Used for RANS Flow Simulation in Single and Compound Channels. Inventions, 8(1), 4. https://doi.org/10.3390/inventions8010004






