Modification of Pulse Decay Method for Determination of Permeability of Crystalline Rocks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Isotropic Permeability
2.1.1. Theoretical Model
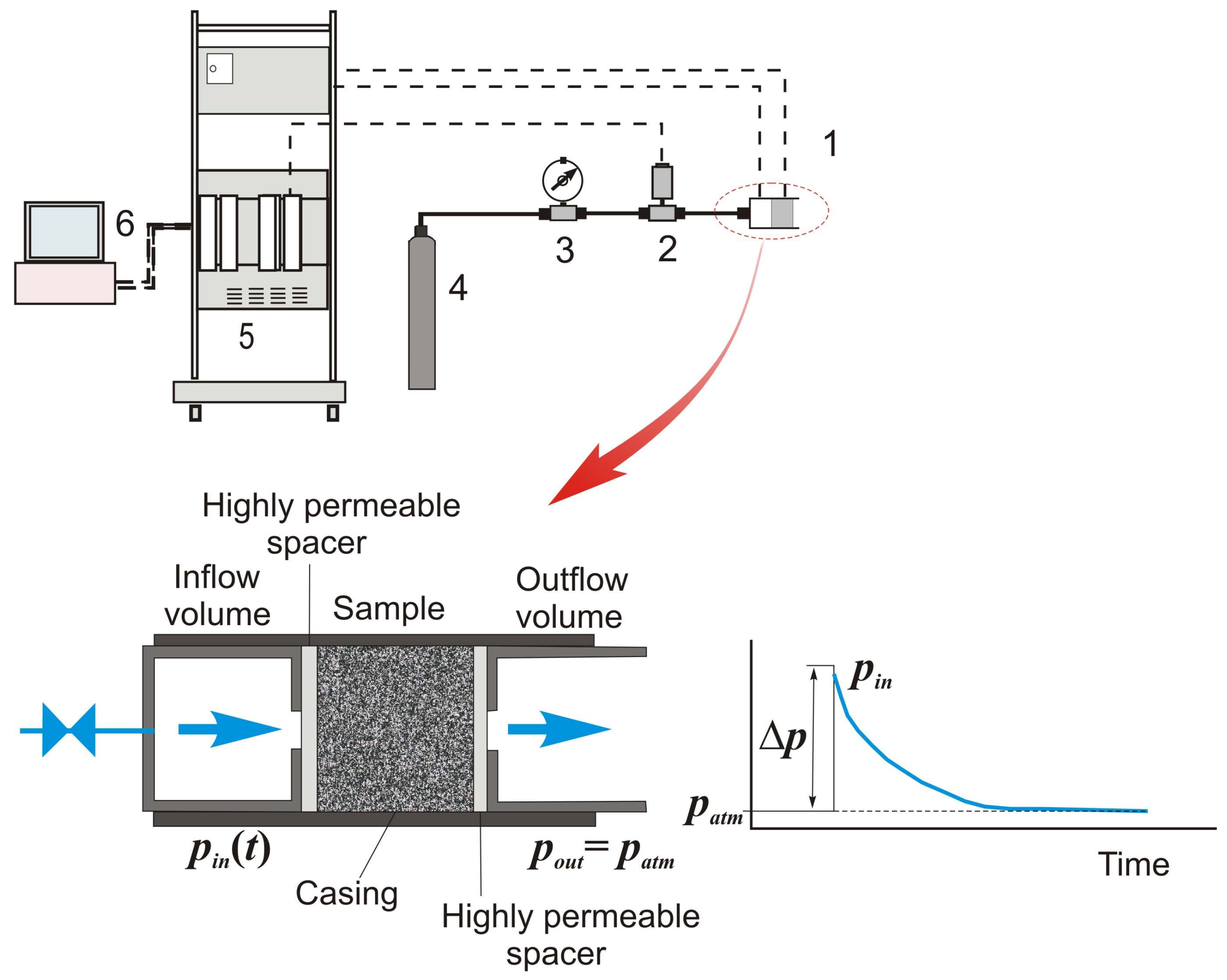
2.1.2. Experimental Apparatus
2.2. Anisotropic Permeability
2.2.1. Experimental Apparatus
2.2.2. Theoretical Model
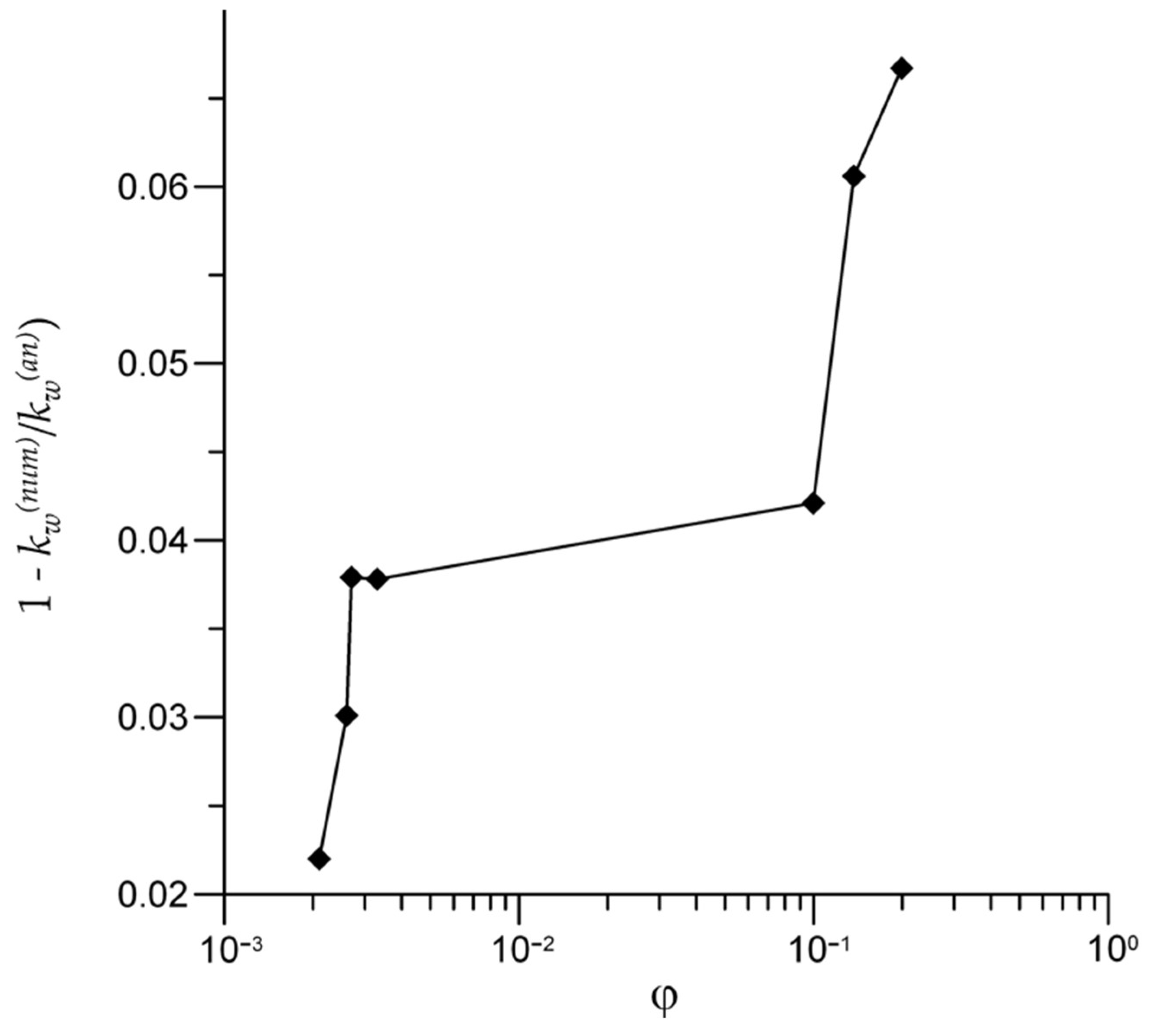
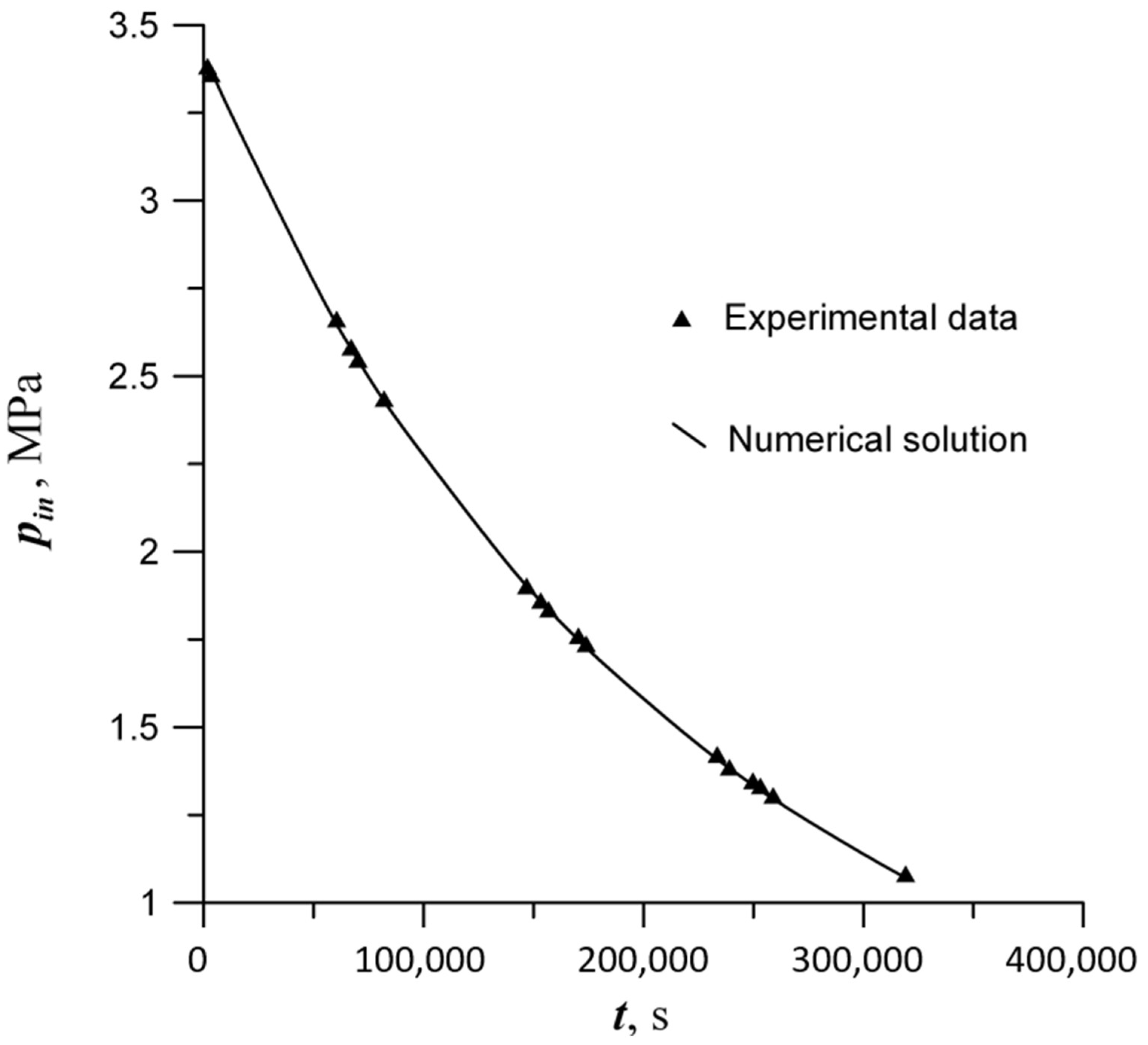
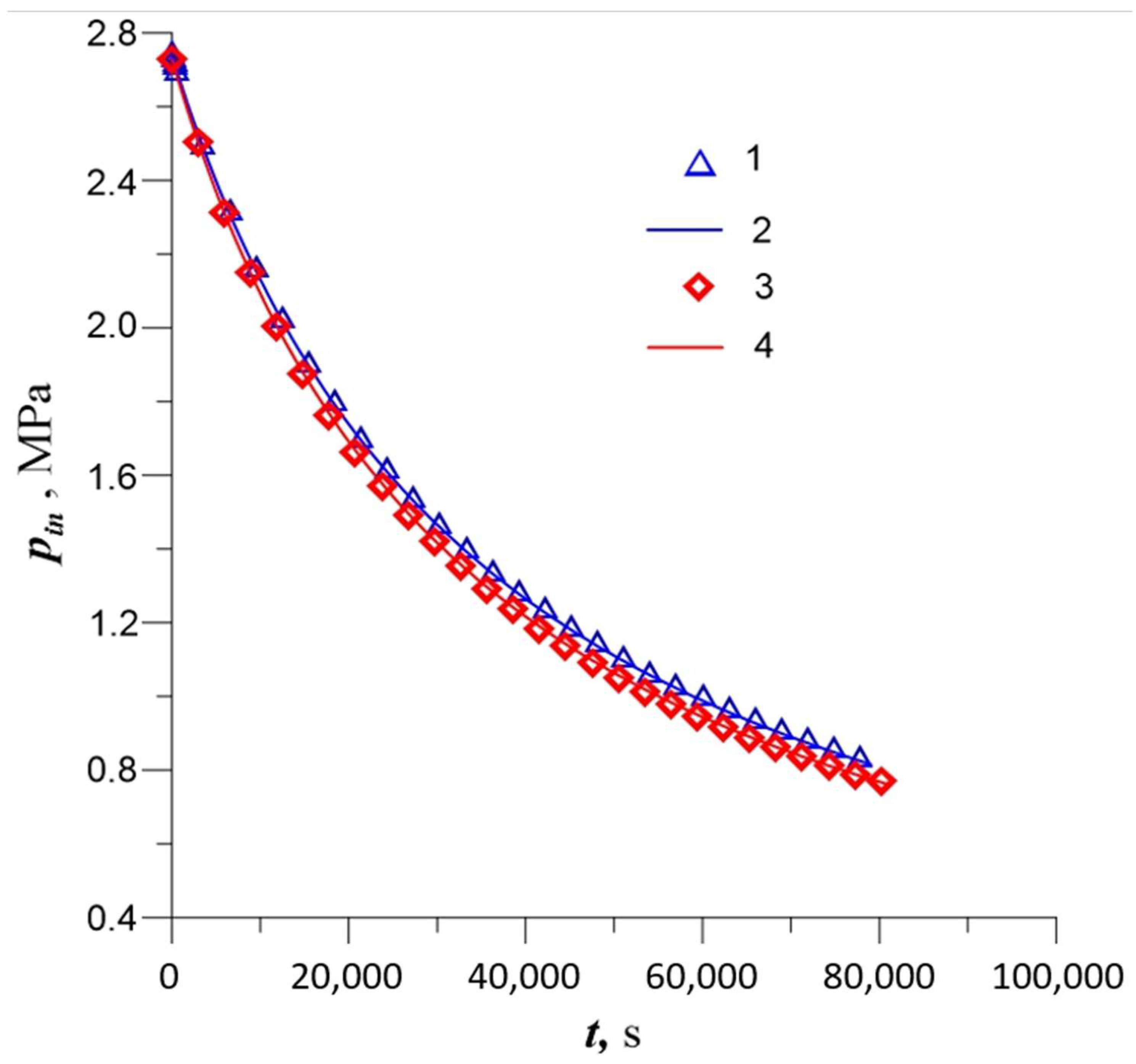
3. Results and Discussion
Isotropic Permeability
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pek, A.A. On the Dynamic of Juvenile Solutions; Nauka: Moscow, Russia, 1968. [Google Scholar]
- Malkovsky, V.I.; Pek, A.A.; Arseniev, P.L.; Topor, D.N. Modeling of convective heat and mass transport at fluids flow along fault zones. Izvestya RAN Phisika Zemli 1988, 12, 57–62. [Google Scholar]
- Tutubalin, A.V.; Grichuk, D.V.; Malkovsky, V.I. A complex hydrodynamic model of a convective hydrothermal system. In Proceedings of the 8th International Symposium “Water-Rock Interaction-WRI-8”, Vladivostok, Russia, 15–19 August 1995; Balkema: Rotterdam, The Netherlands, 1995; pp. 763–766. [Google Scholar]
- Malkovsky, V.I.; Pek, A.A.; Omelyanenko, B.I.; Drojko, E.G. Numerical simulation of thermocon-vective transport of radionuclides by groundwater from the well-type repository of high-level radioactive waste. Izvestya RAN Energ. 1994, 3, 113–122. [Google Scholar]
- Kissin, I.G. Fluids in the Earth’s Crust, 2nd ed.; Nauka: Moscow, Russia, 2015; 328p. [Google Scholar]
- Morrow, C.; Byerlee, J. Permeability of rock samples from Cajon Pass, California. J. Geophys. Res. 1988, 15, 1033–1036. [Google Scholar] [CrossRef]
- Morrow, C.; Lockner, D. Permeability difference between surface-derived and deep drill hole core samples. J. Geophys. Res. 1994, 21, 2151–2154. [Google Scholar]
- Brace, W.F.; Walsh, J.B.; Frangos, W.T. Permeability of granite under high pressure. J. Geophys. Res. 1968, 73, 2225–2236. [Google Scholar] [CrossRef]
- Hsieh, P.A.; Tracy, J.V.; Neuzil, C.E.; Bredehoeft, J.D.; Silliman, S.E. A transient laboratory method for determining the hydraulic properties of tight rocks-I Theory. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 245–252. [Google Scholar] [CrossRef]
- Lin, W. Parametric analyses of the transient method of measuring permeability. J. Geophys. Res. 1982, 87, 1055–1060. [Google Scholar] [CrossRef]
- Trimmer, D.B.; Bonner, H.C.; Duba, A. Effect of pressure and stress on water transport in intact and fractured gabbro and granite. J. Geophys. Res. 1980, 85, 7059–7071. [Google Scholar] [CrossRef]
- Lin, C.; Pirie, G.; Trimmer, D.A. Low Permeability Rocks-Laboratory Measurements and 3-Dimensional Microstructural Analysis. J. Geophys. Res. 1986, 91, 2173–2181. [Google Scholar] [CrossRef]
- Katsube, T.J.; Mudford, B.S.; Best, M.E. Petrophysical Characteristics of Shales from the Scotian Shelf. Geophysics 1991, 56, 1681–1689. [Google Scholar] [CrossRef]
- Le Guen, C.; Deveughele, M.; Billiotte, J.; Brulhet, J. Gas-permeability changes of rock-salt subjected to thermomechanical stresses. Q. J. Eng. Geol. 1993, 26, 327–334. [Google Scholar] [CrossRef]
- Zeynalyandabily, E.M.; Rahman, S.S. Measurement of Permeability of Tight Rocks. Meas. Sci. Technol. 1995, 6, 1519–1527. [Google Scholar] [CrossRef]
- Cao, C. Numerical interpretation of transient permeability test in tight rock. J. Rock Mech. Geotech. Eng. 2018, 10, 32–41. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, K.; Wang, C.; Bi, J. A large pressure pulse decay method to simultaneously measure permeability and compressibility of tight rocks. J. Nat. Gas Sci. Eng. 2022, 98, 104395. [Google Scholar] [CrossRef]
- Wang, Y.; Tian Zh Nolte, S.; Krooss, B.M.; Wang, M. An improved straight-line method for permeability and porosity determination for tight reservoirs using pulse-decay measurements. J. Nat. Gas Sci. Eng. 2022, 105, 104708. [Google Scholar] [CrossRef]
- Fischer, G.J.; Paterson, M.S. Permeability and storage capacity during deformation at elevated temperatures. In Fault Mechanics and Transport Properties of Rocks; Elsevier: St. Diego, CA, USA, 1992; pp. 187–211. [Google Scholar]
- Zhang, S.; Paterson, M.S.; Cox, S.F. Porosity and permeability evolution during hot isostatic pressing of calcite aggregates. J. Geophys. Res. 1994, 99, 15741–15760. [Google Scholar] [CrossRef]
- Sander, R.; Pan, Z.; Connell, L. Laboratory measurement of low permeability unconventional gas reservoir rocks: A review of experimental methods. J. Nat. Gas Sci. Eng. 2017, 37, 248–279. [Google Scholar] [CrossRef]
- Zharikov, A.V.; Vitovtova, V.M.; Shmonov, V.M. Experimental study of permeability of Archean rocks from the Kola super deep drill hole. Geol. Rudn. Mestorojdeniy 1990, 32, 79–88. [Google Scholar]
- Klinkenberg, L.J. The permeability of porous media to liquids and gases. In Drilling and Production Practice; API: New York, NY, USA, 1941; pp. 200–211. [Google Scholar]
- Scott, D.S.; Dullien, F.A.L. The flow of rarefied gases. AIChE J. 1962, 15, 293–297. [Google Scholar] [CrossRef]
- Zaraisky, G.P.; Balashov, V.N. Thermal decompaction of rocks. In Fluids in the Crust; Shmulovich, K.I., Yardley, B.W.D., Gonchar, G.G., Eds.; Springer: Dordrecht, The Netherlands, 1994. [Google Scholar] [CrossRef]
- Lanczos, C. Applied Analysis; Dover Publications Inc.: New York, NY, USA, 1988; 539p. [Google Scholar]
- Gill, P.h.E.; Murray, W.; Wright, M.H. Practical Optimization; SIAM: Philadelphia, PA, USA, 2019; 401p. [Google Scholar]
- Roache, P.J. Computational Fluid Dynamics; Albuquerque: Hemrosa, CA, USA, 1976. [Google Scholar]
- Zubarev, V.N.; Kozlov, A.D.; Kouznetsov, V.M. Thermophysical Properties of Gases Important in Techniques at High Temperature and Pressure; Energoatomizdat: Moscow, Russia, 1989. [Google Scholar]
- Zienkiewicz, O.C.; Morgan, K. Finite Elements and Approximation; Dover Publications: Newburyport, MA, USA, 2013; 574p. [Google Scholar]

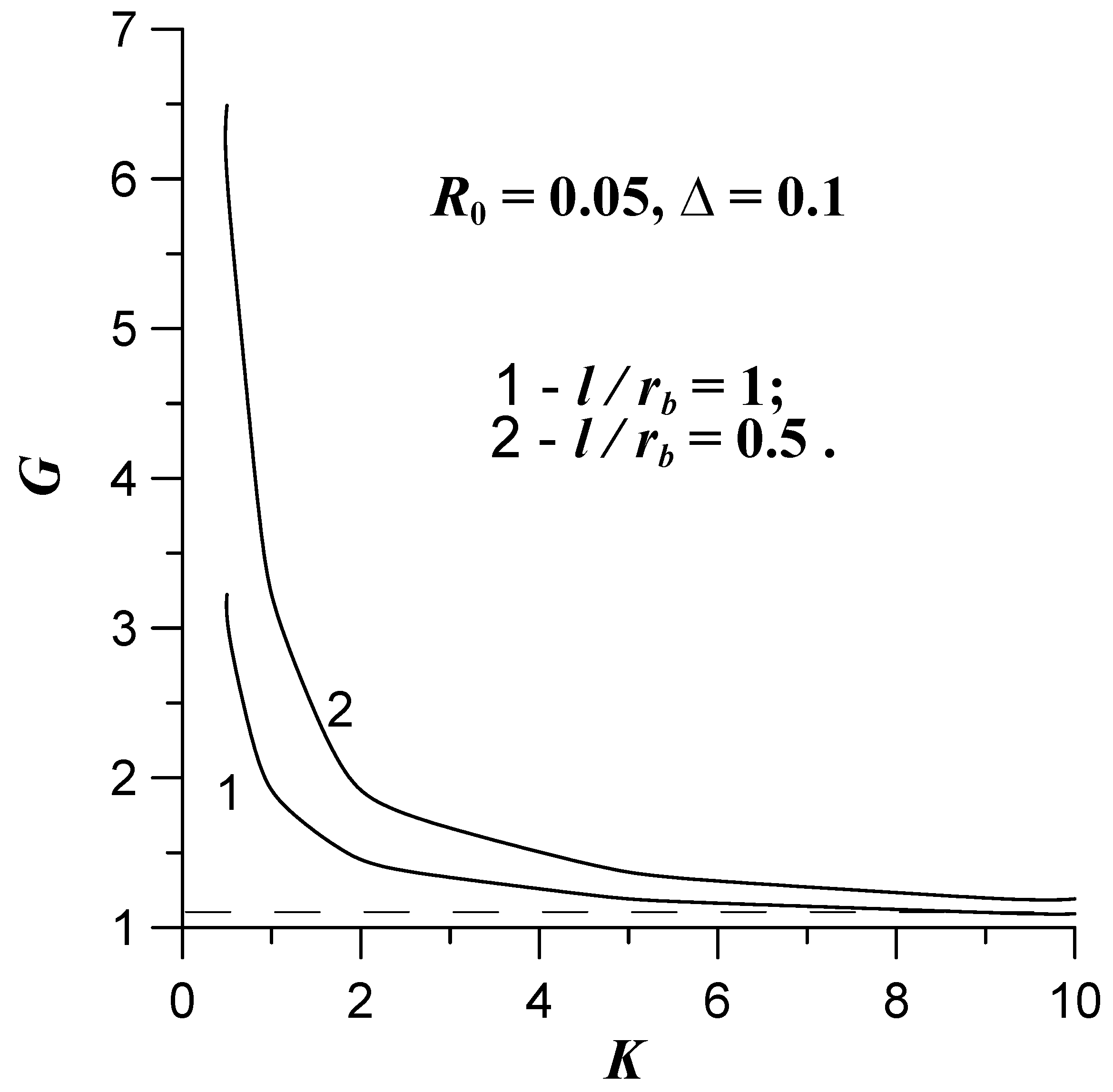
| Sample | , Mpa | kw(Kl) | ||||||
|---|---|---|---|---|---|---|---|---|
| Porf-1 | 0.0021 | 0.154 | 2.48 × 10−20 | 2.427 × 10−20 | 2.499 | 2.568 | 3.8 × 10−20 | −0.541 |
| Porf-2 | 0.0026 | 0.376 | 6.974 × 10−20 | 6.764 × 10−20 | 1.757 | 1.835 | 8.5 × 10−20 | −0.257 |
| Porf-3 | 0.0027 | 0.286 | 3.011 × 10−20 | 2.897 × 10−20 | 1.266 | 1.361 | 2.6 × 10−20 | 0.103 |
| Porf-4 | 0.0033 | 0.117 | 1.111 × 10−19 | 1.069 × 10−19 | 1.182 | 1.259 | 1.1 × 10−19 | −0.029 |
| Sand-1 | 0.1370 | 0.155 | 2.707 × 10−15 | 2.543 × 10−15 | 0.4501 | 0.5088 | 2.0 × 10−15 | 0.214 |
| Sand-2 | 0.0998 | 0.118 | 1.687 × 10−15 | 1.616 × 10−15 | 0.6529 | 0.7014 | 1.6 × 10−15 | 0.010 |
| B-1 | 0.1990 | 0.191 | 1.009 × 10−16 | 9.417 × 10−17 | 1.007 | 1.117 | 1.0 × 10−16 | −0.062 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malkovsky, V.I.; Zharikov, A.V.; Ojovan, M.I. Modification of Pulse Decay Method for Determination of Permeability of Crystalline Rocks. Inventions 2023, 8, 14. https://doi.org/10.3390/inventions8010014
Malkovsky VI, Zharikov AV, Ojovan MI. Modification of Pulse Decay Method for Determination of Permeability of Crystalline Rocks. Inventions. 2023; 8(1):14. https://doi.org/10.3390/inventions8010014
Chicago/Turabian StyleMalkovsky, Victor I., Andrey V. Zharikov, and Michael I. Ojovan. 2023. "Modification of Pulse Decay Method for Determination of Permeability of Crystalline Rocks" Inventions 8, no. 1: 14. https://doi.org/10.3390/inventions8010014
APA StyleMalkovsky, V. I., Zharikov, A. V., & Ojovan, M. I. (2023). Modification of Pulse Decay Method for Determination of Permeability of Crystalline Rocks. Inventions, 8(1), 14. https://doi.org/10.3390/inventions8010014







