2. Derivation of the Basic Equation and It Analysis
To get the equation we need, we will use the law of conservation of power which is elementarily obtained from the law of conservation of energy. Indeed, according to the law of conservation of energy . Differentiating this equality over time we have , where .
We will define this system in the form of two phase components, one of which is a gas and the other is a liquid droplet. Taking into account the interaction of gas phase molecules and molecules in a droplet at the boundary of their contact, the balance equation can be represented in the only way as the sum of three terms (it is easy to understand that there are simply no other components in the problem being solved):
where
is the droplet entropy attributed to the unit of its volume,
is the entropy of the unit of volume of the gas phase surrounding the liquid droplet including the molecules of the already evaporated substance of the droplet,
is the variable volume of the droplet,
is the total volume occupied by the droplet and gas,
is the surface area of the droplet,
is the temperature,
is the surface tension coefficient. The Equation (1) describes the total power balance of the conservative system under study: drop + gas.
Looking ahead a little, we note that as a result of solving Equation (1), we will come to the correct answer both qualitatively and quantitatively which is not in contradiction with the well-known result given in the traditional Fuchs monograph [
3] but complements it with the qualitatively new result obtained below. This also answers the question of the relevance of our approach when comparing it with the results of other authors working in this direction (see the articles mentioned above [
4,
5,
6,
7,
8,
9]).
Once again, we emphasize that the principle of preserving the total full power of any dissipative system (and it does not matter whether it is closed or open) leads to correct equations which was strictly proved in concrete physical examples in study [
1]. We will not reproduce the details of this study here since in this message we are talking about a specific isolated case which will now be considered in detail.
Performing a simple differentiation in (2) we find
(All variables appearing in Equation (2) are explained after Equation (1)).
Introducing here the latent heat of vaporization.
Our problem now is to calculate the first two terms included in Equation (4). According to the definition of entropy in the language of the distribution function which according to the evidence given in ref. [
10] is considered valid for both liquids and gases, we have
where
is the non-equilibrium function of the distribution of liquid molecules in the momenta,
is the normalization factor and
is the equilibrium distribution function, where
is a pressure.
The ratio (5) according to its definition in [
10] is fair in both equilibrium and non-equilibrium cases. Note also that for convenience and reduction of the record, we will consider the Boltzmann constant to be equal to one. That is, we believe that
. This can always be done since in the final result, in which the temperature will appear in order to obtain the correct dimension, it will only need to be multiplied by
.
The relationship between the equilibrium and non-equilibrium distribution functions is determined from the conditions of continuity allowing it to be written that .
is the kinetic energy of molecules in a liquid, is their chemical potential.
Considering the temperature constant (that is
), the differentiation of Formulas (5) and (6) in time leads us to the following relations
According to the Boltzmann kinetic equation we have the right to write that
where
are the integrals of collisions of liquid and gas molecules at the boundary of their contact, respectively.
As for the “internal” collision integrals, that is collisions of gas molecules with each other and liquid molecules with each other in accordance with the Bogolyubov hierarchical principle which allows moving to quasi-equilibrium distribution functions (see (5) and (6)) and “uncoupling” the corresponding correlators, they can be ignored. This remarkable principle makes it possible to find solutions to a variety of problems, the number of which is currently extremely large.
In formal mathematical language, this means that the relaxation times for internal intermolecular collisions are much smaller than the collision times of gas and liquid molecules at the external interface of contact.
That is . Only when this condition is met do we have the right to introduce a quasi-equilibrium (equilibrium) distribution function into consideration.
Taking into account (6)–(8), Equation (4) will take the following form
We will look for the solution of kinetic equations using the BGK method [
11] according to which the collision integrals can be replaced with approximate expressions
where
is the relaxation time of liquid molecules when they are scattered on gas molecules and
is the relaxation time of gas molecules when they are scattered on liquid molecules. It is quite clear that these times are different. We will now find corrections to the distribution function
due to interaction.
According to kinetic Equation (8), we have
Since we are looking for a stationary solution, then . In addition, it should be considered that the force .
We will search for solutions of Equations (12) and (13) by the method of successive approximations assuming that
Therefore, we get
where vectors of free path lengths
are introduced.
It is convenient to search for the solution of Equation (15) by decomposing the desired functions into the Fourier integral. Indeed, we have for an arbitrary (so far) function
where by the symbol of a one-dimensional integral we mean a three-dimensional integral,
Fourier image of function
. Substituting (16) into any of the Equation (15) we easily find
From where
where
Fourier is the image of the equilibrium distribution function of molecules
.
Substituting solution (17) into definition (16), now we obtain the correction to the equilibrium distribution function that interests us
Here and further we simplify the recording of the Fourier integral by omitting the limits of integration. To calculate the resulting integral, it is convenient to use the following artificial technique. Let us represent function
as an integral
Then from (18) it follows
Then after substituting the Fourier image (21) into the solution (20), we will have as a result a simple rearrangement of the multipliers
To calculate the internal integral appearing here we proceed as follows. Let us write it down as
where is the delta function and .
As a result, it follows from (22)
We take the resulting integral using integration in parts. Really
Remembering now the translational transfer operator, namely the rule
we get from (23)
Therefore, for the desired corrections in our case, we obtain such solutions of Equation (15)
and, therefore, in accordance with (9) and (10), we find
where corrections
are given by solutions (25).
By virtue of the definition of the equilibrium distribution functions, then the dissipative balance equation follows from (26)
Note that the last term in (27) is conveniently represented as
where
is some average energy per one particle of a liquid,
is their concentration. In accordance with (25), the solution can be written as an infinite series
.
Integrating each term here by , we come to this solution
Where, for the sake of brevity of the record solutions (25) are presented using the uniform notation
and
, that is
and
. If we now substitute solution (28) into the balance Equation (27), then due to momentum integration
all odd degrees
will disappear and instead of (27) we get
Leaving in (29) only the terms quadratic in the free path length and taking into account the explicit form of the equilibrium distribution function, as a result of elementary differentiation we come to the following equation
Since the entropy continuity condition must be fulfilled at the boundary of the two phases in the absence of chemical reactions, it is quite clear that the following equality takes place
As you can see, this condition is true if the temperature is constant. At the same time, it is quite clear that the equality of entropies at the contact boundary of a droplet and a gas mixture does not at all mean equality of their specific heat capacities since from a formal point of view, equality (31) should be written in a slightly different form namely as
where the limits are taken to the left and right of the contact boundary.
Therefore, due to the piecewise smoothness of entropy, an additional condition for temperature derivatives of entropy follows from (32) which also binds the heat capacities of both phases. This means that the following equality must take place
where
represents the final jump in the heat capacity at the interface of both phases and the isobaric heat capacity is introduced here in accordance with the generally accepted definition [
10]
where the index
numbers the phases.
As for the physical side of Equation (30), it is immediately necessary to emphasize that as soon as we introduce the concept of variable entropy, we automatically proceed to take into account the dissipative properties of matter. That is, in the non-equilibrium case which is described by Equation (30), the entropy increase condition takes place (the famous
Boltzmann theorem [
10]). As it will become clear now, taking into account the interaction between the molecules of both phases that is the transfer of energy from water molecules to gas molecules and vice versa leads to the destruction of the weak surface tension of a droplet. For an analytical description of this process, it is necessary to focus on the remarkable property of any natural physical phenomenon such as the hierarchy of relaxation times [
11,
12,
13].
Indeed, in order of magnitude, the free path length of molecules in a liquid turns out to be significantly less than the free path length of gas molecules , that is the inequality holds.
This means that in terms of the hierarchy of times by virtue of the condition which actually follows from the condition where are the average concentrations of liquid and gas molecules, respectively, the main evaporation process belongs to the first term in (30) and it is this important fact that allows us to neglect the second term.
Otherwise, the first process as the fastest one has already occurred and the droplet has begun to evaporate and the second one has not yet had time to begin. This, however, does not mean at all that it does not contribute to the evaporation process; at a later period of time, this contribution may manifest itself but only if the droplet has not had time to evaporate by this point in time.
Thus, taking into account the condition of continuity of entropy at the contact boundary according to (32) and taking into account all that has been said from Equation (30), we come to such an equation
Note also that for the chemical potentials of both phases at the boundary of their contact, the following equilibrium condition must also be met
Since
, we find the following from (34)
Due to the fact that the distribution of the inhomogeneous chemical potential at the contact of two media (see [
14]) obeys the equation
where
is the length of the inhomogeneity satisfying inequality
where
and
is a certain coefficient leading to a correct solution (see Formula (38)), then in the one-dimensional case, we obtain the following from Equation (37)
Therefore, at the contact boundary we have
and thus Equation (39) takes the following form
from where after direct integration taking into account the initial condition
we get
where the diffusion coefficient is
Equality (41) means that the evaporation time of the liquid droplet we are interested in must be from the condition of equality to zero of the root expression that is
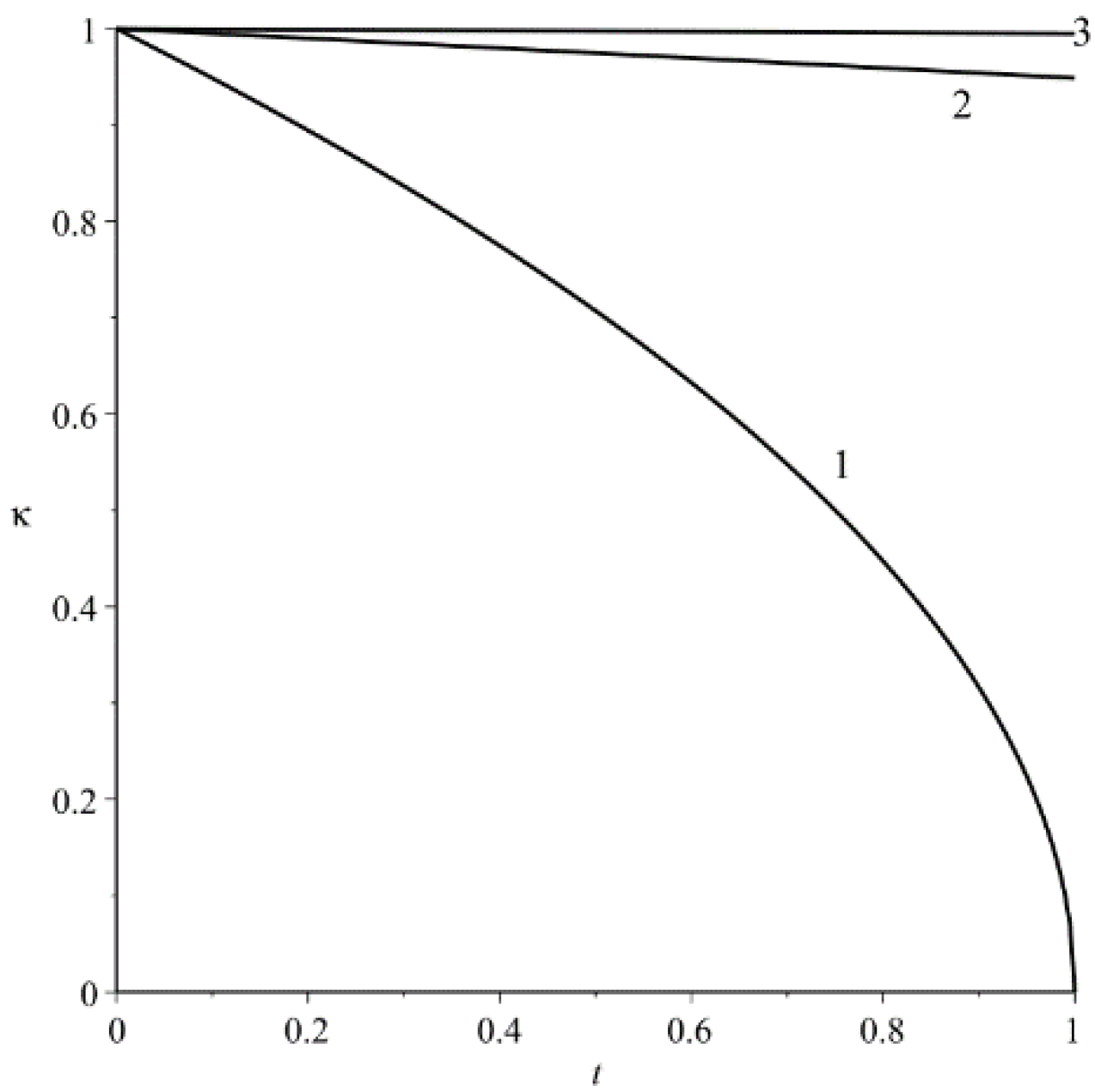
A characteristic change in the size of the evaporating droplet (41) is shown in
Figure 1.
As for the relaxation time
, it can be easily estimated based on the following formula (see [
14])
where
is the radius of a gas molecule,
is their average chemical potential,
is the mass of a water molecule,
is the mass of a gas molecule,
is the average concentration of water molecules. In order of magnitude, it follows from (44) that
s. A similar formula holds for relaxation time
. It is obtained from formula (44) by formally replacing the indices
with
. It can be shown that in order of magnitude
s.
The calculation of the evaporation time by formula (42) also dictates the need to substitute the chemical potentials of gas and liquid into it. If we proceed from the general definition of the average energy of a large statistical system of particles, namely
, where
is the number of particles in the system then for its differential we have
According to example [
10] in variables
, the Helmholtz energy differential is
From the comparison of (45) and (46), we see that
It is known from [
10] that the entropy per particle can be calculated as
where
is the normalization factor and
is the equilibrium Maxwell distribution function,
is the molecule momentum. Neglecting in (48) the processes of scattering of molecules, we have for entropy
The chemical potentials in exponential exponents under the integral in (53) and in the normalization factor will decrease and as a result of a simple calculation, we will come to this answer
Remembering now definition (47), we obtain the following differential equation for determining
Simple integration leads us to the following result
where dependence
is easily found from the second relation in (47), that is
Since the Clapeyron–Mendeleev equation
holds for an ideal gas, we immediately get from here that
where
is the constant.
Assuming
and substituting (55) into (53), we find the desired dependence
where
is the temperature and pressure under normal conditions that is
. That is, for the gas phase, the chemical potential is determined using (56) as
As for a droplet of water, it is very problematic to use the gas approximation for it and in this case you can use for example the Van der Waals equation. As a result, the chemical potential can also be calculated analytically but we will not do this now but will proceed to the estimation of the evaporation time considering for simplicity that . Note, by the way, that this ratio is quite correct.
To numerically estimate the evaporation time, we will use the general expression (40).
The physical parameters present in Formula (40) can be selected as follows:
Note that in all the estimates below we will use the Gaussian system of units.
That is, a droplet of water with a diameter of five millimeters evaporates in about twenty minutes. Result (60) is in full correlation with the traditional formula given in [
3] which gives us reason to assert the correctness of the results obtained above.
Looking at Equation (36), we quite clearly see before us an equation of the type of thermal conductivity equation with a thermal conductivity coefficient
or a diffusion-type equation with a diffusion coefficient
which are determined in order of magnitude by the coefficient of the right side of Equation (36), that is
This remarkable result is evidence that the evaporation process is purely dissipative in nature and under isothermal conditions is determined by the heterogeneity of the chemical potential at the interface between liquid and gas. In light of the above, it can be argued that according to (59), the described evaporation effect is nothing more than isothermal diffusion. In fact, the problem of the analytical description of the droplet evaporation process can be considered solved by evaluation (58).
4. Dynamics of Droplet Passage through A Hot Medium
In the event that a purely technical problem is set related to extinguishing a fire, for example, a burning transformer box, we need to provide an analytical solution to this problem and describe the dynamics of droplets passing through the flame to the surface of the boiling transformer oil taking into account all the basic physical conditions.
If we assume, for example, that the velocity of water from the hose is equal to , and the distance that the water jet passes to the source of ignition is put equal say , then the time of passage of the jet will be about three-tenths of a second.
Based on estimate (61), it can be assumed that the complete evaporation of a droplet with a diameter of half a centimeter occurs in about an hour; therefore, the droplet does not actually have time to evaporate and passing through the flame, it hits the surface of the oil with almost the same size. It is possible for water droplets to reach the oil surface if the obvious inequality is met
Whence it follows that the droplet size must obey the condition
As can be seen from the above assessment, the situation is not quite simple in terms of analytical determination of the most effective droplet size. In fact, if we achieve the droplet size, for example, such , then it simply evaporates quickly without having time to reach the oil surface. This means that here the problem of determining the optimal size of the droplet arises, which despite its small size will still have time to reach the oil surface evaporating directly on it which is the main criterion in the conditions of ignition of oil transformers.
This means that the following strict inequalities must be met
where
and the value of the right side of inequality (66)
must be found. To calculate it, we will use the equation of motion of a droplet in the gravity field taking into account the drag force and the buoyant force in the following form (see, for example, study [
15,
16,
17])
where the attenuation coefficient due to the consideration of the Stokes resistance force is
Recall that index “1” refers to a droplet and index “2” refers to a gas. Function
is given by dependency (41) which is convenient to write taking into account (43) in the following form
Taking into account (68), Equation (67) can be presented in a more convenient form as
where
and
. The solution of Equation (70) is trivial. In fact, by solving a homogeneous equation we get
hence
where
is the index. Considering constant
as a function of time and then substituting (71) into Equation (70), we find
that is
where
is the integration constant. Substituting (72) into (71), we find the following solution
To determine constant
, we use initial condition
. As a result,
and the final solution will take the following form
In a dimensionless view, we have
where
and
.
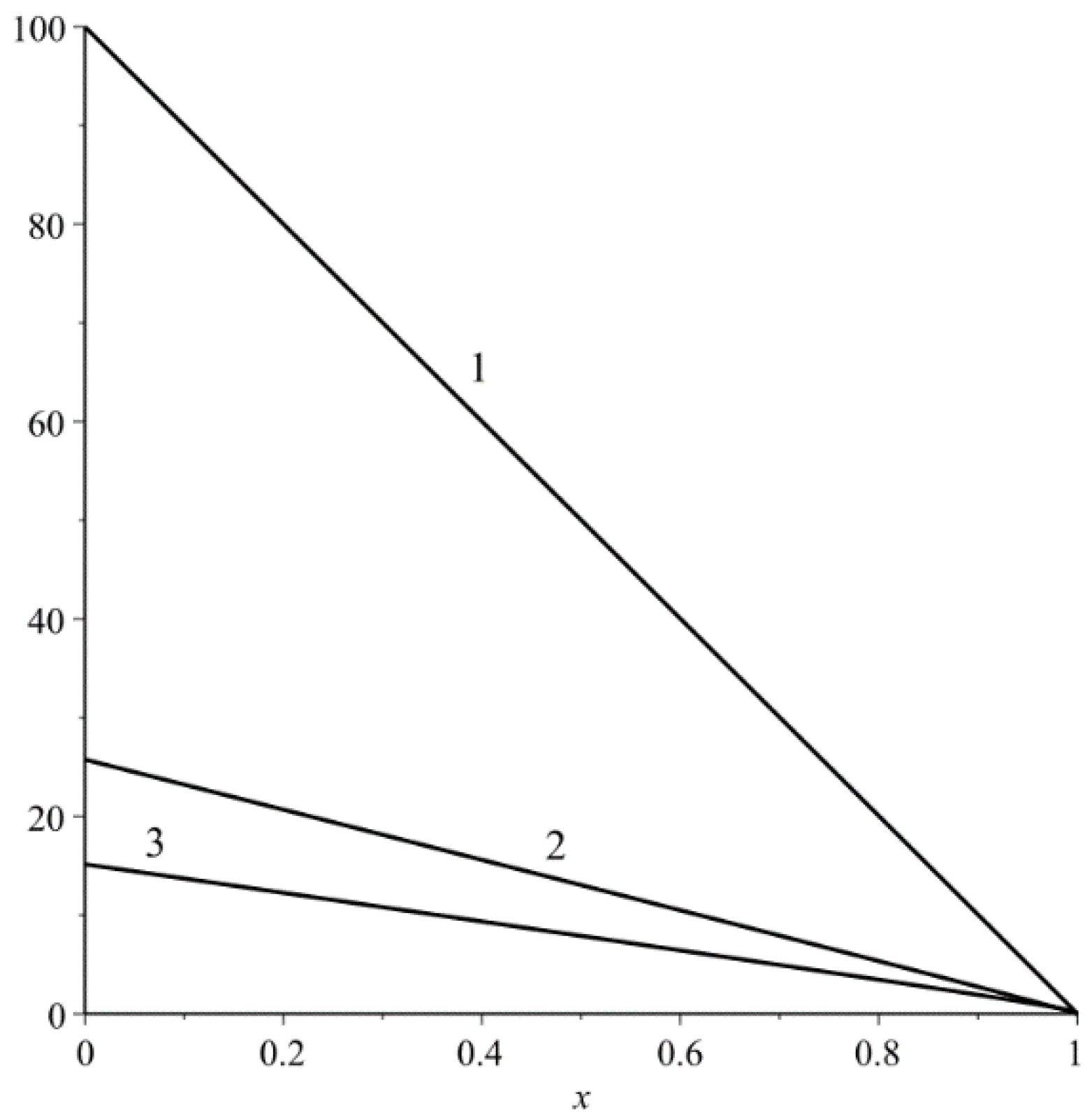
The dependence (74b) is shown in
Figure 2.
It is taken into account here that always
. Integrating (74) in time, we find the droplet path length
From the initial condition
, we get
therefore,
In a dimensionless view, the dependence (77a) can be written as
where the parameters are
,
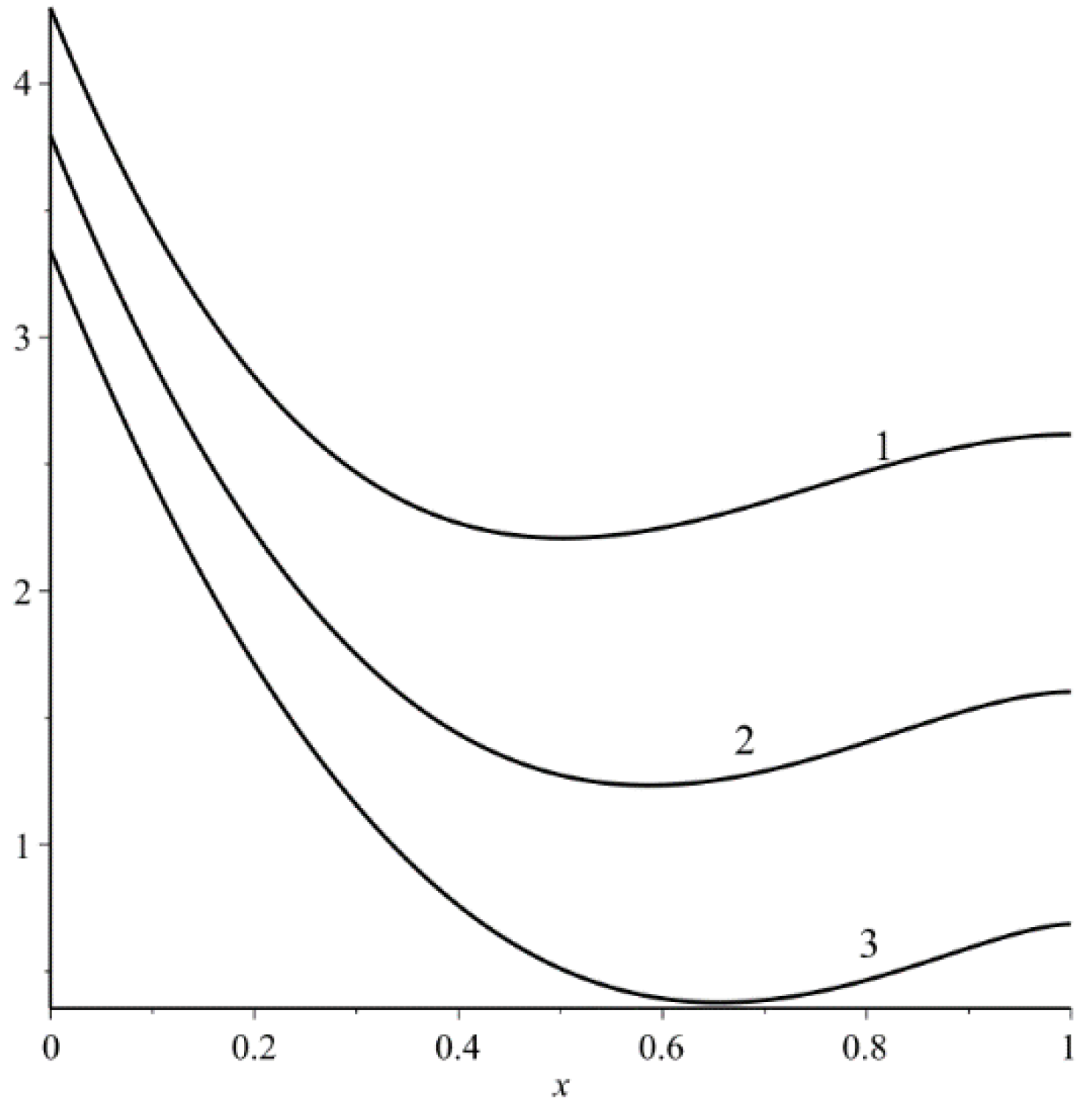
The dependence (77b) is illustrated in
Figure 3.
From condition
, we can calculate the time of the droplet movement to the oil surface of our interest taking into account its evaporation. This algebraic equation must be solved under the condition that
. Therefore, by decomposing function
by degrees of ratio
, we find approximately
From here taking into account evaporation, the travel time will be
During this period of time, the droplet size decreases and becomes equal according to (69)
Thus, from solution (80), taking into account the explicit form for
, it follows that the initial droplet size should be
In turn, remembering that
, we get a biquadrate inequality to determine the possible values
. In fact, from (84) we get
It is convenient to bring this inequality to the following form
where
.
Moreover, the hierarchy of these parameters is as follows
Therefore, using condition
and leaving only one in the lowest fraction, we easily solve the simplified biquadrate inequality which leads us to the following condition
Substituting explicit expressions for radii from (83), we find
From where we find the condition for the initial velocity of the droplet
where
From the example, we can take the following parameters ,
The numerical value (88) is in full accordance with the known practical results; therefore, the solution of the problem can be considered complete in accordance with estimates (86) and (87).