Rheological Properties and Its Effect on the Lubrication Mechanism of PVP K30 and PVP 40-50 G as Artificial Synovial Fluids
Abstract
:1. Introduction
2. Experimental Method and Materials
2.1. Preparation Method of PVP Solution
2.2. Rheological Measurements
2.3. Numerical Analysis
3. Results and Discussion
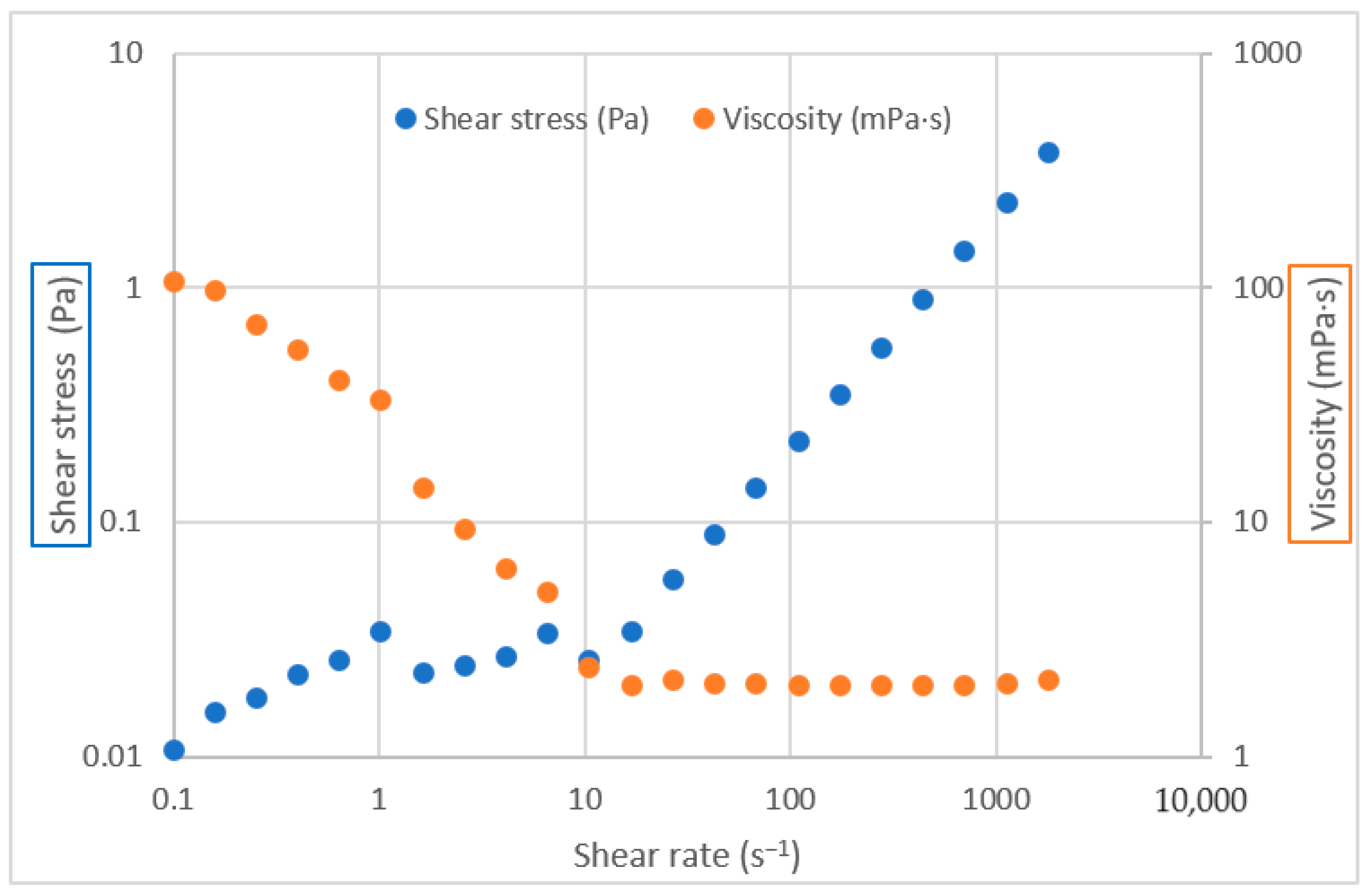
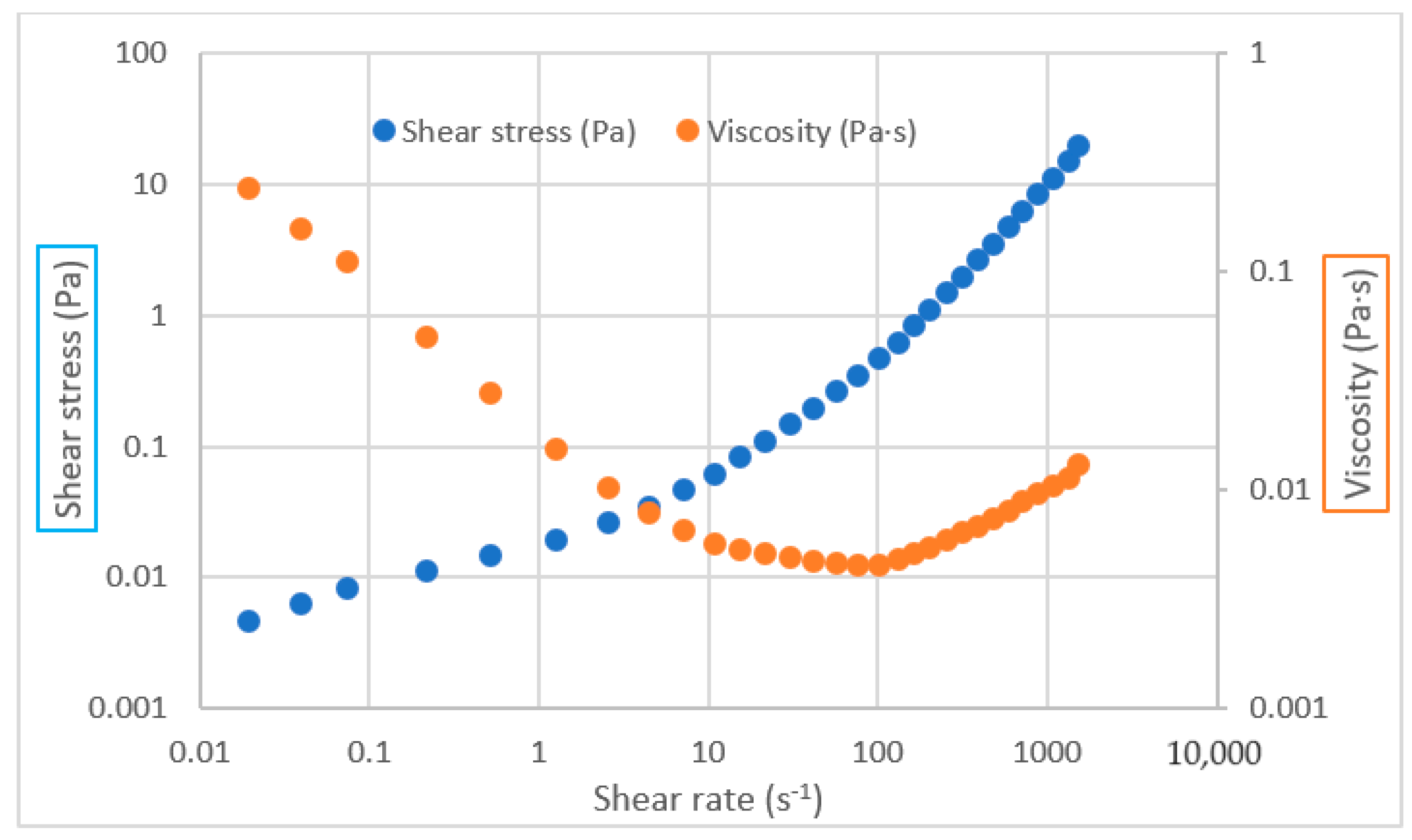
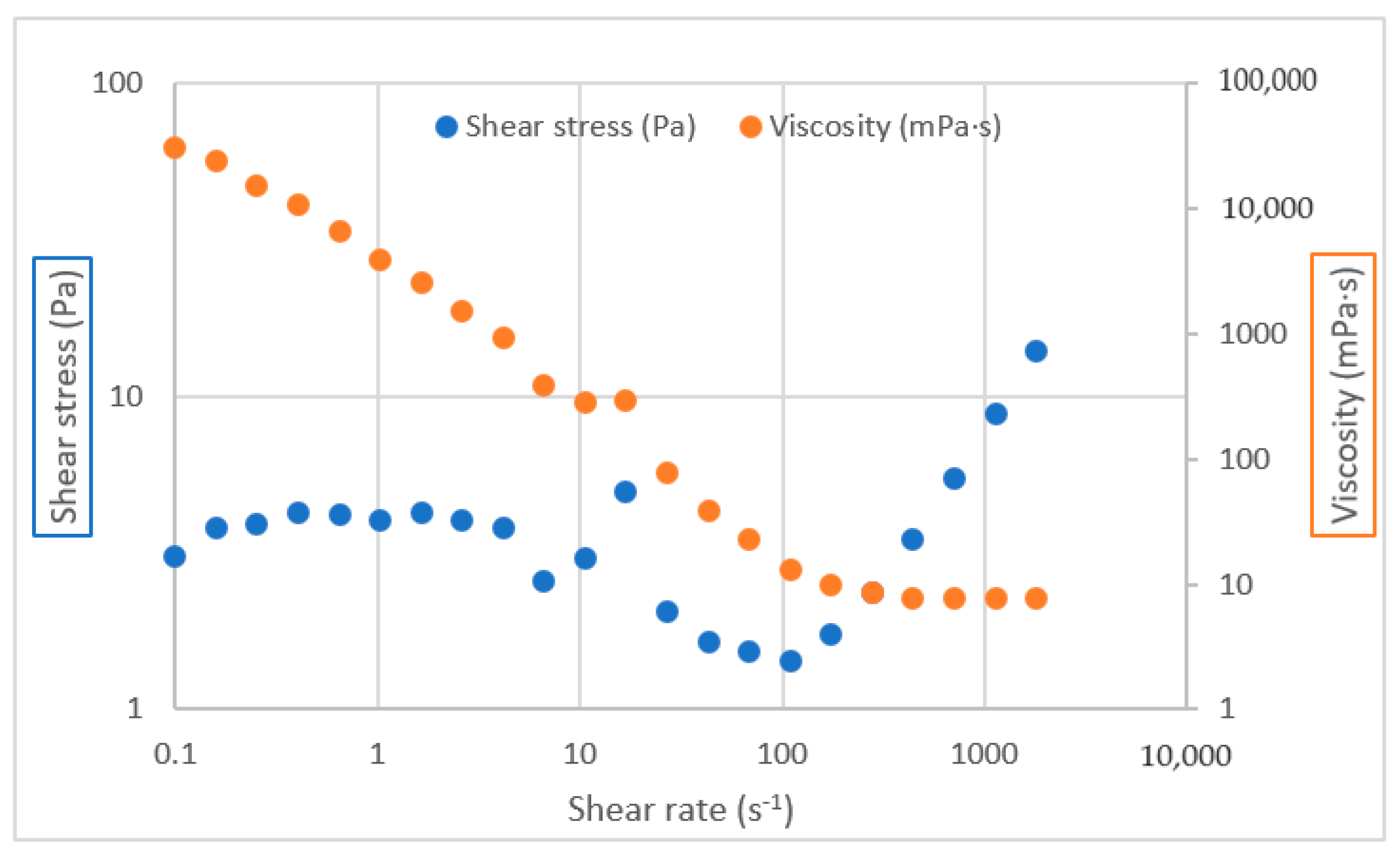
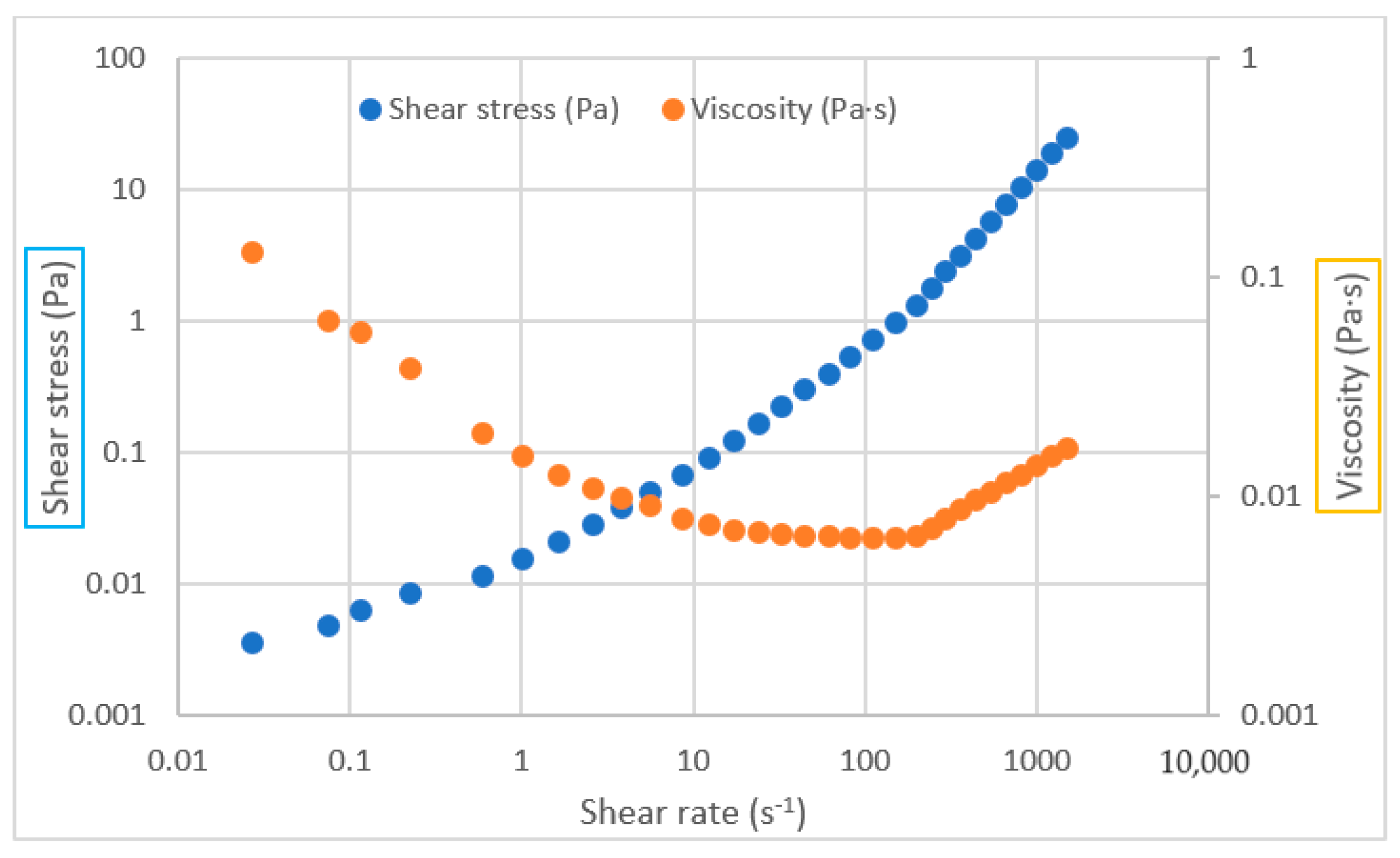
3.1. Viscosity and Shear Stress
3.2. Numerical Analysis Results for Different Samples
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liao, J.; Miramini, S.; Liu, X.; Zhang, L. Computational study on synovial fluid flow behaviour in cartilage contact gap under osteoarthritic condition. Comput. Biol. Med. 2020, 123, 103915. [Google Scholar] [CrossRef] [PubMed]
- Jay, G.D.; Waller, K.A. The biology of lubricin: Near frictionless joint motion. Matrix Biol. 2014, 39, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Cook, S.G.; Guan, Y.; Pacifici, N.J.; Brown, C.N.; Czako, E.; Samak, M.S.; Bonassar, L.J.; Gourdon, D. Dynamics of synovial fluid aggregation under shear. Langmuir 2019, 35, 15887–15896. [Google Scholar] [CrossRef] [PubMed]
- More, S.; Kotiya, A.; Kotia, A.; Ghosh, S.K.; Spyrou, L.A.; Sarris, I.E. Rheological properties of synovial fluid due to viscosupplements: A review for osteoarthritis remedy. Comput. Methods Programs Biomed. 2020, 196, 105644. [Google Scholar] [CrossRef] [PubMed]
- Bhuanantanondh, P.; Grecov, D.; Kwok, E. Rheological study of viscosupplements and synovial fluid in patients with osteoarthritis. CMBES Proc. 2010, 33, 12–16. [Google Scholar] [CrossRef]
- Lundsgaard, C.; Dufour, N.; Fallentin, E.; Winkel, P.; Gluud, C. Intra-articular sodium hyaluronate 2 mL versus physiological saline 20 mL versus physiological saline 2 mL for painful knee osteoarthritis: A randomized clinical trial. Scand. J. Rheumatol. 2008, 37, 142–150. [Google Scholar] [CrossRef] [PubMed]
- Nair, B. Final report on the safety assessment of polyvinylpyrrolidone (PVP). Int. J. Toxicol. 1998, 17, 95–130. [Google Scholar] [CrossRef]
- Haaf, F.; Sanner, A.; Straub, F. Polymers of N-vinylpyrrolidone: Synthesis, characterization and uses. Polym. J. 1985, 17, 143–152. [Google Scholar] [CrossRef] [Green Version]
- Kurakula, M.; Rao, G.K. Pharmaceutical Assessment of Polyvinylpyrrolidone (PVP): As Excipient from Conventional to Controlled Delivery Systems with a Spotlight on COVID-19 Inhibition. J. Drug Deliv. Sci. Technol. 2020, 60, 102046. [Google Scholar] [CrossRef] [PubMed]
- Radin, E.L.; Paul, I.L.; Weisser, P.A. Joint lubrication with artificial lubricants. Arthritis Rheum. Off. J. Am. Coll. Rheumatol. 1971, 14, 126–129. [Google Scholar] [CrossRef] [PubMed]
- Bühler, V. Polyvinylpyrrolidone Excipients for Pharmaceuticals: Povidone, Crospovidone and Copovidone; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Rowe, R.C.; Sheskey, P.; Quinn, M. Handbook of Pharmaceutical Excipients; Pharmaceutical Press: London, UK, 2009. [Google Scholar]
- Frizon, F.; de Oliveira Eloy, J.; Donaduzzi, C.M.; Mitsui, M.L.; Marchetti, J.M. Dissolution rate enhancement of loratadine in polyvinylpyrrolidone K-30 solid dispersions by solvent methods. Powder Technol. 2013, 235, 532–539. [Google Scholar] [CrossRef]
- Budavari, S.; O’Neil, M.J.; Smith, A. The Merck Index, 13th ed.; Merck & Co. Inc.: Whitehouse Station, NJ, USA, 1996. [Google Scholar]
- Kurakula, M.; Koteswara Rao, G.S.N. Moving polyvinyl pyrrolidone electrospun nanofibers and bioprinted scaffolds toward multidisciplinary biomedical applications. Eur. Polym. J. 2020, 136, 109919. [Google Scholar] [CrossRef]
- Teodorescu, M.; Bercea, M.; Morariu, S. Biomaterials of PVA and PVP in medical and pharmaceutical applications: Perspectives and challenges. Biotechnol. Adv. 2019, 37, 109–131. [Google Scholar] [CrossRef] [PubMed]
- Jun, Y.-B.; Min, B.-H.; Kim, S.-I.; Kim, Y.-I. Preparation and evaluation of acetaminophen tablets. J. Pharm. Investig. 1989, 19, 123–129. [Google Scholar]
- Joint FAO/WHO Expert Committee on Food Additives. Technical Report Series; WHO: Geneva, Switzerland, 1987. [Google Scholar]
- Guo, Y.; Hao, Z.; Wan, C. Tribological characteristics of polyvinylpyrrolidone (PVP) as a lubrication additive for artificial knee joint. Tribol. Int. 2016, 93, 214–219. [Google Scholar] [CrossRef]
- Wong, Y.-R.; Sophie, S.H.T.; Mat Jais, I.S.; Leo, H.-L.; Liu, C.-F.; Tay, S.-C. Computational Simulation of Synovial Fluid Kinematics of the Scapholunate Joint. J. Hand Surg. 2019, 24, 169–174. [Google Scholar]
- Wang, Y.; Fan, Y.; Zhang, M. Comparison of stress on knee cartilage during kneeling and standing using finite element models. Med. Eng. Phys. 2014, 36, 439–447. [Google Scholar] [CrossRef] [PubMed]

| Property | Description |
|---|---|
| Description of PVP | Fine, white odorless, hygroscopic, Amorphous powder. |
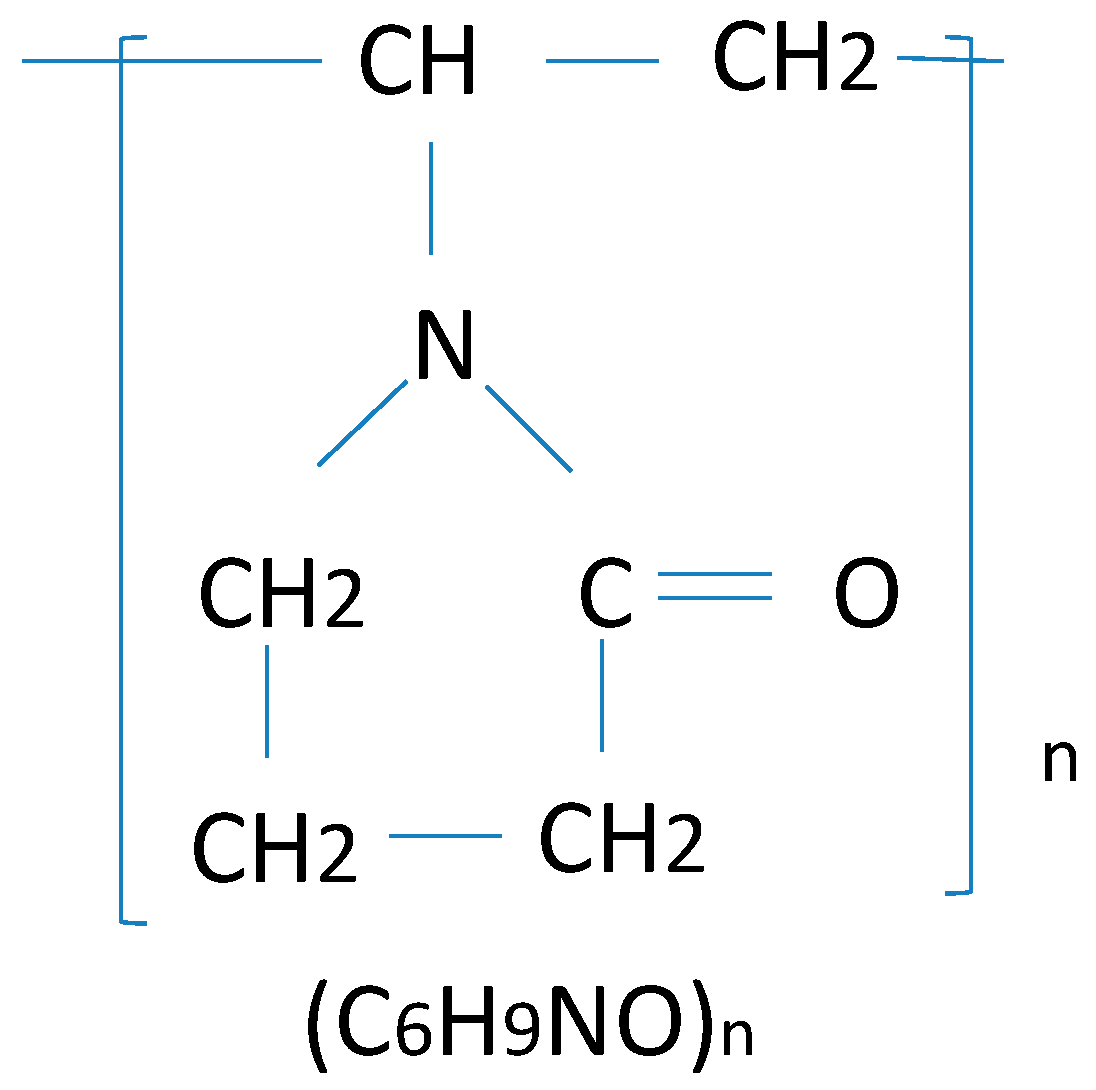
| Molecular formula | (C6H9NO) n |
| Molecular weight | 2500–3,000,000 Da |
| K value range | 10–120 |
| Solubility | Water, ethanol, methanol, chloroform, acids, and amines. Insoluble in ethers, hydrocarbons, some esters, some ketones, and mineral oil. |
| Melting point | Softens at 150 °C and decomposes after 180 °C |
| pH value | 3–7 (varies with concentration and k value of the solution) |
| Compatibility | Hydrophilic and hydrophobic, natural and synthetic resins; inorganic salts and other chemicals. |
| Polymer | K Value | Concentration in Water (%) | Relative Viscosity in Water |
|---|---|---|---|
| PVP | 12 | 5 | 1.2915 ± 0.0695 |
| 17 | 5 | 1.513 ± 0.083 | |
| 25 | 1 | 1.1735 ± 0.0275 | |
| 30 | 1 | 1.241 ± 0.04 | |
| 90 | 1 | 4.2525 ± 0.9425 |
| Pressure (Pa) | Molecular Viscosity (kg/m·s) | |
|---|---|---|
| 1 | Case 1. (Sterile water) | |
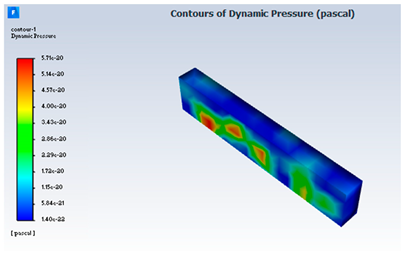 |  | |
| 2 | Case 2. (5%—PVP 40-50 G/sterile water) | |
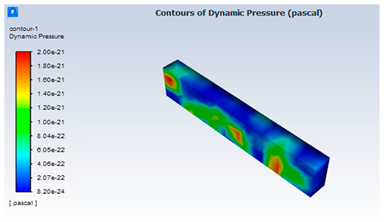 |  | |
| 3 | Case 3. (10%—PVP K30/sterile water) | |
 |  | |
| 4 | Case 4. (20%—PVP40-50 G/sterile water) | |
 |  | |
| 5 | Case 5. (20%—PVP K30/sterile water) | |
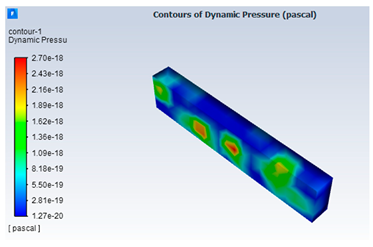 | 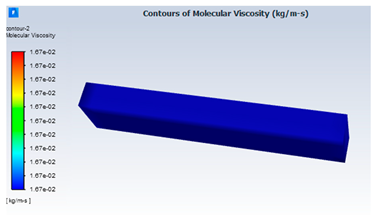 | |
| Sample | Pressure Variation (Pa) | Molecular Viscosity (kg/m·s) | Residuals (Continuity) |
|---|---|---|---|
| Sterile water | 4.132487 × 10−23 to 1.084074 × 10−19 | 0.10617 | 10−15 |
| 5%—PVP 40-50 G/sterile water | 3.906337 × 10−24 to 3.642479 × 10−21 | 0.51632 | 10−8 |
| 10%—PVP K30/sterile water | 6.383177 × 10−21 to 5.806318 × 10−18 | 0.01304 | 10−15 |
| 20%—PVP40-50 G/sterile water | 6.005832 × 10−28 to 1.106963 × 10−24 | 30.605 | 10−15 |
| 20%—PVP K30/sterile water | 2.921407 × 10−21 to 5.371442 × 10−18 | 0.01674 | 10−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotia, A.; More, S.; Yadav, A.; Mohan, T.V.S.Y.; Naidu, A.H.; Rajesh, G.; Sarris, I.E. Rheological Properties and Its Effect on the Lubrication Mechanism of PVP K30 and PVP 40-50 G as Artificial Synovial Fluids. Inventions 2021, 6, 61. https://doi.org/10.3390/inventions6040061
Kotia A, More S, Yadav A, Mohan TVSY, Naidu AH, Rajesh G, Sarris IE. Rheological Properties and Its Effect on the Lubrication Mechanism of PVP K30 and PVP 40-50 G as Artificial Synovial Fluids. Inventions. 2021; 6(4):61. https://doi.org/10.3390/inventions6040061
Chicago/Turabian StyleKotia, Ankit, Sunil More, Aman Yadav, Thota Venkata Sai Yaswanth Mohan, Arnepaplli Harshavardhan Naidu, Golusu Rajesh, and Ioannis E. Sarris. 2021. "Rheological Properties and Its Effect on the Lubrication Mechanism of PVP K30 and PVP 40-50 G as Artificial Synovial Fluids" Inventions 6, no. 4: 61. https://doi.org/10.3390/inventions6040061
APA StyleKotia, A., More, S., Yadav, A., Mohan, T. V. S. Y., Naidu, A. H., Rajesh, G., & Sarris, I. E. (2021). Rheological Properties and Its Effect on the Lubrication Mechanism of PVP K30 and PVP 40-50 G as Artificial Synovial Fluids. Inventions, 6(4), 61. https://doi.org/10.3390/inventions6040061







