A Tutorial on Robust Control, Adaptive Control and Robust Adaptive Control—Application to Robotic Manipulators
Abstract
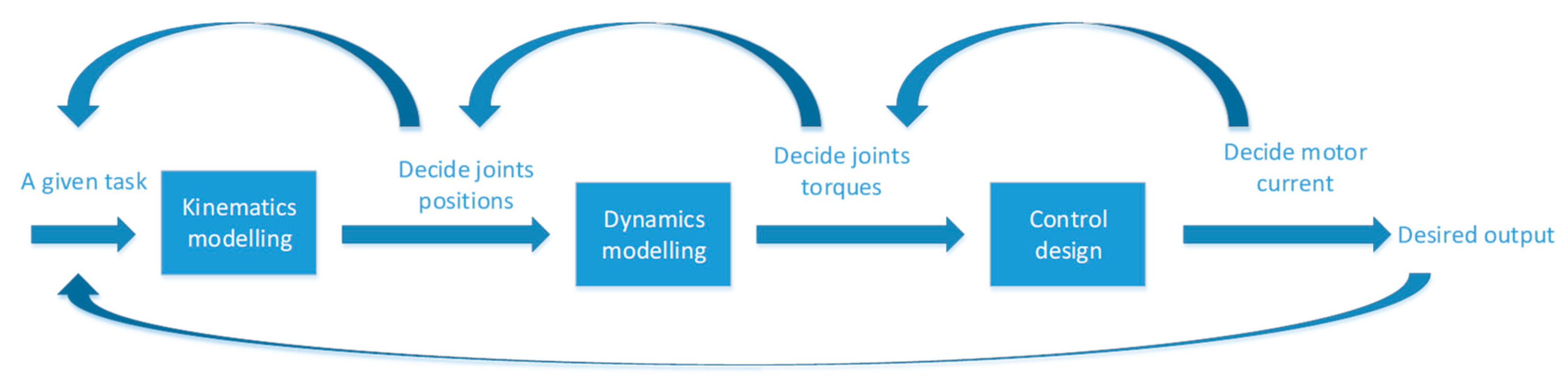
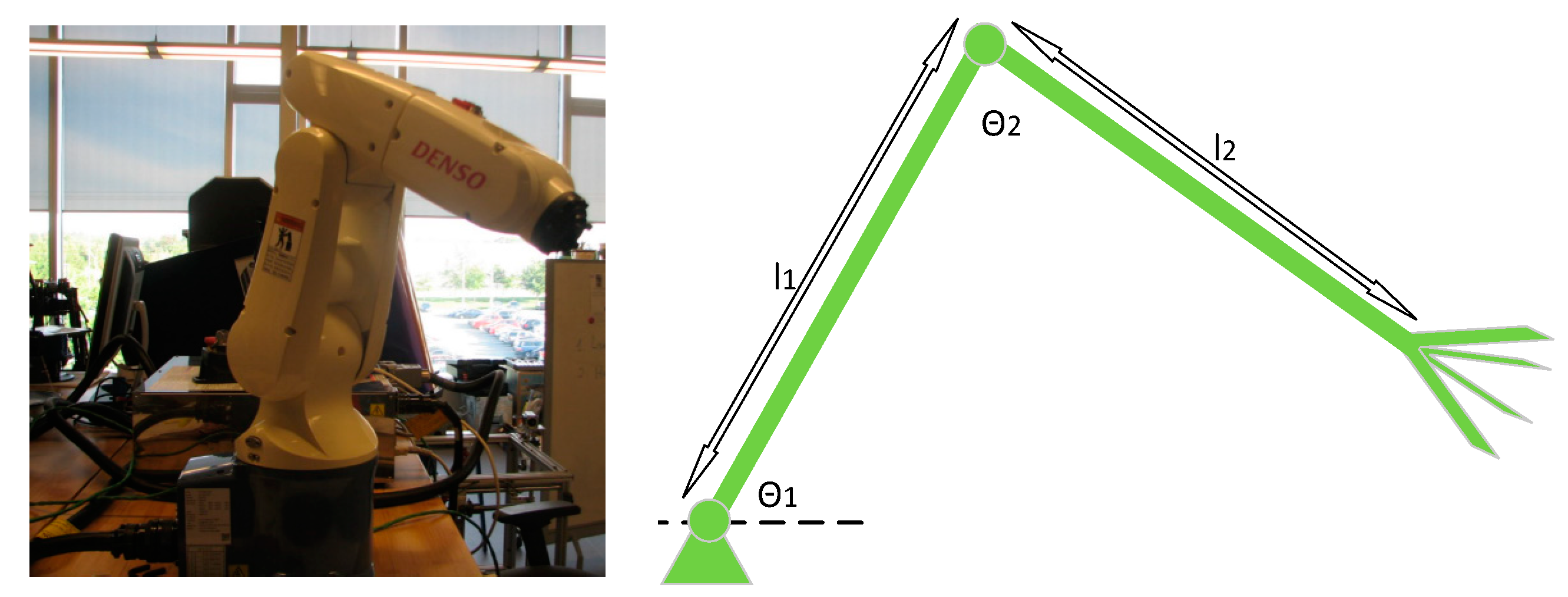
1. Introduction
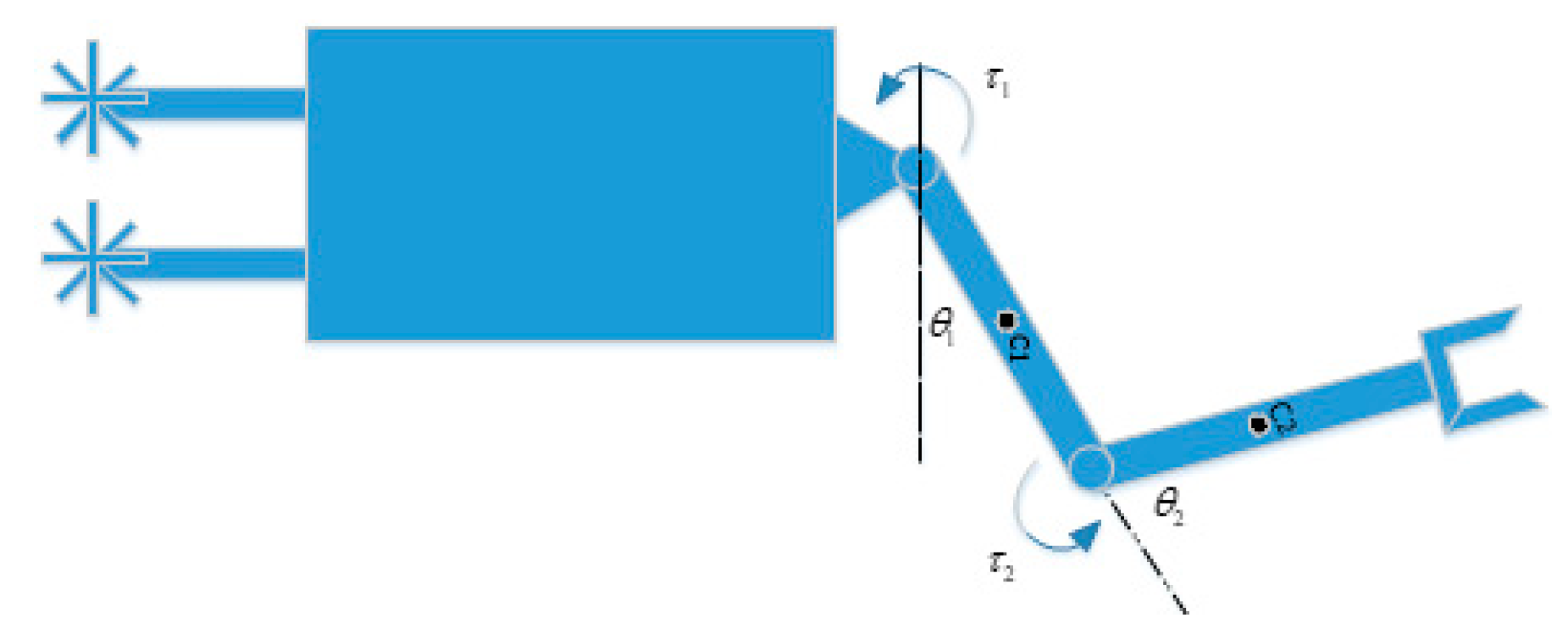
2. Joint Space Control and Operational Space Control
3. Robust Control
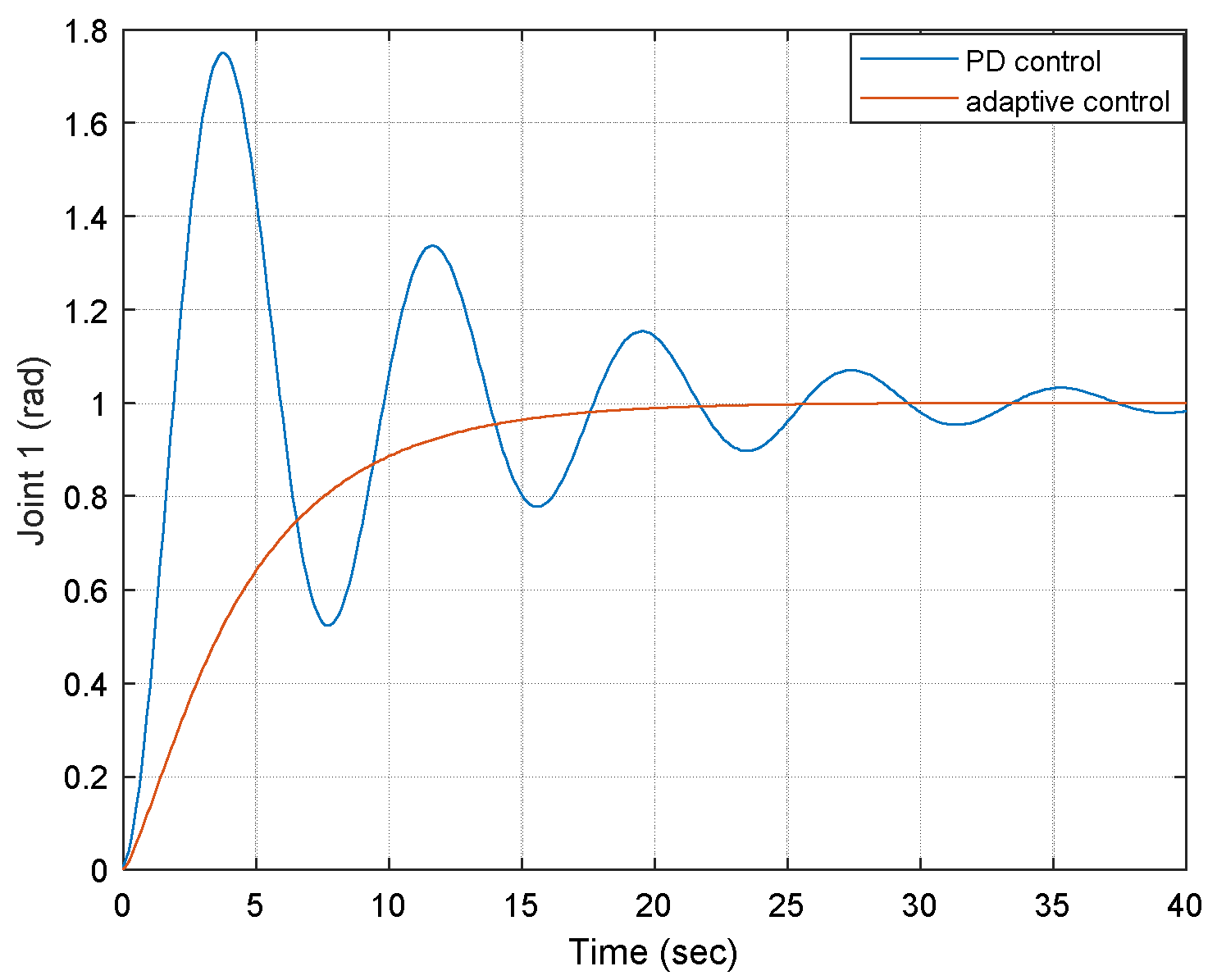
4. Adaptive Control
5. Robust Adaptive Control
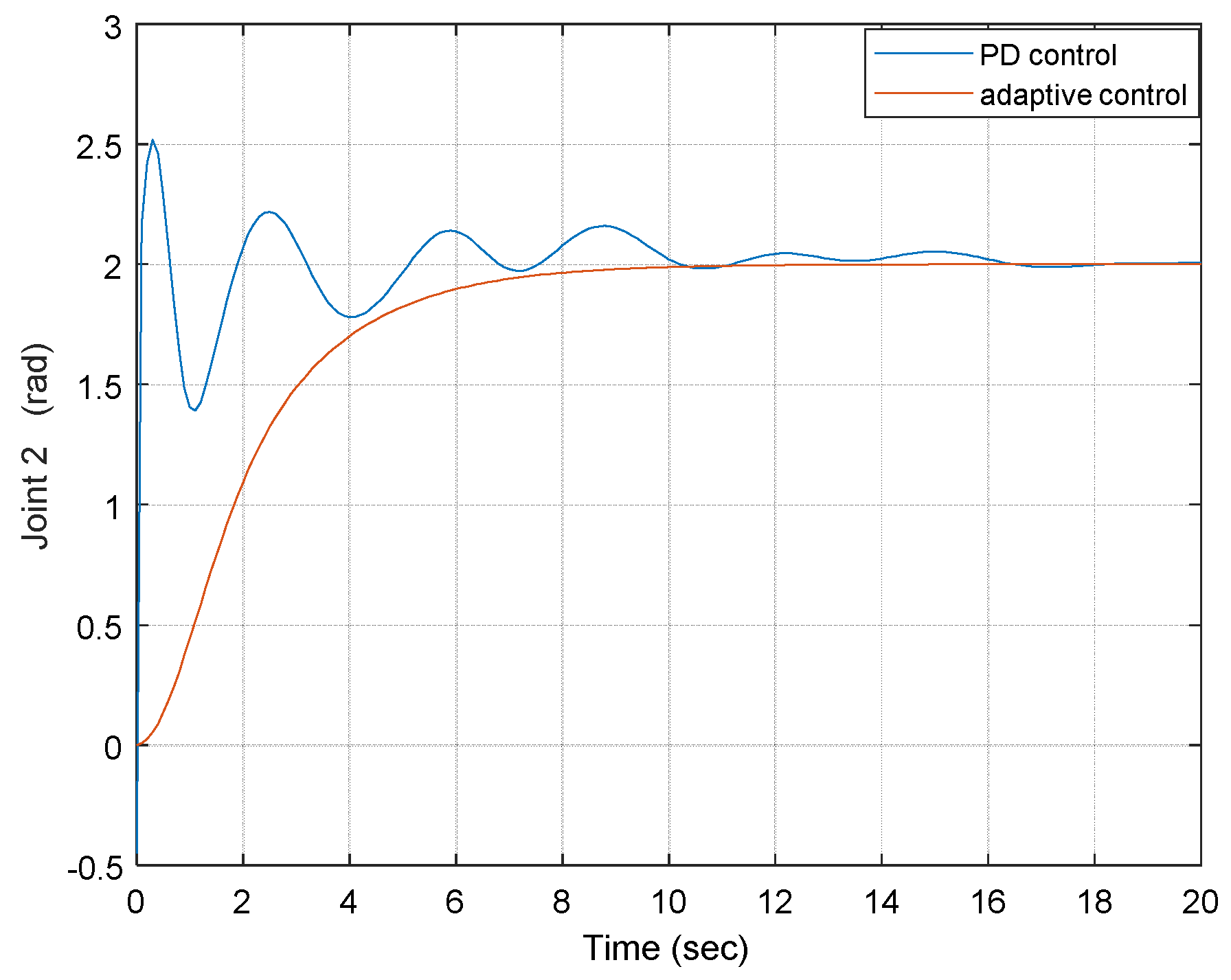
6. Adaptive Control
7. Conclusions
Funding
Conflicts of Interest
Abbreviations
| Term | Meaning |
| unknow constant (see Equation (15)) | |
| estimate of | |
| parameter estimation error | |
| unknown friction term | |
| estimate of |
References
- Schreiber, L.; Gosselin, C.; Laliberte, T. Kinematics and dynamic analysis of a skating robot. Trans. Can. Soc. Mech. Eng. 2014, 38, 185–197. [Google Scholar] [CrossRef]
- St-Onge, D.; Gosselin, C. Synthesis and Design of a One Degree-of-Freedom Planar Deployable Mechanism with a Large Expansion Ratio. J. Mech. Robot. 2016, 8, 021025. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, B. Design and optimization of a Tripod-based hybrid manipulator. Romansy- 2014, CISM-IFToMM Symposium on Theory and Practice of Robots and Manipulators. Mech. Mach. Sci. 2014, 22, 83–91. [Google Scholar]
- Cavusoglu, M.; Villanueva, I.; Tendick, F. Workspace analysis of robotic manipulators for a teleoperated suturing task. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; pp. 2234–2239. [Google Scholar]
- Bouzgou, K.; Ahmed-Foitih, Z. Workspace Analysis and Geometric Modeling of 6 DOF Fanuc 200IC Robot. Procedia Soc. Behav. Sci. 2015, 182, 703–709. [Google Scholar] [CrossRef][Green Version]
- Isaksson, M.; Gosselin, C.; Marlow, K. Singularity analysis of a class of kinematically redundant parallel Schönflies motion generators. Mech. Mach. Theory 2017, 112, 172–191. [Google Scholar] [CrossRef]
- Jiang, Q.; Gosselin, C.M.; Wang, Y.; Fang, C. Maximal singularity-free orientation workspace over a position region of Gough–Stewart platform. Adv. Robot. 2015, 29, 1–10. [Google Scholar] [CrossRef]
- Klimchik, A.; Caro, S.; Wu, Y.; Chablat, D.; Furet, B.; Pashkevich, A. Stiffness modeling of robotic manipulator with gravity compensator. In Proceedings of the 6th International Workshop on Computational Kinematics (CK2013), Barcelona, Spain, 12–15 May 2013; pp. 161–168. [Google Scholar]
- Zhang, D.; Wei, B. Design, kinematic and dynamic modeling of a novel tripod-based manipulator. Robotica 2016, 34, 2186–2204. [Google Scholar] [CrossRef]
- Flacco, F.; De Luca, A.; Khatib, O. Control of Redundant Robots under Hard Joint Constraints: Saturation in the Null Space. IEEE Trans. Robot. 2015, 31, 637–654. [Google Scholar] [CrossRef]
- Menon, S.; Fok, S.; Neckar, A.; Khatib, O.; Boahen, K. Controlling articulated robots in task-space with spiking silicon neurons. In Proceedings of the 5th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, Sao Paulo, Brazil, 12–15 August 2014; pp. 181–186. [Google Scholar]
- Conti, F.; Park, J.; Khatib, O. Interface Design and Control Strategies for a Robot Assisted Ultrasonic Examination System. In Experimental Robotics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 97–113. [Google Scholar]
- Khatib, O. A unified approach for motion and force control of robot manipulators: The operational space formulation. IEEE J. Robot. Autom. 1987, 3, 43–53. [Google Scholar] [CrossRef]
- Sentis, L.; Park, J.; Khatib, O. Compliant control of multi-contact and center of mass behaviors in humanoid robots. IEEE Trans. Robot. 2010, 26, 483–501. [Google Scholar] [CrossRef]
- Slotine, J.E.; Li, W. Applied Nonlinear Control; Prentice-Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Santibáñez, V.; Kelly, R. PD control with feedforward compensation for robot manipulators: Analysis and experimentation. Robotica 2001, 19, 11–19. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, B. Adaptive Control for Robotic Manipulators; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Li, W.; Slotine, J.-J.E. On the Adaptive Control of Robot Manipulators. Int. J. Robot. Res. 1987, 6, 49–59. [Google Scholar]
- Tomizuka, M.; Horowitz, R. An Adaptive Control Scheme for Mechanical Manipulators—Compensation of Nonlinearity and Decoupling Control. J. Dyn. Syst. Meas. Control 1986, 108, 127–135. [Google Scholar]
- Tong, S.; Li, Y.; Sui, S. Adaptive Fuzzy Tracking Control Design for SISO Uncertain Nonstrict Feedback Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2016, 24, 1441–1454. [Google Scholar] [CrossRef]
- Li, Y.; Tong, S.; Liu, L.; Feng, G. Adaptive output-feedback control design with prescribed performance for switched nonlinear systems. Automatica 2017, 80, 225–231. [Google Scholar] [CrossRef]
- Craig, J.J. Adaptive Control of Mechanical Manipulators; Addison-Wesley: Boston, MA, USA, 1988. [Google Scholar]
- Wang, C.; Zhao, Y.; Chen, Y.; Tomizuka, M. Nonparametric statistical learning control of robot manipulators for trajectory or contour tracking. Robot. Comput. Manuf. 2015, 35, 96–103. [Google Scholar] [CrossRef]
- Armin, S.; Goele, P.; Jan, S. Optimization-based iterative learning control for robotic manipulators. In Proceedings of the 2016 Benelux Meeting on Systems and Control, Soesterberg, The Netherlands, 22–24 March 2016. [Google Scholar]
- Verrelli, C.M.; Pirozzi, S.; Tomei, P.; Natale, C. Linear Repetitive Learning Controls for Robotic Manipulators by Padé Approximants. IEEE Trans. Control Syst. Technol. 2015, 23, 2063–2070. [Google Scholar] [CrossRef]
- Ernesto, H.; Pedro, J.O. Iterative Learning Control with Desired Gravity Compensation under Saturation for a Robotic Machining Manipulator. Math. Probl. Eng. 2015, 2015, 187948. [Google Scholar] [CrossRef]
- Delchev, K.; Boiadjiev, G.; Kawasaki, H.; Mouri, T. Iterative learning control with sampled-data feedback for robot manipulators. Arch. Control Sci. 2014, 24, 299–319. [Google Scholar] [CrossRef]
- Delchev, K. Iterative learning control for robotic manipulators: A bounded-error algorithm. Int. J. Adapt. Control Signal Process. 2014, 28, 1454–1473. [Google Scholar] [CrossRef]
- Munadi, M.; Naniwa, T. Experimental verification of adaptive dominant type hybrid adaptive and learning controller for trajectory tracking of robot manipulators. J. Robot. Mechatron. 2013, 25, 737–747. [Google Scholar] [CrossRef]
- Queen, M.P.; Kuma, M.; Aurtherson, P. Repetitive Learning Controller for Six Degree of Freedom Robot Manipulator. Int. Rev. Autom. Control 2013, 6, 286–293. [Google Scholar]
- Marino, R.; Tomei, P.; Verrelli, C.M. Robust adaptive learning control for nonlinear systems with extended matching unstructured uncertainties. Int. J. Robust Nonlinear Control 2012, 22, 645–675. [Google Scholar] [CrossRef]
- Bouakrif, F.; Boukhetala, D.; Boudjema, F. Velocity observer-based iterative learning control for robot manipulators. Int. J. Syst. Sci. 2013, 44, 214–222. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, B. On the development of learning control for robotic manipulators. Robotics 2017, 6, 23. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X. Sliding mode control for robot. In Advanced Sliding Mode Control for Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bennassar, A.; Banerjee, S.; Jamma, M.; Essalmi, A.; Akherraz, M. Real Time High Performance of Sliding Mode Controlled Induction Motor Drives. Procedia Comput. Sci. 2018, 132, 971–982. [Google Scholar] [CrossRef]
- Faris, F.; Moussaoui, A. Design and real-time implementation of a decentralized sliding mode controller for twin rotor multi-input multi-output system. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2016, 231, 3–13. [Google Scholar] [CrossRef]
- Castanos, F.; Fridman, L. Analysis and Design of Integral Sliding Manifolds for Systems with Unmatched Perturbations. IEEE Trans. Autom. Control 2006, 51, 853–858. [Google Scholar] [CrossRef]
- Shi, J.; Liu, H.; Bajcinca, N. Robust control of robotic manipulators based on integral sliding mode. Int. J. Control 2008, 81, 1537–1548. [Google Scholar] [CrossRef]
- Piltan, F.; Sulaiman, N. Review of sliding mode control of robotic manipulator. World Appl. Sci. J. 2012, 18, 1855–1869. [Google Scholar]
- Jin, S.; Bak, J.; Kim, J.; Seo, T.; Kim, H.S. Switching PD-based sliding mode control for hovering of a tilting-thruster underwater robot. PLoS ONE 2018, 13, e0194427. [Google Scholar] [CrossRef] [PubMed]
- Bendaas, I.; Naceri, F. A new method to minimize the chattering phenomenon in sliding mode control based on intelligent control for induction motor drives. Serb. J. Electr. Eng. 2013, 10, 231–246. [Google Scholar] [CrossRef]
- Barambones, O.; Garrido, A. Adaptive sensorless robust control of AC drives based on sliding mode control theory. Int. J. Robust Nonlinear Control 2006, 72, 862–879. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, B. A Tutorial on Robust Control, Adaptive Control and Robust Adaptive Control—Application to Robotic Manipulators. Inventions 2019, 4, 49. https://doi.org/10.3390/inventions4030049
Wei B. A Tutorial on Robust Control, Adaptive Control and Robust Adaptive Control—Application to Robotic Manipulators. Inventions. 2019; 4(3):49. https://doi.org/10.3390/inventions4030049
Chicago/Turabian StyleWei, Bin. 2019. "A Tutorial on Robust Control, Adaptive Control and Robust Adaptive Control—Application to Robotic Manipulators" Inventions 4, no. 3: 49. https://doi.org/10.3390/inventions4030049
APA StyleWei, B. (2019). A Tutorial on Robust Control, Adaptive Control and Robust Adaptive Control—Application to Robotic Manipulators. Inventions, 4(3), 49. https://doi.org/10.3390/inventions4030049



