Temperature Distribution through a Nanofilm by Means of a Ballistic-Diffusive Approach
Abstract
1. Introduction
2. Methods: Constitutional Equation for Ballistic Heat Transport
3. Temperature Distribution in Nanoscaled Materials
3.1. Two-Temperature Model
3.2. Boundary and Initial Conditions
3.3. Comparison with Fourier and Cattaneo Laws
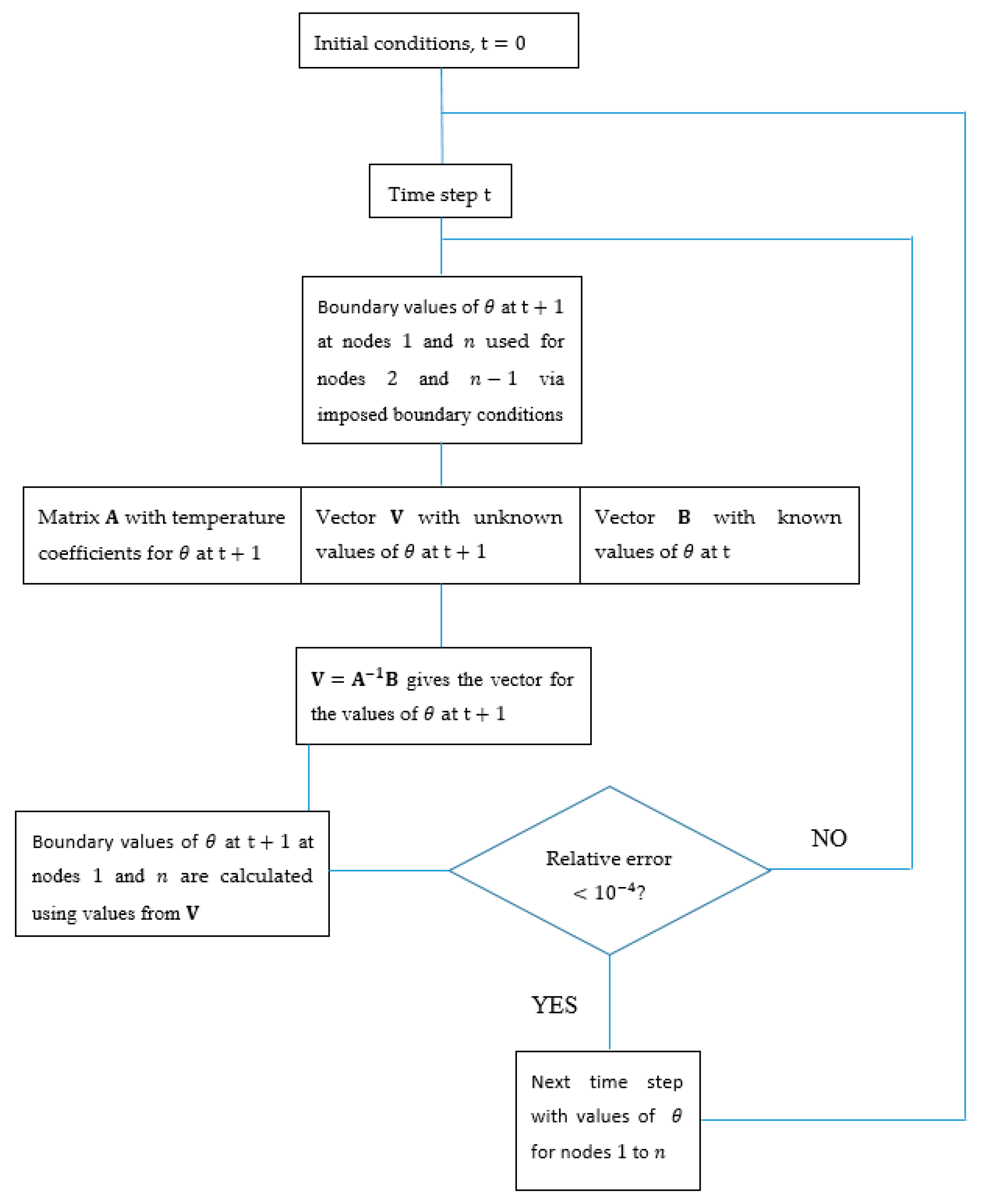
3.4. Numerical Method
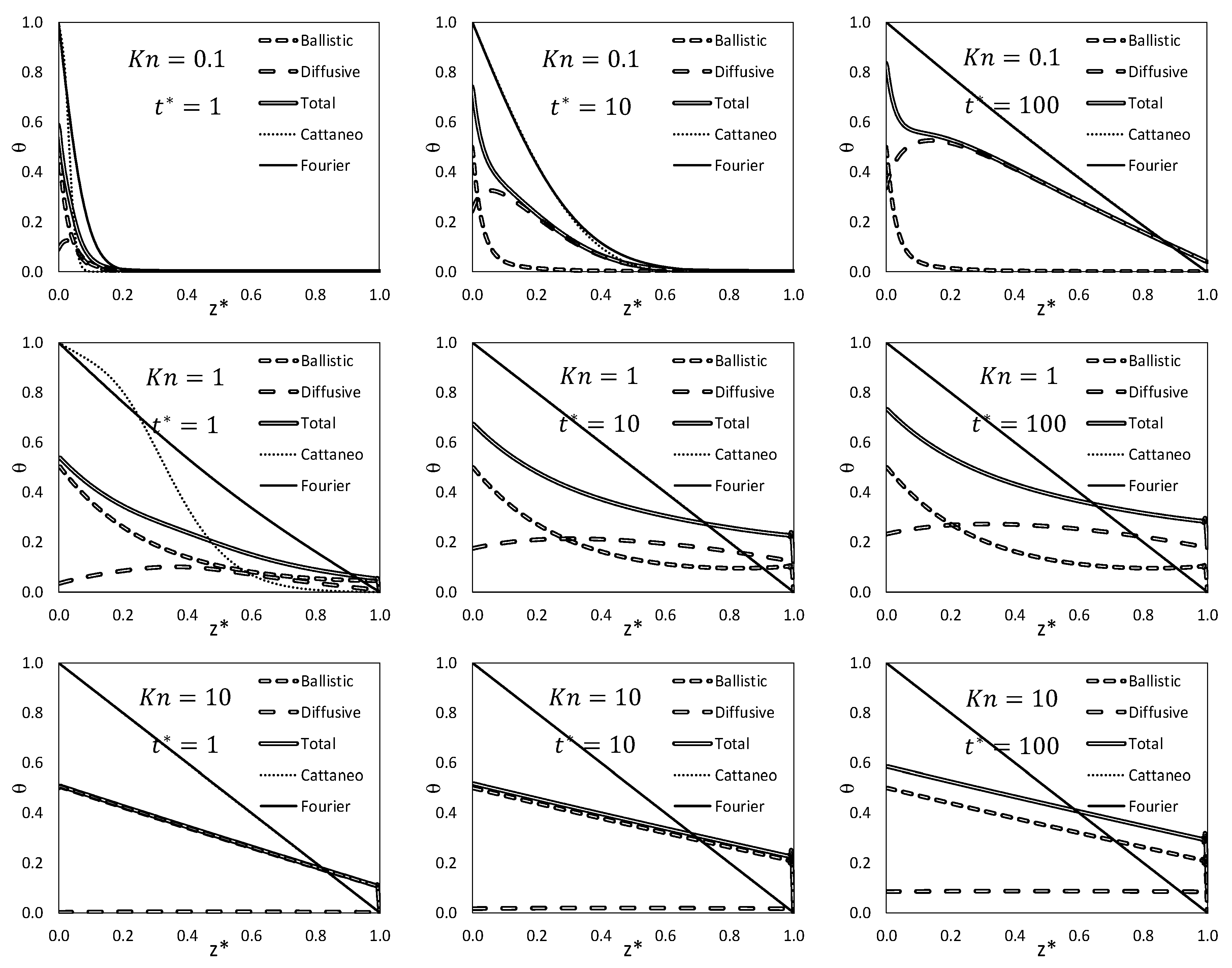
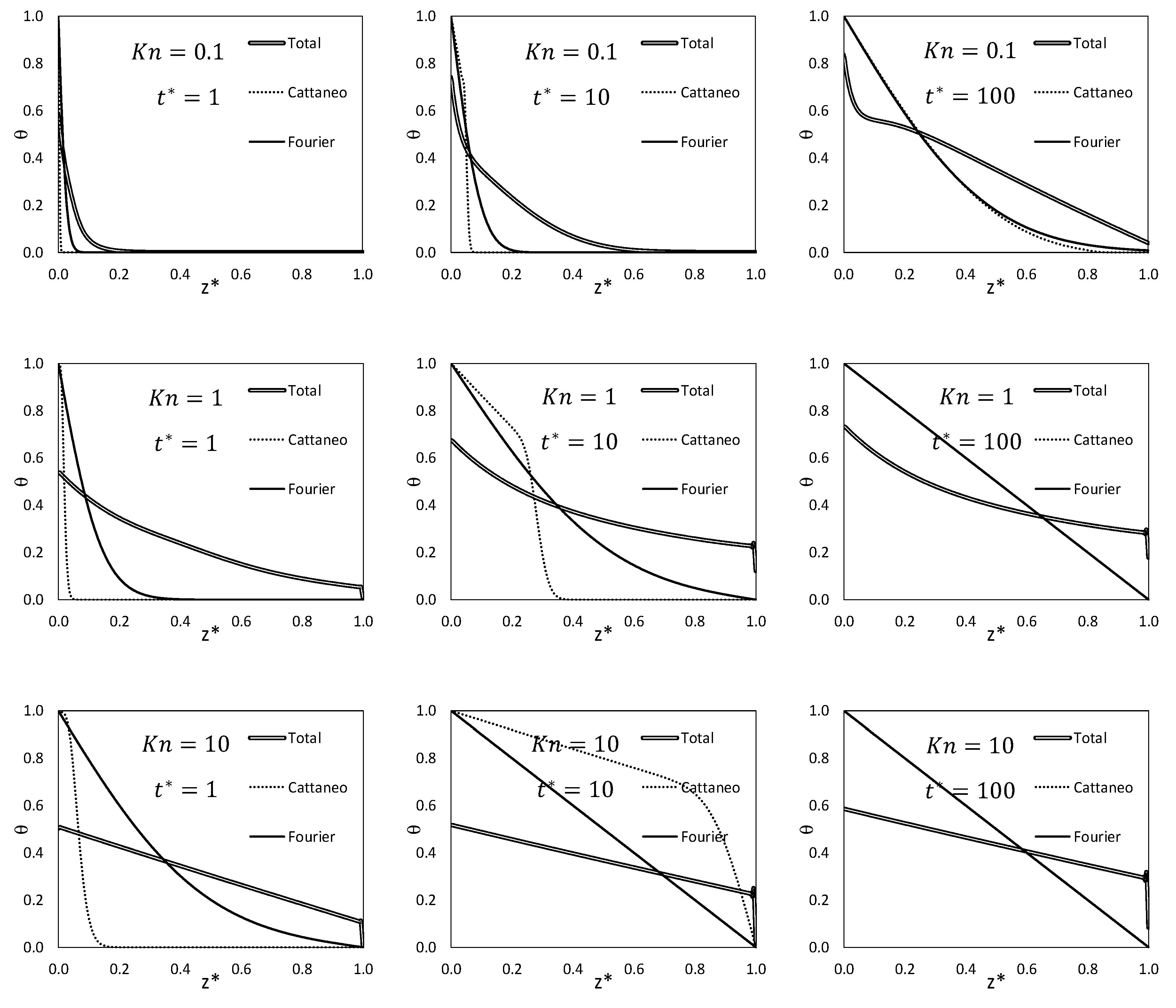
4. Results
4.1. Temperature Distribution of the Two-Temperature Model
4.2. Temperature Distribution of the Fourier and Cattaneo Laws with an Effective Thermal Conductivity
5. Discussion
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| heat capacity per unit volume [J/m3K] | |
| correction factor | |
| entropy flux [Wm/K] | |
| wavenumber vector | |
| Knudsen number | |
| mean free path [m] | |
| characteristic length [m] | |
| heat flux [W/m2] | |
| heat flux of order n [W/m2(m/s)n−1] | |
| position vector | |
| source term [W/m3] | |
| entropy per unit volume [J/Km3] | |
| temperature [K] | |
| time [s] | |
| dimensionless time | |
| internal energy per unit volume [J/m3] | |
| phonon velocity [m/s] | |
| spatial coordinate [m] | |
| dimensionless spatial coordinate | |
| Greek symbols | |
| rate of entropy production [W/K] | |
| dimensionless temperature | |
| thermal conductivity [W/Km] | |
| relaxation time [s] | |
| Subscript | |
| initial state | |
| ballistic | |
| Cattaneo | |
| diffusive | |
| effective value | |
| Fourier | |
| Upperscript | |
| Fourier transformed variable | |
References
- Machrafi, H.; Lebon, G. General constitutive equations of heat transport at small length scales and high frequencies with extension to mass and electrical charge transport. Appl. Math. Lett. 2016, 52, 30–37. [Google Scholar] [CrossRef]
- Hill, T.L. Thermodynamics of Small Systems; Dover: New York, NY, USA, 1994. [Google Scholar]
- Niemann, J.; Härter, S.; Kästle, C.; Franke, J. Challenges of the miniaturization in the electronics production on the example of 01005 components. In Tagungsband des 2. Kongresses Montage Handhabung Industrieroboter; Springer Vieweg: Berlin, Germany, 2017; pp. 113–123. [Google Scholar]
- Moore, A.L.; Shi, L. Emerging challenges and materials for thermal management of electronics. Materialstoday 2014, 17, 163–174. [Google Scholar] [CrossRef]
- Cahill, D.G.; Ford, W.K.; Goodson, K.E.; Mahan, G.D.; Majumdar, A.; Maris, H.J.; Merlin, R.; Phillpot, S.R. Nanoscale thermal transport. J. Appl. Phys. 2003, 93, 793. [Google Scholar] [CrossRef]
- Dinh, T.; Phan, H.P.; Kashaninejad, N.; Nguyen, T.K.; Dao, D.V.; Nguyen, N.T. An on-chip SiC MEMS device with integrated heating, sensing, and microfluidic cooling systems. Adv. Mater. Interfaces 2018, 5, 1800764. [Google Scholar] [CrossRef]
- Zheng, W.; Huang, B.; Li, H.; Koh, Y.K. Achieving huge thermal conductance of metallic nitride on graphene through enhanced elastic and inelastic phonon transmission. ACS Appl. Mater. Interfaces 2018, 10, 35487–35494. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Chen, Z.G.; Dargusch, M.S.; Zou, J. High performance thermoelectric materials: Progress and their applications. Adv. Energy Mater. 2018, 8, 1701797. [Google Scholar] [CrossRef]
- Yang, N.; Xu, X.; Zhang, G.; Li, B. Thermal transport in nanostructures. AIP Adv. 2012, 2, 041410. [Google Scholar] [CrossRef]
- Kuleyev, I.I.; Kuleyev, I.G.; Bakharev, S.M. Phonon focusing and features of phonon transport in silicon nanofilms and nanowires at low temperatures. Phys. Status Solidi B 2015, 252, 323–332. [Google Scholar] [CrossRef]
- Terris, D.; Joulain, K.; Lacroix, D.; Lemonnier, D. Numerical simulation of transient phonon heat transfer in silicon nanowires and nanofilms J. Phys. Conf. Ser. 2007, 92, 012077. [Google Scholar] [CrossRef]
- Gao, Y.; Bao, W.; Meng, Q.; Jing, Y.; Song, X. The thermal transport properties of single-crystalline nanowires covered with amorphous shell: A molecular dynamics study. J. Non-Cryst. Solids 2014, 387, 132–138. [Google Scholar] [CrossRef]
- Kaiser, J.; Feng, T.; Maassen, J.; Wang, X.; Ruan, X.; Lundstrom, M. Thermal transport at the nanoscale: A Fourier’s law vs. phonon Boltzmann equation study. J. Appl. Phys. 2017, 121, 044302. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, M. Phonon hydrodynamics for nanoscale heat transport at ordinary temperatures. Phys. Rev. B 2018, 97, 035421. [Google Scholar] [CrossRef]
- Tang, D.S.; Hua, Y.C.; Cao, B.Y. Thermal wave propagation through nanofilms in ballistic-diffusive regime by Monte Carlo simulations. Int. J. Therm. Sci. 2016, 109, 81–89. [Google Scholar] [CrossRef]
- Li, H.L.; Hua, Y.C.; Cao, B.Y. A hybrid phonon Monte Carlo-diffusion method for ballistic-diffusive heat conduction in nano- and micro-structures. Int. J. Heat Mass Transf. 2018, 127, 1014–1022. [Google Scholar] [CrossRef]
- Guyer, R.A.; Krumhansl, J.A. Solution of the linearized Boltzmann phonon equation. Phys. Rev. 1966, 148, 766–778. [Google Scholar] [CrossRef]
- Guyer, R.A.; Krumhansl, J.A. Thermal conductivity, second sound, and phonon hydrodynamic phenomena in nonmetallic Crystals. Phys. Rev. 1966, 148, 778–788. [Google Scholar] [CrossRef]
- Yu, Y.J.; Li, C.L.; Xue, Z.N.; Tian, X.G. The dilemma of hyperbolic heat conduction and its settlement by incorporating spatially nonlocal effect at nanoscale. Phys. Lett. A 2016, 380, 255–261. [Google Scholar] [CrossRef]
- Koh, Y.K.; Cahill, D.G.; Sun, B. Nonlocal theory for heat transport at high frequencies. Phys. Rev. B 2014, 90, 205412. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro to Microscale Heat Transfer: The Lagging Behaviour; Taylor and Francis: New York, NY, USA, 1997. [Google Scholar]
- Ordonez-Miranda, J.; Alvarado-Gil, J. On the stability of the exact solutions of the dual-phase lagging model of heat conduction. Nanoscale Res. Lett. 2011, 6, 327. [Google Scholar] [CrossRef]
- Cattaneo, C. Sulla conduzione del calore. Atti del Seminario Matematico e Fisico dell’ Universita di Modena 1948, 3, 83–101. [Google Scholar]
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Lebon, G.; Machrafi, H.; Grmela, M.; Dubois, C. An extended thermodynamic model of transient heat conduction at sub-continuum scales. Proc. R. Soc. A 2011, 467, 3241–3256. [Google Scholar] [CrossRef]
- Longshaw, S.M.; Borg, M.K.; Ramisetti, S.B.; Zhang, J.; Lockerby, D.A.; Emerson, D.R.; Reese, J.M. mdFoam+: Advanced molecular dynamics in OpenFOAM. Comput. Phys. Commun. 2018, 224, 1–21. [Google Scholar] [CrossRef]
- Machrafi, H. An extended thermodynamic model for size-dependent thermoelectric properties at nanometric scales: Application to nanofilms, nanocomposites and thin nanocomposite films. Appl. Math. Model. 2016, 40, 2143–2160. [Google Scholar] [CrossRef]
- Lebon, G.; Jou, D.; Casas-Vazquez, J. Understanding Non-Equilibrium Thermodynamics; Springer: Berlin, Germany, 2008. [Google Scholar]
- Modest, M.F. Radiative Heat Transfer; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Alvarez, F.X.; Jou, D. Boundary conditions and Evolution of Ballistic Heat transport. ASME J. Heat Transf. 2010, 132, 0124404. [Google Scholar] [CrossRef]
- Swartz, E.T.; Pohl, R.O. Thermal boundary resistance. Rev. Mod. Phys. 1981, 61, 605–668. [Google Scholar] [CrossRef]
- Hess, S. On Nonlocal Constitutive Relations, Continued Fraction Expansion for the Wave Vector Dependent Diffusion Coefficient. Z. Naturforsch. 1977, 32a, 678–684. [Google Scholar] [CrossRef]
- Machrafi, H. Heat transfer at nanometric scales described by extended irreversible thermodynamics. Commun. Appl. Ind. Math. 2016, 7, 177–195. [Google Scholar] [CrossRef]
- Lebon, G.; Machrafi, H. Effective thermal conductivity of nanostructures: A review. Atti della Accademia Peloritana dei Pericolanti 2019, 96, A14. [Google Scholar] [CrossRef]
- Joshi, A.A.; Majumdar, A. Transient ballistic and diffusive phonon heat transport in thin films. J. Appl. Phys. 1993, 74, 31–39. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machrafi, H. Temperature Distribution through a Nanofilm by Means of a Ballistic-Diffusive Approach. Inventions 2019, 4, 2. https://doi.org/10.3390/inventions4010002
Machrafi H. Temperature Distribution through a Nanofilm by Means of a Ballistic-Diffusive Approach. Inventions. 2019; 4(1):2. https://doi.org/10.3390/inventions4010002
Chicago/Turabian StyleMachrafi, Hatim. 2019. "Temperature Distribution through a Nanofilm by Means of a Ballistic-Diffusive Approach" Inventions 4, no. 1: 2. https://doi.org/10.3390/inventions4010002
APA StyleMachrafi, H. (2019). Temperature Distribution through a Nanofilm by Means of a Ballistic-Diffusive Approach. Inventions, 4(1), 2. https://doi.org/10.3390/inventions4010002



