The Thermodynamics of Internal Combustion Engines: Examples of Insights
Abstract
:1. Introduction
2. Brief Review of the Laws of Thermodynamics
3. Description of the Engine Cycle Simulation
3.1. Basics of the Simulation
3.2. Formulations
3.3. Items Needed for Solutions
3.3.1. Properties
3.3.2. Kinematics
3.3.3. Combustion
3.3.4. Cylinder Heat Transfer
3.3.5. Mass Flow Rates
3.3.6. Mechanical Friction
3.4. Description of the Engine
3.5. Second Law
4. Example One: Thermodynamics of Low Heat Rejection Engines
4.1. Introduction
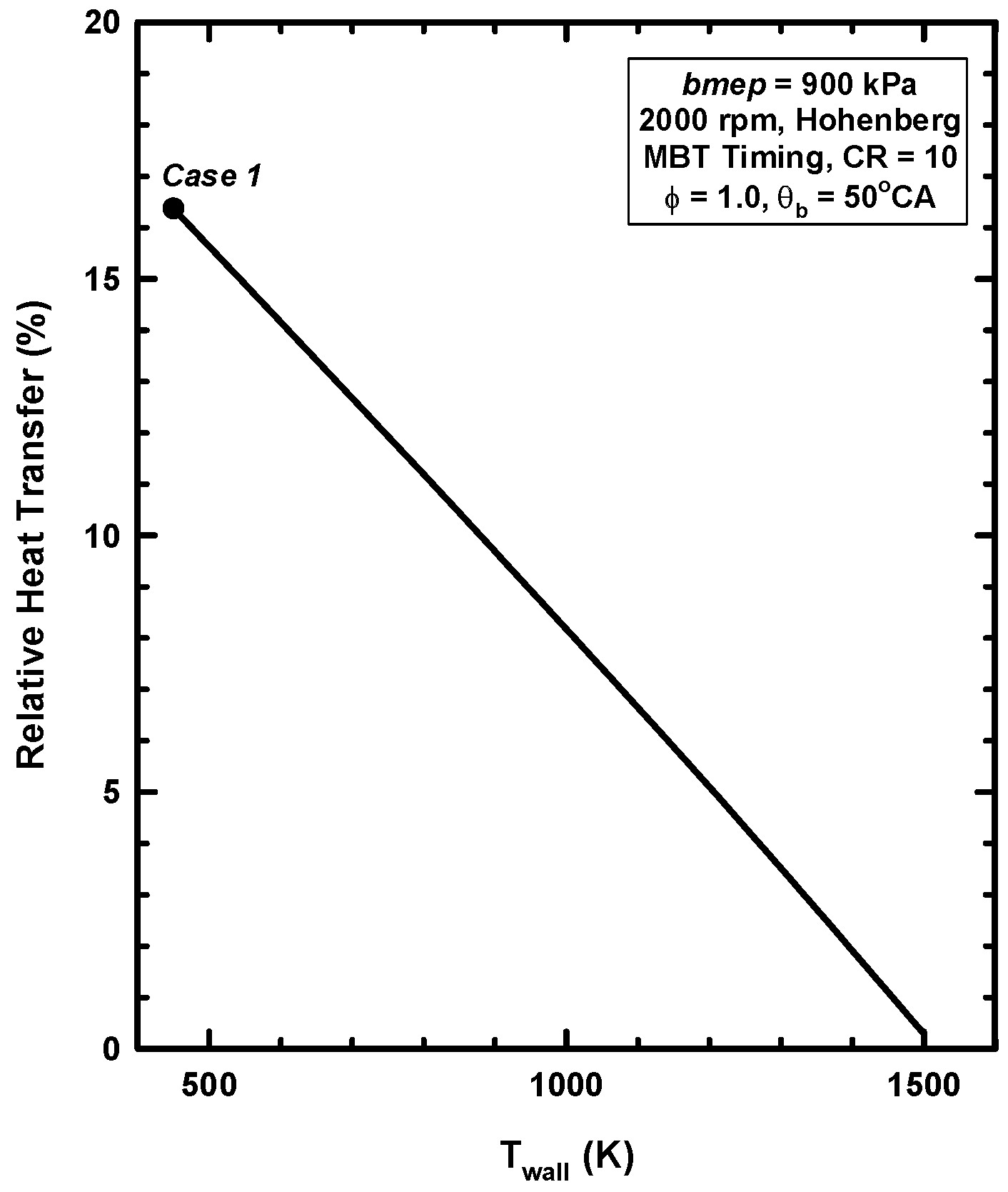
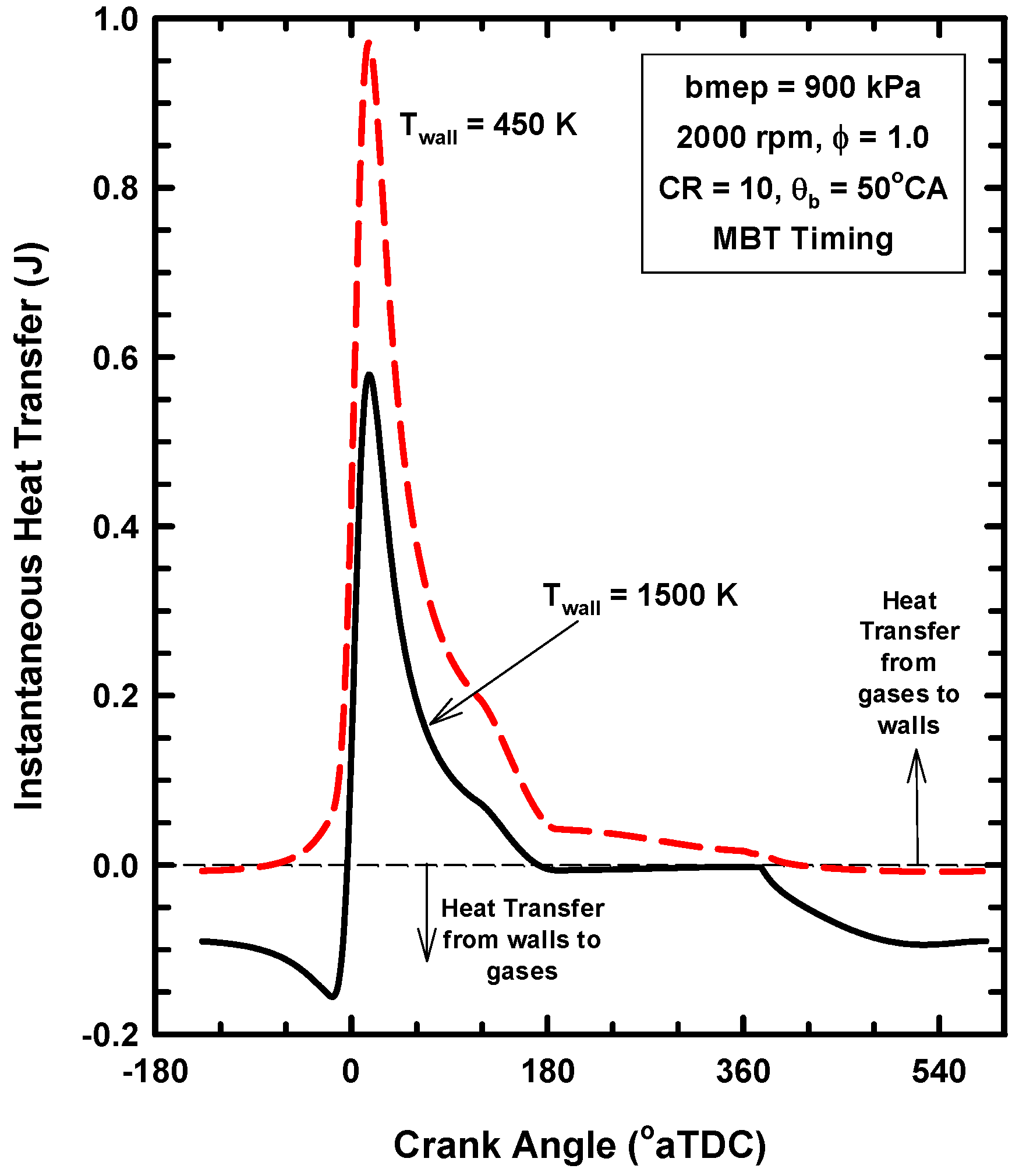
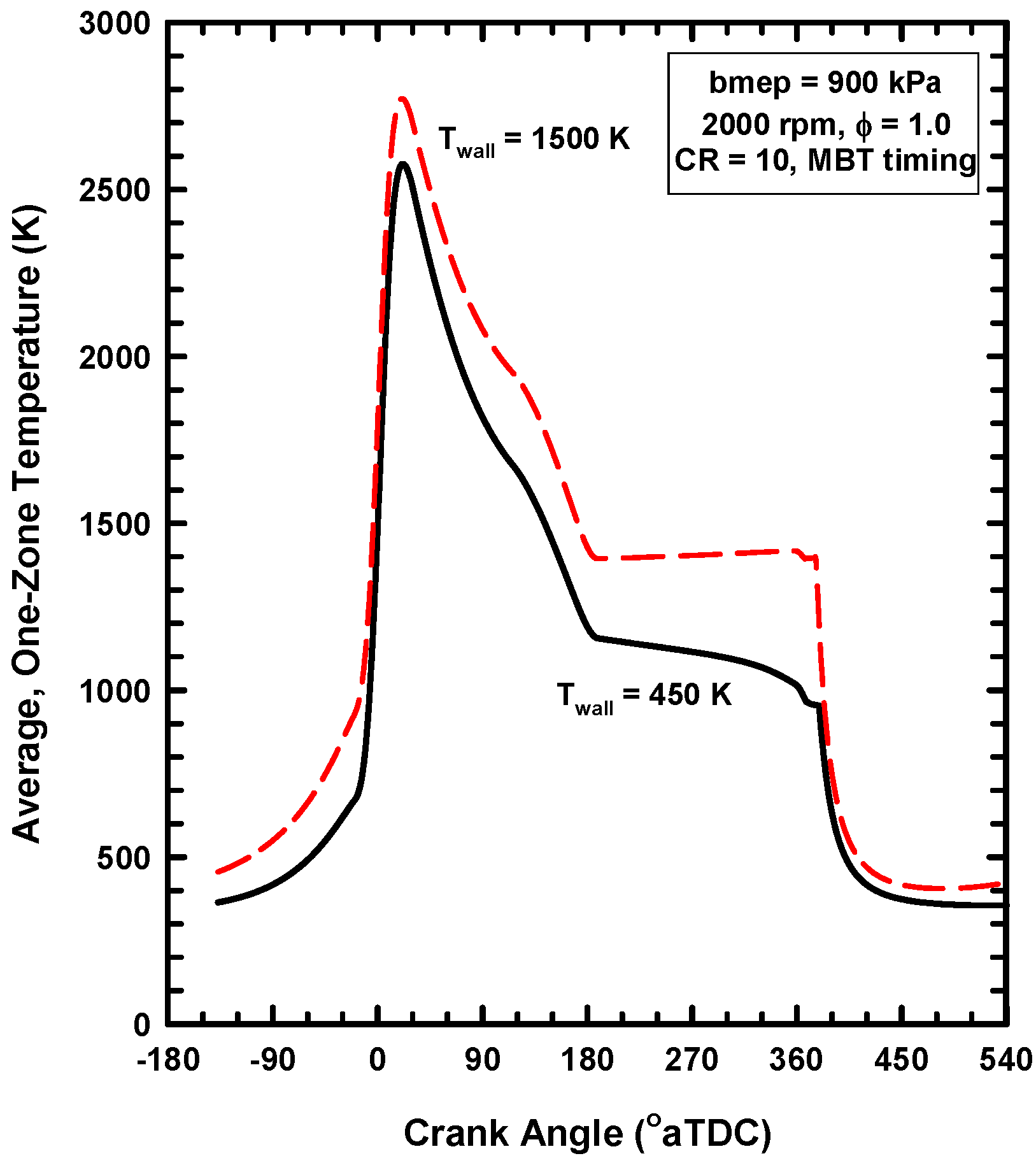
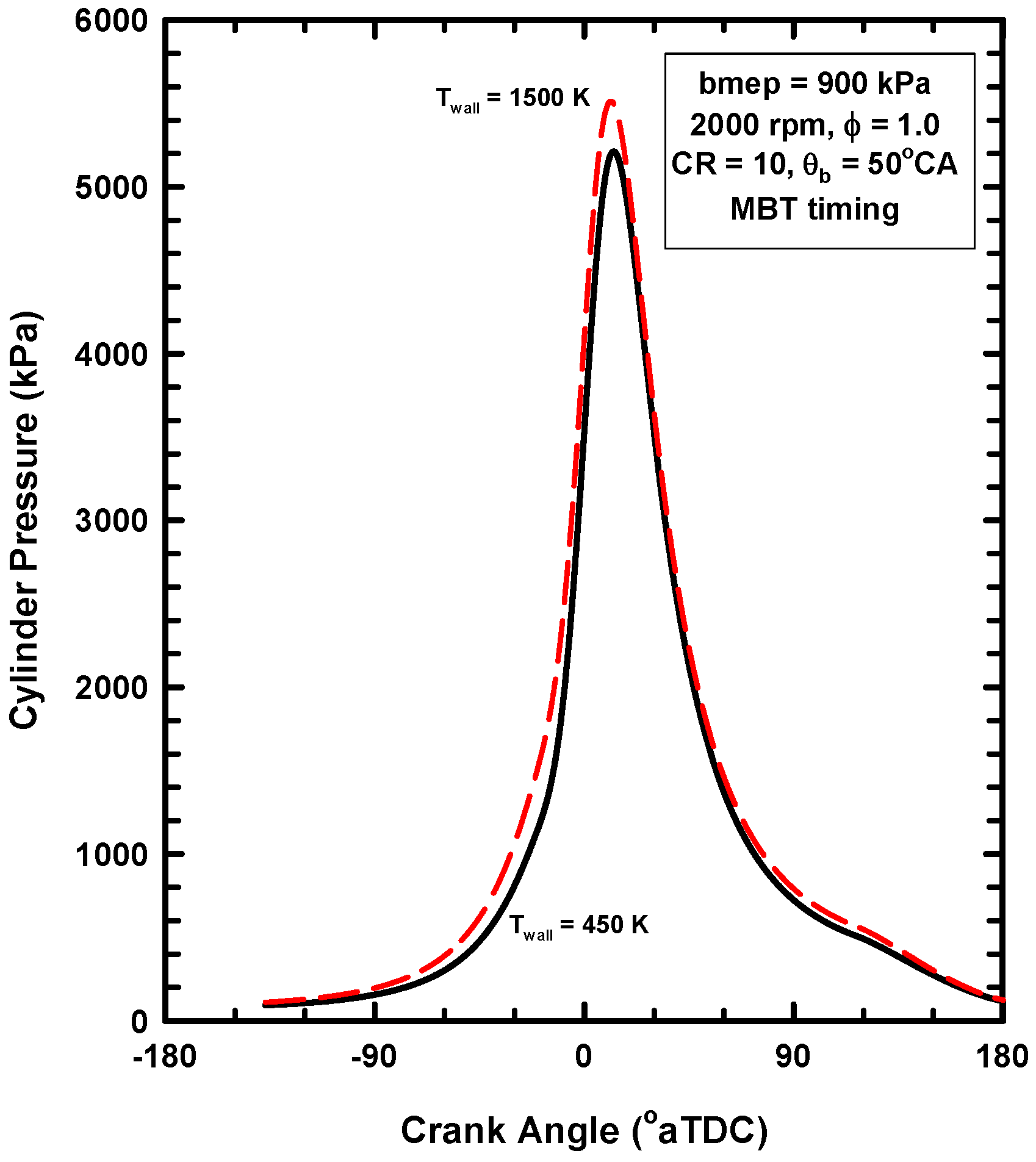
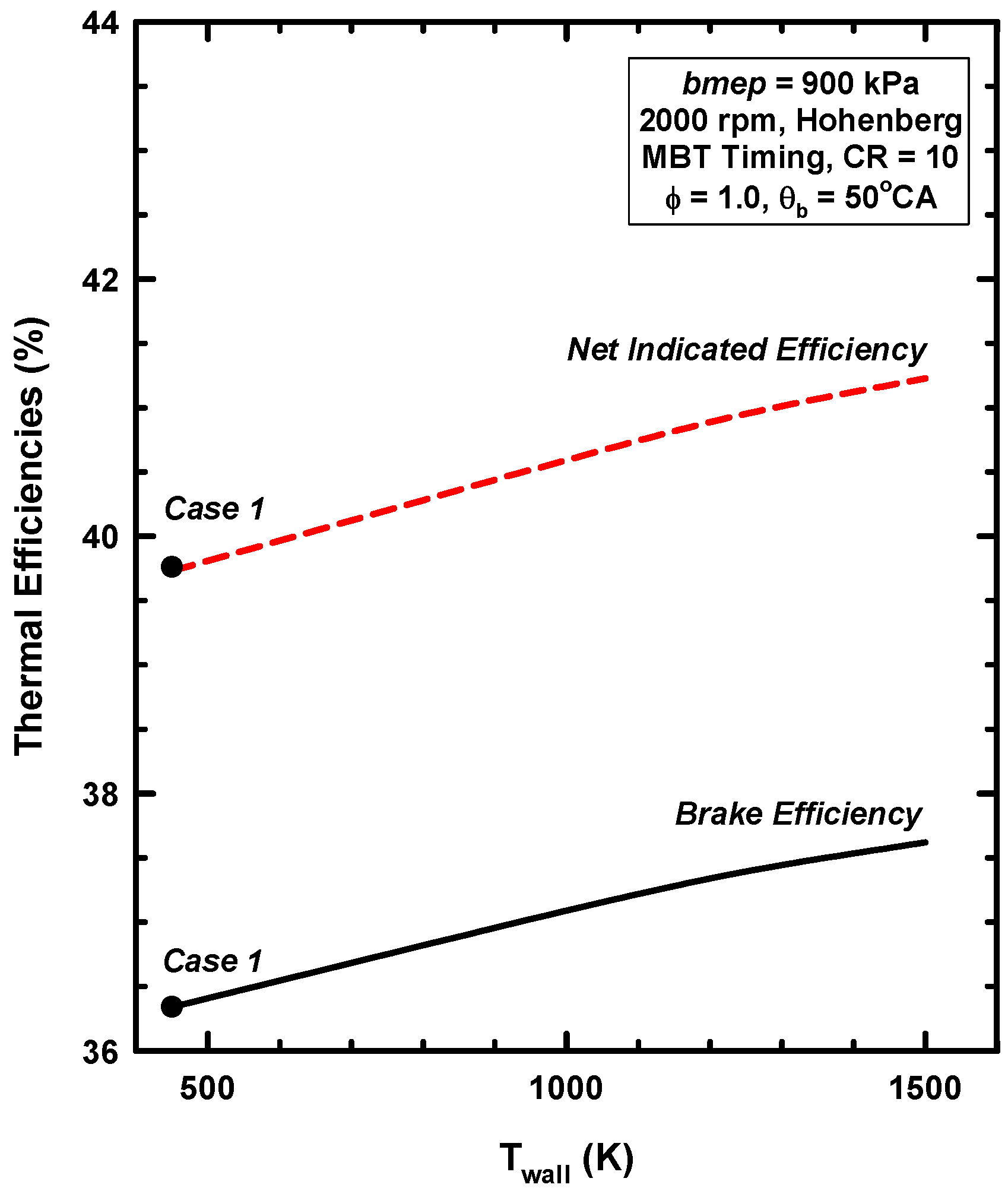
4.2. Results for Increases of the Wall Temperature
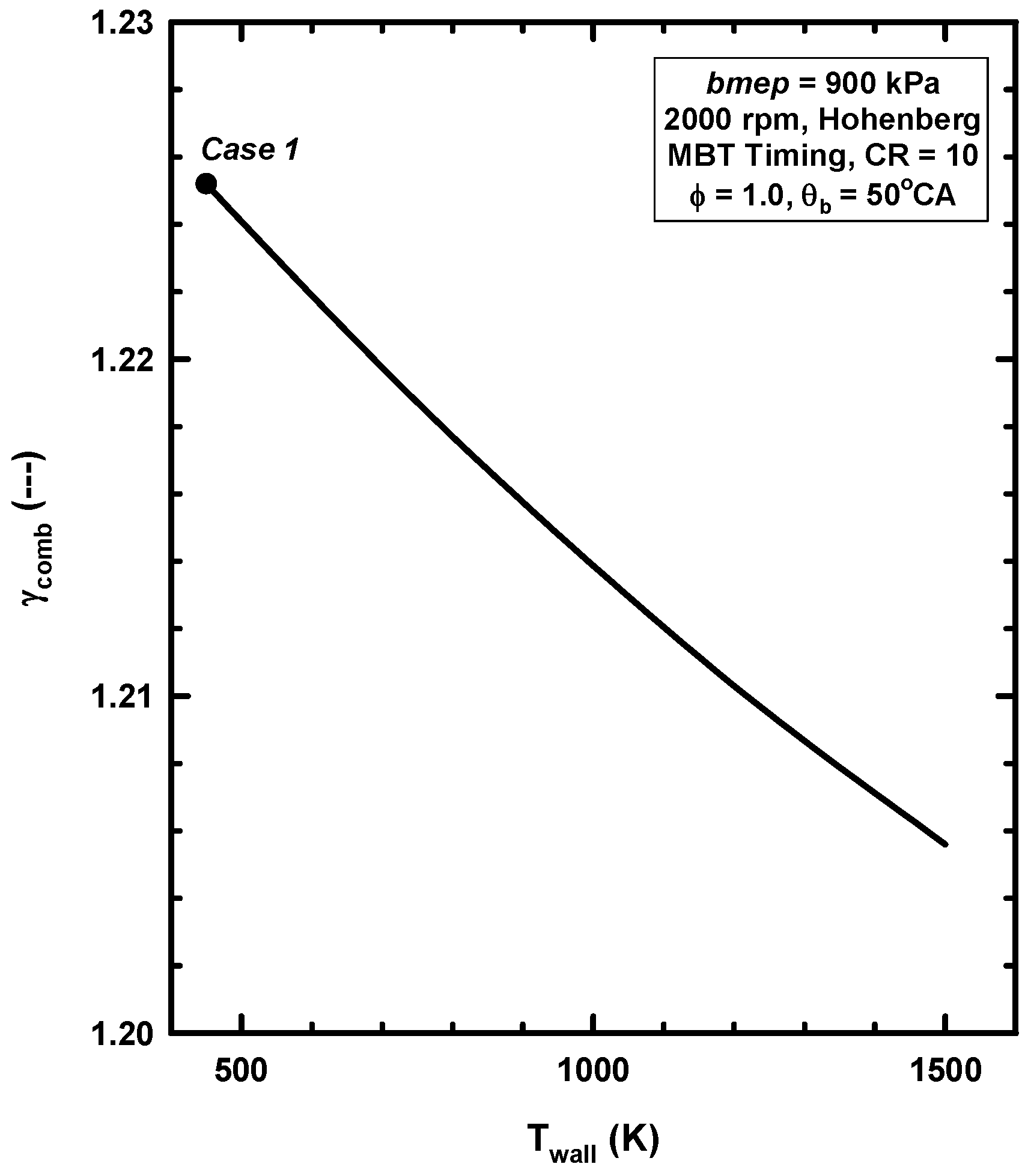
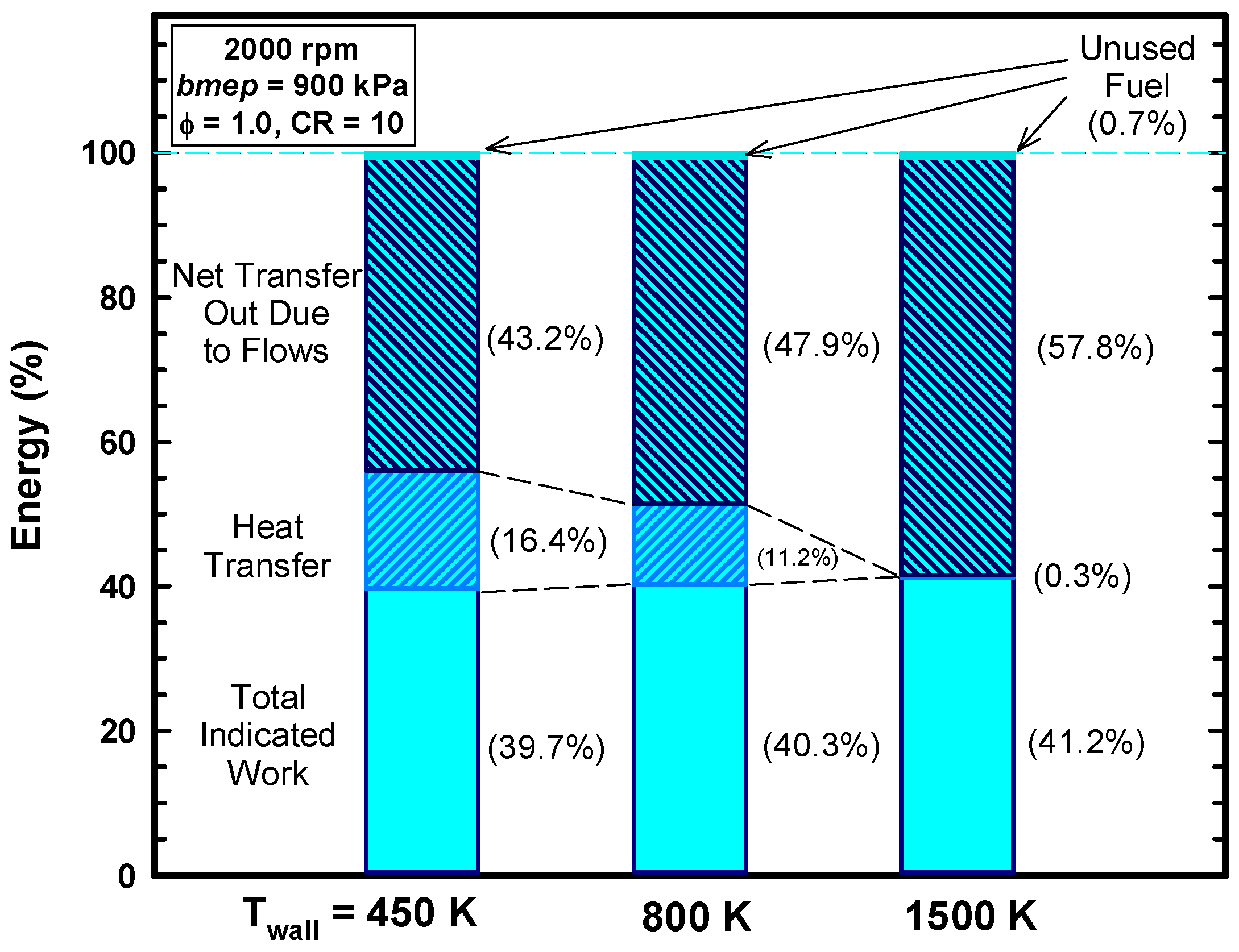
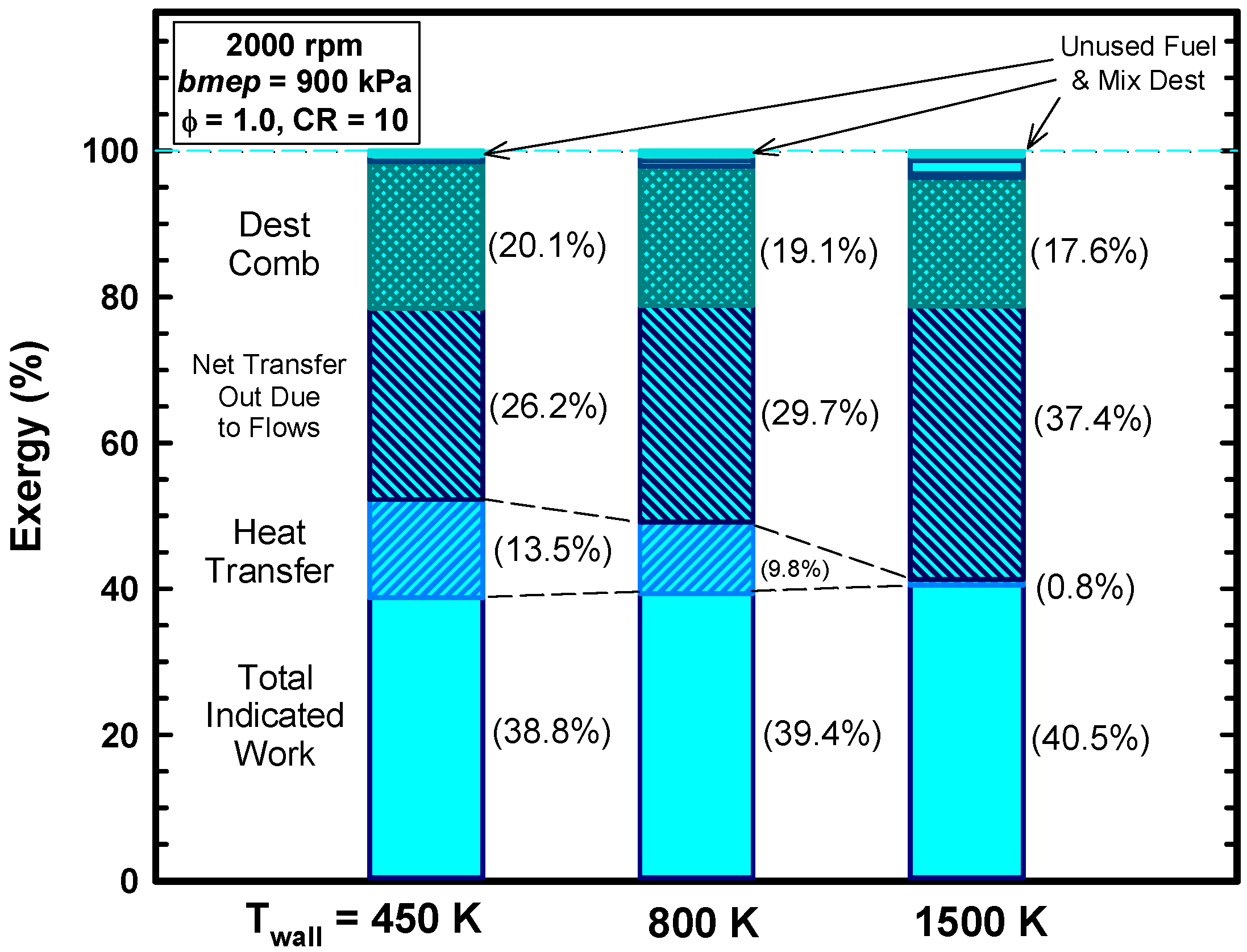
4.3. Reasons for Negligible Efficiency Increases
- Not all the heat energy is available to do work. The total exergy of the heat transfer is about 13% (as opposed to the 16% based on energy).
- Some of the preserved heat transfer is during compression. This increases compression pressures and causes additional compression work, which negates some of the gains during the expansion.
- The volumetric efficiency decreases slightly for the high cylinder wall temperature case due to the higher gas temperatures.
- Only the heat transfer preserved near TDC will contribute to additional expansion work.
- Only a fraction of the preserved thermal energy near TDC can be converted to work.
- As shown above, gamma decreases due to the higher temperatures for the high cylinder wall temperature case. This decreases the conversion of thermal energy to work.
- For this case, the exhaust gas temperature increases from about 1310 K for the 450 K case to about 1600 K for the 1500 K case (Table 4). This is evidence that a considerable amount of the energy preserved remains in the gases.
- Due to the higher gas temperatures, the exergy destroyed during the combustion process is reduced from 20.1% to 17.6% (Table 4). This improvement is offset by the items mentioned above.
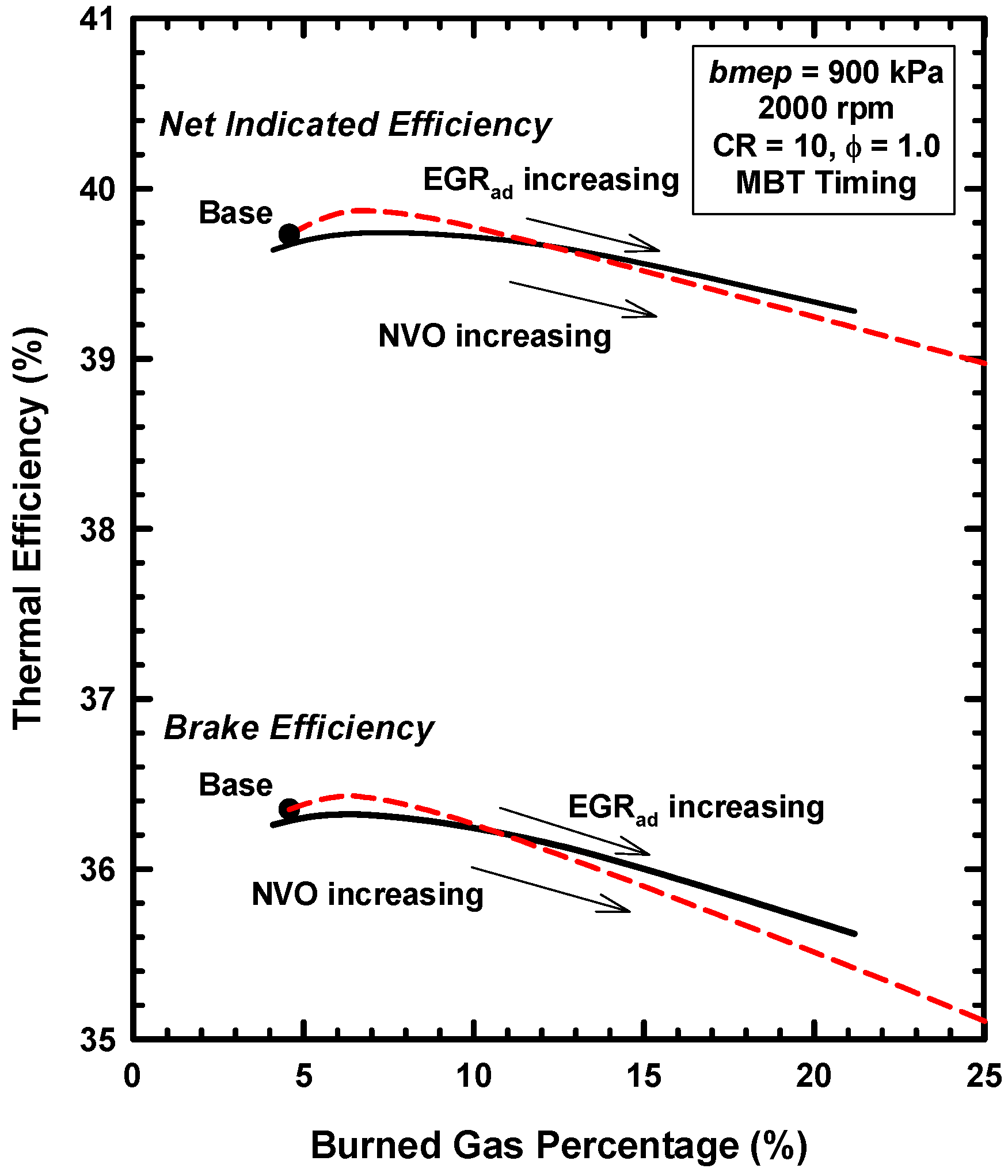
5. Example Two: Thermodynamics of Exhaust Gas Dilution
5.1. Introduction
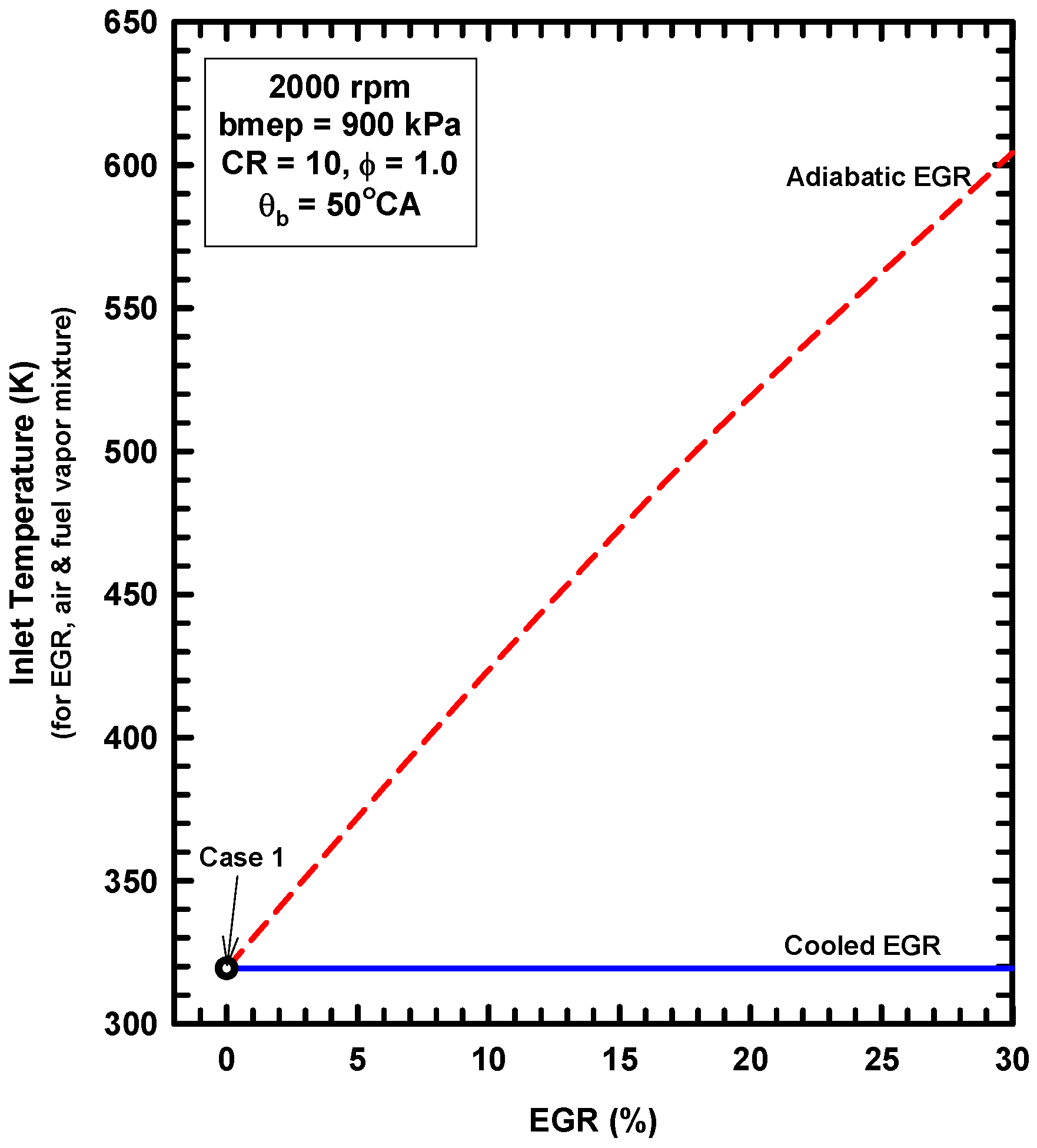
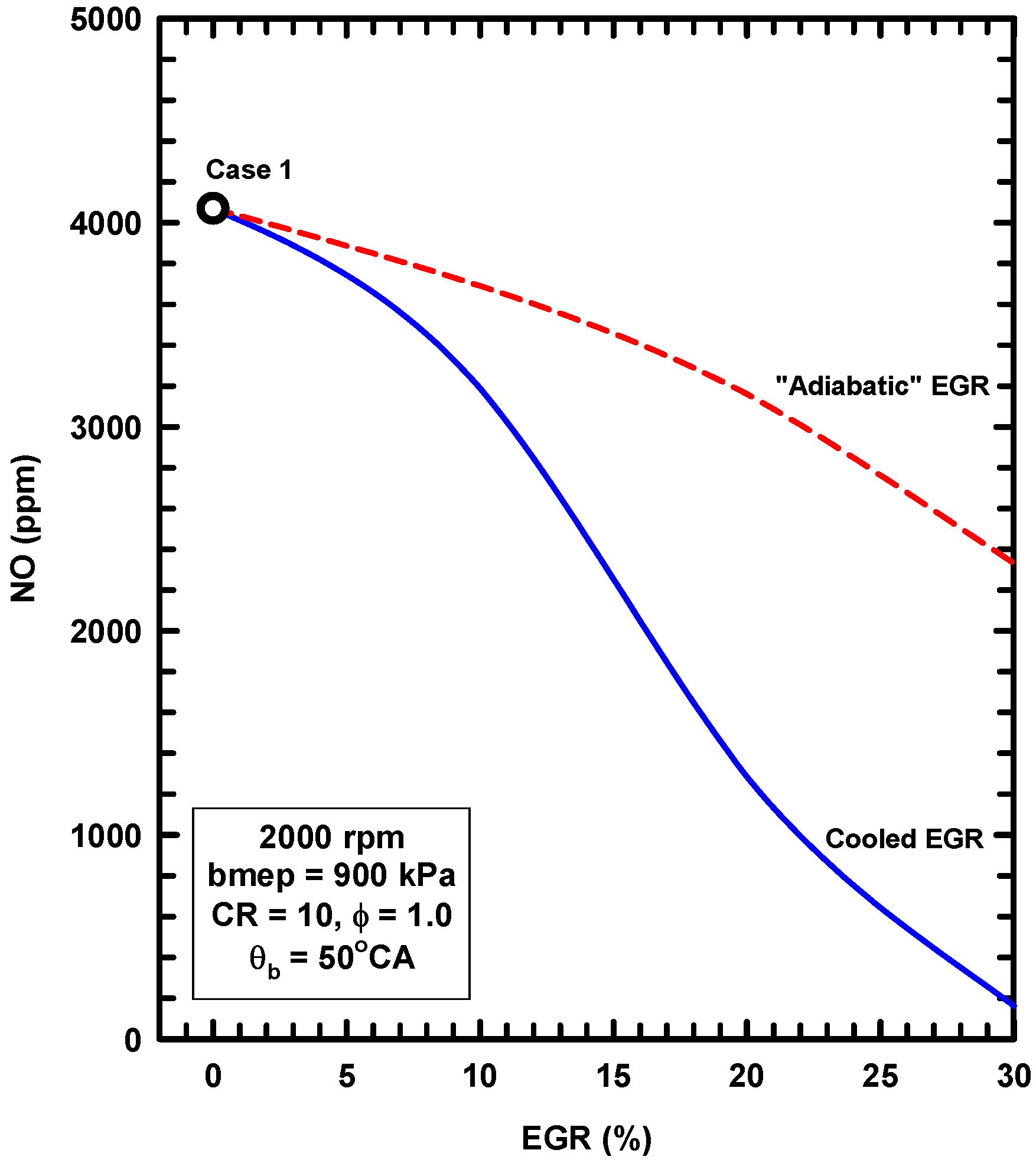
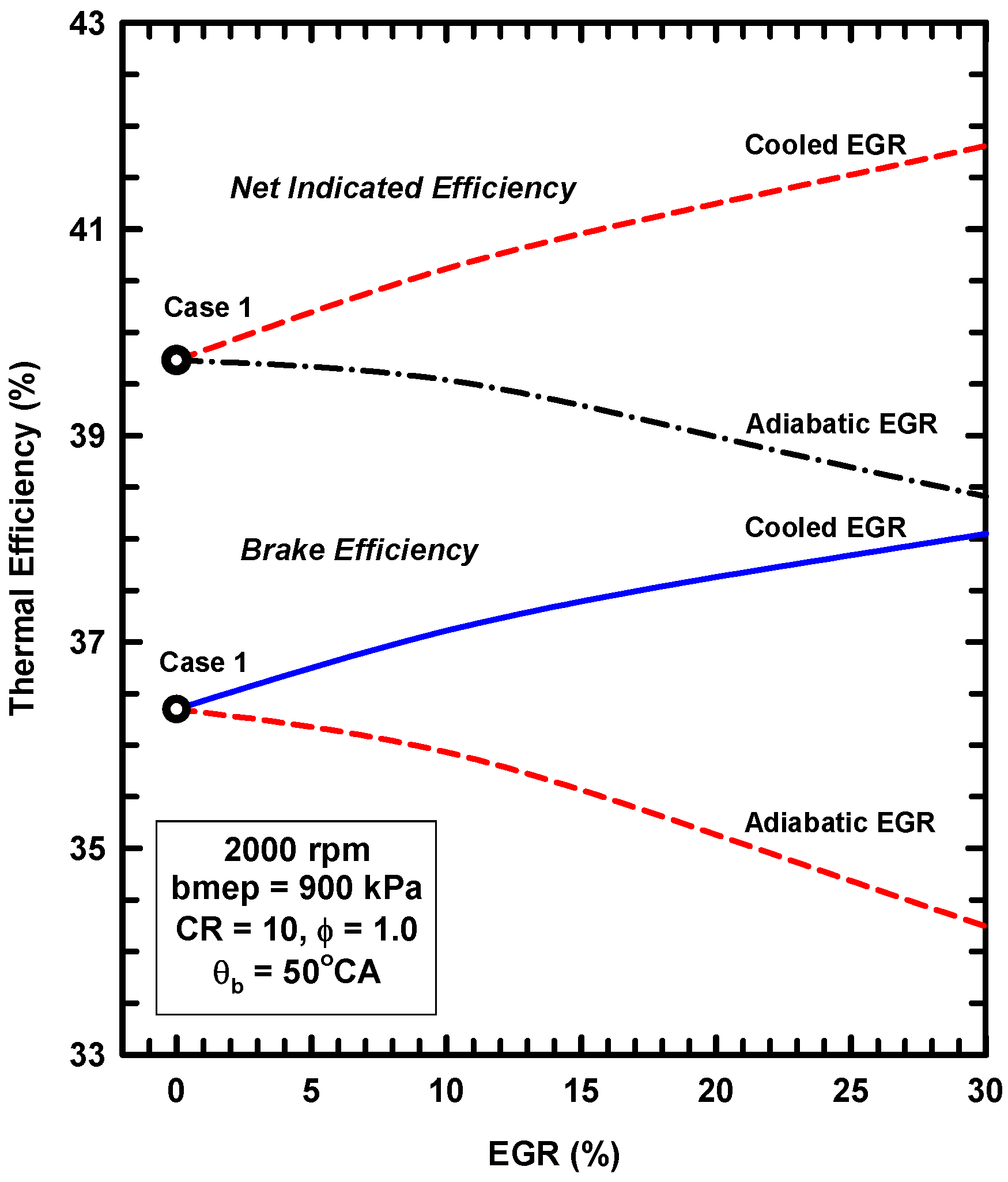
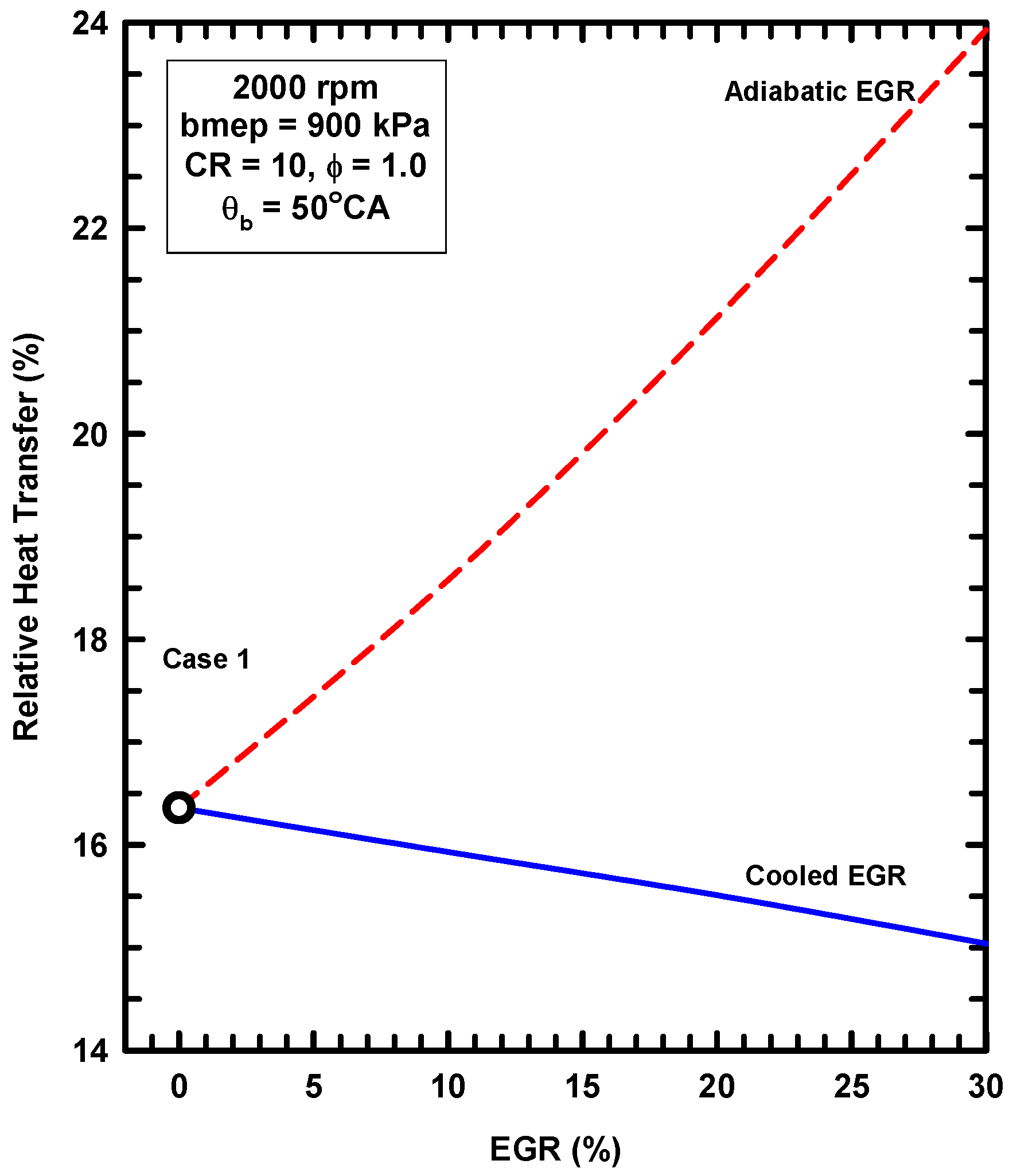
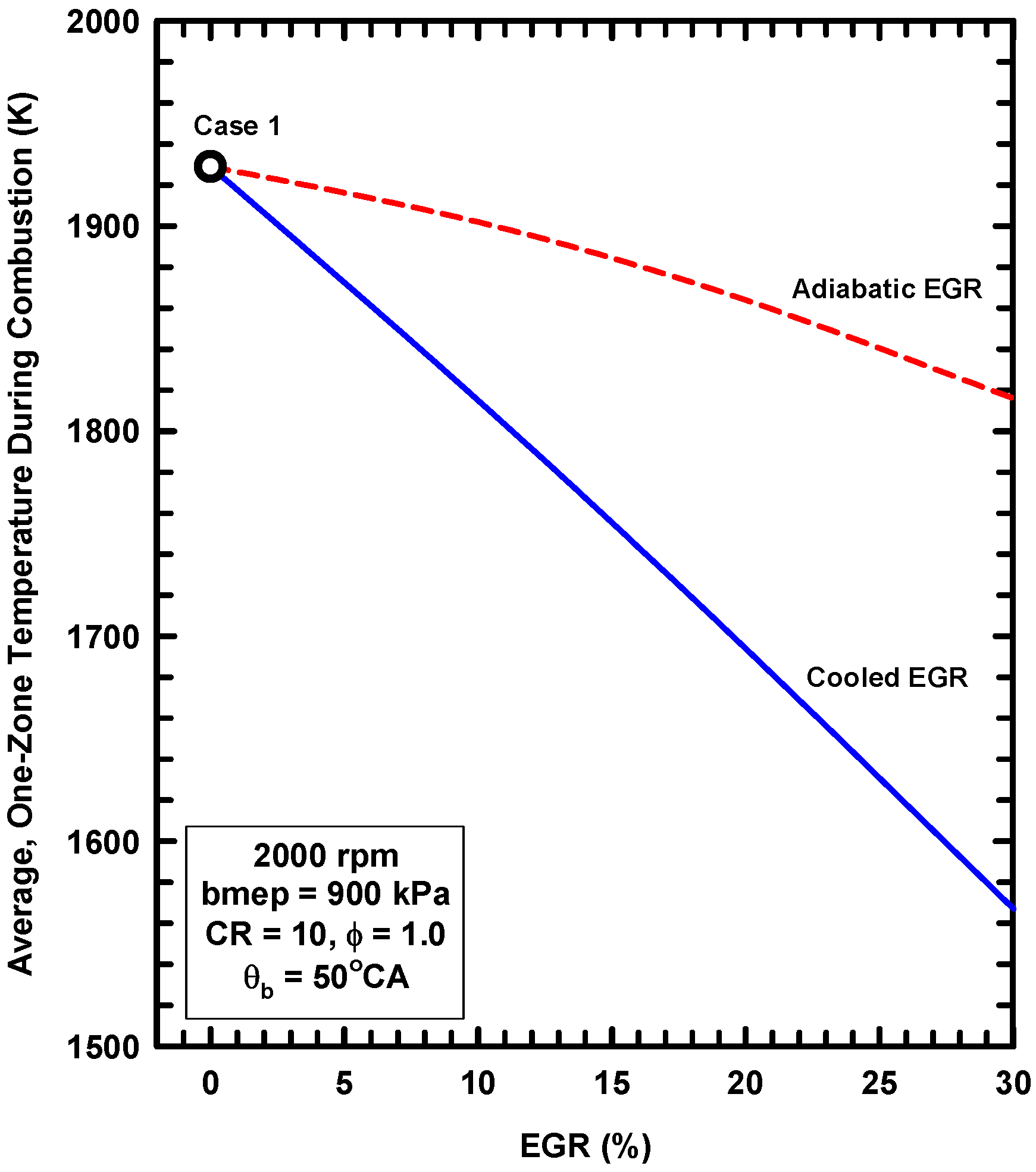
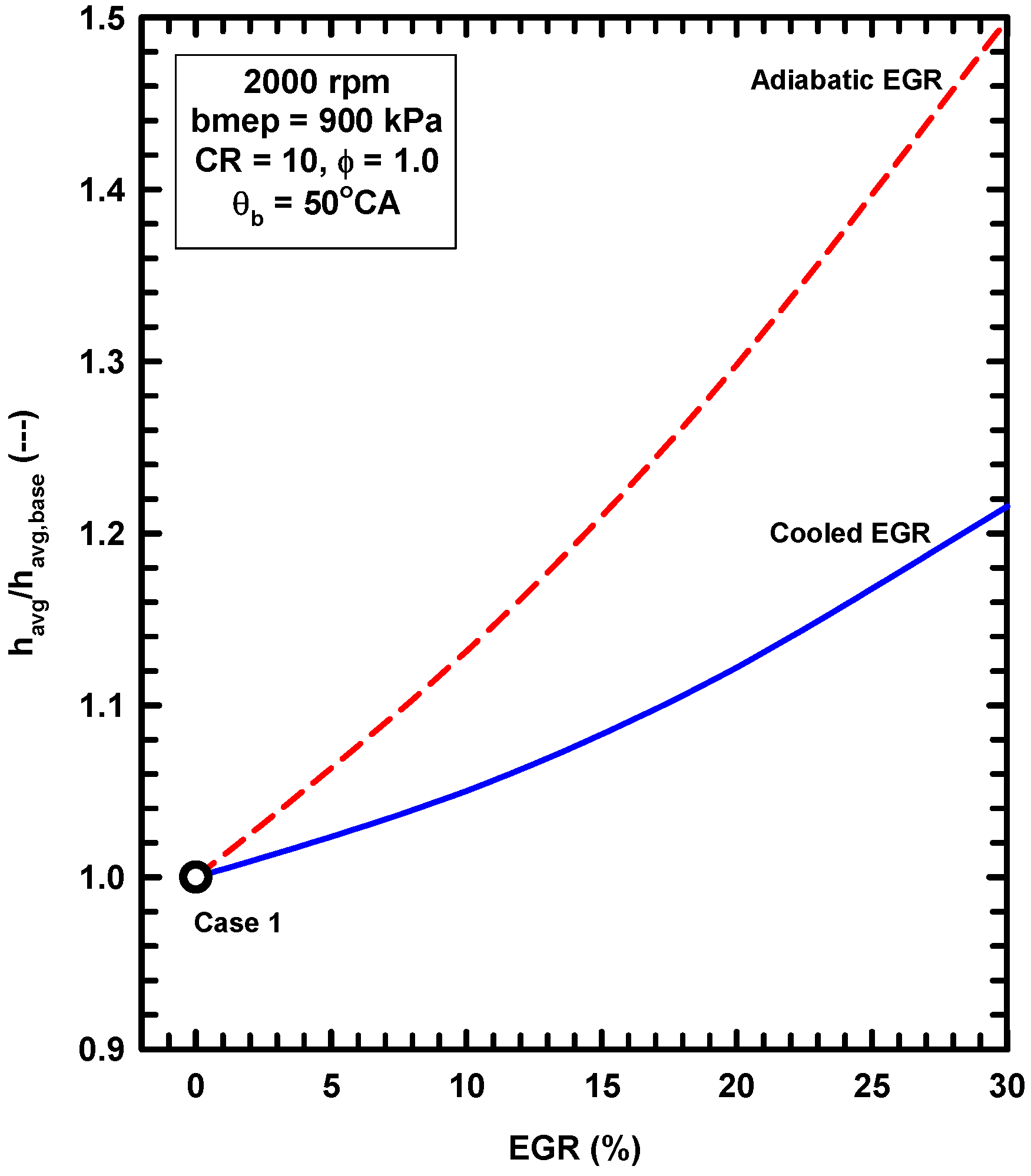
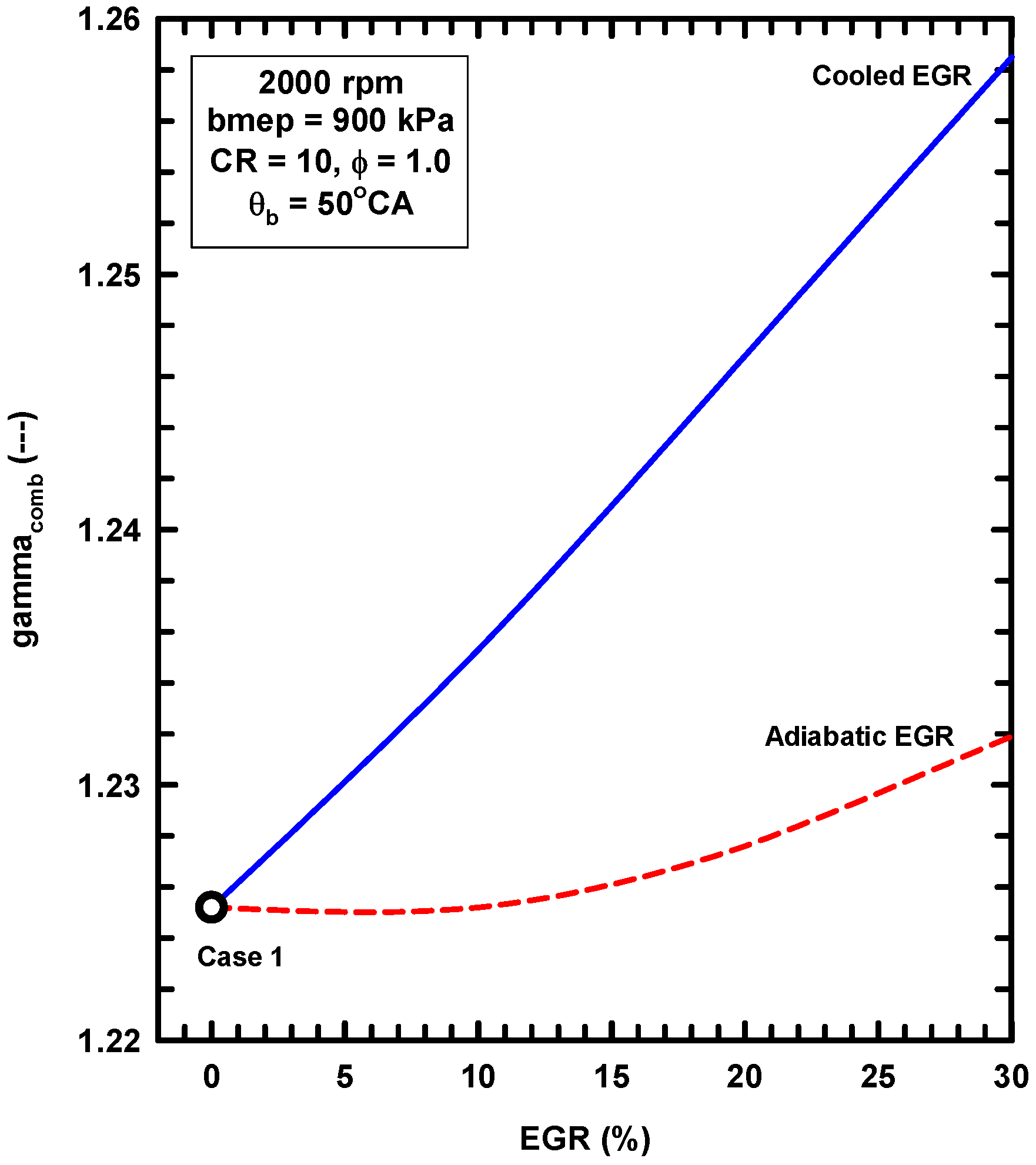
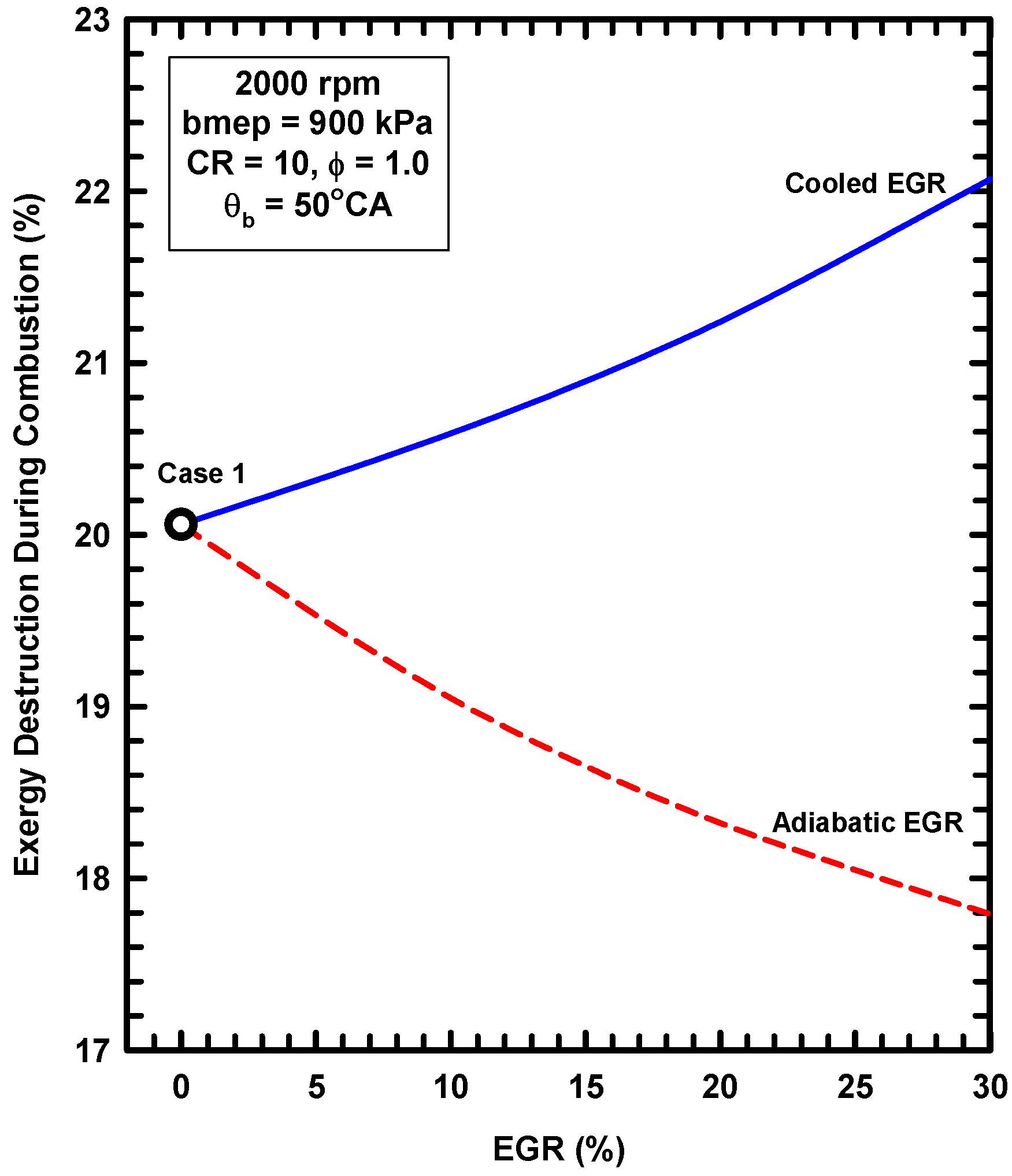
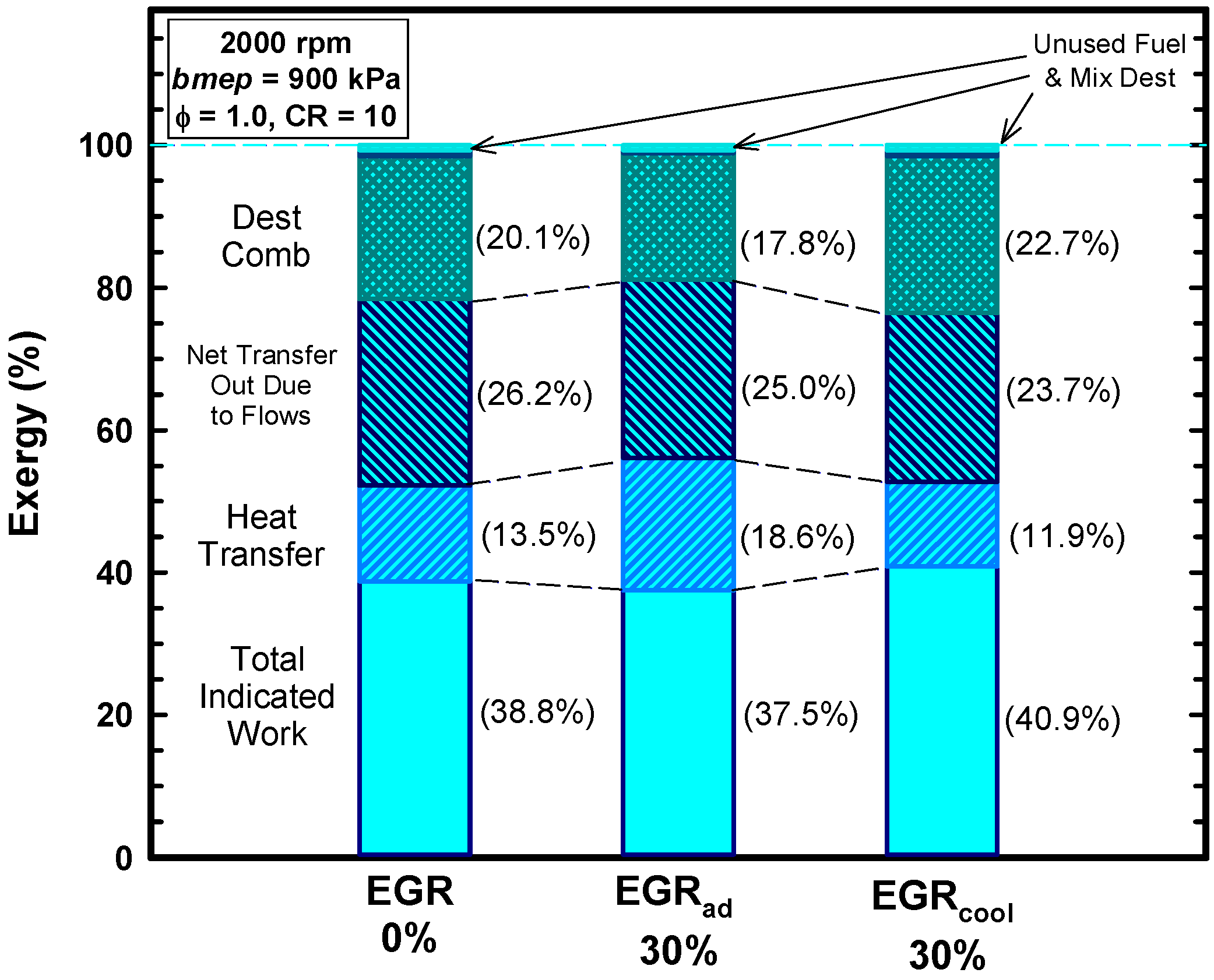
5.2. External Exhaust Gas Dilution
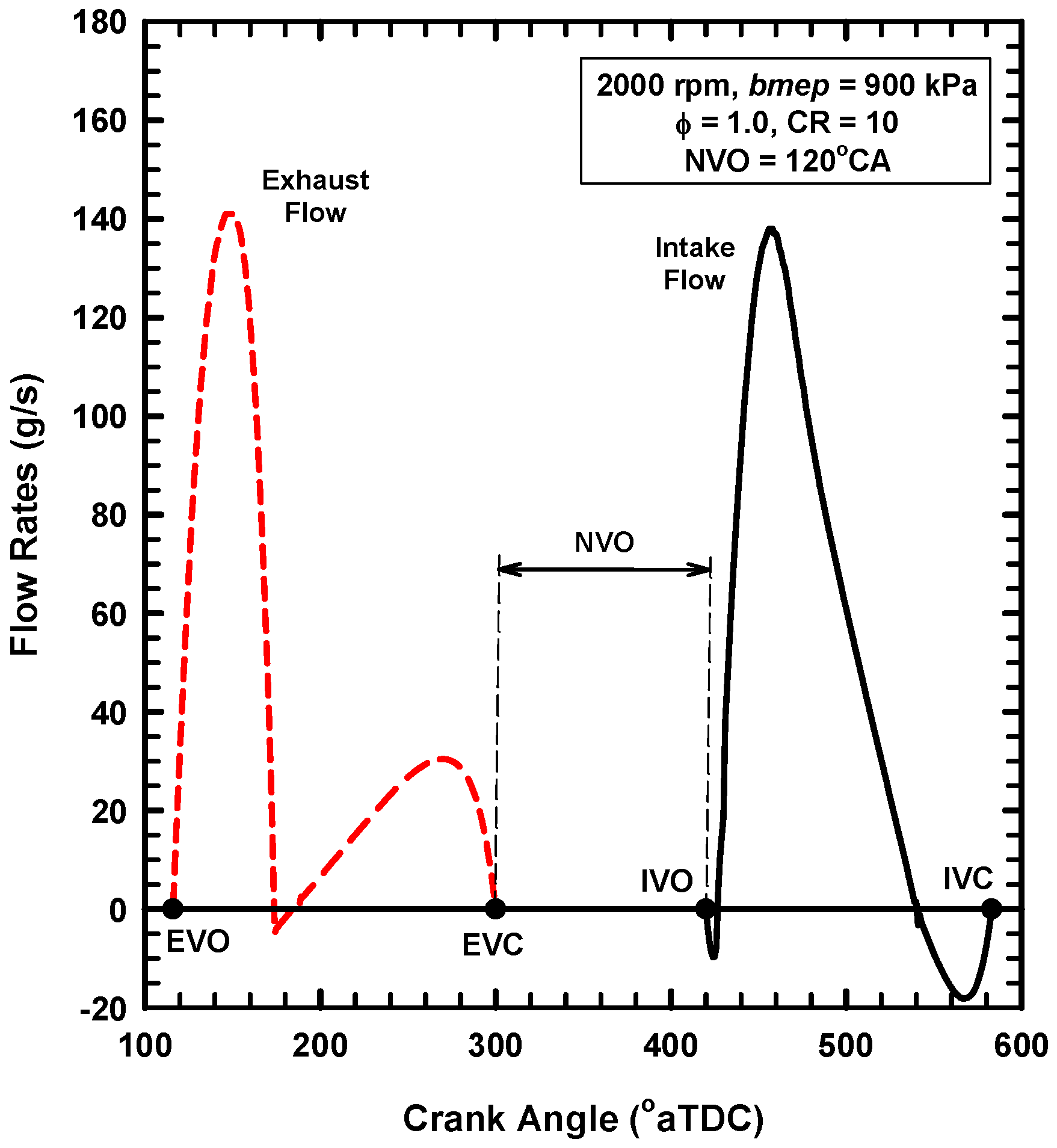
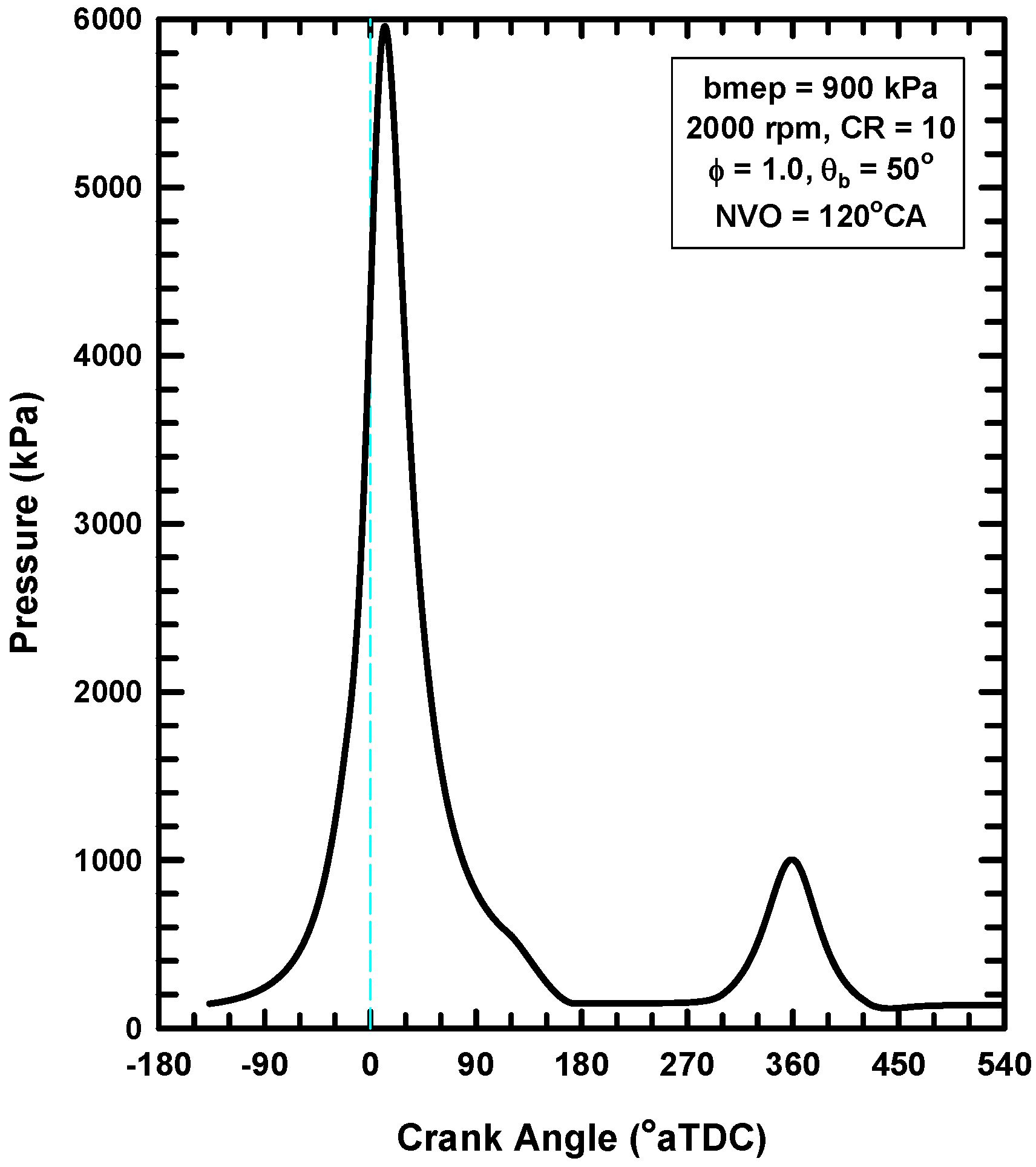
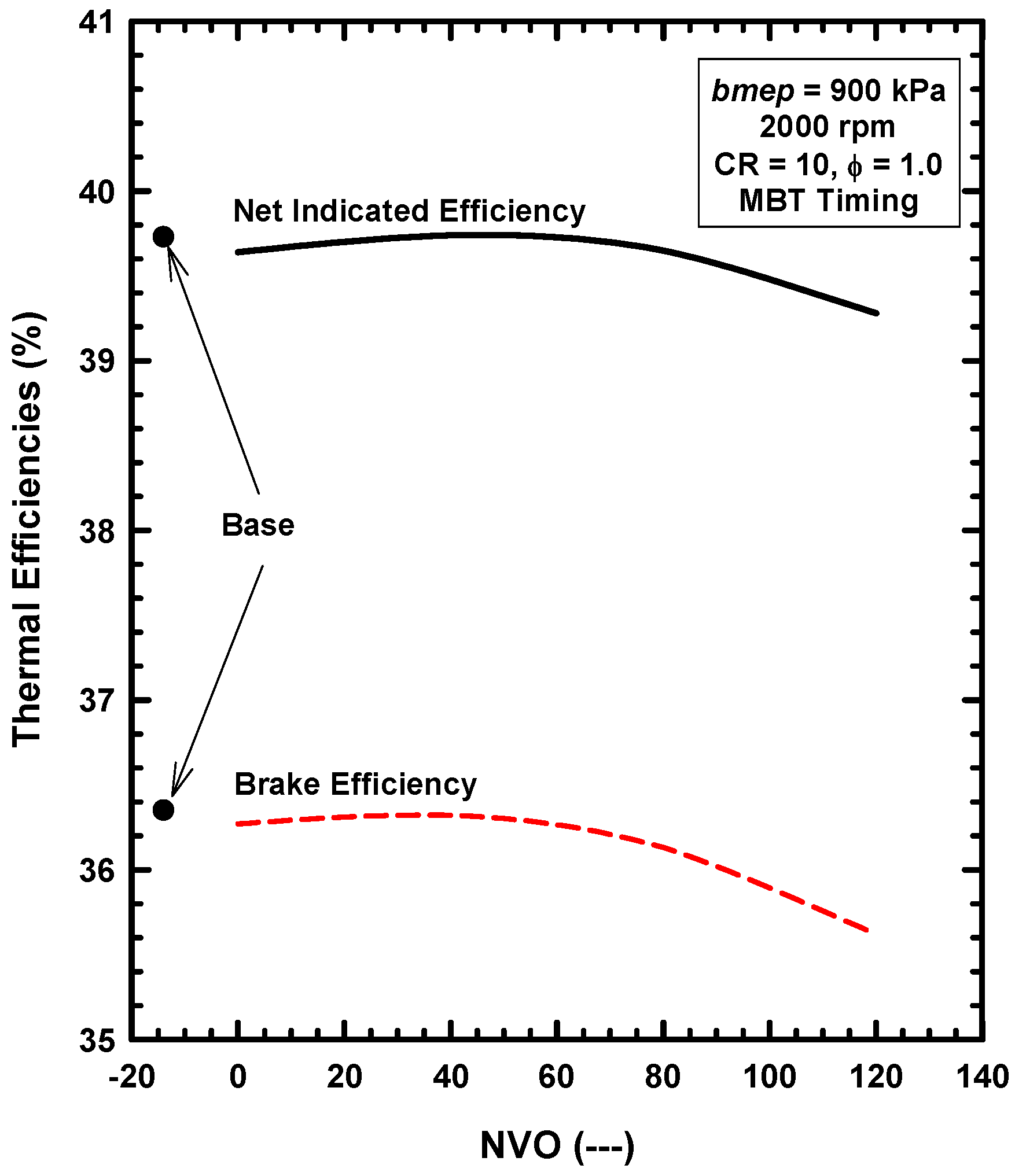
5.3. Internal Exhaust Gas Dilution
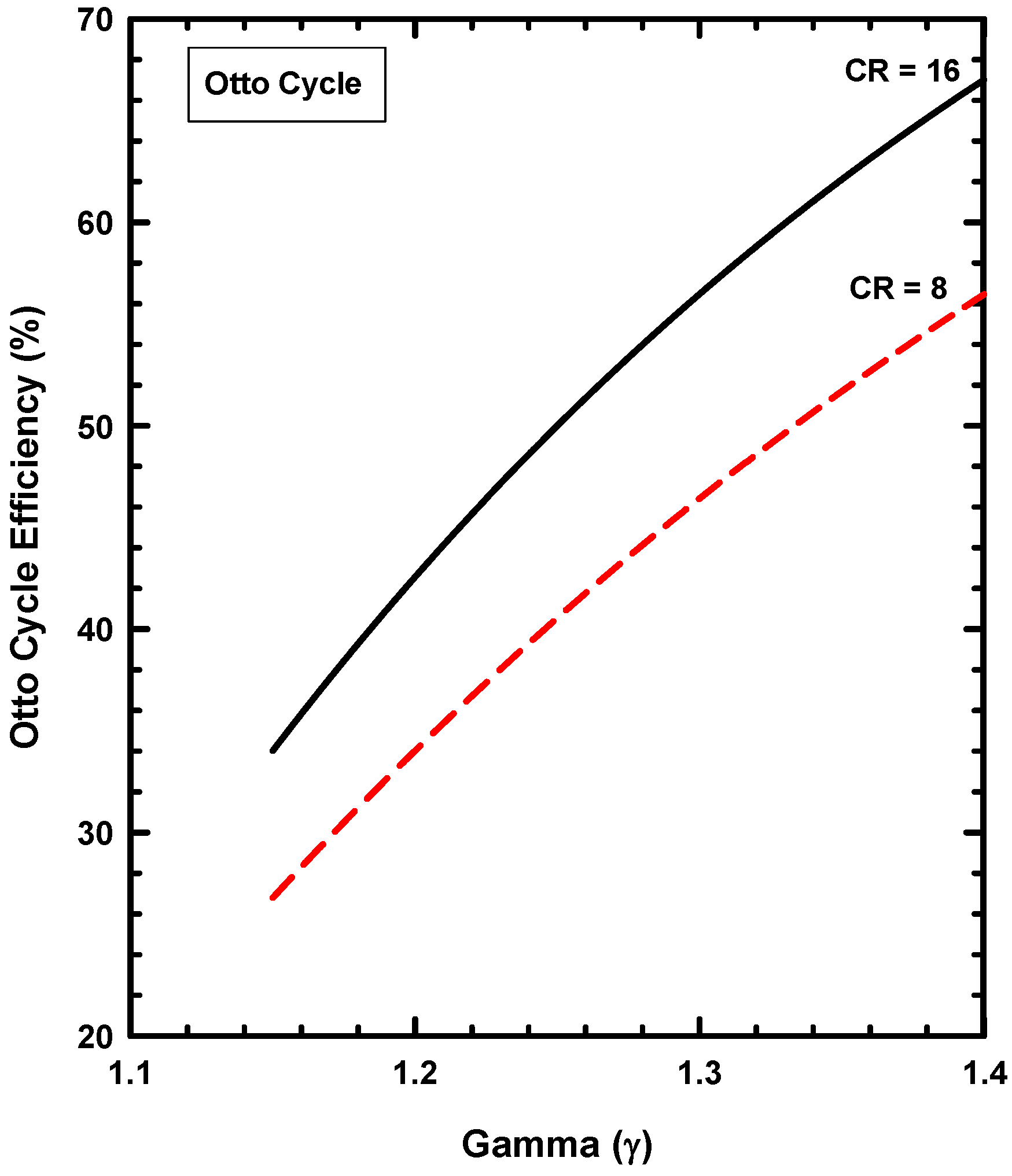
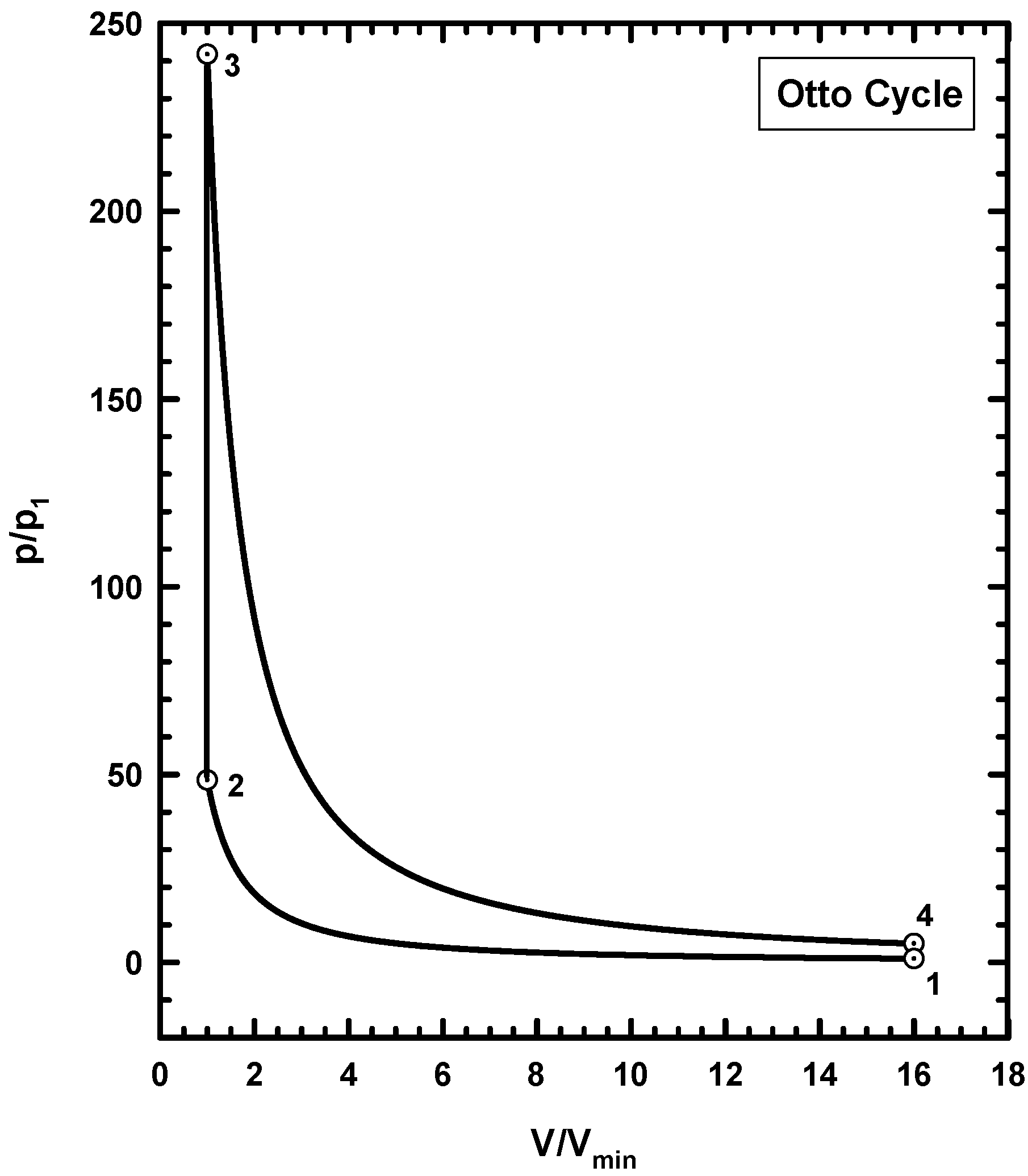
6. Example Three: Thermodynamics of the Otto Cycle
6.1. Basics of the Ideal Otto Cycle
- The working fluid is air;
- The compression and expansion processes are adiabatic and reversible (isentropic);
- The combustion process is replaced with a heat addition process under prescribed conditions;
- The exhaust blow-down process is replaced by a constant volume heat rejection at BDC;
- Inlet and exhaust strokes are not included.
6.2. Features Consistent with IC Engines
- The compression and expansion processes.
- Temperature (and pressure) increases due to thermal energy addition
- The mechanical conversion of pressure increases to work.
6.3. Features Inconsistent with IC Engines
- Heat transfer in actual engines is significant, particularly during combustion and expansion.
- Actual combustion processes require a finite time (of order 50 °CA), and do not occur instantaneously at TDC.
- Flow processes in actual engines may limit the charge mass, and may compromise the network of the cycle due to valve timings (e.g., exhaust valve opening before BDC).
- Other real effects that are not part of the Otto cycle include blow-by, incomplete combustion, chemical dissociation, and mechanical and fluid friction.
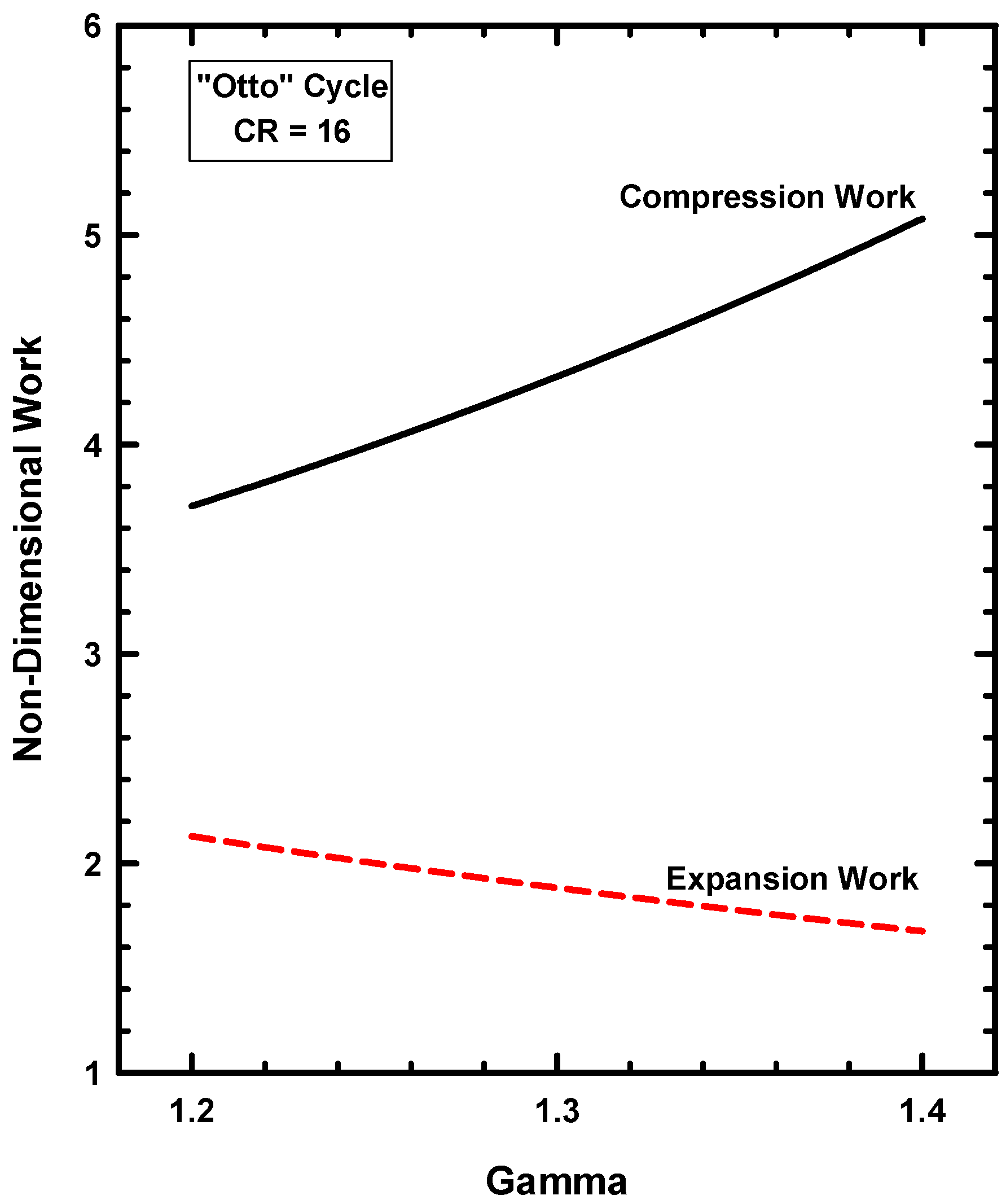
6.4. Thermodynamics of the Otto Cycle
7. Summary and Conclusions
7.1. Summary
7.2. Thermodynamics of LHR Engines
- A low heat rejection engine concept was examined by increasing the cylinder wall temperatures. As the cylinder wall temperature increased, the heat losses decreased, and the thermal energy of the cylinder gases increased.
- Even for the extreme conditions examined (a cylinder wall temperature of 1500 K), very little of the retained thermal energy could be realized as addition work. This is consistent with the majority of the experimental results.
- The paper outlined a series of reasons for the difficulty of converting the reduction of heat losses into work.
- The retention of thermal energy (even if no addition work is produced) could be advantageous, since the exhaust gas energy may be useful for turbo-charging or other applications.
7.3. Thermodynamics of Exhaust Gas Dilution
- Both external and internal exhaust gas dilution were examined.
- External exhaust gas dilution can use some level of cooling. This work examined an adiabatic EGR configuration and a cooled EGR configuration.
- The cooled EGR configuration provides significant efficiency benefits due to decreased heat losses and increases of the ratio of specific heats in spite of modest increases of exergy destruction during combustion.
- The adiabatic EGR configuration resulted in lower efficiencies due to increases of the heat losses in spite of modest reductions of exergy destruction during combustion.
- The use of negative valve overlap results in increased retention of combustion gases. This approach provided results that were similar to the use of the adiabatic EGR configuration.
7.4. Concerning the Otto Cycle
- The classical Otto cycle was reviewed, and identified as an analysis for heat engines and not chemical conversion devices such as IC engines.
- The Otto cycle does, however, possess three thermodynamic characteristics that are consistent with IC engines. These are (1) the mechanical advantage of increasing compression ratio, (2) the conversion of thermal energy to work, and (3) the compression and expansion processes.
- The Otto cycle, however, is inconsistent with IC engines for several reasons. Perhaps the most important of these is that the Otto cycle does not include a combustion process, and therefore completely neglects the combustion irreversibilities.
- The Otto cycle does, however, allow the importance of the ratio of specific heats and compression ratio to be demonstrated.
Acknowledgments
Conflicts of Interest
Appendix A. Brief Review of Combustion Irreversibilities for IC Engines
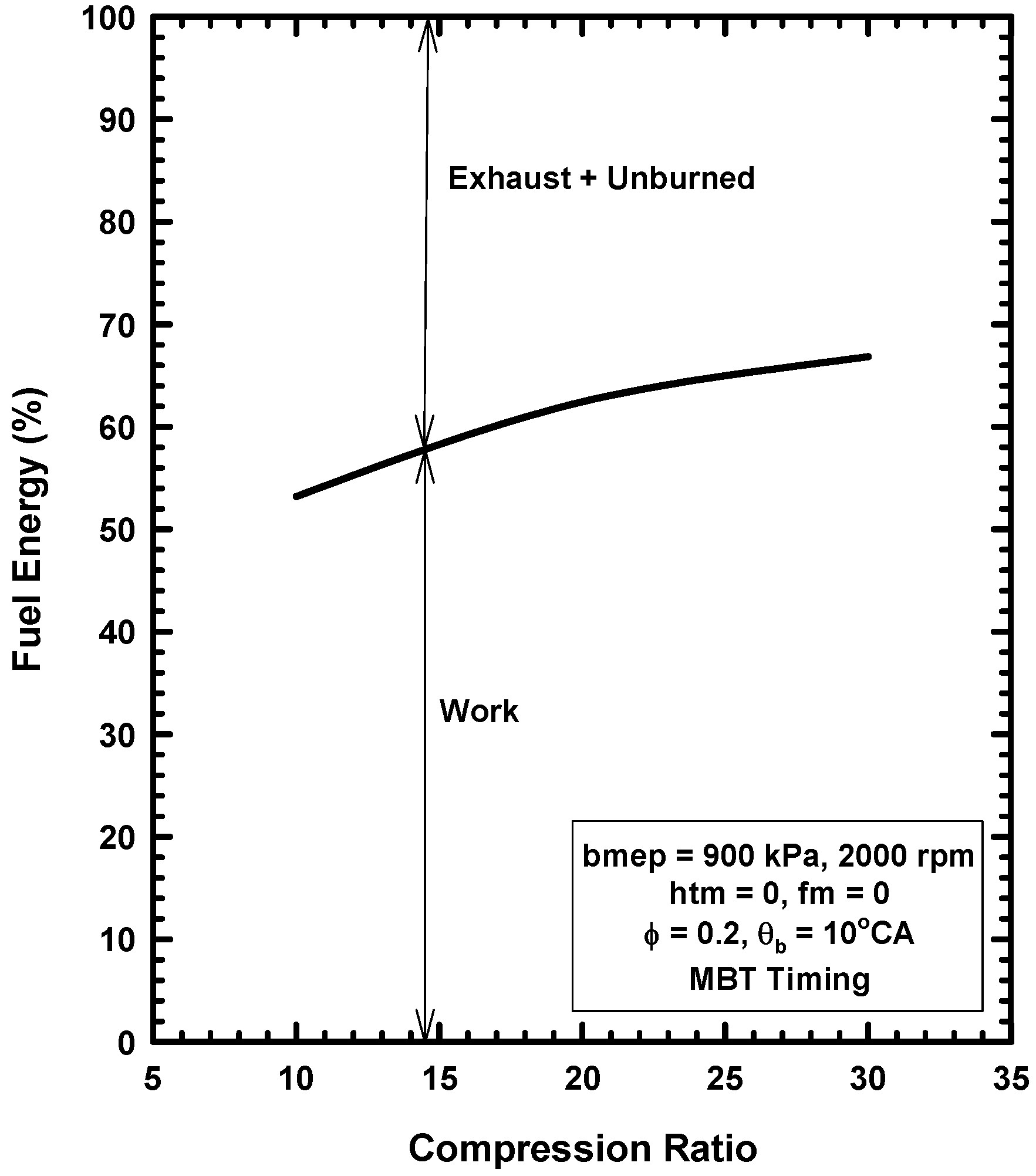
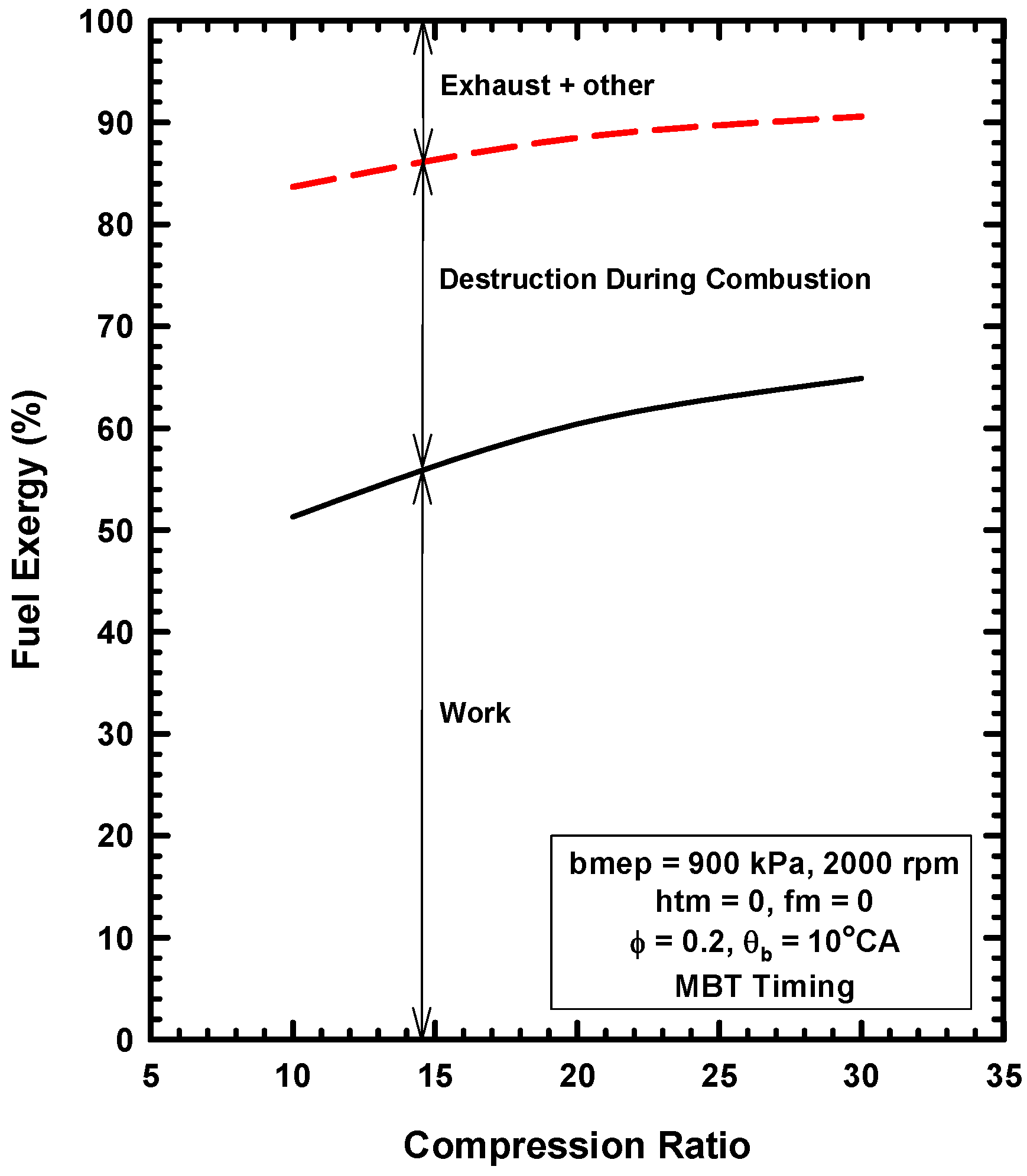
References
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Book Company: New York, NY, USA, 1988. [Google Scholar]
- Ferguson, C.R.; Kirkpatrick, A.T. Internal Combustion Engines—Applied Thermosciences, 3rd ed.; John Wiley & Sons, Inc.: Chichester, UK, 2016. [Google Scholar]
- Tracinski, R. Don’t Count Out the Internal Combustion Engine, RealClearFuture, 29 August 2016. Available online: http://www.realclearfuture.com/articles/2016/08/29/dont_count_out_the_internal_combustion_engine_111937.html (accessed on 14 April 2018).
- Topping, N. The Death of the Internal Combustion Engine, Huffpost, 9 December 2016. Available online: http://www.huffingtonpost.com/we-mean-business/the-death-of-the-internal_b_13533290.html (accessed on 14 April 2018).
- Howell, J.R.; Buckius, R.O. Fundamentals of Engineering Thermodynamics, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics, 8th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2014. [Google Scholar]
- Stone, R. Introduction to Internal Combustion Engines, 4th ed.; Palgrave Macmillan: London, UK, 2012. [Google Scholar]
- Carnot, N.L.S. Reflections on the Motive Power of Fire; Dover Publications: Paris, France, 1824. [Google Scholar]
- Caton, J.A. An Introduction to Thermodynamic Cycle Simulations for Internal Combustion Engines; John Wiley & Sons, Ltd.: Chichester, UK, 2016. [Google Scholar]
- Caton, J.A. On the importance of specific heats as regards efficiency increases for highly dilute IC engines. Energy Convers. Manag. 2014, 79, 146–160. [Google Scholar] [CrossRef]
- Caton, J.A. A multiple-zone cycle simulation for spark-ignition engines: Thermodynamic details. In Large-Bore Engines, Fuel Effects, Homogeneous Charge Compression Ignition, Engine Performance and Simulation, Vol. 2, ICEVol. 37–2, Proceedings of the 2001 Fall Technical Conference, Argonne, IL, USA, 23–26 September 2001; Paper No. 2001-ICE-412; Wong, V.W., Ed.; The ASME Internal Combustion Engine Division, American Society of Mechanical Engineers: New York, NY, USA; pp. 41–58.
- Caton, J.A. A Cycle simulation including the second law of thermodynamics for a spark-ignition engine: Implications of the use of multiple-zones for combustion. Trans. Soc. Autom. Eng. J. Engines 2003, 111–113, 281–299. [Google Scholar]
- Caton, J.A. An assessment of the thermodynamics associated with high efficiency engines. In Proceedings of the ASME 2010 Internal Combustion Engine Division Fall Technical Conference, San Antonio, TX, USA, 12–15 September 2010. [Google Scholar]
- Wiebe, J.J. Brennverlauf und Kreisprozess von Ver-Brennungsmotoren; VEB-Verlag Technik: Berlin, Germany, 1970. [Google Scholar]
- Caton, J.A. Comparisons of global heat transfer correlations for conventional and high efficiency reciprocating engines. In Proceedings of the ASME Internal Combustion Engine Division 2011 Fall Technical Conference, Morgantown, WV, USA, 2–5 October 2011. [Google Scholar]
- Hohenberg, G.F. Advanced Approaches for Heat Transfer Calculations; SAE Paper No. 790825; Society of Automotive Engineers: Warrendale, PN, USA, 1979. [Google Scholar]
- Sandoval, D.; Heywood, J.B. An Improved Friction Model for Spark-Ignition Engines; SAE Paper No. 2003-01-0725; Society of Automotive Engineers: Warrendale, PN, USA, 2003. [Google Scholar]
- Caton, J.A. Correlations of exergy destruction during combustion for internal combustion engines. Int. J. Exergy 2015, 16, 183–213. [Google Scholar] [CrossRef]
- Zucchetto, J.; Myers, P.; Johnson, J.; Miller, D. An assessment of the performance and requirements for “adiabatic” engines. Science 1988, 240, 1157–1162. [Google Scholar] [CrossRef] [PubMed]
- Siegla, D.C.; Alkidas, A.C. Evaluation of the Potential of a Low-Heat-Rejection Diesel Engine to Meet Future EPA Heavy-Duty Emission Standards; SAE Paper No. 890291; Society of Automotive Engineers: Warrendale, PN, USA, 1989. [Google Scholar]
- Reddy, C.S.; Domingo, N.; Graves, R.L. Low Heat Rejection Engine Research Status: Where Do We Go from Here? SAE Paper No. 900620; Society of Automotive Engineers: Warrendale, PN, USA, 1990. [Google Scholar]
- Jaichandar, S.; Tamilporai, P. Low Heat Rejection Engines—An Overview; SAE Paper No. 2003-01-0405; Society of Automotive Engineers: Warrendale, PN, USA, 2003. [Google Scholar]
- Berger, L.B.; Elliot, M.A.; Holts, T.C.; Schrenk, H.H. Diesel Engines Underground—II. Effect of Adding Exhaust Gas to Intake Air; U.S. Department of Interior, Bureau of Mines: Washington, DC, USA, 1940.
- Miller, A.E.; Sullis, S. Recycling Exhaust Gas for Suppressing of Knock in ICE; American Petroleum Institute: Washington, DC, USA, 1953; Section 111; p. 151. [Google Scholar]
- Kopa, R.D.; Kimura, H. Exhaust gas recirculation as a method of nitrogen oxides control in an internal combustion engine. In Proceedings of the APCA 53rd Annual Meeting, Cincinnati, OH, USA, 22–26 May 1960. [Google Scholar]
- Kopa, R.D.; Jewell, R.; Spangler, R.V. Effect of Exhaust Gas Recirculation on Automotive Ring Wear; SAE Paper No. S321; Society of Automotive Engineers, Southern California Section: Los Angeles, CA, USA, 1962. [Google Scholar]
- Onishi, S.; Jo, S.H.; Shoda, K.; Jo, P.D.; Kato, S. Active Thermo-Atmosphere Combustion (ATAC)—A New Combustion Process for Internal Combustion Engines; SAE Paper No. 790501; Society of Automotive Engineers: Warrendale, PN, USA, 1979. [Google Scholar]
- Noguchi, M.; Tanaka, Y.; Tanaka, T.; Takeuchi, Y. A Study on Gasoline Engine Combustion by Observation of Intermediate Reactive Products during Combustion; SAE Paper No. 790840; Society of Automotive Engineers: Warrendale, PN, USA, 1979. [Google Scholar]
- Caton, J.A. A thermodynamic comparison of external and internal exhaust gas dilution for high-efficiency internal combustion engines. Int. J. Engine Res. 2015, 16, 935–955. [Google Scholar] [CrossRef]
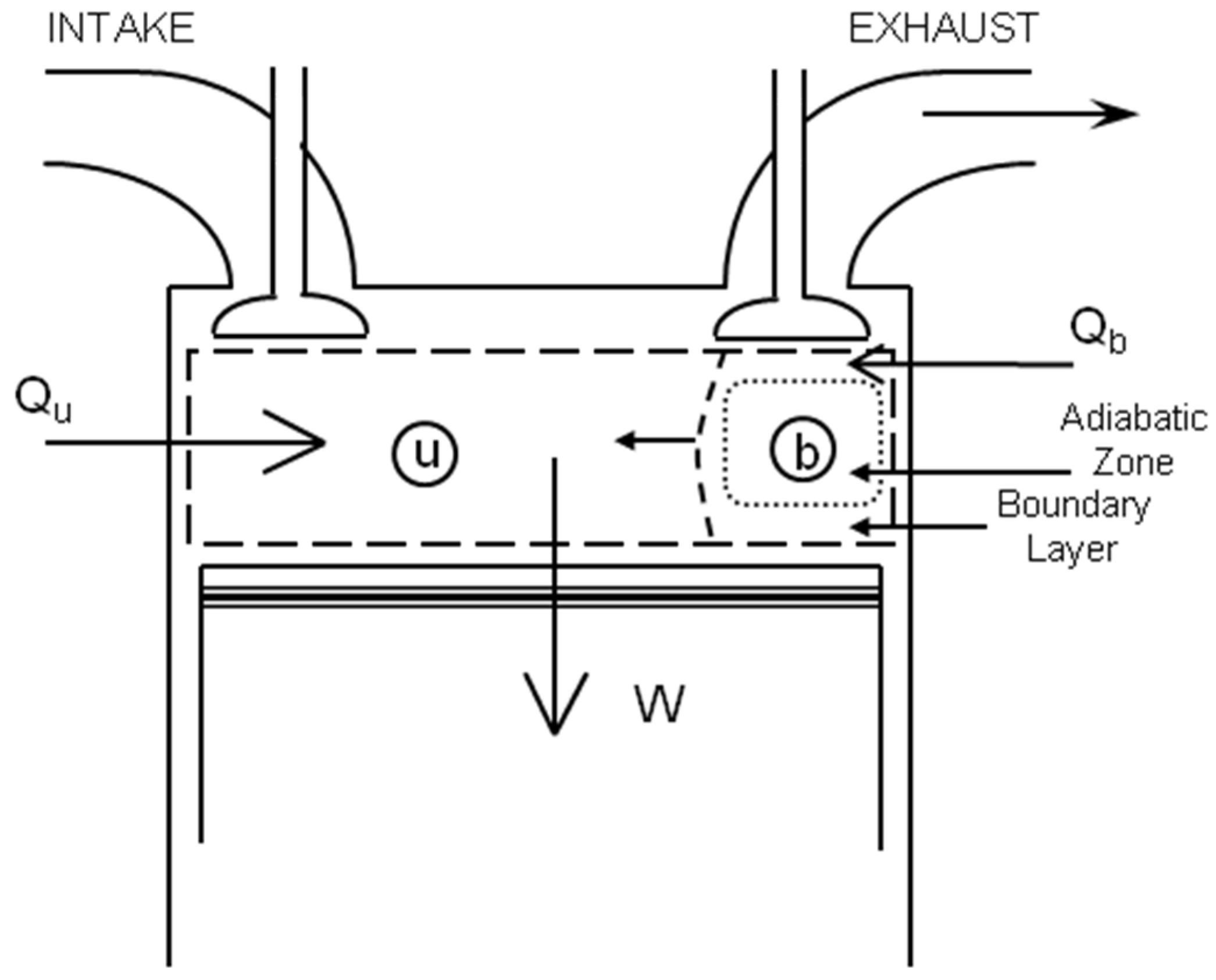
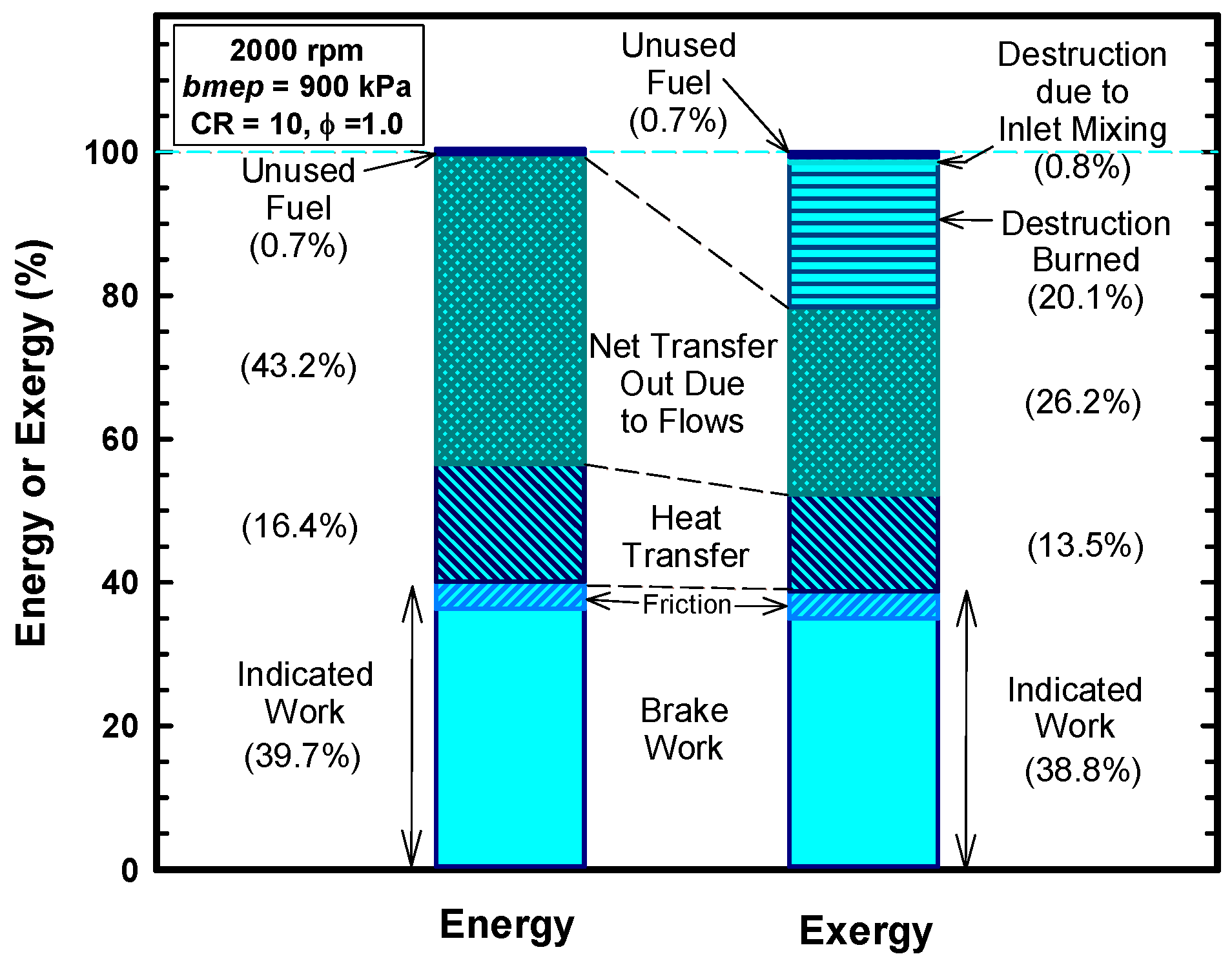
| Item | Value |
|---|---|
| Engine Speed (rpm) | 2000 |
| Bore (mm) | 101.6 |
| Stroke (mm) | 88.4 |
| Crank Rad/Con Rod Ratio | 0.3 |
| Inlet Valves | |
| Diameter (mm) | 50.8 |
| Max Lift (mm) | 10.0 |
| Open (°CA aTDC) | 357 |
| Close (°CA aTDC) | −136 |
| Exhaust Valves | |
| Diameter (mm) | 39.6 |
| Max Lift (mm) | 10.0 |
| Open (°CA aTDC) | 116 |
| Close (°CA aTDC) | 371 |
| Valve Overlap (degrees) | 14° |
| A/V (m−1) at TDC | 469 |
| Item | Value Used | How Obtained |
|---|---|---|
| Fuel | Isooctane | input |
| AFstoich | 15.13 | for isooctane [1] |
| Inlet (air-fuel) Temperature | 319.3 K | Input |
| Compression Ratio | varies | input |
| Equivalence Ratio | varies | Input |
| Inlet pressure (kPa) | varies | Input |
| Exhaust Pressure (kPa) | pin + 10 | computed |
| Fuel LHV (kJ/kg) | 44,400 | for isooctane [1] |
| Fuel Exergy (kJ/kg) | 45,670 | for isooctane [1] |
| Wiebe constant “m” | 2.0 | [1] |
| Wiebe constant “a” | 5.0 | [1] |
| Heat Transfer correlation | Hohenberg | Input [16] |
| Item | Value |
|---|---|
| bmep | 900 |
| rpm | 2000 |
| CR | 10.0 |
| φ | 1.0 |
| θb (°CA) | 50 |
| Twall (K) | 450 |
| Item/Case | 1 | 1a |
|---|---|---|
| Twall (K) | 450 | 1500 |
| bmep (kPa) | 900.9 | 899.7 |
| ηindicated | 39.73 | 41.23 |
| ηbrake | 36.35 | 37.62 |
| θo (°aTDC) | –21.0 | –21.5 |
| pin (kPa) | 86.6 | 100.7 |
| pmax (MPa) | 5.21 | 5.51 |
| MPRR * (MPa/CA) | 0.211 | 0.208 |
| RHT (%) | 16.36 | 0.29 |
| Q (kJ) | 0.291 | 0.005 |
| havg (J/s·m2·K) | 351 | 363 |
| γcomb (---) | 1.2252 | 1.2056 |
| CD ** (%) | 20.06 | 17.57 |
| Tcomb (K) | 1929 | 2171 |
| Texh (K) | 1310 | 1597 |
| Fueling (kJ) | 1.776 | 1.714 |
| Conventional Valve Timings—Positive Valve Overlap (PVO) | 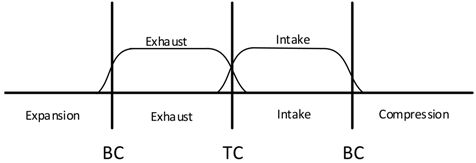 |
| “Recompression”—Negative Valve Overlap (NVO) | 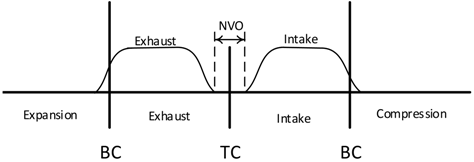 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caton, J.A. The Thermodynamics of Internal Combustion Engines: Examples of Insights. Inventions 2018, 3, 33. https://doi.org/10.3390/inventions3020033
Caton JA. The Thermodynamics of Internal Combustion Engines: Examples of Insights. Inventions. 2018; 3(2):33. https://doi.org/10.3390/inventions3020033
Chicago/Turabian StyleCaton, Jerald A. 2018. "The Thermodynamics of Internal Combustion Engines: Examples of Insights" Inventions 3, no. 2: 33. https://doi.org/10.3390/inventions3020033
APA StyleCaton, J. A. (2018). The Thermodynamics of Internal Combustion Engines: Examples of Insights. Inventions, 3(2), 33. https://doi.org/10.3390/inventions3020033




