Identification of Milling Status Using Vibration Feature Extraction Techniques and Support Vector Machine Classifier
Abstract
:1. Introduction
2. Theory and Method
2.1. Empirical Mode Decomposition
2.2. Fisher Score
2.3. Support Vector Machine
3. Experiment Setup and Process
4. Experiment Result and Analysis
4.1. Fisher Score Feature Selection
4.2. Time Domain Signal Analysis
4.3. Frequency Domain Signal Analysis
4.4. Support Vector Machine Classification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multi-scale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multi-scale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Madzarov, G.; Gjorgjevikj, D.; Chorbev, I. A Multi-class SVM Classifier Utilizing Binary Decision Tree. Informatica 2009, 33, 233–241. [Google Scholar]
- Yang, Y.; Yu, D.J.; Cheng, J.S. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM. Measurement 2007, 40, 943–950. [Google Scholar] [CrossRef]
- Seryasat, O.R.; Shoorehdeli, M.A.; Honarvar, F.; Rahmani, A.; Haddadnia, J. Multi-fault diagnosis of ball bearing using intrinsic mode functions, Hilbert marginal spectrum and multi-class support vector machine. In Proceedings of the International Conference on Mechanical and Electronics Engineering, Taiyuan, China, 1–3 August 2010; Volume 2, pp. 145–149. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.C.; Shih, H.H.; Zheng, Q.N.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Pan, M.C.; Tsao, W.C. Using appropriate IMFs for envelope analysis in multiple fault diagnosis of ball bearings. Int. J. Mech. Sci. 2013, 69, 114–124. [Google Scholar] [CrossRef]
- Liu, Z.; Chai, T.Y.; Yu, W.; Tang, J. Multi-frequency signal modeling using empirical mode decomposition and PCA with application to mill load estimation. Neurocomputing 2015, 169, 392–402. [Google Scholar] [CrossRef]
- Identification of Milling Status Using Vibration Feature Extraction Techniques and Support Vector Machine Classifier. Available online: http://web.nchu.edu.tw/~tianyauwu/data/milling_status/milling_status.htm (accessed on 17 April 2018).
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Song, Q.; Jiang, H.; Liu, J. Feature selection based on FDA and F-score for multi-class classification. Expert Syst. Appl. 2017, 81, 22–27. [Google Scholar] [CrossRef]
- Wu, T.Y.; Chen, J.C.; Wang, C.C. Characterization of gear faults in variable rotating speed using hilbert-huang transform and instantaneous dimensionless frequency normalization. Mech. Syst. Signal Process. 2012, 30, 103–122. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Wu, T.Y.; Wang, C.C. Multi-scale analysis based ball bearing defect diagnostics using mahalanobis distance and support vector machine. Entropy 2013, 15, 416–433. [Google Scholar] [CrossRef]
- Wu, T.Y.; Yu, C.L.; Liu, D.C. On multi-scale entropy analysis of order-tracking measurement for bearing fault diagnosis under variable speed. Entropy 2016, 18, 292. [Google Scholar] [CrossRef]



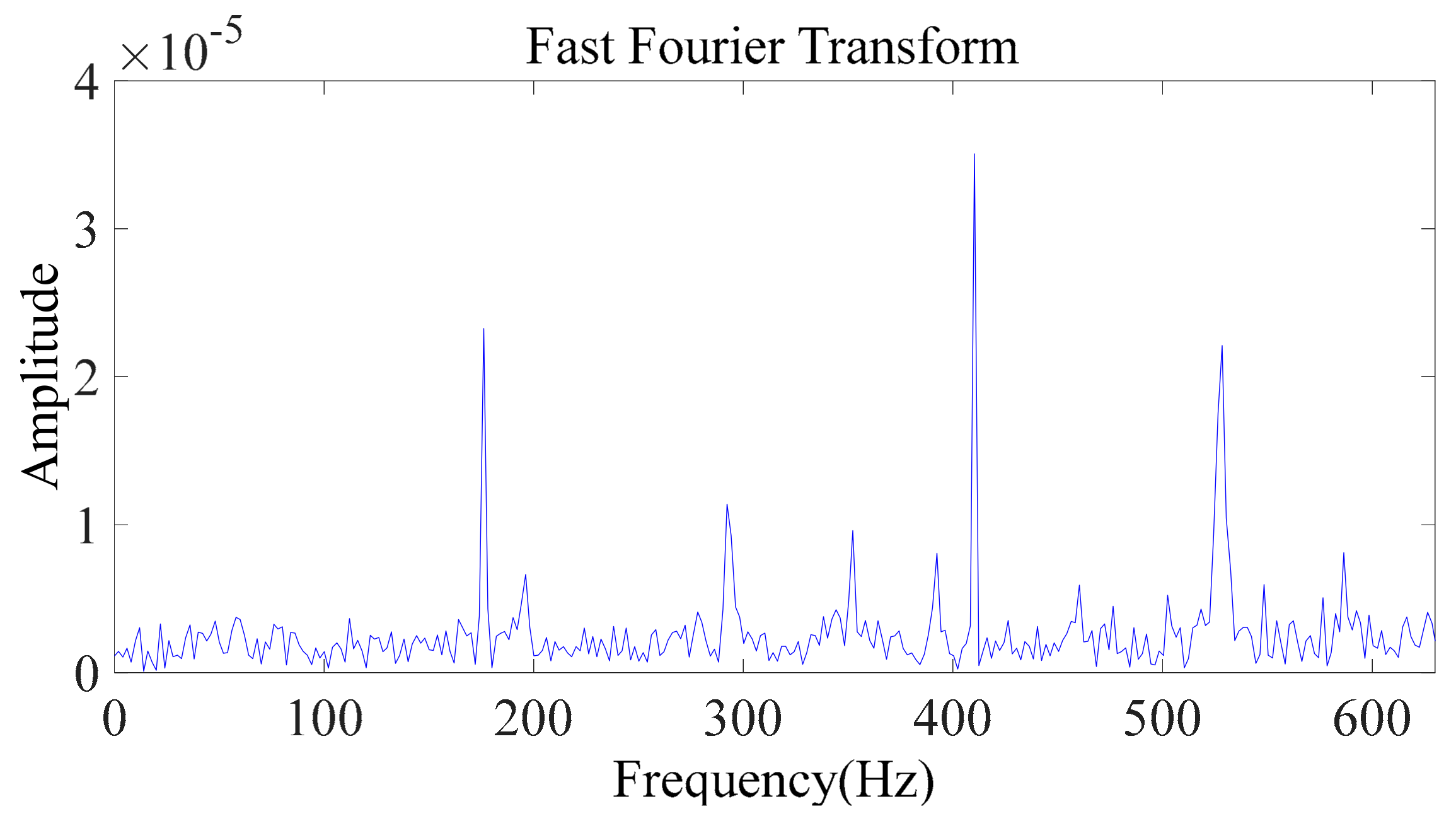
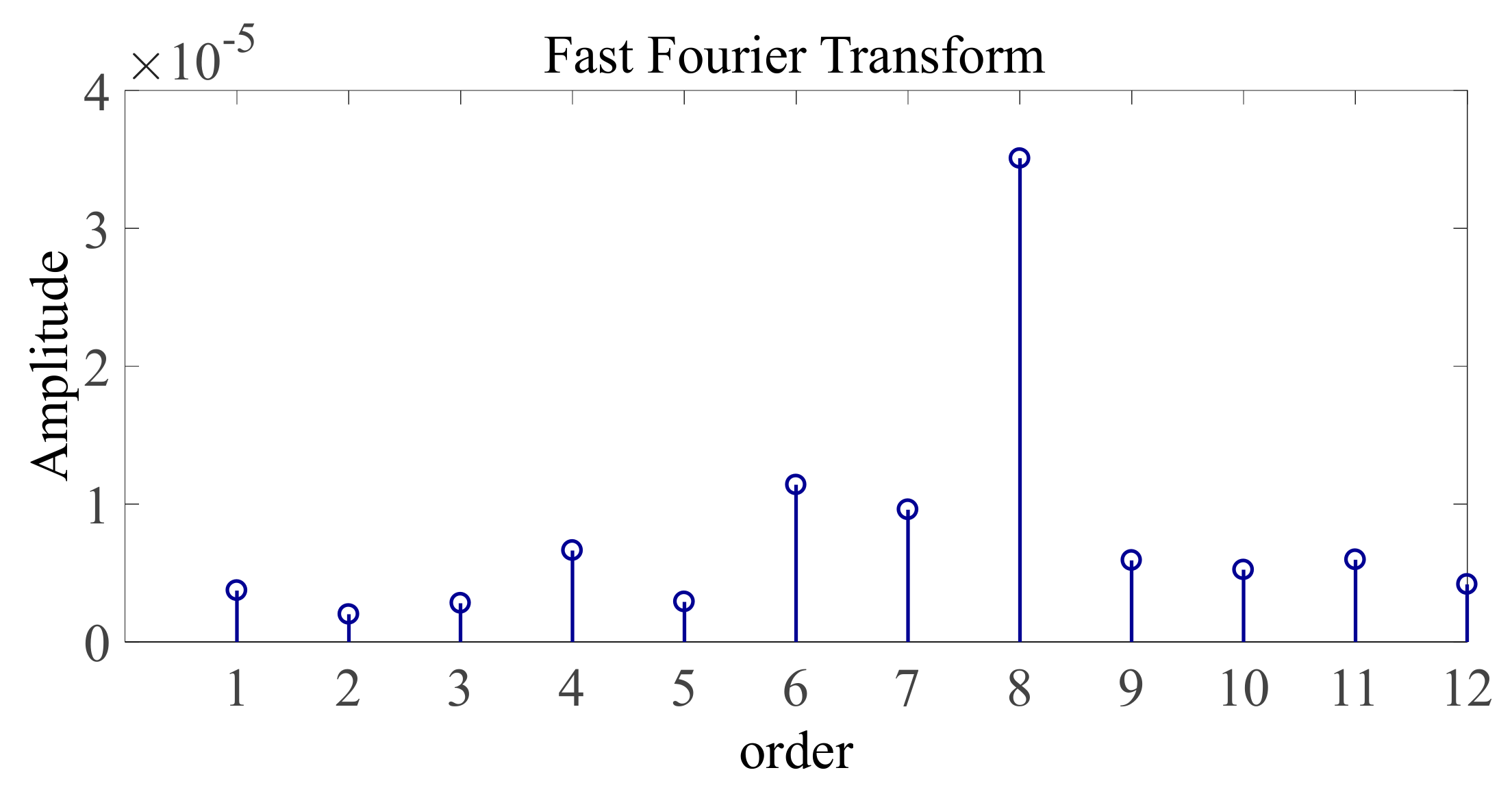

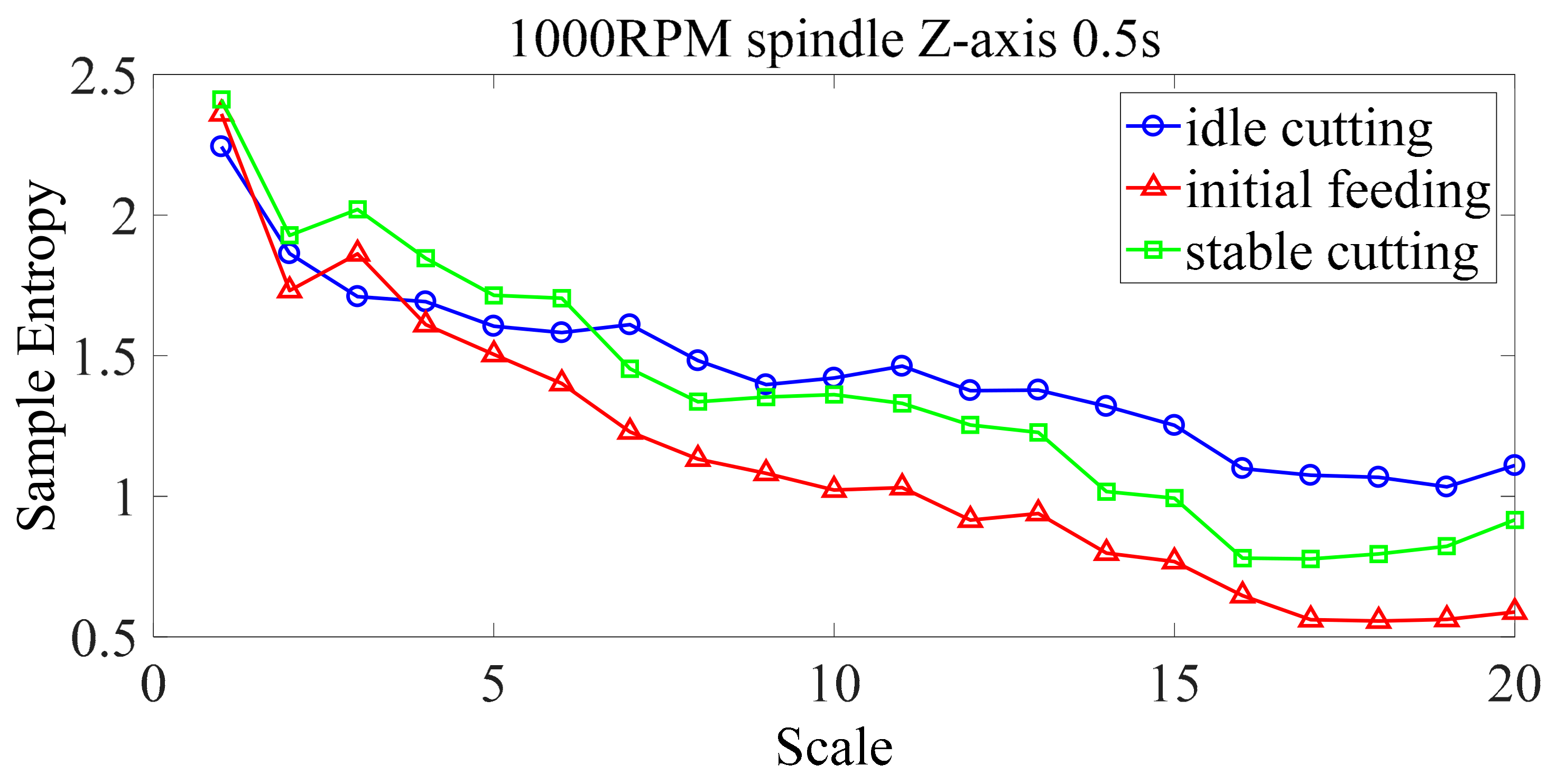
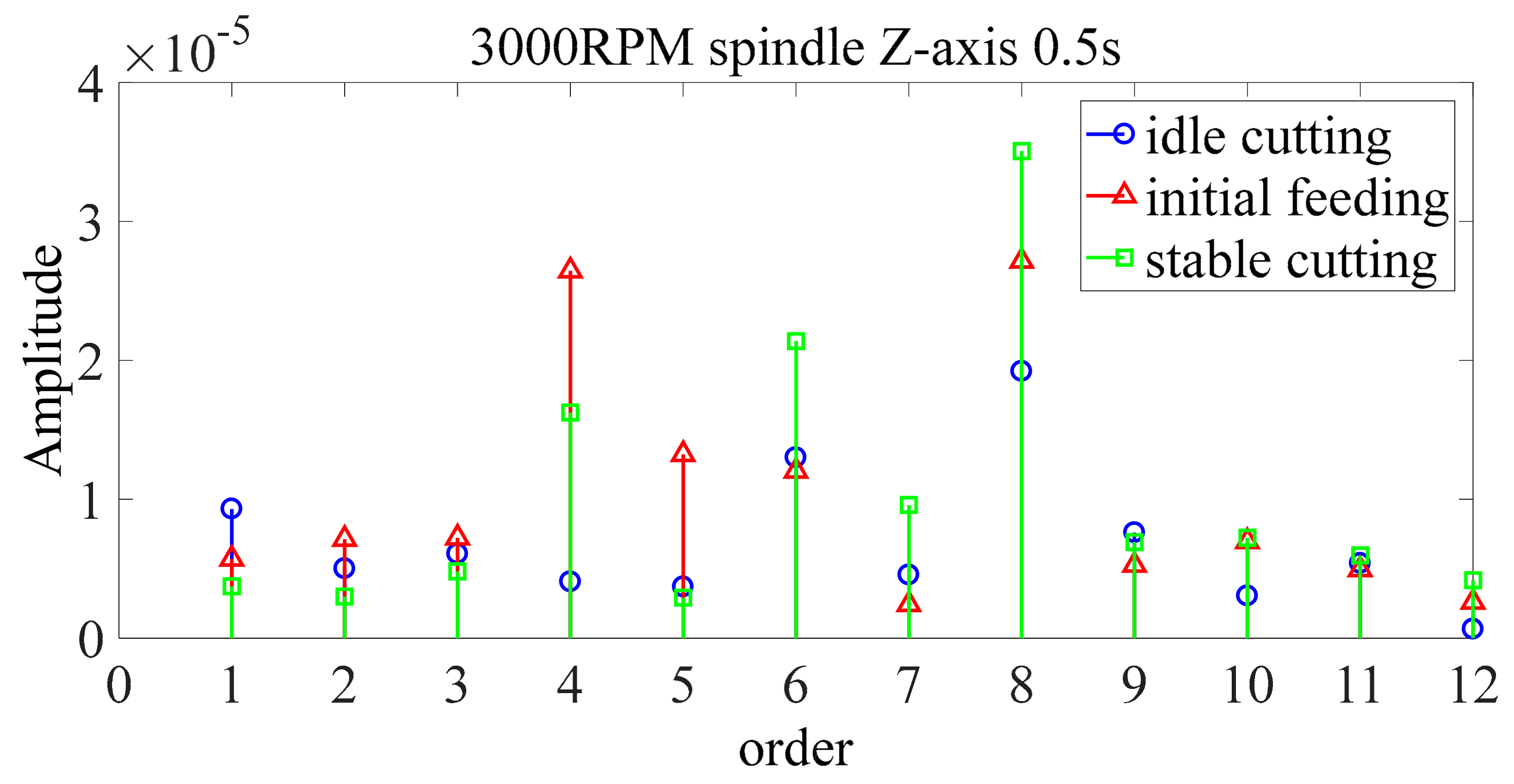
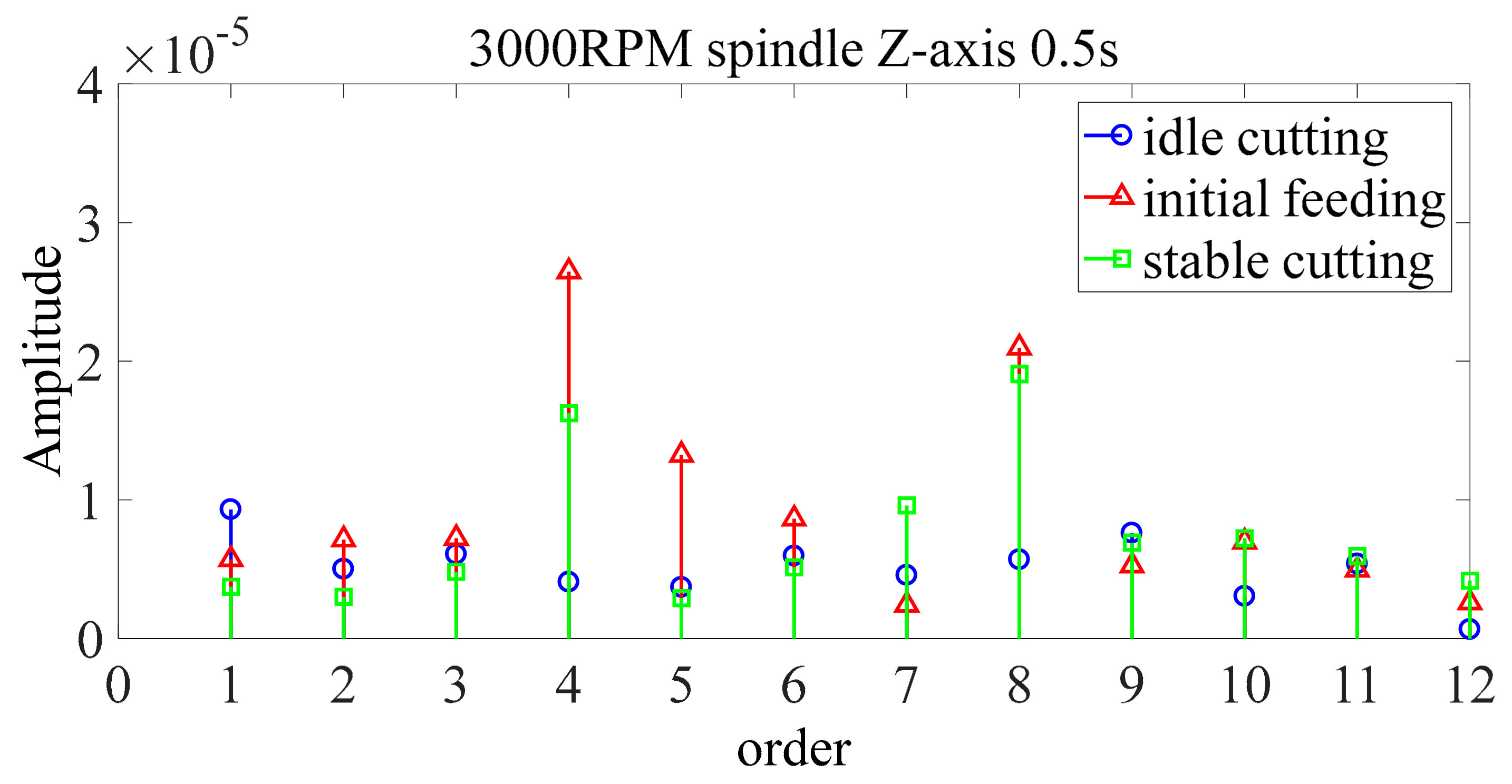
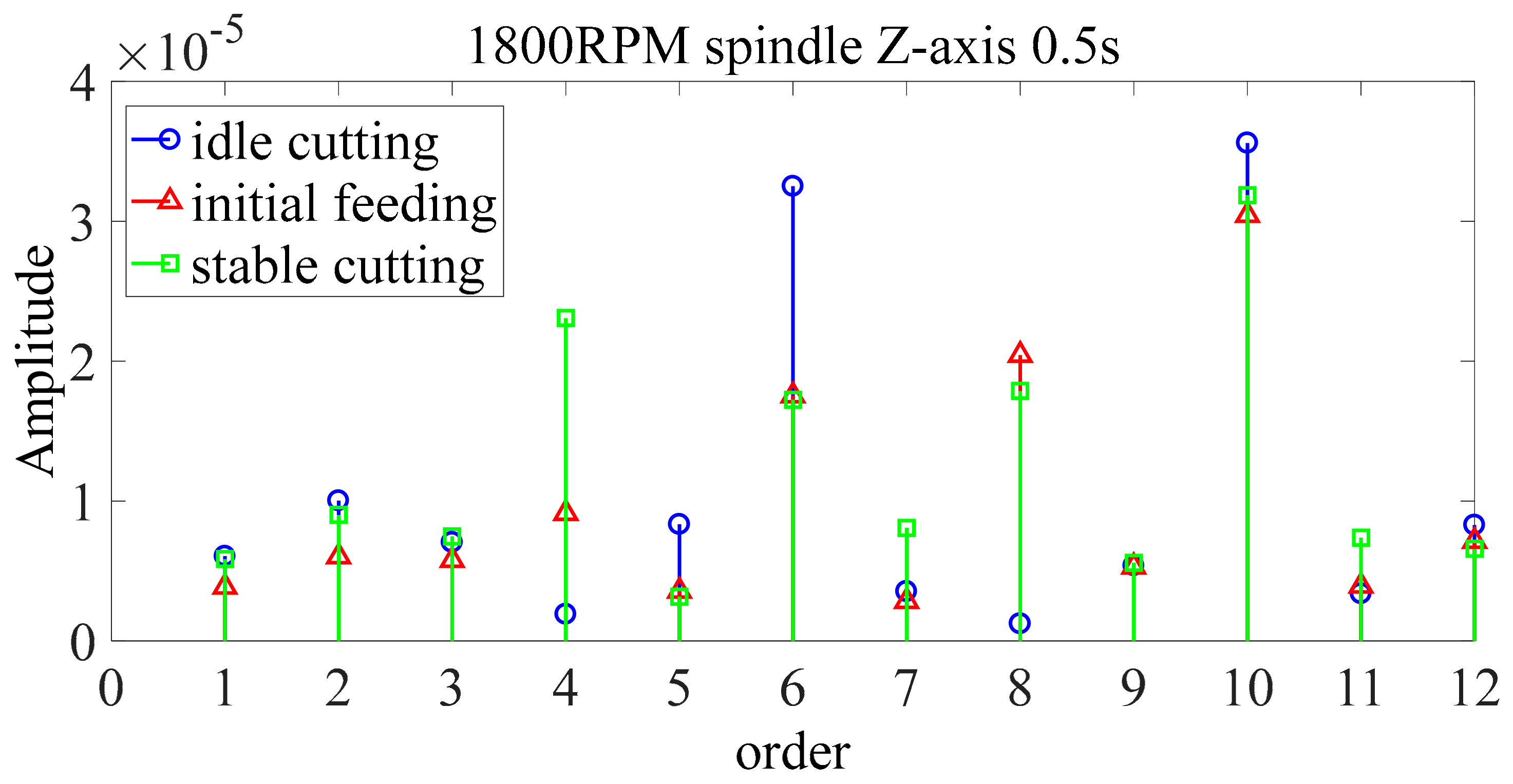
| Category | Idle Cutting and Initial Feeding | Idle Cutting and Stable Cutting | Initial Feeding and Stable Cutting | |
|---|---|---|---|---|
| Feature | ||||
| 1× speed frequency | 0.9175 | 0.5875 | 1.1004 | |
| 2× speed frequency | 0.0336 | 1.9790 | 0.2264 | |
| 3× speed frequency | 0.0432 | 0.1954 | 0.2365 | |
| 4× speed frequency | 2.5395 | 2.5379 | 2.0486 | |
| 5× speed frequency | 0.6767 | 0.1845 | 0.1019 | |
| 6× speed frequency | 0.0674 | 0.6964 | 5.7447 | |
| 7× speed frequency | 0.3298 | 0.7133 | 0.0005 | |
| 8× speed frequency | 2.0440 | 3.1098 | 1.483 | |
| Signal Feature | X Axis | Y Axis | Z Axis | 3 Axes Combination | |
|---|---|---|---|---|---|
| Milling Status | |||||
| Idling cutting | 60.34% | 60.21% | 67.14% | 38.24% | |
| Initial feeding | 44.56% | 41.32% | 40.54% | 33.68% | |
| Stable cutting | 59.32% | 65.28% | 67.42% | 40.38% | |
| Average accuracy | 58.07% | 62.64% | 64.95% | 39.58% | |
| Signal Feature | X Axis | Y Axis | Z Axis | 3 Axes Combination | |
|---|---|---|---|---|---|
| Milling Status | |||||
| Idling cutting | 94.75% | 94.89% | 96.63% | 93.73% | |
| Initial feeding | 90.33% | 92.65% | 94.91% | 91.15% | |
| Stable cutting | 97.38% | 96.94% | 98.75% | 96.68% | |
| Average accuracy | 96.50% | 96.36% | 98.21% | 95.91% | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-Y.; Wu, T.-Y. Identification of Milling Status Using Vibration Feature Extraction Techniques and Support Vector Machine Classifier. Inventions 2018, 3, 25. https://doi.org/10.3390/inventions3020025
Chang C-Y, Wu T-Y. Identification of Milling Status Using Vibration Feature Extraction Techniques and Support Vector Machine Classifier. Inventions. 2018; 3(2):25. https://doi.org/10.3390/inventions3020025
Chicago/Turabian StyleChang, Che-Yuan, and Tian-Yau Wu. 2018. "Identification of Milling Status Using Vibration Feature Extraction Techniques and Support Vector Machine Classifier" Inventions 3, no. 2: 25. https://doi.org/10.3390/inventions3020025
APA StyleChang, C.-Y., & Wu, T.-Y. (2018). Identification of Milling Status Using Vibration Feature Extraction Techniques and Support Vector Machine Classifier. Inventions, 3(2), 25. https://doi.org/10.3390/inventions3020025





