Influence of the Grinding Wheel Topography on the Thermo-Mechanical Stress Collective in Grinding

Abstract

The grinding process is used for both high-performance machining and surface finishing of hardened steel. In addition to the grinding parameters and the grinding fluid supply, the topography of the grinding wheel mainly determines the grinding process behavior and the grinding process result. An alteration of the topography by a variation of the volumetric composition of the grinding wheel, by a variation of the grinding wheel conditioning, or by wear causes a change in the contact conditions. The state of the art shows a substantial knowledge deficit about the influence of the volumetric grinding wheel composition and the resulting grinding wheel topography on the thermo-mechanical stress collective acting on the workpiece external zone. Thus, it is not possible to make a quantitative statement about the influence of the volumetric grinding wheel composition on the external zone properties of a component after grinding. Therefore, the aim of the current research is an empirical-analytical model for the prediction of the thermo-mechanical stress collective as a function of the grinding wheel topography. For this purpose, a methodology is developed, which enables the prediction of the topography-dependent thermo-mechanical load in a grinding process. Therefore, the topography is characterized by means of quantitative parameters and the main influencing variables on the grinding process behavior are investigated. The findings are used to analyze the influence of a change in the topography on the grinding temperature and the grinding force. The obtained results are summarized and are used to explain the thermo-mechanical stress collective as a function of the grinding wheel topography.

1. Introduction

The topography of a grinding wheel represents a functional surface. It is part of a tribological system and causes a stress collective during the engagement with the workpiece material. It determines the chipping of the workpiece material, and thus, the stresses, such as mechanical loads and temperatures. To identify the influence of the grinding wheel topography on this thermo-mechanical stress collective, the topography of the grinding wheel must be described adequately. In principle, the grinding wheel topography is dependent on the grinding wheel specification [1,2]. Further, it is strongly influenced by the grinding-wheel conditioning process and geometrical changes during the grinding process due to wear [3,4]. The characteristics of the topography determine the machining behavior in the grinding process, particularly, so it must be taken into account when designing grinding processes [5].

In the past, several approaches were developed to characterize the grinding wheel topography and to investigate its influence on the grinding behavior. Nowicki proposed a method for selecting topographic characterization parameters for a multi-parameter representation based on low statistical correlation analysis. Based on 100 machined and ground surfaces, he constructed one cross-correlation matrix. Nine parameters were compared, including three height parameters, four spacing parameters, asperity radius, and slope. The three height parameter pairs were found to have correlation coefficients above 0.9, but for the other 29 pairs, he did not find any correlation [6]. Hecker et al. presented a three-dimensional methodology to evaluate the static parameters of a topography to calculate the dynamic parameters. In their model, the individual grain geometries were approximated to a conical or a spherical shape. They found that primarily the protrusion of the grains determines the dynamic grain density and the grinding force [7]. For the characterization of the topography, Nguyen and Butler used the root-mean square parameter Sq to describe its coarseness and the parameters density of summits Sds and summits curvature Ssc to indicate the abrasive grain density and their sharpness. The results show a significant correlation between the parameters Sds and Sq, but the results do not show a correlation between the topography and the investigated grinding force [8]. Uhlmann et al. described the surface of a grinding wheel to develop a reliable method for Numerical Control (NC)-grinding by using a single profile of kinematic cutting edges instead of the whole topography. The simplification of the grinding tool topography proved to be feasible for grinding with abrasive mounted points, in which rotations are high and feed rates are low. A quantitative description of the topography or the kinematic cutting edges is not given [5].

According to Hübert et al., the sufficient characterization of the grinding wheel topography is only possible with the aid of value-supported height, surface, and volume data [9]. Since 2007, DIN ISO 25178 standard [10] has consistently been used to control the acquisition and determination of surface-related and three-dimensional surface parameters. In order to characterize a surface, it is differed between surface-related height parameters and functions, including related function parameters.

The height parameters include the mean arithmetic height of a surface Sa, which indicates the arithmetic mean value of the absolute ordinate values within a definition range, and the mean square height of a surface Sq, which calculates the root from the average square value of the ordinal values of a range. The skewness of a surface Ssk, which corresponds to the quotient of the mean third power of the ordinate values and the third power of Sq, is a measure of the symmetry of the amplitude density curve. Furthermore, the kurtosis of the surface Sku, the steepness of the height distribution within the definition area, as well as the maximum peak and maximum sink height Sp and Sv, and the maximum height Sz (sum of Sp and Sv), are counted to the height characteristics.

Furthermore, the standard specifies the definition of functions for describing the surface texture and the related parameters. In particular, the area-based material ratio curve of scale-limited surfaces, also known as the Abbott-Curve, is of interest in the description of the grinding wheel topography. This function represents the material portion of the scale-bound surface as a function of height, and thus describes the increase in the proportion of material (Mr) of a surface with the increasing depth of the roughness profile.

The Abbott-Curve is formed by cutting the profile of a grinding wheel from the highest peak to the deepest valley at defined intervals from a horizontal plane. Important components of the Abbott-Curve are the core height Sk, which corresponds to the distance between the highest and lowest levels of the core of the surface, the reduced peak height Spk, which indicates the mean height of the protruding peaks above the core height, and the reduced valley height Svk, which indicates the prominent valleys below the core.

The Abbott-Curve also opens the possibility to calculate the area-related empty volume Vv(p) of the cavities for a given material proportion p. Based on this, the empty volume of the valleys of a surface Vvv and the empty volume of the core Vvc is calculable. Analogously to the calculation of the empty volume, the peak material volume Vmp is calculable for a given material proportion. However, the Abbott-Curve does not provide information about the ratio of the proportions of bond and abrasive grains on the surface of a grinding wheel [11].

Weiß, Duscha, and Rasim pursued in their research a different approach for the description of the grinding wheel topography. They quantitatively described the contact conditions in grinding by means of a grain engagement model, which bases on the limiting cutting edge offset angle ε_lim according to Kassen and Werner [12,13]. Therefore, they developed the software Topo-Tool, which focuses on the analysis and quantitative description of the topography by analyzing the kinematic cutting edges. Weiß [14] determined the number of theoretical kinematic grain surfaces N_kin, as well as their respective size, A_kin, and calculated the fractions of these surfaces in the tangential and normal direction to the grinding direction A_kin,t and A_kin,n. He quantified the engagement surfaces of measured topographies of ceramic and synthetic resin bonded grinding wheels depending on their specification, as well as the average tangential and normal cutting engagement surfaces Ā_kin,t and Ā_kin,n as a function of the mean grain diameter [15]. Duscha used the kinematic engagement surfaces of a grinding wheel to determine the maximum surface pressure in the grinding process. In this way, he was able to draw conclusions about the real mechanical loads in the grinding process [16]. Rasim enhanced the Topo-Tool model with the four additional characteristic values peak angle β, rake angle γ, and sharpening angle δ, as well as the opening angle α to describe the kinematic cutting engagement surfaces. He determined the frequency distribution of the grain shapes, which he used to analyze the influence of the shape of the cutting edge surfaces on the energy conversion in the grinding process. In his investigations, he varied the grain type in galvanic bonded grinding wheels, and was thus able to model the influence of the grinding wheel topography on the energy conversion in the grinding process for the first time [17]. However, he did not undertake a comprehensive variation of the volumetric grinding wheel composition. Figure 1 gives an overview of the potential parameters for describing the properties of functional surfaces and grinding wheel topographies.

Despite the previous research, the state of the art shows a substantial knowledge deficit about the influence of the volumetric grinding wheel composition, and the resulting grinding wheel topography on the thermo-mechanical stress collective acting on the workpiece external zone. Thus, it is not possible to make a quantitative statement about the influence of the topography geometry on the thermal and mechanical process load acting on the workpiece external zone of a component. Consequently, the knowledge about the influence of the topography of a grinding wheel on the component’s surface and external zone properties is insufficient.

Therefore, the aim of current research is an empirical-analytical model for the prediction of the thermo-mechanical stress collective as a function of the grinding wheel topography. For this purpose, a methodology has been developed that enables the prediction of the topography-dependent thermo-mechanical load in the grinding process.

2. Materials and Methods

First, grinding tests with multilayered, synthetic resin-bonded cubic boron nitride (CBN) grinding wheels have been carried out. In the grinding experiments, a tool grinding machine S22P turbo of the company ISOG was used to investigate the thermo-mechanical stress collective depending on the grinding wheel topography. During the experimental investigations, 13 synthetic resin-bonded CBN grinding wheels from the company TYROLIT Schleifmittelwerke Swarovski K.G. (Schwaz, Austria) were used to grind the bearing steel 100Cr6. The grinding wheels differed in their volumetric composition, in the average grain size, and in the grain type. The grain types ABN200 and ABN800 from the company Element Six (Burghaun, Germany) were used. The grain type ABN200 is described as “sharp” with high strength and thermal stability. The grains predominantly have an octahedral shape and are rounder than the grains of the grain type ABN800. An overview of the used grinding wheel specifications is shown in Figure 2.

Approximately 160 grinding tests were carried out, each with different experimental conditions to investigate the influence of the grinding wheel topography on the thermo-mechanical stress collective. A full-factor experimental design was chosen in order to fully explore the influence of the individual input factors. By varying only one input variable at otherwise constant input variables, it was possible to identify the influence of each input variable on the process result. Thus, almost-repeated tests were carried out in the experimental design, which could be confirmed on the basis of the results. Both, the composition of the grinding wheels and the dressing process were varied to adjust the topography of the grinding wheels. The experiments were carried out in an up-grinding process. In the experiments, the grinding wheel topography was varied by changing the volumetric composition of the grinding wheels. The CBN abrasive wheels were profiled by a diamond form roller with a mean grain size of 301 µm and were sharpened by means of sharpening blocks of the type A240 H5 V from TYROLIT Schleifmittelwerke Swarovski K.G. company. They were dressed with different dressing overlap ratios U_d = 1; 2; 4, a constant dressing feed a_ed = 2.5 µm and a speed ratio of q_d = 0.8. In addition, the topography was varied by using the sharpening parameters specific sharpening material removal rate Q’_Sb = 100 mm³/mms and specific sharpening material removal V’_Sb = 50, 100 and 150 mm³/mm. The grinding parameters grinding wheel circumferential speed v_s = 30 m/s and infeed a_e = 100 µm were kept constant. The workpiece speed was varied in three steps between 1.5 m/min < v_w < 4.5 m/min to set the specific material removal rate varied between 2.5 mm³/mms < Q’_w < 7.5 mm³/mms.

The interpretation of the thermo-mechanical stress during grinding is only possible with a sufficiently precise knowledge of the occurring grinding force and temperature, as well as the geometric contact conditions along the real contact arc. Therefore, a temperature-force measuring platform has been manufactured to measure the occurring grinding forces and temperatures. In order to determine the thermal loads during the grinding process parallel to the mechanical loads, a temperature measurement method according to Duscha, based on the work of Choi and Batako, was used [16,18,19]. A constantan foil (55% Cu, 44% Ni and 1% Mn) was connected to a constantan wire with the help of a TL-WELD-220V thermocouple welding machine from OMEGA. The resulting metallic conductor was fixed between two screwed workpiece parts. Ceramic mica discs isolated the constantan foil from the two workpiece parts beside. The downstream workpiece part was connected with an iron conductor to a reference point. As a result of the passage of the grinding wheel during the grinding process, the constantan foil was machined, and, due to plastic deformation, a contact with the downstream part of the workpiece was closed over the isolation. The closed contact between the metal pair enabled the temperature measurement due to the occurring thermal stress by means of the electrical charge transfers in a high repeatability and certainty of results.

To ensure that the initial wear of the grinding wheels was overcome before the grinding experiments, each grinding wheel was ground in after the dressing process. Once the grinding wheel produced a constant grinding force, the grinding in process was stopped.

In order to identify the influence of the grinding wheel topography on the thermo-mechanical stress collective, the topography of the grinding wheels was recorded and analyzed by a three-dimensional (3D) Laser Scanning Confocal Microscope VK-X 150 before each experiment. The analysis of the topographies was carried out with the analysis module of the company Keyence (Osaka, Japan) and with the MATLAB-based Topo-Tool developed at the Laboratory for Machine Tools and Engineering (WZL) of RWTH Aachen University [14]. The analysis module of the laser scanning microscope enables the determination of the volume, height, distance and function parameters listed in Figure 1 according to DIN EN ISO 25178 [10]. The Topo-Tool enabled the identification of the kinematic engagement surfaces of a grinding topography, as well as the calculation of the size of the engagement surfaces, depending on the process parameters. The calculation is based on the Formula 1 calculated by Kassen and Werner for the calculation of the limiting cutting edge angle ε_lim [12]. The calculated limiting cutting edge angle ε_lim results from the infeed of the grinding wheel during simultaneous relative movement between the grinding wheel and the workpiece in the circumferential direction of the grinding wheel. In Figure 3, the approach for calculating the kinematic engagement surfaces is shown schematically, using the example of a small grinding wheel cutout.

$${\epsilon }_{\lim }=\frac{{\mathrm{v}}_{\mathrm{w}}}{{\mathrm{v}}_{\mathrm{s}}}\cdot 2\cdot {\left(\frac{{\mathrm{a}}_{\mathrm{e}}}{{\mathrm{d}}_{\mathrm{s}}}\right)}^{\frac{1}{2}}$$

(1)

In addition to the identification of the kinematic engagement surfaces, the size of the individual kinematic engagement surfaces A_kin and the proportions in normal and tangential direction A_kin,n and A_kin,t were determined, according to [14,16]. Based on this, the mean kinematic engagement surfaces in normal and tangential direction Ā_kin,n and Ā_kin,t were calculated. Furthermore, the analysis of the shape of the kinematic cutting edges was carried out using the characteristic values of the peak angle β, the rake angle γ, and the sharpening angle δ [17].

3. Results

The aim of the research was to investigate the influence of the grinding wheel topography on the thermo-mechanical stress collective. Therefore, first the influence of the listed topography parameters on the grinding force and the grinding temperature was analyzed. Parameters with an influence on the thermo-mechanical stress collective were subsequently tested for correlations with each other and were then grouped. Subsequently, the influence of a change of the relevant topography parameters on the process results was examined in detail. The high number of experiments and investigated parameters did not permit any direct analysis and interpretation of all the results. Therefore, first investigations that are presented in this paper were carried out with a constant specific material removal rate of Q’_w = 2.5 mm³/mms, a constant dressing overlap ratio U_d = 1 and with grinding wheels with a grain proportion of V_K = 25% and mean grain size of d_G = 126 µm.

The analysis of the test results was carried out with the aid of the open-source software ORANGE, which is a component-based visual programming software package for data analysis, data visualization, machine learning, and data mining [20]. The visualization of the correlations between topography parameters and process parameters was carried out using scatter plot matrices in MATLAB. This enabled the rapid identification of correlations between the parameters.

3.1. Correlations between the Process Result Parameters

Figure 4 shows the correlation between the maximum temperature T_max and the grinding force in tangential and normal direction F_t and F_n for the specific material removal rate Q’_w = 2.5 mm³/mms. In the present case, the highest value for the degree of determination R² was found with a linear approach to the relationship between the grinding force and the temperature. In particular, there was a very strong linear correlation between the maximum temperature T_max and the grinding forces in normal and tangential direction F_n and F_t. Based on this finding, the influence of the topography on the process behavior was investigated by means of the grinding temperature.

3.2. Correlations between the Topography Parameters

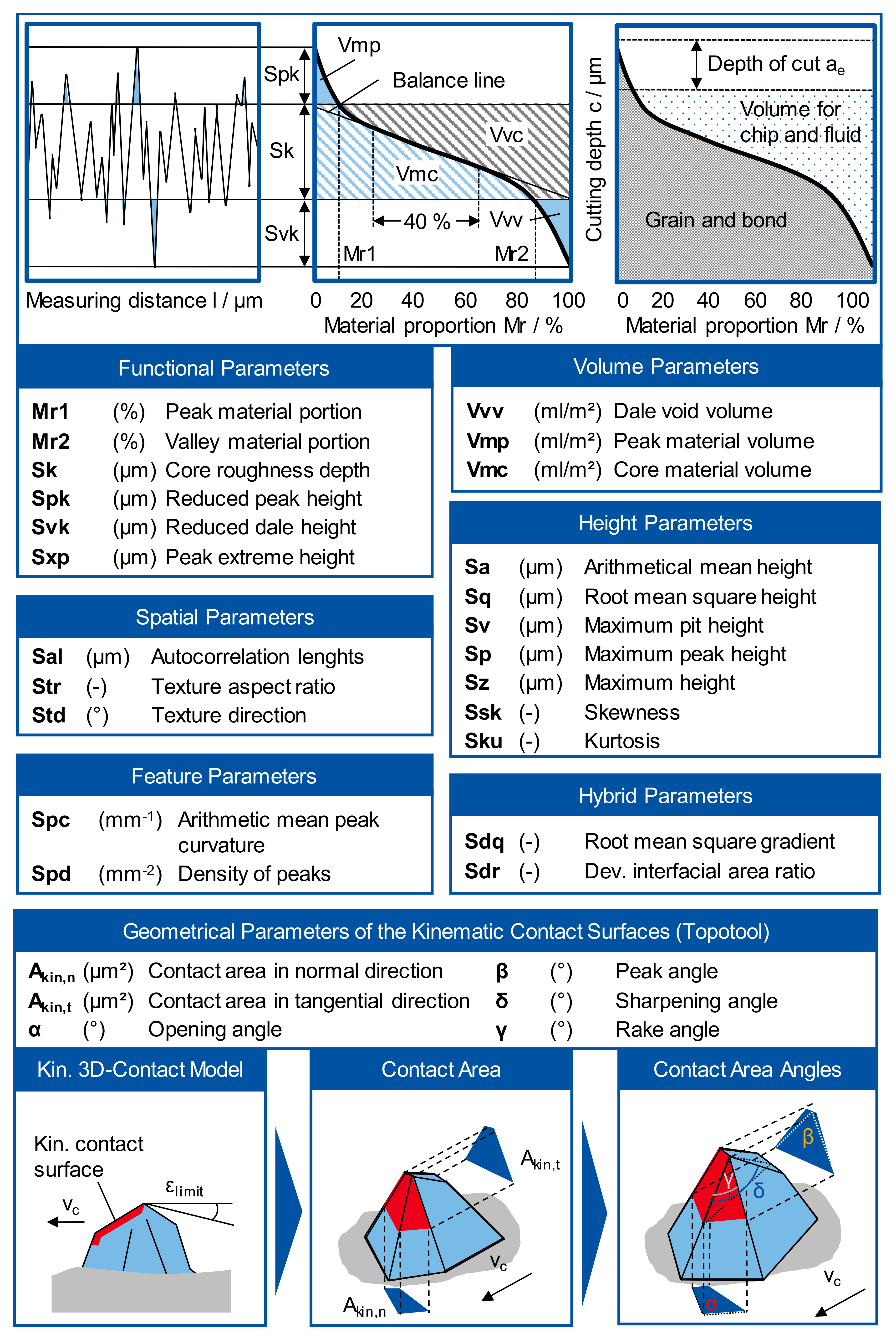
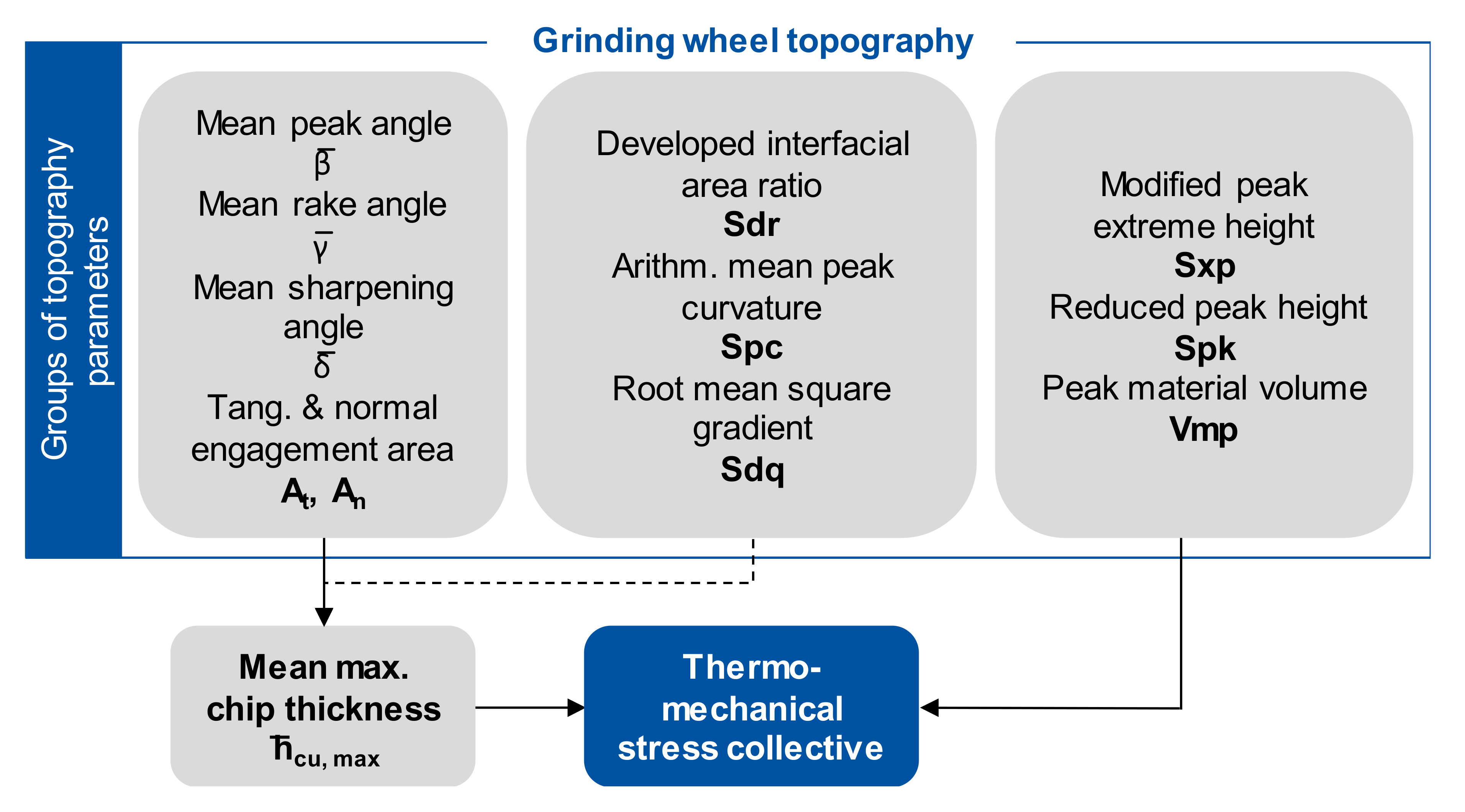
In the following, the characteristic topography parameters, which had a similar influence on the thermo-mechanical stress collective were investigated and grouped. Three parameter groups were identified by the analysis, so that a reduction of the total of 33 investigated topography parameters to three parameter groups could be realized for describing the influence of the grinding wheel topography on the thermo-mechanical stress collective.

The results did show no correlation between the height parameters Sa, Sz, Sq, Ssk, Sku, Sp, and Sv among each other and the process results maximum temperature T_max and the process force components F_n and F_t. The process results also showed no significant dependencies on the height parameters Str, Sal, and Std. Therefore, height parameters are not suitable for describing the influence of the grinding wheel topography on the thermo-mechanical stress collective.

The volume parameter texture aspect ratio of the surface Str, autocorrelation length of the texture Sal, and the texture direction Std, describe the spatial structure patterns of the topography. Significant dependencies of the process variables were not found in the investigations, so that the volume parameters do not seem to be suitable for the quantitative description of the influence of the topography on the grinding process behavior.

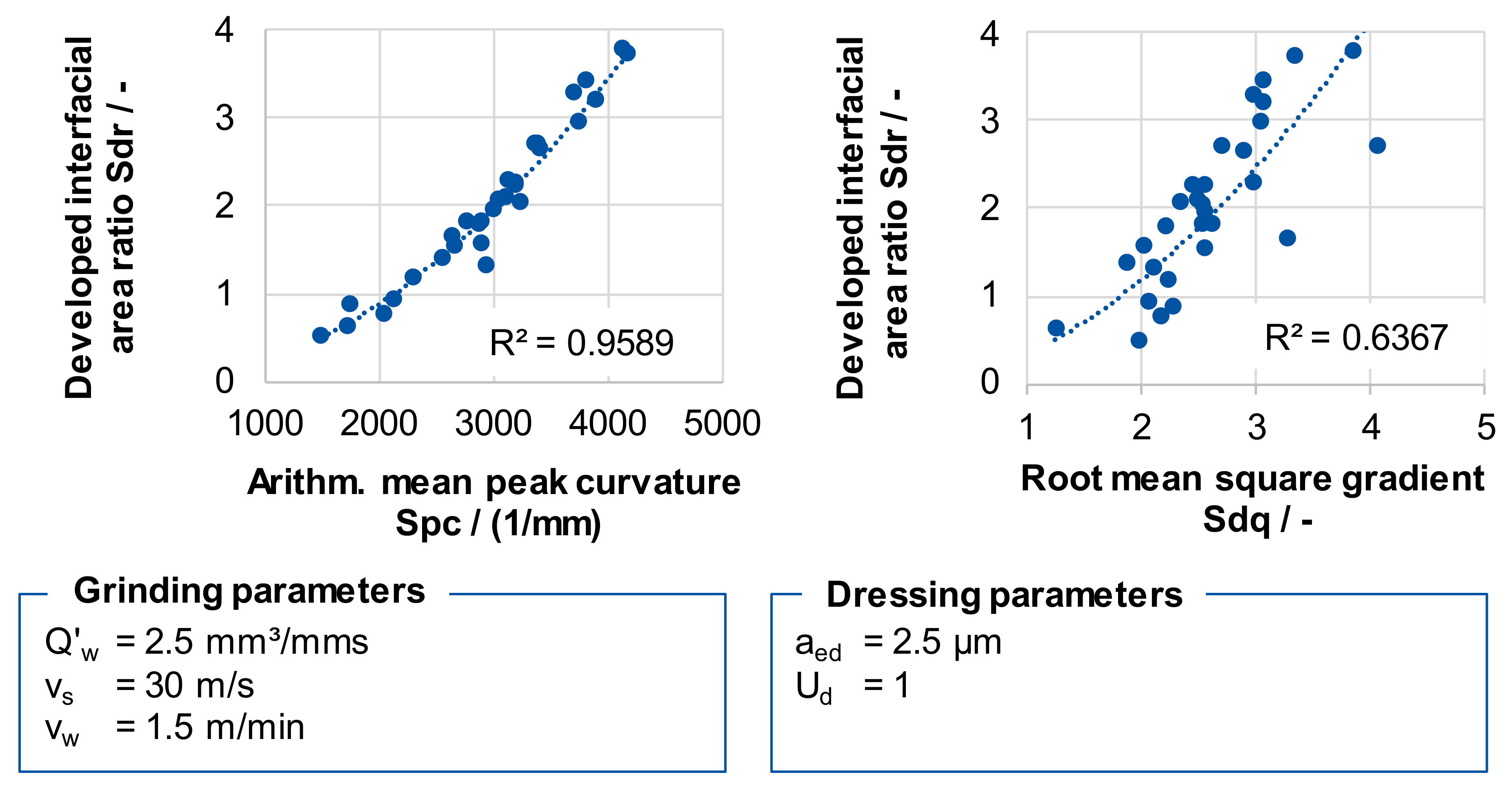
In mechanical engineering, hybrid parameters are used in various applications to describe wear and tribological behavior. They combine spatial and vertical parameters. The developed interfacial area ratio Sdr indicates the ratio between the true surface of the topography and the projected base area in the X–Z plane. Thus, it is a measure of the three-dimensional roughness of the analyzed surface. A perfectly planar surface has a value of Sdq = 0. The arithmetic mean value of the peak curvature Spc, the developed interfacial area ratio Sdr, and the root mean square gradient Sdq showed a particularly strong correlation. The correlation between the arithmetical mean value of the peak curvature Spc and the developed interface area ratio Sdr was best describable by a quadratic function with a coefficient of determination of R² = 0.9589, which corresponds to an excellent correlation (see Figure 5). The correlations between the above-mentioned parameters and the process variables were investigated and they showed identical trends. For the further procedure, the three parameters were grouped and the influence of the arithmetical mean value of the peak curvature Spc was analyzed as representative for the parameter cluster.

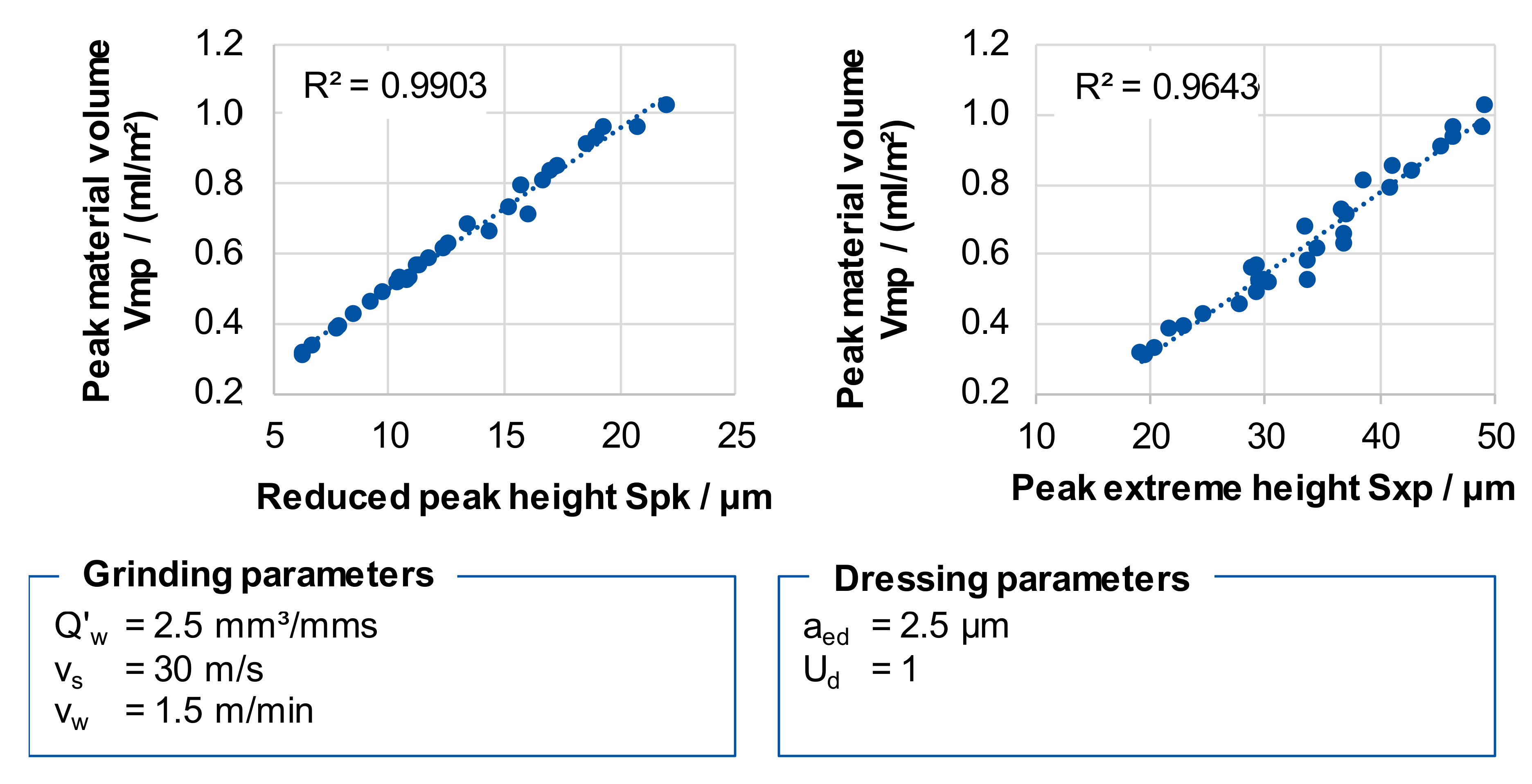
Similarly, there were strong correlations between the functional parameters describing the upper part of the Abbott curve, see Figure 6. Since the correlation coefficients between the reduced peak height Spk, the peak extrem heigt Sxp, and the peak material volume Vmp assume approximately a coefficient of determination of nearly R² = 1, an almost perfect linear relationship exists between the topography characteristics. Here, the formation of a cluster is obvious, since all the parameters also had the same relation to the process variables.

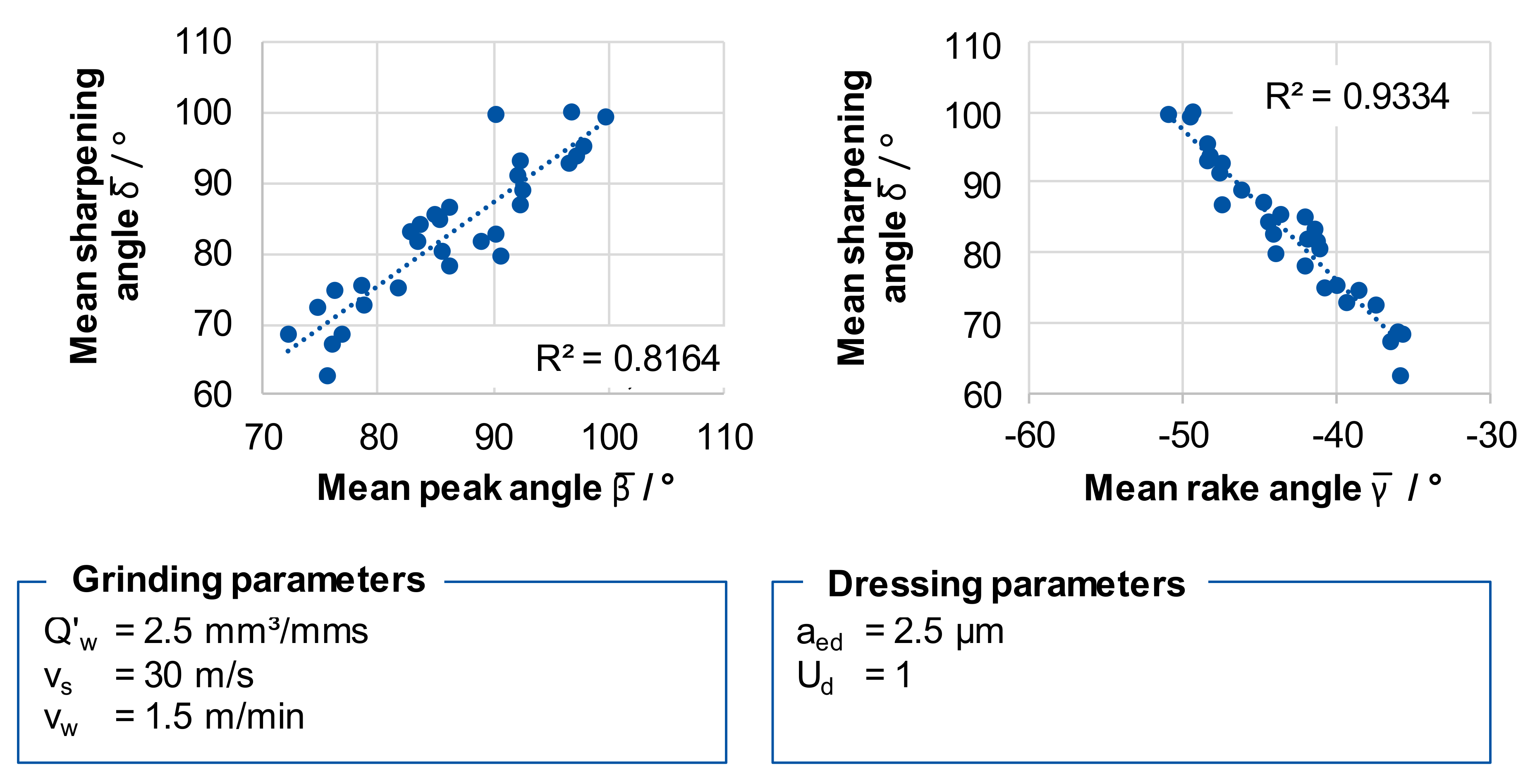
The angles of the kinematic cutting edges, which were identified by the Topo-Tool, also correlated strongly. Figure 7 shows approximately linear relationships between the angles of the kinematic cutting edge areas. When the mean peak angle β or the mean sharpening angle δ increase, the mean rake angle γ decreases. Here, too, a grouping of these parameters was appropriate, in order to reduce complexity for the analysis of the influence of the grinding wheel topography on the thermo-mechanical stress collective.

3.3. Influence of the Topography Parameters on the Chip Thickness and Process Result Parameters

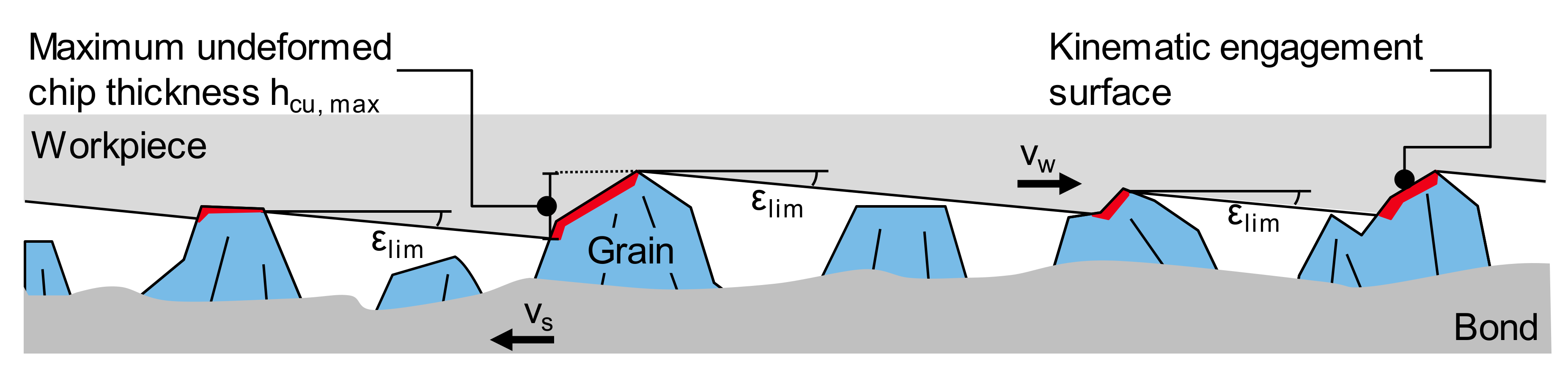
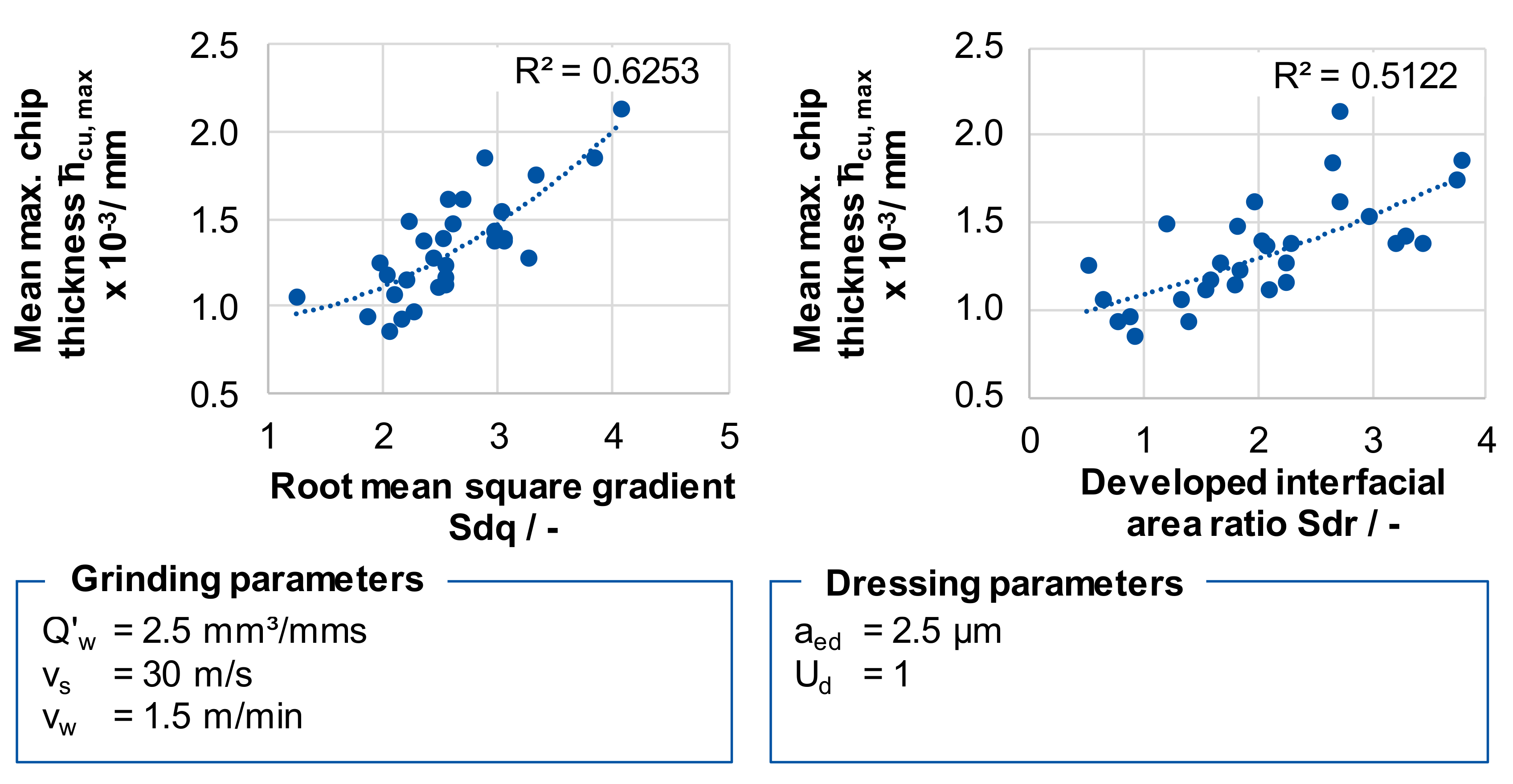
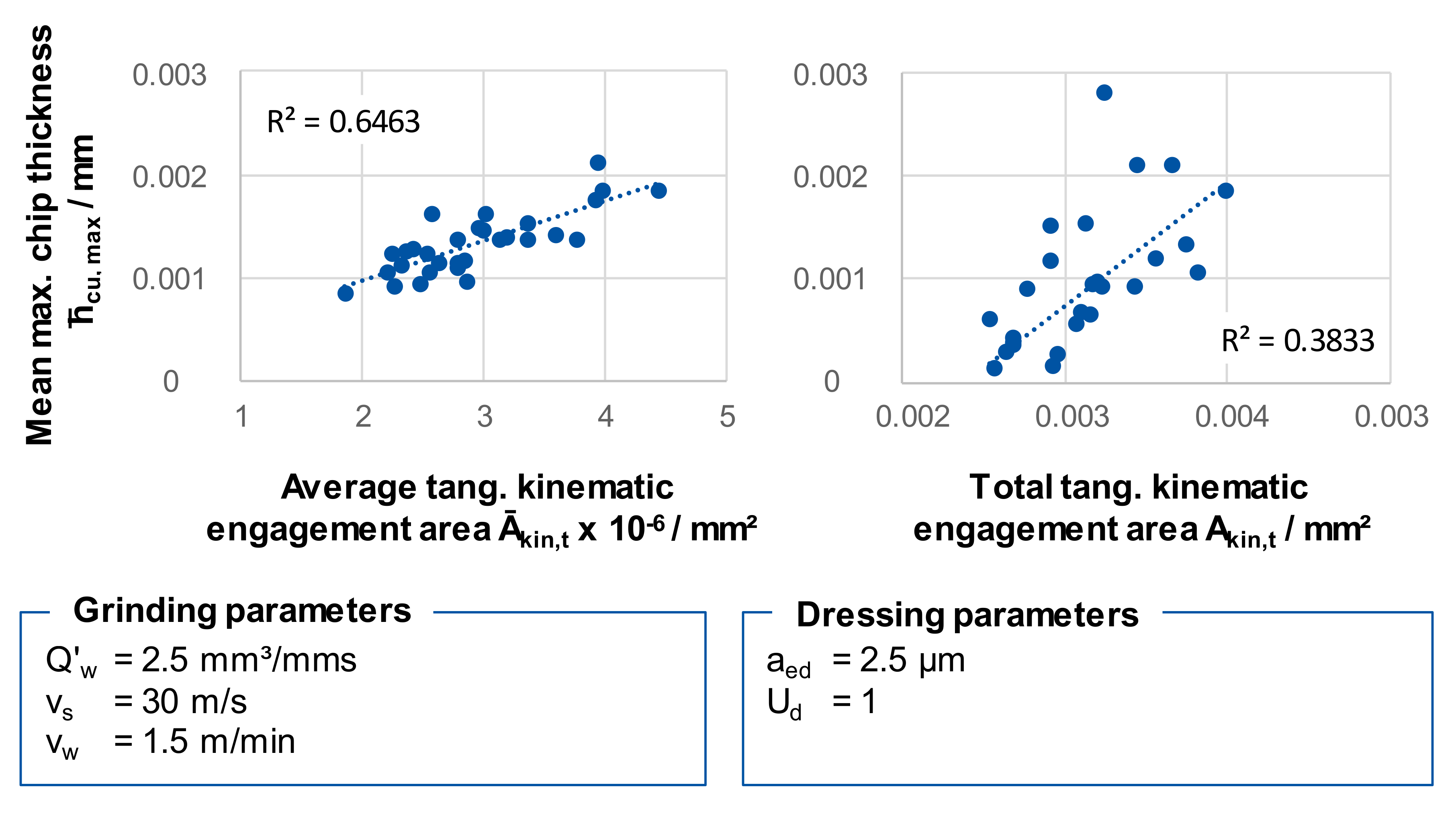
Based on the rapid identification of correlations between the topography parameters and the process parameters, a detailed analysis of the influence of the relevant topography parameters on the thermo-mechanical stress collective was carried out. Figure 8 shows the correlations between the hybrid parameters and the process parameter mean maximum chip thickness h_{cu, max}. The maximum chip thickness was investigated by means of the Topo-Tool, which measures the biggest vertical distance between the lowest and the highest points of the tangential kinematic engagement area, as described in Figure. Between the developed interface ratio Sdr and the process parameters F_n, F_t, and T_max, only weak correlations were identified. An influence of these surface parameters on the process behavior is physically close, but due to the coefficient of determination of only R² = 0.62, a low suitability of these topography characteristics is assumed to describe the influence of the topography on the thermo-mechanical stress collective solely.

The further investigated functional parameters are derived from the Abbott curve, which characterizes the vertical material distribution of a surface structure. The Abbott curve is created by applying the material portion above the profile height. Functional parameters, such as the reduced dale height Svk, or the core material volume Vmc, which describe the geometry and structure of the grooves on a surface, did not influence the force or temperature in the grinding process. In particular, the reduced dale height Svk, which evaluates surfaces with regard to their ability to absorb and to serve fluid to adjust the lubricating properties in tribosystems, did not show any correlation with force and temperature, contrary to expectations.

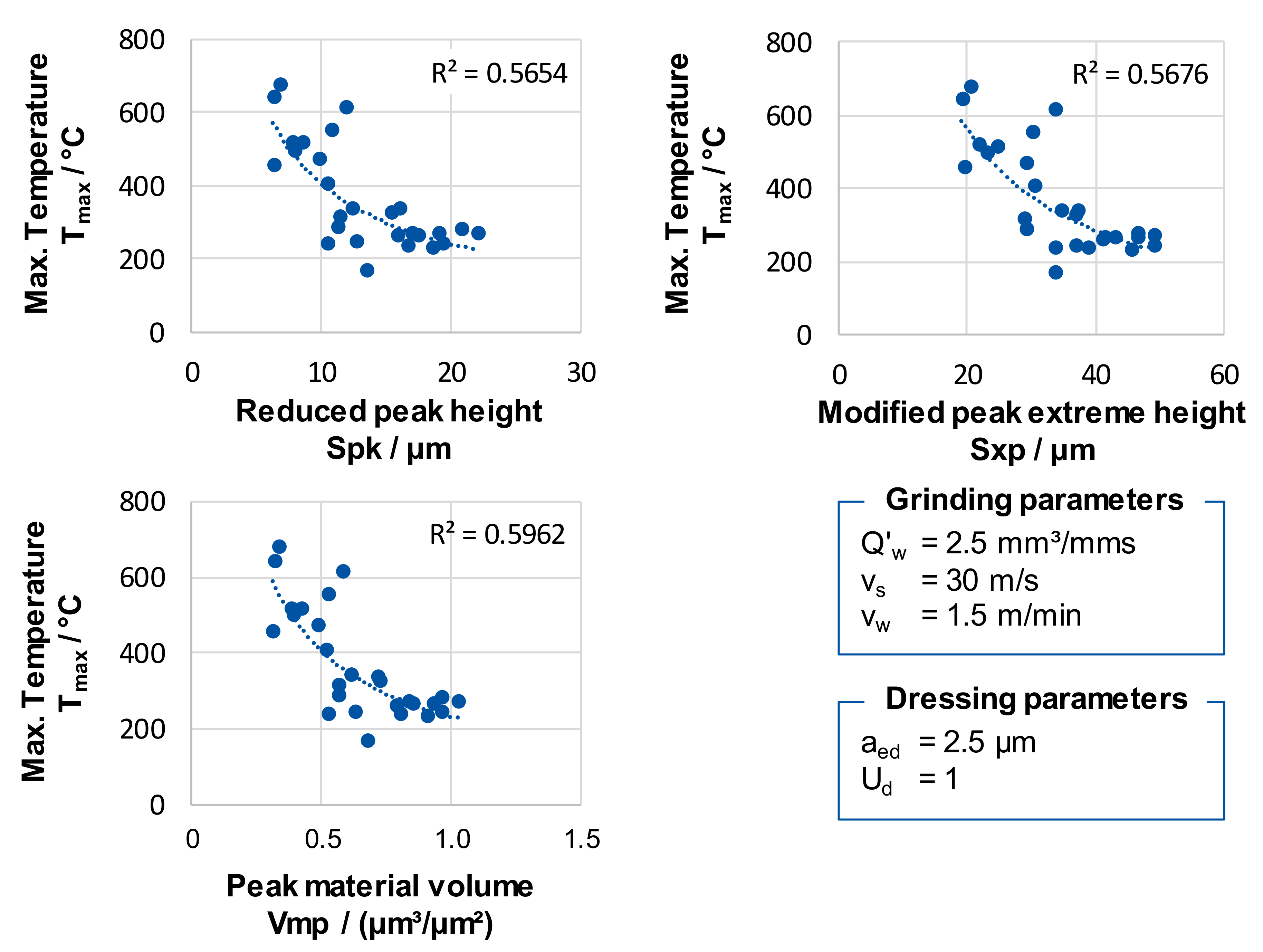
However, topography parameters that describe the characteristics of the peaks of a topography showed correlations with the thermo-mechanical stress collective. The peak extreme height Sxp is the difference of heights at the areal material ratio values p = 0% and q = 50%. The corresponding material portions p and q correlated strongly with the grain protrusion. Influences on the maximum temperature T_max and the occurring grinding forces F_t and F_n were measured. As the grain protrusion increased and the value of Sxp raised, the grinding force and the temperature dropped. The same applied to the relationship between the reduced peak height Spk, which corresponds to the reduced height of the peaks above the core surface, and the grinding forces in the normal and tangential directions.

The peak material volume Vmp describes the material volume for an areal material ratio value of 10%. It corresponds to the volume, which is occupied by the tips of the topography. The larger the volume of the tips, the higher is the protrusion of the grains, or the amount of grains out of the core volume of the topography. If the peak material volume Vmp is small, then the core volume Vmc is correspondingly larger. This is the case if grinding wheels are smooth with a small grain protrusion. In the case of a small grain protrusion, only a small quantity of grinding fluid can enter the contact zone, which influences the contact conditions. As the peak material volume Vmp increased, the tangential grinding force F_t, as well as the maximum temperature T_max, dropped significantly, as presented in Figure 9. The coefficient of determination is in the range of R² = 0.5–0.6. The relatively small R² indicates that the parameters Sxp, Vmp, and Spk influence the thermo-mechanical stress collective, but are likewise not suitable for describing the influence of the grinding wheel topography on the thermo-mechanical stress collective solely.

The feature parameters include the peak density of the surface Spd and the arithmetic mean peak curvature Spc. The peak density Spd indicates the number of roughness peaks of a topography relative to the considered area [10]. This parameter ignores that a large part of the identified tips does not come into engagement because of shading effects during the grinding process. Accordingly, the meaningfulness of this parameter is very low. With regard to the process results, Spc showed a correlation with the maximum grinding force in normal and tangential direction F_n and F_t, as well as to the maximum temperature T_max. The results showed distinctive trends, but the coefficients of determination R² were low. So the feature parameters were not taken into account for detailed investigations. The test results showed a linear correlation between the mean tangential kinematic engagement area Ā_kin,t, and the mean maximum chip thickness h_{cu, max}. This correlation becomes already clear from geometrical considerations. A similar, but lower effect showed an increase of the total tangential kinematic engagement area A_kin,t. The relationship between the average tangential kinematic engagement area Ā_kin,t and the averaged maximum chip thickness h_{cu, max} is described by a linear mathematical function, with a coefficient of determination of R² = 0.6463 (see Figure 10).

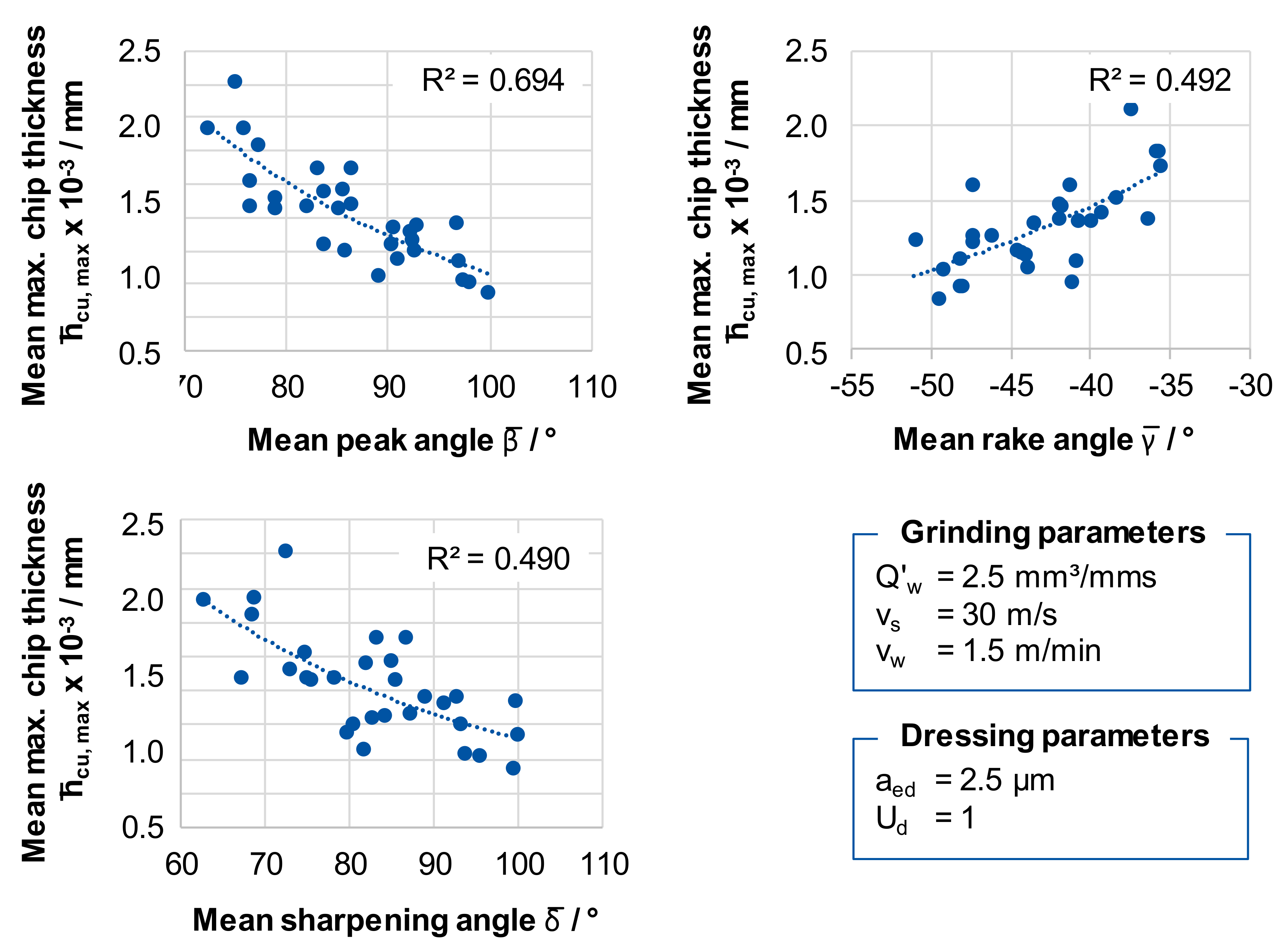
The mean peak angle β, the mean rake angle γ and the mean sharpening angle δ showed a strong influence on the averaged maximum chip thickness h_{cu, max}. The coefficient of determination for a linear relationship between β and h_{cu, max} was about R² = 0.69, which corresponds to a good regression (see Figure 11). Direct connections between the averaged maximum chip thickness h_{cu, max} and the grinding force, as well as the temperature were not detectable. One possible reason is that the calculation of h_{cu, max} solely does not take the different grain protrusions during the investigations into account.

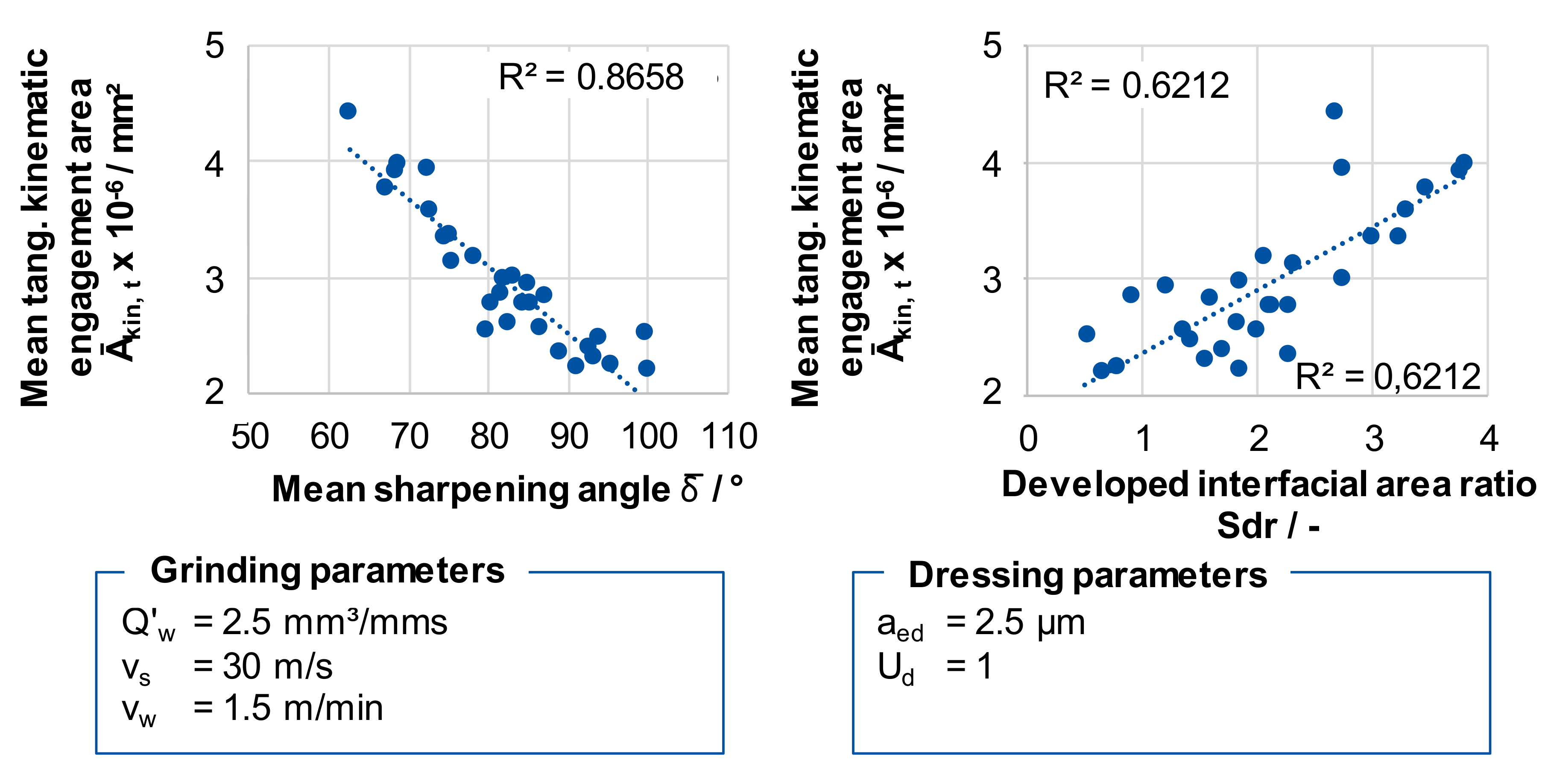
In Figure 12 the relationship between the mean rake angle γ, the developed interfacial area ratio Sdr, and the mean tangential kinematic engagement area Ā_kin,t is shown. A strong correlation prevails between the mean sharpening angle δ and the mean tangential kinematic engagement area Ā_kin,t. An increase in the developed interfacial area ratio Sdr is associated with a rising mean tangential kinematic engagement area Ā_kin,t. Based on these correlations, this means that the mean grain surface contact angle β, γ, and δ as a group, and the topography characteristics Spc, Sdr, and Sdq as a group correlate as well.

The results of the empirical investigations showed that a change of each identified topography parameter group had an influence on the formation of the thermo-mechanical stress collective. However, the results of the investigation also allowed for the conclusion that the thermo-mechanical load in the grinding process is caused by a superposition of the influences of these identified topography parameters. Therefore, the identified topography parameters were investigated in combination.

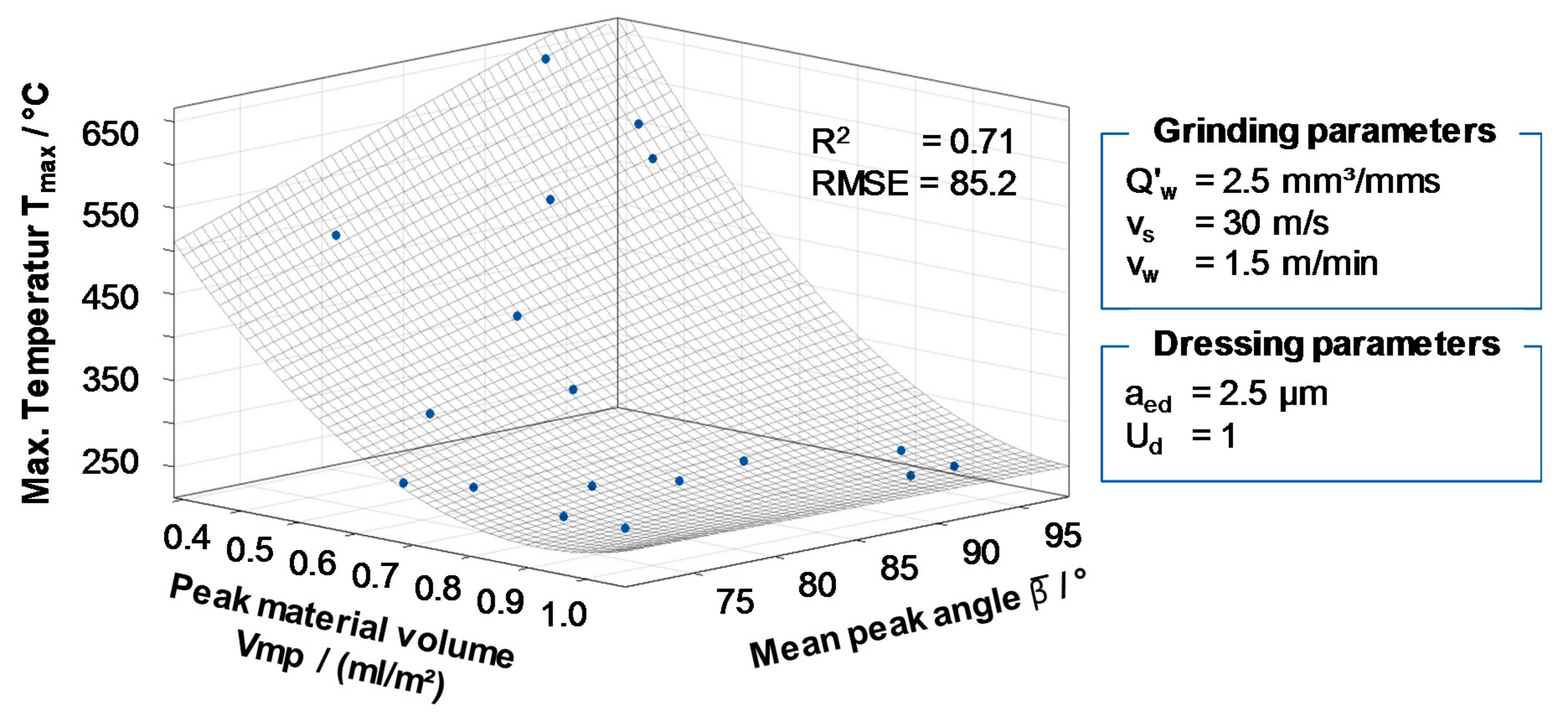
In this context, Figure 13 shows the measured maximum grinding temperature T_max depending on the peak material volume Vmp and the mean peak angle β. The results showed that the maximum grinding temperature T_max decreased strongly with an increasing mean peak material volume Vmp. However, the results show that topographies with a similar peak material volume Vmp did not necessarily lead to a similar maximum grinding temperature T_max. By a combined examination of the mean peak material volume Vmp and the mean peak angle β in Figure 13, it can be seen that the fluctuating maximum grinding temperatures at almost constant Vmp can be attributed to the geometry of the kinematic peak angles. If, for example, the mean peak angle β increased, the maximum grinding temperature T_max increased significantly with a constant peak material volume Vmp. This was especially noticeable at low values of the mean peak material volume Vmp. An increase of the mean peak angle from β = 75° to β = 95° at a constant mean peak material volume of Vmp = 0.4 led to an rising maximum grinding temperature T_max from nearly 500 °C to more than 650 °C. With increasing Vmp, the influence of the angle decreased. It can be assumed that the influence of the mean peak angle β decreased with increasing Vmp, since additional chip space allowed for an increased dissipation of the process heat. The dependence of the grinding temperature on the grinding wheel topography could be approximated with the help of the two parameters with a coefficient of determination of R² = 0.71 and a root mean square error of 85.2, which corresponds to a good accuracy.

4. Discussion of the Results

Based on the presented evaluations, it can be summarized that three groups, which correlated with the temperature and force during the grinding process, with each three characteristic parameters were identified. The first group, consisting of the developed interface area ratio Sdr, the arithmetic mean peak curvature Spc, and the root mean square gradient Sdq describes the shape of the roughness on the grinding wheel surface. An increase of these parameters resulted in a reduction of the normal grinding force F_n and the maximum grinding temperature T_max. The second topography parameter group, consisting of the grain engagement angles mean peak angle β, the mean sharpening angle δ, and the mean rake angle γ, as well as the kinematic grain surface area in tangential and normal direction A_kin,t and A_kin,n showed a strong correlation with the mean maximum chip thickness h_{cu, max}. In addition, they slightly correlated with the first named group. The third group of topography parameters includes functional parameters, which describe the material proportions of the topography by means of the abbott-curve; the reduced peak height Spk, the peak material volume Vmp, and the peak extreme height Sxp. These topography parameters correlated strongly with each other, but did not show any correlation with other parameters. A change of these parameters had a very strong influence on the grinding forces and the temperature. Figure 14 shows a summary of the previously identified groups, which have a strong influence the thermo-mechanical stress collective.

By a combined consideration of the influence of these three groups, the thermal loads in the grinding process were approximated with a high degree of accuracy. Thus, the maximum measured grinding temperature T_max could be approximated with the help of the parameters peak material volume Vmp and the mean peak angle β with a coefficient of determination of R² = 0.71, which corresponds to a good value, due to the high complexity in grinding technique. The research results show that by means of the identified topography parameters, it was possible to describe the influence of the topography’s geometry on the thermo-mechanical stress collective based on only few geometrical parameters quantitatively. Further investigations should confirm and extend these results.

5. Conclusions

The aim of the investigations was to identify the influence of the grinding wheel topography on the thermo-mechanical stress collective during the grinding process, and to determine the topography parameters by which the influence of the topography on the thermo-mechanical stress collective can be described quantitatively. For this purpose, empirical-analytical examinations with different grinding wheels were performed. A high variation of topographies was realized by means of 13 different grinding wheel specifications and by varied dressing and sharpening strategies.

• During empirical investigations, topography parameters could be identified and classified into groups that had an influence on the thermo-mechanical stress collective
• Each group combines topography parameters, which had the same influence on the formation of the thermo-mechanical stress collective (Figure 14).
• The isolated consideration of these groups, however, did not provide a clear explanation of the dependence of the thermal and mechanical loads in the grinding process on the grinding wheel topography.
• The combined consideration of the groups around the topography parameters peak material volume Vmp and mean peak angle β allowed for the quantitative description of the dependence of the thermo-mechanical stress collective on the geometry of the grinding wheel topography. So, it became possible to describe the influence of the topography on the stress collective during grinding by a few topography parameters for the first time quantitatively.

In further investigations, the influence of the dressing overlap ratio, as well as the volumetric composition and the related machining volume on the grinding wheel topography and its kinematic components, as well as on the grinding process result will be investigated.