Control of the Acrobot with Motors of Atypical Size Using Artificial Intelligence Techniques
Abstract
:1. Introduction
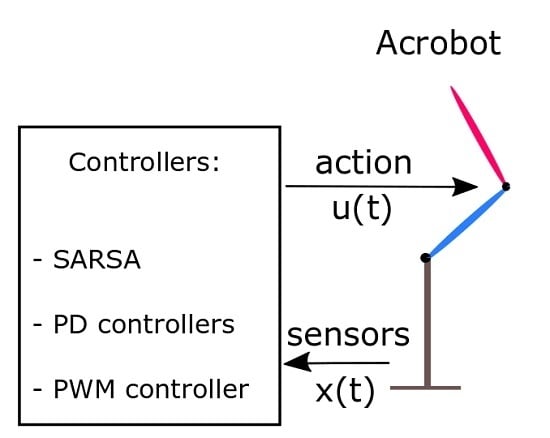
2. Acrobot Model
3. Control Methods
3.1. State-Action-Reward-State-Action (SARSA) Controller
| Algorithm 1: SARSA algorithm |
 |
3.2. Proportional–Derivative (PD) Controller
3.3. Pulse-Width Modulation (PWM) Controller
4. Results
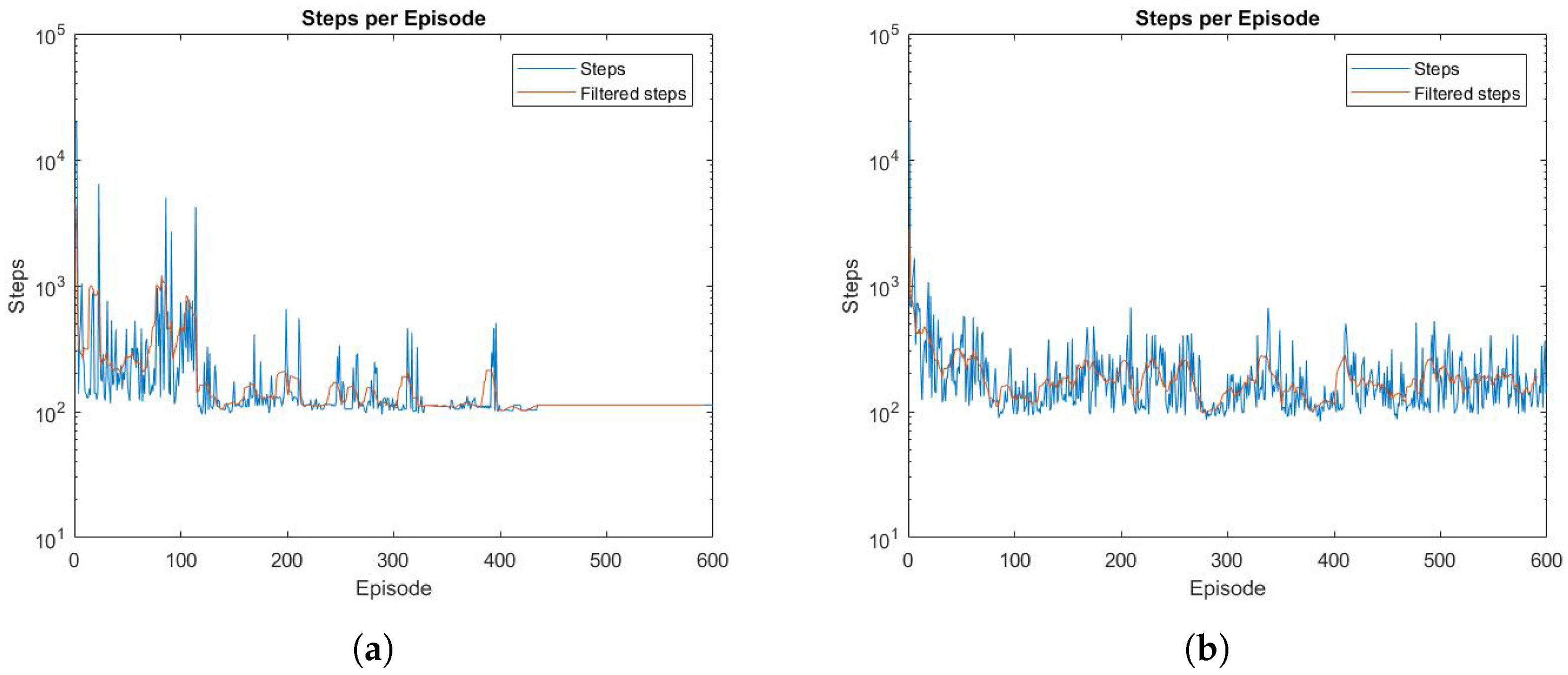
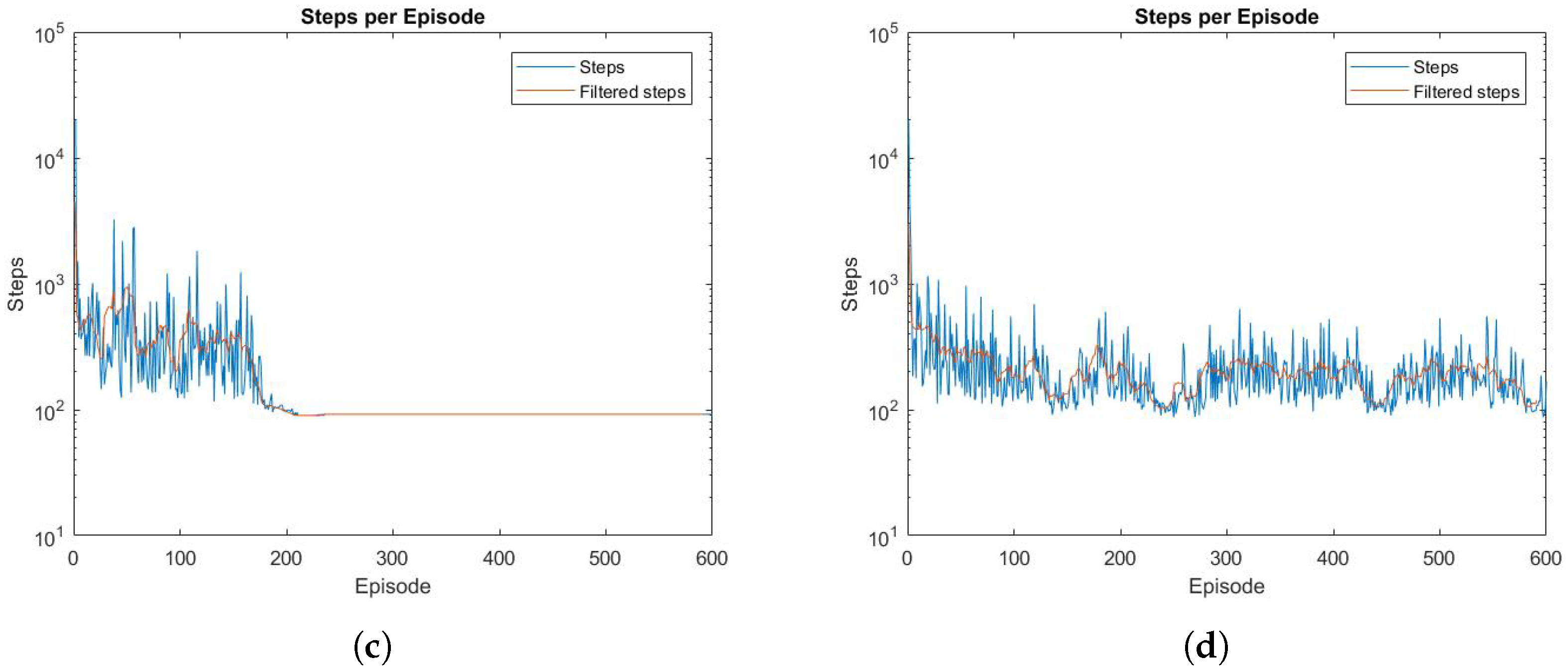
4.1. SARSA
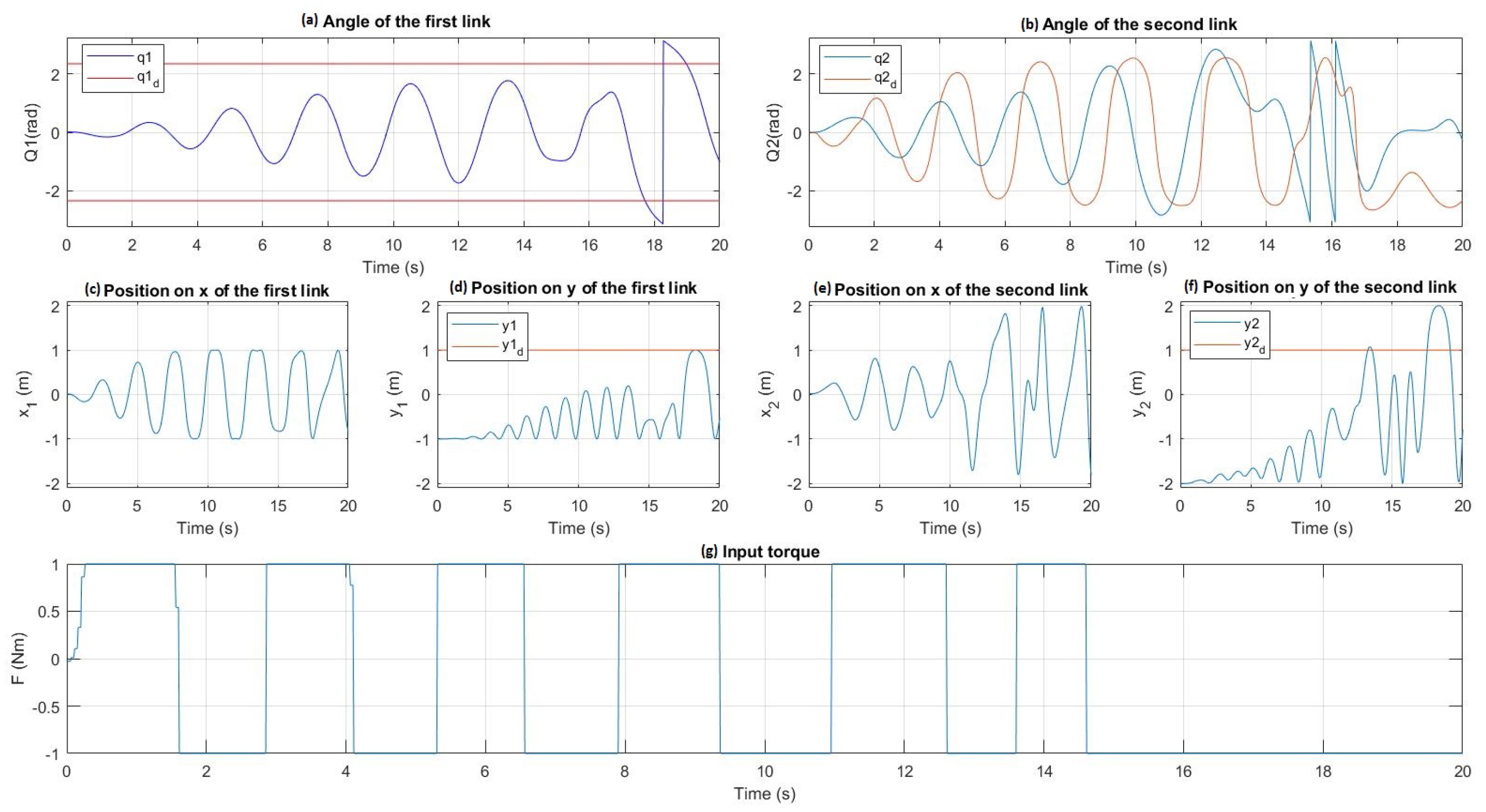
4.2. PD Controller
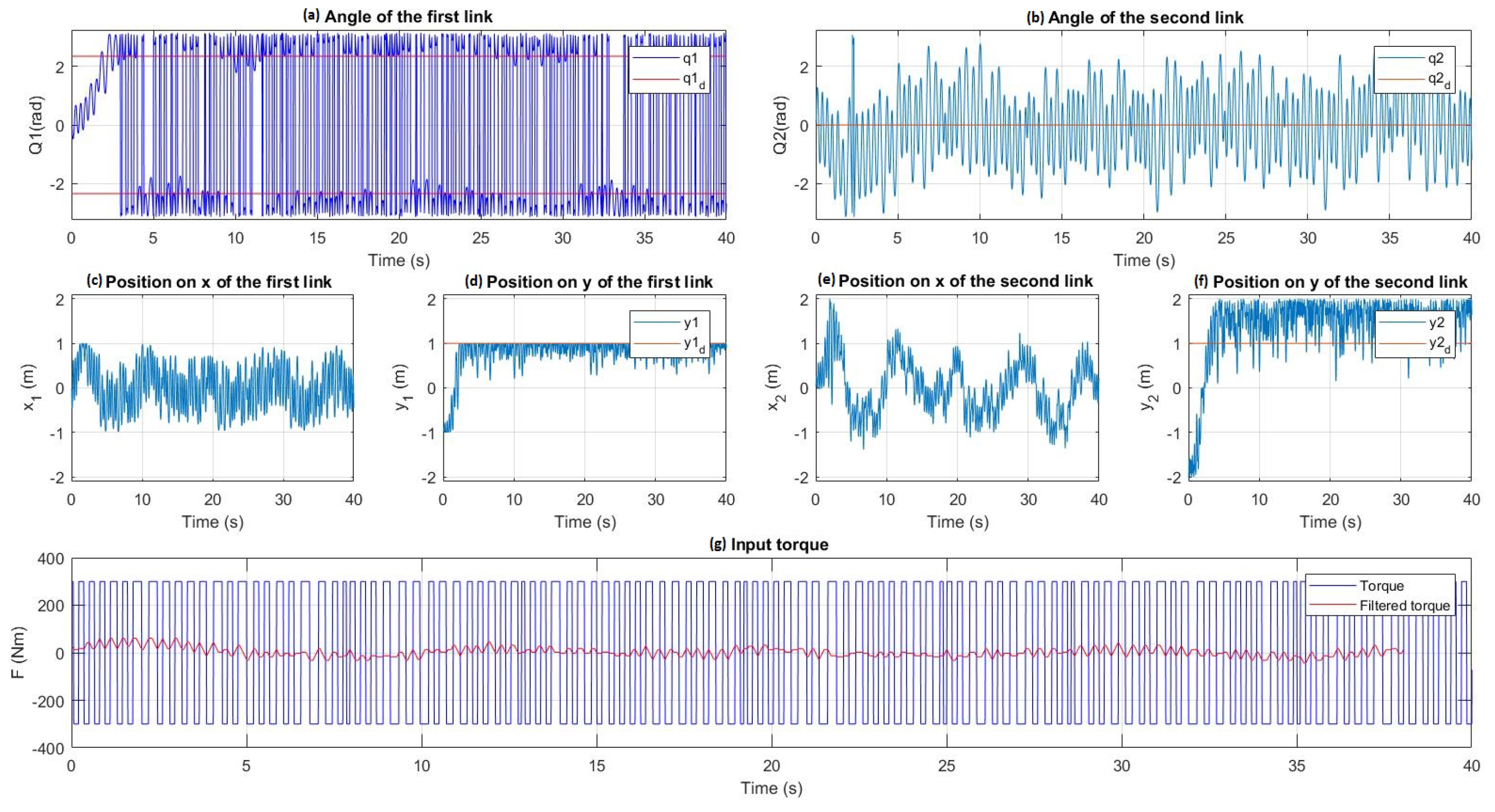
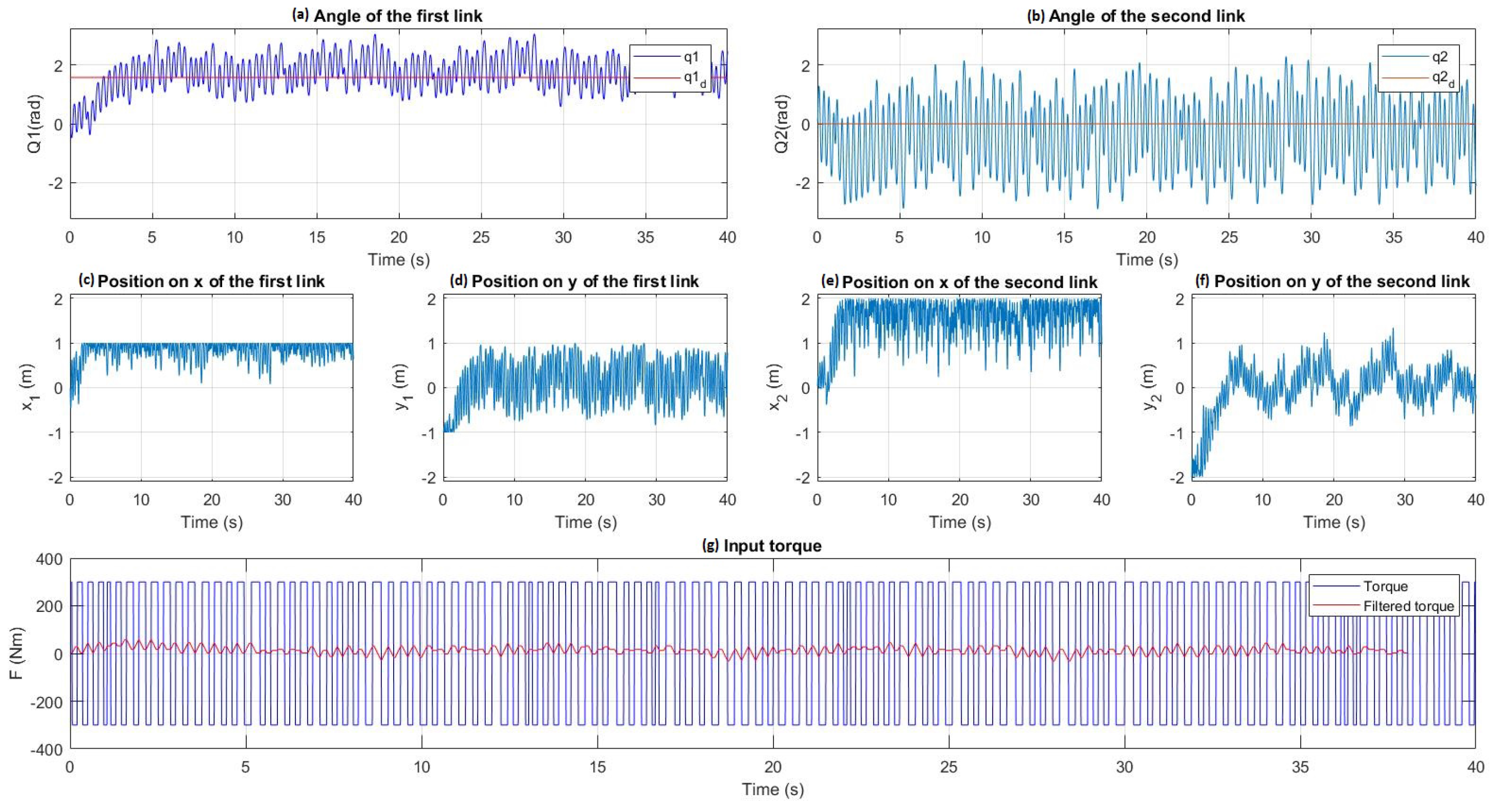
4.3. PWM Controller
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Fantoni, I.; Lozano, R.; Spong, M. Energy based control of the Pendubot. IEEE Trans. Autom. Control 2000, 45, 725–729. [Google Scholar] [CrossRef]
- Boone, G. Minimum-time control of the Acrobot. Proc. Int. Conf. Robot. Autom. 1997, 4, 3281–3287. [Google Scholar]
- Brown, S.C.; Passino, K.M. Intelligent Control for an Acrobot. J. Intell. Robot. Syst. 1997, 18, 209–248. [Google Scholar] [CrossRef]
- Duong, S.C.; Kinjo, H.; Uezato, E. A switch controller design for the acrobot using neural network and genetic algorithm. In Proceedings of the 10th IEEE International Conference on Control, Automation, Robotics and Vision, Hanoi, Vietnam; 2008; pp. 1540–1544. [Google Scholar]
- Duong, S.C.; Kinjo, H.; Uezato, E.; Yamamoto, T. On the continuous control of the acrobot via computational intelligence. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Tainan, Taiwan, 24–27 June 2009; pp. 231–241. [Google Scholar]
- Horibe, T.; Sakamoto, N. Swing up and stabilization of the acrobot via nonlinear optimal control based on stable manifold method. IFAC-PapersOnLine 2016, 49, 374–379. [Google Scholar] [CrossRef]
- Mahindrakar, A.D.; Banavar, R.N. A swing-up of the acrobot based on a simple pendulum strategy. Int. J. Control 2005, 78, 424–429. [Google Scholar] [CrossRef]
- Nichols, B.D. Continuous action-space reinforcement learning methods applied to the minimum-time swing-up of the acrobot. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, SMC 2015, Hong Kong, China, 9–12 October 2016; pp. 2084–2089. [Google Scholar]
- Spong, M.W. The swing up control problem for the acrobot. IEEE Control Syst. 1995, 15, 49–55. [Google Scholar] [CrossRef]
- Sutton, R.S. Generalization in reinforcement learning: Successful examples using sparse coarse coding. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 2–5 December 1996; pp. 1038–1044. [Google Scholar]
- Tedrake, R.; Seung, H.S. Improved dynamic stability using reinforcement learning. In Proceedings of the International Conference on Climbing and Walking Robots (CLAWAR), Paris, France, 25–27 September 2002; pp. 341–348. [Google Scholar]
- Ueda, R. Small implementation of decision-making policy for the height task of the acrobot. Adv. Robot. 2016, 30, 744–757. [Google Scholar] [CrossRef]
- Wiklendt, L.; Chalup, S.; Middleton, R. A small spiking neural network with LQR control applied to the acrobot. Neural Compu. Appl. 2009, 18, 369–375. [Google Scholar] [CrossRef]
- Yoshimoto, J.; Ishii, S.; Sato, M.A. Application of reinforcement learning to balancing of acrobot 3 Nara Institute of Science and Technology 33 ATR Human Information Processing Research Laboratories. Sci. Technol. 1999, 5, 516–521. [Google Scholar]
- Zhang, A.; She, J.; Lai, X.; Wu, M. Global stabilization control of acrobot based on equivalent-input-disturbance approach. Control 2011, 44, 14596–14601. [Google Scholar] [CrossRef]


| Parameters | Real Value | Meaning of the Parameter |
|---|---|---|
| 1 kg | Mass of the first link | |
| 1 kg | Mass of the second link | |
| 1 m | Distance from the beginning to the end of the first link | |
| 1 m | Distance from the beginning to the end of the second link | |
| 0.5 m | Distance from the beginning to the center of mass of the first link | |
| 0.5 m | Distance from the beginning to the center of mass of the second link | |
| 1 kg × m2 | Inertia of the first link | |
| 1 kg × m2 | Inertia of the second link | |
| g | 9.8 m/s2 | Gravity |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mier, G.; Lope, J.D. Control of the Acrobot with Motors of Atypical Size Using Artificial Intelligence Techniques. Inventions 2017, 2, 16. https://doi.org/10.3390/inventions2030016
Mier G, Lope JD. Control of the Acrobot with Motors of Atypical Size Using Artificial Intelligence Techniques. Inventions. 2017; 2(3):16. https://doi.org/10.3390/inventions2030016
Chicago/Turabian StyleMier, Gonzalo, and Javier De Lope. 2017. "Control of the Acrobot with Motors of Atypical Size Using Artificial Intelligence Techniques" Inventions 2, no. 3: 16. https://doi.org/10.3390/inventions2030016
APA StyleMier, G., & Lope, J. D. (2017). Control of the Acrobot with Motors of Atypical Size Using Artificial Intelligence Techniques. Inventions, 2(3), 16. https://doi.org/10.3390/inventions2030016