Abstract
In optical fabrication, brittle-hard materials are used for numerous applications. Especially for high-performance optics for laser or lithography applications, a complex and consistent production chain is necessary to account for the material properties. Particularly in pre-processing, e.g., for shaping optical components, brittle material behavior is dominant which leads to a rough surface layer with cracks that reach far below the surface. This so called subsurface damage (SSD) needs to be removed in subsequent processes like polishing. Therefore, it is essential to know the extent of the SSD induced by shaping for an efficient design of precise corrective processes and for process improvement. Within this work the influence of cutting speed on SSD, in fused silica, induced by grinding has been investigated. To analyze the subsurface crack distribution and the maximum crack depth magnetorheological finishing has been appointed to polish a wedge into the ground surface. The depth profile of SSD was analyzed by image processing. For this purpose a coherent area of the polished wedge has been recorded by stitching microscopy. Taking the form deviation of the ground surface in to account to determine the actual depth beneath surface, the accuracy of the SSD-evaluation could be improved significantly. The experiments reveal a clear influence of the cutting speed on SSD, higher cutting speeds generate less SSD. Besides the influence on the maximum crack depth an influence on the crack length itself could be verified. Based on image analysis it was possible, to predict the maximum depth of cracks by means of crack length.
1. Introduction
Grinding is still an indispensable process step in the manufacturing of high precision optics, due to its high removal rates and well-controlled shaping. However, due to the prevailing material removal mechanisms, the grinding of brittle materials inevitably leads to microscopic cracks beneath the surface. This so called subsurface damage (SSD) influences the operability and lifetime of high-performance optics like semiconductor or high power laser applications [1,2]. The shaping process by grinding is followed by various corrective processes like polishing for smoothing the surface, improving the shape accuracy and removing SSD. The maximum crack depth at each process step decisively determines the extent of the polishing and corrective processes required and thus the costs of the overall optic manufacturing process [3]. According to this, a main issue in the production of high performance optics is to minimize the process-related SSD in grinding.
The undefined cutting edge and brittle material removal behavior make grinding a stochastic process. Single grains with high protrusions lead to a local overload of the normal force and cause the deepest cracks [4]. For fine-grained diamond grinding wheels the influencing variables grain protrusion and number of active grains cannot be determined directly, therefore it is nearly impossible to model the grinding process or to predict SSD. Thus, the process design for optics manufacturing still depends on empirical data. To date, the grain size serves as an orientation [5]. The stability of grinding processes as well as the accuracy in ascertaining the maximum depth of SSD is essential for increasing the efficiency in optics manufacturing. The same counts for the investigation of the influencing variables on the process-induced SSD. The accuracy of the evaluation is even more important for fine grinding where crack depths are only a few micrometers.
Nature and extent of subsurface damage in glasses makes quantitative assessment of damage difficult [6]. To date, it is still challenging to determine subsurface damage in optical glasses. Since the measurement of SSD with destructive methods is complex as well as cost-intensive and time-consuming, several attempts were undertaken to correlate process parameters and measurable output values, like surface roughness. The results of Lambropoulos et al. and Wang et al. show, however, a broad distribution in the results of these methods [7,8]. Even though there are numerous non-destructive approaches to determine the crack depths beneath the machined surface, the destructive methods still provide the most accurate results [7]. Over the past few years, the combination of magnetorheological finishing (MRF) and etching has proven to be the most appropriate strategy [7,8]. MRF provides a highly deterministic material removal process without generating new or propagating existing SSD [9]. The subsequent etching process serves to open the cracks on the polished surface to provide a better contrast in optical imaging. The damage free polishing of a wedge allows for a glance under the ground surface. Thus, not only the maximum crack depth can be determined, but also the density and shape of cracks can be observed at different depths. Resolution of this analysis obviously depends on the wedge gradient, as the area increases with decreasing wedge angles.
Simple investigations of SSD by MRF technique are limited to the determination of the maximum crack depth [10,11]. Miller et al. first analyzed the depth profile of the crack density by single micrographs along the wedge [4]. To enable analysis for a larger wedge area, adjacent microscope images were stitched by using a computer-based microscope system with a driven stage [8]. This method offers the great advantage, to analyze the recorded data by image processing. The SSD depth is calculated from the difference in height between the profiles of the ground surface and the wedge surface. In previous publications, a perfect initial surface was assumed, however, even fine grinding generates form deviations of a few micrometers. For rough cuts and pre-shaping this seems negligible, but in the case of fine grinding these deviations can be on the same scale as the SSD.
Within this work, the influence of cutting speeds on SSD for ground fused silica was investigated. To analyze the maximum crack depth and crack distribution MRF technique was used in conjunction with dry etching. Finally, for the first time, the initial surface profile was considered to enhance the accuracy to determine the actual crack depth.
2. Materials and Methods
Fused silica samples with a diameter of 100 mm were ground on an ultraprecision 5-axis grinding machine (Nanotech 500 Freeform Generator, Moore Nanotechnology Systems). The experiments comprise a variation of cutting speeds between 30 and 62 m/s, in five subdivisions, with three repetitions (Table 1). For process monitoring, the grinding forces were measured by a multicomponent dynamometer (CompactDyn, Kistler, Winterthur, Switzerland) mounted beneath the hydrostatic grinding spindle. The grinding kinematics is shown in Figure 1.

Table 1.
Process parameters.
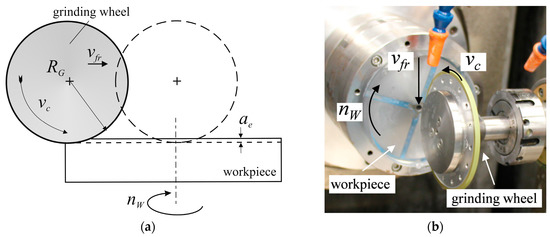
Figure 1.
(a) Grinding kinematics—cross grinding with rotating workpiece; (b) Machine setup.
A resin bonded diamond grinding wheel with a diameter of 100 mm, D20 (C70) was applied. All samples were ground with a constant rotary worktable speed nW = 50 rpm and radial feed vfr = 10 mm/s. Based on a fine grinding process, the material removal was conducted in four passes with 20 µm and one final pass with 10 µm depth of cut. In order to guarantee a uniform initial state, all samples were pre-ground to plane shape before running the actual experiments (pre-processing, ae = 100 µm; four passes with 25 µm). Furthermore, the grinding wheel was dressed and balanced before each grinding experiment. This ensures that the measured SSD results from the actual process parameters.
3. Results
3.1. Grinding Force and Surface Roughness
Based on the constant rotary worktable speed, the feed rate decreases continuously from edge to center. Since the remaining parameters are kept constant, this leads to a reduction in material removal rate and thus a reduction in chip thickness. Consequently, normal forces (Figure 2a) and roughness decrease from edge to center. In conventional grinding, it is generally assumed that higher cutting speeds lead to a lower chip thickness and thus also to lower grinding forces [12]. In the experiments presented in this work, however, the opposite is shown. Larger cutting speeds led to higher normal forces (Figure 2b). For brittle materials like fused silica, the removal mechanisms depend on the chip thickness. Due to a higher rate of ductile material removal, the forces increase with the cutting speed [13]. To make the results comparable and regarding the position of the maximum crack depth cmax at the MRF wedge, the presented values were obtained at a distance of 15 mm from workpiece center.
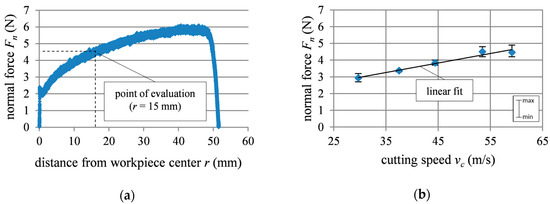
Figure 2.
(a) Typical force curve (Fn) at vc = 62 m/s) for constant worktable speed nW; (b) Normal forces for different cutting speeds (distance from workpiece center 15 mm).
The surface roughness was measured by white light interferometry (WLI, Talysurf CCI HD, Taylor Hobson) with 20× magnification. Along circles of different radii six spots with an area of 840 × 840 µm2 were measured with an angular distance of 60°. To exclude the waviness of the surface a long pass filter was set to 250 µm.
The results of the roughness measurement (e.g., in Figure 3) show an opposite trend towards normal force. This agrees well with the assumption that the proportion of ductile material behavior increases with higher cutting speeds.
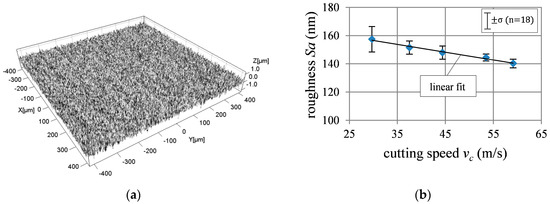
Figure 3.
(a) White light interferometer (WLI) measurement (20× magnification): 2D-surface roughness (vc = 30 m/s, Sa = 160 nm); (b) Surface roughness Sa for different cutting speeds (distance from workpiece center 15 mm) with linear fit.
3.2. Subsurface Damage Evaluation
For the evaluation of subsurface damage, the micrographs of the MRF wedge need to be merged with the depth profile. In order to maintain a high accuracy, the samples were provided with a fiducial mark by laser engraving after grinding. It is thus possible to align the samples for different measurements and to link the data of tactile measurements and microscope images. Figure 4 shows the wedge geometry and the entire evaluation procedure.
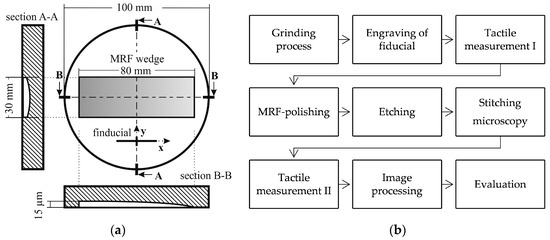
Figure 4.
(a) Position and geometry of the magnetorheological finishing (MRF) wedge; (b) Sample processing chain.
After MRF preparation, the wedge surfaces were dry etched. Compared to wet etching the material removal by dry etching can be controlled with a sub-micron precision [14]. The micrographs of the wedge surface were taken with a ZEISS Axio Imager.Z2 Vario with 500× magnification. 750 micrographs were stitched together to an interrelated area of 40 × 1 mm2. To minimize contamination from particles the samples were cleaned in an ultrasonic bath and microscopy was carried out under clean room conditions (ISO 7). In order to determine the actual depth of the wedge as accurately as possible, the distance between the ground surface (tactile measurement I) and the wedge surface (tactile measurement II) was calculated from the two tactile measurements.
Due to the form deviation, differences between the polished wedge surface and the actual depth profile of up to 2 μm (Figure 5) occur in the individual experiments. This is particularly relevant for fine grinding processes with low SSD. Within the experiments, the differences correspond to 30–40% of the measured maximum crack depth.
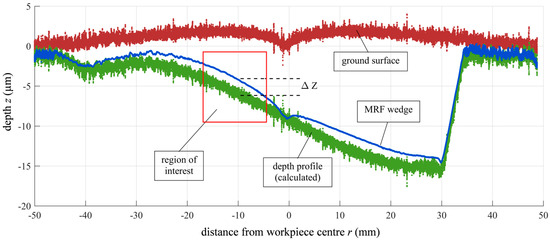
Figure 5.
Tactile measurement of ground surface, MRF wedge and depth profile.
The number of cracks decreases with depth along the MRF wedge. With increasing depth of the wedge, more and more cracks are removed by polishing until the last fracture event can be determined as the maximum crack depth in the micrographs (Figure 6).
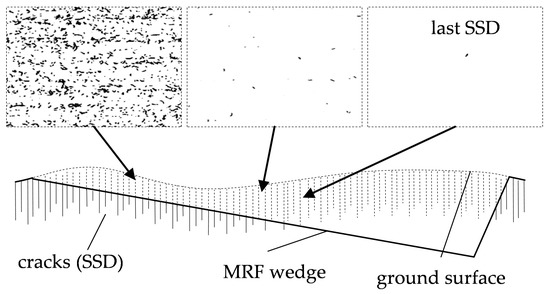
Figure 6.
Sketch of subsurface damage (SSD) appearance along the MRF wedge.
To determine the maximum crack depth cmax the lateral position of the last defect on the micrograph of the polished and etched wedge surface is merged together with the corresponding information of the calculated depth profile (Figure 7).
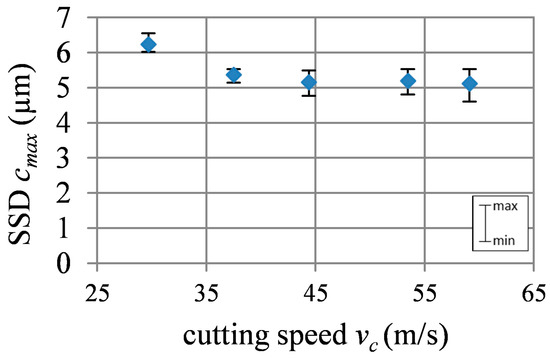
Figure 7.
Maximum crack depth depending on the cutting speed.
3.3. SSD Analysis by Image Processing
Besides the evaluation of the maximum crack depth, the micrographs of the MRF wedge provide the opportunity to examine the crack distribution with increasing depth. Thus, a more extended examination on the influence of process parameters on grinding results is possible. The high number of cracks resulting from the size of the inspected wedge area requires a software-supported evaluation. Therefore the open source software, ImageJ, has been utilized. The software is a highly popular tool in biology in a wide range of applications and provides a segmentation algorithm. This enables the analysis of the position and the geometrically relevant data for each individual crack on the stitched microscope image. After binarization of the images, the cracks appear as uniform black lines on a white background. To specify the crack length, a best fit ellipse is applied to every single crack (Figure 8).
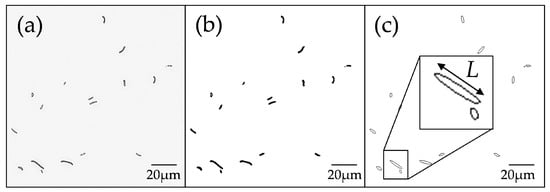
Figure 8.
SSD-Image Processing (ImageJ): (a) raw microscopy data; (b) binary conversion; (c) determination of crack length L by best fit ellipse.
On average, 150,000 cracks were evaluated for each sample with this method. Figure 9 shows the ratio of the number of cracks of different lengths to the total crack number (relative frequency) for different cutting speeds.
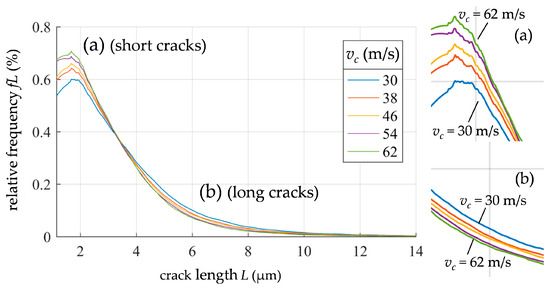
Figure 9.
Relative frequencies of the crack length L (filtered data).
4. Discussion
4.1. Maximum Crack Depth
Typically, the crack density decreases along the wedge, i.e., with increasing depth, following a power law function [15]. At the scale of the surface roughness, the individual cracks intersect and Suratwala et al. describe this as the rubble zone. A few microns below the surface, the cracks can be detected individually. Within our experiments, with the given MRF wedge geometry, the lateral distance between the last cracks could be up to 500 µm. This underlines the importance of size and the slope of the polished wedge.
After an initial decrease in the maximum crack depth with an increasing cutting speed, a seemingly constant depth is obtained above 45 m/s (Figure 7). Besides chip thickness reduction, higher spindle speeds and resulting higher cutting speeds lead to stronger vibrations [16]. This may explain why there is no further improvement of the maximum SSD-depth at cutting speeds higher than 45 m/s. The single-grain load, as the main cause for SSD, seems to be confirmed. In theory, the influence of the material removal rate and thus process parameters such as cutting speed, feed rate and infeed can be easily assessed. In practice, however, the stochastic nature of the grinding wheel as well as other influences such as limited machine rigidity have influence on the maximum crack depth.
Miller et al. have shown that the addition of a small amount of larger grains to a fine slurry for polishing leads to a significant increase in the measured crack depth [4]. The normal force is distributed to a smaller number of particles than in a homogeneous particle distribution and the maximum individual grain loads are increased. In the grinding process, the effective grain size corresponds to the individual grain protrusion, which directly depends on the grain size.
The individually polished and etched wedge surfaces differ considerably, in crack distribution. Figure 10 shows samples with low and high maximum crack depths. The sample with low SSD shows a rather arbitrarily arranged crack pattern (Figure 10a), whereas in case of significantly larger SSD (Figure 10b), the ordered crack formation is particularly remarkable. Large protrusion of individual grains leads to higher individual loads. As a result, it is not possible to assess the process results by means of maximum SSD only in conjunction with the cutting speed e.g., vibrations or variation in grain protrusion.

Figure 10.
Micrograph of the MRF wedge surface after etching: (a) sample with low SSD (vc = 54 m/s; cmax = 4.6 µm); (b) sample with larger SSD (vc = 30 m/s; cmax = 6.8 µm).
As stated above, the maximum crack depth cmax results from one particular or only a few grains. It is thereby subject to a certain variation by the nature of the microstructure of the grinding wheel and the grinding process. Both, crack depth and crack length, depend directly on the grain load. The maximum crack depth cmax should therefore also lead to the maximum crack length Lmax. Within the experiments Lmax shows a linear decay with depth. Figure 11 shows Lmax at intervals of 50 µm along the polished wedge. To avoid the influence of outliers by intersecting cracks on the linear fit, the double median crack length LMdn is set as cut-off criteria.
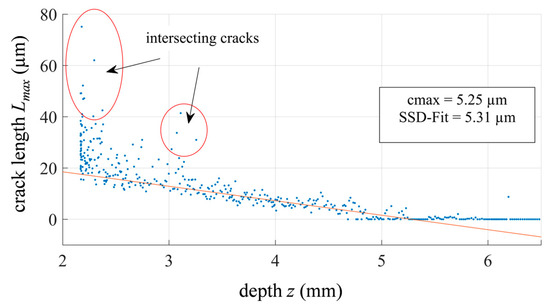
Figure 11.
Maximum crack lengths Lmax as a function of depth (vc = 54 m/s) with linear fit.
The zero point of the fit provides a very good correlation with the measured maximum crack depths (Figure 12).
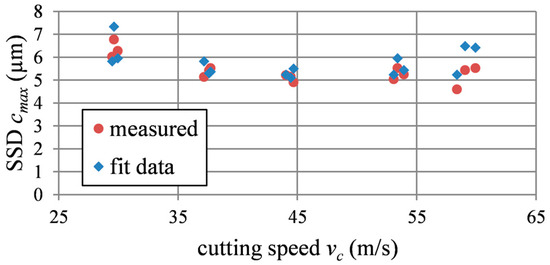
Figure 12.
Measured and calculated maximum crack depths.
4.2. Fracture Mechanics
Determination of the exact surface topography of a grinding wheel is difficult, even for coarse-grained tools. Furthermore, the surface changes continuously by wear or is completely reshaped by dressing. Therefore, attempts are often made to simplify the grinding process by single grain scratch behavior. The basis for most of the considerations is the work of Lawn, who investigated the cracking mechanisms of brittle materials under indentation [17]. His experiments showed the formation of median and lateral cracks as a function of loading and unloading on the workpiece surface. He showed that the maximum radial crack length cr correlates with the load on the indenter, i.e., P~cr3/2[18].
With the indentation constant χr (0.046 for fused silica [19]), indenter load P, fracture toughness KIc, hardness H and Young′s modulus E.
Due to the stochastic nature of the microtopography of grinding wheels, loads on a single grain can not be determined. Equation 1, nevertheless, reveals the maximum grain load to be calculated from the maximum radial crack length cr, which corresponds to the maximum crack depth cmax.
Using equation 2 and the measured maximum crack depths (Figure 7), the maximum individual grain loads P are about 0.2 N for the grinding wheel applied in this work. This corresponds to approximately 5% of the measured average normal force. In addition to the evaluation of the maximum crack depth, the wedge method also makes it possible to determine the crack length L on the polished surface. Based on the Hertzian indentation mechanics Miller et al. found a correlation between average crack length and max crack depth [4].
Assuming that the diamond grains are idealized spherical abrasives the circles of contact are defined by the Hertzian contact zone, with the contact circle radius a.
With the elastic mismatch factor k, the applied load P and the radius of the abrasive r. The factor k relates to the different Young′s moduli and Poisson′s ratio ν of the workpiece and indenter material, where the primes refer to the indenter.
In contrast to static indentation, a sliding indenter causes an asymmetry in the tensile stress field. Since the tensile stresses are relatively small near the front end of the indenter the likelihood of cone cracks increases in this region. This also predicts that the crack may not completely encircle the entire contact radius [20]. Miller et al. assumed that the crack propagates over only a quarter of the contact circumference.
Finally, the calculated crack length Lcalc as a function of cmax according to Equations (2) and (5) shows appropriate accordance with the determined average crack length LMdn from the optical evaluation (Figure 13).
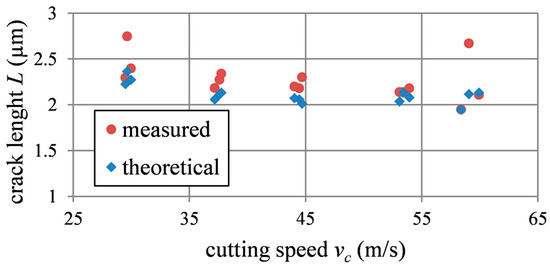
Figure 13.
Measured and calculated crack length for different cutting speeds.
5. Conclusions
To date there is no alternative to the destructive techniques for the evaluation of SSD in optical glasses. By using modern stitching microscopes and image processing, the MRF wedge method offers the highest accuracy in the determination of crack distribution and maximum crack depth. Furthermore, a thorough investigation of the removal mechanisms of the grinding process of optical glasses is enabled.
Within this work subsurface damage (SSD) was directly determined by the MRF wedge technique for a series of fused silica ground with different cutting speeds from 30 to 62 m/s. To improve the accuracy of the SSD evaluation method wet etching was replaced by dry etching. Furthermore, the form deviation of the ground surfaces was taken into account to determine the actual crack depth. Thus, a significant influence of the cutting speed on SSD for a fine grinding process, as it is found in process chains of optical fabrication, could be demonstrated. With stitching microscopy and image processing the gapless evaluation of the density of cracks and the distributions of crack lengths along the wedge surface has been implemented. Thus, a dependency of the crack length distribution on the cutting speed could be confirmed. Based on the model of Miller [4], the relation between calculated crack length Lcalc as a function of cmax and median crack length LMdn could be demonstrated for SSD of only a few microns. Furthermore, a relationship between the maximum crack length as a function of depth and the maximum crack depth could be found. This and the different crack patterns of the SSD samples supports the thesis that the maximum crack depth is caused by a few individual grains that also produce the largest crack length.
Author Contributions
Georg Schnurbusch, Ekkard Brinksmeier and Oltmann Riemer designed the experiments; Schnurbusch performed the experiments and materials investigation; Georg Schnurbusch and Oltmann Riemer analyzed the data. Ekkard Brinksmeier contributed the experimental infrastructure; Georg Schnurbusch, Ekkard Brinksmeier and Oltmann Riemer discussed the results and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| a | Hertzian contact circle radius | LMdn | average crack length (median) |
| ae | depth of cut | MRF | magnetorheological finishing |
| cmax | maximum crack depth | ν | Poisson’s ratio (workpiece) |
| cr | radial crack length | ν’ | Poisson’s ratio (indenter) |
| E | Young’s Modulus (workpiece) | nW | worktable speed |
| E’ | Young’s Modulus (indenter) | P | indenter load |
| fL | relative frequency | R | grain size (radius of the abrasive) |
| Fn | normal force | Sa | average surface area roughness |
| H | hardness | SSD | subsurface damage |
| K | mismatch factor | vc | cutting speed |
| KIc | fracture toughness | vfr | radial feed |
| L | crack length | WLI | white light interferometer |
| Lcalc | calculated crack length | χr | indentation constant |
| Lmax | maximum crack length |
References
- Hed, P.P.; Edwards, D.F.; Davis, J.B. Subsurface damage in optical materials: Origin, measurement & removal. In Proceedings of the Optical fabrication and testing workshop, Santa Clara, CA, USA, 2 November 1988. [Google Scholar]
- Neauport, J.; Ambard, C.; Bercegol, H.; Cahuc, O.; Champreux, J.P.; Charles, J.L.; Cormont, P.; Darbois, N.; Darnis, P.; Destribats, J.; et al. Optimizing fused silica polishing processes for 351 nm high power laser application. In Laser-Inducted Damage in Optical Materials, Proceedings of the SPIE, Volume 7132, Boulder, CO, USA, 22 September 2008; Exarhos, G.J., Ristau, D., Eds.; SPIE: Bellingham, WA, USA, 2008. [Google Scholar] [CrossRef]
- Comley, P.; Morantz, P.; Shore, P.; Tonnellier, X. Grinding metre-scale mirror segments for the E-ELT ground based telescope. CIRP Annals-Manufacturing Technology 2011, 60, 379–382. [Google Scholar] [CrossRef]
- Miller, P.E.; Suratwala, T.I.; Wong, L.L.; Feit, M.D.; Menapace, J.A.; Davis, P.J.; Steele, R.A. The distribution of subsurface damage in fused silica. In Laser-Inducted Damage in Optical Materials, Proceedings of SPIE Volume 5991, Boulder, CO, USA, 19 September 2005; Exarhos, G.J., Guenther, A.H., Eds.; SPIE: Bellingham, WA, USA, 2006. [Google Scholar] [CrossRef]
- Lambropoulos, J.C. From Abrasive Size to Subsurface Damage in Grinding. TOPS 2000, 42, 17–18. [Google Scholar] [CrossRef]
- Lucca, D.A.; Brinksmeier, E.; Goch, G. Progress in Assessing Surface and Subsurface Integrity. CIRP Ann. 1998, 47, 669–693. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Han, J.; Xu, Q.; Guo, Y. Evaluating subsurface damage in optical glasses. JEOS:RP 6 2011, 6, 1–16. [Google Scholar] [CrossRef]
- Menapace, J.A.; Davis, P.J.; Steele, W.A.; Wong, L.L.; Suratwala, T.I.; Miller, P.E. MRF Applications: Measurement of process-dependent subsurface damage in optical materials using the MRF wedge technique. In Laser-Inducted Damage in Optical Materials, Proceedings of SPIE Volume 5991, Boulder, CO, USA, 19 September 2005; Exarhos, G.J., Guenther, A.H., Eds.; SPIE: Bellingham, WA, USA, 2006. [Google Scholar] [CrossRef]
- Menapace, J.A.; Davis, P.J.; Steele, W.A.; Wong, L.L.; Suratwala, T.I.; Miller, P.E. Utilization of magnetorheological finishing as a diagnostic tool for investigating the three-dimensional structure of fractures in fused silica. In Laser-Inducted Damage in Optical Materials, Proceedings of SPIE Volume 5991, Boulder, CO, USA, 19 September 2005; Exarhos, G.J., Guenther, A.H., Eds.; SPIE: Bellingham, WA, USA, 2006. [Google Scholar] [CrossRef]
- Randi, J.A.; Lambropoulos, J.C.; Jacobs, S.D. Subsurface damage in some single crystalline optical materials. Appl. Opt. 2005, 44, 2241–2249. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhenga, N.; Li, H.; Houa, J.; Lei, X.; Chena, X.; Yuana, Z.; Guoa, Z.; Wanga, J.; Guob, Y.; Xua, Q. Morphology and distribution of subsurface damage in optical fused silica parts: Bound-abrasive grinding. Appl. Surf. Sci. 2011, 257, 2066–2073. [Google Scholar] [CrossRef]
- Klocke, F. Manufacturing Processes 2: Grinding, Honing, Lapping; Springer: Heidelberg, Germany, 2009; pp. 251–269. [Google Scholar]
- Wang, H.; Subhash, G.; Chandra, A. Characteristics of single-grit rotating scratch with a conical tool on pure titanium. Wear 2001, 249, 566–581. [Google Scholar] [CrossRef]
- Bollinger, L.D.; Gallatin, G.M.; Samuels, J.; Steinberg, G.; Zarowin, C.B. Rapid, non-contact optical figuring of aspheric surfaces with Plasma Assisted Chemical Etching (PACE). In Advanced Optical Manufacturing and Testing, Proceedings of SPIE 1333, San Diego, CA, USA, 1 July 1990; Sanger, G.M., Reid, P.B., Eds.; SPIE: Bellingham, WA, USA, 1990. [Google Scholar] [CrossRef]
- Suratwala, T.I.; Wong, L.L.; Miller, P.E.; Feit, M.D.; Menapace, J.A.; Steele, R.A.; Davis, P.J.; Walmer, D. Subsurface mechanical damage distributions during grinding of fused silica. J. Non.-Cryst. Solids 2006, 352, 5601–5617. [Google Scholar] [CrossRef]
- Huang, H.; Yin, L. High speed grinding performance and material removal mechanism of silicon nitride. Initiat. Precis. Eng. Begin. Millenn. 2002, 416–420. [Google Scholar] [CrossRef]
- Lawn, B.R.; Swain, M.V. Microfracture beneath point indentations in brittle solids. J. Mater. Sci. 1975, 10, 113–122. [Google Scholar] [CrossRef]
- Lawn, B.R.; Evans, A.G.; Marshall, D.B. Elastic/plastic indentation damage in ceramics: The mediad/radial crack system. J. Am. Ceram. Soc. 1980, 63, 574–581. [Google Scholar] [CrossRef]
- Anstis, G.R.; Chantikul, P.; Lawn, B.R.; Marshall, D.B. A critical evaluation of indentation techniques for measuring fracture toughness: I, direct crack measurements. J. Am. Ceram. Soc. 1981, 64, 533–538. [Google Scholar] [CrossRef]
- Lawn, B.R. Partial cone crack formation in a brittle material loaded with a sliding spherical indenter. Proc. R Soc. Lond. Ser. A 1967, 299, 307–316. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).