Extreme Strengthening of Nickel by Ultralow Additions of SiC Nanoparticles: Synergy of Microstructure Control and Interfacial Reactions During Spark Plasma Sintering

Abstract

Ni–ySiC system (where y = 0.001, 0.005, and 0.015 wt.%) composite materials with enhanced mechanical properties have been fabricated and comprehensively investigated. The composites were synthesized using a combined technology involving preliminary mechanical activation of powder components in a planetary mill followed by consolidation via spark plasma sintering (SPS) at 850 °C. The microstructure and phase composition were studied by scanning electron microscopy (SEM), transmission electron microscopy (TEM), and X-ray diffraction (XRD). The physico-mechanical properties were evaluated by density measurements (hydrostatic weighing), three-point bending tests (25 °C and 400 °C), and Young’s modulus measurement using an ultrasonic method (25–750 °C). It was found that the introduction of ultralow amounts of SiC nanoparticles (0.001 wt.%) leads to an extreme increase in flexural strength: by 115% at 20 °C (up to 1130 MPa) and by 86% at 400 °C (up to 976 MPa) compared to pure nickel. Microstructural analysis revealed the formation of an ultrafine-grained structure (0.15–0.4 µm) with the presence of pyrolytic carbon and probable nickel silicide interlayers at the grain boundaries. Thermodynamic and kinetic modeling, including the calculation of chemical potentials and diffusion coefficients, confirmed the possibility of reactions at the Ni/SiC interface with the formation of nickel silicides (Ni₂Si, NiSi) and free carbon. The scientific novelty of the work lies in establishing a synergistic strengthening mechanism combining the Hall–Petch, Orowan (dispersion), and solid solution strengthening effects, and in demonstrating the property extremum at an ultralow content of the dispersed phase (0.001 wt.%), explained from the standpoint of quantum-chemical analysis of phase stability. The obtained results are of practical importance for the development of high-strength and thermally stable nickel composites, promising for application in aerospace engineering.

1. Introduction

Nickel-based materials are widely used in the aviation, aerospace, engineering, and energy industries due to their high corrosion resistance, heat resistance, and the possibility of targeted modification of mechanical properties [1,2]. Pure nickel is relatively rarely used as a structural material due to its high density and moderate strength. However, its properties can be significantly improved through various strengthening mechanisms: solid solution, dislocation, dispersion, grain boundary, and the Peierls–Nabarro mechanism [2,3].

Dispersion strengthening, achieved by introducing coherent or incoherent nanoparticles, shows high efficiency. The introduction of 0.01–0.1 wt.% spherical nanoparticles of refractory oxides into molybdenum and aluminum led to an increase in ultimate strength by 30–300% compared to pure metals [4,5,6,7]. These results were obtained by powder metallurgy methods, including spark plasma sintering (SPS).

SPS is considered one of the most promising methods for consolidating nickel and its alloy powders, as it combines high heating rates, short holding times, and applied pressure, which minimizes grain growth [8,9,10,11]. It has been shown that the microstructure and properties of sintered nickel materials strongly depend on the characteristics of the initial powder and SPS parameters. When using powders with a bimodal distribution (nanoparticles ~10 nm and particles ~15 µm), the ultimate strength reached 500–650 MPa with a microstructure of 1–2 and 10–25 µm grains [10]. Sintering of nickel powders pre-milled to 52–250 nm yielded a strength of 680–700 MPa [11]. An important strengthening mechanism is also alloying with light elements to form interstitial solid solutions [3,12,13].

The phase diagram of the Ni–C system indicates the possibility of forming FCC Ni + C eutectic and metastable phases, including a hexagonal modification of nickel and carbides. However, carbides are stable only at high carbon content (>15 at.%) [12,14]. The decomposition of the solid solution at elevated temperatures (e.g., at 20 at.% C above 792 K, at 30 at.% C above 663 K [13]) limits the application of such materials. Therefore, the development of thermally stable nickel materials with a carbon content of <15 at.% and a high level of mechanical properties is relevant.

A promising direction is the combination of nickel alloying with carbon and the introduction of refractory nanoparticles using rapid consolidation methods such as SPS [8,9]. SPS not only preserves the fine-grained structure but also promotes the homogenization of the carbon solid solution in nickel. When using graphite molds and carbon paper spacers, diffusion saturation of the sample surface with carbon is possible without its direct introduction into the charge, which simplifies the technology. The additional introduction of small amounts of silicon carbide (SiC) nanoparticles can inhibit recrystallization, increase thermal stability, and promote the formation of a complex composite structure.

The literature data demonstrate an extreme nature of the dependence of nickel strength on the content of dispersed additives. The introduction of 0.05 wt.% boron nitride nanoflakes increased the ultimate tensile strength by 26% (to 562 MPa) while maintaining 36% plasticity; at 750 °C, the strengthening reached 63%, and the flexural strength increased by 121% (from 399 to 883 MPa) [15]. With the addition of 1 wt.% SiC nanoparticles, the yield strength of nickel increased more than fivefold (from 59 to 364 MPa) due to grain growth inhibition [16]. Additions of less than 0.1 wt.% Al₂O₃ nanofibers provided a 10–40% increase in strength at room temperature and property retention at 400–750 °C [17].

The introduction of nanoparticles into the nickel matrix leads to grain refinement by inhibiting boundary migration, increasing dislocation density, strengthening grain boundaries, suppressing creep, and limiting oxidation [18,19,20,21]. Nanoparticles serve as barriers to dislocation motion, promote the formation of Σ3 twin boundaries, inhibit crack propagation, and limit vacancy diffusion [18,19,20,21,22,23,24]. According to the classical Zener theory, the efficiency of grain growth inhibition is determined not only by the volume fraction but also by the particle size [25]. Nanoscale precipitates formed as a result of the controlled decomposition of the dispersed phase, localized precisely at the grain boundaries, are exceptionally effective nuclei for boundary pinning [25]. SPS makes it possible to obtain ultrafine-grained nickel materials with a high content of Σ3 boundaries and a favorable combination of strength and ductility [26,27].

In this work, composite materials of the Ni–ySiC system (y = 0.001, 0.005, 0.015 wt.%) using the combined “mechanical activation + SPS” technology were fabricated and comprehensively investigated. The mechanisms of extreme strengthening at ultralow amounts of SiC nanoparticles were identified. Special attention was paid to the role of the carbon solid solution, pyrolytic carbon, and possible nickel silicides formed at the grain boundaries, using methods of thermodynamic and kinetic modeling, including the analysis of chemical potentials and diffusion.

2. Materials and Methods

2.1. Materials and Powder Preparation

Nickel powder grade PNK UT3 (average particle size ~20 µm, purity 99.9%, Giredmet OJSC, Moscow, Russia) was used as the matrix material. Micrographs of the powder (Figure 1a) show particles of irregular shape with a developed surface, favorable for mechanical interlocking and compaction during pressing.

Silicon carbide nanoparticles with an average size of ~40 nm, synthesized by the plasma–chemical method [28], were used as the modifying phase (Figure 1b). According to XRD and microelectron diffraction data, the SiC powder has a predominantly α-modification with an admixture of β-SiC.

The initial nickel powder was sieved on a vibrating screen to remove contaminants and agglomerates >20 µm. Mechanical activation and mixing were carried out in an “Activator 2SL” planetary mill (Activator LLC, Moscow, Russia) in an argon atmosphere. Steel jars and balls were used with a powder-to-balls ratio = 1:5. The nickel powder was preliminarily “wiped” with steel balls for 20 h to form a protective nickel layer and minimize Fe contamination [29,30]. The main mixing of Ni and pre-dispersed SiC nanoparticles (0.001, 0.005, 0.015 wt.%) was carried out for 20 min at 33 Hz.

After mech activation, the mixture was dispersed in isopropyl alcohol (powder-to-liquid ratio = 1:5) with the addition of oleic acid. Dispersion was carried out with an overhead stirrer (IKA-Werke GmbH & Co. KG, Staufen, Germany) (300–450 rpm) with simultaneous ultrasonic treatment (20 kHz, 5 min). The resulting suspension was dried under a fume hood at room temperature for 24 h.

2.2. Spark Plasma Sintering

Consolidation was carried out by SPS in graphite molds in an argon atmosphere (FCT Systeme Gmbh, Frankenblick, Germany). The sintering temperature was 850 °C, holding time was 20 min, followed by cooling in air. The pressure and pulse mode corresponded to typical parameters for nickel [8,9]. The heating rate was ~100 °C/min, the cooling rate (in an argon atmosphere in the chamber) ~200 °C/min to 600 °C, then with the furnace. The pressure was 50 MPa. A DC pulse mode with a pulse duration of 12 ms and a pause of 2 ms was used.

2.3. Structural Analysis Methods

The density of the sintered samples was determined by the hydrostatic weighing method. To quantify the quality of consolidation, the density and porosity of all the materials studied were determined by hydrostatic weighing. The theoretical density (ρ_theor) was calculated using the mixture rule for the initial charge (Ni and SiC) using the values ρ_Ni = 8.90 g/cm³ and ρ_SiC = 3.21 g/cm³. The contribution of SiC decomposition products (silicides, carbon) to the total density is negligible (<0.1% of ρ_theor) due to their ultrasmall total amount and within the margin of error of the method. The results are presented in

Table 1. Physical and mechanical properties of sintered materials.

Material	Rel. Density, %	Open Porosity, %	HV0.2
Ni	98.7	1.1	70 ± 10
Ni–0.001SiC	98.4	1.4	81 ± 3
Ni–0.005SiC	98.3	1.5	92 ± 4
Ni–0.015SiC	98.2	1.2	82 ± 4

. The relative density for all composites exceeds 98.5%, and the open porosity averages ~1.3%, demonstrating high sintering quality. The standard deviation of the density values is ±0.02 g/cm³, which indicates good repeatability of the results. The microstructure was studied using SEM Quanta 600 and TEM FEI Osiris (FEI Company, Eindhoven, Netherlands/ Hillsborough, OR, USA). The phase composition was analyzed on a HZG 4 (Freiberger Präzisionsmechanik GmbH, Freiberg, Germany) diffractometer in Bragg–Brentano geometry (2θ–θ scanning). The lattice parameter and the size of coherent scattering regions were estimated from the broadening of diffraction peaks. The carbon content in the surface layers was determined by X-ray fluorescence microspectroscopy.

2.4. Mechanical Testing

Test specimens were cut from the sintered pellets for mechanical testing. Vickers microhardness was measured on ground and polished samples using a PMT-3M microhardness tester (JSC LOMO, St. Petersbug, Russia) at a load of 200 gs and exposure time of 10 s. Three-point bending tests were carried out on a “TestSystems VakEto” (TestSystems LLC, Russia) machine at 25 and 400 °C. Young’s modulus were determined by the ultrasonic method using a “MUZA” setup at 25, 400, and 750 °C for samples sized 5 × 15 × 3 mm. At least three samples were produced and tested for each composition to assess the reproducibility of mechanical properties. The standard deviation of the bending strength values did not exceed ±40 MPa, which indicates good repeatability of the results.

2.5. Thermodynamic and Kinetic Modeling

Thermodynamic modeling of phase equilibria in the Ni–Si–C, Ni–C–O₂, Ni–C–SiC–NiO–SiO₂ systems was performed using the OQMD database (for 0 K), TERRA (v. 6.2), MAAT (v.1.0), and the IVTANTERMO (v. 3.0) software package [31,32]. Ternary diagrams of Ni–Si–C were constructed at 1123 K with and without considering ideal solid solutions of Ni–C and Ni–Si. The activities of components and Gibbs mixing energies were calculated to assess the stability of solid solutions and the tendencies for silicide formation.

To estimate the diffusion of carbon in nickel, the Arrhenius dependence was used:

$$D=D_0\exp \left(-{\displaystyle \frac{E}{RT}}\right)=1.04\times {10}^{-5}\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{138300}{8.314\hspace{0.17em}\left(T+273\right)}})\hspace{0.17em}{,\mathrm{m}}^2/\mathrm{s},$$

where D₀ and E are taken from [33,34].

For an in-depth analysis of the stability of phases in the Ni-Si-C system at sintering and operating temperatures (300, 1000, 1273 K), a calculation of chemical potentials (μ) was performed using the “ab-initio thermodynamics” approach, which has proven effective for predicting phase stability in complex systems under conditions far from equilibrium [35]. The free energy of a phase was calculated as the sum of the electronic energy, zero-point vibration energy, phonon contribution, electronic contribution, and configurational entropy. The chemical potential of component i in the phase was defined as the partial derivative of G with respect to the number of Ni particles. This made it possible to construct three-dimensional phase stability diagrams in the coordinates (μ_Ni, μ_Si, μ_C) and analyze their evolution with temperature.

3. Results

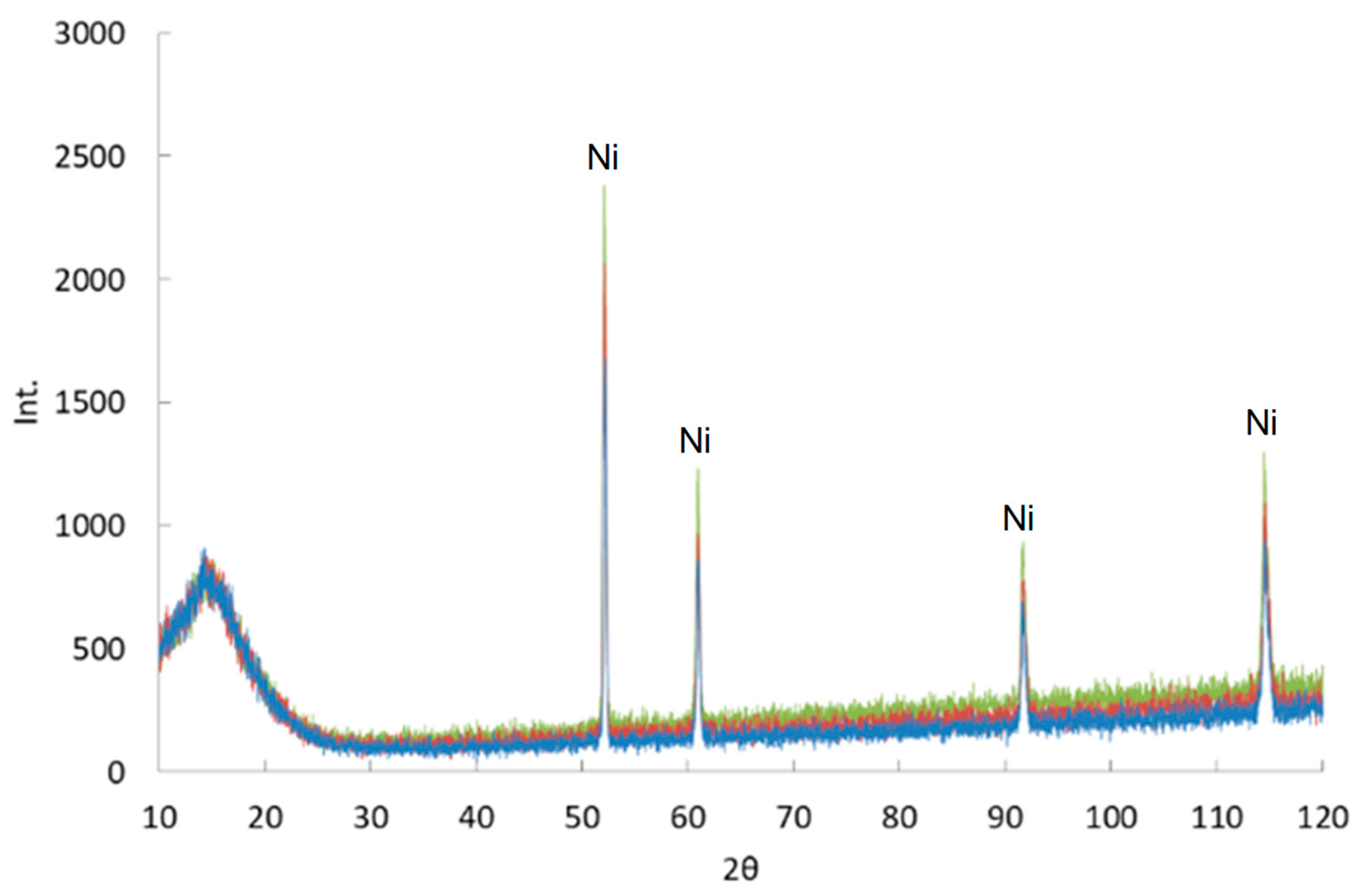
3.1. Structure and Phase Composition of Sintered Nickel

TEM analysis of the pure nickel microstructure (Figure 2a,b) revealed elongated grains with a longitudinal size of >0.4 µm and a transverse size of ~0.15 µm, indicating directional recrystallization under non-equilibrium SPS conditions. Regions of pyrolytic carbon were found at the grain boundaries (Figure 2c). According to X-ray fluorescence analysis, the carbon content in the surface layer reaches 1–2 wt.%, and in the volume it does not exceed ~1 wt.%, indicating a gradient nature of diffusion saturation.

XRD patterns (Figure 3) show the preservation of the FCC nickel lattice. In the region of small angles, a halo characteristic of amorphous carbon is recorded. The lattice parameter of nickel is 3.526–3.527 Å, which slightly exceeds the tabulated value for pure Ni (3.524 Å) and indicates the presence of interstitial carbon in the solid solution. The size of coherent scattering regions, estimated from peak broadening, is ~390 nm, which is in good agreement with the subgrain structure. In the region of small angles (2θ~10–30°), a diffuse halo is detected. That is a characteristic of the presence of an X-ray amorphous phase.

Comparison of the dependence of the Ni lattice parameter on carbon concentration with the literature data [14] (Figure 4) shows that the concentration of carbon in the solid solution is ~0.1–0.3 at.%. Consequently, a significant part of the carbon (up to several at.%) is present in the form of a free carbon phase (pyrolytic carbon, graphite).

The formation of pyrolytic carbon may be associated with (i) the release of excess carbon from the solid solution upon cooling, (ii) the supply of carbon from the spacer paper and graphite tooling, and (iii) thermal decomposition of oleic acid. In terms of morphology and structure, the resulting pyrolytic carbon corresponds to a low-temperature, weakly textured modification [36,37], characteristic of CVD processes at moderate temperatures.

3.2. Structure of Ni–SiC Composites

SEM images of Ni–0.001SiC and Ni–0.005SiC composites microstructure are shown in Figure 5. Submicron and micron pores are observed on the cross-sections, and the grain size reaches 20 µm. After etching, subgrains up to 0.6 µm in size are revealed in the Ni–0.005SiC sample (Figure 5b), indicating a developed substructure and potential for Hall–Petch strengthening. The porous structure of the samples formed during sintering is clearly visible; the pore diameter is on average about 1 µm. Submicron grains and subgrains of less than 500 nm are also visible in the pictures after etching.

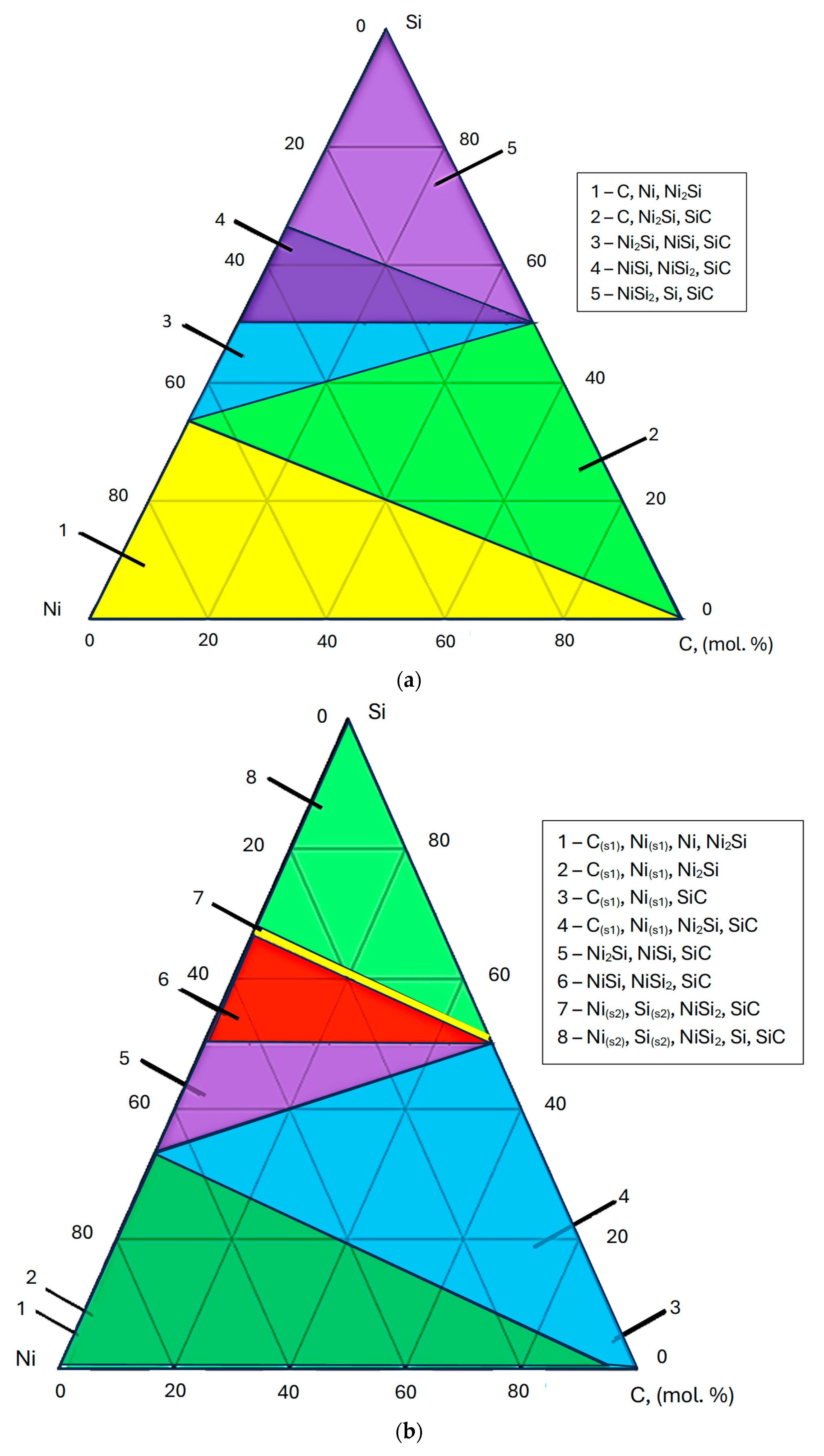
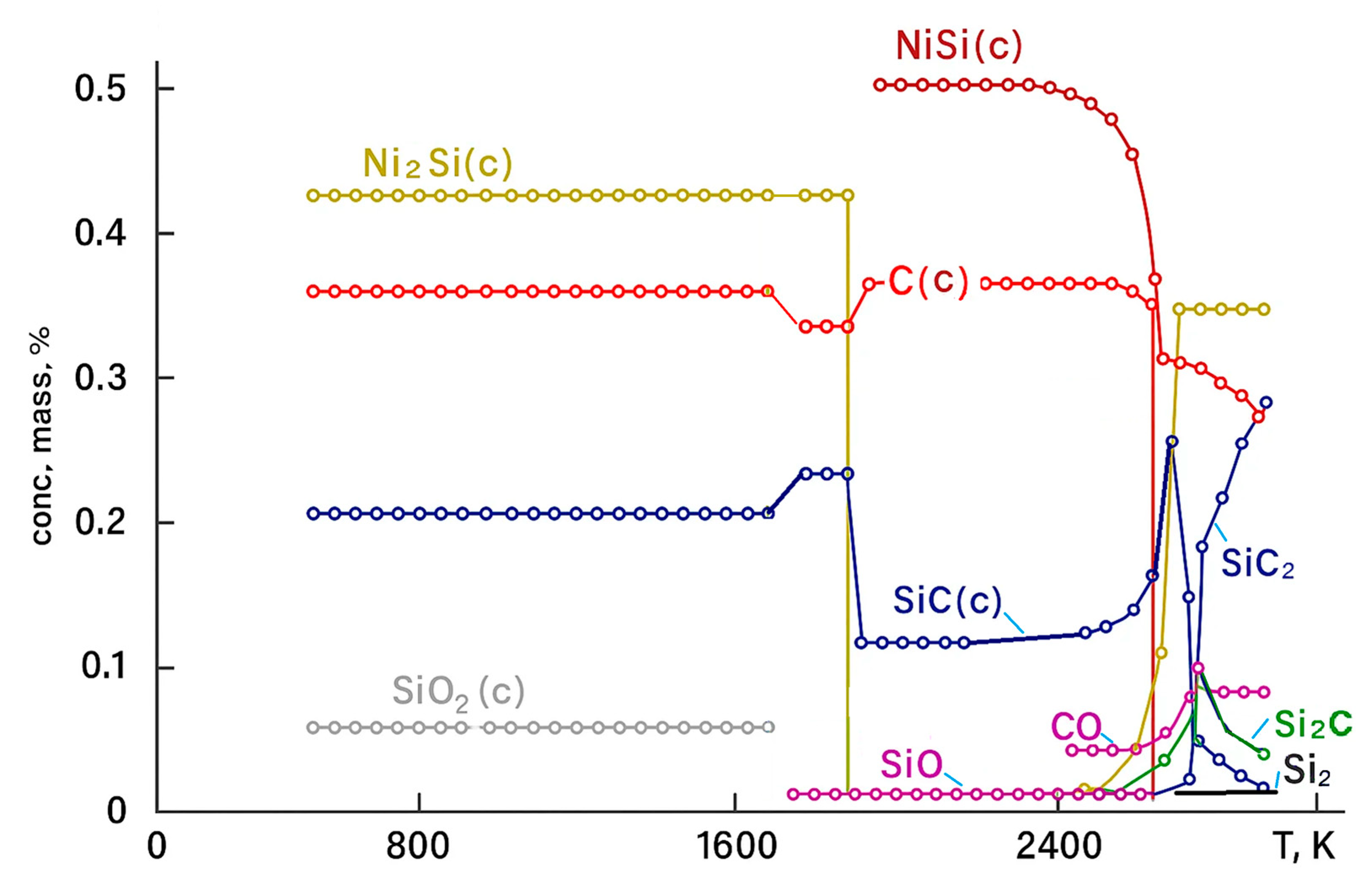
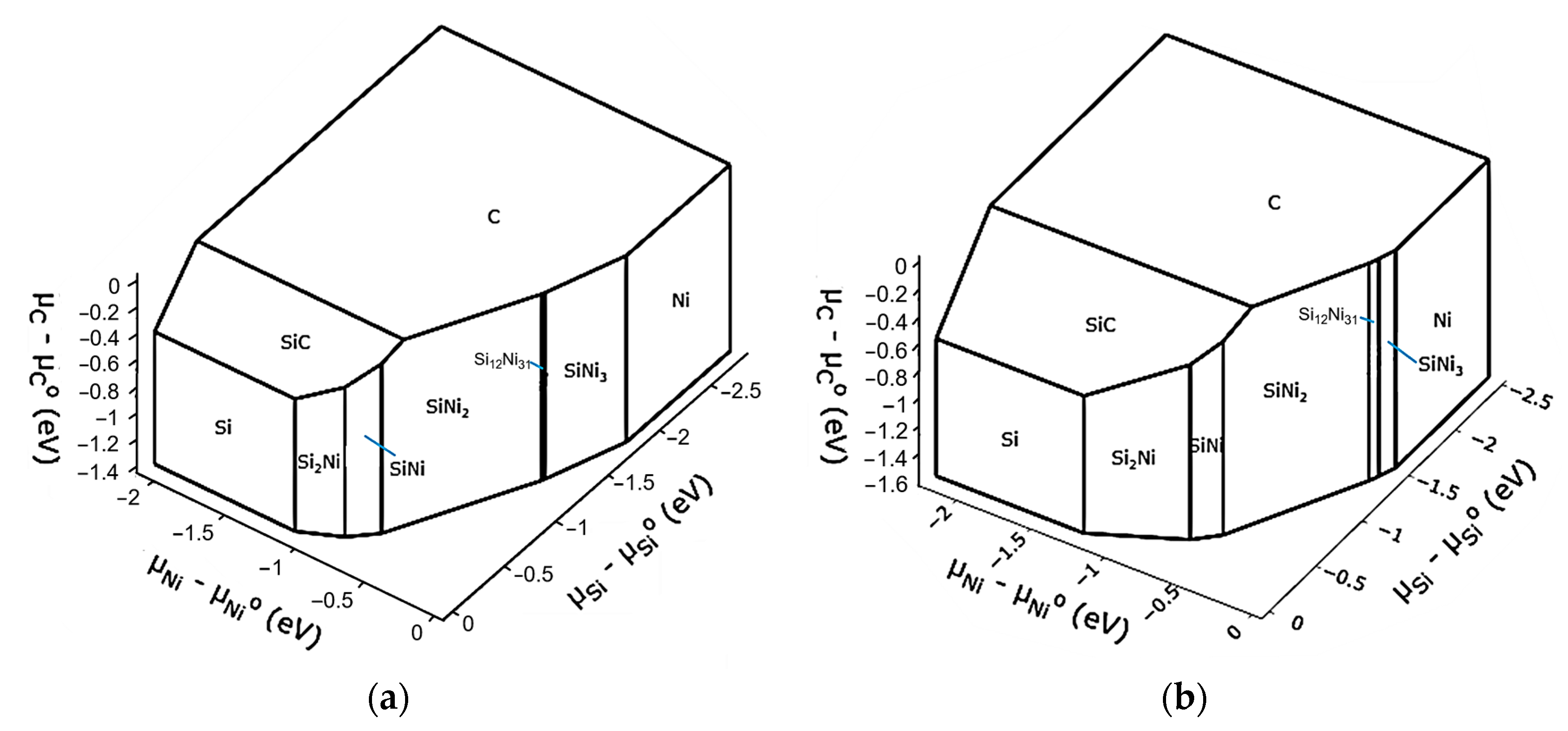
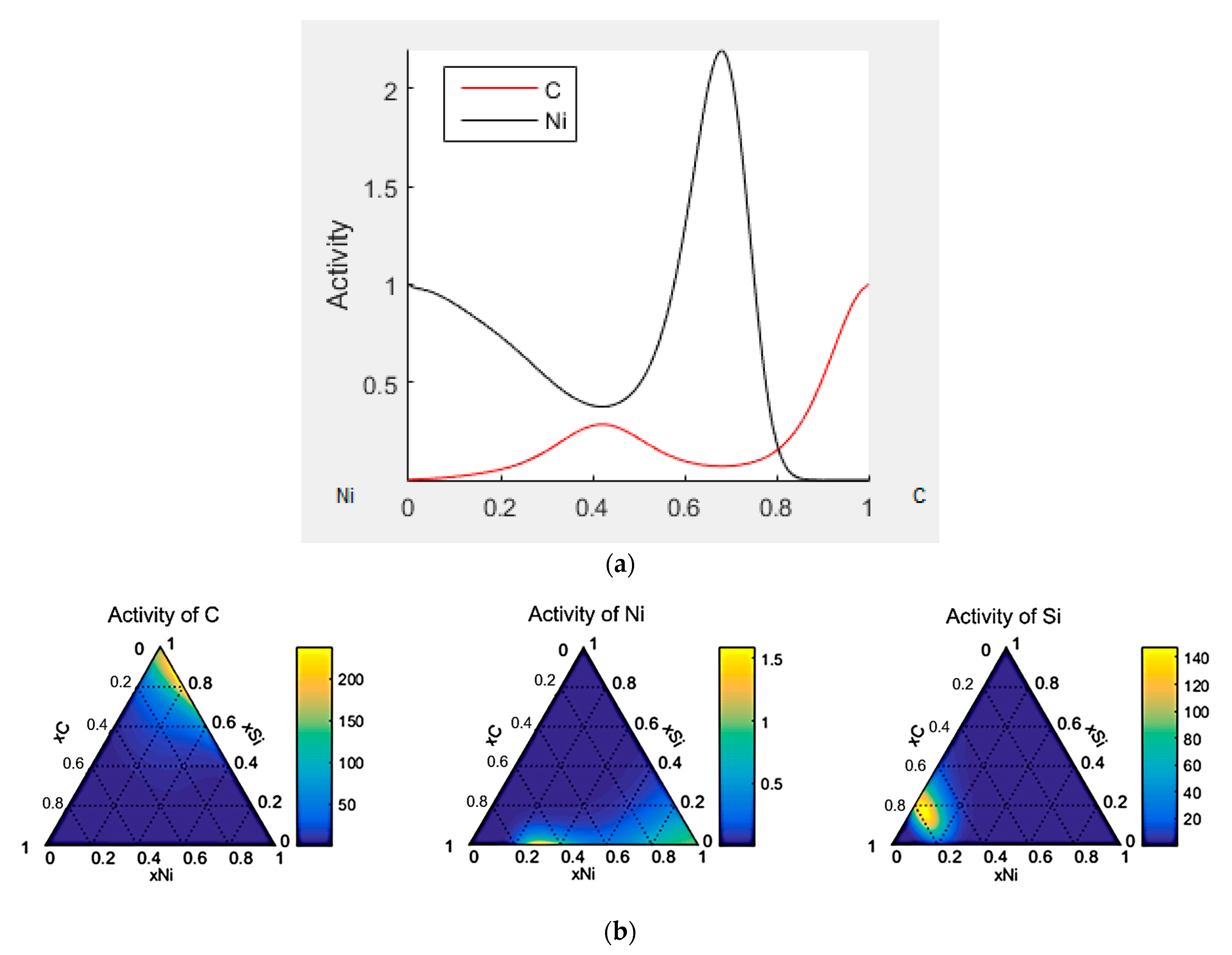
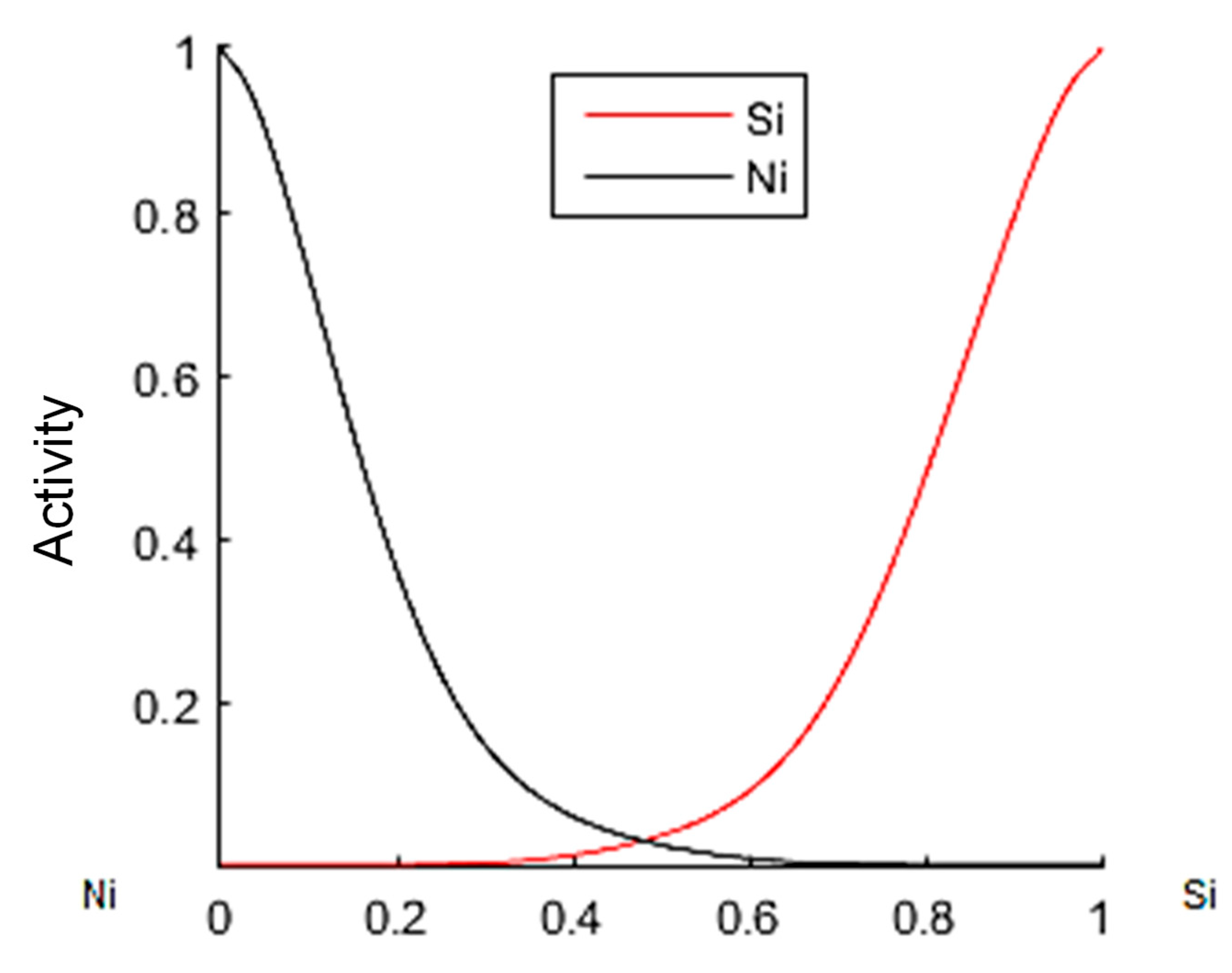
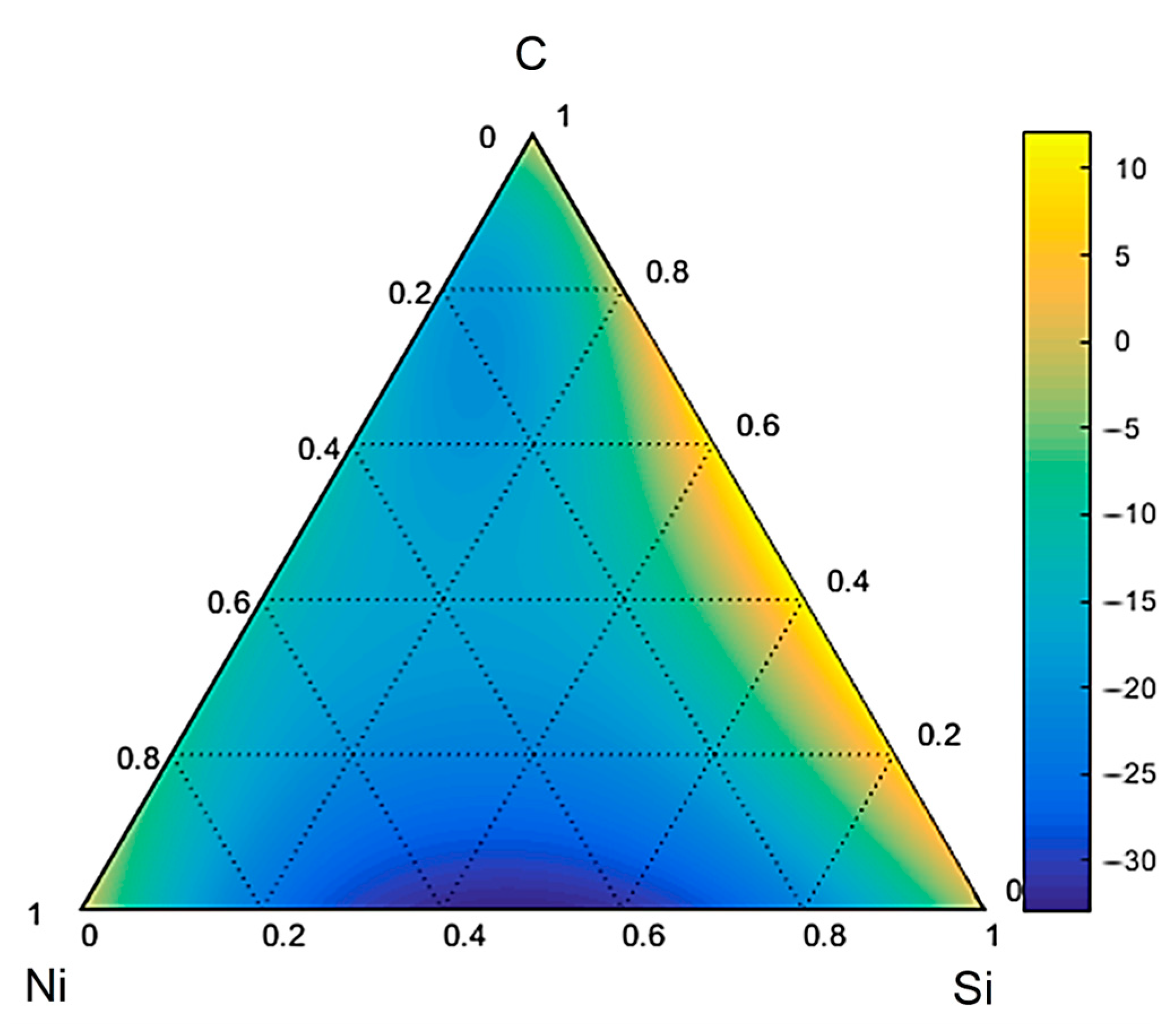
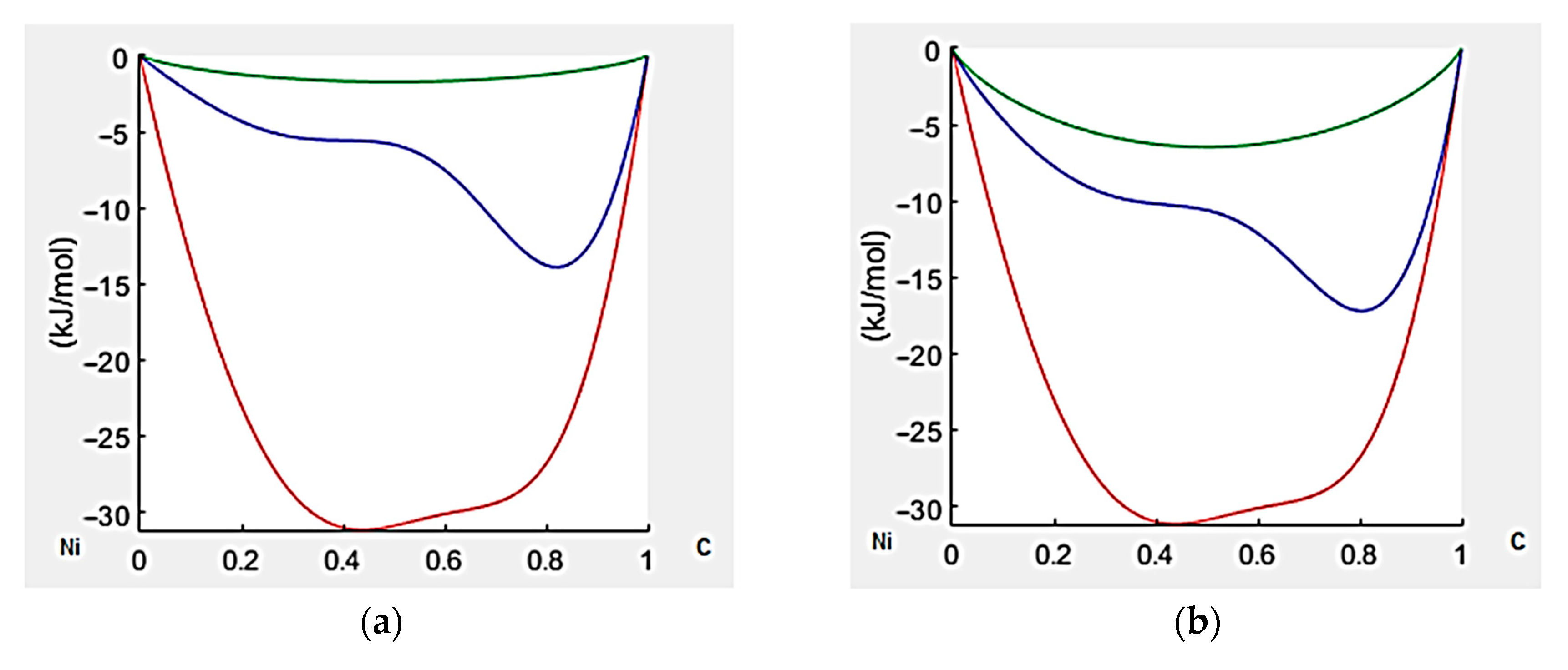
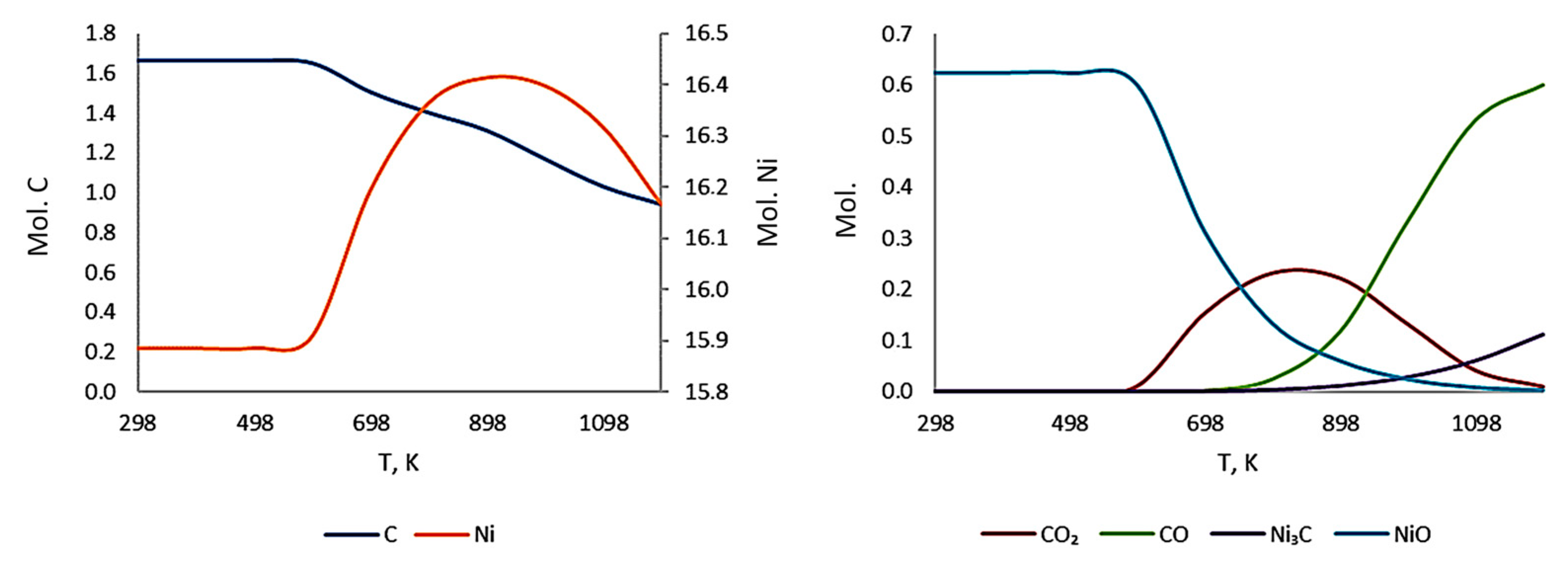
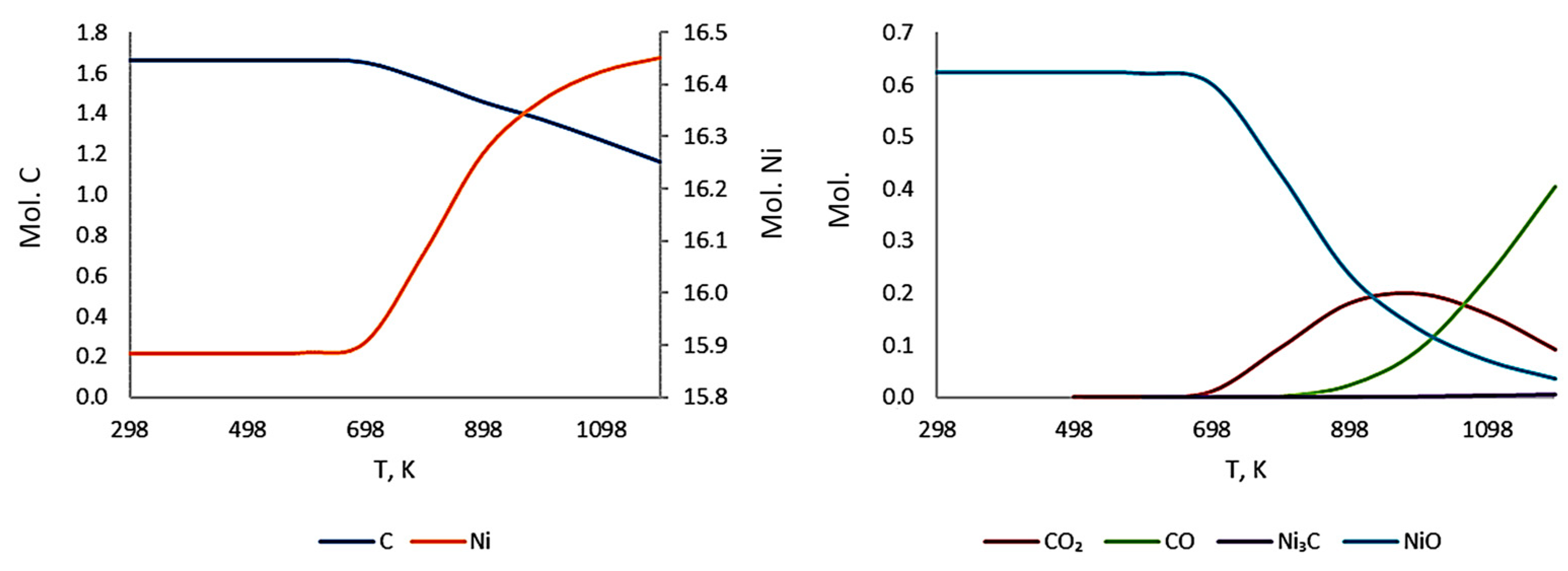
3.3. Thermodynamic Modeling and Analysis of Chemical Potentials

The calculation of the ternary Ni–Si–C diagram at 0 K using the OQMD database (Figure 6) shows the presence of stable phases: SiC, Si₂Ni, NiSi, Ni₂Si, Ni₃Si₂, Ni₃₁Si₁₂, Ni₃Si, and NiSi₂. At 1123 K, without considering solid solutions (Figure 7a), the nickel corner of the diagram includes pure Ni, graphite, and the silicide Ni₂Si. Taking into account the formation of ideal solid solutions Ni–C and Ni–Si (Figure 7b), a wide region of the Ni–C solid solution appears, coexisting with Ni₂Si, while the region of the Ni–Si solid solution is extremely narrow.

The calculation of the equilibrium composition of the Ni–C–SiC–NiO–SiO₂ system with initial concentrations of 0.5 mol% Ni, 0.5 mol% C, 0.5 mol% SiC, 0.05 mol% NiO, and 0.05% mol SiO₂ (Figure 8) shows the formation of silicides NiSi and Ni₂Si with increasing temperature.

The calculation of chemical potentials for the Ni–Si–C system revealed a critical dependence of phase stability regions on temperature. Figure 9 presents three-dimensional diagrams in the coordinates (μNi, μSi, μC) for 300 K and 1273 K.

At 300 K, the stability zones of the phases (SiC, Si, Ni, silicides) have sharp boundaries. The SiC region is extensive, indicating its high thermodynamic stability at room temperature. The regions of silicides Ni₃Si, NiSi, NiSi₂ are relatively narrow.

When the temperature increases to 1273 K, the picture changes radically. The contribution of phonon entropy significantly reduces the free energy of metallic and intermetallic phases. This leads to a significant expansion of the stability regions of nickel silicides, especially nickel-rich phases (Ni₃Si). Simultaneously, the region of SiC stability narrows. This thermodynamic prediction is in excellent agreement with experimental data on the decomposition of SiC in the presence of Ni at sintering temperatures: the system tends to form silicides and dissolve carbon in the nickel matrix. The regions of pure silicon and carbon also shrink, as at high temperatures, these elements are more energetically favorable in solid solutions or intermetallics.

Analysis of component activities in the Ni–C system (Figure 10a) shows that the activity of nickel initially decreases with increasing carbon content, then sharply increases at a carbon mole fraction of ~0.7 and decreases again. In the ternary Ni–Si–C system (Figure 9b), the activities of carbon and silicon significantly exceed unity over a wide range of concentrations, indicating weak interaction between the components at this temperature and significant repulsive forces between silicon and carbon atoms.

On the graph of the change in Ni–Si activity (Figure 11), the activity of nickel gradually decreases with increasing silicon concentration, indicating a strong bond between nickel and silicon in the solid solution.

Figure 12 shows the change in the Gibbs energy of solid solutions formation in the Ni-Si-C system at 1123 K. Interestingly, at low amounts of C and Si, the Gibbs energy is equal to or greater than 0. With a slight increase in carbon concentration (comparable to that reported in this work), the Gibbs energy drops slightly below 0. According to the results of [38], during the interaction of silicon carbide with nickel at 850 °C, the decomposition of silicon carbide occurs with the precipitation of free nanocarbon and the formation of nickel silicides.

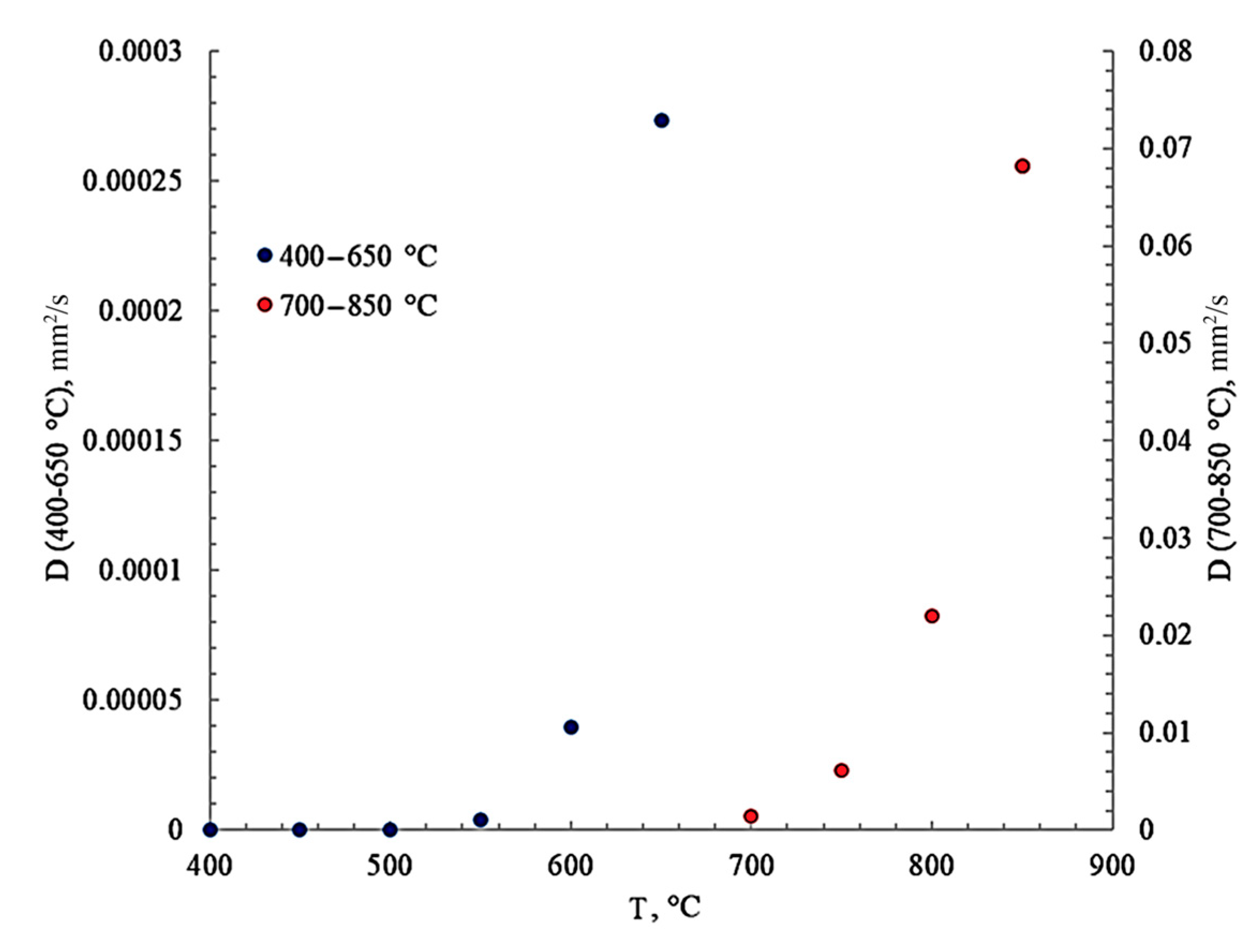
3.4. Kinetics of Carbon Diffusion in Nickel

The calculation of the carbon diffusion coefficient in nickel using the Arrhenius equation (Figure 13) showed that at the sintering temperature of 850 °C (1123 K), the diffusion coefficient (D) is approximately 4 × 10⁻¹² m²/s. This calculation, based on the classical model, is in good agreement with independent experimental data [34,39], according to which carbon from graphite tooling during SPS can penetrate into nickel to a depth of up to 100 µm in 5 min.

However, direct comparison with quantum-chemical modeling (DFT) data revealed some nuances. DFT calculations [40,41] yield a value for the activation energy of carbon migration in the bulk of nickel ~1.62 eV (≈156 kJ/mol), which is higher than the value used in our calculation (138.3 kJ/mol). This discrepancy can be explained by the influence of structural defects (grain boundaries, dislocations) presented in the real material and reducing the effective energy barrier for diffusion. Diffusion along grain boundaries, according to [41], can have a significantly lower activation energy. Thus, the high carbon saturation rate observed in the experiment may be due to the predominance of short-path diffusion (grain boundaries) in the ultrafine-grained structure obtained by SPS.

Figure 14 shows the change in the ideal Gibbs energy, Gibbs mixing energy, and chemical enthalpy of mixing in the Ni–C system depending on the carbon concentration at 298 K and 1123 K. It can be seen that the Gibbs mixing energy is lower than the ideal Gibbs energy and decreases with increasing carbon concentration. This indicates the possibility of forming a solid solution of carbon in nickel with increasing temperature.

Further calculations of the equilibrium states of systems containing carbon either in free form or in a solid solution, at 298–1198 K, led to the results shown in Figure 15 and Figure 16.

The formation of CO₂ begins at 598 K and actively proceeds up to 798 K, when the formation of CO begins to prevail. At the same time, the reduction of NiO and non-intensive formation of Ni₃C occur. This picture is typical for all considered variants. According to [42], nickel carbide Ni₃C is unstable at 400–1600 °C, and a eutectic is observed at 1315 °C at a carbon concentration of 2.2 wt.%. The diffusion of carbon in pure nickel in a sample 5 mm thick was 4 × 10⁻⁸ cm²/s or 4 × 10⁻¹² m²/s at 850 °C [34], which is much lower than the value calculated above for this temperature. However, according to [39], during spark plasma sintering, carbon from punches can penetrate into nickel, similar in composition to that used in this work, to a depth of up to 100 µm at a sintering temperature of 900 °C for 5 min. According to [43], even small additions of carbon (less than 0.01 wt.%) to pure nickel, subjected to high-pressure torsion and nanostructuring, can lead to significant changes in ductility and strength; for example, when the carbon content increases from 0.006 wt.% to 0.06 wt.%, the tensile strength increases by more than 700 MPa.

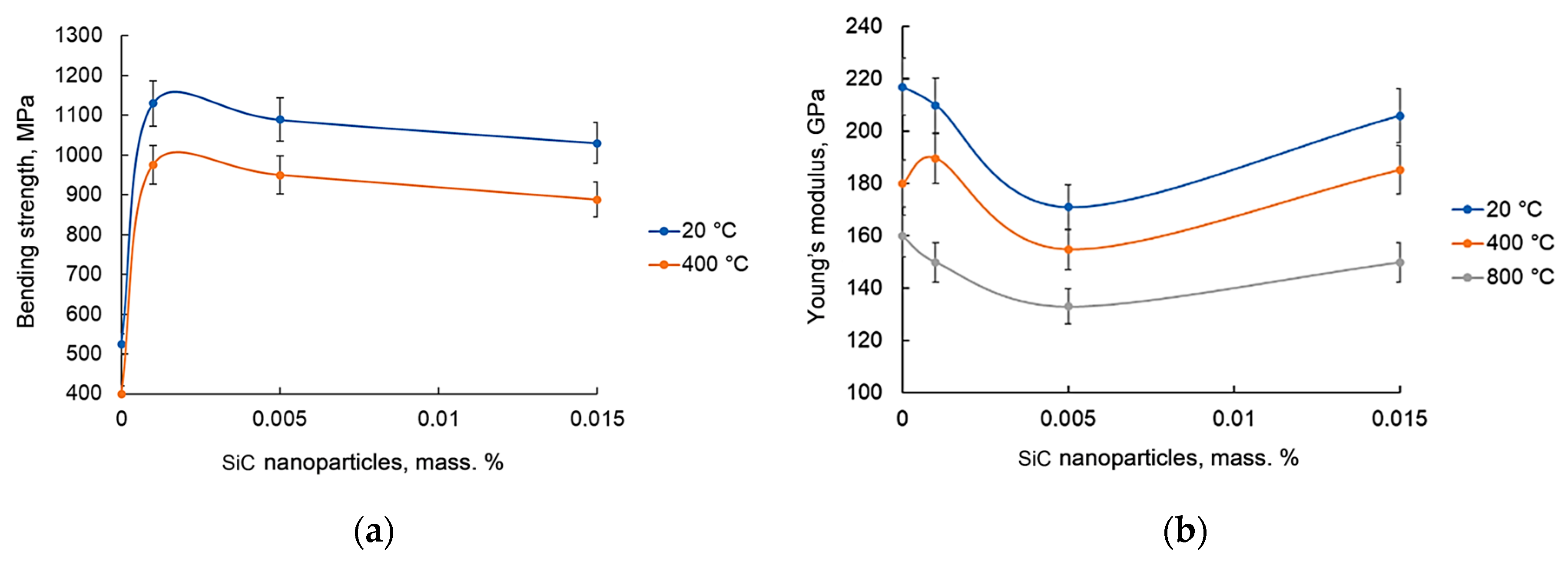
3.5. Mechanical Properties

The open porosity of the samples with nanoparticles averages ~1.3%. The mechanical properties are presented in Figure 17. Even ultralow amounts of SiC nanoparticles provide a significant increase in flexural strength. The relative density for all composites exceeds 98.5% on average, demonstrating high sintering quality (Table 1). The experimental data clearly demonstrate the complex effects of ultralow concentrations of silicon carbide (SiC) nanoparticles and the spark plasma sintering (SPS) method on the microhardness of nickel. The key finding is the observation of extreme hardening at minimum concentrations of the dispersed phase, a phenomenon that cannot be explained by classical models.

Firstly, all of the samples studied, including pure nickel, demonstrated the high quality of SPS consolidation. Relative density values exceeding 98.2% and open porosity values in the range of 1.1–1.5% (see Table 1) indicate the effectiveness of the selected sintering mode, ensuring the formation of a material close to a theoretically dense state. This eliminates the significant influence of pores as stress concentrators and structural defects on the measured hardness, making it possible to correctly analyze the contribution of microstructural factors.

Secondly, a clear non-linear dependence of microhardness on the content of SiC nanoparticles was revealed. Introducing only 0.001 wt.% SiC leads to a statistically significant increase in hardness, from 70 ± 10 HV to 81 ± 3 HV. Increasing the content of the additive to 0.005 wt.% caused a further increase in hardness to a maximum value of 92 ± 4 HV. However, increasing the content to 0.015 wt.% results in a decrease in hardness to 82 ± 4 HV, indicating the presence of an optimum in the region of 0.005 wt.%. This extreme variation in properties is characteristic of a synergistic hardening mechanism, whereby several factors act in concert; however, their balance is disrupted when a certain concentration of the dispersed phase is exceeded.

The addition of 0.001 wt.% SiC increases the flexural strength at 20 °C to 1130 MPa (+115% relative to pure Ni) and at 400 °C to 976 MPa (+86%). The obtained flexural strength value of 1130 MPa for the Ni–0.001SiC composite is one of the highest among those known in the literature for pure ultrafine-grained nickel, exceeding the values achieved, for example, by severe plastic deformation methods [44], which emphasizes the effectiveness of the synergistic strengthening mechanism implemented in this work. With a further increase in SiC content, the strength decreases somewhat, forming an extremum at 0.001 wt.%. The fractures of pure Ni have a ductile dimpled character (Figure 18), while the samples with SiC nanoparticles during bending demonstrate significant plastic deformation before fracture.

4. Discussion

The observed extreme strengthening of nickel at 0.001 wt.% SiC cannot be explained solely by the classical Orowan mechanism, since the volume fraction of particles is extremely small and the calculated contribution Δσ_Or is only 1–5 MPa. The observed strengthening extremum at record-low content of the dispersed phase is consistent with modern concepts of the crucial role of ultralow additions capable of segregating at structural defects and radically affecting their mobility [45]. In our case, such an element is carbon coming from decomposing SiC nanoparticles. The main factors are presented below.

• This is Hall–Petch strengthening due to the ultrafine-grained substructure. For d ≈ 0.25 µm and k_HP ≈ 0.1–0.2 MPa·m^1/2 [46], we obtain Δσ_HP ≈ 200–400 MPa. For regions with larger grains (d ~20 µm), the contribution drops to 20–40 MPa, reflecting the heterogeneity of the structure (0.15–0.4 µm by TEM), giving a contribution of Δσ_HP ≈ 200–400 MPa.
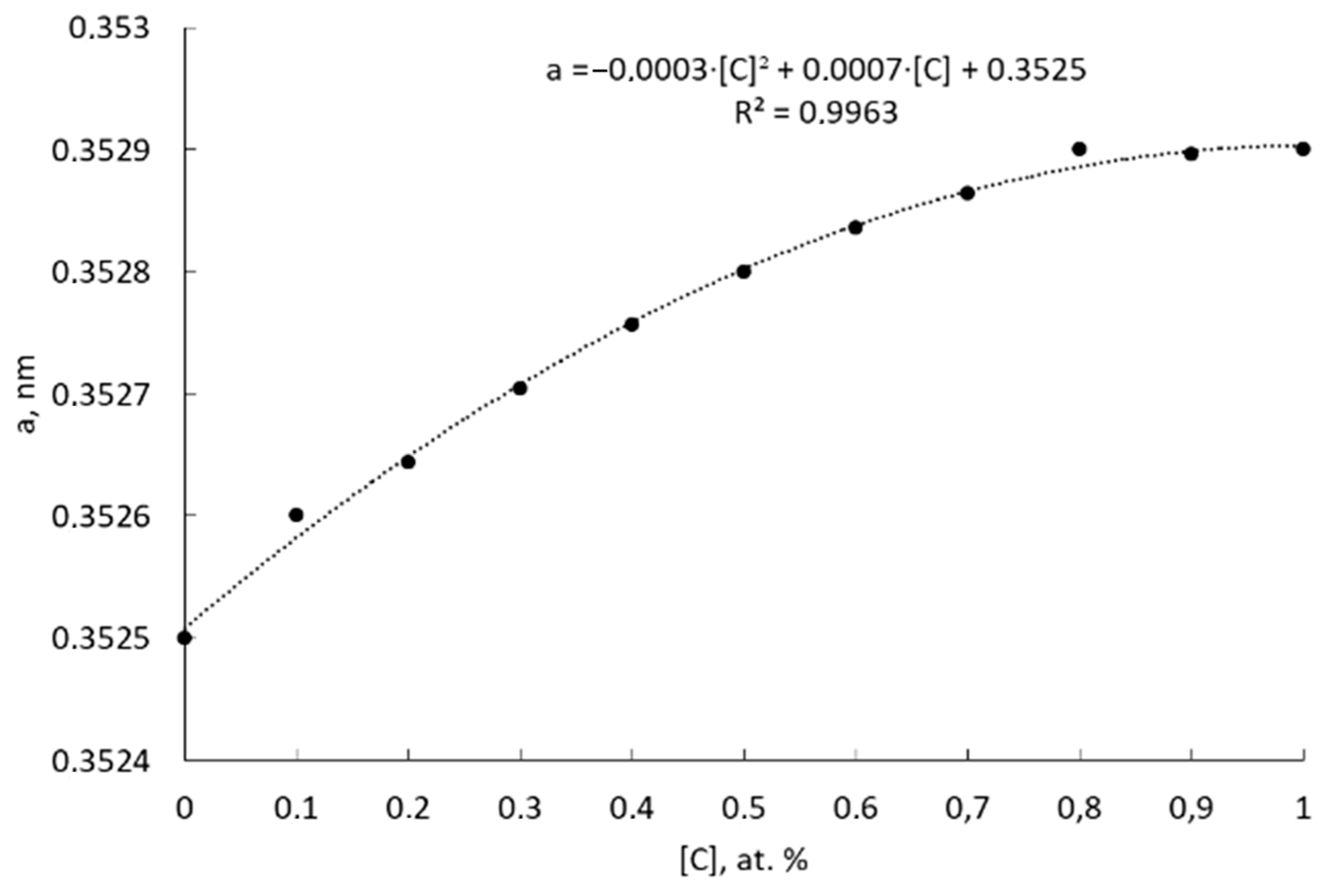
• It is also solid solution strengthening by carbon (0.1–0.3 at.% in the Ni solid solution), giving a contribution of Δσ_SS ≈ 45–135 MPa.
• Texture and elongated grain morphology formed during SPS under pressure create an additional contribution of Δσ_texture ~50–150 MPa. TEM shows pronounced elongation of grains (Figure 1a,b), similar to structures after severe plastic deformation [47]. Models that take into account the shape factor predict an increase in yield strength of 10–30% compared to an isotropic fine-grained structure [48]. For σ ~525 MPa, this yields Δσ_texture ~50–150 MPa.
• It is also the result of the synergistic contribution of SiC decomposition products. Thermodynamic modeling and analysis of chemical potentials unequivocally demonstrated the thermodynamic instability of the Ni-SiC system at a sintering temperature of 850 °C. The decomposition of SiC nanoparticles results in the formation of free carbon (pyrolytic carbon at the boundaries) and, as hypothesis, nickel silicides (Ni₂Si and NiSi). According to classical Zener theory, the efficiency of grain growth inhibition is determined by both the volume fraction and the particle size. The nanoscale silicide and pyrolytic carbon precipitates formed as a result of the controlled decomposition of SiC localize precisely at the grain boundaries. These nuclei are exceptionally effective for boundary pinning, which explains the stability of the UFG structure with such small total additions. At an ultralow SiC content of 0.001 wt.%, the resulting silicide interlayers are discontinuous and serve as effective barriers to dislocations, preventing the formation of continuous brittle phases. At the same time, the released carbon partially dissolves in nickel (solid solution strengthening) and partially forms nanoscale precipitates of pyrolytic carbon, which also inhibits dislocation motion and boundary migration.

Total calculated strength increase:

Δσ_total ≈ Δσ_HP + Δσ_SS + Δσ_texture ≈ 295 to 685 MPa

The high diffusion rate of carbon in nickel at the sintering temperature, confirmed by both calculations and experimental data on the concentration gradient, ensures rapid redistribution of carbon along the grain boundaries, contributing to the stabilization of the ultrafine-grained structure.

Thus, the strengthening extremum at 0.001 wt.% SiC is a consequence of the optimal balance:

−

maximum contribution from grain refinement (Hall–Petch) and elongated texture;

−

significant solid solution strengthening;

−

stabilizing influence of controlled SiC decomposition (pyrolytic carbon, silicides) products without the formation of extensive brittle phases;

−

efficient kinetic provision of these processes due to the high diffusion mobility of carbon.

With an increase in SiC content (>0.001 wt.%), the amount of decomposition products increases, which leads to the formation of more continuous and, possibly, brittle silicide interlayers, which can become centers of crack initiation, explaining the decrease in strength.

For practical application, it is important that the resulting ultrafine-grained structure has good long-term thermal stability. As part of this study, short-term tests were conducted at 400 °C. Based on the results of the microstructural analysis and modeling, the following predictions can be made: (1) According to Zener’s theory, nanoparticles of pyrolytic carbon and, as hypothesis, silicides localized at grain boundaries are effective seeds for their fixation, which should prevent grain coalescence. (2) The solid solution of carbon in nickel is metastable. According to the results of thermodynamic modeling (see Figure 8 and Figure 15), carbon separation from the lattice becomes energetically favorable at temperatures above 600–800 K; therefore, prolonged exposure at elevated temperatures could result in a change to the hardening mechanism due to the decomposition of the solid solution and coagulation of precipitates.

The record bending strength value obtained for the Ni–0.001SiC composite (1130 MPa) is also of interest in a comparative context with nickel hardened by alternative consolidation methods. Direct comparisons of the effectiveness of these methods, as reported in the literature, clearly demonstrate the superiority of technologies with a short processing cycle. For example, in the work of Bousnina et al. [26], consolidation of nickel nanopowder by hot isostatic pressing at 650 °C for one hour resulted in grain growth to 0.4–0.62 µm and a yield strength of 1160 MPa. Using spark plasma sintering (SPS) at a lower temperature (600 °C) and for only 5 min made it possible to preserve a grain size of 0.17–0.2 µm and achieve a yield strength of 1730 MPa [26]. Martinez et al. [49] demonstrated a similar trend, showing that hot pressing (HP) of nanostructured nickel at 300 °C and 900 MPa for 2 min provided a nanohardness of 9.4 GPa. However, GYPSUM at 900 °C and 150 MPa for 1 h led to grain growth and a decrease in hardness to 3.3 GPa [49]. These studies confirm the key advantage of fast methods (SPS and HP): the ability to minimize grain growth, which is critical for implementing the Hall–Petch hardening mechanism.

Further studies have shown that varying the temperature and pressure during sintering allows the microstructure of nickel to be controlled in terms of grain size (from 5 to 45 microns), density, and the fraction of twin boundaries. This directly correlates with the material’s mechanical properties [9]. Notably, SPS enables the production of bulk ultrafine-grained materials with a high proportion of Σ3 boundaries, offering a balance of strength and ductility [46]. However, significant deviation from the Hall–Petch law is observed during the consolidation of nickel nanopowders with an ultrafine-grained structure by the SPS method, due to an additional contribution to hardening from high-density defects and residual stresses [50].

In the context of the present study, the combination of pre-mechanical activation and SPS enabled the preservation of the ultrafine-grained structure (~0.25 microns). Furthermore, the addition of solid solution hardening and dispersion precipitates was observed, a consequence of the controlled decomposition of SiC nanoparticles. This resulted in the attainment of bending strength (1130 MPa), which is comparable to the optimal values for nanostructured nickel achieved through methods of intense plastic deformation (800–1100 MPa [44,46]), yet with the capacity for the fabrication of products of a more intricate nature. It is evident that the selected technological chain exhibits superiority in comparison to conventional powder metallurgy methodologies, particularly with regard to attaining the optimal range of mechanical properties through the synergistic microstructure control at multiple levels.

The mechanical properties of polycrystalline metals, particularly microhardness, are predominantly influenced by the grain size, which is conventionally characterized by the Hall–Petch ratio. This dependence has been repeatedly confirmed in experimental studies of pure nickel. In the research conducted by Yang and Wehoff [51], the electrodeposition of nano- and microcrystalline nickel was examined. The study demonstrated that the microhardness, measured at a load of 490 mN, exhibited a continuous increase with a decrease in the average grain size (d) from 30 µm to 1.5 µm, following a specific dependence. However, when the scale was reduced to the nanoscale (d < 1 µm), saturation of hardness growth was observed. The authors attributed this occurrence to the activation of novel deformation mechanisms, including sliding along grain boundaries. This hypothesis was supported by atomic force microscopy observations at room temperature [51]. Furthermore, it was demonstrated that the process of nanoindenting individual grains resulted in the attainment of maximum hardness when the size of the indent became comparable to the grain size. This underscores the pivotal function of the ratio of the scales of the plastic zone and the microstructure [51].

In the context of materials obtained by spark plasma sintering (SPS), the dependence of hardness on grain size also obeys the Hall–Petch law, but with adjustment for a specific substructure. A study by de la Cruz et al. [46] demonstrated a pronounced correlation between the tensile yield strength and the grain size in the range from 25 to 4.5 microns in pure nickel sintered from pre-mechanically activated powders. In the course of the transition to the ultrafine-grained state (d < 1.2 microns), a deviation from the linear Hall–Petch dependence towards high strength values was observed. The authors attribute this deviation to the heterogeneity of deformation at the yield stage (the Luders effect), as well as to the possible presence of irregular grain boundaries formed as a result of intense plastic deformation during mechanical alloying [46]. It is important to note that all the samples in this study had a high density (>97%) and were characterized by a low level of internal stresses, as confirmed by electron microscopy data and analysis of the spread of crystallographic orientations [46].

In addition to grain size, intragrain substructures such as dislocation cells and deformation twins have a key effect on hardening. A seminal study by Groehlich and Murr [52] on nickel of 99.98% purity, subjected to shock-deformation, demonstrated that the residual microhardness and yield strength are determined by the combined contribution of three scale parameters: grain size (D), dislocation cell size (d), and the distance between twins (Δ). Empirical evidence has demonstrated that, for pressures falling below the twinning threshold (~300 kbar), the residual strength is determined by the first two microstructural factors, following the relation: σ = σ₀ + K⋅D⁻¹/² + K′⋅D⁻², where m varies from 0.5 to 1. In the context of higher pressures, the formation of deformation twins necessitates the incorporation of an additional term that accounts for the intertwin spacing (Δ). This results in the following expression: σ = σ₀ + K⋅D⁻¹/² + K′⋅d⁻¹/² + K″⋅Δ⁻¹/² [52]. It has been demonstrated that dislocation cells and twins function as an effective subgrain, thereby reinforcing the material in accordance with the principle of similarity. The contribution of these subgrains can be comparable to, and in some cases even exceed, that of high-angle grain boundaries [52].

Our experimental microhardness data (Vickers measurements, 200 gs load, 10 s exposure) for materials obtained by the SPS method are consistent with these fundamental patterns and demonstrate the influence of both grain size and dispersed additives (Table 1).

As can be seen from the table, pure sintered nickel powder exhibits the lowest hardness (70 HV), which is typical for a coarser-grained state with minimal dislocation density. The samples obtained by the SPS method with the addition of ultralow amounts of silicon carbide nanoparticles show a significant increase in hardness. This effect cannot be explained solely by classical dispersion hardening by Orowan due to the negligibly small volume content of particles. A key role is played by the synergistic hardening mechanism, which includes (1) Hall–Petch hardening due to the formation of an ultrafine-grained (0.15–0.4 microns) and subgrain structure stabilized by SiC decay products at the boundaries; (2) solid solution hardening by carbon atoms diffusing into the nickel lattice from SiC particles and graphite tooling (concentration ~0.1–0.3 at.%); (3) hardening due to the textural component due to the elongated morphology of the grains formed during SPS. Thermodynamic and kinetic modeling confirm the possibility of SiC decomposition at a sintering temperature (850 °C) with the formation of nickel silicides (Ni₂Si, NiSi) and free carbon. These nanoscale products localized at grain boundaries serve as effective barriers to dislocation movement and boundary migration. When the SiC content is increased above the optimal level (~0.001–0.005 wt.%), it is possible to form more extended and brittle layers of silicides, which become centers of crack nucleation, which explains the decrease in hardness for the composition from 0.015 wt.% SiC.

An important aspect reflected in the review work of Tseluikin [53] is that the introduction of dispersed SiC particles (micro- and nanoscale) into the Ni metal matrix leads to the grinding of the grain of the deposited coating. This effect, observed for nickel composites with nanotubes or carbides, directly contributes to the growth of microhardness by the Hall–Petch mechanism, which is consistent with our results on Ni-SiC composites.

The observed extreme of properties at a certain content of the dispersed phase indicates the need for careful selection of its concentration for an optimal balance between boundary hardening and the risk of embrittlement.

5. Conclusions

• Composites of the Ni–ySiC system (y = 0.001, 0.005, 0.015 wt.%) with improved mechanical properties were obtained by mechanical activation and spark plasma sintering at 850 °C in graphite tooling.
• For the Ni–0.001SiC composite, the flexural strength at 20 °C increased by 115% (to 1130 MPa) and at 400 °C by 86% (to 976 MPa) compared to sintered nickel without additives. At higher SiC contents, a decrease in strength is observed, indicating the presence of a property extremum at 0.001 wt.% nanoparticles.
• Microstructural analysis showed an ultrafine-grained structure of sintered nickel (0.15–0.4 µm), with elongated grains, the presence of pyrolytic carbon at the boundaries, and a carbon concentration in the solid solution of ~0.1–0.3 at.%. A significant part of the carbon (~6–7 at.%) is present in the form of a free phase.
• Comprehensive thermodynamic (chemical potentials) and kinetic (diffusion) modeling confirmed the possibility of SiC decomposition with the formation of free carbon and Ni silicides (Ni₂Si, NiSi) at SPS temperatures. It is shown that with an increase in temperature from 300 K to 1273 K, the stability regions of nickel silicides expand, and the SiC region narrows, which thermodynamically favors reactions at the interface.
• The property extremum at 0.001 wt.% SiC is explained by the synergy of several strengthening mechanisms: solid solution (carbon), grain boundary (Hall–Petch for ultrafine-grained structure), dislocation (high dislocation density and elongated grain shape), as well as structure stabilization by the products of controlled SiC decomposition (pyrolytic carbon, silicides as hypothesis), while minimizing the negative influence of extensive brittle phases.

The obtained results are important for the development of high-strength and thermally stable nickel composites, promising for application in aerospace engineering and power plants.