An Adaptive Concurrent Multiscale Approach Based on the Phase-Field Cohesive Zone Model for the Failure Analysis of Masonry Structures

Abstract

Simulating damage phenomena in masonry structures remains a significant challenge because of the intricate and heterogeneous nature of this material. An accurate evaluation of fracture behavior is essential for assessing the bearing capacity of these structures, thereby mitigating dramatic failures. This paper proposes an innovative adaptive concurrent multiscale model for evaluating the bearing capacity of in-plane masonry structures under in-plane loadings. Developed within a Finite Element (FE) set, the proposed model employs a domain decomposition scheme to solve a combination of fine- and coarse-scale sub-models concurrently. In regions requiring less detail, the masonry is represented by homogeneous linear elastic macro-elements. The material properties for these macro-elements are derived through a first-order computational homogenization strategy. Conversely, in areas with higher resolution needs, the masonry is modeled by accurately depicting individual brick units and mortar joints. To capture strain localization effectively in these finer regions, a Phase Field Cohesive Zone Model (PF-CZM) formulation is employed as the fracture model. The adaptive nature derives from the fact that at the beginning of the analysis, the model is entirely composed of coarse regions. As nonlinear phenomena develop, these regions are progressively deactivated and replaced by finer regions. An activation criterion identifies damage-prone regions of the domain, thereby triggering the transition from macro to micro scales. The proposed model’s validity was assessed through multiscale numerical simulations applied to a targeted case study, with the results compared to those from a direct numerical simulation. The results confirm the effectiveness and accuracy of this innovative approach for analyzing masonry failure.

1. Introduction

Masonry buildings are a significant part of the world’s architectural heritage, and many of these structures, especially residential ones, hold considerable cultural and historical value. Consequently, preserving and restoring them has become a key priority for promoting sustainable urban development and reducing land consumption [1,2,3].

To effectively rehabilitate these buildings, it is essential to have a thorough understanding of their structural behavior under normal and exceptional loads [4]. While masonry is effective at resisting gravitational forces, it is inherently vulnerable to lateral forces, such as those caused by earthquakes [5,6]. These seismic forces can induce severe cracking and a subsequent loss of structural integrity, often leading to partial or total collapse. To address this critical vulnerability, developing accurate and reliable analysis tools is essential for assessing these structures and creating suitable strengthening strategies [7].

In recent years, numerical methods have become a primary tool for evaluating the fracture behavior of materials [8,9,10,11,12]. They allow for the simulation of the complex mechanical behavior of materials and provide valuable insights into the initiation and propagation of cracks. However, accurately modeling masonry’s behavior is a significant challenge due to its heterogeneous nature. The mechanical response of masonry material heavily depends on the properties of its constituent components—namely, brick units and mortar joints—their arrangement, and the quality of the bond between the brick and mortar, often characterized in numerical and experimental analyses by the Interfacial Transition Zone (ITZ). This complexity leads to anisotropic behavior, where the strength properties vary based on the load orientation [13,14]. Additionally, this anisotropy can worsen with deformation and damage, introducing further nonlinearities into the structural response.

Numerical approaches for modeling masonry are typically classified according to the scale of analysis, so that one can distinguish between micro- and macro-modeling methods [15,16].

Micro-modeling approaches represent masonry in detail at the level of its individual components, specifically the blocks or units and mortar joints [17,18]. This feature enables a comprehensive analysis of the mechanical behavior of each material constituent and its interactions, such as adhesion and friction, as well as the overall pattern of the masonry. Notable examples of micro-modeling strategies include detailed and simplified approaches. In the detailed approach [7,19], brick or block units and mortar joints are modeled using continuum elements that are interconnected by discontinuous elements, thereby effectively reproducing damage phenomena (such as adhesion) that occur at the interfaces between units and mortar. On the other hand, the simplified approach [20] represents masonry using expanded brick units modeled with continuum elements that are connected by zero-thickness interface elements. These interface elements replicate both the mechanical behavior of the mortar joint and the interaction mechanics at the brick/mortar interfaces.

While micro-modeling strategies offer better simulation of material anisotropy and a more realistic representation of strain localization and damage mechanisms under various loading conditions, they have significant drawbacks. The most notable limitation is the substantial computational demand required for numerical simulations. This challenge makes it impractical to apply micro-modeling approaches to entire masonry structures, thereby restricting their use to smaller elements, such as portions of masonry buildings.

Macro-modeling approaches schematize the masonry as a fictitious homogeneous and anisotropic material. The mechanical properties assigned to this material are therefore phenomenological [21]. In this category, a notable example is the smeared crack model (SCM), which incorporates the effects of microscale cracking into the continuum constitutive law by degrading the material stiffness (smeared damage) [22,23].

Depending on the specific application, these models can utilize either linear or nonlinear elements. In cases where nonlinear behavior is considered, the structural response of the masonry is modeled using nonlinear frameworks based on damage continuum mechanics and/or plasticity theory. One notable advantage of these modeling approaches is their relatively low computational requirements, making them an effective means of simulating the behavior of entire masonry buildings.

However, macro-modeling approaches also have significant limitations. A major drawback is their reduced accuracy in predicting damage mechanisms and strain localization since they do not explicitly represent individual masonry components. Additionally, these models may struggle to accurately capture the anisotropic behavior of masonry, in which mechanical properties vary according to the orientation of loads in relation to the arrangement of blocks and joints. Furthermore, the calibration of model parameters to align with experimental data or field observations can be complex, time-consuming, and particularly challenging when dealing with various types of masonry that have differing properties.

In recent years, a substantial body of research has underscored the potential of multiscale modeling strategies in accurately predicting and reproducing the mechanical behavior of masonry. Multiscale approaches encompass modeling techniques that simulate the mechanical behavior of a material across various scales, integrating detailed information about material constituents at the microscopic level with the structural behavior of the entire structure at the macroscopic level [24,25].

These multiscale modeling approaches can be categorized into three primary types: (i) hierarchical models, (ii) semi-concurrent models, and (iii) concurrent models [26].

Hierarchical models follow a sequential process in which information flows in a “one-way” direction from the microscale to the macroscale [24,27,28]. In this framework, detailed analyses are executed at smaller scales, and the resultant data informs the parameters and behaviors at larger scales. These models are based on the assumptions that the scales are sufficiently distinct and that the material exhibits macroscopic homogeneity.

The implementation of such models necessitates the definition of a Representative Volume Element (RVE), for which a thorough microscopic analysis is conducted to derive the overall macroscopic constitutive law utilizing a homogenized method amenable to numerical analyses at the macroscale. The mathematical rigor for this multiscale separation, especially concerning materials with a periodically repeating microstructure, is established by the asymptotic homogenization theory, pioneered by Sanchez-Palencia [29]. This framework provides a formal justification for calculating the effective macroscopic properties from the periodic microscale unit cell, aligning conceptually with the initial step of defining the RVE and deriving the constitutive law. Various homogenization methodologies, including those based on Cauchy or Cosserat macro-continuum theories, are applicable [30,31,32,33]. The primary advantage of hierarchical models resides in their efficiency, as computational resources are concentrated on critical aspects at each scale, rendering them less computationally demanding than alternative multiscale methods. Nevertheless, a significant limitation is the potential loss of intricate interaction effects between scales, which can compromise the accuracy of predictions related to complex coupled behaviors. Furthermore, the one-way flow of information may occasionally fail to capture essential feedback mechanisms between scales.

Semi-concurrent models utilize a “two-way” coupling between the microscopic and macroscopic scales [34,35,36]. In this design, the state variables derived from the analyses of the RVE are continuously transferred to the macroscopic model as overall stress fields and tangent operators, thereby facilitating a more precise representation of material behavior.

The principal advantage of semi-concurrent models is their ability to yield a more accurate depiction of strain localization phenomena. However, they may incur heightened computational demands and necessitate sophisticated methodologies to manage the interchange of information between scales effectively.

Concurrent models are distinguished by their simultaneous coupling of scales, wherein microscale behavior directly influences macroscale responses and vice versa throughout the entire simulation [37,38,39]. In contrast to hierarchical and semi-concurrent models that use “scale transitions,” concurrent multiscale models employ “scale embedding.” This means that sub-models of different scales can exist side-by-side in neighboring areas of the computational domain. Consequently, a heterogeneous structural model can be decomposed into fine-scale and coarse-scale regions, which are then solved concurrently.

This methodology confers the advantage of accurately representing strain localization phenomena, which are typically confined to fine regions of the computational domain, while concurrently achieving significant computational efficiencies by modeling undamaged regions with coarse representations.

Numerous concurrent multiscale models have been proposed and successfully employed to assess the structural response of masonry structures. Remarkably, Greco et al. [40] developed a multiscale model intended for analyzing the load-bearing capacity of periodic masonry structures subjected to in-plane loads. This model incorporates a multilevel domain decomposition strategy in conjunction with an adaptive refinement technique that enhances the resolution of computational domains likely to be impacted by strain localization. Specifically, in fine regions, the masonry is represented by expanded brick units interconnected through cohesive interface elements that replicate the mechanical behavior of mortar joints and brick/mortar interfaces during failure events. In contrast, coarse regions consist of macro-elements whose constitutive response is characterized by homogenized moduli derived through a first-order computational homogenization scheme.

Driesen et al. [41] proposed a concurrent multiscale domain activation strategy for the damage analysis of large-scale masonry structures. This model adeptly integrates elastic macroscale elements with nonlinear microscale regions, where the masonry is represented employing a simplified micro-model scheme consistent with expanded brick units connected by interface elements. An effective damage model for the interface is established to reproduce the expected behavior during loading accurately.

Such adaptive methods are rooted in general multiscale strategies like the adaptive Multiscale Finite Element Method (MsFEM) [42], whose combination with discontinuity tracking tools such as the eXtended Finite Element Method (XFEM) [43] enables the efficient handling of non-periodicity and fracture propagation in composite materials, aligning with the principles of enhanced computational efficiency.

The main goal of this research is to present a new adaptive concurrent multiscale model. Based on the Finite Element Method (FEM), this model quantifies the bearing capacity of periodic masonry structures subjected to in-plane loading. This context (periodicity of the masonry and in-plane loadings) ensures computational feasibility of the nonlinear PF-CZM micro-analysis and facilitates rigorous validation against established 2D numerical benchmarks.

Similar to the modeling strategies in [40], the proposed approach uses domain decomposition, splitting the computational domain into coarse and fine regions. The coarse regions consist of linear elastic macroscopic elements, and the homogenized elastic tensor, which describes the constitutive behavior, is determined through a first-order homogenization of an RVE of the masonry [44]. The fine regions utilize a detailed micromechanical model for masonry to accurately capture the failure mechanisms. Precisely, a detailed representation of masonry is adopted, treating it as a two-phase material (brick units and mortar joints). The Phase Field Cohesive Zone Model (PF-CZM) developed by Wu et al. [23,45,46] is then utilized to accurately capture the fracture and failure mechanisms. With its ability to reproduce arbitrary crack paths in homogeneous and heterogeneous materials, this model represents one of the most powerful cohesive fracture approaches available in the literature. A key distinction of the PF-CZM from classical phase-field models lies in its fracture response, which shows an almost negligible dependence on the length scale parameter. This represents a significant improvement, as the length scale parameter strongly influences the numerical predictions of other phase-field models. In particular, the proposed model employs a hybrid isotropic/anisotropic formulation of the PF-CZM model, which is based on an appropriate crack-driving force consistent with a Drucker–Prager model featuring a compressive cap, tailored for analyzing masonry.

The transition from coarse to fine scales is managed by an activation approach, which progressively refines the areas of the computational domain where damage is anticipated. Specifically, coarse regions are deactivated, and fine regions are activated in their place to capture the development of damage.

The assumption of linear elastic behavior for the coarse regions is fundamental to the adaptive multiscale logic. Of course, real masonry exhibits a highly nonlinear response, so that the purely elastic range is very narrow. Nevertheless, in analyzing large-scale masonry structures, vast portions often remain lightly loaded, and for these coarse regions, assuming linear elasticity provides a significant computational saving using homogenized properties. The full nonlinear behavior is captured only where necessary, as the nonlinear PF-CZM micro-scale model is activated only when the elastic limit is reached, ensuring computational efficiency.

To the best of the authors’ knowledge, this work represents the first attempt to develop an adaptive concurrent multiscale approach to analyze the failure behavior of masonry structures using the PF-CZM to replicate fracture mechanisms.

Existing multiscale strategies present significant limitations that hinder their systematic application. Hierarchical models often neglect the mechanical feedback from the micro-scale, while fully concurrent approaches impose an unsustainable computational load for large-scale structures. Semi-concurrent models, while necessary for two-way information exchange, face inherent challenges related to computational demands, implementation complexity, and accuracy. As a matter of fact, managing the continuous and complex two-way exchange of information (like stress fields and tangent operators) requires sophisticated and complex implementation. Besides, the accuracy of these methods can be compromised by approximation errors in the coupling and homogenization processes. These errors are particularly relevant in scenarios with complex nonlinear material behavior or geometric constraints, such as the case of masonry structures. The method proposed in this work aims to fill these gaps. Specifically, the PF-CZM coupling guarantees an accurate, energy-based description of fracture phenomena. Crucially, the use of the first-failure surface concept provides a mechanistically rigorous and predictive activation criterion. This adaptive approach allows for selective and autonomous activation of the micro-scale only when local failure is imminent, thus optimally balancing computational efficiency with predictive accuracy.

Different case studies are conducted to evaluate the reliability and efficiency of the proposed multiscale approach. Initially, the PF-CZM model for fracture is validated through comparisons with experimental and numerical results available in the literature. Following this, we focus on large-scale masonry structures. The results obtained from the proposed multiscale approach are compared to those from equivalent direct numerical simulations, which use a fully microscopic model for masonry.

The remainder of the paper is organized as follows: Section 2 presents the main theoretical concepts underlying the proposed numerical model. Section 3 discusses numerical implementation. Finally, Section 4 and Section 5 report the numerical results and the conclusions of the work.

2. Governing Equations and Theory

This section details the theoretical foundation of the new adaptive concurrent multiscale model. The section starts with a comprehensive description of the micro- and macro-modeling approaches, which are used to represent masonry behavior in the finer and coarser portions of the computational domain, respectively. We then describe the activation criterion that governs the dynamic refinement of the domain, highlighting the importance of the first failure surface in masonry for this process.

2.1. A Detailed Micromechanical Model for Reproducing Failure Mechanisms Inside the Masonry

This section provides a comprehensive description of the micromechanical modeling strategy used to reproduce the complex failure behavior of the masonry accurately. The approach is based on a detailed representation of the material at its constituent level, effectively treating masonry as a two-phase composite material. This model explicitly accounts for the individual characteristics of the solid brick units and the mortar joints, as well as their mechanical interaction.

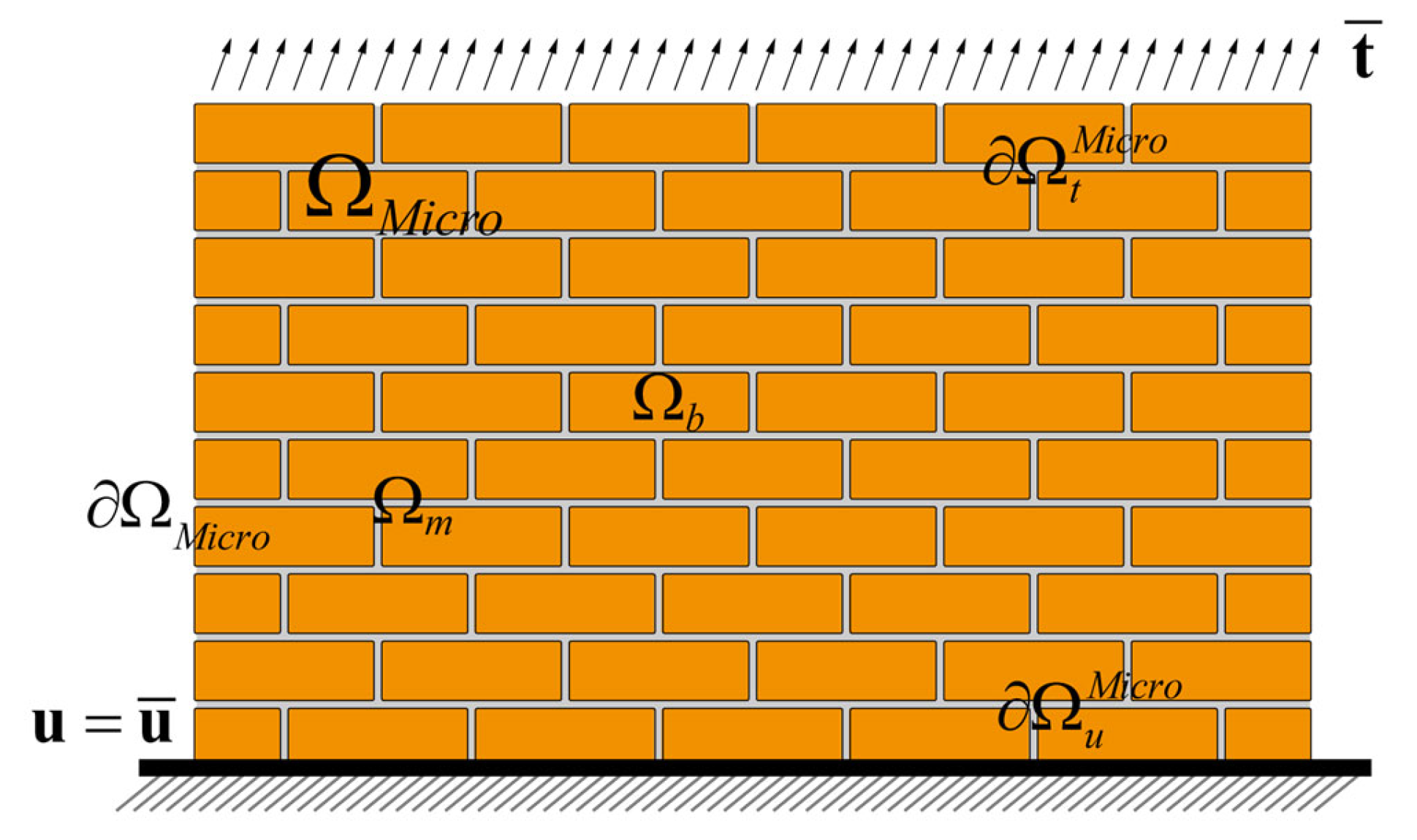
Without loss of generality, consider the conceptual scheme of Figure 1, which illustrates a 2D periodic masonry panel made of regular brick units interconnected by a network of horizontal and vertical mortar joints. This structure occupies a defined computational domain, denoted as Ω_Micro, whose external boundary ∂Ω_Micro is partitioned into two distinct sub-regions, $\partial {\mathsf{\Omega }}_t^{Micro}$ and $\partial {\mathsf{\Omega }}_u^{Micro}$. These sub-regions are used to apply Neumann and Dirichlet boundary conditions, respectively. Precisely, external tractions $\overline{t}$ [N/m²] are applied on $\partial {\mathsf{\Omega }}_t^{Micro}$, while prescribed displacements $\overline{u}$ [m] are imposed on $\partial {\mathsf{\Omega }}_u^{Micro}$ (being $u$ the displacement field).

A fundamental assumption of this model is that the brick units (${\mathsf{\Omega }}_b$) behave as linear elastic and are considered undamaged. In contrast, the mortar joints (${\mathsf{\Omega }}_m$) are assumed to be the primary locations of potential damage.

This hypothesis is well-supported by extensive experimental evidence, which shows that the strength and fracture properties of mortar are typically significantly lower than those of the brick units. Consequently, the failure mechanisms in masonry are predominantly characterized by crack nucleation and propagation within the mortar joints, leading to a typical “staircase” crack pattern. In this framework, the failure of mortar joints are simulated utilizing the Phase Field Cohesive Zone Model (PF-CZM), a method originally introduced by Wu et al. [23]. The primary principle of the PF-CZM is to represent a sharp crack ${\mathsf{\Gamma }}_c$ as a diffuse band of finite width, rather than as a discrete line. The extent of damage within this band is quantified using a continuous scalar field known as the unknown phase-field or damage field $\varphi (x)$, which ranges from 0 to 1. In particular, $\varphi (x)$ = 0 indicates intact material, while $\varphi (x)$ = 1 signifies a fully damaged state.

Under the assumptions of quasi-static loading and small displacements, the governing equations of the solid mechanics problem can be stated in weak form as follows:

$$-{\displaystyle \underset{{\mathsf{\Omega }}_b}{\int }\left(C_b:\nabla u\right)\cdot \delta \nabla u\hspace{0.17em}dV}-{\displaystyle \underset{{\mathsf{\Omega }}_m}{\int }\left(C_m:\nabla u\right):\delta udV}+{\displaystyle \underset{{\mathsf{\Omega }}_{Micro}}{\int }f\cdot \delta udV}+{\displaystyle \underset{\partial {\mathsf{\Omega }}_t^{Micro}}{\int }\overline{t}\cdot \delta udA}=0$$

(1)

where C_b and C_m are the fourth-order constitutive tensors of the brick units and mortar [N/m²], respectively. Besides, $\nabla (·)$ is the gradient operator, f is the body force [N/m³] vector, and u and δu represent the unknown displacement field and the virtual displacement field, respectively, defined as:

$$\begin{array}{l}u=\left\{u\in H^1\left({\mathsf{\Omega }}_{Micro}\right)|u=\overline{u}\hspace{0.17em}\hspace{0.17em}\mathrm{on}\hspace{0.17em}\hspace{0.17em}\partial {\mathsf{\Omega }}_u^{Micro}\right\}\\ \delta u=\left\{\delta u\in H^1\left({\mathsf{\Omega }}_{Micro}\right)|\delta u=0\hspace{0.17em}\hspace{0.17em}\mathrm{on}\hspace{0.17em}\hspace{0.17em}\partial {\mathsf{\Omega }}_u^{Micro}\right\}\end{array}$$

(2)

where $H^1$ represents the Sobolev space defined over the entire domain ${\mathsf{\Omega }}_{Micro}$.

Because the mortar joints are damageable, the fourth-order constitutive tensor is expressed as follows [47]:

$$C_m=C_m\left(\varphi \right)=\omega \left(\varphi \right)C_m^0$$

(3)

In Equation (3) $\omega (\varphi )$ represents the energy degradation function [adim.], while $C_m^0$ is the undamaged elasticity tensor of the mortar [48].

According to the phase field approach, the governing equation of the crack problem can be expressed in weak form as follows:

$${\displaystyle \underset{{\mathsf{\Omega }}_m}{\int }\frac{\partial {\psi }_m(\epsilon ,\varphi )}{\partial \varphi }\delta \varphi dV}+{\displaystyle \underset{{\mathsf{\Omega }}_m}{\int }{G}_c\left[\frac{\partial \gamma }{\partial \varphi }\delta \varphi +\frac{\partial \gamma }{\partial \nabla \varphi }\delta \nabla \varphi \right]dV}\ge 0$$

(4)

where ${\psi }_m(\epsilon ,\varphi )$ is the strain energy of the mortar [J/m³], G_c is the critical energy release rate of the mortar [J/m²], and $\gamma =\gamma \left(\varphi ,\nabla \varphi \right)$ represents the crack surface density function [m⁻¹] generally defined as:

$$\gamma (\varphi ,\nabla \varphi )={\displaystyle \frac{1}{c_0}}\left[{\displaystyle \frac{1}{l_0}}\alpha \left(\varphi \right)+l_0\nabla \varphi \cdot \nabla \varphi \right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{c}_0=4{\displaystyle {\int }_0^1\sqrt{\alpha \left(\varphi \right)}d\varphi }$$

(5)

In Equation (5), l₀ is the length scale parameter that manages the thickness of the spread band reproducing the crack [m], while $\alpha (\varphi )\in [0,1]$ represents the so-called “geometric crack function” [adim.], which describes how the phase-field variable distributes within the band:

$$\alpha \left(\varphi \right)=\xi \varphi +\left(1-\xi \right){\varphi }^2\hspace{0.17em}\hspace{0.17em}\forall \varphi \in \left[0,1\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}\xi \in \left[0,2\right]$$

(6)

The proposed approach adopts a hybrid formulation [22], according to which two different energy functions for the mortar are used to define the damage evolution law and the stress field, specifically:

$${\psi }_m(\nabla u,\varphi )=\omega (\varphi ){\psi }_{m0}\left(\nabla u\right)$$

(7)

$${\overline{\psi }}_m(\nabla u,\varphi )=\omega (\varphi ){\overline{\psi }}_{m0}\left(\nabla u\right)$$

(8)

So that one can write:

$$\sigma ={\displaystyle \frac{\partial {\psi }_m}{\partial \nabla u}}=\omega \left(\varphi \right){\sigma }_0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\sigma }_0={\displaystyle \frac{\partial {\psi }_{0m}}{\partial \nabla u}}=C_m^0:\nabla u$$

(9)

$${\displaystyle \frac{\partial {\overline{\psi }}_m(\nabla u,\varphi )}{\partial \varphi }}={\displaystyle \frac{\partial \overline{{\psi }_m}}{\partial \omega }}{\displaystyle \frac{\partial \omega (\varphi )}{\partial \varphi }}={\overline{Y}}_m{\omega }^{\prime }(\varphi )$$

(10)

In particular, according to Wu et al. [23,46], this degradation function can be expressed in the following general form for cohesive cracks:

$$\omega (\varphi )={\displaystyle \frac{{\left(1-\varphi \right)}^p}{{\left(1-\varphi \right)}^p+a_1\varphi +a_1{a}_2{\varphi }^2+a_1{a}_2{a}_3{\varphi }^3}}$$

(11)

In Equation (11), p ≥ 2, a₁ > 0, a₂, and a₃ govern the softening behavior of the material and are expressed as follows:

$$a_1={\displaystyle \frac{4l_{ch}}{\pi l_0}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{l}_{ch}={\displaystyle \frac{E_m{G}_c}{f_t^2}}$$

(12)

$$a_2=2{\left(-2k_0{\displaystyle \frac{G_c}{f_t^2}}\right)}^{2/3}-\left(p+{\displaystyle \frac{1}{2}}\right)$$

(13)

$$a_3\left\{\begin{array}{cc}0& p>2\\ {\displaystyle \frac{1}{a_2}}\left[{\displaystyle \frac{1}{8}}{\left({\displaystyle \frac{w_c{f}_t}{G_c}}\right)}^2-\left(1+a_2\right)\right]& p=2\end{array}\right.$$

(14)

where E_m is the Young’s modulus of the material [Pa] and f_t is the failure strength of the material [N/m²]. In addition, k₀ ≤ −0.5f_t²/G_c [N/m³] and w_c [m] are the initial modulus (slope) and the limit crack opening width of the cohesive law.

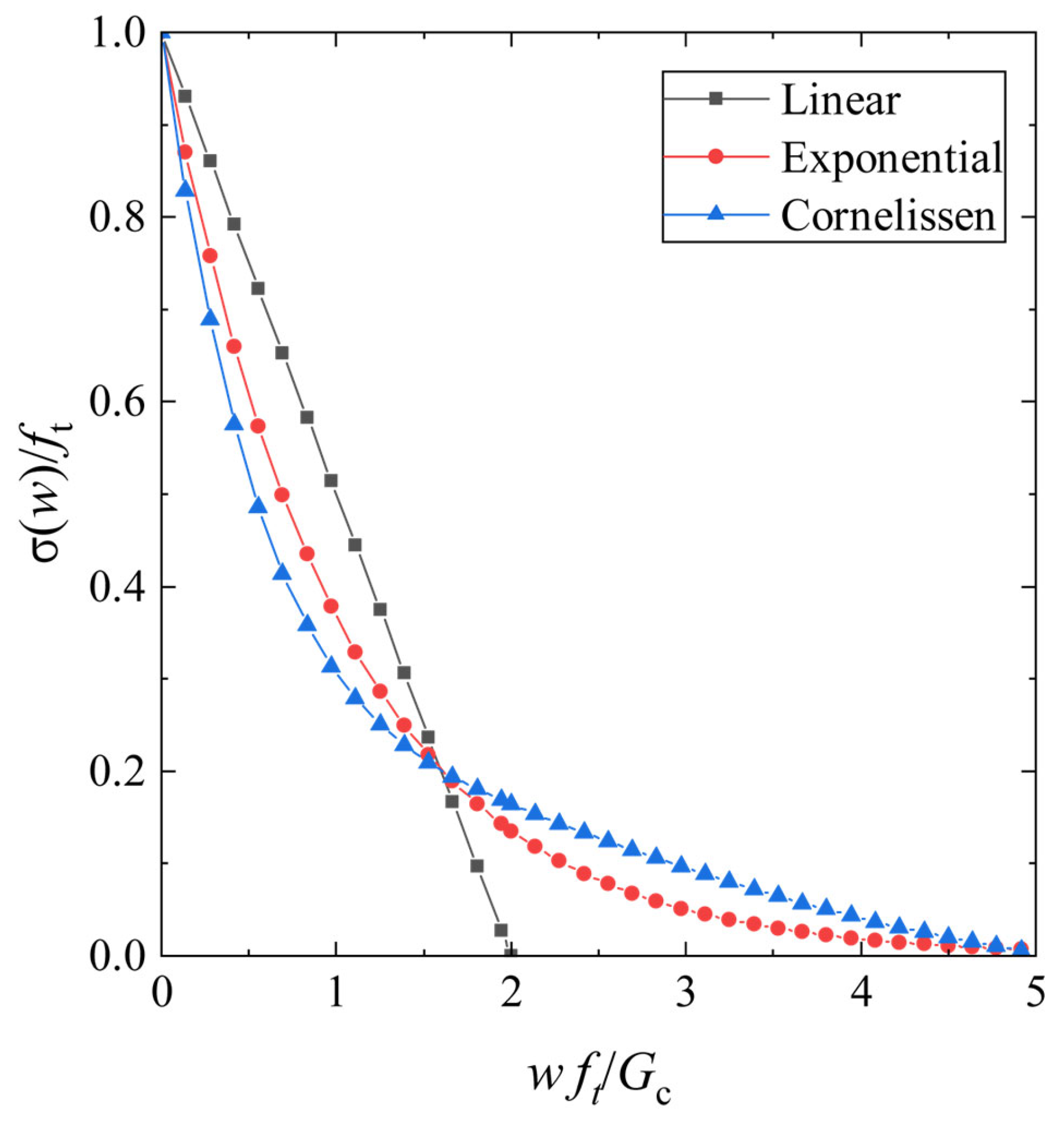
Note that the term l_ch in Equation (12) determines the size of the fracture process zone. In addition, the parameters a₂ and a₃ are determined solely by the chosen softening curves. The technical literature offers various options for these curves, such as linear, exponential, hyperbolic, and Cornelissen’s laws. These can be represented using the following values [22]:

$$\begin{array}{cc}\mathrm{Linear} \mathrm{softening} \mathrm{curve}& p=2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{a}_2=-0.5,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{a}_3=0;\\ \mathrm{Exponential} \mathrm{softening} \mathrm{curve}& p=2.5,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{a}_2=0.1748,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{a}_3=0;\\ \mathrm{Cornelissen}’\mathrm{s} \mathrm{softening} \mathrm{curve}& p=2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{a}_2=1.3868,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{a}_3=0.6567;\end{array}$$

(15)

Figure 2 compares the softening curves predicted by the PF-CZM model corresponding to the Linear, Exponential, and Corneliessen’s laws.

In the present study, the Cornelissen softening law was selected because it accurately represents the quasi-brittle behavior of the mortar after peak stress, which is characterized by a gradual, nonlinear decline in strength. This complex behavior is consistent with experimental evidence found in the literature for masonry joints [49,50].

The exponential represents a good alternative to the Corneliessen’s laws because the nonlinear decreasing trend is quite comparable. On the other hand, the linear softening law was discarded because it implies a constant stress release rate after the peak, which is fundamentally inaccurate for quasi-brittle materials like mortar. The linear model significantly underestimates the energy dissipation (area under the stress–displacement curve) at the beginning of the fracture process and often leads to convergence difficulties in finite element simulations due to the sharp change in stiffness immediately after the peak.

Returning to Equation (10), ${\overline{Y}}_m$ denotes the effective crack driving force. It is important to note that various approaches for defining this force are reported in scientific literature (see, for instance, [23,46,51]), often defined in terms of an equivalent effective stress. For the proposed model, the effective crack driving force is defined in terms of an equivalent strain ${\epsilon }_{eq}$, which is derived from a Drucker–Prager damage model that includes a compression cap [52]. Specifically, the following expressions for the effective crack driving force [N/m²] and the equivalent strain are employed:

$${\overline{Y}}_m={\displaystyle \frac{1}{2}}{E}_m{\epsilon }_{eq}^2$$

(16)

$${\epsilon }_{eq}=\left\{\begin{array}{ccc}A{I}_{1,\epsilon }+B{J}_{2,\epsilon }& \mathrm{if}& J_{2,\epsilon }\ge {\displaystyle \frac{A-C}{D-B}}{I}_{1,\epsilon }\\ C{I}_{1,\epsilon }+D{J}_{2,\epsilon }& \mathrm{if}& J_{2,\epsilon }<{\displaystyle \frac{A-C}{D-B}}{I}_{1,\epsilon }\end{array}\right.$$

(17)

where $J_{2,\epsilon }$ and $I_{1,\epsilon }$ represent the second invariant of the deviatoric strain tensor and the first invariant of the strain tensor, respectively. By assuming plane stress conditions, these variables can be defined as:

$$\begin{array}{l}{I}_{1,\epsilon }=\left({\displaystyle \frac{1-2{\nu }_m}{1-{\nu }_m}}\right)\left({\epsilon }_{xx}+{\epsilon }_{yy}\right)\\ J_{2,\epsilon }={\displaystyle \frac{1}{6}}\left\{{\left({\epsilon }_{xx}-{\epsilon }_{yy}\right)}^2+{\displaystyle \frac{1}{{\left(1-{\nu }_m\right)}^2}}\left[{\left({\nu }_m{\epsilon }_{xx}+{\epsilon }_{yy}\right)}^2+{\left({\epsilon }_{xx}+{\nu }_m{\epsilon }_{yy}\right)}^2\right]\right\}+{\displaystyle \frac{1}{4}}{\gamma }_{xy}^2\end{array}$$

(18)

In Equation (18), ${\nu }_m$ is the Poisson’s ration of the mortar, while A, B, C, and D are parameters expressed as a function of the uniaxial tensile ($f_t$), uniaxial compressive ($f_c$), and biaxial compressive $f_b$ (expressed as $f_b=1.2f_c$). They assume the following expressions:

$$A={\displaystyle \frac{1}{2}}{\displaystyle \frac{f_c-f_t}{f_c}};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}B={\displaystyle \frac{\sqrt{3}}{2}}{\displaystyle \frac{f_c+f_t}{f_c}};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}C={\displaystyle \frac{\left(f_b-f_c\right)f_t}{f_b{f}_c}};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}D=\sqrt{3}{\displaystyle \frac{\left(2f_b-f_c\right)f_t}{f_b{f}_c}}$$

(19)

According to the fundamental irreversibility condition that the crack phase-field $\varphi (x)$ must satisfy ($\dot{\varphi }\ge 0$), the effective crack driving force (${\overline{Y}}_m$) is typically replaced by a history variable $H_m$. This variable, which tracks the maximum value that ${\overline{Y}}_m$ was ever reached over the simulation, is defined as follows:

$$H_m=\max ({\overline{Y}}_{0m},\underset{n\in [0,T]}{\max }{\overline{Y}}_{n,m})$$

(20)

Here, ${\overline{Y}}_{0m}$ is the initial value of the effective crack driving force that fixes the threshold of the undamageable state, while ${\overline{Y}}_{n,m}$ represents the value of the crack driving force reached at time t_n within the time interval [0, T].

By incorporating the expressions from the previously mentioned equations, the weak forms of the solid mechanics and fracture problems assume the following final form:

$$\begin{array}{l}-{\displaystyle \underset{{\mathsf{\Omega }}_b}{\int }\left(C_b:\nabla u\right)\cdot \delta \nabla u\hspace{0.17em}dV}-{\displaystyle \underset{{\mathsf{\Omega }}_m}{\int }\left(\omega \left(\varphi \right)C_m^0:\nabla u\right):\delta udV}+{\displaystyle \underset{{\mathsf{\Omega }}_{Micro}}{\int }f\cdot \delta udV}+{\displaystyle \underset{\partial {\mathsf{\Omega }}_t^{Micro}}{\int }\overline{t}\cdot \delta udA}=0\\ {\displaystyle \underset{{\mathsf{\Omega }}_m}{\int }{H}_m{\omega }^{\prime }(\varphi )\delta \varphi dV}+{\displaystyle \underset{{\mathsf{\Omega }}_m}{\int }{G}_c\left[\frac{1}{c_0{l}_0}{\alpha }^{\prime }\left(\varphi \right)\delta \varphi +2\frac{l_0}{c_0}\nabla \varphi \cdot \delta \nabla \varphi \right]dV}=0\end{array}$$

(21)

2.2. Macroscopic Representation of the Masonry

The concurrent multiscale modeling approach necessitates an efficient strategy for representing the undamaged portions of the masonry structure. For this purpose, the proposed model treats the masonry at the macroscopic scale as a fictitious homogeneous material. This is achieved by schematizing the coarse regions using linear elastic macro-elements.

The mechanical properties of these elements are not phenomenological. Indeed, they are rigorously derived from the underlying microstructural details through a first-order computational homogenization scheme. This approach enables a seamless and accurate transition between scales, while achieving significant computational savings in regions where damage does not occur.

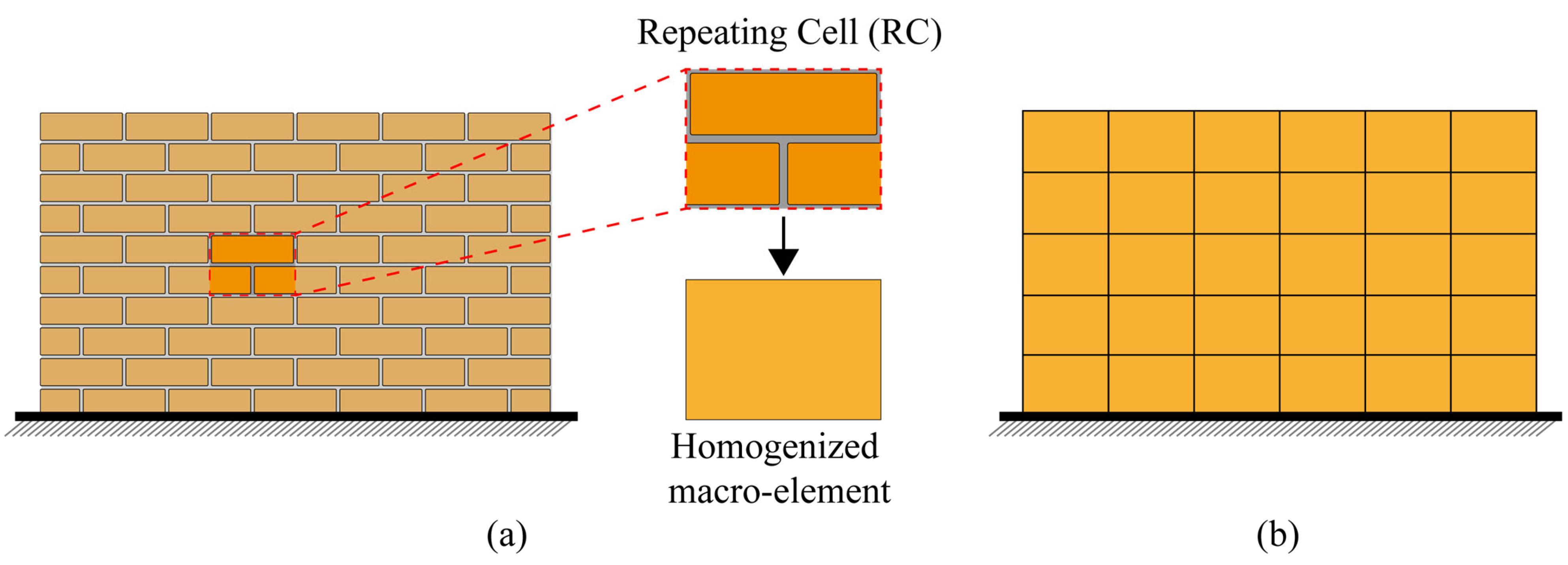
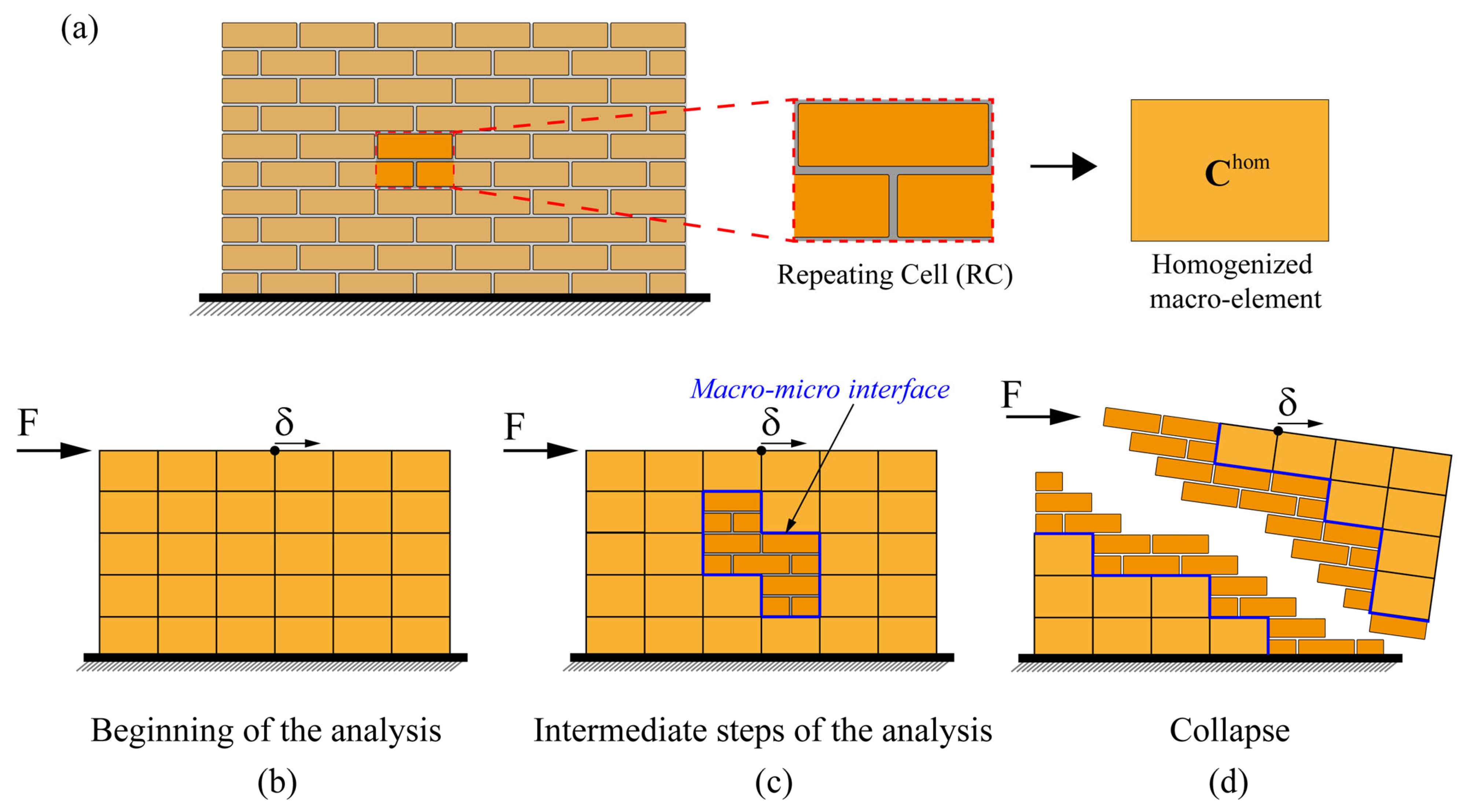
The core of this strategy lies in identifying a Repeating Cell (RC) within the periodic masonry investigated (Figure 3a). The macro-elements (Figure 3b) are defined with a size equal to this RC, and their constitutive behavior is described by a homogenized constitutive tensor $C^{\mathrm{hom}}$.

The elastic moduli of this tensor are derived from a standard numerical homogenization process that applies periodic boundary conditions to the RC. More precisely, using classic strain-driven periodic homogenization, the microscopic displacement field $u(x)$ is controlled by a defined macrostrain $\overline{\epsilon }$, as expressed in the equation:

$$u\left(x\right)=\overline{\epsilon }\cdot x+w\left(x\right)$$

(22)

In this expression, $\overline{\epsilon }\cdot x$ represents the uniform deformation, while the term $w(x)$ is the microscopic displacement fluctuation field, which adheres to the periodic boundary conditions on the opposing boundaries of the RC.

The process involves analyzing the linear elastic response of the RC (i.e., without the crack phase-field) under two uniaxial and one shear loading paths, all with periodic boundary conditions (Figure 4).

The results of these analyses, expressed as stress–strain relations, are used to define the components of the homogenized constitutive tensor, $C^{\mathrm{hom}}$, where ${\sigma }_{ij}^{\mathrm{hom}}=C_{ijhk}^{\mathrm{hom}}{\epsilon }_{hk}$.

It is worth noting that, for materials with highly irregular microstructures (such as the asphalt concrete modeled by Oleksy [53]), alternative approaches are preferable. Nevertheless, the masonry analyzed in the present manuscript, the use of Periodic Boundary Conditions (PBCs) for the RC remains the most appropriate and theoretically sound approach, as the masonry pattern is periodic naturally.

While the constituent materials (brick and mortar) are modeled as isotropic, the specific, regular arrangement of the masonry inside the RC ensures that the resulting homogenized elastic tensor ($C^{\mathrm{hom}}$) is intrinsically orthotropic. This orthotropy is a direct consequence of the periodic geometry, which establishes two distinct principal directions of mechanical behavior (parallel and perpendicular to the bed joints). Due to the intrinsic nature of the periodic masonry, the homogenized constitutive tensor ($C^{\mathrm{hom}}$) is orthotropic. This means that its overall definition requires only four independent moduli: $C_{1111}^{\mathrm{hom}}$, $C_{2222}^{\mathrm{hom}}$, $C_{1122}^{\mathrm{hom}}$ (=$C_{2211}^{\mathrm{hom}}$), and $C_{1212}^{\mathrm{hom}}$. For the remaining components, it results that $C_{ijhk}^{\mathrm{hom}}=0$ $\forall i\ne j$.

It is worth noting that the RVE concept is crucial for bridging the scales. Although a periodic RVE is employed here for computational feasibility and direct validation against established unit cell models, the RVE definition is also applicable to statistically homogeneous materials where the micro-geometry is not strictly repeating. Crucially, the size of this Representative Cell (RC) is not arbitrary: its dimensions are selected to be significantly larger than the microstructural heterogeneities (e.g., brick and mortar width) yet small enough relative to the macroscale domain, thus ensuring the validity of the scale separation principle.

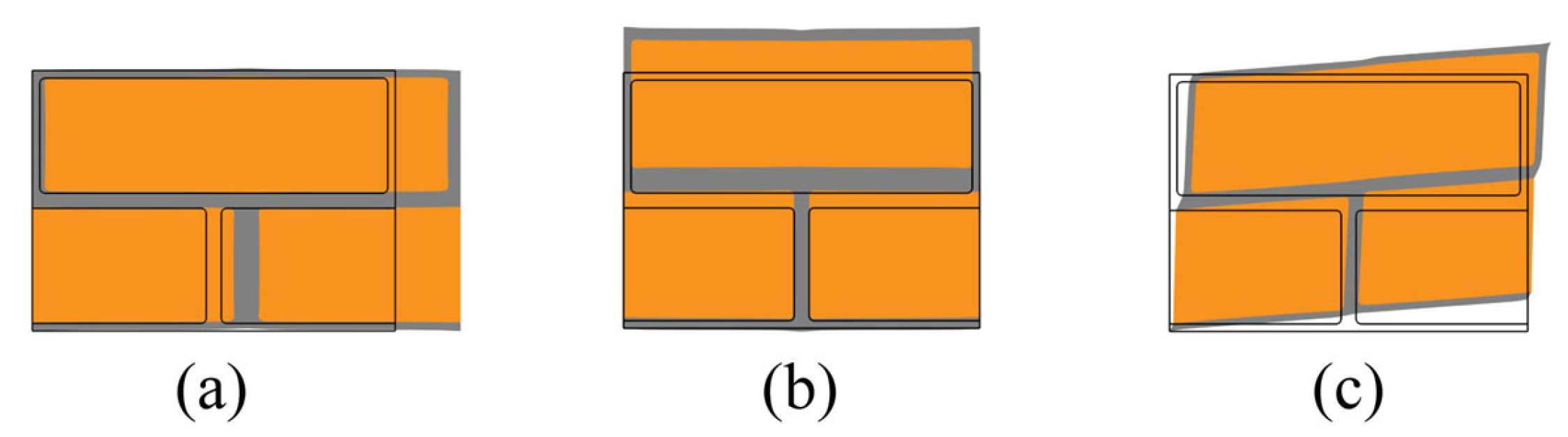
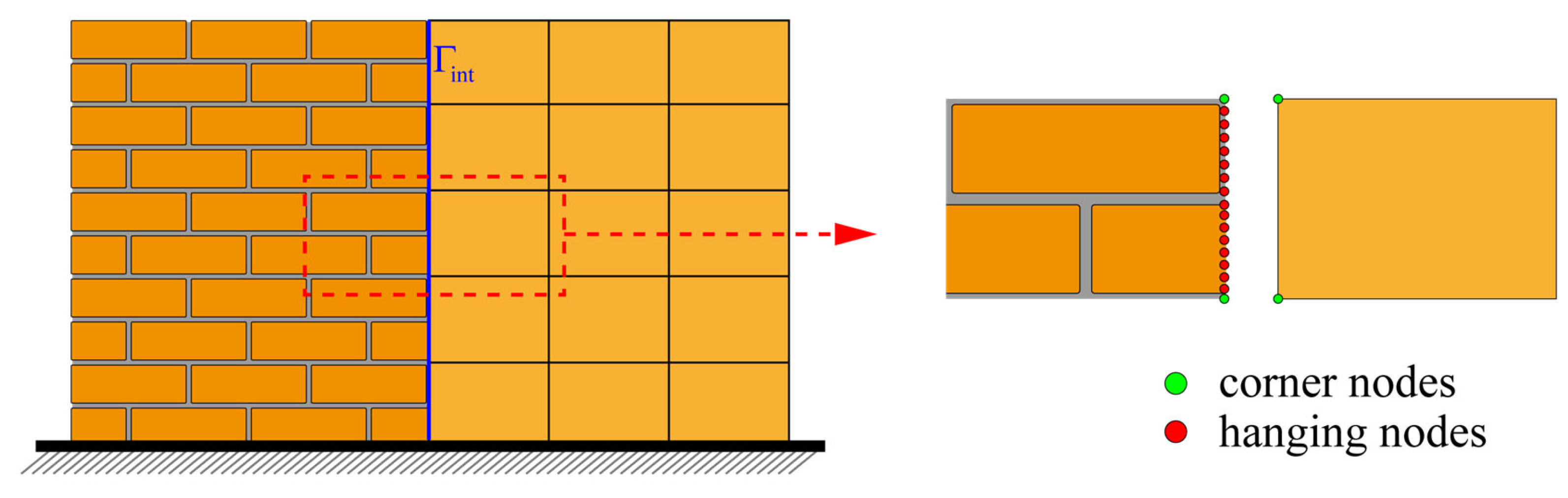
As a consequence of the partition of the original domain, an additional boundary ${\mathsf{\Gamma }}_{\mathrm{int}}$ is introduced into the model, referred to as the micro–macro interface. A significant challenge in this approach is the coexistence of coarse and fine sub-domains, which leads to non-conforming meshes at the micro–macro interfaces (Figure 5). Specifically, the interface contains both “corner nodes”, which are matching nodes between the macro- and micro-sub-domains, and “hanging nodes”, which are non-matching mesh nodes.

The adaptive strategy requires special treatment at the interface between coarse and fine regions to maintain the continuity of the displacement field. The challenge of enforcing continuity at the resulting hanging nodes is a critical aspect of adaptive FEM [54].

To ensure continuity of displacement across these interfaces, a dual-primal FETI (Finite Element Tearing and Interconnecting) approach is employed [55]. According to this technique, the displacement continuity at the corner nodes is enforced pointwise using a primal method, while a Lagrange multiplier technique is used to implement the compatibility condition at the hanging nodes. This advanced coupling strategy ensures the integrity and accuracy of the solution across the entire computational domain.

The concurrent nature of the proposed approach means that the micro-scale and macro-scale sub-problems are not solved in isolation but are coupled together into a single, unified problem for the entire computational domain. This unified problem seeks to determine the displacement fields for both scales and the Lagrange multipliers that enforce continuity at the interfaces.

Based on these considerations, the governing equations for the entire domain can be stated as follows:

$$\begin{array}{l}{\displaystyle \underset{{\mathsf{\Omega }}_b}{\int }\left(C_b:\nabla u\right)\cdot \delta \nabla u\hspace{0.17em}dV}+{\displaystyle \underset{{\mathsf{\Omega }}_m}{\int }\left[\omega \left(\varphi \right)C_m^0:\nabla u\right]:\delta \nabla udV}+{\displaystyle \underset{{\mathsf{\Gamma }}_{\mathrm{int}}}{\int }\lambda \cdot \delta udA}={\displaystyle \underset{{\mathsf{\Omega }}_{Micro}}{\int }f\cdot \delta udV}+{\displaystyle \underset{\partial {\mathsf{\Omega }}_t^{Micro}}{\int }\overline{t}\cdot \delta udA}=0\\ {\displaystyle \underset{{\mathsf{\Omega }}_{Macro}}{\int }[C^{\mathrm{hom}}:\nabla u^m]:\delta \nabla u^m\hspace{0.17em}dV}+{\displaystyle \underset{{\mathsf{\Gamma }}_{\mathrm{int}}}{\int }\lambda \cdot \delta u^{m}dA}={\displaystyle \underset{{\mathsf{\Omega }}_{Macro}}{\int }f\cdot \delta u^{m}dV}+{\displaystyle \underset{\partial {\mathsf{\Omega }}_t^{Macro}}{\int }\overline{t}\cdot \delta u^{m}dA}=0\\ {\displaystyle \underset{{\mathsf{\Gamma }}_{\mathrm{int}}}{\int }\delta \lambda \cdot \left(u-u^m\right)dA=0}\\ {\displaystyle \underset{{\mathsf{\Omega }}_m}{\int }{H}_m{\omega }^{\prime }(\varphi )\delta \varphi dV}+{\displaystyle \underset{{\mathsf{\Omega }}_m}{\int }{G}_c\left[\frac{1}{c_0{l}_0}{\alpha }^{\prime }\left(\varphi \right)\delta \varphi +2\frac{l_0}{c_0}\nabla \varphi \cdot \delta \nabla \varphi \right]dV}=0\end{array}$$

(23)

The first two equations represent the equilibrium conditions for the micro and macro regions of the domain, respectively. The third equation enforces kinematic compatibility at the interface between the micro and macro scales. The fourth equation governs the phase field problem in the detailed regions. It’s important to note that $\lambda$ denotes the unknown Lagrange multiplier field and, and its arbitrary variation, $\delta \lambda$, belongs to the same space Λ, which is the space of Lagrange multipliers.

2.3. First Failure Surface for Periodic Masonry

A crucial component of the proposed concurrent multiscale approach is a robust mechanism for dynamically transitioning from the macroscopic to the microscopic representation. The model must be able to efficiently identify where and when a coarse (homogeneous) region requires a higher-fidelity, heterogeneous description. This transition, or refinement, is triggered precisely at the onset of failure within a macro-element, which is the point where the linear elastic assumption is no longer valid.

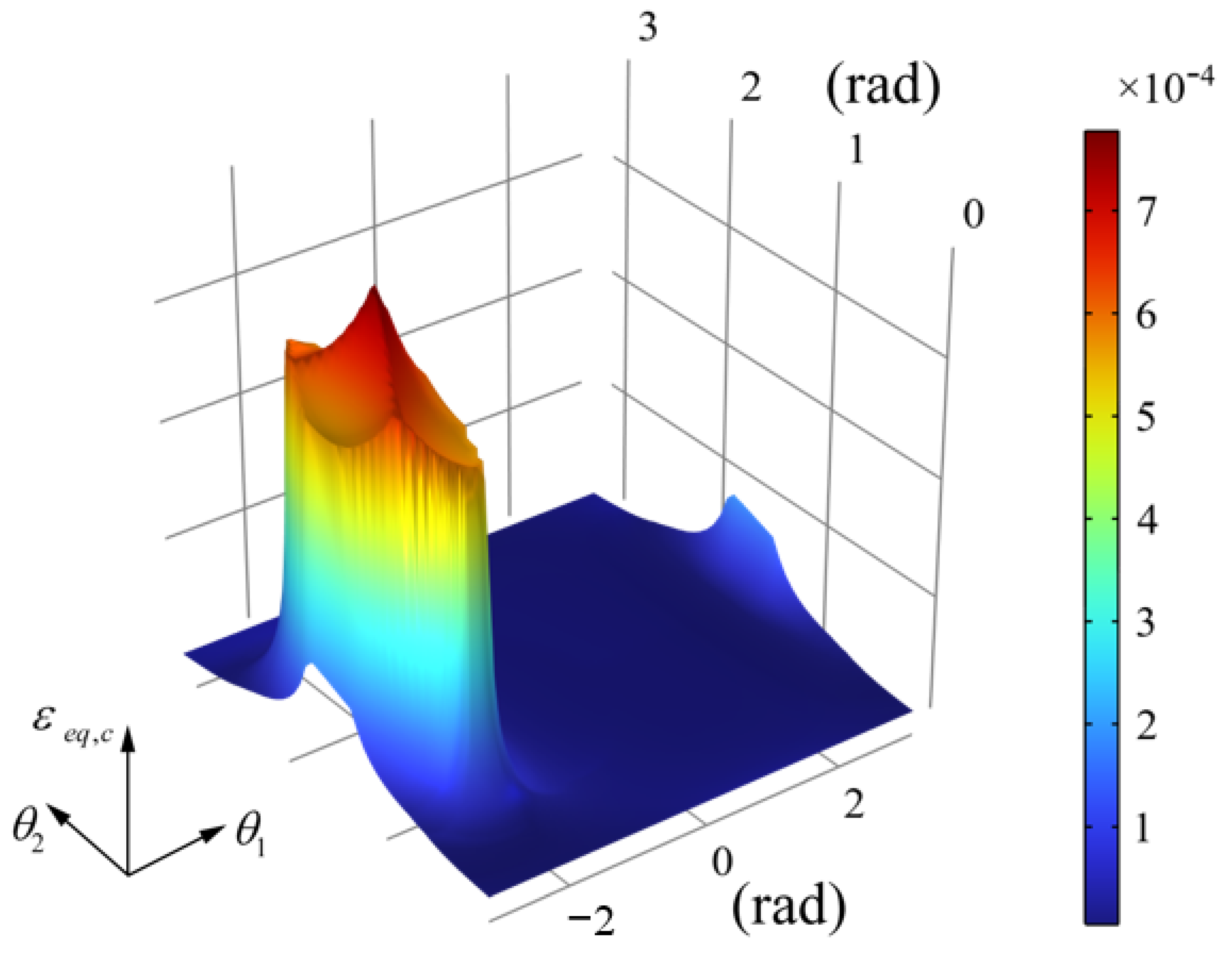
To achieve this, the concept of a first failure surface is introduced. This surface serves as a predictive criterion to define the precise conditions under which damage is initiated within the masonry microstructure. It acts as a bridge between the macroscopic state of the RC and its underlying microscopic behavior.

The first failure surface is constructed by performing a series of detailed finite element analyses on an RC. By subjecting the RC to a wide range of loading conditions along different macroscopic strain paths, the critical stress–strain states at which damage first occurs within the mortar joints are identified. After introducing a properly defined angular coordinate system, any point representing a given macroscopic strain state can be expressed as:

$$\begin{array}{cc}\begin{array}{l}{\epsilon }_x=\beta \cos {\theta }_1\sin {\theta }_2\\ {\epsilon }_y=\beta \sin {\theta }_1\sin {\theta }_2\\ {\gamma }_{xy}=\beta \cos {\theta }_2\end{array}& \begin{array}{c}-180°\le {\theta }_1\le -180°\\ 0\le {\theta }_2\le 180°\end{array}\end{array}$$

(24)

where ${\theta }_1$ and ${\theta }_2$ are the angular coordinates uniquely defining the macrostrain path directions. The parameter $\beta >0$ serves as a loading parameter that controls the magnitude of the imposed strain.

For each macrostrain path, the critical load factor (${\beta }_c$) is obtained in a post-processing step. This multiplier indicates how much the current load state needs to be scaled to reach the onset of failure. In particular, ${\beta }_c$ is achieved by taking advantage of the linear overall response of the microstructure up to this value using the following expression:

$${\beta }_c={\displaystyle \frac{{\epsilon }_{eq}^0}{{\epsilon }_{eq}^1}}$$

(25)

Here, ${\epsilon }_{eq}^0={\sigma }_t/E_0$ represents the critical value of the equivalent deformation, whereas ${\epsilon }_{eq}^1$ is the value of the equivalent deformation for β = 1.

The critical load factor represents the exact amount the current load state needs to be scaled to reach the onset of failure. Figure 6 shows a schematic of the first failure surface of an RC illustrated in Figure 3a.

2.4. The Activation Criterion for Scale Transition

This failure surface forms the basis for the activation criterion. During the simulation, the macroscopic state of each coarse-region element is continuously monitored. If the calculated equivalent deformation of a macro-element reaches the critical value, it signifies that the element is on the verge of failure. In this case, the activation criterion triggers computational refinement, deactivating the linear elastic macro-element and activating a detailed, nonlinear micro-modeling strategy.

The activation criterion is expressed through the following expression:

$${\lambda }_i({\theta }_1,{\theta }_2)\ge \chi {\lambda }_{c,i}({\theta }_1,{\theta }_2)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\mathrm{\dots },n^{macro}$$

(26)

where ${\lambda }_i=\sqrt{{\epsilon }_x^2+{\epsilon }_y^2+{\gamma }_{xy}^2}$ and $\chi$ represents a scale factor of the failure surface (both dimensionless parameters).

The progressive and adaptive approach ensures that the high computational cost of the micro-model is only expended in the specific areas where damage and strain localization are expected.

3. Numerical Implementation

The implementation of the proposed adaptive concurrent multiscale model was carried out using the commercial finite element software COMSOL Multiphysics (Version 6.2) [56]. In particular, a custom-built algorithm was created to manage the adaptive nature of the multiscale model. The steps followed by this algorithm are summarized in the flowchart reported in Figure 7, while Figure 8 depicts a schematic of some steps involved in the proposed model.

To execute the algorithm’s steps automatically, the built-in COMSOL Model Methods interface is adopted. This interface allows for performing COMSOL commands by writing strings in Java. In this context, the Java strings can be configured into “for cycles” or “if statements”, thus allowing a straightforward implementation of the adaptive nature of the proposed approach.

The proposed procedure initiates by defining the necessary input data, including the geometry and material properties of the masonry structure. After that, the analysis starts. The proposed procedure develops into two distinct phases: a series of preliminary “offline” analyses aiming at defining the homogenized elastic modulus and the first failure surface of an RC defined on the investigated masonry, followed by an incremental step-by-step analysis for evaluating the bearing capacity of the investigated masonry structure.

The first step of the offline analyses consists of identifying an RC of the masonry under investigation (Figure 8a). The identified RC is firstly analyzed imposing macroscopically uniform strains through periodic boundary conditions (PBCs), with the materials modeled purely elastic (i.e., the Phase-Field model is inactive). The resulting structural response is used during post-processing to determine the homogenized elastic moduli of the cell. Next, the first failure surface of the RC is evaluated. The same RC sub-model is used, but this time with the PF-CZM model activated for the mortar joints. Various fracture paths are analyzed under different stress combinations to determine the onset of failure, thus establishing the first failure surface of the masonry.

The homogenized elastic moduli and the first failure surface parameters are key input parameters for the incremental step-by-step analysis, which is then used to analyze the structural collapse behavior of the overall masonry structure.

The algorithm establishes a dual-scale discretization of the computational domain associated with the geometry of the investigated masonry structure. The first level of discretization employs a mesh of macro-elements, each matching the size and shape of the RC, arranged in a regular grid (Figure 8b). This discretization provides a coarse-scale representation according to a macro-modeling approach. Simultaneously, a second, finer discretization is performed using numerous finite elements to achieve a detailed, micromechanical representation of the domain. Once these two meshes are generated, they are superimposed, and all macro-elements are initially activated.

The simulation is conducted using a displacement-controlled numerical analysis, where external loads are incrementally applied based on the displacement of a monitored control point (d). In particular, a segregated solver is utilized to handle the nonlinear system of equations that governs the structural mechanics and the phase field problem.

The first-failure surface governs the activation of the micro-scale model through the criterion described by Equation (26). This criterion is implemented in COMSOL Multiphysics by imposing a “stop condition” to the numerical solver so that the analysis is programmed to halt instantaneously when the criterion is satisfied for any macro-element.

Following the interruption, the algorithm deactivates the macro-elements that are starting to damage, thus activating a microscopic representation of the masonry (Figure 8c). In this phase, the displacement field of the deactivated macro-element is projected along the boundaries of the newly formed refined microscopic region. This process ensures the initial conditions of the micro-scale accurately reflect the state of the macro-continuum at the time of arrest. Besides, continuity at the interface between the active macro-domains and the newly activated micro-domain is enforced through pointwise constraints applied at the interface nodes. As specified, these constraints are implemented within the solver sequence using the Lagrange Multipliers method, which is effective for handling the constrained degrees of freedom at the scale interface.

The analysis proceeds, progressively deactivating additional macro-elements as their activation criteria are met, until the full collapse of the structure occurs (Figure 8d).

The proposed adaptive scheme is presented here for periodic masonry, but its core methodology can be generalized for the analysis of nonperiodic masonry. In such circumstances, the primary challenge shifts to the offline homogenization phase. The Representative Cell (RC), used for deterministic calculation of the first-failure surface, must be replaced by a statistical Representative Volume Element (RVE). This is necessary because, in irregular microstructures, the first-failure surface and effective material properties become locally variable. Consequently, the first-failure surface must be determined on a statistical basis, requiring the simulation and averaging over multiple RVEs. While this significantly increases the computational cost of the preliminary offline analysis, the adaptive logic of the flowchart remains conceptually applicable for the online analysis phase.

4. Numerical Results and Discussion

This section is dedicated to presenting the numerical results that validate the accuracy and demonstrate the computational efficiency of our adaptive concurrent multiscale model in analyzing the failure behavior of masonry structures.

The discussion is divided into two parts. First, the reliability of the proposed micro-mechanical model is thoroughly assessed. This is accomplished by comparing its predictions against an established experimental benchmark—the shear test on a masonry wall originally investigated by Vermeltfoort et al. [57]—as well as with the numerical outcomes from various other models reported in the literature.

Subsequently, the computational efficiency of the concurrent multiscale model is demonstrated. This is achieved by applying the model to a large-scale masonry wall and comparing its performance against that of an equivalent direct numerical simulation.

Numerical simulations were conducted using computational meshes of triangular finite elements with linear interpolation functions for both the macroscale and microscale domains. However, it is recognized that alternative multiscale approaches have successfully employed higher-order approximations at the macroscale for improving the convergence rate and the smoothness of the homogenized field variables in multiscale contexts [58].

4.1. Validation of the Proposed Micro-Mechanical Model: A Masonry Wall with an Opening

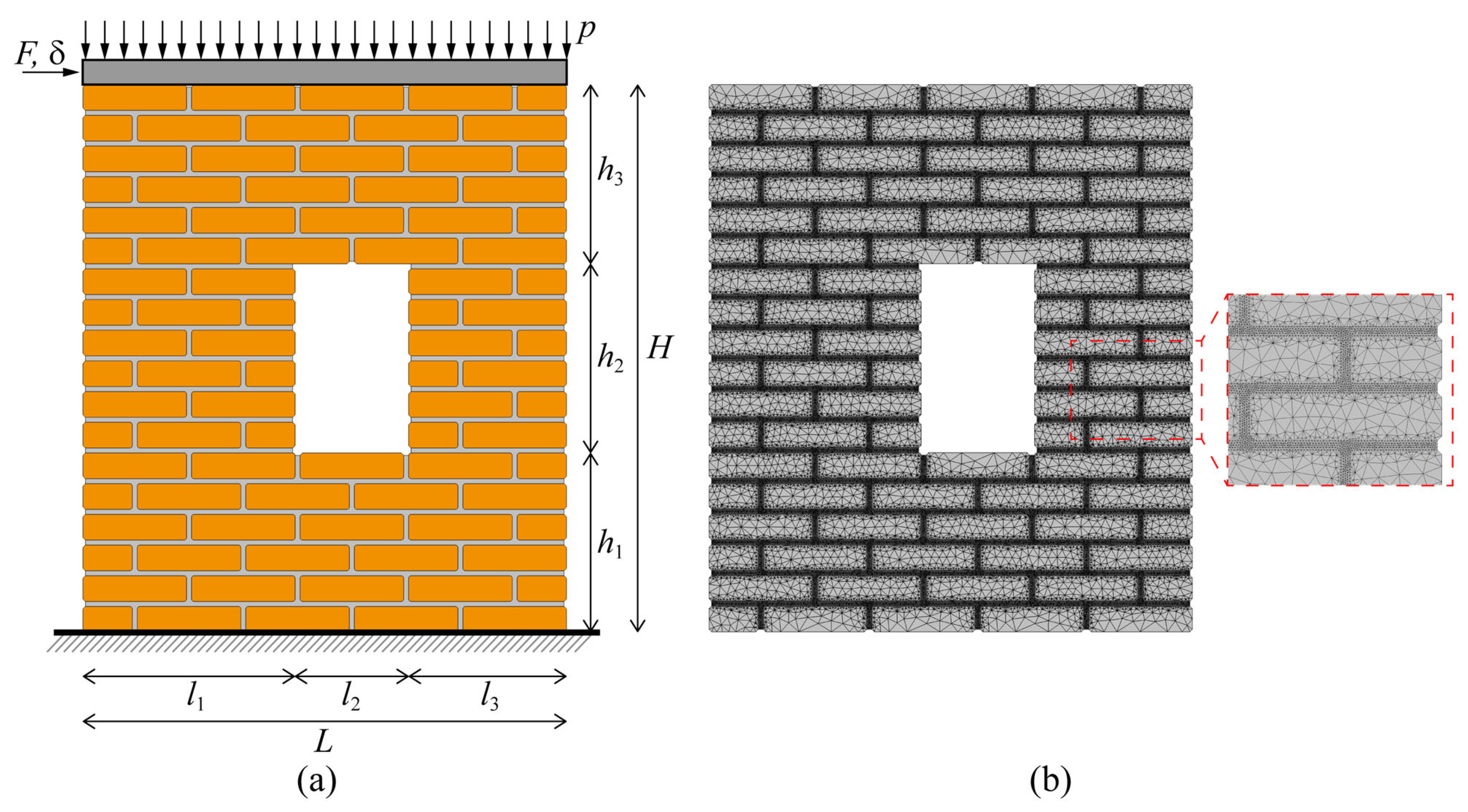
Figure 9 shows a masonry wall measuring L = 900 mm in length and H = 1116 mm in height with a central opening of l₂ = 230 mm and height h₂ = 382 mm. The structure was composed of solid clay bricks (210 × 52 × 100 mm) bonded by 10 mm thick mortar joints.

The wall is subjected to a uniform vertical pressure of p = 0.30 MPa and an increasing shear force, F. This wall was investigated experimentally by Vermeltfoort et al. [57], who provided a comprehensive dataset, including the horizontal displacement–force curves and the corresponding failure modes.

According to their experimental data, Young’s Modulus and Poisson’s ratio for the brick units and mortar joints were assumed to be equal to E_b = 16700 MPa, ν_b = 0.15, and E_m = 782 MPa and ν_m = 0.14, respectively. In addition to the elastic properties, the fracture parameters necessary to define the Phase Field fracture model were also assumed.

Since the proposed model assumes that only the mortar joints are damageable, it is essential to introduce proper values for the fracture parameters.

Consistent with values found in the literature [40], a fracture energy of G_f = 180 N/m and a tensile strength of f_t = 0.25 MPa were assumed. Additionally, the compressive strength was set to f_c =10.5 MPa, and the biaxial compressive strength was assumed to be f_b = 1.2 × f_c.

It is worth noting that the model’s predictions, particularly the peak load and the rate of post-peak softening, are primarily governed by these properties. Among these, the tensile strength (f_t) and the fracture energy (G_f) are the most critical parameters influencing the PF-CZM. The tensile strength controls the stress level required for the onset of fracture and, consequently, the magnitude of the peak load in the macro-response. An increase in f_t directly increases the predicted peak load and slightly delays the initiation of the softening regime. On the other hand, the fracture energy (G_f) dictates the energy dissipation rate during crack opening, directly affecting the rate of post-peak softening. Higher values of G_f imply greater ductility and result in a less steep post-peak slope, sustaining higher residual loads at large displacements. Conversely, lower values of G_f lead to a more brittle response and a rapid load drop. While important, the influence of the compressive strength on the overall shear-compression failure mode of the panel is less dominant than that of f_t and G_f, as tensile and shear mechanisms along the interfaces primarily drive the final failure.

To define the softening behavior consistently with a Cornelissen et al. [59] softening law, the parameters p, a₂, and a₃ of Equation (12)–(14) were assumed to be equal to 2, 1.3868, and 0.6567, respectively (see Equation (15)). The geometry of the wall was discretized using the computational mesh depicted in Figure 9b. Both brick units and mortar joints were discretized using plane stress finite elements with an unstructured Delaunay-type triangulation. In this context, the mortar joints have finite elements of a maximum size equal to 3.18 mm, corresponding to t_m/π, where t_m is the thickness of the mortar joints. This discretization ensures a good reproduction of the phase field. On the contrary, brick units were discretized more coarsely because they are undamageable.

It is worth noting that initial comparative mesh analyses were conducted to confirm the reliability of this fixed discretization. These results, omitted here for the sake of brevity, confirmed that further refinement, especially in the brick units, did not significantly alter the predicted structural response.

To replicate the experimental setup, which involved a metal bracket for transmitting both the vertical and horizontal loads, a rigid connector was implemented between the upper edges of the end bricks of the wall. The scientific community has widely adopted this benchmark case for validating various numerical approaches to analyzing masonry structures [40,60]. Due to the comprehensive experimental data available, it has served as a critical reference for researchers seeking to test the reliability and accuracy of their models in reproducing both the overall structural response and the intricate failure mechanisms of masonry walls. Among these, Lourenço and Rots [61] have modeled the masonry as expanded brick units mutually connected through interface elements. The constitutive behavior of these interfaces was described by a multisurface plasticity model with softening, specifically designed to capture the three main failure modes of masonry: cracking (in tension), sliding (in shear), and crushing (in compression). Vandoren et al. [52] employed a mesoscopic model, where weak and strong discontinuities represented masonry joints. Instead of using classical interface elements that require a pre-aligned mesh, they modeled these discontinuities using the partition of unity property of finite element shape functions. The bricks themselves were assumed to be linear elastic. Like the proposed approach, the degradation of the joints was described using a Drucker–Prager damage model. D’Altri et al. [62] utilized a large-scale approach. In their model, the mortar joints are not explicitly simulated at a micro-structural level; instead, the masonry is treated as a continuous material. Damage is reproduced through a two-step automated procedure: first, an adaptive limit analysis predicts the crack patterns, and then cohesive and frictional interface elements are automatically inserted to simulate the damage behavior during a subsequent pushover analysis.

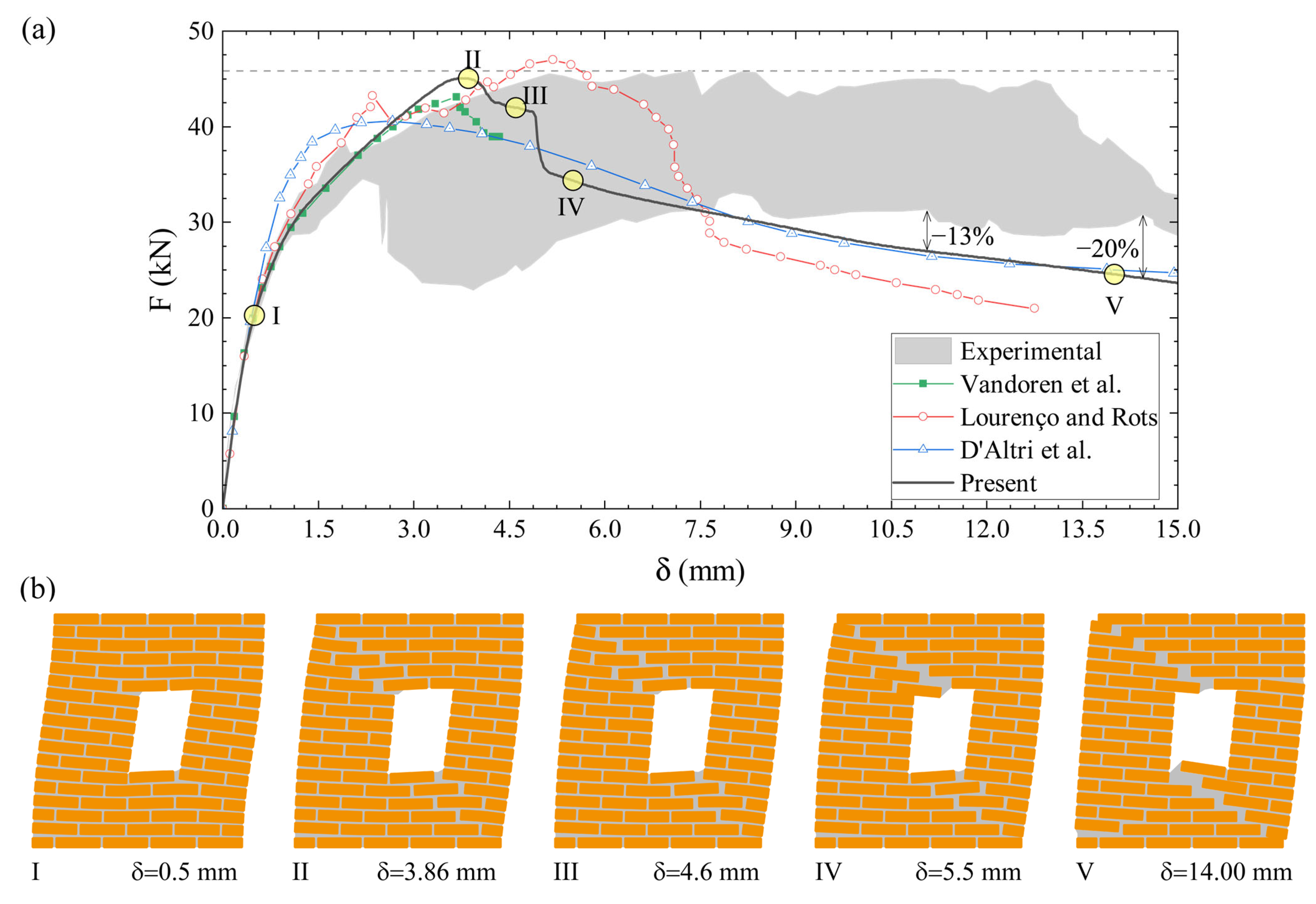
Figure 10a compares the horizontal displacement (δ) vs. lateral force (F) curve predicted by the proposed model with those provided by other authors. On the other hand, Figure 10b shows the geometric configurations of the masonry wall predicted by the proposed model during numerical simulation for increasing values of horizontal displacement (δ).

The results show that the curve predicted by the proposed method lies predominantly within the experimental band, confirming the model’s robustness. The proposed model demonstrates excellent agreement with the experimental results regarding the initial stiffness, as the numerical curve aligns directly with the experimental band. This high fidelity in the initial phase can be attributed to the detailed representation of the geometry of the masonry panel and the elastic properties of both brick units and mortar joints adopted in the numerical model. Besides, the numerical model accurately predicts the peak load, which is lower than the maximum value of the experimental band of about 1.73%. The post-peak softening curve remains well within the bounds of the experimental band up to a value of the controlled displacement (δ) of 8 mm. For δ > 8 mm, the predicted softening curve develops slightly below the lower bound of the experimental band with a maximum difference of −20%. This difference in the softening regime for high values of the controlled displacement parameter (δ) is likely due to the proposed model not explicitly accounting for frictional resistance, which benefits the load-carrying capacity at large crack openings in real masonry. However, this limitation does not significantly undermine the predictive capability of the proposed method, which remains in strong agreement with the predictions of other numerical models, particularly those developed by D’Altri et al. and Lourenço et al.

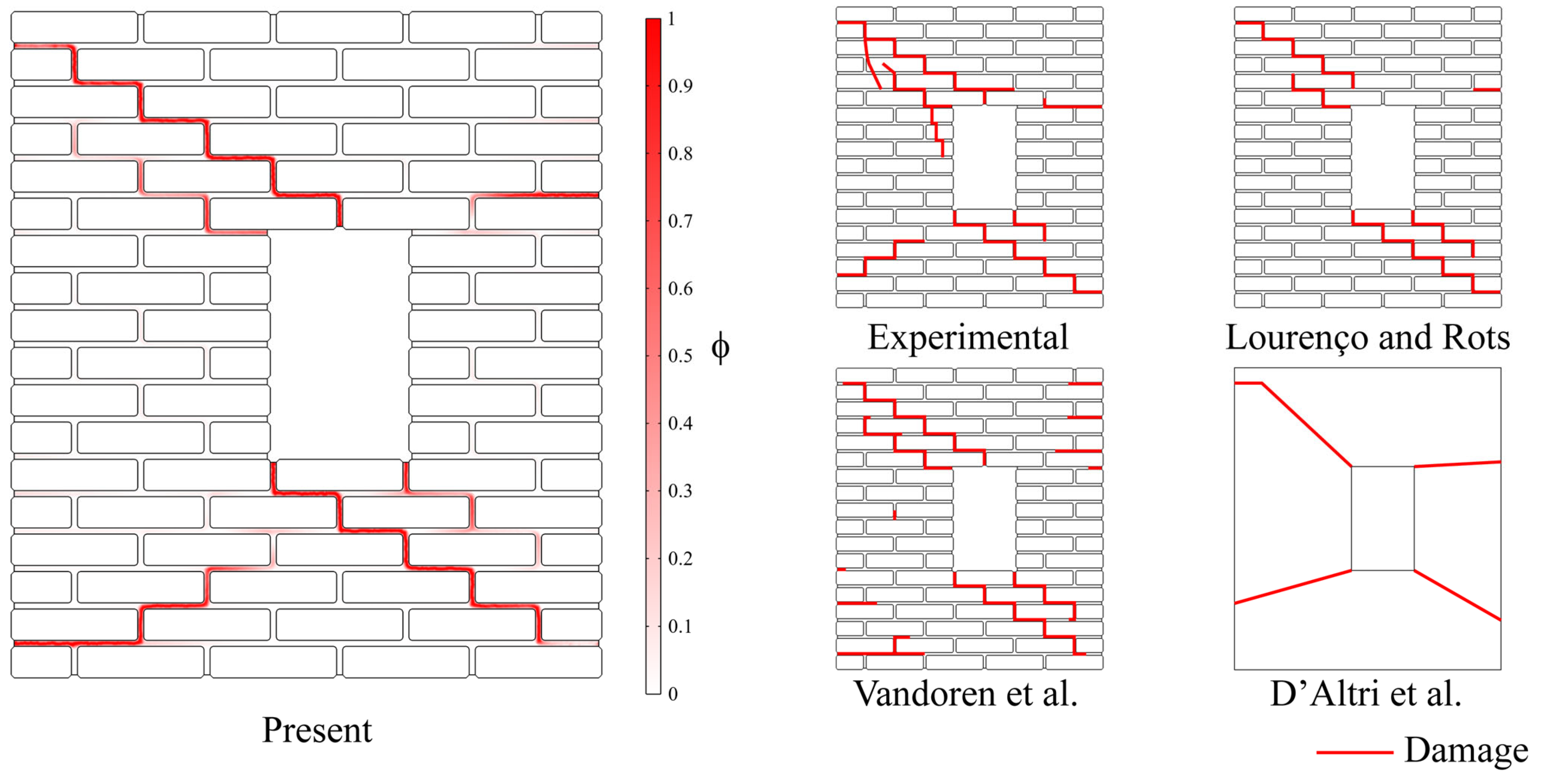
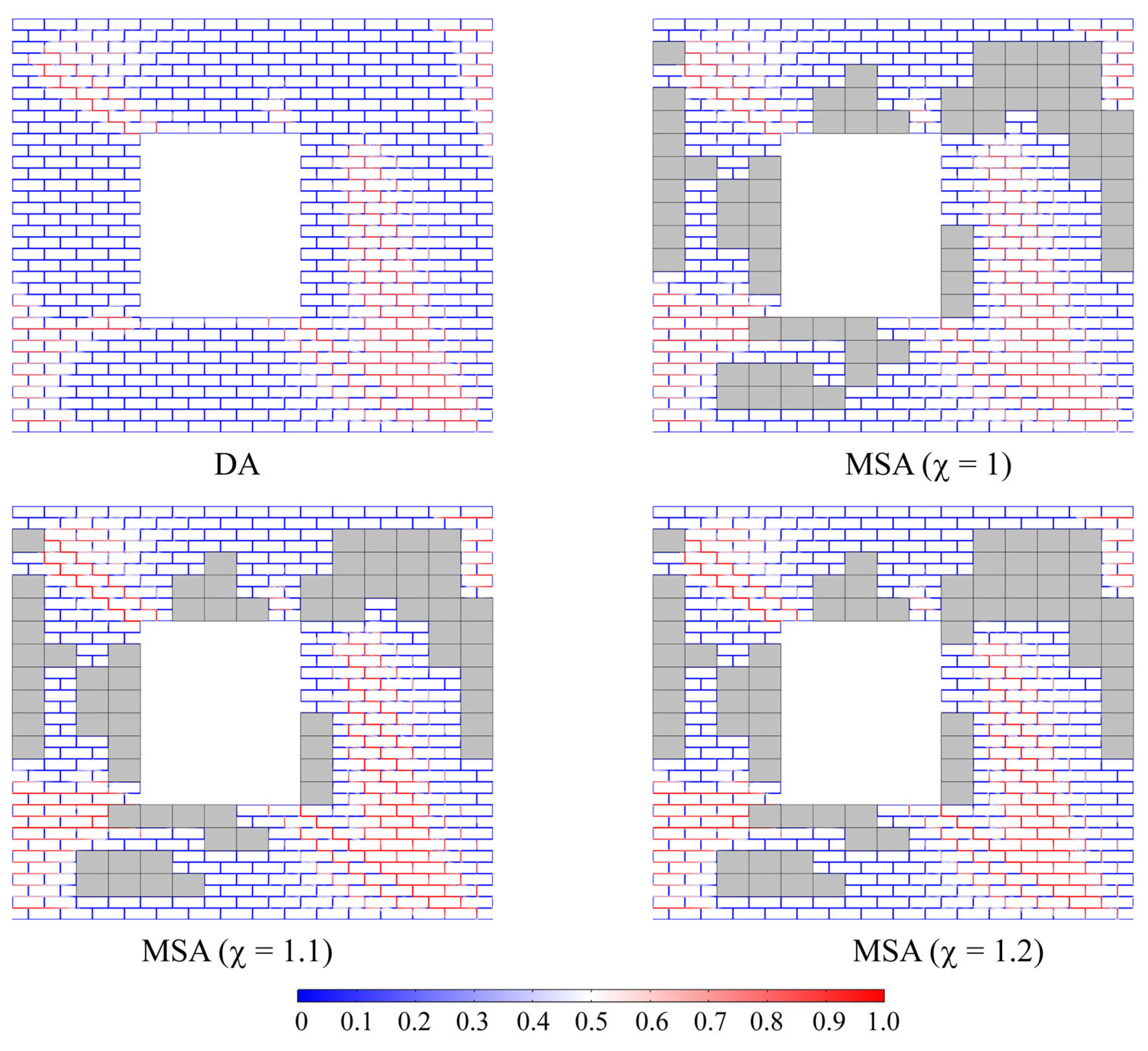
Figure 11 illustrates the damage maps of the masonry wall predicted by the proposed method, alongside experimental data and other numerical results. In this context, the results of the proposed method are expressed in terms of the phase field variable (ϕ). These results indicate that the proposed method yields results in good agreement with the reference data, particularly with the experimental ones.

As expected, the damage to the masonry wall occurs according to a stair-like configuration, propagating exclusively through the mortar joints and following the paths of least resistance. In this context, the damage develops along the diagonal connecting the upper-left corner to the bottom-right one.

This mechanism, characterized by a combination of tensile and shear failures, accurately reproduces the experimental observations and predictions of other numerical techniques (especially with those of Lourenço and Rots [61] and Vandoren et al. [52]). In addition, the proposed method accurately accounts for the damage occurring along the left-bottom portion of the panel, thus confirming its validity and reliability.

4.2. Application of the Proposed Concurred Multiscale Model: Failure Analysis of a Large-Scale Masonry Wall

To validate the accuracy and computational efficiency of the adaptive concurrent multiscale model, this section provides specific numerical results.

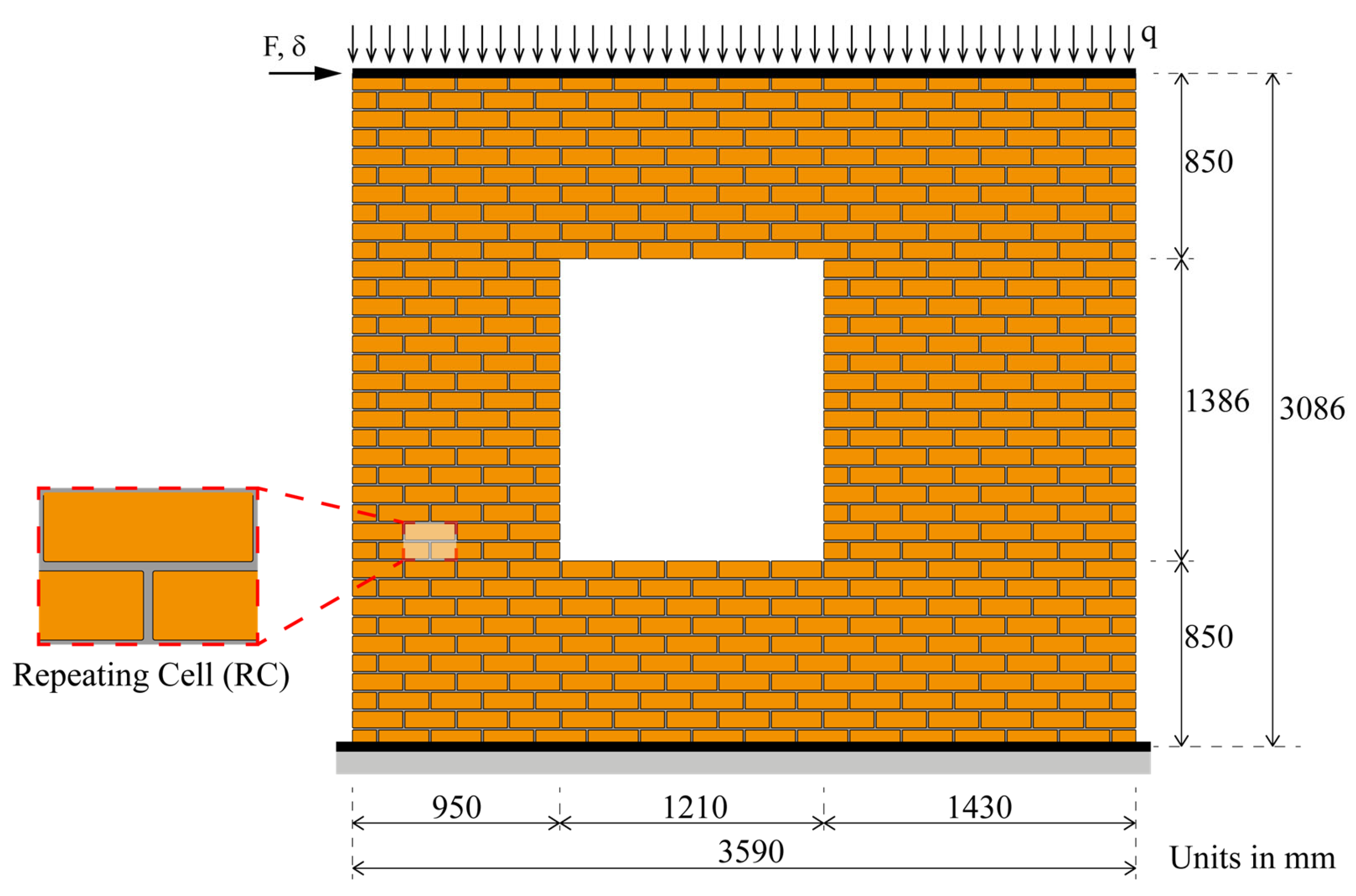
Figure 12 shows a masonry wall of length L = 3590 mm, height H = 3806 mm, and thickness t_w = 25 mm with an opening of 1210 mm × 1386 mm. The masonry exhibits the same mechanical characteristics as the one analyzed in the previous section. As a consequence, the same mechanical properties, including the homogenized elastic tensor $C^{\mathrm{hom}}$ and the first failure surface, are adopted. The wall is fixed at the base and subjected to a uniform vertical pressure q of 0.15 MPa and an increasing horizontal force. To simulate the presence of a horizontal diaphragm, a rigid constraint was applied to the top edge of the wall, linking the top-most bricks. The analysis of the masonry wall was performed using two distinct numerical approaches: a Direct Analysis (DA), which models the entire geometry of the wall with a high-fidelity micro-modeling strategy, and the proposed concurrent adaptive multiscale model (MSA). For the multiscale simulations, analyses were conducted using different scale factors (χ) (see Equation (26)) with values of 1, 1.1, and 1.2 to investigate their influence on the results.

The computational meshes for both DA and MSA are shown in Figure 13. The zoomed-in view reveals that a standard Delaunay-type triangulation was used for both brick units and mortar joints. Given that the brick units are treated as linearly elastic and undamaged components, they can be discretized using a coarser mesh. Conversely, the mortar joints were meshed more finely to achieve an accurate solution to the phase-field problem. To ensure adequate discretization for the damage model, the size of the finite elements within the mortar joints was set to t_m/π, where t_m is the mortar joint thickness.

In the multiscale approach, the wall’s geometry is initially defined by macro-elements equal to the RC size. This preliminary coarse mesh is used across the entire domain, with the exception of the boundaries where kinematic and static conditions are implemented (as in the DA model).

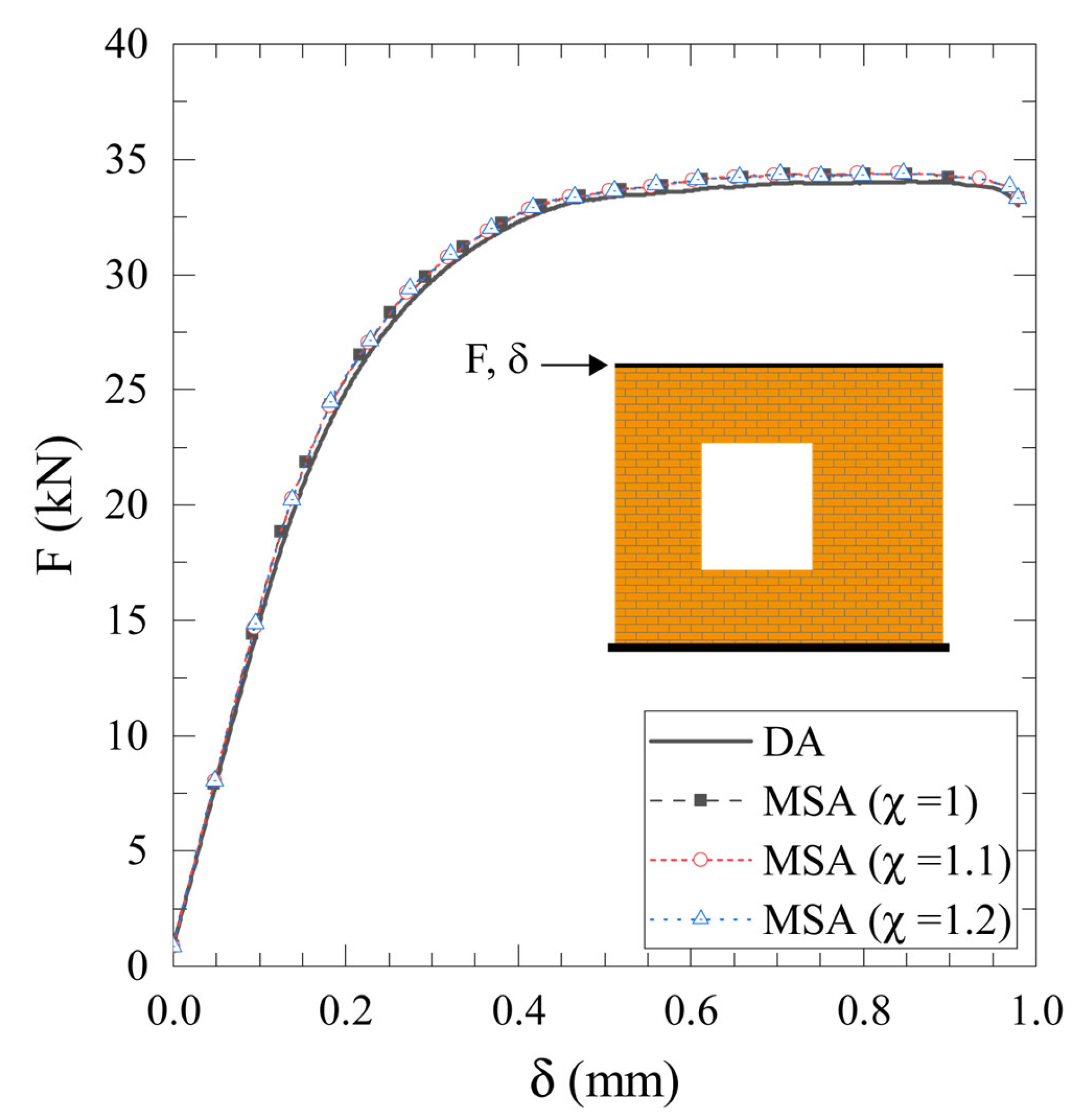
The results from the Direct Analysis (DA) and Multiscale Analysis (MSA) are compared in Figure 14, showing the horizontal displacement of the top diaphragm of the wall (δ) against the applied force (F). Additionally, Figure 15 shows the phase field distributions (ϕ) corresponding to the peak force, respectively. The results highlight that the curves of the multiscale model align well with those obtained from the Direct Analysis (DA), regardless of the scale factor χ. This close match in the load–displacement response serves as a robust validation of the proposed model’s predictive accuracy. Furthermore, a comparison of the phase field variable (ϕ) distribution between DA and MSA reveals a clear consistency between the resulting maps.

In this context, by focusing attention on the blue region predicted by the DA in Figure 15 (i.e., the region where ϕ is quite small, thus denoting sound portions of the masonry), these correspond to linear elastic macro-elements in the MSAs. A comparison of the MSA results reveals that using a larger scale factor (χ) is beneficial. This is because larger χ values prevent the refinement of coarser regions where damage is only moderate.

In fact, by comparing the phase field maps of the MSAs for χ = 1 and χ = 1.2, one can observe that in the map for χ = 1.2, elements remain where a high value of the variable ϕ is not yet present, thus allowing them to be still considered linearly elastic. This behavior is key to the computational efficiency of the multiscale model, as it avoids unnecessary micro-level calculations in regions where damage is not critical.

These results demonstrate that the DA and MSA models predict an identical failure mechanism for the masonry wall. The close correspondence between the phase field distributions and the force–displacement curves obtained with both numerical approaches (i.e., DA and MSA) confirms the robustness and reliability of the proposed multiscale model.

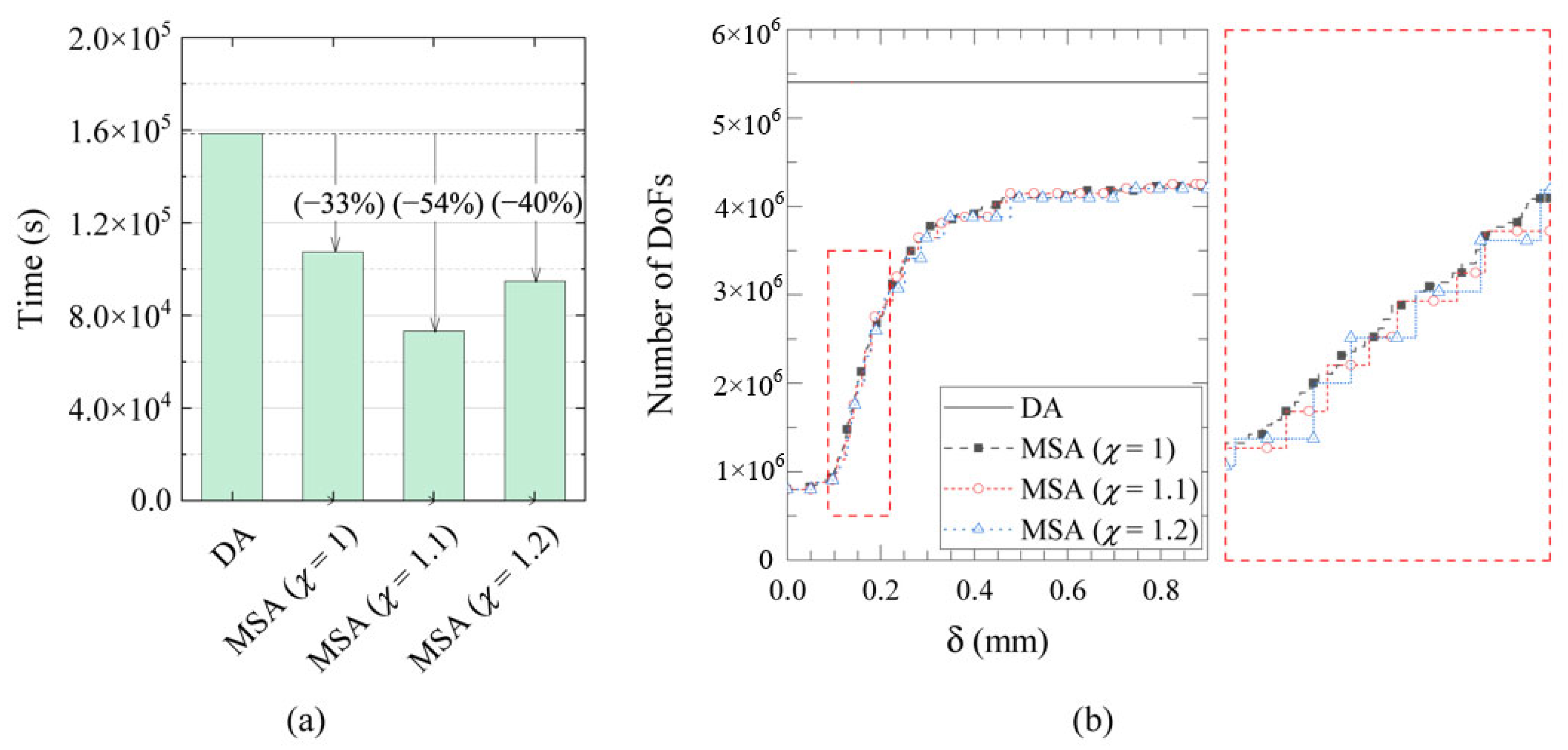
The computational efficiency of the proposed multiscale model is highlighted in Figure 16, which presents a direct comparison of the computational time and the evolution of the DOFs.

As shown in Figure 16a, MSAs achieve a substantial reduction in computational time spent performing numerical simulations compared to the direct analysis. While the DA requires over 16,000 s to perform the entire numerical simulation, the proposed MSA requires only a fraction of this time, demonstrating a significant improvement in efficiency. In this context, the use of a larger scale factor (χ) than 1 contributes significantly to reducing computational time. This is particularly evident for the case with χ = 1.1, which further reduces computational time by 21% compared to the multiscale analysis with χ = 1. Conversely, the use of χ = 1.2 reduces the time by only 40%.

The use of the scaling factor χ = 1.2 means that a microscale region is activated when the macroelement’s utilization is at 120% (i.e., 20% beyond the nominal elastic limit).

Of course, delaying the deactivation of macroelements initially benefits the computational time spent on numerical simulations. However, the achieved results demonstrated that setting a larger value than 1.1 tends to reduce this beneficial effect.

This result is likely to be explained by a primary reason. The magnitude of χ directly influences the initial state of the phase-field variable (ϕ) upon activation of the micro regions. By setting χ = 1.0, microscopic regions are activated when their behavior is at the elastic limit, for which the value of the phase-field variable (ϕ) inside the mortar joints is close to zero. On the other hand, for χ > 1.0, the microscopic regions should already be damaged. Consequently, the initial distribution of ϕ inside the mortar joints for the newly activated micro regions upon activation is non-zero, and this initial damage increases as χ increases. In particular, the distribution of the phase-field variable inside the mortar joints should be determined, considering that it spreads non-uniformly. In this context, for χ = 1.1, ϕ is small and lightly distributed inside the mortar joints, so that the behavior of the microscopic regions is quite similar to that of the sound material. For χ = 1.2, these conditions do not occur, so that the distribution of ϕ inside the mortar joints at the first step after the activation must be evaluated, which is a challenging and burdensome task. This condition forces the segregated solver to spend several additional steps and nonlinear iterations to accurately determine the initial values and distribution of the phase-field variable across the mortar joints of the newly activated microscopic regions. This additional convergence time directly contributes to the reduced overall efficiency and the observed instabilities.

Figure 16b clearly demonstrates the reason for the substantial time saving provided by MSA. This figure plots the evolution of the DOFs as a function of the horizontal displacement of the top of the wall (δ). One can observe that the DA curve remains constant, reflecting that the entire domain is discretized with a fine-scale mesh from the beginning. In contrast, MSAs start with a very low number of DOFs and only increase progressively as damage necessitates the refinement of macro-elements into micro-regions. This adaptive strategy, which applies the high computational cost of the micro-model only where and when it is needed, is the key to the model’s computational efficiency.

The zoomed view of Figure 16b reveals that the evolution of the degrees of freedom (DOFs) for the multiscale models with χ > 1 follows a characteristic sawtooth curve. This behavior highlights the delay in refining the zones that are beginning to be damaged, a deliberate strategy compared to the standard MSA model with χ = 1. This controlled delay is precisely what accounts for the reduced time required to complete the simulation, as it prevents the unnecessary activation of fine-scale elements in regions that are not yet critically affected.

In conclusion, a small increase in the scale factor is highly advisable. This is because, as demonstrated by the results, it does not compromise the predictive accuracy of the model, particularly in terms of the load–displacement response and the final failure mechanism. By strategically delaying the refinement process, this approach significantly enhances the efficiency of the numerical computation, making it an effective investigation tool for the analysis of masonry structures.

Finally, it is worth noting that the computational time considered in Figure 16a is strictly related to the nonlinear pushover analysis. Applying this methodology to nonperiodic masonry would necessitate a statistical homogenization analysis to determine the effective elastic tensor. This procedure would impose a greater initial computational burden compared to the single-RVE homogenization in this case, since the effective properties are not uniquely defined by a single cell but require averaging over multiple statistically relevant volume elements.

5. Conclusions

This work successfully proposed and implemented an innovative adaptive concurrent multiscale model for the in-plane failure analysis of masonry structures. The methodology leverages a domain decomposition strategy that dynamically assigns different levels of resolution based on the material’s constitutive evolution.

The model integrates a Phase Field Cohesive Zone Model (PF-CZM) at the micro-level with an elastic homogenization approach at the macro-level, governed by a custom-built dynamic activation algorithm developed using COMSOL Model Methods.

The primary scientific contributions and quantitative gains of this study are:

• Novel Adaptive Methodology: Successful development and implementation of an adaptive concurrent multiscale algorithm that effectively manages the activation and deactivation of the computationally expensive PF-CZM domain based on a systematic first failure surface criterion.
• Computational Efficiency: The adaptive strategy demonstrated a significant reduction in computational resources. For the case study analyzed, the model achieved a computational speedup of approximately 54% (with χ = 1.1) compared to the direct analysis based on a fully micro-mechanical representation of the computational domain.
• Phase-Field Integration: Successful integration of the Phase-Field Cohesive Zone Model (PF-CZM) within a dual-scale adaptive framework for capturing crack propagation and fracture localization in masonry.

The proposed methodology provides a powerful tool, yet its current formulation presents specific limitations and avenues for future research:

• Applicability: The model relies on the pre-determination of a periodic Representative Cell (RC) of the masonry, limiting its direct application to masonry structures with highly nonperiodic or random geometries. Furthermore, the validation was focused on monotonic loading, requiring extension for dynamic or cyclic analysis.
• Stability: The non-optimal threshold (χ = 1.2) led to a sub-optimal speedup and introduced convergence difficulties upon switching and the non-zero initialization of the Phase-Field variable.

Future work will focus on overcoming these limitations:

• Refining the activation criterion: future research will concentrate on optimizing the adaptive threshold factor (χ) to maximize the computational efficiency and mitigate instabilities by achieving smoother transitions between the scales.
• Solver and constraint robustness: Exploring the use of more robust numerical techniques (e.g., advanced Domain Decomposition methods or specialized Augmented Lagrangian formulations) to handle better the stiff jump in DOFs and the boundary continuity constraints at the macro–micro interface.
• Model extension and 3D Generalization: Extending the model’s capability to simulate complex loading regimes, such as cyclic and dynamic analysis, is a key focus. Furthermore, generalizing the framework to 3D analysis is crucial. This extension, while challenging, is necessary to capture out-of-plane failure mechanisms and requires implementing a full 3D PF-CZM at the micro-scale and defining a 3D first-failure surface under multiaxial stress states, both of which are computationally demanding.
• Extension to finite deformation: The current model operates within the small-displacement framework. Future research will explore extending the adaptive multiscale framework to large-displacement problems, requiring the transition to a finite-deformation kinematic framework and the implementation of a rigorous computational homogenization scheme at finite strains.