An Innovative Solution for Stair Climbing: A Conceptual Design and Analysis of a Tri-Wheeled Trolley with Motorized, Adjustable, and Foldable Features

Abstract

The objective of this study is to design, develop, and analyze a tri-wheeled trolley integrated with a motor that incorporates adjustable and foldable features. The purpose of a trolley is to allow users to easily transport items from one place to another. However, problems arise when transporting objects across challenging surfaces, such as up a flight of stairs, using a conventional cart. This innovation uses multiple engineering skills to determine and develop the best possible design for a stair-climbing trolley. A tri-wheel mechanism is integrated into its motorized design, meticulously engineered for adjustability, ensuring compatibility with a wide range of staircase dimensions. The designed trolley was constructed considering elements and processes such as a literature review, conceptual design, concept screening, concept scoring, 3D modelling, engineering design calculations, and simulations. The trolley was tested, and the measured pulling force data were compared with the theoretical calculations. A graph of the pulling force vs. load was plotted, in which both datasets showed similar increasing trends; hence, the designed trolley worked as expected. The development of this stair-climbing trolley can benefit people living in rural areas or low-cost buildings that are not equipped with elevators and can reduce injuries among the elderly. The designed stair-climbing trolley will not only minimize the user’s physical effort but also enhance safety. On top of that, the adjustable and foldable features of the stair-climbing trolley would benefit users living in areas with limited space.

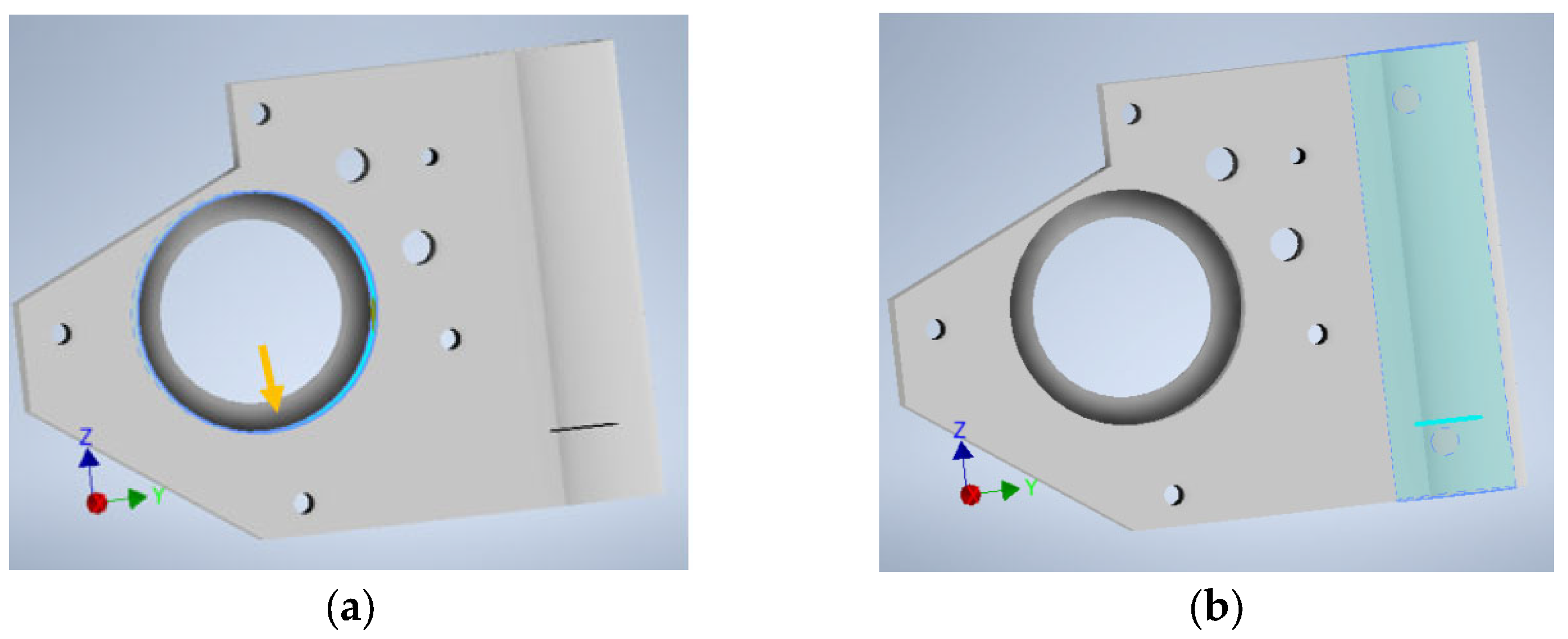
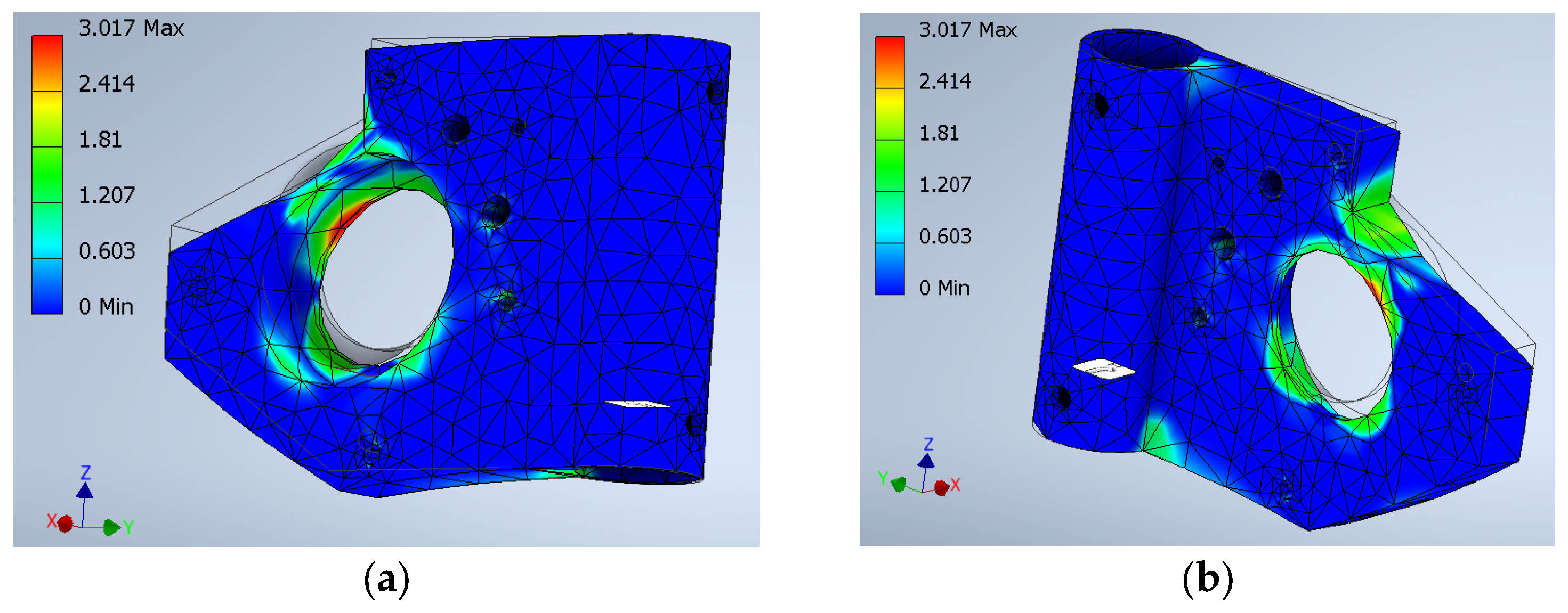
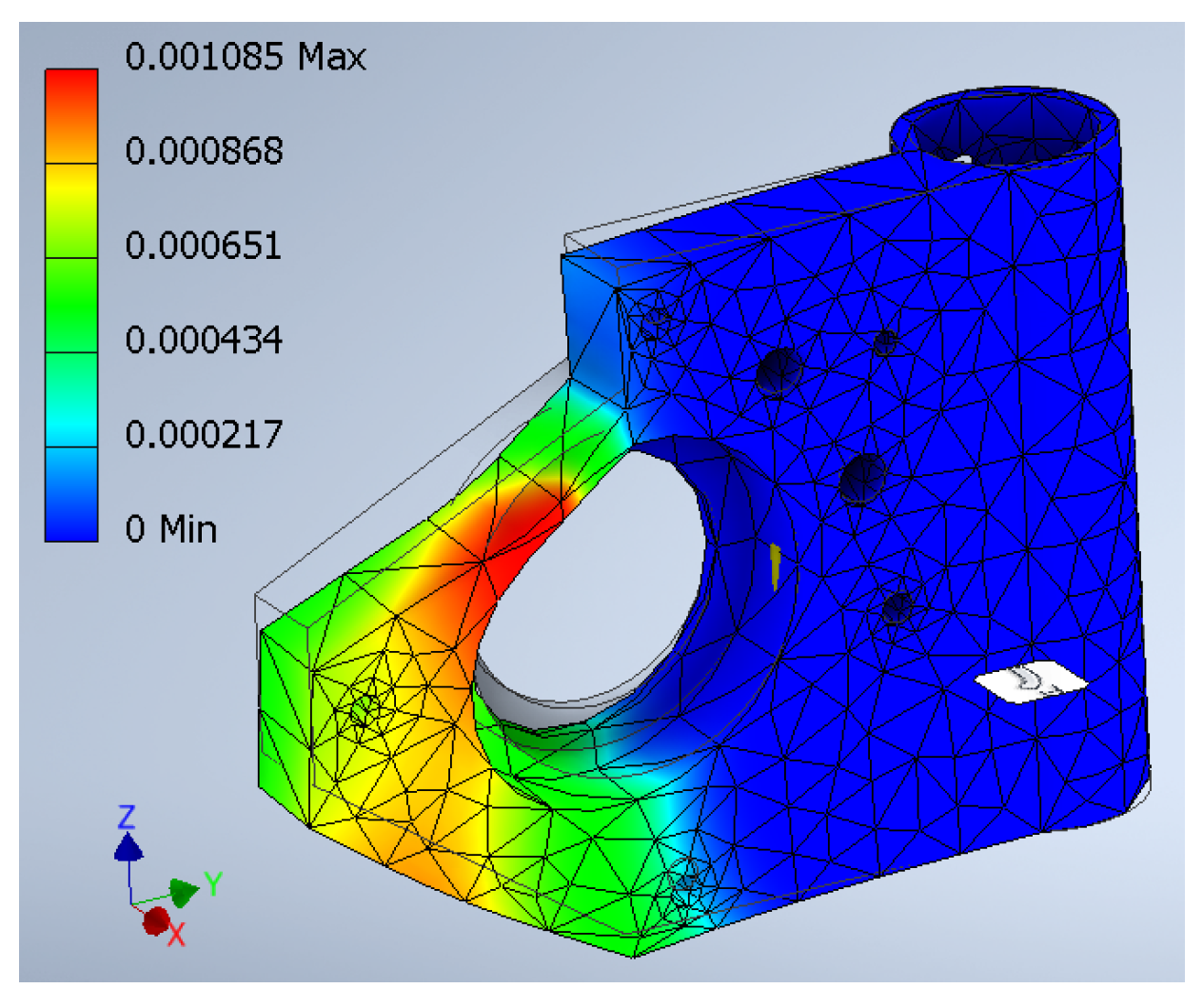
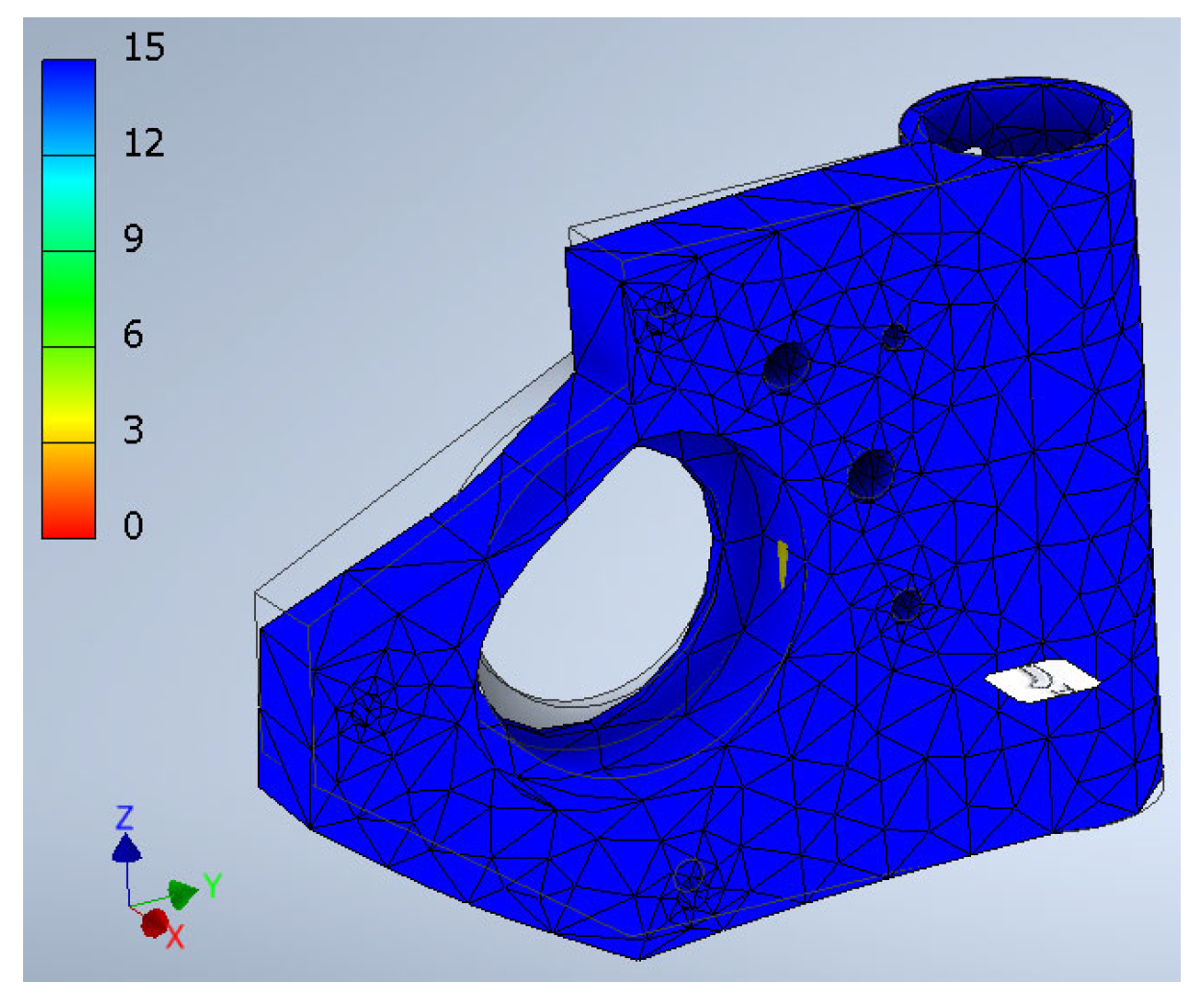
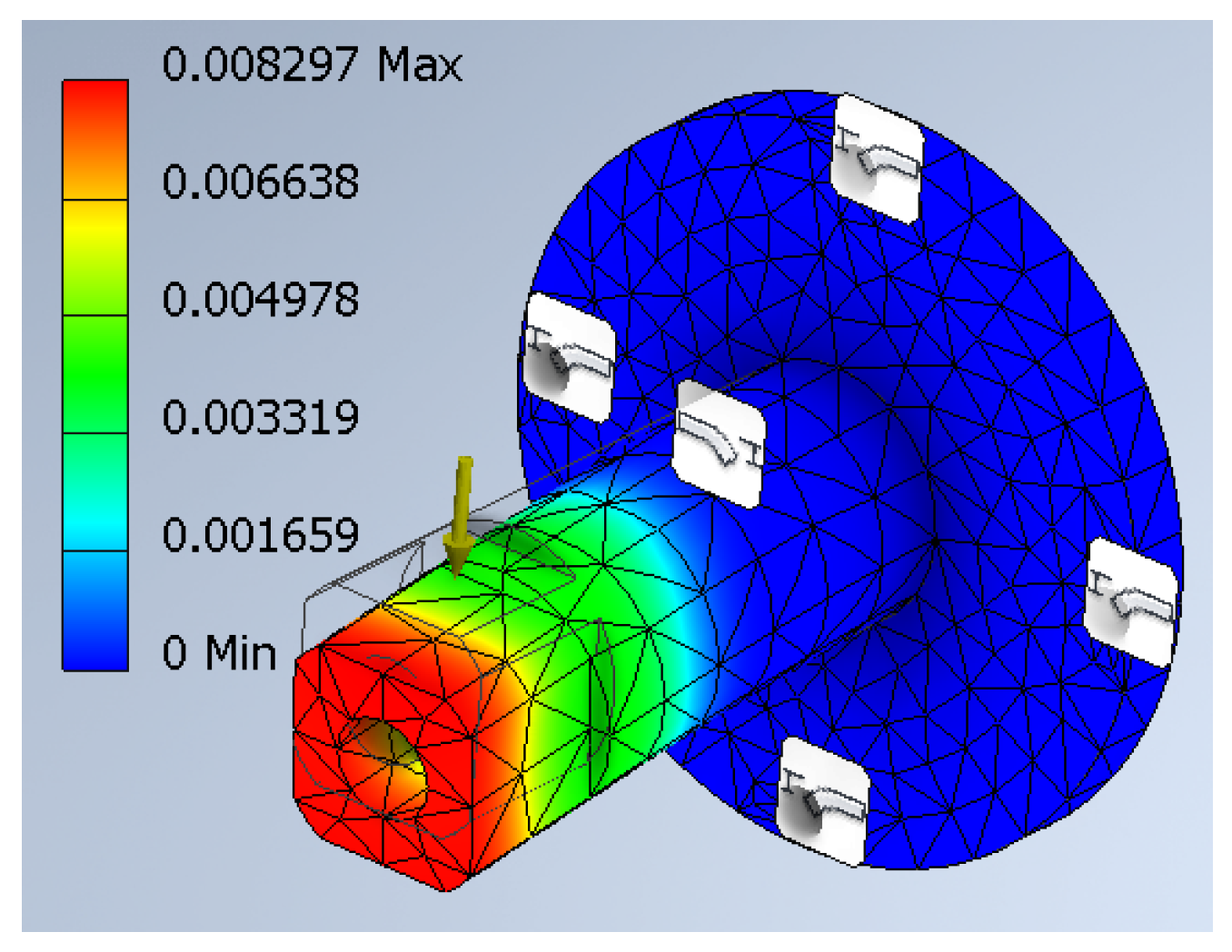
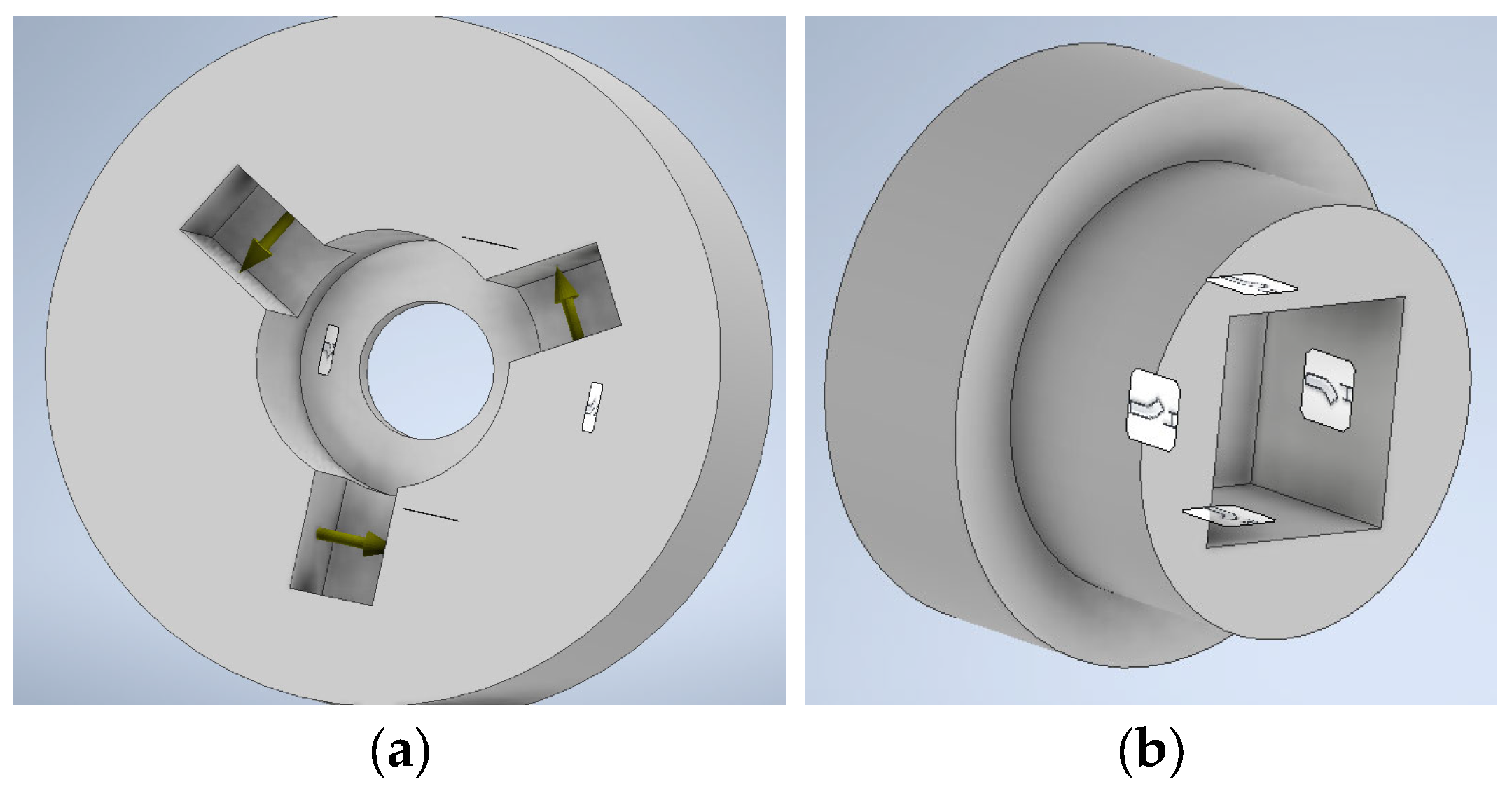
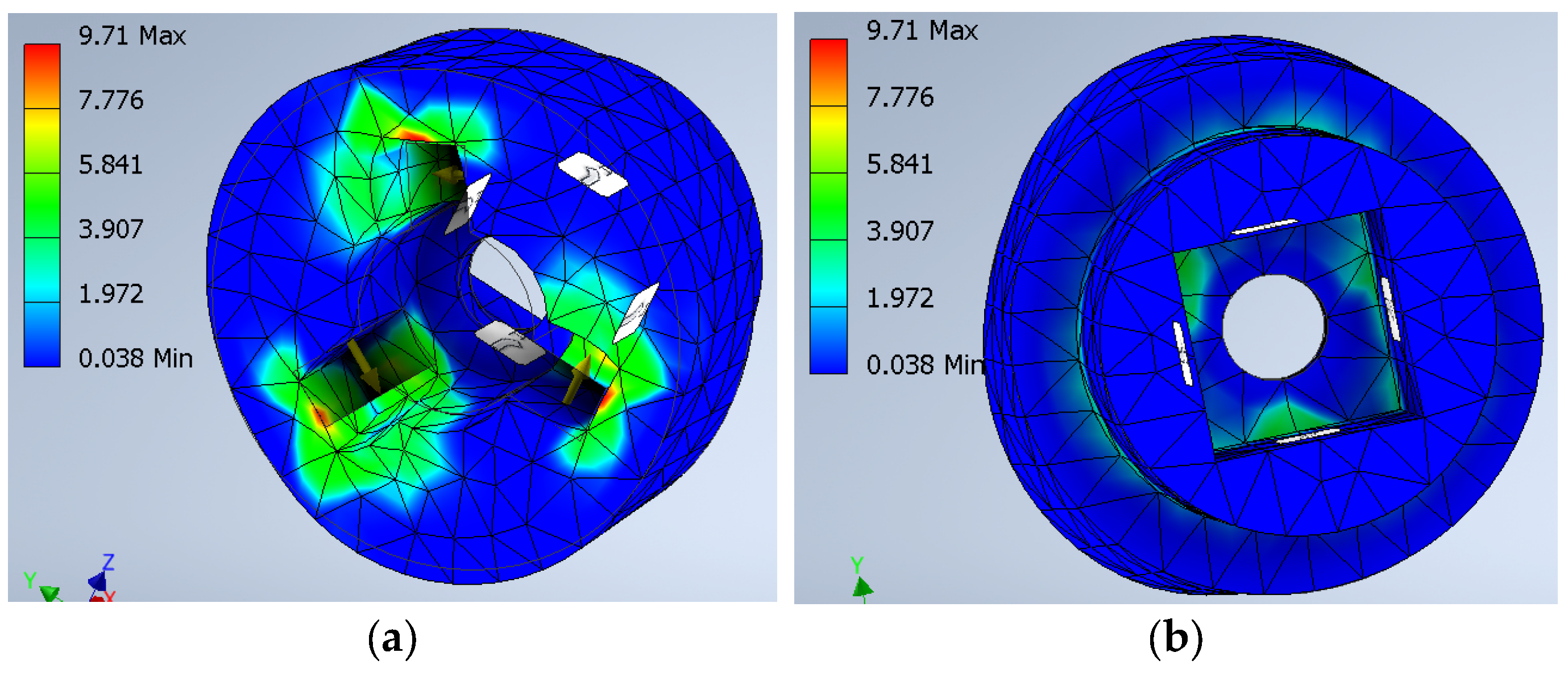
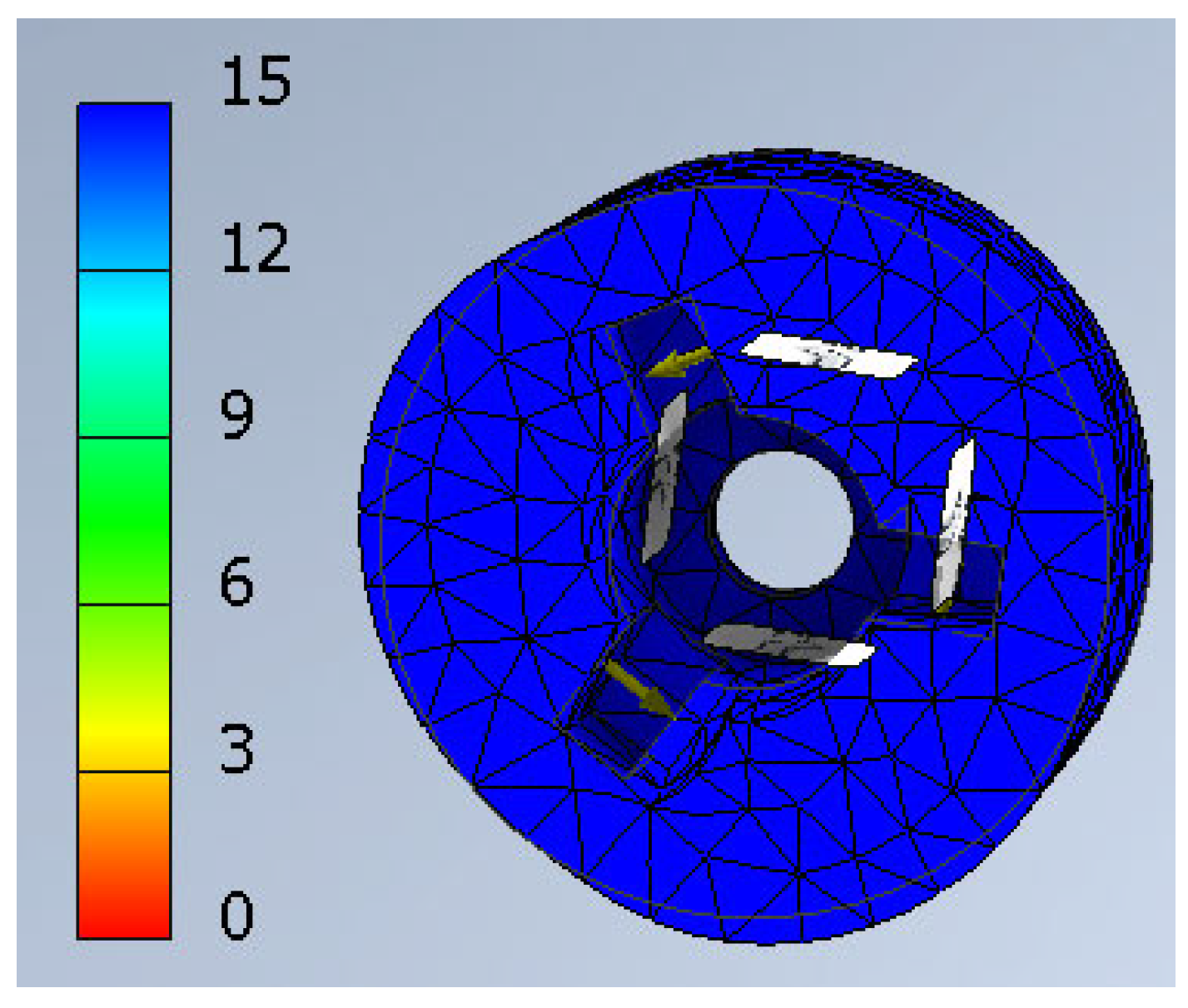
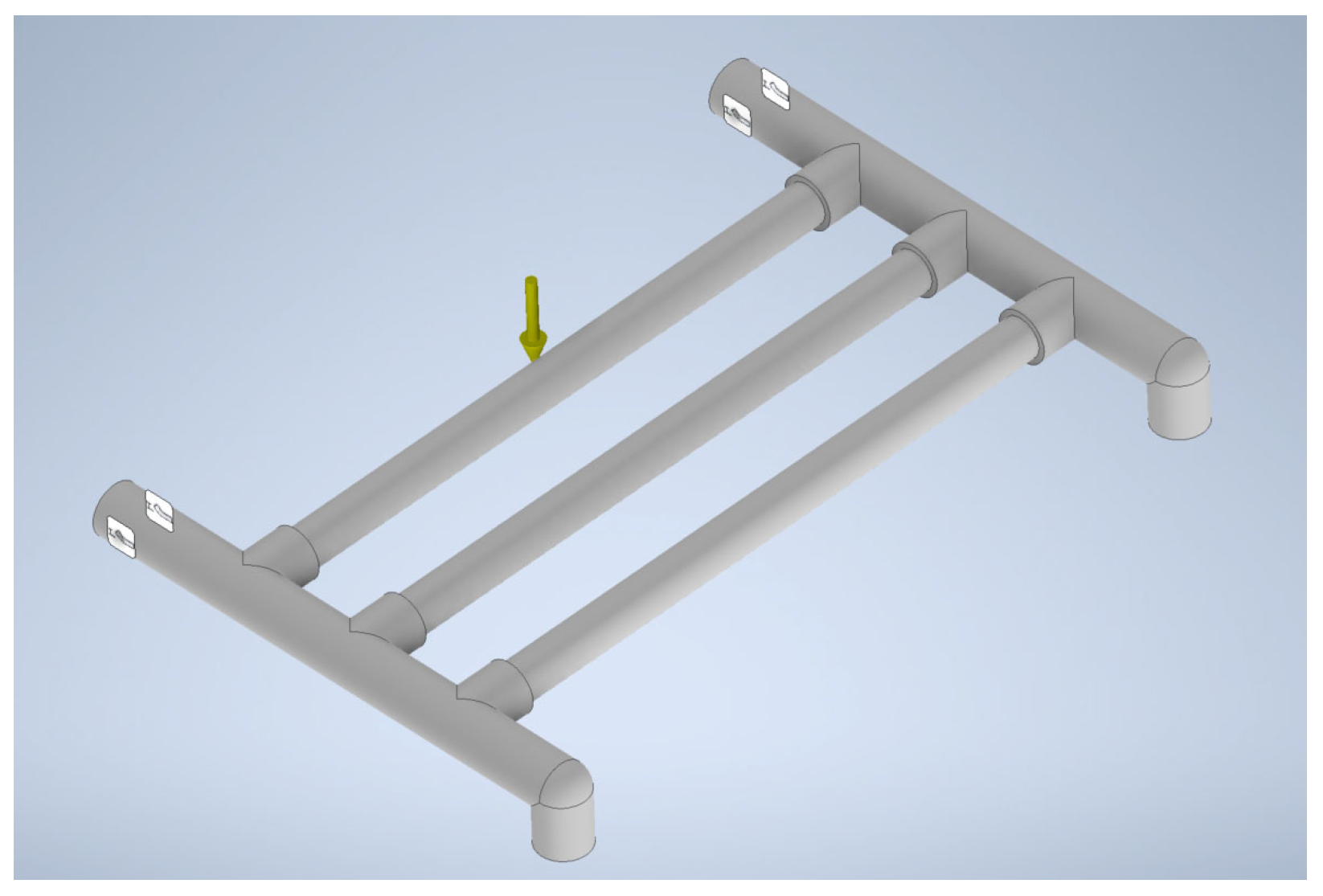
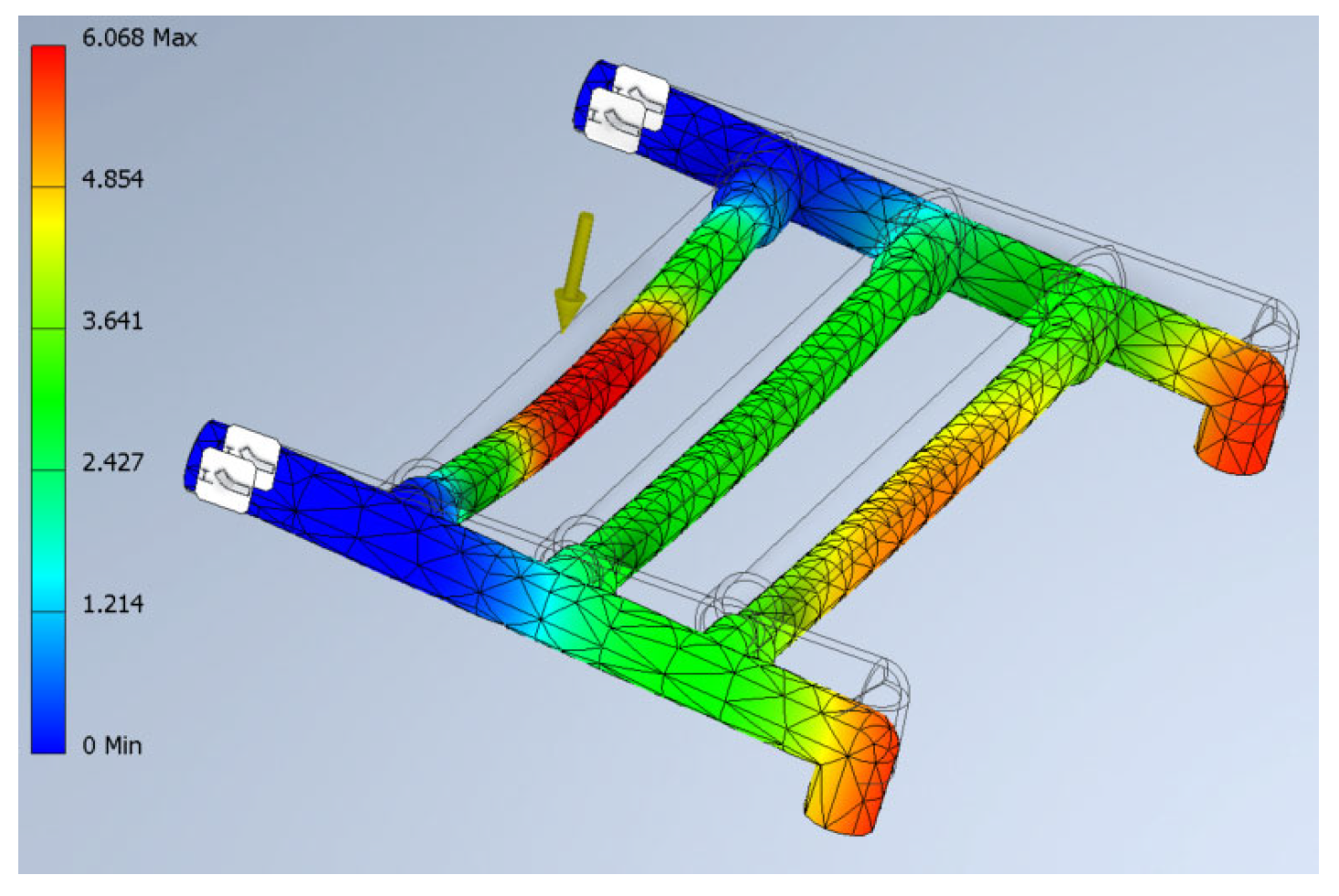
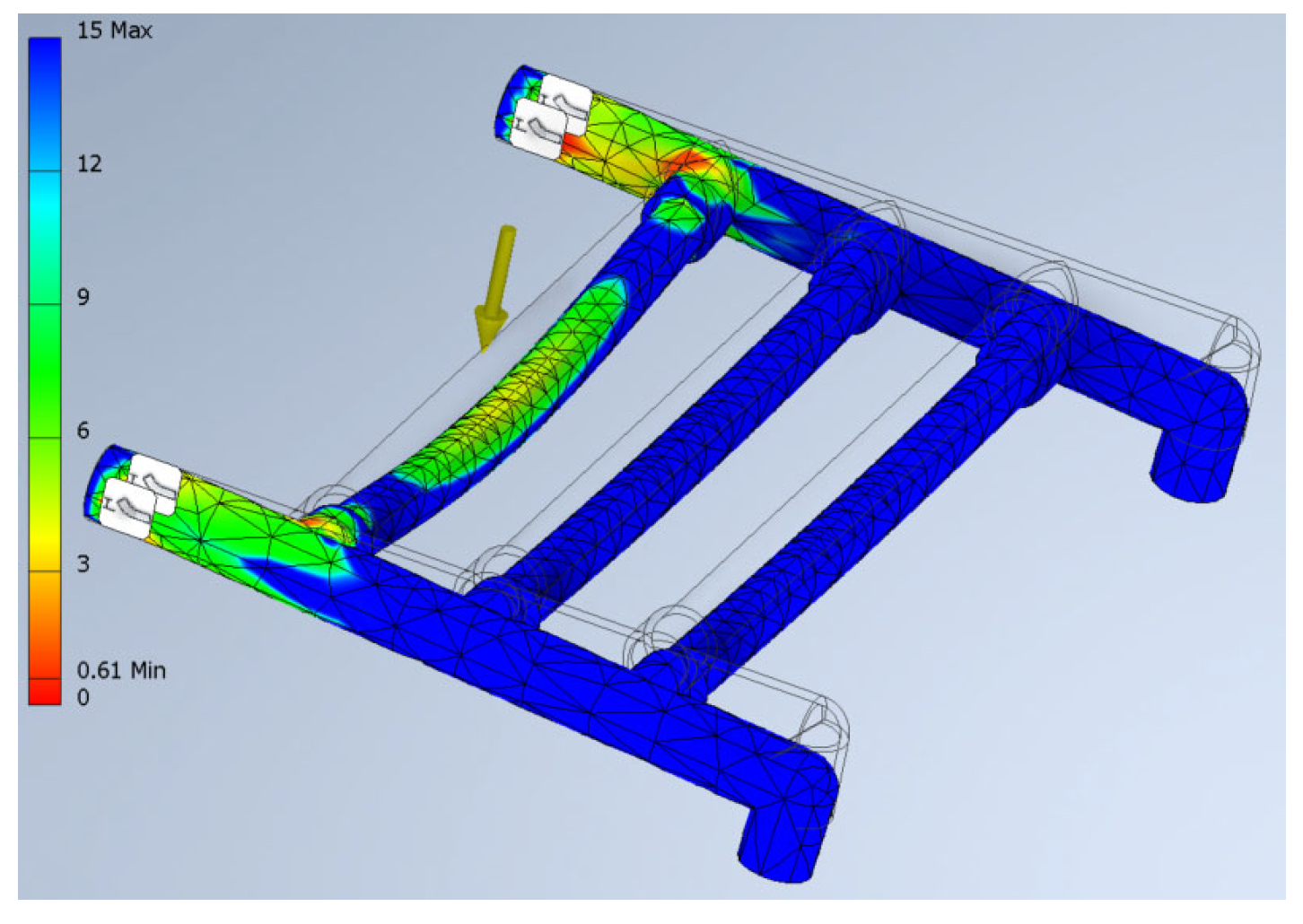
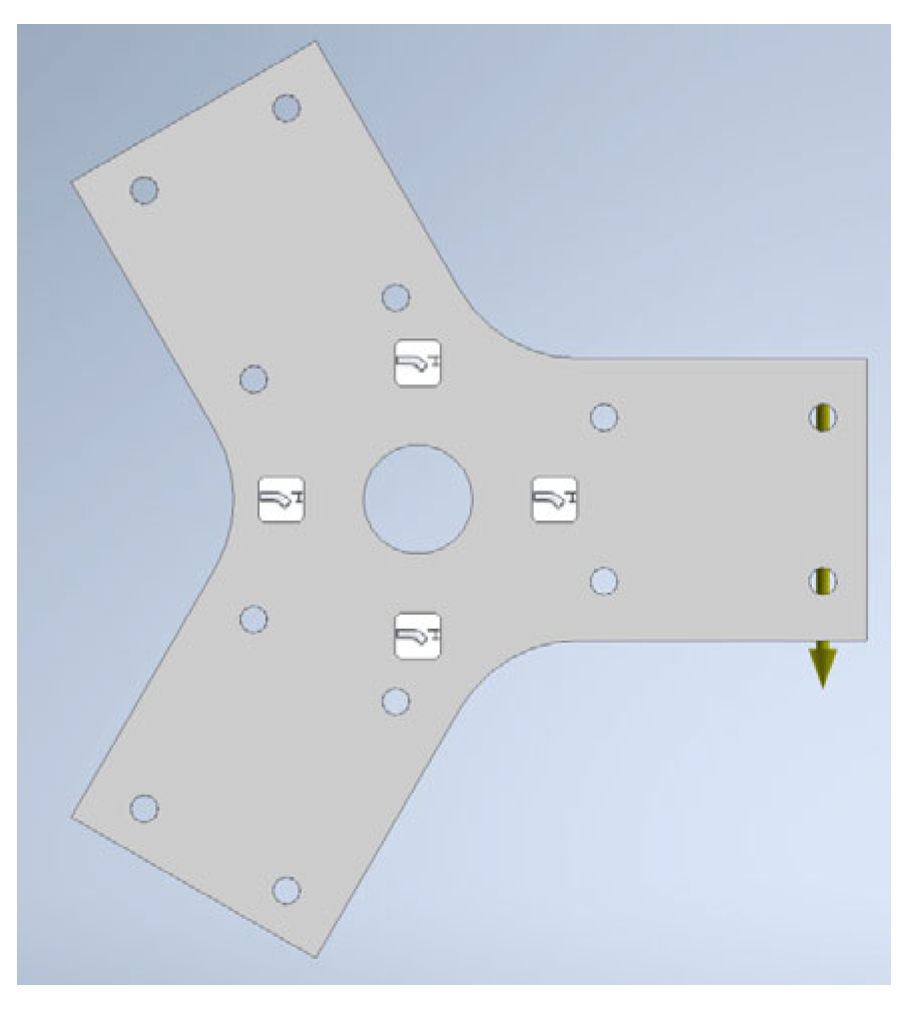
1. Introduction

A trolley is an object with wheels for moving or transporting items from one location to another. The device is a useful mechanism in factories, shops, supermarkets, homes, office complexes [1], warehouses, and marketplaces [2], and its primary aim is carrying items that are difficult to carry due to their weight [2]. When it comes to moving products higher or lower than ground level, there are situations in which a conventional trolley cannot be used, such as when there is uneven terrain or when one is going up to any level above ground level. This task is not simple, especially if there are no lifting facilities, such as elevators or conveyers [3].

In the Regional Regulation Bandung, Indonesia, concerning the reliability requirements of buildings, it was stated that every building with a height above four floors must have an elevator [4]. In developing countries like Pakistan, many buildings do not possess elevators and the primary mode of access between different floors is stairs [5]. In Malaysia, for all non-residential buildings more than four stories above or below the main access level, at least one lift is required [6]. This means that for buildings that have two to four floors, moving goods from the bottom to the top floor would be an issue. For example, several university dormitories located in Bandung have three levels or more with no escalators or elevators. Students come and go every year, forcing them to transport their goods to and from their dormitories via the stairs. If a suitable trolley is available, it would definitely make it easier for students to carry their items [4].

Walking up and down stairs is among the most challenging and hazardous activities of daily living for older individuals. This is evidenced by the reports that stair falls account for more than 10% of fatal fall accidents. The circumstances of stairway falls often include engagement in risky behaviors, such as using stairs laden with objects, using the stairs while wearing socks, not using the handrail, and carrying items when walking up or down stairs [3]. In a study conducted on the safety of older people on stairs, it was found that when needing to move an object up or down the stairs that may cause them a problem, 29% of 157 participants would not ask for help but ‘have a go anyway’ [7].

In a report published by the Bureau of Labor Statistics, over 57% of injuries among laborers and freight, stock, and material movers were to the back and shoulders. Musculoskeletal disorders are injuries or illnesses that result from overexertion or repetitive motion [8]. Bending, twisting, and turning are commonly cited movements that cause back injuries. Strains and sprains from lifting loads improperly or from carrying loads that are either too large or too heavy are common hazards associated with manually moving materials. When employees used smart lifting practices such as using hand trolleys and pushcarts, they are less likely to suffer from back sprains, muscle pulls, wrist injuries, elbow injuries, spinal injuries, or other injuries caused by lifting heavy objects [9]. However, when moving objects between floors, in most cases, specialized mechanical lifting equipment needs to be used to reduce manual handling risks. Thus, the lack of elevators in many facilities, the risky behaviors among older individuals when carrying items on stairs, and the risk of injuries among workers carrying goods in warehouses have driven the need to develop a specialized trolley for stair climbing.

A stair-climbing trolley is a type of trolley that can be pushed, pulled up or down, and stand on a stairway. Stair-climbing trolleys can be manual or battery-powered and, when used properly, can protect people from back injuries and other health problems that can result from lifting heavy loads [10].

A two-wheel (one on each side) trolley was designed by Chhabra et al. (2022) [11] for staircase climbing. The trolley was designed such that its handle extends to an arm that holds a 60 cm diameter wheel. At the same time, the arm is also connected to the base that holds the load for the trolley. The design allows for the base to be lifted when the handle is pulled. When the loaded trolley comes near a step, the wheels stop rotating. By pulling the handle more, the base of the trolley is lifted, shifting the center of gravity towards the next stair step. This causes the wheel to rotate, leading to the trolley being lifted to the next stair step [11]. However, there is no mention of foldability or space-saving features, which may be an issue in areas with limited space. Additionally, its large wheels may add weight to the product, which could burden users during its operation. Nevertheless, this staircase-climbing trolley could be useful for strong workers in large warehouses.

Hasan and Rashid (2019) [12] designed an eight-wheel stair-climbing cart, with four wheels on each side. The four wheels were fastened to connecting sheets with nuts and bolts such that they could rotate about their axis to climb stairs. According to the authors, the unique feature of this design enables users to rest when the cart is placed on two stairs. This is especially important since, when pulling the load and cart upstairs, the tensile stress upon the hand increases a lot. This may result in pain as well as fatigue while carrying loads [12]. Such design is useful for users who may need short breaks while climbing. However, assuming this design uses wheels of a similar size, integrating eight units of wheels instead of four or six definitely would increase the weight of the trolley, thus requiring a greater tensile stress. On top of that, despite the eight-wheel cart design having the added convenience of being able to pause, it may be inefficient and lead to fatigue as users need to exert extra tensile stress to restart the movement. Nevertheless, such design definitely appeals to a specific group of users who require pauses during the cart’s operation. For the rest, a motorized design may offer a less physically demanding alternative.

A six-wheel trolley, which is more commonly known as tri-wheel due to the three wheels used for each side of the product, is the preferred design for many researchers and engineers in the development of staircase-climbing trolleys [13,14,15,16,17,18,19,20,21,22,23]. This is because tri-wheel trolleys work on the principle that when one wheel touches the step, the frame holding the three wheels starts to rotate, landing the next wheel on the next step. As the wheel rotates and touches the step, the frame rotates again, landing the next wheel onto the next step [24]. This process sums up the climbing process of the tri-wheel trolley.

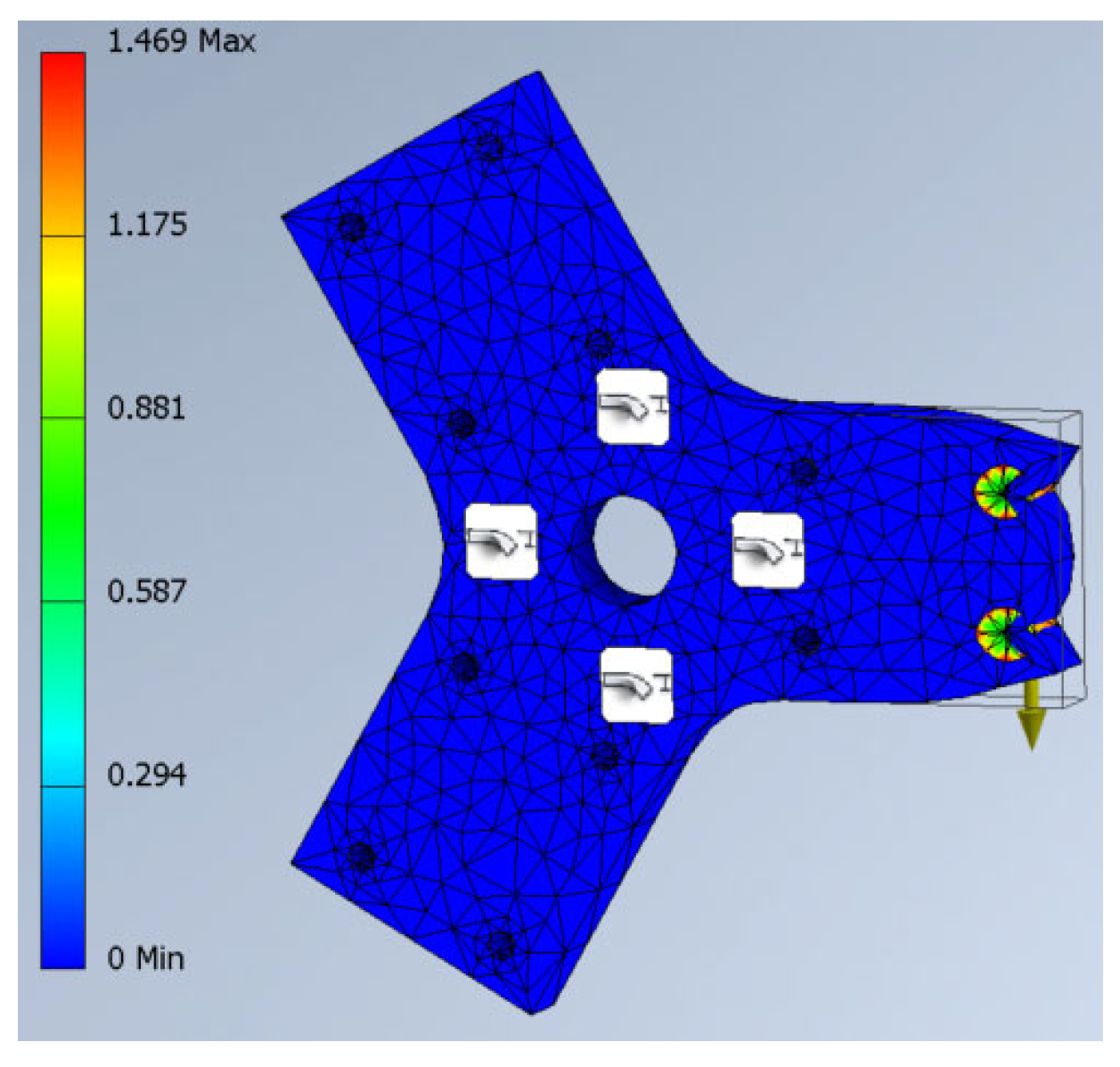
Muhammad and Wan Mohd (2023) [25] designed a tri-wheel stair-climbing trolley following a thorough procedure which included a literature review of previous research, a finite element analysis (FEA) of the trolley structure, material selection, design sketches, a structural analysis using FEA, and a simulation of the motion of the trolley. The final design of the trolley, tested under a 40 kg load, was further improved with an adjustable height feature, which provides added value for various users [25]. However, the absence of an extendable wheel frame may lead it to be unsuitable for different staircase profiles.

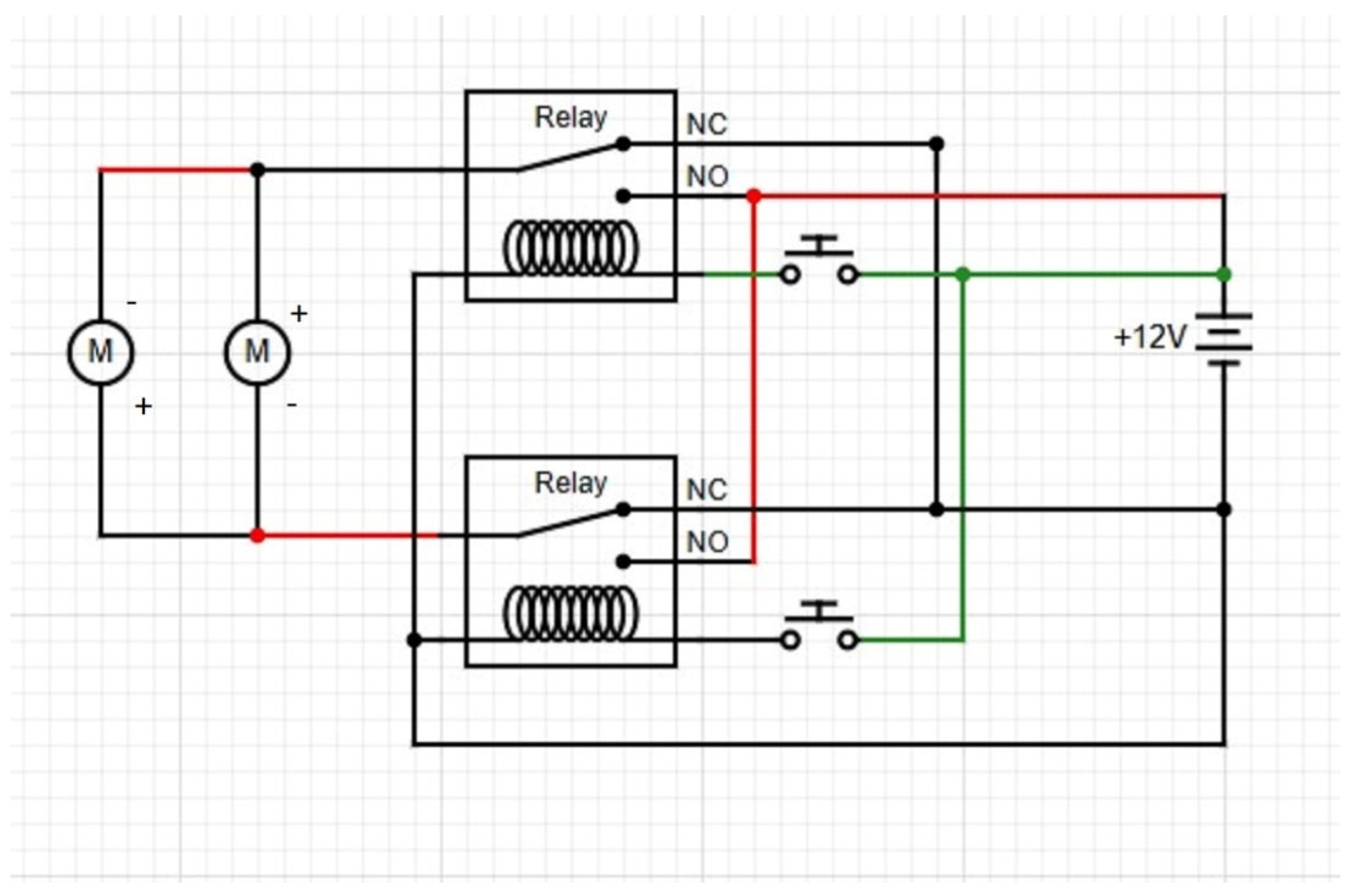
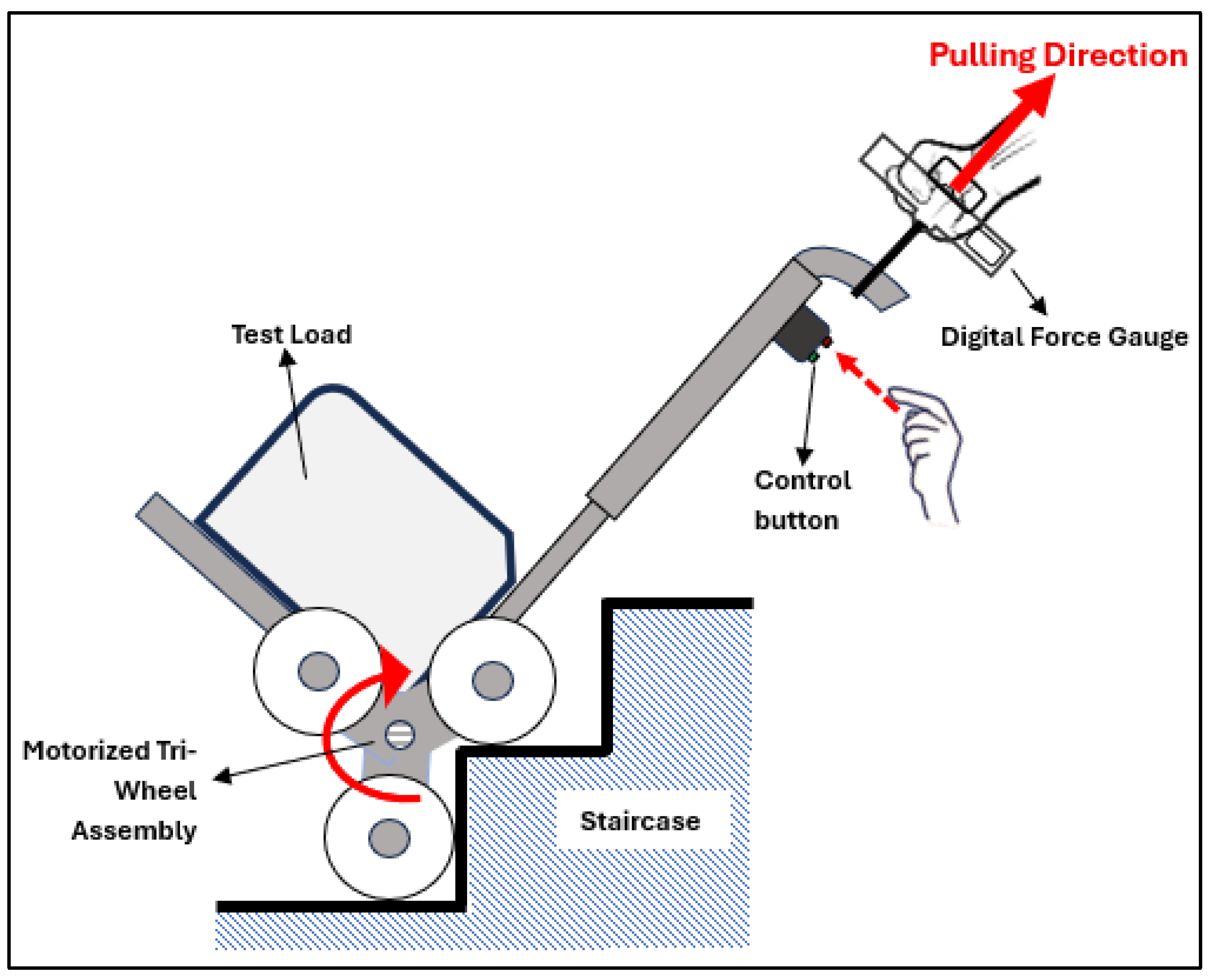
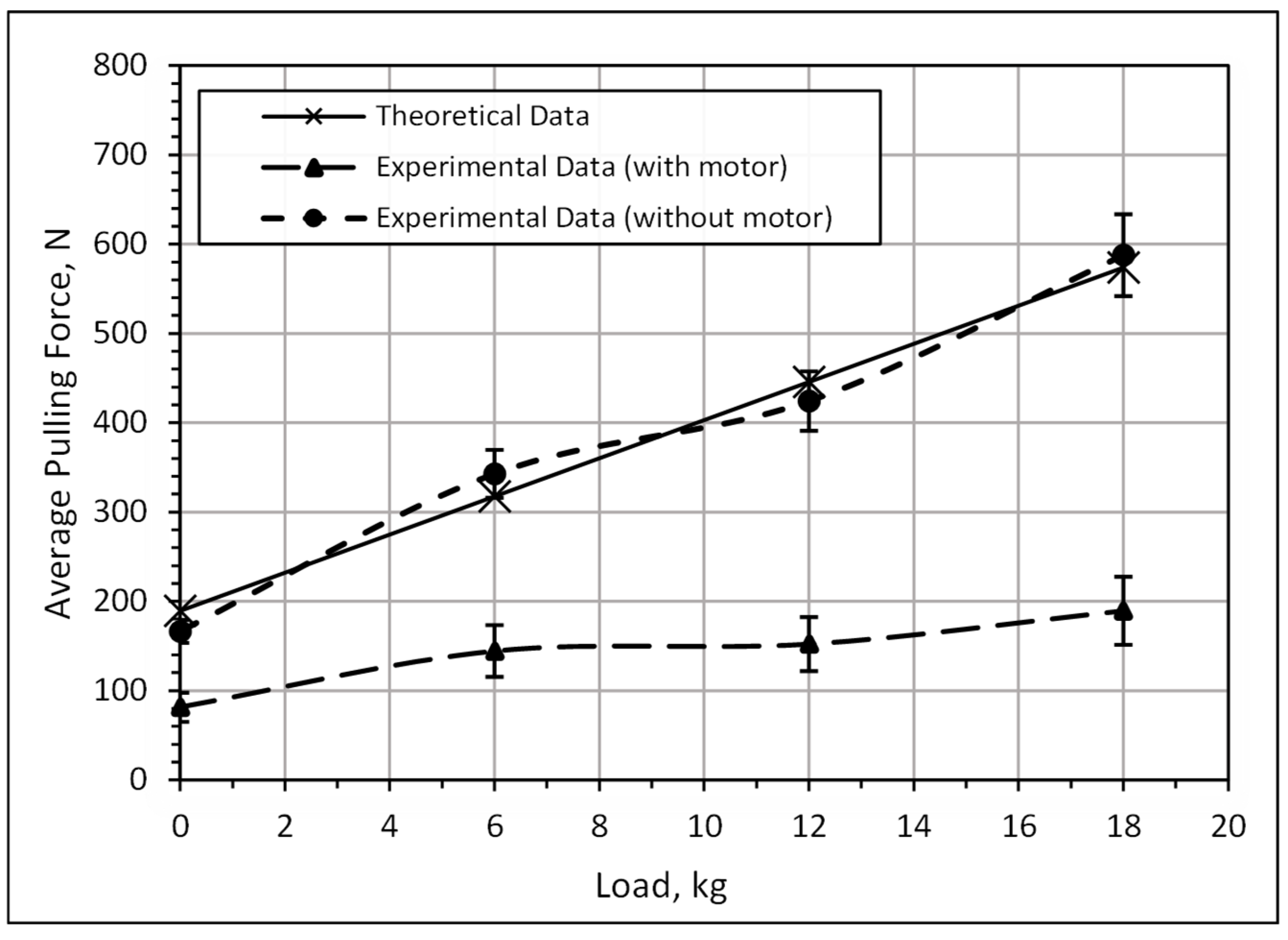
Olodu et al. (2022) [26] designed and fabricated an electric-powered, tri-wheel, stair-climbing trolley that has the ability to climb a 45-degree stairwell while carrying a 50 kg load. The success of the trolley can be contributed to the meticulous design of the tri-wheel, which incorporates five crucial factors, of which two are the height and the width of the stairs. Additionally, when compared to a conventional hand trolley, the electrically powered stair-climbing trolley displayed an enhanced performance efficiency (87%). Nevertheless, the authors admitted that 45 degrees was the maximum gradient the trolley could climb [26].

While the tri-wheel seems like an ideal design for stair-climbing trolleys, it is limited to a narrow range of stair heights due to its fixed frame size. Thus, users struggle to operate the trolley on stairs that are too short or tall relative to the wheel frame. In contrast, trolleys designed with an extendable frame can accommodate a wider range of stair heights, allowing for better adaptability across different stair profiles, as suggested by previously published works [27,28].

Ishak and Pailin (2023) [29] designed and fabricated a prototype of a staircase-climbing trolley, which they coined a hand truck. Prior to its design, the authors first determined the essential needs of trolley users through observations and interviews with students staying in a seven-story hostel, specifically regarding the transportation of goods using a staircase. The students complained that, among other factors, the conventional trolley provided was inadequate to carry goods up the staircase due to its inflexible wheel structure. As a result, the students had to increase their efforts to lift the trolley for staircases with a larger width and height. Then, the authors sketched several concept designs, conducted concept screening, selected the final design, conducted a linear static FEA, and conducted usability testing. The final design consists of an adjustable frame, an adjustable handle length, and foldability, among other features. The usability testing results showed flexibility in extending the wheel frame by 2 cm, 4 cm, and 6 cm, which is advantageous for applications across different staircase sizes [29].

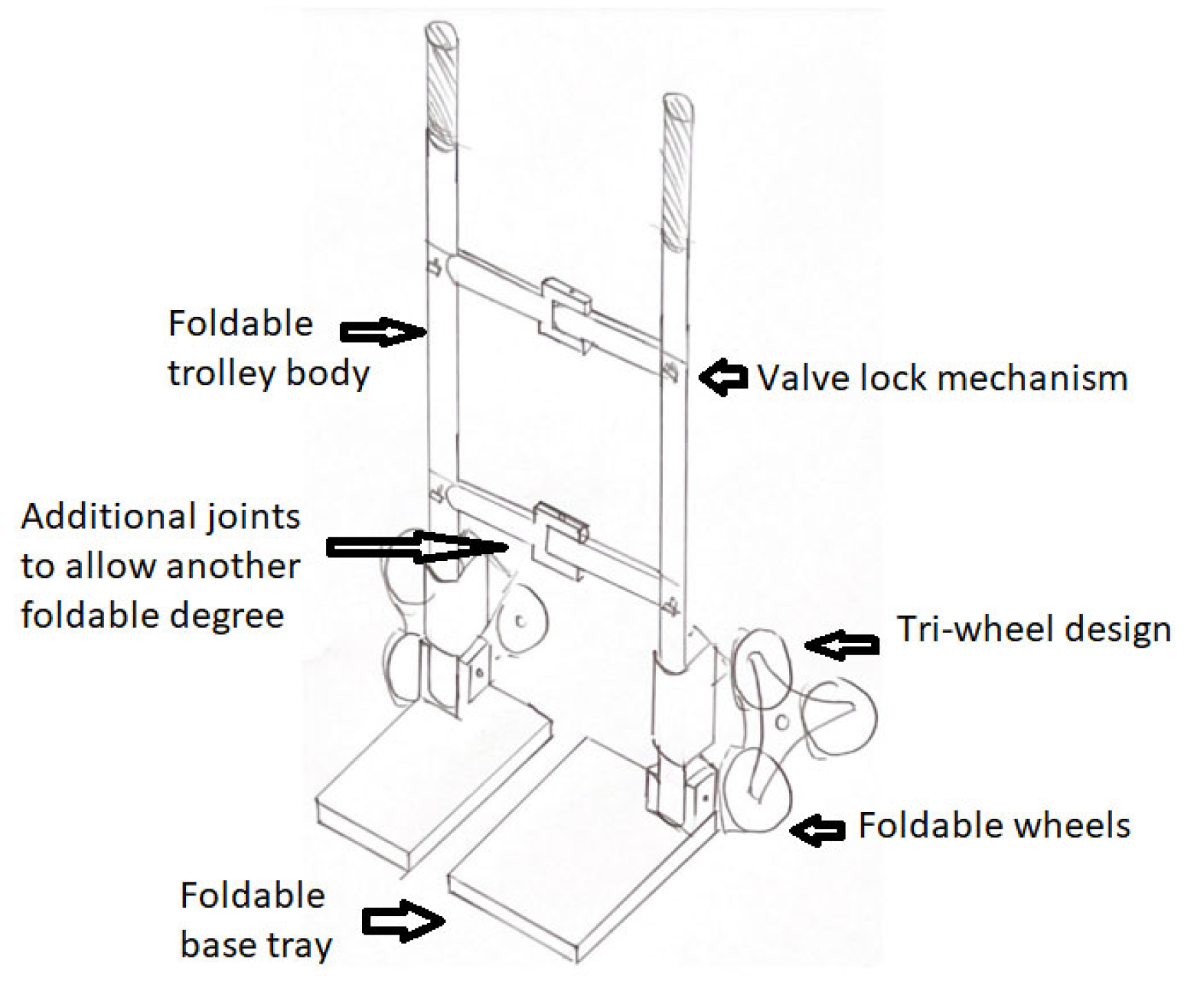
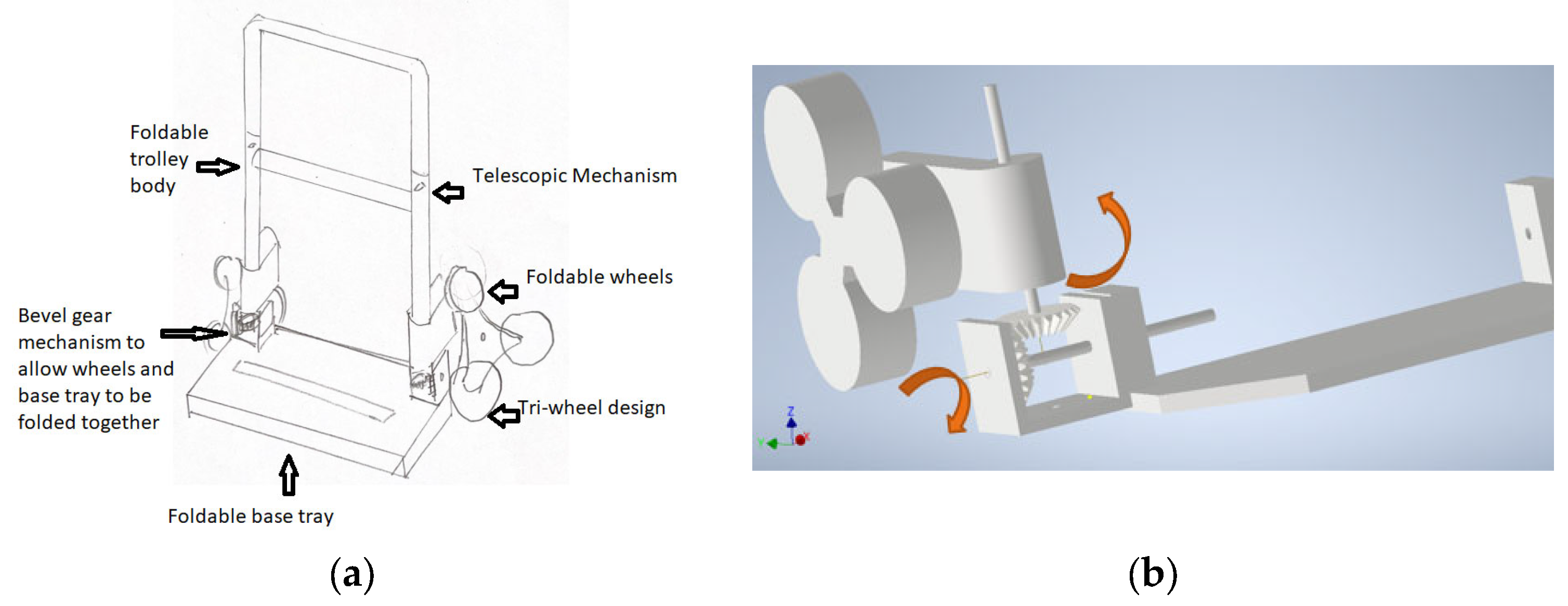
A foldable stair-climbing trolley offers practical advantages by saving space and being easy to store. This design is particularly significant for users working in confined spaces or urban environments where space is limited. Shiau et al. (2015) [30] utilized a mutual pivot junction with supporting frames and a handrail in their development of an innovative foldable trolley. The design not only allowed for changing the folding angle and folding method, but it also allowed it to be easily carried by pulling the handrail on roller wheels after folding it. Through a static analysis, it was found that the safety coefficient was always greater than 1.5; thus, the safety of the entire structure was only impacted to an extremely low extent [30]. Aside from the work by Shiau et al. (2015), the design features of other foldable products, such as multifunctional stretchers, may offer valuable insights for improving portability and storage efficiency [31].

Table 1. Summary of stair-climbing trolley designs and their key features in selected studies.

Author (Year)	Wheel	Frame (Extendable)	Tri-Wheel (Adjustable)	Motorized	Notes
Chhabra et al. (2022) [11]	Two-wheel (one on each side)	No	No	No	The design allows for shifts in its center of gravity, assisting the lift motion for steps
Hasan and Rashid (2019) [12]	Eight-wheel (four on each side)	No	No	No	The design allows the user to rest when two wheels are positioned on a stair step
Muhammad and Wan Mohd (2023) [25]	Six-wheel (three on each side)	No	Yes	No	The design features adjustable height, which accommodates users of varying heights
Olodu et al. (2022) [26]		No	No	Yes	The motorized feature leads to 87% performance enhancement compared to conventional trolley
Ishak and Pailin (2023) [29]		Yes	Yes	No	The wheel frame can be extended by 2 cm, 4 cm, and 6 cm, allowing it to be adapted to various staircase profiles
Tun et al. (2019) [10]		No	No	No	The prototype displays a basic model with several limitations, suggesting the need for more innovation beyond fundamental approach
Sathe et al. (2020) [32]		No	No	No	The motorized design displayed steady performance across uniform step size but faced difficulties when climbing stairs with an inclination above 44 degrees
Bara et al. (2023) [33]		No	Yes	No	The design is equipped with adjustable handle to accommodate users with different heights
Saikrishna et al. (2023) [34]		No	No	No	The trolley travels smoothly over uniform stairs but struggles when faced with stairs with various step sizes
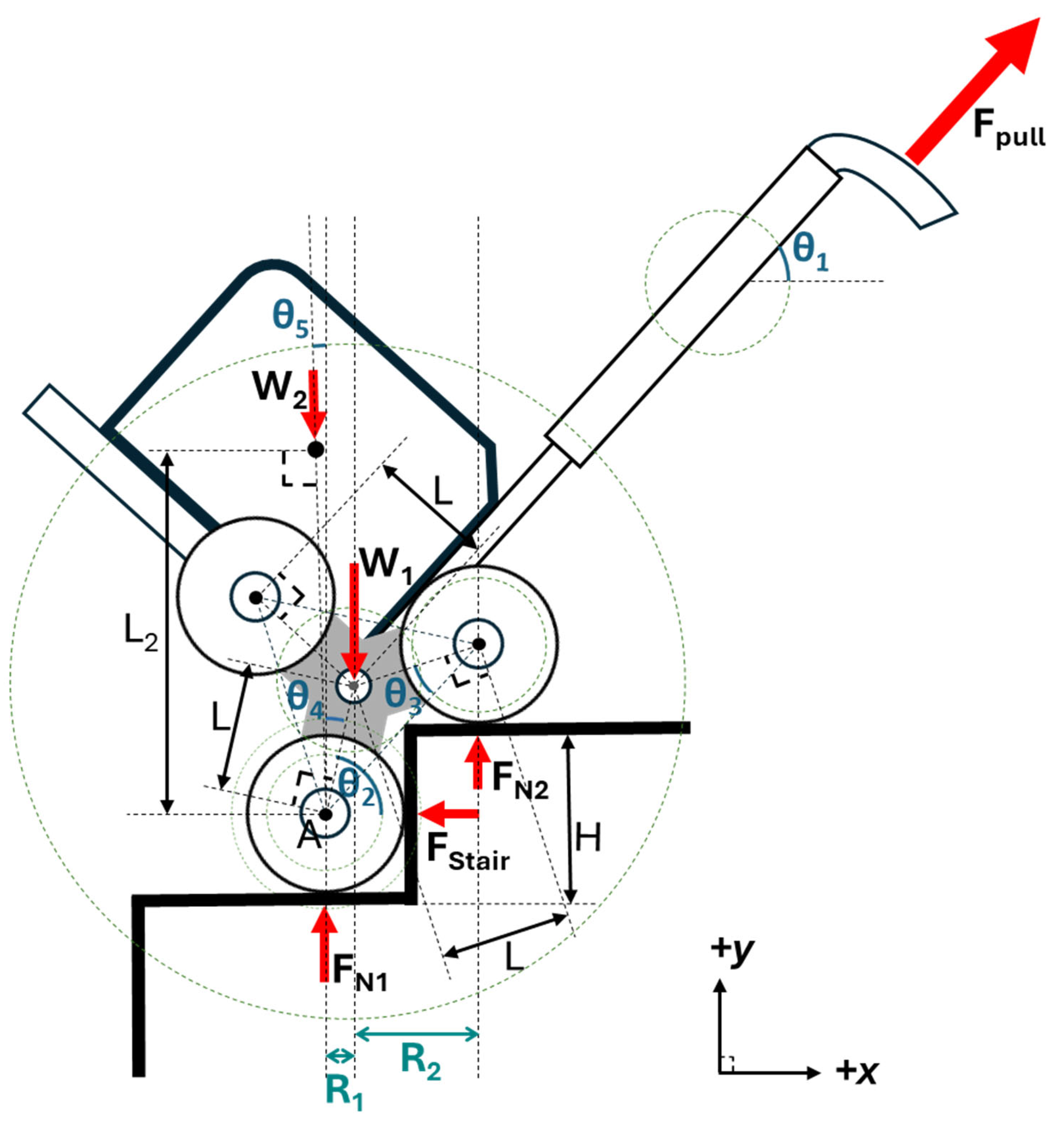
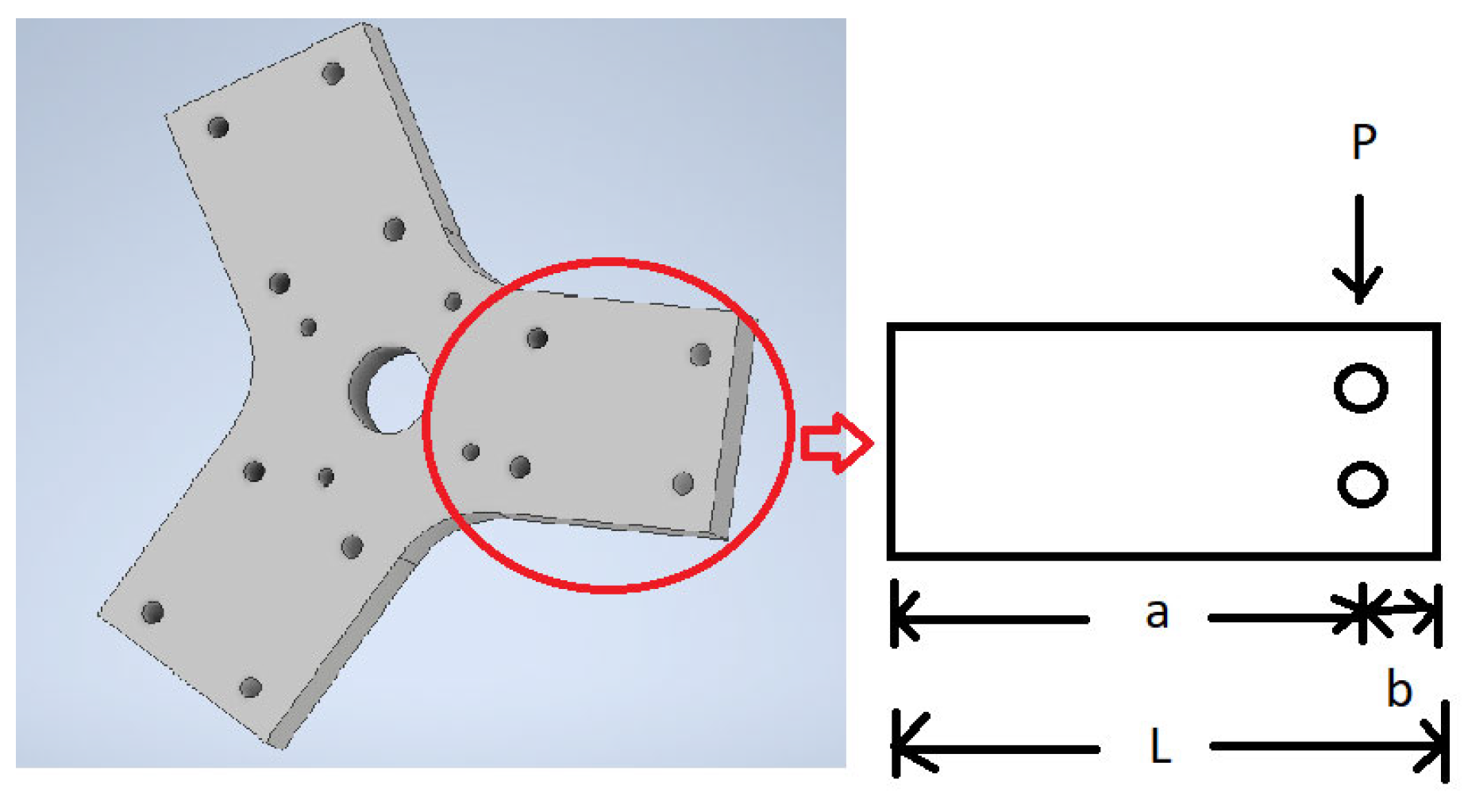
Norain and Yew (2021) [35]		No	Yes	No	The design features manual hand winch, which allows items to be lifted from the ground to higher surfaces, such as tables

displays the summary of stair-climbing trolley designs and key features from the selected studies reviewed above, as well as other relevant works [32,33,34,35]. To the best of the authors’ knowledge, there are no reports of a stair-climbing trolley that incorporates a tri-wheel with an extendable and foldable body frame to save space, adjustable tri-wheel radii, and a motorized design for reduced physical effort while transporting goods up and down staircases. Thus, this project aims to design, develop, and analyze a tri-wheel trolley with motorized, adjustable, and foldable features. The development of this trolley may help reduce physical strain when carrying heavy loads up staircases, especially for workers and residents. Additionally, this trolley may assist elderly people who live alone, giving them the ability to carry out tasks independently.

2. Methodology

2.1. Concept Screening and Scoring

Concept screening and scoring are significant steps in product development, allowing researchers to identify viable design options early in the development process. Various studies have incorporated this method to evaluate and refine their designs [36,37,38]. The concepts reviewed in the literature review were screened and scored. The concept relevant for this innovation was selected to go through both screening and scoring. Each feature or concept had different criteria due to their different use cases. For example, a movable trolley concept should meet the criteria of safety and stability, which allow users to use the trolley safely and efficiently. Potential or better innovations for the current trolley were used for screening and scoring as well. After the best concepts were selected, the concepts were used to draft the conceptual designs.

2.1.1. Criteria for Concept Screening and Scoring

The criteria for concept screening and scoring are weight, durability, ease of manufacturing, cost, size, efficiency during use, safety, and stability.

The weight of the trolley should be functional and lightweight. Lightweight designs will produce a lighter model, which is favorable in the case of a stair-climbing trolley. A heavy trolley will burden users when carrying objects up staircases and cause soreness in their arms. A sales manager from the UK mentioned that lightweight equipment was safer than heavier equipment. Also, lightweight equipment is easier to use compared to heavier equipment [39].

The durability of the trolley should be good: the trolley should withstand high loads and not break. The trolley should be able to withstand shocks and high loads. Also, users expect a trolley to function well after multiple uses. Hence, the trolley should not break easily and should be reliable. Donracks mentioned the important aspects of a stainless-steel shopping cart, including durability. Hence, the trolley should be durable [40].

The ease of manufacturing should be good: the trolley should be easy to make or produce. This reduces the complexity when fabricating its parts. Also, if the trolley is required to be mass-produced, this will reduce the lead time as well. A design methodology called Design for Manufacturing and Assembly (DFMA) is an approach to ease the manufacturing and assembly process. Hence, the design methodology is important in regards to ease of manufacturing [41].

The total cost of making the design should be low and relevant while not sacrificing any functionality or durability. A product with a low final cost can be sold at a lower price and would be more competitive in the market. ProfitWell mentioned the importance of pricing: a price point lets the customers know whether it is worth their investment and time [42].

The storage size should be small for added convenience. The folded trolley should be small enough to fit into a car trunk. The importance of properly sized equipment has been reported. Properly sized equipment can provide more comfort while reducing the total cost at the same time [43].

The efficiency of the trolley during its use should be great. The design should be easily understood and users should be able to operate it after a glance. The design should be easy to use for users’ convenience. Researchers from Oklahoma State University mentioned the importance of equipment efficiency: efficient equipment will require minimal effort to operate [44].

The safety of the trolley should be good. The trolley should be safe to use, which would prevent injuries while using it. The feature or design should not have potential hazards like rotating too fast or having sharp edges.

The trolley should have good stability. The trolley should remain still when not in use. Also, while using the trolley, it should not tilt sideways, which would result in the load falling off the trolley.

Finally, the trolley should be easy to use. The concept should be easily accessed and the trolley should be convenient to use, so that it is more user friendly. The users should easily understand how to use its features.

2.1.2. Concept Screening for Wheels

The concept screening for wheels is shown in

Table 2. Concept screening for wheels.

Wheels	Concepts
Selection Criteria	Tri-Wheel	Quad-Wheel	Custom Wheel	Tracked Wheel
Weight	+	0	+	−
Durability	+	0	−	−
Ease of Manufacturing	+	+	−	−
Cost	0	0	0	−
Size	+	0	+	−
Efficiency During Use	0	0	+	+
Sum of +	4	1	3	1
Sum of 0	2	5	1	0
Sum of −	0	0	2	5
Net Score	4	1	1	−4
Rank	1	2	2	3

. The best designs received +, while the worst received −. Some designs that were decent were given a neutral score of 0. The weight of the mechanism should be as light as possible. Hence, the design with the lowest weight received a plus. The design with the best durability was given a plus. The design with a wheel mechanism that is easy to manufacture received a plus. Furthermore, the mechanism that requires the lowest cost to manufacture was given a plus. The mechanism with the smallest size was given a plus. Finally, the mechanism that had the best efficiency while in use was given a plus.

2.1.3. Concept Screening for Motorized Design

The concept screening for motorized designs is shown in

Table 3. Concept screening for motorized design.

Motorized Design	Concepts
Selection Criteria	Power Window Motor to Define Increments of Steps	Motor Connected to Chain Sprocket	Track-Based
Weight	+	0	−
Size	+	0	−
Ease of Use	0	0	+
Durability	0	0	−
Ease of Manufacturing	+	+	−
Cost	+	0	−
Safety	0	−	0
Stability	0	0	−
Sum of +	4	1	1
Sum of 0	4	6	1
Sum of −	0	1	6
Net Score	4	0	−5
Rank	1	2	3

, in which the best designs received +, while the worst received −. Some designs that were decent were given a neutral score of 0. The motorized design that had the lowest weight was given a plus. The smallest design was given a plus. The motorized design that was the easiest to use was given a plus. Also, the design with best durability was given a plus. The design that was easiest to manufacture was given a plus. The design that required the lowest cost to manufacture was given a plus. Furthermore, the design that provided the greatest level of safety was given a plus. Finally, the design that had the best stability while in use was given a plus.

2.1.4. Concept Screening for Anti-Slippage Mechanism

The concept screening for anti-slippage mechanism is shown in

Table 4. Concept screening for anti-slippage mechanism.

Anti-Slippage Mechanism	Concepts
Selection Criteria	Pin Locking Mechanism	Ratchet Wheel Arrangement	Stopper Mechanism
Weight	0	0	+
Size	+	+	+
Ease of Use	0	+	0
Durability	−	0	0
Ease of Manufacturing	−	0	0
Cost	+	0	0
Sum of +	2	2	2
Sum of 0	2	4	4
Sum of −	2	0	0
Net Score	0	2	2
Rank	2	1	1 (fin wheels only)

, in which the best designs received +, while the worst received −. Some designs that were decent were given a neutral score of 0. The lightest design was given a plus. The mechanism that occupied the least space was given a plus. The mechanism that was the easiest to use was given a plus. Also, the mechanism that had the best durability was given a plus. The mechanism that was the easiest to manufacture was given a plus. Finally, the mechanism that required the lowest cost was given a plus.

2.1.5. Concept Screening for Locking Mechanism

The concept screening for locking mechanism is shown in

Table 5. Concept screening for locking mechanism.

Locking Mechanism	Concepts
Selection Criteria	Telescopic Lock	Valve Lock Mechanism
Durability	0	−
Ease of Manufacturing	+	−
Cost	+	−
Size	+	0
Efficiency During Use	0	0
Sum of +	4	0
Sum of 0	2	3
Sum of −	0	3
Net Score	4	−3
Rank	1	2

, in which the best designs received +, while the worst received −. Some designs that were decent were given a neutral score of 0. The lightest mechanism was given a plus. The mechanism that had the best durability was given a plus. The mechanism that was the easiest to manufacture was given a plus. Also, the mechanism that required the lowest cost to manufacture was given a plus. Furthermore, the smallest mechanism was given a plus. Finally, the mechanism that was the most efficient while in use was given a plus.

2.1.6. Method for Concept Scoring and Decision Making

• The top 2 designs from concept screening are selected for concept scoring;
• The scoring ranged from 1 to 5, with 5 being highest. If scores are close, combination of designs is used;
• Each selected criterion is given a weightage for that specific purpose; for example, a trolley that is expected to be lightweight will have a higher weightage;
• The concepts are given a rating with respect to the selected criteria;
• The rating is multiplied by the weightage and a weighted score is obtained;
• The total weighted score is calculated and compared to that of the other concepts;
• The highest-scoring concept is selected for the final design;
• If 2 designs score the same, their combination and accessibility will be considered.

2.1.7. Concept Scoring for Wheels

Table 6. Concept scoring for wheels.

Wheels		Concepts
		Tri-Wheel		Quad-Wheel		Custom Wheel
Selection Criteria	Weight	Rating	Weighted Score	Rating	Weighted Score	Rating	Weighted Score
Weight	25%	4	1	3	0.75	3	0.75
Durability	25%	4	1	4	1	3	0.75
Ease of Manufacturing	10%	4	0.4	4	0.4	2	0.2
Cost	10%	3	0.3	3	0.3	3	0.3
Size	15%	3	0.45	2	0.3	3	0.45
Efficiency During Use	15%	3	0.45	3	0.45	4	0.6
Total Score			3.6		3.2		3.1
Rank		1		2		3
Continue?		Yes		No		No

shows the concept scoring for wheels. The weight of the wheels was crucial to ensure a lightweight final product; hence, 25% weightage was given for weight. The lightest design was given the highest rating. The durability of wheels plays an important role in ensuring reliability and preventing breakdowns. If one of the wheels breaks, the stair-climbing trolley may not operate as intended; hence, durability was weighted at 25%. The design with the best durability was given the highest rating. The criterion for ease of manufacturing was weighted at 10%, as wheels may be bought directly from suppliers. The design that was the easiest to manufacture was given the highest rating. The cost of the wheels was weighted at 10%, as wheels in general are inexpensive, so this does not greatly affect the final cost of the design. However, cheaper wheels were still desired. The design with the lowest cost was given the highest rating. Next, the size of wheels was weighted at 15%, as smaller designs will produce a smaller product. Hence, the trolley should be small when it is in storage, so it can be stored easily and conveniently. The smallest design was given the highest rating. Efficiency during use was weighted at 15%, as the wheels are bought from suppliers; hence, we cannot determine their efficiency. However, we can anticipate the potential of the designed wheels; for example, the wheels should move smoothly while moving upstairs. The design with the best efficiency while in use was given the highest rating.

2.1.8. Concept Scoring for Motorized Design

Table 7. Concept scoring for motorized design.

Motorized Design		Concepts
		Power Window Motor to Define Increment of Steps		Motor Connected To Chain Sprocket
Selection Criteria	Weight	Rating	Weighted Score	Rating	Weighted Score
Weight	20%	4	0.8	3	0.6
Size	10%	4	0.4	3	0.3
Ease of Use	20%	4	0.8	4	0.8
Durability	15%	4	0.6	3	0.45
Ease of Manufacturing	10%	4	0.4	3	0.4
Cost	5%	4	0.2	3	0.15
Safety	10%	3	0.3	2	0.2
Stability	10%	3	0.3	3	0.3
Total Score			3.6
Rank		1		2
Continue?		Yes		No

shows the concept scoring for motorized design. The weight of the motorized design will highly impact the outcome of final product, as high-torque motors will be heavy, so selections were made carefully for this concept design. Hence, the weight of motorized design was given a weightage of 20%. The lightest design was given the highest rating. The size of the motor had been weighted at 10%, as motors with high torque are generally bulky and may need a big power supply; hence, it may beneficial to select a motor design that is smaller. The smallest design was given the highest rating. The criterion ease of use was weighted at 20%, as the motor will act as the driving force when climbing stairs; hence, the motor must be easy to use to prevent complications. The design that was the easiest to operate was given the highest rating. The durability of the motor should be high, as it will be used consistently while climbing stairs, so this was weighted at 15%. The design with the best durability was given the highest rating. The ease of manufacturing was given 10% weightage, as an oddly shaped motor or motor with multiple components may be hard to install on the trolley. The design that was the easiest to manufacture was given the highest rating. Next, cost was weighted at 5%, as on average, motors will have a higher cost, so making a selection according to price was not necessary. The design that requires the lowest cost to manufacture was given the highest rating. Criteria of safety and stability were added for concept scoring. Both safety and stability were weighted at 10%. The motorized design must be safe to operate to prevent injuries. The design that provided the greatest level of safety was given the highest rating. Finally, the motor must not cause serious stability issues during its use; low stability will result in the trolley falling to the side. The design that provides the best stability while in use was given the highest rating.

2.1.9. Concept Scoring for Anti-Slippage Mechanism

Table 8. Concept scoring for anti-slippage mechanism.

Anti-Slippage Mechanism		Concepts
		Pin Locking Mechanism		Ratchet Wheel Arrangement
Selection Criteria	Weight	Rating	Weighted Score	Rating	Weighted Score
Weight	25%	4	1	3	0.75
Size	15%	3	0.45	4	0.6
Ease of Use	20%	3	0.6	4	0.8
Durability	20%	2	0.4	4	0.8
Ease of Manufacturing	10%	2	0.2	3	0.3
Cost	10%	3	0.3	3	0.3
Total Score			2.96		3.55
Rank		2		1
Continue?		No		Yes

shows the concept scoring for anti-slippage mechanism. The trolley is expected to be lightweight; hence, the weight for the anti-slippage mechanism should be as low as possible, so the weight criterion had a 25% weightage. The lightest design was given the highest rating. The size of the anti-slippage mechanism was given a weightage of 15%, as the mechanism should not be huge or hinder the stair-climbing process. The smallest design was given the highest rating. The criterion ease of use was weighted at 20%, as the mechanism should work immediately as the trolley falls downwards, so any delay in the mechanism is not desirable. The mechanism that was the easiest to use was given the highest rating. Next, the durability was weighted at 20%, as the anti-slippage mechanism should withstand the full load of the trolley; hence, it should not break. The design with the best durability was given the highest rating. Ease of manufacturing was weighted at 10%, as the mechanism should be easy to combine with other parts, like a motor. A complicated anti-slippage mechanism is hard to fabricate and install on the trolley. The design that was the easiest to manufacture was given the highest rating. Finally, cost was weighted at 10%. This low weightage was due to the criterion being less significant, as other criteria play a more important role for this concept. The design that requires the lowest cost to manufacture was given the highest rating.

2.1.10. Concept Scoring for Locking Mechanism

Table 9. Concept scoring for locking mechanism.

Locking Mechanism		Concepts
		Telescopic Lock		Valve Lock Mechanism
Selection Criteria	Weight	Rating	Weighted Score	Rating	Weighted Score
Weight	15%	4	0.6	3	0.45
Size	25%	4	1	3	0.75
Ease of Use	20%	3	0.6	4	0.8
Durability	20%	4	0.8	3	0.6
Ease of Manufacturing	10%	4	0.4	2	0.2
Cost	10%	4	0.4	3	0.3
Total Score			3.8		3.1
Rank		1		2
Continue?		Yes		No

shows the concept scoring for locking mechanism. The weight of locking mechanism was given a 15% weightage, as the mechanism should not be heavy so that it does not contribute much to the total weight. The lightest design was given the highest rating. The size of the locking mechanism was weighted at 25%, as the lock should not be bulky. The smallest design was given the highest rating. The ease-of-use criterion was weighted at 20%, as the mechanism should be easy to operate; for example, it should be easy to adjust. The design that was the easiest to use was given the highest rating. The durability was weighted at 20%, as the lock mechanism should not fail when the mechanism latches. The design with the best durability was given the highest rating. Ease of manufacturing was weighted at 10%, as lock mechanism should be easily installed, so that future repairs can be easily carried out. The design that was the easiest to manufacture was given the highest rating. Finally, the cost of the locking mechanism was weighted at 10%, as locking mechanisms are generally small and the cost will not be too high. The design that requires the lowest cost to manufacture was given the highest rating.

2.2. Conceptual Design

2.2.1. Conceptual Design 1

Figure 1 shows conceptual design 1, which is for a foldable trolley that can be collapsed down twice to become a portable size. The wheels are connected to a foldable bracket linked to the body. A tri-wheel design is used for this conceptual design. Next, the valve lock mechanism is designed so that the handles can collapse down and height adjustments can be made. Also, two small wheels are at the base plate of the trolley. Finally, the base tray and wheels can be folded inwards to form a flat model. The foldable wheels and base tray can save storage space. The 2 wheels at the base plate are convenient to use. Furthermore, the valve locking design is easier to adjust compared to telescopic mechanism.

2.2.2. Conceptual Design 2

Figure 2 shows conceptual design 2, which is for a foldable trolley that can be collapsed down twice to become a portable size. The wheels are connected to a foldable bracket linked to the body. A tri-wheel design is used for this conceptual design. Next, the valve lock mechanism is designed so that the handles can collapse down and height adjustments can be made. The base tray and wheels can be folded inwards to form a flat model so that it can save storage space. A unique aspect of this concept design was additional joints at the center of the trolley, which allow for greater foldability. The additional joints allow the trolley to be folded into a small model. Finally, the base plate is separated into two parts to allow the trolley to be folded inwards. The downside for this design is that it would be hard to fabricate and the trolley would not be sturdy if it was not used properly. There would be more possible critical points at which it is vulnerable to failure.

2.2.3. Conceptual Design 3

Figure 3 shows conceptual design 3. This concept design involves the folding mechanism between the wheel bracket and trolley body. The concept of using bevel gears is applied in this case. The mechanism would work as follows: the base tray would rotate down, rotating the vertical bevel gear anti-clockwise, and the vertical bevel gear would rotate the horizontal bevel gear clockwise, which will unfold the wheel bracket. The design requires more parts to fabricate, and a smaller gear setup would be desirable to achieve a smaller model. The disadvantage of this design is potential gear failures. If the bevel gears get stuck, the trolley will rest at an unusable state and must be repaired. The design features a foldable trolley body that can be adjusted through the telescopic mechanism. A tri-wheel mechanism is used in this conceptual design.

2.2.4. Final Design

The concepts selected through screening and scoring were tri-wheel design, stepper motor to define increments of steps, ratchet wheel arrangement for anti-slippage mechanism, and telescopic locking mechanism, as shown in

Table 10. Concepts selected through screening and scoring.

Concepts Selected Through Screening and Scoring
Design	Concept
Wheels	Tri-wheel
Motorized Design	Power window motor to define increments of steps
Anti-slippage Mechanism	Ratchet wheel arrangement
Locking Mechanism	Telescopic lock
	Extendable wheel frame
	Foldable wheels
	Wheels with ball bearings
	Foldable base plate

. The tri-wheel design was proven to be efficient at climbing stairs, the design can save costs due to having fewer components, and it will be lighter in weight. The power window motor is installed on the wheel bracket, while connecting directly to the tri-wheels. The power window motor was selected due to its small size and high torque. Next, a ratchet wheel arrangement acts as a safety mechanism that prevents the trolley from slipping downstairs. A telescopic lock is used to allow for adjustments of the body and the foldable wheel bracket. The telescopic lock is easier to fabricate and lightweight, which both are favorable in this design. The wheels should have ball bearings at their center to allow for smoother rotations. Finally, a foldable base plate is used so the trolley can be stored in small spaces. The final design sketch is shown in Figure 4.

Figure 4a shows the full assembly of the stair-climbing trolley when opened. The base tray and wheel bracket can be folded inwards to achieve a flat model. The locking mechanism for each fold is locked using telescopic mechanism. The telescopic pins can be pushed in to allow the parts to be adjusted and folded, and the pin will pop back up when it reaches its final point. A tri-wheel design is implemented and the wheels can be extended (Figure 4b) to fit higher stair steps. Next, a ratchet wheel is placed in between the wheel bracket and wheel frame. The ratchet wheel’s pawl is installed on the wheel bracket. A power window motor is designed to be installed directly on the wheel bracket, and the motor shaft connects to the wheel bracket shaft. The power window motor will rotate the wheel frame, which will aid the stair-climbing process. Furthermore, the wheel bracket has a bearing that connects with the wheel frame, which allows the wheel frame to rotate smoothly. The wheel source has a bearing as well. The buttons to control the power window motor are placed on the handles, which can be easily accessed when climbing the stairs.

2.3. Engineering Design Calculations

2.3.1. Tri-Wheel Mechanism with Load Applied

Figure 5 displays the free body diagram used to determine the required pulling force for the tri-wheel mechanism under load, where:

F_Pull is the pulling force required;

W₁ is the weight of the stair-climbing trolley in newton;

W₂ is the weight of the load in newton;

L is the length between the center point of wheel to the center of wheel frame;

L₂ is the length between the equilibrium position of load to the center of lower wheel;

H is the height of stair step;

F_Stair is the reaction force in newton against the staircase;

F_N1 is the normal force in newton acting on the lower wheel;

F_N2 is the normal force in newton acting on the wheel above the stair step;

${\theta }_1$ is the pulling angle at 45 degrees;

${\theta }_2$ is the angle of a wheel frame link from the horizontal axis;

${\theta }_3$ is the inner angle of the tri-wheel mechanism, in this case, 30 degrees;

${\theta }_4$ is the angle of wheel frame link from the vertical axis;

${\theta }_5$ is the angle between the vertical axis and the line crossing point A and W₂.

The following is the summation of forces along x-axis, where direction to the right was positive.

$$\overrightarrow{+}\sum F_x=0$$

$$F_{Pull}\cos {\theta }_1-F_{Stair}=0$$

(1)

The following is the summation of forces along y-axis, where direction facing up was positive.

$$+\uparrow \sum F_y=0$$

$$F_{Pull}\sin {\theta }_1+F_{N1}+F_{N2}-W_1-W_2=0$$

(2)

The following is the moment at point A, where anti-clockwise direction was positive.

$$+\circlearrowleft \sum M_A=0$$

$$(F_{Pull}\sin {\theta }_1\left)\right(L\sin {\theta }_4)-(F_{Pull}\cos {\theta }_1\left)\right(L\cos {\theta }_4)-(W_1\left)\right(L\sin {\theta }_4)+(F_{N2}\left)\right(2L\cos {\theta }_3)\cos \left({\theta }_2-{\theta }_3\right)+\left(W_2\right)\left(L_2\mathrm{t}\mathrm{a}\mathrm{n}{\theta }_5\right)=0$$

(3)

F_N1 and F_N2 are not equal; hence, a constitutive equation is required, as shown below:

$$F_{Pull}\sin {\theta }_1-W_1-W_2=-R_1{F}_{N1}-R_2{F}_{N2}$$

(4)

where R₁ and R₂ are ratio corresponding to the distance from the center of wheel frame to the center of wheels, R₁ is the distance between the center of the wheel frame to the center of the lower wheel and R₂ is the distance from center of the wheel frame to the center of the wheel above the stair step

$$R_1={\displaystyle \frac{L\sin {\theta }_4}{2Lcos{\theta }_3\mathrm{c}\mathrm{o}\mathrm{s}({\theta }_2-{\theta }_3)}}$$

(5)

$$R_2={\displaystyle \frac{2L\cos {\theta }_3\cos \left({\theta }_2-{\theta }_3\right)-L\sin {\theta }_4}{2\mathit{Lcos}{\theta }_3\cos \left({\theta }_2-{\theta }_3\right)}}$$

(6)

The angle of ${\theta }_2$ was not constant. It was a dependent variable, and the value changes according to the orientation of the tri-wheel on the step. Therefore, ${\theta }_2$ can be written as follows:

$${\theta }_2={\mathrm{s}\mathrm{i}\mathrm{n}}^{-1}{\displaystyle \frac{H}{2Lcos{\theta }_3}}+{\theta }_3$$

(7)

Substituting (4) into (2), we get:

$$F_{\mathrm{N}2}={\displaystyle \frac{F_{N1}\left(R_1-1\right)}{\left({1-R}_2\right)}}$$

(8)

$$F_{\mathrm{N}1}={\displaystyle \frac{{W_1+W_2-R_2{F}_{N2}-F}_{pull}sin{\theta }_1}{R_1}}$$

(9)

Substituting (9) into (8), we get:

$$F_{\mathrm{N}2}={\displaystyle \frac{\left({1-R}_1\right)\left({W_1+W_2-F}_{pull}sin{\theta }_1\right)}{\left(R_2-R_1\right)}}$$

(10)

Substituting (10) into (3) and rearranging for F_pull, we get:

$$F_{Pull}={\displaystyle \frac{W_{1}sin{\theta }_4-W_2\frac{L_2}{L}\left(\frac{sin{\theta }_5}{cos{\theta }_5}\right)-{2(W}_1+W_2\left)\left(\frac{1-R_1}{R_2-R_1}\right)cos{\theta }_{3}cos\right({\theta }_2{-\theta }_3)}{\left(sin{\theta }_1{sin\theta }_4-cos{\theta }_1{cos\theta }_4\right)-2\left(\frac{1-R_1}{R_2-R_1}\right)sin{\theta }_{1}cos{\theta }_{3}cos({\theta }_2-{\theta }_3)}}$$

(11)

2.3.2. Bolt Selection

Bolt selection was carried out for the wheel frame only. The other parts do not require bolts with specific bolt diameters as the bolts are used to secure the position only, so a lower load is applied to the bolt. Also, some parts with specific dimensions have to be paired with specific bolt diameter. For example, the wheels require M8 bolt, as the center hole diameter is approximately 8 mm.

Assumptions for this calculation are that one side of the wheel frame is considered. Only 2 bolts are locked on the wheel frame. A weight of 60 kg is applied on the trolley; hence, each side will experience 30 kg load. Also, 2 bolts are installed there. Hence, the load will be shared by the 2 bolts. The free body diagram is shown in Figure 6.

The following is the formula for max deflection, δ_max, for cantilever beam:

$${\delta }_{max}={\displaystyle \frac{P{a}^2(3L-a)}{6EI}}$$

(12)

where:

P is the force applied, 15 kg;

L is the length of the beam, 82 mm;

E is the Young’s modulus for steel, 190 GPa;

I is the second moment of inertia of bolt;

a is the length from the fixed region to the applied force, 74 mm.

b is the length from the applied force to the end of the wheel frame

Different bolt diameters were used for calculations to obtain the maximum deflection values.

Table 11. Max deflection for different bolt diameters.

Diameter of Bolt	Moment of Inertia	${\mathit{\delta }}_{\mathit{m}\mathit{a}\mathit{x}}$ (m)	${\mathit{\delta }}_{\mathit{m}\mathit{a}\mathit{x}}$ (mm)
0.001	4.90874 × 10−14	2.4767228	2476.7228
0.002	7.85398 × 10−13	0.1547952	154.79518
0.003	3.97608 × 10−12	0.0305768	30.576825
0.004	1.25664 × 10−11	0.0096747	9.6746984
0.005	3.06796 × 10−11	0.0039628	3.9627565
0.006	6.36173 × 10−11	0.0019111	1.9110515
0.007	1.17859 × 10−10	0.0010315	1.031538
0.008	2.01062 × 10−10	0.0006047	0.6046687

shows the max deflection for different bolt diameters. For 0.005 m diameter bolt, which was M5 bolt, the deflection was small. Hence, M5 bolts or thicker bolts should be selected.

2.3.3. Motor Selection

Figure 7 shows the free body diagram used to determine the required torque for motor selection. The free body diagram shows the stair-climbing trolley vaulted up one step, where the top front wheel rests on the higher step. The black line shows the shape of stairs. The target of this free body diagram was to determine the torque necessary to rotate the trolley at origin O. Mass of M₁, M₂, and M₃ shows the mass at the center of the wheel, and the weight for each region was calculated separately. For example, M₂ consists of the weight of wheel, 1/3 of a wheel frame, 2 extension brackets, and 1 extension link. W₁ was the weight of trolley, while W₂ was the weight of a 20 kg load. Autodesk Inventor Professional 2022 was used to obtain the dimensions to determine the required torque. The pulling force, F_pull, is omitted from the free body diagram in order to calculate the actual torque required by the motor to rotate the tri-wheel frame of the trolley without any assistance from human-applied force.

Where:

M₁ is the total mass in kg experienced at the center of the lower wheel;

M₂ is the total mass in kg experienced at the center of the top left wheel;

M₃ is the total mass in kg experienced at the center of the wheel above the stair step;

M_a is the total mass in kg experienced at the center of the lower extension link;

M_b is the total mass in kg experienced at the center of the top left extension link;

M_c is the total mass in kg experienced at the center of the extension link on the stair step;

W₁ is the weight in newton of trolley experienced by one side of the wheel;

W₂ is the weight in newton of load experienced by one side of the wheel;

F_Stair is the reaction force in newton against the staircase;

F_N1 is the normal force in newton acting on the lower wheel;

F_N2 is the normal force in newton acting on the wheel above the stair step;

g is the gravitational acceleration;

L_M1 is the length from origin O to the center of the wheel perpendicular to M₁;

L_M2 is the length from origin O to the center of the wheel perpendicular to M₂;

L_M3 is the length from origin O to the center of the wheel perpendicular to M₃;

L_Ma is the length from origin O perpendicular to the center of the extension bracket M_a;

L_Mb is the length from origin O perpendicular to the center of the extension bracket M_b;

L_Mc is the length from origin O perpendicular to the center of the extension bracket M_c;

L_N1 is the length from origin O perpendicular to F_N1;

L_N2 is the length from origin O perpendicular to F_N2;

L_W1 is the length from origin O perpendicular to W₁ (which is zero since it coincides with y-axis);

L_W2 is the length from origin O perpendicular to W₂

The equation for each mass was obtained through these combinations, and the weight for each component was simulated using Autodesk Inventor Professional 2022.

$$M_1=Wheel Frame+\left(3\times Extension Link\right)+\left(6\times Extension Bracket\right)+\left(3\times Wheels\right)$$

(13)

$$M_2=\left({\displaystyle \frac{1}{3}}Wheel frame\right)+Extension Link+\left(2\times Extension Bracket\right)+Wheel$$

(14)

$$M_3=\left({\displaystyle \frac{1}{3}}Wheel frame\right)+Extension Link+\left(2\times Extension Bracket\right)+Wheel$$

(15)

$$M_a=Wheel frame+\left(3\times Extension link\right)+\left(6\times Extension Bracket\right)+\left(2\times Wheels\right)$$

(16)

$$M_b=\left({\displaystyle \frac{1}{3}}Wheel frame\right)+Extension Link+\left(2\times Extension Bracket\right)$$

(17)

$$M_c=\left({\displaystyle \frac{1}{3}}Wheel frame\right)+Extension Link+\left(2\times Extension Bracket\right)$$

(18)

The following is the summation of forces along x-axis, where direction to the right was positive.

$$\overrightarrow{+}\sum F_x=0$$

$$-F_{Stair}=0$$

(19)

The following is the summation of forces along y-axis, where direction facing up was positive.

$$+\uparrow \sum F_y=0$$

$$F_{N1}+F_{N2}-{\displaystyle \frac{W_1}{2}}-{\displaystyle \frac{W_2}{2}}-M_{1}g-M_{2}g-M_{3}g-M_{a}g-M_{b}g-M_{c}g=0$$

(20)

F_N1 was approximately zero while climbing; hence, we can obtain F_N2.

The moment at point O, which is also the required torque, is the summation of moment for all the forces.

$$Torque, T_o=\sum M_o$$

$$\begin{array}{ll}Torque,{ T}_o=& \left(M_{1}g\right)\left(L_{{\mathrm{M}}_1}\right)+\left(M_{2}g\right)\left(L_{{\mathrm{M}}_2}\right)+\left(M_{3}g\right)\left(L_{{\mathrm{M}}_3}\right)+\left(M_{a}g\right)\left(L_{{\mathrm{M}}_a}\right)\\ & \hspace{1em}+\left(M_{b}g\right)\left(L_{{\mathrm{M}}_b}\right)+\left(M_{c}g\right)\left(L_{{\mathrm{M}}_c}\right)+\left(F_{N1}\right)\left(L_{N1}\right)+\left(F_{N2}\right)\left(L_{N2}\right)\\ & \hspace{1em}+\left({\displaystyle \frac{W_2}{2}}\right)\left(L_{W2}\right)\end{array}$$

(21)

The calculated torque required to rotate the wheel was 8.31 Nm, while the torque of a power window motor was 2.942 Nm. In this case, the power window motor will only aid the stair climbing process and will not rotate the wheel frame up the staircase unassisted.

2.4. Simulation and Analysis

2.4.1. Simulation of the Bracket for Tri-Wheel

The set conditions included a force acting downwards at the center hole. The material was steel. We assumed a 60 kg load was applied on the trolley. Each side had to approximately withstand 30 kg load. Force simulated was 294.3 N, as shown by the yellow arrow in Figure 8a. The fixed constraint was set at the cylindrical tube connected to the trolley body, as shown in Figure 8b.

In stress analysis as shown in Figure 9, the weakest point of the bracket was at the thinnest region, located just above the bearing. The weakest point falls at the point of greatest stress. Additionally, the region with the most displacement falls in the thinnest region. However, the displacement was only 0.001 mm due to overdesigning, as shown in Figure 10.

Table 12. Simulated data for bracket.

Name	Minimum	Maximum
Volume	135,024 mm3
Mass	1.05994 kg
Von Mises Stress	0.00000433834 MPa	3.01694 MPa
Displacement	0 mm	0.00108509 mm
Safety Factor	15 ul	15 ul

shows the simulated data for the bracket. The bracket design for both sides was the same, so only one simulation was performed. The bracket was designed using the power window motor dimensions and the available bearing size. Hence, the bracket was limited to a specific shape and thickness. The thickness of the bracket was slightly thicker than the bearing, so that there was a slot into which the bearing could be installed. The thick bracket was categorized as “overdesigned” when referring to a simulated safety factor of 15 ul (ultimate load), as shown in Table 12 and Figure 11. The possibility of overdesign was expected while designing this bracket. The bracket underwent optimization using Autodesk Inventor Professional 2022, and only the required shape was generated. However, the bracket cannot be further optimized, as all the holes had to be selected as preserved region and the dimensions and features could not be removed. This limited our ability to optimize the model, and the final optimized part was the same as it was in the initial model. Hence, the model is used as the finalized part.

2.4.2. Simulation on the Bracket Holder

The set conditions included a force acting downwards at the square cross-section, as shown in Figure 12a. The material was steel. The region was connected to the bracket coupling, where the load from the bracket was transferred to this specific region. We assumed a 60 kg load was applied on the trolley. Each side had to approximately withstand 30 kg load. Force simulated was 294.3 N, as shown by the yellow arrow in Figure 12a. Fixed constraint was set at inner face region, which is highlighted in green in Figure 12b. The four screw holes were set as fixed constraint, as shown in Figure 12c.

Table 13. Simulated data for bracket holder.

Name	Minimum	Maximum
Volume	23,594 mm3
Mass	0.185213 kg
Von Mises Stress	0.000139598 MPa	33.4892 MPa
Displacement	0 mm	0.00829714 mm
Safety Factor	6.1811 ul	15 ul

shows the simulated data for bracket holder. The bracket holder design for both sides was the same, so only one simulation was performed. An approximate load of 30 kg was applied onto the part, which applied 294.3 N of force on the region, as shown in Figure 13a. The inner surface and the four screw holes were set as fixed constraints, as they were fixed on the wheel frame. They rotate together with the wheel frame, which allows the power window motor to aid the stair-climbing process. Referring to the Von Mises stress shown in Figure 13, the greatest stress occurs at the edge between the shaft and top base. The maximum Von Mises stress was 33.49 MPa. As the trolley moves, the shaft rotates with the wheel frame. Hence, the stress experienced is parallel to the acting force and occurs in the red region. The simulated displacement is shown in Figure 14, in which the maximum displacement occurs at the end of shaft. The maximum displacement simulated was 0.008 mm. The top base had 0 mm displacement; it was caused by the fixed constraint added when the wheel frame was installed on it in the simulation. Finally, in regards to safety factor shown in Figure 15, the critical zone had the lowest safety factor at 6.2 ul, as shown in Table 13. The other regions were also shown to be overdesigned.

2.4.3. Simulation for Coupling

The set conditions included the force acting on the coupling, as shown in Figure 16a. The material was steel. The power window motor drives the coupling in the direction shown by the yellow arrow. Force of approximated 30 kg was simulated, and a magnitude of 294.3 N was calculated for each arrow. The square cross-section that connects to the bracket holder was set as fixed constraint. The four flat surfaces were set as fixed constraints, as shown in Figure 16b.

Table 14. Simulated data for coupling.

Name	Minimum	Maximum
Volume	19,356.1 mm3
Mass	0.151945 kg
Von Mises Stress	0.0377509 MPa	9.70995 MPa
Displacement	0 mm	0.000506277 mm
Safety Factor	15 ul	15 ul

shows the simulated data for coupling. The coupling for both sides was the same; hence, only one simulation was performed. The coupling was driven by a power window motor, whose operation was simulated here. The power window motor shaft drives on a flat surface, as shown in Figure 16a. An approximated load of 30 kg was applied on each yellow arrow, which, in this case, was 294.3 N of force for each arrow. The inner face of the square cross-section was set as fixed constraints, as it is connected to the bracket holder. The four flat surfaces set as fixed constraint are shown in Figure 16b. The Von Mises stress is shown in Figure 17; the greatest stress occurs at the edges on each cut out, as shown by the red region. The maximum Von Mises stress simulated was 9.71 MPa. The displacement is shown in Figure 18. The maximum displacement occurs at the surface applied by the force, as shown in red. The maximum displacement simulated was 0.0005 mm. The coupling had low level of displacement, as it was constrained by multiple parts in the full assembly, resulting in less room for displacement. Also, the part was made with steel; hence, less displacement was expected. Finally, the safety factor is shown in Figure 19, where the whole part has a safety factor of 15 ul. The part was shown to be overdesigned. The coupling had to follow the power window motor shaft and bearing dimensions; hence, it was thicker and bigger than required.

2.4.4. Simulation for Base Tray

The base tray had a constraint fixed at the through holes for bolts, as shown in Figure 20. An approximated force of 60 kg was placed at the yellow arrow. PVC was assigned as the material for the base tray.

Table 15. Simulated data for base tray.

Name	Minimum	Maximum
Volume	514,215 mm3
Mass	0.719901 kg
Von Mises Stress	0.00114951 MPa	76.6039 MPa
Displacement	0 mm	6.06771 mm
Safety Factor	0.60741 ul	15 ul

shows the simulated data for base tray. A load of 60 kg was placed on the yellow region, where 588.6 N was simulated, as shown by the yellow arrow. PVC was the material assigned for this base tray. The Von Mises stress is shown in Figure 21, where the maximum occurs at the bolt holes. The stress was similar for both sides. The maximum Von Mises stress was 76.60 MPa. The displacement is shown in Figure 22, where the maximum displacement occurs at the region of the load. The displacement is expected to shift according to the location of the load. For example, when the load is applied on the middle bar, the maximum displacement will occur there. The maximum displacement was 6.06 mm. Finally, the safety factor is shown in Figure 23, where the critical region occurs at the joint around the first T joint region and the region of load. The lowest safety factor was 0.607 ul. Hence, this part might need to be strengthened to achieve a higher safety factor. The base tray was strengthened by slotting an aluminum tube into the PVC pipe.

2.4.5. Simulation for Wheel Frame

The fixed constraints and force acting on the wheel frame are shown in Figure 24. The wheel frame had a fixed constraint at the four screw holes, where it was fixed using bolts. The force of 15 kg for each hole was acting downwards (yellow arrow), and, in this case, the simulated load was 147.15 N. The assigned material was aluminum.

Table 16. Simulated data for wheel frame.

Name	Minimum	Maximum
Volume	138,018 mm3
Mass	0.372648 kg
Von Mises Stress	0.000000027932 MPa	1.46867 MPa
Displacement	0 mm	0.0000572834 mm
Safety Factor	15 ul	15 ul

shows the simulated data for wheel frame. The simulation depicts a scenario of a user climbing up a staircase, in which only one wheel on each side has to withstand the total load of the trolley. A 60 kg load was simulated; hence, each side will carry 30 kg of load. On each side, 2 bolts will share the load—hence, 15 kg for each hole. The Von Mises stress of wheel frame is shown in Figure 25, where the maximum was 1.47 MPa at the edge of the bolt holes. The displacement of wheel frame is shown in Figure 26, and the maximum displacement is 0.000057 mm. The safety factor for wheel frame is shown in Figure 27, and the wheel frame had a safety factor of 15 ul. The wheel frame is safe to use.

2.5. Circuit Development

The circuit was developed to operate the two-power window motor, as shown in Figure 28. The power window motors must rotate in opposite directions to fulfil the requirement for climbing motion: one rotates clockwise and the other rotates anticlockwise. A button was installed on the trolley body, and the power window motor rotates when the button is pressed. The trolley was intended to aid the climbing process, so only 1 button was expected to turn on the power window motor. However, the circuit was developed to allow rotations in both directions. To allow for rotations in both directions, two relays were used in this circuit. The relay used was Single Pole Double Throw Relay (SPDT). The SPDT relay has a coil and 3 terminals. The 3 terminals were common terminal, normally closed terminal (NC), and normally open terminal (NO). When the coil of the relay is not energized, the common terminal and the normally closed terminal (NC) are connected for current flow. When the coil is energized, the common terminal and the normally open terminal (NO) allow current to flow through [35]. Two buttons were used for the circuit to energize a specific SPDT relay. One of the power window motors was connected in opposite direction to allow the power window motors to rotate in different directions.

2.6. Experimental Setup

A digital force gauge with maximum load of 40 kg was locked onto the trolley handle to measure the experimental pulling force. Then, varying loads of 0 kg, 6 kg, 12 kg, and 18 kg were placed onto the trolley by using required amount of 1.5 L bottles, with the assumption that 1 L is equivalent to 1 kg. The trolley was then pulled through the digital force gauge, as shown in Figure 29. While transitioning to the new step, the pulling force required was measured using the digital force gauge. The load measured was used to calculate the pulling force. The experiment was then repeated by pressing the corresponding control button to initiate the power window motor to aid the stair-climbing process. The load was again measured and used to calculate the pulling force.

3. Results

Figure 30 shows a complete view of the foldable tri-wheeled stair-climbing trolley. Figure 30a shows the open configuration, in which the wheel and base were opened. The trolley body was extended to the highest height, the base was opened and ready for the items to be loaded, and the wheels were positioned such that they were ready for operation. On the other hand, Figure 30b shows the folded configuration of the trolley, in which the body was shortened, the bases were folded up, and the wheels were positioned such that the trolley would take up the smallest amount of space for storage. The folded configuration displays significantly smaller dimensions than the open configuration.

4. Discussion

Figure 31 shows the graph of average pulling force as a function of load, in which the theoretical data and experimental data were compared. The theoretical data and experimental data were about the same, though the experimental data with the motor were much lower compared to the theoretical data, as the stair-climbing trolley had power window motors attached to it, aiding the stair-climbing process. Hence, a lower pulling force was expected. The comparison between the theoretical and experimental results shows the validity of each calculation and the measurements. The theoretical data showed how a graph might look and potential measurement readings from the scale. Also, the lower experimental readings proved the motorized design aided the stair-climbing process, and a lower pulling force was required to pull the load up the staircase. The design was improved, as the pulling force slightly increased with the increased load. The slight increase in pulling force shows the motorized design aided the climbing process.

The designed foldable stair-climbing trolley used a tri-wheel design. Most researchers have found this to be the best design to lift weight upstairs with less effort. The stair-climbing trolley designed used a curved wheel frame rather than a straight wheel frame, and it was found that the curved wheel frame requires less power to tilt it compared to a straight frame. Bearings were installed at the wheel bracket to reduce the rotational friction. The bearing sourced was an NTN 6006ZZ ball bearing. The trolley had extendable links to lengthen the wheel frame. A longer wheel frame link arm would fit higher stair steps. The users can adjust the link’s length to fit their staircase’s specifications. Next, the stair-climbing trolley used power window motors to aid the stair-climbing process. The data proved the motorized design aided the stair-climbing process, and less pulling force was required to pull the load up the staircase. Also, a ratchet wheel arrangement was used for this design, which allowed for rotations in one direction only. The designed trolley had great foldability as well: the base tray, wheels, and body could be folded and adjusted.

5. Conclusions

• A tri-wheeled stair-climbing trolley with motorized, adjustable, and foldable features was successfully designed, developed, and analyzed. The theoretical and experimental results were consistent, as indicated by the similar trends observed in the comparison graph. Notably, the experimental data obtained with motor assistance showed significantly lower values, attributed to the additional support provided by the power window motor during stair climbing;
• The innovative motorized trolley has the potential to reduce physical strain for workers and residents in buildings without escalators or elevators. The experimental results indicate that it can decrease the required human pulling force by approximately 30%, thereby also helping to lower the risk of injuries, particularly among the elderly;
• The adjustable functionality of the tri-wheel mechanism enhances the trolley’s adaptability, allowing it to be effectively used in buildings with varying stair step dimensions;
• The trolley’s foldable design provides a practical advantage for users who require space-saving solutions.