Experimental Determination of Excitation Function Curves through the Measurement of Thick Target Yields in Liquid Targets: The Examples of the 68Zn(p,n)68Ga and 64Zn(p,α)61Cu Nuclear Reactions
Abstract
:1. Introduction
2. Materials and Methods
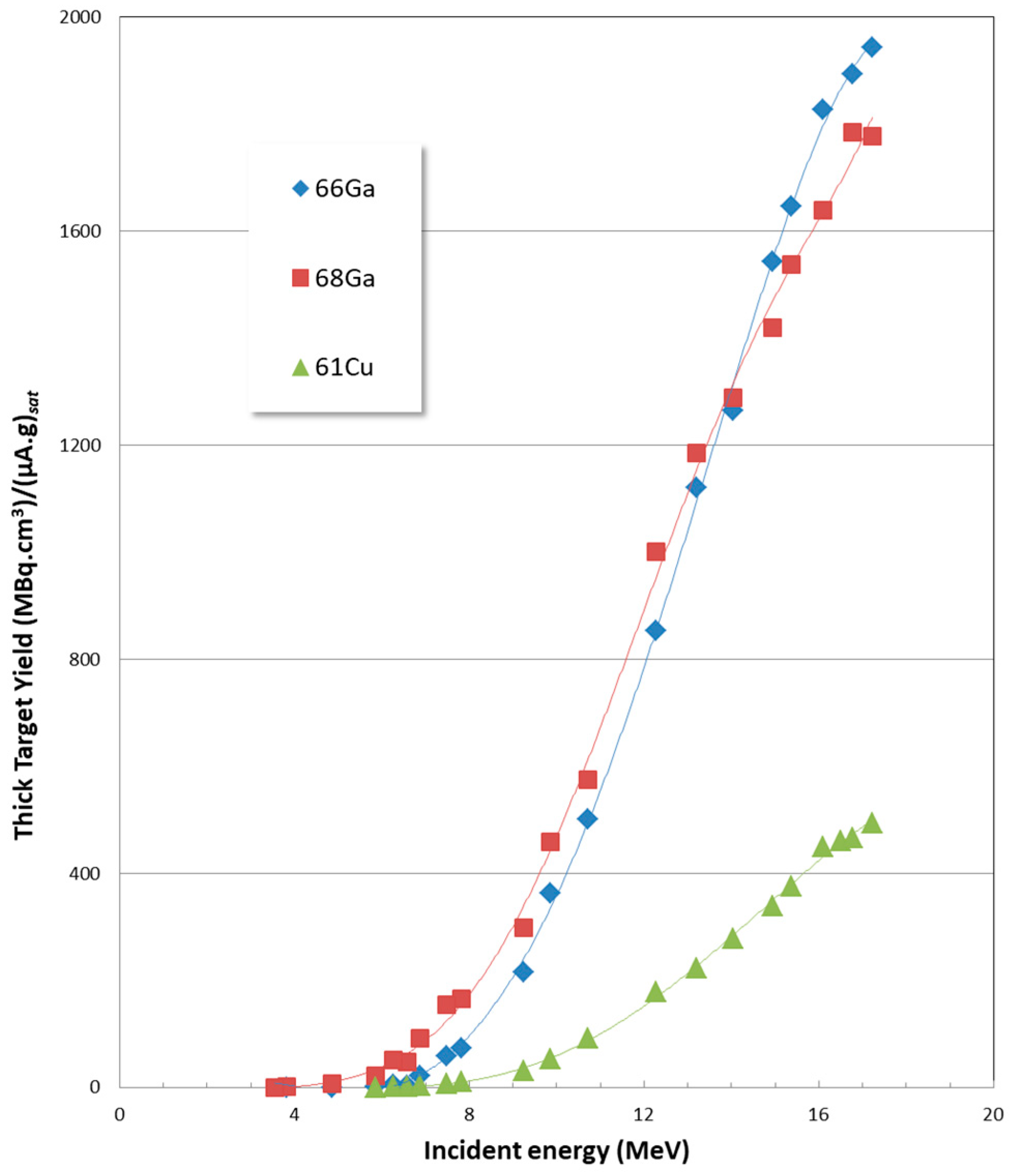
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qaim, S.M. Development of novel positron emitters for medical applications: Nuclear and radiochemical aspects. Radiochim. Acta 2011, 99, 611–625. [Google Scholar] [CrossRef]
- Qaim, S.M.; Scholten, B.; Spahn, I.; Neumair, B. Positron-emitting radionuclides for appliactions, with special emphasis on their production methodologies for medical use. Radiochim. Acta 2019, 107, 1011–1026. [Google Scholar] [CrossRef]
- Alves, F.; Alves, V.H.; Neves, A.C.B.; do Carmo, S.J.C.; Natergal, B.; Hellas, V.; Kral, E.; Gonçalves-Gameiro, C.; Abrunhosa, A.J. Cyclotron production of Ga-68 for human use from liquid targets: From theory to practice. AIP Conf. Proc. 2017, 1845, 020001. [Google Scholar]
- Alves, F.; Alves, V.H.; do Carmo, S.J.C.; Neves, A.C.B.; Silva, M.; Abrunhosa, A.J. Production of copper-64 and gallium-68 with a medical cyclotron using liquid targets. Mod. Phys. Lett. A 2017, 32, 1740013. [Google Scholar] [CrossRef]
- European Pharmacopeia. Gallium (68Ga) Chloride (Accelerador-Produced) Solution for Radiolabelling. Available online: http://radiofarmacia.org/wp-content/uploads/2018/10/MONOGRAF%C3%8DA-GA68Cl.pdf (accessed on 2 May 2019).
- Takacs, S.; Tarkanyi, F.; Sonck, M.; Hermanne, A. Investigation of the natMo(p,x)96mgTc nuclear reaction to monitor proton beams: New measurements and consequences on the earlier reported data. Nucl. Instr. Methods B 2002, 198, 183–196. [Google Scholar] [CrossRef]
- Takacs, S.; Tarkanyi, F.; Hermanne, A.; Paviotti de Corcuera, R. Validation and upgrading of the recommended cross section data of charged particle reactions used for production of PET radioisotopes. Nucl. Instr. Methods B 2003, 211, 169–189. [Google Scholar] [CrossRef]
- Qaim, S.M.; Hussain, M.; Spahn, I.; Neumaier, B. Continuing Nuclear Data Research for Production of Accelerator-Based Novel Radionuclides for Medical Use: A Mini-Review. Front. Phys. 2021, 9, 639290. [Google Scholar] [CrossRef]
- IAEA-TECDOC-1211, Charged Particle Cross-Section Database for Medical Radioisotope Production: Diagnostic Radioisotopes and Monitor Reactions. Available online: https://www-pub.iaea.org/MTCD/Publications/PDF/te_1211_prn.pdf (accessed on 27 May 2021).
- Hermanne, A.; Ignatyuk, A.V.; Capote, R.; Carlson, B.V.; Engle, J.W.; Kellett, M.A.; Kidedi, T.; Kim, G.; Hussain, M.; Lebeda, O.; et al. Reference cross sections for charged-particle monitor reactions. Nuclear Data Sheets 2018, 148, 338–382. [Google Scholar] [CrossRef]
- do Carmo, S.J.C.; de Oliveira, P.M.; Alves, F. Simple, Immediate and Calibration-Free Cyclotron Proton Beam Energy Determination Using Commercial Targets. Instruments 2019, 3, 20. [Google Scholar] [CrossRef] [Green Version]
- Campajola, L.; Braccini, S.; Casolaro, P.; de Luca, D.; Ereditato, A.; Haffner, P.D.; Scampoli, P. Measurement of the proton beam energy of a medical cyclotron based on Rutherford Back-scattering Analysis. Nucl. Instr. Methods B 2019, 440, 114–117. [Google Scholar] [CrossRef]
- Nesteruk, K.P.; Ramseyer, L.; Carzaniga, T.S.; Braccini, S. Measurement of the beam energy distribution of a medical cyclotron with a multi-leaf farady cup. Instruments 2019, 3, 4. [Google Scholar] [CrossRef] [Green Version]
- Haffner, P.; Aguilar, C.B.; Braccini, S.; Scampoli, P.; Thonet, P.A. Study of the extracted beam energy as a function of operational parameters of a medical cyclotron. Instruments 2019, 3, 63. [Google Scholar] [CrossRef] [Green Version]
- Gagnon, K.; Jensen, M.; Thisgaard, H.; Publicover, J.; Lapi, S.; McQuarrie, S.A.; Ruth, T.J. A new and simple calibration-independent method for measuring the beam energy of a cyclotron. Appl. Radiat. Isot. 2011, 69, 247–253. [Google Scholar] [CrossRef] [PubMed]
- Tarkanyi, F.; Qaim, S.M.; Stocklin, G. Excitation functions of 3He- and α-particle induced Nuclear reactions on natural krypton: Production of 82Sr at a compact cyclotron. Appl. Radiat. Isot. 1988, 39, 135–143. [Google Scholar] [CrossRef]
- Gyurky, G.; Vakulenko, M.; Fulop, Z.; Halasz, Z.; Kiss, G.G.; Somorjai, E.; Szucs, T. Cross section and reaction rate of the 92Mo(p,γ)93Tc determined from thick target yield measurements. Nucl. Phys. A 2014, 922, 112–115. [Google Scholar] [CrossRef] [Green Version]
- Basbas, G.; Brandt, W.; Laubert, R. Universal Cross Sections for K-Shell Ionization by Heavy Charged Particles. I. Low Particle Velocities. Phys. Rev. A 1973, 7, 983. [Google Scholar] [CrossRef]
- do Carmo, S.J.C.; Borges, F.I.G.M.; Trindade, A.M.F.; Conde, C.A.N. K X-ray production cross sections in Aluminium for 15 keV, 20 keV and 25 keV protons. Nucl. Instr. Methods B 2012, 293, 16–20. [Google Scholar] [CrossRef]
- Rashiduzzaman Khan, M.; Crumpton, D.; Francois, P.E. Proton-induced X-ray production in titanium, nickel, copper, molybdenum and silver. J. Phys. B 2001, 9, 455–460. [Google Scholar] [CrossRef]
- do Carmo, S.J.C.; Alves, V.H.P.; Alves, F.; Abrunhosa, A.J. Fast and cost-effective cyclotron production of 61Cu using a natZn liquid target: An opportunity for radiopharmaceutical production and R&D. Dalton Trans. 2017, 46, 14556–14560. [Google Scholar]
- do Carmo, S.J.C.; Scott, P.J.H.; Alves, F. The production of radiometals in liquid targets. EJNMMI Radiopharm. Chem. 2020, 5, 1–21. [Google Scholar] [CrossRef]
- IAEA-TECDOC-1955. Production of Emerging Radionuclides towards Theranostic Applications: Copper-61, Scandium-43 and -44, and Yttrium-86; International Atomic Energy Agency: Vienna, Austria, 2021; Available online: https://www-pub.iaea.org/MTCD/Publications/PDF/TE-1955web.pdf (accessed on 29 November 2022).
- Courtyn, J.; Devillet, F.; Geets, J.-M.; Ghyoot, M.; Kral, E.; Michaux, O.; Mooij, R.; Nactergal, B.; Nuttens, V.; Perk, L. Performance of IBA New Conical Shaped Niobium [18O] Water Targets. Proceedings of Cyclotrons 2013, Vancouver, BC, Canada. 2013. Available online: https://accelconf.web.cern.ch/CYCLOTRONS2013/papers/wepsh043.pdf (accessed on 12 May 2021).
- Experimental Nuclear Reaction Data (EXFOR) Database Version of 2021-05-18. Available online: https://www-nds.iaea.org/exfor/ (accessed on 21 May 2021).
- Levkovskij, V.N. Activation Cross Section Nuclides of Average Masses (A = 40–100) by Protons and Alpha-Particles with Average Energies (E = 10–50 MeV). 1991. Available online: https://www-nds.iaea.org/CRP-CP-monitor/2RCM/Hussain-2RCM-2014.pdf (accessed on 29 November 2022).
- Szelecseny, F.; Kovacs, Z.; Nagatsu, K.; Fukumura, K.; Suzuki, K.; Mukai, K. Investigation of direct production of 68Ga with low energy multiparticle accelerator. Radiochim. Acta 2012, 100, 5–11. [Google Scholar] [CrossRef]
- Zhuravlev, Y.Y.; Zarubin, P.P.; Zeic, Y.V.; Kolozhvari, A.A.; Chelgunov, I.V. Excitation functions of (p,n) reactions on nuclei of isotopes Zn from E(p)=5.6 To 6.8 MeV. J. Izv. Rossiiskoi Akademii Nauk Ser. Fiz. 1995, 59, 118, (EXFOR entry A0550:1). [Google Scholar]
- Vinogradov, V.M.; Zhuravlev, Y.Y.; Zarubin, P.P.; Kolozhvari, A.A.; Sergeev, V.O.; Sitnikova, I.V. Excitation functions of (p,n) reactions on zinc isotopes in the range of E(p) from 4.9 to 5.9 MeV. J. Izv. Rossiiskoi Akademii Nauk Ser. Fiz. 1993, 57, 154, (EXFOR entry A0841:1). [Google Scholar]
- Hermanne, A. Evaluated cross section and thick target yield data of Zn+P processes for practical applications. 1997. Private communication for EXFOR entry D4093. [Google Scholar]
- Naik, H.; Suryanarayana, S.V.; Murali, M.S.R.; Noy, K. Excitation function of 68Zn(p,n)68Ga reaction for the production of 68Ga. J. Radioanal. Nucl. Chem. 2020, 324, 285–289. [Google Scholar] [CrossRef]
- Esat, M.T.; Spear, R.H.; Zyskind, J.L.; Shapiro, M.H.; Fowler, W.A.; Davidson, J.M. Test of global Hauser-Feshbach calculations for proton-induced reactions on 68Zn. Phys. Rev. C 1981, 23, 1822–1825. [Google Scholar] [CrossRef]
- Cohen, B.L.; Newman, E.; Charpie, R.A.; Handley, T.H. (p,pn) and (p,αn) Excitation Functions. Phys. Rev. 1954, 94, 620–625. [Google Scholar] [CrossRef]
- Gyurky, G.; Fulop, Z.; Halasz, Z.; Kiss, G.G.; Szucs, T. Direct study of the α-nucleus optical potential at astrophysical energies using the 64Zn( p,α)61Cu Reaction. Phys. Rev. C 2014, 90, 052801(R). [Google Scholar] [CrossRef] [Green Version]
- Szelecsenyi, F.; Kovcs, Z.; Suzuki, K.; Okada, K.; van der Walt, T.N.; Steyn, G.F.; Mukherjee, S. Production possibility of 61Cu using proton induced nuclear reactions on zinc for PET studies. J. Radioanal. Nucl. Chem. 2005, 263, 539–546. [Google Scholar] [CrossRef]
- Uddin, M.S.; Khandaker, M.U.; Kim, K.S.; Lee, Y.S.; Kim, G.N. Excitation functions of the proton induced nuclear reactions on natZn up to 40 MeV. Nucl. Instrum. Methods B 2007, 258, 313–320. [Google Scholar] [CrossRef]
- Asad, A.H.; Chan, S.; Morandeau, L.; Cryer, D.; Smith, S.V.; Price, R.I. Excitation functions of natZn(p,x) nuclear reactions with proton beam energy below 18 MeV. Appl. Radiat. Isot. 2014, 94, 67. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
do Carmo, S.J.C.; Alves, F. Experimental Determination of Excitation Function Curves through the Measurement of Thick Target Yields in Liquid Targets: The Examples of the 68Zn(p,n)68Ga and 64Zn(p,α)61Cu Nuclear Reactions. Instruments 2022, 6, 3. https://doi.org/10.3390/instruments6010003
do Carmo SJC, Alves F. Experimental Determination of Excitation Function Curves through the Measurement of Thick Target Yields in Liquid Targets: The Examples of the 68Zn(p,n)68Ga and 64Zn(p,α)61Cu Nuclear Reactions. Instruments. 2022; 6(1):3. https://doi.org/10.3390/instruments6010003
Chicago/Turabian Styledo Carmo, Sergio J. C., and Francisco Alves. 2022. "Experimental Determination of Excitation Function Curves through the Measurement of Thick Target Yields in Liquid Targets: The Examples of the 68Zn(p,n)68Ga and 64Zn(p,α)61Cu Nuclear Reactions" Instruments 6, no. 1: 3. https://doi.org/10.3390/instruments6010003
APA Styledo Carmo, S. J. C., & Alves, F. (2022). Experimental Determination of Excitation Function Curves through the Measurement of Thick Target Yields in Liquid Targets: The Examples of the 68Zn(p,n)68Ga and 64Zn(p,α)61Cu Nuclear Reactions. Instruments, 6(1), 3. https://doi.org/10.3390/instruments6010003